Multimodal hyperspectral fluorescence and spatial frequency domain imaging for tissue health diagnostics of the oral cavity

Abstract

A multimodal, hyperspectral imaging system was built for diagnostics of oral tissues. The system, termed Hyperspectral-Fluorescence-Spatial Frequency Domain Imaging (Hy-F-SFDI), combines the principles of spatial frequency domain imaging, quantitative light fluorescence, and CIELAB color measurement. Hy-F-SFDI employs a compact LED projector, excitation LED, and a 16 channel hyperspectral camera mounted on a custom platform for tissue imaging. A two layer Monte Carlo approach was used to generate a reference table for quick tissue analysis. To demonstrate the clinical capabilities of Hy-F-SFDI, we used the system to quantify gingival tissue hemoglobin volume fraction, detect caries, bacterial activity, and measure tooth color of a volunteer at different time points. Hy-F-SFDI was able to measure quantitative changes in tissue parameters.

1. Introduction

Changes in bio-chromophores, such as blood, are indicators of disease and morbidity [1–4]. Qualitatively determining longitudinal changes in bio-chromophore concentration using the trained eye is complicated by the convolution of chromophore absorption with tissue scattering. Development of quantitative spectroscopic imaging systems capable of fast, in vivo mapping of bio-chromophore concentrations has potential to positively impact health diagnostics and drug development [5–11]. Spectrally and spatially mapping of chromophores can be clinically used to monitor or diagnose disease and pathology, as well as quantitatively measuring drug and treatment efficacy longitudinally [12–14]. A hurdle to applying spectroscopic imaging in clinical applications is long image acquisition time and limited field-of-view (FOV).

Hyperspectral imaging has been applied for in vivo monitoring of tissue parameters such as blood perfusion, hemoglobin saturation, melanin concentration, oxygen metabolism, as well as mapping other optically absorbing bio-chromophores [15–17]. Conventional spectral imaging techniques require time consuming multiplexing of light sources or tuning spectral filters [18–23]. A fast method for large FOV spectroscopic imaging is snap-shot hyperspectral imaging [6]. Snap-shot hyperspectral imaging utilizes broadband illumination, placing the burden of spectroscopy on the camera. Fast image acquisition improves spectroscopic analysis by capturing functional changes on shorter time-scales and minimizing motion artifacts. Motion artifacts cause spatial mismatch in subsequent images that are used in chromophore mapping [24]. Due to the temporal advantages of snap-shot hyperspectral imaging, the technique is being exploited for tissue diagnostics and chromophore mapping; especially in compact form factors for clinical applications [25]. Another challenge in spectral diagnostics is separating the optical absorption from scattering in tissues. Light incident on tissues is absorbed and scattered from multiple layers at depths with different light absorbing biomolecules. A simplified approach for quantitative determination of tissue optical properties is to decouple the absorption and scattering components of chromophores and tissues.

Spatial frequency domain imaging (SFDI) is a quantitative imaging technique that can separate the optical absorption and scattering components of a sample [14,23–31]. In general, SFDI relies on measuring the percentage of light reflected and the change in modulation depth of projected fringe patterns on a sample at different phases and frequencies, though alterations exist [32–34]. In reflection based SFDI, optical absorption and the modulation depth changes in the illumination field yield quantitative information about the absorption and scattering properties of the sample. The most common illumination field is described by $I_{field}(r)=\frac{1}{2}[1+cos({\omega }_r\cdot r)]$ , where r is the central position of the illumination field on the illumination plane and ${\omega }_r$ is the spatial frequency of the illumination field in radians per unit length. When combined with tissue models, the optical coefficients derived by SFDI can be used to calculate in vivo quantitative measurements of tissue chromophores (e.g., melanin and hemoglobin). However, reflection based SFDI is limited to chromophores with high optical absorption in the detector's spectral range, such as melanin and hemoglobin for visible light. Fluorescence based techniques have also proven powerful in accessing chromophores that are difficult to detect using reflection based SFDI [32,33]. Fluorescence based SFDI has demonstrated feasibility for three-dimensional guided surgery, tissue optical property mapping, as well as determining the depth and concentration of fluorescent molecules in tissue.

In contrast, quantitative light fluorescence (QLF) is a clinical technique which also gives access to fluorescent chromophores that are difficult to detect using reflection based techniques [35]. QLF is often applied clinically to assess oral tissue health indicators such as hard tissue lesion area, porphyrin produced by bacterial activity, and changes in hard tissue mineralization using autofluorescence that originates from collagen in the dentin layer [36,37]. QLF informs of changes in mineralization by comparing the fluorescence intensity per unit area to that of surrounding healthy hard tissue. Combining hyperspectral imaging and QLF allows for identification of fluorescent chromophore spectral signatures. Furthermore, in the case of hard tissue fluorescence, the shape of the fluorescence spectra can be used to classify tissue health [38].

This report describes a quantitative chromophore mapping system, Hyperspectral-Fluorescence-SFDI (Hy-F-SFDI), that the authors developed, which increases the number of measurable chromophores by harnessing optical absorption, scattering, and fluorescence spectral mapping. This system takes advantage of snap-shot hyperspectral imaging for multimodal SFDI and fluorescence imaging to investigate tissue health and hygiene in the oral cavity at a 0.6 Hz data acquisition rate. Analyzing the SFDI results using oral tissue Monte Carlo modeling yields in vivo quantitative melanin concentration and hemoglobin volume fraction information. In addition, spectral reflection and absorption is utilized for CIELAB measurements of hard tissue. The fluorescence information is used to detect measures of hard tissue health and porphyrin metabolites produced by bacteria.

2. Materials and methods

2.1. Snapshot Hy-F-SFDI instrument setup

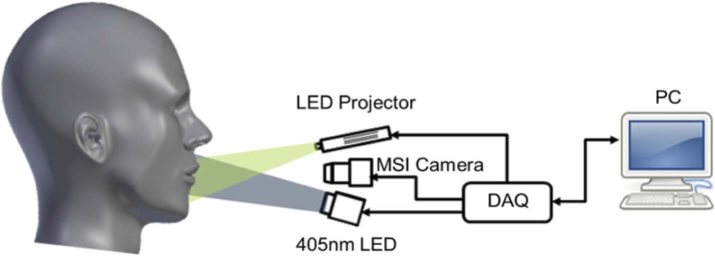
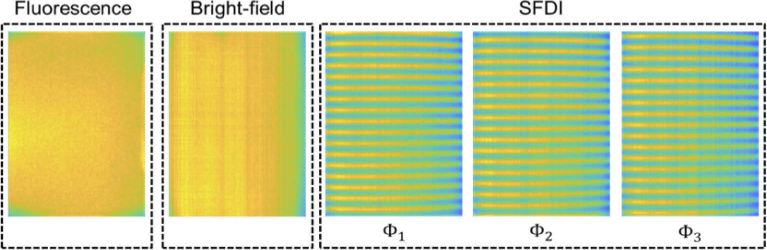
Figure 1 shows a simplified schematic of the Hy-F-SFDI system setup. For SFDI and bright-field illumination, we used a compact LED projector (P2-A, AAXA Technologies). Light from the projector was directed through a polarizer before being incident on the sample. Patterned light on the sample was projected at spatial frequencies of 0 and 0.2 mm^-1 for the low and high frequency components, respectively. Each projected pattern was incident on the sample for 100 ms. Images were acquired for an 80 ms integration time, which started 10 ms after each projected pattern. Figure 2 shows images acquired from a silicone calibration phantom sample for SFDI for the 502 nm channel. A total of five images were acquired for SFDI (2–bright field, 3–structured light) in addition to two background images. The two bright-field images we averaged and used for comparison with demodulated AC images. For fluorescence imaging, a 1200 mW 405 nm LED (M405LP1, Thorlabs) was used to excite the sample. The excitation light was passed through a diffuser for homogenization. Next, the light was shaped using a condenser lens before passing through a linear polarizer (25.5 AUF, Schneider Kreuznach) and being incident on the sample. A total of two fluorescence images were acquired at 80 ms integration times. Finally, backscattered and fluorescent light from the sample passed through a cross-polarizer before being collected by a lens (C1614-M, Pentax) and detected with a 16 channel hyperspectral camera (MQ022HG-IM-SM4X4-VIS, Ximea). The camera was adjusted to be 34 cm from the front sample surface. The measured central peak of the hyperspectral camera channels ranged from 464–636 nm (central peak: 464, 468, 477, 487, 502, 512, 524, 538, 562, 573, 586, 598, 611, 620, 632, 636) and have spectral bandwidths ranging from 12–22 nm for the full-width at half-max [16,39].

Fig. 1.

Simplified schematic of the Hy-F-SFDI system.

Fig. 2.

Intensity profiles and illumination patterns of the Hy-F-SFDI system scattered from a phantom sample. The projected intensity decreases across the horizontal field by 13.56% for the 502 nm channel. Other channels had similar intensity fields.

2.2. Acquisition software

We wrote a custom program in LabVIEW (LabVIEW 2019, National Instruments) to synchronize optical irradiation and camera acquisition. A DAQ device (USB-6211, National Instruments) was used for triggering camera acquisition and excitation LED illumination, while projector control was handled using serial commands from the host computer. A total of nine images for analysis (2–bright-field image, 3–structured light, 2–fluorescence, 2–background) were collected. Each image was collected using an integration time of 80 ms. Illumination intensity and integration time were carefully chosen to avoid camera saturation while allowing for sufficient signal. Image acquisition started and ended 10 ms after and before the illumination to allow for light source stabilization. Total sample image acquisition time, including background images, was approximately 1.7 seconds due to software latency and hardware response.

2.3. Hyperspectral image calibration and preprocessing

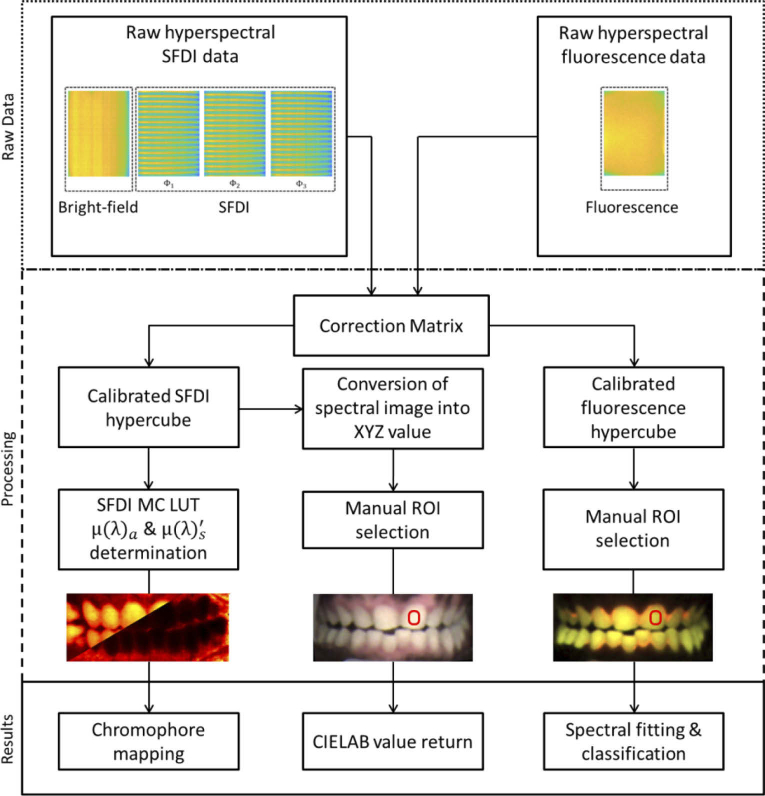
Image calibration and processing was performed using routines written in Matlab. Figure 3 shows the flow chart of the data processing steps. To analyze hyperspectral images, we first calibrated the hyperspectral camera. To calibrate the camera, we applied the manufacturer-supplied correction matrix to raw images (Fig. 4(a)) using a custom Matlab program and measured the spectral response of each channel using a supercontinuum laser (SuperK Extreme, NKT) connected to an AOM. The laser was routed through the Hy-F-SFDI system, passed through an integrating sphere for homogenous illumination, and reflected from a reflection standard (SG3151, SphereOptics) placed in the imaging plane. Using the AOM we controlled the wavelength in 1 nm steps across the spectral range of the camera. Images were acquired at each wavelength step. Average output power and illumination area of the laser were kept constant over the wavelengths in order to measure the system response. To remove camera noise, background images were acquired in a dark room with illumination sources turned off. The background images were averaged and subtracted from all illuminated images. Each hyperspectral snapshot image (2048 × 1088 pixels) was converted into a 512 × 272 × 16 hypercube (Fig. 4(b)). Four blue channels displayed a similar spectral cross-talk artifact from red illumination centered at 638 nm with a 21 nm FWHM, but each blue channel had different artifact transmission intensities. Specifically, for the 625 nm illumination LED used in the projector, the 464 nm, 468 nm, 477 nm, and 487 nm channels respectively detected approximately 7.7, 4.9, 5.0, and 6.7 percent of the light as compared to the sum of the detected signal in all channels. Comparatively, 73 percent of the 625 nm LED was detected in the summed red channels (611 nm, 620 nm, 632 nm, and 636 nm). To account for large cross-talk in the blue channels and smaller levels of cross-talk in other channels, we created our own correction matrix. To create the correction matrix we used the technique reported in reference 40, but modified for the 16 channel camera. Our correction matrix reduced spectral crosstalk to less than 0.5 percent for all channels other than the blue channels. Cross-talk for the 464 nm, 468 nm, 477 nm, and 487 were respectively 5.0, 5.0, 3.3, and 3.4 percent during illumination of the 625 nm LED. Because we were unable to correct cross-talk sufficiently, the blue channels (464 nm, 468 nm, 477 nm, 487 nm) were discarded in SFDI analysis. In fluorescence imaging, spectral cross-talk was not as significant because the illumination was sufficiently filtered by the camera. Cross-talk from red fluorescence was still visible in the blue channels, but was reduced in each channel. The improvement is likely due to less red light radiating in the red cross-talk transmission region. Lastly, we validated our spectral calibration by measuring the absorption spectra of a color checker (ColorChecker Classic, X-Rite) using the hyperspectral camera and compared the spectra with that acquired from a sub-nanometer resolution spectrometer (USB2000+VIS-NIR-ES, Ocean Optics).

Fig. 3.

Flow chart of the Hy-F-SFDI system data processing. Raw data is first acquired. In the processing steps, a correction matrix is applied and data is converted into a hypercube. Next, SFDI scattering & absorption, CIELAB, and fluorescence maps are created. Finally the parameter calculation algorithms are applied for generating results.

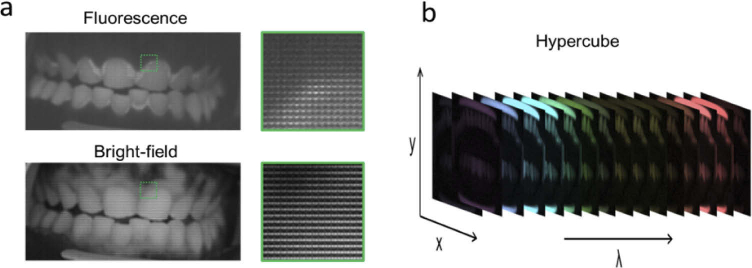
Fig. 4.

(a) Example of the raw hyperspectral fluorescence (top) and bright-field (bottom) images acquired from a volunteer. A zoomed image from the raw data, indicated by the green square in the image, is displayed to show the 4X4 filter matrix over the pixels. Porphyrin emission can visually be distinguished from the raw fluorescence image around the hard and soft tissue, but is not obvious in the bright-field. (b) Example of a reconstructed hypercube displaying the spectral imaging ability of the detector.

To correct for non-uniform illumination from the light sources and system setup, the intensity profiles of the projector and excitation LED at the sample plane were measured (Fig. 2). For the projector illumination, we reflected the projected DC and patterned light from the reflection standard. For the excitation LED, we illuminated and measured the fluorescence from a homogenous silicone sample. The projector horizontal field intensity changed by 13.56 percent. The vertical field also had variation in illumination intensity of 8.6 percent. However, the intensity changes were consistent and could be corrected. Using a reflectance calibration standard, we normalized the projector light distribution profiles over the FOV and corrected for instrument response:

$$R=0.95\ast \frac{I-I_{dark}}{I_{white}-I_{dark}},$$

where I is the image, $I_{dark}$ is the background image, and $I_{white}$ is the white reflectance standard image. The fluorescence intensity profile was also post corrected by dividing the raw image by a normalized intensity field. Notably, curvature of the sample surface and variation in distance is not considered in the system calibration or final results. Deviations in distance and curvature induce intensity error. Therefore, only the tissue areas above the front to the lateral incisors were used for SFDI analysis. Using a 3D intraoral scanner (3Shape, Trios 4), we measured a 2.3 mm change in distance in depth over the FOV from the front to lateral incisors of the subject used in this report.

After hyperspectral image calibration and correcting for non-uniform illumination, the corrected hyperspectral images were first segmented by Matlab based on modal-type (SFDI, CIELAB, fluorescence) and sent to their respective processing algorithm for analysis as described below.

2.4. SFDI calibration and analysis

For SFDI calibration, we first determined the spatial resolution for each channel by measuring the minimum resolvable feature of a USAF target (62-465, Edmund Optics). The minimum resolvable feature was 280 µm for all spectral channels (Group Number 0, Element 6). We also used the target to calibrate the representative pixel size in the imaging plane. Next, the optical properties of a silicone phantom sample were measured using the inverse adding-doubling method (IAD) [41,42]. The same phantom sample was used as the calibration sample for the SFDI. The modulated AC components were individually calculated to remove the mode noise in the system and calibrated with the phantom. The calibration allows the units to be converted to absolute reflectance by comparing measured reflectance with the predicted Monte Carlo (MC) simulation. For SFDI analysis, we utilized single frequency, three-phase SFDI for measuring absorption and reduced scattering coefficients of the samples. We modified an open source SFDI Matlab code (Open SFDI) for use with our hyperspectral camera and our custom MC lookup table (LUT) [30]. The principles of SFDI have previously been described [26,31], but briefly, to extract subsurface optical properties we first recovered the AC components ( $M_{AC}$ ) of the high frequency data using the demodulation equation:

$$M_{AC}(x,y)=\frac{\sqrt{2}}{3}\ast \sqrt{{[I_{1,A}(x,y)-I_{2,A}(x,y)]}^2+{[I_{2,A}(x,y)-I_{3,A}(x,y)]}^2+{[I_{3,A}(x,y)-I_{1,A}(x,y)]}^2}$$

where $I_{1,A}$ , $I_{2,A}$ , and $I_{3,A}$ are the high frequency structured images. We calculated the DC components of the images:

$$M_{DC}(x,y)=\frac{1}{3}\ast [I_{1,A}(x,y)+I_{2,A}(x,y)+I_{3,A}(x,y)]-I_{dark}(x,y).$$

The $M_{DC}$ components should be equivalent to the two bright-field images. We compared the $M_{DC}$ to the averaged bright-field to ensure the quality of illumination. The diffuse reflectance of the sample ( $R_d$ ) was calculated using the equation:

$$R_d=\frac{M_{AC}}{M_{AC,ref}}\ast R_{d,ref},$$

where $M_{AC,ref}$ is the modulated AC components measured from a reflection standard and $R_{d,ref}$ is the measured diffuse reflectance of the same standard.

2.5. Monte Carlo simulation

There are two MC LUTs used in our approach. Both MC models were developed using MCXLAB program in Matlab [43]. A two-layer inverse forward MC simulation was used to determine the expected absorption ( ${\mu }_a$ ) and reduced scattering coefficients ( ${\mu }_s^{\mathrm{\prime }}$ ) for the SFDI MC LUT. The tissue layers were modeled to mimic melanin absorbers in the first layer and only blood absorbers in the second layer. The thickness of the top layer was allowed to vary between 10 to 100 µm. The ${\mu }_{a1}$ value was varied between 0 and 5.0 cm^-1 to account for large variation in melanin. The second layer was considered to be semi-infinite and the ${\mu }_a$ value was varied between 0 and 2.0 cm^-1. The ${\mu }_s^{\mathrm{\prime }}$ was equal for both layers, but allowed to vary between 1 and 120 cm^-1 in the model. The refractive index was set to n = 1.4 for both layers. The output of the MC simulation was used to generate a LUT that yielded a ${\mu }_{a1}$ , ${\mu }_{a2}$ , and ${\mu }_s^{\mathrm{\prime }}$ , which was called by the SFDI program to generate a pixel-by-pixel absorption and reduced scattering coefficient map. To determine chromophore concentration, a second MC LUT was generated to fit the ${\mu }_{a1}(\lambda )$ and ${\mu }_{a2}(\lambda )$ values at each pixel of the absorption maps. In general, solving a system of linear equations at each wavelength of the measured ${\mu }_a(\lambda )$ using known chromophore extinction spectra can give the volume fraction. We chose to use a MC fitting to model the melanin layer, which is mostly concentrated in the superficial tissue, and a separate blood layer behind the superficial melanin layer. In the model, melanin fraction ( $C_{mel}$ ) is fit for the ${\mu }_{a1}(\lambda )$ , whereas blood fraction ( $C_{blood}$ ) and blood oxygen saturation ( $S_b$ ) are fit for ${\mu }_{a2}(\lambda )$ . The model is generated for each layer using the known absorption and scattering coefficients of the chromophore and tissues:

$${\mu }_a(\lambda )=C_{mel}\ast {\mu }_{mel}(\lambda )+C_{blood}\ast S_b\ast {\mu }_{oxy}(\lambda )+C_{blood}\ast (1-S_b)\ast {\mu }_{oxy}(\lambda )$$

where scattering is described by the Henyey-Greenstein phase function for both layers:

$${\mu }_s^{\mathrm{\prime }}=\alpha \ast {\left(\frac{\lambda }{500}\right)}^{-\beta }$$ (.)

Here a is the wavelength scaling factor and $\beta$ is the scattering power, as described by Jacques [44].

2.6. CIE-LAB calibration and analysis

The hyperspectral camera for CIE-LAB measurements was calibrated using squares 1–10 and 19–24 of a Macbeth ColorChecker. Knowing the spectrum of the illumination allows reconstruction of images in different color scales. To convert the hyperspectral image to the CIE-LAB 1976 color system, each 4 X 4 hyperspectral pixel was converted into XYZ values. Then the XYZ values were transformed into LAB values. The channels were linearized using the neutral color squares 19–24 and scaled to the camera dynamic range. All processing was conducted using routines written in Matlab. Lastly, squares 11–18 were measured to confirm calibration and check for over fitting. For measurements, we averaged 100 pixels in a 10 X 10 square on the selected part of the color checker. Cross-talk is still present in the ColorChecker calibration. However, it has less impact on the analysis in CIE-LAB since it is not as sensitive to small changes in intensity.

2.7. Fluorescence calibration and analysis

The custom correction matrix described in section 2.3 was applied to the raw fluorescence hyperspectral image for cross-talk correction. To determine the spectral accuracy, we created ex vivo samples using bovine teeth and porphyrin IX (Sigma Aldrich, P8293). We suspended small amounts of porphyrin on one side of the teeth using Sylgard 184. Spectra of the teeth, porphyrin, and Sylgard 184 were measured with a spectrometer using 405 nm excitation to determine the ground-truth spectrum. The samples were then measured with the hyperspectral camera using the fluorescence mode of the Hy-F-SFDI system. For fluorescence imaging, the calibrated camera allows accurate detection of spectral profiles with lower levels of spectral cross-talk present in the blue channels. By measuring pure porphyrin samples, we determined the cross-talk for the 464 nm, 468 nm, 477 nm, and 487 were respectively 4.0, 0.9, 2.2, and 2.4 percent. Cross-talk in other channels was less than one percent. It is likely cross-talk was less for fluorescence since the illumination does not correspond directly to a spectral cross-talk region. We utilized all 16 channels of the detector for fluorescence imaging. After calibrating using ex vivo samples, the system was used for in vivo analysis. The acquired spectra were used to distinguish spectral signatures of caries, porphyrin, dentine and enamel, which have well-documented spectra. Unlike canonical QLF, which measures changes in fluorescence intensity over time or in comparison with surrounding tissue using a RGB channels, we used the spectral emission profile to distinguish biomolecules and caries lesions. Fluorescence also detects dental restoration in the oral cavity due to their lack of fluorescence.

2.8. Phantom experiments

Homogeneous phantoms were used to validate the Hy-F-SFDI system ${\mu }_a$ and ${\mu }_s^{\mathrm{\prime }}$ measurements. We measured ${\mu }_a$ and ${\mu }_s^{\mathrm{\prime }}$ of silicone phantoms using the inverse adding-doubling method (IAD) [41,42]. In the setup, a single integrating sphere (819C-SL-5.3-CAL2, Newport) was used for transmission and absorption measurements of the samples and reference target. The supercontinuum laser, in combination with the AOM, was used to illuminate the samples at the central wavelengths of the spectral channels used in the MC simulations. To measure absorbed and transmitted light, a spectrometer coupled to the detector port of the integrating sphere with a multimode fiber (79-100272-00, C Technologies Inc.) was used. The samples were uniformly cut to 1 mm thickness; and the collimated laser beam diameter was 2 mm. Two phantom samples were measured using IAD. The first sample was a silicone scattering sample which was used as the SFDI calibration sample. A second skin mimicking silicone phantom was used to compare Hy-F-SFDI with IAD measurements.

2.9. In vivo experiments

In vivo Hy-F-SFDI measurements of oral tissues were acquired from a single volunteer. Two measurements were taken at different time points and under different oral hygiene conditions. The baseline measurement was acquired from the volunteer during their normal hygiene regimen. The second measurement was acquired from the same volunteer after three weeks of non-brushing in order to induce mild tissue inflammation [18,45]. The volunteer was given an oral exam by a dental professional at both time points to measure the gingival index (GI) of the gingival tissues surrounding the hard tissue (GI is an ordinal index used to record the presence and severity of gingival inflammation) [18]. To keep the volunteer’s oral cavity fixed at the correct distance in the imaging plane, a chin rest with a head harness was used. To expose the gingiva and hard tissue, the volunteer wore a cheek retractor during the imaging sessions. The volunteer also wore safety goggles to prevent eye exposure to the excitation LED. The volunteer was instructed to remain still during image acquisition to reduce motion artifacts. Image acquisition lasted 1.7 seconds, including 200 ms for background images acquired after the SFDI and fluorescence images. All experiments in the study were approved by the US Institutional Review Board, Inc (IRB#U.S.URB2019CP/13).

3. Experimental results

3.1. Color checker evaluation

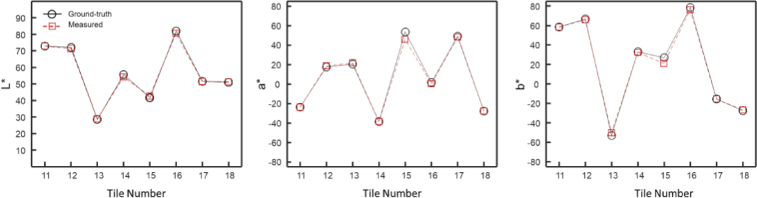
Figure 5 shows the accuracy of the CIE-LAB measurements for tiles 11–18 of the Macbeth color checker. Only tiles 11–18 are used for accuracy measurement since tiles 1–10 and the neutral tiles are used for calibration. The ‘L*’ values were within ±2.4% of the known values of the MacBeth ColorChecker, whereas ‘a*’ and ‘b*’ values were within ±5.4%.

Fig. 5.

Hy-F-SFDI color measurements. (Left) A plot of the L* intensity values as reported by the manufacturer (black circles with solid black line) and values measured by the Hy-F-SFDI (red squares with dashed red line). (Center) Same as (Left), but for a* values. (Right) Same as (Left), but for b* values.

3.2. Phantom sample

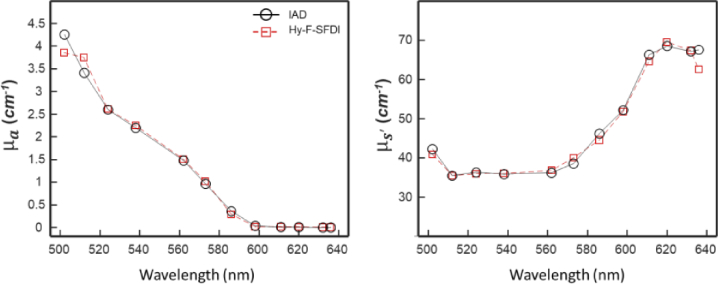
Figure 6 shows the results of the IAD and Hy-F-SFDI measurements of the skin mimicking phantom for the relevant spectral channels. For comparison with IAD, the convolved ${\mu }_a$ for the SFDI layer values were used. IAD and Hy-F-SFDI ${\mu }_a$ and ${\mu }_s^{\mathrm{\prime }}$ measurements were similar across the spectrum. Absorption coefficient measurements were also in relative agreement across the two techniques; however the 586, 598, and 636 nm channels had lower values of ${\mu }_a$ compared with IAD. For the 586 and 598 nm channels, the error is likely due to using a narrow band laser for the IAD experiments and a broad LED for Hy-F-SFDI. The larger bandwidth of the channels can result in different ${\mu }_a$ and ${\mu }_s^{\mathrm{\prime }}$ values. Reduced scattering coefficient measurements were within 5 percent agreement, with the exception of the 636 nm channel. Some spectral cross-talk may be present in the post-corrected Hy-F-SFDI, which can induce error in the final measurement. Though IAD is known to have experimental error [46], it was used as the ground-truth in our investigation.

Fig. 6.

IAD and Hy-F-SFDI optical coefficient comparison of a skin mimicking phantom. (Left) Absorption coefficient plot of IAD (black circles with solid black line) and Hy-F-SFDI (red square with dashed red line) measurements. (Right) Same as (Left), but for the reduced scattering coefficient.

3.3. In vivo analysis

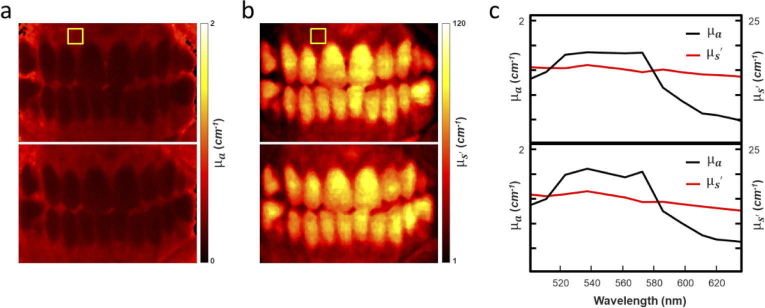
Figure 7 shows a single channel analysis from the Hy-F-SFDI of the volunteers’ oral tissue before and after abstaining from brushing for three weeks. We mapped the convolved ${\mu }_a$ and the ${\mu }_s^{\mathrm{\prime }}$ of the oral cavity. The convolved ${\mu }_a$ and ${\mu }_s^{\mathrm{\prime }}$ for an area in the upper gingiva, indicated by a yellow box in Fig. 7(a) and (b), was averaged and plotted over the spectral range for the base and three-week data (Fig. 7(c)). In the plots, a change in the absorption and less pronounced change in scattering coefficient can be distinguished at the two time points.

Fig. 7.

Hy-F-SFDI analysis results. (a) Mapped of the tissue convolved absorption coefficient at the 502 nm spectral channel for the base (top map) and 3-week (bottom map) time points. (b) Same as (a), but for reduced scattering coefficient. (c) Plot of the averaged absorption and reduced scattering coefficients for each spectral channel. The data were averaged from the region indicated in the yellow box in (a) and (b).

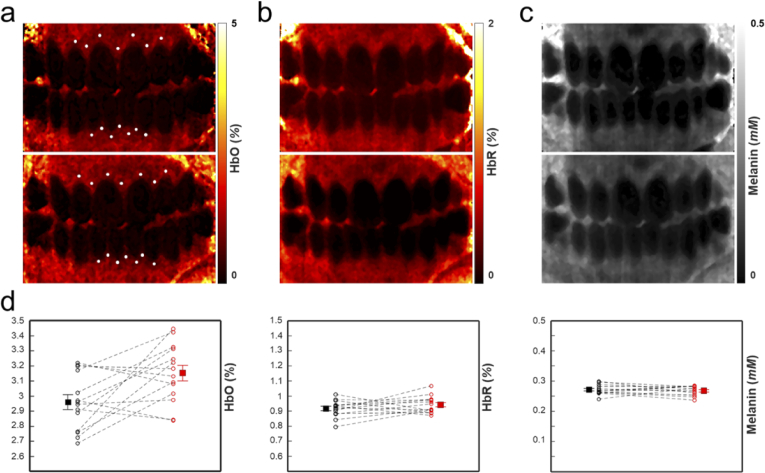
We calculated the volume fraction change in total hemoglobin (Hb), deoxygenated hemoglobin (HbR), oxygenated hemoglobin (HbO) and melanin at different sections of the gingiva, as shown in Fig. 8. Spectral MC fitting for the HbR, HbO, and melanin chromophores was used at each hyperspectral pixel to determine chromophore concentration. Finally, chromophore maps were generated for both time points, as shown in Fig. 8(a)-(c). To understand how chromophore concentration in localized regions of the tissue changes, the average value at 14 locations in the oral cavity of the chromophores were taken at both time points. A 4 X 4 pixel region was averaged at the locations indicated by the dots in Fig. 8(a). We approximated the locations in the two images by matching features in the corresponding white light images. Though large FOV blood volume maps of the oral cavity have not been thoroughly investigated [45,47], the measured values (shown in Fig. 8(d)) are within the expected biological range [48]. Comparison shows a change in oxygenated blood volume fraction near the gingival margin (ΔHbO = +0.210), whereas deoxygenated blood (ΔHbR = +0.033) and melanin concentration (Δmelanin = +0.0023 mM) are similar at the different time points. These quantitative results are consistent with the average measured GI score of the front teeth (base = 1.25, final = 2.08), which qualitatively describes increased inflammation at these sites. Small changes in melanin should be expected due to tissue conformational changes from swelling and minor alignment changes in the system [49]. We limited analysis to relatively flat regions of the tissue to limit curvature induced error.

Fig. 8.

(a) Oxygenated blood map of the base (top) and three-week (bottom) time points. (b) Same as (a), but for deoxygenated blood. (c) Same as (a), but for melanin. (d) Measurements of the oxygenated blood volume fraction (left), deoxygenated blood volume fraction (middle), and melanin molar concentration (right). The locations of the measurements are indicated by the white dots in (a). Error bars indicate the standard error of the mean (SEM).

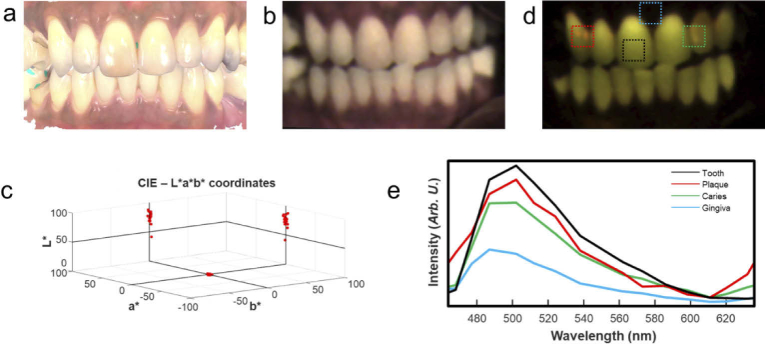
Figure 9 shows CIE-LAB and fluorescence results from Hy-F-SFDI analysis of the volunteer. An en-face white light 3D image acquired from a 3D intraoral scanner (Fig. 9(a)) is shown for comparison. The 3D white light image is not color corrected, but does have high structural resolution. We generated a color corrected white light image using the previously described CIE-LAB calibration procedure (Fig. 9(b)). The CIE-LAB values of 17 well exposed teeth were measured. Using the International Standards Organization Designation System (ISO System), numbers 11–14, 21–23, 31–35, and 41–45 were assigned to the measured teeth. The CIE-LAB values were collectively plotted (Fig. 9(c)). The measurements ranged from -0.3–2.1 and 1.9–14.4 for the ‘a*’ and ‘b*’ values, respectively. Intensity measurements, L*, of each tooth ranged from 42 to 91. Restorations placed on implants in positions 14, 35 and 45 had the highest L* values compared to real teeth (real teeth had an average L* value of 74.3). It should be noted that CIE-LAB calibration was performed across the entire spectral range of the camera.

Fig. 9.

White light and autofluorescence analysis of tissue hygiene. (a) An en-face white light image acquired by an intraoral 3D scanner. The color information is not correctly calibrated, contains specular reflection, and is saturated for display. (b) Reconstructed white light image of the oral cavity using Hy-F-SFDI. (c) CIELAB measurements of 17 visible teeth. The molar implants have higher L values in the reconstructed image. (d) Pseudo colored fluorescence image displaying hard-tissue, caries and porphyrin fluorescence. (e) Measured spectra of different sections of the oral cavity. The spectra are averaged from the region indicated by the boxes in (d).

Fluorescence imaging (Fig. 9(d)) clearly identifies restorative procedures due to their lack of fluorescence. Hyperspectral fluorescence imaging also captured the spectral signatures of dentine, porphyrins from plaque and white spot caries lesion (Fig. 9(e)). Depending on severity, spectra of surface caries (Fig. 9(d), green box) are characterized by a blue shifted peak with a slight red peak (centered at 630 nm) when compared with healthy dentine fluorescence (Fig. 9(d), black box). The subsurface red peak is due to the presence of porphyrin producing bacteria present in the porous lesion, whereas plaque (Fig. 9(d), red box) is easily distinguished by a red porphyrin emission peak on the surface [36].

4. Discussion

Sample motion was not a significant factor for in vivo Hy-F-SFDI. The acquisition time and stable chin rest with head restraint minimized movement from the volunteer during imaging. Although the system uses a total of nine images for complete diagnostics, only five images are necessary for the SFDI modality. Of the nine images, two images were background and were not sensitive to the motion of the target. The total time for the SDFI acquisition was 0.9 seconds (1.1 Hz). This time could be improved by using the summed high frequency components for the DC image, increasing illumination intensity, decreasing detector integration time, and reducing latency of software and hardware [50]. On the other hand, averaging the two background and two DC images had the benefit of improving signal-to-noise and extending the usable dynamic range of the detector. The improved signal-to-noise is beneficial in clinical investigations since differences in bio-chromophores are diverse across subjects and can consequently lead to signals beyond the dynamic range or below the sensitivity of the detector. Therefore, a balance between integration time, signal intensity, and diversity of chromophores need to be determined during system calibration or multiple calibrations are required. In our system, the SFDI modality imaging rate was fundamentally limited by the projector DMD array to 30 Hz per image (6 Hz for all five SFDI images). Addition of a faster DMD array or lowering bit resolution could double the acquisition rate (>12 Hz for all SFDI). Higher frame rates can make real-time monitoring of hemoglobin possible. Lastly, a large limitation in the current setup is resolution. Our hyperspectral snapshot camera sacrifices resolution for spectral information. The lower resolution also contributes to reducing apparent motion artifacts in the reconstructed images, but prevents structural evaluation of smaller vasculature. Higher pixel cameras can overcome the resolution limitation, but might produce larger errors from motion.

A source of error in the current system is the uncorrected changes in sample distance, angle, and topology [51]. Changes in distance are likely the largest source of error for our system. Intensity is inversely proportional to imaging distance, $I(d)\propto I_o/d^2$ , where I(d) is the distance dependent intensity, d is the distance, and $I_o$ is the intensity at a location on the sample. In our system the camera is 34 cm from the front surface of the sample. The change in the distance from the front to lateral incisor of the subject in this study was approximately 2.3 mm, as measured using a 3D intraoral scanner (3Shape, Trios 4). Therefore, changes in distance can result in approximately 1.3% intensity error across the measured FOV. Small changes in angle (< 3 degrees) of the subjects head are negligible due to their cosine dependence and high repeatability of position allowed by the chin and head rest. Angle of curvature of the tissue also contributes to error with a cosine dependence on tissue angle. However, because we only measured relatively flat regions (angles less than five degrees from the surface normal), angle induced intensity error should be minimized to less than 1%.

Another limitation of the current implementation is the use of a two-layer MC model to generate expected optical parameters. The MC model was validated using homogeneous phantoms with known optical properties. Multilayer phantoms to validate the two-layer measurements would be advantageous for clinical applications. Furthermore, MC models that specifically capture the layer diversity of the oral cavity can improve the system.

5. Conclusion

Hy-F-SFDI offers a simplified, non-invasive approach for in vivo oral tissue diagnostics. The strength of Hy-F-SFDI is the large FOV, imaging rate, and ability to simultaneously detect more chromophores than visible SFDI alone has demonstrated. Here, Hy-F-SFDI was used to generate quantitative longitudinal maps of chromophore tissue concentrations, bacterial activity, hard tissue, and CIE-LAB color values in the oral cavity. Accounting for surface curvature by implementing three-dimensional SFDI will improve system accuracy and applicability for future tissue investigations.

Funding

Colgate-Palmolive Company10.13039/100004368.

Disclosures

The authors declare no conflicts of interest.

Data availability

Data and algorithms generated in this paper are not publicly available at this time but may be obtained at a future date from the authors upon reasonable request.