Abstract
Glaucoma is a leading cause of blindness. The measurement of vertical cup-to-disc ratio combined with other clinical features is one of the methods used to screen glaucoma. In this paper, we propose a deep level set method to implement the segmentation of optic cup (OC) and optic disc (OD). We present a multi-scale convolutional neural network as the prediction network to generate level set initial contour and evolution parameters. The initial contour will be further refined based on the evolution parameters. The network is integrated with augmented prior knowledge and supervised by active contour loss, which makes the level set evolution yield more accurate shape and boundary details. The experimental results on the REFUGE dataset show that the IoU of the OC and OD are 93.61% and 96.69%, respectively. To evaluate the robustness of the proposed method, we further test the model on the Drishthi-GS1 dataset. The segmentation results show that the proposed method outperforms the state-of-the-art methods.
1. Introduction
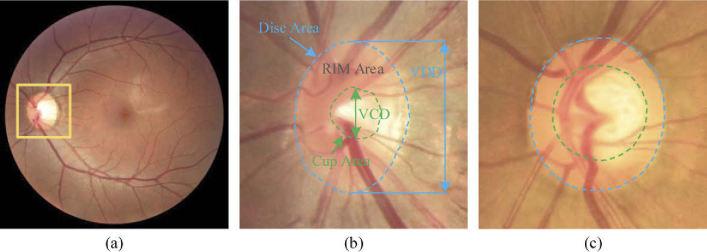
Retinal image analysis has a wide range of clinical applications in the diagnosis of ophthalmic diseases. Many eye diseases can be revealed by the morphology of the optic cup (OC) and optic disc (OD). For instance, glaucoma, the leading cause of chronic and irreversible blindness globally, is usually characterized by the thinning of the neuro retinal rim and the growing of optic cup [1]. Glaucoma can lead to progressive damage to the vision system. Therefore, it is of great significance to accurately diagnose and treat glaucoma at an early stage. The symptoms of glaucoma include the structural changes on the nerve fiber layer and/or optic nerve head (ONH), which occurs preferentially at the superior and inferior poles of the OD, and the OC enlarges vertically more than horizontally [2]. These characteristics can be evaluated by the vertical cup-to-disc ratio (vCDR), which is computed as the division of the vertical diameter of the OC by the vertical diameter of the OD. Due to glaucoma usually leads to a significant increase in the vCDR values, the measurement of vCDR combined with other clinical features in ONH assessments is widely used to diagnose glaucoma [1,3]. In clinical application, color fundus photography is the most effective imaging modality for the examination of retinal disorders [4]. The OD appears as a bright yellow elliptical region in the fundus image, and the center depression of the OD is OC. Examples of normal eye and glaucoma are shown in Fig. 1.
Fig. 1.
Examples of the (a) whole fundus image and the enlarged optic disc area for the (b) normal and (c) glaucoma cases. The optic disc and cup are indicated by the outer blue and inner green dash lines, respectively. VCD and VDD indicate the vertical diameter of the optic cup and disc, respectively.
Manually segmenting the OC and OD and measuring the vCDR are time-consuming and are affected by the clinical experience of the ophthalmologist. Therefore, a lot of significant progress has been made in the field of automatic fundus image segmentation. Based on the working principle, the existing methods for OC and OD segmentation can be mainly divided into three categories, which are non-model-based method, model-based method, and deep learning-based method. The non-model-based methods usually use traditional algorithms to detect the boundary of OD and OC, like clustering, thresholding, and morphological operation [5]. The model-based methods include template matching and deformable model-based methods.
For the template-based method, Lalonde et al. [6] proposed a Hausdorff-based template matching method, which is guided by a pyramidal decomposition and confidence assignment to localize the OD. Youssif et al. [7] proposed a two-dimensional Gaussian matched filter to segment retinal vessels and predict a vessels direction map. An OD edge map can be obtained by training a classifier based on structure learning. Aquino et al. [8] and Cheng et al. [9] modeled the OD as a circle and an ellipse boundary, respectively. They utilized edge detection techniques followed by the Hough transform to detect the edges in the image. Zheng et al. [10] integrated prior information with the OC and OD. The segmentation task was performed by using a general energy function based on the graph cut technique. Mukherjee et al. [11] localized the OD region based on a parameterized membership function defined on the cluster regions and the convergence point of the retinal vasculature. The template matching focuses on incorporating the shape of OC and OD by matching the edge with a circle or an ellipse. However, they often require a lot of sampling points and fail to detect the object shape irregularity due to the shape variation.
Deformable model-based methods need an initial contour for initialization and deformation towards the target contour according to various energy terms. The energy terms are usually defined by image gradient, image intensity, and boundary smoothness [12]. Typical deformable models include the active contour model, level set model, and Chan-Vese level set model. Osareh et al. [13] and Lowell et al. [14] localized the OD region through active contour fitting combined with grey-level morphology and specialized template matching, respectively. Xu et al. [15] proposed a boundary detection method for OC and OD region based on snake model, which includes knowledge-based clustering and smooth updating. They labeled the contour points as positive or uncertain points after each snake deformation, which is used to refine the object boundary before the next contour deformation. Joshi et al. [16] improved the Chan-Vese model by using two texture feature spaces near the analyzed pixels and local red channel intensities. A modified region-based active contour model was used to segment OD boundary. A deformable model could acquire desirable results and have shown promise for segmentation tasks of OC and OD. However, due to they are sensitive to the initialization, and the OD usually has a blurred edge against OC or outside region of OD, the deformable models still have challenges for the segmentation of OC and OD.
Recently, the deep learning-based method has gained a lot of attention for segmentation tasks of the OC and OD in fundus images. The deep convolutional neural network has the ability to explore intricate structures from high-dimensional data. Most methods of fundus images segmentation are based on the classic convolutional neural network (CNN) [17–20]. Maninis et al. [21] performed OD segmentation by using fully-convolutional neural network [17] based on VGG-16 [22] and the transfer learning technique. Based on U-Net, Sevastopolsky et al. [23] and Fu et al. [24] proposed a modified U-Net for joint segmentation of OC and OD in retinal images, respectively. Shankaranarayana et al. [25] employed the concept of residual block and proposed a dilated residual inception network for OC and OD segmentation.
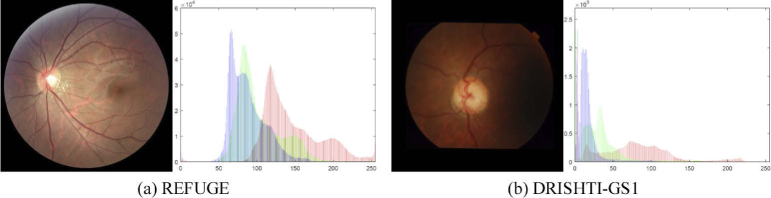
Although significant progress has been achieved, the following difficulties still need to be solved. Firstly, the deep learning-based methods tend to perform well when being applied to well-annotated datasets with consistent image distributions. However, the distribution of retinal fundus image datasets is usually inconsistent. Due to the variance among the diverse data domains, most of the state-of-the-art methods can not give a satisfying segmentation result on the test set that has a different data distribution from the training set. Figure 2 illustrates fundus images from different datasets captured by different fundus cameras. Secondly, the segmentation of OC and OD is challenging due to the pathological lesions on the boundaries or regions, which lead to the variations in the shape, size, and color in the OC and OD regions. Thirdly, the pixel-wise segmentation methods focused on inferring label for each pixel independently, which may come short at yielding compact and uniform predictions and require more computation resources. In this respect, the contour-based method, level set, formulates the segmentation problem as an energy minimization problem. However, the traditional level set method is usually used as a post-processing tool. Recent works [26,27] proposed modified level set methods for image segmentation, which combine the traditional level set method with deep learning architecture. Although these methods have achieved outstanding performance on natural image segmentation, are still insufficiently accurate for clinical use due to the fundus images features mentioned above.
Fig. 2.
Examples of REFUGE and DRISHTI-GS1 dataset, and the RGB histogram of the corresponding image.
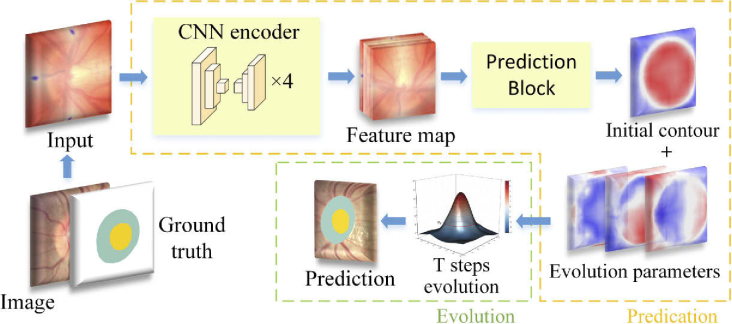
In this paper, to overcome the aforementioned problems, we propose a semi-auto deep level set model for the OD and OC segmentation. The proposed method includes two main parts, as illustrated in Fig. 3. The first part is a multi-scale convolutional neural network, which is used to predict the level set evolution parameters. The second part is based on level set evolution to further refine the predicted contour. The input of the evolution part is the initial contour and evolution parameters predicted by the prediction part. The proposed method takes the segmentation task as a contour prediction problem, which can generate compact and uniform predictions. Moreover, the augmented prior knowledge is proposed to make the level set evolution have a more accurate shape. The network is supervised by weighted cross-entropy loss and active contour loss, which can introduce more boundary details to the deep level set model. The proposed method can be trained in an end-to-end manner.
Fig. 3.
Overview of the proposed method. The yellow and green dash frames represent the prediction part and the evolution part, respectively. The prediction part predicts an initial contour and three parameters for level set evolution. After T steps evolution, the initial contour is further updated to obtain the refined prediction result.
The rest of the paper is organized as follows. The details of the proposed method are described in Section 2. Experimental results are shown in Section 3, including the data description, evaluation results of the proposed method, and the comparison with other segmentation methods. Finally, a discussion is provided with a conclusion in Section 4.
2. Methods
2.1. Network architecture
The network architecture consists of two parts, the prediction part and the evolution part. The prediction part is a multi-scale convolutional neural network, which is used to predict the level set evolution parameters. The evolution part is based on level set and is used to evolve the initial contour. An overview of the proposed method is shown in Fig. 3.
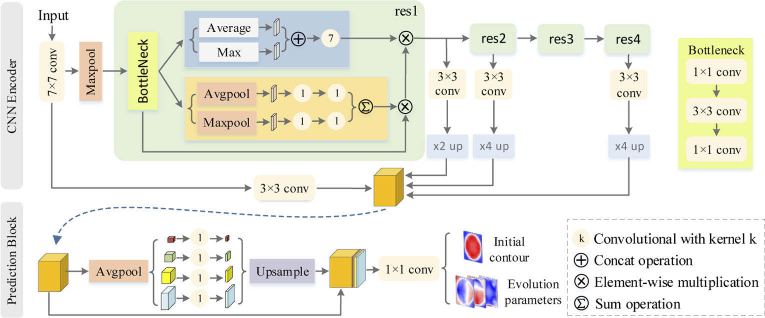
The CNN encoder is a modified ResNet-101 [28] with skip connections and attention module [29] for getting multi-scale and more powerful representation features of the input images. The last average pooling layer and the fully connected layer of ResNet-101 are removed. Four convolution operations are used to encode features from the convolution, residual block 1, 2, 4, respectively. To concatenate features from the four convolution operations, the bilinear up-sampling operations with 2 and 4 scale factors are used to make the feature maps have the same spatial size of . Finally, the concatenated feature map is feed into the prediction block, which predicts three level set evolution parameters and an initial contour. The prediction block is based on the pyramid parsing module [19] to extract multiscale features. The structure of the CNN encoder and the prediction block is shown in Fig. 4.
Fig. 4.
Architecture of the CNN encoder and prediction block. conv represents the convolution operation with kernel size . up and up represent the bilinear up-sampling operation with 2 and 4 scale factors, respectively. The orange tensor is the input of the prediction block.
Given an input image, users can click on the top, bottom, left-most and right-most parts of the region of interest (RoI) to get four extreme points. Moreover, two intersecting segments are derived by pairing and connecting the four extreme points [30]. Then, the addition of the two intersecting segments and the four extreme points are taken as our augmented prior knowledge and feed into the CNN network together with the input image. Feature maps will be extracted by the CNN encoder and fed into the prediction block, which is used to predict the initial contour and the evolution parameters. The evolution parameters include external energy and internal energy. The external energy is used to promote the initial contour to the desired position. The internal energy is used to avoid excessive smoothing. Based on the evolution parameters, the initial contour is evolved steps to get the final prediction. To make the level set evolution result yield more accurate shape and boundary details, we take the inside and outside area and the size of boundaries into account by using the active contour (AC) loss. Moreover, the prediction block is designed to predict the foreground and background binary probability map. The AC loss can be calculated by the binary probability map and the binary masks obtained from the ground truth. The network is supervised by the weighted cross-entropy (CE) loss and the AC loss. Finally, the CNN parameters are updated by backpropagation.
2.2. Level set evolution
Level set method represents the curve as the intersection of zero level set with level set function:
| (1) |
The target of segmentation task is to find the curve . The inside and the outside area of the curve indicate the foreground and background, respectively.
The level set function is usually represented as a signed distance function (SDF). In this paper, the initial contour is represented as a truncated signed distance function (TSDF), which makes the training process more stable and reduce the deviation of the output. The TSDF is defined as:
| (2) |
where the represents step function, and the represents truncated threshold.
The initial contour is represented as a distance map, where the zero distance point set represents the initial contour, the positive and negative distance points represent the inside and outside points of the contour, respectively. The closer the point to the object boundary is, the smaller the absolute distance. The evolution parameters include external and internal energy. External energy is designed as the gradient map at and direction, indicating the evolution direction of the contour. Generally, the level set evolution is regularized by moving the contour along the direction of curvature, which smooth the contour and eliminates boundary noise. Internal energy is designed as a probability map to selectively smooth the contour and give the model more flexibility. The initial contour is iteratively evolved based on the evolution parameters. After T steps of evolution, the prediction result is obtained. T is set by experience.
2.3. Confidence map
To improve the segmentation performance, the prior knowledge is expanded based on the extreme points [31]. The main idea is using the four extreme points to generate two intersecting segments, and taking the combination of the segments and extreme points as an augmented prior knowledge. Specifically, each pixel in the image has a distance from the intersecting segments. The distance is used to generate a confidence map, which assigns a confidence score to each pixel in the image domain. Then, the extreme points are combined with the confidence map together as an additional channel concatenates with the input image to feed into the network.
Through the extreme points, the following information is suitable for most situations: 1) Four extreme points can be paired and connected to form two intersecting line segments , . 2) The intersection point of the two line segments is more likely to belong to the RoI. 3) The point in the image have a distance from the line segments, the smaller the distance between and the two line segments, the more likely it is to belong to the RoI, and vice versa. The line segments , and intersection point are collectively used as a coordinate frame, the confidence map can be calculated as the following formula:
| (3) |
where and are the weight distances from pixel to line segments and . is the Euclidean distance from point to line segment . is the variance along segment .
| (4) |
| (5) |
| (6) |
where and measure the Chebyshev and Mahalonobis distance of the point to line segments and , respectively.
2.4. Loss function
To let the network learn more discriminative features and improve the segmentation performance. Inspired by Chen et al. [32], the inside and outside area and the size of boundaries are taken into account by combining the active contour loss with the weighted cross-entropy loss as follows:
| (7) |
where is the AC loss weight. In the experiment, we set it to 1e-4. Specifically, the AC loss function is defined as follows:
| (8) |
| (9) |
| (10) |
where the and measure the area of region and length of contour, respectively. The parameter is used to balance the weight of area loss and contour length loss. In the experiment, we set it to 0.5. The range of is [0,1]. The parameter represent the segmentation result, represent the given image. and represent the energy inside and outside the object curve, respectively. and from and represent the horizontal and vertical directions, respectively. is a parameter to avoid square root is zero.
3. Results
3.1. Materials
The proposed method is evaluated on two public retinal fundus datasets, REFUGE [4] and Drishti-GS1 [33]. The REFUGE dataset contains a total of 1200 two-dimensional color fundus images in JPEG format, 120 with glaucoma and 1080 without. The dataset is divided into three subsets officially, each of them contains 400 fundus images and has an equal proportion of glaucomatous (10%) and non-glaucomatous (90%) cases. The training and testing set are captured by different cameras so that the color and texture of the images are different. Specifically, the training set is acquired by Zeiss Visucam 500 fundus camera with a resolution of pixels, and the validation and test set are acquired by Canon CR-2 camera with a resolution of pixels. The Drishti-GS1 dataset comprises 101 fundus images with a resolution of to pixels, and stored in PNG format. All images were taken with the eyes dilated centered on OD with a Field-of-View of 30-degrees. No other imaging constraints were imposed on the acquisition process. The dataset is officially split into 50 and 51 images for training and test, respectively. Manual annotations of the OD and OC were provided by 7 and 4 independent glaucoma experts for REFUGE and DRISHTI-GS1 dataset, respectively. All the experts independently reviewed and delineated the OD and OC in all the images. For the REFUGE dataset, a senior expert adjudicates the 7 segmentation results to remove incorrect ones. For the DRISHTI-GS1 dataset, it does not involve the adjudication process.
3.2. Evaluation metrics
For the segmentation task of OD and OC, Intersection over Union (IoU) and Dice similarity coefficient (DSC) are used to evaluate the overlap between the prediction result and ground truth. For classification of glaucoma and normal cases, Sensitivity and Specificity are used to show the percentage of glaucoma and normal cases correctly identified by the proposed method, respectively. The classification of glaucoma cases is based on the vCDR, which is calculated by the vertical diameter of the OD and OC. The mean absolute error (MAE) is used to evaluate the estimation of vCDR. Furthermore, ROC graph is used to visualize the classification performance of the proposed method.
The IoU and DSC are defined as:
| (11) |
| (12) |
where the and are the ground truth and predicted segmentations of the region of interest , respectively (with = OD or OC).
The Sensitivity (Sen.) and Specificity (Spec.) are defined as:
| (13) |
| (14) |
where TP, TN, FP, and FN present true positive, true negative, false positive, and false negative, respectively.
The MAE is defined as:
| (15) |
where the is a function that estimates the vCDR based on the vertical diameter of the segmentations of the OD and the OC, respectively.
3.3. Training details and parameter setting
The proposed method is implemented by the deep learning framework PyTorch 0.4.0. and all experiments were performed using GTX 1080Ti GPU. The training process of the proposed method executes 30 epochs with a mini-batch size of 8, and converges around 25 epochs. It is validated every 5 epochs during the training process. The training process takes a total of 1.5 hours, including 30 epochs of training and 6 validations. We perform the image normalization on each image for the two datasets and resize the region of interest to for input into the network. Apart from this, no additional pre-processing and data augmentation were used in the training and testing processes. For a fair comparison, we preprocess the images with RoI crop for all automatic methods. The level set evolution phase uses both in the training and testing. Specifically, random noise was added to the ground-truth annotation to get extreme points used for training. A 2D Gaussian is placed around each of the extreme points to get a heatmap. For other hyperparameters, the initial learning rate is 3e-4 and decayed by 0.3. Momentum is 0.9 and weight decay is 1e-6. The training loss curve and the validation results are shown in the Fig. 5.
Fig. 5.
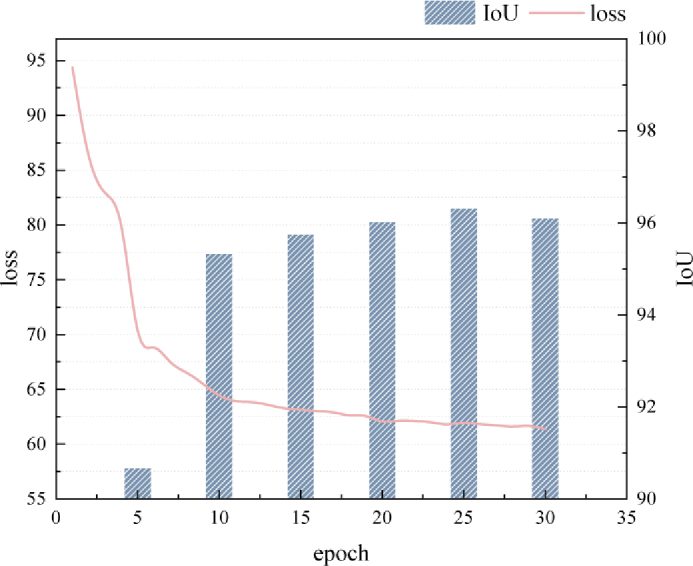
Training loss curve of the proposed method and the validation results for the corresponding epochs.
3.4. Experimental results
The quantitative results of the proposed method on the REFUGE validation set and test set are shown in Table 1. From the table, it can be observed that the segmentation accuracy on the test set is close to the validation set. It demonstrates the effectiveness of the proposed method. The average IoU of OD is higher than that of OC. It is mainly because glaucoma leads to changes in the morphology and structure of the OC. Figure 6 shows the maximum and minimum IoU index of the OD and OC for the test set, respectively.
Table 1. Quantitative results of the proposed method on the REFUGE validation and test set. Avg., Std., Max and Min represent average values, standard deviations, maximum and minimum, respectively.
| Cup | DISC | ||||||||
|---|---|---|---|---|---|---|---|---|---|
|
|
|||||||||
| Avg. | Std. | Max | Min | Avg. | Std. | Max | Min | ||
| Test | IoU(%) | ||||||||
| DSC(%) | |||||||||
| Val | IoU(%) | ||||||||
| DSC(%) | |||||||||
Fig. 6.
The maximum and minimum IoU of segmentation result for optic cup and disc.
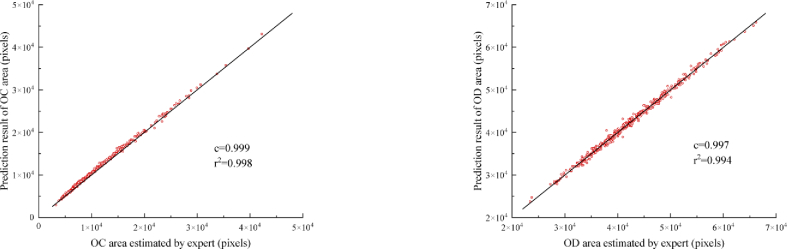
Correlation analysis is performed to assess the reliability of the proposed method, which is shown in Fig. 7. The predicted area (total number of pixels) and the expert manually labeled area are used as the assessment criteria. The high correlation coefficient demonstrates the proposed method can predict the OD/OC area with satisfactory performance. A high determination coefficient means most points are near to the line, which shows no systematic difference.
Fig. 7.
Correlation analysis of the segmentation results with expert labeled results for optic cup and disc in REFUGE test set. c and represent the correlation coefficient and determination coefficient, respectively. The black line represents no systematic difference.
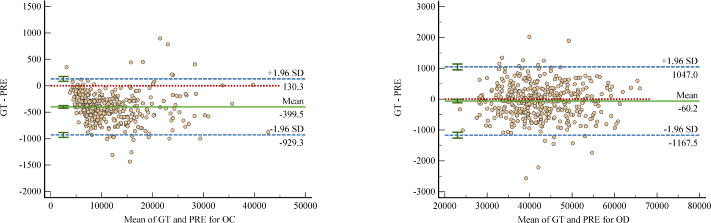
The area deviations of OD and OC are shown in the Bland-Altman plot (Fig. 8), which measures the agreement between the ground truth and the segmentation result obtained from the proposed method. Two blue dotted lines indicate the average 1.96 standard deviations, and the interval formed by the two blue dotted lines indicates the 95% limits of agreement (LoA). The prediction result and ground truth are consistent as most of the scattered points fall within the 95% LoA. Specifically, 5% (20/400) points fall outside of the 95% LoA for OC and 4% (16/400) for OD. The green solid and red dotted lines indicate the mean value of the differences and zero bias line, respectively. The closer the green line with the red line, the better the segmentation performance. In the region of 95% LoA, the maximum difference between the ground truth and the prediction for OC is -1400 (bottom point), for OD is -2600, and the average difference for OC and OD is -399.5 and -60.2, respectively. It can be observed that for the segmentation of OC, the model slightly tends to be over-segment.
Fig. 8.
Bland-Altman plot of the agreement between the ground truth and the segmentation result. The horizontal and vertical axis represent the average value and the difference of the predicted (PRE) area and the ground-truth (GT) area, respectively.
The proposed method is compared with classic networks in segmentation tasks under identical and unbiased settings. The official implementation codes were used for all the experiments, and the parameters were established by the authors. Moreover, the proposed method is also compared with other state-of-the-art segmentation methods for OD and OC segmentation. The experimental results are shown in Table 2. We preprocess the images with RoI crop for all automatic methods. The evaluation results are reported as average standard deviation. From the table, it can be observed that the proposed method achieves the highest IoU and the lowest standard deviation. Table 3 shows the comparison of the proposed method with the state-of-the-art segmentation methods on the REFUGE leaderboard. Ranked first and second methods are chosen for comparison.
Table 2. Comparison with other segmentation methods on the REFUGE test set. The method with * represent semi-auto segmentation method.
Table 3. Comparison with the REFUGE leaderboard. DSC is used for evaluating the segmentation of optic cup and disc, and the MAE is used for evaluating the vertical cup-to-disc ratio (vCDR).
| Method | Disc rank | Cup rank | vCDR MAE rank | Disc DSC(%) | Cup DSC(%) | MAE |
|---|---|---|---|---|---|---|
| CUHKMED | 1 | 2 | 2 | 96.02 | 88.26 | 0.0450 |
| Masker | 7 | 1 | 1 | 94.64 | 88.37 | 0.0414 |
| Ours | - | - | - | 98.45 | 96.69 | 0.0015 |
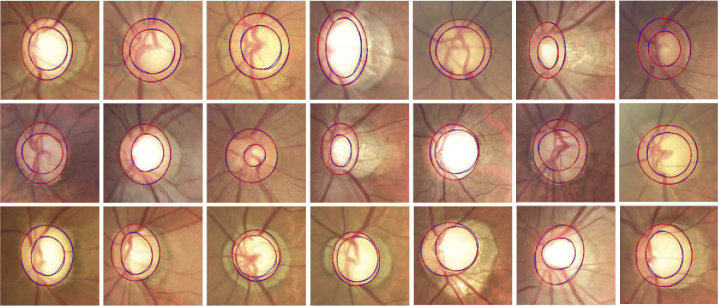
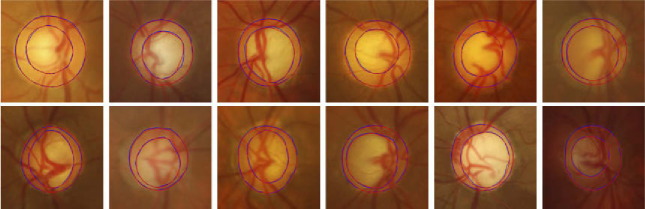
Figure 9 shows several segmentation results of the OD and OC with different appearance situations, where red and blue lines indicate the segmentation results of the proposed method and the ground truth. It can be observed that the existence of a blurred border confuses the other methods and causes erroneous segmentation results. In contrast, the proposed method works well for most cases in the given examples and the segmentation results are relatively accurate. Figure 10 shows the segmentation results of 21 glaucoma cases in the REFUGE test set. The colors of OD include yellowish, reddish, brownish, and whitish. The structure of the OC is vertically enlarged, and the border between OC and OD is blurred. From the segmentation results, the proposed method derives a relevant satisfying prediction for most glaucoma situations.
Fig. 9.
Segmentation result visualization of the optic cup (OC) and optic disc (OD), where the blue and red lines indicate the ground truth and the predictions of the proposed method. The first column shows five fundus image with different appearance and structure of OC and OD, including boundary blurring or structural changes. The rest of each column represents the segmentation results of different segmentation method.
Fig. 10.
Segmentation results of the proposed method for glaucoma cases in the REFUGE test set, where the blue and red lines indicate the ground truth and the predictions of the proposed method.
To evaluate the robustness of the model, the model trained on the REFUGE training set is directly tested on the Drishti-GS1 test set (51 images). The evaluation results are shown in Table 4. From the table, it can be observed that the proposed method has more advantages in OC segmentation. The visualization result is shown in Fig. 11. To verify the robustness of the proposed method on the normal and glaucoma cases, the segmentation results of the two classes are evaluated respectively. Table 5 illustrates the segmentation results on the REFUGE and Drishti-GS1 test set, respectively.
Table 4. Comparison with other state-of-the-art methods on Drishti-GS1 test set.
Fig. 11.
Segmentation results of the proposed method in Drishti-GS1 test set. The blue and red lines represent the ground truth and the prediction result, respectively. The model is trained on the REFUGE dataset, and test on the Drishti-GS1 test set directly without any preprocess.
Table 5. The segmentation result of the proposed method for glaucoma and normal cases on the REUFGE and Drishti-GS1 test set, respectively.
| Glaucoma | Normal | ||||
|---|---|---|---|---|---|
|
|
|||||
| Cup | Disc | Cup | Disc | ||
| REFUGE | IoU(%) | ||||
| DSC(%) | |||||
| Drishti-GS1 | IoU(%) | ||||
| DSC(%) | |||||
Figure 12 shows the receiver operating characteristics (ROC) curve of the proposed method and ground truth on two datasets, respectively. The classification of glaucoma and normal cases is based on vCDR without using any other additional processing. The ROC curve is plotted by calculating the true positive rate (TPR) against the false positive rate (FPR) at various threshold settings. From the figure, we can observe that the calculation of the vCDR derived from the proposed method performs similarly to the ground truth.
Fig. 12.
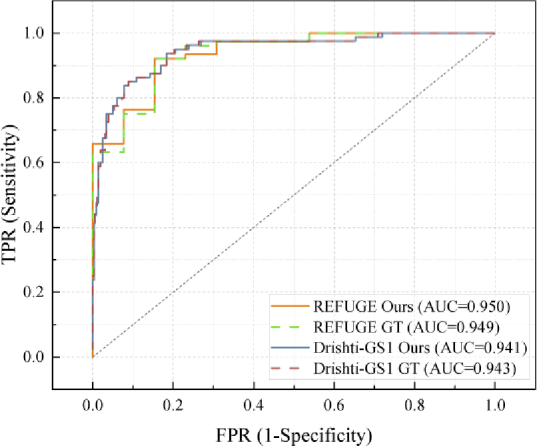
The receiver operating characteristics (ROC) curves of the proposed method and ground truth for REFUGE and Drishti-GS1, respectively.
The ablation study of the proposed method is shown in Table 6. The segmentation accuracy is the IoU of OD and OC, respectively. From the table, we can see the effectiveness of the level set evolution and the modified ResNet-101, respectively.
Table 6. Ablation study of the proposed method. LSE represent level set evolution.
| Model | ResNet-101 | ResNet-101+LSE | Modified ResNet-101 | Modified ResNet-101+LSE (Ours) |
|---|---|---|---|---|
| Cup IoU (%) | 81.39 | 82.52 | 93.24 | 93.61 |
| Disc IoU (%) | 89.58 | 92.69 | 95.00 | 96.95 |
Based on the encoder ResNet-101 and modified ResNet-101, we calculated the cost of computation resources and the segmentation accuracy of the proposed method, respectively. The results are shown in Table 7. From the table, the parameters and the FLOPs of modified ResNet-101 are larger than ResNet-101. However, the average segmentation accuracy of the OD and OC improves 7.52%.
Table 7. The cost of computation resource and the segmentation accuracy on the REFUGE test set of the proposed method based on the ResNet-101 and the modified ResNet-101, respectively. The segmentation accuracy is the average Intersection over Union (IoU) of the optic disc and optic cup.
| Backbone | Training time (second/epoch) | Testing time (second/image) | Parameters (M) | FLOPs (G) | IoU (%) |
|---|---|---|---|---|---|
| ResNet-101 | 69 | 0.4 | 67.69 | 53.22 | 87.76 |
| Modified ResNet-101 | 104 | 0.5 | 109.31 | 78.05 | 95.28 |
4. Discussion and conclusion
In this work, a semi-auto deep level set method for the segmentation task of OC and OD in fundus images is proposed. There are two main elements, including the prediction part and the evolution part. The prediction part is designed as a multi-scale convolutional neural network (CNN) with a prediction block. The CNN is employed as a feature extractor, and the prediction block is used to predict the parameters of the level set evolution. The evolution part takes the prediction result as an initial contour and further refines the contour based on the evolution parameters.
A series of experiments were performed on the REFUGE and Drishti-GS1 datasets to evaluate the accuracy and robustness of the proposed method. Quantitative results and the correlation analysis demonstrate the effectiveness of the proposed method, which gets the mean IoU of 93.61% and 96.95% for optic cup and disc, respectively. The model is evaluated on the Drishti-GS1 test set without extra training. The quantitative results show that the mean IoU of optic cup and disc are 94.7% and 96.5%, respectively. The results demonstrate that the proposed method is robust between different datasets. For the estimation of vCDR, we calculated the vCDR by the segmentation result of the optic cup and disc directly. The mean absolute error of vCDR is 0.0015, which shows that the proposed method achieves comparable results to the ground truth. For the classification of glaucoma, ROC curves show the classification result on the two datasets, respectively. We can observe that the curve derived from the proposed method is close to the curve derived from the ground truth. It also demonstrates that the results from the proposed method are comparable to the expert manually annotated one. From the visualization of the segmentation results, it can be observed that other segmentation methods tend to be affected by structural changes and blurred edges. However, the proposed method gives more reliable results for both normal and glaucoma cases. The proposed method also have some limitations. The level set evolution may rely on the predictions of the initial contour and the evolution parameters. Therefore, the prediction network needs to be able to predict the parameters well, otherwise the evolution result may deviate from expectations. A potential solution is to design a more reliable prediction network, which can balance the hardware requirements and segmentation accuracy.
In summary, we propose a contour-based optic cup and disc segmentation method, which can segment the object with more boundary details. The proposed method can give a reliable result for both optic cup and disc and is robust in different datasets. In our subsequent studies, we will further study the advantages of the contour-based segmentation method and apply the proposed method to more organ segmentation tasks.
Funding
National Key Research and Development Program of China10.13039/501100012166 (2017YFA0700800); National Natural Science Foundation of China10.13039/501100001809 (61876148, 61971343); Key Research and Development Projects of Shaanxi Province10.13039/501100015401 (2020GXLH-Y-008).
Disclosures
The authors declare no conflicts of interest.
Data availability
Data underlying the results presented in this paper are available in Ref. [4] and [33].
References
- 1.Tham Y.-C., Li X., Wong T. Y., Quigley H. A., Aung T., Cheng C.-Y., “Global prevalence of glaucoma and projections of glaucoma burden through 2040: a systematic review and meta-analysis,” Ophthalmology 121(11), 2081–2090 (2014). 10.1016/j.ophtha.2014.05.013 [DOI] [PubMed] [Google Scholar]
- 2.Yohannan J., Boland M. V., “The evolving role of the relationship between optic nerve structure and function in glaucoma,” Ophthalmology 124(12), S66–S70 (2017). 10.1016/j.ophtha.2017.05.006 [DOI] [PubMed] [Google Scholar]
- 3.Jonas J. B., Bergua A., Schmitz-Valckenberg P., Papastathopoulos K. I., Budde W. M., “Ranking of optic disc variables for detection of glaucomatous optic nerve damage,” Invest. Ophthalmol. Vis. Sci. 41, 1764–1773 (2000). [PubMed] [Google Scholar]
- 4.Orlando J. I., Fu H., Breda J. B., van Keer K., Bathula D. R., Diaz-Pinto A., Fang R., Heng P.-A., Kim J., Lee J., “Refuge challenge: A unified framework for evaluating automated methods for glaucoma assessment from fundus photographs,” Med. Image Anal. 59, 101570 (2020). 10.1016/j.media.2019.101570 [DOI] [PubMed] [Google Scholar]
- 5.Vishnuvarthanan A., Rajasekaran M. P., Govindaraj V., Zhang Y., Thiyagarajan A., “An automated hybrid approach using clustering and nature inspired optimization technique for improved tumor and tissue segmentation in magnetic resonance brain images,” Appl. Soft Comput. 57, 399–426 (2017). 10.1016/j.asoc.2017.04.023 [DOI] [Google Scholar]
- 6.Lalonde M., Beaulieu M., Gagnon L., “Fast and robust optic disc detection using pyramidal decomposition and hausdorff-based template matching,” IEEE Trans. Med. Imaging 20(11), 1193–1200 (2001). 10.1109/42.963823 [DOI] [PubMed] [Google Scholar]
- 7.A.-R. Youssif A. A.-H., Ghalwash A. Z., A.-R. Ghoneim A. A. S., “Optic disc detection from normalized digital fundus images by means of a vessels’ direction matched filter,” IEEE Trans. Med. Imaging 27(1), 11–18 (2008). 10.1109/TMI.2007.900326 [DOI] [PubMed] [Google Scholar]
- 8.Aquino A., Gegúndez-Arias M. E., Marín D., “Detecting the optic disc boundary in digital fundus images using morphological, edge detection, and feature extraction techniques,” IEEE Trans. Med. Imaging 29(11), 1860–1869 (2010). 10.1109/TMI.2010.2053042 [DOI] [PubMed] [Google Scholar]
- 9.Cheng J., Liu J., Wong D. W. K., Yin F., Cheung C., Baskaran M., Aung T., Wong T. Y., “Automatic optic disc segmentation with peripapillary atrophy elimination,” in 2011 Annual International Conference of the IEEE Engineering in Medicine and Biology Society (IEEE, 2011), pp. 6224–6227. [DOI] [PubMed] [Google Scholar]
- 10.Zheng Y., Stambolian D., O’Brien J., Gee J. C., “Optic disc and cup segmentation from color fundus photograph using graph cut with priors,” in International Conference on Medical Image Computing and Computer-Assisted Intervention (Springer, 2013), pp. 75–82. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Mukherjee N., Dutta H. S., “Automated localization of optic disk in retinal fundus images using cluster region membership and vessel network,” Int. J. Comput. Appl. 41(5), 343–358 (2019). 10.1080/1206212X.2018.1437658 [DOI] [Google Scholar]
- 12.Dai B., Wu X., Bu W., “Optic disc segmentation based on variational model with multiple energies,” Pattern Recognit. 64, 226–235 (2017). 10.1016/j.patcog.2016.11.017 [DOI] [Google Scholar]
- 13.Osareh A., Mirmehdi M., Thomas B., Markham R., “Comparison of colour spaces for optic disc localisation in retinal images,” in Object Recognition Supported by User Interaction for Service Robots, vol. 1 (IEEE, 2002), pp. 743–746. [Google Scholar]
- 14.Lowell J., Hunter A., Steel D., Basu A., Ryder R., Fletcher E., Kennedy L., “Optic nerve head segmentation,” IEEE Trans. Med. Imaging 23(2), 256–264 (2004). 10.1109/TMI.2003.823261 [DOI] [PubMed] [Google Scholar]
- 15.Xu J., Chutatape O., Sung E., Zheng C., Kuan P. C. T., “Optic disk feature extraction via modified deformable model technique for glaucoma analysis,” Pattern Recognit. 40(7), 2063–2076 (2007). 10.1016/j.patcog.2006.10.015 [DOI] [Google Scholar]
- 16.Joshi G. D., Sivaswamy J., Krishnadas S., “Optic disk and cup segmentation from monocular color retinal images for glaucoma assessment,” IEEE Transactions on Medical Imaging 30, 1192–1205 (2011). [DOI] [PubMed] [Google Scholar]
- 17.Long J., Shelhamer E., Darrell T., “Fully convolutional networks for semantic segmentation,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (2015), pp. 3431–3440. [DOI] [PubMed] [Google Scholar]
- 18.Ronneberger O., Fischer P., Brox T., “U-net: Convolutional networks for biomedical image segmentation,” in International Conference on Medical Image Computing and Computer-assisted Intervention (Springer, 2015), pp. 234–241. [Google Scholar]
- 19.Zhao H., Shi J., Qi X., Wang X., Jia J., “Pyramid scene parsing network,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (2017), pp. 2881–2890. [Google Scholar]
- 20.Chen L.-C., Zhu Y., Papandreou G., Schroff F., Adam H., “Encoder-decoder with atrous separable convolution for semantic image segmentation,” in Proceedings of the European Conference on Computer Vision (ECCV) (2018), pp. 801–818. [Google Scholar]
- 21.Maninis K.-K., Pont-Tuset J., Arbeláez P., Van Gool L., “Deep retinal image understanding,” in International Conference on Medical Image Computing and Computer-assisted Intervention (Springer, 2016), pp. 140–148. [Google Scholar]
- 22.Simonyan K., Zisserman A., “Very deep convolutional networks for large-scale image recognition,” arXiv preprint arXiv:1409.1556 (2014).
- 23.Sevastopolsky A., “Optic disc and cup segmentation methods for glaucoma detection with modification of u-net convolutional neural network,” Pattern Recognit. Image Anal. 27(3), 618–624 (2017). 10.1134/S1054661817030269 [DOI] [Google Scholar]
- 24.Fu H., Cheng J., Xu Y., Wong D. W. K., Liu J., Cao X., “Joint optic disc and cup segmentation based on multi-label deep network and polar transformation,” IEEE Trans. Med. Imaging 37(7), 1597–1605 (2018). 10.1109/TMI.2018.2791488 [DOI] [PubMed] [Google Scholar]
- 25.Shankaranarayana S. M., Ram K., Mitra K., Sivaprakasam M., “Fully convolutional networks for monocular retinal depth estimation and optic disc-cup segmentation,” IEEE J. Biomed. Health Inform. 23(4), 1417–1426 (2019). 10.1109/JBHI.2019.2899403 [DOI] [PubMed] [Google Scholar]
- 26.Tang M., Valipour S., Zhang Z., Cobzas D., Jagersand M., “A deep level set method for image segmentation,” in Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support (Springer, 2017), pp. 126–134. [Google Scholar]
- 27.Wang Z., Acuna D., Ling H., Kar A., Fidler S., “Object instance annotation with deep extreme level set evolution,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, (2019), pp. 7500–7508. [Google Scholar]
- 28.He K., Zhang X., Ren S., Sun J., “Deep residual learning for image recognition,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (2016), pp. 770–778. [Google Scholar]
- 29.Woo S., Park J., Lee J.-Y., So Kweon I., “Cbam: convolutional block attention module,” in Proceedings of the European Conference on Computer Vision (ECCV) (2018), pp. 3–19. [Google Scholar]
- 30.Khan S., Shahin A. H., Villafruela J., Shen J., Shao L., “Extreme points derived confidence map as a cue for class-agnostic segmentation using deep neural network,” arXiv preprint arXiv:1906.02421 (2019).
- 31.Maninis K.-K., Caelles S., Pont-Tuset J., Van Gool L., “Deep extreme cut: From extreme points to object segmentation,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, (2018), pp. 616–625. [Google Scholar]
- 32.Chen X., Williams B. M., Vallabhaneni S. R., Czanner G., Williams R., Zheng Y., “Learning active contour models for medical image segmentation,” in Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, (2019), pp. 11632–11640. [Google Scholar]
- 33.Sivaswamy J., Krishnadas S., Chakravarty A., Joshi G., Tabish A. S., “A comprehensive retinal image dataset for the assessment of glaucoma from the optic nerve head analysis,” JSM Biomed. Imaging Data Papers 2, 1004 (2015). [Google Scholar]
- 34.Wang S., Yu L., Yang X., Fu C.-W., Heng P.-A., “Patch-based output space adversarial learning for joint optic disc and cup segmentation,” IEEE Trans. Med. Imaging 38(11), 2485–2495 (2019). 10.1109/TMI.2019.2899910 [DOI] [PubMed] [Google Scholar]
- 35.Liu P., Kong B., Li Z., Zhang S., Fang R., “Cfea: collaborative feature ensembling adaptation for domain adaptation in unsupervised optic disc and cup segmentation,” in International Conference on Medical Image Computing and Computer-Assisted Intervention, (Springer, 2019), pp. 521–529. [Google Scholar]
- 36.Wang Z., Dong N., Rosario S. D., Xu M., Xie P., Xing E. P., “Ellipse detection of optic disc-and-cup boundary in fundus images,” in 2019 IEEE 16th International Symposium on Biomedical Imaging (ISBI 2019) (IEEE, 2019), pp. 601–604. [Google Scholar]
- 37.Zhang Z., Fu H., Dai H., Shen J., Pang Y., Shao L., “Et-net: A generic edge-attention guidance network for medical image segmentation,” in International Conference on Medical Image Computing and Computer-Assisted Intervention (Springer, 2019), pp. 442–450. [Google Scholar]
- 38.Shah S., Kasukurthi N., Pande H., “Dynamic region proposal networks for semantic segmentation in automated glaucoma screening,” in 2019 IEEE 16th International Symposium on Biomedical Imaging (ISBI 2019) (IEEE, 2019), pp. 578–582. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data underlying the results presented in this paper are available in Ref. [4] and [33].