Abstract
Partition coefficients describe the relative concentration of a chemical equilibrated between two phases. In the design of air samplers, the sorbent-air partition coefficient is a critical parameter, as is the ability to extrapolate or predict partitioning at a variety of temperatures. Our specific interest is the partitioning of plant-derived terpenes (hydrocarbons formed from isoprene building blocks) and terpenoids (with oxygen-containing functional groups) in polydimethylsiloxane (PDMS) sorbents. To predict as a function of temperature for compounds containing carbon, hydrogen, and oxygen, we developed a group contribution model that explicitly incorporates the van’t Hoff equation. For the 360 training compounds, predicted values strongly correlate (R2 > 0.987) with values measured at temperatures from 60 °C to 200 °C. To validate the model with available literature data, we compared predictions for 50 additional C10 compounds, including 6 terpenes and 22 terpenoids, with values measured at 100 °C and determined an average relative error of 3.1 %. We also compared predictions with values measured at 25 °C. The modeling approach developed here is advantageous for properties with limited experimental values at a single temperature.
Graphical Abstract

Introduction
Passive air sampling is an important technique for characterizing exposure to hazardous chemicals in indoor and outdoor environments.1–3 Commercially-available personal exposure badges utilize activated carbon sorbents and are generally intended to capture industrial chemicals such as benzene, toluene, ethylbenzene, and xylenes (BTEX). Direct capture of vapor samples (e.g., with evacuated canisters) can also be effective for volatile organic chemicals but may not be effective for semi-volatile chemicals present in lower concentrations. For these chemicals, sampling schemes rely on capture and concentration by a sorbent material. Passive air samplers may utilize activated carbon, polyurethane foam, styrene-divinylbenzene copolymer resins, semi-permeable membranes filled with triolein, or polydimethylsiloxane (PDMS) sheets.1–5 With the exception of activated carbon, these materials are intended to capture persistent organic pollutants (POPs) such as polybrominated diphenyl ethers (PBDEs), polycyclic aromatic hydrocarbons (PAHs), polychlorinated biphenyls (PCBs), and organochlorine pesticides (OCPs). Interestingly, butter acts as an indirect sampling matrix for POPs that are captured from the air by pasture crops and fed to livestock, allowing them to concentrate in milk fats.6
Passive headspace sampling is a related technique that permits volatile or semi-volatile organic chemicals to be extracted from a complex solid or liquid matrix, concentrated, and released for identification. Sampling schemes often rely on capture by a sorbent material because direct capture of vapor samples (e.g., with gas-tight syringes) does not permit the detection of trace chemicals. For example, in current forensic science practice, the headspace of fire debris is sampled with activated carbon, which must be eluted with solvent to recover the adsorbed chemicals. Headspace solid phase microextraction (SPME) was developed as a solvent-free alternative in which adsorbed chemicals can be recovered by heating.7 This technique utilizes a short (1 cm long), sorbent-coated glass fiber that is retracted into a stainless steel needle for protection once adsorption is complete. PDMS or other sorbents coat the fiber; PDMS is valued for its ability to capture a wide range of organic chemicals and withstand high injector temperatures. SPME has been applied to simulated fire debris samples8 and illicit drugs and explosives.9 Capillary microextraction of volatiles (CMV) is a related technique that utilizes a wide (2 mm diameter, 2 cm long) glass capillary packed with PDMS-coated glass microfibers, resulting in high surface area and sampling capacity.10 Equilibration is accelerated by forcing headspace air through the capillary. Depending on the target analyte and matrix, the equilibration time can be reduced to as little as 30 s. Breath collection devices were recently created by connecting CMVs to a mouth piece to capture organic chemicals from the exhaled breath of cigarette smokers.11
The uptake profile of a passive air sampler has three regions. Mathematical models to predict uptake have been described in detail by others4 and will only be discussed briefly here. The concentration of a target analyte in the sorbent initially increases linearly with time (kinetic region) but eventually equilibrates (thermodynamic region). The linear uptake region is often considered to end when the sampler has accumulated 25 % of the eventual equilibrium value. Similarly, when the sampler has accumulated 95 % of the eventual equilibrium value, it is in the thermodynamic region. The transition region from approximately 25 % to 95 % of capacity requires consideration of kinetics and thermodynamics. In the kinetic region, Eq. 1 defines the mass of target analyte captured by the sorbent ().
| [1] |
In this equation, is the air-side mass transfer coefficient (cm/s), is the planar area of the exposed sorbent material (cm2), is the concentration of target analyte in air (ng/cm3) and t is the sampling time (s). The sampling rate, , which has units of cm3/s, provides a sense of how much air is sampled by the sorbent. In the thermodynamic region, Eq. 2 defines the sorbent-air partition coefficient (), which is dimensionless. is the measured concentration of target analyte in the sorbent (ng/cm3) and one can calculate if is known.
| [2] |
Passive air samplers can be designed to operate in either region. To sample in the kinetic region, the capacity of the sorbent must be high enough to avoid reaching the transition (or curvilinear) region. Personal exposure badges generally operate in the kinetic region; manufacturers provide values and maximum sampling times for each chemical that can be sampled by their badges. Generic, chemical-independent values have also been proposed for chemicals predominantly found in the vapor-phase rather than the particle-phase.5,12 To sample in the thermodynamic region, the sorbent configuration must facilitate rapid equilibration. PDMS-coated glass fibers (100 μm sorbent thickness) equilibrate with volatile organic chemicals within minutes to hours,13,14 whereas PDMS sheets (104 μm sorbent thickness) might require years to equilibrate with semi-volatile chemicals.15 Ethylene vinyl acetate has been coated onto glass to create thin films that equilibrate with POPs within days or weeks.16 For environmental monitoring, one advantage to operating in the thermodynamic region is that once equilibrium is reached, samplers can be retrieved at any time. More analyte mass is generally recovered, leading to a lower detection limit. However, the same sorbent may be in the kinetic region with respect to some analytes and in the thermodynamic region with respect to others.4 Partition coefficients are needed for two purposes: to estimate the duration of the kinetic region and to calculate equilibrium concentrations in the thermodynamic region during adsorption or desorption.
There are several approaches to determining partition coefficients, depending on the sorbent and analyte(s) of interest. can be measured by equilibrating PDMS-coated fibers13,14,17,18 or other PDMS-coated materials19 with single compounds or mixtures. Sorbent thickness does not matter if equilibrium is achieved.17 For semi-volatile compounds, constant linear airflow has been utilized to reduce the equilibration time.17 can also be measured by isothermal gas chromatography and extrapolated to lower temperatures within the linear range of the van’t Hoff equation. For example, Okeme et al. determined for 76 semi-volatile organic compounds at temperatures from 60 °C to 190 °C and extrapolated these values to 25 °C.15 Such measurements, again, do not depend on the stationary phase (sorbent) thickness because the specific retention volume is normalized by the stationary phase volume; however, the accuracy of stationary phase dimensions must be verified.20 Furthermore, extrapolation can introduce errors because the relationship between log and 1/T may not be linear over a large range of temperatures.
Semi-empirical prediction approaches have also been developed – most commonly a polyparameter linear free energy relationship (ppLFER) equation that models solute transfer between two phases at a single temperature.21,22 For gas-liquid partition coefficients, this approach includes five solute descriptors: excess molar refractivity (E), dipolarity/polarity (S), hydrogen bond acidity (A) and basicity (B), and the logarithm of the Ostwald partition coefficient (L) into hexadecane at 298 K. The predictive equation has the form log K = c + eE + sS + aA + bB + lL, where c, e, s, a, b, and l are sorbent-specific constants. Solute descriptors must be measured or predicted; sorbent-specific constants are determined by regression with training compounds for which the partition coefficient is known. Starting with values for 142 training compounds, Sprunger et al. developed a ppLFER equation to predict at a single temperature (25 °C).23 Okeme et al. applied the equation developed by Sprunger et al. to 76 compounds; the authors concluded that the semi-empirical ppLFER approach was more successful than the theoretical COSMO-RS approach in predicting at 25 °C.15 To predict at other temperatures, sorbent-specific constants must be determined from values at these temperatures, essentially developing a ppLFER equation at each temperature. Analogous ppLFER equations have been developed to predict the enthalpy of sorption (ΔHS) on polyurethane foam24 and styrene-divinylbenzene resin.25 Although ΔHS predictions can be used to adjust log K values to different temperatures, thus far training compounds have been limited (N < 55) and the quality of the correlation has been similarly limited (R2 ~ 0.85).24,25
Group contribution models are based on the concept that pure component thermophysical and transport properties can be predicted solely by molecular structure. Group contribution models are additive – the contributions of each group, multiplied by its frequency within the compound, are summed to give the value for the pure compound.26 While property data for training compounds are required to determine group contributions by regression, solute descriptors are not required. Joback & Reid27 predicted temperature-independent properties such as the enthalpy of vaporization (Hv, widely used for the design of vapor-liquid equilibrium-based processes) with 41 first-order groups. Their approach was expanded to treat compounds of greater complexity by additional first-order groups, second-order groups28 and third-order groups.29,30 While first-order groups describe the entire molecule with small, non-overlapping groups, second-order groups typically do not describe the entire molecule and may overlap. Second-order groups were created to provide more information for aliphatic and aromatic compounds with one ring, and to distinguish between isomers. Similarly, third-order groups were created for polycyclic compounds. Octanol-water partition coefficients (KOW, a measure of lipophilicity that influences biodistribution and environmental fate) have been predicted at 25 °C with models containing second-order groups31 and third-order groups.32 has not been modelled by group contribution methods.26
Identification or quantitation of plant-derived compounds by vapor-phase analysis is important for determining intoxication, monitoring the air quality of indoor cannabis production facilities, and enforcing legal limits for cannabis possession. Cannabis plant material can be distinguished from similar plants by its major cannabinoids (Δ-9-tetrahydrocannabinol or cannabidiol); however, cannabinoids have low vapor pressures33 and only small quantities will be captured at ambient temperatures. Furthermore, highly-odorous compounds which may be important for cannabis detection by humans or trained canines are not necessarily the compounds present in the highest concentration in the vapor phase.34,35 Recent investigations indicated that three sesquiterpenes (α-santalene, valencene, and β-bisabolene) are unique to cannabis,36 suggesting that terpenoids may be effective markers for cannabis for some applications. Cigarette smokers were distinguished from non-smokers by twelve chemicals in their exhaled breath, including the terpenes β-myrcene and limonene and the terpenoid citral.11 Nicotine alone was a poor indicator of recent smoking, whereas detection of multiple chemicals in combination was more successful.11 Recent cannabis users are likely to exhibit analogous differences in their breath profiles compared to non-users.
We are interested in quantitative measurements of exhaled breath, indoor environments such as greenhouses, isolated plant material, and thermal desorption of adsorbed compounds. These applications require partition coefficients at breath temperature (34 °C), greenhouse temperature (21 °C to 27 °C), or ambient temperature (−40 °C to 40 °C). Higher temperatures (60 °C to 80 °C) may be employed for passive headspace sampling in the lab, while 200 °C may be an appropriate desorption temperature for many compounds. Our goal is to enable prediction within the range 20 °C to 200 °C. In this work, we developed a group contribution model with 18 first-order groups to predict as a function of temperature. We created the model with data from 360 training compounds and validated the model at 100 °C with 50 additional C10 compounds. values for the training compounds were calculated from Kovats retention indices and isothermal gas chromatography measurements at temperatures from 60 °C to 200 °C. The 360 training compounds contain only carbon, hydrogen, and oxygen, reflecting our interest in phytochemicals such as terpenoids. For the 360 training compounds, values predicted by the resulting model correlate with measured values (R2 > 0.987). For the 50 additional C10 validation compounds, values predicted at 100 °C have an average relative error of 3.1% compared to measured values. We find that the modeling approach developed here is advantageous for properties with limited experimental values at a single temperature.
Materials and Methods
Determining partition coefficients by IGC (isothermal gas chromatography).
We can calculate from isothermal retention times when the stationary phase is the sorbent of interest (Eq. 3).37 values have been determined by this method for volatile organic compounds (n-alkanes and substituted benzenes)20 and semi-volatile organic compounds containing bromine, chlorine, and/or phosphate functional groups.15
| [3] |
In Eq. 3, F is the flow rate of mobile phase (mL/min), is the retention time of the analyte (min), is the retention time of a non-retained chemical (min), and is the volume of the liquid stationary phase (mL). F was calculated at each temperature by measuring the flow rate of nitrogen carrier gas with a bubble flowmeter and applying corrections for water vapor and gas compressibility. was calculated from the column dimensions and the manufacturer-specified stationary phase thickness. Retention times were determined with a flame ionization detector and the non-retained tracer was methane for all experiments. For isothermal measurements, the practical temperature range depends on the compound of interest, because long retention times result in wide chromatographic peaks that are difficult to distinguish from baseline and short retention times result in peaks that cannot be distinguished from the non-retained tracer. Retention time measurements for C6 to C16 n-alkanes were made at a series of temperatures from 60 °C to 200 °C, with at least 5 temperatures spanning a range of at least 60 °C for each chemical. For example, hexane was measured at temperatures from 60 °C to 140 °C, whereas hexadecane was measured from 140 °C to 200 °C. We employed an Agilent 6890 gas chromatograph with a flame ionization detector and ChemStation software. The J&W Scientific DB-1 capillary column had an inner diameter of 0.25 mm and a stationary phase thickness of 0.1 μm. The column was 29.0 m in length. Nine replicate measurements were made at each temperature. We calculated average retention times () and average values for use in Eq. 4 and Eq. 8, respectively, as will be described.
Determining partition coefficients by combining IGC with literature values.
Kovats retention indices () convert isothermal retention times into dimensionless values by normalizing the retention time of any analyte by the retention times of the n-alkanes that elute before and after it.38 We can calculate the retention time for our experimental conditions if has been reported for a column with equivalent stationary phase chemistry (Eq. 4). This equation is simply a rearrangement of the equation defining the Kovats retention index. In Eq. 4, and are the retention times of n-alkanes with < < , where n and N are the number of carbons in the smaller and larger n-alkanes, respectively. Importantly, data from capillary or packed columns can be employed and experimental parameters such as column dimensions, stationary phase thickness, mobile phase flow rate, and/or pressure can be different. Once is obtained for our experimental conditions, we calculate from Eq. 3.
| [4] |
We determined values for a series of n-alkylbenzenes by both methods and compared them to values reported by Kloskowski et al.20 (Fig. 1). Note that benzene could not be measured at 200 °C because it did not separate sufficiently from the non-retained tracer. At higher temperatures (150 °C and 200 °C), there is greater variability in the measured values, which suggests that temperature is the greatest source of uncertainty. The correspondence between our values for benzene, toluene, and ethylbenzene and values for these compounds measured with three stationary phases by Kloskowski et al.20 provides verification of our stationary phase volume. The data in Fig. 1 also clearly demonstrates that values determined by combining IGC measurements with literature values (Eq. 4 and Eq. 3) are equivalent to values determined by IGC measurements alone (Eq. 3). This is important because we need values for a diverse set of training compounds and the second approach enables us to utilize Kovats retention indices reported by other laboratories. Kovats retention indices were identified through the NIST Chemistry Webbook39 for stationary phases equivalent to 100% polydimethylsiloxane.
Figure 1.
Log as a function of 1 / T [K] for a series of n-alkylbenzenes. IGC (Eq. 3) was conducted at 50 °C, 75 °C, 100 °C, 150 °C, and 200 °C. Nine measurements are shown at each temperature. IGC was combined with literature Ix values (Eq. 4 and Eq. 3) at 60 °C, 80 °C, 100 °C, 120 °C, 140 °C, 160 °C, and 180 °C. Only the regression lines are shown. Average values reported by Kloskowski et al. include columns with 1 μm, 5 μm, and 18 μm thick stationary phases.20 Abbreviations: B = benzene; T = toluene; EB = ethylbenzene, PB = propylbenzene; BB = butylbenzene.
Model development and evaluation.
Fig. 1 demonstrates that log is proportional to 1/T over the temperatures investigated, in accordance with the van’t Hoff equation (Eq. 5). Therefore, the slope (proportional to ΔHS, the enthalpy of sorption) and intercept (proportional to ΔSS, the entropy of sorption) can be determined by linear regression, permitting values to be calculated at temperatures of interest within the linear range of the van’t Hoff equation. Eq. 5 provides the starting point for a group contribution model that explicitly incorporates temperature dependence by predicting the slope and intercept as a function of molecular structure. We determined values by Eq. 3 for 21 training compounds, which included 11 n-alkanes and 10 compounds with aldehyde and/or ether groups. We determined values for all other training compounds by Eq. 4 and Eq. 3. To do this, we first identified compounds with = 600 – 1600 at three or more temperatures from the following: 60 °C, 80 °C, 100 °C, 120 °C, 140 °C, 150 °C, 160 °C, 180 °C, and 200 °C. We calculated from each value and plotted log vs. 1/T for each compound. We used these plots to verify that values are consistent with the van’t Hoff equation by examining the R2 values resulting from linear regression for the slope and intercept. We eliminated compounds with R2 < 0.95 from the training data. One compound was eliminated by this quality control check: α-phellandrene (R2 = 0.87). The remaining 339 compounds were added to the 21 compounds described above, resulting in 360 training compounds (Supplementary Table S1). Apart from the n-alkanes which ranged from C6 to C16, training compounds ranged in size from C4 alcohols to C15 terpenes.
| [5] |
| [6] |
| [7] |
| [8] |
We selected 18 first-order groups to describe the molecular structure of each training compound. For each training compound at each temperature, we predicted log with the van’t Hoff equation (Eq. 5). In this equation, the slope (Eq. 6) and intercept (Eq. 7) are the sum of contributions by first-order structural groups, and , respectively, multiplied by their frequency, , and T is the absolute temperature. To determine values of and for the 18 first-order groups, we minimized the sum of the squared errors (Eq. 8). We applied a multistart approach to run a generalized reduced gradient (GRG) local solver from multiple starting points to reach a solution with high probability of being a global solution. N = 1625 and is greater than the number of training compounds, because each compound at each temperature generates a squared error. We chose this approach to minimize the error of the value we wish to predict () without reducing the model input to two values per compound. In this way, compounds measured at more temperatures were weighted by the model more than compounds measured at fewer temperatures.
Results and Discussion
Group Contribution Model with 18 Groups.
The groups utilized here were compared with first-order groups utilized for carbon, hydrogen, and oxygen containing compounds by Joback & Reid (25 groups total),27 Marrero & Gani (64 groups total),32 and Stefanis et al. (37 groups total)31 (Supplementary Table S2). There are significant differences in group definitions. Joback & Reid27 define five cyclic groups for aliphatic and aromatic rings. Marrero & Gani32 use cyclic groups for aliphatic rings only, whereas Stefanis et al.31 do not define any cyclic groups for aliphatic rings. Marrero & Gani32 and Stefanis et al.31 both define groups for aromatic carbons, but Marrero & Gani32 define a variety of additional groups for substituents that replace hydrogen (e.g. aromatic carbon bound to alcohol, methoxy, acetyl, aldehyde, or acetate). Stefanis et al.31 define only five such substituents and delineate fewer groups in general (e.g., compare ethers, ketones, and esters). Our groups match the Joback & Reid27 groups, however, we utilized only one ether group and one ketone group due to the limited number of training compounds with these groups (18 and 12, respectively). Furthermore, the training compounds contain only one compound with a cyclic ether group (eucalyptol) and one compound with a cyclic ketone group (cyclohexanone).
Group contributions (Table 1) are provided with six digits to avoid roundoff error when these values are used for prediction. To qualitatively examine model performance, correlation plots were separated based on functional groups (Fig. 2). Compounds in the plots for alkanes-alkenes, isoalkanes, cycloalkanes, or aromatic hydrocarbons appear only once, whereas compounds may appear more than once in the plots for alcohols-phenols, aldehydesketone-ethers, esters, or terpenoids, based on multiple oxygen-containing groups. For example, vanillin contains a phenol group, an aldehyde group, and an ether group, and therefore appears in two plots. Furthermore, each compound generates several pairs of predicted/measured values – one at each temperature included in the training data. Fig. 2 indicates the absolute error between model predictions and measurements in the form of vertical distance from the solid black line. For an individual compound, higher log values are associated with lower temperatures. Predictions for the simplest compounds, alkanes and alkenes, require only three groups and, not surprisingly, have small absolute errors. Predictions for esters, which includes linear esters and benzoates, and therefore many more groups, also have small absolute errors. The model systematically underpredicts a subset of isoalkanes, whereas aromatic hydrocarbon outliers are both under- and over-predicted. Note that aromatic hydrocarbons include fused ring compounds such as indane and naphthalene. Compounds with alcohol, phenol, aldehyde, ketone, or ether functional groups have the largest absolute errors, which may reflect the simplified group assignments, the limited number of training compounds with these functional groups, or the presence of multiple oxygen-containing groups.
Table 1.
First-order groups and their contributions to the slope and intercept.
| Group | Slope (Si) | Intercept (Ii) |
|---|---|---|
| CH3 | 144.865 | 0.221633 |
| CH2 | 174.012 | 0.203179 |
| CH | 175.625 | 0.222433 |
| C | 135.718 | 0.127316 |
| =CH2 | 177.947 | 0.348045 |
| =CH | 128.264 | 0.089427 |
| =C | 241.677 | 0.272969 |
| CH2 (cyc)a | 160.692 | 0.170520 |
| CH (cyc) | 123.224 | 0.063547 |
| C (cyc) | 96.295 | 0.075337 |
| =CH (cyc) | 158.186 | 0.171851 |
| =C (cyc) | 223.060 | 0.225132 |
| OH (alcohol) | 339.926 | 0.415119 |
| OH (phenol) | 480.871 | 0.783309 |
| O | 192.570 | 0.209433 |
| CO | 411.400 | 0.398990 |
| CHO | 398.877 | 0.431350 |
| COO | 459.731 | 0.519668 |
| CONSTANT | 578.918 | 1.500359 |
Specifies groups found within a ring structure, which includes aromatic rings.
Figure 2.
Correlation between predicted log values and measured log values for 360 training compounds. Solid black lines indicate 1:1 correspondence. Solid blue lines are regression lines.
Model performance statistics (Table 2) indicate that the overall correlation between predicted and measured values is high (R2 > 0.987). Many of the qualitative observations from Fig. 2 are quantified here; for example, the average absolute error (AAE) of 0.07 log units for compounds with alcohol or phenol groups indicates lower predictive capability for these compounds. However, the maximum absolute error (AEMAX) is equal to 0.3 log units for individual compounds with a variety of functional groups, suggesting that model performance could be improved by a variety of approaches. AAE is frequently utilized to compare the performance of different models when the training compounds remain the same. For example, Marrero & Gani32 developed a three-level group contribution model to predict KOW at 25 °C with a diverse set of more than 9500 training compounds. AAE for the training data decreased from 0.35 log units when first-order groups were employed, to 0.27 log units and 0.24 log units when second-order and third-order groups, respectively, were included. AAE for the training data modeled here is nearly an order of magnitude smaller (0.05 log units) but cannot be directly compared because the training compounds were different. One advantage to creating small models for compounds of interest rather than large, inclusive models is minimizing absolute errors. Average relative error (ARE) provides an estimate of uncertainty for model predictions based on the functional groups involved, meaning that predictions for a compound with an ester group have lower uncertainty than predictions for a compound with aldehyde or alcohol groups.
Table 2.
Statistical performance of the group contribution model.
| COMPOUNDS | N | R2 | SDa | AAEb | AEMAX | AREc | RE > 5%d |
|---|---|---|---|---|---|---|---|
| Alkane-Alkene (18) | 102 | 0.998 | 0.04 | 0.02 | 0.1 | 1.4 | 1 |
| Isoalkane (29) | 121 | 0.987 | 0.07 | 0.05 | 0.2 | 3.0 | 4 |
| Cycloalkane (30) | 128 | 0.985 | 0.06 | 0.05 | 0.2 | 2.6 | 2 |
| Aromatic Hydrocarbon (71) | 318 | 0.984 | 0.07 | 0.05 | 0.3 | 2.2 | 3 |
| Alcohol-Phenol (66) | 306 | 0.979 | 0.09 | 0.07 | 0.3 | 3.2 | 8 |
| Aldehyde-Ketone-Ether (43) | 183 | 0.974 | 0.09 | 0.06 | 0.3 | 3.0 | 5 |
| Ester (95) | 422 | 0.990 | 0.05 | 0.04 | 0.3 | 1.7 | 1 |
| Terpenoid (38) | 184 | 0.980 | 0.07 | 0.06 | 0.2 | 2.5 | 6 |
| Training Compounds (360) | 1625 | 0.987 | 0.07 | 0.05 | 0.3 | 2.3 | 23 |
Standard deviation (SD) is estimated by calculating the root mean squared error: .
Average absolute error (AAE) measures the deviation of predicted values from measured values: .
Average relative error (ARE) normalizes each deviation by the measured value: .
At three or more temperatures.
Relative error (RE) can be used to identify compounds that are poorly described by the model. We identified compounds with RE > 5 % at three or more temperatures to provide direction for selecting second-order groups. Twenty-three compounds fell into this category; most had multiple substituents, such as multiple methyl groups or multiple oxygen-containing groups. Our model consistently underpredicts for four isoalkanes with multiple methyl groups: 2,2,3-trimethylbutane, 2,3,3-trimethylpentane, 2,3,4-trimethylpentane, and 2,2,3,3-trimethylbutane. This leads to multiple points below the y = x line in Fig. 2. There are no alternative approaches to selecting first-order groups; however, the following second-order groups30 provide additional structural information: (CH3)2CH, (CH3)3C, CH(CH3)CH(CH3), CH(CH3)C(CH3)2, and C(CH3)2C(CH3)2. Only nine of the isoalkanes do not include a second-order group and the four compounds identified above include up to four second-order groups (2 unique groups in each molecule). Second-order groups such as (CH3)2CH are also found in many terpenoids. Second-order groups have also been created to distinguish isomers, especially the isomers that result from substituted aromatic rings. Many training compounds with aromatic rings have multiple substitutions and predicted values for compounds such as o-, m-. and p-xylene or o-, m-, and p-ethyltoluene are approximately equal to the average value. For example, our model predicts for the isomers durene (1,2,4,5-tetramethylbenzene), isodurene (1,2,3,5-tetramethylbenzene), and prehnitene (1,2,3,4-tetramethylbenzene) identically. Durene and isodurene have similar (lower) values than prehnitene. Another example is o-hydroxybenzaldehyde, which our model overpredicts, and p-hydroxybenzaldehyde, which our model underpredicts. Second-order groups that distinguish these isomers are expected to improve predictions.
Model Predictions for Validation Compounds at 100 °C.
Terpenes are based on a five-carbon isoprene unit (2-methyl-1,3-butadiene); monoterpenes consist of 2 isoprene units and sesquiterpenes consist of 3 isoprene units. We identified 50 ten-carbon (C10) validation compounds with Kovats retention indices at 100 °C, including 6 terpenes and 22 terpenoids (Supplementary Table S3). Compared to the training compounds, the validation compounds have more alcohol, ether, ketone, and aldehyde functional groups (Fig. 3). The reliability of values for these compounds is also lower because there was no possibility to verify consistency with the van’t Hoff equation. Predicted values are correlated with measured values (Fig. 4). AAE and ARE for the validation compounds are comparable to values from the alcohol-phenol and ether-ketone-aldehyde classes of training compounds.
Figure 3.
Distribution of oxygen-containing functional groups within the training compounds (360) and the C10 validation compounds (50).
Figure 4.
Log values for 50 C10 compounds were predicted at 100 °C and compared with log values calculated from Kovats retention indices. Solid black line indicates 1:1 correspondence. Solid red line is a regression line. AAE is 0.09 log units and ARE is 3.1 % for all 50 compounds.
Model Predictions from 20 °C to 40 °C.
We first compare model predictions to extrapolated values for the 360 training compounds. This approach assumes a constant slope over a wide temperature range (20 °C to 200 °C) and the error (log – log ) indicates how well the model replicates single compound extrapolation. We examined histograms of the error at intervals of 20 °C and found that they were normally distributed (Supplementary Figure S1). The mean error is within ± 0.01 log units at each temperature. The standard deviation decreases from 0.14 log units at 20 °C to 0.06 log units at 200 °C, which indicates that predictions at 20 °C to 40 °C have greater absolute errors than predictions at higher temperatures, as we expect based on the temperature distribution of the training compounds (60 °C to 200 °C). However, the standard deviation is less than 3 % of the average log value at 20 °C, demonstrating that predictions at 20 °C to 40 °C do not a priori lead to greater uncertainty than predictions at higher temperatures (e.g., 100 °C). We next compare model predictions to measured values, which are limited.
Martos et al.13 measured at 25 °C by equilibrating PDMS-coated fibers with a mixture of 29 isoalkanes (100 μm coating) or 33 aromatic hydrocarbons (30 μm coating). We used our model to predict at 25 °C (Fig. 5). The training data included 10 of the isoalkanes and 26 of the aromatic hydrocarbons. Fig. 5 shows that model predictions can be successfully extended to 25 °C, however, our model tends to overpredict for both isoalkanes and aromatic hydrocarbons. For the isoalkanes, RE was greater than 5 % for four compounds – 3-methylpentane, 2,4-dimethylpentane, 2-methylhexane, 2,5-dimethylhexane – and in each case the model overpredicted . This is particularly interesting because the model underpredicts for several isoalkane training compounds. Here the result may reflect the general observation that the model’s RE at 25 °C is smallest for decane (0.0%); the model overpredicts smaller n-alkanes and underpredicts larger n-alkanes. This is a consequence of the training compounds, whose average carbon number is in the range C9 – C10, and the n-alkane structure, which has two CH3 groups and therefore only differs by the number of CH2 groups. For the aromatic hydrocarbons, RE was greater than 5 % for one compound – isobutylbenzene.
Figure 5.
Log values for 29 isoalkanes, 33 aromatic hydrocarbons, and 10 n-alkanes were predicted at 25 °C and compared to log values measured by Martos et al.13 Solid black lines indicate 1:1 correspondence. Solid red lines are regression lines. AAE is 0.08 log units and ARE is 2.3 % for all 72 compounds.
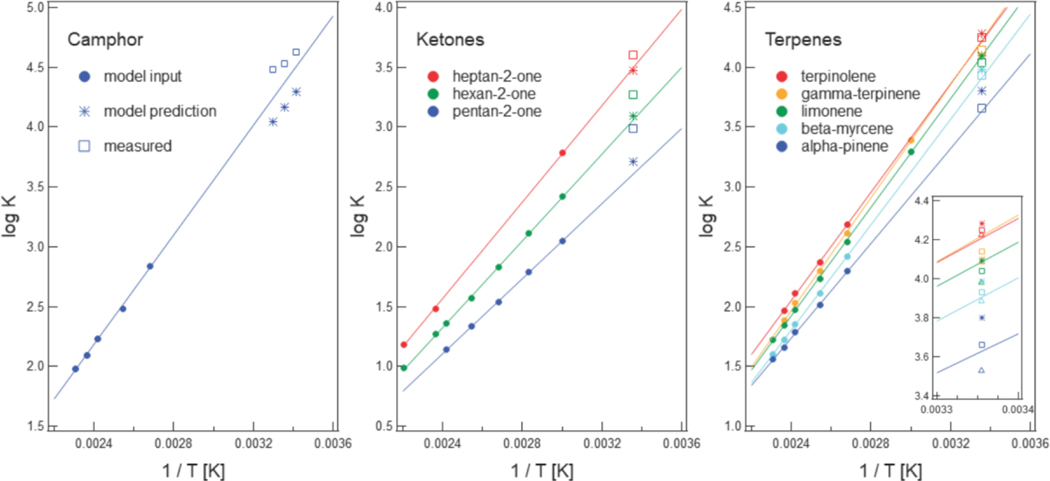
was directly measured at 20 °C to 30 °C by equilibrating PDMS-coated stir bars with headspace vapors of naphthalene and camphor19 and at 25 °C by equilibrating PDMS-coated fibers with aliphatic alcohols, aliphatic ketones and monoterpenes.14,18 Each of these compounds was part of the training data, so several useful comparisons can be made (Fig. 6). Regression lines based on model input (at higher temperatures) indicate that extrapolated log values were consistently lower than measured log values for oxygen-containing compounds. On average, extrapolated values were 8 % lower. In contrast, extrapolated and measured log values for the five monoterpenes were within 2 % of each other. Fig. 6 indicates that the predictive ability of the group contribution model at 25 °C depends on whether extrapolation from higher temperatures is valid. This is true whether values at higher temperatures are measured or predicted. We also predicted log values at 25 °C by combining the predictive equation developed by Sprunger et al.23 with solute descriptors for terpenes.40 Our predictions were consistently larger than predictions from the Sprunger et al. model; both models had the highest absolute error for α-pinene. This limited comparison indicates similar performance by the two approaches.
Figure 6.
Log values for camphor were predicted at 20 °C, 25 °C, and 30 °C (stars) and compared to log values measured by De Coensel et al.19 (open squares) and to log values extrapolated from higher temperatures (solid regression line). Predicted, measured, and extrapolated log values for three ketones and five terpenes are similarly plotted. Measurements by Isidorov et al.14 and Nilsson et al.18 Inset compares log measurements at 25 °C (open squares) to Sprunger et al.’s model23,40 (triangles; AAE is 0.07 log units and ARE is 1.9 %) and our model (stars; AAE is 0.06 log units and ARE is 1.5 %).
values can be calculated from Kovats retention indices at many temperatures; however, the data at any one temperature is limited. For example, our model incorporates training data for nearly 300 compounds at 140 °C, whereas at 60 °C there are fewer than 200 compounds. By incorporating multiple temperatures, the group contribution method developed here increases model input. We further note that Kovats retention indices have been measured for hundreds of hydrocarbons and oxygen-containing organics at one (or perhaps two) temperatures.39 values for such compounds cannot be extrapolated to other temperatures of interest. The quality control check that we implemented in this work only eliminated one compound from the training data. Incorporating such compounds into a future model would further increase model input.
Conclusions
We developed a group contribution model to predict from 20 °C to 200 °C. Our model employs 18 first-order groups to describe the molecular structure of 360 training compounds containing carbon, hydrogen, and oxygen. Predictions at 25 °C for 72 hydrocarbons have an average relative error of 2.3 %. Predictions at 100 °C for 50 C10 validation compounds, including 6 terpenes and 22 terpenoids, have an average relative error of 3.1 %, which is comparable to average relative errors for the alcohol-phenol and aldehyde-ketone-ether classes of training compounds. We are interested in the partitioning of plant-derived terpenoids; additional training compounds with oxygen-containing groups are a priority to improve the model. Ideas for acquiring such compounds were discussed. Our results demonstrate that incorporating the van’t Hoff equation into a predictive group contribution model is a viable approach to estimating at multiple temperatures. The value of this modeling approach lies in its ability to incorporate all available data, which is particularly advantageous for properties with limited experimental values at a single temperature.
Supplementary Material
Acknowledgments
The authors thank the NIST Special Programs Office (SPO) for its financial support of this work. Funding to E. Holland was provided through the Professional Research Experience Program (PREP) partnership between NIST and the University of Colorado at Boulder.
Footnotes
Disclaimer
Certain commercial entities are identified in order to specify experimental procedures as completely as possible. In no case does such identification imply a recommendation or endorsement by the National Institute of Standards and Technology, nor does it imply that any of the entities identified are necessarily the best available for the purpose.
Supporting Information
Document containing IUPAC InChI Keys, R2 values from van’t Hoff plots of log vs. 1/T, carbon number (#C), and classification for 360 training compounds (Table S1); first-order functional group definitions and comparisons to other group contribution models (Table S2); IUPAC InChI Keys, log values at 100 °C, log values at 100 °C, relative error (RE), and classification for 50 validation compounds (Table S3); an example of an error histogram for log − log at 100 °C, and mean error, standard deviation, and number of training compounds as a function of temperature.
References
- 1.Lamplugh A; Harries M; Xiang F; Trinh J; Hecobian A; Montoya LD Occupational exposure to volatile organic compounds and health risks in Colorado nail salons. Environ. Pollut 2019, 249, 518–526. [DOI] [PubMed] [Google Scholar]
- 2.Wilford BH; Harner T; Zhu J; Shoeib M; Jones KC Passive sampling survey of polybrominated diphenyl ether flame retardants in indoor and outdoor air in Ottawa, Canada: implications for sources and exposure. Environ. Sci. Technol 2004, 38, 5312–5318. [DOI] [PubMed] [Google Scholar]
- 3.Wania F; Shen L; Lei YD; Teixeira C; Muir DCG Development and calibration of a resin-based passive sampling system for monitoring persistent organic pollutants in the atmosphere. Environ. Sci. Technol 2003, 37, 1352–1359. [Google Scholar]
- 4.Shoeib M; Harner T. Characterization and comparison of three passive air samplers for persistent organic pollutants. Environ. Sci. Technol 2002, 36, 4142–4151. [DOI] [PubMed] [Google Scholar]
- 5.Okeme JO; Nguyen LV; Lorenzo M; Dhal S; Pico Y; Arrandale VH; Diamond ML Polydimethylsiloxane (silicone rubber) brooch as a personal passive air sampler for semi-volatile organic compounds. Chemosphere 2018, 208, 1002–1007. [DOI] [PubMed] [Google Scholar]
- 6.Kalantzi OI; Alcock RE; Johnston PA; Santillo D; Stringer RL; Thomas GO; Jones KC The global distribution of polychlorinated biphenyls and organochlorine pesticides in butter. Environ. Sci. Technol 2001, 35, 1013–1018. [DOI] [PubMed] [Google Scholar]
- 7.Zhang Z; Pawliszyn J. Headspace solid-phase microextraction. Anal. Chem 1993, 65, 1843–1852. [Google Scholar]
- 8.Steffen A; Pawliszyn J. Determination of liquid accelerants in arson suspected fire debris using headspace solid-phase microextraction. Anal. Comm 1996, 33, 129–131. [Google Scholar]
- 9.Guerra-Diaz P; Gura S; Almirall JR Dynamic planar solid phase microextraction-ion mobility spectrometry for rapid field air sampling and analysis of illicit drugs and explosives. Anal. Chem 2010, 82, 2826–2835. [DOI] [PubMed] [Google Scholar]
- 10.Fan W; Almirall JR High-efficiency headspace sampling of volatile organic compounds in explosives using capillary microextraction of volatiles (CMV) coupled to gas chromatography-mass spectrometry (GC-MS). Anal. Bioanal. Chem 2014, 406, 2189–2195. [DOI] [PubMed] [Google Scholar]
- 11.Hamblin D; Almirall JR Analysis of exhaled breath from cigarette smokers using CMV-GC/MS. Forensic Chem. 2017, 4, 67–74. [Google Scholar]
- 12.Okeme JO; Saini A; Yang C; Zhu J; Smedes F; Klanova J; Diamond ML Calibration of polydimethylsiloxane and XAD-pocket passive air samplers (PAS) for measuring gas- and particle-phase SVOCs. Atmos. Environ 2016, 143, 202–208. [Google Scholar]
- 13.Martos PA; Saraullo A; Pawliszyn J. Estimation of air/coating distribution coefficients for solid phase microextraction using retention indexes from linear temperature-programmed capillary gas chromatography: application to the sampling and analysis of total petroleum hydrocarbons in air. Anal. Chem 1997, 69, 402–408. [DOI] [PubMed] [Google Scholar]
- 14.Isidorov VA; Vinogorova VT Experimental determination and calculation of distribution coefficients between air and fiber with polydimethylsiloxane coating for some groups of organic compounds. J. Chromatogr. A 2005, 1077, 195–201. [DOI] [PubMed] [Google Scholar]
- 15.Okeme JO; Parnis JM; Poole J; Diamond ML; Jantunen LM Polydimethylsiloxane-air partition ratios for semi-volatile organic compounds by GC-based measurement and COSMO-RS estimation: rapid measurements and accurate modelling. Chemosphere 2016, 156, 204–211. [DOI] [PubMed] [Google Scholar]
- 16.Genualdi S; Harner T. Rapidly equilibrating micrometer film sampler for priority pollutants in air. Environ. Sci. Technol 2012, 46, 7661–7668. [DOI] [PubMed] [Google Scholar]
- 17.Isetun S; Nilsson U; Colmsjo A. Evaluation of solid-phase microextraction with PDMS for air sampling of gaseous organophosphate flame retardants and plasticizers. Anal. Bioanal. Chem 2004, 380, 319–324. [DOI] [PubMed] [Google Scholar]
- 18.Nilsson T; Larsen TO; Montanarella L; Madsen JO Application of headspace solid-phase microextraction for the analysis of volatile metabolites emitted by Penicillium species. J. Microbiol. Meth 1996, 25, [Google Scholar]
- 19.De Coensel N; Desmet K; Gorecki T; Sandra P. Determination of polydimethylsiloxane-air partition coefficients using headspace sorptive extraction. J. Chromatogr. A 2007, 1150, 183–189. [DOI] [PubMed] [Google Scholar]
- 20.Kloskowski A; Chrzanowski W; Pilarczyk M; Namiesnik J. Partition coefficients of selected environmentally important volatile organic compounds determined by gas-liquid chromatography with polydimethylsiloxane stationary phase. J. Chem. Thermodynamics 2005, 37, 21–29. [Google Scholar]
- 21.Abraham MH Scales of solute hydrogen-bonding: their construction and application to physicochemical and biochemical processes. Chem. Soc. Rev 1993, 22, 73–83. [Google Scholar]
- 22.Abraham MH; Ibrahim A; Zissimos AM Determination of sets of solute descriptors from chromatographic measurements. J. Chromatogr. A 2004, 1037, 29–47. [DOI] [PubMed] [Google Scholar]
- 23.Sprunger L; Proctor A; Acree WE; Abraham MH Characterization of the sorption of gaseous and organic solutes onto polydimethylsiloxane solid-phase microextraction surfaces using the Abraham model. J. Chromatogr. A 2007, 1175, 162–173. [DOI] [PubMed] [Google Scholar]
- 24.Kamprad I; Goss K-U Systematic investigation of the sorption properties of polyurethane foams for organic vapors. Anal. Chem 2007, 79, 4222–4227. [DOI] [PubMed] [Google Scholar]
- 25.Hayward SJ; Lei YD; Wania F. Sorption of a diverse set of organic chemical vapors on XAD-2 resin: measurement, prediction, and implications for air sampling. Atmos. Environ 2011, 45, 296–302. [Google Scholar]
- 26.Harini M; Adhikari J; Rani KY A review on property estimation methods and computational schemes for rational solvent design: a focus on pharmaceuticals. Ind. Eng. Chem. Res 2013, 52, 6869–6893. [Google Scholar]
- 27.Joback KG; Reid RC Estimation of pure-component properties from group-contributions. Chem. Eng. Comm 1987, 57, 233–243. [Google Scholar]
- 28.Constantinou L; Gani R. New group contribution method for estimating properties of pure compounds. AIChE J. 1994, 40, 1697–1710. [Google Scholar]
- 29.Kolska Z; Ruzicka V; Gani R. Estimation of the enthalpy of vaporization and the entropy of vaporization for pure organic compounds at 298.15 K and at normal boiling temperature by a group contribution method. Ind. Eng. Chem. Res 2005, 44, 8436–8454. [Google Scholar]
- 30.Marrero J; Gani R. Group-contribution based estimation of pure component properties. Fluid Phase Equilibr. 2001, 183–184, 183–208. [Google Scholar]
- 31.Stefanis E; Constantinou L; Panayiotou C. A group-contribution method for predicting pure component properties of biochemical and safety interest. Ind. Eng. Chem. Res 2004, 43, 6253–6261. [Google Scholar]
- 32.Marrero J; Gani R. Group-contribution-based estimation of octanol/water partition coefficient and aqueous solubility. Ind. Eng. Chem. Res 2002, 41, 6623–6633. [Google Scholar]
- 33.Lovestead TM; Bruno TJ Determination of cannabinoid vapor pressures to aid in vapor phase detection of intoxication. Forensic Chem. 2017, 5, 79–85. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Rice S; Koziel JA (2015) Characterizing the smell of marijuana by odor impact of volatile compounds: an application of simultaneous chemical and sensory analysis. PLOS One, 10: e0144160. 10.1371/journal.pone.0144160 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Rice S; Koziel JA The relationship between chemical concentration and odor activity value explains the inconsistency in making a comprehensive surrogate scent training tool representative of illicit drugs. Forens. Sci. Int 2015, 257, 257–270. [DOI] [PubMed] [Google Scholar]
- 36.Wiebelhaus N; Hamblin D; Kreitals NM; Almirall JR Differentiation of marijuana headspace volatiles from other plants and hemp products using capillary microextraction of volatiles (CMV) coupled to gas-chromatography-mass spectrometry (GC-MS). Forensic Chem. 2016, 2, 1–8. [Google Scholar]
- 37.Conder JR; Young CL Physicochemical Measurements by Gas Chromatography. John Wiley & Sons: Chichester, 1979. [Google Scholar]
- 38.Kovats E. Gas chromatographic characterization of organic compounds: retention indices of aliphatic halides, alcohols, aldehydes, and ketones. Helv. Chim. Acta 1958, 41, 1915–1932. [Google Scholar]
- 39.NIST Mass Spectrometry Data Center, Wallace William E., Director, “Retention Indices” in NIST Chemistry WebBook, NIST Standard Reference Database Number 69, Eds. Linstrom PJand Mallard WG, National Institute of Standards and Technology, Gaithersburg, MD: 20899, 10.18434/T4D303 [DOI] [Google Scholar]
- 40.Abraham MH; Gola JRM; Gil-Lostes J; Acree WE; Cometto-Muniz JE Determination of solvation descriptors for terpene hydrocarbons from chromatographic measurements. J. Chromatogr. A 2013, 1293, 133–141. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.