A Tool for Automatic Scoring of Spelling Performance

Abstract

Purpose

The evaluation of spelling performance in aphasia reveals deficits in written language and can facilitate the design of targeted writing treatments. Nevertheless, manual scoring of spelling performance is time-consuming, laborious, and error prone. We propose a novel method based on the use of distance metrics to automatically score spelling. This study compares six automatic distance metrics to identify the metric that best corresponds to the gold standard—manual scoring—using data from manually obtained spelling scores from individuals with primary progressive aphasia.

Method

Three thousand five hundred forty word and nonword spelling productions from 42 individuals with primary progressive aphasia were scored manually. The gold standard—the manual scores—were compared to scores from six automated distance metrics: sequence matcher ratio, Damerau–Levenshtein distance, normalized Damerau–Levenshtein distance, Jaccard distance, Masi distance, and Jaro–Winkler similarity distance. We evaluated each distance metric based on its correlation with the manual spelling score.

Results

All automatic distance scores had high correlation with the manual method for both words and nonwords. The normalized Damerau–Levenshtein distance provided the highest correlation with the manual scoring for both words (r_s = .99) and nonwords (r_s = .95).

Conclusions

The high correlation between the automated and manual methods suggests that automatic spelling scoring constitutes a quick and objective approach that can reliably substitute the existing manual and time-consuming spelling scoring process, an important asset for both researchers and clinicians.

The evaluation and remediation of spelling (written language production) plays an important role in language therapy. Research on poststroke dysgraphia (Buchwald & Rapp, 2004; Caramazza & Miceli, 1990) and on neurodegenerative conditions, such as primary progressive aphasia (PPA), has shown effects of brain damage on underlying cognitive processes related to spelling (Rapp & Fischer-Baum, 2015). For example, spelling data have been shown to facilitate reliable subtyping of PPA into its variants (Neophytou et al., 2019), identify underlying language/cognitive deficits (Neophytou et al., 2019; Sepelyak et al., 2011), monitor the progression of the neurodegenerative condition over time, inform treatment decisions (Fenner et al., 2019), and reliably quantify the effect of spelling treatments (Rapp & Kane, 2002; Tsapkini et al., 2014; Tsapkini & Hillis, 2013).

For spelling treatment and evaluation, spelling-to-dictation tasks are included in language batteries, such as the Johns Hopkins University Dysgraphia Battery (Goodman & Caramazza, 1985) and the Arizona Battery for Reading and Spelling (Beeson et al., 2010). These evaluations can identify the cognitive processes involved in the spelling of both real words and nonwords (pseudowords). Spelling of real words involves access to the speech sounds and to lexicosemantic/orthographic representations stored in long-term memory, whereas nonword spelling requires only the learned knowledge about the relationship between sounds and letters to generate plausible spellings (phonology-to-orthography conversion; Tainturier & Rapp, 2001).

However, the task of scoring spelling errors manually is exceptionally time-consuming, laborious, and error prone. In this research note, we propose to apply automated distance metrics commonly employed in string comparison for the scoring of spelling of both regular words (i.e., words with existing orthography) and nonwords (i.e., words without existing orthography). We used manually scored spelling data for individuals with PPA to evaluate the distance metrics as a tool for assessing spelling performance. The ultimate goal of this work is to provide a tool to clinicians and researchers for automatic spelling evaluation of individuals with spelling disorders, such as PPA and stroke dysgraphia.

Spelling Performance Evaluation: Current Practices

Manual scoring of spelling responses is currently a time-consuming process. The spelling evaluation proposal by Caramazza and Miceli (1990) involves the comparison of an individual's spelling response with the standard spelling of that word, letter by letter. The comparison is based on a set of rules, which consider the addition of new letters that do not exist in the target word, the substitution of letters with others, the deletion of letters, and the movement of letters to incorrect positions within words. There is also a set of rules that account for double letters, such as deleting, moving, substituting, or simplifying a double letter, or doubling what should be a single letter. According to this scoring approach, each letter in the target word is worth 1 point. If the individual's response includes changes such as those listed above, a specified number of points are subtracted from the overall score of the word. For example, if the target word is “cat,” the maximum number of points is 3. If the patient's response is CAP, the word will be scored with 2 out of 3 points because of the substitution of “T” with “P.”

The process applies slightly differently in words and nonwords, given that for nonwords there are multiple possible correct spellings. For instance, for “foit,” both PHOIT and FOIT are plausible spellings and, therefore, should be considered correct. In one approach to scoring nonword spelling, the scorer considers each response separately and selects as the “target” response the option that would maximize the points for that response as long as there is adherence to the phoneme-to-grapheme correspondence rules. Following the example above, if a participant is asked to spell “foit” and they write PHOAT, PHOIT would be chosen as the “intended” target and not FOIT, because PHOIT would assign 4 out of 5 points (i.e., substitute “I” with “A”), while assuming FOIT as the target would only assign 2 out of 4 points (i.e., substitute “I” with “A” and “PH” with “F”). This process assumes that even if two participants get the same nonwords, the target orthographic forms might be different across participants (depending on their responses), and therefore, the total possible points for each nonword might be different across participants. Clearly, when there is more than one error in a response, nonword scoring depends on the clinician's assumptions about the assumed target word, making the process extremely complex. The manual spelling evaluation of spelling performance is currently the gold standard of spelling evaluation, but it is often error prone, takes a lot of time, and requires high interrater reliability scores from at least two clinicians to ensure consistency.

Attempts to automatically evaluate spelling performance have been proposed before. For instance, McCloskey et al. (1994) developed a computer program to identify the different types of letter errors, namely, deletions, insertions, substitutions, transpositions, and nonidentifiable errors. The study has mostly focused on identifying error types rather than error scores. More recently, Ross et al. (2019) devised a hierarchical scoring system that simultaneously evaluates both lexical and sublexical processing. More specifically, this system identifies both lexical and sublexical parameters that are believed to have shaped a given response, and these parameters are matched to certain scores. Scores are coded as S0–S9 and L0–L9 for the sublexical and lexical systems, respectively. Each response gets an S and an L score. This system was first constructed manually and was then automatized with a set of scripts. Undoubtedly, both of these studies provide valuable tools in qualitatively assessing the cognitive measures that underly spelling but rely on complex rules and do not offer a single spelling score for every response, which is the measure that most clinicians need in their everyday practice.

Other studies have used computational connectionist models to describe the underlying cognitive processes of spelling production (Brown & Loosemore, 1994; Bullinaria, 1997; Houghton & Zorzi, 1998, 2003; Olson & Caramazza, 1994), which are often inspired by related research on reading (Seidenberg et al., 1984; Sejnowski & Rosenberg, 1987). These approaches aim to model the functioning of the human brain through the representation of spelling by interconnected networks of simple units and their connections. Although some of this work involves modeling acquired dysgraphia, the aim of these models is not to score spelling errors but rather to determine the cognitive processes that underlie spelling. To the best of our knowledge, there have been no attempts to provide automated single response accuracy values.

Alternative Approaches Using “Distance Functions”

The comparison of different strings and the evaluation of their corresponding differences are commonly carried out using distance metrics, also known as “string similarity metrics” or “string distance functions” (Jurafsky & Martin, 2009). A distance is a metric that measures how close two elements are, where elements can be letters, characters, numbers, and more complex structures such as tables. Such metrics measure the minimum number of alternations, such as insertions, deletions, substitutions, and so on, required to make the two strings identical. For example, to make a string of letters such as “grapheme” and “graphemes” identical, you need to delete the last “s” from “graphemes,” so their distance is 1; to make “grapheme” and “krapheme” identical, you need to substitute “k” with “g”; again, the distance is 1. In many ways, the automatic approach described above is very similar to the manual approach currently being employed for the calculation of spelling, making automatic distance metrics exceptionally suitable for automating spelling evaluation. Commonly employed measures are as follows: sequence matcher ratio, Damerau–Levenshtein distance, normalized Damerau–Levenshtein distance, Jaccard distance, Masi distance, and Jaro–Winkler similarity distance. These measures have many applications in language research, biology (such as in DNA and RNA analysis), and data mining (Bisani & Ney, 2008; Damper & Eastmond, 1997; Ferragne & Pellegrino, 2010; Gillot et al., 2010; Hathout, 2014; Heeringa et al., 2009; Hixon et al., 2011; Jelinek, 1996; Kaiser et al., 2002; Navarro, 2001; Peng et al., 2011; Riches et al., 2011; Schlippe et al., 2010; Schlüter et al., 2010; Spruit et al., 2009; Tang & van Heuven, 2009; Wieling et al., 2012). In a study by Smith et al. (2019), the phonemic edit distance ratio, which is an automatic distance function, was employed to estimate error frequency analysis for evaluating the speech production of individuals with acquired language disorders, such as apraxia of speech and aphasia with phonemic paraphasia, highlighting the efficacy of distance metrics in automating manual measures in the context of language pathology.

The Current Study

The aim of this research note is to propose an automatic spelling scoring methodology that employs distance metrics to generate spelling scores for both real-word and nonword spellings. Therefore, we compared scoring based on the manual spelling scoring method to six established distance metrics: (a) sequence matcher ratio, (b) Damerau–Levenshtein distance, (c) normalized Damerau–Levenshtein distance, (d) Jaccard distance, (e) Masi distance, and (f) Jaro–Winkler similarity distance (see Appendix A for more details). We have selected these methods because they have the potential to provide results that can automate the manual method for scoring of spelling errors using conceptually different approaches. We selected two types of distance metrics in this research note: those that treat words as sets of letters and those that treat words as strings of letters. The sequence matcher ratio (a.k.a. gestalt pattern matching), the Jaccard distance, and the Masi distance compare sets and employ set theory to calculate distance; in a set, a letter can appear only once. On the other hand, the Damerau–Levenshtein distance and the normalized Damerau–Levenshtein distance treat words as strings and are estimating the movements of letters, namely, the insertions, deletions, and substitutions required to make two strings equal. The only difference between these two metrics is that the normalized Damerau–Levenshtein distance calculates transpositions as well. Finally, the Jaro–Winkler similarity distance is a method similar to the Levenshtein distance, but it gives more favorable scores to strings that match from the beginning of the word (see Appendix A for details).

By comparing the outcomes of these metrics to the manual spelling scoring, this study aims to identify the metric that best matches the manual scoring and can therefore be employed to automatically evaluate the spelling of both real words and nonwords. The automated metrics can be employed in the clinic to facilitate spelling evaluation and provide a quantitative approach to spelling scoring that would greatly improve not only speed and efficiency but also consistency relative to current practice.

Method

Participants

Forty-two patients with PPA were administered a test of spelling-to-dictation with both words and nonwords. The patients were recruited over a period of 5 years as part of a clinical trial on the effects of transcranial direct current stimulation in PPA (ClinicalTrials.gov Identifier: NCT02606422). The data evaluated here were obtained from the evaluation phase preceding any treatment. All patients are subtyped into the three PPA variants following the consensus criteria by Gorno-Tempini et al. (2011; see Appendix B).

Data Collection and Scoring

Spelling-to-dictation tasks were administered to 42 patients with PPA to assess patients' spelling performance. Twenty-five patients received a 92-item set (73 words and 19 nonwords), 11 patients received a 138-item set (104 words and 34 nonwords), three patients received a 184-item set (146 words and 38 nonwords), two patients received a 168-item set (134 words and 34 nonwords), and one patient received a 62-item set (54 words and eight nonwords; 4,768 words in total, 3,729 words and 1,039 nonwords). See also Appendix C for the words included in the five sets of words and nonwords.

Manual Scoring

For the manual scoring, we followed the schema proposed by Caramazza and Miceli (1990; see also Tainturier & Rapp, 2003), as summarized in Appendix D. Clinicians identify letter errors (i.e., additions, doublings, movements, substitutions, and deletions), and on that basis, they calculate a final score for each word. The outcome of this scoring is a percentage of correct letters for each word, ranging between 0 and 1, where 0 indicates a completely incorrect response and 1 indicates a correct response. The mean score for words was 0.84 (0.26), and for nonwords, it was 0.78 (0.27). To manually score all the data reported here, the clinician, who was moderately experienced, required approximately 120 hr (about 1–2 min per word), but this time can differ, depending on the experience of clinicians.

To evaluate reliability across scorers (a PhD researcher, a research coordinator, and a clinician), 100 words and 100 nonwords were selected from different patients, and the Spearman correlations of the scorers were calculated. From these 200 selected items, 90% had incorrect spellings, and 10% had correct spellings. As shown in Table 1, real words exhibited higher interscorer correlations compared to nonwords, underscoring the need for a more reliable nonword scoring system.

Table 1.

Correlation statistics between the three manual raters (N = 100).

X	Y	Real words		Nonwords
		rs	p	rs	p
Rater A	Rater B	.93	.0001	.77	.0001
Rater A	Rater C	.95	.0001	.78	.0001
Rater B	Rater C	.97	.0001	.88	.0001

Automated Scoring

The automated scoring consisted of several steps. Both the targets and the responses were transformed into lowercase, and all leading and following spaces were removed. Once the data were preprocessed, we calculated the distance between the target and the response for every individual item. Different approaches were taken for words and nonwords.

• The spelling scoring of words was obtained by comparing the spelling of the target word to that of the written response provided by the participant.

• The spelling scoring of nonwords was estimated by comparing the phonemic transcriptions of the target and the response. To do this, both the target and the response were transcribed into the International Phonetic Alphabet (IPA). To convert words into IPA, we employed eSpeak, which is an open-source software text-to-speech engine for English and other languages, operating on Linux, MacOS, and Windows. The reason we decided to compare the phonetic transcriptions of target and response instead of the spelling directly is that, as indicated in the introduction, nonwords (in English) can potentially have multiple correct orthographic transcriptions yet only one correct phonetic transcription (see example in the Spelling Performance Evaluation: Current Practices section). To simplify string comparison, we removed two symbols from the phonetic transcriptions: the stress symbol /ˈ/ and the length symbol /ː/. For example, using the automated transcription system, a target nonword “feen” is converted to a matching phonemic presentation /fin/ (instead of /fiːn/).

The string comparison process was repeated for each of the six distance metrics described in the introduction, namely, (a) the sequence matcher ratio, (b) the Damerau–Levenshtein distance, (c) the normalized Damerau–Levenshtein distance, (d) the Jaccard distance, (e) the Masi distance, and (f) the Jaro–Winkler similarity distance (see Appendix A). The distance values for each of these metrics are values ranging between 0 and 1. For the sequence matcher ratio, a perfect response is equal to 1, while for the normalized Damerau–Levenshtein distance, the Jaccard distance, the Masi distance, and the Jaro–Winkler similarity distance, a perfect response is equal to 0. The only distance metric that does not have values ranging between 0 and 1 is the Damerau–Levenshtein distance, which provides a count of the changes (e.g., deletions, insertions) required to make two strings equal. The algorithm required less than 1 s to calculate spelling scores for the whole database of words and nonwords.

Method Comparison

Once all the distance metrics were calculated for the entire data set, we estimated their correlation to manual scoring. The output of the comparison was a Spearman's rank correlation coefficient, indicating the extent to which the word accuracy scores correlate. All distance metrics were calculated in Python 3. To calculate correlations and their corresponding significance tests (significance tests for correlations and the resulting p values are calculated using t tests from 0), we employed the Python packages, namely, SciPy (Jones et al., 2001), Pingouin (Vallat, 2018), and pandas (McKinney, 2010).

Results

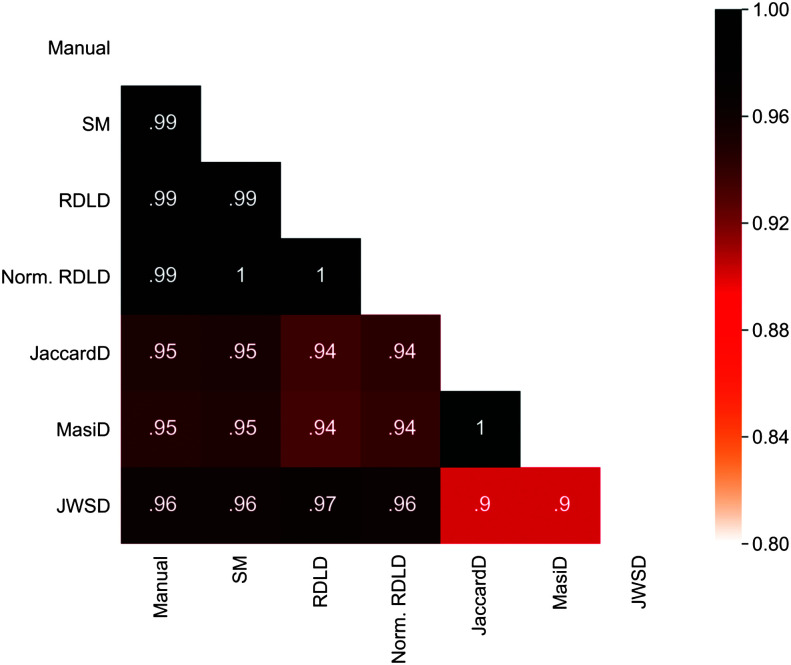
The results of the Spearman correlations between manual and automatic scorings for words and nonwords are shown in Figures 1 and 2 and in Tables 2 and 3, respectively. The first column of the correlation matrix shows the correlations of the manual evaluation with each of the estimated distance metrics. The other columns show the correlations of the automatic distance metrics with one another. For words, the manual scoring and the automated metric scoring provided correlations over .95, which are high correlations. Specifically, there was a high correlation of the normalized Damerau–Levenshtein distance, the Damerau–Levenshtein distance, and the sequence matcher with the manual scoring of spelling productions, r_s (3538) = .99, p = .001, which indicates that distance metrics provide almost identical results to the manual evaluation. There was a slightly lower correlation of the Jaro–Winkler similarity distance with the manual scores, r_s (3538) = .96, p = .001. The Jaccard distance and the Masi distance had the lowest correlations with the manual scoring, r_s (3538) = .95, p = .001.

Figure 1.

Correlation matrix for words. JaccardD = Jaccard distance; JWSD = Jaro–Winkler similarity distance; Manual = manual spelling estimation; MasiD = Masi distance; Norm. RDLD = normalized Damerau–Levenshtein distance; RDLD = Damerau–Levenshtein distance; SM = sequence matcher ratio.

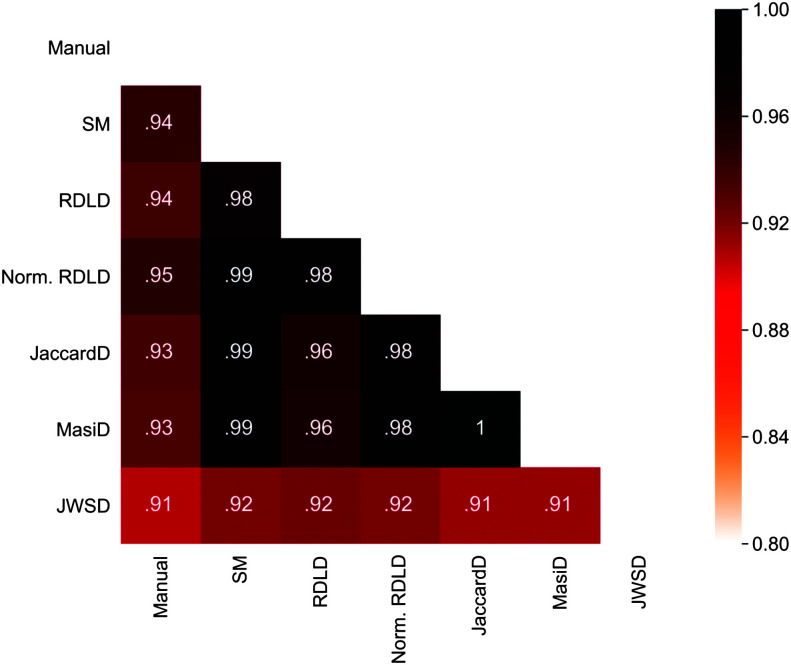
Figure 2.

Correlation matrix for nonwords. JaccardD = Jaccard distance; JWSD = Jaro–Winkler similarity distance; Manual = manual spelling estimation; MasiD = Masi distance; Norm. RDLD = normalized Damerau–Levenshtein distance; RDLD = Damerau–Levenshtein distance; SM = sequence matcher ratio.

Table 2.

Correlation statistics between the manual method and the automatic distance metrics for real words (N = 3,540).

Distancemetric	Correct and incorrect spellings		Incorrect spellings
	rs	95% CI	rs	95% CI
SM	.994*	[.99, .99]	.92*	[.91, .92]
RDLD	−.990*	[−.99, −.99]	−.86*	[−.87, −.84]
Norm. RDLD	−.995*	[−.99, −.99]	−.92*	[-.93, −.91]
JaccardD	−.952*	[−.96, −.95]	−.86*	[−.88, −.85]
MasiD	−.950*	[−.95, −.95]	−.83*	[−.84, −.81]

Note. The table provides correlations of the manual approach with the automated distance metrics on all stimuli (Correct and incorrect spellings; N = 3,540) and correlations of the manual approach and the automated distance metrics based only on spellings that were spelled incorrectly (Incorrect spellings; N = 1,327). Shown in the table are the correlation coefficient (r_s ) and the parametric 95% confidence intervals (CIs) of the coefficient, while the asterisk signifies that p < .0001. In bold is the distance metric with the highest score overall. SM = sequence matcher ratio; RDLD = Damerau–Levenshtein distance; Norm. RDLD = normalized Damerau–Levenshtein distance; JaccardD = Jaccard distance; MasiD = Masi distance.

Table 3.

Correlation statistics between the manual method and the automatic distance metrics of nonwords (N = 987).

Distancemetric	Correct and incorrect spellings		Incorrect spellings
	rs	95% CI	rs	95% CI
SM	.945*	[.94, .95]	.799*	[.77, .81]
RDLD	−.936*	[−.94, −.93]	−.780*	[−.79, −.76]
Norm. RDLD	−.947*	[−.95, −.94]	−.821*	[−.86, −.78]
JaccardD	−.935*	[−.94, −.93]	−.786*	[−.79, −.76]
MasiD	−.933*	[−.94, −.92]	−.778*	[−.78, −.74]

Note. The table provides correlations of the manual approach with the automated distance metrics on all stimuli (Correct and incorrect spellings; N = 987) and correlations of the manual approach and of the automated distance metrics on spellings that were spelled incorrectly (Incorrect spellings; N = 520). Shown in the table are the correlation coefficient (r_s ) and the parametric 95% confidence intervals (CIs) of the coefficient, while the asterisk signifies that p < .0001. In bold is the distance metric with the highest score overall. SM = sequence matcher ratio; RDLD = Damerau–Levenshtein distance; Norm. RDLD = normalized Damerau–Levenshtein distance; JaccardD = Jaccard distance; MasiD = Masi distance.

The normalized Damerau–Levenshtein distance outperformed all other distance metrics on nonwords with r_s (985) = .95, p < .001, followed by the Damerau–Levenshtein distance and sequence matcher ratio that correlated with the manual estimate of spelling with r_s (985) = .94, p < .001, for both. The Jaccard distance and the Masi distance had correlations of r_s (985) = .93, p < .001, and finally, the Jaro–Winkler similarity distance had the lowest correlation for nonwords, with a value of r_s (985) = .91, p < .001. Importantly, for the normalized Damerau–Levenshtein distance, which outperforms the other distance metrics, if we remove the correct cases from the data set (the items on which participants scored 100%), the correlation remains very high with r_s (3538) = .92 (see Table 2) for words and r_s (985) = .82 for nonwords (see Table 3).

Discussion

This study aimed to provide a tool for scoring spelling performance automatically by identifying a measure that corresponds closely to the current gold standard for spelling evaluation, the manual letter-by-letter scoring of spelling performance (Caramazza & Miceli, 1990). We compared six distance functions that measure the similarity of strings of letters previously used in other scientific fields for estimating distances of different types of sequences (e.g., sequencing DNA and in computational linguistics). The results showed that all six automated measures had very high correlations with the manual scoring for both words and nonwords. However, the normalized Damerau–Levenshtein distance, which had a .99 correlation with the manual scores for words and .95 correlation with the manual scores for nonwords, outperformed the other distance metrics. An important reason for the high correlation between the normalized Damerau–Levenshtein distance and the manual method is the fact that it considers all four types of errors, namely, deletions, insertions, substitutions, and transpositions, whereas the simple Damerau–Levenshtein distance calculates only deletions, insertions, and substitutions (see Appendix A for more details on the two methods). Therefore, the findings provide good support for using the normalized Damerau–Levenshtein distance as a substitute for the manual process for scoring spelling performance. An important advantage of this method over the manual methods is that it provides objective measures of spelling errors. The present tool will facilitate the evaluation of written language impairments and their treatment in PPA and in other patient populations.

A key characteristic of the approach employed for the scoring of words and nonwords is that both types of items are treated as sequences of strings. The evaluation algorithm provides a generic distance that can be employed to score both words and nonwords. The only difference in evaluating spelling performance in words and nonwords is that, as nonwords do not have a standard orthographic representation, rather, they can be transcribed in multiple different ways that are all considered to be correct. As discussed earlier, this is because, in English orthography, different characters and sequences of characters may be used to represent the same sound (e.g., /s/ can be represented as 〈ps〉 in psychology, 〈s〉 in seen, and 〈sc〉 in scene). Also, as shown by the interrater reliability check, for real words, the correlations were high between the three manual scorers, but for nonwords, the correlations were lower. This further highlights the need for a more efficient and consistent way of scoring nonwords.

With the innovative inclusion of IPA transcription to represent nonwords phonemically, we have provided a unitary algorithm that can handle both words and nonwords. For nonwords, once the targets and responses were phonemically transcribed, we estimated their distance in the same fashion as we estimated the distance between targets and responses for real words. For example, if the target word is KANTREE, eSpeak will provide the IPA form /kantɹi/. If the patient transcribed the word as KINTRA, the proposed approach will compare /kantɹi/ to /kɪntɹə/. An advantage of using IPA is that it provides consistent phonemic representations of nonwords. This approach contrasts with the challenges faced in manual scoring to estimate the errors for nonwords that can be orthographically represented in multiple ways. In these cases, clinicians have to identify the target representation that the patient probably had in mind so that the scoring is “fair.” For instance, in the manual approach, if the target word is FLOPE and the patient wrote PHLAP, a clinician may not compare the word to the target word FLOPE but to a presumed target PHLOAP, as this is orthographically closer to the response. This would give a score of 5/6. However, a different clinician may compare this response to PHLOPE and provide a different score, specifically, 4/6 (see also the Alternative Approaches Using “Distance Functions” section for discussion). As a result, each scorer's selection of a specific intended target can influence the scoring by enabling a different set of available options for the spelling of the targets. This clearly poses additional challenges for manual scoring of nonword spelling responses.

The phonemic transcription of nonwords generates a single pronunciation of a spelled word that was produced using grapheme to pronunciation rules of English, without accessing the lexicon. The pronunciation rules prioritize the most probable pronunciation given the context in which a letter appears (i.e., what letters precede and follow a given letter). What is novel about the proposed approach is that it does not require generating an “intended target.” Instead, the patients' actual response is converted to IPA and compared to the IPA of the target. If the IPA transcription of the target nonword and the transcription of the response match on their pronunciation, the response is considered correct. Since the IPA transcription always provides the same representation for a given item, without having to infer a participant's intended target, the algorithm produces a consistent score, which we consider a valuable benefit of the proposed approach.

The pronunciation rules convert an orthographic item to the most probable pronunciation transcription. For example, the nonwords KANTREE, KANTRY, or KANTRI will all be transcribed by the program into /kæntɹi/, and all of these spellings would be scored as correct. However, a less straightforward example is when, for instance, for the stimulus /raInt/, a patient writes RINT. A clinician might choose to score this as correct based on the writing of the existing word PINT /paInt/. On the other hand, the automated algorithm will transcribe RINT into /rInt/ and mark this as an error. However, because such cases are ambiguous, they could also create discrepancies between clinicians. However, because the automated algorithm provides consistent phonemic representation for every item, it eliminates discrepancies that might occur between different clinicians and in human scoring in general, helping to offset the discrepancies between manual and automated scoring.

A problem that might arise is the generalizability of the algorithm for patients and clinicians with different English accents, which may lead to different spellings. Some of these cases can be addressed by selecting the corresponding eSpeak pronunciation when using the algorithm. For example, the system already includes pronunciations for Scottish English, Standard British English (received pronunciation), and so on, and further pronunciation dictionaries can be added. However, in future work and especially when this automated method is used in areas of the world with distinct dialects, the target items can be provided in IPA format as well, especially for the nonwords.

Lastly, it is important to note that, for the purpose of demonstrating this new methodology, this study used the spelling data from individuals with PPA. However, tests evaluating spelling performance are currently being employed across a broad variety of patient populations, including children with language disorders, as well as adults with stroke-induced aphasia and acquired neurogenic language disorders. Therefore, the proposed method can be employed to estimate spelling performance across a range of different populations, for a variety of different purposes.

A limitation of the automated method described here is that it provides item-specific scores, but it does not identify error types, for example, it does not identify semantic and phonologically plausible errors. For instance, if the target is “lion” but the response is TIGER, then this is a semantic substitution error. On the other hand, if the target is “lion” but the response is LAION, then this is a phonologically plausible error. Although this labeling is not provided by the scoring algorithm as currently configured, it can be a useful feature to implement both in clinical and research work (Rapp & Fischer-Baum, 2015). Error type labeling such as this can extend this work even further, adding to the value of this new tool, and it thus constitutes important direction for future research.

Conclusions

The aim of this study has been to provide an objective method for scoring spelling performance that can be used both in clinical and research settings to replace the current manual spelling scoring process, which is both time-consuming and laborious. We obtained spelling scorings using several automatic distance metrics and evaluated their efficiency by calculating their correlations with manual scoring. Our findings showed that the normalized Damerau–Levenshtein distance provides scores very similar to manual scoring for both words and nonwords, with .99 and .95 correlations, respectively, and can thus be employed to automate the scoring of spelling. For words, this distance is estimated by comparing the orthographic representation of the target and the response, while for nonwords, the distance is calculated by comparing the phonemic, IPA-transcribed representation of both the target and response. Finally, it is important to note that, while the manual scoring for a data set of the size discussed here can take many hours to complete, the automated scoring can be completed in less than 1 s. These results provide the basis for developing a useful tool for the clinicians and the researchers to evaluate spelling performance accurately and efficiently.

Appendix A

Distance Metrics

1. The sequence matcher ratio proposed by Ratcliff and Metzener (1988) provides the similarity of two strings as the number of matching characters divided by the total number of characters in the two strings. It recursively identifies common characters in the longest common substring (a.k.a. longest common subsequence) and the characters in the string without matched characters preceding or following the longest common subsequence.

2. The Damerau–Levenshtein distance calculates the minimal number of insertions, deletions, and substitutions required to make two strings equal. The Levenshtein function lev _a,b (i, j) between two strings a and b is the distance between an i-symbol prefix (initial substring) of string a and a j-symbol prefix of b. Levenshtein distance is symmetric so that 0 ≤ lev(a, b) ≤ max(|a|, |b|). Therefore, the Levenshtein distance between two strings a, b (of length |a| and |b|, respectively) is given by lev _{a, b} (|a|, |b|), where

$${\mathrm{lev}}_{a,b}\left(i,j\right)=\left\{\begin{array}{ll}max\left(i,j\right)& \text{if}min\left(i,j\right)=0,\\ min\left\{\begin{array}{l}{\mathrm{lev}}_{a,b}\left(i-1,j\right)+1\\ {\mathrm{lev}}_{a,b}\left(i,j-1\right)+1\\ {\mathrm{lev}}_{a,b}\left(i-1,j-1\right)+1_{\left(a_i\ne {\mathit{b}}_{\mathit{j}}\right)}\end{array}\right.& \text{otherwise},\end{array}\right.$$ (1)

where $1_{\left(a_i\ne b_j\right)}$ is the indicator function equal to 0 when a_i = b_j and equal to 1 otherwise and lev _{a, b} (i, j) is the distance between the first i characters of a and the first j characters of b. The first element (lev _{a, b} (i − 1, j) + 1) in the minimum corresponds to deletion (from a to b), the second (lev _{a, b} (i, j − 1) + 1) corresponds to insertion, and the third to match (lev _{a, b} (i − 1, j − 1) + 1) or mismatch, depending on whether the respective symbols are the same.

3. Normalized Damerau–Levenshtein distance extends the basic Levenshtein distance described above by adding transposition as an operation in addition to insertions, deletions, and substitutions. The normalized Damerau–Levenshtein distance provides the Damerau–Levenshtein distance divided by the number of characters of the longest string in characters. The Damerau–Levenshtein function dlev _a,b (i, j) between two strings a and b is the distance between an i-symbol prefix (initial substring) of string a and a j-symbol prefix of b. The “restricted distance” function is defined recursively as follows:

$${\text{dlev}}_{a,b}\left(i,j\right)=min\left\{\begin{array}{ll}0& \text{if}i=j=0\\ {\text{dlev}}_{a,b}\left(i-1,j\right)+1& \text{if}i>0\\ {\text{dlev}}_{a,b}\left(i,j-1\right)+1& \text{if}j>0\\ {\text{dlev}}_{a,b}\left(i-1,j-1\right)+1_{\left(a_i\ne b_j\right)}& \text{if}i,j>0\\ {\text{dlev}}_{a,b}\left(i-2,j-2\right)+1& \text{if}i,j>1\text{and}a\left[i\right]=b\left[j-1\right]\text{and}a\left[i-1\right]=b\left[j\right]\end{array}\right.$$ (2)

where $1_{\left({\mathit{a}}_{\mathit{i}}\ne {\mathit{b}}_{\mathit{j}}\right)}$ is equal to 0 when a_i = b_j and equal to 1 otherwise.

As in the Damerau–Levenshtein distance, the elements in the minimum match one of the following processes:

1. A deletion (from a to b) is denoted by dlev _a,b (i − 1, j) + 1.

2. An insertion (from a to b) is denoted by dlev _a,b (i, j − 1) + 1.

3. A (mis)match is denoted by dlev _a,b (i − 1, j − 1) + $1_{\left({\mathit{a}}_{\mathit{i}}\ne {\mathit{b}}_{\mathit{j}}\right)}$

4. A transposition is denoted by dlev _a,b (i − 2, j − 2) + 1.

4. The Jaccard distance is defined as the ratio of the size of the symmetric difference ((A ∪ B) − (A ∩ B)); the symmetric difference is the set of elements that are in either of the sets and not in the intersection of the two sets. The Jaccard distance calculates the dissimilarity between sets, and it is estimated by calculating the intersection over the union (a.k.a. Jaccard similarity coefficient), which is the division of the difference of the sizes of the union and the intersection of two sets by the size of the union and then subtracting the intersection over the union from 1.

$$d_J\left(A,B\right)=1-J\left(A,B\right)=\frac{\mid A\cup B\mid -\mid A\cap B\mid }{\mid A\cup B\mid }$$ (3)

5. The Masi distance is measuring the agreement on items of sets (Passonneau, 2006). Like the Jaccard distance, the Masi distance compares sets, rather than a string of characters. To estimate the Masi distance, the length of the intersection of strings a and b (a ∩ b) and the length of the union of string a and b (a ∪ b) are estimated.

$$\text{dmasi}\left(a,b\right)=1-\frac{\text{lengthof}a\cap b}{\text{lengthof}a\cup b}\ast \text{score}$$ (4)

The score value is estimated as follows:

• If the length of string a is equal to string b and to the length of a ∩ b, then the score is equal to 1.

• If the length of a ∩ b is equal to the smallest string (a or b), then the score is 0.67.

• Else if the length of the intersection is greater than 0, then the score is 0.33.

• If nothing holds, then the score is 0.

Appendix B

Demographic and Neuropsychological Data on the Participants

Variant	Gender	Education (years)	Age	Years from disease onset	Language severity a	Overall severity b
nfvPPA = 10 lvPPA = 17 svPPA = 6 mixed = 9	F = 18 M = 24	M = 13.4 (SD = 7)	M = 67.1 (SD = 6.9)	M = 4.4 (SD = 2.9)	M = 1.8 (SD = 0.9)	M = 6.6 (SD = 4.9)

Note. nfvPPA = nonfluent variant primary progressive aphasia; lvPPA = logopenic variant primary progressive aphasia; svPPA = semantic variant primary progressive aphasia.

^a Language severity was measured with the Frontotemporal Dementia Clinical Dementia Rating (FTD-CDR Language subscale; see Knopman et al., 2008; range: 0–3).

^b Overall severity was measured with the FTD-CDR Language subscale (see Knopman et al., 2008)—rating (FTD-CDR “sum of boxes”; see Knopman et al., 2008; range: 0–24).

Appendix C

Five Sets of Words and Nonwords Evaluated in the Study

184-set		168-set		138-set		92-set		62-set
target	type	target	type	target	type	target	type	target	type
REMMUN	nonword	MURNEE	nonword	MURNEE	nonword	REMMUN	nonword	REMMUN	nonword
MUSHRAME	nonword	HERM	nonword	HERM	nonword	MUSHRAME	nonword	MUSHRAME	nonword
SARCLE	nonword	DONSEPT	nonword	DONSEPT	nonword	SARCLE	nonword	SARCLE	nonword
TEABULL	nonword	MERBER	nonword	MERBER	nonword	TEABULL	nonword	TEABULL	nonword
HAYGRID	nonword	TROE	nonword	TROE	nonword	HAYGRID	nonword	HAYGRID	nonword
CHENCH	nonword	PYTES	nonword	PYTES	nonword	CHENCH	nonword	CHENCH	nonword
MURNEE	nonword	FOYS	nonword	FOYS	nonword	MURNEE	nonword	MURNEE	nonword
REESH	nonword	WESSEL	nonword	WESSEL	nonword	REESH	nonword	REESH	nonword
BOKE	nonword	FEEN	nonword	FEEN	nonword	BOKE	nonword	BOKE	nonword
HERM	nonword	SNOY	nonword	SNOY	nonword	HERM	nonword	HERM	nonword
HANNEE	nonword	PHLOKE	nonword	PHLOKE	nonword	HANNEE	nonword	HANNEE	nonword
DEWT	nonword	DEWT	nonword	DEWT	nonword	DEWT	nonword	DEWT	nonword
KWINE	nonword	GHURB	nonword	GHURB	nonword	KWINE	nonword	KWINE	nonword
DONSEPT	nonword	PHOIT	nonword	PHOIT	nonword	DONSEPT	nonword	DONSEPT	nonword
PHOIT	nonword	HAYGRID	nonword	HAYGRID	nonword	PHOIT	nonword	PHOIT	nonword
KANTREE	nonword	KROID	nonword	KROID	nonword	KANTREE	nonword	KANTREE	nonword
LORN	nonword	KITTUL	nonword	KITTUL	nonword	LORN	nonword	LORN	nonword
FEEN	nonword	BRUTH	nonword	BRUTH	nonword	FEEN	nonword	FEEN	nonword
SKART	nonword	KANTREE	nonword	KANTREE	nonword	SKART	nonword	SKART	nonword
REMMUN	nonword	BERK	nonword	BERK	nonword	SHOOT	word	ENOUGH	word
MUSHRAME	nonword	WUNDOE	nonword	WUNDOE	nonword	HANG	word	FRESH	word
SARCLE	nonword	SARCLE	nonword	SARCLE	nonword	PRAY	word	QUAINT	word
TEABULL	nonword	SORTAIN	nonword	SORTAIN	nonword	SHAVE	word	FABRIC	word
HAYGRID	nonword	LORN	nonword	LORN	nonword	KICK	word	CRISP	word
CHENCH	nonword	BOKE	nonword	BOKE	nonword	CUT	word	PURSUIT	word
MURNEE	nonword	TEABULL	nonword	TEABULL	nonword	SPEAK	word	STREET	word
REESH	nonword	HANNEE	nonword	HANNEE	nonword	ROPE	word	PRIEST	word
BOKE	nonword	KWINE	nonword	KWINE	nonword	DEER	word	SUSPEND	word
HERM	nonword	REMMUN	nonword	REMMUN	nonword	CANE	word	BRISK	word
HANNEE	nonword	SUME	nonword	SUME	nonword	LEAF	word	SPOIL	word
DEWT	nonword	SKART	nonword	SKART	nonword	DOOR	word	RIGID	word
KWINE	nonword	REESH	nonword	REESH	nonword	ROAD	word	RATHER	word
DONSEPT	nonword	MUSHRAME	nonword	MUSHRAME	nonword	BOOK	word	MOMENT	word
PHOIT	nonword	CHENCH	nonword	CHENCH	nonword	BALL	word	HUNGRY	word
KANTREE	nonword	SHOOT	word	DECIDE	word	SEW	word	PIERCE	word
LORN	nonword	HANG	word	GRIEF	word	KNOCK	word	LISTEN	word
FEEN	nonword	PRAY	word	SPEND	word	SIEVE	word	GLOVE	word
SKART	nonword	SHAVE	word	LOYAL	word	SEIZE	word	SINCE	word
SHOOT	word	KICK	word	RATHER	word	GAUGE	word	BRING	word
HANG	word	CUT	word	PREACH	word	SIGH	word	ARGUE	word
PRAY	word	SPEAK	word	FRESH	word	LAUGH	word	BRIGHT	word
SHAVE	word	ROPE	word	CONQUER	word	CHOIR	word	SEVERE	word
KICK	word	DEER	word	SHALL	word	AISLE	word	CARRY	word
CUT	word	CANE	word	SOUGHT	word	LIMB	word	AFRAID	word
SPEAK	word	LEAF	word	THREAT	word	HEIR	word	WHAT	word
ROPE	word	DOOR	word	ABSENT	word	TONGUE	word	STARVE	word
DEER	word	ROAD	word	SPEAK	word	SWORD	word	MEMBER	word
CANE	word	BOOK	word	ENOUGH	word	GHOST	word	TALENT	word
LEAF	word	BALL	word	CAREER	word	EARTH	word	UNDER	word
DOOR	word	SEW	word	CHURCH	word	ENOUGH	word	LENGTH	word
ROAD	word	KNOCK	word	BRIGHT	word	FRESH	word	BORROW	word
BOOK	word	SIEVE	word	ADOPT	word	QUAINT	word	SPEAK	word
BALL	word	SEIZE	word	STRICT	word	FABRIC	word	FAITH	word
SEW	word	GAUGE	word	LEARN	word	CRISP	word	STRICT	word
KNOCK	word	SIGH	word	QUAINT	word	PURSUIT	word	HAPPY	word
SIEVE	word	LAUGH	word	BECOME	word	STREET	word	GRIEF	word
SEIZE	word	CHOIR	word	STRONG	word	PRIEST	word	ABSENT	word
GAUGE	word	AISLE	word	BUGLE	word	SUSPEND	word	POEM	word
SIGH	word	LIMB	word	STARVE	word	BRISK	word	THOUGH	word
LAUGH	word	HEIR	word	DENY	word	SPOIL	word	GREET	word
CHOIR	word	TONGUE	word	LENGTH	word	RIGID	word	PROVIDE	word
AISLE	word	SWORD	word	PILLOW	word	RATHER	word	WINDOW	word
LIMB	word	GHOST	word	CAUGHT	word	MOMENT	word
HEIR	word	EARTH	word	BEFORE	word	HUNGRY	word
TONGUE	word	DECIDE	word	AFRAID	word	PIERCE	word
SWORD	word	GRIEF	word	BODY	word	LISTEN	word
GHOST	word	SPEND	word	HUNGRY	word	GLOVE	word
EARTH	word	LOYAL	word	COLUMN	word	SINCE	word
ENOUGH	word	RATHER	word	THESE	word	BRING	word
FRESH	word	PREACH	word	STRIPE	word	ARGUE	word
QUAINT	word	FRESH	word	MUSIC	word	BRIGHT	word
FABRIC	word	CONQUER	word	CRISP	word	SEVERE	word
CRISP	word	SHALL	word	HURRY	word	CARRY	word
PURSUIT	word	SOUGHT	word	PIERCE	word	AFRAID	word
STREET	word	THREAT	word	TINY	word	WHAT	word
PRIEST	word	ABSENT	word	ARGUE	word	STARVE	word
SUSPEND	word	SPEAK	word	DIGIT	word	MEMBER	word
BRISK	word	ENOUGH	word	COMMON	word	TALENT	word
SPOIL	word	CAREER	word	ANNOY	word	UNDER	word
RIGID	word	CHURCH	word	STREET	word	LENGTH	word
RATHER	word	BRIGHT	word	COULD	word	BORROW	word
MOMENT	word	ADOPT	word	RIGID	word	SPEAK	word
HUNGRY	word	STRICT	word	OFTEN	word	FAITH	word
PIERCE	word	LEARN	word	BRING	word	STRICT	word
LISTEN	word	QUAINT	word	LISTEN	word	HAPPY	word
GLOVE	word	BECOME	word	FIERCE	word	GRIEF	word
SINCE	word	STRONG	word	NATURE	word	ABSENT	word
BRING	word	BUGLE	word	UNDER	word	POEM	word
ARGUE	word	STARVE	word	MOTEL	word	THOUGH	word
BRIGHT	word	DENY	word	SHOULD	word	GREET	word
SEVERE	word	LENGTH	word	VULGAR	word	PROVIDE	word
CARRY	word	PILLOW	word	CHEAP	word	WINDOW	word
AFRAID	word	CAUGHT	word	SPOIL	word
WHAT	word	BEFORE	word	CERTAIN	word
STARVE	word	AFRAID	word	ABOVE	word
MEMBER	word	BODY	word	LOUD	word
TALENT	word	HUNGRY	word	SINCE	word
UNDER	word	COLUMN	word	SLEEK	word
LENGTH	word	THESE	word	REVEAL	word
BORROW	word	STRIPE	word	BOTH	word
SPEAK	word	MUSIC	word	NOISE	word
FAITH	word	CRISP	word	INTO	word
STRICT	word	HURRY	word	STRANGE	word
HAPPY	word	PIERCE	word	CARRY	word
GRIEF	word	TINY	word	SOLVE	word
ABSENT	word	ARGUE	word	OCEAN	word
POEM	word	DIGIT	word	DECENT	word
THOUGH	word	COMMON	word	THOUGH	word
GREET	word	ANNOY	word	SHORT	word
PROVIDE	word	STREET	word	ABOUT	word
WINDOW	word	COULD	word	BOTTOM	word
SHOOT	word	RIGID	word	FRIEND	word
HANG	word	OFTEN	word	LOBSTER	word
PRAY	word	BRING	word	VIVID	word
SHAVE	word	LISTEN	word	BROAD	word
KICK	word	FIERCE	word	WHILE	word
CUT	word	NATURE	word	CHILD	word
SPEAK	word	UNDER	word	HAPPEN	word
ROPE	word	MOTEL	word	SEVERE	word
DEER	word	SHOULD	word	AFTER	word
CANE	word	VULGAR	word	PRIEST	word
LEAF	word	CHEAP	word	MERGE	word
DOOR	word	SPOIL	word	GLOVE	word
ROAD	word	CERTAIN	word	ONLY	word
BOOK	word	ABOVE	word	GREET	word
BALL	word	LOUD	word	MEMBER	word
SEW	word	SINCE	word	BEGIN	word
KNOCK	word	SLEEK	word	BRISK	word
SIEVE	word	REVEAL	word	WHAT	word
SEIZE	word	BOTH	word	BORROW	word
GAUGE	word	NOISE	word	JURY	word
SIGH	word	INTO	word	SLEEVE	word
LAUGH	word	STRANGE	word	BOUGHT	word
CHOIR	word	CARRY	word	HAPPY	word
AISLE	word	SOLVE	word	SPACE	word
LIMB	word	OCEAN	word	ANGRY	word
HEIR	word	DECENT	word	THOSE	word
TONGUE	word	THOUGH	word	FAITH	word
SWORD	word	SHORT	word
GHOST	word	ABOUT	word
EARTH	word	BOTTOM	word
ENOUGH	word	FRIEND	word
FRESH	word	LOBSTER	word
QUAINT	word	VIVID	word
FABRIC	word	BROAD	word
CRISP	word	WHILE	word
PURSUIT	word	CHILD	word
STREET	word	HAPPEN	word
PRIEST	word	SEVERE	word
SUSPEND	word	AFTER	word
BRISK	word	PRIEST	word
SPOIL	word	MERGE	word
RIGID	word	GLOVE	word
RATHER	word	ONLY	word
MOMENT	word	GREET	word
HUNGRY	word	MEMBER	word
PIERCE	word	BEGIN	word
LISTEN	word	BRISK	word
GLOVE	word	WHAT	word
SINCE	word	BORROW	word
BRING	word	JURY	word
ARGUE	word	SLEEVE	word
BRIGHT	word	BOUGHT	word
SEVERE	word	HAPPY	word
CARRY	word	SPACE	word
AFRAID	word	ANGRY	word
WHAT	word	THOSE	word
STARVE	word	FAITH	word
MEMBER	word
TALENT	word
UNDER	word
LENGTH	word
BORROW	word
SPEAK	word
FAITH	word
STRICT	word
HAPPY	word
GRIEF	word
ABSENT	word
POEM	word
THOUGH	word
GREET	word
PROVIDE	word
WINDOW	word

Note. Set 1: 184 items, Set 2: 168 items, Set 3: 138 items, Set 4: 92 items, and Set 5: 62 items.

Appendix D

Instructions for Manual Scoring

Values are assigned to letters in the target, not the response. For nonwords, use the target spelling that maximizes points for given response.

Each letter of the target word is assigned a value between 0 and 1, with the general guidelines being:

• any letter that is present and in the correct position (relative, not absolute) gets 1 point;

• any letter that is present but in the incorrect position gets 0.5 points;

• any letter that is not present gets 0 points.

To determine the value:

1. Maximally align the target item and the response.

2. If the response is correct, give each target letter a value of 1.

3. If the response is incorrect, score depending upon error type:

   a. ADDITION: give each of the letters that allow the addition (i.e., the letters adjacent to the added letter) a value of 0.5.

   b. SUBSTITUTION: give the letter that is substituted a value of 0.

   c. DELETION: give the letter that is deleted a value of 0.

   d. TRANSPOSITION: give a value of 0.5 to each transposed letter.

   e. MOVEMENT: give value of 0.5 to the moved letter.

   f. DOUBLING: give a value of 0.5 to doubled letter.

   g. DELETION OF DOUBLE LETTER: give a value of 0.5 to both letters of double.

   h. MOVEMENT OF GEMINATE: give a value of 0.75 to both letters of geminate and a value of 0.5 to the letter the geminate moved to.

   i. SUBSTITUTION/DELETION COMBINATION: give a value of 0 to missing letters.

   j. SUBSTITUTION/ADDITION COMBINATION: give 0 to incorrect letter and 0.75 to surrounding letters.

Funding Statement

This study was supported by the Science of Learning Institute at Johns Hopkins University and National Institute on Deafness and Other Communication Disorders Grant R01 DC014475 (to Kyrana Tsapkini).