Abstract
Background:
Transcranial Magnetic Stimulation (TMS) is a widely used non-invasive brain stimulation method. However, its mechanism of action and the neural response to TMS are still poorly understood. Multi-scale modeling can complement experimental research to study the subcellular neural effects of TMS. At the macroscopic level, sophisticated numerical models exist to estimate the induced electric fields. However, multi-scale computational modeling approaches to predict TMS cellular and subcellular responses, crucial to understanding TMS plasticity inducing protocols, are not available so far.
Objective:
We develop an open-source multi-scale toolbox Neuron Modeling for TMS (NeMo-TMS) to address this problem.
Methods:
NeMo-TMS generates accurate neuron models from morphological reconstructions, couples them to the external electric fields induced by TMS, and simulates the cellular and subcellular responses of single-pulse and repetitive TMS.
Results:
We provide examples showing some of the capabilities of the toolbox.
Conclusion:
NeMo-TMS toolbox allows researchers a previously not available level of detail and precision in realistically modeling the physical and physiological effects of TMS.
Keywords: transcranial magnetic stimulation, electric field simulation, neuron compartmental modeling, calcium simulation, three-dimensional reconstructions, synaptic plasticity, dendrites
Introduction
Transcranial Magnetic Stimulation (TMS) is a popular non-invasive brain stimulation method to safely modulate brain activity in the human brain. TMS generates a strong magnetic field by passing a transient current through a magnetic coil [1]. This time-varying magnetic field crosses the skull and induces an electric field which can depolarize neurons in the underlying brain areas [2]. TMS is used both in research and clinical applications for neuropsychiatric and neurological disorders [3]. Despite the growing use of TMS, there is still a lack of understanding of its mechanism of action.
Direct in vivo recordings of neural activity in rodents and non-human primates have led to key insights into TMS mechanisms [4–8]. However, due to differences in brain structure and functional neuroanatomy compared to humans, great care has to be taken when translating findings across species to account for dosing, coil placement and other parameters [9]. Besides in vivo animal studies, in vitro experiments in hippocampal slice cultures have been instrumental for our understanding of cellular and molecular mechanisms of TMS [10–13]. In vitro preparations allow studying the effects of TMS on a single neuron basis in detail, however, as for animal studies, translating findings to humans needs mindful assessment.
Computational modeling is a key tool to complement experimental studies to investigate TMS mechanisms. Computational models can provide a framework to understand experimental results as well as allow efficient screening of a large range of stimulation parameters. Most TMS modeling studies have focused on the spatial distribution of TMS-induced electric fields in the brain [14–19]. These studies have been successful in predicting TMS stimulation regions and guiding TMS targeting for human experiments. However, they are limited in expanding our understanding of the TMS physiological response which depends on a variety of factors such as neuron type, electric field orientation, and ongoing activity [20,21]. Consequently, there has been a growing interest in developing neuron models to predict the physiological outcome of TMS.
In early modeling work, the effects of magnetic stimulation on elongated cables representing axonal tracts were studied [16,22–25]. More recent work [26–32] used more realistic neuronal geometries. Aberra and colleagues [33] highlighted the need to include realistic axonal reconstructions and myelination to more accurately predict neuronal responses. These studies have commonly focused on single-pulse TMS. However, for clinical applications, TMS is applied repeatedly in specific temporal patterns (repetitive TMS [rTMS]). Also, these rTMS protocols are designed to induce neural plasticity that is guided by several subcellular processes including somatic and dendritic calcium accumulation [34–36]. Despite the importance of rTMS-induced plasticity on intracellular calcium signaling pathways [10,13,37], subcellular calcium-dependent processes have only been incorporated in computational models of TMS utilizing mean-field theory [38–40] where volume averaged effects such as mean calcium concentration are modeled. However, it is important to spatially resolve the intracellular processes in the models.
To address the limitations of available TMS models, we developed a multi-scale modeling toolbox coupling TMS electric fields with anatomically and biophysically realistic neuron models, and their intracellular calcium signaling. TMS multi-scale modeling requires the detailed knowledge of a broad range of computational tools, and so far, no such toolboxes exist. Here, we describe a newly developed Neuron Modeling for TMS (NeMo-TMS) pipeline that allows simulating and visualizing realistic multi-scale models from neuronal reconstructions without the need for technical expertise in all the related fields. Our modeling toolbox allows researchers to explore TMS mechanisms computationally and embed experimental findings in a theoretical framework that can facilitate our understanding of TMS mechanisms across scales.
Materials and Methods
Overview of Multi-scale Modeling Paradigm
We give an overview of the concept of multi-scale modeling to study the effects of TMS on neurons at the cellular and subcellular levels as shown in Figure 1. First, we use the Finite Element Method (FEM) to numerically calculate the electric fields induced in the geometry of interest (e.g. in vitro model or head model, Fig. 1A). However, the resulting electric fields at the macroscopic and mesoscopic scale cannot directly predict the physiological outcome. Therefore, we model the neuron membrane response to these external electric fields. To this end, we reconstruct CA1 pyramidal neurons based on microscopic images of enthorhino-hippocampal tissue cultures prepared from rodent brains (Fig. 1B). Based on the neuron morphology, we then generate a discretized numerical model of the neuron. Then, to couple the electric fields from the FEM model to the neuron model, we calculate quasipotentials (Fig. 1C) across all the neuron compartments [41]. Afterward, the neuron model is numerically solved to estimate the membrane potential across the whole neuron over time (Fig. 1D). Based on the calculated voltage traces, we solve the equations governing the calcium dynamics to calculate the calcium concentrations in the neuron over time at the subcellular level (Fig. 1E).
Figure 1.
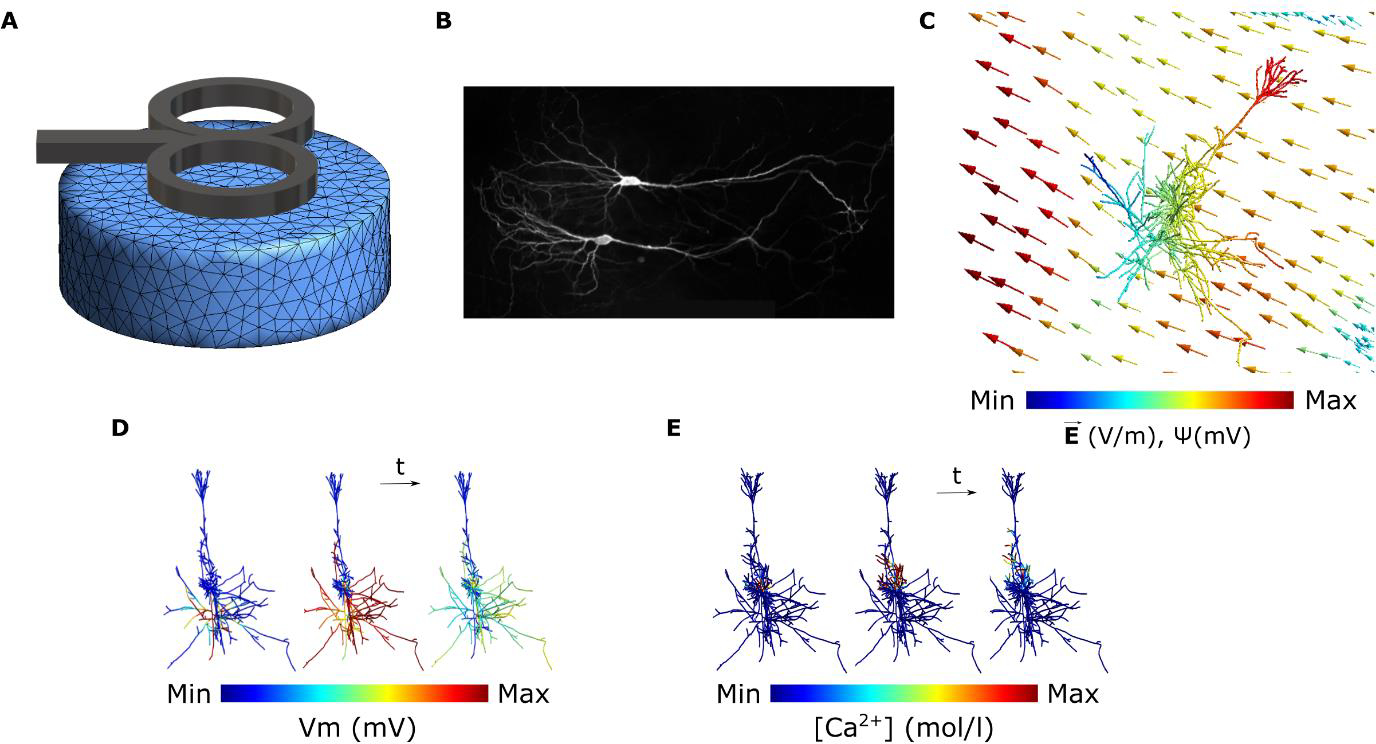
Overview of the multi-scale modeling paradigm. (A) Electric field calculation in the FEM model of interest. (B) Neuron reconstruction of CA1 pyramidal cells from microscopic images. (C) Coupling the electric fields to the morphologically accurate neuron model by calculating quasipotentials (ψ). (D) Simulating the membrane voltage (Vm) using the quasipotentials and computing the voltage traces of the neuron compartments over time. (E) Simulating the release of calcium ions from the voltage-dependent calcium channels (VDCC) over time by solving the calcium diffusion equations.
Neuron Modeling for TMS (NeMo-TMS) Toolbox
To facilitate the process of multi-scale modeling, we have developed a new toolbox (NeMo-TMS) and share it as an open-source resource with instructions (https://github.com/OpitzLab/NeMo-TMS) accessible to the research community. We tested the toolbox on Microsoft Windows 10 and Linux (Ubuntu 18.4/20.04). We have tested all the steps except the model generation (step 1) on macOS Catalina. Here, we outline the toolbox functionality and the steps to perform multi-scale simulations. Furthermore, we provide examples to show how it can be used to investigate TMS-related research questions.
As shown in Figure S1, the pipeline is comprised of multiple steps that allow the user to run multi-scale models. We have shared all the necessary codes and instructions to run multi-scale models with minimal prerequisites from the user. Below we summarize typical steps in the modeling process:
Neuron models are generated from realistic neuron reconstructions and the biophysics of CA1 or neocortical pyramidal cells are automatically added to these models.
Coordinates of the neuron model compartments are exported to be used in later steps.
The macroscopic electric fields are numerically calculated in the geometry of interest (e.g. in vitro model, head model). This accounts for the spatial distribution of the electric fields.
The electric fields computed in step 3 are coupled to the neuron model by calculating the quasipotentials at the coordinates exported in step 2.
The desired rTMS waveform is generated which accounts for the temporal pattern of the electric fields. User can also select the time step for subsequent simulations.
The membrane voltage of the neuron is simulated based on the spatial and temporal distribution of the TMS-induced electric fields calculated in the previous steps. Alternatively, the user can also run this step under the assumption of a spatially uniform electric field (in this case, steps 2 to 4 can be skipped).
The calcium concentration is simulated based on solving the calcium diffusion-reaction equations with voltage-dependent calcium channels.
The simulation results are visualized.
This toolbox is developed by utilizing multiple software packages, methods, and algorithms. Because of this and to make the toolbox accessible to a broad range of researchers with varying computational skills, we have simplified and automated the process to a great degree. For all the steps described above, the user can run the simulations using either graphical interfaces or through scripting. This feature is useful as it makes the computational workflow reproducible and gives advanced users the ability to run multiple simulations programmatically. With the NeMo-TMS toolbox, we provide a set of ten morphologically accurate neuron reconstructions with detailed dendritic and axonal branches to run example simulations. The morphology of these neurons is shown in Figure S2. For further technical details on the pipeline procedure, see below.
Neuron Reconstructions
Ethics Statement
Animals were maintained in a 12 h light/dark cycle with food and water available ad libitum. Every effort was made to minimize distress and pain in animals. All experimental procedures were performed according to German animal welfare legislation and approved by the local animal welfare officer of Freiburg University.
Tissue Cultures and Imaging
Enthorhino-hippocampal tissue cultures were prepared at postnatal days 4−5 from Wistar rats of either sex as described previously [37]. Single CA1 pyramidal neurons were identified under a microscope equipped a Dodt-Gradient-Contrast system. The bath solution contained 126 mM NaCl, 2.5 mM KCl, 26 mM NaHCO3, 1.25 mM 337 NaH2PO4, 2 mM CaCl2, 2 mM MgCl2 and 10 mM glucose and was saturated with 95% O2 / 5% CO2. Patch pipettes were filled with a solution containing 126 mM K-gluconate, 4 mM KCl, 4 mM ATP-Mg, 0.3 mM GTP-Na2, 10 mM PO-Creatine, 10 mM HEPES, and 0.1% Biocytin (pH = 7.25, 290 mOsm). The cells were held at −60 mV and the whole-cell configuration was maintained for at least 10 min to ensure complete filling of the cells. Patch pipettes were retracted carefully, and the tissue cultures were fixed in a solution of 4 % PFA (w/v) and 4 % (w/v) sucrose in 0.01 M PBS for 1 h. The staining and imaging procedures have been described previously [42]. Briefly, the tissue cultures were counterstained with Alexa-488 conjugated streptavidin (1:1000) and multiple z-stacks were obtained using a laser scanning confocal microscope (step size 0.5 μm; voxel size x and y = 0.3784 μm).
Neuronal Reconstructions
CA1 pyramidal cells were reconstructed using Neurolucida 360 (ver. 2019.1.3; MBF Bioscience). Somata were reconstructed using manual contour tracing, with the contour tracing set to ‘Cell Body’. Dendrites were subsequently reconstructed in the Neurolucida 3D environment under the ‘User-guided’ tracing option using the ‘Directional Kernels’ method. The raw reconstructed morphological data with detailed axonal and dendritic branching were then imported into the TREES toolbox for additional processing [43]. To correct for diameter overestimation due to fluorescence halo, a quadratic diameter taper algorithm [44] was applied across the dendritic arbor, with separate consideration for the basal dendrites, apical tuft, apical oblique projections, and primary apical dendrite. Parameters for the diameter tapering algorithm were adapted from [10]. Internodal segments of the axon were assigned a fixed diameter of 1μm and 0.8μm for nodes of Ranvier. As abrupt changes in the direction of neurites cause anomalous local effective electric fields along the neurite, a smoothing algorithm was also applied to the neurites. Using ProMesh4 (Goethe-Universität, Germany), we applied a Laplacian smoothing to all neurites (alpha = 0.25, 20 iterations) as well as manually removing any remaining anomalous sharp direction changes. These ten sample neuron reconstructions are shared with the toolbox.
Neuron Model Generation
We integrated a series of software tools into an automated pipeline for generating NEURON compartmental models [45]. This pipeline can generate models from commonly used file formats, i.e., SWC and Neurolucida ASCII files. Note that it is up to the user to ensure the input morphologies are correct, high-quality and without artifacts, otherwise the model generation may fail in the process or the simulation results would not be reliable. We tested the pipeline on the ten reconstructions of rat CA1 pyramidal cells provided here, as well as other morphology files.
Since the axonal reconstructions do not include myelination, this pipeline allows the user to myelinate the axon automatically, or to leave the neuron unmyelinated. For this, we implemented a modified variant of the myelination algorithm used in [46]. Nodes of Ranvier were placed at all bifurcation points in the axon arbor, as well as regularly at 100μm intervals. All internodal segments except terminal segments shorter than 20μm were myelinated. As most publicly available reconstructions of pyramidal neurons do not have an axon, the pipeline also features a provision for potential automatic addition of a straight artificial axon; in this case, the axon is a straight line emanating from the basal region of the soma with the first 10um a hillock segment, the next 15μm the axon initial segment, followed by six 100μm long myelinated internodal segments with regularly spaced 1μm long nodes of Ranvier.
Then, the NEURON compartmental models are generated using the T2N extension of the TREES Toolbox [47] in MATLAB (Mathworks, Inc., Natick, MA, USA), which translates the TREES Toolbox morphological data into NEURON’s HOC format and adds biophysics to the model. Our models implement a generalized version of the Jarsky model of the CA1 pyramidal cell [48,49]. This includes the passive properties: Cm = 0.75 μF/cm2, Ra = 200 Ω-cm, Rm = 40000 Ω/cm2. Additionally, axon myelinated segments had a significantly reduced Cm of 0.01 μF/cm^2, while axon nodes had Rm of 50 Ω/cm2. The models included three voltage-gated conductances: a Na+ conductance, a delayed rectifier K+ conductance, and two A-type K+ conductances. The values of these conductances are assigned according to distance from the soma as described in [49]. While the Na+ and conductances are fixed at 0.04 S/cm2, the value of the conductances steadily increases from 0.05 S/cm2 at the soma to 0.3 S/cm2 at 500μm from the soma. There is a crossover point between the two different conductances at 100μm from the soma. Furthermore, the extracellular mechanism [45], which accounts for the extracellular electric potentials, was inserted into the models by T2N simultaneously with the other biophysics. A synapse is also automatically placed in the proximal apical dendrite at a user-specified distance from the soma. Following the generation of the model files by T2N, other necessary files for the next steps are also generated and automatically placed in the correct location.
Additionally, we implement two human-inspired neocortical pyramidal cell models[46], one for layer 2/3 and one for layer 5 in the T2N-TREES framework for use with NeMo-TMS. As myelination is already implemented for these models, the myelination step of model generation is bypassed. These morphologies are extracted directly from the code provided in [46] using the neu_tree function of TREES Toolbox. This process preserves the diameter scaling and myelination of that model.
FEM Modeling of the TMS induced Electric field
To study the behavior of neurons under non-invasive brain stimulation, we first calculate the electric field generated at the macro- and mesoscopic scale. This includes computing the spatial distribution and time course of the TMS electric field. Since the stimulation frequency is relatively low, we can use the quasi-static approximation to separate the spatial and temporal components of the electric field [50–52]. For the spatial component, we calculate TMS-induced electric fields using FEM models implemented in the open-source software SimNIBS v3.1 [53]. SimNIBS is a versatile simulation platform that can simulate TMS-induced electric fields for various geometries and a variety of TMS coils.
Furthermore, since the electric field simulation accuracy depends on the resolution of the FEM mesh, we also provide a refined version of the Ernie head model from SimNIBS [54] as a sample. This mesh was generated by increasing the number of triangles in the gray matter (5.8X) and white matter (13.1X) surfaces from the original file first using MeshFix [55]. Then, the tetrahedral elements were generated from the triangular surfaces in Gmsh [56]. This refined mesh file can be downloaded from https://zenodo.org/record/5209082 [57].
Under the quasi-static assumption, the time course of the TMS-induced electric field is the same as that of the TMS stimulation output (rate of change [dI/dt] of the coil current). Therefore, after determining the spatial distribution of the electric field, the electric field can be found at any time point by scaling the spatial distribution to the TMS waveform. It is thus, very important to accurately represent the TMS waveform to investigate the temporal interaction of the external electric fields with neurons. For repetitive TMS (rTMS) a TMS pulse train is generated based on the parameters of the rTMS protocol. The user has the option to choose the TMS pulse type, inter-pulse interval, and the number of pulses. We included TMS pulse types commonly used in commercial TMS machines i.e. monophasic, and biphasic pulses [58]. We used the waveforms provided in a previous modeling study which were recorded from TMS pulses from a MagPro X100 TMS machine with a MCF-B70 figure-of-8 coil (MagVenture, Denmark) [33]. Based on the specified parameters, the pulses are concatenated to generate a pulse train and then written in a file that is used later in the neuron simulation. Note that advanced users can create custom-waveforms e.g. TBS and cTMS [59] as long as they follow the correct waveform format.
Electric field Coupling to Neuron Models
After calculating the macroscopic TMS-induced electric fields induced in the FEM model of interest, these external fields need to be coupled with the neuron models. While neurons are known to generate and affect electric fields around them, these fields are negligible compared to the strong TMS-induced electric fields. Therefore, it is common to exclude neurons during electric field modeling and couple the electric fields to neurons afterward [30,33,41]. In this pipeline, this is performed by: 1) Coordinates of the neuron compartments from the neuron model in the NEURON environment are exported to a text file. 2) The FEM model including the electric fields and the neuron coordinate files are imported to MATLAB. 3) The user enters the desired location and depth (relative to the grey matter surface) for the neuron placement. Additionally, the user has the option to manually specify the neuron orientation or choose a default orientation which is perpendicular to the grey matter surface. [60–62]. 4) The microscopic electric field at the location of neuronal compartments is interpolated from the mesoscopic TMS-induced electric fields calculated in the FEM model. 5) In this step, the user can scale the electric field strength if needed.
Since the electric field strength scales linearly with the stimulation intensity, one can easily scale the electric fields instead of rerunning the FEM simulations at different intensities. 7) The quasipotentials are computed over all compartments as described in [41] and written in a file that will be used later in the pipeline for the NEURON simulations. Additionally, the neuron (transformed to the desired location) and the FEM model are exported as mesh files for visualization.
To simplify the multi-scale modeling process, we have also enabled an alternative method to skip the FEM electric field modeling and the corresponding coupling step. In this case, the electric field is assumed to be spatially uniform over the extent of the neuron. This allows the user to specify the TMS-induced electric field everywhere using a single scalar for the amplitude and a vector for orientation. Typically, since neurons are considerably smaller than the TMS coil and the head model, the electric field distribution confined to a single neuron region is mostly uniform. Therefore, the uniform electric field approximation provides sufficiently accurate results in most cases. However, note that the uniform electric field approximation is not always valid. This occurs mainly in the following cases: 1) The neuron crosses a tissue boundary e.g. between Grey matter and white matter [16]. Due to the difference in electrical conductivities between tissues, a difference in the electric fields can arise between tissues. 2) The neuron is spatially extended (e.g. neurons with long axonal projections) so that the homogeneity of the electric field over small scales does not apply anymore. 3) The tissue surrounding the neuron is highly inhomogeneous. It should be noted that at the microscopic scale, the medium around the neurons is never fully homogeneous. However, due to computational demand, the electromagnetic characteristics of the grey matter is typically assumed to be locally homogeneous in modeling studies.
In the case of a uniform electric field, the quasipotentials equation can be simplified to the following expression:
| (1) |
Where is the electric field, is the displacement vector, Ex, Ey, and Ez stand for the Cartesian components of the electric field, and x, y, and z denote the Cartesian coordinates of each compartment. This step is computed in the NEURON environment.
Regardless of whether the electric field is uniform or based on the FEM model, the quasipotentials are calculated at each neuron segments (as exported from the NEURON model) and applied to the neuron simulations by using the extracellular mechanism available in the NEURON environment [45,46]. This process accounts for the exogenous fields induced by TMS.
Neuron Model Simulations
In this step, the simulation is run based on the generated NEURON model, the quasipotentials and TMS waveform files. During this stage, the user is prompted to choose to use the quasipotentials file calculated previously or to proceed with a uniform electric field. In the latter case, the user should enter the intensity of the electric field and its orientation, either in spherical or Cartesian coordinates. Then, the parameters for the random and synchronous synaptic inputs are entered by the user. Both of these synaptic inputs are supplied to the same synapse specified during the model generation. One input is synchronous with the TMS pulse, differing by a user-specified offset (2 ms default). The other input is random, with a user-selectable frequency and noise. Both inputs are disabled by default and can be enabled by setting non-zero synaptic weights. After running the simulation, the output files are automatically created. This includes voltage traces of all neuron segments over time and the coordinates of the segments and their connections.
Calcium Simulations
The calcium modeling tool of NeMo-TMS simulates the changes in calcium concentration based on Ca2+ influx via voltage dependent calcium channels (VDCCs). The VDCCs are simulated using the Borg-Graham model [63] and intracellular changes are modeled by solving diffusion-reaction equations on a one-dimensional tree geometry. Accordingly, the effects of the electric field on plasma membrane depolarization, activation of VDCCs and Ca2+ influx can be studied. Calcium mechanisms are either lacking in NEURON models or are typically simplified models that do not include the detailed calcium dynamics such as calcium diffusion. Therefore, realistic models of calcium diffusion such as the one incorporated in NeMo-TMS can provide more accurate results as shown in Fig. S8.
All necessary components were implemented in the simulation toolbox NeuroBox [64]. NeuroBox is a simulation toolbox that combines models of electrical and biochemical signaling on one- to three-dimensional computational domains. NeuroBox allows the definition of model equations, typically formulated as ordinary and partial differential equations, of the cellular computational domain and specification of the mathematical discretization methods and solvers [65,66]. The user can specify simulation parameters for the end time, time step size, and load the geometry. The following parameters are set by default based on previous literature [67]: plasma membrane Ca2+ -ATPase pumps (PMCA), Na+/Ca2+ exchangers (NCX), and VDCC densities, initial cytosolic calcium concentration, and diffusion constant for cytosolic calcium. However advanced users can modify the variables if necessary (discussed in the tutorial).
Calcium Model Equations
The model equations that are used for the calcium simulations have been utilized in [67,68]. In particular, the authors of [68] utilize the plasma membrane model equations in conjunction with intracellular calcium stores to verify necessary conditions to initiate stable calcium waves. For our simulations we study Ca2+ influx through VDCCs, in [67], this would be analogous to the passive/no-endoplasmic reticulum case and the authors concluded that minimal calcium reaches the dendritic compartments of the neuron. We observe this effect since the calcium remains localized near the soma and does not diffuse into all the distal dendrites of the neuron. Calcium mobility in the cytosol is described by the diffusion equation
| (2) |
where u(x, t) is the vector quantity of calcium concentration in the cytosol [Ca2+] and calbindin-D28k. The diffusion constants D are defined using data from (4). The interaction between cytosolic calcium and calbindin-D28k are described by
| (3) |
The rate constants and are defined in [67]. The calcium dynamics are modeled by a system of diffusion-reaction equations on a one-dimensional tree geometry with three spatial coordinates, the equations are as follows:
| (4) |
| (5) |
where the concentration of the CalB-Ca2+ compound is expressed by the difference of the total concentration of CalB present in the cytosol (btot) and free CalB, the former of which is assumed to be constant in space and time (this amounts to the assumption that free calcium and CalB have the same diffusive properties). The parameters used in this study are taken from [67].
In order to study the influence of the intracellular organization on Ca2+ signals, we include Ca2+ exchange mechanisms on the plasma membrane (PM). For the plasma membrane, we consider PMCA, NCX, Ca2+ influx through VDCCs, and a leakage term. This amounts to the flux equations (number of ions per membrane area and time)
| (6) |
with the Hill equations
| (7) |
| (8) |
The flux equations for the voltage-dependent calcium channels are described in the Appendix.
Numerical Methods for Calcium Simulations
For numerical simulations, the equations are discretized in space using a finite volumes method. Current densities, across the plasma membranes, can be incorporated into the reaction-diffusion process very naturally and easily this way. Time discretization is realized using a backward Euler scheme, i.e., for each point in time t, the term is approximated by
| (9) |
where τ is the time step size. For the results we present here, the emerging linearized problems were solved using a Bi-CGSTAB [67] linear solver preconditioned by an incomplete LU decomposition.
Although the intracellular calcium can affect the membrane potential, the effect on neuronal spiking is small for isolated neurons in short time scales as shown in Figure S7. Therefore, due to computational performance, only a feedforward implementation of calcium simulations based on the membrane potentials is implemented in this pipeline.
Visualization
Additionally, we have provided a GUI that can visualize the 3D distribution of the membrane potentials and the calcium concentrations based on the simulated data from the previous steps. Alternatively, users can visualize the data with Paraview [69].
Examples
To demonstrate some of the abilities of NeMo-TMS, we provide a few examples here. In example 1, we run a full multi-scale simulation on an in vitro model and show the membrane potential and calcium activity of the neuron when a TMS pulse is delivered. As shown in Figure 2A, the in vitro model consists of a tissue culture placed inside a Petri dish surrounded by artificial cerebrospinal fluid (aCSF). The Petri dish is modeled as a cylinder with 30 mm in diameter and 10 mm in height. The tissue culture is 2 × 1.5 × 0.3 mm in size and is placed at the center of the Petri dish 8 mm above the bottom surface. The mesh file for this model is available for download (https://zenodo.org/record/4009465) [70]. The electrical conductivity of the aCSF and the tissue culture are set to those of CSF (1.654 S/m) and grey matter (0.275 S/m) respectively [71]. A dipole-equivalent model of a 70 mm figure-8 coil (MagVenture MC-B70, Farum, Denmark) was placed 4 mm above the center of the Petri dish. We ran the FEM electric field simulation with a stimulator output of dI/dt = 240 A/μs. A biphasic TMS pulse was used, and all the simulations were run at a 5 μs time step. In example 2, we examine the effect of rTMS protocols on calcium accumulation. For this, we keep all parameters the same as example 1 and only change the rTMS waveform. We compare a 10 Hz rTMS protocol with a Theta Burst Stimulation (TBS) protocol [72]. In the TBS protocol, a burst of three TMS pulses is delivered at 50 Hz repeated at 5 Hz (200 ms delay between bursts). The TMS waveform is biphasic for this example, and all the simulations were run at a 25 μs time step. In example 3, we show how the orientation of the TMS electric field can affect the neural activation site and subsequently calcium dynamics. Since the spatial distribution of the electric field plays a key role in TMS effects [15], we compared two different electric field directions and their effects on the neuronal response. For this, we used one of the features of the pipeline to apply a spatially uniform electric field rather than from FEM modeling. We applied a monophasic TMS pulse in two different orientations: i) along the somatodendritic axis from the apical dendrite to the longest axon branch, ii) At 45° relative to the somatodendritic axis, along the second-longest axon branch. All the simulations were performed at a 5 μs time step in this example. In example 4, we run the pipeline for a human neocortical pyramidal neuron [46] for differing TMS intensities. The neuron is placed in the hand knob region of the primary motor cortex (M1), normal to the surface of the grey matter (soma is 1 mm deep). We used the refined Ernie head model explained in the methods and placed the figure-8 MC-B70 TMS coil (MagVenture, Denmark) at a 45° angle relative to the midline, at the location of the C3 electrode based on the international 10–20 system. Then, we apply 10 Hz biphasic rTMS at three stimulus intensities (dI/dt) and synaptic inputs: 1) 120 A/ μs with no synaptic input, 2) 120 A/ μs with random synaptic input, and 3)100 A/μs with synchronous synaptic input. The simulations were run at a 5 μs time step.
Figure 2.
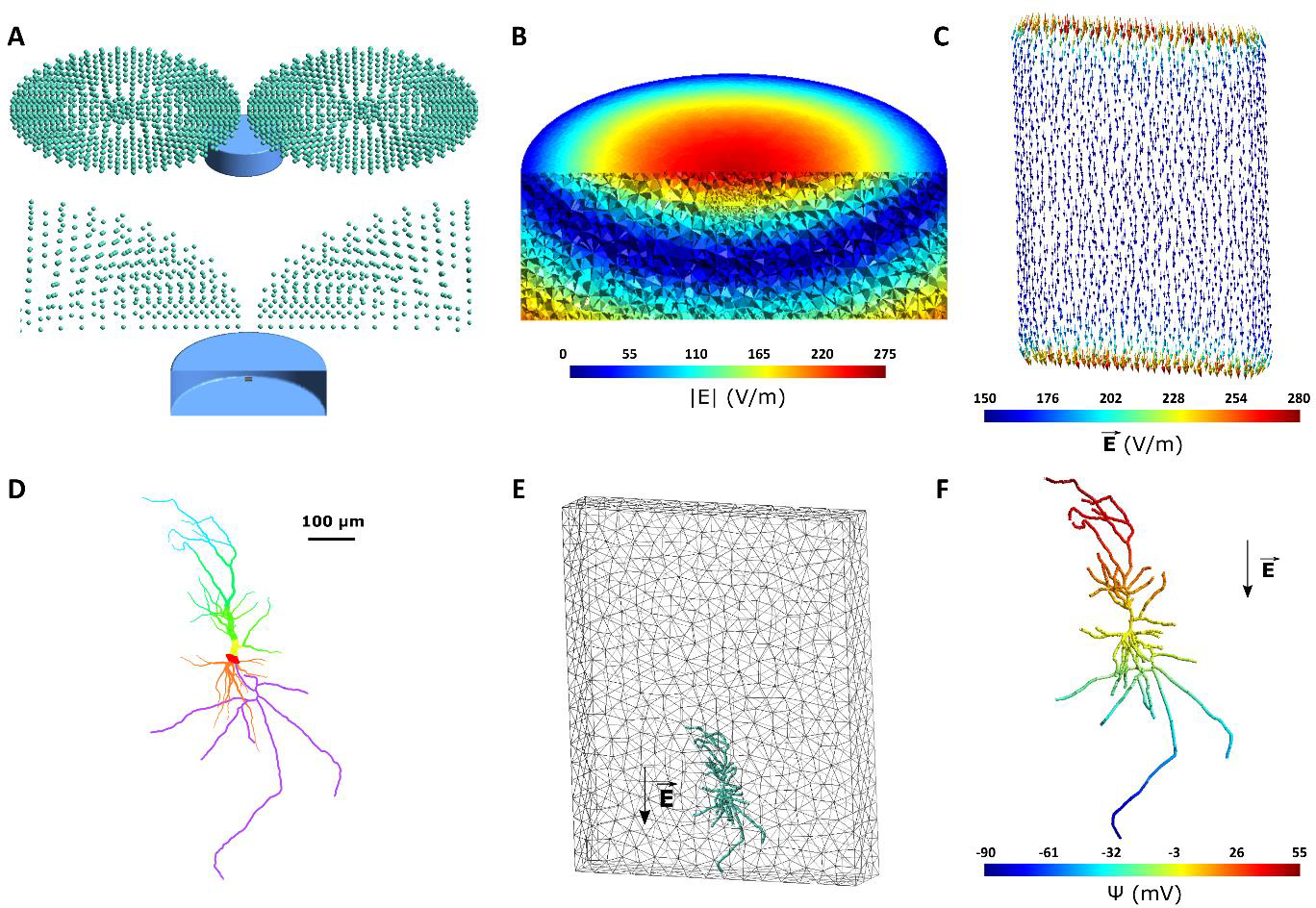
In vitro model of tissue culture in a Petri dish. (A) Geometry of the in vitro model. Top: TMS coil is represented through green magnetic dipoles. The Petri dish, shown in blue, is 30 mm in diameter with a height of 10 mm and is filled with aCSF. The figure-8 coil is placed 4 mm above the center of the Petri dish. Bottom: A cut-through image of the TMS coil and Petri dish is shown. The tissue culture with a size of 2 × 1.5 × 0.3 mm is placed at the center of the Petri dish 8 mm above the bottom surface. The tissue culture is modeled with grey matter conductivity. (B) Electric field magnitude induced in the in vitro model for a TMS stimulator output of dI/dt = 240 A/μs. (C) Electric field vector induced in the tissue culture. Electric fields are aligned unidirectionally along the handle of the figure-8 coil. Due to the conductivity mismatch between the culture and aCSF in the Petri dish, the electric field is enhanced at the borders along the electric field direction. (D) Reconstructed neuron morphology. Red, orange, yellow, green, blue, and purple respectively denote soma, basal dendrites, proximal apical, distal apical, apical tufts, and axon. Line thickness increased for better visualization. (E) Neuron (green) placement inside the tissue culture (grey mesh). The arrow shows the orientation of the electric field at the second peak of the biphasic TMS pulse. (F) The quasipotential distribution across the neuron compartments. In this model, the electric field is applied along the somatodendritic axis, thus a gradient can be seen from the apical dendrites to the axon.
Results
Example 1: Effects of TMS on the membrane potential and calcium concentration for an in vitro neuron model
For the in vitro model, the resulting electric fields are strongest at the top center of the model since these regions are closest to the center of the TMS coil (Fig. 2B). Electric fields are aligned unidirectionally in the tissue culture (Fig. 2C). Due to a conductivity difference between grey matter and CSF, an increase in the electric field occurs at these border walls [73]. The morphology of the reconstructed neuron is shown in Figure 2D. We placed the neuron model inside the tissue culture close to the border of the tissue culture and oriented it in a way that the electric fields are in the direction of the neuron somatodendritic axis (Fig. 2E). Then, we coupled the electric fields to the neuron by calculating the quasipotentials across the neuron (Fig. 2F). A gradient of quasipotentials occurs in the direction of the electric field.
Subsequently, we simulated the membrane dynamics of the neuron compartmental model using the CA1 pyramidal cell biophysics [48,49] in response to the applied electric field with the quasipotential mechanism. The resulting membrane voltage traces are then used as input to the simulation of the calcium dynamics for this neuron. While action potential initiation occurs on a millisecond timescale, calcium accumulation in the soma occurs with a delay and can be slower. Figure 3 and the corresponding Video S1 show the membrane potential of the neuron and its corresponding calcium concentrations over time during a single biphasic TMS pulse (simulated at 5 μs). Before the TMS pulse delivery, the neuron is at resting membrane voltage all across the cell (−70 mV). At time 0, the TMS pulse is delivered. Shortly after the TMS pulse, the axon terminal at the bottom of the cell is depolarized enough to induce an action potential. Since the axon is myelinated, the action potential quickly travels across all axonal branches and reaches the soma around 1 ms later. Afterward, the dendrites slowly depolarize as a result of ionic diffusion. Since basal dendrites are shorter, they depolarize faster than the apical dendrites. Over time (approximately 4 ms), the neuron gradually recovers back to the resting potential. Apical and tuft dendrites are the last neurites to depolarize and therefore the last ones to return to rest. The bottom panel in Figure 3 shows the calcium densities across the neuron for the same neuron spike. Once the action potential reaches the soma at around 1 ms after the TMS pulse, with a short delay of less than 1 ms, calcium accumulation is initiated in the soma. Then, the calcium levels start to rise slowly at the basal and apical dendrites. For these simulations, calcium exchange and release mechanisms are not considered in the axon region of the neuron; therefore, the calcium concentration remains constant in the axon of the cell. Afterward, the calcium densities in the rest of the neuron decrease and approach the resting values again (~5 ms). However, it takes longer for the calcium in the soma to fully restore to the baseline.
Figure 3.
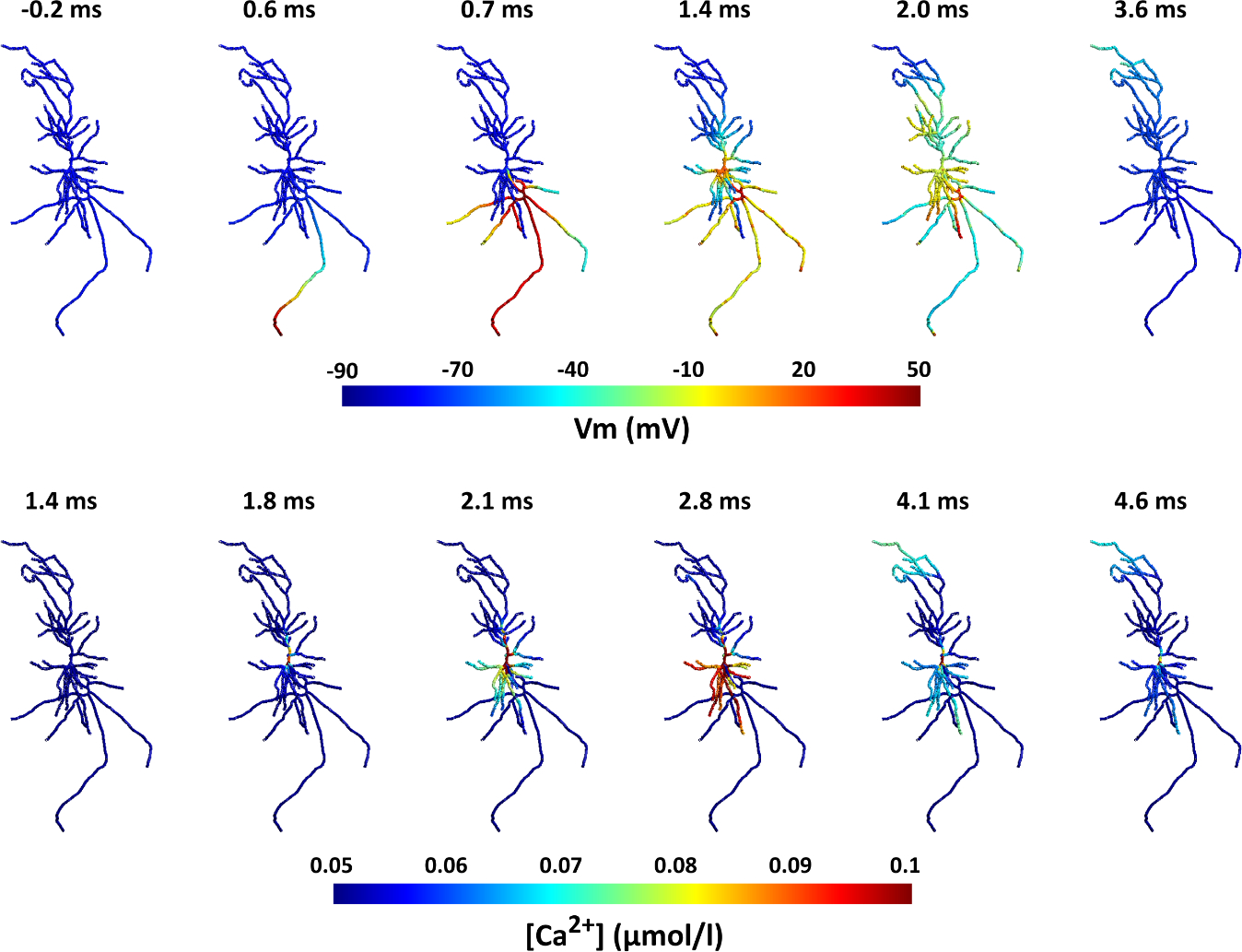
Action potential and calcium propagation over time in the neuron for the in vitro model. Note that time scales of membrane potentials and calcium dynamics differ between the upper and lower panel. Top: Spatial distribution of membrane potentials over time. The action potential starts at the axon terminal shortly after the TMS pulse (t = 0) and quickly propagates to the rest of the neuron. In the following ~4 ms, the neuron recovers back to its resting potential. Bottom: Distribution of the calcium concentrations displayed for the same TMS action potential. After the action potential reaches the soma ~1 ms after the TMS pulse, shortly after < 1 ms), the calcium concentration increases in the soma and then propagates to the dendrites. After several ms calcium levels resort to baseline. The range of the color bar for the calcium concentrations was adjusted for improved visualization and does not represent the maximum values. Also see Video S1.
Example 2: Effect of rTMS pulse parameters on calcium dynamics
For the comparison of the rTMS pulses, the membrane potential and the calcium concentration in the soma over several TMS pulses for 10Hz rTMS and TBS protocols are shown in Figure 4. After each TMS pulse, the neuron spikes, and therefore calcium accumulation in the soma follows. For the 10 Hz rTMS protocol, after each neuron spike, there is a rapid increase and then a decrease in the calcium level in the soma. However, after this initial activity, the decay rate slows dramatically. Since the calcium concentration does not completely recover to baseline before the subsequent pulse, there is a gradual increase in the overall calcium level. On the other hand, for the TBS protocol, since TMS pulses are very close together in each burst, calcium reaches higher concentrations after each burst but also decays quicker than the 10 Hz protocol. Although, because the bursts are fairly close together, the calcium level stays higher than the baseline (Fig. 4D). Overall, a buildup of calcium occurs in the soma over time in both rTMS protocols, but the temporal patterns are different. The experimental data (refer to supplementary methods) shows that 10 Hz repetitive magnetic stimulation (rMS) of the hippocampal tissue culture induces a gradual increase in the somatic Ca2+ concentration (Fig. S5). This slow buildup of the calcium is in line with the simulation results (Fig. 4). In this example, we used a 25 μs time step for the simulations. We also investigated the effect of simulation time steps on neuronal activity. Figure S4 shows that the results for 5 and 25 μs time steps are consistent. Except for a short delay (<0.2 ms), we found no difference in the temporal pattern and the thresholds. Thus, we recommend using a 25 μs time step due to lower computational cost unless the exact timing of neuronal activity is necessary. The simulation times depend on the model, parameters and the hardware setup of the computer. On a Microsoft Windows 10 computer (Intel Core i7–4790 Processor, 32 GB memory), it takes approximately 30 minutes and 24 hours to run the neuron and calcium simulations of example 2 respectively, performed at a 25 μs time step. Furthermore, to see the effect of neuron morphology on the rTMS response, refer to Figure S6.
Figure 4.
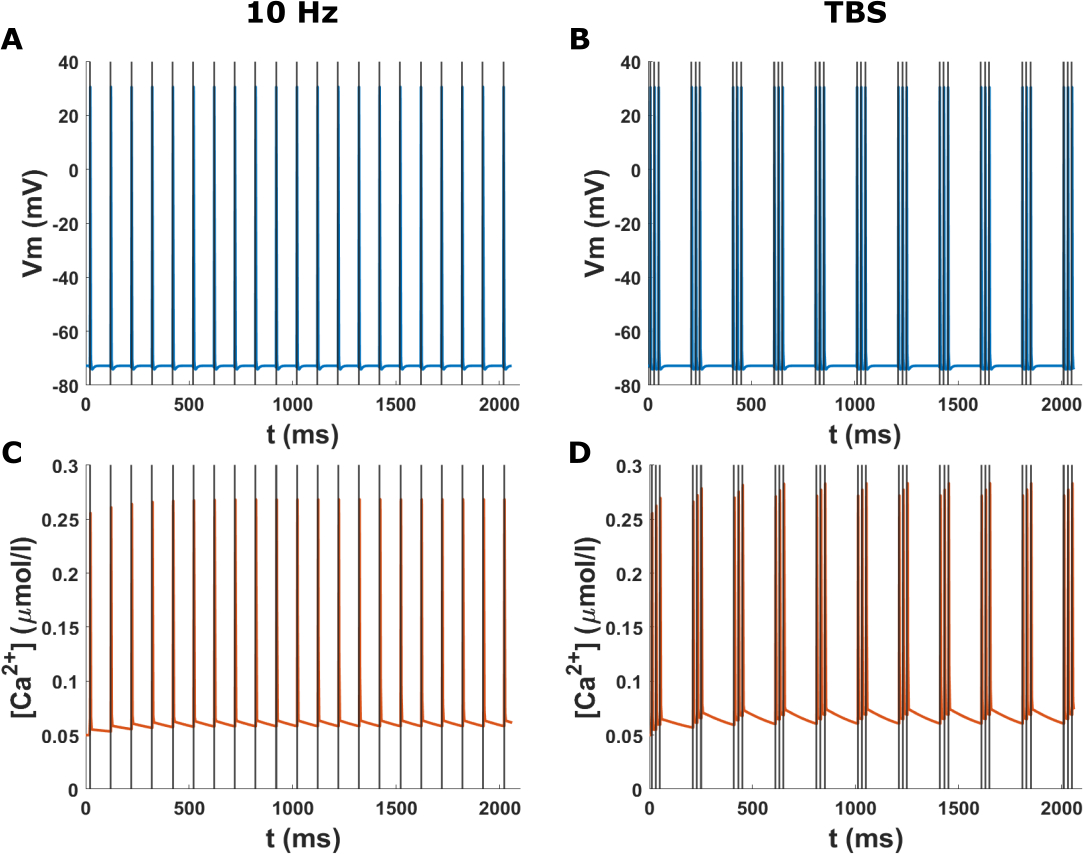
Time course of the membrane potential and calcium concentration at the soma in the in vitro model for two rTMS protocols. The grey lines indicate the TMS pulses. (A) Membrane potential at the soma for the 10 Hz biphasic rTMS protocol. The neuron spikes immediately after each TMS pulse. (B) Membrane potential at the soma for the TBS protocol with a biphasic TMS pulse. (C) Calcium concentration at the soma for the 10 Hz rTMS protocol corresponding to (A). Calcium levels rise after each spike and then slowly recover. Over time, there is a buildup of calcium. (D) Calcium concentration at the soma for the TBS protocol corresponding to (B). The calcium levels rise after each burst of pulses and then subside. The calcium levels stay higher than the baseline.
Example 3: Effect of the electric field orientation on neural activation
In this example, the neuron activation pattern is shown in Figure 5 and Video S2 for two electric field orientations. In the first case, since the electric field is aligned with the long axon branch, the action potential is initiated in the terminal of the long axon branch. However, in the second scenario, the action potential is initiated in the terminal of the second-longest axon since it is more suitably aligned to the electric field. Additionally, in the first scenario, the neuron fires at an electric field strength of 275 V/m, while in the second case, a slightly higher field strength (280 V/m) is needed for the neuron to fire. Also, there is a time shift (~0.1 ms) between the action potential initiation and propagation between these electric field orientations. This time shift causes a delay in calcium accumulation between these conditions as shown in Video S3. This example shows that the electric field orientation plays a role not only in the activation thresholds but also in the neuron firing pattern, and calcium dynamics timing.
Figure 5.
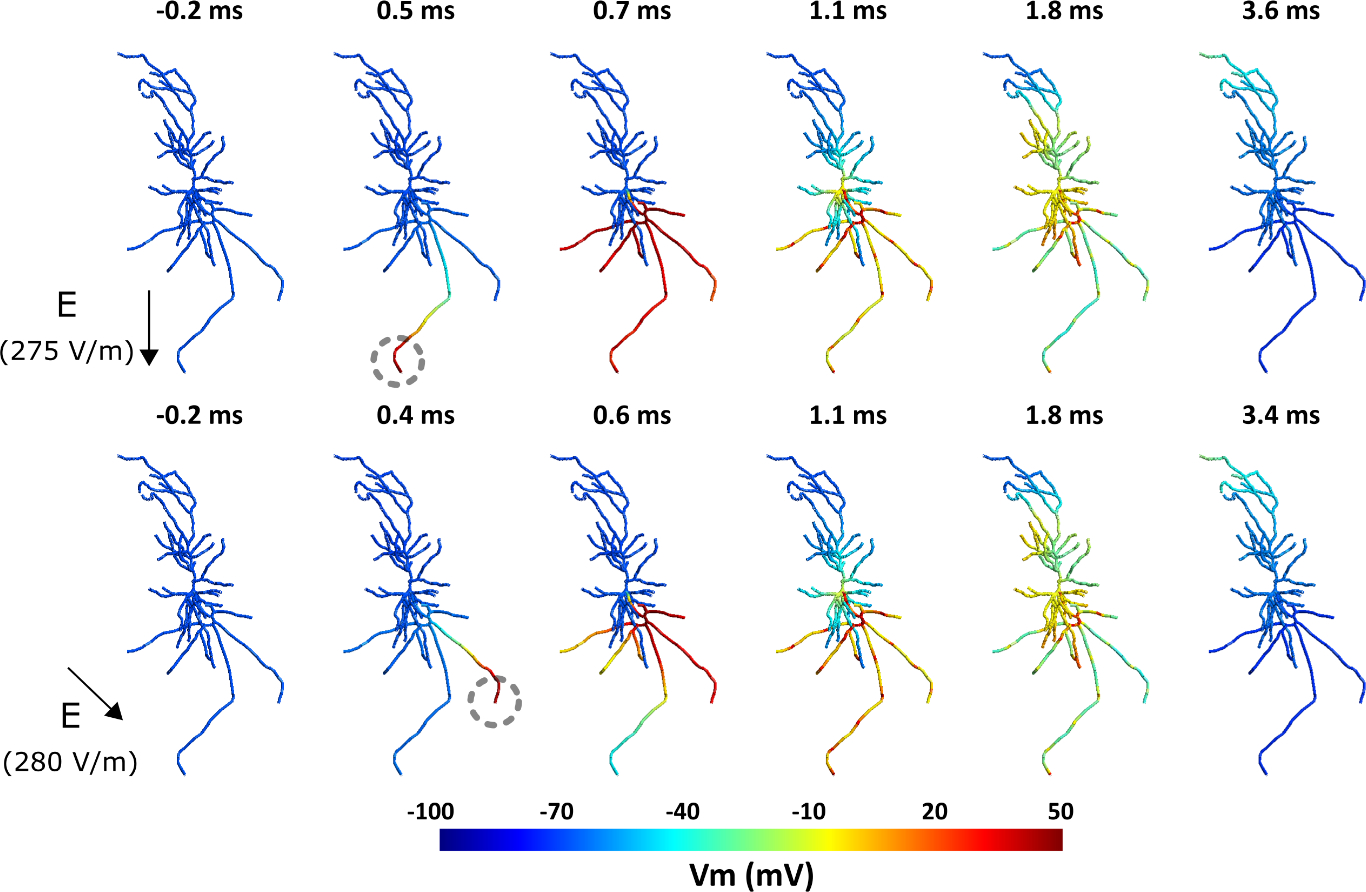
Effect of the TMS electric field orientation on membrane dynamics and spiking threshold. Top: Spiking activity in the neuron for a 275 V/m intensity uniform electric field with a monophasic TMS pulse oriented along the somatodendritic axis. The action potential initiates at the bottom-most axon terminal indicated with a grey dashed circle. Bottom: Spiking activity for a 280 V/m intensity uniform electric field with a monophasic TMS pulse oriented at 45° relative to the somatodendritic axis. The action potential starts at the axon terminal on the right. Also see Video S2. For the corresponding calcium concentration, see Video S3.
Example 4: Effects of TMS on the membrane potential and calcium concentration for a human neocortical neuron model in a realistic head model
In this example, we examine the behavior of a human neocortical pyramidal neuron in a realistic head model for multiple stimulus intensities of biphasic 10Hz rTMS. Figure 6A shows the placement of the coil on the head, targeting the left primary motor cortex. The electric field induced in the grey matter is strongest in motor and somatosensory areas (Fig. 6B). The white circle denotes the hand knob area of the M1 at the lip of the gyrus. We place the neuron at the center of this region perpendicular to the grey matter surface (Fig. 6C). Figure 6D illustrates the morphology of the pyramidal neuron. Somatic membrane potentials of the neuron at different conditions show that spike activity depends on the TMS intensity and synaptic inputs (Fig. 6E). For the studied rTMS protocols we observe that the neuron does not fire with every TMS pulse due to its slow recovery. However, random synaptic input can increase the neuron recovery to some degree. Furthermore, a synaptic input with synchronous timing to TMS pulses, can decrease the firing threshold of the neuron. This example shows that the temporal characteristics of the neuronal activity and synaptic inputs play a major role in its response to rTMS. Furthermore, we conducted a control analysis comparing the effect of FEM mesh size on the estimated microscopic electric fields used for multi-scale modeling. Figure S3 shows that a typical FEM head model used in electric field modeling, generates similar results to a locally refined mesh. We therefore conclude, that in most cases, the typical FEM models are accurate, however, depending on the simulation, a more refined mesh can increase the accuracy of the estimated electric fields. Additionally, to compare the effect of FEM mesh refinement on the neuronal activity, we ran the same simulations as in Figure 6, while only altering the FEM head model to the unrefined original mesh used for electric field calculation (Fig S9). Except for minor shifts in the neuron firing timing (some action potentials occur one TMS pulse earlier or later, without any change in overall firing rate pattern) and TMS activation threshold in some conditions (5 A/μs less for the no synaptic and random synaptic inputs in the unrefined case), we do not see major differences between the original and refined mesh. Thus, the typical mesh size used for electric field simulations is suitable for most cases of neuron modeling. However, the user can opt to use a refined FEM model (e.g., the one provided here) to have a higher accuracy in electric field calculations [74], albeit with additional computational cost. The higher accuracy of refined meshes may be more pronounced around the tissue boundaries which can be important if the axon of the neuron used in the multi-scale modeling crosses the grey matter/white matter boundary [16].
Figure 6.
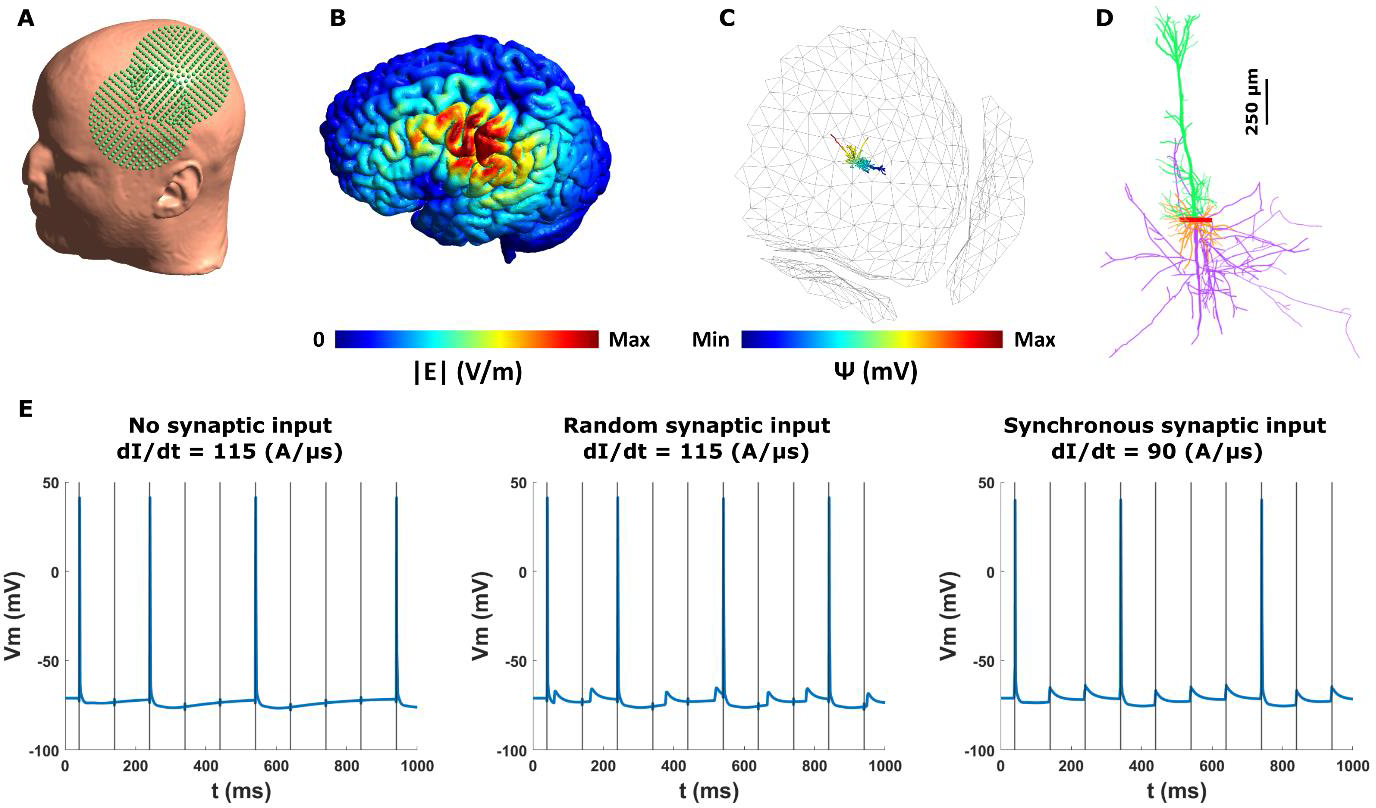
TMS effects in a human neocortical neuron model in a realistic head model (refined Ernie model). (A) TMS coil placement over the left primary motor cortex (M1) at 45° relative to midline. (B) Spatial distribution of the electric field magnitude on the grey matter. The white circle shows the location of the neocortical neuron in the hand knob area of the M1. (C) Neuron placement at the center of the white circle (radius = 5 mm) at the lip of the gyrus. The neuron is oriented normal to the grey matter surface. The quasipotentials induced by the electric fields are overlaid on the neuron. The grey matter surface is made transparent to visualize the neuron. (D) Neocortical neuron morphology. Soma, apical dendrites, basal dendrites, and the axon is shown with red, green, orange, and purple, respectively. (E) Somatic membrane voltage for left. dI/dt = 115 A/μs and no synaptic input; middle. dI/dt = 115 A/μs and random synaptic input (weight = 0.05); and right. dI/dt = 90 A/μs and synchronous synaptic input (weight = 0.05). The neuron does not fire at every TMS pulse due to slow recovery period. Neuronal spiking depends on the synaptic input. Synchronous synaptic input decreases the TMS firing threshold. The grey vertical lines mark the TMS pulses.
Discussion
We developed an open-source multi-scale modeling toolbox to enable researchers to model the effects of (r)TMS on single neurons and study their cellular and subcellular behavior. NeMo-TMS toolbox allows users to simulate the TMS-induced electric fields in geometries of interest (such as an in vitro model or a head model), to couple the TMS electric fields to morphologically accurate neuron models, and to simulate the membrane voltage and calcium concentration in the neurons. Our pipeline provides a graphical user interface, as well as an interface to run the process through scripts that will allow researchers with different computational skill sets to efficiently use our software.
To our knowledge, NeMo-TMS is the first modeling toolbox that enables studying single neuron behavior under TMS at macro-/mesoscopic, microscopic, and subcellular levels at the same time. Additionally, our toolbox can incorporate sophisticated neuron geometries and morphologies. Complementing modeling results with experimental studies can help to improve our understanding of the basic mechanisms of TMS.
Besides the technical implementation of the pipeline, we discuss several examples to showcase some of its capabilities. In the first example, we simulate the effect of single-pulse TMS on a morphologically reconstructed neuron embedded inside a tissue culture as an in vitro model. We show how the action potential is initiated at the axon terminal from which it propagates to the rest of the neuron. The voltage-dependent calcium concentrations increase after the action potential reaches the soma from which they spread into the dendrites. Both processes occur at different timescales with the calcium propagation following the action potential. In the second example, we compare the neuron response to two classical plasticity-inducing rTMS protocols: a 10 Hz rTMS protocol and a TBS protocol. We show that calcium induction varies between the protocols and that TBS results in a build-up of calcium levels. We provide initial experimental evidence for somatic calcium increase in response to rTMS as would be expected from simulation results. A more comprehensive experimental validation will be necessary in future studies. In the third example, we examine how the neuron response to TMS depends on the orientation of the electric field. For this, we applied a spatially uniform electric field at two orientations and show that the initiation site of the action potential changes as a result as well as the activation threshold. The site of the action potential initiation and the overall field intensity to initiate action potentials are in line with a recent study using morphologically accurate neuron models [33]. The differences in action potential initiation also resulted in slight delays in calcium accumulation in the soma. The exact timing between pre- and postsynaptic activity has a major impact on synaptic plasticity [10,75,76]. It is thus conceivable that in the context of rTMS these effects may add up over the course of several hundred pulses. However, further work is required to test this prediction. In the final example, we run the Nemo-TMS pipeline for a human neocortical pyramidal neuron and show how the neuron spiking pattern is dependent on the stimulus intensity and synaptic inputs. The electric field intensities reported in this manuscript for TMS-induced action potentials are in line with previous realistic neuron modeling studies [33,46]. Although these examples demonstrate some of the capabilities of this toolbox, its use is not limited to the examples discussed and researchers have the freedom to apply it to questions of their interest.
While our toolbox significantly advances the field of TMS multi-scale modeling, future studies are expected to validate the accuracy of neuronal membrane voltage and calcium dynamics. Further developments can also be envisioned. Neurons vary drastically in terms of their biophysics depending on their type. Here, we focused on implementing the biophysics for CA1 and neocortical pyramidal neurons. Currently, the Ca2+ simulations do not consider internal calcium stores and only simulate the Ca2+ influx from voltage-dependent calcium channels (VDCCs), sodium-calcium exchangers (NCX), and plasma membrane Ca2+ ATPase (PMCA). Future versions of our pipeline can provide biophysics for more diverse neurons, and allow users to define their own biophysics. Further developments can also be implemented to incorporate modeling of Ca2+ release from intracellular Ca2+ stores. In future work, our framework allows to integrate the models from [67,68], using the 3D cell generator AnaMorph [77], to extend the current 1D intracellular calcium dynamics to solve the 3D calcium models in NeMo. Additionally, our toolbox can be expanded to include other non-invasive or invasive brain stimulation techniques such as transcranial Alternating Current Stimulation (tACS), transcranial Direct Current Stimulation (tDCS), or Deep Brain Stimulation (DBS). In the future versions, the pipeline can be streamlined even more by removing the dependency of the toolbox on multiple software packages. Finally, many of the behavioral and physiological neural responses to TMS arise from network interactions between the neurons. Thus, investigating the neural behavior at the population level will be vital for a fundamental understanding of TMS responses. Future hardware and software developments will be necessary to implement tools to model networks of neurons in response to TMS.
In conclusion, NeMo-TMS is a unique tool that provides an easy-to-use platform for multi-scale TMS modeling and enables researchers to incorporate sophisticated modeling approaches into their research.
Supplementary Material
We developed a new toolbox (NeMo-TMS) to simulate the cellular and subcellular activity of single neurons in response to (repetitive) TMS
TMS-induced electric fields from the macroscopic models are coupled with a morphologically realistic neuron model to simulate the membrane potential and the spiking pattern
Membrane potentials are used to model the voltage-gated calcium dynamics important for understating neuronal plasticity
All necessary codes can be found in an open-source repository (https://github.com/OpitzLab/NeMo-TMS)
Acknowledgments
We thank Dr. Zsolt Turi for the helpful discussions and testing of the toolbox, and Swathi Anil for her help with the neuronal reconstructions and testing of the toolbox. This work was supported by the National Institutes of Health (R01MH118930 to GQ and AO and R01NS109498 to AV and AO and RF1MH117428 to AO), Federal Ministry of Education and Research Germany (BMBF, 01GQ1804A to AV; BMBF, 01GQ1804B to PJ), and the von Behring Röntgen Foundation (to PJ).
Appendix
The flux equations for the voltage-dependent calcium channels are given by
| (1) |
where G is the gating function and F is the flux function [63]. Both depend on the voltage at the channel at a particular time t. For F, Δ[Ca2+]is the difference in the internal and external ion concentration
| (2) |
and
| (3) |
where R is the gas constant, F is Faraday’s constant, T is in Kelvin, is the permeability of the calcium channel, and z is the valence of the ion [63].
The gating function g is described by a finite product
| (4) |
where xiis the open probability of the gating particle, in this case, it is only calcium, and n is the number of particles. The open probability is described by the ODE
| (5) |
where x∞is the steady-state value of x, and τx is the time constant for the particular particle x, formulas are given in [63].
Footnotes
Conflict of Interest
There are no conflicts of interest to report.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- [1].Barker AT, Jalinous R, Freeston IL. NON-INVASIVE MAGNETIC STIMULATION OF HUMAN MOTOR CORTEX. The Lancet 1985;325:1106–7. 10.1016/S0140-6736(85)92413-4. [DOI] [PubMed] [Google Scholar]
- [2].Hallett M. Transcranial Magnetic Stimulation: A Primer. Neuron 2007;55:187–99. 10.1016/j.neuron.2007.06.026. [DOI] [PubMed] [Google Scholar]
- [3].Lefaucheur J-P, André-Obadia N, Antal A, Ayache SS, Baeken C, Benninger DH, et al. Evidence-based guidelines on the therapeutic use of repetitive transcranial magnetic stimulation (rTMS). Clinical Neurophysiology 2014;125:2150–206. 10.1016/j.clinph.2014.05.021. [DOI] [PubMed] [Google Scholar]
- [4].Allen EA, Pasley BN, Duong T, Freeman RD. Transcranial Magnetic Stimulation Elicits Coupled Neural and Hemodynamic Consequences. Science 2007;317:1918–21. 10.1126/science.1146426. [DOI] [PubMed] [Google Scholar]
- [5].Li B, Virtanen JP, Oeltermann A, Schwarz C, Giese MA, Ziemann U, et al. Lifting the veil on the dynamics of neuronal activities evoked by transcranial magnetic stimulation. ELife 2017;6:e30552. 10.7554/eLife.30552. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6].Mueller JK, Grigsby EM, Prevosto V, Petraglia FW, Rao H, Deng Z-D, et al. Simultaneous transcranial magnetic stimulation and single-neuron recording in alert non-human primates. Nature Neuroscience 2014;17:1130–6. 10.1038/nn.3751. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Romero MC, Davare M, Armendariz M, Janssen P. Neural effects of transcranial magnetic stimulation at the single-cell level. Nature Communications 2019;10:2642. 10.1038/s41467-019-10638-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [8].Murphy SC, Palmer LM, Nyffeler T, Müri RM, Larkum ME. Transcranial magnetic stimulation (TMS) inhibits cortical dendrites. ELife 2016;5:e13598. 10.7554/eLife.13598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [9].Alekseichuk I, Mantell K, Shirinpour S, Opitz A. Comparative modeling of transcranial magnetic and electric stimulation in mouse, monkey, and human. NeuroImage 2019;194:136–48. 10.1016/j.neuroimage.2019.03.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Lenz M, Platschek S, Priesemann V, Becker D, Willems LM, Ziemann U, et al. Repetitive magnetic stimulation induces plasticity of excitatory postsynapses on proximal dendrites of cultured mouse CA1 pyramidal neurons. Brain Struct Funct 2015;220:3323–37. 10.1007/s00429-014-0859-9. [DOI] [PubMed] [Google Scholar]
- [11].Tang A, Thickbroom G, Rodger J. Repetitive Transcranial Magnetic Stimulation of the Brain: Mechanisms from Animal and Experimental Models. The Neuroscientist 2015. 10.1177/1073858415618897. [DOI] [PubMed] [Google Scholar]
- [12].Tokay T, Holl N, Kirschstein T, Zschorlich V, Köhling R. High-frequency magnetic stimulation induces long-term potentiation in rat hippocampal slices. Neuroscience Letters 2009;461:150–4. 10.1016/j.neulet.2009.06.032. [DOI] [PubMed] [Google Scholar]
- [13].Vlachos A, Müller-Dahlhaus F, Rosskopp J, Lenz M, Ziemann U, Deller T. Repetitive Magnetic Stimulation Induces Functional and Structural Plasticity of Excitatory Postsynapses in Mouse Organotypic Hippocampal Slice Cultures. J Neurosci 2012;32:17514–23. 10.1523/JNEUROSCI.0409-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14].Laakso I, Hirata A, Ugawa Y. Effects of coil orientation on the electric field induced by TMS over the hand motor area. Phys Med Biol 2013;59:203–18. 10.1088/0031-9155/59/1/203. [DOI] [PubMed] [Google Scholar]
- [15].Opitz A, Legon W, Rowlands A, Bickel WK, Paulus W, Tyler WJ. Physiological observations validate finite element models for estimating subject-specific electric field distributions induced by transcranial magnetic stimulation of the human motor cortex. NeuroImage 2013;81:253–64. 10.1016/j.neuroimage.2013.04.067. [DOI] [PubMed] [Google Scholar]
- [16].Opitz A, Windhoff M, Heidemann RM, Turner R, Thielscher A. How the brain tissue shapes the electric field induced by transcranial magnetic stimulation. NeuroImage 2011;58:849–59. 10.1016/j.neuroimage.2011.06.069. [DOI] [PubMed] [Google Scholar]
- [17].Salinas FS, Lancaster JL, Fox PT. 3D modeling of the total electric field induced by transcranial magnetic stimulation using the boundary element method. Phys Med Biol 2009;54:3631–47. 10.1088/0031-9155/54/12/002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Laakso I, Murakami T, Hirata A, Ugawa Y. Where and what TMS activates: Experiments and modeling. Brain Stimulation 2018;11:166–74. 10.1016/j.brs.2017.09.011. [DOI] [PubMed] [Google Scholar]
- [19].Bungert A, Antunes A, Espenhahn S, Thielscher A. Where does TMS Stimulate the Motor Cortex? Combining Electrophysiological Measurements and Realistic Field Estimates to Reveal the Affected Cortex Position. Cerebral Cortex 2017;27:5083–94. 10.1093/cercor/bhw292. [DOI] [PubMed] [Google Scholar]
- [20].Di Lazzaro V, Rothwell J, Capogna M. Noninvasive Stimulation of the Human Brain: Activation of Multiple Cortical Circuits. Neuroscientist 2018;24:246–60. 10.1177/1073858417717660. [DOI] [PubMed] [Google Scholar]
- [21].Hannah R, Rothwell JC. Pulse Duration as Well as Current Direction Determines the Specificity of Transcranial Magnetic Stimulation of Motor Cortex during Contraction. Brain Stimulation 2017;10:106–15. 10.1016/j.brs.2016.09.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22].Basser PJ, Roth BJ. Stimulation of a myelinated nerve axon by electromagnetic induction. Med Biol Eng Comput 1991;29:261–8. 10.1007/BF02446708. [DOI] [PubMed] [Google Scholar]
- [23].Nagarajan SS, Durand DM. A generalized cable equation for magnetic stimulation of axons. IEEE Transactions on Biomedical Engineering 1996;43:304–12. 10.1109/10.486288. [DOI] [PubMed] [Google Scholar]
- [24].Salvador R, Silva S, Basser PJ, Miranda PC. Determining which mechanisms lead to activation in the motor cortex: A modeling study of transcranial magnetic stimulation using realistic stimulus waveforms and sulcal geometry. Clinical Neurophysiology 2011;122:748–58. 10.1016/j.clinph.2010.09.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25].Wagner T, Eden U, Rushmore J, Russo CJ, Dipietro L, Fregni F, et al. Impact of brain tissue filtering on neurostimulation fields: A modeling study. NeuroImage 2014;85:1048–57. 10.1016/j.neuroimage.2013.06.079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [26].Goodwin BD, Butson CR. Subject-Specific Multiscale Modeling to Investigate Effects of Transcranial Magnetic Stimulation. Neuromodulation: Technology at the Neural Interface 2015;18:694–704. 10.1111/ner.12296. [DOI] [PubMed] [Google Scholar]
- [27].Kamitani Y, Bhalodia VM, Kubota Y, Shimojo S. A model of magnetic stimulation of neocortical neurons. Neurocomputing 2001;38–40:697–703. 10.1016/S0925-2312(01)00447-7. [DOI] [Google Scholar]
- [28].Pashut T, Wolfus S, Friedman A, Lavidor M, Bar-Gad I, Yeshurun Y, et al. Mechanisms of Magnetic Stimulation of Central Nervous System Neurons. PLOS Computational Biology 2011;7:e1002022. 10.1371/journal.pcbi.1002022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29].Seo H, Jun SC. Relation between the electric field and activation of cortical neurons in transcranial electrical stimulation. Brain Stimulation 2019;12:275–89. 10.1016/j.brs.2018.11.004. [DOI] [PubMed] [Google Scholar]
- [30].Seo H, Schaworonkow N, Jun SC, Triesch J. A multi-scale computational model of the effects of TMS on motor cortex. F1000Res 2017;5:1945. 10.12688/f1000research.9277.3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Wu T, Fan J, Lee KS, Li X. Cortical neuron activation induced by electromagnetic stimulation: a quantitative analysis via modelling and simulation. J Comput Neurosci 2016;40:51–64. 10.1007/s10827-015-0585-1. [DOI] [PubMed] [Google Scholar]
- [32].Rusu CV, Murakami M, Ziemann U, Triesch J. A Model of TMS-induced I-waves in Motor Cortex. Brain Stimulation 2014;7:401–14. 10.1016/j.brs.2014.02.009. [DOI] [PubMed] [Google Scholar]
- [33].Aberra AS, Wang B, Grill WM, Peterchev AV. Simulation of transcranial magnetic stimulation in head model with morphologically-realistic cortical neurons. Brain Stimulation 2020;13:175–89. 10.1016/j.brs.2019.10.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Eilers J, Callewaert G, Armstrong C, Konnerth A. Calcium signaling in a narrow somatic submembrane shell during synaptic activity in cerebellar Purkinje neurons. PNAS 1995;92:10272–6. 10.1073/pnas.92.22.10272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Limbäck-Stokin K, Korzus E, Nagaoka-Yasuda R, Mayford M. Nuclear Calcium/Calmodulin Regulates Memory Consolidation. J Neurosci 2004;24:10858–67. 10.1523/JNEUROSCI.1022-04.2004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Shoop RD, Chang KT, Ellisman MH, Berg DK. Synaptically Driven Calcium Transients via Nicotinic Receptors on Somatic Spines. J Neurosci 2001;21:771–81. 10.1523/JNEUROSCI.21-03-00771.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Lenz M, Galanis C, Müller-Dahlhaus F, Opitz A, Wierenga CJ, Szabó G, et al. Repetitive magnetic stimulation induces plasticity of inhibitory synapses. Nature Communications 2016;7:10020. 10.1038/ncomms10020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Fung PK, Robinson PA. Neural field theory of synaptic metaplasticity with applications to theta burst stimulation. Journal of Theoretical Biology 2014;340:164–76. 10.1016/j.jtbi.2013.09.021. [DOI] [PubMed] [Google Scholar]
- [39].Fung PK, Robinson PA. Neural field theory of calcium dependent plasticity with applications to transcranial magnetic stimulation. Journal of Theoretical Biology 2013;324:72–83. 10.1016/j.jtbi.2013.01.013. [DOI] [PubMed] [Google Scholar]
- [40].Wilson MT, Fung PK, Robinson PA, Shemmell J, Reynolds JNJ. Calcium dependent plasticity applied to repetitive transcranial magnetic stimulation with a neural field model. J Comput Neurosci 2016;41:107–25. 10.1007/s10827-016-0607-7. [DOI] [PubMed] [Google Scholar]
- [41].Wang B, Grill WM, Peterchev AV. Coupling Magnetically Induced Electric Fields to Neurons: Longitudinal and Transverse Activation. Biophysical Journal 2018;115:95–107. 10.1016/j.bpj.2018.06.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42].Galanis C, Fellenz M, Becker D, Bold C, Lichtenthaler SF, Müller UC, et al. Amyloid-beta mediates homeostatic synaptic plasticity. J Neurosci 2021. 10.1523/JNEUROSCI.1820-20.2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Cuntz H, Forstner F, Borst A, Häusser M. One Rule to Grow Them All: A General Theory of Neuronal Branching and Its Practical Application. PLOS Computational Biology 2010;6:e1000877. 10.1371/journal.pcbi.1000877. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Cuntz H, Borst A, Segev I. Optimization principles of dendritic structure. Theoretical Biology and Medical Modelling 2007;4:21. 10.1186/1742-4682-4-21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Hines ML, Carnevale NT. The NEURON Simulation Environment. Neural Computation 1997;9:1179–209. 10.1162/neco.1997.9.6.1179. [DOI] [PubMed] [Google Scholar]
- [46].Aberra AS, Peterchev AV, Grill WM. Biophysically realistic neuron models for simulation of cortical stimulation. J Neural Eng 2018;15:066023. 10.1088/1741-2552/aadbb1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Beining M, Mongiat LA, Schwarzacher SW, Cuntz H, Jedlicka P. T2N as a new tool for robust electrophysiological modeling demonstrated for mature and adult-born dentate granule cells. ELife 2017;6:e26517. 10.7554/eLife.26517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48].Cuntz H, Bird AD, Beining M, Schneider M, Mediavilla L, Hoffmann FZ, et al. A general principle of dendritic constancy – a neuron’s size and shape invariant excitability. BioRxiv 2019:787911. 10.1101/787911. [DOI] [PubMed] [Google Scholar]
- [49].Jarsky T, Roxin A, Kath WL, Spruston N. Conditional dendritic spike propagation following distal synaptic activation of hippocampal CA1 pyramidal neurons. Nature Neuroscience 2005;8:1667–76. 10.1038/nn1599. [DOI] [PubMed] [Google Scholar]
- [50].Plonsey R Bioelectric Phenomena. New York, NY: McGraw-Hill; 1969. [Google Scholar]
- [51].Plonsey R, Heppner DB. Considerations of quasi-stationarity in electrophysiological systems. Bulletin of Mathematical Biophysics 1967;29:657–64. 10.1007/BF02476917. [DOI] [PubMed] [Google Scholar]
- [52].Windhoff M, Opitz A, Thielscher A. Electric field calculations in brain stimulation based on finite elements: An optimized processing pipeline for the generation and usage of accurate individual head models. Human Brain Mapping 2013;34:923–35. 10.1002/hbm.21479. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Saturnino GB, Madsen KH, Thielscher A. Electric field simulations for transcranial brain stimulation using FEM: an efficient implementation and error analysis. J Neural Eng 2019;16:066032. 10.1088/1741-2552/ab41ba. [DOI] [PubMed] [Google Scholar]
- [54].Saturnino GB, Puonti O, Nielsen JD, Antonenko D, Madsen KH, Thielscher A. SimNIBS 2.1: A Comprehensive Pipeline for Individualized Electric Field Modelling for Transcranial Brain Stimulation. In: Makarov S, Horner M, Noetscher G, editors. Brain and Human Body Modeling: Computational Human Modeling at EMBC 2018, Cham: Springer International Publishing; 2019, p. 3–25. 10.1007/978-3-030-21293-3_1. [DOI] [PubMed] [Google Scholar]
- [55].Attene M. A lightweight approach to repairing digitized polygon meshes. Vis Comput 2010;26:1393–406. 10.1007/s00371-010-0416-3. [DOI] [Google Scholar]
- [56].Geuzaine C, Remacle J-F. Gmsh: A 3-D finite element mesh generator with built-in pre- and post-processing facilities. International Journal for Numerical Methods in Engineering 2009;79:1309–31. 10.1002/nme.2579. [DOI] [Google Scholar]
- [57].Shirinpour S, Opitz A. A high-resolution finite element method (FEM) human head model for non-invasive brain stimulation 2021. 10.5281/zenodo.5209082. [DOI] [Google Scholar]
- [58].Kammer T, Beck S, Thielscher A, Laubis-Herrmann U, Topka H. Motor thresholds in humans: a transcranial magnetic stimulation study comparing different pulse waveforms, current directions and stimulator types. Clinical Neurophysiology 2001;112:250–8. 10.1016/S1388-2457(00)00513-7. [DOI] [PubMed] [Google Scholar]
- [59].Peterchev AV, Jalinous R, Lisanby SH. A Transcranial Magnetic Stimulator Inducing Near-Rectangular Pulses With Controllable Pulse Width (cTMS). IEEE Transactions on Biomedical Engineering 2008;55:257–66. 10.1109/TBME.2007.900540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [60].Amunts K, Zilles K. Architectonic Mapping of the Human Brain beyond Brodmann. Neuron 2015;88:1086–107. 10.1016/j.neuron.2015.12.001. [DOI] [PubMed] [Google Scholar]
- [61].DeFelipe J, Hendry SHC, Hashikawa T, Molinari M, Jones EG. A microcolumnar structure of monkey cerebral cortex revealed by immunocytochemical studies of double bouquet cell axons. Neuroscience 1990;37:655–73. 10.1016/0306-4522(90)90097-N. [DOI] [PubMed] [Google Scholar]
- [62].Mountcastle VB. The columnar organization of the neocortex. Brain 1997;120:701–22. 10.1093/brain/120.4.701. [DOI] [PubMed] [Google Scholar]
- [63].Borg-Graham LJ. Interpretations of Data and Mechanisms for Hippocampal Pyramidal Cell Models. In: Ulinski PS, Jones EG, Peters A, editors. Models of Cortical Circuits, Boston, MA: Springer US; 1999, p. 19–138. 10.1007/978-1-4615-4903-1_2. [DOI] [Google Scholar]
- [64].Breit M, Stepniewski M, Grein S, Gottmann P, Reinhardt L, Queisser G. Anatomically Detailed and Large-Scale Simulations Studying Synapse Loss and Synchrony Using NeuroBox. Front Neuroanat 2016;10. 10.3389/fnana.2016.00008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [65].Reiter S, Vogel A, Heppner I, Rupp M, Wittum G. A massively parallel geometric multigrid solver on hierarchically distributed grids. Comput Visual Sci 2013;16:151–64. 10.1007/s00791-014-0231-x. [DOI] [Google Scholar]
- [66].Vogel A, Reiter S, Rupp M, Nägel A, Wittum G. UG 4: A novel flexible software system for simulating PDE based models on high performance computers. Comput Visual Sci 2013;16:165–79. 10.1007/s00791-014-0232-9. [DOI] [Google Scholar]
- [67].Breit M, Kessler M, Stepniewski M, Vlachos A, Queisser G. Spine-to-Dendrite Calcium Modeling Discloses Relevance for Precise Positioning of Ryanodine Receptor-Containing Spine Endoplasmic Reticulum. Scientific Reports 2018;8:15624. 10.1038/s41598-018-33343-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [68].Breit M, Queisser G. What Is Required for Neuronal Calcium Waves? A Numerical Parameter Study. The Journal of Mathematical Neuroscience 2018;8:9. 10.1186/s13408-018-0064-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [69].Ahrens J, Geveci B, Law C. 36 - ParaView: An End-User Tool for Large-Data Visualization. In: Hansen CD, Johnson CR, editors. Visualization Handbook, Burlington: Butterworth-Heinemann; 2005, p. 717–31. 10.1016/B978-012387582-2/50038-1. [DOI] [Google Scholar]
- [70].Alekseichuk I, Shirinpour S, Opitz A. Finite element method (FEM) models for translational research in non-invasive brain stimulation 2020. 10.5281/zenodo.4009465. [DOI] [Google Scholar]
- [71].Wagner TA, Zahn M, Grodzinsky AJ, Pascual-Leone A. Three-dimensional head model Simulation of transcranial magnetic stimulation. IEEE Transactions on Biomedical Engineering 2004;51:1586–98. 10.1109/TBME.2004.827925. [DOI] [PubMed] [Google Scholar]
- [72].Huang Y-Z, Edwards MJ, Rounis E, Bhatia KP, Rothwell JC. Theta Burst Stimulation of the Human Motor Cortex. Neuron 2005;45:201–6. 10.1016/j.neuron.2004.12.033. [DOI] [PubMed] [Google Scholar]
- [73].Opitz A, Paulus W, Will S, Antunes A, Thielscher A. Determinants of the electric field during transcranial direct current stimulation. NeuroImage 2015;109:140–50. 10.1016/j.neuroimage.2015.01.033. [DOI] [PubMed] [Google Scholar]
- [74].Gomez LJ, Dannhauer M, Koponen LM, Peterchev AV. Conditions for numerically accurate TMS electric field simulation. Brain Stimulation 2020;13:157–66. 10.1016/j.brs.2019.09.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [75].Brzosko Z, Mierau SB, Paulsen O. Neuromodulation of Spike-Timing-Dependent Plasticity: Past, Present, and Future. Neuron 2019;103:563–81. 10.1016/j.neuron.2019.05.041. [DOI] [PubMed] [Google Scholar]
- [76].Feldman DE. The Spike-Timing Dependence of Plasticity. Neuron 2012;75:556–71. 10.1016/j.neuron.2012.08.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [77].Mörschel K, Breit M, Queisser G. Generating Neuron Geometries for Detailed Three-Dimensional Simulations Using AnaMorph. Neuroinformatics 2017;15:247–69. 10.1007/s12021-017-9329-x. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


