Growth and thermal maturation of the Toba magma reservoir

Significance

Understanding the thermal state of magma reservoirs before supereruptions is crucial for interpreting the processes leading to such catastrophic events. Here, we show that the two supereruptions of Toba were preceded and followed by protracted magma influx at relatively constant average volumetric rate over the past 2.2 My. This suggests that increased magma flux is not essential before supereruptions. Instead, long-term thermal maturation of the magma reservoir related to significant magma pulses primes the system for eruption. Importantly, our results indicate that significant variations of monitoring parameters, such as increased surface deformation or degassing, may not occur before supereruptions. Our method can be widely applied to other large silicic magmatic systems to evaluate their potential to feed a supereruption.

Abstract

The Toba volcanic system in Indonesia has produced two of the largest eruptions (>2,000 km³ dense-rock equivalent [DRE] each) on Earth since the Quaternary. U–Pb crystallization ages of zircon span a period of ∼600 ky before each eruptive event, and in the run-up to each eruption, the mean and variance of the zircons’ U content decrease. To quantify the process of accumulation of eruptible magma underneath the Toba caldera, we integrated these observations with thermal and geochemical modeling. We show that caldera-forming eruptions at Toba are the result of progressive thermal maturation of the upper crustal magma reservoir, which grows and chemically homogenizes, by sustained magma influx at average volumetric rates between 0.008 and 0.01 km³/y over the past 2.2 My. Protracted thermal pulses related to magma-recharge events prime the system for eruption without necessarily requiring an increased magma-recharge rate before the two supereruptions. If the rate of magma input was maintained since the last supereruption of Toba at 75 ka, eruptible magma is currently accumulating at a minimum rate of ∼4.2 km³ per millennium, and the current estimate of the total volume of potentially eruptible magma available today is a minimum of ∼315 km³. Our approach to evaluate magma flux and the rate of eruptible magma accumulation is applicable to other volcanic systems capable of producing supereruptions and thereby could help in assessing the potential of active volcanic systems to feed supereruptions.

Supereruptions are events that eject ≥450-km³ dense-rock equivalent (DRE) of magma with a volcanic explosivity index of ≥8 (1, 2). They are commonly fed by giant silicic magma reservoirs in the upper continental crust (less than or equal to ∼15 km in depth; refs. 3–5). While it is clear that these reservoirs are assembled by protracted input of magma into the crust, it is debated whether a sudden increase of the rate of magma input is required to initiate large eruptions (6–9). High-precision zircon dating has confirmed the prolonged lifetime (10⁵ to 10⁶ y) of large magma reservoirs, but the total duration of zircon crystallization varies for different systems (8, 10–12). The varying “incubation” times could reflect differences in the rate of magma input into the reservoir, thermal maturity, and/or extrusive–intrusive ratio (e.g., ref. 7). Due to the rarity of these events, it is difficult to statistically determine the recurrence rate of supereruptions (13, 14). Thus, identifying the processes leading to these events is vital to quantify the potential hazard associated with supereruptions at a local and global scale.

The Toba volcanic system has produced two supereruptions within the past 1 My (15), which provides a natural laboratory for investigating the processes that repeatedly lead to large volcanic events. Toba is located on the continental margin of the Sunda arc on Sumatra Island, Indonesia (Fig. 1A). The onset of explosive volcanism was marked by the 1.20 ± 0.16 Ma Haranggaol Dacite Tuff (HDT; ref. 16), followed by the 0.84 ± 0.03 Ma Oldest Toba Tuff (OTT; ref. 17), the 0.501 ± 0.005 Ma Middle Toba Tuff (MTT; ref. 18), and the 75.0 ± 0.9 ka Youngest Toba Tuff (YTT; ref. 19). Intense structural uplift of the Samosir Island until at least ∼2700 B.P. indicates post-YTT magmatic unrest underneath the Toba caldera (e.g., ref. 20). The OTT and YTT are supereruptions that released at least 2,300 km³ and 2,800 km³ of magma, respectively (21, 22), and generated calderas that are partly occupied by Lake Toba today. The HDT and MTT are relatively small in volume (tens of cubic kilometers DRE; ref. 15) and sourced from a similar vent location in the northern part of the large caldera (Fig. 1A). Based on a present-day low-velocity zone beneath Toba, the magma reservoir footprint is estimated to be a minimum of 70 × 30 km (23). Comparatively, using the caldera floor as a proxy for the magma reservoir footprint, it was ∼55 × 20 km for the OTT and 100 × 30 km for the YTT (15).

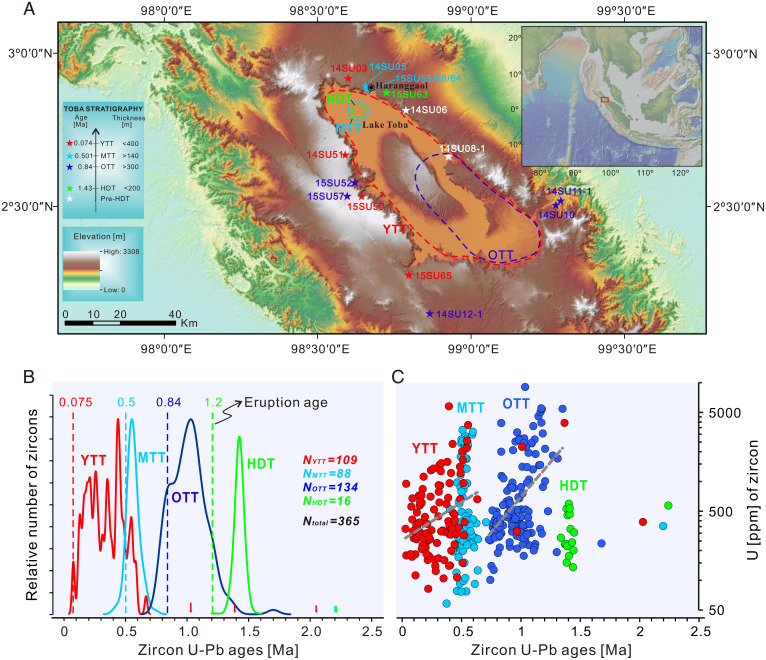
Fig. 1.

Topographic map of the Toba caldera, along with age-distribution spectrum and U content of zircons from the four eruptions of Toba. (A) Approximate source-caldera areas of the HDT, OTT, MTT, and YTT are outlined (15). Stars represent the sampling locations. (Inset) The location of the Toba caldera in northern Sumatra, Indonesia. (B) Zircon age distributions for the HDT, OTT, MTT, and YTT. The colored arrows pointing to the x axis indicate zircons with older ages in respective eruptions. We present the density of the natural ages with a bandwidth equal to 1σ analytical error. Eruption ages (Ma) and number of zircon (N) analyzed in each eruption are also specified. (C) Variation of U content of zircons as a function of age for each eruption. Gray dotted lines represent the mean trend of zircon U contents of the OTT and YTT eruptions with age.

Results and Discussion

We synthesized all information gathered from field geology and geophysics, zircon geochronology, and geochemistry, in combination with numerical modeling, to constrain the average rate of magma input and eruptible magma accumulation in the Toba plumbing system. We obtained 365 zircon model ages from 15 samples of the 4 major explosive eruptions of Toba. The ages span a continuous range from ∼1.7 Ma to ∼75 ka B.P., with a few ages as old as 2.2 Ma (Dataset S1). Specifically, the distributions of zircon ages for the HDT and MTT span ∼100 ky, significantly shorter than those of the OTT and YTT, which crystallized over a period in excess of 600 ky before eruptions (Fig. 1B). Zircons from the HDT have consistently low U contents (<500 ppm), whereas those from the MTT have variable U contents similar to YTT zircons of similar ages (Fig. 1C). The U contents of zircons from both the OTT and YTT spread a large range from tens of ppm to >5,000 ppm. Interestingly, the mean U content of zircons in the OTT decreases from ∼1,800 ppm at 1.4 Ma to ∼350 ppm before eruption, whereas zircons in the YTT decrease from ∼700 ppm at 0.67 Ma to 300 ppm before eruption (Fig. 1C). The zircon age range we measured for the YTT agrees with those of ref. 24 and highlights that zircon spans a notably longer crystallization period than allanite (25). These results suggest that a minority of zircons of the OTT and YTT can be considered as either antecrysts or xenocrysts. Core to rim profiles obtained on zircons from different samples of the same eruption show similar age range, but different Th/U trends (24), suggesting that the erupted magma was sampled from portions of the magma reservoir with distinct thermal histories.

We generated zircon populations using thermal modeling and explored a variety of input parameters that most affect the distribution of zircon crystallization ages. We then compared natural and synthetic distributions to estimate the average rate of magma input and volume of eruptible magma accumulation preceding the OTT and YTT eruptions, using 1) the duration of zircon crystallization, 2) the relationship between age and average U content of zircons, and 3) the eruptive volumes. The comparison between the synthetic and natural distribution of crystallization ages should account for potential sampling biases because the natural distribution is a subsample of the true population distribution of all erupted zircons. Thus, from the synthetic population of zircons, we subsampled zircon ages 100 times (to simulate the analyses of 100 zircons from a single eruption). Repeating this process 1,000 times, we show that the range (i.e., oldest age minus youngest age) in zircon ages is susceptible to sampling bias (SI Appendix, Fig. S1). This is because subsampling manifests especially for older ages, which appear as a tail in natural distributions and represent periods during which fewer zircons crystallize (Fig. 1B). Therefore, we compared natural and synthetic distributions using sample SD as a proxy for the duration of zircon crystallization. Given that for both the OTT and the YTT 1) the sample SD is an order of magnitude larger than the mean analytical error, 2) each sample has a large number of analyses (>100), and 3) within-sample age and analytical error are uncorrelated, then the analytical error will have little impact on the sample SD, which will be dominantly controlled by the spread in zircon ages.

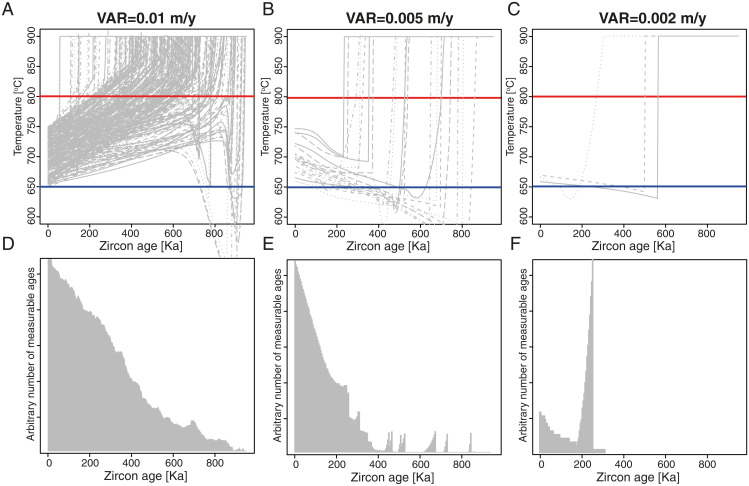
The parameters of the modeled magma reservoir were set up according to those of the Toba upper crustal magma reservoir. Specifically, the modeled magma reservoir was assembled by injection at 10 km below the surface as cylindrical sills of 18 and 36 km in radius, generating a footprint for the magmatic system that encompasses those of the OTT and YTT. Magma was injected at 900 °C either in thermally unconditioned (20 °C/km, initial wall-rock temperature of 200 °C; ref. 26) or preconditioned crust (40 °C/km, wall-rock temperature of 400 °C). Our calculations showed that the lateral extent of the magma reservoir, zircon saturation temperature (T_zr = 850 to 750 °C; ref. 27), and minimum eruptible temperature (T_min = 725 to 650 °C; ref. 28) play minor roles in controlling the time span of zircon crystallization (Fig. 2), which is consistent with previous studies (9, 29–31). The vertical accretion rate (VAR), initial temperature of the wall rock, and duration of the magma input were the most important factors controlling the synthetic populations of zircon ages (Fig. 2). Among them, VAR exerted a fundamental control on the age range of zircon crystallizing in the eruptible portion of a magma reservoir. Modeling results showed that when increasing the VAR from 0.002 m/y to 0.01 m/y for 1 My of magma input, the spread in zircon ages increased from ∼300 ky to ∼900 ky (Fig. 3).

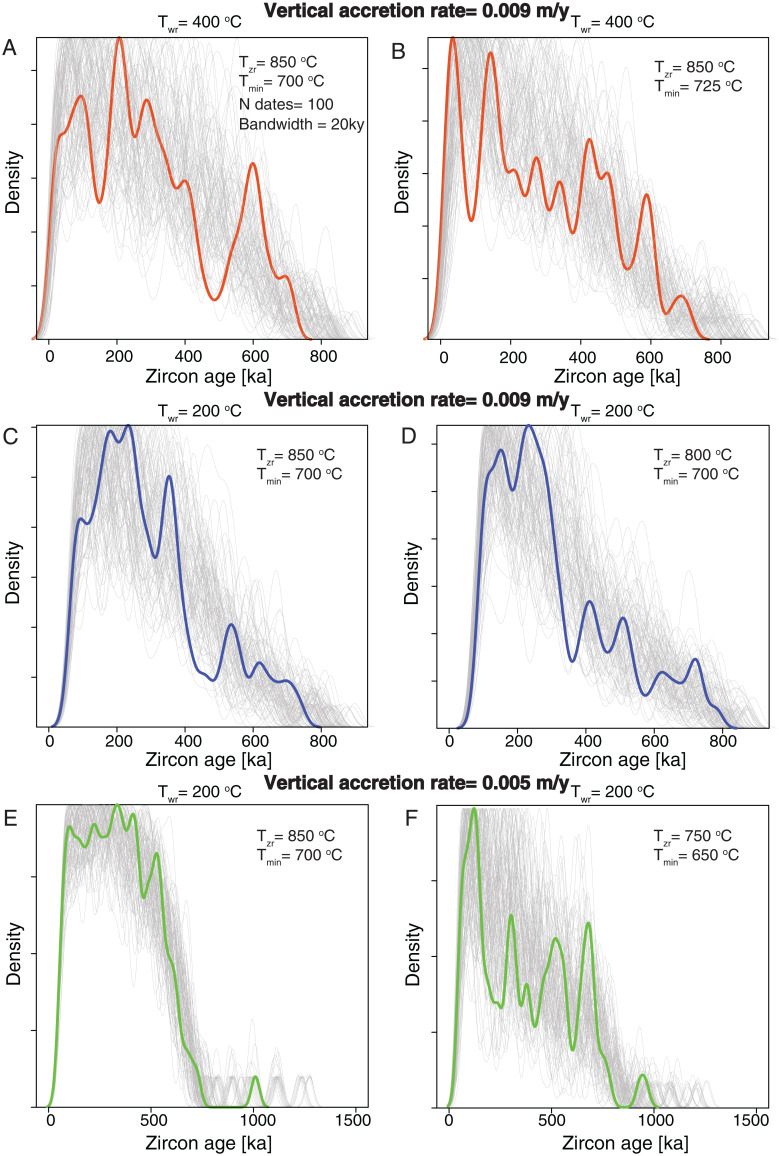
Fig. 2.

Distribution of zircon crystallization ages for different rates of magma input (VAR), temperature of the wall rocks (T_wr), and temperature range of zircon saturation and eruption (T_zr, temperature of zircon saturation; T_min, minimum temperature of eruption). (A–F) The gray lines are bootstrapped distributions obtained by subsampling the synthetic populations of zircon crystallization 100 times with a probability proportional to the number of calculated measurable crystallization times. The thick colored lines show an example of a distribution. Note the different scales of E and F. The peaks in crystallization times are randomly distributed and do not have a geological meaning.

Fig. 3.

Relationships between rate of magma input and distribution of zircon ages. (A–C) Each gray line shows the evolution of temperature for one of the passive tracers injected throughout the modeled period. The red line at 800 °C is the zircon-saturation temperature, and the blue line at 650 °C is the minimum temperature of zircons that are eruptible (in this case, we consider equal to the solidus temperature for simplicity). (D–F) Distribution of measurable zircon ages (no assumption on the location of age in a single zircon) for the simulation presented in A–C, respectively.

Results show that the models performed, considering continuous versus pulsed injection of magma, at the same average rate generated the same distribution of zircon ages (SI Appendix, Fig. S2). This is in agreement with the finding that the thermal evolution of a magmatic system depends chiefly on the average rate of magma input (9, 32). To assess if the peaks observed especially in the YTT zircon ages have a geological meaning, using the same setup as described earlier and subsampling the synthetic zircon population, we show for a sample of 100 zircons that multimodality is not consistent. This multimodality in the zircon distributions was more likely to persist for younger eruptions, due to covariance of the analytical uncertainty and absolute age between different units. Hence, 100 age determinations are not sufficient to assign a geological meaning to the peaks observed in natural distributions (Fig. 2; ref. 9) and give no credence to modeling discretized magma injection. Thus, apparent peaks in the natural distributions are the result of subsampling.

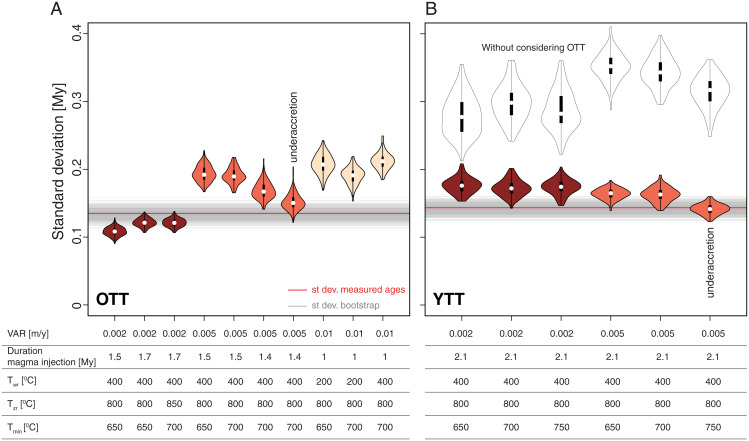
For Toba volcanic rocks, the oldest zircon age dates back to 2.2 Ma (Fig. 1B), which indicates that some zircons are either antecrysts or xenocrysts. In addition to zircon, all amphibole and some plagioclase were considered to be xenocrysts, and the oldest crystallized at around 1.5 Ma (33). Earlier volcanic activity of Toba at ∼1.6 Ma was also recorded in a marine tephra layer in Southeast Asia (34). We therefore inferred that magma input in the upper crustal magma reservoir of Toba started at about 2.2 Ma. Accordingly, the minimum duration of magma input into the plumbing system preceding the OTT eruption is ∼1.4 My. Modeling results showed that the sample SD of natural zircon ages for the OTT is closest to the values calculated for either 1.7 My of pre-eruptive magma injection at a VAR of 0.002 m/y or 1.4 My at a VAR of 0.005 m/y within a thermally conditioned crust (Fig. 4A). For higher magma fluxes, the SDs of synthetic samples are always higher with respect to the natural ones, even considering only 1 My of magma injection (Fig. 4A). For YTT, considering that zircons with ages predating the OTT eruption are sporadic and account for only <3% of the sample, we removed from our synthetic populations all zircon ages predating OTT. This is equivalent to assuming that the OTT eruption removed the totality of zircons from the eruptible portion of the reservoir, leaving highly crystallized magma. Thermally, this assumption implies that the impact of the leftover magma on the thermal evolution of the reservoir was more important than the removal of the magma volume erupted by OTT. Without removing the zircons predating OTT, no simulations returned sample SDs similar to the natural sample for the YTT (Fig. 4B). With this assumption, the sample SDs were similar to the natural samples with the best match for the highest VAR of 0.005 m/y by underaccretion. The natural zircon ages measured for the HDT and MTT span a range that is within analytical error and are therefore not suitable for estimating magma fluxes using our approach.

Fig. 4.

Summary of the thermal modeling results for zircon crystallization. (A–B) The red line is the SD (st. dev.) of zircon ages for the natural OTT and YTT samples. The gray lines are SDs for the bootstrapped zircon age distributions. The violin plots present the distributions of SDs for 1,000 samples from a larger population, for the same number of measurements collected for the OTT (n = 134) and the YTT (n = 109). The colors of the violins relate to the VAR used in the model. The white violin plots show the results obtained without considering the removal of zircons by the OTT eruption. Each of the violin plots shows the results of models performed for different scenarios, as specified at the bottom of the figure. The best-fit models are considered those for which the violin plot overlaps with the gray lines.

The U content of zircons provides additional insights into the thermal and chemical architecture of the magma reservoir before the four eruptions investigated here. A wide range of U content of zircons suggests their crystallization from a heterogenous magma body characterized by a wide range of temperatures and melt fractions. Consequently, both low values and low variance in the U content of zircons erupted in the HDT indicate that they were produced by a thermally and chemically homogeneous magma reservoir at relatively high temperature, which is in agreement with the andesitic–dacitic compositions of HDT (15). Conversely, the progressive decrease of variance and mean U content of zircons erupted in both the OTT and YTT indicates progressive homogenization of the reservoir accompanied by an increase of temperature (Fig. 1). MTT zircons showed similar ages and U distributions with the oldest zircons erupted by the YTT, which suggests that the MTT probably represents partial eruption of the reservoir that finally grew to feed the YTT eruption. Given that the MTT consists purely of high-Si rhyolite (72 to 76 wt% SiO₂), with the most enriched Sr isotopic compositions (⁸⁷Sr/⁸⁶Sr = 0.71470 to 0.71521) among the four eruptions (15), it is likely that the MTT only erupted an evolved portion of the magma body.

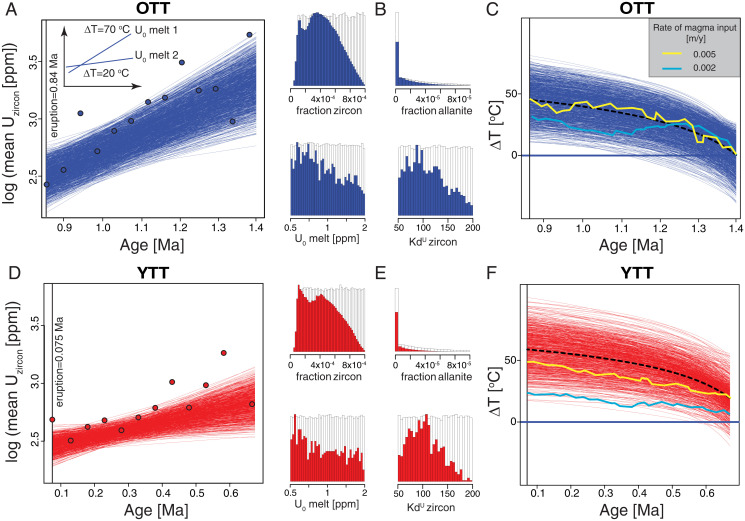
To refine our estimates of the VARs, we modeled the U content of zircon as a function of time for the OTT and YTT (Methods; Fig. 1C). Considering that U is incompatible in all mineral phases of the Toba magmatic system, except in zircon and allanite, such a decrease indicates a progressive increase of temperature (25, 35). This is in agreement with the increasing average Ti content with decreasing zircon ages (SI Appendix, Fig. S3 and Dataset S2). Our calculations showed that the temperature increase during the assembly of OTT and YTT magma was the main parameter influencing the evolution of the average U content of zircon (Fig. 5). Using a VAR of 0.005 m/y, the average U content of zircon of the OTT decreased from ∼1,800 to 300 ppm and that of the YTT changed slightly less, from ∼560 to 300 ppm (Fig. 5 A and D). These results match well the average U content of natural zircons for the OTT and YTT eruptions (Fig. 1C). Moreover, the temperature increase we obtained from the calculations for the OTT and YTT best matches that obtained with a VAR of 0.005 m/y (Fig. 5 C and F). These temperatures also agree with the pre-eruptive temperatures calculated by ref. 28.

Fig. 5.

Summary of the modeling results of the U content in zircon. (A) The circles show the mean U content of zircons as a function of age (binned for 50-ky range) for the OTT (blue). The blue lines show the best-matching simulations. (Inset) The impact of different total increase of temperature (ΔT) and initial U content of the melt from which zircons crystallize (U₀), on the slope and intercept of the calculated lines in the semilog plot. (B) The white histograms show the distributions of the simulated range for each of the relevant parameters of the models, and the blue histograms show the distributions for the best-matching simulations. (C) The blue lines show the evolution of relative temperature as a function of zircon ages for the best-matching simulations shown in A. The dashed black line is the mean temperature increase for the best-matching simulations. The yellow and cyan lines show the evolution of relative temperature for VARs of 0.005 and 0.002 m/y, respectively. (D–F) Same as A–C, but for the YTT eruption.

As a final parameter to consider for our estimates of the average rate of magma input in the Toba plumbing system, we compared modeled volumes of eruptible magma (temperature >750 °C and all interstitial melt) with those erupted by the two large caldera-forming eruptions of the OTT and YTT. In our model, with a VAR of 0.005 m/y and an equivalent radius of 18 km, a total of ∼7,125 km³ magma would have been injected before the OTT eruption, of which ∼1,450 km³ was eruptible at the moment of eruption. This eruptible volume is smaller than the erupted OTT volume. Either prolonging the duration of magmatism or increasing the rate of magma input would increase the volume of eruptible magma present within the reservoir at the moment the OTT eruption occurred. However, such variations would also increase the difference between the natural and synthetic zircon age distributions (Fig. 4). We further tested the injection at the base of previous sills (underaccretion), as this is thermally more efficient (32). However, this only yielded an ∼20% increase of eruptible magma volume for the same duration of magma input, which is not sufficient to account for the total volume erupted by the OTT. The only remaining option is that the reservoir footprint was larger than the surface of the caldera, which has been shown to be plausible by numerical modeling (36) and seems appropriate for the Toba magma reservoir (4). To constrain the effect of the radius of the system on the rate of accumulation of eruptible magma, we performed a simulation considering a VAR of 0.005 m/y and a radius of the magma reservoir of 36 km. As expected, the vertical rate of eruptible magma accumulation dropped, while the total amount of eruptible magma available after a given duration of magma input increased (SI Appendix, Fig. S4). This is because the quadratic dependency of volume on the radius of the system overwhelmed the impact of the decreased rate of vertical accumulation of eruptible magma. Assuming a linear dependence of the vertical rate of eruptible magma accumulation and radius of the magma reservoir for values between 18 and 36 km (32), we calculated the rate of eruptible magma accumulation in such a reservoir. An equivalent radius of 22 km of the reservoir would be sufficient to accumulate 2,300 km³ of eruptible magma when OTT occurred (i.e., after 1.4 My of magma influx; SI Appendix, Fig. S4). With this footprint, over 10,640 km³ of magma would have been injected into the OTT magma reservoir during the 1.4 My preceding the eruption, of which ∼22% is eruptible. Likewise, for the YTT eruption, the footprint of the magma reservoir could have grown further in the time period between OTT and YTT, which seems in line with the increase of caldera size from 55 × 20 km to 100 × 30 km. To obtain 2,800 km³ of eruptible magma in the 0.76-My time period between the OTT and YTT, the reservoir should have grown to an equivalent radius of ∼25 km. Such progressive growth of a magma reservoir is plausible because the addition of large amounts of heat to the crust changes its rheological properties and favors the merging of discrete magma bodies (37), which has been demonstrated to occur in rather short timescales (tens to hundreds of ky; ref. 38). Therefore, the average volumetric rate of magma input was ∼0.008 km³/y in the period preceding OTT eruption and potentially increased, because of the increasing footprint of the reservoir, to 0.01 km³/y before the YTT eruption.

Our study shows that repeated supereruptions at Toba occur because of the progressive thermal maturation of the magmatic system and surrounding crust by prolonged magma influx over timescales of hundreds of thousands to millions of years. A similar maturation process was documented for the Glass Mountain–Bishop Tuff volcanic system (39). Importantly, these two supereruptions were not caused by a sudden increase of the rate of magma input. Thermal maturation at Toba is represented by the increase of the average temperature of the entire magma reservoir (i.e., the weighted average temperature between solidus and liquidus). The period of magma accumulation for the OTT and YTT was accompanied by an increase of the weighted average temperature of ∼50 °C and 30 °C, respectively (Fig. 5 C and F). This is consistent with studies of titanium content in quartz of the YTT, which show that significant thermal pulses related to magma-recharge events prime the system for eruption (40). Thermal maturation of the Toba magma reservoir characterized by increasing temperature and therefore mildly less evolved average magma composition is similar to those predicted by ref. 41 for constant magma flux. This is in contrast to more active volcanoes, such as the Taupo volcanic system, which has produced smaller eruptions characterized by consistently high SiO₂ contents (>72 wt%) and more evolved compositions at low temperatures with time (42).

The effect of thermal maturation of the crust is also manifested by the time interval between supereruptions. The OTT occurred after at least 1.4 My of magma influx, while the YTT occurred 0.76 My after the OTT. We can calculate the total volume of magma injected into the Toba magma reservoir since the YTT eruption and the potential volume of eruptible magma present today using our results and some assumptions. We consider that 1) replenishment of the subvolcanic reservoir at Toba started immediately after the YTT (20), 2) magma accumulates at a VAR of 0.005 m/y, and 3) the current reservoir has a footprint similar to the YTT caldera (i.e., 100 × 30 km and 27.4-km equivalent radius). This calculation returns a volumetric rate of magma input of 0.012 km³/y, which implies that after the YTT eruption, about 900 km³ of magma has been injected into the reservoir. For the same proportion of eruptible magma accumulation as in the period preceding the YTT (i.e., 0.0018 m/y), about 315 km³ of magma would be eruptible. Indeed, molten magma has been detected accumulating beneath Toba as horizontal sills (4), which could be formed at an early stage of thermal maturation. It is important to note that the estimated magma volume is a minimum because the footprint of the reservoir could be now larger than the YTT caldera (37, 38). We suggest that applying our approach to other systems already associated with supereruptions, such as the Yellowstone, the Altiplano–Puna Volcanic Complex, and the Taupo Volcanic Zone, will help us to identify the most likely location for the next supereruption and to obtain an upper limit of plausible eruptive magnitudes.

Methods

Zircon U–Pb Ages and Trace Element Analyses.

Zircon concentrates were separated from ∼2 kg of rock samples by using standard density and magnetic-separation techniques. Zircon separates, together with zircon standards Plešovice and Qinghu, were mounted in epoxy and polished to expose half of the crystals. All zircons were documented with transmitted- and reflected-light photomicrographs as well as cathodoluminescence images to reveal their internal textures. Measurements of U, Th, and Pb isotopes were conducted by using CAMECA IMS-1280HR at the Institute of Geology and Geophysics, Chinese Academy of Sciences in Beijing. The O²⁻ primary ion beam was accelerated at −13 kV, with an intensity of ca. 10 nA. The aperture illumination mode (Kohler illumination) was used to produce an elliptical spot of about 20 × 30 μm in size. Mass resolution was set at ∼7,000 (at 50% peak height). A dynamic multicollector mode was used to measure secondary ion-beam intensities, including Pb isotope measurements by multicollectors and U–Th species by peak jumping sequence (43). Pb/U and Th/U ratios were determined relative to the standard zircon Plešovice (44), analyses of which were interspersed with those of unknown grains.

The very young (<2 Ma) zircon samples were dated on the condition of ²³⁸U–²³⁰Th disequilibrium, and the initial Th in zircon was corrected on a spot-by-spot basis by Th/U fractionation in zircon and the magma from which it was crystallized. The following equation represents the relationship between the ²⁰⁶Pb/²³⁸U ratio and age t (modified from ref. 45):

$$\frac{{ }^{206}{\text{Pb}}_{\text{Zircon}}^{ }{}_{ }}{{}_{ }{}^{238}\text{U}{}_{\text{Zircon} }}=\frac{{ }^{206}{\text{Pb}}_{\text{common}}{}_{ }}{{}_{ }{}^{238}\text{U}{}_{\text{Zircon} }}+\left({\text{e}}^{{\text{λ}}_{238 }\text{t}}-1\right)+ \frac{{\text{λ}}_{238 }}{{\text{λ}}_{230 }}\left({\text{f}}_{\frac{\text{Th}}{\text{U}}}-1\right)\left(1-{\text{e}}^{-{\text{λ}}_{230 }\text{t}}\right){\text{e}}^{{\text{λ}}_{238 }\text{t}},$$

where

$$f_{\frac{Th}{U}}=\frac{{\frac{Th}{U}}_{\mathit{zircon}}}{{\frac{Th}{U}}_{\mathit{magma}}}.$$

It is assumed that the ²³⁴U/²³⁸U ratio is the same in zircon and source magma (²³⁴U and ²³⁸U hold the radioactive equilibrium), and the radioactive equilibrium is established in the source magma. Th/U_magma is represented by the Th/U ratio of whole rock. Common Pb correction used the ²⁰⁷Pb-correction method (45) with an average present-day crustal composition for the common Pb (46). Detailed analytical methods can be found in our recently published paper (47).

Trace element contents of zircon were analyzed by using a New Wave UP213 laser ablation system connected to an Agilent 7500s quadruple inductively coupled plasma mass spectrometer at the Department of Geosciences, National Taiwan University. Detailed analytical protocols can be found in ref. 48.

Thermal and Zircon Crystallization Modeling.

Thermal modeling was performed by using an upgraded finite element approach identical to that presented in ref. 29, modified to add the injection of passive tracers together with magma throughout the duration of the simulations. With this approach, each passive tracer provides the temporal evolution of temperature for a hand specimen of magma. We modeled the continuous injection of magma as cylindrical sills of 18 and 36 km in radius at 10-km depth using two thermal gradients (20 and 40 °C/km). To assess the eventual impact of periodic injection of discrete sills on the temporal evolution of temperature of single passive tracers, we performed one simulation in which single sills were injected every 10 ky. It turned out that there was no significant difference in the synthetic zircon age distributions (SI Appendix, Fig. S2). We did not simulate convection. However, we noticed that thermal modeling studies have shown that variations of the modality of magma injection and geometry of the magmatic system or convection play a secondary-order role on the long-term thermal evolution of magmatic systems and therefore on the zircon age distributions (7, 30, 32, 49, 50). On the other hand, convection of fluids around the reservoir can increase the rate of heat release (51). Thus, our estimates for the rate of magma input and the rate of accumulation of eruptible magma should be considered as minimum.

The average VAR (the parameter controlling the thermal evolution of the magmatic system for this model geometry; ref. 52) was varied between 0.002 and 0.9 m/y. Magma was injected at 900 °C, and the crystal fraction (x_f) increased with decreasing temperature (T in °C; ref. 53) as:

$$x_f=1-\frac{1}{1+e^{\mathit{\theta }}},$$ [1]

where

$$\mathit{\theta }=\frac{(800-T)}{23}.$$ [2]

The fundamental assumptions of our approach are 1) zircon crystallizes within a specific range of temperatures (T_Zr), which is a function of the melt composition and the distribution coefficient of Zr between zircon and melt (54, 55), and 2) the number of zircons crystallizing within a given period of time is proportional to the volume of magma at different temperatures within T_Zr (29, 30). We consider the time–temperature (t–T) trajectories of 1,000 passive tracers injected at constant time intervals between the onset and the end of magma injection. On the basis of these t–T paths, we calculated zircon crystallization ages. The cumulative fraction of zircon (F_zr) for each unit of magma increases with decreasing temperature as (56):

$$F_{zr}=\left\{1.62-1.8\cdot {10}^4{e}^{-\frac{{10}^4}{T}}\right\}\cdot z{r}_m,$$ [3]

where T is the temperature in Kelvin (range between 973 and 1,073), and zr_m is the maximum fraction of zircon crystallizing between zircon saturation temperature (T_zr) and the solidus temperature (T_s). To calculate the distribution of zircon ages for different T_zr, we maintained the same topology of Eq. 3 and modified the temperature range according to T_zr and T_s.

Each tracer contained an arbitrary number of measurable ages (e.g., 100), and the rate of zircon crystallization decreased with decreasing temperature following the derivative of Eq. 3. When an eruption occurred, we considered only the tracers with a temperature higher than a minimum temperature (T_min) can be erupted. T_min can be considered either as the minimum temperature at which magma (and zircons) can be erupted or the temperature of the interstitial melt extracted (together with zircon) to feed a volcanic eruption. The tracer that spent the longest period of time within the temperature interval of zircon saturation provided the maximum possible duration of continuous zircon crystallization. Once this was determined, we summed all measurable ages between the oldest age and the time of eruption. However, due to the artificial bias that zircons with large sizes are preferentially chosen for analysis and that the smallest zircon analyzed in the OTT was 123 μm and that in the YTT was 131 μm, we only sampled zircons larger than this size in respective eruptions. Thus, zircons crystallized close to eruption could be small in size and may not be sampled. This could account for the tailing off of zircon numbers before eruptions and the offset of age peaks in our data and in the modeling result.

To determine the significance of eventual peaks in the distribution of zircon ages, we subsampled our total distribution of zircon ages (generally a total of a few hundred thousand measurable ages) and selected 100 values, with a probability that is proportional to the number of measurable ages calculated for each time interval of the model. We repeated this sampling procedure 100 times. This approach highlights how peaks at different ages vary with each aliquot of 100 dates. In fact, zircons from a different set of YTT samples (24) show distinct U–Pb age spikes in probability-density-distribution diagrams compared with ours. These indicate that the spikes randomly occurred and are closely related to the individual samples and the number of zircon analyzed. Any attempts to assign a geological meaning to the spikes may lead to overinterpretation.

Sensitivity Test.

The calculation of synthetic zircon age distributions involves assumptions for a number of parameters (29, 30, 56). Thus, we performed a series of sensitivity tests to identify those that most affect the distribution of zircon ages. We started by testing for the effect of the lateral extent of the magmatic system on the population of zircon ages. In agreement with previous findings, changing the horizontal dimension of the system while keeping the VAR constant did not affect the distribution of zircon ages (29, 52). However, the eruptible/injected magma ratio decreased for more laterally extensive magmatic systems. Furthermore, zircon saturation temperature (T_zr) and the minimum eruptible temperature (T_min) were tested within reasonable ranges from 850 to 750 °C and 725 to 650 °C, respectively, according to previous studies (27, 28). The results showed that the total spread of zircon crystallization ages did not change appreciably for different temperature ranges assigned (Fig. 2). We also tested for the effect of the initial temperature of the wall rock surrounding the magma reservoir (T_wr = 200 °C and 400 °C). The effect of T_wr was minor, as the comparison of the age distribution obtained for the same rate of magma input, but different initial wall-rock temperature, demonstrated a similar age range of zircon crystallization (Fig. 2). Finally, we found that the VAR has the most significant effect on the age distribution of zircon. The higher the VAR is, the longer the zircon ages can be erupted.

To evaluate the impact of local temperature variations on the synthetic population of zircon ages, we tested a scenario that is more extreme than convection, which is the periodic (as opposed to continuous, as all other models we performed) injection of magma at its liquidus temperature. The simulation was repeated by injecting magma at the same average VAR of 9 × 10⁻³ m/y and a T_wr of 200 °C for the same time, but adding pauses between pulses of 10 ky. The results showed that the thermal evolution of the tracers was essentially the same, except for small temperature oscillations visible in the model with pulsed magma injection (SI Appendix, Fig. S2). The results also showed that the effect of the arrival of the magma pulses is too local to be visible in the final distribution of zircon ages. This is consistent with previous studies (50 showing that for large-caldera volcanic systems like Yellowstone and Long Valley, convection would not promote heat release and therefore has little effect on the cooling rate of the intrusion.

In conclusion, our sensitivity tests showed that the main parameter controlling the zircon age distributions and particularly the age interval of continuous zircon crystallization is the rate of magma input. More precisely, the SD of the synthetic zircon crystallization age distribution increases with increasing rate of magma input and with the duration of magmatism (Fig. 4).

Modeling U Content of Zircons.

We first calculated the U content of the magma as a function of temperature considering a pure fractional crystallization model that U is incompatible in all mineral phases, except for zircon and allanite (35, 57). We then calculated the U content of zircon that crystallized at each temperature according to the U content of melt and a fixed partition coefficient of 254 (58). These calculations require the relationship between temperature and melt fraction (Eq. 1), the calculation of the bulk partition coefficient of U, the fractions of zircon and allanite as a function of temperature, and the initial U content of the magma. Due to the lack of defined estimates for these parameters, we adopted an Approximate Bayesian Computation approach. For all parameters, we started with uninformative uniform prior distributions with these ranges: U between 2 and 4 ppm, which reflects the range we obtained by performing whole-rock measurements of our samples; zircon saturation temperature between 725 and 850 °C; allanite saturation temperature between 710 and 750 °C; initial temperature between 650 and 800 °C, temperature at the moment of eruption up to 825 °C (always higher than the magma input temperature of 900 °C to account for the drop of U content of zircons with time and always lower than the zircon saturation temperature); zircon fraction up to 5 × 10⁻³, varying with temperature and zircon saturation temperature, as stated in Eq. 3; and allanite fraction up to 5 × 10⁻⁴, increasing linearly from saturation temperature to the solidus. To identify the best-matching solutions, we first bootstrapped the natural zircon ages and U content 5,000 times to obtain a distribution of slopes and the intercepts for the best-fitting curve. We considered as the best-matching models those that resulted in slopes and intercepts that are within one sigma of the distributions obtained by bootstrapping. The values of input parameters of the best-matching models are reported in the blue and red histograms in Fig. 5 B and E for the OTT and YTT, respectively.

Data Availability

All study data are included in the article and/or supporting information.