Significance
Synapses connecting granule cells to Purkinje neurons are considered essential sites for learning in the cerebellum. Strikingly, most of them appear to be silent: they do not transmit any electrical information. This may relate to information storage capacity and reliability, which are expected to improve during postnatal maturation. Here, we quantify the proportion of silent synapses in mice by combining optogenetic mapping of synaptic inputs and Purkinje neuron patch-clamp recording. We show that this proportion remains stable between the stage immediately following the postnatal establishment of cerebellar circuitry and 3 wk later when cerebellar function has maturated, presumably as a result of natural learning processes. Our results suggest that information storage capacity and reliability are optimized early during cerebellar maturation.
Keywords: cerebellum, memory, synaptic weight, development, quantitative neuroanatomy
Abstract
Cerebellar Purkinje neurons integrate information transmitted at excitatory synapses formed by granule cells. Although these synapses are considered essential sites for learning, most of them appear not to transmit any detectable electrical information and have been defined as silent. It has been proposed that silent synapses are required to maximize information storage capacity and ensure its reliability, and hence to optimize cerebellar operation. Such optimization is expected to occur once the cerebellar circuitry is in place, during its maturation and the natural and steady improvement of animal agility. We therefore investigated whether the proportion of silent synapses varies over this period, from the third to the sixth postnatal week in mice. Selective expression of a calcium indicator in granule cells enabled quantitative mapping of presynaptic activity, while postsynaptic responses were recorded by patch clamp in acute slices. Through this approach and the assessment of two anatomical features (the distance that separates adjacent planar Purkinje dendritic trees and the synapse density), we determined the average excitatory postsynaptic potential per synapse. Its value was four to eight times smaller than responses from paired recorded detectable connections, consistent with over 70% of synapses being silent. These figures remained remarkably stable across maturation stages. According to the proposed role for silent synapses, our results suggest that information storage capacity and reliability are optimized early during cerebellar maturation. Alternatively, silent synapses may have roles other than adjusting the information storage capacity and reliability.
Typical central excitatory synapses are formed onto dendritic spines, the distinctive morphology of which enables their unambiguous identification (1–3). It has generally been assumed that the presence of a dendritic spine equates to the existence of a functional excitatory transmission (4). Based on this assumption, the observation of spine motility in several brain areas (motor cortex and somatosensory cortex) has been considered to reflect synaptic plasticity (5). Indeed, a number of studies have established a correlation between learning and spine formation (6–8) or pruning (9, 10). However, in some conditions, morphological and synaptic plasticity have been shown to be dissociated (11), in line with the view that morphology does not provide all the information necessary to infer synaptic function.
The cerebellum contains the majority of brain neurons (12, 13) and the predominant excitatory synapses found in this structure connect granule cells (GC) to Purkinje cells (PC). These synapses are formed on typical spines borne by PC dendrites (14), the majestic shape of which is likely related to the huge amount of independent inputs they receive. The GC-to-PC synapse is generally acknowledged to be an essential site for plasticity (15–19). However, in sharp contrast to other parts of the brain such as motor and somatosensory cortices, PC spines appear to be constitutive (20, 21), i.e., they appear to be an inherent property of PCs, independent of external factors. Indeed, pruning of these synapses has not been reported. Novel spine formation has been reported, but likely as a result of dendritic tree expansion (22, 23). The high density of spines along PC dendritic branchlets (5 to 17 per linear micrometer in rat; refs. 14 and 24–27) and their regular ordering in a helical pattern (28) support the idea that they optimize space occupancy with little room for spine addition, in accordance with their constitutive nature.
The apparent morphological homogeneity of PC spines is in sharp contrast with the spectacular heterogeneity observed in the strength of GC-to-PC synapses. An in vivo study has reported that the receptive field of a PC was much smaller than that of the GCs putatively connecting to it (29), suggesting that most GC-to-PC synapses are electrically silent. This has been confirmed by an in vitro report (30) showing that synaptic transmission between paired-recorded GC and PC was detected nearly 10 times less frequently than expected from the occurrence of morphologically defined synaptic connections predicted by anatomical data (14, 31–33). Taken together, these two studies conducted in adult rats suggest that most (85% according to ref. 30) morphologically and molecularly defined GC-to-PC synapses are silent, i.e., they do not transmit any detectable electrical signal.
If silent synapses do not transmit information, what is their role? Are they a reserve for additional information storage? Or do they result from information storage optimization (34)? According to this latter proposal (17, 34), since the requirement for optimized information storage is more and more critical as the amount of learned information increases, one might expect that the proportion of silent synapses increases with the amount learning. As previously suggested (34), this hypothesis could be tested by comparing the proportion of silent synapses in young versus adult animals. Indeed, the mouse cerebellar circuitry is not fully in place until the third postnatal week. Then, for at least 3 wk, the mouse acquires basic skills (eating, walking, and social interactions), adapts to changes in muscle strengths and sensitivity to stimuli, and improves its agility (35). Although the amount of cerebellar learning occurring over this maturation period is unclear, it can be reasonably assumed that cerebellar operation continuously optimizes. Here, we investigate how the proportion of silent synapses changes over this period of maturation.
We determine the proportion of silent GC-to-PC synapses by a method based on the determination of the average postsynaptic response per activated synapse (average synaptic weight, ) in superfused acute slices. Thanks to the geometrical and repetitive architecture of the cerebellar cortex, calcium imaging is used to quantitatively map GC inputs. This mapping, combined with postsynaptic recording of transmission, and the determination of two cerebellar anatomical features (the average synapse density and spacing between PC planar dendritic trees) enables the determination of . By comparison with the properties of synapses that produce an electrical postsynaptic response (investigated by paired recording and quantal analysis), we show that the proportion of silent synapses is higher than 70% and stable between the postnatal stages of interest. This suggests that cerebellar maturation has insignificant impact on the proportion of silent synapses.
Results
An Approach to Determine the Average Strength of Cerebellar Synapses.
Our approach is based on combined imaging of input activity and recording of postsynaptic responses in superfused acute sagittal slices from mouse cerebellum and relies on cerebellar anatomical features. The GC axon ascends from the soma to the molecular layer (ascending axon) where it bifurcates to form the parallel fiber (PF). Both sections of the axon form presynaptic boutons at 5- to 10-µm intervals with grossly similar properties (36). The PF being at least 20 times longer than the ascending axon (37), the vast majority of boutons are on PFs. In this study, we focused on the synapses formed by these boutons on PC dendrites, also called PF-to-PC synapses.
The average synaptic strength (or “weight”), denoted , is defined as the average fast excitatory postsynaptic potential (EPSP) per activated PF-to-PC synapse. This average takes into account synapses for which the evoked EPSP was undetectable, i.e., silent synapses. In this section, we explain how was determined.
Epifluorescence imaging was used to monitor the activation of PFs as a relative change in calcium indicator fluorescence (ΔF/F) following extracellular stimulation (see below and Fig. 1A). Typically, the evoked ΔF/F response was spread over the image plane (SI Appendix, Fig. S1A) with a peak value, denoted for simplicity (SI Appendix, Fig. S1B). To quantify the total response to the stimulation, ΔF/F was integrated over the image plane. The integrated ΔF/F value was denoted (SI Appendix, Fig. S1B). Since the calcium indicator was homogeneously expressed in more than 93% of GCs (see below), could be considered as linearly related to the number of activated PFs (SI Appendix, Fig. S1F and Supplementary Information Text). The average EPSP per unit was denoted . When the number of nearby activated PFs rises, increases due to the spatial overlap of the ΔF/F responses from individual PFs (SI Appendix, Fig. S1 A and D). This increase is expected to tend toward an asymptotic value, denoted (SI Appendix, Fig. S1F), that corresponds to in the theoretical situation where all functional PFs are simultaneously activated in an infinite and homogeneous molecular layer.
Fig. 1.
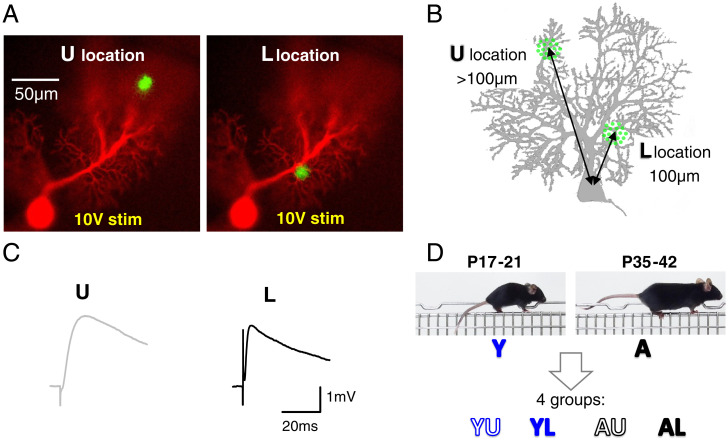
Experimental protocol outline. (A) Images of a patch-clamp-recorded PC loaded with morphological marker Alexa 594 superimposed to the GCaMP6f-mediated ΔF/F response to stimulation in PFs. Two locations were examined: in the middle of the upper (U) or lower (L) half of the molecular layer. (B) Schematic PC showing how the U and L locations were measured relative to the PC soma. (C) EPSPs evoked by a 10-V × 100-µs stimulation pulse at the U or L loci shown in A. (D) Definition of the four groups of data considered, depending on the mouse age (Y or A) and the location of the stimulation (U or L).
As detailed below, and were determined from single experiments combining PF calcium imaging and PC patch-clamp recordings (Fig. 2). Their product , for each experiment, provides a measure of the EPSP per sagittal area of activated PFs (see below). In this section, we demonstrate that is proportional to and can be calculated in a simple manner, provided that two anatomical parameters are determined. This demonstration uses abbreviations defined below (and listed in SI Appendix, Table S1). It relies on the slice orientation (sagittal) and the repetitive organizational features of the GC-to-PC circuitry (PC dendritic trees are flat, with a sagittal planar orientation, and PFs intersect them orthogonally).
Fig. 2.
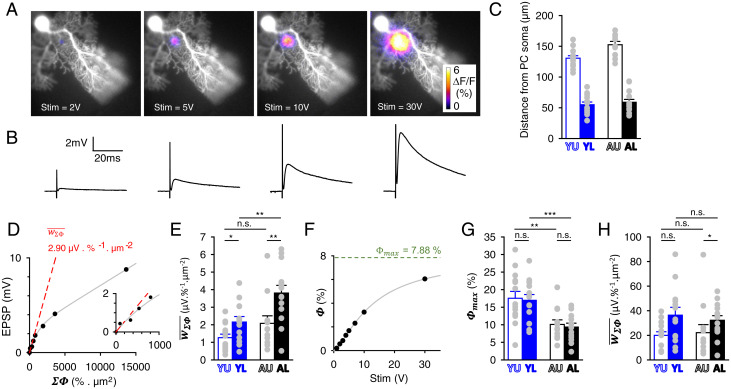
Combined patch-clamp recording of PC and epifluorescence imaging PF activity to determine the EPSP relative to presynaptic activity. (A) Images as in Fig. 1A, for stepwise increased stimulation strengths. (B) Corresponding recorded EPSPs evoked by single stimulation pulses of step-increased strengths. The data obtained from this representative experiment example (AL group) are shown in D and F and SI Appendix, Fig. S4. (C) Averaged distance of the PF stimulation site from the recorded PC soma for each of the four groups studied. (D) Plot of the EPSP against . Note the sublinearity. The value of is determined as the initial slope (dashed red line) of the fit of the data (gray line; see main text). (Inset) Zoom on the initial slope. (E) Values of for the four groups studied. (F) Peak of GCaMP6f fluorescence change () plotted against the stimulation strength. Fit with a three-coefficient sigmoid Hill function, from which the value of the asymptote for infinite stimulation strength was obtained. (G) Average determined for the four groups of data. (H) Average determined for the four groups of data. *P ≤ 0.05; **P ≤ 0.01; ***P ≤ 0.005; n.s., not statistically significant.
Let us consider the PFs intersecting the dendrites of a recorded PC and define as the average number of synapses at each intersection. The average EPSP evoked by the activation of a single PF intersecting the dendrites of a PC is denoted and defined by
| [1] |
Let be the average produced by the activation of a single PF, so we have
| [2] |
Combining Eqs. 1 and 2, we have
| [3] |
and do not need to be determined as they decompose as follows.
can also be defined as , where and are the average numbers of PF synapses and intersections over the dendrites of a PC. Let , , , and be the average spacing in the transverse axis between adjacent planar PC trees (center to center), the average area covered by the PC dendrites in the sagittal plane, the volumetric density of PF-to-PC synapses, and the areal density of PFs in the sagittal plane. is given by and by . It follows that
| [4] |
can be expressed as a function of the ΔF/F responses evoked by molecular layer stimulations. Since corresponds to ΔF/F that would be measured in the theoretical situation of an infinite homogeneous molecular layer, we deduce that is proportional to and . We have
| [5] |
where is the fraction of PFs which remain functional in our acute slice preparation (i.e., generate an action potential-induced calcium transient in response to stimulation).
| [6] |
This equation expresses that is the quotient between the average EPSP per activated sagittal area and the average areal density of functional PF synapses contacting one PC. In the following sections, we determine through combined patch-clamp and PF activity imaging. Next, we determine and though optical microscopy. Finally, we estimate from PF activity imaging and transmitted electronic microscopy images.
Quantitative Mapping of PF Activity.
We produced mice expressing GCaMP6f (38) in GCs by crossing the Tg(Gabra6-cre)B1 driver line constitutively expressing the site-specific Cre recombinase from the GABA-R alpa6 promoter (39, 40) with the Ai95(RCL-GCaMP6f)-D floxed reporter strain (Materials and Methods). The obtained double-heterozygous mice, hereafter denoted G6-Cre;GCaMP6f, were used to map presynaptic calcium transients evoked by PF stimulation in superfused acute slices. In the sagittal plane, GCaMP6f imaging provided a view of activated beams of PFs, seen in cross-section (Fig. 1A). By imaging the dendritic tree of the recorded PC (revealed with the morphological dye Alexa 594 dialyzed through the patch pipette), we selectively activated inputs at restricted locations of the PC dendrites of interest. Recordings were performed in 10 µM GABAzine in order to strictly isolate the AMPA-mediated GC-to-PC synaptic responses from feed-forward interneuron-mediated inhibition. For each recorded PC, we systematically interleaved stimulations at two molecular layer locations: upper (U) or lower (L) than 100 µm from the PC soma (Figs. 1B and 2C). Evoked EPSPs were recorded in current clamp and showed slower time courses for U locations (Fig. 1C), as expected from dendritic filtering effect (41). We examined four groups of data defined by the age of animals: young (postnatal day [P]17 to 21, named Y) or near-adult (P35 to 42, named A), and the location of the stimulation: U or L. Accordingly, groups were named YU, YL, AU, and AL (Fig. 1D).
GCaMP6f expression in cerebellar GCs yielded ΔF/F responses to molecular layer stimulation that were about five times larger than those reported with GCaMP2 (42) and at least ten times larger than autofluorescence responses (SI Appendix, Fig. S2). We confirmed that these ΔF/F responses specifically reported GC activity as follows. First, green fluorescent protein–targeted immunocytochemistry supported selective GCaMP6f expression in GCs, with no detectable ectopic expression (SI Appendix, Fig. S3 A, B, D, and E). Second, we crossed the Tg(Gabra6-cre)B1 line with a CAG-Cytbow multicolor reporter mouse that stochastically produces distinct fluorescent proteins (red, yellow, or cyan) in a Cre-dependent manner, based on the strategy described in ref. 43. In the granular layer, 92.6 ± 0.4% of cells were labeled by this approach [SI Appendix, Fig. S3 C and F; no significant differences between age groups Y (n = 5) and A (n = 6) or between lobules of interest; see Materials and Methods]. Since among the unlabeled cells other cell types are expected (astrocytes, Golgi cells, and unipolar brush cells), this percentage represents an underestimate. The lack of other cell types expressing fluorescent markers supported the absence of ectopic Cre expression. Third, we checked whether PC calcium signaling yielded some detectable fluorescence responses, given that PCs express an extended palette of calcium signaling mechanisms (44) which, even with a very low calcium indicator expression, might have compromised the selectivity of our PF activity mapping. We stimulated the climbing fiber input to evoke large calcium transients that propagate in the entire dendrites (45). We previously showed that this propagation was considerably enhanced when PCs were allowed to fire (by reducing current injection through the patch pipette) and in the presence of 4-AP (44). Even then, no change in fluorescence could be detected (SI Appendix, Fig. S3G; see SI Appendix, Fig. S6A for comparison with the effect of PF stimulation).
In conclusion, the G6-Cre;GCaMP6f mouse model was suitable to quantify the activity of PF input on PC: Ectopic expression of the transgene was either absent or negligible, ensuring that fluorescence changes in the molecular layer could be solely attributed to calcium signaling in GC axons, and nearly all GCs expressed GCaMP6f at the two age groups of interest. Activity of PF inputs could be quantitatively mapped while recording the postsynaptic response. This combined input–output monitoring enabled the determination of and to calculate .
Determination of the Average EPSP Relative to PF Activity.
Locations U or L were stimulated with stepwise increased strength while the ΔF/F presynaptic responses and evoked EPSPs were recorded (Fig. 2 A and B). Presynaptic activity was quantified by measuring and (SI Appendix, Fig. S4 A and B). In contrast to (SI Appendix, Fig. S4A), exhibited a saturation when the stimulation strength increased (SI Appendix, Fig. S4B). The EPSP amplitude did not correlate linearly with the stimulation strength (SI Appendix, Fig. S4C), exhibiting a supralinear increase for low strengths, consistent with supralinear increase (SI Appendix, Fig. S4A). Since provided a linear readout of the number of activated PFs (see SI Appendix, Supplementary Information Text), we plotted the EPSP against (Fig. 2D). Surprisingly, the EPSP increase with was found to be sublinear. It was satisfactorily described by fitting a single exponential multiplied by an affine function (gray line in Fig. 2D). The same sublinearity was observed for all groups (SI Appendix, Fig. S5). We concluded that the EPSP increased sublinearly with the number of activated PFs.
Given that physiological spatial patterns of PF activation are likely much sparser than those evoked by molecular layer stimulation (46), and that a single activated synapse produces an average EPSP of less than 100 µV (see Fig. 6 B–D and ref. 30), we considered that the lower the extracellular stimulation the more physiologically relevant it was to determine the average EPSP per input activity (measured as ΣΦ), . Therefore, the asymptote at zero of the EPSP against plot was taken as the best estimate of (dashed red lines in Fig. 2D and SI Appendix, Fig. S5; see also insets). increased from Y to A stages (P = 0.09 and 0.006 at U and L locations, respectively; Fig. 2E and Table 1). Besides, at both stages, was significantly higher for L locations (P = 0.03 and 0.01 for Y and A mice, respectively; Fig. 2E).
Fig. 6.
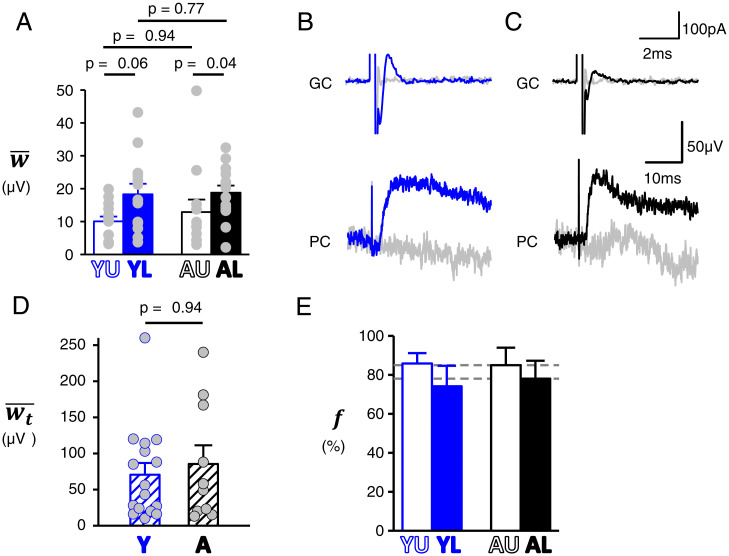
Average synaptic strength () and proportion of silent synapses (). (A) Average synaptic strength calculated according to Eq. 6 for the four groups of data. (B and C) Paired GC and PC recordings. Representative examples of GCs recorded in loose cell attach mode while PCs are recorded in current clamp for Y (B) and (C) A mice. GCs are stimulated with a 12-µs single voltage pulse at 0.5 Hz near the threshold that evokes an action potential. The action potential is detected as a capacitive current. Sweeps with or without detected action potential are averaged separately (plain and gray traces, respectively). Averaged evoked postsynaptic responses (bottom traces) show unambiguous EPSP detection. (D) EPSP amplitudes (determined from paired recordings), the average of which provide for Y and A mice. For about a third of recordings (including those with undetected postsynaptic response), we performed burst stimulation at 100 Hz to confidently conclude the talkative vs. silent nature of the GC input. (E) Proportion of silent synapses calculated from and values (Eq. 7; propagated error).
Table 1.
Summary of determined parameters
| Determination | YU | YL | AU | AL | Change with age | Test | P value | ||
| U location | L location | ||||||||
| (µV⋅%−1⋅µm−2) | Meas. | 1.27 ± 0.20 | 2.15 ± 0.32 | 2.08 ± 0.43 | 3.81 ± 0.44 | Increase | M-W | 0.09 | 0.006 |
| (%) | Meas. | 17.6 ± 1.9 | 17 ± 1.6 | 10.1 ± 1.3 | 9.4 ± 1.1 | Decrease | M-W | 0.005 | 0.001 |
| (µV⋅µm−2) | Meas. | 20 ± 2.9 | 36.4 ± 6.4 | 22.1 ± 6.5 | 32.2 ± 3.7 | M-W | 0.74 | 0.79 | |
| (µm) | Meas. | 3.99 ± 0.26 | 4.11 ± 0.21 | 3.82 ± 0.11 | 3.92 ± 0.28 | Stu | 0.58 | 0.63 | |
| (µm−3) | Meas. | 0.73 ± 0.05 | 0.72 ± 0.03 | 0.86 ± 0.06 | 0.73 ± 0.08 | Stu | 0.13 | 0.96 | |
| (µm−2)* | Calc. | 3.02 | |||||||
| (%) | Meas. | 0.66 ± 0.04 | 0.52 ± 0.02 | 0.43 ± 0.02 | 0.49 ± 0.02 | Decrease | M-W | <0.0001 | 0.17 |
| (%⋅µm2)†,‡ | Calc. | 4.11 ± 1.24 | 3.20 ± 0.93 | 2.68 ± 0.81 | 3.03 ± 0.89 | ||||
| (µm−2)†,‡ | Calc. Eq. 5 | 4.27 ± 1.77 | 5.3 ± 2.06 | 3.77 ± 1.63 | 3.09 ± 1.27 | ||||
| (µm−2) | Meas. | 7.85 | 6.8 | 6.3 | 5.75 | ||||
| § | Calc. | 0.66 | 0.57 | ||||||
| (µV) | Calc. Eq. 6 | 10 ± 1.5 | 18.3 ± 3.2 | 12.9 ± 3.8 | 18.8 ± 2.2 | M-W | 0.94 | 0.77 | |
| (µV) | Meas. | 70.6 ± 16.2 | 85.4 ± 25.9 | M-W | 0.94 | ||||
| (%)‡ | Calc. Eq. 7 | 86 ± 5 | 74 ± 11 | 85 ± 9 | 78 ± 9 | ||||
Determination (measured [Meas.] or calculated [Calc.]), values, change with age, and statistical test (Mann–Whitney U [M-W] or Student’s t [Stu]).
*In vivo areal synapse density per PC, assumed constant based on the similarity of and values between groups and their low variation coefficient (see main text).
†Calculated from (see SI Appendix).
‡Propagated errors.
§Calculated values were 0.54, 0.78, 0.60, and 0.54 for YU, YL, AU, and AL groups, respectively. Since U and L groups were from the same slice preparations, was averaged between U and L loci.
The peak of the spatially spread ΔF/F responses, denoted (SI Appendix, Fig. S1 B and D), was determined by graphical approach. As theoretically expected (SI Appendix, Fig. S1F), saturated as the number of activated PFs increased (SI Appendix, Fig. S4B). When plotting against stimulation strength (Fig. 2F), we found that the plots were accurately fitted by three-parameter sigmoid Hill functions, with an almost perfect correlation (R values were all above 0.97: 46 experiments with R > 0.99 and 2 experiments with R > 0.97; see SI Appendix, Fig. S5 for other examples from other groups). The quality of this fitting prompted us to confidently use it to estimate as the value extrapolated at an infinite stimulation strength (Fig. 2F and SI Appendix, Fig. S5). was similar for the U and the L locations (Fig. 2G). However, it was half lower in A mice (P = 0.005 or 0.001, U or L locations, respectively; Fig. 2G and Table 1). As shown by Eq. 5, these differences must reflect differences in , , or (see Discussion). For each experiment, was obtained, providing a measure of the average EPSP per areal input in our acute slice preparations. It was not significantly different between Y and A stages (P = 0.64 and 0.57 at U and L locations, respectively; Fig. 2H and Table 1). This lack of difference reflects the cancellation of differences in and between Y and A stages in opposite directions (Fig. 2 E and G).
Determination of Anatomical Parameters and .
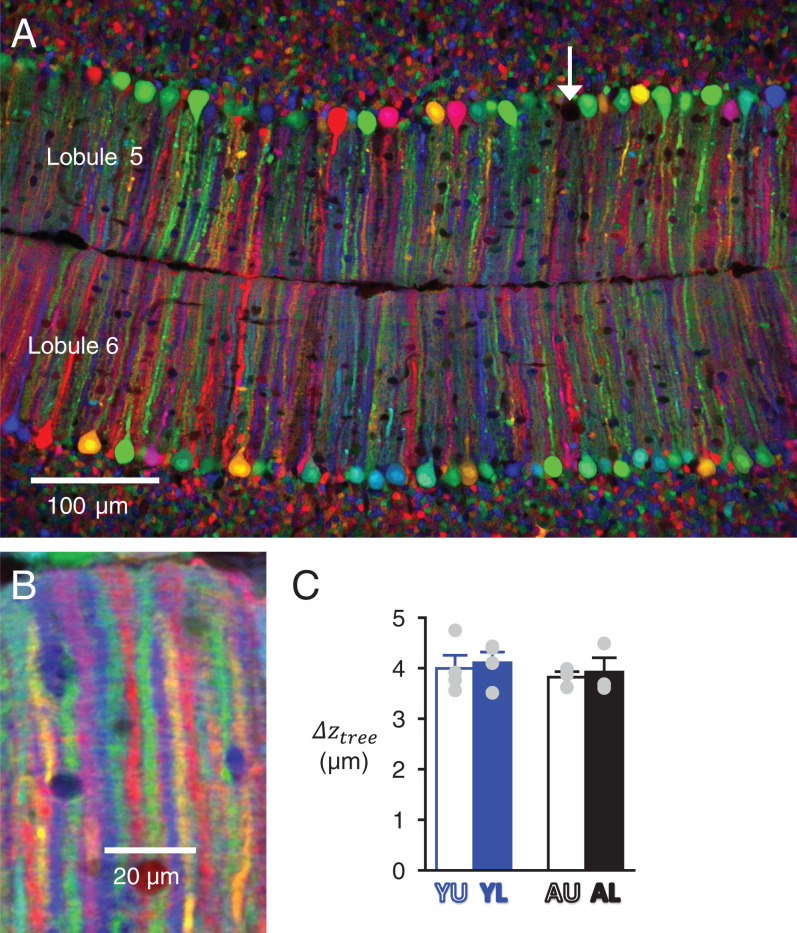
Our method to calculate (Eq. 6) requires the use of two anatomical parameters: the average spacing between adjacent PC dendritic trees () and the volumic density of PF-to-PC synapses (). The average spacing between adjacent PC dendritic trees in the transverse plane () was estimated using the abovementioned CAG-Cytbow multicolor reporter mouse line, using a Wnt1-Cre driver to trigger fluorescent protein expression in PCs (see Materials and Methods). In mice homozygous for the CAG-Cytbow allele, a vast majority of PCs were labeled at the Y and A stages (98.1 ± 0.4%, n = 3 and 95.7 ± 0.5%, n = 3, respectively), expressing six to eight randomly distributed colors. This pattern enabled clear separation of adjacent dendritic trees from distinct PCs imaged in the horizontal plane (Fig. 3A). The fluorescent proteins were also expressed by GCs and their axons, but thanks to the geometrical architecture of the cerebellar cortex, signal arising from GC axons was easily cancelled out by averaging fluorescence intensity over a few optical planes without compromising the ability to resolve adjacent PC trees (Fig. 3B). values were 3.99 ± 0.26 µm (n = 4), 4.11 ± 0.21 µm (n = 4), 3.82 ± 0.11 µm (n = 3), and 3.92 ± 0.28 µm (n = 3) for the YU, YL, AU, and AL groups, respectively (Fig. 3C and Table 1). Based on the lack of significant differences between groups, pooling the results led to an average of 3.96 ± 0.12 µm.
Fig. 3.
Determination of the spacing between adjacent PC dendritic trees. (A) Confocal image of lobules 5 and 6 in a horizontal slice from a Y-stage Wnt1-Cre;CAG-Cytbow mouse. Recombination has occurred in almost all PCs; the arrow points at a rare unlabeled PC. (B) High-magnification view of PC dendrites with averaging of a series of optical plans over 6 µm enabling unambiguous measure of the spacing between successive planar PC trees along the transverse axis (). (C) Average for the four groups of data.
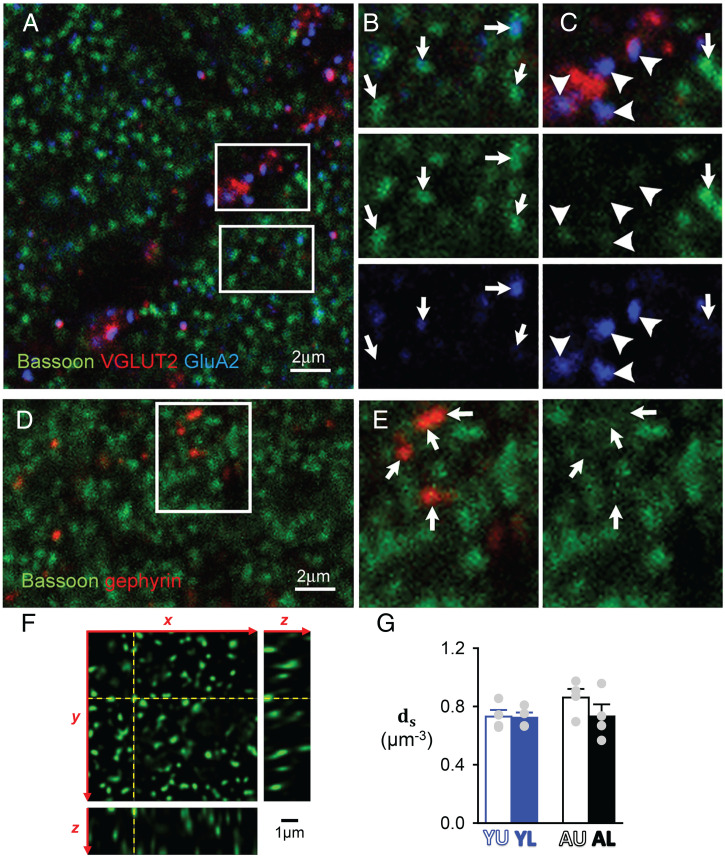
The density of PF-to-PC synapses () was determined by immunostaining against bassoon, a protein of the presynaptic active zone (47). In line with previous studies (48), intense punctate immunostaining was found in the molecular layer as a result of strong bassoon expression at PF-to-PC synapses (Fig. 4A). Bassoon puncta frequently exhibited immunoreactivity for the AMPA receptor subunit GluA2 but the intensity of the GluA2 immunoreaction was highly variable between puncta, suggesting differences in the number and/or the subunit composition of AMPA receptors (Fig. 4B). Reportedly, bassoon expression also occurs at synapses between climbing fibers and PCs, as well as at inhibitory cerebellar synapses (48). In our hands bassoon immunolabeling in the molecular layer was mostly restricted to PF-to-PC synapses. Bassoon expression at climbing fiber synapses, identified as GluA2 immunoreactive puncta apposed to terminals expressing the specific marker VGLUT2 (Fig. 4C), was light and easily distinguishable from the intense labeling at PF-to-PC synapses (Fig. 3C). Likewise, immunolabeling at inhibitory synapses identified by gephyrin immunoreactivity was either faint or absent (Fig. 4 D and E). After deconvolution, the dense punctate staining present at PF-to-PC synapses could be appropriately resolved (Fig. 4F). Bassoon puncta were counted by unbiased stereological methods (49) using an optical dissector probe (400-nm-spaced deconvolved confocal sections). Having taken into account tissue shrinkage and the average fraction of the molecular layer (ML) space not occupied by synapses (PC primary dendrites and blood vessels), PF-to-PC synapse densities were 0.73 ± 0.05 (n = 4), 0.72 ± 0.03 (n = 4), 0.86 ± 0.06 (n = 4), and 0.73 ± 0.08 μm−3 (n = 4) in YU, YL, AU, and AL groups, respectively (Fig. 4G and Table 1). These values were clearly similar, with an average of 0.76 ± 0.03 μm−3. Note that these are slight overestimations as bassoon puncta presumably include synapses made by ascending GC axons, which may account for up to 5% of GC-to-PC synapses (37).
Fig. 4.
Determination of GC-to-PC synapse density ds by immunocytochemistry. (A) GC-to-PC synapses in the molecular layer identified by punctate bassoon labeling (green). VGLUT2 labeling (red) was performed in conjunction with AMPA receptor labeling (GluA2, blue) to identify climbing fibers (CF) synapses. (B) Inset from A showing GluA2 immunolabeling (blue) apposed to bassoon immunoreactive puncta at PF-to-PC synapses (indicated by arrows). Note that the intensity of GluA2 labeling was highly variable across bassoon puncta. (C) Inset from A showing that bassoon expression at CF-to-PC synapses (arrowheads) was low and easily distinguishable from the intense labeling occurring at GC-to-PC synapses. (D) Inhibitory synapses identified by gephyrin immunoreactivity in the molecular layer. (E) Inset showing that bassoon expression was either low or absent at these inhibitory synapses. (F) Three-dimensional view of a deconvolved optical section stack used for GC-to-PC synapses counting. The y–z and the x–z images correspond to the yellow dashed lines on the x–y image. Note that bassoon puncta were well-resolved, allowing individual counting of GC-to-PC synapses. (G) Average ds for the four groups of data.
and exhibited no significant differences between groups and very low variation coefficients (: 0.13, 0.1, 0.05, 0.12 and : 0.12, 0.1, 0.14, 0.23 for YU, YL, AU, and AL groups, respectively) compared to the variation coefficient of (0.55, 0.64, 1.02, and 0.43 for YU, YL, AU, and AL groups, respectively). Therefore, for calculation (see below) we assumed that (the in vivo areal density of PF synapses per PC in the sagittal plane) was constant with a value of 3.02 µm−2 (Table 1).
Calculation of the Fraction of Functional PFs, , and the Average Synaptic Strength, .
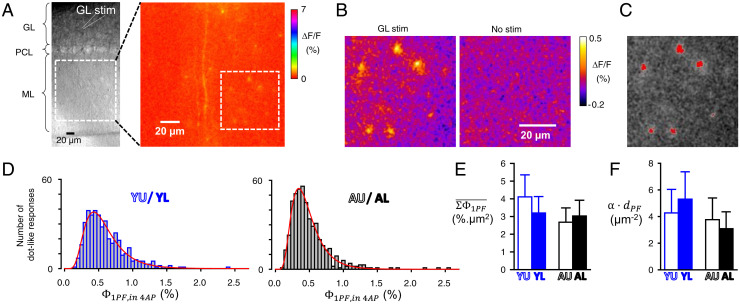
In the initial study that reported silent GC-to-PC synapses, all PFs have been assumed to remain functional in acute slices (30). However, given that the slicing procedure will truncate all PFs, the functionality of a fraction of them is likely to be impaired. We named , the fraction of PFs which remained functional in our acute slice preparations. Although could not be determined directly, we could determine (the areal density of PFs for which a calcium response could be evoked by stimulation). Indeed, this areal density can be derived from ΔF/F responses to molecular layer stimulation, provided that the average ΔF/F response arising from a single activated PF is known (see Eq. 5). Using granular layer stimulation, ΔF/F responses from single isolated PF could be imaged provided they were amplified by 4-AP application (Fig. 5 A–C; see SI Appendix, Supplementary Information Text). This approach enabled the determination of for single activated PFs (; Fig. 5D), which was found significantly higher in the Y group (Table 1), from which we calculated the average (; Fig. 5E and Table 1; see SI Appendix, Supplementary Information Text and Figs. S6 and S7). Once and were known, could be calculated from Eq. 5. Its value was 4.27 ± 1.77, 5.3 ± 2.06, 3.77 ± 1.63, and 3.09 ± 1.27 µm−2 for the YU, YL, AU, and AL groups, respectively (Fig. 5F and Table 1). Although the calculation (with error propagation) did not allow statistical comparisons, a trend for lower in A mice can be noted.
Fig. 5.
Determination of the average GCaMP6f-mediated ΔF/F response produced by a single activated PF in order to calculate the areal density of functional PFs. (A) (Left) Transmitted light image of a superfused sagittal cerebellar slice showing the position of a stimulation electrode in the granular layer relative to the field of view in the molecular layer for which the ΔF/F image following stimulation in the granular layer is displayed (Right). In the presence of 50 µM 4AP to enhance the ΔF/F responses (see SI Appendix, data). (B) Zoom of the part of the ML delimited by a dotted square in A, Right, with a ΔF/F scale enabling unambiguous detection of spot-like ΔF/F responses (not present in the absence of stimulation: Right). (C) Thresholding for identification of spot-like ΔF/F responses (6 responses on this image). Their peak values () were determined as detailed in SI Appendix, Fig. S7. (D) Distribution of for data from Y and A mice (data from individual groups, with spot-like ΔF/F responses attributed to U or L loci according to their distance from the PC soma closest to the stimulating electrode, are shown in Table 1). (E) Average values calculated from values (see SI Appendix, Supplementary Information Text) for the four groups of data. (F) Average (areal density of functional PFs) calculated from and according to Eq. 5. Calculations with error propagation.
The calculation of required the knowledge of , the in vivo areal density of PFs, which surprisingly is poorly known. It has been reported for adult rats, with an averaged value of 6.07 µm−2 (33). We measured from electronic micrographs from Y (n = 2) and A (n = 2) mice (SI Appendix, Fig. S8). Mean was found to be 7.85, 6.8, 6.3, and 5.75 µm−2 in YU, YL, AU, and AL groups, respectively (Table 1). These means were used to calculate , the value of which was averaged between U and L locations since both locations went through identical slice preparation conditions. Calculated was 0.66 and 0.57 for Y and A mice, respectively (Table 1) and could be calculated for each group. was 10 ± 1.5, 18.3 ± 3.2, 12.9 ± 3.8, and 18.8 ± 2.2 µV for the YU, YL, AU, and AL groups, respectively (Fig. 6A). Strikingly, even though some parameters used to calculate changed with age ( and ; Table 1), appeared remarkably stable across the two stages of interest (no significant difference, P ≥ 0.8; Table 1).
Calculation of the Proportion of Silent Synapses .
The study by Isope and Barbour (30) strongly supports the idea that GC-to-PC synapses are divided into two populations: silent and nonsilent. For convenience, we named the latter “talkative” synapses and their average strength . The proportion of silent synapses can be calculated from and (see below). We performed a quantal analysis of EPSPs evoked by PF stimulation that showed no significant differences in quantal parameters between groups (SI Appendix, Supplementary Information Text and Fig. S9). However, the evidence that GC-to-PC synaptic vesicular release occurs through a multivesicular mechanism (50) precludes simple determination of from quantal parameters. Therefore, we determined directly by PC current-clamp recording while single GCs were recorded and stimulated in loose-cell attached mode (30) (Fig. 6 B–D). As expected (30), less than 10% of recorded pairs exhibited a detectable synaptic response. When detected, EPSPs were evoked by stimulation close to threshold. Recording from the loose cell attached pipette enabled unambiguous detection of evoked action potentials (Fig. 6 B and C). Responses to successfully evoked action potential were averaged to determine , which was 70.6 ± 16.2 µV (n = 16) and 85.4 ± 25.9 µV (n = 10) in Y and A mice, respectively (Fig. 6D; note that this method did not enable us to distinguish between U and L locations). The lack of a significant difference (P = 0.94) and the similarity of quantal parameters (SI Appendix, Fig. S9), in line with reports in rats (30, 50), strongly support the conclusion that the average properties of talkative synapses are similar at both postdevelopmental stages.
The proportion of silent synapses can be expressed as a function of and :
| [7] |
Calculated from calculated and measured was 86 ± 5, 74 ± 11, 85 ± 9, and 78 ± 9% for the YU, YL, AU, and AL groups, respectively (with error propagation; Fig. 6E and Table 1). Although the calculation does not allow statistical comparison, these data suggest a tendency for the presence of more silent synapses at U locations. Remarkably, values obtained for the two investigated stages of postnatal development were very similar.
Discussion
About 20 y ago, two independent studies supported the notion that cerebellar PF-to-PC synapses are, in a large proportion, silent in the adult rat (29, 30). The role of these silent synapses has been addressed by modeling studies, which concluded that they ensure a trade-off between maximizing information storage capacity and reliability (34, 51). According to this proposed role, a tight relationship between learning (which requires an increase in stored information) and the proportion of silent synapses might be expected. However, such a relationship has remained unestablished. Here, we determined the proportion of PF-to-PC silent synapses in mice at stages P17–21 and P35–42 of postnatal maturation. We provide quantitative evidence supporting that the proportion of silent synapses is large (75 to 85%). We further show that this proportion remains remarkably stable across the maturation stages studied. Since mouse agility strikingly improves between the third and the sixth postnatal week, we may reasonably assume that this period is critical for natural cerebellar learning processes that mediate this improvement. Based on this assumption, our results suggest that the proportion of silent synapses is poorly related to the natural learning that likely takes place during the first few weeks after birth.
Quantitative Mapping of PF Activity and Presynaptic Calcium Signaling.
Our method to determine is based on quantitative mapping of activated inputs. G6-Cre;GCaMP6f mice show GCaMP6f expression specific to and in more than 93% of GCs (SI Appendix, Fig. S3), providing a suitable model for unambiguous mapping of PF activity in the molecular layer, by imaging ΔF/F responses to stimulation. This method is highly quantitative as the total ΔF/F response () can be considered as a linear readout of the number of activated PFs (SI Appendix, Supplementary Information Text).
The ΔF/F responses were calibrated by estimating their maximum amplitude, noted (Fig. 2F). Strikingly, was 44% smaller in A than in Y mice (Fig. 2G and Table 1). Eq. 5 indicates that decrease must reflect a decrease in , or . Our data show that each of these three parameters tends to decrease from Y to A stage (Table 1). These decreases, albeit not statistically significant, could be interpreted as follows. A decrease in is expected if PFs have reached their full length by Y stage (52), while the molecular layer continues to expand due to PC tree expansion (53). Consistently, we observed about 27% increase in the molecular layer thickness between the Y and the A stages. A decrease in would indicate that PF survival is more compromised in acute slices from older animals, which is in line with the general observation that acute slices from young animals are healthier. Finally, the nonsignificance of the decrease is presumably due to its indirect determination (involving error propagation). was derived from measured , which shows a highly significant decrease with age for upper locations (Table 1). This decrease is unlikely to be due to a difference in GCaMP6f expression because the ratiometric nature of ΔF/F measurements makes it independent of probe concentration. Rather, this decrease may reflect a change in calcium signaling properties: Either the stimulation-evoked presynaptic [Ca2+]i rise gets smaller or the resting [Ca2+]i gets higher (impacting the dynamic range of ΔF/F responses) as the animal matures, as suggested by the higher GCaMP6f fluorescence baseline observed in A mice (SI Appendix, Fig. S2). However, the latter could also reflect higher GCaMP6f expression in A mice. We have no explanation as to why the change in with age was only observed for the U location.
To conclude, we have introduced a method that enables quantitative mapping of presynaptic inputs by GCaMP6-mediated monitoring of PF activation. This monitoring reveals that calcium signaling properties change with postnatal maturation, likely because of a rise in baseline presynaptic calcium. Such a change might be expected to be associated with a change in release probability. However, the latter is poorly related to the residual calcium signals (54) (as monitored by GCaMP6f), and we did not observe any significant change in release probability between the two stages investigated (SI Appendix, Fig. S9E).
Cooperative Effect during Activation of Neighboring Synapses.
PC patch-clamp recording combined with quantitative PF mapping provides a mean to normalize the postsynaptic response to the presynaptic input quantified as the unit. The use of a single stimulation strength could have been thought to suffice to perform this normalization and derive from it the postsynaptic response per activated PF. However, unexpectedly, we found a sublinear relationship between the postsynaptic response and the number of activated PFs, indicating a negative cooperativity between neighboring activated synapses. This is surprising since the high expression of voltage-activated calcium channels in PC dendrites (44) could have been expected to amplify the depolarization initially caused by AMPA receptors opening (55) and produce, on the contrary, a supralinear relationship. We have not investigated further the cause of the negative cooperative effect, which could be local depolarization in spiny branchlets reducing the driving force through AMPA receptors. However, we carefully took it into account to determine (Fig. 2D).
This negative cooperativity is likely to have impacted our determination of the quantal size (Q). Indeed, the quantal analysis method assumes that the compound EPSP (evoked by multiple inputs) is a linear summation of the EPSPs evoked by each individual input. Although the stimulation strength was adjusted to evoke EPSPs below 2 mV (SI Appendix, Fig. S9D) for which the relationship between the EPSP and ΣΦ appeared quasi-linear (Fig. 2D, Inset), detailed investigation of EPSP against ΣΦ in the 0- to 2.5-mV EPSP range showed that the sublinearity could not be ignored (SI Appendix, Fig. S10 A–D). However, these data show that the resulting underestimation was similar for all groups (SI Appendix, Fig. S10E) and thus do not impact our conclusion that Q is similar across groups (SI Appendix, Fig. S9F).
Finally, this negative cooperativity means that the determined (Fig. 2H), which in appearance represents the average EPSP evoked by square micrometer of activated PF inputs, cannot be used to linearly extrapolate the value of the EPSP evoked by simultaneous activation of numerous PFs in a beam of known section. However, in the case of physiological inputs, expected to be more spatially scattered, the negative cooperativity may not apply and comparing the 20 to 36 µV⋅µm−2 determined for to the average area of a PC tree (200 × 200 µm) suggests that simultaneous firing of 1% of PFs evokes an about 10-mV EPSP.
Determination of , the Proportion of PF-to-PC Synapses Which Are Silent.
Until now, the only quantitative determination of has been through paired GC–PC recordings in acute slices (30). This approach requires an enormous number of recordings and raises two issues. First, the functionality of the stimulated GC axon presumably intersecting the dendrites of the recorded PC is uncertain. Our finding that nearly half of PFs lose their functionality in acute slices ( close to 0.5) suggests that the probability of recording a pair of connected cells (based on anatomical data, respective cell location, and geometrical considerations) has been overestimated (30). Second, for any given PC, GCs connecting it with a talkative synapse appear not randomly distributed in the granular layer but rather in microzones (56). Therefore, the experimenter must ensure that paired recordings are obtained from samples large enough to encompass different microzones. Our method is less affected by this potential bias since the beams of activated PFs considered to determine are made of inputs originating from diverse microzones.
Our determination of is based on the determination of the average synaptic weight of all synapses () and its comparison to the average synaptic weight of talkative synapses () measured from paired recordings. The values we found for A mice are 85 ± 9 and 78 ± 9% for the U and L molecular layers, respectively. These values are close to the 87% estimate from the study of paired recordings in adult rats (30), which may be an overestimate since PF loss of functionality following slice preparation was ignored. The apparent difference between the U and L molecular layer locations (also observed for young mice; Fig. 6E and Table 1) reflects differences in (Fig. 6A and Table 1). However, since in our paired recordings the location of the activated synapses could not be ascertained, possible differences in between U and L locations cannot be ruled out and preclude any conclusion on differences in between U and L locations. In contrast, the lack of significant differences between age groups for both and (P ≥ 0.8 and P = 0.9, respectively; Table 1) supports the conclusion that remains stable between Y and A stages.
Organization and Morphological Features of PF-to-PC Connections.
The distance between successive PF varicosities has been consistently reported to be >5 μm (32, 33, 57, 58), while the average spacing between adjacent PC trees () in the adult rat has been estimated to be around 4 μm (33, 58), in good agreement with our measures (Table 1). In addition, the number of GC-to-PC synapses per varicosity has been estimated to be 1.05 (14), in line with the report that about 5% of bouton are multiple synapse boutons (59, 60). Altogether, the published data support that is below 1. Using Eq. 4, we calculated values of 0.37, 0.44, 0.52, and 0.50 for YU, YL, AU, and AL groups, respectively. Our values in A mice are consistent with the 0.54 value calculated from Napper and Harvey data in adult rats (14, 30–33). The overall synapse density () that we found (Fig. 4G and Table 1) is in very good agreement with estimates in adult rats (33, 61). The stability of and across molecular layer locations and maturation stages supports the notion that the GC-to-PC microcircuit is optimally organized from early postdevelopmental stages.
The Properties of Newly Formed Synapses.
Although the occurrence of a small, undetected change in between the Y and A stages cannot be excluded, our data rule out the hypothesis that most synapses would start being talkative before getting silenced during postnatal maturation; 74 to 85% of PF-to-PC synapses are silent at the early P17–21 stage, i.e., a few days after being formed. During postnatal maturation, the molecular layer volume expands (53). In mice, we observed a 27% expansion from Y to A stages. Since did not significantly increase between these two stages (Fig. 3D), we deduce that the absolute number of synapses must have increased by about 27%. Most of these synapses will be in the upper part of the molecular layer. Lower at the upper locations (Fig. 6) suggests that newly added synapses are silent before being assigned talkative/silent status in a stable proportion.
The Role of Silent Synapses.
Since we could not establish any correlation between the cerebellar maturation (and the presumed associated natural learning) and the proportion of silent synapses, their role remains unclear. These synapses may be silent only apparently: They may in fact transmit information in a form that we have not detected by looking at fast postsynaptic depolarization evoked by short bursts of presynaptic action potentials (Fig. 6D, legend). For example, they may transmit nonelectrical postsynaptic responses which yet contribute to information processing by modifying properties of branchlet microdomains. Alternatively, silent synapses may result from heterosynaptic plasticity (59, 62) and be a homeostatic by-product required to modulate the overall amount of PC excitability in response to GC inputs (63).
To date, the proposed role for cerebellar silent synapses has been associated with information storage optimization. The perceptron is a model of supervised information learning by a neuron receiving inputs with modifiable (plastic) synaptic entries (34). For a perceptron model analogous to the GC-to-PC network, it has been proposed that silent synapses enable an optimization of the information storage: a balance between maximization of the amount of stored information and reliability of stored information (34). In this model, if we ignore the reliability issue (which accounts for noise, inherent to biological systems), the maximized amount of stored information is obtained for 50% of synapses being silent. To improve reliability, additional silent synapses are required. Accordingly, it can be predicted that, if less than 50% of newly formed synapses are silent, increasing the amount and the reliability of stored information will both require an increase in the proportion of silent synapses. Alternatively, if more than 50% of newly formed synapses are silent, the optimization of information storage capacity or reliability will require changes in the proportion of silent synapse in opposite directions: a decrease or an increase, respectively.
The latter scenario can be decomposed into the three following hypotheses. First, learning requires a larger storage capacity (fewer silent synapses), while reliability is not so critical. The proportion of silent synapses would then be expected to decrease with learning. Second, learning primarily requires an increased reliability of stored information (more silent synapses). The information storage capacity would need to be reduced (elimination of nonconsolidated memory), and the proportion of silent synapses would increase. Third, the initial information storage capacity and reliability are optimal to start with. The balance between these two components of information storage is maintained through learning processes. Learning may modify synaptic weights or silent vs. talkative synaptic properties, but the average proportion of silent synapses would remain stable.
The first and second hypotheses cannot be ruled out, as changes might occur below our detection threshold, but overall the third hypothesis is best supported by our data: Despite the tremendous gain in agility over the critical postnatal period that we investigated and the presumed associated increase in stored information, the proportion of silent synapses remains stable. This suggests that information storage capacity is optimal at a very early stage and remains optimal during postnatal maturation. While the information storage capacity has been used as an adjustable variable in the perceptron model (34), it may in fact not vary during cerebellum maturation and improvement in performance. Instead, the spatial distribution of the stored information (talkative synapses) or synaptic properties which were not assessed in this study (59) could be the adjusted variables. The nature of stored information would change, but the total amount of stored information would remain stable. Therefore, we propose that, unlike a computer, the cerebellum increases its performance mostly by modifying rather than expanding its stored information, which already uses its full capacity as soon as neurons have migrated to their final location.
Materials and Methods
Mice.
Mice were housed in a 12-h light/12-h dark cycle with free access to food, and animal procedures were carried out in accordance with institutional guidelines. Experiments performed at University College London were in accordance with the United Kingdom Animal (Scientific Procedures) Act of 1986 and covered by the Home Office project license PPL 70/05771 for the breeding of GCaMP2 (transgenic) mice. Experiments at INMED were covered by the National Institute of Health and Medical Research animal care and use agreement (D-13-055-19) and the European community council directive (2010/63/UE). Animal protocols used at Institut de la Vision were approved by the Charles Darwin animal experimentation ethical board (CEEACD/No 5). Mice were either humanely killed by cervical dislocation or anesthetized by intraperitoneal injection of mixed ketamine and xylazine in 0.9% NaCl solution (147 and 7.8 mg/kg, respectively) before being decapitated. Wild-type, GCaMP6f, and Wnt1-Cre had a C57BL/6J background, CAG-Cytbow mice a C57BL/6N background, and GCaMP2 mice had an ICR background. GCaMP2 mice expressed the fluorescent calcium indicator protein GCaMP2 under the control of the regulatory sequences of the gene coding Kv3.1 potassium channel (64). G6-Cre;GCaMP6f mice were generated by crossing driver Tg(Gabra6-cre)B1Lfr mice (39, 40) with reporter Ai95(RCL-GCaMP6f)-D mice (The Jackson Laboratory). Wnt1-Cre;CAG-Cytbow mice were generated by crossing transgenic Wnt1-Cre animals (65), a gift from A. Chédotal, Institut de la Vision, Paris, France, and multicolor reporter mice broadly expressing a CAG-Cytbow transgene (66) designed on the model of ref. 43, modified to achieve random expression of mTurquoise2, mEYFP, or tdTomato from the broadly active CAG promoter following Cre recombination (this line will be described elsewhere). Two stages were chosen for the analysis: P17–P21 (Y) and P35–P42 (A). At P17–21, GC have completed their migration (67). Anatomical data from rat (53) translated to mouse suggest that at P17–21 PC dendrites are about 70% developed, while they reach their full size at P35–42 (53). Our study was limited to vermal lobules 4 to 6, whose implication in motor coordination has been reported (68–70).
Immunocytochemistry.
Following decapitation, brains were swiftly removed, frozen, and kept at −20 °C. Fourteen-micrometer-thick sagittal sections were cut 0.2 to 0.8 mm from the midline with a cryostat. Antigen retrieval was performed on sections intended for GluA2 immunolabeling. This was done by combining microwave irradiation and postfixation in 0.5% paraformaldehyde for 45 s as previously described (71). Remaining sections were postfixed at room temperature in 2% paraformaldehyde for 10 to 15 min. Sections were then incubated in 10% normal goat serum for 1 h before being incubated with primary antibodies overnight at 4 °C. Primary antibodies were mouse anti-Bassoon (Enzo Life Science, ADI-VAM-P5003, 2 to 3 μg/mL), rabbit anti-GluA2 (Epitomics, 18281, EP966Y, 1 μg/mL), guinea pig anti-VGLUT2 (Millipore AB2251-l, 1 μg/mL), and mouse anti-gephyrin (Synaptic System, mAb7A, 1.25 μg/mL). Secondary antibodies were incubated at 5‰ concentration for 1 h at room temperature. Isotype-specific anti-mouse secondary antibodies were used for gephyrin-bassoon double labeling. Sections were mounted in 50% glycerol and 50% phosphate-buffered saline.
Confocal Imaging.
Images of sections labeled for synapse counting were acquired on a confocal microscope (Leica TCS SP5 X or Zeiss LSM 510) using a 1.4 numerical aperture (N.A.) oil immersion objective. Voxel size was adjusted to 70 nm in x and y and to 200 nm in z (for stacks). Fluorophores Alexa 488, Alexa 555, Cy3, and Alexa647 were excited at 488, 550, and 649 nm (Leica TCS SP5) or 488, 543, and 633 nm (Zeiss LSM 510). Image stacks were deconvolved using the Huyghens software. Image stacks from Cytbow-labeled PC dendritic arbors were acquired from 90-μm-thick horizontal brain sections using an Olympus FV1200 confocal microscope equipped with 440-, 515-, and 560-nm laser lines using a 40× 1.3 N.A. oil immersion objective. Sampling was adjusted to 155 nm in x and y and 41 nm in z.
Electron Microscopy.
Mice were anesthetized with a mixture of ketamine (50 mg/kg) and xylazine (15 mg/kg) and perfused through the ascending aorta with 30 mL of 2.5% glutaraldehyde. Sagital cerebellar sections cut 0.2 to 0.8 mm from the midline with a vibratome were stained with 1% osmium tetroxide followed by 1% uranyl acetate, dehydrated in increasing alcohol concentrations and propylene oxide, and flat-embedded in Durcupan ACM Fluka. Ultrathin sections (80 nm) were collected on formvar-coated single-slot grids. Images were acquired at a magnification of 17,000×. The amount of tissue sampled per animal and per region (i.e., upper or lower molecular layer) for PF counting was 300 µm2.
Cerebellar Acute Slice Preparation.
Following decapitation, the GCaMP6 mouse brain was swiftly extracted and immersed in 95%O2/5%CO2 equilibrated BBS (bicarbonate buffered solution, see below) at 4 °C. The cerebellum was dissected and glued on the slicer holder using Loctite superglue-3 before being immersed in gluconate cutting medium (GCS; see solution recipes below) at 4 °C. Vermis sagittal slices 300 to 325 µm thick were cut in GCS with an ethanol-washed Wilkinson razor blade mounted on a VT1200S slicer (Leica), vibration amplitude 0.65 mm. For paired recordings, slices were cut with an angle for a configuration similar to that described in ref. 30. The angle was about 45° relative to the sagittal plane and an axis parallel to the main direction of lobules 4, 5, and 6, in order to ensure pairs connected by PF–PC synapses could be recorded. Slices were then immersed for 2 to 3 min in 95%O2/5%CO2 equilibrated mannitol cutting solution (MCS) at 34 °C, then in 95%O2/5%CO2 equilibrated bicarbonate-buffered solution (BBS) for 30 min at 34 °C, and then for up to 6 h at room temperature.
Slice Superfusion and Electrophysiology.
Slices were superfused at a constant 3 mL⋅min−1 rate on both sides in a 3-mL recording chamber on the stage of an Olympus BX51 microscope. Experiments were performed at room temperature. Patch-clamp and loose-patch recording electrodes were made from 1.5-mm outside diameter (OD) × 1.05-mm borosilicate glass capillaries (Hilgenberg), with typical 3- to 3.5-MΩ and 7- to 8-MΩ resistances, respectively. Stimulating pipette were made from 1.5-mm OD × 1.17-mm borosilicate capillaries (GC150TF-10; Harvard Apparatus), pulled on a P97 puller (Sutter) with setting adjusted to obtain narrow tips (less than 10-µm diameter along more than 100 µm, in order to be able to insert them deep in the tissue with minimum mechanical damage), filled with standard BBS, with a resistance of 3.3 to 3.5 MΩ. The PCs were whole-cell current-clamped with injected current (typically 300 pA) to maintain their potential at −70 mV. Cells that required an injected current higher than 800 pA were discarded. It was checked that the bridge balance remained stable over the course of experiments with no more series resistance compensation than 25 MΩ. Recordings were made using a Multiclamp 700 B (Molecular Devices). Stimulations were negative 100-µs square voltage pulses applied between the stimulating pipette tip and a ground in the chamber. Loose cell-attached recordings of GCs were obtained using a ELC-03XS amplifier (npi electronic).
Solutions.
The medium used for slice incubation and superfusion, BBS, contained (in millimolar) NaCl 126, KCl 2.5, NaH2PO4 1.25, NaHCO3 26, CaCl2 2, MgCl2 1, and glucose 25, bubbled with 95% O2–5% CO2. The slicing medium, GCS, contained (in millimolar) KGluconate 130, KCl 15, EGTA 2, Hepes 20, glucose 25, and D-AP5 0.05 (to block NMDA receptors), pH-adjusted to 7.4 with NaOH. This high-potassium/EGTA (intracellular-mimicking) medium was used solely during slicing at 4 °C (42, 44) to enable better protection despite unavoidable mechanical membrane damage produced by slicing. Immediately following slicing, slices were immerged in a recovery medium (MCS) for a transition from the high-K+, low-Ca2+ GCS to the low-K+, high-Ca2+ BBS. MCS contained (in millimolar) d-mannitol 225, KCl 2.5, NaH2PO4 1.25, NaHCO3 25, and glucose 25. All superfusion solution contained 10 µM GABAzine. For patch-clamp experiments, normal intracellular (pipette) solution contained (in millimolar) KMeSO4 145, NaCl 6, Hepes 10, K2.5EGTA 0.5, MgCl2 1, MgATP 4, and Na2GTP 0.5, pH-adjusted to 7.35 with KOH. This medium was stored at −80 °C. Alexa Fluor 594 hydrazide was added at 15 µM just before patching.
Electrophysiology and Calcium Imaging.
Images were acquired through a 40× objective (Olympus; N.A. 0.8). The excitation light was produced by a 468-nm light-emitting diode (LED) controlled with an OptoLED (Cairn), the power of which was set for an irradiance of 4 mW⋅mm−2 over the imaged sample, or a 568- to 588-nm band sampled by an Optoscan monochromator (Cairn) from a 75-W Xenon arc lamp. Both excitations passed through a dual band-pass filter 452 to 490 nm, 554 to 589 nm (59022X; Chroma). Dual excitation/emission was enabled through a beamsplitter 59022bs (Chroma). Epifluorescence was collected through a dual-emission filter 502 to 542 nm, 602 to 663 nm (59022 m; Chroma) by an electron-multiplying charge-coupled device camera (iXon DU-897E; Andor). Imaging of Alexa Fluor 594 enabled the visualization of the dendrites of the recorded PC. According to the shape of the dendritic tree, stimulating electrodes were positioned over the molecular layer to ensure that stimulated PF beams crossed regions entirely filled with spiny branchlets of the recorded PC. Stimulation was done with a negative 100-µs square pulse; maximum amplitude was 30 V. When studying the effect of increased stimulation intensity, the stimulation amplitude was stepped increased from 1.5 to 2 V to 10 V and back. This bracketing of the 10-V stimulation intensity was used to improve the accuracy of our data acquisition. Stimulations consisted of 13 stimulations at 1 Hz followed by a train of 10 stimulations at 10 Hz. This pattern was repeated every 30 s. The average of the 13 EPSP evoked by the single stimulations was used to measure the EPSP peak. The 10-Hz train was used for the mapping of PF input. Following this bracketing, the 30-V stimulation intensity was used just once, at the end of the experiment (for our collected data not to be affected by putative long-term effect of high stimulation intensity). Activated PFs were imaged as the stimulation-evoked change in GCaMP fluorescence (42, 72). The stimulator DS2A (Digitimer) and the camera were driven externally by pCLAMP (Molecular Devices) to synchronize imaging, stimulation, and electrophysiological recordings. One-second frames were collected every 15 s. Changes in GCaMP fluorescence (ΔF) were determined by subtracting the frame acquired during the 10 stimuli at 10 Hz from the frame acquired just before when no stimulation occurred. The relative change in fluorescence (ΔF/F) was derived. The ΔF/F 512- × 512-pixel image (pixel size 0.16 μm2) was smoothed by a one-pixel Gaussian blur in ImageJ before determining the two signals and (see SI Appendix, Fig. S1).
Mapping of Activated PFs.
The epifluorescence imaging did not restrict excitation and photon collection to the focal plane. With this imaging method, light diffusion and scattering made ΔF/F responses of single PFs much wider than the actual PF section (Fig. 5C and SI Appendix, Fig. S7 A–D compared to SI Appendix, Fig. S8). However, this method was ideally suited to map PF activation irrespective of their reported heterogeneity of calcium responses along their length (36). Due to their orientation perpendicular to the sagittal plane, the epifluorescence imaging of PFs is equivalent to the average imaging of lengths of PFs that comprise several boutons. Let Imax be the maximal irradiance received at the slice surface. Given the irradiance attenuation through the depth of the tissue (73) and the direction of PFs (parallel to the optic path), the total amount of blue light received by a PF crossing the 300-μm thickness of the slice is expected to be equivalent to Imax received without attenuation over a 102-µm length of the PF. Since PFs bear more than 100 boutons per mm (32, 37), the ΔF/F response actually collected from each PF could be considered as the average of signals arising from more than 10 consecutive excited boutons and their in-between axon segments and, as such, be considered as little dependent on the heterogeneity of presynaptic bouton properties.
Analysis and Statistics.
The ΔF/F epifluorescence signals arising from PFs were spread out over a large surface area (SI Appendix, Fig. S1 A and B), even those arising from a single activated fiber (SI Appendix, Fig. S7 A–D). The geometrical arrangement of PFs (perpendicular to the image plane) was advantageously used for analysis: ΔF/F signals exhibited a radial symmetry and could hence be fully described by radial plotting, which was used to measure (SI Appendix, Fig. S1D). Data are presented as mean ± SEM. Significance was determined by an unequal variances two-tailed t test (when appropriate) or a Mann–Whitney U test (M-W as indicated in Table 1). In order to control type II error, we verified for each statistical comparison that the achieved power, given actual alpha and effect size, was above 0.8.
Acknowledgments
We thank D. Debanne, M. Seagar, F. Tell, and L. Kerkerian-Le Goff for critical reading of the manuscript. We thank the Luminy imaging facility (member of the national infrastructure France-BioImaging supported by the French National Research Agency, ANR-10-INBS-04), the INMED (Institut de Neurobiologie de la Méditerranée) imaging facility (InMagic), the Institut de la Vision imaging facility, the PBMC (Pateforme de Biologie Moléculaire et Cellulaire) of the INMED, and the animal housing facilities of the INMED and the Institut de la Vision for provision of helpful resources. We thank T. Knöpfel, M. Mark, and A. Chédotal for providing the GCaMP2, Tg(Gabra6-cre)B1Lfr and Wnt1-Cre transgenic mouse lines, respectively. This work was supported by the Career Development Award G0600064 from the United Kingdom Medical Research Council and a Pépinière d’Excellence award from the Amidex (Aix-Marseille Université) to P.M., a PhD studentship from the Amidex (Aix-Marseille Université) ICN (Integrative and Clinical Neuroscience) PhD program to S.H., the Laboratoire d'Excellence “SENSES FOR A LIFETIME” (LabEx LIFESENSES, ANR-10-LABX-65), the Institut Hospitalo-Universitaire “Enabling Vision Restoration” (IHU FOReSIGHT, ANR-18-IAHU-01), the Centre National de la Recherche Scientifique, and the Institut National de la Santé et de la Recherche Médicale.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2024890118/-/DCSupplemental.
Data Availability
All study data are included in the article and/or SI Appendix.
References
- 1.Yuste R., The discovery of dendritic spines by Cajal. Front. Neuroanat. 9, 18 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Yuste R., Dendritic spines and distributed circuits. Neuron 71, 772–781 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Gray E. G., Electron microscopy of synaptic contacts on dendrite spines of the cerebral cortex. Nature 183, 1592–1593 (1959). [DOI] [PubMed] [Google Scholar]
- 4.Gipson C. D., Olive M. F., Structural and functional plasticity of dendritic spines—Root or result of behavior? Genes Brain Behav. 16, 101–117 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Holtmaat A., Caroni P., Functional and structural underpinnings of neuronal assembly formation in learning. Nat. Neurosci. 19, 1553–1562 (2016). [DOI] [PubMed] [Google Scholar]
- 6.Fu M., Yu X., Lu J., Zuo Y., Repetitive motor learning induces coordinated formation of clustered dendritic spines in vivo. Nature 483, 92–95 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Moczulska K. E., et al. , Dynamics of dendritic spines in the mouse auditory cortex during memory formation and memory recall. Proc. Natl. Acad. Sci. U.S.A. 110, 18315–18320 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Yang Y., et al. , Selective synaptic remodeling of amygdalocortical connections associated with fear memory. Nat. Neurosci. 19, 1348–1355 (2016). [DOI] [PubMed] [Google Scholar]
- 9.Joachimsthaler B., Brugger D., Skodras A., Schwarz C., Spine loss in primary somatosensory cortex during trace eyeblink conditioning. J. Neurosci. 35, 3772–3781 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lai C. S., Franke T. F., Gan W. B., Opposite effects of fear conditioning and extinction on dendritic spine remodelling. Nature 483, 87–91 (2012). [DOI] [PubMed] [Google Scholar]
- 11.Wang X. B., Yang Y., Zhou Q., Independent expression of synaptic and morphological plasticity associated with long-term depression. J. Neurosci. 27, 12419–12429 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Azevedo F. A., et al. , Equal numbers of neuronal and nonneuronal cells make the human brain an isometrically scaled-up primate brain. J. Comp. Neurol. 513, 532–541 (2009). [DOI] [PubMed] [Google Scholar]
- 13.Herculano-Houzel S., Coordinated scaling of cortical and cerebellar numbers of neurons. Front. Neuroanat. 4, 12 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Napper R. M., Harvey R. J., Quantitative study of the Purkinje cell dendritic spines in the rat cerebellum. J. Comp. Neurol. 274, 158–167 (1988). [DOI] [PubMed] [Google Scholar]
- 15.Albus J. S., A theory of cerebellar function. Math. Biosci. 10, 26–51 (1971). [Google Scholar]
- 16.Bouvier G., et al. , Burst-dependent bidirectional plasticity in the cerebellum is driven by presynaptic NMDA receptors. Cell Rep. 15, 104–116 (2016). [DOI] [PubMed] [Google Scholar]
- 17.Dean P., Porrill J., Ekerot C. F., Jörntell H., The cerebellar microcircuit as an adaptive filter: Experimental and computational evidence. Nat. Rev. Neurosci. 11, 30–43 (2010). [DOI] [PubMed] [Google Scholar]
- 18.Ito M., Yamaguchi K., Nagao S., Yamazaki T., Long-term depression as a model of cerebellar plasticity. Prog. Brain Res. 210, 1–30 (2014). [DOI] [PubMed] [Google Scholar]
- 19.Marr D., A theory of cerebellar cortex. J. Physiol. 202, 437–470 (1969). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Deng J., Dunaevsky A., Dynamics of dendritic spines and their afferent terminals: Spines are more motile than presynaptic boutons. Dev. Biol. 277, 366–377 (2005). [DOI] [PubMed] [Google Scholar]
- 21.Lippman Bell J. J., Lordkipanidze T., Cobb N., Dunaevsky A., Bergmann glial ensheathment of dendritic spines regulates synapse number without affecting spine motility. Neuron Glia Biol. 6, 193–200 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Kleim J. A., et al. , Selective synaptic plasticity within the cerebellar cortex following complex motor skill learning. Neurobiol. Learn. Mem. 69, 274–289 (1998). [DOI] [PubMed] [Google Scholar]
- 23.Black J. E., Isaacs K. R., Anderson B. J., Alcantara A. A., Greenough W. T., Learning causes synaptogenesis, whereas motor activity causes angiogenesis, in cerebellar cortex of adult rats. Proc. Natl. Acad. Sci. U.S.A. 87, 5568–5572 (1990). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Harris K. M., Stevens J. K., Dendritic spines of rat cerebellar Purkinje cells: Serial electron microscopy with reference to their biophysical characteristics. J. Neurosci. 8, 4455–4469 (1988). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Hillman D. E., Chen S., Reciprocal relationship between size of postsynaptic densities and their number: Constancy in contact area. Brain Res. 295, 325–343 (1984). [DOI] [PubMed] [Google Scholar]
- 26.Meek J., Nieuwenhuys R., Palisade pattern of mormyrid Purkinje cells: A correlated light and electron microscopic study. J. Comp. Neurol. 306, 156–192 (1991). [DOI] [PubMed] [Google Scholar]
- 27.Spacek J., Hartmann M., Three-dimensional analysis of dendritic spines. I. Quantitative observations related to dendritic spine and synaptic morphology in cerebral and cerebellar cortices. Anat. Embryol. (Berl.) 167, 289–310 (1983). [DOI] [PubMed] [Google Scholar]
- 28.O’Brien J., Unwin N., Organization of spines on the dendrites of Purkinje cells. Proc. Natl. Acad. Sci. U.S.A. 103, 1575–1580 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Ekerot C. F., Jörntell H., Parallel fibre receptive fields of Purkinje cells and interneurons are climbing fibre-specific. Eur. J. Neurosci. 13, 1303–1310 (2001). [DOI] [PubMed] [Google Scholar]
- 30.Isope P., Barbour B., Properties of unitary granule cell-->Purkinje cell synapses in adult rat cerebellar slices. J. Neurosci. 22, 9668–9678 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Harvey R. J., Napper R. M., Quantitative study of granule and Purkinje cells in the cerebellar cortex of the rat. J. Comp. Neurol. 274, 151–157 (1988). [DOI] [PubMed] [Google Scholar]
- 32.Harvey R. J., Napper R. M., Quantitative studies on the mammalian cerebellum. Prog. Neurobiol. 36, 437–463 (1991). [DOI] [PubMed] [Google Scholar]
- 33.Napper R. M., Harvey R. J., Number of parallel fiber synapses on an individual Purkinje cell in the cerebellum of the rat. J. Comp. Neurol. 274, 168–177 (1988). [DOI] [PubMed] [Google Scholar]
- 34.Brunel N., Hakim V., Isope P., Nadal J. P., Barbour B., Optimal information storage and the distribution of synaptic weights: Perceptron versus Purkinje cell. Neuron 43, 745–757 (2004). [DOI] [PubMed] [Google Scholar]
- 35.Brust V., Schindler P. M., Lewejohann L., Lifetime development of behavioural phenotype in the house mouse (Mus musculus). Front. Zool. 12(suppl. 1), S17 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Zhang W., Linden D. J., Calcium influx measured at single presynaptic boutons of cerebellar granule cell ascending axons and parallel fibers. Cerebellum 11, 121–131 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Pichitpornchai C., Rawson J. A., Rees S., Morphology of parallel fibres in the cerebellar cortex of the rat: An experimental light and electron microscopic study with biocytin. J. Comp. Neurol. 342, 206–220 (1994). [DOI] [PubMed] [Google Scholar]
- 38.Chen T. W., et al. , Ultrasensitive fluorescent proteins for imaging neuronal activity. Nature 499, 295–300 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Fünfschilling U., Reichardt L. F., Cre-mediated recombination in rhombic lip derivatives. Genesis 33, 160–169 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Maejima T., et al. , Postnatal loss of P/Q-type channels confined to rhombic-lip-derived neurons alters synaptic transmission at the parallel fiber to Purkinje cell synapse and replicates genomic Cacna1a mutation phenotype of ataxia and seizures in mice. J. Neurosci. 33, 5162–5174 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Roth A., Häusser M., Compartmental models of rat cerebellar Purkinje cells based on simultaneous somatic and dendritic patch-clamp recordings. J. Physiol. 535, 445–472 (2001). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Bergerot A., Rigby M., Bouvier G., Marcaggi P., Persistent posttetanic depression at cerebellar parallel fiber to Purkinje cell synapses. PLoS One 8, e70277 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Loulier K., et al. , Multiplex cell and lineage tracking with combinatorial labels. Neuron 81, 505–520 (2014). [DOI] [PubMed] [Google Scholar]
- 44.Otsu Y., et al. , Activity-dependent gating of calcium spikes by A-type K+ channels controls climbing fiber signaling in Purkinje cell dendrites. Neuron 84, 137–151 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Konnerth A., Dreessen J., Augustine G. J., Brief dendritic calcium signals initiate long-lasting synaptic depression in cerebellar Purkinje cells. Proc. Natl. Acad. Sci. U.S.A. 89, 7051–7055 (1992). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Marcaggi P., Attwell D., Endocannabinoid signaling depends on the spatial pattern of synapse activation. Nat. Neurosci. 8, 776–781 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Gundelfinger E. D., Reissner C., Garner C. C., Role of bassoon and piccolo in assembly and molecular organization of the active zone. Front. Synaptic Neurosci. 7, 19 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Richter K., et al. , Presynaptic cytomatrix protein bassoon is localized at both excitatory and inhibitory synapses of rat brain. J. Comp. Neurol. 408, 437–448 (1999). [DOI] [PubMed] [Google Scholar]
- 49.Sterio D. C., The unbiased estimation of number and sizes of arbitrary particles using the disector. J. Microsc. 134, 127–136 (1984). [DOI] [PubMed] [Google Scholar]
- 50.Valera A. M., Doussau F., Poulain B., Barbour B., Isope P., Adaptation of granule cell to Purkinje cell synapses to high-frequency transmission. J. Neurosci. 32, 3267–3280 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Barbour B., Brunel N., Hakim V., Nadal J. P., What can we learn from synaptic weight distributions? Trends Neurosci. 30, 622–629 (2007). [DOI] [PubMed] [Google Scholar]
- 52.Huang C. M., Miyamoto H., Huang R. H., The mouse cerebellum from 1 to 34 months: Parallel fibers. Neurobiol. Aging 27, 1715–1718 (2006). [DOI] [PubMed] [Google Scholar]
- 53.McKay B. E., Turner R. W., Physiological and morphological development of the rat cerebellar Purkinje cell. J. Physiol. 567, 829–850 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Atluri P. P., Regehr W. G., Determinants of the time course of facilitation at the granule cell to Purkinje cell synapse. J. Neurosci. 16, 5661–5671 (1996). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Ly R., et al. , Contribution of postsynaptic T-type calcium channels to parallel fibre-Purkinje cell synaptic responses. J. Physiol. 594, 915–936 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Spaeth L., et al. , Cerebellar connectivity maps embody individual adaptive behavior. bioRxiv [Preprint] (2021). https://www.biorxiv.org/content/10.1101/2021.02.24.432563v1.full (Accessed 6 September 2021).
- 57.Brenowitz S. D., Regehr W. G., Reliability and heterogeneity of calcium signaling at single presynaptic boutons of cerebellar granule cells. J. Neurosci. 27, 7888–7898 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Palay S., Chan-Palay V., Cerebellar Cortex (Springer, New York, 1974). [Google Scholar]
- 59.Lee K. J., et al. , Motor skill training induces coordinated strengthening and weakening between neighboring synapses. J. Neurosci. 33, 9794–9799 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Federmeier K. D., Kleim J. A., Greenough W. T., Learning-induced multiple synapse formation in rat cerebellar cortex. Neurosci. Lett. 332, 180–184 (2002). [DOI] [PubMed] [Google Scholar]
- 61.Ruela C., Matos-Lima L., Sobrinho-Simões M. A., Paula-Barbosa M. M., Comparative morphometric study of cerebellar neurons. II. Purkinje cells. Acta Anat. (Basel) 106, 270–275 (1980). [DOI] [PubMed] [Google Scholar]
- 62.Tong R., Chater T. E., Emptage N. J., Goda Y., Heterosynaptic cross-talk of pre- and postsynaptic strengths along segments of dendrites. Cell Rep. 34, 108693 (2021). [DOI] [PubMed] [Google Scholar]
- 63.Bannon N. M., Chistiakova M., Volgushev M., Synaptic plasticity in cortical inhibitory neurons: What mechanisms may help to balance synaptic weight changes? Front. Cell. Neurosci. 14, 204 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Díez-García J., Akemann W., Knöpfel T., In vivo calcium imaging from genetically specified target cells in mouse cerebellum. Neuroimage 34, 859–869 (2007). [DOI] [PubMed] [Google Scholar]
- 65.Danielian P. S., Muccino D., Rowitch D. H., Michael S. K., McMahon A. P., Modification of gene activity in mouse embryos in utero by a tamoxifen-inducible form of Cre recombinase. Curr. Biol. 8, 1323–1326 (1998). [DOI] [PubMed] [Google Scholar]
- 66.Abdeladim L., et al. , Multicolor multiscale brain imaging with chromatic multiphoton serial microscopy. Nat. Commun. 10, 1662 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Galas L., et al. , Postnatal migration of cerebellar interneurons. Brain Sci. 7, 1–17 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Akaike T., The tectorecipient zone in the inferior olivary nucleus in the rat. J. Comp. Neurol. 320, 398–414 (1992). [DOI] [PubMed] [Google Scholar]
- 69.Barash S., et al. , Saccadic dysmetria and adaptation after lesions of the cerebellar cortex. J. Neurosci. 19, 10931–10939 (1999). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Glickstein M., Sultan F., Voogd J., Functional localization in the cerebellum. Cortex 47, 59–80 (2011). [DOI] [PubMed] [Google Scholar]
- 71.Lachamp P., et al. , Early expression of AMPA receptors and lack of NMDA receptors in developing rat climbing fibre synapses. J. Physiol. 564, 751–763 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Pachoud B., Sharma P., Bergerot A., Knöpfel T., Marcaggi P., Quantification of the density of cooperative neighboring synapses required to evoke endocannabinoid signaling. Neuroscience 256, 412–425 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Al-Juboori S. I., et al. , Light scattering properties vary across different regions of the adult mouse brain. PLoS One 8, e67626 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All study data are included in the article and/or SI Appendix.