Stochastic chromatin packing of 3D mitotic chromosomes revealed by coherent X-rays

Significance

The structural link between meter-long DNA molecules and chromosomes a few microns in size and their highly space-effective and fault-free packing and unpacking mechanisms remain a puzzle. This research addressed this fundamental issue by resolving a three-dimensional (3D) structure of human chromosomes using cryogenic coherent X-ray diffraction tomography. Structures of metaphase chromosomes, preserved in a frozen hydrated condition, with quantitative details on 3D electron density distributions were obtained at nanometer-scale resolution. The geometrical analysis of the 3D structures with the statistical modeling unveils that the stochastic process is the essence of the structure formation. While supporting the structural analysis, molecular dynamics simulations further elucidate the critical role of short-range attraction between chromatins and DNA-binding proteins in forming micrometer-sized chromosomes.

Abstract

DNA molecules are atomic-scale information storage molecules that promote reliable information transfer via fault-free repetitions of replications and transcriptions. Remarkable accuracy of compacting a few-meters-long DNA into a micrometer-scale object, and the reverse, makes the chromosome one of the most intriguing structures from both physical and biological viewpoints. However, its three-dimensional (3D) structure remains elusive with challenges in observing native structures of specimens at tens-of-nanometers resolution. Here, using cryogenic coherent X-ray diffraction imaging, we succeeded in obtaining nanoscale 3D structures of metaphase chromosomes that exhibited a random distribution of electron density without characteristics of high-order folding structures. Scaling analysis of the chromosomes, compared with a model structure having the same density profile as the experimental results, has discovered the fractal nature of density distributions. Quantitative 3D density maps, corroborated by molecular dynamics simulations, reveal that internal structures of chromosomes conform to diffusion-limited aggregation behavior, which indicates that 3D chromatin packing occurs via stochastic processes.

The discovery of the double-helical structure of DNA, arguably one of the most important scientific discoveries made in the 20th century, has opened the path to understanding various biological phenomena on a molecular basis (1, 2). This has motivated research on the human intervention of genes to regulate cell functions. Despite notable accomplishments, various challenges have also emerged because of the incomplete knowledge of the nanoscale three-dimensional (3D) structures of the chromosome, including the puzzling compaction mechanism from a DNA molecule to a chromosome and its error-free unpacking into DNA molecules again in the nucleus (1, 3–5). Understanding the structure-forming mechanism of the chromosome can begin with the chromatin chains of 11-nanometer-scale nucleosomes that consist of DNA molecules wrapped around the histone octamer. The question is how these 11-nanometer-scale molecular complexes are spatially organized to form micrometer-sized chromosomes (1, 6, 7).

High-resolution structures of chromosomes are expected to reveal the underlying mechanisms behind chromatin packing, especially in metaphase, which has prompted active research (3, 8–10). There has been increasing experimental evidence on the spatial arrangements of intermixed chromatin in cell nuclei and compacted 3D structures from Hi-C map analysis, optical fluorescence imaging, electron microscopy, atomic force microscopy, superresolution optical imaging, and X-ray diffraction (3, 6, 8, 11–14). These results have led to the proposal of various structural models for mitotic chromosomes such as the hierarchical multiscale model and loops/scaffold model. The hierarchical model proposes that the 11-nm nucleosomal DNA builds up 30-nm-scale chromatin fibers and subsequent putative higher-order folding structures to establish the mitotic chromosome of a few microns in scale (2, 5, 6, 15–18). The loops/scaffold model suggests that the mitotic chromosome consists of arrays of radial loops emanating from a central scaffold formed by structure-forming proteins including condensin and topoisomerase-II (19–21). However, a unifying structure model still remains to be established, which has been largely delayed by insufficient information on the high-resolution 3D structure of the specimens preserving its native structure (3, 4, 16, 22–26). By performing cryogenic coherent diffraction imaging (cryo-CDI) experiments, we obtained a nanoscale 3D density distribution of isolated human chromosomes in the mitotic phase. The specimens were frozen rapidly in hydrated conditions to best preserve the native structure. X-ray imaging under cryogenic temperature, compared to ambient temperature, helps to acquire a higher-resolution structure by allowing a few tens of times higher X-ray dose (27–30). We performed geometrical analysis of the 3D structures in comparison with a statistical model, which provides physical and biological insights into structure-forming mechanisms.

Results

Three-Dimensional Structure of Mitotic Human Chromosomes.

Nanoscale 3D structures of mitotic chromosomes were acquired from cryo-CDI (30). The experiments were performed at BL29XUL of SPring-8 with the incident X-ray energy at 5.5 keV. We prepared the specimens by rapidly freezing hydrated chromosomes dispersed on an Si₃N₄ membrane. The 3D data were collected by rotating the membrane with the specimen at the center of the cryogenic helium gas stream at 100 K. The entire cryo-CDI system was enclosed by a custom-designed acrylic box at helium ambience (Fig. 1A and Materials and Methods) (31). X-rays enable the probing of specimens too thick for electron microscopy, which allows for noninvasive and quantitative 3D imaging of whole chromosomes (27, 32, 33).

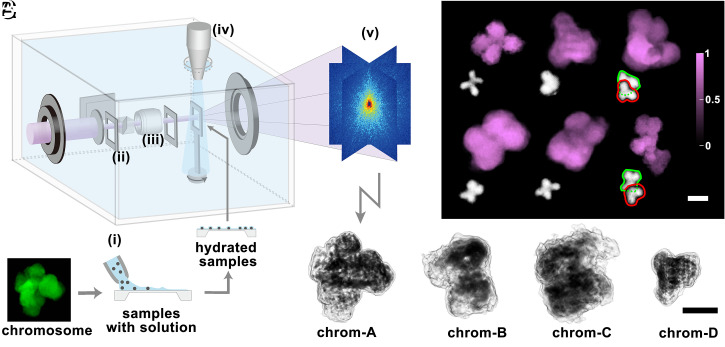
Fig. 1.

Cryogenic coherent X-ray diffraction imaging of frozen hydrated chromosome. (A) Cryogenic coherent diffraction 3D imaging (cryo-CDI) of isolated human chromosomes. Specimens in the buffer solution were dispersed on a 30-nm thin Si₃N₄ membrane (i). The hydrated chromosomes are rapidly frozen using the cryogenic helium gas stream (iv). The location of the sample on the membrane is found with an inline microscope (iii), and X-rays are irradiated to generate coherent diffraction patterns from single isolated chromosome. The two slits (ii) block parasitic scatterings from upstream of the beamline. X-ray diffraction patterns (v) are collected and phase retrieved to obtain 3D images. (B) Two-dimensional projection images of chromosomes were obtained displaying the characteristic shapes of the chromosome. Optical microscope images of human chromosomes with similar morphologies were compared (Inset). (C) Three-dimensional structures of four different chromosomes were obtained using tomographic reconstructions. Images displayed in gray tone with the dark regions with higher electron density. (Scale bars, 1 μm.)

Using isolated single chromosomes as specimens, we collected coherent X-ray diffraction patterns in the far field that are equivalent to the Fourier moduli of chromosome electron densities projected along the incident X-ray direction. By performing numerical phase retrievals of the diffraction patterns, we obtained images that displayed plane-projected electron densities of the mitotic chromosomes from HCT116 cells (Fig. 1B and Materials and Methods) (30, 32). Images were obtained at the spatial resolution of ∼44 nm estimated from the phase retrieval transfer function (PRTF) (SI Appendix, Fig. S1). Characteristic shapes of the chromosomes were observed along with variants from reconstructed images that compared well with the gallery of human chromosomes (Fig. 1B, Insets) (34). Images with more complex shapes were attributed to two overlaid chromosomes. We have not attempted to identify the chromosome number given the experimental limitations, such as the difficulty in collecting all 23 pairs from one nucleus for self-consistent numbering.

The 3D structure was obtained by performing tomographic reconstructions of two-dimensional (2D) images from the same chromosome collected by rotating the specimen perpendicular to incident X-rays (Movie S1 and Materials and Methods). We acquired four independent sets of 3D data from different chromosomes. Reconstructed 3D images displayed the internal structures of chromosomes (Fig. 1C). In all four chromosome structures, we noticed that the electron density was distributed with irregular mixtures of relatively higher- and lower-density regions (Fig. 2A and SI Appendix, Fig. S2). The high-density regions can be understood as local spaces well-packed with chromatin and related proteins. The zoomed-in volume manifested a nonuniform distribution of densities, indicating irregular compaction of the chromatin without a well-defined structural pattern (Fig. 2A, Inset). Instead, we observed that overall structures were established in a disordered manner from the smaller length scale of a few tens of nanometers to a several-hundred-nanometer scale.

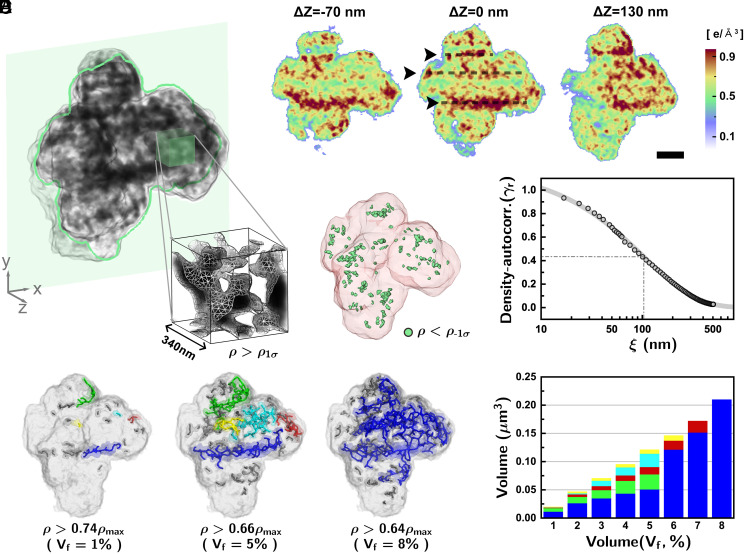
Fig. 2.

Quantitative 3D structure of the metaphase human chromosome. (A) Three-dimensional density distributions of the mitotic chromosomes (chrom-A). The internal structures displayed a disordered density distribution. (B) Sectioned images of the 3D structure to exhibit internal structures clearly along with the repeating high-density structures at the interval of 250 to 300 nm. (Scale bar, 500 nm.) (C) Low-density regions in the 3D density distribution were identified (green) to represent cavities. (D) The density–density autocorrelation was estimated to show that the spatial correlation in the density distribution decreased monotonically without any particular ordering tendency. The gray solid line is a fit to ${\text{γ}}_r\left(\mathit{\xi }\right)=\text{A} \text{exp}\left(-{\left(\mathit{\xi }/l_c\right)}^{\mathit{\beta }}\right)$ with the best-fit parameters $\mathit{\beta }\cong 0.83$ and $l_c\cong 104 \text{nm}$. The characteristic length $l_c$ can be viewed as the typical domain size of the high-density regions. (E) High-density structures originated from well-packed chromatins were identified with their topological features displayed through the skeleton images. Each skeleton of the connected body was painted using the same color, identifying the connectivity of the high-density structure. (F) Relative size and volume fraction of the five largest skeletons with high electron density were traced by changing the density threshold levels. The structures became merged for a volume fraction level of 8%.

The internal density distribution was shown clearly in numerically sectioned 2D images (Fig. 2B). Repeated high-density structures at intervals of 250 to 300 nm were observed in two of the four structures: chrom-A and chrom-D. This was reminiscent of chromosomal bands reported earlier (14). Further attempts to extract biological implications were avoided due to its presence only on two of the four chromosomes and the absence of an established structure model accounting for this (11).

Geometrical Analysis of 3D Chromosome Structures.

From the 3D density maps, we identified the regions with significantly lower density at the level out of the one-sigma range, $\mathit{\rho }\left(\overrightarrow{r}\right)< {\mathit{\rho }}_{\text{avg}}-{\mathit{\rho }}_{\mathit{\sigma }}$, with ${\mathit{\rho }}_{\mathit{\sigma }}$ being the SD from the average density (${\mathit{\rho }}_{\text{avg}}$), which can be regarded as cavities within the metaphase chromosome (Fig. 2C). Most of the cavities were present deep inside the chromosome with a volume fraction smaller than 1% of the total volume, which can be compared with the ∼4.5% volume fraction reported for prophase chromosomes (8). This lower cavity concentration indicates that metaphase chromosomes were more densely packed (3). Cavities extended to the surface were not explicitly identified here.

The statistical characteristics of the density distribution were identified by estimating the density autocorrelation, ${\mathit{\gamma }}_r\left(\mathit{\xi }\right)={{\displaystyle \int }}^{\text{}}d{\text{Ω}}_{\mathit{\xi }}{\int }_{V}d\overrightarrow{r}\left\{\mathit{\rho }\left(\overrightarrow{r}+\overrightarrow{\mathit{\xi }}\right)-{\mathit{\rho }}_{\text{avg}}\right\}\left\{\mathit{\rho }\left(\overrightarrow{r}\right)-{\mathit{\rho }}_{\text{avg}}\right\}$, showing the spatial correlation in the density distribution. The density autocorrelation obtained along the radial direction exhibited a stretched-exponential decay with a characteristic length ($l_c$) of 104 nm (Fig. 2D). Similar monotonic decreases in the density autocorrelation were observed along any particular radial directions. Such characteristics of the density autocorrelation suggest that the metaphase chromosome may not have a well-defined ordered chromatin structure (e.g., the 30-nm chromatin fiber) and the structure of chromatin packing is disordered at the length scale from tens to hundreds of nanometers.

The topological nature of the density distribution was investigated further to understand chromatin packing. By gradually lowering the density threshold starting from the maximum (${\mathit{\rho }}_{\text{max}})$, the high-density regions became connected accordingly. We have represented such connected high-density structures using skeletons to emphasize topological features (Fig. 2E and Materials and Methods). The results showed that the chrom-A had several segmented linear structures of high electron density (Fig. 2E, level corresponding to the volume occupancy of high-density regions, $V_f$, to be 1%). Upon decreasing the density threshold, the linear structures became extended by connecting small segments nearby. Not all of the linear structures were connected in the beginning to show that those high-density regions did not necessarily form one main scaffold but remained fragmented. By lowering the threshold level further, small structures were newly branched out from the major linear structure to form meshed structures (Fig. 2E; $V_f$ = 5%). Upon decreasing the density threshold to accommodate 8% of the high-density volume occupancy, most of the major skeletons merged into one large structure (Fig. 2 E and F). We may regard the growth of the largest cluster into a spanning cluster as a percolation transition in finite-size systems with the fraction of percolation as an order parameter (see further discussion in SI Appendix, section S2.1). The percolation transition was observed for the four chromosome structures in our experiment (see the fraction of percolation vs. the volume fraction $V_f$; SI Appendix, Fig. S3). This happened randomly and did not accompany any regular pattern, which favors the disorder structure model description of the 3D chromatin packing (3). The observed large meshed network at sufficiently low threshold levels was reminiscent of interconnected 3D chromatin complex network in metaphase chromosomes reported before from focused ion beam scanning electron microscope imaging (35) and electron microscopy tomography (36).

Comparative Statistical Structure Models.

We performed a comparative analysis of the chromosome structure with a statistical model to gain physical insight into the internal structure. The statistical structure model was built using the density profile conforming to the Gaussian random field (GRF) distribution with the same density autocorrelation characteristics observed in the experiments (Materials and Methods). The established GRF structure was then wrapped with the 3D morphology of chrom-A for direct visual comparison. Overall, it well reproduced the random distribution of the 3D density map observed in the experiments (Fig. 3A), except for a major difference that the GRF structure does not allow the globally connected high-density network (Fig. 3A, Inset and SI Appendix, Fig. S3). To quantify such differences in its geometrical features, we compared the asphericities of all the high-density structures ($V_f=5\%$) found in the GRFs and the four chromosomes (Fig. 3B). The x and y axes are asphericity ($\text{Δ}$) and the nature of asphericity ($\text{Σ}$), which measures the anisotropy and ellipticity of an object, respectively (Materials and Methods) (37). It showed that for both the GRF model and real chromosomes the high-density structures are prolate and anisotropic. However, metaphase chromosome’s folding structure is distinguished from the GRFs in the sense that its high-density parts have substantial directional persistence to reach the rod-like limit ($\text{Δ}\approx 1$ and $\text{Σ}\approx 1$). This analysis elucidates that the chromatin packing is accommodated randomly and the size increases with a strong tendency for directional growth.

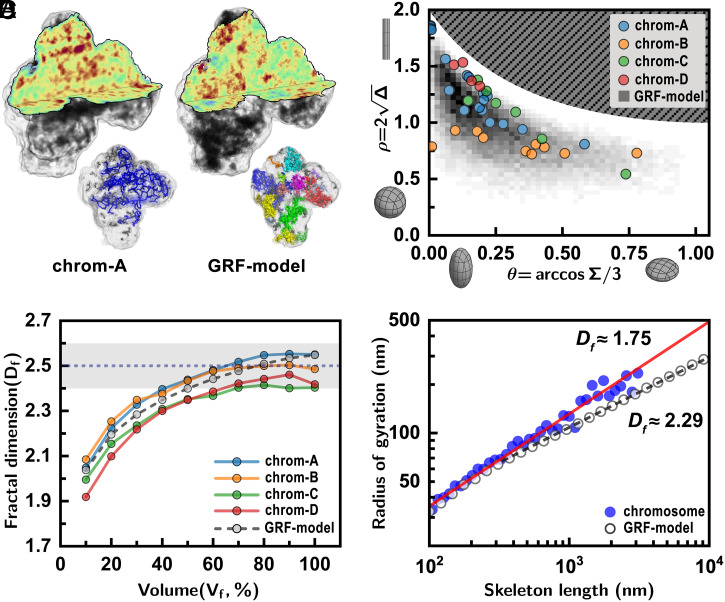
Fig. 3.

Scaling analysis of the chromosomes compared with a structure model. (A) Three-dimensional density distribution of the chromosome (chrom-A) was compared with the GRF structure model (GRF model) that has the same density profile as chrom-A. Details on the construction of the GRF model structure are found in the main text. Random distributions of the high-density regions are similarly noted, but the GRF model structure does not form a globally connected high-density structure (Inset). (B) The shapes of high-density structures showed that well-packed regions formed favoring a prolate geometry similar to the GRF model. (C) High-density structures ($V_f\mathrm{\gtrsim }70\text{\%}$) in the chromosomes filled the space with the fractal dimension $D_f=2.5(\pm 0.1)$ (shaded region). The same convergence in the fractal dimension was found for the GRF model as well as other chromosomes investigated. (D) The radii of gyration ($R_g$) of the high-density skeletons of the chromosome from experimental data showed that their volume increases with the skeleton’s linear size with $D_f\approx 1.75$ (red solid line). Here, the $R_g$ displays the average value from all four chromosomes. The high-density skeletons of the GRF model exhibited a different scaling behavior with $D_f\approx 2.29$ (dashed line).

To understand the chromatin packing behavior, we performed a scaling analysis of the space-filling fractal dimension. The image voxels with densities higher than a threshold level ($V_f$) were identified to represent highly packed regions (Fig. 3C and Materials and Methods). The dimensions of the filled regions were traced for different threshold levels. The fractal dimension ($D_f$) of the high-density regions was calculated using the box-counting method, $D_f={\lim }_{\epsilon \to 0}\frac{\log N\left(\epsilon \right)}{\log (1/\epsilon )},$ where $N(\mathit{\epsilon })$ is the number of boxes of side length $\mathit{\epsilon }$ (Materials and Methods). The fractal dimension reached its saturated value of 2.5 (± 0.1) for $V_f \mathrm{\gtrsim }70\%.$ A similar fractal dimension was found consistently for all four chromosomes (Fig. 3C and SI Appendix, Fig. S4).

The aforementioned dimensional analysis delivers several important messages. The fractal nature of the space filling indicates a self-similar packing of the chromatin across the length scale. The obtained fractal dimension of 2.5 falls in the range between 2.2 and 3 reported for interphase chromosomes (12, 38, 39). The GRF model also led to the same fractal dimension of ∼2.5, which suggests that the fractal dimension indeed reflects the intrinsic property of the random density distributions found in our experiments. The fractal dimension of ∼2.5 is close to that for 3D percolation clusters at criticality with $D_f$ = 2.53, such as a cross-linking polymer at the gel point (40) or random structures via diffusion-limited particle-cluster aggregation with $D_f$ = 2.5 (41).

We further scrutinized the fractal dimension of the high-density structures by investigating the relationship between their radii of gyration, $R_g$, and occupied voxel volume, n (i.e., linear length). The fractal dimension was estimated from the scaling relation, $R_g \propto n^{1/D_f}$ (Materials and Methods). We obtained $D_f=\mathrm{2.44-}‒2.80$ for the high-density clusters in chrom-A and chrom-D (SI Appendix, Fig. S5A), consistent with the box-counting method. We then estimated $D_f$ for the skeletonized high-density structures of both experimental and model structures (Fig. 3D). It should be noted that this is the fractal dimension solely for the backbone structure and accordingly gives relevant information on the large-scale connectivity of high-density clusters. The $R_g$ of the skeletonized clusters was plotted as a function of their linear length (Fig. 3D). The results showed an interesting distinction between the metaphase chromosome and the GRF structures. For the chromosome skeletons, $R_g$ followed a power-law behavior with $D_f\approx 1.75$ throughout the whole length scale. The value of $D_f$ smaller than 2 (of the random walk) indicates that the backbone configuration resembles a persistent random walk having a positive directional correlation. Meanwhile, those from the GRF model had the fractal dimension $D_f\approx 2.29$ (>2), following an antipersistent random walk. This strongly suggests that the backbone of the high-density chromosome structures, represented by skeletons, is formed with directional preference in the midst of random growth.

We investigated possible physical mechanisms to account for the fractal dimension of 1.75 observed for the high-density skeletons. This skeleton configuration is distinguished from a self-avoiding walk of $D_f\approx 1.70$ and shows a close similarity to the diffusion-limited cluster aggregation (DLCA) with the fractal dimension $D_f=\mathrm{1.7-}–1.8$ (42). The DLCA is a growth process that the diffusing particles self-aggregate into a giant cluster via shear-rigid bonds (42). In this process, the particles in proximity aggregate into small clusters, and then these clusters slowly self-aggregate into bigger ones to become a giant fractal object with $D_f=\mathrm{1.7-}‒1.8$.

We found that neither of two major chromosome models—the hierarchical multiscale model or loops/scaffold model—explains the observed DLCA-like inhomogeneous high-density structure. Based on the reported model structures (20), we simulated the two chromosome polymer models explicitly to obtain the voxelized density map (SI Appendix, Figs. S7 and S8 and text). The density autocorrelation of the hierarchical model showed a monotonically decreasing density profile analogous to our chromosome data. However, the density distribution of the hierarchical model is rather homogenous over the entire volume, distinguished from the fractal-patterned chromosome density map (SI Appendix, Fig. S7). The density map for the loops/scaffold model displays two distinct density regions (SI Appendix, Fig. S8). The scaffold-containing central part forms a high-density region, whereas the off-axis outer part shows a homogeneous distribution with low density. Further discussion on the chromosome models and simulations can be found in SI Appendix. Our simulation results do not necessarily exclude the existence of high-order structures, chromatin loops, or scaffold in mitotic chromosomes. Instead, the results suggest that the inhomogeneous chromatin packing at the length scale of hundreds nanometer is governed by physical mechanism(s) neglected in the abovementioned models. We propose that the experimentally observed DLCA-like high-density structure can be established from concentrated DNA-binding proteins with self-aggregation and binding onto chromatin fibers. To our best knowledge, the roles of protein self-aggregation on the chromatin packing have not been explicitly taken into account in the above two major chromosome models (see further discussion on the chromosome models in SI Appendix, section S2.2).

To demonstrate the proposed chromatin-packing mechanism, we generated the chromosome structure from Langevin molecular dynamics simulations of a coarse-grained polymer model system; our model structure consists of highly packed chromatin polymers together with the concentrated DNA-binding proteins (Fig. 4). For the length scale of interest, the chromosome was viewed from the 11-nm-scale “beads-on-a-string” chromatin with each bead representing a nucleosome. The DNA-binding proteins were described as spherical blobs that bind themselves upon contact or attached to the chromatin polymers via an interprotein attractive interaction (SI Appendix, Fig. S6) (43). This chromatin–protein system was subject to strong spatial confinement to accommodate the packing density similar to the mitotic chromosome (SI Appendix, section S1) (44). The molecular dynamics simulations confirmed the formation of DLCA-like fractal structure under a highly condensed state (Fig. 4). The fractal dimension of the simulated structure was extracted to have $D_f\approx 1.78$ (Fig. 4D), consistent with the experimental results. See SI Appendix, sections S1 and S2.3 for further information on the model and parameters and additional analyses on the simulation results.

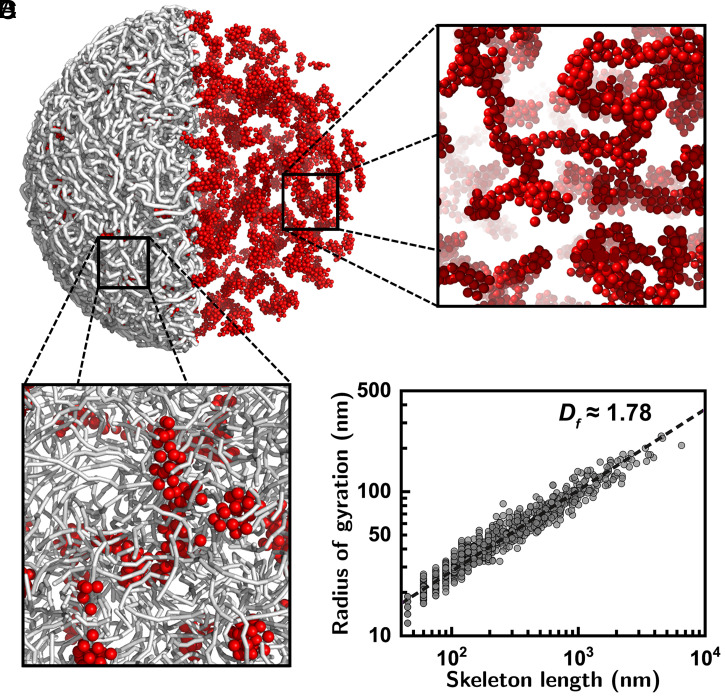
Fig. 4.

Langevin molecular dynamics simulations displaying formation of high-density structures. (A) Molecular dynamics simulation of a coarse-grained polymer model for describing the chromatins and DNA-binding protein complex systems. Here, the gray sticks visualize the chromatin fiber and the red spheres depict the DNA-binding proteins. For further information on the model and simulation details see SI Appendix. Simulations confirmed the formation of high-density structures via aggregations of the proteins and chromatins. For visual inspection of the protein aggregations the chromatin was not displayed in the right hemisphere. (B and C) Zoomed-in views of the snapshot images with (B) and without (C) the chromatin. Molecular dynamics simulations ascertained that the chromatin–protein complex forms a DLCA-like high-density structure. (D) The radii of gyration were estimated at different length scales for the skeletons of the high-density structures from 10 independent simulation runs. The best fit shown in the dashed line leads to $D_f\approx 1.78$, consistent with the experimental results. The obtained $D_f$ is a time-independent stationary value (see $D_f$ vs. simulation time in SI Appendix, section S1.2.

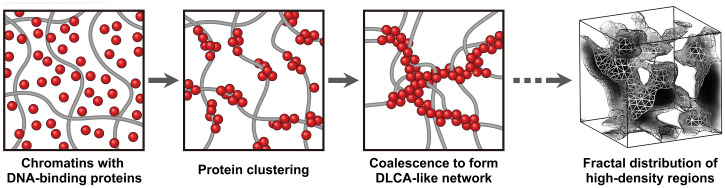
We can describe the chromatin-packing process as follows (Fig. 5). The proteins in the neighborhood stick together through random diffusion to form small clusters with shear rigidity. The clusters are then mingled with the chromatins via the proteins attached to them. Then, the chromatin–protein clusters become connected to the others via coalescence, forming a DLCA-like backbone structure of the mitotic chromosome (Fig. 5 and Movies S2 and S3). As evidenced by the molecular dynamics simulations, this chromatin-packing model emphasizes the critical role of the self-aggregation of proteins in forming the DLCA-like chromosome regions. Our molecular dynamics simulations confirmed that without a proper aggregation interaction the protein-mediated high-density regions failed to grow into a large fractal object: In the absence of the interprotein interaction, the proteins became evenly scattered over the chromosome globule as small fragments (SI Appendix, Fig. S9 A and D). Meanwhile, if the proteins aggregate without shear rigidity, they eventually render a chromatin–protein complex having a spherical morphology (SI Appendix, Fig. S9 B and E). Only when the proteins aggregate with shear rigidity do they lead to DLCA-like fractal high-density regions (SI Appendix, Fig. S9 C and F). We confirmed that the high-density regions are correlated with the location of protein clusters (SI Appendix, section S2.3). It was proposed that condensin-I and -II show intercondensin attraction (45, 46), which may find relevance to our model. However, we do not attempt to pinpoint the involved binding proteins from the current investigations.

Fig. 5.

Stochastic chromatin packing with DNA-binding proteins via diffusion-limited cluster aggregation. A mechanistic model describing the chromatin packing process to form randomly distributed high-density structures in the metaphase chromosome is proposed. The complex networks with dispersed chromatins and DNA-binding proteins start to form small clustering with self-aggregation of proteins. With further development of the self-aggregating reaction, enlarged protein clusters becomes coalesced while driving random concentration of chromatins accordingly, which leads to the formation of large-scale chromatin–protein networks following a DLCA structure. As verified by the Langevin molecular dynamics simulations, this stochastically driven chromatin condensation model can describe the fractal distribution of high-density structures observed in metaphase chromosomes.

Our model emphasizes the role of physical interactions among DNA and proteins in the condensation and structure formation of mitotic chromosomes. This proposed model is compatible with the previous in vitro experimental observations that compaction of mitotic chromosome can be caused by histone posttranslational modification and increase of Mg²⁺ ions in the chromosome without ATP-involved loop extruding proteins, which demonstrates there are in fact multiple players in the chromosome condensation and the role of nucleosome-mediated interactions along with DNA-associated proteins are prominent (47–50). However, our stochastic structure model is not intended to explain the whole process of mitotic chromosome condensation in the nucleus, which would require the concerted play of ATP-consuming proteins, for instance the active loop extrusions by condensins (21, 51, 52). In this regard, our model may provide an insightful complement to the existing chromosome structure models (SI Appendix, section S2.2).

Summary

We have obtained quantitative 3D structures of mitotic chromosomes at tens-of-nanometers resolution by preserving their structures in frozen-hydrated conditions. In direct comparison with the statistical model structure constructed to follow the Gaussian-type random density distribution, systematic characterization of the 3D structures using density autocorrelation and topological characteristics of the high-density regions has unveiled that the mitotic chromosomes can be characterized by random 3D packing of chromatins at the length scale of hundreds nanometers (4). The scaling analysis of the experimental data has also elucidated that well-packed, high-density regions and their backbone structures share close similarity with the 3D percolation and DLCA systems, respectively. Being further corroborated by Langevin molecular dynamics simulations of coarse-grained polymer models, the statistical analysis of the 3D density profiles of the metaphase chromosome provides a key insight into the physical mechanism behind the chromosome condensation to form DLCA-like high-density regions in the mitotic chromosome. This work, while consistent with the disorder structure model for the 3D chromosome structure (3), adds new understanding that the coalescence process with short-ranged attractions among chromatin fibers and DNA-associated proteins plays a dominant role in the structure formation of the mitotic chromosome.

Materials and Methods

Cryogenic Coherent Diffraction Imaging Experiment.

The coherent X-ray diffraction imaging experiment was performed at BL29 of SPring-8 using a custom-built cryogenic coherent diffraction imaging chamber. The imaging chamber is made of several components as follows. A pinhole with a diameter of 10 μm is located 370 mm upstream from the sample to improve the spatial coherence of incoming X-rays from synchrotrons. Two slits made of Si block parasitic scattering from upstream optics. The helium stream was cooled to 100 K with the open flow of the helium gas cooled by circulating around the Cu cold head of the closed-type displex. The cryogenic nozzle was positioned a few millimeters above the sample to rapidly freeze the specimens and maintain the sample temperature below 100 K. Continuous flow of the helium stream maintained the imaging chamber at ambient helium, which helped to minimize the ice formation caused by residual water molecules and to reduce air scattering. The exhaust vent was installed to prevent overpressurization of the chamber by discharging excess helium gas and air. The sample is located at the center of the helium stream and is isolated from the surrounding area. An in-line optical microscope was installed in front of the sample stage to inspect the specimens prior to X-ray data collection. We made a 300-μm-diameter hole at the center of the inline microscope lens for the X-rays to pass through, which enabled simultaneous operation of visual inspection and X-ray diffraction.

The diffraction signals from the specimens were collected by a liquid nitrogen-cooled charge-coupled device (CCD) detector (PI-LCX-1300; Princeton Instruments). An edge-polished metal plate made of a Ta block was installed in front of the CCD chip as a beam stopper to prevent direct illumination of the incident X-ray beam. The path after the sample to the CCD detector was maintained in vacuum at a pressure lower than 10⁻² Pa. The imaging chamber itself was operated at helium ambience.

We inspected well-isolated chromosomes of sizes between 1.5 and 2.5 μm using X-rays. For ultrastructural characterization of the chromosomes preserved close to the native condition, we prepared the specimens by rapidly freezing isolated chromosomes in hydration. Specimens in buffer solution were dispersed on the membrane, and hydrated chromosomes were frozen instantaneously under a concentrated flow of cryogenic helium gas (Fig. 1). Specimens mounted on thin Si₃N₄ membrane were preserved at a cryogenic temperature of 100 K during data collection and simultaneously monitored by inline optical microscopy to inspect the samples. For the tomographic 3D data collection, the identified chromosome was rotated, and the 2D diffraction pattern corresponding to each tilting angle was measured. The diffraction pattern was measured at 25 angles within the range between +63° and −63°. The tilt angles were determined fulfilling the equal-slope increments.

Metaphase Chromosome Preparation.

HCT116 cells were cultured at 37 °C in an atmosphere with 5% CO₂ in Dulbecco’s modified Eagle’s medium supplemented with 10% fetal bovine serum. Mitotic chromosomes were prepared from those cells essentially as described previously (53) but with minor modifications. Cells were first treated with 100 ng/mL nocodazole for 14 to 16 h, and then mitotic cells were shaken off and collected by centrifugation at 190 × g at room temperature for 5 min. The cells were resuspended in 75 mM KCl solution and placed at room temperature for 30 min. The cells were again collected by centrifugation at 780 × g at 4 °C for 10 min, resuspended in ice-cold polyamine-EDTA buffer (15 mM Tris·HCl [pH 7.4], 80 mM KCl, 2 mM EDTA, 0.2 mM spermine [S1141; Sigma-Aldrich], 0.5 mM spermidine [S2501; Sigma-Aldrich], 20 mM 2-mercaptoethanol, 0.1 mM phenylmethylsulfonyl fluoride, and 0.05% Empigen BB [Merck Millipore]) supplemented with a complete protease inhibitor mixture (Roche) and lysed by 20 gentle strokes with a tight-fitting stainless homogenizer. Mitotic chromosomes were collected in the supernatant (and other subcellular components were sedimented) by centrifugation of the lysate at 440 × g at 4 °C for 3 min. Contaminating subcellular components in the supernatant were eliminated by repeating the centrifuge operation once more. The supernatant was overlaid on isolation buffer (50 mM Tris·HCl [pH 7.4], 20 mM KCl, 20 mM EDTA, 0.25 mM spermidine, 0.05% Empigen BB, and 70% glycerol) and centrifuged at 1,750 × g at 4 °C for 20 min. After centrifugation, most of the mitotic chromosomes were collected in isolation buffer. The light layer that was originally the cell lysate layer was removed by aspiration, and the boundary between the two layers was carefully washed several times with polyamine-EDTA buffer. Collected chromosomes were chemically fixed with 2% formaldehyde (064-00406; FUJIFILM Wako Pure Chemical) by mixing gently with twofold concentrated fixative (4% formaldehyde in isolation buffer) of the same volume.

Numerical Phase Retrieval and 3D Reconstructions.

We retrieved the phase of the measured coherent diffraction patterns using the generalized proximal smoothing (GPS) algorithm (54). The diffraction patterns were first numerically binned to have 3-by-3 pixels into one, which helped to improve the signal-to-noise ratio of the data. Binned diffraction patterns were deconvoluted to have exactly oversampled diffraction patterns (55). The image reconstruction began using loose support at first. For one 2D diffraction pattern, numerical phase retrievals were performed using 100 initial random phases, and each random seed underwent 1,000 iterations before obtaining the first reconstructed image. Out of 100 images, the best three images with lower errors were selected to generate the average image. This average image of the first reconstruction step was used to refine the support. The second stage of image reconstruction was performed again using the GPS algorithm with refined support. The reconstruction started from 100 seeds. In this stage, the concept of the guiding from genetic algorithm of guided hybrid input–output (56) method was adopted. The reconstruction ran up to the fifth generation. Three out of 100 images with the lowest errors were averaged to generate final reconstructed images. The PRTF of the each reconstructed 2D projection image shows that the reconstruction results converge well (SI Appendix, Fig. S1). Each 3D image was obtained for tomographic reconstructions of 2D projection images. Each 2D projection image was aligned to have the same center of mass position. We employed the GENFIRE algorithm for 3D reconstruction (57).

Fractal Dimension Estimation.

The fractal dimension of the chromosome was calculated for the high-density region of the chromosome. First, a high-density region was segmented from the chromosome via a density threshold corresponding to each volume fraction. The 3D density map was then binarized and divided into regions of higher density than the threshold and lower densities. These binary images were used to calculate fractal dimensions by assigning the high-density region as regions occupied by the chromatin. The fractal dimension was then calculated using the box-counting method.

The Construction of the GRF.

The GRF imprinted with a given density–density correlation function $\text{Cov}\left(\mathit{x}\right)$ is obtained via the transformation (58)

$$G\left(\mathit{x}\right)=\left({\mathcal{F}}^{-1}{\gamma }^{1/2}\mathcal{F}W\right)\left(\mathit{x}\right).$$

In this expression, $W$ is a white Gaussian noise of zero mean and unit variance, $\mathbb{E}\left[W\left(\mathit{x}\right)W\left(\mathit{y}\right)\right]={\mathit{\delta }}^3\left(\mathit{x}-\mathit{y}\right)$. The $\mathrm{\gamma }=\mathcal{F}\left(\text{Cov}\left(\mathit{x}\right)\right)$ is the spectral density of $\text{Cov}\left(\mathit{x}\right)$, and $\mathcal{F}$ (${\mathcal{F}}^{-1}$) denotes the (inverse) Fourier transformation. The constructed GRF has the statistical property of $\mathbb{E}\left[G\left(\mathit{x}\right)G\left(\mathit{y}\right)\right]=\text{Cov}\left(\mathit{x}-\mathit{y}\right)$. To numerically implement the GRF, we first generated a 3D covariance array $C$ having experimentally obtained density correlation of the chromosomes (Fig. 2D) and a 3D array $W$ filled with Gaussian white noise of unit variance. Then, a GRF having the same density correlation with the chromosomes was numerically obtained by $G=\text{IFFT}\left(\text{FFT}{\left(C\right)}^{1/2}\circ \text{FFT}\left(W\right)\right)$, where $\text{FFT}$ ($\text{IFFT}$) is the fast Fourier (inverse Fourier) transform, and the operator $\circ$ represents the elementwise product. Once $G$ was obtained, it was multiplied and shifted by constants to fit the mean and variance of chrom-A. Finally, we trimmed the $G$ using a morphological mask of chrom-A.

Image Skeletonization.

Skeletonization reduces a 3D volumetric object into a one-dimensional skeleton representation while preserving its connectivity and topology. We used Lee’s method (59) in the Python scikit-image package (60). As preprocessing, the isolated clusters were converted to binary maps where small cavities were filled to prevent an empty shell-like structure after skeletonization.

Gyration Tensor, Radius of Gyration, and Asphericity.

The gyration tensor is defined in terms of its matrix element as $S_{ij}=\frac{1}{N}{\sum }_{k=1}^N{r}_i^{\left(k\right)}{r}_j^{\left(k\right)}$, where $r_i^{\left(k\right)}$ is the i-th Cartesian coordinate of the k-th voxel from the origin being the center of mass so that ${\mathit{r}}_{\text{CM}}=\frac{1}{N}{\sum }_{k=1}^N{\mathit{r}}^{(k)}=0$. The eigenvalues of the gyration tensor (${\mathit{\lambda }}_1\ge {\mathit{\lambda }}_2\ge {\mathit{\lambda }}_3$) are called principal moments, which represent the semiaxis lengths of the gyration ellipsoid.

A variety of shape descriptors can be defined using the principal moments. Among them, in our study, we calculated three quantities, namely, the radius of gyration, asphericity (61), and the nature of asphericity (62), which are useful shape descriptors in polymer physics (37). The radius of gyration is given by $R_G^2\equiv \frac{1}{N}{\sum }_{k=1}^N{\left({\mathit{r}}^{\left(k\right)}\right)}^2={\text{λ}}_1+{\text{λ}}_2+{\text{λ}}_3$=$\text{Tr}S$. The asphericity is defined by $\text{Δ}=\frac{3}{2}\frac{\text{Tr}{\widehat{S}}^2}{{\left(\text{Tr}S\right)}^2}$, where ${\widehat{S}}_{ij}=S_{ij}-{\mathit{\delta }}_{ij}\frac{1}{3}\left(\text{Tr}S\right)$ is a traceless tensor. It quantifies shape anisotropy, which has a value between 0 and 1 such that $\text{Δ}=0$ corresponds to a spherically symmetric object and $\text{Δ}=1$ to a linear object. The nature of asphericity is defined by $\text{Σ}\equiv \frac{4\det \widehat{S}}{{\left(\frac{2}{3}\text{Tr}{\widehat{S}}^2\right)}^{\frac{3}{2}}}$. It has a value between −1 and 1, which indicates that an object is more oblate (prolate) as $\text{Σ}\to -1 \left(+1\right)$. The nature of asphericity is alternatively represented by $\mathit{\theta }=\frac{\arccos \left(\text{Σ}\right)}{3}\in \left[0,\frac{\pi }{3}\right]$. In Fig. 3B, the joint distribution of $2\sqrt{\text{Δ}}$ and $\mathit{\theta }$ is plotted for the high-density large clusters from the chromosomes and from GRFs.

To calculate the shape descriptors of the high-density clusters, we first transformed the original image voxels into binary voxels based on a rule that a voxel is occupied if its density is above a threshold level and unoccupied otherwise. We then examined the connectivity status for the occupied binary voxels (60) and identified isolated clusters from them. The isolated clusters of size smaller than 27 voxels were neglected from our analysis. Finally, each isolated cluster’s structure and its skeleton structure’s shape descriptors were calculated. The isolated clusters from several threshold levels were used to increase the number of data points (Fig. 3D and SI Appendix, Fig. S5).

Data Availability

All study data are included in the manuscript and/or supporting information.