Modular origins of high-amplitude cofluctuations in fine-scale functional connectivity dynamics

Significance

Brain regions engage in complex patterns of activation over time. Relating these patterns to neural processing is a central challenge in cognitive neuroscience. Recent work has identified brief intermittent bursts of brain-wide signal cofluctuations, called events, and shown that events drive functional connectivity. The origins of events are unclear. Here, we address this gap in knowledge by implementing computational models of neural oscillators coupled by anatomical connections derived from maps of the human cerebral cortex. Analysis of the emerging large-scale brain dynamics reveals brief episodes with high system-wide signal amplitudes. Simulated events closely correspond to those seen recently in empirical recordings. Notably, simulated events are significantly aligned with underlying structural modules, thus suggesting an important role of modular network organization.

Abstract

The topology of structural brain networks shapes brain dynamics, including the correlation structure of brain activity (functional connectivity) as estimated from functional neuroimaging data. Empirical studies have shown that functional connectivity fluctuates over time, exhibiting patterns that vary in the spatial arrangement of correlations among segregated functional systems. Recently, an exact decomposition of functional connectivity into frame-wise contributions has revealed fine-scale dynamics that are punctuated by brief and intermittent episodes (events) of high-amplitude cofluctuations involving large sets of brain regions. Their origin is currently unclear. Here, we demonstrate that similar episodes readily appear in silico using computational simulations of whole-brain dynamics. As in empirical data, simulated events contribute disproportionately to long-time functional connectivity, involve recurrence of patterned cofluctuations, and can be clustered into distinct families. Importantly, comparison of event-related patterns of cofluctuations to underlying patterns of structural connectivity reveals that modular organization present in the coupling matrix shapes patterns of event-related cofluctuations. Our work suggests that brief, intermittent events in functional dynamics are partly shaped by modular organization of structural connectivity.

Structural and functional brain networks exhibit complex topology, and functional brain networks display rich temporal dynamics (1–3). The topological organization of structural connectivity (SC; the connectome) is characterized by broad degree distributions, hubs linked into cores and rich clubs, and multiscale modularity (4–6). Functional connectivity (FC), as measured with resting-state functional MRI (fMRI), displays consistent system-level architecture (7–9) as well as fluctuating dynamics (10–12) and complex spatiotemporal state transitions (13, 14). Resting brain dynamics exhibit metastable behavior. The lack of a fixed attractor allows for exploration of a large repertoire of network states and configurations (15–17).

Recent work has uncovered fine-scale dynamics of FC as measured with fMRI during rest and passive movie watching (18, 19). The approach leverages an exact decomposition of averaged FC estimates into patterns of edge cofluctuations resolved at the timescale of single image frames (20). These studies reveal that ongoing activity is punctuated by brief, intermittent, high-amplitude bursts of brain-wide cofluctuations of the blood-oxygenation level–dependent (BOLD) signal. The approach is reminiscent of an earlier approach proposed for electroencephalography (EEG) data in which an exact frame-wise analysis of modeled and human scalp EEG data using the Hilbert transform revealed brief large-scale desynchronous bursts (21). In the BOLD literature, episodes of high-amplitude cofluctuations, referred to as “events,” drive long-time estimates of FC and represent patterns with consistent topography across time and across individuals (18, 19, 22). The occurrence of events appears unrelated to nonneuronal physiological processes, head motion, or acquisition artifacts. A better understanding of how events originate may illuminate the basis for individual differences in FC and its variation across cognitive state, development, and disorders. Here, we aim to provide a generative model for the origin of events in neuronal time series and uncover potential structural bases for their emergence in fine-scale dynamics.

The relationship of structure to function has been a central objective of numerous empirical and computational studies, leveraging cellular population recordings (23, 24), electrophysiological (25), and neuroimaging techniques (26–28). While there is broad consensus that “structure shapes function” on long timescales (29, 30), relating specific dynamic features to the topology of the underlying structural network is an open problem. Computational models have made important contributions to understanding how SC (31, 32), time delays, and noisy fluctuations (33) contribute to patterns of FC as estimated over long and short timescales. Model implementations range from biophysically based neural mass models to much simpler phase oscillators such as the Kuramoto model (34). Despite their overt simplicity, phase oscillator models can generate a wide range of complex synchronization and coordination states, and they reproduce patterns of empirical FC (35), including temporal dynamics at intermediate timescales (36). These modeled dynamics reproduce ongoing fluctuations between integrated (less modular) and segregated (more modular) network states (37, 38), a key characteristic of empirical fMRI resting-state dynamics (39).

Here, we pursue a computational modeling approach that seeks to relate high-amplitude cofluctuations to whole-brain network structure. We simulate spontaneous BOLD signal dynamics on an empirical SC matrix of the human cerebral cortex using an implementation of a coupled phase oscillator model incorporating phase delays, the Kuramoto–Sakaguchi (KS) model (40). The KS model is well suited for this purpose because its parsimonious parametrization allows for drawing specific links between network structure and synchronization patterns. The KS model also allows simulation focused on a specific frequency band of interest so that it can more closely replicate the oscillatory behavior of neural populations often found in the gamma band (41). We find that over broad parameter ranges, BOLD signals exhibit significant high-amplitude network-wide fluctuations strongly resembling intermittent events observed in empirical data. Model dynamics reproduce several key characteristics of empirical events, including their strong contribution to long-time averages of FC as well as recurrent patterns across time. Simulated events are significantly related to network structure. They fall into distinct clusters aligned with different combinations of modules in underlying SC. Disruption of structural modules largely abolishes the occurrence of events in BOLD dynamics. These findings suggest a modular origin of high-amplitude cofluctuations in fine-scale FC dynamics.

Results

Empirical data were derived from 95 subjects included as part of the Human Connectome Project (HCP), with SC reconstructed from diffusion imaging and tractography and FC derived from four resting-state scans (792 s, 1,100 frames). The brain was parcellated into 200 functionally defined regions of approximately equal size (42), covering both cerebral hemispheres but excluding subcortical or cerebellar structures. SC data comprised estimates of connection weights as well as tract lengths used to compute time delays based on a uniform conduction velocity. Connection weights were retained in all simulations reported in this article. Most simulations employed a consensus average of SC across all 95 subjects that preserved mean density as well as the distance distribution of tracts (43). A total of 10 structural modules (labeled M1, M2, … M10; SI Appendix, Fig. 1) were derived from an implementation of multiresolution consensus clustering (Methods).

The computational model implemented the KS phase-delay oscillator (ref. 40; Fig. 1 A and B) simulated at 1 ms time resolution. A frustration matrix derived from empirical connection lengths carried phase delays computed from connection lengths and a biophysically realistic conduction velocity. Oscillator signal amplitudes (Fig. 1C) were convolved with a standard hemodynamic response function (HRF; Fig. 1D) to yield simulated BOLD signals, which were then low-pass filtered (cutoff at 0.25 Hz) and down-sampled to match the fMRI sampling rate used in the HCP data. For a single simulation run, the resulting time series extended over 792 s, composed of 1,100 time steps (720 ms). An initial transient of 20 s was discarded. Simulated BOLD time courses were processed into edge time series computed as the element-wise product of the edge’s BOLD time series standard scores (Fig. 1 E and F). The mean across all time steps of a single edge in the edge time series corresponded exactly to that edge’s FC (18–20, 22). The “root sum square” (RSS) of edgewise cofluctuations, computed across all edges on each time step, recorded system-wide instantaneous cofluctuations (Fig. 1G). Events were detected by applying a nonparametric permutation-based null model that randomly offset time series relative to each other (Fig. 1G), thus preserving (approximately) each time series’ autocorrelation while randomizing their temporal alignment (cross-correlation).

Fig. 1.

KS model schematic, computational workflow, and event detection. (A) SC weight and length matrix. (B) Node pair $(i,j)$ linked by an edge $ij$ and its corresponding phases $\mathit{\theta }(t)$. (C) Oscillator time series $\text{sin}(\theta \left(t\right))$. (D) HRF used for convolving oscillator time series to yield BOLD time series (E). (F) Elementwise product of normalized BOLD time series yields edge time series. (G) RSS of all edge time series yields RSS amplitude time series. The null model consists of a distribution of null RSS amplitudes computed from randomly shifted node time series. Gray dots show amplitudes from 100 null models, stippled line indicates the $P<0.001$ cutoff derived from 1,000 permutation nulls. Peaks exceeding the cutoff indicated by inverted triangles correspond to events. Data shown here computed from a representative run ($k=280$, 12 events detected).

Most simulations were carried out using a group-averaged SC coupling matrix (Fig. 2A) while varying the global coupling parameter $k$, yielding simulated BOLD time series and average FC patterns. Comparison of empirical (Fig. 2A) to simulated FC (Fig. 2B) exhibited modest levels of similarity (Fig. 2 B and C), in line with previous studies. A single value of the coupling parameter ($k=280$), which provided a near-optimal match with empirical FC, was selected for further detailed analysis. Empirical FC was significantly correlated with the strengths of the SC weights (Pearson correlation, all node pairs: $r_a=0.214, P=0$; Pearson correlation, intrahemispheric node pairs: $r_i=0.343, P=0$; Fig. 2C) as well as the coclassification matrix summarizing multiscale modular organization of SC (Fig. 2B). The latter finding agrees with prior observations in modeling studies that have linked structural to functional modules (31, 35) and expands on these observations by demonstrating that SC multiscale coclassification alone can significantly predict the long-time covariance structure of FC derived from empirical ($r_a=0.257, P=0; r_i=0.359, P=0$) and modeled time series ($r_a=0.756, P=0; r_i=0.732, P=0;k=280$). Model fit remained significant when simulations were carried out on SC matrices of individual participants ($r_a=0.200, P=0; r_i=0.341, P=0;$ 10 randomly selected subjects, 4 simulations each; correlations computed against the mean of the same subject’s empirical FC). Realistic FC patterns emerged with only partial synchronization of phase oscillators, as documented by relatively low means of the order parameter [$\mathit{mean}(R(t))=0.0825 \pm 0.0002$; SD; 12 runs, $k=280$], accompanied by consistently high SDs [$\mathit{std}\left(R(t)\right)=0.0414 \pm 0.0001$; SD; 12 runs, $k=280$], indicative of persistent variability in synchronization patterns and metastability.

Fig. 2.

SC and FC. (A) Empirical data. (Left) SC consensus weight matrix; (Middle) SC connection lengths (conduction delays); (Right) FC, average of 95 subjects, four runs each; all panels shown in FC module node order (FC modules marked at Left, cf. SI Appendix, Fig. 1A). (B) SC consensus and simulated FC. (Left) Coclassification (agreement) matrix derived from the consensus SC matrix; (Right) simulated FC, average of 12 runs, $k=280$; both panels shown in SC consensus module node order (SC consensus modules marked at Left, cf. SI Appendix, Fig. 1B). (Right) Scatter plot showing comparison of empirical and simulated FC (orange: all node pairs; blue: intrahemispheric node pairs only). (C) (Left) Similarity (Pearson correlation) between empirical and simulated FC across all values of $k$; (Middle) Spearman’s rho between empirical SC weights ($K_{ij}$) and simulated FC; (Right) similarity (Pearson correlation) between empirical SC coclassification matrix and simulated FC. All panels in C show data for the full range of the coupling parameter $k$, with orange dots indicating full-brain coverage (both cerebral hemispheres and their interconnections) and blue dots indicating intrahemispheric connections only. Large dots indicate data for $k=280$ (stippled vertical lines) averaged over 12 runs.

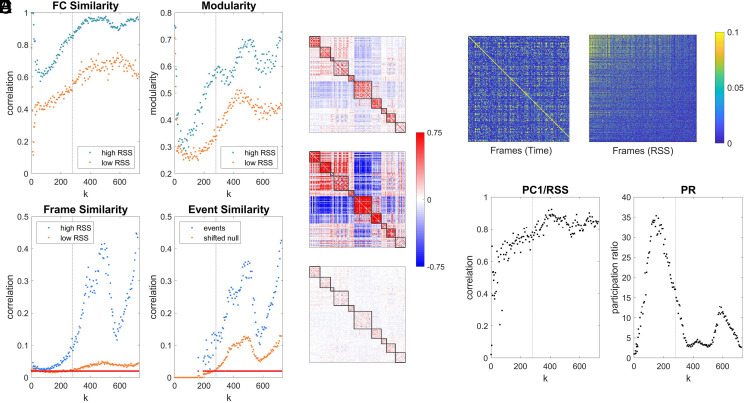
Examining the RSS of simulated edge time series reveals brief, intermittent, high-amplitude peaks, or events, over a wide range of the coupling parameter $k$ (Fig. 3). In empirical data, events exhibit several characteristic features, including their disproportionate contributions to long-time estimates of FC and somewhat stereotypic topography (18). Simulations reproduced these features (Fig. 4). We tested whether the simulated edge time series exhibited some of the same features attributed to empirical edge time series. First, we constructed FC separately using either high- or low-RSS frames. We found that FC components constructed from high-RSS frames exhibited much greater similarity to the full FC estimate than those obtained from low-RSS frames and that high-RSS FC components were significantly more modular (Fig. 4 A and B). Additionally, the cofluctuation patterns expressed during high-RSS frames were more similar to each other than low-RSS patterns, and these frames exhibited significant stereotypy across distant time points (Fig. 4 C and D).

Fig. 3.

Events in simulated edge time series. (A) Number of events (Left) and event amplitudes (RSS; Right) over the full range of $k$. Application of the null model for event detection suppresses low RSS-amplitude peaks. (B) Example of simulated edge time series ($k=280$) and RSS amplitudes, with event peaks surviving null model comparison indicated by inverted triangles.

Fig. 4.

Properties of simulated edge time series. (A) Comparison of FC components derived from the top 10% (“high RSS,” blue dots) or bottom 10% (“low RSS,” orange dots) RSS frames. (Left) Similarity (Pearson correlation) with full FC; (Right) modularity. Both panels show data across the full range of $k$. (B) Example FC matrix (all frames, Top; cf. Fig. 2) and FC components (high-RSS frames, Middle; low-RSS frames, Bottom). Data averaged over 12 simulation runs of KS model at $k=280$. (C) Similarity of frame sets sampled during high-/low-RSS epochs and during events. (Left) Mean similarity (Pearson correlation) of frames within high-/low-RSS sets (110 frames each). Red dots indicate values of $k$ for which significant differences between distributions were detected (Wilcoxon rank-sum test, one-sided, $P<0.0001$, uncorrected). (Right) Mean similarity (Pearson correlation) of event frames compared to mean of 250 randomly offset frame sets. Red dots indicate values of $k$ with $P<0.01$ (uncorrected). (D) Example plot of similarity of edge time series (Pearson correlation) across all frames within one simulation run (KS model, $k=280$; Left: frames in original time sequence; Right: frames sorted by RSS amplitude). (E) (Left) Correlation of the largest PC (PC1) of the edge time series with the RSS amplitude across all values of $k$. (Right) Participation ratio (dimensionality) computed from the FC covariance matrix. Stippled vertical line marks $k=280$ in panels A, C, and E.

We performed a principal components analysis (PCA) of edge time series, which yielded a distribution of principal components (PCs) that differed in spatial pattern and temporal expression. The score (level of expression across time) of the largest PC (PC1) was significantly correlated with global RSS amplitude (Fig. 4E), suggesting that the PC1 captured a consistent component associated with high-RSS time steps. Consistent with the emergence of a significant PC1 component, the structure of the FC covariance matrix indicated the presence of low-dimensional dynamics (low participation ratio, $PR$) over most of the parameter range, coinciding with the occurrence of high numbers of events.

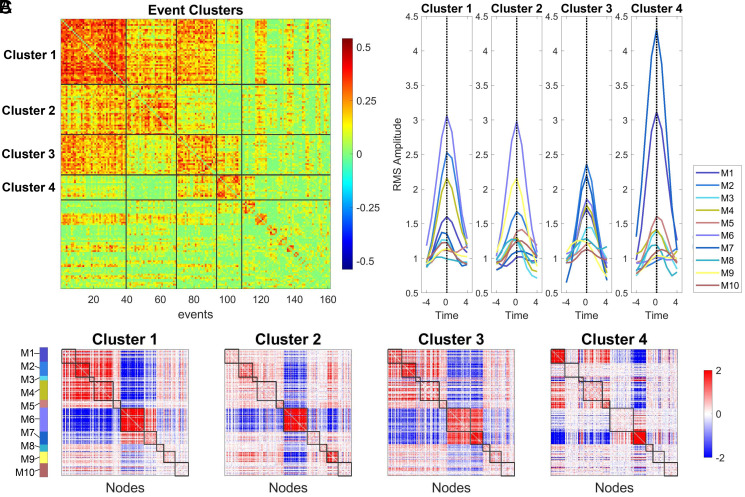
Next, we assessed the relationship of simulated events with the underlying SC. Data from 12 simulation runs ($k=280$) were aggregated to explore the topography of events and their temporal recurrence in greater detail (Fig. 5). A total of 161 events, each represented by a vector of 19,900 edge cofluctuation values, were extracted, and their mutual similarity (Pearson correlation) matrix was clustered to detect distinct sets of event patterns (Fig. 5A). We tested whether patterns for the four largest event clusters were significantly aligned with SC consensus module boundaries (Fig. 5B). The test employed a null model that rotates the structural modules on the cortical surface, thus approximately preserving their spatial contiguity (spin test, 100,000 rotations; ref. 44). Total cofluctuation magnitude within all SC modules significantly exceeded that obtained for 100,000 null model rotations (event cluster 1: P = 2 × 10⁻⁵; event cluster 2: P = 0; event cluster 3: P = 10⁻⁵; event cluster 4: P = 0.02). Testing for contributions of individual SC modules confirmed significant coalignment of specific modules with cofluctuation patterns (all P < 0.01, uncorrected; event cluster 1: M6, P = 2.3 × 10⁻⁴; event cluster 2: M2, P = 0.0026; M6; P = 1.7 × 10⁻⁴; event cluster 3: M7, P = 0.0039; M8, P = 0.006; event cluster 4: M1, P = 1.7 × 10⁻⁴; M7, P = 6 × 10⁻⁵). Different classes of events aligned with different subsets of structural modules and exhibited different time courses of cofluctuations (Fig. 5C). Our findings suggest that events belonging to different clusters are shaped by different combinations of modules present in the underlying SC.

Fig. 5.

Event clusters and relation to SC consensus modules. (A) Clustered correlation matrix of event patterns (k = 280, 161 events). Matrix is reordered to show event clusters from largest to smallest. The top four clusters are delineated and contain 37, 30, 26, and 15 events, respectively. (B) Means of the events clusters (cluster centroids) displayed in matrix form, with nodes arranged in SC consensus order (cf. Fig. 2). (C) Mean time courses of RMS, computed for each SC consensus module, with time courses aligned to the event peak for each of the four main event clusters (means of 37, 30, 26, and 15 events, respectively). Time courses show mean cofluctuation amplitude for each SC consensus module.

Several additional analyses were carried out to establish the robustness of these findings. Simulations employing different settings of the conduction velocity were analyzed to examine the frequency of events as well as the match between empirical and simulated FC (SI Appendix, Fig. 2A). Findings indicated that events occurred over a wide range of velocities (6 m/s to 21 m/s), covering a range of plausible conduction velocities for interregional projections in primate cortex (45). Events did not occur when simulations were carried out using a randomized SC matrix with near-absent modular organization (SI Appendix, Fig. 3). In contrast, events were readily observed in simulations that employed a synthetic (manually configured) SC matrix with strongly modular organization spanning specific node sets, and these events appear aligned to the provided SC modular architecture (SI Appendix, Fig. 4). Finally, simulated BOLD time courses were generated by implementing a neural mass model (NMM, as employed in ref. 31) using the same SC consensus matrix and processed identically as implemented for the KS model (SI Appendix, Fig. 5). The model matched empirical FC, exhibited robust structure–function correlations, and showed events over a range of coupling parameters. NMM model events exhibited characteristics very similar to those found in empirical as well as KS model data. Importantly, as for the KS model, NMM event clusters were significantly aligned with structural consensus modules (SI Appendix, Fig. 5). Total cofluctuation magnitude within all SC modules significantly exceeded that obtained for 100,000 null model rotations for three out of four event clusters (event cluster 1: P = 0.0508; event cluster 2: P = 1.1 × 10⁻⁴; event cluster 3: P = 0; event cluster 4: P = 0). Testing for contributions of individual SC modules confirmed significant coalignment of specific modules with cofluctuation patterns (all P < 0.01, uncorrected; event cluster 1: M3, P = 2.1 × 10^-4; M7, P = 0.0035; event cluster 2: M2, P = 1.2 × 10⁻⁴; event cluster 3: M4, P = 9.8 × 10⁻⁴; M6, P = 0.0056; M9 P = 2.4 × 10⁻⁴; event cluster 4: M2, P = 5.5 × 10⁻⁴; M7, P = 0.0032).

Discussion

Here, we show that computational models of large-scale brain dynamics exhibit brief, intermittent, high-amplitude bursts of edge cofluctuations (events) across broad ranges of coupling and conduction velocity parameters. Simulated events exhibit several characteristics that match those observed in empirical data, including a strong similarity to full-length FC and recurrence across time. We find that simulated events display brain-wide patterns of cofluctuation that are significantly aligned with network communities (consensus modules) present in the underlying SC. This relationship is reproduced in simulations that employ synthetic SC with defined modular architecture, is absent in randomized SC in which modular structure has been degraded, and is replicated in an independent model implementation. Overall, our study suggests a significant role for SC network modules in driving and shaping brief burst-like events that occur in fine-scale FC dynamics.

Recent studies have demonstrated that cofluctuations of spontaneous brain activity as measured with fMRI exhibit brief, intermittent, and high-amplitude events (18–20, 22). These patterns contribute disproportionately to time-averaged FC, contain participant-specific information, and amplify brain–behavior correlations. However, their origins are poorly understood. We address this question using computational models, which have a long-established history as generative models of resting-state FC and FC dynamics (34). Prior work has shown that their ability to match empirical data depends on the topology and weights of the underlying coupling matrix (31), noisy or chaotic dynamics, and time delays (33), as well as the lack of fixed attractors, giving rise to metastable dynamics and forming a rich repertoire of functional patterns (11). Here, we build on this body of work by extending model performance and analysis to fine temporal scales in BOLD time series. We show that model dynamic matches several recently described characteristics of empirically observed BOLD dynamics, including the recurrence of high-amplitude events in edge time series that drive full FC. Importantly, analyzing simulated FC with respect to the SC shows that specific patterns recurring in high-amplitude events are aligned with modular boundaries in the underlying SC matrix, suggesting a mechanistic basis of events in the topology of structural modules. This finding, in conjunction with the fact that events drive average long-time FC, may account for the observation that modules form a consistent “core structure” in FC (46). Previous work has implicated “cluster synchronization” in patterning of FC (35) and in temporal fluctuations related to near-critical and metastable dynamics (47). A recent model (48) adopted the FC decomposition approach to track fine-scale cofluctuation patterns linking them to neuronal cascades and nodal network structure. The model demonstrated that node centrality highly influences the node’s likelihood to participate in coordinated activations that may, in turn, spread within structurally densely connected clusters or communities. These findings are compatible with the role, proposed in the present study, of structural modules in shaping spatially organized coactivity and burst-like events.

The relationship between modular network topology and synchrony has been extensively investigated in the complex systems and networks literature (49–54). In agreement with previous simulation studies, our model produced metastable dynamics and partial synchronization (as measured by the Kuramoto order parameter), which has been shown to manifest within clusters contained in the connectivity matrix (47). Applied to brain models, previous work demonstrated that slow fluctuations in modular FC topology on slower time scales (tens of seconds) depended on the integrity of structural modules (31) and that modular metastable states were driven by “cluster synchronization” (36). Our findings suggest that these structural factors can act on fast timescales, yielding burst-like events that carry signatures of SC. At intermediate coupling, networks with a strong community structure are conducive to fast, local synchronization but not global synchronization (52). Additionally, when moving toward full synchronization, smaller, more highly connected communities synchronize before larger communities, creating a mechanism by which network structure may impose different timescales on the system (55, 56). More generally, the finding that events are related to synchronization along the underlying modular structure resonates with this larger body of literature and supports the notion that the brain’s modular network architecture facilitates communication within modules while preventing global synchronization.

What causes events to occur? In simulations, we can confidently exclude scanner artifacts, spurious physiological signals, head movement, or variations in internal state as drivers of events. Indeed, analysis of empirical data has not found any significant correlation of timings or frequencies of events with nuisance variables related to acquisition, motion, or physiology (18). Notably, in both KS and NMM models, the origin of events does not require a specific “built-in” driving mechanism that triggers events at specific times. This observation is reminiscent of the emergence of complex dynamics on multiple timescales in high-dimensional neuronal systems (57). While no forcing mechanisms are needed for events to occur, they are shown to depend critically on the topology of the SC matrix. We demonstrate that events are enabled by the presence of modular SC and that the modular topology is imprinted in the specific dynamic patterns that manifest as events. We also emphasize that the model as presented here is implemented as a fully deterministic high-dimensional system of coupled differential equations that capture how elementary (microscale) processes give rise to emergent and collective (macroscale) system behavior. While many stochastic processes necessarily contain extremal events, our model is generative in a mechanistic, rather than purely stochastic, sense: observed fluctuations are localized in space and time, and their origin is rooted in the structure of the underlying anatomical network.

Our focus has been on extremal events, sharp excursions of global cofluctuation amplitudes that drive FC. The cognitive relevance of such events is a current subject of investigation, with studies suggesting that fMRI event profiles carry subject-specific information (22). Intriguing links may emerge between fMRI events and transient phase-locking of BOLD signals (58) and activity pulses (59), stereotypic patterns of propagation of intrinsic activity (60), and brain-wide traveling waves (61, 62). If events do support adaptive function, then we may speculate that specific network topological features have been selected to facilitate events. More work is needed to determine whether events have adaptive roles in promoting specific neuronal functions. For example, the brief and system-wide nature of events suggests relations to episodic synchronous neuronal activity, such as avalanches (63) or ripples (64, 65), that involve large multiregional neuronal populations and may facilitate distribution of packets of neural information. The generative model furnished in this article may prove useful for examining and testing these and other hypotheses.

Recent research (66) has shown that many characteristics of the edge time series, including high-amplitude cofluctuations, can be reproduced with a null model using independently and identically distributed Gaussian random variables derived from the static node FC (nFC). This is an important contribution to any work using edge time series and touches on the present work in two important ways. First, the authors take an analytic approach, working backward from the covariance (FC) matrix. Our generative model is complementary, as it suggests a specific structural mechanism by which high-amplitude cofluctuations might occur and thus goes beyond describing statistical characteristics of the nFC. While the Gaussian null model requires prior knowledge of the nFC, our model generates this connectivity from the underlying structure, capturing how fluctuations across time accumulate to yield the observed nFC. Second, the authors suggest that the size of the cofluctuations is directly related to the eigenspectrum of the FC matrix, with larger modules allowing for larger eigenvalues and so producing cofluctuations of the greatest amplitude. Though this reasoning is not a causal chain, it complements our findings so far as the structural modules and the functional modules are highly correlated. As disrupting modules in the SC will disrupt both functional modules and events in our generative model, disrupting empirical functional modules will likewise disrupt events in the Gaussian null model. Broadly, we view ref. 66 as supporting some of our key findings, since they show that brief fluctuations are an intrinsic part of the RSS time series and that FC modules are analytically related to these fluctuations.

Limitations of the study should be discussed. Both model implementations documented in this article represent major simplifications of real anatomy and physiology. The models do not include subcortical regions and are carried out on connectivity data that is processed into a specific nodal parcellation at intermediate spatial resolution (200 nodes). Finer spatial scales of connectivity, more realistic dynamics, inclusion of region-specific model parameters (67), the addition of neuromodulatory systems (68), individualized connectomes, and geometric embedding of connectivity (69) may improve model performance and match with empirical data. These limitations can be addressed in more accurate and data-driven multiscale implementations (e.g., linking microscale anatomy and physiology to large-scale population responses). Future work may also include implementation of more conservative null models for edge time series, for example by preserving both the auto- and cross-correlation linear statistics while preserving higher-order statistics such as irregular joint desynchronization (70).

Additional directions for future work, beyond increasing model realism, include application to task-driven dynamics, extrinsic perturbations, and the analysis of individual differences. Further understanding of the possible structural origins of events in empirical data may come from comparing empirical event patterns to SC modules. Because models give access not only to observed BOLD patterns but also to the underlying (phase-oscillator or neural population) time series sampled at millisecond resolution, fine-scale BOLD dynamics could be traced to fast fluctuations in synchrony at the microscale. These directions may provide additional valuable insights into the network basis of neuron-level dynamics that drive and shape FC.

Methods

Dataset and Acquisition.

All empirical data used for this study were derived from the set of 100 unrelated subjects acquired by the HCP (71). Informed consent was obtained from all participants, and all study protocols and procedures were approved by the Washington University Institutional Review Board. A detailed description of HCP data acquisition protocols can be found in refs. 71 and 72. All data were collected on a Siemens 3T Connectom Skyra equipped with a 32-channel head coil. SC was derived from diffusion imaging and tractography. Briefly, subjects underwent two diffusion MRI scans, which were acquired with a spin-echo planar imaging sequence (repetition time [TR] = 5520 ms, echo time [TE] = 89.5 ms, flip angle = 78°, 1.25 mm isotropic voxel resolution, b-values = 1,000, 2,000, 3,000 s/mm², 90 diffusion weighed volumes for each shell, 18 b = 0 volumes). These two scans were taken with opposite phase encoding directions and averaged. FC was derived from resting-state functional MRI (rs-fMRI), acquired with a gradient-echo echo-planar imaging (EPI) sequence over four scans on two separate days (scan duration: 14:33 min; eyes open). Main acquisition parameters were TR = 720 ms, TE = 33.1ms, flip angle of 52°, 2 mm isotropic voxel resolution, and a multiband factor of 8. Both SC and FC were mapped to regions (nodes) using a common parcellation scheme [n = 200 nodes in cerebral cortex (42)], mapped to canonical resting state networks derived from ref. 9.

For inclusion in the present study, we selected a subset of 95 (out of 100 total) subjects. Subjects were considered for exclusion based on the mean and mean absolute deviation of the relative root mean square (RMS) motion across either four resting-state MRI scans or one diffusion MRI scan, resulting in four summary motion measures. If a subject exceeded 1.5 times the interquartile range (in the adverse direction) of the measurement distribution in two or more of these measures, the subject was excluded. These exclusion criteria were established before the current study. Four subjects were excluded based on these criteria. One subject was excluded for software error during diffusion MRI processing. The remaining subset of 95 subjects had the following demographic characteristics: 56% female, mean age = 29.29 ± 3.66, age range = 22 to 36.

Structural Preprocessing.

Diffusion images were minimally preprocessed according to the description provided in ref. 40. Briefly, these data were normalized to the mean b0 image, corrected for EPI, eddy current, and gradient nonlinearity distortions, corrected for motion, and aligned to the subject anatomical space using a boundary-based registration (73). In addition to this minimal preprocessing, images were corrected for intensity nonuniformity with N4BiasFieldCorrection (74). FSL’s (FMRIB Software Library) dtifit was used to obtain scalar maps of fractional anisotropy, mean diffusivity, and mean kurtosis. The Dipy toolbox (version 1.1) (75) was used to fit a multishell, multitissue constrained spherical deconvolution (76) to the diffusion data with a spherical harmonics order of 8, using tissue maps estimated with FSL’s fast (77). Tractography was performed using Dipy’s Local Tracking module. Multiple instances of probabilistic tractography were run per subject (78), varying the step size and maximum turning angle of the algorithm. Tractography was run at step sizes of 0.25 mm, 0.4 mm, 0.5 mm, 0.6 mm, and 0.75 mm with the maximum turning angle set to 20°. Additionally, tractography was run at maximum turning angles of 10°, 16°, 24°, and 30° with the step size set to 0.5 mm. For each instance of tractography, streamlines were randomly seeded three times within each voxel of a white matter mask, retained if longer than 10 mm and with valid endpoints, following Dipy’s implementation of anatomically constrained tractography (79), and errant streamlines were filtered based on the cluster confidence index (80).

The number of streamlines between nodes of the volumetric parcellations was recorded for each tractography instance. Fractional anisotropy, mean diffusivity, and mean kurtosis maps were sampled from the middle 80% of each streamline’s path, which were averaged within the streamline and then across all streamlines between each pair of nodes. Streamline counts were normalized by dividing the count between nodes by the geometric average volume of the nodes. Since tractography was run nine times per subject, edge values had to be collapsed across runs. To do this, the weighted mean was taken, with weights based on the proportion of total streamlines at that edge. This operation biases edge weights toward larger values, which reflect tractography instances better parameterized to estimate the geometry of each connection.

A single group-averaged SC matrix was constructed by forming a consensus average preserving the length distribution of fiber tracts as well as matching the global connection density to the mean over all individual subjects (43). The resulting matrix (200 nodes, 6,040 connections, 30.4% density, and 72.4 mm mean connection length) was used as a coupling matrix for the simulations. In addition to these group averages, some simulations used SC matrices estimated on data from single participants.

Functional Preprocessing.

Minimal preprocessing of rs-fMRI data included the following steps (72): 1) distortion, susceptibility, and motion correction; 2) registration to subjects’ respective T1-weighted data; 3) bias and intensity normalization; 4) projection onto the 32k_fs_LR mesh; and 5) alignment to common space with a multimodal surface registration (81). This preprocessing resulted in ICA+FIX time series in the CIFTI grayordinate coordinate system. Additional preprocessing steps included: 6) global signal regression and 7) detrending and band pass filtering (0.008 to 0.08 Hz) (82). Following confound regression and filtering, the first and last 50 frames of the time series were discarded, resulting in a final scan length of 13.2 min (1,100 frames).

For comparing simulated to empirical FC, a single group-averaged FC matrix was derived by computing the mean FC over all 95 subjects and all four scans. When reporting correlations of full FC against other metrics, raw FC values were first passed through the Fisher z-transform.

SC Consensus Clusters.

Human connectome SC displays modular organization. To detect network communities in our SC consensus matrix, we employed multiresolution consensus clustering (83), which allowed us to capture communities across multiple scales. The algorithm for modularity maximization was based on the Louvain method, employed a spatial resolution parameter $\mathit{\gamma }$, and operated in three stages. First, a coarse sweep (1,000 steps) of the resolution parameter established outer bounds that yielded between two and N communities. Second, a finer sweep (10,000 steps) over this range collected partitions across the full range. These partitions were aggregated into a coclassification matrix, followed by subtracting a null model (constant across all node pairs) corresponding to an expected level of coclassification based on number and size of modules (83). Finally, this null-adjusted coclassification matrix was reclustered under a variable consensus threshold $\tau$ (84). Resulting consensus partitions for different values of $\tau$ were collected. The most frequently sampled consensus partition contained 10 modules and was selected for subsequent analysis (SI Appendix, Fig. 1).

KS Model Implementation.

We implemented a version of the model that generates fast oscillatory dynamics and incorporates a coupling structure consisting of weighted undirected connections and the corresponding time delays, encoded in a phase delay (frustration) matrix. The fundamental equation of this KS model (Fig. 1) is given as

$$\frac{d{\mathit{\theta }}_i}{dt}=2\mathit{\pi }f+k{\displaystyle \sum }_{j=1}^N{K}_{ij} \text{sin}({\mathit{\theta }}_j\left(t-d_{ij}\right)-{\mathit{\theta }}_i\left(t\right)).$$

The global coupling parameter $k$ was systematically varied. The mean natural frequency $f$ was set to 40 Hz, with variability at each node (SD = 0.1 Hz). The coupling matrix $K_{ij}$ corresponded, in most simulations, to the empirical SC consensus matrix. A global scaling constant was applied to normalize $K_{ij}$ for use in the simulations. The matrix of phase delays was derived from the physical lengths of each SC connection, computed as the group-averaged mean of its constituent streamlines, expressed in millimeters. Each SC connection length was converted to a time delay $d_{ij}$ computed from a constant conduction velocity $v$. Most simulations in the paper use $v=12 \text{ms}$, resulting in a mean time delay of $6.1 \text{ms}$, averaged over all connections in $K_{ij}$. The conduction velocity was varied between $v=3 \text{ms}$ and $v= 24 \text{ms}$, a range that was systematically explored in prior work (36) and roughly corresponds to the plausible physiological range for cortico-cortical projections in primates (45). Because the unique nature of oscillators allows time to be expressed as phase, time delays can be introduced without the extra computational load of using delay differential equations. Accordingly, each time delay was converted to a phase delay aij using the average intrinsic frequency to calculate the amount of phase change expected per unit time. It should be noted that this method is only valid for phase delays less than half a rotation. At an average intrinsic frequency of 40 Hz, the phase delay is greater than half a rotation on less than 0.05% of all connections, with no discernable impact on RSS events or system dynamics. Simulations have been tested for a range of frequencies from 15 to 50 Hz, and the core phenomenon of events in RSS time series is observed over all frequencies in this range (SI Appendix, Fig. 2B). Notably, at slower intrinsic frequencies, all connections are less than half a rotation, further confirming that the very few above that mark at 40 Hz are negligible. We have chosen 40 Hz as the main frequency for analysis following the example of previous literature that both uses this frequency for simulation (85) and demonstrates population activity in this range (41). No noise was added to the phase time series.

The system of N coupled equations was integrated (using MATLAB’s ode45 solver) at 1 ms time resolution, based on an implementation of the KS model in the Brain Dynamics Toolbox (86). For each simulation, the initial condition consisted of phases drawn randomly and uniformly between $[0, 2\mathit{\pi }]$. Simulations proceeded for 812 s, which resulted, after removal of an initial 20-s transient, in 792 s of simulated time. Synchronization behavior of the system was tracked by computing the global order parameter

$$R\left(t\right)=\frac{1}{N} {\displaystyle \sum }_{n=1}^N{e}^{i{\mathit{\theta }}_n(t)}.$$

$R\left(t\right)$ quantifies the global phase synchronization, with $R\left(t\right)=0$ indicting complete asynchrony and $R\left(t\right)=1$ indicating complete synchrony. After converting phases into signal amplitudes $\text{sin}(\mathit{\theta }\left(t\right)$ (Fig. 1C), the time series were convolved with a canonical HRF (ref. 86; Fig. 1D) resulting in synthetic BOLD time series (Fig. 1E). These were low-pass filtered [0.25 Hz (36)] and down-sampled at intervals of 720 ms, corresponding to the empirical TR in rs-fMRI acquisitions, thus yielding an $[N\times T]$ simulated BOLD activity matrix, with T = 1,100 time points (“frames”). Finally, the global mean of these BOLD time series was regressed out, and the residuals were retained for computing edge time series and FC (Pearson correlation).

NMM Implementation.

To demonstrate the robustness of our principal findings, we configured a second dynamic model closely based on earlier work (31). Briefly, the NMM equations were adopted from a conductance-based model of neuronal dynamics designed to capture local population activity. Local populations of densely interconnected inhibitory and excitatory neurons, whose behaviors are determined by voltage- and ligand-gated membrane channels, were placed at each node, and the SC matrix provided internode couplings between excitatory neuronal populations. Parameter values were identical to those reported in ref. 31. No time delays were implemented, nor was stochastic noise added to the voltage time series. While other work has shown contributions made by time delays and noise to BOLD dynamics (33), here, we were interested in whether a minimal set of ingredients (the SC weights and their modular network structure) could yield realistic event-like patterns. Only the global coupling parameter $k$ was varied across runs.

Following numerical integration of the system of Nx3 coupled differential equations (using MATLAB’s ode45 solver) and removal of a 20-s initial transient, the remaining time series were down-sampled and converted to 792 s and 1,100 frames of synthetic BOLD data, as described for the KS model. All analyses were carried out identically for BOLD time series derived from both KS and NMM models.

Edge Time Series and Cofluctuation Amplitude.

Simulated BOLD time series were processed into edge time series as previously described for empirical fMRI data (18–20, 22). Nodal BOLD signals were z-scored, and edge time series (one for each node pair) were computed as the element-wise product of the respective node time series:

$$E_{ij}\left(t\right)=z_i\left(t\right)\cdot z_j(t).$$

The mean of each edge time series is exactly equal to the corresponding Pearson correlation (FC) [i.e., $F{C}_{ij}=\frac{1}{T-1}{{\displaystyle \sum }}_{t=1}^T{E}_{ij}\left(t\right)$]. Edge time series, representing edge cofluctuations, formed a $[K\times T]$ matrix, with $K=19,900$ (for $N=200$) and $T=1,100$. The system-wide amplitude of all cofluctuations was computed as the RSS or, in cases in which different-sized node sets were compared, as the RMS.

Prior work in empirical fMRI data established that FC components derived from high RSS frames have higher similarity to full FC and have higher modularity than those derived from low-RSS frames (18). We computed FC components for subsets of frames corresponding to the top and bottom deciles of RSS (“high” and “low” RSS) by taking the means across the respective subsamples of the edge time series. Modularity was computed on the resulting FC component matrix by applying modularity maximization (Louvain algorithm) adapted for use with matrices that contain both positive and negative edges (87). The modularity metric $Q^{*}$ summed contributions by positive and negative edges as

$$Q^{*}=\frac{1}{v^{+}}{\displaystyle \sum }_{i,j}\left(w_{i,j}^{+}-e_{i,j}^{+}\right){\mathit{\delta }}_{c_i,c_j}-\frac{1}{v^{+}+v^{-}}{\displaystyle \sum }_{i,j}\left(w_{i,j}^{-}-e_{i,j}^{-}\right){\mathit{\delta }}_{c_i,c_j},$$

where ${\mathit{\delta }}_{c_i,c_j}=1$ if nodes i and j are within the same community and ${\delta }_{c_i,c_j}=0$ otherwise. The positive and negative superscripts to the edge weight w_i,j between nodes i and j are used for separating positive and negative edge weights, where $w_{i,j}^{+} =w_{i,j}$ and $w_{i,j}^{-}=0$ if w_i,j > 0 and $w_{i,j}^{+} =0$ and $w_{i,j}^{-} =-w_{i,j}$ otherwise. The term $e_{i,j}^{\pm }=s_i^{\pm }{s}_j^{\pm }/v^{\pm }$, where $s_i^{\pm }={{\displaystyle \sum }}_j{w}_{i,j}^{\pm }$ and $v^{\pm }={{\displaystyle \sum }}_{i,j}{w}_{i,j}^{\pm }$, is the expected positive or negative edge weight between nodes i and j if edges were randomly distributed. All edges were retained, and the value of the modularity metric was computed while setting the resolution parameter to the default of $\mathit{\gamma }=1$. Very similar results were obtained for other (higher and lower) settings of $\mathit{\gamma }$.

Another previous finding indicated that frames obtained when RSS is high were more similar (stereotypic) across time than low-RSS frames (18, 20, 22). In the simulation data, two related tests were performed to examine the similarity of high-/low-RSS frames as well as the similarity of event frames versus a time-shifted null. High-/low-RSS frame sets were extracted and the distribution of all pairwise Pearson correlations among their constituent edge cofluctuation patterns was compared (Wilcoxon rank-sum test for equal medians, one-tailed, $P<0.0001$, uncorrected). Event peaks were extracted and the set of all Pearson correlations among these events was compared against 250 sets computed from an equal number of randomly shifted time points, with offsets chosen uniformly from the interval $[-1100 1100]$. The mean correlation of the actual events was compared against these 250 random values and considered significant if $P<0.01$ (uncorrected; actual value exceeds null model at least 247/250 times).

Two additional analyses delivered insights on the relation of edge time series patterns and RSS as well as on the dimensionality of the edge dynamics. First, performing PCA on edge time series yields a series of PCs. The correlation between the scores of the largest PC (PC1; taken to represent its expression over time) and the RSS is computed as Spearman’s $\mathit{\rho }$. Second, the eigen-decomposition of the covariance matrix of the neural activity (BOLD time series) yields a series of eigenvalues $\left\{{\mathit{\lambda }}_i\right\}$ from which the participation ratio ($PR$) can be computed as a measure of the dimensionality of the system (88):

$$PR= \frac{{({{{\displaystyle \sum }}^{\text{}}}_i{\mathit{\lambda }}_i)}^2}{{{{\displaystyle \sum }}^{\text{}}}_i{\mathit{\lambda }}_i{}^2}.$$

The value of $PR$ is highly correlated with the cumulative explained variance of the largest PCs of a PCA decomposition of the BOLD covariance matrix.

Event Detection and Statistics.

Peaks in the RSS statistic that exceed a statistical criterion are termed events. To determine statistical significance, we performed nonparametric permutation tests on each model run (ref. 22; Fig. 1G). BOLD time series were randomly shifted (using MATLAB’s circshift operator), each separately with an offset chosen uniformly from the interval $\left[-1100 1100\right]$, thus approximately preserving each node’s autocorrelation while randomizing the cross-correlation between nodes. This null model was applied 1,000 times to each model run, and edge time series and RSS were computed for each instance. Time points in the original time series for which the empirically observed RSS amplitude exceeded all RSS values for all null model instantiations ($P<0.001$) were retained. The intersection between all peaks in the original RSS and these time points constituted significant events in the model run. Event amplitudes corresponded to the RSS value at the time each such peaks occurred.

At very low coupling ($k\le 35$ in the KS model), we observed occasional excursions in single-node time series, which resulted in sharply fluctuating BOLD signal amplitudes and extremal z-scores. Extreme z-scores in single or very few nodes can result in sharp RSS spikes at the system level due to the transitive and multiplicative nature of the edge time series calculation. This phenomenon did not match characteristics of events observed in empirical fMRI data. Hence, RSS peaks that coincided with excursions of at least one BOLD time series above or below $z=\pm 4.5$ (the 99.99th percentile of empirically observed BOLD signal amplitudes) were excluded from the analysis. Such peaks occurred infrequently (at most once per 1,100 frames) at couplings $k>35$.

Event Clustering.

Once statistically valid events were detected, their corresponding edge cofluctuation patterns were extracted and aggregated across multiple runs ($k=280$ for the KS model; $\text{k}=0.175$ for the NMM model; 12 runs each). The Pearson correlation matrix for these event patterns was clustered using a version of modularity maximization (employing the Potts model) and multiresolution consensus clustering (83). The resolution parameter was stepped through a range of 10,000 values covering modular partitions yielding between two and N modules. All partitions were aggregated into a single coclassification matrix, which was scaled between $[0 1]$ followed by subtraction of the analytic null (83) and subjected to consensus clustering with $\tau =0$.

The four largest clusters were retained for subsequent analyses (labeled event clusters 1 through 4). A single mean edge cofluctuation pattern (cluster centroid) was computed for each cluster. Applying the SC consensus module partition to the four centroids yields a representation of how event-related cofluctuations distribute relative to the SC. To test whether mean cofluctuations within each of the structural modules were significantly above or below chance, the modular components of edge cofluctuations were recomputed using the spin test (44), which rotates the structural modular partition 100,000 times on the cortical surface. This procedure preserves not only the number but also (approximately) the spatial proximity of nodes contained in the original SC consensus modules.

SC Randomization and Synthetic SC.

The SC consensus matrix was randomized using a rewiring algorithm (89) that preserved the degree sequence exactly and the strength sequence approximately. Connection lengths (delays) were preserved at each connection such that the connection weight/delay relationship was retained. The resulting randomized matrix matched the SC consensus in all summary statistics pertaining to weight or delays while comprising a globally randomized architecture. The modular architecture, as revealed through multiscale consensus clustering (SI Appendix, Fig. 3), was significantly muted.

A synthetic SC matrix was constructed such that the modular arrangement of the connections was predetermined (four modules in the case of the matrix displayed in SI Appendix, Fig. 4) while retaining some summary statistics of the empirical SC consensus matrix. Specifically, the synthetic matrix approximately (maximal deviation less than 0.1%) retained connection density, total sum of connection weights, mean connection weight, and mean connection length. Weights and lengths were inversely related, with the strongest weights and shortest lengths assigned to within-module connections. Simulation parameters (e.g., intrinsic frequency and conduction velocity) matched those employed for simulations with the empirical SC matrix. The matrix was used in KS model simulations with a rescaled coupling parameter of $k=25$. This rescaling ensured that the global coupling strength provided by the synthetic SC matrix approximately matched that provided by the empirical SC consensus at $k=280$.

Data Availability

Data and code, including a package to carry out simulations of the KS model, have been deposited in GitHub: https://github.com/brain-networks/KSmodel_fMRIdynamics.