Skip to main content
PMC home page
Royal Society of Chemistry logoLink to Royal Society of Chemistry
. 2019 Feb 25;21(19):9651–9664. doi: 10.1039/c8cp07671e

Understanding the differences between iron and palladium in cross-coupling reactions†

Xiaobo Sun 1, Marcus V J Rocha 1,2, Trevor A Hamlin 1, Jordi Poater 3,4,✉, F Matthias Bickelhaupt 1,5,✉
PMCID: PMC8610147  PMID: 30847454

Abstract

We aim at developing design principles, based on quantum chemical analyses, for a novel type of iron-based catalysts that mimic the behavior of their well-known palladium analogs in the bond activation step of cross coupling reactions. To this end, we have systematically explored C–X bond activation via oxidative addition of CH3X substrates (X = H, Cl, CH3) to model catalysts mFe(CO)4q (q = 0, −2; m = singlet, triplet) and, for comparison, Pd(PH3)2 and Pd(CO)2, using relativistic density functional theory at the ZORA-OPBE/TZ2P level. We find that the neutral singlet iron catalyst 1Fe(CO)4 activates all three C–X bonds via barriers that are lower than those for Pd(PH3)2 and Pd(CO)2. This is a direct consequence of the capability of the iron complex to engage not only in π-backdonation, but also in comparably strong σ-donation. Interestingly, whereas the palladium complexes favor C–Cl activation, 1Fe(CO)4 shows a strong preference for activating the C–H bond, with a barrier as low as 10.4 kcal mol−1. Our results suggest a high potential for iron to feature in palladium-type cross-coupling reactions.

We aim at developing design principles, based on quantum chemical analyses, for a novel type of iron-based catalysts that mimic the behavior of their well-known palladium analogs in the bond activation step of cross coupling reactions.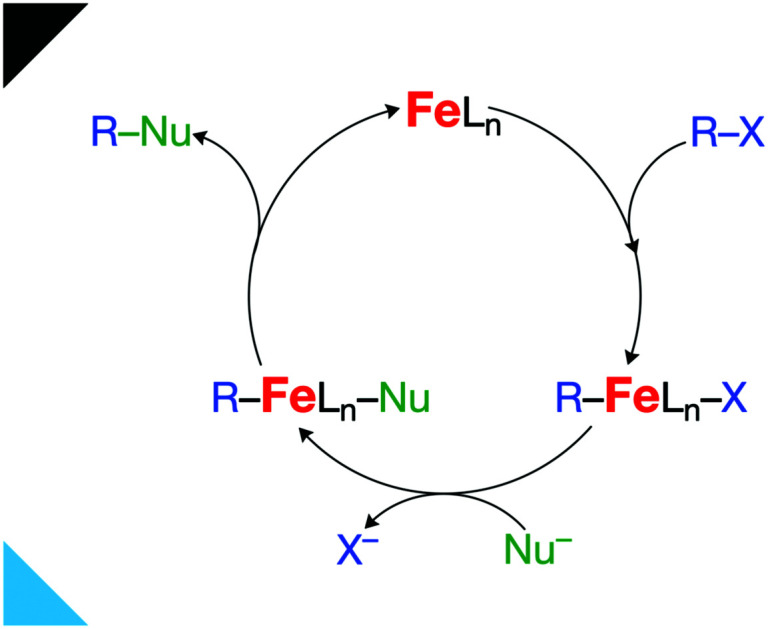graphic file with name c8cp07671e-ga.jpg

Introduction

Catalysis is ubiquitous in modern synthetic and industrial chemistry, and plays a key role in reducing the consumption of energy and feedstocks. Yet, “designing” catalysts with the desired activity and selectivity is still a formidable task, and to a large extent, an empirical undertaking that proceeds through trial and error.1–3 In order to facilitate this process, a fragment-based approach, called the activation strain model4–6 (ASM, also known as the distortion/interaction model7,8) of chemical reactivity, which will be explained later on, can be used to understand how and why a certain combination of a metal center, ligands and solvent is able to selectively catalyze one particular bond in the substrate. Using this model, our group has performed a series of studies to systematically investigate the effect of a specific variation on the reactivity of the catalysts, especially for palladium in key steps for cross-coupling reactions.9,10 For example, we have explored not only how the reaction barrier varies when different bonds are activated by palladium,11,12 or different ligands are attached to palladium,13 but also how different metal centers perform compared to palladium.14

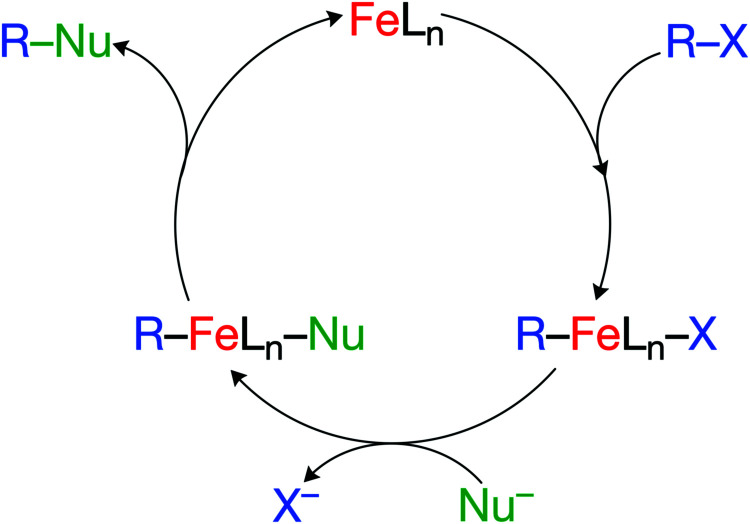
Proceeding from the insights obtained in the above studies, we now aim at a next step: the exploration of iron's potential to take over from palladium in archetypal, closed-shell catalytic cross-coupling reactions, as illustrated by the generic catalytic cycle in Scheme 1. There are processes known in which iron-centers feature in such pathways (vide infra) although, in general, they react often via radical mechanisms.15–17 Our purpose, here, is not to optimize the latter. Instead, we wish to understand how and why FeLn complexes behave in general differently from PdLn complexes. In this way, we develop a theoretical framework that facilitates a more systematic development of iron-based cross-coupling chemistry.

Scheme 1. Key steps in catalytic cross-coupling model reactions.

Scheme 1

Open in a new tab

Cross-coupling reactions constitute one of the most important tools for efficiently creating a bond between two carbon atoms, and have been widely investigated, both experimentally and theoretically.18,19 The first and generally rate-determining step in the catalytic cycle of a typical cross-coupling reaction is the activation of a bond, such as C–H, C–C and C–X (where X = halogen), by oxidative addition to a transition-metal complex. Moreover, activation of these bonds is also an important step towards the efficient conversion of abundant and inert compounds into more useful products.15,20,21 While iron plays an important role in other areas of modern synthetic chemistry, it has been traditionally eclipsed by other transition metals such as palladium in cross-coupling reactions.22,23 However, the growing concern about environmental damage and energy consumption nowadays demands cheap, nontoxic and highly selective catalysts.24 For this reason, iron-based catalysts, started by the pioneering work of Kochi25–28 in the early 1970s, and later carried on by Cahiez,29–32 have quickly become an important tool in the cross-coupling arsenal. Based on recent work by Fürstner,33–37 Nakamura and Nakamura,38–42 Hayashi,43–45 and Bedford46–49 new catalysts have been developed which tolerate both a rich manifold of reactivity patterns and various functional groups. However, despite the growing number of studies, their applicability in synthesis is still scarce,3,16 and the mechanism of iron-catalyzed cross-coupling reactions is not fully understood yet, in contrast with Pd.50–60

Here, we wish to explore a different idea: as opposed to developing a separate and different iron chemistry, is it possible to “teach” iron to do the tricks of palladium? This is a quantum chemical proof-of-concept study that requires several questions to be answered: what are the major electronic and structural differences between iron and palladium systems? Why, so far, have these differences made palladium the most favorite metal in cross-coupling reactions? How could iron complexes mimic the behavior of palladium catalysts by careful choice of suitable ligands? To answer these questions, we have systematically explored iron-mediated C–X bond activation via oxidative addition of CH3X substrates (X = H, Cl, CH3) to model catalysts mFe(CO)4q (q = 0, −2; m = singlet, triplet) as well as selected reactions involving analogous palladium model catalysts, using relativistic density functional theory at the ZORA-OPBE/TZ2P level in combination with the activation strain model and quantitative molecular orbital (MO) theory.

There are several reasons to choose the prototypical iron-carbonyl complexes mFe(CO)4q as model catalysts in our quest: (i) these model systems have the required simplicity to focus on, and uncover, the underlying physical factors of their properties and to compare them with simple bis-ligated Pd catalyst complexes; (ii) at the same time, Fe(CO)4 is feasible to use in the lab and has been extensively studied for its properties and interactions with various species such as hydrogen, nitrogen, hydrocarbon and so on;61–66 and (iii) importantly, iron-based carbonyl complexes constitute one of the most important families in organometallic chemistry, displaying a wealth of structural complexity and chemical reactivity. This stability and diversity have their roots in the very nature of the carbonyl ligand: CO has the right orbital electronic structure for balanced σ-donation through the 5σ orbital and π-backdonation through the 2π orbitals, which is crucial in the formation of stable metal–ligand bonds.67,68 Furthermore, CO can be easily replaced by other ligands, such as BR or PR3, which offer an arsenal of tuning possibilities.69

Methods

General procedure

All calculations were carried out using the Amsterdam Density Functional (ADF)70–79 and the quantum-regions interconnected by local descriptions (QUILD) program80 using relativistic density functional theory at the ZORA-OPBE/TZ2P81–90 level. The frozen core approximation (small frozen core) was applied in all calculations to reduce the computational cost, as the relative energies of stationary points differ by less than 1 kcal mol−1 if computed with or without frozen core. Our early work and extensive benchmarking91 (see Tables S1–S7 in the ESI†) have proven this approach to be well suited for the systems of interest. In particular, OPBE is suggested by Truhlar92 and Swart93 to accurately perform in the determination of the ground spin state of iron complexes, which is important in answering the tricky question as to whether the singlet or triplet is the ground state for Fe(CO)4 in our study. Geometries were optimized without any symmetry constraints. Through vibrational analysis, all energy minima and transition state structures were confirmed to be either equilibrium structures (zero imaginary frequencies) or transition states (a single imaginary frequency). The character of the normal mode associated with the imaginary frequency was analyzed to ensure that the correct transition state was found. Where computationally feasible, intrinsic reaction coordinate (IRC) calculations have been performed to obtain the potential energy surfaces (PES) of the reactions. Throughout this paper, our discussion is based on the electronic energies of the molecular systems. Notably, Gibbs free activation barriers and free reaction energies have also been calculated and the trends in reactivity remain unchanged (see Table S1 of the ESI†). The PyFrag program was used to facilitate the analyses of the potential energy surfaces (PESs).94 All computations, including analysis, were carried out in the gas-phase, as the trends in the oxidative insertion potential energy surfaces of iron model catalysts into H3C–X bonds (X = H, Cl, CH3) in solution (THF) remained unchanged (see Table S3, ESI†). Further details are provided in the ESI.†

Activation strain model analysis

Insight into the overall reaction energies is obtained through activation strain model (ASM) analyses.95 The activation strain model of chemical reactivity is a fragment-based approach to understand the energy profile of a chemical process and to explain it in terms of the original reactants. This allows an easy assessment of the influence of geometrical deformation and the electronic structure of the catalyst and the substrate. Obviously, in the current work, our main interest is the interplay between one fragment, the catalyst, and another fragment, the substrate. Subsequently, the division of the reaction system into catalyst and substrate is used in the PyFrag computation to generate the activation strain profile. Thus, the bonding energy ΔE is decomposed along the intrinsic reaction coordinate (IRC) into the strain energy ΔEstrain, which is associated with the geometrical deformation of the individual reactants as the process takes place, plus the actual interaction energy ΔEint between the deformed reactants. We project the reaction coordinate on the stretch of the activated C–X bond, which has been shown to be a suitable choice.96,97 Furthermore, the strain energy ΔEstrain can be readily split into contributions from the deformation of the substrate and that of the catalyst (see eqn (1)).

ΔE = ΔEstrain[substr] + ΔEstrain[cat] + ΔEint 1

The interaction energy ΔEint between the deformed reactants is further analyzed in the conceptual framework provided by the Kohn–Sham molecular orbital (KS-MO) model, using a quantitative energy decomposition scheme (see eqn (2)):98

ΔEint = ΔVelstat + ΔEPauli + ΔEoi 2

The term ΔVelstat corresponds to the classical Coulomb interaction between the unperturbed charge distributions of the deformed reactants and is usually attractive. The Pauli repulsion energy ΔEPauli comprises the destabilizing interactions between occupied orbitals on the respective reactants and is responsible for steric repulsion. The orbital interaction energy ΔEoi accounts for charge transfer (interaction between occupied orbitals on one fragment and unoccupied orbitals on the other fragment, including the HOMO–LUMO interactions) and polarization (empty-occupied orbital mixing on one fragment due to the presence of another fragment).

Results and discussion

Model catalysts

In the following, we first examine the geometric and electronic structure of our model iron-catalysts mFe(CO)4q for: q = 0 with m = singlet or triplet states; and for q = −2 with m = the singlet state. Also, we address the proof-of-concept character of this study, in particular, the fact that model iron-based catalysts of the type we focus on in this study cover all key steps of a full cross-coupling catalytic cycle, in the same way as, for example, the palladium-based model catalyst Pd(PH3)2. Subsequently, we explore the various reaction pathways for activating C–H, C–C and C–Cl bonds via oxidative addition to the model mFe(CO)4q complexes, followed by detailed activation strain and bonding analyses that serve to uncover the physical factors that are behind the reactivity trends. In the last section, palladium-mediated reactions are included to enable the development of design principles for iron-complexes that mimic the bond-activation behavior of the palladium systems. The results of our ZORA-OPBE/TZ2P calculations are collected in Tables 1–3 and shown in Fig. 1–8 (detailed structural data are available in the ESI†).

Geometry parameters (in Å and degrees) of singlet and triplet Fe(CO)4, and 1Fe(CO)42− a.

Fe–Cax Fe–Ceq C–Oax C–Oeq Cax–Fe–Cax Ceq–Fe–Ceq Fe–Cax–Oax Fe–Ceq–Oeq
1Fe(CO)4 1.777 1.732 1.151 1.158 181.7 126.6 178.2 170.5
3Fe(CO)4 1.810 1.761 1.151 1.154 154.5 96.0 175.8 178.8
1Fe(CO)42− 1.727 1.727 1.201 1.201 109.7 109.7 179.8 179.8
Open in a new tab
a

Computed at ZORA-OPBE/TZ2P.

Reaction profile (in kcal mol−1) for the oxidative insertion of iron and palladium model catalysts into H3C–X bonds (X = H, Cl, CH3)a.

RC TS P
1Fe(CO)4 C–H −1.3 10.4 0.8
C–Cl −9.0 25.5 −15.1
C–C 0.1 48.0 10.2
3Fe(CO)4 C–H 0.0 64.4 45.2
C–Cl 0.0 43.3 29.4
C–C −0.1 76.9 51.1
1Fe(CO)42− C–H −2.4 74.1 66.3
Pd(PH3)2 C–H −0.2 30.5 28.1
C–Cl −0.5 30.6 −8.0
C–C −0.3 51.7 29.8
Pd(CO)2 C–H −0.0 33.4 31.7
C–Cl −0.2 34.7 5.1
C–C −0.1 53.9 32.8
Open in a new tab
a

Computed at ZORA-OPBE/TZ2P. 1Fe(CO)4 is 0.2 kcal mol−1 less stable than 3Fe(CO)4.

Analysis of transition states for oxidative insertions of 1Fe(CO)4 into H3C–H, H3C–Cl and H3C–CH3 bondsa.

CH4 CH3Cl C2H6
EDA (in kcal mol−1)
ΔEstrain[“Fe”] 6.1 5.2 4.0
ΔEstrain[“X”] 54.4 31.2 57.3
ΔEstrain 60.5 36.4 61.3
ΔVelstat −104.9 −47.8 −63.6
ΔEPauli 151.8 87.8 104.7
ΔEσ −37.4 −22.5 −22.8
ΔEπ −49.7 −19.8 −23.4
ΔErest −9.9 −8.6 −8.2
ΔEoi −97.0 −50.9 −54.4
ΔEint −50.1 −10.9 −13.3
ΔE 10.4 25.5 48.0
FMO energy (in eV)
“Fe”: dσ −4.6 −4.6 −4.5
“X”: σc–x −7.3 −8.9 −7.0
Δεdonation 2.7 4.3 2.5
“Fe”: dπ −5.3 −5.3 −5.3
“X”: σc–x* −1.3 −3.4 −0.9
Δεbackdonation 4.0 1.9 4.4
FMO overlap
〈Fe: dσ|X: σc–x〉 0.30 0.15 0.20
〈Fe: dπ|X: σc–x*〉 0.35 0.05 0.09
FMO population (in e)
“Fe”: dσ 0.42 0.37 0.25
“X”: σc–x 1.44 1.73 1.62
“Fe”: dπ 1.54 1.63 1.75
“X”: σc–x* 0.58 0.36 0.35
Open in a new tab
a

Computed at ZORA-OPBE/TZ2P.

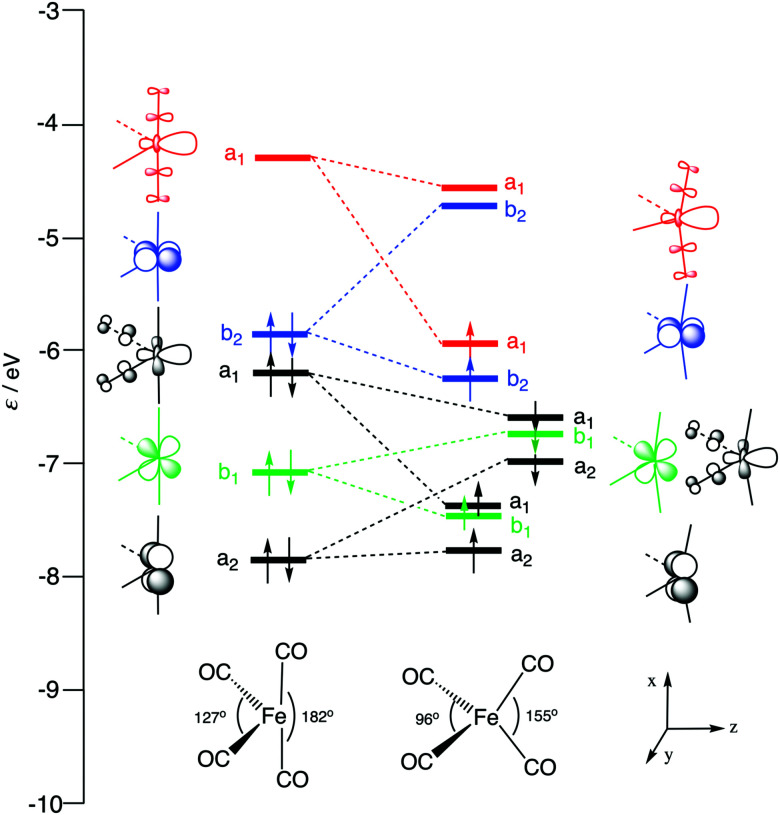
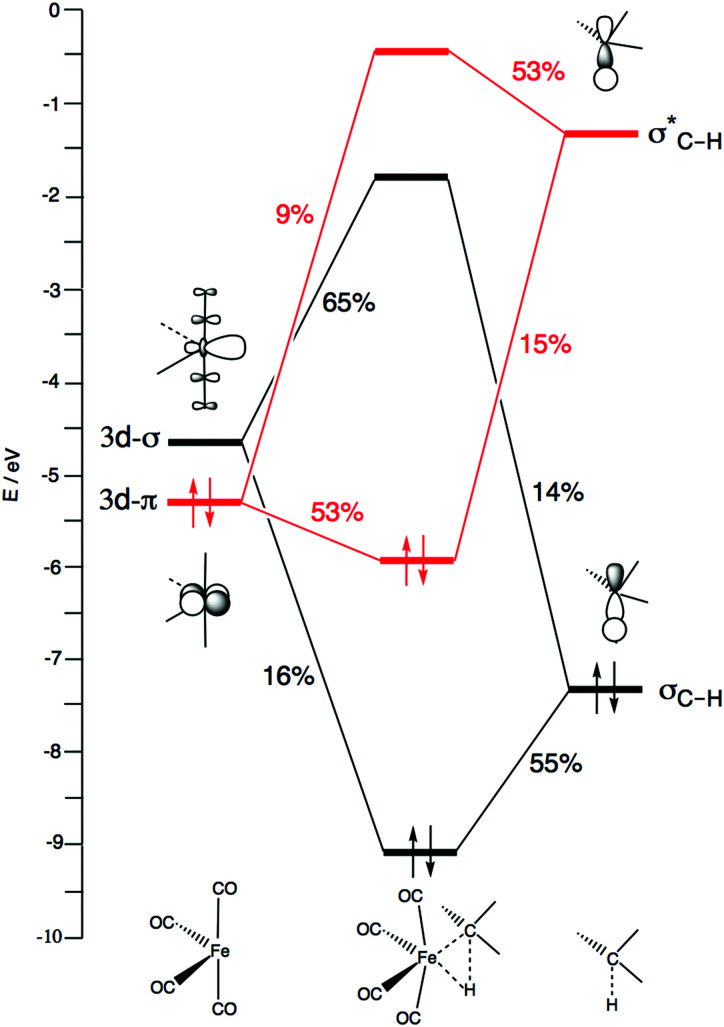
Fig. 1. Schematic molecular orbital (MO) diagrams of 1Fe(CO)4 (left) and 3Fe(CO)4 (right: α- and β-spin levels), computed at ZORA-OPBE/TZ2P.

Fig. 1

Open in a new tab

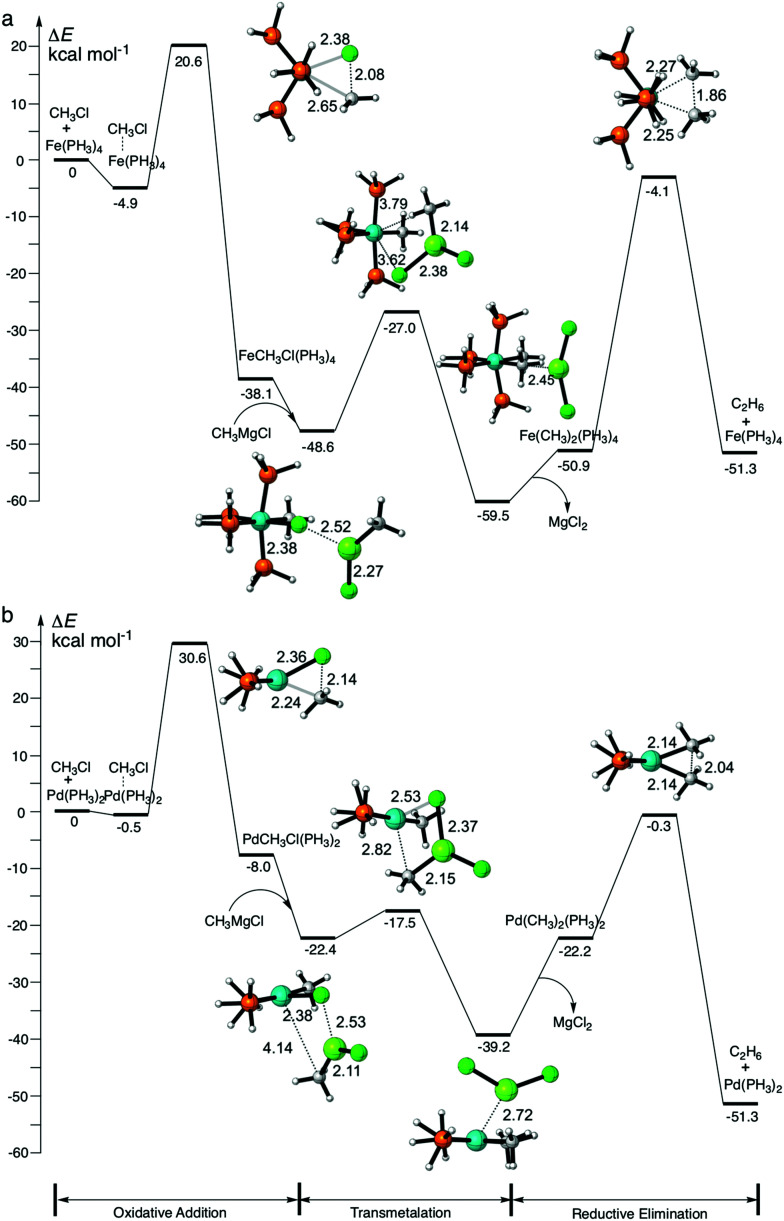
Fig. 2. Reaction profiles and key structures (in Å) for cross coupling of chloromethane with methylmagnesium chloride, catalyzed by: (a) Fe(PH3)4 and (b) Pd(PH3)2 (see eqn (3)), computed at ZORA-OPBE/TZ2P.

Fig. 2

Open in a new tab

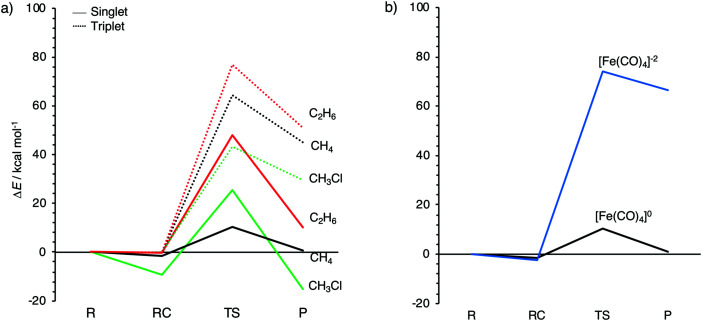
Fig. 3. Reaction profiles for the oxidative insertion of: (a) singlet and triplet Fe(CO)4 into CH3X (X = H, Cl, CH3); and (b) neutral and dianionic singlet Fe(CO)4 into CH4, computed at ZORA-OPBE/TZ2P.

Fig. 3

Open in a new tab

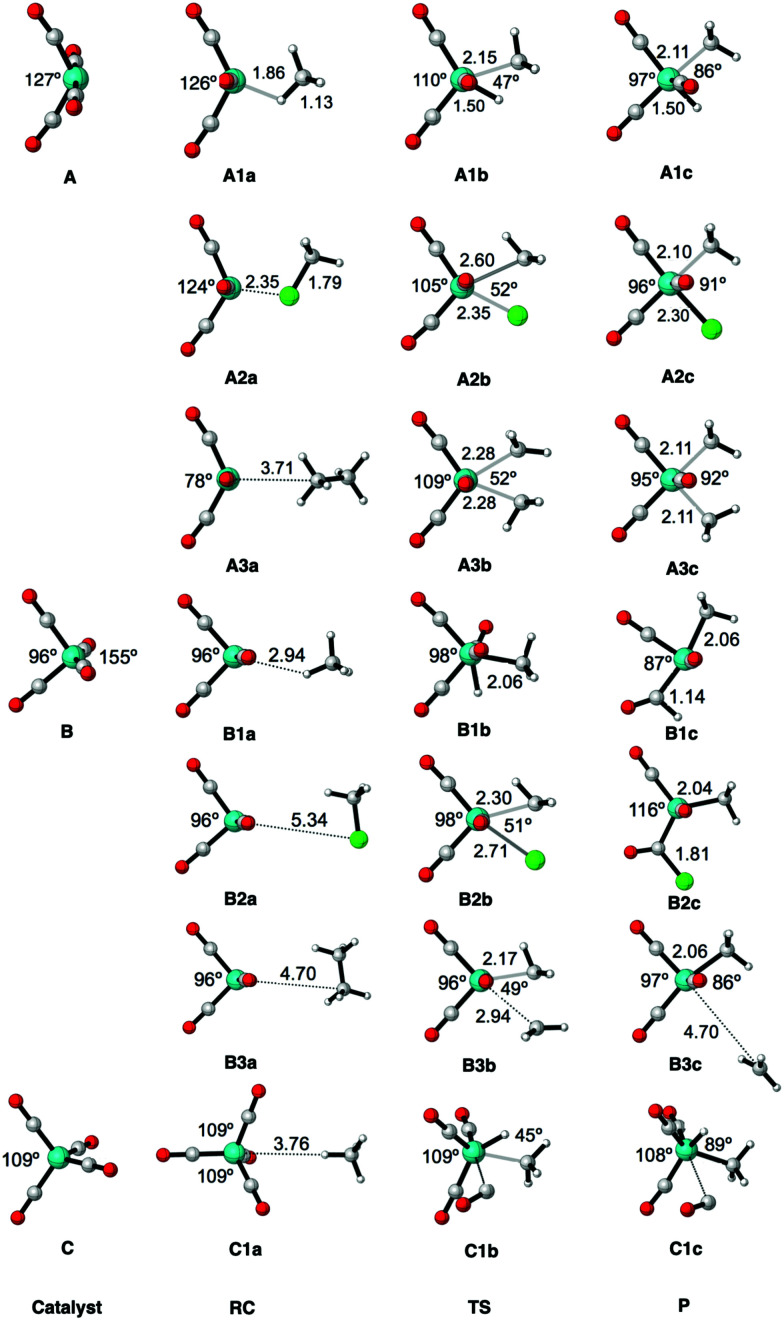
Fig. 4. Structure parameters (the bite angle of OC–Fe–CO, and the bond lengths of Fe–X, Fe–C and C–X in Å) of the stationary points along the reaction coordinate for the oxidative insertion of Fe(CO)4 into CH4, CH3Cl and C2H6, computed at ZORA-OPBE/TZ2P. Uppercase letters A, B, and C represent Fe(CO)4 in the neutral singlet state, neutral triplet state and anionic (2−) singlet state, respectively. Numbers 1, 2, and 3 represent the three substrates CH4, CH3Cl, and C2H6, respectively. Lowercase letters a, b, and c represent the three stages along the oxidative reaction, namely the reactant complex, transition state and final product, respectively.

Fig. 4

Open in a new tab

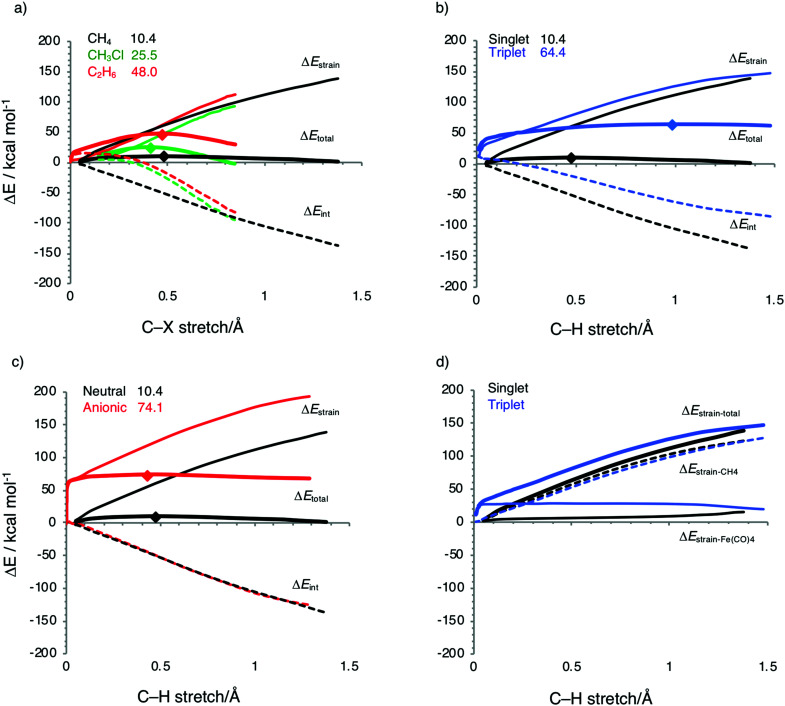
Fig. 5. Activation strain diagrams (ASD) for the oxidative addition of: (a) CH3–X bonds (X = H, Cl, CH3: black, green, red) to singlet Fe(CO)4; (b) CH3–H bonds to singlet and triplet Fe(CO)4 (black and blue); and (c) CH3–H bonds to neutral and dianionic Fe(CO)4 (black and red); and (d) decomposition of the total strain energy into catalyst and substrate strain. Energy barriers relative to reactants for the TSs are also included (see upper left corner panel) and the positions of TSs are marked by dots.

Fig. 5

Open in a new tab

Fig. 6. Catalyst–substrate orbital interactions in the TS for the oxidative insertion of 1Fe(CO)4 into the CH4 C–H bond, with gross Mulliken percentage contributions of FMOs to MOs.

Fig. 6

Open in a new tab

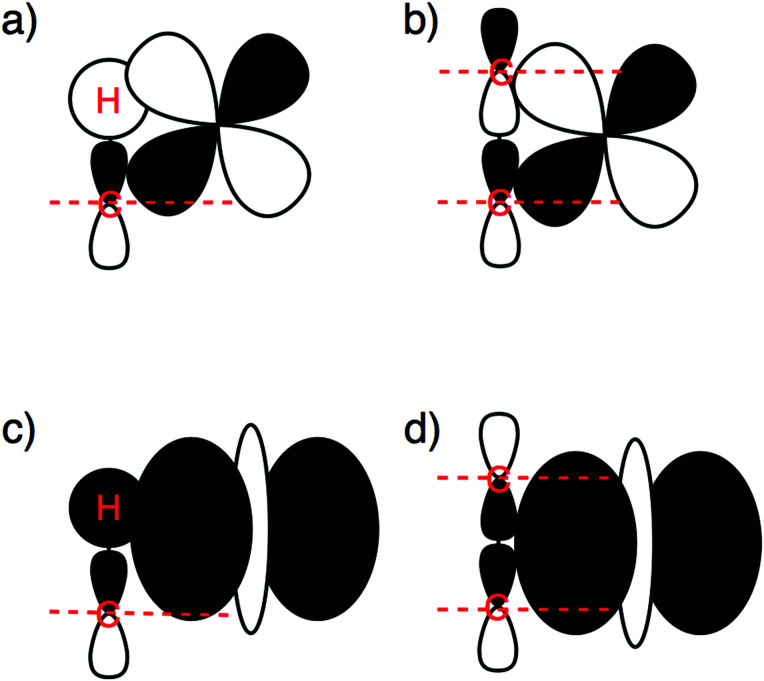
Fig. 7. Orbital overlap pattern for catalyst–substrate π-backdonation (a and b) and σ-donation (c and d) in the case of the C–H bond (a and c) and C–Cl and C–C bonds (b and d).

Fig. 7

Open in a new tab

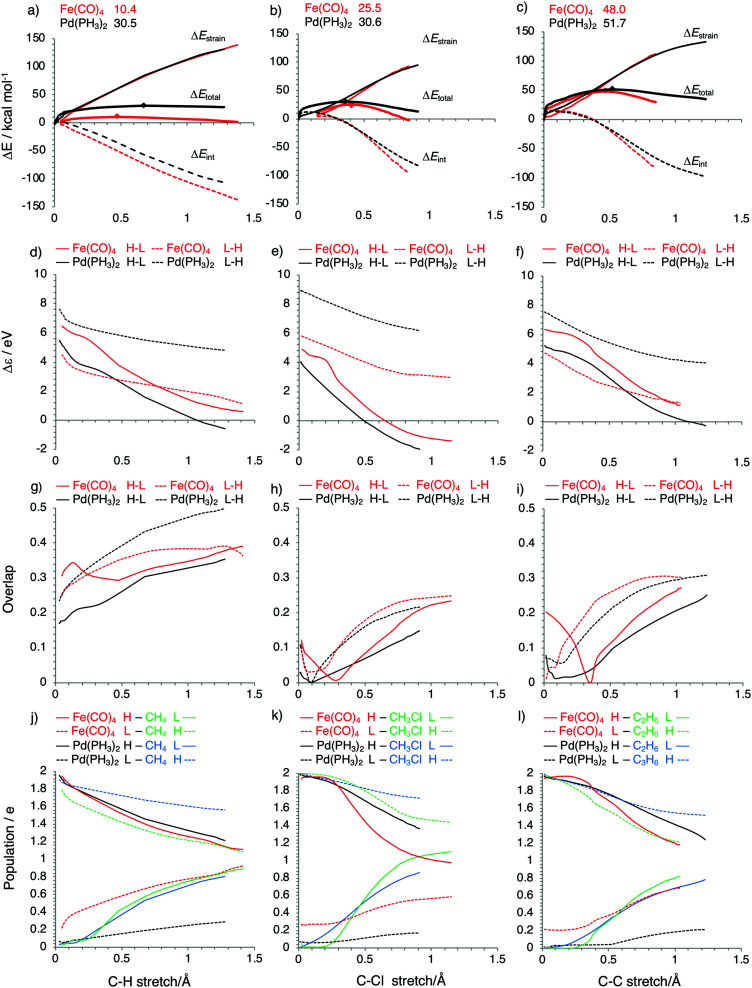
Fig. 8. Activation strain diagrams (ASD) for the oxidative addition of Fe(CO)4 (red) and Pd(PH3)2 (black) into CH3–H (a), CH3–Cl (b) and CH3–CH3 bonds (c). Energy barriers relative to reactants for the TSs are also included and the positions of TSs are marked by diamonds (a–c). FMO energy gap and overlap between metal complex Fe(CO)4 (red) or Pd(PH3)2 (black) and CH3–H (d, g), CH3–Cl (e, h) and CH3–CH3 bonds (f, i). H–L (solid line) designates [metal-complex dπ]–[substrate σc–x*]. L–H (dashed line) designates [metal-complex dσ]–[substrate σc–x]. (j, k and l) depict the populations of these orbitals (Fe(CO)4 d–π in the red solid line, Fe(CO)4 d–σ in the red dashed line, Pd(PH3)2 d–π in the black solid line, Pd(PH3)2 s in the black dashed line, substrate σc–x in the green or blue dashed line, substrate σc–x* in the green or blue solid line).

Fig. 8

Open in a new tab

Let us first inspect the three prototypical iron complexes 1Fe(CO)4, 3Fe(CO)4 and 1Fe(CO)42−. Fig. 1 depicts the frontier MOs of neutral Fe(CO)4 and their occupation in the singlet and triplet states, i.e., in 1Fe(CO)4 and 3Fe(CO)4. The triplet state is the ground state. Its open-shell nature gives rise to iron's tendency to react via radical pathways. But, the singlet state is only slightly, that is, 0.2 kcal mol−1, higher in energy than the triplet state. Herein, we are mainly interested in iron's less common closed-shell chemistry on the singlet potential energy surface (PES), which shows striking similarities and, yet, also characteristic differences to palladium chemistry.

Our computed geometries and energies of model iron complex 1Fe(CO)42−, singlet 1Fe(CO)4, and triplet 3Fe(CO)4 agree well with data from previous theoretical and experimental studies.99–105 While the anionic d10-metal complex 1Fe(CO)42− is tetrahedrally coordinated,3 the neutral d8-Fe(CO)4 complexes, both singlet and triplet, have C2v symmetry (see Fig. 1 and Table 1). The larger axial and equatorial OC–Fe–CO angles in 1Fe(CO)4 make this system resemble a trigonal bipyramid in which one of the equatorial sites is vacant. On the other hand, the geometry of 3Fe(CO)4 approaches more closely a distorted tetrahedron. Later on, we will see that the larger OC–Fe–CO angle of 1Fe(CO)4 is responsible for a significantly less destabilizing activation strain and, thus, lower barrier for C–X bond activation by this catalyst complex.

Proof-of-concept character of model catalytic cycles

Next, we address the proof-of-concept character of this study. Whereas the main emphasis of our analyses is to obtain an understanding of the differences between iron- and palladium-based model catalysts in the initial, selectivity-determining step of C–X bond activation, we stress that ultimately it is, of course, not only this step, but the entire catalytic cycle that determines whether such a process is kinetically feasible. Therefore, we precede these more detailed analyses by a helicopter-view exploration of the full catalytic cycle for a representative model cross-coupling reaction for both an iron- and an analogous palladium model catalyst. For that purpose, we choose the cross coupling of chloromethane with the Grignard reagent methylmagnesium chloride leading to the formation of ethane, catalyzed by both Fe(PH3)4 and Pd(PH3)2 (eqn (3)). For our purpose, Fe(CO)4 is replaced by Fe(PH3)4 to allow for a more direct comparison with the model palladium system, Pd(PH3)2. Iron catalysts with carbonyl and phosphine ligands, such as Fe(CO)4, Fe(PH3)4, Fe(DPE)2, Fe(DMPE)2 and Fe(CO)2(DPPE) [DPE = H2PCH2CH2PH2, DMPE = (CH3)2PCH2CH2P(CH3)2 and DPPE = Ph2PCH2CH2PPh2] have similar yet slightly different properties and thus have been applied as models in the exploration of various reactions.106–108 Moreover, use of the simplified and generic model catalysts, Fe(PH3)4 and Pd(PH3)2, allows the physical factors governing their activity and selectivity in cross coupling reactions to be directly compared and understood.

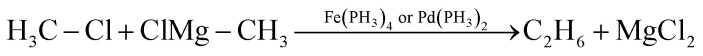graphic file with name c8cp07671e-t1.jpg 3

We have computationally modelled all key steps of the catalytic cycles, involving first oxidative addition, then transmetalation, and finally reductive elimination (see Scheme 1). As illustrated in Fig. 2, the overall potential energy surfaces for catalytic cycles involving Fe(PH3)4 and Pd(PH3)2 are qualitatively similar. Note that both model catalysts, Fe(PH3)4 and Pd(PH3)2, used to investigate the intrinsic properties of “real” catalysts,9,109 have unfavorable energetics for key steps of their respective catalyst cycles. The rate determining step for Pd(PH3)2 is the oxidative addition,1 while for 1Fe(PH3)4, it is the reductive elimination step.2 The insight gained in the model study is to be used, in particular, to tune these unfavorable steps in the model processes to achieve the desired (lower) barriers while keeping also the overall energy-span of the mechanism small.110

A rather unexpected finding is that Fe(PH3)4 has a 10.0 kcal mol−1 lower barrier than Pd(PH3)2 in the oxidative-addition step. This points to the enhanced bond activating capability for iron-based catalysts compared to the ubiquitous palladium analogs. Other than the previously mentioned differences, similar qualitative features emerge when comparing the catalytic cycles for Fe(PH3)4 and Pd(PH3)2. Thus, the use of our generic catalysts is justified and is a useful tool to understand the fundamental differences between iron- and palladium-based model catalysts.

General reaction profiles

The aim of the present work is to design iron-based catalysts that, as closely as possible, mimic the mechanism of bond activation for cross-coupling as performed by palladium catalysts. With this in mind, we have chosen three prototypical C–X bond activations that feature in palladium-catalyzed cross-coupling mechanisms, namely, that of the methane C–H, the chloromethane C–Cl, and the ethane C–C bond, and explored their activation by the three iron carbonyl complexes introduced above. The computed energies, relative to the reactants, of the stationary points along all seven model reactions are collected in Table 2. The corresponding energy profiles are depicted in Fig. 3. In addition, geometries and designations of the stationary points located for each model reaction are depicted in Fig. 4.

The oxidative insertions of the iron complexes start from a weakly bound reactant complex (RC), at only 0 to −9.0 kcal mol−1 relative to the separate reactants, in which CH3–X (X = H, Cl, CH3) coordinates via its C–X bond (or via its C–X and a C–H bond) to the iron center (see Table 2 and Fig. 4). The only RC of a more substantial stability is that of the chloromethane C–Cl bond coordinating to the singlet 1Fe(CO)4 (A2a), at −9.0 kcal mol−1. The reactant complexes of neutral Fe(CO)4 have a singlet ground state in the case of C–H and C–Cl and a triplet ground state for C–C activation; the latter is, however, only 0.2 kcal mol−1 above the singlet state. Proceeding from the RC, the catalyst approaches the C–X bond, which elongates as we approach the transition state (TS), which is a triangular [FeCX] unit involving partially formed Fe–C and Fe–X bonds and a partially broken C–X bond. The lowest barriers in all cases occur for the neutral singlet-complex 1Fe(CO)4 (see Fig. 3 and Table 2). In the case of the anionic d10-iron catalyst, the occurrence of a 20-electron species in the reaction with methane is prevented as one CO ligand begins to dissociate. This ligand dissociation also generates extra room for the approaching C–H bond. Our activation strain analyses reveal that this metal–ligand bond breaking causes a larger strain energy in 1Fe(CO)42− and, therefore, a substantially higher energy barrier than in the reactions of the neutral d8-iron complex 1Fe(CO)4: 74.1 versus 10.4 kcal mol−1 (see Fig. 3b). The TS geometries for 1Fe(CO)4 and 3Fe(CO)4 are quite similar (see Fig. 4). Nevertheless, the former has significantly lower barriers than the latter: 10.4 vs. 64.4 kcal mol−1 for C–H, 25.5 vs. 43.3 kcal mol−1 for C–Cl, and 48.0 vs. 76.9 kcal mol−1 for C–C bond activation, respectively. Our activation strain analyses reveal that this increase in barrier height, from 1Fe(CO)4 to 3Fe(CO)4, is associated with a more destabilizing catalyst strain associated with the necessity of a larger widening of the initially smaller OC–Fe–CO angle in the more tetrahedral 3Fe(CO)4 complex (vide infra).

The reactions involving the neutral singlet complex 1Fe(CO)4 proceed not only with the lowest barrier, but also lead to the most stable products (P): in all cases, this is the direct-insertion product, in which the C–X bond has been effectively reduced and broken (see P, in Fig. 3). The reaction energies of 1Fe(CO)4 are 0.8, −15.1, and 10.2 kcal mol−1 for C–H, C–Cl, and C–C activation (see Table 2 and Fig. 3). This has to be compared with the substantially more endothermic reaction energies of the triplet complex 3Fe(CO)4, which are 45.2, 29.4 and 51.1 kcal mol−1, respectively. These observations agree with the experimental findings by Poliakoff and Turner, who suggested that the adduct (CO)4–HFeCH3 has a singlet ground state.99,100 The associated radical reactions differ in nature from those of the closed-shell reactions of the singlet model catalyst. These radical reactions comprise the transfer of one methyl group of the substrate to iron under formation of an electron-pair bond while the X-group either leaves (in the case of CH3–CH3) or migrates to the carbon of a CO ligand (in the case of CH3–H and CH3–Cl). The most endothermic insertion among our model reactions is C–H activation by the anionic d10-complex 1Fe(CO)42− with a reaction energy of 66.3 kcal mol−1. Note that the straight oxidative-insertion product is not stable for both 3Fe(CO)4 and 1Fe(CO)42−: in the former case, an X˙ radical migrates to the carbon of a CO ligand (C–H and C–C) or it dissociates and leaves (C–C). In the latter case, that is, for 1Fe(CO)42− + CH4, a CO ligand departs (see Fig. 4). In this way, the formation of an unfavorable 20-electron species is avoided.

In addition to oxidative addition, we have also considered the SN2 reaction path for the activation of CH3X substrates (X = H, Cl, CH3) by the anionic iron complex 1Fe(CO)42−. It has been suggested that Na2Fe(CO)4 (Collman's reagent) proceeds through a rapid SN2 reaction with alkyl bromides.111 Our calculations indeed find a low barrier for C–Cl activation, but high barriers for C–H and C–C activation. As we wish to focus on developing design principles for tuning the oxidation addition step of model iron catalysts, we provide the SN2 results in the ESI.†

In conclusion, the kinetically and thermodynamically most favorable pathways proceed via oxidative addition on the singlet-state energy surfaces. The associated triplet–singlet interconversion of the initial iron-carbonyl complex is a common phenomenon for first row transition-metals, especially for those that exhibit multiple spin states, such as iron (cf. spin-cross reaction).112,113

Activation strain analysis

Next, we analyze the origin of the trends in reactivity and selectivity for the oxidative addition of iron-based catalyst complex Fe(CO)4 to the series of archetypal C–X bonds (X = H, Cl, CH3) by means of the activation strain model and Kohn–Sham molecular orbital analyses. A comparison with the corresponding palladium-mediated reactions follows, later on. Our activation strain analyses show that the reaction barrier increases from C–H to C–Cl activation because of a weaker catalyst–substrate interaction, whereas the increase from C–Cl to C–C activation arises from an increase in the destabilizing activation strain. The physical factors behind the variation in strain and interaction curves for the three types of bonds are similar to those behind the corresponding trends in reactivity of palladium-mediated C–X bond activation, as will be explained later on.11

Before we address the catalytic activity of 1Fe(CO)4, we first examine why 3Fe(CO)4 and 1Fe(CO)42− are not active and thus are not viable candidates for designing catalysts for cross coupling reactions. The substantial rise in barriers from 1Fe(CO)4 to either 3Fe(CO)4 or 1Fe(CO)42− mainly originates from a more destabilizing strain energy. For example, the strain energy is almost 60 kcal mol−1 higher for 1Fe(CO)42− than for 1Fe(CO)4 in the early stage of addition to the C–H bond (Fig. 5c), which pushes up the total energy immediately. The comparison of Fig. 5b and d shows that this prohibitively high strain mainly comes from the iron complex, which occurs because the 3Fe(CO)4 and 1Fe(CO)42− complexes are (near-)tetrahedral and lack an open site for docking the incoming substrate, at variance to 1Fe(CO)4, which has an open equatorial position in its incomplete trigonal bipyramidal geometry (Fig. 4). As a consequence, essentially no deformation is needed in the case of 1Fe(CO)4 to coordinate the incoming substrate, while 3Fe(CO)4 and 1Fe(CO)42− must undergo a substantial structural deformation. The axial CO–Fe–CO angle for 3Fe(CO)4 is widened from 155° in equilibrium geometries to 165°, 170° and 168° in TS for C–H, C–Cl and C–C activation, respectively. The larger expansion of the smaller angle (109°) eventually causes the dissociation of one ligand from the metal center in the case of 1Fe(CO)42−. Note that the bending of the bite angle to make room for the approaching substrate is crucial, to avoid otherwise even stronger steric repulsion between the catalyst and the substrate.13,114

Next, we continue with our analyses of the physical factors behind the selectivity of 1Fe(CO)4 towards C–H, C–Cl and C–C activation, followed by the core of our work, that is, a comparison of the underlying factors of the similarities and differences in activity between our iron model catalyst and archetypal d10-PdL2 model catalysts.

C–H, C–Cl and C–C bond activation by 1Fe(CO)4

As pointed out above, the barrier for 1Fe(CO)4-mediated bond activation increases from 10.4 to 25.5 to 48.0 kcal mol−1 along C–H, C–Cl and C–C bonds (see Table 2). The increase in the barrier from C–H to C–Cl and C–C activation is caused by two factors. One factor is the delay in the interaction curves ΔEint for the two latter bonds (see Fig. 5a). In the case of C–H activation, the interaction curve ΔEint becomes steadily more stabilizing, right from the beginning of the reaction. This makes the barrier lowest for C–H activation despite a relatively unfavorable strain curve which is comparable to that of C–C activation. At variance, in the case of C–Cl and C–C activation, the build-up in interaction energy ΔEint lags behind until the C–X bond is stretched sufficiently. Only then do the ΔEint curves for C–Cl and C–C gain quickly and eventually catch up with the ΔEint curve for C–H activation (see Fig. 5a). We come back to the different behavior in the interaction curves in a moment.

The second factor behind the trend in C–X bond activation is the higher strain curve for C–C compared to C–Cl activation, which causes the barrier for C–C activation to be highest. The elongation and eventual breaking of the covalent C–X bond is the main source of the strain energy, while the bending of the OC–Fe–CO angle contributes only a little (see Fig. 4 and 5d). The more destabilizing strain from C–Cl to C–C activation simply reflects the higher bond strength of the latter bond (see also ref. 11).

To understand why C–Cl and C–C bond activations have a delayed interaction, we further analyzed the bonding mechanism behind the interaction energy profiles by means of Kohn–Sham molecular orbital analysis. All three C–X bond activations have in common that the basic interaction pattern consists mainly of two features: (i) backdonation from the dπ of Fe(CO)4 to the σC–X* of CH3X; and (ii) donation from the σC–X of CH3X to the dσ of Fe(CO)4. This bonding mechanism is depicted in Fig. 6 for the case of oxidative addition of CH4 to 1Fe(CO)4. The remaining three d-type orbitals of Fe are not included since they are involved only very weakly in the bonding, or not at all. Our catalyst–substrate bonding analyses at the transition states reveal that the stabilizing electrostatic (ΔVelstat) and orbital-interaction (ΔEoi) contributions to the interaction energy ΔEint are of comparable magnitude and, at this stage of the reaction, outweigh the Pauli repulsion between occupied orbitals in the activation of all three bonds, C–H, C–Cl and C–C (see Table 3). Note also that the orbital overlaps, the extent of charge transfer from the HOMO to the LUMO in both π-backdonation and σ-donation, and the strength of orbital interactions ΔEoi are substantially larger for C–H than for C–Cl and C–C activation.

Now, there is a fundamental difference between the σC–H and σ* orbitals of the C–H bond and the σC–X and σC–X* orbitals of the C–Cl and C–C bonds, which is responsible for the delay in the catalyst–substrate interaction in the case of the two latter bonds. Fig. 7 schematically depicts the HOMO and LUMO of our three substrates CH3X, i.e., σC–X and σC–X*, which are composed of the in-phase and out-phase combination of orbitals between CH3 and the X unit (p-type for CH3 and Cl, 1s for H). Therefore, the σC–X and σC–X* orbitals of the C–Cl and C–C bonds have one additional nodal surface on the X moiety as compared to the σC–H and σC–H* orbitals of the C–H bond. This is depicted in Fig. 7, which also shows how the additional nodal surface of the C–Cl and C–C orbitals cuts into the lobes of the metal d orbital, in the early stages of C–Cl and C–C activation reactions at which the bonds have not yet been elongated much. This results in poor catalyst–substrate orbital overlap and thus less stabilizing π-backdonation and σ-donation for C–Cl and C–C activation compared to C–H activation, as shown by our EDA-NOCV115,116 calculations. Accordingly, the ΔEπ and ΔEσ terms, which quantity the backdonation from the dπ of Fe(CO)4 to the σC–X* of CH3X and the donation from the σC–X of CH3X to the dσ of Fe(CO)4, respectively, are more stabilizing in the TS for C–H activation (ΔEπ = −49.7 and ΔEσ = −37.4 kcal mol−1) than in the TS for C–Cl (ΔEπ = −19.8 and ΔEσ = −22.5 kcal mol−1) and C–C activation (ΔEπ = −23.4 and ΔEσ = −22.8 kcal mol−1; Table 3). Also, note that the net interaction energy curve ΔEint for C–Cl and C–C activation is even slightly positive, that is, repulsive, in the early stages of C–Cl and C–C activation, because the weak orbital interactions cannot overcome the unfavorable Pauli repulsion between occupied orbitals (see Fig. 5a).

Only in more advanced stages of the reaction, that is, after the C–Cl and C–C bonds have been stretched sufficiently to move the p-nodal surfaces of the substrate σC–X and σC–X* orbitals out of the way of the iron 3dσ and 3dπ lobes, do favorable overlap and interaction energy ΔEint build up, and quickly catch up with the overlap and interaction values in the case of C–H activation (see Fig. 5 and also the discussion later on). Note that the steeper interaction curves ΔEint in these more advanced stages of the reaction pull the TS for C–Cl and C–C activation to an earlier point along the reaction coordinate than the TS for C–H activation. Interestingly, this constitutes an example of anti-Hammond behavior: the more endothermic C–C activation reaction has a more reactant-like, not a more product-like, TS than C–H activation (see Fig. 4 and especially 5).

Iron versus palladium complexes

Finally, we turn to our initial question: is it possible to “teach” iron to do the tricks of palladium? The answer is a clear yes! We have seen this already in the discussion above: 1Fe(CO)4 can activate C–X bonds to an extent similar to d10-PdL2 complexes. Here, we undertake a more detailed and direct comparison of 1Fe(CO)4- versus Pd(PH3)2- and Pd(CO)2-mediated activation of methane C–H, chloromethane C–Cl, and ethane C–C bonds via oxidative addition. We choose these two palladium-d10 model catalysts because Pd(PH3)2 is, electronically, a representative model for the often bulkier palladium–phosphine complexes used in practice,109 whereas Pd(CO)2 allows for a more systematic comparison with the iron-carbonyl complex Fe(CO)4. Note that we recomputed the selected palladium-mediated bond activation pathways with the DFT approach of the present study, ZORA-OPBE/TZ2P, for a consistent comparison (see Table 2). Earlier work13,117 on the activity of Pd(PH3)2 and Pd(CO)2 was done with ZORA-BLYP/TZ2P, which yields the same reactivity trends, however slightly, i.e., by up to 1.8 kcal mol−1, different barriers or reaction energies.

We recall the main observations. In the first place, our iron-based model catalyst 1Fe(CO)4 is similarly, in fact, even slightly more reactive towards C–X bond activation than the archetypal palladium-based complexes Pd(PH3)2 and Pd(CO)2 (see Table 2). Furthermore, the iron model catalyst 1Fe(CO)4 achieves a particularly low barrier for C–H activation, even lower than for C–Cl activation. This contrasts with the palladium complexes Pd(PH3)2 and Pd(CO)2 which both activate C–H and C–Cl bonds via nearly identical reaction barriers (see Table 2). This is in line with an early experimental observation that showed the d8-iron complex Fe(DMPE)2 [DMPE = 1,2-bis(dimethylphosphino)ethane], which is similar in geometry to 1Fe(CO)4, to undergo oxidative addition to unactivated alkane C–H bonds at temperatures below −90 °C.108 In contrast, palladium-based cross coupling reactions tend to activate carbon–halogen bonds, not carbon–hydrogen bonds.1,18,19 This indicates that properly designed iron-catalysts can be used not only to replace palladium analogs, but they may also be deployed to achieve a different selectivity.

The results of our analyses of 1Fe(CO)4- and Pd(PH3)2-induced activation of C–H, C–Cl and C–C bonds are collected and one-on-one compared in Fig. 8, which depicts the activation strain diagrams (ASD), FMO energy gaps, and FMO overlaps as well as the FMO populations for all reactions: red and black curves in each subdiagram for 1Fe(CO)4versus Pd(PH3)2 reactions, respectively. First, we focus on the activation of the C–H bond, for which the largest difference in barriers occurs: 30.5 vs. 10.4 kcal mol−1 for Pd(PH3)2 and Fe(CO)4, respectively. The corresponding ASD in Fig. 8a shows a clearly more stabilizing interaction curve ΔEint for Fe(CO)4 along the entire reaction coordinate, leading to an earlier and lower barrier than for Pd(PH3)2. The strain curves ΔEstrain essentially coincide because the main source of strain energy is in both cases the breaking of the C–H bond.

The more stabilizing interaction energy curve for Fe(CO)4 comes from the characteristic difference that Fe(CO)4 has an incomplete d-shell, which features both a high-energy dπ HOMO and a low-energy dσ LUMO that can participate in strong π-backdonation as well as strong σ-donation, respectively (see Fig. 6, vide supra). The Pd(PH3)2 complex has a filled d-shell, which still provides a high-energy HOMO that can be deployed only for strong π-backdonation. The LUMO of Pd(PH3)2 is a higher-energy Pd-5s derived orbital, which is less capable of entering into a favorable σ-donation interaction. Thus, as can be seen in Fig. 8d–f, the LUMO–HOMO energy gap involving σ-donation is significantly larger for Pd(PH3)2 (black dashed curves) than for Fe(CO)4 (red dashed curves). Pd(PH3)2 thus has weak σ-donation, especially in the reaction with CH4. This is also reflected by the hardly changing populations of the Pd(PH3)2 5s-type LUMO and the CH4 σC–H HOMO, which remain relatively close to 2 and 0, respectively (see Fig. 8j). For comparison, π-backdonation in the case of Pd(PH3)2 is as strong as that for Fe(CO)4, as reflected by the small orbital-energy gap, the favorably large overlap and the relatively strong charge transfer from dπ to σC–H* (see Fig. 8d, g and j).

However, the σ-donation of 1Fe(CO)4 does not immediately come into action in the cases of C–Cl and C–C bond activations. This is why the energy barrier is reduced only slightly from Pd(PH3)2 to Fe(CO)4: from 30.6 to 25.5 kcal mol−1 for C–Cl and from 51.7 to 48.0 kcal mol−1 for C–C (see Table 2 and Fig. 8). This is so even though for the 1Fe(CO)4-induced bond activation the orbital-energy gap for σ-donation is still the smallest and charge transfer the strongest (see Fig. 8). However, for the C–Cl and C–C bond activation, the overlap interferes with the orbital-energy gap and codetermines the reactivity trend. Similar to the situation for the iron complex, the overlap is considerably smaller for C–Cl and C–C than for C–H activation by Pd(PH3)2. This again originates from the delayed donation and backdonation interaction, and is again caused by the cancelation between the d orbital of the metal complex and the substrate frontier orbitals at the early stage of the reaction (see Fig. 7a and b). As shown in Fig. 8h and i, due to the cancelation, the overlap for both the iron and the palladium complex remains close to zero at first and then increases quickly once the C–X bond is stretched enough. The small overlaps at early stages of the reaction lead to weak orbital interactions and, consequently, to higher energy barriers. Even though the poor overlap situation leaves little room for σ-donation to play a role, a close look at Fig. 8b and c shows that stronger orbital interaction for Fe(CO)4, due to the smaller orbital-energy gap, is still noticeable. Therefore, the ΔEint curves decrease more steeply for Fe(CO)4 than for Pd(PH3)2 at the later stages of the reactions.

The above comparison reveals an important difference in the interaction pattern between Pd and Fe complexes and substrates. Because of the saturated d10-shell and high-energy s orbital of Pd complexes, π-backdonation is usually the determining interaction and the focus of tuning. The employment of ligands that can push-up the palladium d orbitals, such as σ-donating ligands, can reduce the orbital-energy gap and enhance the catalyzing capability. The approach however differs if one wishes to tune iron-d8 catalysts: here, one has to consider both π-backdonation to and σ-donation from the substrate. How to achieve the simultaneous tuning of these two orbital mechanisms in the design of iron-complexes for C–X bond activation and catalytic cross coupling is the subject of future work in our laboratory.

Conclusions

Closed-shell iron-d8 complexes can be excellent candidates for replacing the more classical palladium-d10 systems in catalytic cross-coupling reactions. Our proof-of-concept quantum chemical investigation shows that a simple model system such as Fe(CO)4 has access to viable, non-radical pathways for C–X bond activation that closely mimic the oxidative-addition pathways of PdL2 complexes. This follows from our detailed analyses of the similarities of, and differences between, the reactivity of singlet 1Fe(CO)4, triplet 3Fe(CO)4, Fe(CO)42−, Pd(CO)2 and Pd(PH3)2 towards C–H, C–Cl, and C–C bonds, using the activation-strain model in combination with relativistic density functional theory. The full catalytic cycles associated with the cross coupling of chloromethane with the Grignard reagent methylmagnesium chloride catalyzed by our model iron-based catalyst, Fe(PH3)4, and a prototypical palladium catalyst, Pd(PH3)2, exhibit similar qualitative features, thus justifying the use of the generic Fe(L)4 catalyst for our current investigations. Interestingly, the oxidative addition is the rate determining step for Pd(PH3)2, while the reductive elimination step plays a more important role for Fe(PH3)4.

In fact, Fe(CO)4 is even slightly more active in closed-shell (i.e., singlet-state) activation of representative C–X bonds than archetypal PdL2 complexes. There are two major reasons for the good performance of 1Fe(CO)4. One is that FeL4 complexes, such as singlet 1Fe(CO)4, have an incomplete valence d8 shell. Consequently, they do not only have a high-energy dπ HOMO for effective π-backdonation to the σC–X* LUMO of the substrate, a feature they share with the d10-complexes of palladium, but also possess an empty 3dσ orbital, which is at relatively low energy as compared to the empty 5s-derived LUMO of palladium systems. This low-energy dσ LUMO of the iron complex can enter into a stronger, more stabilizing orbital interaction with the occupied σC–X orbital of the substrate resulting in a lower reaction barrier. A second reason for the good performance of 1Fe(CO)4 is that 1FeL4 complexes adopt the geometry of a “trigonal bipyramid missing one equatorial ligand”. This gap in the coordination sphere can straightforwardly accommodate the incoming substrate without inducing much activation strain in the catalyst complex during the bond activation process.

Interestingly, 1Fe(CO)4 favors C–H over C–Cl activation, at variance to archetypal PdL2 complexes, which show more facile C–Cl than C–H activation. The reason is that the additional σ-donation into the 3dσ LUMO, taking place in the iron-mediated reactions, achieves the most beneficial orbital overlap with the σC–H orbital, which is essentially 2pσ(C) + 1s(H). Both C–Cl and C–C activation suffer from the cancelation of orbital overlap with the iron 3dσ that arises from the additional 2p-nodal surface in their σC–X orbitals, which are essentially 2pσ(C) + npσ(X). For all model catalysts, C–C activation has the highest barrier because this is the strongest bond in the series, giving rise to the highest activation strain.

Conflicts of interest

There are no conflicts to declare.

Supplementary Material

CP-021-C8CP07671E-s001

Acknowledgments

We thank the China Scholarship Council (CSC), the Ministry of Education of Brazil/CAPES (1938/14-2), the Spanish MINECO (CTQ2016-77558-R and MDM-2017-0767), the Generalitat de Catalunya (2017SGR348), and the Netherlands Organization for Scientific Research (NWO) for financial support.

†

Electronic supplementary information (ESI) available. See DOI: 10.1039/c8cp07671e

References

  1. Hartwig J. F., Organotransition Metal Chemistry-From Bonding to Catalysis, University Science Books, Sausalito, CA, 2010 [Google Scholar]
  2. Smith M. B., March's Advanced Organic Chemistry: Reactions, Mechanisms and Structure, Wiley, New York, 2013 [Google Scholar]
  3. Bauer I. Knolker H. J. Chem. Rev. 2015;115:3170–3387. doi: 10.1021/cr500425u. [DOI] [PubMed] [Google Scholar]
  4. Bickelhaupt F. M. Houk K. N. Angew. Chem. 2017;129:10204–10221. doi: 10.1002/ange.201701486. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. van Zeist W. J. Bickelhaupt F. M. Org. Biomol. Chem. 2010;8:3118–3127. doi: 10.1039/B926828F. [DOI] [PubMed] [Google Scholar]
  6. Bickelhaupt F. M. J. Comput. Chem. 1999;20:114–128. doi: 10.1002/(SICI)1096-987X(19990115)20:1<114::AID-JCC12>3.0.CO;2-L. [DOI] [Google Scholar]
  7. Ess D. H. Houk K. J. Am. Chem. Soc. 2008;130:10187–10198. doi: 10.1021/ja800009z. [DOI] [PubMed] [Google Scholar]
  8. Ess D. H. Houk K. J. Am. Chem. Soc. 2007;129:10646–10647. doi: 10.1021/ja0734086. [DOI] [PubMed] [Google Scholar]
  9. Wolters L. P. van Zeist W. J. Bickelhaupt F. M. Chem. – Eur. J. 2014;20:11370–11381. doi: 10.1002/chem.201403237. [DOI] [PubMed] [Google Scholar]
  10. Wolters L. P. Koekkoek R. Bickelhaupt F. M. ACS Catal. 2015;5:5766–5775. doi: 10.1021/acscatal.5b01354. [DOI] [Google Scholar]
  11. de Jong G. T. Bickelhaupt F. M. ChemPhysChem. 2007;8:1170–1181. doi: 10.1002/cphc.200700092. [DOI] [PubMed] [Google Scholar]
  12. Vermeeren P. Sun X. Bickelhaupt F. M. Sci. Rep. 2018;8:10729–10739. doi: 10.1038/s41598-018-28998-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. van Zeist W. J. Visser R. Bickelhaupt F. M. Chem. – Eur. J. 2009;15:6112–6115. doi: 10.1002/chem.200900367. [DOI] [PubMed] [Google Scholar]
  14. de Jong G. T. Bickelhaupt F. M. Can. J. Chem. 2009;87:806–817. doi: 10.1139/V09-009. [DOI] [Google Scholar]
  15. Souillart L. Cramer N. Chem. Rev. 2015;115:9410–9464. doi: 10.1021/acs.chemrev.5b00138. [DOI] [PubMed] [Google Scholar]
  16. Bedford R. B. and Brenner P. B., Iron Catalysis II, 2015, vol. 50, pp. 19–46 [Google Scholar]
  17. Shang R. Ilies L. Nakamura E. Chem. Rev. 2017;117:9086–9139. doi: 10.1021/acs.chemrev.6b00772. [DOI] [PubMed] [Google Scholar]
  18. Negishi E.-I. Angew. Chem. 2011;123:6870–6897. doi: 10.1002/ange.201101380. [DOI] [Google Scholar]
  19. Suzuki A. Angew. Chem. 2011;123:6854–6869. doi: 10.1002/ange.201101379. [DOI] [Google Scholar]
  20. Garcia-Melchor M. Braga A. A. Lledos A. Ujaque G. Maseras F. Acc. Chem. Res. 2013;46:2626–2634. doi: 10.1021/ar400080r. [DOI] [PubMed] [Google Scholar]
  21. Murakami M. Matsuda T. Chem. Commun. 2011;47:1100–1105. doi: 10.1039/C0CC02566F. [DOI] [PubMed] [Google Scholar]
  22. Biajoli A. F. P. Schwalm C. S. Limberger J. Claudino T. S. Monteiro A. L. J. Braz. Chem. Soc. 2014;25:2186–2214. [Google Scholar]
  23. Zhang S. L. Yu Z. L. Org. Biomol. Chem. 2016;14:10511–10515. doi: 10.1039/C6OB01979J. [DOI] [PubMed] [Google Scholar]
  24. Czaplik W. M. Mayer M. Cvengros J. von Wangelin A. J. ChemSusChem. 2009;2:396–417. doi: 10.1002/cssc.200900055. [DOI] [PubMed] [Google Scholar]
  25. Tamura M. Kochi J. K. J. Am. Chem. Soc. 1971;93:1487–1489. doi: 10.1021/ja00735a030. [DOI] [Google Scholar]
  26. Tamura M. Kochi J. K. Synthesis. 1971:303–305. doi: 10.1055/s-1971-35043. [DOI] [Google Scholar]
  27. Kochi J. K. Acc. Chem. Res. 1974;7:351–360. doi: 10.1021/ar50082a006. [DOI] [Google Scholar]
  28. Neumann S. M. Kochi J. K. J. Org. Chem. 1975;40:599–606. doi: 10.1021/jo00893a013. [DOI] [Google Scholar]
  29. Cahiez G. Marquais S. Pure Appl. Chem. 1996;68:53–60. [Google Scholar]
  30. Cahiez G. Avedissian H. Synthesis. 1998:1199–1205. doi: 10.1055/s-1998-2135. [DOI] [Google Scholar]
  31. Dohle W. Kopp F. Cahiez G. Knochel P. Synlett. 2001:1901–1904. doi: 10.1055/s-2001-18748. [DOI] [Google Scholar]
  32. Cahiez G. Habiak V. Duplais C. Moyeux A. Angew. Chem. 2007;119:4442–4444. doi: 10.1002/ange.200700742. [DOI] [PubMed] [Google Scholar]
  33. Fürstner A. Leitner A. Méndez M. Krause H. J. Am. Chem. Soc. 2002;124:13856–13863. doi: 10.1021/ja027190t. [DOI] [PubMed] [Google Scholar]
  34. Fürstner A. Leitner A. Angew. Chem. 2002;114:632–635. doi: 10.1002/1521-3757(20020215)114:4<632::AID-ANGE632>3.0.CO;2-M. [DOI] [Google Scholar]
  35. Fürstner A. Méndez M. Angew. Chem. 2003;115:5513–5515. doi: 10.1002/ange.200352441. [DOI] [Google Scholar]
  36. Sherry B. D. Fürstner A. Acc. Chem. Res. 2008;41:1500–1511. doi: 10.1021/ar800039x. [DOI] [PubMed] [Google Scholar]
  37. Fürstner A. Martin R. Krause H. Seidel G. Goddard R. Lehmann C. W. J. Am. Chem. Soc. 2008;130:8773–8787. doi: 10.1021/ja801466t. [DOI] [PubMed] [Google Scholar]
  38. Nakamura M. Hirai A. Nakamura E. J. Am. Chem. Soc. 2000;122:978–979. doi: 10.1021/ja983066r. [DOI] [Google Scholar]
  39. Hatakeyama T. Hashimoto T. Kondo Y. Fujiwara Y. Seike H. Takaya H. Tamada Y. Ono T. Nakamura M. J. Am. Chem. Soc. 2010;132:10674–10676. doi: 10.1021/ja103973a. [DOI] [PubMed] [Google Scholar]
  40. Nakamura E. Yoshikai N. J. Org. Chem. 2010;75:6061–6067. doi: 10.1021/jo100693m. [DOI] [PubMed] [Google Scholar]
  41. Ilies L. Ichikawa S. Asako S. Matsubara T. Nakamura E. Adv. Synth. Catal. 2015;357:2175–2179. doi: 10.1002/adsc.201500276. [DOI] [Google Scholar]
  42. Shang R. Ilies L. Nakamura E. J. Am. Chem. Soc. 2015;137:7660–7663. doi: 10.1021/jacs.5b04818. [DOI] [PubMed] [Google Scholar]
  43. Nagano T. Hayashi T. Org. Lett. 2005;7:491–493. doi: 10.1021/ol047509+. [DOI] [PubMed] [Google Scholar]
  44. Shirakawa E. Itoh K. Higashino T. Hayashi T. J. Am. Chem. Soc. 2010;132:15537–15539. doi: 10.1021/ja1080822. [DOI] [PubMed] [Google Scholar]
  45. Uchiyama N. Shirakawa E. Nishikawa R. Hayashi T. Chem. Commun. 2011;47:11671–11673. doi: 10.1039/C1CC14694G. [DOI] [PubMed] [Google Scholar]
  46. Bedford R. B. Betham M. Bruce D. W. Danopoulos A. A. Frost R. M. Hird M. J. Org. Chem. 2006;71:1104–1110. doi: 10.1021/jo052250+. [DOI] [PubMed] [Google Scholar]
  47. Adams C. J. Bedford R. B. Carter E. Gower N. J. Haddow M. F. Harvey J. N. Huwe M. Cartes M. A. N. Mansell S. M. Mendoza C. J. Am. Chem. Soc. 2012;134:10333–10336. doi: 10.1021/ja303250t. [DOI] [PubMed] [Google Scholar]
  48. Bedford R. B. Brenner P. B. Carter E. Cogswell P. M. Haddow M. F. Harvey J. N. Murphy D. M. Nunn J. Woodall C. H. Angew. Chem. 2014;126:1835–1839. doi: 10.1002/ange.201308395. [DOI] [PubMed] [Google Scholar]
  49. Bedford R. B. Acc. Chem. Res. 2015;48:1485–1493. doi: 10.1021/acs.accounts.5b00042. [DOI] [PubMed] [Google Scholar]
  50. Smith R. S. Kochi J. K. J. Org. Chem. 1976;41:502–509. doi: 10.1021/jo00865a019. [DOI] [Google Scholar]
  51. Hedström A. Izakian Z. Vreto I. Wallentin C. J. Norrby P. O. Chem. – Eur. J. 2015;21:5946–5953. doi: 10.1002/chem.201406096. [DOI] [PubMed] [Google Scholar]
  52. Hashimoto T. Hatakeyama T. Nakamura M. J. Org. Chem. 2011;77:1168–1173. doi: 10.1021/jo202151f. [DOI] [PubMed] [Google Scholar]
  53. Sharma A. K. Sameera W. C. Jin M. Adak L. Okuzono C. Iwamoto T. Kato M. Nakamura M. Morokuma K. J. Am. Chem. Soc. 2017;139:16117–16125. doi: 10.1021/jacs.7b05917. [DOI] [PubMed] [Google Scholar]
  54. Lee W. Zhou J. Gutierrez O. J. Am. Chem. Soc. 2017;139:16126–16133. doi: 10.1021/jacs.7b06377. [DOI] [PubMed] [Google Scholar]
  55. Kneebone J. L. Brennessel W. W. Neidig M. L. J. Am. Chem. Soc. 2017;139:6988–7003. doi: 10.1021/jacs.7b02363. [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Hung C. H. Gandeepan P. Cheng L. C. Chen L. Y. Cheng M. J. Cheng C. H. J. Am. Chem. Soc. 2017;139:17015–17021. doi: 10.1021/jacs.7b05981. [DOI] [PubMed] [Google Scholar]
  57. Hu L. Chen H. J. Am. Chem. Soc. 2017;139:15564–15567. doi: 10.1021/jacs.7b06086. [DOI] [PubMed] [Google Scholar]
  58. Hong S. Lu X. Lee Y. M. Seo M. S. Ohta T. Ogura T. Clémancey M. Maldivi P. Latour J. M. Sarangi R. J. Am. Chem. Soc. 2017;139:14372–14375. doi: 10.1021/jacs.7b08161. [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Kleimark J. Hedström A. Larsson P. F. Johansson C. Norrby P. O. ChemCatChem. 2009;1:152–161. doi: 10.1002/cctc.200900061. [DOI] [Google Scholar]
  60. Kleimark J. Larsson P. F. Emamy P. Hedström A. Norrby P. O. Adv. Synth. Catal. 2012;354:448–456. doi: 10.1002/adsc.201100392. [DOI] [Google Scholar]
  61. Burdett J. K. Coord. Chem. Rev. 1978;27:1–58. doi: 10.1016/S0010-8545(00)80352-5. [DOI] [Google Scholar]
  62. Poliakoff M. Turner J. J. Dalton Trans. 1973:1351–1357. doi: 10.1039/DT9730001351. [DOI] [Google Scholar]
  63. Newlands M. Ogilvie J. Can. J. Chem. 1971;49:343. doi: 10.1139/v71-056. [DOI] [Google Scholar]
  64. Harvey J. N. Poli R. Dalton Trans. 2003:4100–4106. doi: 10.1039/B302916F. [DOI] [Google Scholar]
  65. Poliakoff M. Weitz E. Acc. Chem. Res. 1987;20:408–414. doi: 10.1021/ar00143a004. [DOI] [Google Scholar]
  66. Cedeño D. L. Weitz E. J. Phys. Chem. A. 2000;104:8011–8026. doi: 10.1021/jp0011894. [DOI] [Google Scholar]
  67. Ehlers A. W. Baerends E. J. Bickelhaupt F. M. Radius U. Chem. – Eur. J. 1998;4:210–221. doi: 10.1002/(SICI)1521-3765(19980210)4:2<210::AID-CHEM210>3.0.CO;2-T. [DOI] [Google Scholar]
  68. Radius U. Bickelhaupt F. M. Hoffmann R. Inorg. Chem. 1998;37:1080–1090. doi: 10.1021/ic970897+. [DOI] [Google Scholar]
  69. Michael D. Mingos P. J. Organomet. Chem. 2001;635:1–8. doi: 10.1016/S0022-328X(01)01155-X. [DOI] [Google Scholar]
  70. ADF, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands, http://www.scm.com
  71. Bérces A. Dickson R. M. Fan L. Jacobsen H. Swerhone D. Ziegler T. Comput. Phys. Commun. 1997;100:247–262. doi: 10.1016/S0010-4655(96)00120-8. [DOI] [Google Scholar]
  72. Boerrigter P. M. te Velde G. Baerends E. J. Int. J. Quantum Chem. 1988;33:87–113. doi: 10.1002/qua.560330204. [DOI] [Google Scholar]
  73. Deng L. Q. Ziegler T. Fan L. Y. J. Chem. Phys. 1993;99:3823–3835. doi: 10.1063/1.466129. [DOI] [Google Scholar]
  74. Fonseca Guerra C. Snijders J. G. te Velde G. Baerends E. J. Theor. Chem. Acc. 1998;99:391–403. [Google Scholar]
  75. Fukui K. Acc. Chem. Res. 1981;14:363–368. doi: 10.1021/ar00072a001. [DOI] [Google Scholar]
  76. te Velde G. Bickelhaupt F. M. Baerends E. J. Fonseca Guerra C. van Gisbergen S. J. A. Snijders J. G. Ziegler T. J. Comput. Chem. 2001;22:931–967. doi: 10.1002/jcc.1056. [DOI] [Google Scholar]
  77. Jacobsen H. Berces A. Swerhone D. P. Ziegler T. Comput. Phys. Commun. 1997;100:263–276. doi: 10.1016/S0010-4655(96)00119-1. [DOI] [Google Scholar]
  78. te Velde G. Baerends E. J. J. Comput. Phys. 1992;99:84–98. doi: 10.1016/0021-9991(92)90277-6. [DOI] [Google Scholar]
  79. Versluis L. Ziegler T. J. Chem. Phys. 1988;88:322–328. doi: 10.1063/1.454603. [DOI] [Google Scholar]
  80. Swart M. and Bickelhaupt F. M., Computer software (QUILD), Vrije Universiteit, Amsterdam (The Netherlands), 2006 [Google Scholar]
  81. Swart M. Bickelhaupt F. M. Int. J. Quantum Chem. 2006;106:2536–2544. doi: 10.1002/qua.21049. [DOI] [Google Scholar]
  82. Swart M. Sola M. Bickelhaupt F. M. J. Comput. Chem. 2007;28:1551–1560. doi: 10.1002/jcc.20653. [DOI] [PubMed] [Google Scholar]
  83. van Lenthe E. Baerends E. J. J. Comput. Chem. 2003;24:1142–1156. doi: 10.1002/jcc.10255. [DOI] [PubMed] [Google Scholar]
  84. Becke A. D. J. Chem. Phys. 1986;84:4524–4529. doi: 10.1063/1.450025. [DOI] [Google Scholar]
  85. Becke A. D. Phys. Rev. A. 1988;38:3098–3100. doi: 10.1103/PhysRevA.38.3098. [DOI] [PubMed] [Google Scholar]
  86. Johnson B. G. Gill P. M. W. Pople J. A. J. Chem. Phys. 1993;98:5612–5626. doi: 10.1063/1.464906. [DOI] [Google Scholar]
  87. Lee C. T. Yang W. T. Parr R. G. Phys. Rev. B. 1988;37:785–789. doi: 10.1103/PhysRevB.37.785. [DOI] [PubMed] [Google Scholar]
  88. Russo T. V. Martin R. L. Hay P. J. J. Chem. Phys. 1994;101:7729–7737. doi: 10.1063/1.468265. [DOI] [Google Scholar]
  89. van Lenthe E. van Leeuwen R. Baerends E. J. Snijders J. G. Int. J. Quantum Chem. 1996;57:281–293. doi: 10.1002/(SICI)1097-461X(1996)57:3<281::AID-QUA2>3.0.CO;2-U. [DOI] [Google Scholar]
  90. van Lenthe E. Baerends E. J. Snijders J. G. J. Chem. Phys. 1994;101:9783–9792. doi: 10.1063/1.467943. [DOI] [Google Scholar]
  91. de Jong G. T. Bickelhaupt F. M. J. Chem. Theory Comput. 2006;2:322–335. doi: 10.1021/ct050254g. [DOI] [PubMed] [Google Scholar]
  92. Verma P. Varga Z. Klein J. E. Cramer C. J. Que L. Truhlar D. G. Phys. Chem. Chem. Phys. 2017;19:13049–13069. doi: 10.1039/C7CP01263B. [DOI] [PubMed] [Google Scholar]
  93. Swart M. Gruden M. Acc. Chem. Res. 2016;49:2690–2697. doi: 10.1021/acs.accounts.6b00271. [DOI] [PubMed] [Google Scholar]
  94. van Zeist W. J. Fonseca Guerra C. Bickelhaupt F. M. J. Comput. Chem. 2008;29:312–315. doi: 10.1002/jcc.20786. [DOI] [PubMed] [Google Scholar]
  95. van Zeist W. J. Bickelhaupt F. M. Dalton Trans. 2011;40:3028–3038. doi: 10.1039/C0DT01550D. [DOI] [PubMed] [Google Scholar]
  96. Fernandez I. Bickelhaupt F. M. Chem. Soc. Rev. 2014;43:4953–4967. doi: 10.1039/C4CS00055B. [DOI] [PubMed] [Google Scholar]
  97. Wolters L. P. Bickelhaupt F. M. WIREs Comput. Mol. Sci. 2015;5:324–343. doi: 10.1002/wcms.1221. [DOI] [PMC free article] [PubMed] [Google Scholar]
  98. Bickelhaupt F. M. and Baerends E. J., in Reviews in Computational Chemistry, ed. K. B. Lipkowitz and D. B. Boyd, Wiley-VCH, New York, 2000, vol. 15, pp. 1–86 [Google Scholar]
  99. Poliakoff M. Turner J. J. Dalton Trans. 1974:2358–2363. [Google Scholar]
  100. Poliakoff M. Turner J. J. Angew. Chem., Int. Ed. 2001;40:2809–2812. doi: 10.1002/1521-3773(20010803)40:15<2809::AID-ANIE2809>3.0.CO;2-U. [DOI] [PubMed] [Google Scholar]
  101. Lyne P. D. Mingos D. M. P. Ziegler T. Downs A. J. Inorg. Chem. 1993;32:4785–4796. doi: 10.1021/ic00074a022. [DOI] [Google Scholar]
  102. Wang W. Weitz E. J. Phys. Chem. A. 1997;101:2358–2363. doi: 10.1021/jp964090z. [DOI] [Google Scholar]
  103. Krapp A. Pandey K. K. Frenking G. J. Am. Chem. Soc. 2007;129:7596–7610. doi: 10.1021/ja0691324. [DOI] [PubMed] [Google Scholar]
  104. Ihee H. Cao J. Zewail A. H. Angew. Chem. 2001;113:1580–1584. doi: 10.1002/1521-3757(20010417)113:8<1580::AID-ANGE1580>3.0.CO;2-2. [DOI] [Google Scholar]
  105. Sun Z. Schaefer III H. F. Xie Y. Liu Y. Zhong R. J. Comput. Chem. 2014;35:998–1009. doi: 10.1002/jcc.23585. [DOI] [PubMed] [Google Scholar]
  106. Schott D. Callaghan P. Dunne J. Duckett S. B. Godard C. Goicoechea J. M. Harvey J. N. Lowe J. P. Mawby R. J. Müller G. Perutz R. N. Poli R. Whittlesey M. K. Dalton Trans. 2004:3218–3224. doi: 10.1039/B407457B. [DOI] [PubMed] [Google Scholar]
  107. Bedford R. B. Brenner P. B. Carter E. Clifton J. Cogswell P. M. Gower N. J. Haddow M. F. Harvey J. N. Kehl J. A. Murphy D. M. Neeve E. C. Neidig M. L. Nunn J. Snyder B. E. R. Taylor J. Organometallics. 2014;33:5767–5780. doi: 10.1021/om500518r. [DOI] [Google Scholar]
  108. Baker M. V. Field L. D. J. Am. Chem. Soc. 1987;109:2825–2826. doi: 10.1021/ja00243a046. [DOI] [Google Scholar]
  109. Wassenaar J. Jansen E. van Zeist W. J. Bickelhaupt F. M. Siegler M. A. Spek A. L. Reek J. N. Nat. Chem. 2010;2:417–421. doi: 10.1038/nchem.614. [DOI] [PubMed] [Google Scholar]
  110. Kozuch S. Shaik S. Acc. Chem. Res. 2010;44:101–110. doi: 10.1021/ar1000956. [DOI] [PubMed] [Google Scholar]
  111. Pearson A. J., Iron Compounds in Organic Synthesis, Academic Press, 1994 [Google Scholar]
  112. Sun Y. Tang H. Chen K. Hu L. Yao J. Shaik S. Chen H. J. Am. Chem. Soc. 2016;138:3715–3730. doi: 10.1021/jacs.5b12150. [DOI] [PubMed] [Google Scholar]
  113. Carreón-Macedo J.-L. Harvey J. N. Phys. Chem. Chem. Phys. 2006;8:93–100. doi: 10.1039/B513325D. [DOI] [PubMed] [Google Scholar]
  114. Wolters L. P. Bickelhaupt F. M. ChemistryOpen. 2013;2:106–114. doi: 10.1002/open.201300009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  115. Mitoraj M. P. Michalak A. Ziegler T. J. Chem. Theory Comput. 2009;5:962–975. doi: 10.1021/ct800503d. [DOI] [PubMed] [Google Scholar]
  116. Mitoraj M. Michalak A. J. Mol. Model. 2007;13:347–355. doi: 10.1007/s00894-006-0149-4. [DOI] [PubMed] [Google Scholar]
  117. Wolters L. P. Bickelhaupt F. M. Chem. – Asian J. 2015;10:2272–2282. doi: 10.1002/asia.201500368. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

CP-021-C8CP07671E-s001
CP-021-C8CP07671E-s001.pdf (469.7KB, pdf)

Articles from Physical Chemistry Chemical Physics are provided here courtesy of Royal Society of Chemistry

RESOURCES