Applying Propensity Score Methods in Clinical Research in Neurology

Abstract

Propensity score–based analysis is increasingly being used in observational studies to estimate the effects of treatments, interventions, and exposures. We introduce the concept of the propensity score and how it can be used in observational research. We describe 4 different ways of using the propensity score: matching on the propensity score, inverse probability of treatment weighting using the propensity score, stratification on the propensity score, and covariate adjustment on the propensity score (with a focus on the first 2). We provide recommendations for the use and reporting of propensity score methods for the conduct of observational studies in neurologic research.

Introduction

Observational studies are increasingly being used to estimate the effects of treatments and exposures. Such studies can often be conducted rapidly and at less expense than randomized controlled trials (RCTs) and can estimate the effects of treatments as they are used in real-world clinical practice. Furthermore, they permit the study of exposures for which it would be unethical to randomize patients (e.g., tobacco smoking), or, in some cases, not possible to randomize (e.g., sex). However, in observational studies, unlike in RCTs, treated participants (used hereafter for exposed participants) frequently differ at baseline from those receiving the control intervention. Studies are said to be subject to confounding when the distribution of variables that influence the outcome differs between treated and control participants. In the presence of confounding, differences in outcomes between treatment groups may be due, at least in part, to these systematic differences between treated and control participants.

In observational studies, statistical methods are required to reduce the effects of confounding when estimating the effects of treatments. Methods based on the propensity score are increasingly being used for this purpose. The objective of this article is to introduce the propensity score and its application to neurologic research. We define the propensity score, describe how it can be estimated in an observational cohort study, and review different methods for using the propensity score.

Two Types of Questions

There are 2 common questions that one can ask when estimating the effect of a treatment. First, what is the effect of treatment in the entire population or sample of eligible patients? This is equivalent to asking how outcomes would differ if everyone received the treatment of interest compared to if everyone received the control treatment. Second, what is the effect of treatment in those patients who ultimately received the treatment of interest? This is equivalent to asking how outcomes would differ in the treated participants if, contrary to what occurred, they had not been treated. The former question is about the average treatment effect (ATE), while the latter is about the average treatment effect in the treated (ATT). Understanding the type of question that one is asking will help determine the most appropriate propensity score method to use.

In many pharmacoepidemiologic studies, the ATE may be of greater interest, as one can think of everyone in the eligible population as being treated with either agent. However, the ATT may be of greater interest in settings in which, despite all participants being eligible for either treatment, there are barriers or burdens imposed by one of the treatments. For example, if the cost of a drug is not routinely covered by insurance, it may make more sense to estimate the effect of this drug in those participants who ultimately decide to pay for it out of pocket.

Defining and Estimating the Propensity Score

We assume an observational cohort study design with a binary treatment (treated vs control) that is assessed at baseline (i.e., time of cohort entry). Treatment can either involve 2 active treatments (e.g., natalizumab vs another disease-modifying therapy for patients with multiple sclerosis) or an active treatment compared with a null control treatment (e.g., edavarone vs standard care in patients with amyotrophic lateral sclerosis). Baseline characteristics are measured on each participant. The outcome is measured after cohort entry (and implicitly after the treatment has been applied). Outcomes can be of types that are commonly seen in clinical research: continuous (e.g., blood pressure), binary (e.g., disabled on discharge vs not disabled on discharge), time-to-event (e.g., time to death), or a count (e.g., number of health care encounters). Any outcome that one can use in an RCT can be used in a study that uses propensity score methods.

The propensity score is defined as the probability of receiving the treatment of interest (vs the control treatment) conditional on measured participant covariates.^1,2 The primary property of the propensity score is that it is a balancing score.¹ This means that in a subgroup of participants, all of whom have the same value of the propensity score, the distribution of measured baseline covariates will be the same in treated and control participants in that subgroup. Thus, we can remove the effects of confounding by comparing outcomes between treated and control participants who share a similar value of the propensity score. This balancing is analogous to that induced by randomization in RCTs, with the key difference being that conditioning on the propensity score balances measured covariates, whereas randomization ideally balances both measured and unmeasured covariates. Note that balance is a large sample property, and that a sufficiently large sample is necessary in order to expect to observe balance in a given sample.

The validity of conclusions drawn from an analysis that uses propensity score methods rests on 2 assumptions: (1) the assumption that the investigators have measured all confounding variables and that there are no unmeasured confounders and (2) the positivity assumption that each participant has a nonzero probability of receiving each treatment.¹ This implies that no participant has an absolute contraindication to either the active or control treatment. Participants with an absolute (or relative) contraindication to either treatment should be excluded at the design stage, as is done in the design of RCTs. We refer the reader elsewhere for a discussion of positivity and methods to identify its presence.³ As an example, in a study comparing outcomes between immigrants to Ontario and long-term residents, participants residing in rural areas were excluded because, in Ontario, immigrants reside almost exclusively in urban areas.⁴ These assumptions are no different from those required by other methods for estimating causal effects in observational studies.

The propensity score is frequently estimated using a logistic regression model in which treatment status (treatment vs control) is regressed on the measured baseline covariates. While logistic regression is the most frequently used approach, researchers can also use algorithmic approaches from the machine learning literature, such as random forests or generalized boosting models. Strategies for variable selection for the propensity score model have been described elsewhere; see the Table for a summary of 2 strategies that perform well.⁵

Table.

Strategies for Selecting Variables to Include in a Propensity Score Model

Once the propensity score has been estimated, there are 4 main ways of using it: matching on the propensity score, inverse probability of treatment weighting (IPTW) using the propensity score, stratification on the propensity score, and covariate adjustment using the propensity score.

Matching on the Propensity Score

Matching on the propensity score entails forming matched sets of treated and control participants who share a similar value of the propensity score. The most common implementation is pair-matching, in which pairs of treated and control participants are formed. There are 2 common implementations of pair-matching. The first is greedy nearest neighbor matching (NNM), in which a treated participant is selected at random and then matched to the control participant whose propensity score is closest to that of the treated participant. The process is described as greedy because at each stage the control is selected who is closest to the currently considered treated participant, even if that untreated participant would serve better as a control for a subsequent treated participant. This process is then repeated until a matched control participant has been selected for each treated participant. This process generally uses matching without replacement, so that once a control participant is matched to a treated participant, that control participant is no longer available for matching to a subsequent treated participant. A refinement to NNM is NNM with a caliper restriction. Using this approach, a control participant is an acceptable match for a treated participant only if the difference in their propensity scores is less than a maximum amount (the caliper width or distance). For technical reasons, one typically matches on the logit of the propensity score and uses a caliper width that is defined as a proportion of the SD of the logit of the propensity score.⁶ Prior research has shown that a caliper of width equal to 0.2 of the SD of the logit of the propensity score works well in a variety of settings.⁷ Readers are referred elsewhere for a discussion and examination of different matching algorithms.^8,9 An alternative to greedy matching is optimal matching, which forms matched pairs to minimize the total within-pair difference in the propensity score. Alternative matching algorithms to pair-matching have been described in the literature. These include fixed ratio M:1 matching, variable ratio matching, and full matching.^10-15 While NNM with a caliper restriction is often a preferred approach, an attraction of these alternative matching algorithms is the ability to include a larger number of control participants in the analytic sample.

Matching on the propensity score can be combined with exact matching on a small number of baseline covariates. This will ensure perfect balance on these variables between treated and control participants in the matched sample. This approach is important if one wants to conduct subsequent subgroup analyses, so that matched pairs are included in the same subgroup. If one wanted to conduct subsequent sex-specific analyses, one could match on the propensity score and on sex, so that matched participants were of the same sex. When matching on a variable such as sex, it is not necessary that that variable be excluded from the propensity score model. Matching on the propensity score does not guarantee that matched participants will be identical on all measured variables. Rather, the distribution of the covariates will be similar between treated and control participants in the matched sample.

A crucial step in any study that uses propensity score matching is to assess the degree to which matching on the propensity score resulted in the formation of a matched sample in which the distribution of baseline characteristics is similar between treated and control participants. This assessment is critical as it allows both the researcher and readers to assess whether matching on the estimated propensity score has removed systematic baseline differences between treatment groups. This assessment should always be conducted while blinded to the outcomes (i.e., before any comparison of outcomes between treated and control participants). The use of statistical significance testing for assessing differences in baseline characteristics has been criticized by different sets of authors.^16,17 Instead, we recommend the use of statistics that are properties of samples and that, unlike statistical hypothesis testing, do not refer to hypothetical superpopulations. The use of the standardized difference, which is the difference in means in units of SD, is often used for assessing the similarity of matched treated and control participants. Some authors have suggested that a threshold of 0.10 (or 10%) be used to denote acceptable balance after matching.¹⁸ While most researchers limit balance assessment to using standardized differences to compare the means and prevalences of covariates between treatment groups, a comprehensive suite of balance diagnostics is described elsewhere for those wanting to conduct a more extensive assessment.¹⁹ If inadequate balance is observed, the researchers are encouraged to modify the specification of the propensity score model. Possible modifications include allowing for nonlinear relationships between continuous covariates and the log-odds of treatment (e.g., using restricted cubic splines) or the inclusion of interaction terms.²⁰ For example, Rosenbaum and Rubin,²⁰ in the first application of propensity score methods, described an iterative process that required 4 iterations to achieve acceptable balance.

Once acceptable balance has been achieved, analysts can unblind themselves to the outcome and compare outcomes between treated and control participants in the matched sample. The analyses conducted in the propensity score–matched sample can be similar to those that would be done in an RCT with a similar outcome. Thus, if the outcome is continuous (e.g., the Unified Parkinson's Disease Rating Scale), one can compute the mean blood pressure in each treatment group and then compute the difference in mean blood pressure. Similarly, if the outcome is binary (e.g., resolution of symptoms), one can compute the proportion of successes in each treatment group. One can then compute the absolute risk reduction (difference in the estimated proportions in each treatment group) and the relative risk (ratio of the estimated proportions in each treatment group). From the former, one can estimate the number needed to treat (NNT), which some have described as a key statistic for medical decision-making.^21,22 Note that there is no need to report an odds ratio. If the outcome is time-to-event in nature, one can estimate Kaplan-Meier survival curves (or cumulative incidence functions if there are competing risks) in treated and control participants.^23,24 These survival curves can be complemented by estimating a univariate Cox model (or cause-specific hazard model if there are competing risks) in which the hazard of the outcome is regressed on treatment status.

While estimation of the effect of treatment (e.g., estimating the hazard ratio or risk difference) can be done using analyses that reflect those that would be conducted in a similar RCT, the standard error of the estimated effect (used for constructing confidence intervals) should account for the matched nature of the sample.^25-28 Thus, for instance, with a Cox model, a robust variance estimator can be used,²⁶ while one can use the McNemar test for comparing proportions between groups.²⁷

When using matching on the propensity score, one is estimating the ATT. One cannot make inferences about the effect of treatment in the entire population of treated and control participants.

Propensity Score Matching in the Neurology Literature

Yu and colleagues²⁹ used matching on the propensity score to estimate the efficacy of IV thrombolysis with recombinant tissue-type plasminogen activator (tPA) for acute ischemic stroke in routine clinical practice. In order to account for baseline differences between groups, they used propensity score matching using NNM caliper matching with a caliper of 0.2 times the SD of the logit of the propensity score. The authors used standardized differences to confirm that there were no meaningful differences in measured baseline covariates between treated and control participants in the matched sample. Having satisfied themselves that matching had substantially decreased differences between the 2 groups, the authors compared mortality in those who did and did not receive tPA using Kaplan-Meier survival curves (compared using a stratified log-rank test to account for the matched nature of the sample) and a Cox proportional hazards model to compare the hazard of death between treated and control participants.

An advantage to using propensity score matching in this context is that it discards those untreated participants who are dissimilar to any treated participant and retains only controls who are similar to the treated participants. Yu and colleagues²⁹ estimated the effect of tPA in those who received it. Some applied researchers are wary of using propensity score matching for fear of excluding participants from the matched sample, but this concern is generally unwarranted. It is important to identify a matched control for each treated participant, as failure to do so can result in bias due to incomplete matching (because one is trying to estimate the effect of treatment in only a subset of treated participants who may differ systematically from the overall population of treated participants). However, once a control participant has been identified for each treated participant, the remaining unused control participants are superfluous and their exclusion from the analysis is unimportant. For this reason, matching works best in those settings in which there are substantially more controls than treated participants, as this increases the likelihood of identifying a suitable control for each treated participant.

IPTW Using the Propensity Score

IPTW using the propensity score creates weights based on the propensity score.³⁰ In the weighted sample, the distribution of measured baseline covariates will be the same in treated participants as in control participants. Thus, the presence of confounding is removed by weighting and outcomes can be compared directly between treated and control participants in the weighted sample. IPTW can be understood through the lens of complex surveys that incorporate sampling weights. Just as survey weights allow one to standardize the survey sample so that it is reflective of a given population, the use of IPTW standardizes each of the treated and control samples to a common reference sample.

Let Z be a binary variable denoting treatment status (Z = 1 for treated vs Z = 0 for control) and e denote the propensity score. Conventional inverse probability of treatment weights are defined as 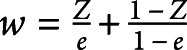. Thus, all participants are weighted by the reciprocal of the probability of receiving the treatment that they actually received. This set of weights uses the combined sample of treated and control participants as the target population to which each is standardized. A modification of these weights is stabilized weights: 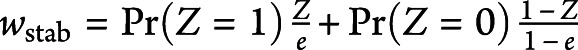.³¹ The use of stabilized weights may reduce the effect of a small number of participants with very high weights, which can result in improved variance estimation. The use of either conventional inverse probability of treatment weights or stabilized weights allows the investigator to estimate the ATE. An alternative set of weights allows one to estimate the ATT: 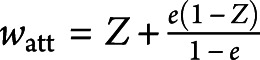.^32,33 Thus, treated participants have a weight of 1, while control participants have a weight of e/(1–e). This implies that the treated participants are the reference population to which each of the treated and control samples are standardized. The investigator must choose the set of weights (ATE vs ATT) that is appropriate to address the specific study question. While ATE and ATT weights are the most commonly used propensity score–based weights, matching weights, overlap weights, and entropy weights are alternatives.³⁴

Once the weights have been estimated, it is important to examine the distribution of the weights, as very large weights can affect variance estimation of the treatment effect and participants with very large weights can exert undue influence on the analyses and result in unstable estimates. There is no definition as to what constitutes a large weight. Strategies to address the presence of large weights include trimming large weights, so that weights that exceed a given threshold are truncated to equal this threshold (e.g., weights that exceed the 99th percentile of weights are set equal to the 99th percentile) or excluding participants whose propensity score is less than 0.1 or greater than 0.9.³⁵ Additional weight-based diagnostics are described elsewhere.³⁶

Once the propensity score has been estimated and the appropriate set of weights has been constructed, an assessment of the degree to which using the weights has allowed one to balance measured baseline covariates between treatment groups must be conducted prior to examining the effect of treatment on outcomes. An extensive set of balance diagnostics for use with propensity score weighting has been described elsewhere.³⁶ As with matching, the use of standardized differences in the weighted sample is recommended and the process of specifying the propensity score can proceed iteratively until acceptable balance is achieved.

Because weighting has removed the effects of confounding, one can estimate the effect of treatment using methods similar to those used in a comparable RCT. For continuous outcomes, one can estimate the weighted mean outcome in treated and control participants separately and then compute the difference in means. For binary outcomes, one can estimate the weighted proportion of successes in treated and control participants and then compute an absolute risk reduction, a relative risk, and an NNT. As with matching, there is no need to estimate an odds ratio. With time-to-event outcomes, weighted Kaplan-Meier survival curves (or cumulative incidence functions in the presence of competing risks) can be estimated, along with a weighted Cox proportional hazards model. Lunceford and Davidian³⁷ describe methods to estimate the variance of differences in means (which can also be used with risk differences). Xie and Liu³⁸ describe a test for equality of weighted survival curves. When using a regression model (e.g., a Cox model) in the weighted sample, variance estimation must account for the within-participant homogeneity induced by the weights.^39,40 One option is to use a robust variance estimator.²⁶ For all estimated measures of effect (e.g., a relative risk or a hazard ratio), one can use bootstrapping to construct confidence intervals. When using the bootstrap, it would be important to estimate the propensity score within each bootstrap sample in order to reflect the variability in the estimated statistic.

IPTW in the Neurology Literature

Vyas and colleagues⁴ used IPTW to compare mortality after ischemic stroke between immigrants and long-term residents. They used standardized differences to compare baseline covariates between immigrants and long-term residents in the weighted sample and confirmed that these were <0.10. Both Kaplan-Meier survival curves and a Cox regression model were used to compare mortality between immigrants and long-term residents in the weighted sample.

Hersh and colleagues⁴¹ used IPTW to compare relapse between switching from natalizumab to a moderate-efficacy disease-modifying therapy vs high-efficacy therapy in patients with multiple sclerosis. The authors used ATT weights with those switching to a moderate-efficacy disease-modifying therapy as the reference population. The authors used standardized differences to assess the balance in baseline covariates induced by weighting; after weighting, all but 5 of the standardized differences were less than 10%. The authors then used a Poisson regression model to compare the relapse rate between treatment groups.

Stratification and Covariate Adjustment Using the Propensity Score

Stratification on the propensity score involves ranking participants on the estimated propensity score and then dividing the sample into approximately equal size strata based on specified percentiles of the propensity score. Using 5 strata based on quintiles of the propensity score is the most common approach in practice. One then compares treated and control participants in each stratum and computes stratum-specific estimates of treatment effect, which are then pooled to generate an overall estimate of treatment effect.

Covariate adjustment using the propensity score involves regression of the outcome on an indicator variable denoting treatment status and the propensity score. This method was initially suggested for use with continuous outcomes and when estimating a linear treatment effect (e.g., a difference in means). However, it was subsequently frequently applied in settings with binary or time-to-event outcomes.

Lunceford and Davidian³⁷ suggest that stratification is affected by “biased inference due to residual confounding, and the effect of this bias becomes more serious with increasing sample size”. Other research has shown that both stratification on the propensity score and covariate adjustment using the propensity score can lead to biased estimation of odds ratios and hazard ratios,^26,42,43 and that covariate adjustment using the propensity score resulted in a greater magnitude of residual confounding than did matching on the propensity score or IPTW.⁴⁴ A further limitation of covariate adjustment using the propensity score is that it relies on a regression model to relate the outcome to treatment status and other variables (the propensity score). This approach requires the assumption that the outcomes regression model has been correctly specified.

For these reasons, while these 2 propensity score methods may be preferable in specific settings, we generally encourage researchers to consider either matching or weighting as the first propensity score approach to be considered.

Using the Propensity Score to Estimate Effects of Nonbinary Treatments

In the preceding sections we have focused on methods to use the propensity score to estimate the effects of binary treatment (treated vs control), as this is the most common application of propensity score methods. The generalized propensity score is an extension of propensity score methods to continuous or quantitative treatments (e.g., number of antiepileptic medications).^45-48 When considering a nonbinary categorical treatment (e.g., glatiramer acetate vs interferon-β 1b vs interferon-β 1a for treatment of multiple sclerosis), one possible approach is to conduct a sequence of analyses, each consisting of a comparison of 2 of the different levels of the treatment. Alternatively, methods using a multinomial logistic regression model to estimate the propensity score have been described.⁴⁹ Further research is necessary to determine the relative performance of these approaches.

Propensity Score vs Regression-Based Methods

Many researchers are familiar with regression-based approaches to account for confounding and may wonder whether it is worthwhile to learn a new technique. There are several advantages to the use of propensity score matching and weighting over conventional regression adjustment. First, when outcomes are binary, one can report absolute risk differences, relative risks, and NNTs. Similarly, with time-to-event outcomes, one can report absolute differences in survival at specific time points (obtained from the estimated survival curves) and hazard ratios. In contrast, with conventional regression adjustment, one is generally limited to reporting odds ratios and hazard ratios. Although the other measures can be estimated with additional work, this is rarely done in practice. Second, through describing the distribution of baseline covariates in treated and control participants in the matched or weighted sample, one can illustrate the degree to which matching or weighting has removed systematic baseline differences between treatment groups. It is much more difficult to determine the degree to which regression adjustment has minimized differences between groups. Finally, in settings in which outcomes are rare and the sample size is low to moderate, regression-based approaches would be limited in terms of the number of covariates that could be included in the regression model. This limitation does not apply to propensity score methods.

Limitations of Propensity Score Methods

Propensity score methods allow one to remove the effects of confounding due to measured baseline covariates. They make no claim to remove the effects of confounding due to unmeasured covariates, and findings from observational studies must be interpreted with care given this potential for residual confounding (a limitation shared by regression adjustment). Rosenbaum⁵⁰ described sensitivity analyses that can be used with propensity score matching to assess the robustness of study conclusions to unmeasured confounding.

Summary

Propensity score methods reduce the effects of confounding due to measured baseline covariates by creating a matched or weighted sample in which the distribution of measured baseline covariates is similar in treated and control participants. This allows for a direct comparison of outcomes between treatment groups and the use of metrics of treatment effect similar to what would be done in a comparable RCT. We have provided a checklist of study design and analysis considerations in Figure 1 and a reporting checklist for manuscripts that use propensity score matching or weighting in Figure 2.

Figure 1. Author Checklist for the Design and Analysis of Studies Using Propensity Score Methods.

Figure 2. Author Checklist for the Reporting of Studies Using Propensity Score Methods.

We hope this brief introduction will be of use to neurologic researchers and that the checklists and recommendations provided will strengthen the quality of observational studies that use propensity score methods.

Glossary

ATE

average treatment effect

ATT

average treatment effect in the treated

IPTW

inverse probability of treatment weighting

NNM

nearest neighbor matching

NNT

number needed to treat

RCT

randomized controlled trial

tPA

tissue-type plasminogen activator

Appendix. Authors

Study Funding

This research was supported by an operating grant from the Canadian Institutes of Health Research (CIHR) (PJT 166161). Drs. Austin and Kapral are supported by Mid-Career Investigator awards from the Heart and Stroke Foundation of Ontario. Dr. Kapral holds the Lillian Love Chair in Women's Health at the University Health Network/University of Toronto. Dr. Yu is supported by a national new investigator award from the Heart and Stroke Foundation of Canada.

Disclosure

The authors report no disclosures relevant to the manuscript. Go to Neurology.org/N for full disclosures.