Artificial intelligence applications in intensity modulated radiation treatment planning: an overview

Abstract

Artificial intelligence (AI) refers to methods that improve and automate challenging human tasks by systematically capturing and applying relevant knowledge in these tasks. Over the past decades, a number of approaches have been developed to address different types and needs of system intelligence ranging from search strategies to knowledge representation and inference to robotic planning. In the context of radiation treatment planning, multiple AI approaches may be adopted to improve the planning quality and efficiency. For example, knowledge representation and inference methods may improve dose prescription by integrating and reasoning about the domain knowledge described in many clinical guidelines and clinical trials reports. In this review, we will focus on the most studied AI approach in intensity modulated radiation therapy (IMRT)/volumetric modulated arc therapy (VMAT)—machine learning (ML) and describe our recent efforts in applying ML to improve the quality, consistency, and efficiency of IMRT/VMAT planning. With the available high-quality data, we can build models to accurately predict critical variables for each step of the planning process and thus automate and improve its outcomes. Specific to the IMRT/VMAT planning process, we can build models for each of the four critical components in the process: dose-volume histogram (DVH), Dose, Fluence, and Human Planner. These models can be divided into two general groups. The first group focuses on encoding prior experience and knowledge through ML and more recently deep learning (DL) from prior clinical plans and using these models to predict the optimal DVH (DVH prediction model), or 3D dose distribution (dose prediction model), or fluence map (fluence map model). The goal of these models is to reduce or remove the trial-and-error process and guarantee consistently high-quality plans. The second group of models focuses on mimicking human planners’ decision-making process (planning strategy model) during the iterative adjustments/guidance of the optimization engine. Each critical step of the IMRT/VMAT treatment planning process can be improved and automated by AI methods. As more training data becomes available and more sophisticated models are developed, we can expect that the AI methods in treatment planning will continue to improve accuracy, efficiency, and robustness.

Introduction

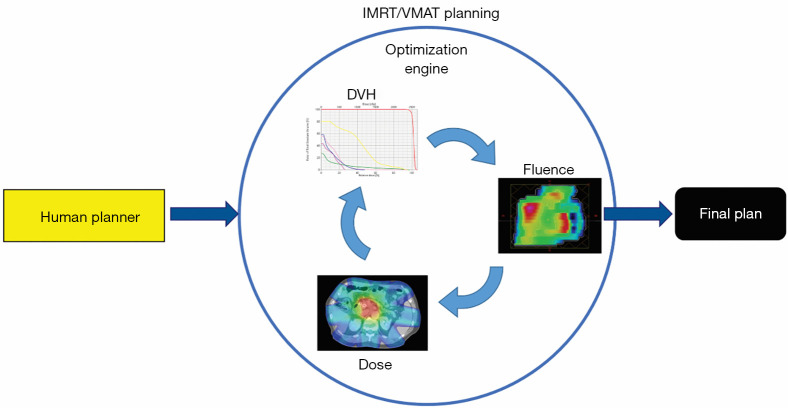
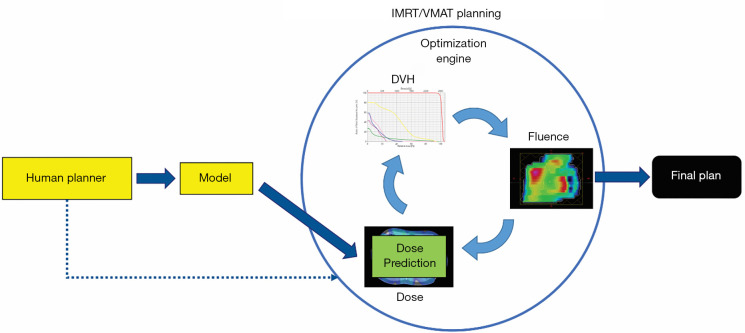
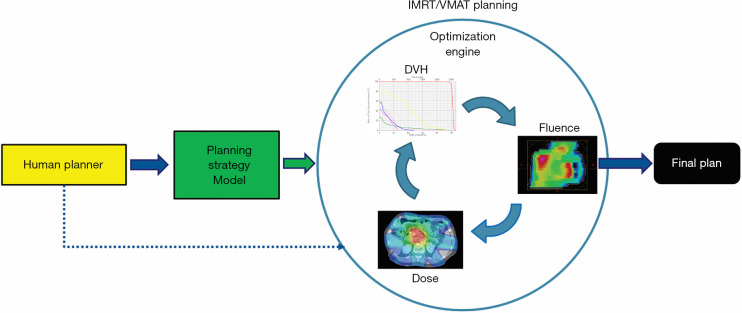
With the wide adoption of intensity modulated radiation therapy (IMRT) and volumetric modulated arc therapy (VMAT) technologies in the past two decades, treatment planning has become one of the most time-consuming processes in the clinic workflow. During IMRT/VMAT treatment planning, the planner interacts with the treatment planning system (TPS) to guide the inverse planning process. Typically, planners assign optimization constraints in the form of planning target volume (PTV) and organ-at-risk (OAR) dose-volume histogram (DVH) points and their relative weights/priorities. These constraints are subsequently used by TPS to construct a cost function that guides the optimization algorithm to apply changes to the fluence maps of the IMRT plan or multi-leaf collimator (MLC) segments of the VMAT plan. The updated fluence map/MLC segments are passed to the dose calculation engine to update the dose distribution. This is then led to the update of the DVH values of the current plan. The optimization DVHs are compared to the planner’s DVH constraints, in the form of cost-function, for further changes of the fluence maps/MLC segments. This iterative process is shown in the circle of “optimization engine” in Figure 1. In addition, the planner may change the DVH constraints or their associated weights to guide the optimization process to reach a clinically optimal solution, such control is represented by the dark blue arrow pointing from yellow box “Human Planner” to the optimization engine as shown Figure 1. This planning process continues until the cost function converges or the maximum number of iterations is reached. The complete workflow of the inverse planning, including the interaction of the optimization engine and the iterative process of IMRT/VMAT optimization is illustrated in Figure 1. Without patient-specific estimates of best achievable DVH results, planners usually assign generic optimization constraints based on previous experience and knowledge that often require multiple trial-and-error iterations and make the treatment planning process highly subjective and plan quality highly variable (1-5).

Figure 1.

IMRT/VMAT manual planning process. IMRT, intensity modulated radiation therapy; VMAT, volumetric modulated arc therapy; DVH, dose-volume histogram.

Artificial intelligence (AI) refers to methods that improve and automate challenging human tasks by systematically capturing and applying relevant knowledge in these tasks. Over the past decades, a number of approaches have been developed to address different types and needs of system intelligence ranging from search strategies to knowledge representation and inference to robotic planning. In the context of radiation treatment planning, multiple AI approaches may be adopted to improve the planning quality and efficiency. For example, knowledge representation and inference methods may improve dose prescription by integrating and reasoning about the pieces of knowledge described in the many clinical guidelines and clinical trials reports (6,7). In this review, we will focus on the most studied AI approach in IMRT/VMAT—machine learning (ML) and describe our recent efforts in applying ML to improve the quality, consistency, and efficiency of IMRT/VMAT planning.

ML aims to develop models that capture the essential relationships and patterns between input and output variables in the data. As long as high-quality data is available, we can build models to accurately predict critical variables for each step of the planning process and thus automate and improve its outcomes. Specific to the IMRT/VMAT planning process outlined in Figure 1, we can build models for each of the four boxes in the figure: DVH, Dose, Fluence, and Human Planner. These models can be divided into two general groups. The first group focuses on encoding prior experience and knowledge through ML and more recently deep learning (DL) from prior clinical plans and using these models to predict the optimal DVH (DVH prediction model), or 3D dose distribution (dose prediction model), or fluence map (fluence map model). The goal of these models is to reduce or remove the trial-and-error process and guarantee consistently high-quality plans. The second group of models focuses on mimicking human planners’ decision-making process (planning strategy model) during the iterative adjustments/guidance of the optimization engine. In the following sections, we describe several example models to demonstrate some currently available AI methods for improving and automating IMRT/VMAT treatment planning. Specifically, this review paper is organized as follows. Section “DVH prediction models”, “Dose prediction models” and “Fluence map prediction models” focus on the first group of DVH/dose/fluence map prediction ML algorithms. Section “Planning strategy models” reviews the second group of human decision mimicking techniques. “Summary” section provides a summary of all AI techniques commonly seen in radiation therapy treatment planning.

DVH prediction models

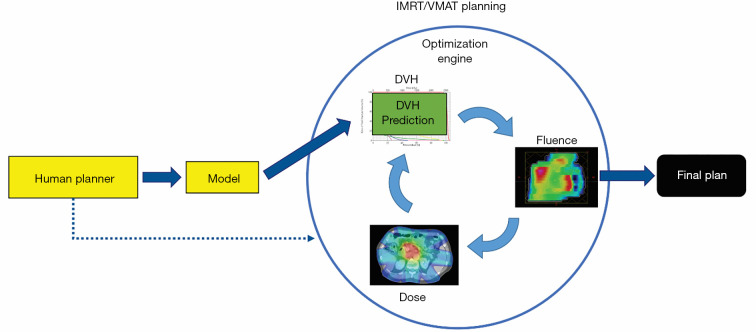
Most of the earlier ML models in IMRT are DVH prediction models that predict the best achievable OAR dose sparing using knowledge embedded in high-quality prior treatment plans (8-11). In this approach, the correlations of OAR DVHs and patient anatomical features are learned from previously treated patients and used to predict the optimal DVHs for new patients. Therefore, this group of models aims to replace planner’s experience-based and protocol-driven generic DVH objectives with model-based and patient-specific predictions. Clinical implementations of these models have demonstrated better plan quality and consistency (12-14). This group of models is also known as knowledge-based planning (KBP) models (8,10,11,15-21). A general workflow is illustrated in Figure 2. Human planners (yellow box) could refer to the DVH (green box) predicted by the model (yellow box) while executing the optimization engine (blue dotted arrow).

Figure 2.

The application DVH Prediction Models in the automation of IMRT/VMAT planning. DVH, dose-volume histogram; IMRT, intensity modulated radiation therapy; VMAT, volumetric modulated arc therapy.

Feature design and dimensionality reduction

In radiation therapy treatment planning, DVHs, 1-dimensional representations of dose distributions, are commonly used to interpreting OAR toxicity quantitatively. In order to predict OAR DVHs, a low dimensional representation of the spatial relationship between OAR voxels and the PTV is needed. Considering that the determinant factor for dose levels near the PTV is the distance to the PTV, the histogram of OAR volume percentages within certain distances from the PTV surface, or distance-to-target histogram (DTH) (8), is a natural choice for predictive features. Alternative representations of patient anatomy include overlap volume histogram (OVH) (22,23) and OAR sub-volumes (11).

In some of our DVH prediction models, DVH and DTH are processed using principal component analysis (PCA) to further reduce their dimensions. This method enables efficient learning with limited available clinical training samples. The variability of the histograms can be summarized by a few principal component directions, and the individual variations can be represented by a small number of principal components. Typically, the first three components of the principal component scores (PCSs) are selected as anatomical features (8,9). Other anatomical information, such as OAR/PTV volume, percentage of OAR volume overlapping with the PTV, and fraction of OAR volume outside the treatment fields, are combined with DTH PCSs to form a feature vector and used as the model input.

Example model training and validation

Yuan et al. (8) used 88 prostate IMRT plans to develop a DVH model. The treatment plans used in the study were previously treated clinical plans. Among these plans, 64 prostate patients were selected for training purposes, and the remaining 24 prostate plans were reserved for validation.

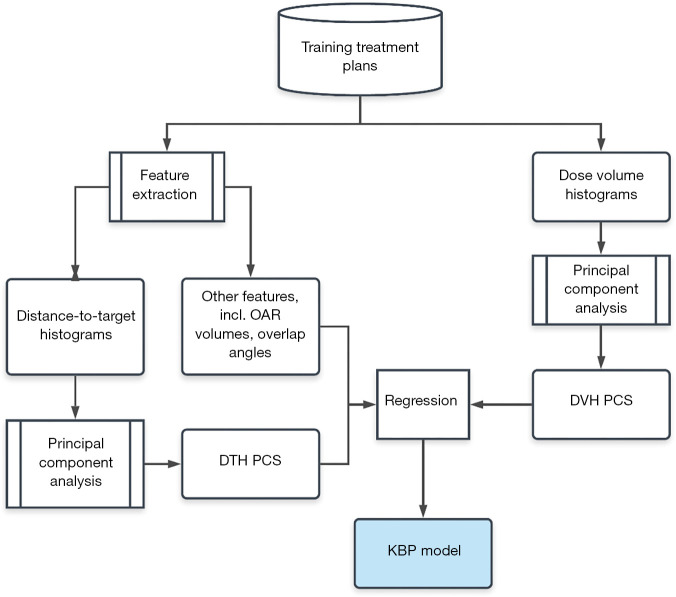
The training workflow, as summarized in Figure 3, starts with data extraction and preprocessing. After the feature vector and the DVH PCSs are prepared, DVH PCSs are fitted to anatomical features using a stepwise multiple regression method. The stepwise regression method selects the most significant feature to the model by the coefficient of partial determination, which measures the correlation between that factor and the DVH variation not explained by the factors already included in the model. The result of the training process is a KBP model consisted of regression coefficients and the DTH/DVH PCA basis vectors. After obtaining the regression coefficients in the training process, the model can be used to predict OAR DVHs for future patients.

Figure 3.

The workflow of the KBP training process. KBP, knowledge-based planning; OAR, organ-at-risk; DVH, dose-volume histogram; PCS, principal component score; DTH, distance-to-target histogram.

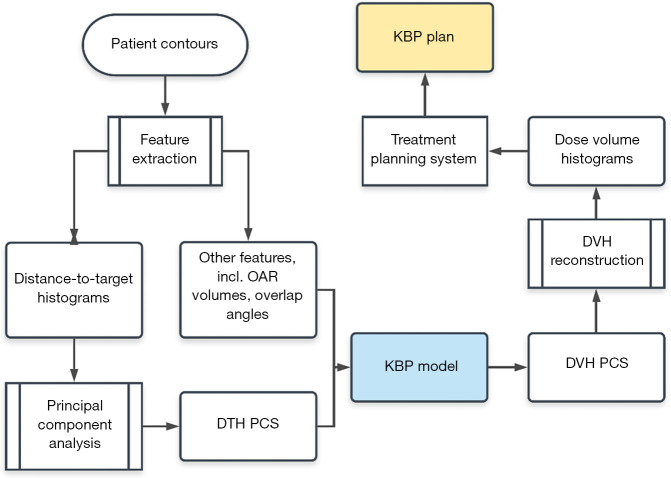
Following the flowchart shown in Figure 4, the DVHs are calculated by the trained regression model using anatomical features extracted from the new patients. These model-predicted DVHs are compared to the DVHs in the corresponding clinical plans to evaluate the prediction accuracy of the trained model. In Yuan et al. (8), V99%, V85%, V50% for both bladder and rectum were evaluated. Considering both bladder and rectum, 71% of the validation plans were within 6% error bound, and 85% were within 10% error bound.

Figure 4.

The workflow of a KBP prediction. KBP, knowledge-based planning; OAR, organ-at-risk; DVH, dose-volume histogram; PCS, principal component score; DTH, distance-to-target histogram.

This KBP model has been modified and adopted by Varian Medical Systems and integrated into Eclipse TPS as a module known as RapidPlan (Varian Medical Systems, Palo Alto, CA) (24). RapidPlan replaces the DTH feature with a similar geometric expected dose (GED) feature, which incorporates beam geometry and multiple prescribed dose levels, in addition to OAR-to-PTV distance information. Clinical uses of RapidPlan for various treatment sites have been extensively studied. The results suggest that the DVH prediction models and the RapidPlan KBP models, if trained properly, can produce optimal clinical plans efficiently (2,3,17,25-42).

Expanding DVH prediction to include clinical tradeoff options

In treatment sites with complex OAR sparing tradeoffs, such as head-and-neck (HN), physicians often prescribe OAR dose constraints based on estimates of the best achievable DVHs with desired tradeoffs, and planners need to interact with the TPS and the physicians iteratively in order to achieve patient-specific optimal OAR-sparing. For such treatment sites, one set of DVH predictions provided by a standard KBP model may not be sufficient, considering the tradeoff needs. A pre-planning tradeoff estimation method (43) has been proposed to support tradeoff decision-making by modeling the clinically viable tradeoff experience embedded in prior clinical plans.

The workflow, as shown in Figure 5, starts with building a patient-specific KBP model, which is a model based on only those prior cases that are similar to the current case. Given a case to predict, a case reference set (CRS) consisted of N reference cases are selected from a reference database. The generalized distance-to-target (gDTH) feature (44) is modified to select similar plans in terms of all OARs. After the KBP model is built, it is applied to all the cases in the CRS to extract tradeoff related variations. The difference between the predicted and the actual DVH PCS (from clinical plans) for all OARs is estimated and formulated as E∈R^N×MP, which is essentially the fitting residuals of N training cases in the CRS, each with M OARs and P DVH PCS per OAR. The purpose of subtracting the predicted PCS is to remove the variations caused by anatomical differences and extract only the discrepancy between the KBP model and the clinical plans that are likely linked to tradeoff decisions. The matrix E of OAR DVH fitting residuals is subsequently processed by PCA to further reduce the dimensionality with the first three PCSs taken as the principal tradeoff directions. The tradeoff directions effectively reveal the most prominent DVH variation patterns in the CRS after adjusting for anatomy variations.

Figure 5.

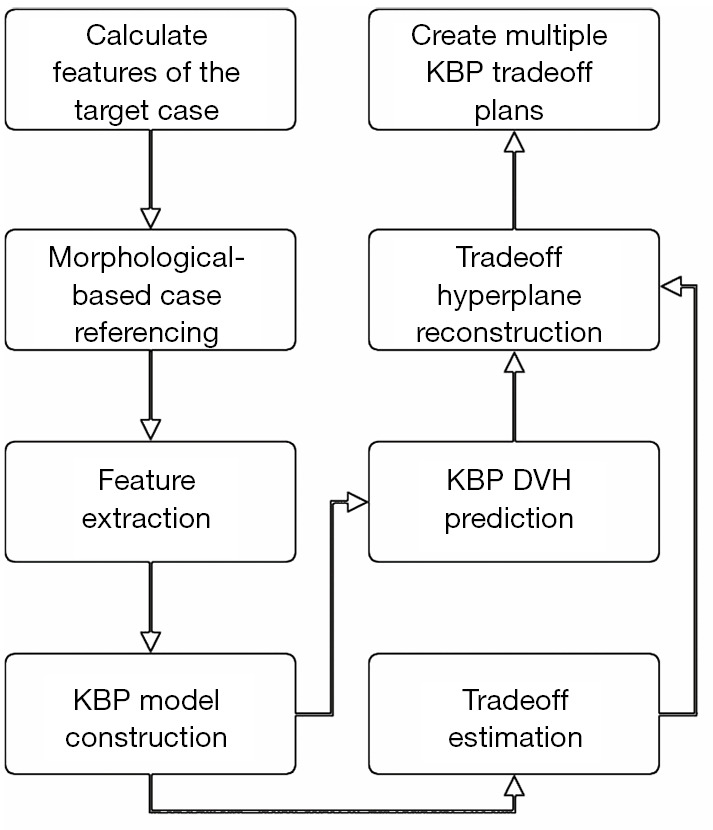
The workflow of a knowledge-based tradeoff model. KBP, knowledge-based planning; DVH, dose-volume histogram.

Example tradeoff simulation and validation

In Zhang et al.’s study (43), 244 anonymized HN IMRT cases were retrieved from the clinical database. The dataset was divided into a 214-case training set and a 30-case validation set. After the model was trained, it was applied to the validation set to generate 12 sets of OAR DVH predictions (3 tradeoff directions, 4 plans sampled in each tradeoff direction). A conventional KBP plan and a clinical-DVH-fitted plan were also generated for each case. Figure 6 shows the root-mean-squared error (RMSE) between the DVHs predicted by the tradeoff hyperplane and the corresponding DVHs realized by the auto-generated tradeoff plans. These RMSE values represent the fidelity of the auto-generated tradeoff plans compared with hyperplane model predictions and are evaluated against the KBP model baselines as well as the clinical-DVH-fitted results. RMSEs of the max-dose constrained OARs (cord, brainstem, mandible) have higher values in general compared to dose-volume constrained OARs (e.g., parotid). In clinical planning, when OARs are max-dose constrained, planners tend to place very low priorities on sparing these OARs at dose-volume points other than the D_max. This results in large DVH variations not attributed to anatomy differences. Therefore, these DVH curves are not predicted as accurately as DVHs of other OARs, such as parotid and oral cavity. Due to such variations, RMSE values, even for the KBP plans, are not expected to be zero. However, as it has been shown in the literature that the KBP model predicted DVHs are indeed achievable (45), the non-zero RMSE of the KBP model predictions can establish the baseline for the hyperplane model. The RMSE of all 12 tradeoff-guided plans are not significantly different from the baseline RMSE (P>0.05; paired t-test; n=30 validation samples). These results suggest that all tradeoff plans are as achievable as the KBP plans.

Figure 6.

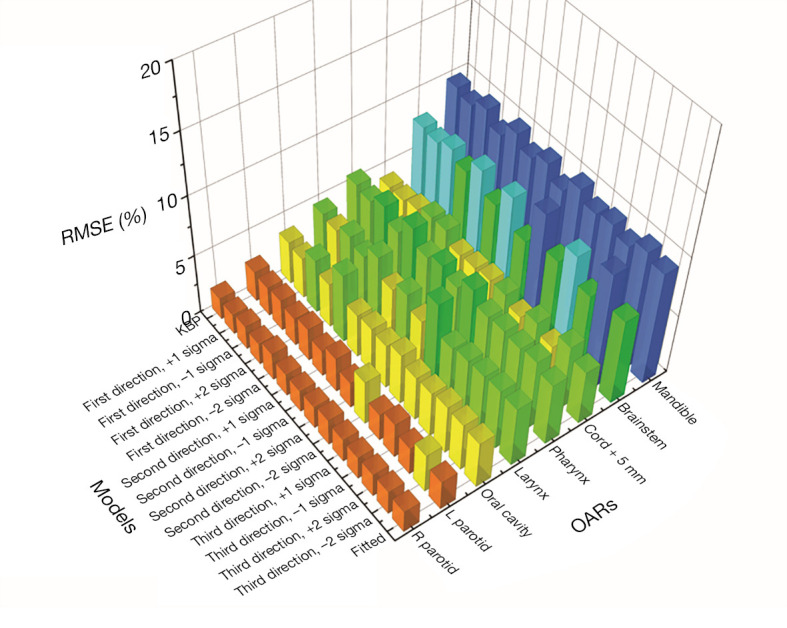
RMSE values for model predicted DVHs measured against corresponding TPS plan DVHs. Small RMSE values indicate that hyperplane predicted DVHs closely resemble the realized DVHs of auto-generated plans and hence provide evidence that the hyperplane DVH predictions are highly achievable. Different colors denote different ranges of RMSE values. RMSE, root-mean-squared error; DVH, dose-volume histogram; TPS, treatment planning system.

The feature extraction, regression, and DVH prediction of the tradeoff model work similarly to the conventional model-based KBP. The endpoint of the new workflow, however, is an ensemble of best achievable plans with various tradeoff preferences. Additionally, the hyperplane model generates preplanning estimations of achievable OAR tradeoffs, thereby providing systematic guidance on the best achievable dosimetric parameters for informed decision-making in clinical environments.

Dose prediction models

Similar to DVH prediction, dose distribution prediction can also be utilized as the optimization objectives in the inverse planning process. A general workflow is shown in Figure 7. Compared to DVH prediction, dose distribution prediction could provide more spatial information of dose (46). Furthermore, dose distribution prediction could be converted to a plan through dose mimicking (47-49). Dose mimicking driven planning process is similar to inverse planning in terms of iterative updates of the machine parameters. The difference is dose mimicking algorithms’ objective functions could be calculated between model-predicted dose and optimizing dose.

Figure 7.

IMRT/VMAT planning workflow based on dose prediction algorithms. IMRT, intensity modulated radiation therapy; VMAT, volumetric modulated arc therapy; DVH, dose-volume histogram.

While it is possible to estimate dose distribution using algorithms such as deformable image registration (50), most recent dose prediction algorithms are based on ML or DL models (51). Categorized by prediction algorithms, dose distribution could be predicted by shallow ML models (49,51), deep neural network models such as the convolutional neural network (CNN) (47,52-59) and the generative adversarial network (GAN) (48,60,61). Categorized by input/output dimensions, dose distribution could be predicted voxel by voxel (49,51), slice by slice (47,48,52,56,59,62), or as a 3D volume (53,54,57,58,60,61). In the following section, we present one example of a DL based dose prediction model for prostate VMAT.

Example prostate VMAT dose prediction using residual network

In Jensen et al.’s study (63), a 2D patch dose prediction algorithm was designed for prostate VMAT plans. Predicting dose distribution of 2D patches could be regarded as a combination of voxel-wise and slice-wise dose prediction algorithms. The dose distribution was initialized on a voxel-wise basis using a fitted model:

$$D\left(\stackrel{\rightharpoonup }{x}\right)={\left(1+a_1\times IS{D}_1{\left(\stackrel{\rightharpoonup }{x}\right)}^{a_2}+c\times IS{D}_2{\left(\stackrel{\rightharpoonup }{x}\right)}^{a_3}\right)}^{-1}$$ [1]

where $D\left(\stackrel{\rightharpoonup }{x}\right)$ is the dose of the voxel at position $\stackrel{\rightharpoonup }{x}$, ISD₁ stands for the voxel’s nearest inter-slice distance to the PTV within the axial plane, ISD₂ stands for the voxel’s nearest intra-slice distance to the PTV along the interior-superior direction, a₁, a₂, and a₃ are fitting parameters. The root mean squared error (RMSE) for the dose initialization fit was about 5.5% of the prescription dose.

A series of 9-by-9-pixel 2D patches were generated from structure contours and initial dose estimation and was fed as network input. The DL network started with 3 parallel convolutional layers with a filter size of 3 by 3 and atrous rates of 1, 3, and 10, respectively. Outputs from these three convolutional layers were flattened and concatenated with optimization priorities to form a vector. By involving optimization priorities, the model is designed to predict dose distributions with different tradeoffs. The rest of the network contains 6 residual blocks. A residual block contains two fully connected layers followed by leaky rectified linear unit (Leaky ReLu) activation layers with a slope of 0.2 and one fully connected layer followed by a softsign activation layer scaled by 0.3 in sequence. The output of each residual block is added to the dose map before entering the following layers. The loss function was RMSE between the predicted and ground truth dose maps. In a 10-fold cross-validation, the RMSE of the dose predicted by the DL network was about 2.4% of the prescription dose, which showed a significant improvement from the initialization fit.

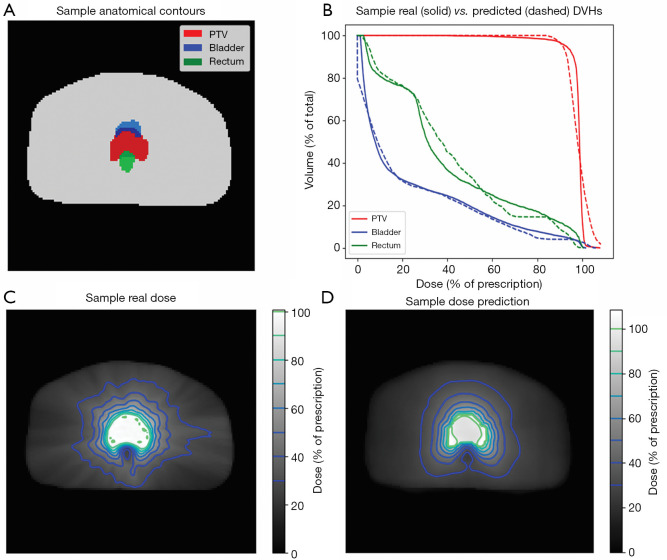
Figure 8 shows structure contours and dose prediction results of a test patient. Patient anatomy was shown in Figure 8A as uniform structure contours. Figure 8C and D show the ground truth and predicted dose distribution in axial view, respectively. The predicted dose distribution is smoother than the ground truth, but they share similar overall dose fall-off patterns outside PTV. As a result, the DVHs of PTV (red), bladder (blue), and rectum (green) between the ground truth and model predictions are in high agreement (Figure 8B).

Figure 8.

Dose prediction input and results of a test patient. (A) Structure contours; (B) DVH comparison between ground truth dose distribution and predicted dose distribution; (C) ground truth dose distribution; (D) predicted dose distribution. DVH, dose-volume histogram.

Fluence map prediction models

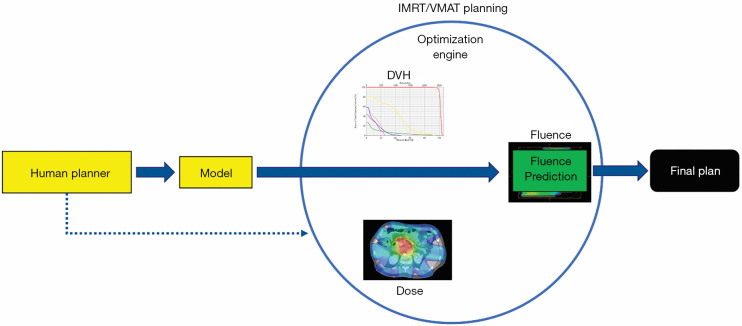
Both DVH prediction models and dose prediction models generate the best achievable dose constraints that guide an inverse optimization engine to produce final plans. A recent research direction in automatic treatment planning is to directly predict actual plan parameters (e.g., fluence maps or MLC segments) that can be converted into final treatment plans without invoking the iterative inverse planning algorithms (64-68). Figure 9 illustrates that the iterative inverse optimization process was replaced by a direct prediction approach achieved by the AI model. Therefore, it is expected that using these AI models, the planning efficiency will be further improved.

Figure 9.

IMRT/VMAT planning workflow of fluence map prediction based planning. IMRT, intensity modulated radiation therapy; VMAT, volumetric modulated arc therapy; DVH, dose-volume histogram.

Example breast fluence model using random forest

For whole breast radiation therapy (WBRT), Sheng et al. (68) developed an automatic TPS, which consists of energy selection, fluence estimation, and fluence fine-tuning. A binary decision model was created to select between single (6 MV) or mixed (6/15 MV) energy based on the beam’s digitally reconstructed radiographs (DRR). PCA was performed to reduce the dimension of the gray level histogram of the DRRs. Fluence maps were then predicted pixel-wise by a random forest (RF) model with shape-based features as inputs. The final fluence fine-tuning included a centrality correction step to adjust fluence intensities and provide patient-specific coverage or dose reduction. A separate program developed by Wang et al. (64) provided an automated solution for WBRT beam setting. This program used patient Computed Tomography (CT) images and contours as inputs to generate optimal beam settings (gantry angles, isocenter, field size, etc.) for WBRT. An initial beam was placed to fit the breast wires in the CT images. An optimization of gantry angles and isocenter was performed to minimize the objective function, which aimed to improve PTV coverage and reduce lung dose. A coefficient, which determined the relative importance of PTV and lung, was learned from existing clinical plans and used in the objective function. A complete treatment planning workflow for WBRT, from beam setting to fluence prediction, was established by using both the auto beam setting tool and the auto planning tool in conjunction.

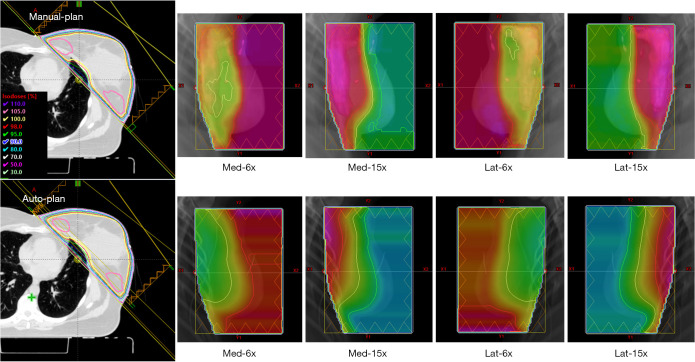
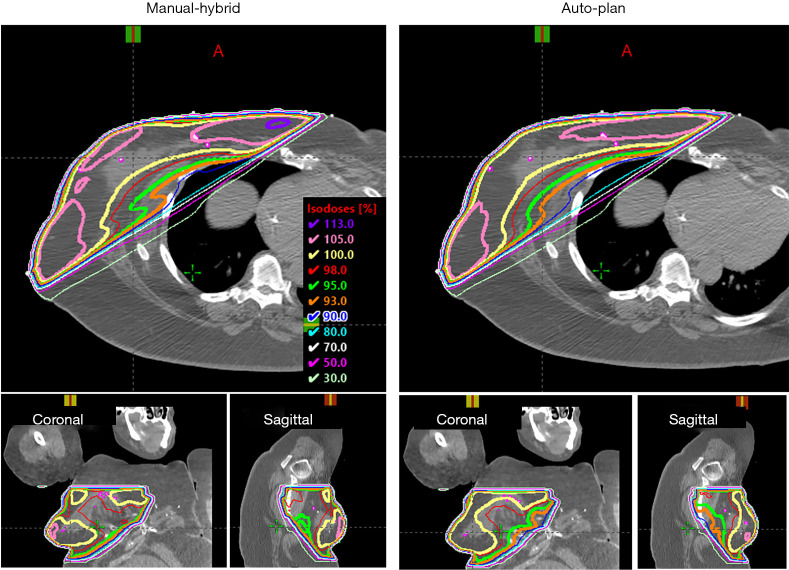
Figure 10 shows an example of a standard breast case. In the clinical plan, the planner decided mixed high and low energy beam configurations to meet the need of different regions with different lengths. Similarly, the AI plan also predicted mixed energy as the optimal solution. Overall, the fluence maps of the two plans are similar. However, the AI plan’s fluence maps contain more detailed intensity variations, while the human planer’s fluence painting has a more uniform intensity in blocks of areas. Figure 11 shows another example patient with large separation. As can be seen, the auto plan has better overall homogeneity (less 105% and 110% volume) as compared to the manual plan that used the hybrid technique. This type of challenging hybrid plan would take hours of manual effort while the AI plan is generated in minutes. Overall, the manual planning for breast cases took 110.2 minutes on average, and the AI plan took 6.4 minutes (69). Clinical target volume (CTV) mean V95% was 96.7% for the manual planning and 96.7% for the AI-based planning (P=0.89, two-tailed Wilcoxon Signed-Rank test).

Figure 10.

Dose distribution and fluence map comparison between manual plan and auto-plan.

Figure 11.

Dose distribution comparison between manual plan and auto plan.

This breast fluence map prediction model has been implemented in our institution for clinical treatment. For the first 30 patients, both manual and AI plans were generated. All plans passed physician review and met clinical quality criteria. The manual planning time varies significantly ranging from 25 to 270 minutes, while the AI planning time remains highly consistent (6–8 min) with the majority of time consumed by importing-exporting plan data between TPS and AI module. The planning time comparison of two plans is shown in Figure 12. To date, our clinic has treated about 800 cases using this AI-driven auto-planning technology.

Figure 12.

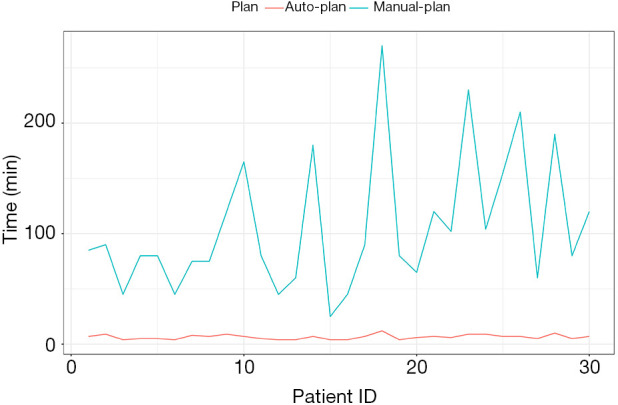
Planning time comparison between auto-plan (red) and manual plan (blue).

Example prostate fluence model using Dense-Res hybrid network

In the study by Li et al. (65), a DL-based fluence prediction based AI planning for prostate IMRT was designed. The DL network, Dense-Res Hybrid Network (DRHN), contains 3 DenseNet blocks, 3 ResNet blocks, and 4 convolutional layers. All layers in the DenseNet blocks were concatenated to the following DenseNet blocks. A ResNet block contains 2 convolutional layers, which were summed before sent to the following layers. All convolutional layers have a filter size of 3 by 3 by 3 and were followed by an exponential unit activation.

The patient anatomy information was compressed into two types of 2D projections, intra-structure projections and interface projections. Intra-structure projections contain attenuation information within a specific structure and were projected along a specific beam angle. Interface projections also contain attenuation information in front of the structure along the beam entrance. The intra-structure projections of PTV70Gy, PTV58.8Gy, and seminal vesicle, and the interface projections of PTV70Gy, PTV58.8Gy, seminal vesicle, bladder, and rectum were generated for each patient. These 8 projections relative to each of 9 template beam angles were stacked as a single 4D input for DRHN. The 4 dimensions are fluence map rows, fluence map columns, different beams, and different projections.

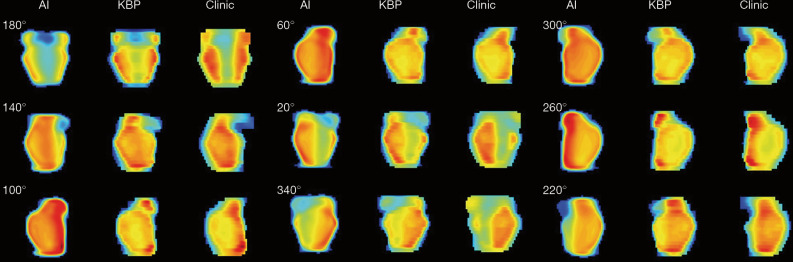
The ground truth in this study are the fluence maps of the KBP IMRT plans generated using an Eclipse Scripting Application Programing Interface (ESAPI) script. All KBP plans used 9 IMRT beams. The KBP model was pretrained on a reserved patient cohort (43 cases) and was used to predict DVH objectives for the training cases. The ESAPI script applied these optimization objectives based on KBP predictions and then iteratively and automatically adjusted these objectives. Using these KBP plans as ground truth could avoid the inter-patient variation on treatment modality, delivery machine, and beam configuration. During the training process, DRHN’s output was compared with ground truth using a soft band pass filter in the Fourier space to improve learning accuracy in middle frequency. The filter was designed based on clinical experience. Figure 13 shows the fluence map comparison between the predicted AI, clinical plan, and KBP plan of a test case.

Figure 13.

Comparison of AI, KBP, and clinic plan fluence maps in all 9 template beam angles of a test patient. AI, artificial intelligence; KBP, knowledge-based planning.

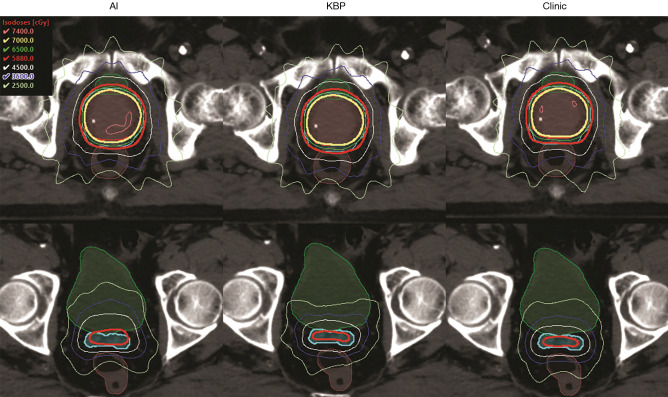
In the final planning step, these predicted fluence maps were directly converted into a treatment plan after leaf sequencing and dose calculation in the TPS. The predicted fluence maps were converted into AI plans in TPS using the same leaf sequencing and dose calculation algorithm as those used for the training plans. All AI plans were normalized to the same target coverage as the clinic plans and KBP plans. Figure 14 shows the dose distribution comparison of the AI plan, KBP plan, and clinical plan of the same test patient as in Figure 13. This AI plan achieved comparable dose distribution. Both primary target (cyan) and boost target (red) have sufficient and comparable dose coverage from the 58.8 Gy isodose lines (red) and the 70 Gy isodose lines (yellow), respectively. The 35 Gy isodose lines (pink) and 25 Gy isodose lines (lime) show rectum sparing in all plans. The maximum dose in the AI plans is higher than those in the KBP plans and clinical plans, but the values are acceptable according to clinical criteria. Overall, the study found that rectum and bladder dose sparing in the AI plans was statistically comparable to or had no clinically related difference with those in the clinic plans and KBP plans.

Figure 14.

Dose distribution comparison of AI, KBP, and clinic plan of a test patient. Red segment: PTV70Gy. Cyan segment: PTV58.8Gy. Green segment: bladder. Orange segment: rectum. AI, artificial intelligence; KBP, knowledge-based planning.

Example pancreas SBRT fluence model using CNN

In the study by Wang et al. (67), a DL framework was designed to predict fluence maps for pancreas stereotactic body radiation therapy (SBRT), as illustrated in Figure 15. A total of 100 pancreatic cancer cases were included in the study, with 85 for training and 15 for testing. As a feasibility study, all cases had 9-beam IMRT plans using the same dosimetric objectives as benchmark plans (ground truth).

Figure 15.

The workflow of the pancreas fluence prediction study. FD-CNN, field-dose convolutional neural network; BEV, beam’s eye view; FM-CNN, fluence-map convolutional neural network; TPS, treatment planning system.

The framework consists of two CNNs, which predict beam dose and fluence maps separately. The first network, the field dose (FD) CNN, which has a customized encoder-decoder structure, uses the contours of PTV and OAR as inputs and predicts 9 individual beam doses simultaneously. The network architecture includes a downsampling block, an upsampling block, and a convolutional block. The loss function is the weighted sum of the field dose mean square error and the total dose mean square error. All PTV axial slices plus a margin of 1 cm are fed into the network for field dose prediction. For each beam, the predicted dose is concatenated into a 3D volume, projected along the beam’s eye view (BEV), and used as the input for the second network, the fluence map (FM) CNN, which predicts the final fluence map. The FM-CNN adopts a customized U-Net architecture with 3 resolution levels. The loss function is a modified mean absolute error of the fluence map. The field doses and fluence maps of the benchmark plans in the training set are used to train the two networks separately. The predicted fluence maps are converted to deliverable MLC control points by the Eclipse leaf sequencing algorithm.

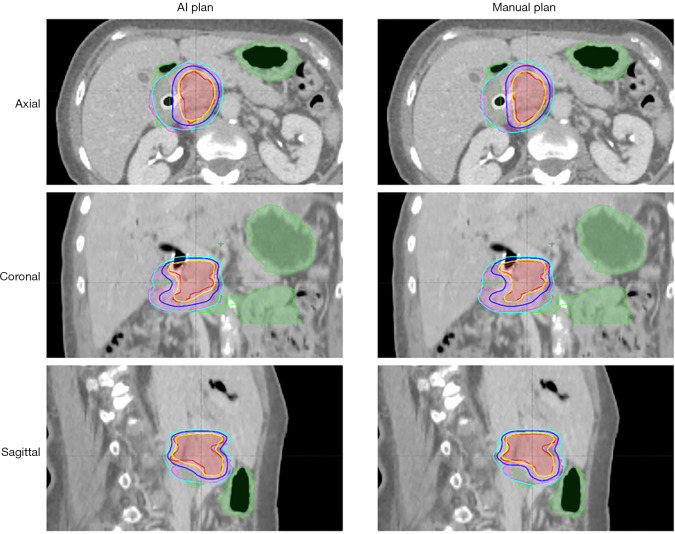
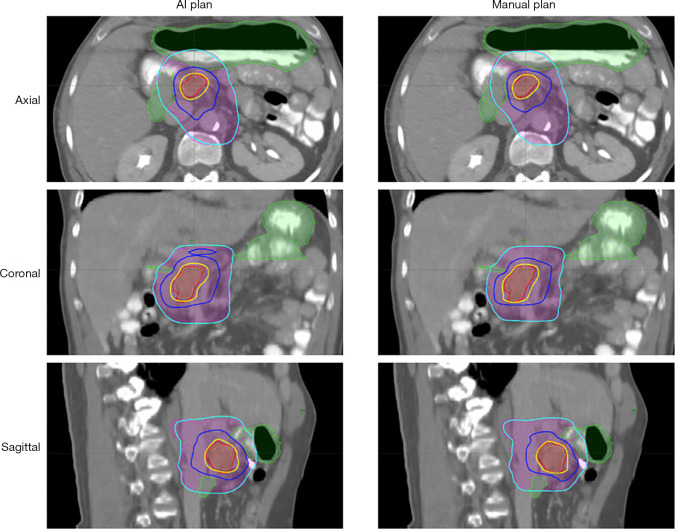
Compared to manual inverse planning, the main advantage of this workflow is fast plan generation. The average prediction time for one patient was 7.1 seconds, including 5.97 seconds for BEV dose projection. In the dosimetric evaluation, the model-predicted plans achieved similar PTV and OAR mean dose as the benchmark plans, while the maximum dose was higher for both structures. The averaged voxel dose difference was 2.41% (of prescription dose) for the PTV and 2.70% for the OAR. Two pancreas SIB-SBRT cases are shown in Figures 16,17. The GTV (red) was prescribed to 33 Gy (yellow isodose line), and the PTV (purple) was prescribed to 25 Gy (cyan isodose line). The GI-OAR (green) was limited to a maximum dose of 29 Gy (blue isodose line). The two cases differ in the relative size of PTV and GTV, as well as the shapes of the structures. The AI plans achieved similar dose distribution as the manual plan in both cases. The AI plan’s dose for some sharp edges of the GTV Figure 16 was not as conformal as the manual plan. In Figure 17, the 29 Gy isodose volume was larger in the AI plan, but the OAR constraint was still satisfied. Although some limitations exist for this preliminary study, such as unified beam geometry and dose constraints, it demonstrates one viable pathway for fluence map prediction in IMRT planning.

Figure 16.

Isodose line comparison between an AI plan and the corresponding manual plan for a simultaneous integrated boost pancreas case. AI, artificial intelligence.

Figure 17.

Isodose line comparison between an AI plan and the corresponding manual plan for a simultaneous integrated boost pancreas case. AI, artificial intelligence.

Planning strategy models

While DVH, dose, and fluence map prediction models are expected to improve the quality, consistency, and efficiency of IMRT/VMAT planning for most patient cases, it is inevitable that some complex and out-of-sample cases will require multiple iterations of inverse optimization to achieve optimal clinical planning goals. To plan for these cases, the setting of planning objectives for the TPS is highly dependent on the shape, size, and location of the PTVs and requires complex strategies for adjustments between iterations. One such example is the pancreas SBRT. For these cases, the planner often needs to interact with the TPS multiple times and perform various actions, including adjusting dose-volume constraints and creating necessary auxiliary structures in order to get desirable dose distributions.

We can capture the complex planning strategies into a planning strategy model and automate the iterative planning process using a reinforcement learning (RL) framework (70). Figure 18 shows the overall workflow of AI planning using RL. The optimization engine is replaced by the proposed planning strategy model executing the optimum strategy (green arrow) and is supervised by the human planner (blue dotted arrow) to generate the final plan.

Figure 18.

IMRT/VMAT planning workflow of AI robot using reinforcement learning. IMRT, intensity modulated radiation therapy; VMAT, volumetric modulated arc therapy; AI, artificial intelligence.

Example design of a RL framework for treatment planning

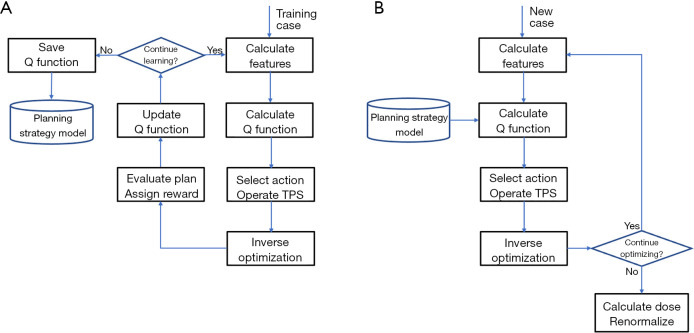
In the study by Zhang et al. (70), the RL training and validation workflow, as shown in Figure 19, has been implemented in a research TPS environment (Eclipse™ Treatment Planning System Version 13.7, Varian Medical Systems, CA). In this RL framework, Zhang et al. defined the concepts of state, action, and reward in the context of IMRT treatment planning. Here, states and rewards are related to plan and plan quality. Actions are modeled after human planners and can be categorized into a few types, including adding dose-volume constraints to existing structures and assigning constraints to new auxiliary structures based on intermediate dose distribution. For human planners, the underlying strategies of applying proper actions to reach better states, i.e., better treatment plans, are acquired through years of planning experience. This learning process can vary significantly because there is no ground truth in terms of optimal decisions or actions. RL is well-suited for solving this type of problems. A RL AI agent can learn to make decisions to optimize expected plan quality by repetitively interacting with the TPS and evaluating plan dose distributions. A widely used RL framework called the state-action-reward-state-action (SARSA) (71) is based on the following learning formula:

Figure 19.

The workflow of the proposed RL planning framework: (A) training phase (B) validation/application phase. RL, reinforcement learning.

$$Q\left(s,a\right)\leftarrow Q\left(s,a\right)+\alpha \cdot \left[r\left(s,a,s^{\prime }\right)+\gamma \cdot Q\left(s^{\prime },a^{\prime }\right)-Q\left(s,a\right)\right]$$ [2]

where s and a denote the current state and action; s' and a' denote the next state and action; Q denotes the action-value function, which reflects the overall quality of an action; r denotes the immediate reward; α denotes the learning rate of the agent; and γ denotes the discount factor of the system. In particular, the action-value function Q predicts the expected long-term reward. The goal of the iteration during the training phase is to estimate the Q function, which is the core of the RL model that, when it is fully learned, can be subsequently used to guide future planning. The action-value function can be formulated as a linear function approximation of the form:

$$Q_{\theta }\left(s,a\right)={\theta }^T\phi \left(s,a\right)$$ [3]

where Q_θ(s,a) represents the expected value at state s when action a is taken, θ^T denotes the feature weighting vector that will be learned through the training process, and φ(s,a) is a feature vector carefully engineered to reduce the complexity of the RL problem without losing generalization. On choice of the feature φ(s,a) is the outer product of a state vector f(s) and an action vector g(a): φ(s,a)=vec[f(s)⨂g(a)]. Here ⨂ denotes the outer product operator, which multiplies each element of the row vector f(s) with each element of the column vector g(a). The state vector f(s) is formulated as $f\left(s\right)=\left[△D_1,△D_2,\dots ,△D_N\right]$, where $△D_n={\overline{D}}_n-D_n,n\in \left[1,2,3,\dots ,N\right]$ denotes the differences between the predicted/estimated dose constraints and the actual dose values at the current iteration, and N denotes the total number of involved dose constraints. The action vector g(a)=[1(a=A₁),1(a=A₂),…,1(a=AM)]^T is an array of M indicators that represent indices of M actions. The M action options are designed based on the actions commonly taken by human planners during pancreas SBRT treatment planning. In this study, the actions include adding constraints to liver, kidney, cord, and auxiliary structures associated with stomach, duodenum, bowel, primary PTV, and boost PTV. The agent takes one action per interaction and is allowed to take repeated actions. The reward r is assigned as the plan quality score improvement after each step: r=S'−S, where S and S' denote the plan quality score before and after taking the current action, respectively. The plan score metric S is set as a weighted combination of various clinical plan quality metrics:

$$S=-{\displaystyle \sum _i{W}_i}\max \left(K_i-\overline{K_i},0\right)-{\displaystyle \sum _j{W}_j}\max {\left(H_j-\overline{H_j},0\right)}^2$$ [4]

where $\overline{K_i}$, $\overline{H_j}$ denote prescribed soft and hard constraints and K_i, H_j denote achieved soft and hard constraint values. In this study, hard constraints refer to the constraints assigned to bowel, duodenum, stomach, and cord. Soft constraints are the constraints for liver and kidney.

To evaluate the performance of the proposed planning strategy model, 40 anonymized pancreas SBRT cases were retrieved. Sixteen randomly selected cases were used for RL training while the remaining 24 cases were used for validation, which compares the plans generated by the planning agent (agent plans) with the corresponding clinical plans.

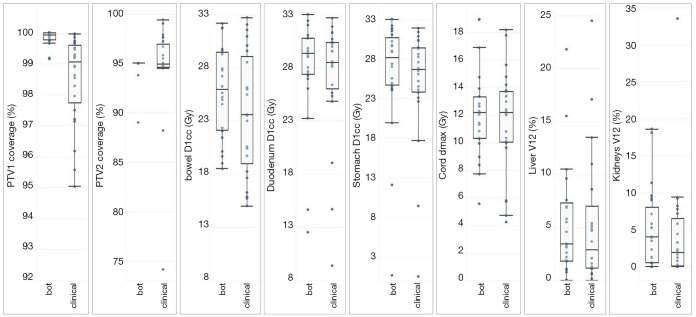
Figure 20 shows the planning results for cases in the validation set. All 24 clinical plans and agent plans meet pre-defined GI constraints (V_33Gy <1 cc) and have sufficient PTV coverages. At a more detailed level, many dose metrics are comparable: PTV_33Gy coverage (clinical: 94.6%±4.8%, agent: 94.7%±1.2%; P=0.924), duodenum D_1cc (clinical: 27.2±5.4 Gy, agent: 27.9±4.8 Gy, P=0.174), kidney V_12Gy (clinical: 4.2±6.9 Gy, agent: 5.1±5.2 Gy, P=0.303), and cord D_max (clinical: 11.7±3.6 Gy, agent: 12.1±3.1 Gy, P=0.425). The agent plans have higher PTV_25Gy coverage (clinical: 99.8%±0.2%, agent: 98.5%±1.4%, P<0.001), while the clinical plans have lower bowel D_1cc (clinical: 23.7±5.6 Gy, agent: 25.7±4.2 Gy, P<0.001), stomach D_1cc (clinical: 25.1±7.0 Gy, agent: 26.3±7.0 Gy, P=0.007), and liver V_12Gy (clinical: 5.2±6.0 Gy, agent: 6.1±6.8 Gy, P=0.007). The mean MU value is also higher in the agent plans (clinical: 1,742±271 MU, agent: 1,995±351 MU; P=0.002).

Figure 20.

Dosimetric comparison between RL agent plans and clinical plans. The boxes represent quartiles, and the whiskers mark the datapoints within the 1.5 IQR from the median values. The clinical constraints for bowel D1cc, duodenum D1cc, stomach D1cc are 33 Gy. Cord Dmax is limited below 20 Gy, and kidney V12Gy is limited below 25–50%. All clinical plans and RL agent plans meet these clinical constraints. Reprinted from An interpretable planning bot for pancreas stereotactic body radiation therapy. Int J Radiat Oncol Biol Phys, 109(4):1076-1085, with permission from Elsevier. RL, reinforcement learning; IQR, interquartile ranges.

These results demonstrate the feasibility of the proposed intelligent planning agent to automatically acquire planning strategies using a RL framework. We expect that furthermore improvement in plan quality can be achieved by refining the RL model, extending training time and training samples, as well as improving the learning algorithms.

Summary

As we can see from the previous examples, each critical step of the IMRT/VMAT treatment planning process can be improved and automated by AI methods. Other research groups have also proposed many variations of AI methods in recent years. They all target one of the steps in Figure 1 and especially focus on the first two boxes, i.e., DVH and dose predictions (67). As more training data becomes more available and more sophisticated models are developed, we can expect that the AI methods in treatment planning will continue to improve accuracy, efficiency, and robustness.

With so many models targeting various steps of the planning process, one may naturally wonder whether a single best model will eventually emerge as the ultimate AI method for the entire process or multiple models will need to work together to address different challenges in the planning process. We conjecture that the future of AI applications in radiation treatment planning will follow the latter scenario due to the complexity of patient anatomy, cancer types, and clinical tradeoff requirements. We can envision a comprehensive AI planning agent that uses a fluence map prediction model to quickly generate clinically viable treatment plans for most straightforward patient cases, while for some more complex cases, it applies a DVH prediction model to determine the tradeoff of some dose-volume constraints and a dose prediction model to adjust the tradeoff between a max dose constraint and PTV coverage. Furthermore, when the agent detects an out-of-sample case that no existing models are suitable, it deploys the planning strategy model to guide the optimization engine to generate a clinically optimal plan iteratively.

We should emphasize again that AI does not simply mean ML and predictive model development. AI could be customized to assist human planner under various specific clinical scenarios and function as carriers of clinical knowledge and experience. We are still in the early phase of developing AI applications for radiation treatment planning. In addition to further advancing the performance of AI models described in this paper, we must also examine other aspects of AI models and methods that ultimately make up an intelligent planning agent. For example, we should investigate the uncertainty and bias of model predictions and the interpretability and trustworthiness of prediction models. And perhaps more importantly, we should ensure that human operators continue to play an essential and central role in all AI applications in treatment planning that will ultimately affect patient health and lives.

Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The study was approved by DUHS Institutional Review Board (Protocol ID: Pro00046706).

Open Access Statement: This is an Open Access article distributed in accordance with the Creative Commons Attribution-NonCommercial-NoDerivs 4.0 International License (CC BY-NC-ND 4.0), which permits the non-commercial replication and distribution of the article with the strict proviso that no changes or edits are made and the original work is properly cited (including links to both the formal publication through the relevant DOI and the license). See: https://creativecommons.org/licenses/by-nc-nd/4.0/.