Computational Prediction of ω-Transaminase Specificity by a Combination of Docking and Molecular Dynamics Simulations

Abstract

ω-Transaminases (ω-TAs) catalyze the conversion of ketones to chiral amines, often with high enantioselectivity and specificity, which makes them attractive for industrial production of chiral amines. Tailoring ω-TAs to accept non-natural substrates is necessary because of their limited substrate range. We present a computational protocol for predicting the enantioselectivity and catalytic selectivity of an ω-TA from Vibrio fluvialis with different substrates and benchmark it against 62 compounds gathered from the literature. Rosetta-generated complexes containing an external aldimine intermediate of the transamination reaction are used as starting conformations for multiple short independent molecular dynamics (MD) simulations. The combination of molecular docking and MD simulations ensures sufficient and accurate sampling of the relevant conformational space. Based on the frequency of near-attack conformations observed during the MD trajectories, enantioselectivities can be quantitatively predicted. The predicted enantioselectivities are in agreement with a benchmark dataset of experimentally determined ee% values. The substrate-range predictions can be based on the docking score of the external aldimine intermediate. The low computational cost required to run the presented framework makes it feasible for use in enzyme design to screen thousands of enzyme variants.

Introduction

ω-Transaminases (ω-TAs) are pyridoxal-5′-phosphate-(PLP)-dependent enzymes that catalyze the reversible transfer of an amino group from an amino donor to a keto acceptor, yielding a keto product and a chiral amine in the process.¹ The high enantioselectivity of most ω-TAs makes them attractive catalysts in the industrial production of chiral amines.^2,3 Classical chemical synthesis methods usually involve the use of expensive catalysts and hazardous conditions. Using ω-TAs for the production of chiral amines can be advantageous because ω-TAs offer high enantioselectivity, do not require external cofactors, allow high reactant concentrations, and give good product yields under mild reaction conditions.⁴ However, the selectivity of ω-TAs needs to be tailored to the substrate of interest for industrial application.

The range of substrates that can be accepted by ω-TAs of the class III transaminases (fold-type I PLP enzymes) is mainly limited by the size of the small binding pocket, which rarely accommodates side chains larger than a methyl group. These ω-TAs also have a large binding pocket that can easily accept more bulky substituents such as an aryl or alkyl group.⁵ The size duality of the small and large binding pockets is what confers ω-TAs their high enantioselectivity. Both binding pockets are hydrophobic, and both can be targeted to expand the substrate range of the enzymes.^6,7 Tailoring the reactivity of ω-TAs to accept non-natural substrates is usually achieved via repetitive rounds of mutagenesis and testing. In general, rational design and in silico approaches can be very effective for enzyme selectivity engineering but require case-specific fine-tuning to produce reliable results.⁸ Therefore, we aimed to develop a computational framework that can be used in enzyme design for assessing the substrate scope and enantioselectivity of ω-TA variants. The accuracy of the presented framework for the prediction of enantioselectivity and substrate scope was evaluated on a benchmark dataset of 62 compounds gathered from the literature.

The (S)-selective ω-TA from Vibrio fluvialis (Vf-TA) was chosen as the model system for the benchmarking of the presented framework because it is a well-characterized enzyme. Vf-TA was first described in 1999 by Shin and Kim,⁹ and a high-resolution crystal structure was reported in 2013.¹⁰Vf-TA has enzymatic activity toward both aliphatic and aromatic substrates,⁵ generally producing highly enantiopure amines from ketones. Vf-TA tolerates mutations in both the small and large binding pockets. Tailoring Vf-TA to accept non-natural substrates via computational methods has previously been attempted with varying degrees of success.^11,12 A common feature of these studies is their qualitative nature and the small range (less than 5) of screened substrates.^11,13

Previous computational approaches aimed at understanding or engineering the reactivity of ω-TAs have examined the keto substrate,¹¹⁻¹⁴ amino substrate,¹⁵ quinonoid intermediate,^12,16 ketimine intermediate,¹⁷ or external aldimine intermediate¹⁷ as the ligand. The external aldimine intermediate was chosen for the current study because it is the first chiral intermediate in the second half reaction and is involved in the rate-limiting transamination step. Protonation of the quinonoid intermediate by the catalytic lysine leads to the formation of the external aldimine, which is subsequently cleaved to form the resting enzyme and the amine product. Cassimjee et al.¹ estimated the energy profiles of a half-transamination reaction catalyzed by an ω-TA from Chromobacterium violaceum (Cv-TA) going from (S)-1-phenylethylamine to acetophenone using density functional theory calculations of all the involved intermediates and transition states. The energy profile showed that the external aldimine intermediate is fenced by two large energy barriers corresponding to transition states in the forward or backward reaction direction, to form the quinonoid or the geminal diamine intermediates, respectively. Hence, we hypothesized that the enantiomer better accommodated by the enzyme in the external aldimine form would display a higher overall turnover rate.

To test the hypothesis that modeling the external aldimine intermediate is enough to predict the enantioselectivity (and substrate scope) of Vf-TA, we compared the results of the presented molecular modeling protocol against experimentally measured values for the asymmetric synthesis reactions (ketone → amine). The approach makes three assumptions: (1) the energy profile for the half-transamination reaction is the same in Vf-TA as in Cv-TA; (2) the formation of all other reaction intermediates is not rate-limiting for the tested compounds; and (3) the forward and backward half-transamination reactions behave similarly. The first assumption is based on the fact that both Vf-TA and Cv-TA are (S)-selective ω-TAs belonging to the PLP fold-type I superfamily class III in which active site groups and the catalytic mechanism are conserved.¹⁸ The second assumption requires that the relative energy profile for the half-transamination reaction described for (S)-1-phenylethylamine to acetophenone¹ be maintained regardless of the substituents attached to the reacting C_α. The third assumption is based on the fact that the transamination reaction is reversible at every step of the catalytic cycle, and therefore, the principle of microscopic reversibility or detailed balance applies.¹⁹ An additional advantage of modeling the external aldimine intermediate is the reduced computational cost. Because the C_α is covalently bound via a Schiff base to the PLP cofactor, the search space in the docking stage is substantially reduced, thereby eliminating the need for initial placement algorithms.²⁰

The results demonstrate the potential of using a combination of docking and molecular dynamics (MD) simulations for computational screening of different transaminase substrates. The developed protocol can give quantitative predictions of ω-TA selectivity and enantioselectivity at a low computational cost, which can be employed in enzyme engineering efforts aimed at tailoring catalytic activity.

Methods

Collection of the Benchmark Dataset

A list of 62 compounds was gathered from existing literature to test the accuracy of the presented computational protocol (Figure 1). The gathered dataset contains experimentally determined values for enantiomeric excess (ee%) of amines (compounds 01−49) obtained in asymmetric synthesis catalyzed by Vf-TA. The ee% values obtained from kinetic resolution of racemic amines were not included in the dataset because of the dependance of observed ee% values on reaction progress. Additionally, data of compounds 50–62 were gathered for the substrate scope prediction task. The range of molecules explored is large, with the majority of the diversity coming from the substituent that binds to the large binding pocket. By contrast, the substituent that binds to the small binding pocket is a methyl or a short-chain alkyl group, with a few exceptions (e.g., compounds 28, 32, 33, 35, and 36).

Figure 1.

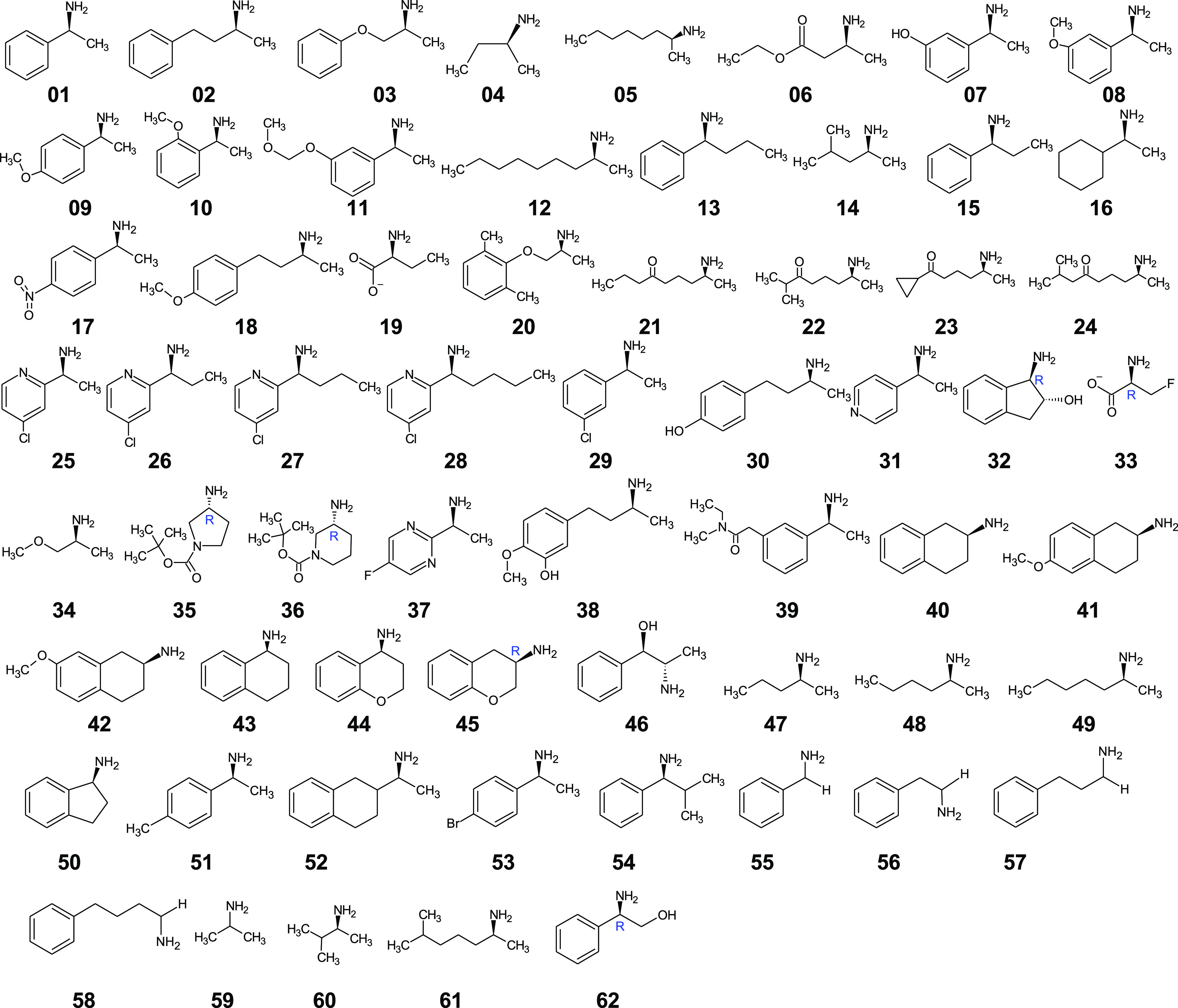
Compound dataset used in this study as benchmark to test the reliability of the developed protocol. The dataset was gathered from the existing literature, and sources are cited in Table 1. The enantiomeric excess for the asymmetric synthesis reactions used to obtain amines 01–49 from their respective ketones has been reported. Compounds 50–62 were only used for substrate-scope predictions because they are nonchiral or the experimental ee% for asymmetric synthesis was not found in the literature. All structures represent the preferred enantiomer of Vf-TA and are drawn with the bulkiest substituent to the left, i.e., in the position corresponding to the phenyl group of the (S)-enantiomer of 01. Following CIP rules, all compounds are (S)-amines, except 32, 33, 35, 36, 45, and 62 which formally are (R)-enantiomers.

Preparation of Ligand Structures

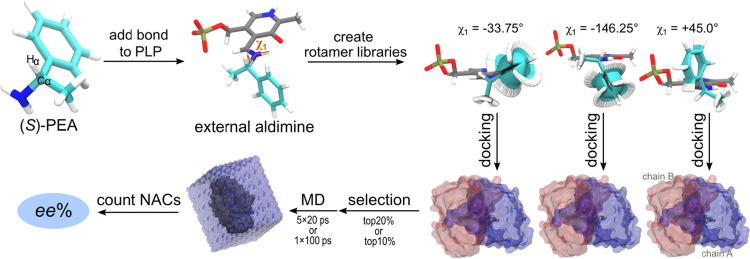
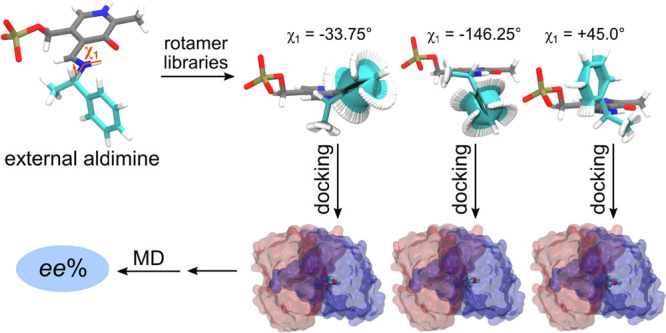
Initial atom coordinates for the (S)- and (R)-amine dataset (Figure 1) were created using Avogadro software²¹ and optimized with 500 steps of steepest descent minimization in the MMFF94 force-field.²² The subsequent steps were made in YASARA (www.yasara.org).²³ Each amino compound was covalently bonded to the pyridoxal cofactor via a Schiff base to form the corresponding external aldimine complex, hereafter referred to simply as the ligand. The geometry of the ligand was then optimized in AM1 with implicit solvent.²⁴ Atomic charges were assigned for the ligand using the restrained electrostatic potential approach included in the Gaussian09 software package.²⁵ A library of relevant low-energy rotamers was generated for each compound by random perturbation of all torsion angles that contained at least one heavy atom (SampleDih YASARA routine), with the exception of ligand atoms originally belonging to the PMP cofactor. The latter were kept frozen during the rotamer generation stage. A total of 32 independent libraries were created for each ligand, with each library containing rotamers where the χ₁ dihedral was set to a fixed value (χ₁ = {−180°, −168.75°, −157.50°, ..., +180°}) (Figure 2). The χ₁ dihedral indicates the orientation of the C_α–H_α bond with respect to the PLP ring, and the precise definition is shown in Figure 3A. The initial size of each of the 32 libraries was 1000 rotamers, but after pruning for uniqueness (pair-wise RMSD between any two rotamers >0.005 Å) the size of each library ended in between 100 and 800 unique rotamers. In other words, the entire dataset contained 49 unique chemical compounds, each compound had two external aldimine forms (one for the (S)- and one for the (R)-enantiomer), each of them had 32 unique rotamer libraries, and each of those libraries contained 100–800 unique rotamers.

Figure 2.

General overview of the presented framework for the enantioselectivity prediction of ω-TAs. The χ₁ dihedral was set to fixed values, χ₁ = {−180°, −168.75°, −157.50°, ..., +180°}, adding up to 32 independent rotamer libraries per examined ligand.

Figure 3.

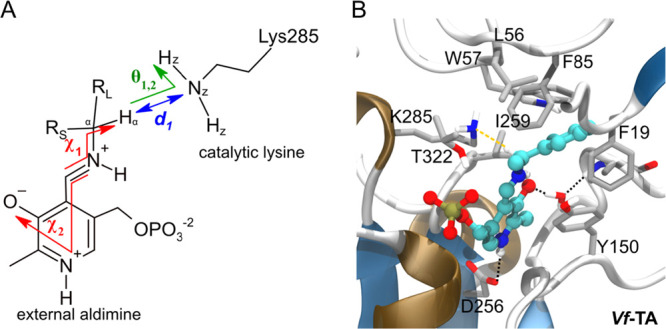
(A) An enzyme–ligand complex was considered to be in a NAC when the following criteria were simultaneously met: d₁ < 2.65 Å, −75 < χ₁ < −105°, −15 < χ₂ < +15°, 90 < θ₁ < 130°, and 90 < θ₂ < 130°. Distances are colored in blue, angles in green, and dihedrals in red. θ₁ and θ₂ are the angles between the abstracting hydrogen H_α, the N_Z atom of Lys285, and either of the two H_Z atoms. R_L = large substituent and R_S = small substituent. (B) Structure of a NAC obtained from a simulation frame of the external aldimine of compound 01S.

Preparation of the Enzyme Scaffold Structure

The crystal structure of an (S)-selective ω-TA from Vibrio fluvialis (PDB: 4E3Q) was used as scaffold.¹⁰ Molecular modeling was performed using the dimer derived from subunits A and B. The dimer contains two PMP cofactors located in the subunit interface approximately 15 Å apart, forming two binding sites. Se-Met residues were converted into Met by the YASARA CleanObj routine. The protonation states of Asp, Glu, His, and Lys were predicted by a YASARA automated routine (OptHyd).²⁶ All Asp, Glu, and Lys were in their standard protonation states at neutral pH, and histidine residues were in the HIP (charge +1, both δ- and ε-nitrogens protonated; His at 26 and 178), HID (neutral, δ-nitrogen protonated; His at 35, 151, and 362), and HIE (neutral, ε-nitrogen protonated, His at 65, 83, 132, 183, 319, and 326) forms. All water molecules were removed from the crystal structure for the docking stage but were later added back in for the MD simulations.

Rosetta Docking of the External Aldimines

Docking of the external aldimine intermediates (ligand) into the active site of Vf-TA was performed with the Rosetta Enzyme Design application (build number 57927).²⁷ The following steps were performed on the binding site that is mainly composed of subunit A residues. Ligands were initially placed in the binding site by superimposing the pyridine ring heavy atoms to the equivalent PMP atoms found in the crystal structure. The following command-line arguments were used when running Rosetta: −enzdes, −cst_predock, −cst_design, −cut1 0.0, −cut2 0.0, −cut3 8.0, −cut4 10.0, −cst_min, −chi_min, −bb_min, −packing::use_input_sc, −packing::soft_rep_design, −design_min_cycles 3, −ex1:level 4, −ex2:level 4, −ex1aro:level 4, −ex2aro:level 4.²⁷ For the enantioselectivity predictions, 10 docking structures were produced for each χ₁ dihedral, and from the resulting 320 structures (32 × 10), the top-scoring solutions, that is, the low energy conformations, were selected to serve as starting conformations for MD simulations. The selection was carried out on the basis of the Rosetta interface energy, adding up to a total of 64 (top20%) or 32 (top10%) starting structures for MD simulations. For substrate-range predictions, 200 Rosetta structures were generated for each enzyme–ligand complex (all with χ₁ = −90°).

MD Simulations of the Docked Structures

Short MD simulations were performed using the top-ranking docked complexes to estimate the enantiomeric excess. All simulations were carried out in YASARA, using the knowledge-based YAMBER3 force field²⁸ for protein residues and the GAFF force field²⁹ for ligands. As for the identity of the ligands, the binding site of subunit A contained the docked external aldimine form of the query compound, while the binding site of subunit B contained the crystallographic PMP cofactor. The protein–ligand complexes were placed in a cubic simulation cell extending at least 10 Å beyond the protein. Crystallographic water molecules, formerly removed in the docking stage, were added back to the enzyme. Any water molecule with its center of mass closer than 1.1 Å from any non-water heavy atom was deleted from the simulation box. Enough TIP3P water molecules were added to fill the simulation cell, along with Na⁺ and Cl^– ions to a final concentration of 0.150 M. The pK_a values for residues Asp, Glu, His, and Lys were predicted using the YASARA neutralization experiment routine³⁰ at pH 8, resulting in standard protonation states for Asp, Glu, and Lys, and the following protonation states for histidine: HID (35, 151, and 362) and HIE (26, 65, 83, 132, 178, 183, 319, and 326). The protonation states of histidine residues 26 and 178 differed from the protonation states obtained using the OptHyd YASARA routine. The cell charge was neutralized with Na⁺ ions. Next, 25 steps of steepest descent minimization were carried out to remove conformational stress followed by simulated annealing to find an energy-minimum conformation. Simulated annealing was performed by slowly cooling down the system for 100 steps from 298 to 0 K by rescaling atom velocities by a factor of 0.9 each step, after which 100 steps of classical MD are performed at 298 K. After obtaining an energy-minimized conformation, the system was gradually warmed up from 0 to 298 K in 3.0 ps. A short equilibration of 2.0 ps (timestep = 2.0 fs) preceded the production run of 20.0 or 100.0 ps. The simulations were performed using the leap-frog integration step method of YASARA,³¹ with a timestep of 2.5 fs. To gain performance, the nonbonded interactions were evaluated every second step. To enable such a large timestep for the intermolecular interactions, high-frequency bonds and angles (involving hydrogens) were replaced by constraints. LINCS was used to constrain all covalent bonds involving hydrogen atoms with a relative geometric tolerance of 10^–4.³² Pressure (1.0 bar) and temperature (298 K) were maintained with a modified Berendsen barostat and thermostat, respectively.^28,33 Long-range electrostatic interactions were treated with the particle mesh Ewald algorithm and short-range interactions with direct-space Coulombic interactions with a cutoff of 8.0 Å.³⁴ The production run was 20 ps in length with five seeds (5 × 20 ps setup) or 100 ps with one seed (1 × 100 ps setup), bringing the total simulation time to 6400 ps per examined ligand in either setup.

Calculation of ee% from MD Trajectories

The MD trajectories of each ligand were scored by counting the number of frames in which a near-attack-conformation (NAC) was observed (Figure 3). NACs were measured on-the-fly every 20 fs, adding up to 1000 datapoints for a 20 ps trajectory. For each compound (01–49 in Figure 1), the relative frequency of NACs produced by the docked complexes of the (S)- and (R)-enantiomer was used to calculate the expected ee% and compared against the experimentally determined value.

NAC Criteria

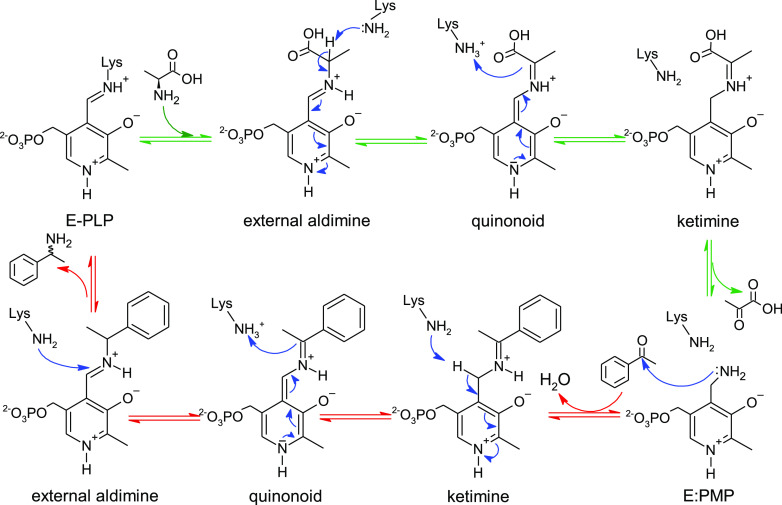
NACs were defined by a combination of geometric parameters important for the transamination reaction to take place, in particular the nucleophilic proton abstraction of the external aldimine intermediate to form the quinonoid intermediate (Scheme 1). In order for Lys285 to perform a nucleophilic attack on the external aldimine, the reacting atoms must be positioned at a short distance, where their van der Waals radii start overlapping (d₁). Furthermore, the cleavable bond H_α–C_α needs to be positioned perpendicular to the Schiff base (χ₁ ≈ −90°) to allow the nascent p orbital to align with the electrons of the PLP-conjugated π system (χ₂ ≈ 0°). Additionally, the free electrons of the attacking lysine nitrogen (:N_Z) need to be pointing directly toward H_α (θ₁, θ₂ > 90°). The complete set of geometric criteria for a frame to be considered a NAC is listed in Figure 3. The precise criteria have been found to have a large influence on the absolute NAC values but not on the relative ratios observed between different states that are compared.³⁵⁻⁴³

Scheme 1. Transamination Reaction Mechanism.

The fully reversible reaction consists of two half-transamination reactions.¹ In the first half reaction (green arrows), l-alanine is converted into pyruvate, resulting in the generation of the E/PMP intermediate (PMP is pyridoxamine-5′-phosphate). The second half (red arrows) consists of substrate entry and formation of the Michaelis complex with E:PMP. A nucleophilic attack on the carbonyl carbon of the substrate (acetophenone shown as an example) by the amino group of PMP leads to the formation of the ketimine intermediate. A further rearrangement involves the catalytic lysine (Lys285), acting first as a base and later as an acid, to form the quinonoid and external aldimine intermediates, respectively. Finally, Lys285 performs a nucleophilic attack on the iminium carbon of the external aldimine, resulting in the formation of amine (1-phenylethylamine) and an internal aldimine (E-PLP).

Results

General Approach

As outlined in Figure 2, the first step of the approach for predicting the activity of Vf-TA toward a query compound was to generate enzyme–ligand conformations by Rosetta docking. The ligand is the external aldimine intermediate of the query compound. The generated docked structures were ranked based on the Rosetta interface energy, and the top-scoring structures (top10% or top20%) were used as starting conformations for MD simulations. The MD trajectories (1 × 100 ps or 5 × 20 ps) were scored based on a set of geometric parameters. In particular, we looked at the occurrence of NACs during the trajectories. NACs are ground-state conformers that lie close to the transition path of a chemical reaction.⁴⁴

For prediction of stereoselectivity, an ee% value is obtained from MD simulations by combining the proportion of NACs found in the simulation for the (R)- and the (S)-enantiomer, using the following formula:

1

We thus use docking algorithms to reach the ground-state conformations of the external aldimine and MD simulations to sample the Boltzmann distribution of ground-state conformers and their propensity to adopt reactive poses. The proportion of ground-state conformers that are NACs gives an estimate of the free energy of NAC formation.⁴⁵ Comparing the free energy of NAC formation for the (R)- and (S)-enantiomer gives a direct estimate of the ee%. The use of NAC frequencies as indication of enzymatic selectivity has been adopted successfully in previous studies on a variety of enzymes.^36−42,46

For the substrate-range prediction, we found the Rosetta interface energy between the enzyme and the external aldimine form of the query compound to be in agreement with the experimental activities of the whole transamination reaction. Conversely, there was no apparent correlation between the percentage of NACs and the enzymatic activity (results not shown).

Enantioselectivity Predictions with the Benchmark Compounds

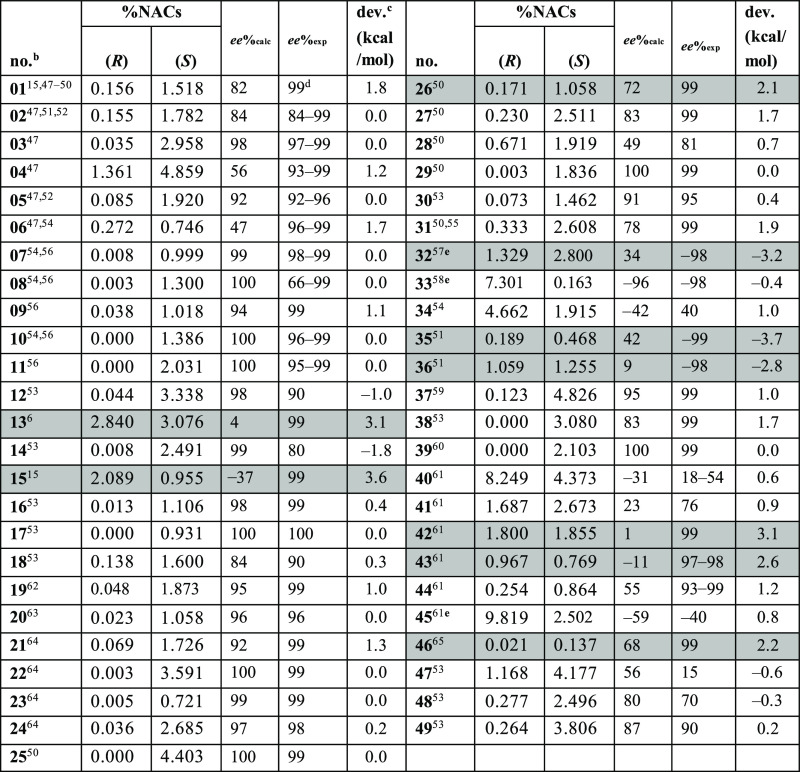
To estimate the ee% of compounds 01–49, the best Rosetta structures were selected to serve as starting conformations for short MD simulations, and the trajectories were scored by computing the NAC occurrence. The enantiomeric excess was calculated with eq 1, where the number of NACs produced by each enantiomer is thought of as being an indication of the ability of the enantiomer to adopt a conformation optimal for catalysis. The calculated ee% (ee%_calc) was then compared against the experimental ee% values (ee%_exp). In most cases, the ee%_calc matched the expected values (Table 1).

Table 1. Comparison between the ee%_calc and ee%_exp Enantioselectivities for the Benchmark^a Dataset^15,47−65.

^aThe ee% was calculated from the 5 × 20 ps setup using eq 1. The ee%_calc of most compounds closely matches the ee%_exp compounds with deviations indicating an error in energy calculations larger than 2 kcal/mol shaded in gray. The formulas to calculate deviations are provided in the Supporting Information.

^bNo: query compound number (Figure 1) with literature reference in superscript.

^cdev: ΔΔG^‡ deviation (kcal/mol) between calculated and experimental values.

^dPositive ee% values mean preference for the (S)-enantiomer.

^ePreferred enantiomer with a similar stereoconfiguration to (S)-01 but a different R/S notation because of the shift in CIP.

The high enantioselectivity of ω-TAs is an attractive feature in the synthesis of chiral amines but also hinders validation of the presented protocol because the dataset gathered from the literature is strongly unbalanced. Most of the compounds in the presented dataset have an ee%_exp of around 99%, and the ee%_calc values are correctly predicted to be in this range. The enantioselectivity calculations situated the numeric ee%_calc values of most compounds as large and positive (a positive sign means (S)-enantiopreference, and a negative sign means (R)-enantiopreference), which is in agreement with the highly (S)-enantioselective nature of Vf-TA (Table 1). Compounds 32, 33, 35, 36, and 45 are the exception, but 32, 33, and 45 are only designated as (R)-amines because of CIP rules and retain a similar stereoconfiguration to (S)-01 (the bulky substituent binds in the large pocket). By contrast, compounds 35 and 36 do not maintain the stereoconfiguration of (S)-01. Here, the ee%_calc for 35 (42%) and 36 (9%) was not in agreement with the ee%_exp (−99 and −98%, respectively). While the predictions incorrectly favor the (S)-enantiomer, the experiments suggested that the (R)-enantiomer was preferred in both 35 and 36. The ee%_exp reported by Höhne et al.⁵¹ suggests that Vf-TA would strongly prefer to place the N-Boc substituent of compounds 35 and 36 in the small binding pocket to yield the corresponding amines. Nevertheless, structural analysis of the docked complexes of ligands 35(R/S) and 36(R/S) did not provide an explanation as to why Vf-TA should prefer one enantiomer over the other (Figure S1).

Additionally, it can be noted that there are a few compounds in the dataset with low absolute ee%_exp values (i.e., 34, 40, 41, 45, 47, and 48) that were correctly predicted to have a poor enantioselectivity. For example, the ee%_exp of 47 is 15%, which suggests that Vf-TA does not produce an enantiopure mixture of amines (ratio of (S)- to (R)-amine is 1.35:1), and the ee%_calc has a low absolute value of 56% (3.5:1). On the other hand, there are a few compounds in the dataset with high absolute ee%_exp values (i.e., 13, 15, 32, 35, 36, 42, and 43) that were incorrectly predicted to have much lower ee%_calc values. For example, the ee%_exp of 13 (99%) suggests a strong preference for the (S)-enantiomer, but the ee%_calc (4%) would wrongly predict that Vf-TA produces both enantiomers in almost equal amounts. Compounds 35 and 36 were discussed earlier, and an explanation for the failure of the protocol in predicting the enantiopreference of compounds 13 and 15 could not be found.

The enantioselectivity predictions for compounds containing the indan or tetralin moieties (i.e., 32, 40–45) were generally not in agreement with the reported experimental values. For example, for compounds 42 and 43, Vf-TA was expected to have a strong preference toward the (S)-enantiomer, but the ee%_calc values (1 and −11%, respectively) suggest no preference. Inspection of the docked structures provided no explanation for these inaccurate ee%_calc values. Within the tetralin compounds, the ee%_calc (−31%) for 40 deviates in 49 percentual points from the ee%_exp (18%), which might lead to the conclusion that the prediction for 40 is incorrect. However, because the enantiomeric excess does not follow a linear scale, these deviations need to be interpreted accordingly. The ee%_calc for compound 40 corresponds to a small enantiopreference for the (R)-enantiomer (enantiomeric ratio 0.52:1), whereas the ee%_exp suggests a slight enantiopreference for the (S)-enantiomer (1.4:1). Accordingly, the energy deviations suggest that the enantioselectivity calculations are rather accurate (0.6 kcal/mol deviation), and the same holds for compounds 34, 45, and 47. Gawley⁶⁶ provides an excellent overview of the limitations of using enantiomeric excess as a metric to describe the enantiomeric composition. For that reason, we also calculated the ΔΔG^‡ deviations from experimental data (see the Supporting Information for calculation details). In many cases (26 out of 49), the deviations are below ±1.0 kcal/mol (Table 1), which corroborates the predictive power of the presented methodology for modeling the enantioselectivity of ω-TAs.

The ability of Arg415 to form salt bridge interaction with carboxyl groups is corroborated by the enantiopreference of Vf-TA toward compounds 19 (L-alanine) and 33 (3-fluoroalanine). Synthesis of (S)-19 and (R)-33 requires placing the carboxyl substituent in the large binding pocket, where Arg415 is located (Figure S2). The formation of a salt bridge between the guanidinium group of Arg145 and the COO^– group of the ligand to occur, the carboxyl substituent needs to be deprotonated. In fact, when the simulations (docking and MD) were performed with the carboxyl groups in the neutral form (COOH), the ee%_calc of compounds 19 and 33 was found to be 76 and –36%, respectively. The results presented in Table 1 are from simulations with the deprotonated form (COO^–), where the preference is toward salt bridge formation (ee%_calc was 95 and –96% for compounds 19 and 33, respectively).

Additional Simulation Setups

Additional simulation setups were used to test the robustness of the presented protocol (Table S1). We tested whether the number and length of the simulations (5 × 20 ps vs 1 × 100 ps), or the fraction of docked structures selected for MD (top20% vs top10%), affected the outcome of the calculations. When comparing the 5 × 20 ps against the 1 × 100 ps setups, no large differences were found in the predicted ee% values. In fact, NAC-producing frames were found to be evenly spaced across the MD trajectories (Figure S5), which means that the percentage of NACs produced by a trajectory was not dependent on the simulation length. Still, the length of the simulations should be long enough to generate conformational sampling of the ground-state region set at the docking stage, but short enough to maintain a conformation close to the initial structure. Our research group has previously shown that ps-scale MD simulations are long enough to allow meaningful counting of binding poses and that running multiple-independent MD simulations is better for sampling than performing a single long simulation.^36,37,46,67 Additionally, no large difference was found when comparing the ee% obtained from using the top10% or top20% of Rosetta structures for MD simulations (Table S1). Again, only low-energy conformations should be used to avoid working with unfavorable ground states (unfavorable Rosetta interface energies), but the structures should be diverse enough to prevent single outliers from dominating the averaged frequency of NAC conformations. Within the set of selected structures, the number of NACs that each trajectory produced was not correlated with the Rosetta interface energy of the starting structure (Figure S6). All in all, the choice of limiting the proportion of docking structures (top20%) to be used as starting conformations for multiple short MD simulations (5 × 20 ps) was adequate.

Sampling of the χ₁ Dihedral Is Key to Modeling the Enantioselectivity of Vf-TA

In this section, we provide further results that illustrate why sampling the χ₁ dihedral using the Rosetta energy function can be advantageous.

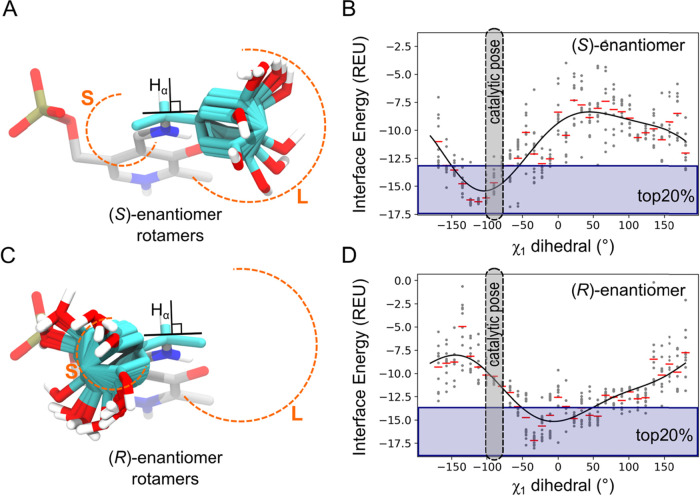
The most important difference between the preferred and nonpreferred enantiomers is that the former can position their cleavable H_α–C_α bond perpendicular to the PMP plane, ready for proton abstraction by Lys285. By contrast, the nonpreferred enantiomers cannot position the H_α close to Lys285, because this would require placing the large substituent in the small binding pocket, which is unfavorable (Figure 4). Therefore, the initial approach for modeling the enantioselectivity of Vf-TA was to dock the ligands of compounds 01–49 in a conformation that resembled as much as possible a catalytic conformation (setting χ₁ to −90°) and allow the nonpreferred enantiomer to reorient itself into a more favorable (and probably noncatalytic) conformation during the simulation (Figure 4A,C). In this way, the fraction of NACs produced by the nonpreferred enantiomer would be lower than the fraction produced by the preferred enantiomer (NAC criterium χ₁). However, we found that the nonpreferred enantiomer (i.e., the (R)-enantiomer) was not able to invert to a more favorable conformation in simulation time scales realistic for application in rapid computational screening (i.e., tens of ps). When the external aldimine form of both enantiomers was docked in a catalytic orientation (χ₁ = −90°), followed by MD simulations, the ee%_calc showed no correlation with the ee%_exp values (Table S1). Hence, docking all external aldimine intermediates in a catalytic orientation was unsuitable for discerning between reactive and nonreactive enantiomers.

Figure 4.

Comparison between the (R)- and (S)-enantiomers. (A) Preferred enantiomer (the (S)-enantiomer of compound 07) can position H_α perpendicular to the plane of the PMP ring and ready for proton abstraction by Lys285. (B) Preference for the preferred enantiomer to adopt a catalytic orientation (χ₁ = −90°) is evident when comparing the Rosetta score at different χ₁ values. (C) By contrast, the nonpreferred enantiomer is unable to adopt a catalytic orientation (χ₁ = −90°), where the H_α is positioned close to the catalytic lysine, because of steric hindrance with the small binding pocket (S: small, L: large binding pockets). (D) Scanning through the χ₁ dihedral shows that the energy minimum is not located near the optimal value for catalysis to take place. In panels (A) and (C), carbon atoms originally belonging to the cofactor are colored gray, while carbon atoms originally belonging to the amino compound are colored cyan. All panels correspond to compound 07, shown as an example.

Longer MD simulations of the external aldimine complex of compounds 01R and 01S showed that the χ₁ dihedral evolves too slowly to obtain convergence in short time scales (Figure S7). We sorted out this limitation by using the Rosetta energy function to scan through the χ₁ dihedral and produce enzyme–ligand complexes with staggered χ₁ values (χ₁ = {−180°, −168.75°, −157.50°, ..., +180°}) (Figure 2). The top-scoring Rosetta structures (top20%: 64 out of 320 total structures; top10%: 32 out of 320 total structures) were then used as starting conformations for MD simulations (Figure 4B,D). This way, the docking algorithm makes larger jumps in conformational space, and the short MD simulations subsequently sample the local region of said conformational space, yielding a fast and accurate protocol to model ω-TA enantioselectivity.

Influence of NAC Definitions on ee%_calc

Among the set of geometric criteria (d₁, θ₁, θ₂, χ₁, and χ₂), the dihedral χ₁ was the criterion with greater influence on the number of NACs produced in the trajectory because of its slow dynamics. The MD simulations (20–100 ps) were not of sufficient length as to allow χ₁ to move away from the starting value set at the docking stage (Figure S3). Hence, ligands docked in a catalytic conformation (χ₁ = −90°) were more likely (but not guaranteed) to produce NACs than ligands docked in a noncatalytic conformation (χ₁ ≠ −90°). Because a ligand docked in a catalytic conformation is not necessarily guaranteed to produce NACs (as NAC production also depends on other geometric parameters), performing MD simulations on the docked structures is still necessary to determine ee%_calc. Similarly, a ligand docked in a noncatalytic conformation is still capable of producing NACs (Figure S4). Additionally, MD simulations allow the inclusion of explicit water molecules. All in all, the presented strategy of scanning the χ₁ dihedral landscape using the Rosetta energy function and then performing more accurate ps-scale MD simulations of the top-scoring docked structures enables a fast and accurate way of modeling the enantioselectivity of ω-TAs.

Substrate Scope Prediction Using the Rosetta Interface Energy

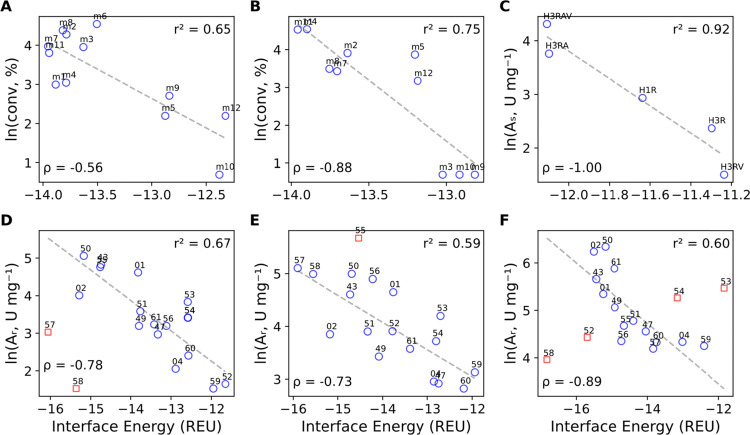
After examining enantioselectivity, we investigated if the sole modeling of the external aldimine intermediate would suffice to predict the substrate range. Six independent sets of substrates were examined. The first three sets keep the query compound constant but explore different Vf-TA variants (Figure 5A–C), and the remaining three sets keep the enzyme variant constant but explore different compounds (Figure 5D–F). The Rosetta interface energy was found to be well correlated with the observed experimental activity for the six independent sets of compounds, once major outliers were omitted from the latter three datasets. The correlation is surprising because the interface energy only accounts for interactions between the ligand and the protein while ignoring other factors that may cause differences in catalytic activity, such as differences in the chemical potential of the reacting compounds or in desolvation free energy upon substrate binding across substrates or mutants.⁶⁸ Calculating only the interface energy of the external aldimine complex also ignores other steps in the catalytic cycle for a given substrate to undergo transamination, such as formation of the Michaelis complex or formation of reaction intermediates other than the external aldimine. However, because all these reaction intermediates are structurally similar (Scheme 1), a good interaction energy for the modeled intermediate might also reflect a good interaction energy for the nonmodeled intermediates. Whereas substrate binding (affinity) would mainly influence K_M, the affinity of an intermediate can also influence k_cat, which would be in agreement with inspecting the relationship between the Rosetta interface energy and experimental data, namely, yield and conversion. Another point to consider is the scale on which the observed correlation between Rosetta scores and enzymatic activity exhibits monotonicity. On short scales, two mutants with different activities may receive a similar Rosetta score (e.g., mutants m10 and m12 in Figure 5A, m3 vs m12 and m5 in Figure 5B, and H3RV vs H3R in Figure 5C). Despite these potential pitfalls, the good correlation found between interface energies and experimental substrate specificity suggests that the Rosetta score can be used as the objective function to guide the design of ω-TA mutants.

Figure 5.

Correlation between the Rosetta interface energy and substrate range. Panels A–C show the relation between the Rosetta score of the external aldimine of compounds 13, 62, and 54, respectively, and the experimental conversion across different Vf-TA mutants. In panels D–F, we show the relation between the Rosetta score of wild-type Vf-TA, Vf-TA + W147G, and Vf-TA + W57G, respectively, and the experimental activity on a dataset of 17 compounds. All Rosetta calculations were performed using the external aldimine of the (S)-amine. The red squares are outliers, that is, datapoints that do not follow the overall trend and were not used to do the linear regression (dotted lines). Experimental data were obtained from the existing literature: panels A and B from Nobili et al.;⁶ panel C from Genz et al.;¹⁵ and panels D and F from Cho et al.⁵ Abbreviations are as follows. For panels A and B: m1, wild-type; m2, mutant V153A; m3, mutant F85L; m4, mutant Y150F; m5, mutant Y150M; m6, mutant F85L_V153A; m7, mutant F85L_Y150F; m8, mutant F85L_Y150F_V153A; m9, mutant F85L_Y150M; m10, mutant F85L_Y150M_V153A; m11, mutant Y150F_V153A; m12, mutant Y150M_V153A. For panel C: H1R, mutant L56V_W57F_F85V; H3R, mutant L56V_W57C; H3RV, mutant L56V_W57C_F85V; H3RA, mutant L56V_W57C_V153A; H3RAV, mutant L56V_W57C_F85V_V153A. For panels D, E, and F, the numbers correspond to the dataset presented in Figure 1. REU: Rosetta Energy Units., A_s: specific activity, A_r: relative specific activity, and ρ: Spearman’s correlation coefficient.

Discussion

Modeling the enzymatic enantioselectivity is a complicated task because of the small energy differences that need to be reproduced and the number of intermediates and transition states that need to be considered. Very accurate but computationally demanding methods, such as quantum mechanics (QM), molecular mechanics, empirical valence bond, and the quantum chemical cluster approach, have been used successfully in the study of enzymatic enantioselectivity.⁶⁹ In this work, we explored a strategy that combines molecular docking and MD simulations to yield a computationally inexpensive but accurate framework for predicting the specificity of Vf-TA in the production of chiral amines. Modeling was performed using only the external aldimine intermediate of the query compounds. Docking allows a computationally efficient generation of ground-state conformations, while the MD simulations quantify the Boltzmann distribution of ground-state conformers, including the occurrence of reactive poses. Estimating the proportion of ground-state conformers that resemble a NAC provides an indication of the free energy of NAC formation⁴⁵ and a direct means for predicting the ee% (Eq 1). The MD simulations are intended to account for the loss of accuracy arising from the discreteness of rotamers of docking approaches^70,71 and the lack of explicit water molecules.⁷² The computational cost of the presented framework is around 37 CPU-h (using an HP workstation Z4 with Intel Xeon W-2135 Processor with six CPUs) per assayed compound (setup: 5 × 20 ps, top20%), and parallel computing is possible.

With six independent compound sets, it was shown that the Rosetta interface energy, measured between the enzyme variant and the external aldimine form of the query compound, correlates well with the experimental substrate scope of Vf-TA (Figure 5). At least for the presented datasets, this correlation shows that modeling the amino donor (typically l-alanine or isopropylamine) is not necessary for the reactivity prediction task, in contrast to the approach of Seo et al.,⁴⁹ where differential binding energies were considered for the substrates of both half-transamination reactions. We recently also reported the correlation between interface energies and experimental conversion in other Vf-TA and Pj-TA datasets⁷³ and used the Rosetta interface energy as the target function for the computational engineering of the Pj-TA substrate scope.⁶⁸ The protocol allowed the rapid design of Pj-TA variants accepting sterically hindered substrates. The computational cost of scanning for enzyme variants using Rosetta interface energy is circa 2 CPU-h per enzyme variant. Generating every enzyme–ligand structure takes approximately 60 s, but producing at least 100 structures per scanned variant is recommended. Other more sophisticated methodologies for predicting ω-TA reactivity can be useful in later stages of the search for new mutants but tend to be more expensive. For example, the methodology of Voss et al.,¹³ which used a combination of QM calculations and MD simulations, has a computational cost of around 60 CPU-h per enzyme variant.

Although validation was made solely on a Vf-TA dataset, the presented approach may be applicable to other (S)-selective ω-TAs owing to their similarities. We have tested the substrate scope prediction task in Pj-TA^68,73 and Cv-TA.⁷³ In contrast, this approach may or may not be applicable to (R)-selective ω-TAs, because the two enzymes evolved separately and belong to a completely different PLP fold type (fold type IV).¹⁸

Conclusions

We presented a framework for calculating the enantioselectivity of an ω-TA from V. fluvialis toward a variety of compounds. The framework is computationally inexpensive and can assist in the enzyme design of ω-TAs. In general, the retrospectively predicted ee% values were in agreement with those found in the literature, but there were cases where the predictions did not correspond to the expected values. Furthermore, we showed that the Rosetta interface energy of the external aldimine complex is a good predictor of the activity of Vf-TA across mutants or across different compounds. Using the Rosetta interface energy as the target scoring function can therefore aid in the search for enzyme variants with a broadened substrate range.

Glossary

Abbreviations

ω-TA

ω-transaminase

PLP

pyridoxal 5-phosphate

PMP

pyridoxamine 5-phosphate

E

enzyme

Vf-TA

ω-TA from Vibrio fluvialis

Cv-TA

ω-TA from Chromobacterium violaceum

Pj-TA

ω-TA from Pseudomonas jessenii

NAC

near-attack conformation

ee%

percentual enantiomeric excess

REU

Rosetta energy units

MD

molecular dynamics

QM

quantum mechanics.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jcim.1c00617.

• Equations to calculate ΔΔG^‡ deviations; structures of docked complexes; plots showing the variation of the χ₁ dihedral at the start and end of the MD simulations; 3D histogram of the dependency of NACs and docked dihedral; heatmaps showing the NAC count independency on the simulation time window and on the Rosetta score of the starting conformation; time evolution of the χ₁ dihedral in long MD simulations; and table comparing the ee%_calc obtained from different setups (PDF)

Author Contributions

C.R.P. performed the computational work and wrote the manuscript. H.J.W. supervised docking and initial MD simulations. H.J.W. and D.B.J. conceived the project. S.T. supervised the MD simulation work. D.B.J. supervised the overall project. D.B.J. and S.J.M. revised the manuscript.

The authors declare no competing financial interest.

Notes

Scripts necessary for running the presented protocol are publicly available at: https://github.com/crp-mol/transaminases. Usage instructions and example input and output files are provided.