Abstract
The coronavirus disease 2019 (COVID-19) pandemic caused by the novel severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) has led to a sharp increase in hospitalized patients with multi-organ disease pneumonia. Early and automatic diagnosis of COVID-19 is essential to slow down the spread of this epidemic and reduce the mortality of patients infected with SARS-CoV-2. In this paper, we propose a joint multi-center sparse learning (MCSL) and decision fusion scheme exploiting chest CT images for automatic COVID-19 diagnosis. Specifically, considering the inconsistency of data in multiple centers, we first convert CT images into histogram of oriented gradient (HOG) images to reduce the structural differences between multi-center data and enhance the generalization performance. We then exploit a 3-dimensional convolutional neural network (3D-CNN) model to learn the useful information between and within 3D HOG image slices and extract multi-center features. Furthermore, we employ the proposed MCSL method that learns the intrinsic structure between multiple centers and within each center, which selects discriminative features to jointly train multi-center classifiers. Finally, we fuse these decisions made by these classifiers. Extensive experiments are performed on chest CT images from five centers to validate the effectiveness of the proposed method. The results demonstrate that the proposed method can improve COVID-19 diagnosis performance and outperform the state-of-the-art methods.
Keywords: COVID-19 diagnosis, Histogram of oriented gradient, 3D-CNN, Multi-center sparse learning, Decision fusion
1. Introduction
The coronavirus disease 2019 (COVID-19) pandemic caused by the novel severe acute respiratory syndrome coronavirus 2 (SARS-CoV-2) has led to a sharp increase in hospitalized patients with multi-organ disease pneumonia. In the early stages of the disease, patients with COVID-19 may be asymptomatic or appear some common symptoms, such as fever and cough [1]. With the disease worsening, these patients can appear viral sepsis, which may further lead to life-threatening organ dysfunction and even failure [2]. According to the data from the world health organization (WHO), COVID-19 has caused more than 239.4 million confirmed cases and 4.8 million deaths worldwide as of 15 October 2021 [3]. Since it spreads rapidly mainly through respiratory droplets from face-to-face contact, infection cases are increasing with a mortality rate of up to 2%, which causes the clinicians’ shortage and the increase of their workloads. Many clinical measures have been used to diagnose whether the suspected cases are infected with SARS-CoV-2, such as reverse transcription-polymerase chain reaction testing (RT-PCR) [4], [5], manual chest X-ray [2], [6], and computed tomography (CT) [7], [8] screening. However, RT-PCR easily has a low sensitivity problem [9], and the limited RT-PCR test kits cannot detect all the suspected cases. Meanwhile, manual X-ray and CT screening are time-consuming and cannot quickly and accurately diagnose COVID-19.
As a good plan B, artificial intelligence methods based on medical image data are playing an increasing role in automatic COVID-19 diagnosis [10], [11], [12]. In the early diagnosis of the disease, chest CT images can better reflect lung abnormalities than chest X-ray images and have captured widespread attention [2]. For example, Li et al. [10] first used RestNet50 as the backbone to extract features of each slice from CT images and then fused these features by a max-pooling operation. The final fused features were input to a fully connected layer and softmax activation function for pneumonia diagnosis. Wang et al. [13] proposed a transfer learning model based on the inception network, where the pre-trained inception network is used to extract features from CT slices, and the fully connected network is exploited for COVID-19 diagnosis. However, most of these methods treat 3D CT images as a series of slices [10], [14] or manually select several pathological slices [15], [16] and input them into a 2-dimensional convolutional neural network (2D-CNN) model for COVID-19 diagnosis. Therefore, they are inherently unable to exploit the context of adjacent slices to improve classification performance. Also, the manual selection of some slices consumes the doctor’s time. Since the 3-dimensional CNN (3D-CNN) model can effectively and automatically learn the inter-slice context information, it has been widely used for classification and segmentation tasks of 3D data [17].
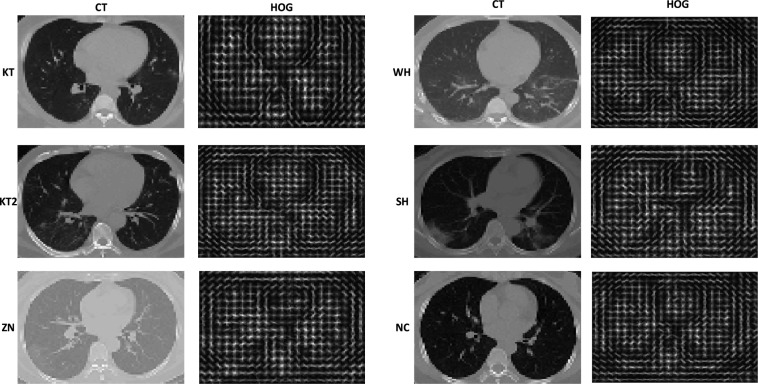
Due to the large-scale outbreak of COVID-19 around the world, the data studied in the literature are collected from different centers or hospitals, such as two centers [18], five centers [19], six centers [10], [20], seven centers [21], [22], and ten centers [14]. These multi-center data acquired from different devices and parameter settings are structurally inconsistent, and the lesion characteristics of some center data are not obvious. For example, in this paper, we have collected chest CT images of COVID-19 patients from Keting hospital (KT1), Wuhan shelter hospital (WH), another Keting hospital (KT2), Wuhan No. 7 Hospital (SH), and Zhongnan hospital (ZN) of Wuhan University, China, respectively. We also collect chest CT images of their corresponding normal control (NC). As shown in Fig. 1, we can see that CT images in SH and ZN centers are quite different from the other three centers, and CT images of COVID-19 patients in KT center are similar to those of the NC group, which has undoubtedly augmented the difficulties of COVID-19 diagnosis. Since the histogram of oriented gradient (HOG) representation can capture gradient structure with local shape characteristics, it is easy to control the invariance of local geometry and photometric conversion [23], [24]. Inspired by the above, considering the inconsistency of data in multiple centers, we first convert 3D CT images into HOG images, which can reduce the structural differences between multi-center data. We then design a 3D-CNN model to learn the useful information between and within 3D HOG image slices and extract multi-center features, which can also save the doctor’s time to screen the pathological slices.
Fig. 1.
Examples of CT images and corresponding HOG images in COVID-19 patients and NC.
Furthermore, most existing methods are restricted to treat multiple centers into one center [21], [25], which ignores the relationship between and within multi-center data. There are some methods proposed to learn the relationship of multi-center data. For example, in [26], Wang et al. proposed a united learning scheme to facilitate the diagnosis of COVID-19 by learning heterogeneous information from different centers. In our method, considering the inconsistency of data in multiple centers, we convert 3D CT images into HOG images to reduce the structural differences between multi-center data, thereby enhancing generalization performance. These two methods solve the problem of multi-center data differences from two aspects, which form an effective complementarity. In [27], Song et al. first used a 3D-CNN to extract features from multi-center CT images and then constructed an augmented multi-center graph to consider the heterogeneity of multi-center data and disease state information. Finally, the multi-center graph is input into a graph convolutional network (GCN) for COVID-19 diagnosis. In the process of constructing the multi-center graph, this method only constructs edges for samples with the same category at the same center, that is, it only considers the relationship within each center, while ignoring the relationship between multi-center data. Also, this method inputs the constructed graph directly into the GCN for classification and does not consider the multi-center fusion strategy to enhance the classification performance. There is redundancy in the relatively high-dimensional features extracted from CNN models, which can negatively affect the generalization ability of the model [28], [29]. Besides, since information fusion can gather all kinds of useful information to enhance generalization performance, various fusion strategies (e.g., center fusion, feature fusion, and decision fusion) have received wide attention from researchers [11], [30], [31], [32]. Center fusion treats multiple centers into one center [21]. Feature fusion concatenates/encodes multi-modal features into high-dimensional/another form of features [33]. Decision fusion combines the decisions made by multiple data [34]. However, center fusion can eliminate the relationship between multi-center data, and feature fusion can result in high feature dimensionality, which can reduce model generalization performance. For decision fusion, it can comprehensively consider the relationship between multi-center data and jointly analyze the diagnosis results of different classifiers to improve the diagnostic performance. Inspired by the above, we devise a multi-center sparse learning (MCSL) method to learn the intrinsic structure information between multiple centers and within each center for COVID-19 diagnosis. Specifically, we use the group sparseness regularizer to learn the intrinsic relationship between multiple centers and the global sparseness regularizer to enhance the generalization performance. Furthermore, we consider the similarity among subjects of each center to preserve the local structure information within each center. Finally, we select discriminative features from our MCSL model to jointly learn multiple classifiers. The decision is determined by fusing the results of multi-center classifiers.
We highlight the main contributions of our paper as follows.
-
•
Considering the inconsistency of data in multiple centers, we convert 3D CT images into HOG images to reduce the structural differences between multi-center data and enhance the generalization performance.
-
•
We propose a 3D-CNN model to learn the useful information between and within 3D HOG image slices and extract multi-center features, which saves the doctor’s time to screen the pathological slices.
-
•
We propose a MCSL method to learn the intrinsic structure information between multiple centers and within each center and select discriminative features to jointly train multi-center classifiers.
-
•
The decision fusion is used to comprehensively consider the relationship between multi-center data and jointly analyze the diagnosis results of different classifiers to improve the diagnostic performance.
2. Related work
2.1. Feature learning
Feature learning methods aim to automatically learn deep features to improve the diagnostic performance of COVID-19. However, due to the differences between multi-center data, it is challenging to use a deep learning model to learn discriminative features that meet the accuracy requirements of multiple centers. Researchers have made some attempts by using different CNN models to handle this challenge. Ghoshal et al. [18] proposed a Bayesian convolutional neural network (BCNN) to estimate network uncertainty to improve the accuracy of pneumonia screening. Li et al. [10] first used RestNet50 as the backbone to extract features of each slice from CT images and then fused these features by a max-pooling operation. The final fused features were input to a fully connected layer and softmax activation function for pneumonia diagnosis. Gao et al. [14] used the segmented lesion features to facilitate classification at the slice level and then used a slice probability mapping method to reduce the potential influence of different imaging parameters from individual facilities for COVID-19 diagnosis. Jie et al. [22] proposed an artificial intelligence system, where CT images were divided into different cohorts to train the deep learning-based model for COVID-19 diagnosis. Wang et al. [21] developed a fully automatic deep learning system, where lung segmentation network, non-lung area suppression operation, and lung- ROI normalization were used to obtain standard lung region, and then the standardized lung-ROI was input into the COVID-19Net for COVID-19 diagnosis.
These methods show great potential by using various models to learn deep features for COVID-19 diagnosis. However, they do not fully consider processing at the data level to reduce the differences between multi-center data. Meanwhile, most of these methods treat 3D images as a series of slices or manually select several pathological slices and then input these slices into 2D-CNN models for COVID-19 diagnosis. This ignores related information between slices, and manual selection of some slices also consumes the doctor’s time. In this paper, considering the inconsistency of data in multiple centers, we first convert the original CT images into HOG images, which can reduce the structural differences between multi-center data. We then propose a 3D-CNN model to automatically learn the useful information between and within 3D HOG image slices and extract multi-center features, which can also save the doctor’s time to screen the pathological slices.
2.2. Sparse learning
Sparse learning methods aim to select discriminative features for various tasks such as classification, regression, and prediction. For example, in [35], the least absolute shrinkage and selection operator method (Lasso) method used linear regression and penalty to perform feature selection. In [36], the elastic net method used linear regression, norm and penalties for feature selection. Zhang et al. [37] proposed a multi-modal multi-task method to select common relevant features for Alzheimer’s disease diagnosis. Sun et al. [20] first extracted the location-specific handcrafted features from chest CT images and then used the adaptive feature selection guided deep forest (AFS-DF) model for COVID-19 classification. Shaban et al. [38] proposed a COVID-19 detection strategy based on a hybrid sparse learning and enhanced k-nearest neighbor classifier. In [39], Zhu et al. first extracted handcrafted features from CT images and then used joint logistic and linear regression to select the discriminative features for COVID-19 classification and prediction.
These methods have good performance in different tasks. However, these methods do not consider the relationship between and within multi-center or multi-modal data at the same time. In this paper, to handle this problem, we propose a MCSL method to capture the intrinsic structure between multiple centers and within each center and selects discriminative features to jointly train multi-center classifiers.
2.3. Information fusion
Information fusion aims to gather all kinds of useful information to enhance generalization performance [11], [30], [40], [41]. There are currently three main fusion strategies, i.e., center fusion, feature fusion, and decision fusion. Center fusion treats multiple centers into one center [21]. Feature fusion concatenates/encodes multiple modal features into higher-dimensional/another form of features [33]. For example, Zhu et al. [42] first linearly fused the multi-modal features and then input the fused feature into a sparse learning model to select the discriminative features for Alzheimer’s disease diagnosis. Decision fusion combines the decisions made by multiple data [34]. For example, Xie et al. [30] used decision fusion to combine texture, shape, and deep model features for the classification of lung nodules.
These fusion strategies have good performance in different scenarios. However, center fusion can eliminate the relationship between multi-center data, and feature fusion can result in high feature dimensionality, which can reduce model generalization performance. For decision fusion, it can comprehensively consider the relationship between multi-center data and jointly analyzes the diagnosis results of different classifiers to improve the diagnostic performance. Thus, in this paper, we use decision fusion to obtain the final result.
3. Method
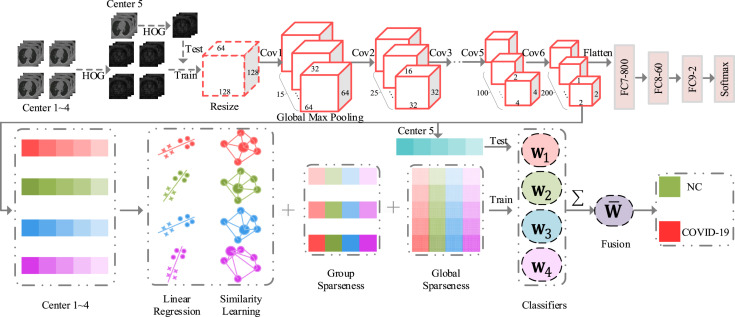
Fig. 2 shows our method for automatic COVID-19 diagnosis. Specifically, considering the inconsistency of data in multiple centers, we first convert 3D CT images into HOG images, which can reduce the structural differences between multi-center data. We then use a 3D-CNN to learn deep features from each center. Finally, we employ the proposed MCSL model to learn the intrinsic structure between multiple centers and within each center and select discriminative features for COVID-19 diagnosis.
Fig. 2.
Illustration of the proposed method for COVID-19 diagnosis.
3.1. Notations
In this paper, boldface uppercase typefaces indicate matrices, boldface lowercase typefaces indicate vectors, and normal italic typefaces indicate scalars. For a matrix , we use , , , and to indicate the transposition, trace, -norm and Frobenius norm of , respectively.
3.2. Multi-center deep feature extraction
For each CT slice, the corresponding HOG image is generated through the following steps: (1) divide the CT slice into many small spatial cells of equal size; (2) compute gradients and accumulate histogram of gradient directions over the pixels of each cell; (3) conduct contrast normalization on local responses; (4) generate a pictorial rendition of HOG descriptors. As shown in Fig. 2, we construct a 3D-CNN to automatically learn multi-center deep features from HOG images. Specifically, the input of this network is a down-sampled HOG image with a size of 128 × 128 × 64. It has six convolutional layers and three fully connected (FC) layers (i.e., FC7-800, FC8-60, and FC9-2). The size of each convolutional kernel is 3 × 3 × 3 and its stride, padding, and data format equal one, ‘same’, ‘channel first’, respectively. The number of convolutional kernels in each convolutional layer is 15, 25, 50, 50, 100, and 200, respectively. Each convolution layer is followed by a rectified linear unit activation function and a max-pooling operation. The size of each max-pooling operation is 2 × 2 × 2 and its stride, padding, and data format equal two, ‘same’, and ‘channel first’, respectively. After building the network model, we first use four central data to train the network model to identify whether patients have COVID-19. Finally, we pop FC9-2, FC8-60, and FC7-800 and add a global max-pooling layer to extract multi-center deep features. The feature dimension of each center is 200. Table 1 also shows the detailed information of our 3D-CNN.
Table 1.
The architecture of our 3D-CNN used in this paper.
| Layer | Kernels, channels, stride, padding, data format |
|---|---|
| Conv1 | 3 × 3 × 3, 15, 1, same, channel first |
| ReLU | |
| Max pooling, 2 × 2 × 2, 15 | |
| Conv2 | 3 × 3 × 3, 25, 1, same, channel first |
| ReLU | |
| Max pooling, 2 × 2 × 2, 25 | |
| Conv3 | 3 × 3 × 3, 50, 1, same, channel first |
| ReLU | |
| Max pooling, 2 × 2 × 2, 50 | |
| Conv4 | 3 × 3 × 3, 50, 1, same, channel first |
| ReLU | |
| Max pooling, 2 × 2 × 2, 50 | |
| Conv5 | 3 × 3 × 3, 100, 1, same, channel first |
| ReLU | |
| Max pooling, 2 × 2 × 2, 100 | |
| Conv6 | 3 × 3 × 3, 200, 1, same, channel first |
| ReLU | |
| Max pooling, 2 × 2 × 2, 200 | |
| FC, 1 × 1 × 1, 800 | |
| FC, 1 × 1 × 1, 60 | |
| FC, 1 × 1 × 1, 2 | |
| Softmax | |
3.3. Multi-center sparse learning
After learning the multi-center features, we need to use these features to build a regression model for COVID-19 diagnosis. Generally speaking, the linear multi-center regression model can be expressed as follows:
| (1) |
where indicates the training data of n subjects and d features in the th center, and is the corresponding true label vector (i.e., patient with COVID-19 or NC). indicates the feature weight matrix of C center data, where is the feature weight vector of the th center. The larger the value of , the more important the corresponding feature. However, there is redundancy in relatively high-dimensional features, which can lead to the over-fitting problem. To solve this problem, we add the group sparseness and global sparseness regularizers into Eq. (1), which is indicated as:
| (2) |
In multi-center data, the importance of features with the same index should be similar. Thus we use the -norm to conduct the group sparseness to learn the intrinsic relationship between multiple centers. The -norm can make the weight matrix have many zero rows. In other words, the features corresponding to non-zero rows in will be selected for COVID-19 diagnosis. Meanwhile, we use the Frobenius norm to conduct the global sparseness to reduce the overall feature weight, which can further enhance the generalization performance of the model.
Further, considering that in each center, the smaller the Euclidean distance between two subjects, the more similar their predicted target values should be. Thus, we introduce the following formula to learn this similarity relationship among subjects in each center:
| (3) |
where and indicate the th and th subjects in the th center, respectively, and is their similarity value. indicates the similarity matrix of subjects in the th center. indicates the Laplacian matrix of , where is the diagonal matrix whose th element value on the diagonal equals to . Eq. (3) aims to preserve the local structure information within each center. To compute the similarity matrix in the th center, we use a radial basis function kernel as follows:
| (4) |
where t indicates a kernel width. If and are among the k nearest neighbors, we use Eq. (4) to compute , otherwise, we set it to zero. Finally, we add Eq. (3) into Eq. (2) and we can get our MCSL model:
| (5) |
where , , and are three regularization parameters. The larger their value, the stronger the binding force of the corresponding regularization terms. By our MCSL model, we can learn the intrinsic structure between multiple centers and within each center and selects discriminative features to jointly train multi-center classifiers.
3.4. Optimization of MCSL model
Since the objective function in Eq. (5) contains the non-smooth part (i.e., -norm), it is difficult to solve this function directly. Thus, as shown in Algorithm 1, we exploit the accelerated proximal gradient method (APG) [43] to optimize it. First, we divide Eq. (5) into a smooth part and a non-smooth part :
| (6) |
| (7) |
Then, we introduce the following function to approximate Eq. (6):
| (8) |
where indicates the gradient of at the search point in the th iteration, and we can use Algorithm 2 to compute . l indicates the step length. Meanwhile, we compute by the following formula:
| (9) |
where and ( and ).
Finally, according to the APG method [43], we update as follows:
| (10) |
where and indicate the th row of and , respectively. Meanwhile, is obtained by the following formula:
| (11) |
According to the work in [44], we can compute each of Eq. (10) and obtain :
| (12) |
We dynamically update until convergence using Algorithm 1 and then use the optimal as multi-center classifiers.
3.5. Decision fusion
Since information fusion can gather all kinds of useful information to enhance the generalization performance, various fusion strategies (e.g., center fusion, feature fusion, and decision fusion) have received wide attention from researchers [11], [30], [40], [41]. In this paper, we select the third method, namely decision fusion. Specifically, we first exploit Algorithm 1 to optimize the feature weight of Eq. (13):
| (13) |
We then use the optimal multi-center weight parameter as multi-center classifiers, where each is a central classifier like a clinician. To comprehensively consider the diagnosis results of each clinician, we introduce the following formula to fuse the decision of each center to obtain the final diagnosis result for test subjects:
| (14) |
| (15) |
where indicates the training data, and the decision weight of each center is 0.25. To further prove the advantages of decision fusion, we attempt to conduct fusion at the center level, i.e., concatenating training subjects from multiple centers, and input these subjects to the MCSL model to learn a feature weight vector for COVID-19 diagnosis. Meanwhile, we also try to perform fusion at the feature level, that is, to concatenate the features of CT images and HOG images, and then input these features to the MCSL model to learn a feature weight vector for COVID-19 diagnosis.
4. Experiments
4.1. Data acquisition
We have collected a total of 1034 chest CT images of COVID-19 patients from five hospitals or centers in Wuhan, China, including 178 subjects from KT1 center, 130 subjects from WH center, 417 subjects from KT2 center, 104 subjects from SH center, and 205 subjects from ZN center. We have also collected a total of 2298 chest CT images of NC. These NC subjects are allocated to each center in proportion to the number of their corresponding patients with COVID-19, namely, 395 NC subjects in KT1 center, 288 NC subjects in WH center, 926 NC subjects in KT2 center, 231 NC subjects in SH center, and 458 NC subjects in ZN center. In Table 2, we also show the data distribution in the five centers. In this paper, all the data we used have passed the corresponding ethical approval, and the use of these data has been approved.
Table 2.
The number of subjects in five centers.
| Center | COVID-19 | NC |
|---|---|---|
| KT1 | 178 | 395 |
| WH | 130 | 288 |
| KT2 | 417 | 926 |
| SH | 104 | 231 |
| ZN | 205 | 458 |
| Total | 1034 | 2298 |
4.2. Experimental setting
As for data preprocessing, we first down-sample CT images to a size of 128 × 128 × 64. We then exploit the VLfeat tool package ( https://www.vlfeat.org/index.html) to generate HOG images from the down-sampled CT images. Finally, we down-sample these HOG images to a size of 128 × 128 × 64 again. These preprocessing procedures can not only ensure that the generated HOG images can be normally input to the 3D-CNN network for training, but also ensure the clarity of these images.
In this paper, we collect chest CT images from five centers. We use four central data as the training set and the remaining one as the test set. In this way, we can get the classification results of each center as the test set. In the 3D-CNN model, we set the following parameters: the learning rate is 0.0001, the optimizer is Adam, the loss is categorical cross-entropy, the number of epochs is 15, and the batch size is 16. In Eq. (4), we set t equal to 1 and . We also tune the regularization parameters of the MCSL method as follows: , . Finally, we also show the running environment of our framework to facilitate researchers to reproduce our experiments in Table 3. It is worth noting that we use the Transplant package of python to call the MATLAB program, and then we use MATLAB to generate HOG images and optimize the MCSL model in the paper. We compare our MCSL method with state-of-the-art multi-center sparse learning methods including: (1) the logistic regression (LogisticR) method is a multi-center learning method consisting of the logistic regression and -norm in the MALSAR1.1 package [45]. (2) The LogisticR-G method is obtained by adding a global sparse norm to the LogisticR method. (3) The least-square regression (LeastR) method is a special case of our proposed MCSL method by setting . This method does not have the subject similarity norm and the global sparse norm. (4) The LeastR-G method is also a special case of our method by setting . This method does not have the subject similarity norm. (5) A library for support vector machines (LIBSVM) [46] is a widely used classifier without feature selection. (6) We directly use the proposed 3D-CNN for COVID-19 diagnosis.
We evaluate our method on the five center datasets and the experimental results are given in Table 4, Figs. 3, and 4. To estimate its diagnostic performances, we use the quantitative metrics of accuracy (ACC), sensitivity (SEN), specificity (SPE), precision (PRE), unweighted average recall (UAR), F1-score, and area under the receiver operating characteristic (ROC) curve (AUC).
Table 4.
Sensitivity results of the competing methods for different input images in different centers.
| Image | Method | SEN (%) |
||||
|---|---|---|---|---|---|---|
| KT | WH | KT2 | SH | ZN | ||
| CT | SVM | 79.78 | 96.92 | 96.16 | 50.00 | 93.17 |
| LogisticR | 41.57 | 92.31 | 70.98 | 19.23 | 15.61 | |
| LogisticR-G | 45.51 | 93.85 | 74.34 | 18.27 | 47.80 | |
| LeastR | 41.01 | 96.15 | 93.05 | 27.88 | 13.17 | |
| LeastR-G | 84.27 | 97.69 | 93.05 | 58.65 | 27.80 | |
| 3D-CNN | 57.87 | 96.92 | 94.24 | 19.23 | 9.27 | |
| MCSL | 91.57 | 97.69 | 94.72 | 93.27 | 93.17 | |
| HOG | SVM | 84.27 | 94.62 | 98.80 | 96.15 | 88.29 |
| LogisticR | 73.03 | 87.69 | 98.80 | 87.50 | 84.39 | |
| LogisticR-G | 73.60 | 91.54 | 98.56 | 90.38 | 80.98 | |
| LeastR | 87.08 | 90.77 | 99.04 | 90.38 | 72.68 | |
| LeastR-G | 87.08 | 90.77 | 99.28 | 97.12 | 92.20 | |
| 3D-CNN | 86.52 | 93.08 | 99.28 | 94.23 | 80.00 | |
| MCSL | 94.38 | 93.08 | 99.76 | 99.04 | 93.17 | |
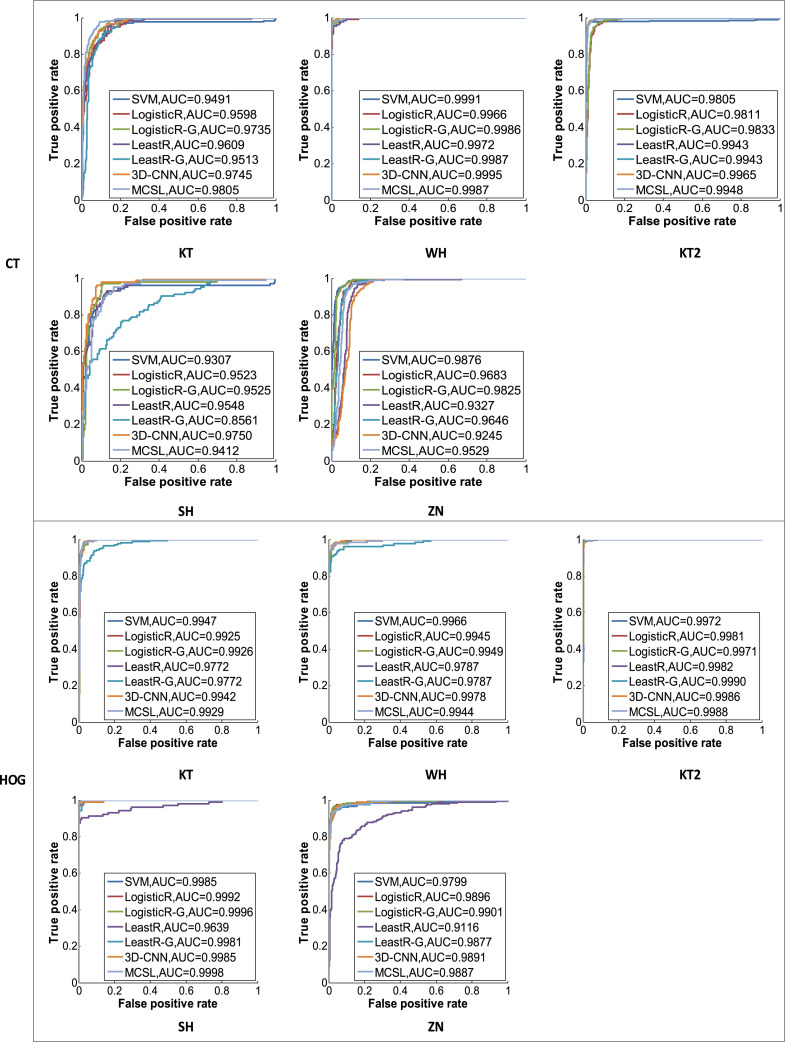
Fig. 3.
ROC curves for the competing methods in CT images and HOG images.
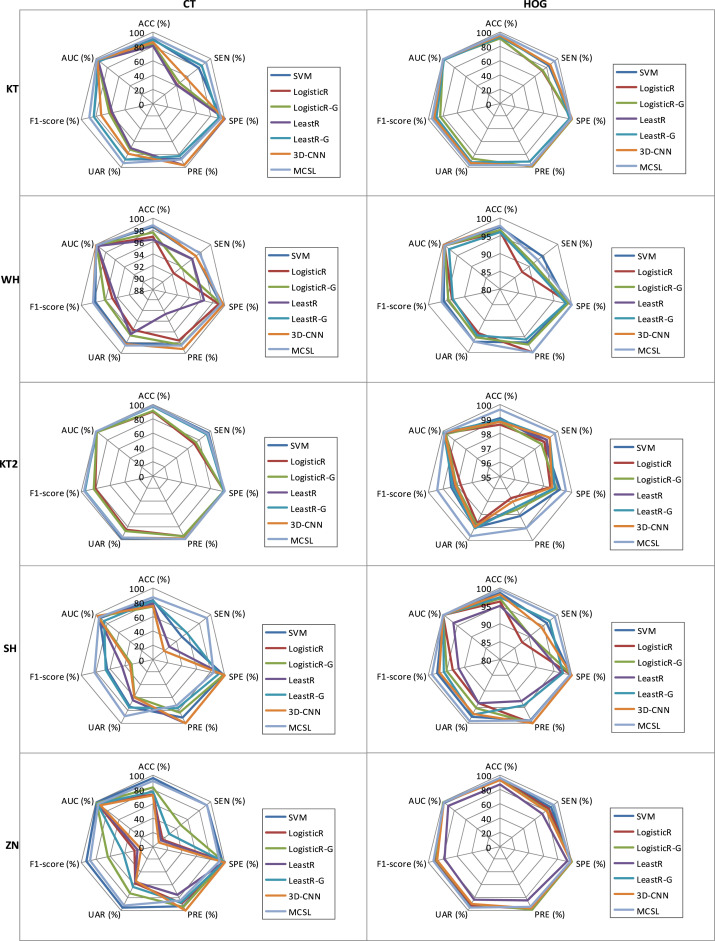
Fig. 4.
Diagnostic performance of the competing methods on radar charts.
Table 3.
The running environment of our framework.
| Server | Information | Number/size/version | Remark |
|---|---|---|---|
| Operating system | Ubuntu | 18.04.4 | Version |
| Hardware | CPU | 48 | Number |
| GPU | 2/12GB/TITAN X | Number/size/version | |
| Memory | 120 GB | Size | |
| Data disk | 4.4T | Size | |
| Software/package | CUDA | 10.0.130 | Version |
| cuDNN | 7.6.3 | Version | |
| Python | 3.6.10 | Version | |
| Transplant | 0.8.10 | Version (Call MATLAB) | |
| Tensorflow-gpu | 2.0.0 | Version | |
| Keras | 2.3.1 | Version (3D-CNN) | |
| MATLAB | R2017b | Version (MCSL) | |
| VLfeat | 0.9.21 | Version | |
4.3. Diagnostic performance for COVID-19
Table 4 shows the sensitivity results of the competing methods for different input images in different centers. Based on the above results, we can make the following findings. Compared with using CT images, we can get better and robust performance by using corresponding HOG images. For example, the diagnosis of WH and KT2 centers is relatively easy, since images of the two centers have small differences and their lesions are relatively easy to distinguish. In KT center, we can see that chest CT images are directly input to our 3D-CNN model and have low sensitivity since the lesions are not very clear. As shown in Fig. 1, the diagnosis on KT, SH, and ZN centers is difficult, since CT images with COVID-19 patients in KT center are similar to those of the NC group, and CT images in SH and ZN centers are different from the other 3 centers. However, we can easily see that HOG images are input to our 3D-CNN model and always achieve good performance. For example, there are sensitivities of 86.52%, 93.08%, 99.28%, 94.23%, and 80.00% in KT, WH, KT2, SH, and ZN centers, respectively. Because there are differences between multi-center CT images, and HOG images can maintain good invariance to image geometric and optical deformations. We convert 3D CT images into HOG images, which can reduce the structural differences between multi-center data and thus improve the diagnostic performance of COVID-19.
Meanwhile, in HOG images, compared with the LogisticR, LogisticR-G, LeastR, and LeastR-G methods that do not consider the relationship between and within multi-center data at the same time, our MCSL method uses multiple regularizers to learn the relationship between and within multiple centers and thus has achieved higher performance. For example, our MCSL method has the highest sensitivity and achieves results of 94.38%, 93.08%, 99.76%, 99.04%, and 93.17% in KT, WH, KT2, SH, and ZN centers, respectively, which also has higher sensitivity than RT-PCR such as sputum (72%) and nasal swabs (63%) [47]. In addition, although there are structural differences between multi-center CT images, our MCSL method always maintains a sensitivity of up to 90% in all centers. The reason is that our method contains the sample similarity constraint, which can learn the local spatial structure of each center and capture the heterogeneous information of multiple centers. Meanwhile, it includes the group sparsity and global sparsity constraints, which can learn the common features of multiple centers and enhance the generalization ability. Therefore, our method can adapt to multi-center changes and maintain good performance. However, the LogisticR, LogisticR-G, LeastR, and LeastR-G methods cannot adapt to changes in multi-center CT images, and hence their sensitivities are low in KT, SH, and ZN centers. Finally, the ROC curves of the competing methods are compared using CT images and HOG images in Fig. 3. Fig. 4 also shows the performance of the competing methods vividly on radar charts. We can see that our method has more robust performance than other competing methods.
4.4. The influence of regularization parameters of MCSL on performance
From Table 4, we get that using HOG images has more robust performance, and our MCSL method has the best performance in HOG images. Further, to study the influence of each regularization term of our MCSL method on the classification performance, we use HOG images with better performance for ablation experiments on our MCSL method. Table 5 shows the sensitivity results of our MCSL method using HOG images under different settings of regularization parameters. From this table, we can obtain the following findings. First, when setting , the MCSL method only contains a multi-center least square regression term without regularization terms. We can see that its diagnostic performance is acceptable in KT2 and SH centers, but poor in KT, WH, and ZN centers. For example, the MCSL method without regularization term obtains a sensitivity of 90.38% in SH center, but only has a sensitivity of 30.34% in KT center.
Second, when gradually adding regularization terms to our method, we can see that its performance is improved. For example, in KT center, the MCSL method including global sparseness (i.e., ) has a sensitivity of 87.08%. The MCSL method including global sparseness and similarity constraint (i.e., and ) obtains a sensitivity of 89.89%. The MCSL method including group sparseness, global sparseness, and similarity constraint (i.e., ) obtains a sensitivity of 94.38%, which shows that each regularization term of our method can affect the performance improvement.
Table 5.
Sensitivity results of our MCSL method using HOG images under different regularization terms.
| Image | Hyper-parameter | SEN (%) |
||||
|---|---|---|---|---|---|---|
| KT | WH | KT2 | SH | ZN | ||
| HOG | 30.34 | 20.77 | 99.76 | 90.38 | 57.56 | |
| 87.08 | 90.77 | 99.04 | 90.38 | 72.68 | ||
| 87.08 | 90.77 | 99.76 | 97.12 | 92.20 | ||
| 87.64 | 88.46 | 99.52 | 95.19 | 81.46 | ||
| 87.08 | 90.77 | 99.28 | 97.12 | 92.20 | ||
| 90.45 | 88.46 | 99.76 | 99.04 | 84.88 | ||
| 89.89 | 96.92 | 99.28 | 99.04 | 92.20 | ||
| 94.38 | 93.08 | 99.76 | 99.04 | 93.17 | ||
4.5. Fusion strategies
For multi-center data, information fusion can occur at the center, feature, or decision level. In this paper, we first use 3D-CNN to extract deep features from multi-center data using HOG images. We then input these multi-center features to the MCSL model to jointly learn the feature weight matrix , where each is denoted as a clinician. Finally, to comprehensively consider the diagnosis results of each clinician, we fuse the decision of each center to obtain the final diagnosis result for test subjects, namely, . Meanwhile, we attempt to conduct fusion at the center level, i.e., concatenating training subjects from multiple centers, and input these subjects to the MCSL model to learn a feature weight vector for COVID-19 diagnosis. We also attempt to perform fusion at the feature level, that is, to concatenate the features of CT images and HOG images, and then input these linearly connected features to the MCSL model to learn a feature weight vector for COVID-19 diagnosis. In Table 6, we compare the diagnosis performance of the three fusion methods, and the results show that decision fusion has better performance. For example, decision fusion, center fusion, and feature fusion methods have accuracies of 97.21%, 96.51%, and 96.51% in KT center, accuracies of 97.85%, 96.41%, and 94.74% in WH center, accuracies of 99.63%, 99.18%, and 98.88% in KT2 center, accuracies of 99.40%, 92.24%, and 95.52% in SH center, and accuracies of 96.08%, 91.86%, and 93.36% in ZN center. Decision fusion can comprehensively consider the relationship between multi-center data and jointly analyze the diagnosis results of different classifiers to obtain the best performance, which is very similar to the situation in real life where multiple doctors jointly diagnose suspected cases to improve the diagnosis accuracy. The disadvantage of center fusion may be that multiple centers are merged into one center, and the relationship between multi-center data is ignored, thereby eliminating the advantages of multi-center decision-making. The disadvantage of feature fusion may be that the fused features have higher dimensionality, and different features may also interfere with each other, which reduces the diagnostic performance. Meanwhile, in feature fusion, high-dimensional features take more time to train, and the time consumption is about three times that of decision fusion and central fusion, which is not conducive to fast training of the model to suit different scenarios.
Table 6.
Diagnosis performance of center fusion, feature fusion, and decision fusion.
| Center | Method | ACC (%) | SEN (%) | SPE (%) | PRE (%) | UAR (%) | F1-score (%) | AUC (%) |
|---|---|---|---|---|---|---|---|---|
| KT | Center fusion | 96.51 | 94.94 | 97.22 | 93.89 | 96.08 | 94.41 | 98.79 |
| Feature fusion | 96.51 | 91.01 | 98.99 | 97.59 | 95.00 | 94.19 | 99.24 | |
| Decision fusion | 97.21 | 94.38 | 98.48 | 96.55 | 96.43 | 95.45 | 99.29 | |
| WH | Center fusion | 96.41 | 93.08 | 97.92 | 95.28 | 95.50 | 94.16 | 98.75 |
| Feature fusion | 94.74 | 98.46 | 93.06 | 86.49 | 95.76 | 92.09 | 99.38 | |
| Decision fusion | 97.85 | 93.08 | 100.00 | 100.00 | 96.54 | 96.41 | 99.44 | |
| KT2 | Center fusion | 99.18 | 99.28 | 99.14 | 98.10 | 99.21 | 98.69 | 99.94 |
| Feature fusion | 98.88 | 99.04 | 98.81 | 97.41 | 98.93 | 98.22 | 99.57 | |
| Decision fusion | 99.63 | 99.76 | 99.57 | 99.05 | 99.66 | 99.40 | 99.88 | |
| SH | Center fusion | 92.24 | 87.50 | 94.37 | 87.50 | 90.94 | 87.50 | 96.29 |
| Feature fusion | 95.52 | 94.23 | 96.10 | 91.59 | 95.17 | 92.89 | 97.78 | |
| Decision fusion | 99.40 | 99.04 | 99.57 | 99.04 | 99.30 | 99.04 | 99.98 | |
| ZN | Center fusion | 91.86 | 81.95 | 96.29 | 90.81 | 89.12 | 86.15 | 96.77 |
| Feature fusion | 93.36 | 92.68 | 93.67 | 86.76 | 93.18 | 89.62 | 97.39 | |
| Decision fusion | 96.08 | 93.17 | 97.38 | 94.09 | 95.28 | 93.63 | 98.87 | |
5. Discussions
5.1. Comparison with the related methods for COVID-19 diagnosis
Based on HOG images corresponding to chest CT, we evaluate our MCSL methods against eleven state-of-the-art COVID-19 diagnosis methods. Table 7 shows the performance of these competing methods. We can see that although the method from Toraman et al. [48] has high sensitivity, they use limited X-ray images for the diagnosis, and hence their robustness needs to be verified. Meanwhile, most of these methods are based on CT images instead of X-ray images for imaging screening of COVID-19 since chest CT can better reflect lung abnormalities in the early diagnosis of the disease [2]. In addition, compared with CNN methods, we also can see that our 3D-CNN has the overall best performance, such as mean accuracy of 96.64%, mean sensitivity of 90.62%, and mean specificity of 99.35% in five centers. After using our 3D-CNN model to extract multi-center features, we use the MCSL method for diagnosis. We can see that diagnostic performance has been further improved. The reason is that these competing methods are restricted to a single-center or treat multiple centers into one center and thus ignore the relationship between and within multi-center data. However, our MCSL method can select the most discriminative features by learning the relationship between and within multiple centers for COVID-19 diagnosis and thus has achieved higher performance. For example, our MCSL method has the best performance overall and obtains mean accuracy of 98.03%, mean sensitivity of 95.89%, and mean specificity of 99.00% in five centers.
Table 7.
Performance comparison of some related methods for COVID-19 diagnosis (Mean).
| Image | Method | Ref. | Subject | ACC | SEN | SPE |
|---|---|---|---|---|---|---|
| X-ray | BCNN | [18] | Two centers: 68 COVID-19, 2786 bacterial pneumonia, 1504 non-COVID-19 viral pneumonia, 1583NC |
89.82 | / | / |
| X-ray | CapsNet | [48] | One center: 231 COVID-19, 500 NC | 91.24 | 96.00 | 80.95 |
| CT | ResNet | [10] | Six centers: 468 COVID-19, 1551 CAP, 1303 NC | / | 90.33 | 94.67 |
| CT | U-net, DCN, FCN | [14] | Ten centers: 704 COVID-19, 498 NC | 94.81 | 95.39 | 94.46 |
| CT | DenseNet | [21] | Seven centers: 924 COVID-19, 342 other pneumonia | 81.15 | 79.70 | 76.40 |
| CT | U-net, DeCoVNet | [52] | One center: 313 COVID-19, 229 NC | 90.10 | 84.00 | 98.20 |
| CT | U-Net, ResNet | [22] | Seven centers: 3084 COVID-19, 5941 others | / | 87.03 | 96.60 |
| CT | U-Net++, ResNet | [19] | Five centers: 723 COVID-19, 413 NC | / | 97.40 | 92.20 |
| CT | Feature selection, KNN | [38] | Unknown: 216 COVID-19, unknown | 96.00 | 74.00 | / |
| CT | AFS-DF | [20] | Six centers: 1495 COVID-19, 1027 CAP | 91.79 | 93.05 | 89.95 |
| CT-H | 3D-CNN | Ours | Five centers: 1034 COVID-19, 2298 NC | 96.64 | 90.62 | 99.35 |
| CT-H | 3D-CNN, MCSL | Ours | Five centers: 1034 COVID-19, 2298 NC | 98.03 | 95.89 | 99.00 |
Note: CT-H denotes the HOG images corresponding to chest CT images; boldface denotes the best performance; community-acquired pneumonia (CAP).
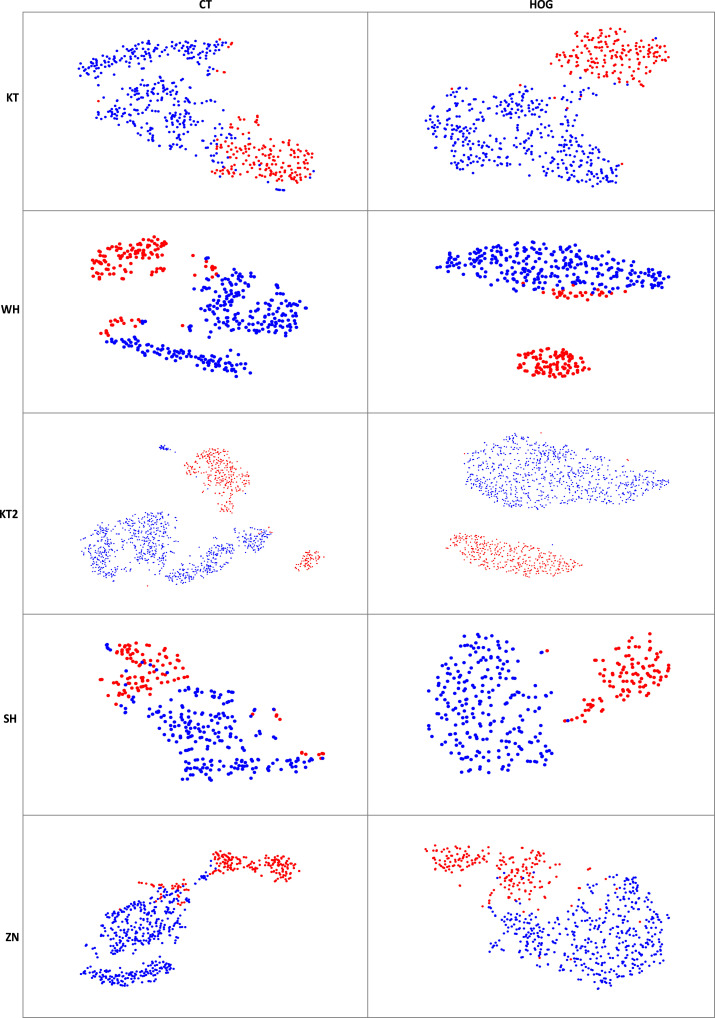
5.2. Visualization analysis
We use the t-distributed stochastic neighbor embedding (t-SNE) method of MATLAB software to visualize high-level features. We pop FC9-2, FC8-60, and FC7-800 layers and add a global max-pooling layer to extract these features from testing images (e.g., CT images and HOG images). Fig. 5 shows the t-SNE visualization results of the features extracted from 3D-CNN using CT images and HOG images, respectively, where red dots indicate patients with COVID-19 and blue dots indicate NCs. From the t-SNE feature distribution maps, we can get the following findings. The features extracted from CT images have large intra-class differences and small inter-class differences. For example, in KT center, blue dots of the same category are divided into two pieces, and blue and red dots of different categories are close to each other. After we convert CT images to HOG images, we can see that the intra-class differences of the corresponding feature maps have become smaller, while the inter-class differences have become larger, which indicates that HOG images can improve the diagnostic performance.
Fig. 5.
The t-SNE visualization results illustrate features extracted from 3D-CNN using CT images and HOG images in five centers. (Red dots indicate patients with COVID-19 and blue dots indicate NCs).
5.3. Limitations and future direction
Our approach has achieved appealing performance, but there are still limitations, which we highlight here. First, when using 3D-CNN to extract deep features, we do not consider the relationship between multi-center data. We can add the relationship among multi-center data to this network to further learn the more discriminative features. Second, in this paper, we only use a single modality (i.e., chest CT image) for COVID-19 diagnosis. We can use multi-modal data (e.g., chest CT, chest radiograph, and clinical information) to improve diagnosis accuracy [30]. Third, our MCSL model is supervised, and we can further explore a semi-supervised method to adapt to scenarios with a large number of suspected cases [49]. Finally, we do not conduct the lung segmentation and lesion area positioning tasks in the paper [50]. Since SARS-CoV-2 mainly infects human lungs, we can perform the lung segmentation task to further improve diagnostic performance for COVID-19 in the future, and conduct the lesion area positioning tasks to assist doctors in diagnosing COVID-19 [22], [51].
6. Conclusions
In this paper, we propose a MCSL and decision fusion scheme exploiting chest CT images for automatic COVID-19 diagnosis. Specifically, considering the inconsistency of data in multiple centers, we first convert 3D CT images into HOG images to reduce the structural differences between multi-center data and enhance the generalization performance. We then employ a 3D-CNN model to learn the useful information between and within 3D HOG image slices and extract multi-center features, which saves the doctor’s time to screen the pathological slices. Furthermore, we employ the proposed MCSL model that learns the intrinsic structure between multiple centers and within each center and selects discriminative features to jointly train multi-center classifiers. Finally, the decision fusion is used to comprehensively consider the relationship between multi-center data and jointly analyze the diagnosis results of different classifiers to improve the diagnostic performance. The extensive experiments are performed on the chest CT images from the five centers to validate the effectiveness of the proposed method, where four central data are used as the training set and the remaining one as the testing set. The results demonstrate that the proposed method can improve COVID-19 diagnosis performance and precede state-of-the-art methods.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
This work was supported partly by National Natural Science Foundation of China [Nos. 61871274, 61801305, and 81571758], National Natural Science Foundation of Guangdong Province, China [Nos. 2020A1515010649 and 2019A1515111205], (Key) Project of Department of Education of Guangdong Province, China [No. 2019KZDZX1015], Guangdong Province Key Laboratory of Popular High Performance Computers, China [No. 2017B030314073], Guangdong Laboratory of Artificial-Intelligence and Cyber-Economics (SZ), Shenzhen Peacock Plan, China [Nos. KQTD2016053112051497 and KQTD2015033016104926], Shenzhen Key Basic Research Project, China [Nos. JCYJ20190808165209410, 20190808145011259, JCYJ20180507184647636, GJHZ20190822095414576, JCYJ20170302153337765, JCYJ20170302150411789, JCYJ20170302142515949, GCZX2017040715180580, GJHZ20180418190529516, and JSGG20180507183215520 ], NTUT-SZU Joint Research Program [No. 2020003], Hong Kong Research Grants Council [No. PolyU 152035/17E], Beijing Municipal Science and Technology Project, China [Z211100003521009], and Guangzhou Science and Technology Planning Project, China [202103010001].
References
- 1.Bai Y., Yao L., Wei T., Tian F., Jin D.-Y., Chen L., Wang M. Presumed asymptomatic carrier transmission of COVID-19. JAMA. 2020;323:1406–1407. doi: 10.1001/jama.2020.2565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Wiersinga W.J., Rhodes A., Cheng A.C., Peacock S.J., Prescott H.C. Pathophysiology, transmission, diagnosis, and treatment of coronavirus disease 2019 (covid-19): a review. JAMA. 2020;324:782–793. doi: 10.1001/jama.2020.12839. [DOI] [PubMed] [Google Scholar]
- 3.WHO . 2021. Who coronavirus disease (COVID-19) dashboard. https://covid19.who.int/ (accessed 15 2021) [Google Scholar]
- 4.Corman V.M., Landt O., Kaiser M., Molenkamp R., Meijer A., Chu D.K., Bleicker T., Brünink S., Schneider J., Schmidt M.L., Mulders D.G., Haagmans B.L., van der Veer B., van den Brink S., Wijsman L., Goderski G., Romette J.-L., Ellis J., Zambon M., Peiris M., Goossens H., Reusken C., Koopmans M.P., Drosten C. Detection of 2019 novel coronavirus (2019-nCoV) by real-time RT-PCR. Euro Surveill. 2019;25(2020) doi: 10.2807/1560-7917.ES.2020.25.3.2000045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ai T., Yang Z., Hou H., Zhan C., Chen C., Lv W., Tao Q., Sun Z., Xia L. Correlation of chest CT and RT-PCR testing for coronavirus disease 2019 (COVID-19) in China: A report of 1014 cases. Radiology. 2020;296:E32–E40. doi: 10.1148/radiol.2020200642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Chandra T.B., Verma K., Singh B.K., Jain D., Netam S.S. Coronavirus disease (COVID-19) detection in chest X-ray images using majority voting based classifier ensemble. Expert Syst. Appl. 2021;165 doi: 10.1016/j.eswa.2020.113909. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Kanne J.P., Little B.P., Chung J.H., Elicker B.M., Ketai L.H. Essentials for radiologists on COVID-19: An update-radiology scientific expert panel. Radiology. 2020;296:E113–E114. doi: 10.1148/radiol.2020200527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Long C., Xu H., Shen Q., Zhang X., Fan B., Wang C., Zeng B., Li Z., Li X., Li H. Diagnosis of the coronavirus disease (COVID-19): rRT-PCR or ct? Eur. J. Radiol. 2020;126 doi: 10.1016/j.ejrad.2020.108961. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Fang Y., Zhang H., Xie J., Lin M., Ying L., Pang P., Ji W. Sensitivity of chest CT for COVID-19: Comparison to RT-PCR. Radiology. 2020;296:E115–E117. doi: 10.1148/radiol.2020200432. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Li L., Qin L., Xu Z., Yin Y., Wang X., Kong B., Bai J., Lu Y., Fang Z., Song Q., Cao K., Liu D., Wang G., Xu Q., Fang X., Zhang S., Xia J., Xia J. Using artificial intelligence to detect COVID-19 and community-acquired pneumonia based on pulmonary CT: Evaluation of the diagnostic accuracy. Radiology. 2020;296:E65–E71. doi: 10.1148/radiol.2020200905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Wang S.-H., Govindaraj V.V., Górriz J.M., Zhang X., Zhang Y.-D. Covid-19 classification by fgcnet with deep feature fusion from graph convolutional network and convolutional neural network. Inf. Fusion. 2021;67:208–229. doi: 10.1016/j.inffus.2020.10.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Nour M., Cömert Z., Polat K. A novel medical diagnosis model for COVID-19 infection detection based on deep features and Bayesian optimization. Appl. Soft Comput. 2020;97 doi: 10.1016/j.asoc.2020.106580. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Wang S., Kang B., Ma J., Zeng X., Xiao M., Guo J., Cai M., Yang J., Li Y., Meng X., Xu B. A deep learning algorithm using CT images to screen for corona virus disease (COVID-19) Eur. Radiol. 2021;31:6096–6104. doi: 10.1007/s00330-021-07715-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Gao K., Su J., Jiang Z., Zeng L.-L., Feng Z., Shen H., Rong P., Xu X., Qin J., Yang Y., Wang W., Hu D. Dual-branch combination network (DCN): Towards accurate diagnosis and lesion segmentation of COVID-19 using CT images. Med. Image Anal. 2021;67 doi: 10.1016/j.media.2020.101836. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Castiglione A., Vijayakumar P., Nappi M., Sadiq S., Umer M. Covid-19: Automatic detection of the novel coronavirus disease from CT images using an optimized convolutional neural network. IEEE Trans. Ind. Inf. 2021;17:6480–6488. doi: 10.1109/TII.2021.3057524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Wang S.-H., Nayak D.R., Guttery D.S., Zhang X., Zhang Y.-D. Covid-19 classification by ccshnet with deep fusion using transfer learning and discriminant correlation analysis. Inf. Fusion. 2021;68:131–148. doi: 10.1016/j.inffus.2020.11.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ji S., Xu W., Yang M., Yu K. 3D convolutional neural networks for human action recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2013;35:221–231. doi: 10.1109/TPAMI.2012.59. [DOI] [PubMed] [Google Scholar]
- 18.Ghoshal B., Tucker A. 2020. Estimating uncertainty and interpretability in deep learning for coronavirus (COVID-19) detection. arXiv preprint arXiv:2003.10769. [Google Scholar]
- 19.Wang B., Jin S., Yan Q., Xu H., Luo C., Wei L., Zhao W., Hou X., Ma W., Xu Z., Zheng Z., Sun W., Lan L., Zhang W., Mu X., Shi C., Wang Z., Lee J., Jin Z., Lin M., Jin H., Zhang L., Guo J., Zhao B., Ren Z., Wang S., Xu W., Wang X., Wang J., You Z., Dong J. Ai-assisted CT imaging analysis for COVID-19 screening: Building and deploying a medical AI system. Appl. Soft Comput. 2021;98 doi: 10.1016/j.asoc.2020.106897. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Sun L., Mo Z., Yan F., Xia L., Shan F., Ding Z., Song B., Gao W., Shao W., Shi F., Yuan H., Jiang H., Wu D., Wei Y., Gao Y., Sui H., Zhang D., Shen D. Adaptive feature selection guided deep forest for COVID-19 classification with chest CT. IEEE J. Biomed. Health Inf. 2020;24:2798–2805. doi: 10.1109/JBHI.2020.3019505. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Wang S., Zha Y., Li W., Wu Q., Li X., Niu M., Wang M., Qiu X., Li H., Yu H., Gong W., Bai Y., Li L., Zhu Y., Wang L., Tian J. A fully automatic deep learning system for COVID-19 diagnostic and prognostic analysis. Eur. Respir. J. 2020;56 doi: 10.1183/13993003.00775-2020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Jin C., Chen W., Cao Y., Xu Z., Tan Z., Zhang X., Deng L., Zheng C., Zhou J., Shi H., Feng J. Development and evaluation of an artificial intelligence system for COVID-19 diagnosis. Nature Commun. 2020;11:5088. doi: 10.1038/s41467-020-18685-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Dalal N., Triggs B. 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. 2005. Histograms of oriented gradients for human detection; pp. 886–893. [Google Scholar]
- 24.Tian S., Bhattacharya U., Lu S., Su B., Wang Q., Wei X., Lu Y., Tan C.L. Multilingual scene character recognition with co-occurrence of histogram of oriented gradients. Pattern Recognit. 2016;51:125–134. [Google Scholar]
- 25.Zhou T., Lu H., Yang Z., Qiu S., Huo B., Dong Y. The ensemble deep learning model for novel COVID-19 on CT images. Appl. Soft Comput. 2021;98 doi: 10.1016/j.asoc.2020.106885. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Wang Z., Liu Q., Dou Q. Contrastive cross-site learning with redesigned net for COVID-19 CT classification. IEEE J. Biomed. Health Inf. 2020;24:2806–2813. doi: 10.1109/JBHI.2020.3023246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Song X., Li H., Gao W., Chen Y., Wang T., Ma G., Lei B. Augmented multicenter graph convolutional network for COVID-19 diagnosis. IEEE Trans. Ind. Inf. 2021;17:6499–6509. doi: 10.1109/TII.2021.3056686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Lei H., Huang Z., Zhang J., Yang Z., Tan E.-L., Zhou F., Lei B. Joint detection and clinical score prediction in parkinson’s disease via multi-modal sparse learning. Expert Syst. Appl. 2017;80:284–296. [Google Scholar]
- 29.Lei B., Yang P., Wang T., Chen S., Ni D. Relational-regularized discriminative sparse learning for alzheimer’s disease diagnosis. IEEE Trans. Cybern. 2017;47:1102–1113. doi: 10.1109/TCYB.2016.2644718. [DOI] [PubMed] [Google Scholar]
- 30.Xie Y., Zhang J., Xia Y., Fulham M., Zhang Y. Fusing texture, shape and deep model-learned information at decision level for automated classification of lung nodules on chest CT. Inf. Fusion. 2018;42:102–110. [Google Scholar]
- 31.Liu Y., Jiang C., Zhao H. Using contextual features and multi-view ensemble learning in product defect identification from online discussion forums. Decis. Support Syst. 2018;105:1–12. [Google Scholar]
- 32.Wang Y., Xu W. Leveraging deep learning with LDA-based text analytics to detect automobile insurance fraud. Decis. Support Syst. 2018;105:87–95. [Google Scholar]
- 33.Alexandre L.A. Gender recognition: A multiscale decision fusion approach. Pattern Recognit. Lett. 2010;31:1422–1427. [Google Scholar]
- 34.Lei H., Huang Z., Zhou F., Elazab A., Tan E., Li H., Qin J., Lei B. Parkinson’s disease diagnosis via joint learning from multiple modalities and relations. IEEE J. Biomed. Health Inf. 2019;23:1437–1449. doi: 10.1109/JBHI.2018.2868420. [DOI] [PubMed] [Google Scholar]
- 35.Tibshirani R. Regression shrinkage and selection via the lasso. J. R. Statist. Soc. Ser. B-Methodol. 1996;58:267–288. [Google Scholar]
- 36.Zou H., Hastie T. Regularization and variable selection via the elastic net. J. R. Stat. Soc. Ser. B Stat. Methodol. 2005;67:301–320. [Google Scholar]
- 37.Zhang D., Shen D. Multi-modal multi-task learning for joint prediction of multiple regression and classification variables in alzheimer’s disease. NeuroImage. 2012;59:895–907. doi: 10.1016/j.neuroimage.2011.09.069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Shaban W.M., Rabie A.H., Saleh A.I., Abo-Elsoud M.A. A new COVID-19 patients detection strategy (CPDS) based on hybrid feature selection and enhanced KNN classifier. Knowl.-Based Syst. 2020;205 doi: 10.1016/j.knosys.2020.106270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Zhu X., Song B., Shi F., Chen Y., Hu R., Gan J., Zhang W., Li M., Wang L., Gao Y., Shan F., Shen D. Joint prediction and time estimation of COVID-19 developing severe symptoms using chest CT scan. Med. Image Anal. 2021;67 doi: 10.1016/j.media.2020.101824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Mokhtari M., Rabbani H., Mehri-Dehnavi A., Kafieh R., Akhlaghi M.-R., Pourazizi M., Fang L. Local comparison of cup to disc ratio in right and left eyes based on fusion of color fundus images and OCT B-scans. Inf. Fusion. 2019;51:30–41. [Google Scholar]
- 41.Dian R., Li S., Fang L., Wei Q. Multispectral and hyperspectral image fusion with spatial–spectral sparse representation. Inf. Fusion. 2019;49:262–270. [Google Scholar]
- 42.Zhu X., Suk H.I., Shen D. A novel matrix-similarity based loss function for joint regression and classification in AD diagnosis. NeuroImage. 2014;100:91–105. doi: 10.1016/j.neuroimage.2014.05.078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Beck A., Teboulle M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Imaging Sci. 2009;2:183–202. [Google Scholar]
- 44.Chen X., Pan W., Kwok J.T., Carbonell J.G. 2009 Ninth IEEE International Conference on Data Mining. 2009. Accelerated gradient method for multi-task sparse learning problem; pp. 746–751. [Google Scholar]
- 45.Zhou J., Chen J., Ye J. Arizona State University; 2011. Malsar: Multi-Task Learning Via Structural Regularization, Vol. 21; pp. 1–50. [Google Scholar]
- 46.Chang C.-C., Lin C.-J. Libsvm: A library for support vector machines. ACM Trans. Intell. Syst. Technol. (TIST) 2011;2:1–27. [Google Scholar]
- 47.Wang W., Xu Y., Gao R., Lu R., Han K., Wu G., Tan W. Detection of SARS-CoV-2 in different types of clinical specimens. JAMA. 2020;323:1843–1844. doi: 10.1001/jama.2020.3786. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Toraman S., Alakus T.B., Turkoglu I. Convolutional capsnet: A novel artificial neural network approach to detect COVID-19 disease from X-ray images using capsule networks. Chaos Solitons Fractals. 2020;140 doi: 10.1016/j.chaos.2020.110122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Adeli E., Thung K., An L., Wu G., Shi F., Wang T., Shen D. Semi-supervised discriminative classification robust to sample-outliers and feature-noises. IEEE Trans. Pattern Anal. Mach. Intell. 2019;41:515–522. doi: 10.1109/TPAMI.2018.2794470. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Wu Y.H., Gao S.H., Mei J., Xu J., Fan D.P., Zhang R.G., Cheng M.M. Jcs: An explainable COVID-19 diagnosis system by joint classification and segmentation. IEEE Trans. Image Process. 2021;30:3113–3126. doi: 10.1109/TIP.2021.3058783. [DOI] [PubMed] [Google Scholar]
- 51.Shan F., Gao Y., Wang J., Shi W., Shi N., Han M., Xue Z., Shen D., Shi Y. Abnormal lung quantification in chest CT images of COVID-19 patients with deep learning and its application to severity prediction. Med. Phys. 2021;48:1633–1645. doi: 10.1002/mp.14609. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Wang X., Deng X., Fu Q., Zhou Q., Feng J., Ma H., Liu W., Zheng C. A weakly-supervised framework for COVID-19 classification and lesion localization from chest CT. IEEE Trans. Med. Imaging. 2020;39:2615–2625. doi: 10.1109/TMI.2020.2995965. [DOI] [PubMed] [Google Scholar]