Exploring Dynamics and Structure of Biomolecules, Cryoprotectants, and Water Using Molecular Dynamics Simulations: Implications for Biostabilization and Biopreservation

Abstract

Successful stabilization and preservation of biological materials often utilize low temperatures and dehydration to arrest molecular motion. Cryoprotectants are routinely employed to help the biological entities survive the physicochemical and mechanical stresses induced by cold or dryness. Molecular interactions between biomolecules, cryoprotectants, and water fundamentally determine the outcomes of preservation. The optimization of assays using the empirical approach is often limited in structural and temporal resolution, whereas classical molecular dynamics simulations can provide a cost-effective glimpse into the atomic-level structure and interaction of individual molecules that dictate the macroscopic behavior. Computational research on biomolecules, cryoprotectants, and water has provided invaluable insights into the development of new cryoprotectants and the optimization of preservation methods. Here, we describe the rapidly evolving state of the art for molecular simulations of these complex systems, summarize the molecular-scale protective and stabilizing mechanisms, and discuss the challenges that motivate continued innovation in this field.

1. INTRODUCTION

The preservation of living cells, tissues, and organs has immense significance for many fields such as human reproduction, organ transplantation, regenerative medicine, and germplasm resource banking. With the new era of precision medicine on the horizon, biobanking of an overwhelming number of well-phenotyped biospecimens will accelerate and reduce the cost of gene and biomarker discovery for detecting disease progression and treatment response. Major breakthroughs in liposome technology and recent advances in molecular biology and recombinant technology have fueled the rapid development of liposome-based drug delivery systems (1) and therapeutic proteins (2), respectively. Stabilization methods are urgently needed to maintain the high quality of these biopharmaceuticals for extended shelf life.

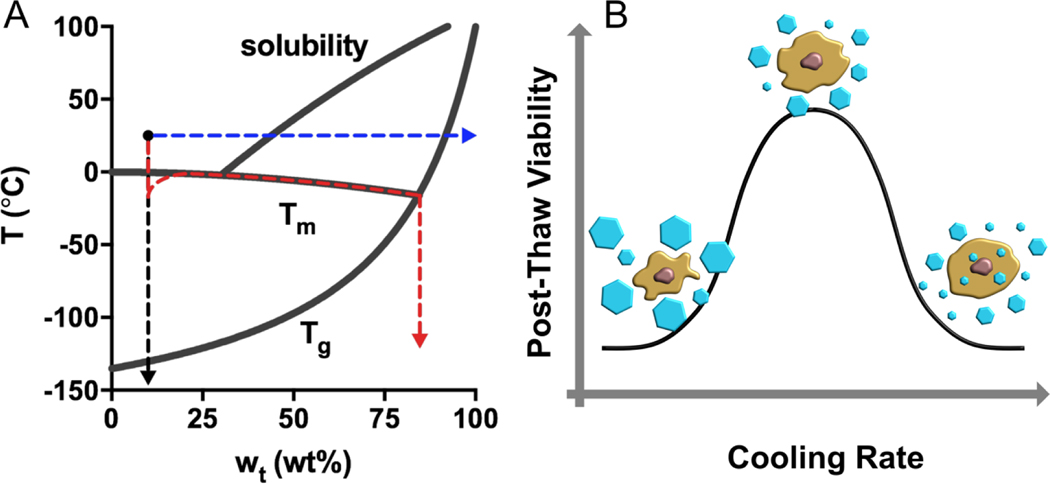
Stabilization and preservation methods include four major approaches: slow freezing, vitrification, freeze-drying, and drying (Figure 1). Slow freezing is a classic preservation method for cellular products in which the sample is frozen at an optimal rate. The freezing rate is selected to be slow enough to avoid intracellular ice formation (IIF) but fast enough to prevent excessive dehydration in the presence of extracellular ice. Minimizing these two components of potential freezing-induced damage is referred to as the two-factor hypothesis (Figure 1) (3). Avoiding IIF has been a common practice in most cryopreservation applications, but the presence of intracellular ice may not necessarily be lethal, depending on multiple factors such as the ice nucleation temperature and cooling and thawing rates (4).

Figure 1.

Preservation pathways for a trehalose solution (initial condition: 10 wt% and 25 °C) and the two-factor hypothesis for slow-freezing of living cells. (A) In a slow-freezing method, ice crystallization drives the unfrozen trehalose solution to follow the liquidus curve until it crosses the $T_g$ (red). Direct vitrification strategy brings the temperature of the solution below $T_g$ ultra-rapidly in the absence of ice formation (black). Isothermal vitrification removes water from the solution until the concentration yields a $T_g$ that is below 25 °C (blue). (B) High cooling rates may be associated with intracellular ice formation that causes mechanical disruption of membranes and organelles; Slow cooling rates may result in excessive cell dehydration and prolonged exposure of cells to a high electrolyte concentration. There is an optimal cooling rate at which the two mechanisms of damage are balanced, yielding the highest post-thaw viability.

Vitrification is an ice-free process in which the liquid is cooled rapidly to outrun ice crystallization and transits into a noncrystalline solid state below the glass transition temperature (T_g) (5), which almost always requires the combination of an ultrarapid cooling rate and a very high concentration of glass-forming solutes (which can themselves be toxic). During thawing, the rewarming rate must be sufficiently high to prevent devitrification, especially in large-volume systems such as thick tissues or solid organs (6).

Freeze-drying, also known as lyophilization, works by freezing the aqueous material, then reducing the pressure and adding heat to allow the frozen water to sublimate, leaving the residual solution phase to become amorphous (7). Dry preservation is facilitated by isothermal vitrification in which water is removed from the aqueous material by drying at a constant temperature (usually the ambient temperature) until the T_g of the residual concentrated solution becomes higher than ambient to complete the glass transition (8). Without exception, ice formation and/or glass transition occur(s) in the above-mentioned processes, inducing a variety of physicochemical and mechanical stresses on the preserved biological materials such as low temperature, dehydration, ice crystallization, high salt concentration, and pH fluctuation.

Glass transition:

a second-order phase transition in amorphous materials from a brittle “glass” into a viscous liquid as the temperature increases

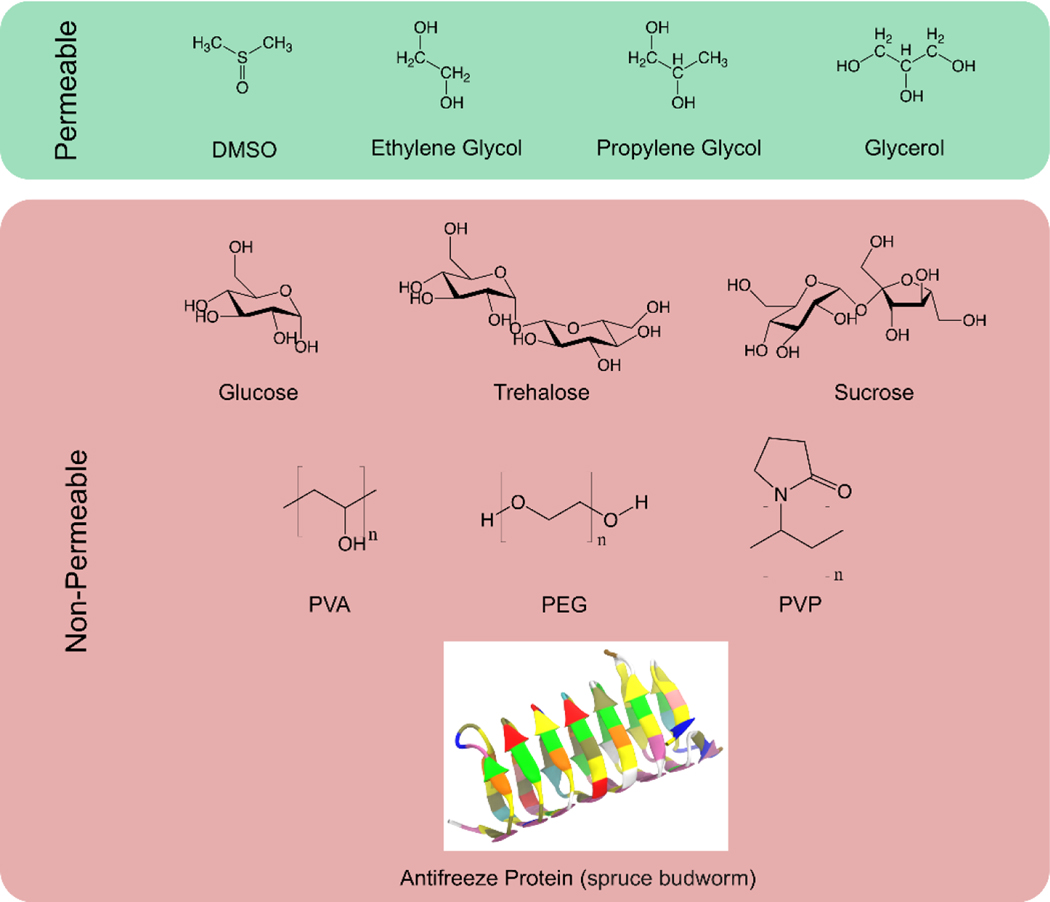
The use of cryoprotective agents (CPAs), also known as cryoprotectants, has become routine to help preserved biologics overcome the detrimental stresses induced by stabilization methods. CPAs can depress ice nucleation, promote glass transition, help preserve the integrity of plasma membranes, or stabilize the native structure of proteins. There are two main two categories of cryoprotectants (Figure 2). Permeable CPAs, including alcohols, sulfoxides, and amides, can readily penetrate the cell membrane by diffusion, acting in both extra- and intracellular spaces. Dimethyl sulfoxide (Me₂SO), for example, is the mostly frequently used cryoprotectant in cell-banking applications due to its high membrane permeability, low cost, and ease of use (9). Nonpermeable CPAs, such as sugars, sugar alcohols, and polymers, are typically excluded from the intracellular milieu unless artificial interruption is involved (10). In nature, certain insects, nematodes, rotifers, and tardigrades accumulate sugars in the body to help survive severe dryness or extreme temperatures they often encounter, a phenomenon called anhydrobiosis (11). Because of their ability to mimic nature’s strategy, various sugars, especially trehalose, have been employed for protecting pharmaceuticals, food, and cells during freezing and drying (12). In addition, antifreeze proteins (AFPs) and antifreeze glycoproteins (AFGPs) are produced by many species of fish, insects, and plants that inhabit cold environments, which can modulate the unfavorable effect of ice on their lives (13, 14). As a synthetic mimic of AF(G)Ps, poly(vinyl alcohol) (PVA) has been recognized as an ice recrystallization inhibitor of unusually high activity (15, 16). Both AF(G)Ps and their synthetic mimics have been included in a number of cryoprotective formulations (17, 18).

Figure 2.

Representative permeable or non-permeable cryoprotectants that have been widely employed for the stabilization and preservation of a variety of biologics.

Cryoprotective agent (CPA), or cryoprotectant:

a substance used to protect biological materials from freezing and/or drying damage

Ice recrystallization:

a process in which large ice crystals grow at the cost of small ones to effectively reduce interfacial energy

Despite the prevalence of CPA use, our knowledge about the interactions between cellular components (e.g., proteins, lipid bilayers, or nuclei acids), cryoprotectants, and water is far from comprehensive. These interactions fundamentally dictate the effectiveness of CPAs and the outcomes of preservation. Therefore, a better understanding of such interplay would significantly advance the optimization of preservation methods and rationalize the development of novel CPAs. The past two decades have witnessed a growing body of research focusing on the complexity of the systems consisting of macromolecules or biostructures, cryoprotectants, and water. Experimental approaches such as nuclear magnetic resonance (NMR) (19), infrared spectroscopy (20, 21), Raman spectroscopy (22), neutron diffraction (23–25), and neutron scattering (26) have been used to investigate the dynamics and structure of the CPA–water mixtures or lipid bilayers or proteins that are solvated in aqueous CPA solutions.

Nuclear magnetic resonance (NMR) spectroscopy:

an analytical chemistry technique for determining the content, molecular structure, or purity of a sample

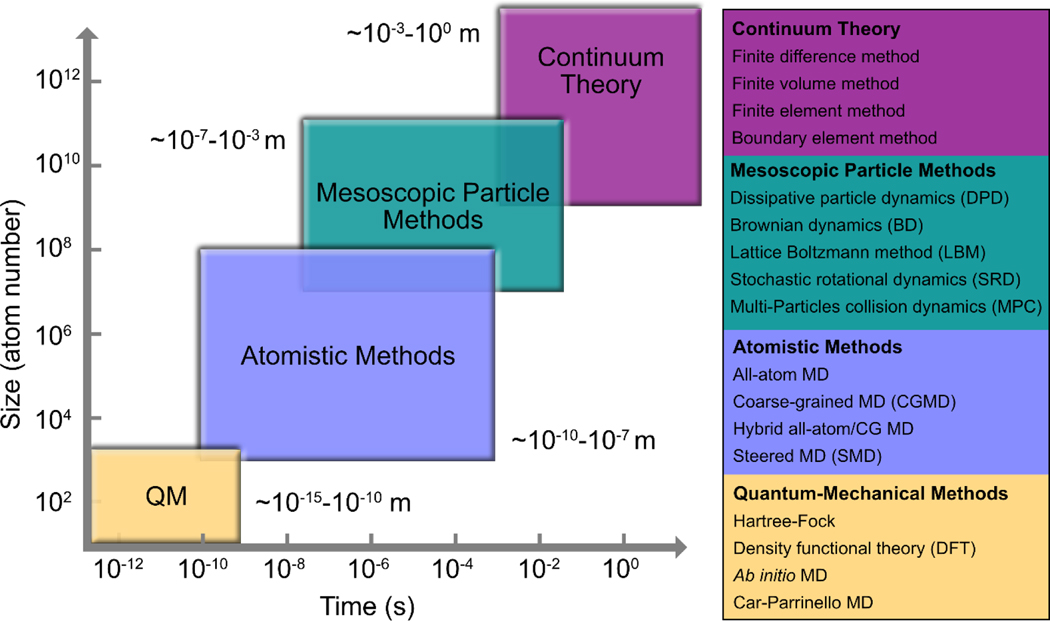
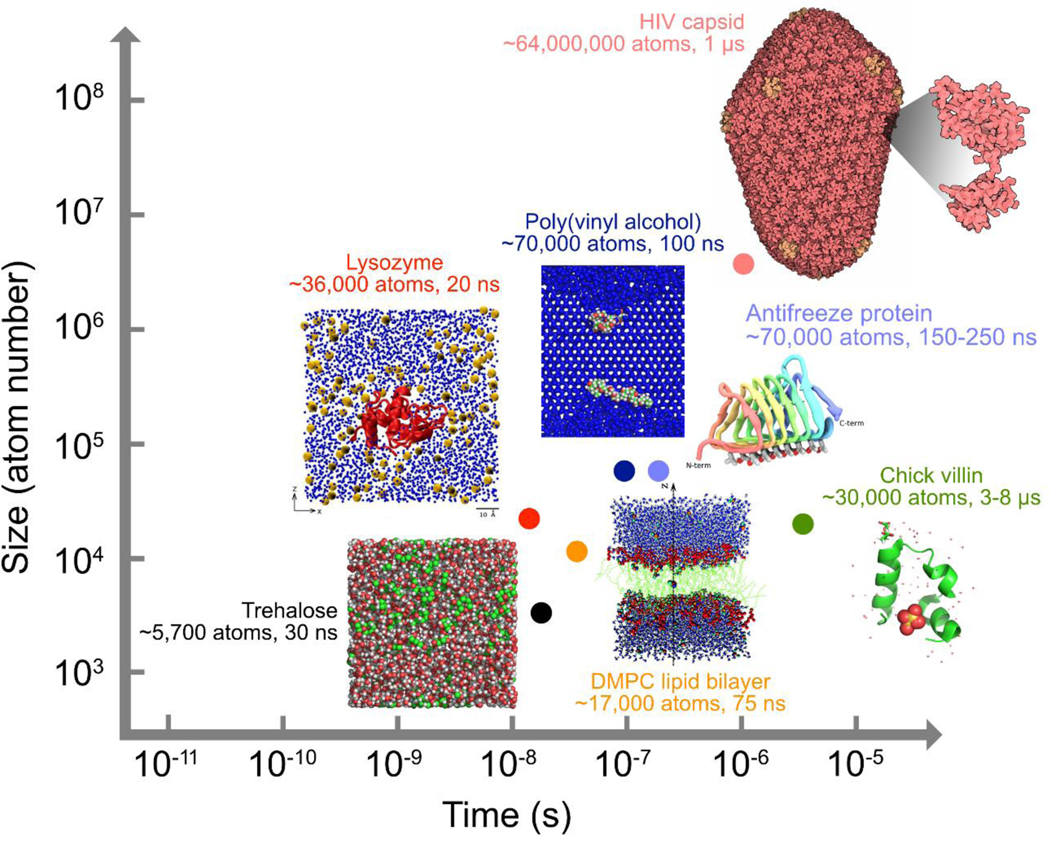
However, experimental techniques are generally limited in their spatial and temporal resolution, yielding ensemble average properties rather than the motion of individual molecules (27). For example, NMR is a remarkably successful technique for determining the conformational state of solutes, but it provides little structural information about the hydrogen-bonding network between solutes and the solvent through their exchangeable hydrogen sites (28). In contrast, molecular dynamics (MD) simulations are able to capture sets of time-evolved snapshots of atomic coordinates (i.e., trajectories) and produce detailed “movies” of how a biomolecule behaves over time under a variety of tunable conditions (see the sidebar) (29). MD simulations have been a powerful tool to probe the structure, dynamics, and interactions of biological molecules such as proteins, lipids, carbohydrates, and nucleic acids, providing adequate spatial and temporal resolution (Figure 3) at a reasonable computational cost. Other computational modeling techniques cover a range of spatial and temporal scales (Figure 3). Quantum mechanical (QM) calculations investigate bond cleavage and formation, distribution of charge and spin, and reaction mechanisms by simulating the electronic properties of a subset of atoms within a molecule. But the applicability of QM methods is limited to small systems or short timescales due to their excessive computational cost (29a). Coarse-grained (CG) MD simulations typically map several heavy atoms, along with the associated hydrogen atoms, to a single united particle. But the atomistic details of the intermediate structures that are often overlooked by CG MD simulations are desirable for the analysis of molecular interactions such as hydrogen bonding. Monte Carlo (MC) methods employ system sizes (i.e., from a few hundred to a few million molecules) similar to those used in MD simulations. But MC simulations are less favorable than MD for liquid systems because they are subject to a large number of rejected moves and a decrease in the sampling efficiency due to a large probability of selecting random moves for which two or more molecules overlap (29b). Mesoscopic particle methods provide a link between the lower spatiotemporal scales that MC and MD simulations focus on and the macroscopic behavior of a system. Popular mesoscopic particle methods include dissipative particle dynamics (DPD), Brownian dynamics (BD), and the lattice Boltzmann method (LBM). Simulation at the mesoscale is efficient in capturing hydrodynamic interactions, whereas the “all-atom” simulations with explicit solvent particles such as MD are too expensive computationally. Nonetheless, thanks to the recent advances in specialized hardware, parallelization algorithms, and simulation methodology, the speed, size, and accuracy of MD simulations have improved substantially over the past few years. MD simulations have now been performed on large macromolecular systems such as ribosomes (30) and HIV-1 capsid (30a) as well as on smaller systems on longer timescales of up to 10–100 μs (31). Figure 4 has presented the spatial and temporal scales covered by the MD simulations for biopreservation and some μs-long biomolecular simulations beyond the field.

Figure 3.

The hierarchy of size and time scales covered by various computational modeling techniques

Figure 4.

Size and time scales covered by representative MD simulations for biopreservation and some state-of-the-art biomolecular simulations beyond the field. Inset pictures were adapted from References [33], [64], [67], [106] and [114] under the Creative Commons Attribution license or with permission from American Chemical Society. Images of HIV capsid and chick villin were adapted from entries 3J3Q and 1YRF deposited at the Protein Data Bank (PDB).

Hydrogen bond:

an attractive force between a hydrogen atom and an electronegative atom composed of one molecule and another electronegative atom

Monte Carlo (MC) method:

a stochastic determination of the properties of a system by sampling configurations from a statistical ensemble by a random walk algorithm

Coarse-grained (CG):

refers to an approach to representing a group of atoms by a pseudoatom to handle large system sizes and simulation timescales

MOLECULAR DYNAMICS SIMULATION

In MD, a molecule is described as a series of charged atoms linked by bonds. MD simulation steps through time, alternately computing the forces acting on each atom and using Newton’s laws of motion to update the positions and velocities of all the atoms in the system. The forces are computed using a set of force-field parameters. The force field is a collection of equations to describe the time evolution of bond lengths, bond angles, torsions, and the nonbonding van der Waals and electrostatic interactions between atoms. The associated constants are typically obtained from ab initio or semiempirical quantum mechanical calculations or by fitting to experimental data such as neutron, X-ray, and electron diffraction; NMR; and infrared, Raman, and neutron spectroscopy.

The predictive role of MD simulations has been well documented in the fields of materials science and drug discovery. In 2000, a pioneering MD simulation study predicted that a hypothetical isolated graphene monolayer could have unusually high thermal conductivity due to the lack of interlayer coupling (31a), four years before the actual experimental discovery of graphene (31b). It was not until 2008 that researchers experimentally demonstrated the extremely high thermal conductivity of a graphene monolayer (31c). MD simulations have also been widely used to identify and optimize bioactive compounds for the development of new drugs (31d). In the field of biopreservation, however, most MD simulations have been aiding our understanding of existing experimental data.

One of the purposes of this review is to stimulate researchers in related areas to fully realize the potential of MD simulations in designing and predicting the outcome of future experiments such as new CPA development and protocol optimization. We review recent progress in the MD simulations of biomolecules or biostructures, cryoprotectants, and water. Since computer simulations that are closely coupled with experimental techniques are not uncommon, we also include complementary experimental findings, if any. We begin by summarizing the MD simulations on aqueous cryoprotectant solutions. We then review the state of the art in terms of lipid bilayer–cryoprotectant and protein–cryoprotectant interactions by MD investigations. Finally, we discuss the challenges that can stimulate the continued innovation through MD simulations with implications for stabilization and preservation of biologics.

2. MOLECULAR INTERPLAY BETWEEN CRYOPROTECTANT AND WATER/ICE

2.1. Structure and Dynamics of Cryoprotectant–Water Mixtures

Determining the molecular structures of cryoprotectants and water in their mixtures is an important step toward understanding the mechanisms of cryoprotection, such as the colligative property and the structuring or destructuring effect of the solute (25, 32). A series of MD simulations have revealed that, in a mixture of water and cryoprotectants, particularly polyhydroxy cryoprotectants (e.g., alcohols and sugars), the hydrogen-bonding interactions between cryoprotectant and water contribute to the diminution of bulk water and the establishment of the hydration shell of the cryoprotectant as the solute concentration increases. Accordingly, both the structure and the hydrogen-bonding network of the CPA–water mixture are heterogeneous and transit from being solvent dominant to being solute dominant as the CPA concentration increases, as demonstrated by the MD simulation investigations described below.

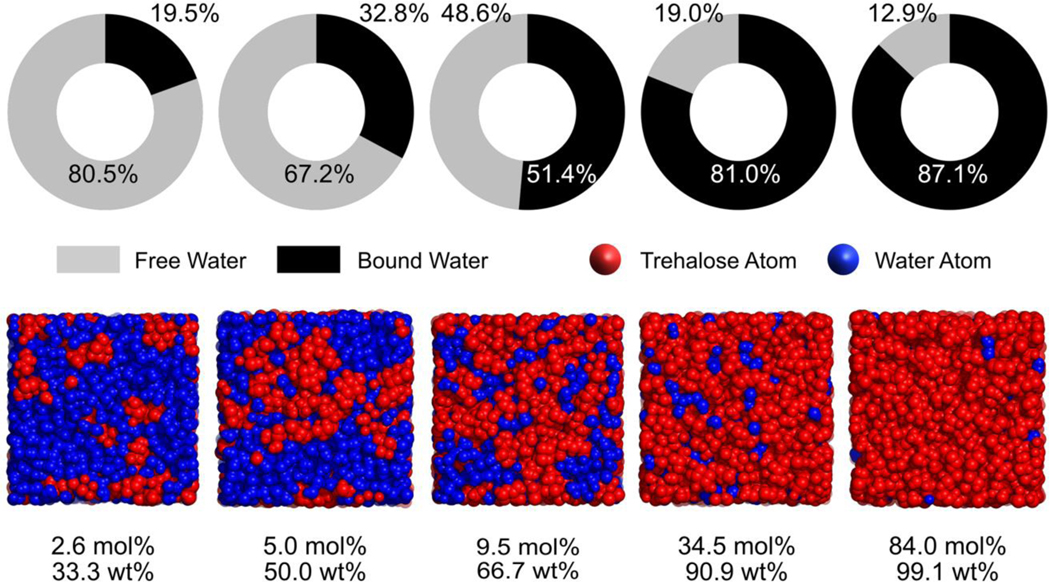
In relatively dilute aqueous cryoprotectant solutions, the nature of bulk water can be retained since the average number of hydrogen bonds associated with one water molecule is almost the same as the value for pure water (23, 33), although the tetrahedral ordering of the hydrogen-bonding network of water reduces in the presence of cryoprotectants (34). In glycerol–water mixtures of x_g ≤ 0.1 (where x_g is the mole fraction of glycerol) (23, 35), for example, the average number of hydrogen bonds per water molecule maintains equivalent to that in pure water, even though the bulk water is gradually recruited by the first hydration shell of glycerol with the increasing solute concentration. In other words, hydrogen bonds between glycerol and water can replace a portion of the original water–water hydrogen bonds, thereby keeping the number of hydrogen bonds per water molecule constant (23, 35). In the dilute glycerol region of x_g = 0.05, 40% of the total glycerol molecules were isolated by the percolating, bulky water clusters (23). As a result, any glycerol molecule can interact with no more than one other glycerol molecule through hydrogen bonding at this concentration. A similar phenomenon has been observed for aqueous trehalose solutions (33). In a trehalose–water mixture of x_t= 0.026 (where x_t is the mole fraction of trehalose), for instance, more than 80% of the total water molecules are identified as “free” water, which has no interaction with trehalose, whereas trehalose molecules are scattered within the bulk water (Figure 5) (33).

Figure 5.

Shares of “bound” and “free” water in trehalose-water mixtures at 295 K (upper panel); Snapshots of the MD simulation box showing the water or trehalose percolation at each of the trehalose–water concentrations under investigation (lower panel, 295 K). This figure was created using the raw data from Ref (33).

In highly concentrated cryoprotectant–water mixtures, however, the bulk water molecules are completely depleted and thus the structure of the cryoprotectant–water mixture becomes significantly solute dominant. For example, the large, percolating glycerol clusters are able to span the full dimensions of the glycerol–water system when the glycerol mole fraction reaches 0.8 (i.e., 95.3 wt%), with the majority (56%) of water molecules existing as single monomers (23). Consequently, the water–water hydrogen-bonding interaction becomes rare. In contrast, each glycerol molecule can form more than five intermolecular glycerol–glycerol hydrogen bonds at such a high concentration (23). Similarly, as the trehalose mole fraction approaches 0.345, an interconnected trehalose skeleton (consisting of ≥92.6% of the total trehalose molecules) emerges, but water molecules are only scattered within the matrix (33). Meanwhile, more than 80% of the total water molecules have become “bound” to trehalose (Figure 5). The formation of an extended solute network may have various implications for the stabilization and preservation of biologics. On one hand, the large, percolating sugar clusters have been suggested to increase the mixture’s resistance to shear deformation and mechanical stability (36). On the other hand, when the cells are compressed within the void volumes in a rigidified sugar network, the mechanical shear may induce physical injury to the cells (33).

During the transition from a solvent-dominant mode to a solute-dominant one, there is a narrow, intermediate region where both cryoprotectant and water clusters of medium sizes exist. Within this region, the number of intercryoprotectant hydrogen bonds increases as the solute concentration increases, accompanied by the gradual decrease in the hydration number of cryoprotectant (23, 33, 37, 38). For the glycerol–water mixtures, a so-called bipercolating cluster regime exists at a concentration range of x_g= 0.25–0.5. Similarly, in the trehalose–water mixture of x_t= 0.095, about half of the total water molecules are “bound” and the other half stay “free,” wheras no giant trehalose clusters can be found at this concentration (Figure 5) (33). In this intermediate region, the disruption of cryoprotectant against the hydrogen-bonding characteristics of bulk water becomes significant, as shown by in the distribution (f_i) of water molecules forming i hydrogen bonds with neighboring water molecules (32, 39, 40). For an aqueous trehalose solution of 66 wt% (equivalent to x_t= 0.1), the peak of f_i shifts to i= 2, versus i= 4 for pure water (40). Likewise, for a Me₂SO–water mixture with a mole fraction of x_D= 0.35, a given water molecule has the highest probability (42%) of forming only two hydrogen bonds with the neighboring water molecules (32).

Although the computational simulations discussed above were conducted at around room temperature (298 K), the transition of structure and hydrogen bonding in the mixture across the full concentration range of the cryoprotectant is independent of temperature (25, 33, 38). The combined neutron diffraction and computational simulation study on glycerol–water mixtures of three concentrations (i.e., x_g = 0.1, 0.25, and 0.8) at their respective melting point demonstrated that the characteristics of nanosegregation of glycerol and water molecules persist at low temperatures (25). Similarly, the proportions of “bound” and “free” water and the clustering of trehalose molecules at 150 K follow the same trends as those observed at 295 K over the concentration range under investigation, although the respective quantities change due to the depressed molecular mobility at 150 K (33).

Dynamically, MD simulations showed that the translational mobility of both water and cryoprotectant decreases as the cryoprotectant concentration increases (33, 41, 42). In pure water, the self-diffusion coefficient of water molecules is 2.212 × 10⁻⁹ m²/s at 300 K, but it is only 0.844 × 10⁻⁹ m²/s in a glycerol–water mixture of x_g= 0.13 at the same temperature (43). The slowing down of water diffusion in the presence of CPA globally delays the clustering of water molecules to form ice embryos in a supercooled liquid, which can postpone ice formation and promote ice-free vitrification. The self-diffusion coefficient of trehalose is 1.645 × 10⁻¹⁰ m²/s in the aqueous solution of ~30 wt%, whereas the diffusivity is only 0.067 × 10⁻¹⁰ m²/s when the solution concentration is 79.6 wt% (42). Furthermore, in the cryoprotectant–water system, the diffusivity of water could be up to two orders of magnitude larger than that of cryoprotectant, depending on temperature and concentration (42, 44). For example, the self-diffusion coefficient of water is more than one order of magnitude larger than that of sucrose or trehalose at a concentration of 6 wt%, but the difference increased to two orders of magnitude at a concentration of 72.4 wt%, which is consistent with the accompanying NMR results (44). Depending on the extent of heterogeneity of the CPA–water mixture, the slower CPA molecules may perform as “roadblocks” to prevent the local gathering of water molecules to form ice embryos, which can delay ice nucleation and cause the mixture to favor glass formation.

Self-diffusion coefficient:

the diffusion coefficient of species in the absence of a chemical potential gradient

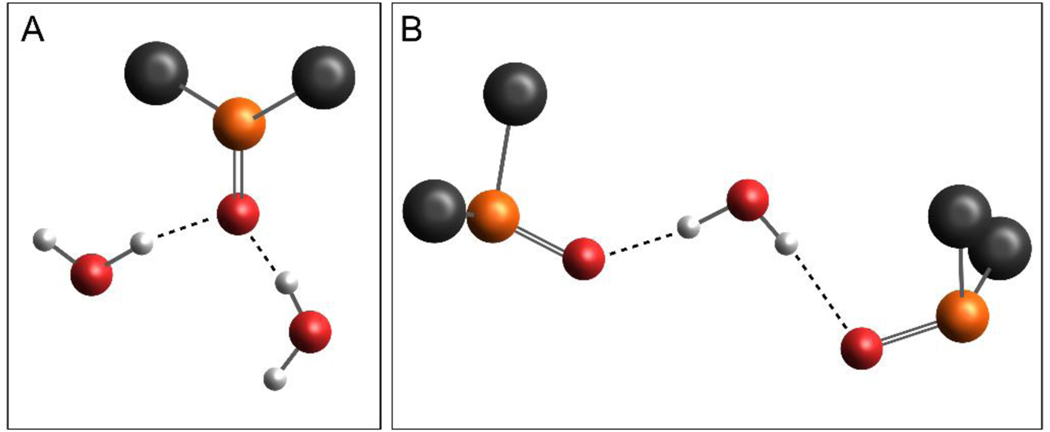
Me₂SO is an exception to the above-mentioned solute clustering phenomenon. The S=O group of Me₂SO restricts it to be primarily a hydrogen-bond acceptor, eliminating the possibility of Me₂SO molecules to connect with each other to form solute clusters through O–H···O hydrogen-bonding. But the highly polar S=O group facilitates the formation of two prevalent arrangements with water: 1Me₂SO–2H₂O and 2Me₂SO–1H₂O (Figure 6). The 1Me₂SO–2H₂O aggregate is formed when two water molecules hydrogen-bond to the oxygen atom of the same Me₂SO molecule, whereas the 2Me₂SO–1H₂O structure features a central water molecule with one Me₂SO hydrogen-bonded to each of its hydrogen atoms (39). Several MD simulations suggest that the 1Me₂SO–2H₂O aggregates dominate in the dilute region of Me₂SO–water mixtures (32, 39, 45, 46). The average angle between the two hydrogen bonds in this molecular arrangement is nearly tetrahedral (32), which may contribute to the ordered structure of the first hydration shell of Me₂SO (45, 47). A chain may form as the 1Me₂SO–2H₂O complexes connect with each other using one of the two water molecules as the bridge (46). Also, the prevalence of 1Me₂SO–2H₂O aggregates is suggested to be responsible for the strong deviation of the aqueous Me₂SO solution from the ideal mixing behavior (39). For example, the self-diffusion coefficient profiles for both water and Me₂SO present the global minimum at the mole fraction of ~0.33, coinciding with a molar ratio of Me₂SO to water of 1:2 (39). But the 2Me₂SO–1H₂O aggregates become more abundant than the 1Me₂SO–2H₂O ones in the concentrated region (39). Moreover, the stronger Me₂SO–water hydrogen bonds generally have longer lifetime than those formed between water molecules (32). The water–water hydrogen bonds within the first hydration shell tend to be shorter and more linear, thereby living longer than their counterparts in the bulk water region (47).

Figure 6.

(A) Snapshot of a typical 1Me₂SO–2H₂O aggregate in which one Me₂SO molecule acting as the hydrogen-bond acceptor forms hydrogen bonds with two water molecules. The 1Me₂SO-2H₂O structure was adapted with permission from Ref (45) Copyright (1992) American Chemical Society. (B) Snapshot of a 2Me₂SO–1H₂O aggregate which includes a central water molecule acting as the hydrogen-bond donor and two Me₂SO molecules being the hydrogen-bond acceptors. The image was adapted from Ref (39), with the permission of AIP Publishing. (Color index: grey-carbon, orange-sulfur, red-oxygen, and white-hydrogen)

The superiority of trehalose as a cryoprotectant partially results from its perturbation to the hydrogen-bonding network of water (i.e., the destructuring effect) and the retarded dynamics of water with its hydration shell (24, 40, 48–50). MD simulation studies suggest that trehalose has a destructuring effect on the tetrahedral hydrogen-bonding network of water near the solute especially, at a concentration of 30 wt% and above (49, 50). The hydration number for trehalose ranges from 12 to 16 in a trehalose–water mixture of as low as 4–6 wt% (37, 40). A recent combined neutron diffraction and empirical potential structure refinement (EPSR) simulation study found that there were ~11 trehalose–water hydrogen bonds per trehalose molecule, although no significant clustering of trehalose was observed due to the relatively dilute concentration (x_t = 0.026) (24). Note, however, that in comparison with a previous study using neutron diffraction and EPSR simulation (28), both the deuteration of nonexchangeable hydrogen of trehalose and the rapid exchange of hydrogen and deuterium between water and the hydroxyl groups of trehalose seem to be critical to reveal the destructuring effect of trehalose on water using the neutron scattering method (24). The translational and rotational mobilities of water in the vicinity of trehalose are also restricted. Furthermore, intramolecular hydrogen bonds in trehalose can confine the movement of sugar rings and hydroxyl groups involved in these internal hydrogen bonds, particularly in the concentrated region (e.g., 50 wt% and above) (37, 40).

2.2. Glass Transition of Cryoprotectant Solution

Vitrification is a unique strategy to achieve the stabilization and preservation of biologics. The mobility of biomolecules can be drastically retarded in a noncrystalline amorphous solid such that the degradation of biomolecules is inhibited. MD simulation of the glass transition phenomenon provides a glimpse of the changing profile of dynamics and structure of cryoprotectants and their mixtures with water over temperature, which can be useful in predicting the T_g and determining the characteristics of the glass-forming liquid (42, 51–54). We emphasize the implication of using MD simulation to predict the T_g, as it could be the only feasible approach to determine the T_g of the compositions that are not accessible by current experimental techniques (54). When the temperature of the simulation system decreases rapidly, the temperature dependence of heat capacity (42, 53), density (37), specific volume (52, 54), or diffusion coefficient (42, 51) exhibits a discontinuity at a certain temperature, which is identified as the T_g with varying consistency with experimental values (usually an overestimate of 10–50 K).

One of benefits that certain cryoprotectants confer is to make a stronger glass. A strong glass tends to maintain its glassy structure and resist crystallization under T_g and exhibits a gradual change from a glass to a liquid upon heating (55). In contrast, the structure of a fragile glass changes abruptly even with a small deviation from the T_g (55–57). Fragile glass-forming liquids typically feature a sharp peak of heat capacity near T_g due to the rapid change in relaxation time with the temperature. In contrast, strong glass-forming liquids exhibit a transition that extends for tens of degrees in temperature (56). The presence of Me₂SO significantly broadens the glass transition of the Me₂SO–water system in the profile of the constant-volume heat capacity (c_V) as a function of temperature (53), thereby contributing to a stronger glass that confers kinetic stability against ice crystallization at low temperatures (58). Similarly, when a trehalose–water system of 80 wt% or 98 wt% was cooled in a series of MD simulations, the mean-squared displacement (MSD) profile for trehalose presented a so-called boson peak near T_g (37), indicating a strong glass-forming system (59). Moreover, the hydrogen-bonding lifetime for any type of the glass in trehalose–water is an order of magnitude larger than that in the liquid state, but interestingly, the composition of the hydrogen-bonding network exhibits no noticeable change through the glass transition (42).

Boson peak:

a low-frequency vibrational feature in the energy range of 2–10 meV at low temperatures, a characteristic of amorphous materials

Increasing the T_g will offer more flexibility in storage temperature and increase the minimum cooling rate needed for vitrification. The discovery of salts as T_g-enhancing agents is particularly attractive given that various salts have already been routinely supplemented to maintain a physiological milieu. Thermal analysis experiments have revealed that the T_g increases upon the addition of Na₂HPO₄ into anhydrous trehalose (60, 61). In contrast, the addition of NaH₂PO₄ gradually decreases the T_g of the trehalose–NaH₂PO₄ mixture (60, 61). Understanding the molecular mechanism governing the T_g-enhancing phenomenon would be critical for discovering new ionic additives that can promote the glass transition.

MD simulations of trehalose–phosphate mixtures proposed that trehalose molecules and HPO₄²⁻ anions formed shorter, more linear, and therefore longer-lived hydrogen bonds, yielding significantly strengthened hydrogen-bonding network between trehalose and HPO₄²⁻ compared with the network within the trehalose–H₂PO₄⁻ mixtures (60). HPO₄²⁻ anions only slightly self-aggregate, forming clusters comprising no more than five anions. However, large clusters (containing more than 10 anions) of H₂PO₄⁻ were observed within the trehalose–H₂PO₄⁻ mixtures (60). On one hand, the strengthened hydrogen-bonding network and few small self-aggregates of HPO₄²⁻ are responsible for the enhanced T_g of the trehalose–HPO₄²⁻ mixtures, compared with trehalose alone. On the other hand, the weak trehalose–anion hydrogen bonds and the prevalence of large-sized clusters contribute to the decrease in T_g of the trehalose–H₂PO₄⁻ mixtures (60).

Compared with trehalose, which is a nonpermeable cryoprotectant, T_g-enhancing compositions based on permeable cryoprotectants may offer more benefits due to the achievement of reinforced glass transition in both the extra- and intracellular spaces. Divalent cations including Mg²⁺ and Ca²⁺ elevate the final T_g of the anhydrous glycerol–salt mixtures. For example, a mixture of MgCl₂ and glycerol (molar ratio 3:2) has a T_g of ~320 K which is approximately 130 K higher than glycerol alone (62). MD simulations of glycerol mixed with MgCl₂, CaCl₂, KCl, or NaCl revealed that the presence of a strong interaction between the divalent cations and the negatively charged oxygen atoms of glycerol significantly strengthened the networking within mixtures of MgCl₂–glycerol and CaCl₂–glycerol, yielding an increase in T_g (63). The divalent cations are homogeneously distributed and act as ionic bridges to connect the neighboring glycerol–cation complexes in a manner analogous to polymerization (Figure 7) (63). For monovalent cations such as Na⁺ or K⁺, a limited effect on T_g was observed since the interactions between the hydroxyl groups of glycerol and Na⁺ or K⁺ are of the same order of magnitude as the original glycerol–glycerol hydrogen bonds (63). Also, due to salt crystallization, the heterogeneity of the of NaCl–glycerol and KCl–glycerol mixtures (Figure 7) confines the cation–dipole interactions to the interfaces between the glycerol-rich and electrolyte-rich regions (63).

Figure 7.

Snapshots of the simulation boxes of MgCl₂–glycerol (left) and NaCl-glycerol (right) mixtures, respectively, at 560 K. The molar ratio of electrolyte to glycerol is 2. Only Mg²⁺ (green), Na⁺ (yellow), and Cl⁻ (grey) are shown. While the MgCl₂–glycerol mixture is homogeneous, the NaCl–glycerol mixture has become heterogeneous with indication of NaCl crystallization. This figure was created using the raw data from Ref (63).

Overall, at least two factors seem to be necessary for ions to be qualified as T_g-enhancing additives. First, the candidate ions need to form interactions with the cryoprotectant molecules that are stronger than the original cryoprotectant–cryoprotectant hydrogen bonds, preferably acting as bridges to connect the neighboring pairs into a polymer-like network. Second, the candidate ions and their accompanying counterions should be resistant to self-aggregation, especially crystallization. A highly heterogeneous mixture may diminish the interactions between ions and cryoprotectants by limiting these interactions to the cluster–cluster interfaces.

2.3. Antifreeze Agent at the Interface Between Water and Ice

In nature, many species of fish, insects, and plants that inhabit cold environments produce antifreeze proteins and/or antifreeze glycoproteins. Such specialized adaptation can modulate the effect of ice on these species’ lives through thermal hysteresis, dynamic ice shaping, and ice recrystallization inhibition (64). These fascinating strategies have inspired the utilization of AFPs in the cryopreservation of red blood cells, although there is a delicate balance between AFP-induced cell preservation and AFP-induced cell damage (17, 65). Understanding the atomic-scale interactions of antifreeze compounds at the ice–water interface can provide valuable guidance for the rational design of synthetic antifreeze compounds, which could overcome the shortcomings of natural AF(G)Ps such as high cost, low availability, and instability. These disadvantages impede the large-scale production of AF(G)Ps and their use in industrial applications.

Recent MD simulations have suggested that the effectiveness of AF(G)Ps in inhibiting ice recrystallization lies in the Gibbs–Thomson effect, caused by the ice-binding phenomenon (66, 67) and long-range interaction by protein-induced water dynamics (68). The curvature generated at the ice–water interface due to ice binding leads to the depression of the local equilibrium freezing temperature, which can retard ice growth (69). The ice crystal planes that AF(G)Ps prefer to bind to depend on the species that those proteins come from. One MD simulation study proposed that the shorthorn sculpin antifreeze protein stereospecifically binds to the secondary prism face of ice, utilizing both α-helical backbone-matching to the secondary prism surface topography and matching of side chains of polar/charged residues with specific water-molecule positions in the ice surface (70). Another MD investigation on a mutant of winter flounder AFP suggests that the protein tends to stably bind to the pyramidal plane of the ice lattice with its hydrophobic residues, yielding a dramatic decrease in the ice growth rate near the ice-binding site (66). The spruce budworm Choristoneura fumiferana AFP binds indirectly to the prism face of ice crystals through a linear array of ordered water molecules that are structurally distinct from ice (67). Around the ice-binding face of the spruce budworm AFP, the water structure is ordered and the dynamics is slowed down (71). Therefore, the preconfigured solvation shell around the ice-binding face should be involved in the initial recognition and binding of spruce budworm AFP to ice, perhaps by lowering the barrier for binding and consolidation of the AFP–ice interaction surface (71).

Gibbs–Thomson effect:

the depression of the local equilibrium freezing temperature across a curved surface or interface

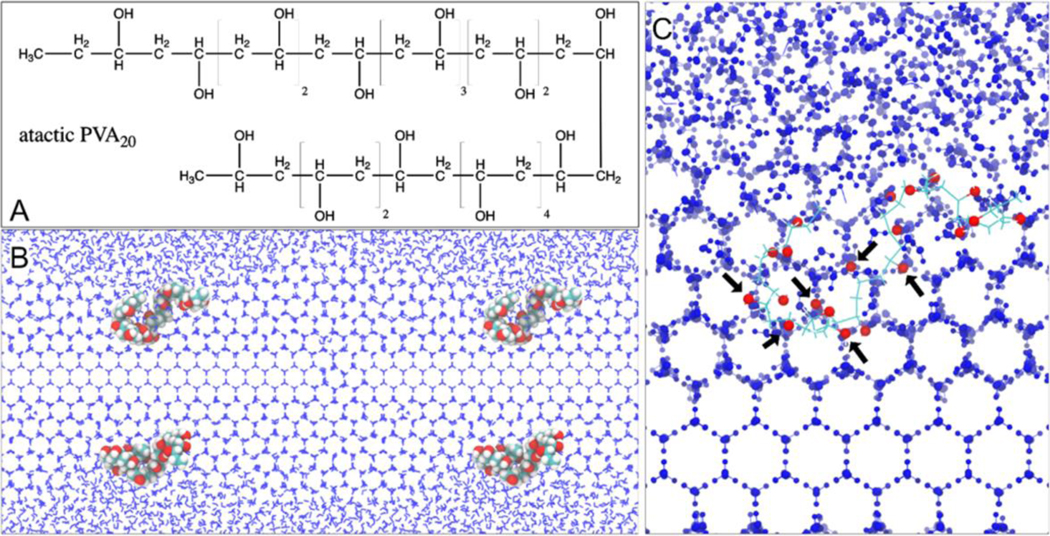
Numerous synthetic AF(G)Ps mimics have been discovered or developed in recent years, such as PVA (15, 18), double hydrophilic block copolymers (72), d-glucose derivatives bearing β-linked para-methoxyphenyl (73), and graphene oxide (74). Among them, PVA seems to be the most potent synthetic ice recrystallization inhibitor found to date. Large-scale MD simulations have been conducted to elucidate the mechanism by which PVA recognizes ice (75). Molecular recognition of ice by PVA (30–240 repeat units) involves cooperative hydrogen bonding through a zipper mechanism facilitated by matching of the distances between water molecules in the ice surface and the hydroxyl groups along the PVA chain (75). As a result, PVA molecules selectively bind to both the primary and secondary prism faces of ice (75). However, branched architectures do not improve the ice-binding activity of PVA (75). Another MD simulation study on short-chain PVA molecules (5–20 repeat units) also observed a stereoscopic, geometrical match between the hydroxyl groups of PVA and the water molecules of ice, which supports the adsorption of PVA molecules to both the basal and prism faces of ice (Figure 8) (64). Short-chain PVAs, such as PVA₅, is also incorporated into the ice lattice when the ice front engulfs the polymer molecule (64). The number of hydroxyl groups of PVA has been suggested to be a key factor determining the performance of ice recrystallization inhibition, since the PVA molecule must be large enough to prevent the joining together of adjacent curvatures in the ice front (Figure 8) (64).

Figure 8.

Role of PVA in inhibiting ice recrystallization. (A) An atactic PVA₂₀ chain with a random arrangement of the −OH groups. (B) Illustration of the Gibbs–Thomson effect due to the PVA₂₀–ice binding with two adjacent periodic images joined together. (C) Geometrical match between some of the −OH groups of PVA₂₀ (indicated by the black arrows) and the lattice of ice front. Reprinted with permission from Ref (64). Copyright (2017) American Chemical Society.

2.4. Ice Nucleation Catalysis

Ice nucleating proteins are a family of proteins that are generally localized at the outer membrane of some species of gram-negative bacteria such as Pseudomonas syringae (76) and Erwinia herbicola (77). These proteins can promote ice nucleation at a temperature close to the melting point of ice. Initiation of ice nucleation at a relatively high subzero temperature is known to reduce the probability of detrimental intracellular ice formation during slow freezing (78). In nature, diverse freeze-tolerant species such as wood frog (Rana sylvatica) rely on ice nucleating agents in the hemolymph and in the gut or skin to control the freezing of extracellular water (79). Therefore, it is critical to understand the molecular dynamics of ice nucleating proteins at the ice–water interface, which may guide the rational design of synthetic mimics of ice nucleating protein.

One MD simulation study reveals that the ice nucleating protein from Pseudomonas syringae and antifreeze proteins from spruce budworm and Tenebrio molitor may share a similar β-helical fold and interact with water through threonine-based repeat units (80). Since the surface of an ice nucleating protein is presumably larger than the size of a critical ice embryo, it may serve as the template for ice nucleation. In contrast, the small size of AFPs allows them to bind only to the ice front and inhibit the growth of ice crystal due to the Gibbs–Thomson effect (80). In another MD investigation, a different β-helical model for the ice nucleating protein produced by Pseudomonas borealis suggests that both sides of the structure can be the ice-forming template, since the tandem arrays of amino acids are able to organize water molecules into the ice-like clathrate structures (81). A recent study of the ice nucleating protein inaZ from the bacterium Pseudomonas syringae, employing a combination of interface-specific sum frequency generation (SFG) spectroscopy and MD simulation, demonstrated that the hydrogen bonding at the water–protein interface imposed structural ordering on the adjacent water network, driving the ice nucleation in the hydration shell (82). Ice nucleation is further facilitated by the unique hydrophilic–hydrophobic patterns on the surface of inaZ and by the highly effective removal of latent heat from the nucleation site (82).

3. MOLECULAR INTERACTION BETWEEN CRYOPROTECTANT AND CELL MEMBRANE

Although the effect of CPAs on the dynamics and structure of aqueous matrix helps protect biologics from freezing- or drying-induced damages, this effect is not solely responsible for the stabilization of biomolecules or biostructures (83). MD simulations provide a powerful approach to understanding the direct interactions between CPAs and biomolecules or biostructures, providing a comprehensive picture of the protection mechanisms rendered by CPAs.

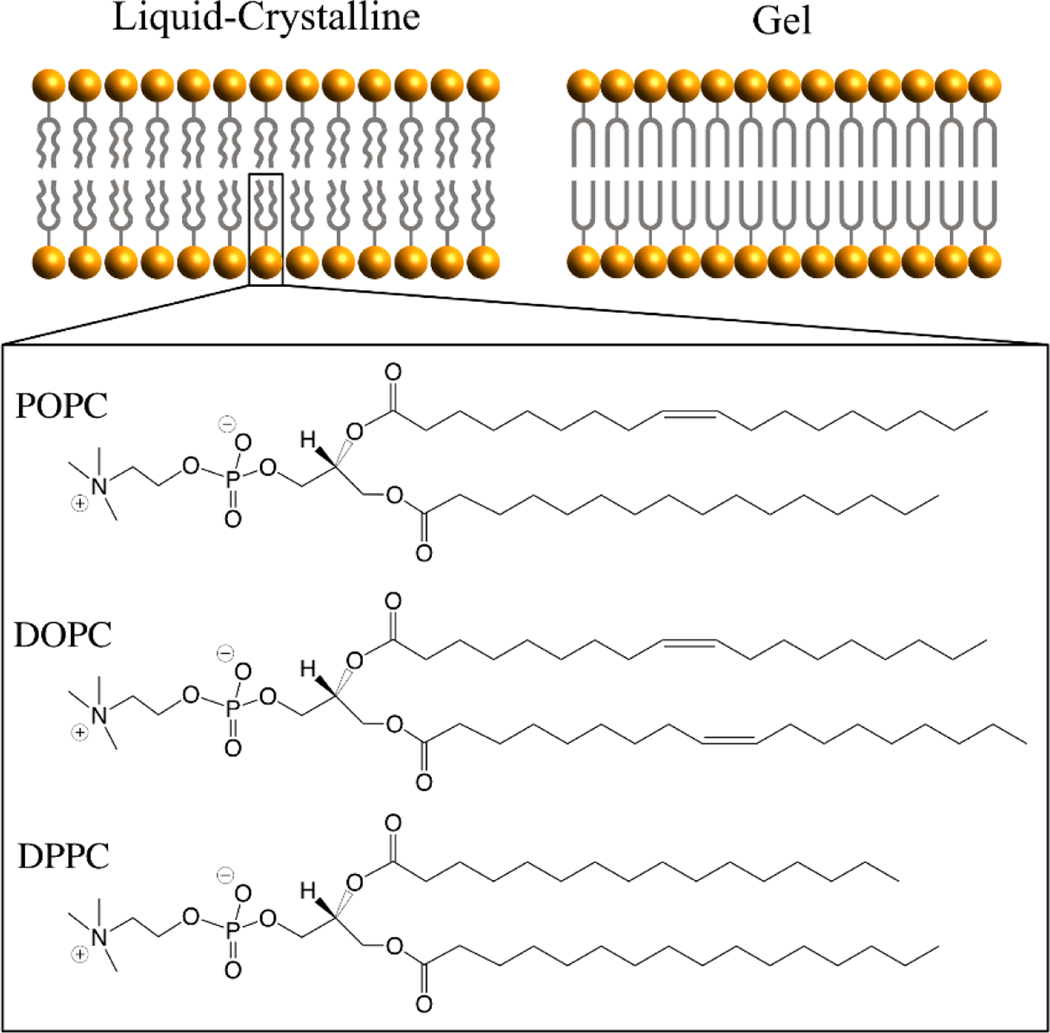
Cell membranes serve as the barrier and gatekeeper to the intracellular milieu by semipermeability. Most cellular membranes, especially plasma membranes, are made of (glycero)phospholipids that are composed of choline, phosphate, and glycerol linked to two fatty acid chains. At low temperatures, the lipid acyl chains can pack tightly to form a rigid, ordered arrangement (i.e., the gel state), whereas the lipid bilayers transit to a fluid, disordered arrangement (i.e., the liquid-crystalline state) when the temperature increases above a characteristic temperature known as the phase-transition temperature (Figure 9). Planar phospholipid bilayers, especially in the liquid-crystalline state, have become the most important model system for understanding the interactions between cryoprotectants and cell membranes using MD simulation. For instance, 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphatidylcholine (POPC), 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC), and 1,2-dipalmitoyl-sn-glycero-3-phosphatidylcholine (DPPC) (Figure 9) are three of the most simulated phospholipids. A number of MD simulation studies have explored the effect of either penetrating or nonpenetrating CPAs on the structure, dynamics, and function of those lipid bilayers in a fully or less hydrated state (84–88).

Figure 9.

Cartoon structure of lipid bilayers and chemical structures of three widely-studied phospholipids (POPC, DOPC, and DPPC). The liquid-crystalline phase features randomly oriented and fluid acyl chains. Below the phase transition temperature, lipid bilayers change into the gel phase in which acyl chains are fully extended and closely packed.

3.1. Saccharide–Lipid Bilayer Interaction

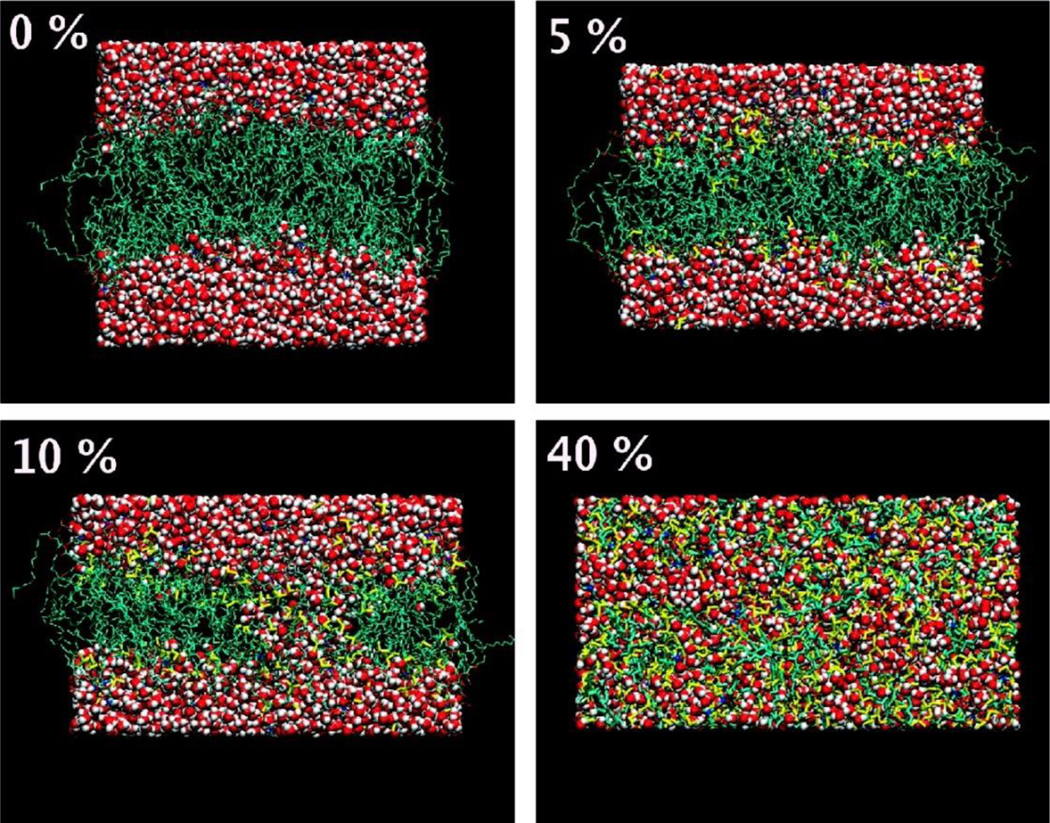
Sugars are well known as extraordinary cryoprotectants or lyoprotectants for biologics subjected to freezing, freeze-drying, or desiccation (89). In addition to the high vitrification tendency that sugars usually exhibit, the water replacement hypothesis is suggested to be the other major mechanism that regulates the sugar-mediated stabilization of cell membranes (11, 90, 91) The direct hydrogen-bonding interaction between sugars and lipids plays a critical role in the water replacement phenomenon, which has been demonstrated by solid-state NMR (92), Fourier transform infrared spectroscopy (93, 94), and differential scanning calorimetry and X-ray diffraction (95) experiments and a number of MD simulations. Through the use of liquid-crystalline phospholipid bilayers hydrated in aqueous sugar solutions as a model system, MD simulations revealed that sugar molecules could interact with the lipid headgroups without significant interruption to the structure of the lipid bilayers (96–98). At a concentration up to 18.1 wt% (~0.65 molal), trehalose can adjust its conformation to fit the space between DPPC lipid headgroups and can hydrogen-bond preferentially with the phosphate and ester groups (96). As a result, the hydration level of the lipid headgroups is reduced compared with the lipid bilayers in pure water (96). Meanwhile, neither the area per lipid headgroup (APL) nor the lipid tail order parameter is significantly affected due to the presence of trehalose (96). These phenomena were also observed for hydrated DPPC bilayers in the presence of sucrose (96). Although another MD simulation study reported that the DPPC bilayers slightly expanded laterally in the presence of 2 molal trehalose at 325 K, the difference in APL induced by trehalose was not statistically significant, since it was of the same order of magnitude as the fluctuation monitored for the DPPC bilayers in pure water (97). The total number of trehalose–DPPC and water–DPPC hydrogen bonds in the presence of 1 or 2 molal trehalose was equal to the total number of water–DPPC hydrogen bonds in the absence of trehalose, which supports the water replacement hypothesis. In addition to trehalose and sucrose, both maltose (up to 2 molal) and glucose (up to 4 molal) could also replace approximately one-fifth to one-quarter of the original water–DPPC hydrogen bonds in a bilayer system hydrated with pure water (98).

The above MD simulations were performed mostly under fully hydrated conditions, where the ratio of water to lipid is close to 30:1 (96–98). However, a dehydrated CPA–membrane system may be more relevant for our understanding of the response of cell membranes to dehydration induced by either freezing or desiccation. Leekumjorn & Sum (99) set up unilamellar bilayers with a ratio of water to lipid of 10:1 in which an inert gas layer of argon molecules kept the lipid bilayer from interacting with its periodic images due to the periodic boundary conditions. These authors discovered that the structure of lipid bilayers remained stable in the presence of either glucose (32.8 wt%) or trehalose (16.5 wt%) during the 30-ns simulation. In contrast, the bilayer structure was destroyed in the absence of sugars at the temperatures considered (290–310 K) (99).

3.2. Polyol–Lipid Bilayer Interaction

In contrast to sugars, alcohols such as ethylene glycol, propylene glycol, and glycerol typically disrupt the structure of lipid bilayers by interacting with the lipid headgroups, as demonstrated by several MD simulation studies (100, 101). The area per lipid headgroup of DPPC or DOPC bilayers becomes larger in the presence of alcohol molecules and increases as the solute concentration increases (100, 101). Accordingly, the acyl tail ordering of the lipid bilayers is reduced in the presence of alcohol (100, 101). In the presence of 15% propylene glycol, the APL increases by ~45% and the thickness of the bilayer decreases by ~18% compared with values in the absence of propylene glycol (101). Propylene glycol also exhibits a comparable, analogous action to Me₂SO (discussed in the following paragraph), that is, inducing the formation of water pores through the lipid bilayers, which has not been observed for other alcohols including ethylene glycol and glycerol (100, 101). At concentrations up to 15 mol%, glycerol and ethylene glycol tend to reside in the outer surface region of the lipid bilayers, whereas propylene glycol tends to accumulate near the phosphate groups of lipids (101), which is attributed to the more hydrophobic character of propylene glycol compared with ethylene glycol and glycerol. Overall, the lipid headgroups are partially dehydrated in the presence of alcohols in that the hydrogen bonds between alcohols and lipid headgroups replace the original water–lipid bonds, yielding reduced structural stability (e.g., lateral expansion and thinning of the bilayers) (100, 101).

3.3. Me₂SO–Lipid Bilayer Interaction

Me₂SO exerts a membrane thinning effect similar to that observed for alcohols. However, Me₂SO–lipid bilayer interactions exhibit a relatively unique phenomenon, namely pore formation in the membrane in the presence of high-concentration Me₂SO, which is in part responsible for various pharmacological effects of Me₂SO (100–104). A number of MD simulation studies have proposed three distinct regimes when Me₂SO interacts with phospholipid bilayers. Consider, for example, DPPC lipid bilayers (Figure 10). First, the dilute Me₂SO solution (e.g., 2.5–7.5 mol%) results in the lateral expansion of the bilayers with increased APL and reduced bilayer thickness. Due to the lack of interaction between Me₂SO and the polar groups of the lipid headgroups, Me₂SO molecules tend to insert between lipid molecules and reside near the phosphate groups (103). Depending on the balance of its hydrophilic and hydrophobic nature that is evaluated by the force field, the residence of Me₂SO within the membrane could be either just above (104) or slightly below (103) the phosphate groups. Second, within the range of 10–20 mol%, Me₂SO induces and stabilizes the formation of transient water pores that can spontaneously grow across the membrane. The number and the life span of these water pores are highly dependent on the concentration of Me₂SO (103). The presence of water pores may facilitate the diffusion of hydrophilic molecules across the membrane (103). Third, a further increase in the Me₂SO concentration beyond 25 mol% leads to the collapse of the structure of DPPC lipid bilayers (103, 104). Note that an extended period of time is necessary for all-atom MD simulation to observe the collapse of lipid bilayers by Me₂SO (104). Lateral expansion and pore formation have also been observed for other phospholipid compositions, including DOPC (104), POPC (105), and dipalmitoylphosphatidylcholine (DMPC) (105), when they interact with Me₂SO. This finding indicates that the disrupting effect of Me₂SO is independent of the lipid composition (i.e., the acyl chain length and unsaturation or saturation).

Figure 10.

Distinct modes of action of Me₂SO on phospholipid membranes (DPPC). Presented are side views of the final structures for the bilayer systems containing 0, 5, 10, and 40 mol% of Me₂SO (lipid-free basis). Lipids are shown in cyan, water in red, and Me₂SO in yellow. Reprinted with permission from Ref (103). Copyright (2007) American Chemical Society.

Force field:

the energy function or interatomic potentials used to calculate the forces acting on atoms during the molecular simulation

Note that the characteristic time of pore formation in MD simulations is strongly dependent on the Me₂SO concentration. In a system of DPPC bilayers hydrated with 10 mol% Me₂SO solution, at least 20 ns are needed for water pores to form (103). In one study that did not use such prolonged simulations, however, significantly enhanced membrane permeability to both water and Me₂SO was observed in the absence of water pores and at a concentration as low as 3 mol% (106). In this study, computation of the free energy and diffusion coefficient profiles across the DMPC bilayer enabled the estimation of permeability coefficient based on an inhomogeneous solubility-diffusion model (106).

4. MOLECULAR MECHANISMS OF PROTEIN STABILIZATION

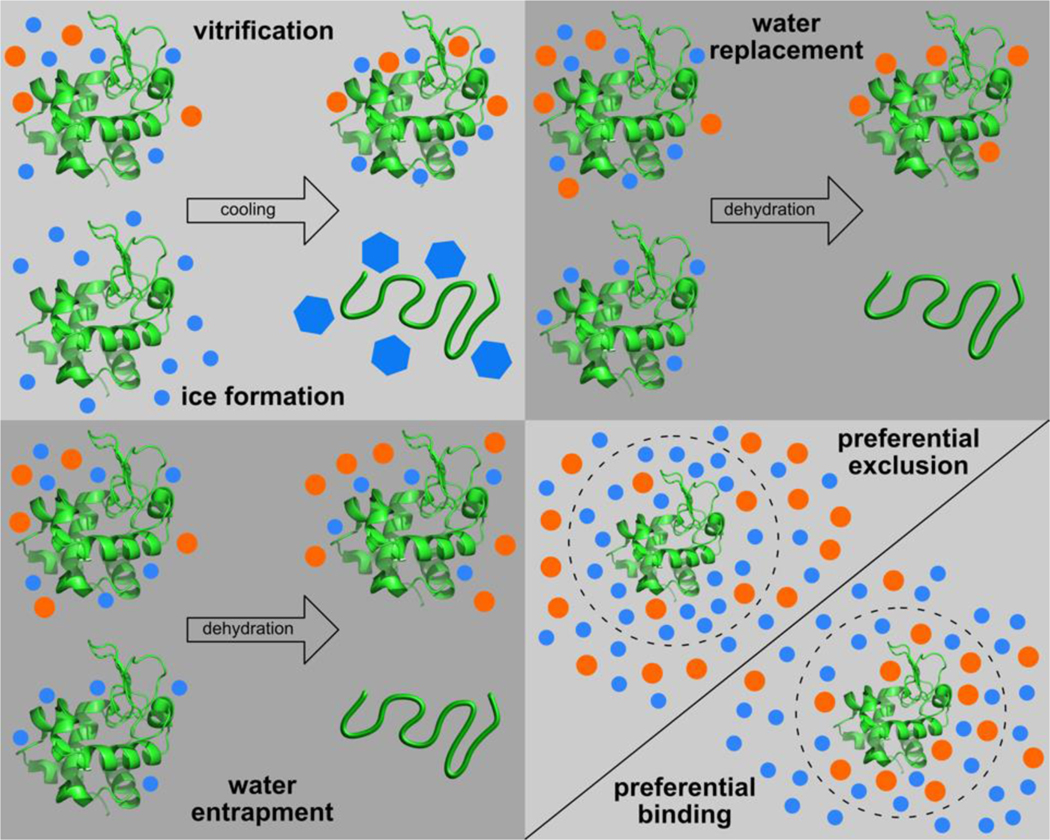
Four main hypotheses have been proposed to explain the stabilization of biomolecules or cellular structures during freezing, freeze-drying, or drying. Figure 11 illustrates these hypotheses using the example of protein stabilization and denaturation in a sugar–water matrix. First, the vitrification hypothesis suggests that molecular motions and structural fluctuations of protein residues are arrested in a noncrystalline, glassy state of high viscosity, thereby preventing the denaturation of the embedded protein (107). Second, the water replacement hypothesis suggests that, during dehydration, sugar molecules can substitute water molecules by forming hydrogen bonds with the protein residues to preserve the native structure of the embedded protein (90, 91). Third, the water entrapment hypothesis proposes that sugar molecules help trap the water molecules within the very vicinity of protein residues during dehydration, thereby maintaining the hydration and native structure of the embedded protein (108). The water entrapment hypothesis seems to be an extension of the following preferential hydration theory, especially for a dehydrated condition. Fourth, the preferential exclusion/hydration theory suggests that the presence of sugar molecules results in the preferential hydration (i.e., preferential exclusion of sugar) for proteins such that protein denaturation becomes thermodynamically unfavorable because it will increase the solvent (water) accessible surface area of proteins (109, 110).

Figure 11.

Hypothesized mechanisms about cryoprotectants protecting proteins against damages induced by freezing or dehydration. (Orange circles represent cryoprotectant molecules like trehalose and blue ones represent water molecules.)

The growing number of MD simulations focusing on the interactions between proteins, cryoprotectants, and water have provided converging evidence about the mechanisms of protein stabilization (111), suggesting high dependence on the hydration level and temperature of the system. Interestingly, most of these MD simulation studies investigated protein(s) embedded within a sugar-only or sugar–water matrix, with trehalose being the single best-studied stabilizing molecule (112).

4.1. Preferential Exclusion and Water Entrapment in Hydrated Proteins

When a protein is solvated in an aqueous sugar solution that is not highly concentrated (e.g., less than ~90 wt% on a protein-free basis), the mechanisms of preferential exclusion and water entrapment take effect in the stabilization of the protein in the hydrated condition. One MD simulation study on a trehalose solution of approximately 18 wt% found that the number of “bound” water molecules within a radial distance of 1.5 nm from the geometric center of the lysozyme is essentially unchanged in the presence of trehalose clusters, indicating that a thin layer of water persistently surrounds the protein (113). Trehalose molecules form only a limited number of hydrogen bonds with the protein due to the excluded volume effect at this concentration (113). Another MD investigation shows that the dominance of water in the vicinity of lysozyme (within the 1.5-nm radius) is maintained even when the trehalose concentration increases to 40 wt% (114). The preferential exclusion of sugar molecules (including trehalose, maltose, and sucrose) from the lysozyme surface becomes more pronounced as the solute concentration increases from 37 wt% to 60 wt% (115). In contrast, the replacement of water–lysozyme hydrogen bonds by sugar–lysozyme bonds is rather limited. The presence of sugar molecules seems to dominate at approximately 2 nm from the protein geometric center, given that the radius of gyration of lysozyme is approximately 1.4 nm. The relaxation times of lysozyme, sugar, and water molecules also significantly increase within the concentration range under investigation, implying that the dynamics of lysozyme is retarded in the presence of these sugars (115).

Another series of MD simulations has validated the preferential exclusion and water entrapment hypotheses in the stabilization of human growth hormone in the presence of various sugars and polyols (116) and carboxy-myoglobin in the presence of trehalose, maltose, or sucrose at a concentration as high as 89 wt% (117–120). A classic structure, that is, sugar shell–water shell–protein, has emerged from these MD simulation studies. Specifically, a preferential hydration shell intimately surrounds the protein with only a few sugar molecules interacting with the protein within the hydration shell through single hydrogen bonds. A layer of sugar molecules extends radially outward. Water molecules between the protein and the sugar, with a dramatic decrease in dynamics (114), act as bridges between the dynamics of the protein with the dynamics of the external sugar–water matrix (117–120). This double-shell structure reduces both the nonharmonic motions and the motions of the loop and helix structures of carboxy-myoglobin, resulting in the stabilization of the protein conformation with respect to the water-only solvated system (117–120).

4.2. Water Replacement in Dehydrated Proteins

MD simulations propose that the water replacement hypothesis begins to take effect as the system becomes highly dehydrated (26) or is subjected to combined stresses of dehydration and low temperatures (116). When lysozyme is solvated in a trehalose–water mixture at the hydration level of 0.075 or 0.15 gH₂O/gdw (grams of water per gram of protein-free dry weight, corresponding to 93 wt% or 87 wt% of trehalose, respectively), in which the hydration shell is no longer intact, the total number of hydrogen bonds that the protein forms remains almost the same as when the protein is solvated with water alone (26). In other words, some of the hydrogen bonds formed between water and lysozyme are replaced by trehalose–lysozyme bonds such that the overall hydrogen-bonding network embedding the protein is preserved; a similar observation has been made for the stabilization of lipid bilayers in the presence of sugars, as discussed in the previous section (26). Moreover, at the hydration level of 0.075 gH₂O/gdw, hydrogen bonds between trehalose and lysozyme dominate the protein’s hydrogen-bonding network compared with bonds between water and lysozyme, demonstrating the prevalence of water replacement (26). But when the hydration level increases to 0.15 gH₂O/gdw, the water–lysozyme hydrogen bonds outnumber the trehalose–lysozyme bonds by a small margin, implying that the mechanisms of water replacement and preferential exclusion/water entrapment take effect largely equally (26). A further increase in the hydration level, that is, a decrease in the solute concentration, causes preferential exclusion and water entrapment to predominate, as discussed above (115).

4.3. Antiplasticization of Small Molecules

The antiplasticization role of water is an intriguing phenomenon that has been observed in the MD simulation studies of highly dehydrated protein systems. The density of the lysozyme–trehalose system increases significantly upon the addition of a small amount of water (0.075 gH₂O/gdw), as revealed by both MD simulation and inelastic neutron scattering, suggesting that water fills the free volumes scattered within the otherwise anhydrous matrix (26). Although the presence of trehalose helps reduce the free volume in pure lysozyme (e.g., void spaces larger than ~200 ų dramatically decrease in the trehalose–lysozyme system) and contributes to denser packing of the trehalose–lysozyme system, the void spaces are not completely eliminated due to the excluded volume effect of the solute molecules, which may still allow a certain extent of structural fluctuation of protein residues (26). The addition of a small amount of water that will fill up the small void spaces remaining in the anhydrous lysozyme–trehalose system can further increase the packing density and therefore hinder the vibrational motions of lysozyme and trehalose at the picosecond scale (i.e., fast dynamics) (26).

This antiplasticization role of small molecules has also been observed for glycerol (57, 121–125) and sorbitol (126) as well as in binary trehalose–water mixtures (26, 33). Upon the addition of a small amount of glycerol, the T_g of the lysozyme–trehalose(–water) system gradually decreases due to the plasticization effect of glycerol, but the molecular packing of the matrix embedding the protein improves in the presence of glycerol (125). Facilitated by the glycerol–lysozyme hydrogen bonds that exist in the spaces occupied by glycerol, the molecular motions at the picosecond and nanosecond scales of lysozyme and trehalose decrease nonmonotonically with the addition of glycerol, with a local minimum within the range of 5–10 wt% glycerol (based on dry solids excluding the protein), in the conditions under investigation (0, 0.075, or 0.15 gH₂O/gdw and 300 K or 100 K). Overall, the antiplasticization role of glycerol contributes to improved stabilization of the embedded protein in compositions containing a small amount of glycerol (e.g., 10 wt% on a protein-free basis) (121, 127, 128).

4.4. Role of Vitrification in Protein Stabilization

The vitrification mechanism is not necessarily excluded by the hypothesis of water replacement, water entrapment, or preferential exclusion. In addition to experimental evidence, MD results support the critical role of vitrification in the stabilization of proteins (129, 130). The viscosity of the solution increases with an increasing concentration of stabilizing solute (0.38–2.5 M) and a decreasing temperature (272–233 K) (116). Also, the increase in viscosity in the presence of disaccharides such as trehalose or sucrose is much greater than that in the presence of glucose, which helps account for the superiority of disaccharides over monosaccharides (116). In addition, at temperatures of 260–300 K, the dynamics of water in the lysozyme–trehalose system is significantly slower than that in the lysozyme alone system. The large retardation factor τ_long/τα (≈6; where τα is the $\alpha$ relaxation time and τ_long corresponds to a slower relaxation time, given the presence of water in the sugar hydration shell) indicates the glass-like behavior of water, which could inhibit protein molecular motion and prevent a change in protein conformation (114, 131, 132).

5. FUTURE FRONTIERS OF MOLECULAR DYNAMICS SIMULATIONS FOR BIOSTABILIZATION AND BIOPRESERVATION

In this section, we discuss future challenges and opportunities for MD simulations. We believe that we are witnessing an exciting time, in which the rate of progress in computational power is matched by our rapidly growing knowledge of chemical structures and biological details. We envision that, when combined with the increasing cost of empirical assays, MD simulations will play a critical role in advancing our understanding of optimal strategies for biological stabilization and preservation.

Despite recent improvements, force fields remain imperfect and in short supply for many cryoprotectant molecules, since most of the available force fields have been parameterized specifically for biologically relevant macromolecules such as amino acids, peptides, and phospholipids. Novel potential protectants, such as room-temperature ionic liquids (133), deep eutectic solvents (134) and synthetic ice recrystallization inhibitors (72–74, 135), have received limited attention. An immediate solution to this problem could be the use of parameterization programs, which perform atom typing and assignment of parameters and charges to new molecules by analogy in a fully automated fashion. However, the parameters generated by these programs have only limited accuracy, and further validation is often necessary. The development of force fields based on first-principles calculations and parameter fitting is highly recommended for molecules with relevance for stabilization.

Ionic liquid:

a salt that is liquid below 100°C or even at room temperature due to poor coordination of ions

Deep eutectic solvent:

a eutectic mixture of salts and hydrogen-bond donors with a melting point lower than that of each individual component

Although genes conferring the activity of ice nucleating proteins have been sequenced from bacterial species such as Pseudomonas syringae (136, 137), for various reasons the structure of these large proteins, consisting of approximately 1,200 amino acids, has not been determined by X-ray crystallography or NMR spectroscopy (82). For example, the nonglobular form of these proteins is not amenable to X-ray diffraction, and it is difficult to achieve crystallization of membrane-associated proteins (138). The structure of ice nucleating proteins has been estimated only from analog peptide templating and theoretical modeling (80, 81, 138). The evolution of cryoelectron microscopy (cryo-EM) with new technological and computational developments (139, 140) may allow us access to the near-atomic-resolution three-dimensional structures of ice nucleating proteins in their near-native states, especially associated with the outer membrane surface, which will enable MD simulations to gain unprecedented information about the ice nucleation process catalyzed by these proteins.

X-ray crystallography:

a technique for determining the atomic and molecular structure of crystals on the basis of diffraction of the beam of incident X-rays

Cryoprotectant toxicity is one of the major challenges for the successful vitrification of thick tissues or solid organs. Although several pairs of CPAs, such as Me₂SO–formamide (141), are able to neutralize each CPA’s toxic effects, the molecular mechanisms underlying such synergy between two or more CPAs have not yet been clarified. MD simulations could be a unique approach to probe the synergetic interactions between certain pairs of CPAs, which will accelerate the discovery of new toxicity neutralizers.

To date, the clear majority of all-atom MD simulations that investigate CPA–membrane interactions have employed a planar lipid bilayer model. This universally applied model typically consists of only 64–128 lipid molecules on each leaflet. As computational hardware and molecular simulation algorithms have improved substantially, it will be more relevant to simulate an entire lipid vesicle solvated in the aqueous cryoprotectant solution. De Vries et al. (142) have found that small vesicles with high curvature have marked differences in the structural and dynamic properties between lipids in the inner and outer leaflets. Coarse-grained (CG) force fields have enabled us to simulate large systems such as lipid vesicles on a long timescale at a reasonable computational cost (143). But CG simulations often overlooked the atomistic details of the intermediate structures, which are necessary for hydrogen-bonding analysis.

Most of the lipid bilayers investigated by MD simulations are made of only one type of phospholipid. It is recommended that future simulations could consider more complicated compositions that better mimic plasma membranes of different species (85, 87, 100, 144). For example, recent MD simulations have found that the presence of β-sitosterol in DOPC bilayers makes the bilayers more structured and more resistant to the perturbation by permeable CPAs like Me₂SO or polyols than in the absence of β-sitosterol (100, 144).

MD studies of lipid bilayers or proteins in the frozen and/or dehydrated state are currently lacking and would be an important addition to the field. For instance, most lipid bilayers studied are fully hydrated. Therefore, simulation results cannot be directly compared with results from many experiments that reproduce the freezing and/or drying process (97). There are several challenges when simulating a dehydrated biomolecule system (99). On one hand, the force fields for biomolecules are typically developed under full hydration and thus may not be compatible with dehydrated biomolecules; for example, they may cause overcompression of the dehydrated biomolecules. On the other hand, the periodic boundary conditions that are often used in MD simulations may result in unnecessary interaction between the simulated biomolecules and their periodic image when the water layer separating the periodic images is too thin. Therefore, adjustment of the force fields and special treatment of the setup of the simulation system are required to simulate lipid bilayers or proteins in frozen and/or dehydrated conditions.

SUMMARY POINTS

1. The structure and hydrogen-bonding network of polyhydroxylated CPA–water systems have been investigated by a number of MD simulations. These simulations consistently revealed a heterogeneous hydrogen-bonding network that transits from being water dominant to being CPA dominant as the solute concentration is increased. In the middle of the transition, there is a “bipercolating” clustering regime in which medium-sized CPA clusters and water clusters coexist.

2. The addition of simple salts has been demonstrated to be exceptional in enhancing the T_g of several CPA formulations, but current experimental approaches fail to gain detailed insight into this phenomenon. Recent MD simulations found that the ions that can enhance the T_g of CPA typically establish stronger interactions with CPA molecules, compared with the original CPA–CPA hydrogen bonding. The bridging effect of CPA–ion–CPA networks may yield a polymerized network. These ions are also resistant to self-aggregation with the accompanying counterions.

3. A series of MD simulations has demonstrated that AF(G)Ps and their synthetic mimics inhibit ice crystallization through specific binding to one or more faces of the ice crystal. The ice-binding action generates curvatures at the ice–water interface, depressing the local equilibrium freezing temperature. These findings have enriched our mechanistic understanding of ice recrystallization inhibition and could advance the rational design of synthetic ice recrystallization inhibitors.

4. MD simulations have elucidated the thinning effect of Me₂SO on biomembranes, similar to alcohol CPAs. These direct atom-scale observations demonstrate that the Me₂SO–lipid interaction uniquely results in pore formation in the membrane with high concentrations of Me₂SO, which facilitates the cross-membrane diffusion of hydrophilic molecules.

5. Mechanisms underlying biomolecule stabilization are generally hypothesized on the basis of existing experimental observations. However, MD simulations directly “visualize” the selective presence of these mechanisms, which depends on the hydration state. For example, preferential exclusion and water entrapment mechanisms play important roles in the stabilization of hydrated proteins, but the water replacement phenomenon becomes noticeable when the proteins become highly dehydrated or are subjected to a combination of dryness and low temperatures. The vitrification mechanism is not necessarily excluded by these three hypotheses.

FUTURE ISSUES

1. Force fields remain inadequate for emerging stabilizing substances such as ionic liquids, deep eutectic solvents, and ice recrystallization inhibitors. The force fields for these novel CPAs should be developed on the basis of a combination of first-principles physics and parameter fitting to QM computations and experimental data for reasonable accuracy.

2. Water is highly relevant to biomolecular simulations. Unfortunately, each of the water models available so far matches only certain limited properties of water. Some models are less robust due to their sensitivity to the precise model parameters, system size, or simulation method. Some are polarizable; others reproduce only “average” structures. Furthermore, the solid phase of water exhibits one of the most complex phase diagrams, with 17 experimentally confirmed ice phases under positive pressures. Therefore, in addition to TIP4P, TIP4P/2005, TIP4P/Ice, and mW, MD simulations for cryopreservation still require water models that can better represent the structure and dynamics of low-temperature water and its various crystalline phases without sacrificing simplicity and computational ease and speed.

3. Advanced configuration-imaging approaches such as cryo-EM and SFG vibrational spectroscopy may be capable of determining the three-dimensional structures of ice nucleating proteins that are associated with the bacterial membrane surface. The atomic resolution structures will allow MD simulations to provide unprecedented insights into the catalysis of ice nucleation by these proteins.

4. In-depth MD simulations of CPA cocktails will likely unravel the synergistic mechanisms between multiple CPAs, such as the neutralization of CPA toxicity.

5. MD simulations of lipid bilayers with curvature and made of biomembrane-mimicking compositions and simulations of biomolecules in a frozen or dehydrated state will provide more relevance and guidance for biostabilization applications.