Significance
The use of enhanced sampling simulations is essential in the study of complex physical, chemical, and biological processes. We devise a procedure that, by combining machine learning and biased simulations, removes the bottlenecks that hinder convergence. This approach allows different types of challenging processes to be studied in a near-blind way, thus extending significantly the scope of atomistic simulations.
Keywords: enhanced sampling, collective variables, machine learning, molecular dynamics
Abstract
The development of enhanced sampling methods has greatly extended the scope of atomistic simulations, allowing long-time phenomena to be studied with accessible computational resources. Many such methods rely on the identification of an appropriate set of collective variables. These are meant to describe the system’s modes that most slowly approach equilibrium under the action of the sampling algorithm. Once identified, the equilibration of these modes is accelerated by the enhanced sampling method of choice. An attractive way of determining the collective variables is to relate them to the eigenfunctions and eigenvalues of the transfer operator. Unfortunately, this requires knowing the long-term dynamics of the system beforehand, which is generally not available. However, we have recently shown that it is indeed possible to determine efficient collective variables starting from biased simulations. In this paper, we bring the power of machine learning and the efficiency of the recently developed on the fly probability-enhanced sampling method to bear on this approach. The result is a powerful and robust algorithm that, given an initial enhanced sampling simulation performed with trial collective variables or generalized ensembles, extracts transfer operator eigenfunctions using a neural network ansatz and then accelerates them to promote sampling of rare events. To illustrate the generality of this approach, we apply it to several systems, ranging from the conformational transition of a small molecule to the folding of a miniprotein and the study of materials crystallization.
Atomistic simulations and in particular, molecular dynamics (MD) play an important role in several fields of science, serving as a virtual microscope that is of great help in the study of physical, chemical, and biological processes. However, any time the free energy barrier between metastable states is large relative to the thermal energy, transitions between states become rare events, taking place on timescales too long to be simulated by standard methods (1). This severely hampers the study of many important phenomena, such as phase transitions, chemical reactions, protein folding, and ligand binding.
To alleviate this problem, different advanced sampling techniques have been developed. A large family of these methods relies on the identification of a small set of collective variables (CVs) that are functions of the system atomic coordinates R. In all these approaches, an external bias potential is added to the system in order to enhance the fluctuations (2). If the CVs are able to activate the slowest degrees of freedom involved in the state-to-state transitions, this procedure results in an enhanced sampling of the transition state. This in turn leads to an increase in the frequency with which rare events are sampled. Different ways of constructing appropriate bias potentials have been suggested. Examples are umbrella sampling (3, 4), hyperdynamics (5), metadynamics (6), variational enhanced sampling (7, 8), Gaussian mixture-based enhanced sampling (9), and on the fly probability-enhanced sampling (OPES) (10).
Regardless of the method used, identifying appropriate CVs is a crucial requisite for a successful enhanced sampling simulation (11, 12). Ideally, one would choose the CVs solely on a physical and chemical basis. However, especially for complex systems, this can be rather cumbersome. For this reason, a number of data-driven approaches and signal analysis methods have been proposed for CV construction (13–15). Some of these methods can be applied when the metastable states involved in the rare event are known beforehand (16–18), such as the folded and the unfolded states of a peptide or the reactants and products of a reaction. A line of attack in these cases has been to collect a number of configurations from short unbiased MD runs in the different metastable states and use these data to train a supervised classification algorithm. The classifier is then used as a CV. Our group has also contributed to this literature and developed an approach named harmonic linear discriminant analysis (LDA) (16, 19) that derives from Fisher’s LDA. Later, we have further improved this method by applying a nonlinear version of linear discriminant analysis (Deep-LDA) (20). The greater flexibility provided by the neural network (NN) architectures is of great help in dealing with complex problems (21, 22). These methods have proven to be successful despite the fact that they do not necessitate prior knowledge of reaction paths or transition states.
Clearly, if we had access to the transition dynamics, we could further improve the CV effectiveness by making use of this dynamical information. To this purpose, several methods have been suggested to extract CVs from reactive simulations in which the system translocates spontaneously from one metastable state to another. Among all these methods, those based on the variational approach to conformational dynamics (VAC) (23–33), both in its linear and nonlinear versions, are of particular relevance here. In ref. 34, it has been argued that the resulting variables are natural reaction coordinates since they 1) perform a dimensionality reduction, 2) are determined by the sampling dynamics, and 3) are maximally predictive of the system evolution. Furthermore, an interesting feature of these CVs is that they measure the progress along any pathway connecting the metastable states, rather than focusing on a single path (34). Hence, these variables can be of great help both to understand and to enhance MD simulations. However, a difficulty in using VAC-generated CVs is that it becomes superfluous to perform enhanced sampling if unbiased reactive trajectories are already available. Thus, one is in a chicken-and-egg situation; to find good CVs, one needs to collect unbiased state-to-state transitions, but to promote transitions, good CVs are needed (35).
A solution to this conundrum may come from an iterative approach, in which the CVs are computed using data generated in a previous enhanced sampling simulation (36–44), even if this initial run is far from optimal. In our group, we have followed this strategy and modified the VAC protocol to identify the slow modes from biased trajectories (29, 45). In this way, we can identify the modes that hinder convergence and enhance their sampling.
Here, we generalize the approach of ref. 29 in two ways. First, we employ a nonlinear variant of VAC, which greatly increases its variational flexibility. Second, we propose strategies for the collection of the initial trajectories, such as sampling generalized ensembles rather than using trial CVs, and for making full use of the information gathered during the initial trajectory. We also employ OPES to construct the bias, which has several advantages over metadynamics and other methods. These improvements lead to a general procedure that is proven to be effective in the study of a variety of rare events.
We organize the structure of this paper as follows. First, we give a brief account of the VAC theory, highlighting the points that are most relevant to our work. Then, we discuss how we can use NNs as trial functions for the variational principle and how to adapt it when starting from enhanced sampling simulations. We initially test our method on the didactically informative example of the alanine dipeptide and then move on to more substantial applications such as folding a small protein and studying a crystallization process.
CVs as Eigenfunctions of the Transfer Operator
An MD simulation can be seen as a dynamical process that takes a density distribution at time t and evolves it toward the equilibrium Boltzmann one: . Here, β is the inverse temperature, and is the interaction potential. An analysis of sampling dynamics can be done by studying the properties of the transfer operator . We assume the dynamics to be reversible, thus satisfying the detailed balance condition. In the following, we quote some of the properties of and refer the interested reader to the literature for a more formal discussion (24, 46).
The transfer operator is defined by its action on the deviation of the probability distribution from its Boltzmann value as measured by :
| (1) |
| (2) |
The action of the transfer operator depends both on the equilibrium distribution μ and the transition probability , which is a property of the sampling dynamics. Thus, we will have different operators even when sampling the same equilibrium distribution (e.g., with standard or enhanced sampling MD).
The transfer operator is self-adjoint with respect to the Boltzmann measure. This implies that its eigenvalues are real and that its eigenfunctions form an orthonormal basis:
| (3) |
where the orthonormality condition reads
| (4) |
Furthermore, its eigenvalues are positive and bounded from above: . In particular, the eigenfunction corresponding to the highest eigenvalue is the function . This trivial solution corresponds to the fact that the Boltzmann distribution is the fixed point of . In fact, if we apply k times to a generic density ψt, we find
| (5) |
from which we see that if we let , only the contribution coming from the eigenfunction survives. The eigenvalues can be reparametrized as , where ti is an implied timescale measuring the decay time of the ith eigenfunction. Thus, the leading eigenvalues are to be associated with the longest implied timescales, meaning that their corresponding eigenfunctions have a slow relaxation toward the equilibrium. For this reason, the first eigenfunctions are good CV candidates since they describe the slow dynamical process that we need to accelerate.
Of course, in a multidimensional system, there is no chance of exactly diagonalizing the transfer operator. Nonetheless, we can use a variational approach akin to the Rayleigh–Ritz principle in quantum mechanics. In the present context, the variational principle reads
| (6) |
where are lower bounds for the true eigenvalues and are variational eigenfunctions satisfying the orthogonality condition . The equality holds only when coincides with the exact eigenfunction. In addition, we have used the property that the matrix elements of can be written in terms of time correlation functions (25). Thus, they can be straightforwardly computed from the sampling trajectories.
Time-Lagged Independent Component Analysis
In order to solve the variational problem, we have to choose a set of trial functions. As a first step, we select a set of Nd descriptors and build the variational eigenfunctions as a linear combination of them:
| (7) |
where the expansion coefficients are the variational parameters. This amounts to applying to the problem the time-lagged independent component analysis (TICA) method (23, 25, 26), a signal analysis technique that, given a set of variables, aims at finding the linear combination for which their autocorrelation is maximal. By imposing the variational functions to have zero mean, we ensure that they are orthogonal to the trivial solution. As in quantum mechanics, finding the variational solution to a problem in which a trial wave function is expressed as a linear expansion leads to solving an eigenvalue problem (46). Recalling that the matrix elements of the transfer operator can be expressed as time correlation functions, the generalized eigenvalue problem can be written as
| (8) |
where
| (9) |
A Neural Network Ansatz for the Basis Functions
Instead of using a predetermined set of descriptors as basis functions, as done in TICA, we employ an NN to learn the basis functions through a nonlinear transformation of the descriptors in a lower-dimensional space. In this way, we can exploit the flexibility of NNs to drastically improve the variational power of ansatz functions and at the same time, extend the VAC method to the case of a large number of descriptors.
The architecture of the NN follows here the implementation of ref. 33, where descriptors and are fed one after the other into a fully connected NN parametrized by a set of parameters θ, obtaining as outputs the corresponding latent variables and , respectively (Fig. 1). The average of the latent variables is subtracted to obtain mean free descriptors. Then, these values are used to compute the time-lagged covariance matrices, from which the eigenvalues and the corresponding eigenfunctions are obtained as the solution of Eq. 8. This information is used to optimize the parameters of the NN as to maximize the first D eigenvalues by minimizing the following loss function with gradient descent methods:
| (10) |
which also corresponds to the so-called variational approach for Markov processes (VAMP)-2 score (32).
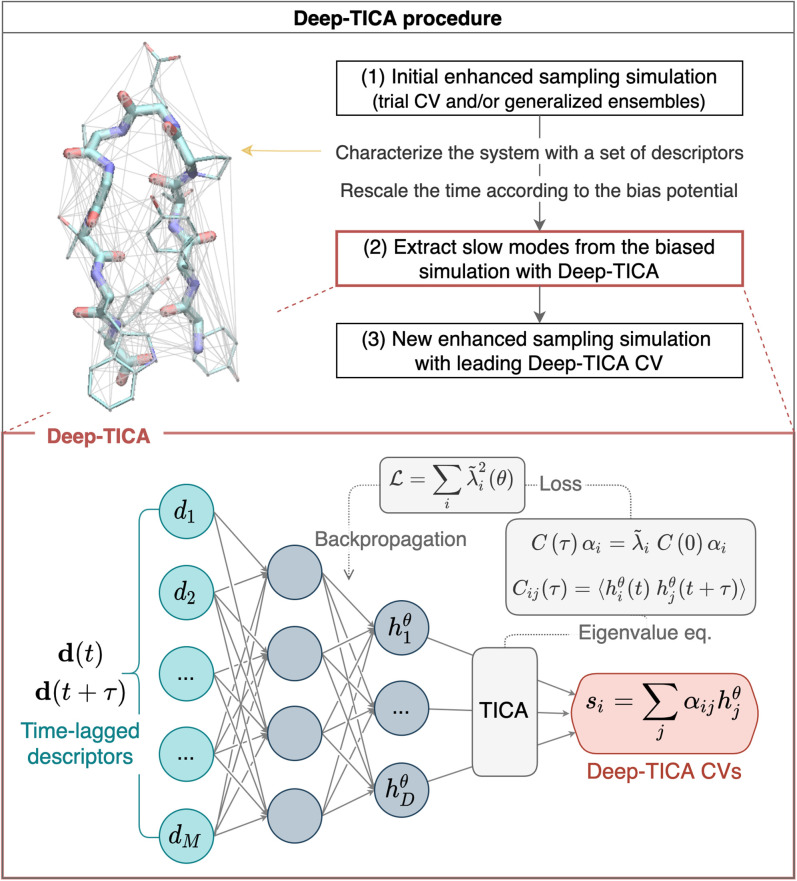
Fig. 1.
(Upper) The Deep-TICA protocol used in this paper. On the left, the miniprotein chignolin is shown, with lines denoting pairwise distances used as descriptors. (Lower) NN architecture and optimization details of Deep-TICA CVs.
This architecture is an end-to-end framework that takes as input a set of descriptors and returns as output the few TICA eigenfunctions of interest. Since these CVs are given by the combination of NN basis functions and the TICA method, we will refer to them in the following as Deep-TICA CVs.
Extending TICA to Enhanced Sampling Simulations
Most of the developments and applications of VAC have been focused on the analysis of long unbiased MD runs. Our purpose is different since we want to identify the slowest dynamical processes from enhanced sampling simulations. The application of an external potential can be seen as an importance sampling technique that samples a modified probability distribution in which the transition rate is accelerated. To recover the equilibrium properties over the Boltzmann distribution, one needs to perform the reweighting procedure (2, 27). When the bias is in a quasistatic regime, the expectation value of any operator can be written as
| (11) |
where represents a time average in the biased simulation. Another way of looking at the reweighting procedure is to rewrite Eq. 11 as an ordinary time average in a time scaled by the value of the bias potential:
| (12) |
where we have performed a change of variable and represents the total scaled time. This means that we can interpret the enhanced sampling simulation as a dynamics that samples the Boltzmann distribution on the timescale. Thus, the VAC procedure can be straightforwardly applied provided that the correlation functions of Eq. 8 are calculated in time (29, 45). Additional details are reported in Materials and Methods.
It is important to note that, even though the enhanced sampling simulation in time asymptotically samples the Boltzmann distribution, its sampling speed does differ from the unbiased one. As a result, the spectrum of the transfer operator will be different since the degrees of freedom that have already been accelerated in the initial simulation will have a smaller contribution. In fact, our group has previously shown that a successful enhanced sampling simulation leads to small leading eigenvalues of the transfer operator as the slow modes are accelerated (29).
Among the many enhanced sampling methods that allow the reweighting procedure of Eqs. 11 and 12, we choose here to use OPES for a variety of reasons that will be discussed later, but first, we sketch the main features of this method. OPES (10, 47) first builds an on the fly estimate of the equilibrium probability distribution , and the bias is then chosen to drive the system toward a desired target distribution :
| (13) |
At convergence, the free energy surface (FES) as a function of s is computed from . An appropriate choice of the target distribution allows one to sample a variety of ensembles including the well-tempered (48) with , uniform distribution, up to generalized ensembles (47). The latter possibility is used here to sample the multithermal ensemble, where configurations relevant to a preassigned range of temperatures are sampled. This is similar to replica-exchange methods but does not involve abrupt exchange of configurations. In the OPES version, the multithermal ensemble is sampled by using the potential energy as a CV.
One important factor that made us choose OPES is that it reaches the quasistatic regime more rapidly than metadynamics (10). Thus, the bias varies more smoothly, and the noise in the calculation of scaled time correlation functions is reduced.
A Recommended Strategy
We outline here the key steps of our recommended procedure (Fig. 1).
-
1)
Exploration. Harness a number of reactive events using a CV-based OPES simulation with a trial CV s0, multithermal sampling [in such a case, ], or even a combination of the two. Store the final bias potential of this initial simulation.
-
2)
CV construction. Select the descriptors to be used as inputs of the NN. Train the Deep-TICA CVs using the trajectories generated in step 1 by calculating the correlation functions in time.
-
3)
Sampling. Perform an OPES simulation using the leading Deep-TICA eigenfunction as CV on the Hamiltonian modified by the addition of the bias potential .
This procedure can be iterated, but usually at this stage, the FES is well converged. In the examples presented in this work, we enhance the fluctuations of the eigenfunction associated with the slowest mode (Deep-TICA 1) while using the others for analysis purposes.
Unlike the approaches developed earlier (29, 45), in step 3 we also add the bias to the Hamiltonian. In this way, we take into account the fact that the slow modes computed in step 2 reflect the rate of convergence to the Boltzmann distribution sampled by reweighting (Eq. 11) from the trajectories generated using the Hamiltonian .
Results and Discussion
Alanine Dipeptide from Multicanonical Simulations and CV-Biased Dynamics
A simple yet informative test of enhanced sampling methods is offered by the study of the conformational equilibrium of alanine dipeptide in vacuum. At room temperature, this small peptide exhibits two metastable states, namely the more stable composed of two substates and the less populated . The conformational transition between the two states is well described by the torsional angles and ψ, with the former being close to an ideal CV. However, since our scope is mostly didactical, we shall on purpose ignore this information and build efficient CVs using as descriptors all the heavy atom interatomic distances. To illustrate the flexibility and power of the method, we consider here two scenarios that differ in the way the initial reactive trajectories are generated.
We start with illustrating the first strategy, which consists of using OPES to sample the multithermal ensemble. As can be seen from Fig. 2A, this procedure is not very efficient and promotes only a small number of transitions, and thus, the free energy estimate is noisy (SI Appendix, Fig. S4). Rather remarkably, this limited information is enough to extract the slow modes of the system using Deep-TICA and obtain CVs that are efficient in promoting sampling. We find the training to be robust concerning the choice of lag time (SI Appendix, Fig. S1) and also, to the number of configurations used (SI Appendix, Fig. S2). The leading Deep-TICA 1 variable is associated with the transition between and , while the second describes the transition between the substates (SI Appendix, Fig. S6).
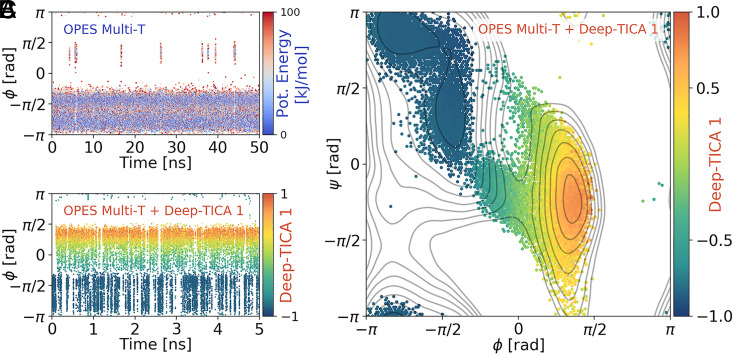
Fig. 2.
The Deep-TICA procedure applied to a multithermal simulation of alanine dipeptide. (A) Time evolution of the -angle in the exploratory OPES multithermal simulation, colored according to the potential energy. (B) Time evolution of the same angle for the simulation in which also the bias on Deep-TICA 1 is added, colored with the value of the latter variable. It can be seen that the system immediately reaches a diffusive behavior. (C) Ramachandran plot of the configurations explored in the Deep-TICA simulation, colored with the average value of Deep-TICA 1. Gray lines denote the isolines of the FES, spaced every 2 . Note that the sampling is focused on the minima and the transition regions that connect them.
Subsequently, a new OPES multithermal simulation is performed biasing in addition Deep-TICA 1. The first remarkable result is a 200-fold increase in the number of transitions per unit time as compared with the initial simulation (Fig. 2B). The system immediately reaches a quasistatic regime in which the average interval between interstate transitions is about 25 ps, to be compared with the pure multithermal simulation in which the same rate was as large as 3 ns. As a consequence of this speedup, the free energy difference between metastable states converges in just 1 ns to the reference value within 0.1 . A quantitative analysis of the convergence of the simulations can be found in SI Appendix, Fig. S4, together with a comparison of the simulations with and without the static bias potential and the FES as a function of the two Deep-TICA CVs (SI Appendix, Fig. S3).
The time to convergence is comparable with what one finds when using as CVs the physically informed dihedral angles and ψ (10), but here, it is the result of a procedure that is generally applicable and does not require any previous understanding of the system. There is also a clear improvement with respect to discriminant-based CVs that use the same set of descriptors (20).
Notably, the Deep-TICA CV promotes sampling along the two different pathways connecting and (Fig. 2C), as it measures the sampling progress along all transition pathways (34). Combined with the OPES ability to set an upper bound to the value of the added bias, this results in focusing the sampling on the most interesting parts of the FES, which are the minima and the transition region.
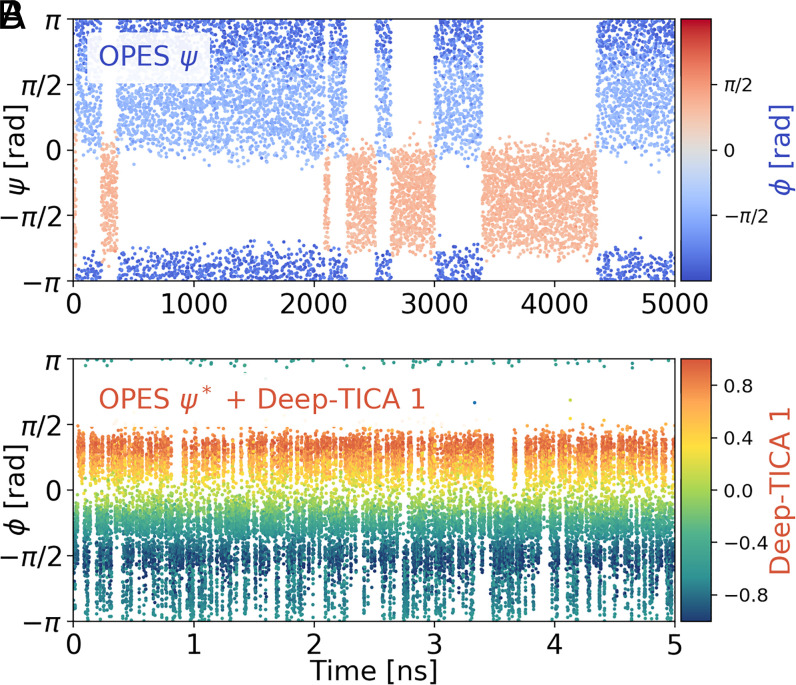
The above-described procedure was based on the ability of the initial multithermal simulation to induce transitions between the local minima. However, in many cases multithermal simulations are not able to induce even a single transition, and the use of a CV to generate a reactive trajectory is called for. Thus, we found it instructive to exemplify the performance of Deep-TICA when the initial biased simulation is driven by a CV. Again, we want to challenge the method, and we choose the angle ψ as the starting CV. A cursory look at the alanine dipetide FES in Fig. 2C makes one realize that ψ is a very poor CV, being almost perpendicular to the direction of the most likely transition paths. For this reason, it is an exemplary case of a CV that should not be used (49). The low quality of the CV is reflected in the fact that we need to simulate the system for 5 µs to observe a handful of transitions (Fig. 3A). As before, we feed these scant data to the Deep-TICA machinery and compute the highest eigenfunctions of the transfer operator. When we perform a new OPES calculation biasing Deep-TICA 1, the simulation immediately reaches a diffusive regime similarly to the previous example (Fig. 3B), which allows for converging the free energy in a very short timescale of 1 ns (SI Appendix, Fig. S5). This is possibly an extreme example but shows that remarkable speedups can be attained when the slow modes are correctly identified and their sampling accelerated. In real life, one tries not to use CVs as bad as ψ, but the use of suboptimal CVs is far from rare. In this respect, the Deep-TICA method holds the promise of remedying a poor initial CV choice.
Fig. 3.
(A) Time evolution of the ψ-angle in the exploratory simulation driven by ψ. The points are colored with the values of the -angle. (B) Time evolution of the -angle in the final Deep-TICA simulation, colored with the value of Deep-TICA 1. This results in a diffusive simulation similar to the previous example, which is even more impressive here given the poor quality of the exploratory sampling.
As discussed in the previous sections, the eigenfunctions that we obtain describe the slowly converging modes of the sampling dynamics performed in step 1. In SI Appendix, we investigated this point by comparing the CVs extracted from the multicanonical simulation with those obtained from the ψ-biased dynamics, highlighting the effect of initial simulation (SI Appendix, Fig. S6). Furthermore, it should be noted that for these cases in which the quality of the initial CV s0 is poor, the advantage of using the bias from the previous simulation is less significant but still nonnegligible (SI Appendix, Figs. S4 and S5).
A Blind Approach to Chignolin Folding
Chignolin is one of the smallest proteins that can be folded into a stable structure. Here, we focus on its variant CLN025, which has been extensively studied using molecular simulations by performing long simulations on the Anton supercomputer (50) and using enhanced sampling techniques (51–54).
Once again, we pretend that we are unaware of the progress made in the understanding of Chignolin behavior and follow the same blind approach pursued in the first alanine dipeptide simulation reported above. That is, in the exploratory phase we perform an OPES multithermal sampling, this time boosted by the use of multiple replicas (Fig. 4A). This leads to observing a few folding–unfolding events. Using these trajectories, we construct a Deep-TICA CV using as descriptors all the 4,278 interatomic distances between heavy atoms.
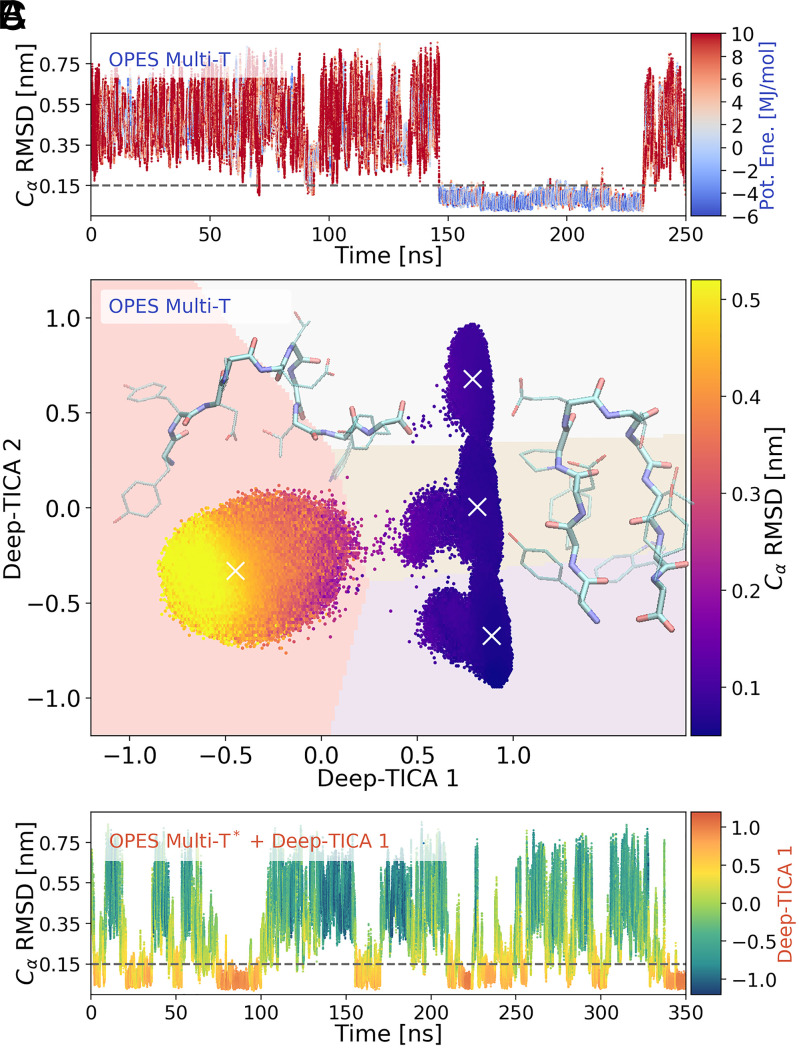
Fig. 4.
The Deep-TICA procedure applied to chignolin folding. (A) Time evolution of the rmsd for one replica during the initial multithermal run. The points are colored according to their potential energy value. Low energy values reflect the fact that configurations relevant at lower temperatures are sampled. (B) Scatterplot of the two leading Deep-TICA CVs in the exploratory simulation. Points are colored according to the average rmsd values. A weighted k-means clustering identifies four clusters whose centers are denoted by a white ×. The pale background colors reflect how space is partitioned by the clustering algorithm. Snapshots of chignolin in the folded (high values of Deep-TICA 1) and unfolded (low values of Deep-TICA 1) states are also shown, realized with the Visual Molecular Dynamics (VMD) software (69). (C) Time evolution of rmsd for a replica in the multithermal simulation also biasing Deep-TICA 1, colored with the value of the latter variable. The time evolution for the other replicas is reported in SI Appendix, Fig. S7.
Since enhancing the sampling of a CV that depends on thousands of descriptors would have been computationally inefficient, we decided to reduce their number by selecting the most relevant one for the leading CV via a sensitivity analysis (20). In this way, we selected 210 descriptors (which are also reported in Fig. 1). We retrain the NN using this reduced set and find out that the leading eigenvalue is only decreased by just 0.5%, thanks to the variational flexibility of the NN. Interestingly, the selected distances involve both backbone and side-chain atoms, suggesting that the latter also have a significant role in the folding process.
As expected, the first CV (Deep-TICA 1) describes the folded to unfolded transition that is the slowest mode of the system. Instead, the second one (Deep-TICA 2) characterizes the fine structure of the folded state, as we will discuss later. This can be seen in Fig. 4B, where we colored the points sampled in the initial trajectory with the value of the backbone rmsd. It should be noted that we find no evidence of stable misfolded states along the dominant folding CVs, in agreement with simulations using the same force field (50, 53, 55).
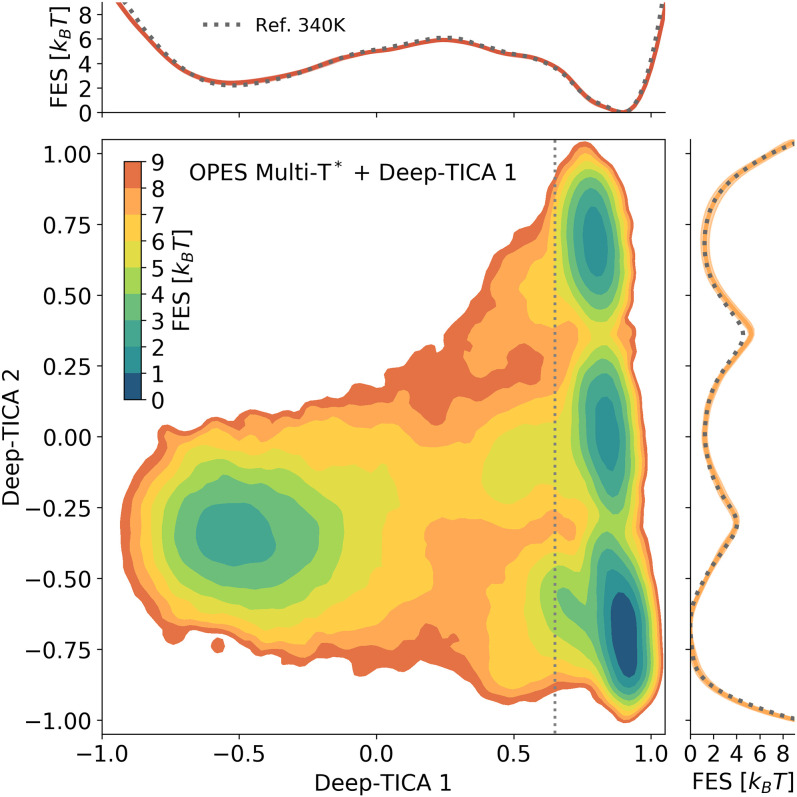
Performing a new simulation with a bias potential along Deep-TICA 1 results in an enhanced sampling of the transition region (SI Appendix, Fig. S8), with a 20-fold increase in the rate of folding events compared with the multithermal simulation (Fig. 4C). Due to the use of the multithermal approach, all the free energy profiles in the chosen range of temperatures can be calculated with great accuracy (SI Appendix, Figs. S10–S12). Indeed, the average statistical error calculated with a weighted block-average technique (47) is about 0.5 kJ/mol, improving on classifier-based approaches applied to the same system (54). In particular, we find an excellent agreement with an unbiased 106-µs reference trajectory (50) at T = 340K (SI Appendix, Fig. S9). Note that a study of the protein behavior at lower temperatures using standard MD would have been significantly more difficult to perform.
In Fig. 5, we report the FES relative to T = 340K plotted as a function of the two leading eigenfunctions, together with their projections along with Deep-TICA CVs. We find two major states divided by a significant free energy barrier, which correspond to the unfolded and folded basins. However, the latter exhibits a fine substructure that can be traced back to the Threonine side chains (THR6 and THR8) occupying different dihedral conformations (SI Appendix, Fig. S13). At 340 K, these states can interconvert on the timescale of nanoseconds, but of course, this time is significantly slower at lower temperatures (SI Appendix, Fig. S11). Notably, the most likely conformation is stabilized by the presence of a hydrogen bond between the two threonine (THR) side chains (SI Appendix, Table S3), as previously observed in a structural analysis study for wild-type chignolin (56). This is remarkable because it was discovered with prior knowledge of neither structural conformation of the system nor the dynamics of folding, and it suggests that going beyond backbone-only structural descriptors is necessary to obtain an accurate representation of the folding dynamics.
Fig. 5.
FES of chignolin at T = 340 K as a function of the two leading Deep-TICA CVs. In Upper and Lower Right are shown the projections of the FES along the corresponding axis (solid lines), confronted with the reference value obtained from a long unbiased MD trajectory at 340 K (50) (dotted lines). Note that the projection of Deep-TICA 2 is obtained by integrating only the region of space with Deep-TICA 1 > 0.65 (marked by a dotted line in Lower Left) to highlight the barriers between the folded metastable states.
Improved Data-Driven Description of Silicon Crystallization
Silicon crystallization is a first-order phase transition hindered by a large free energy barrier. This implies that in step 1 of the Deep-TICA procedure, one has to resort to CV-based simulations to harness reactive trajectories. Our group has previously investigated the application of TICA to simulate Na and Al crystallization (57). The study of Si crystallization is, however, more difficult due to the directional nature of the bonds and the ease with which defective and glassy structures can arise.
To address this problem, we make use of a recently developed set of descriptors that have proven to be useful in a machine learning context (22). These are the peaks of the three-dimensional structure factor of a crystal that is commensurate with the MD simulation box. Compared with the spherically averaged structure factors used in refs. 57 and 58, these descriptors have the advantage that they facilitate the formation of crystal structures aligned with the axes of the box. Since they measure the presence of long-range order in the system, they are a natural choice in the study of crystallization.
In ref. 22, these peaks were combined into a CV using the Deep-LDA classification method. The question that we address here is whether we can improve upon the Deep-LDA description and obtain a CV that incorporates dynamical information. In order to make a fair comparison between Deep-LDA and Deep-TICA, we use the same set of descriptors chosen with a well-defined universal concept. That is, we use in both cases the first 95 Bragg peaks with modulus (SI Appendix, Fig. S15), which amounts to fixing the CV spatial resolution.
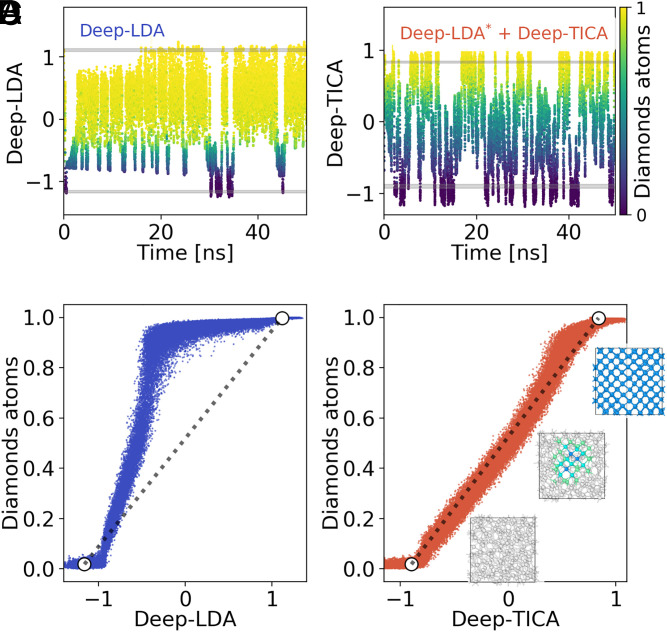
The Deep-LDA CV is trained using short MD simulations in the liquid and the cubic diamond states. Afterward, an OPES simulation is performed, which promotes a few crystallization and melting events, although the system struggles to find its way to the liquid state (Fig. 6A). From this trajectory, a Deep-TICA CV is extracted and subsequently used to enhance sampling together with the final static bias (Fig. 6B). Similar to what happened in the previous examples, this procedure leads to an increase in the number of transitions between the solid and liquid states, which allows converging of the free energy estimate already after 20 ns. The statistical uncertainty on the free energy difference is reduced compared with the Deep-LDA simulation (SI Appendix, Fig. S16). Furthermore, the free energy difference between the two states is close to zero at T = 1,700 K, in excellent agreement with the melting point of the interatomic potential (58, 59).
Fig. 6.
Comparison between (A and C) a Deep-LDA–driven simulation and (B and D) the one based on the present Deep-TICA approach. In A and B, we report the time evolution of (A) the Deep-LDA CV in the initial simulation and (B) the Deep-TICA CV in the improved one. In A and B, the points are colored according to the fraction of diamond-like atoms in the system, computed as in ref. 70. Gray shaded lines indicate the values of the two CVs in unbiased simulations of the liquid (bottom lines) and solid (top lines). C and D report the correlation between the two data-driven CVs and the fraction of diamond-like atoms. White circles denote the mean values of the two CVs in the liquid and solid states, while the dotted gray line interpolates between them. In D, we report also a few snapshots of the crystallization process made with the Open Visualization Tool (OVITO) software (71).
As a final comment, we argue that the different degree of sampling efficiency between the two data-driven CVs has to be rooted in their different training objectives. Being trained as a classifier, Deep-LDA very accurately discriminates between the solid and the liquid phases, but it has no information about the transition region that connects them. Consequently, in almost the entire range of values spanned by the variable during the simulation, the system is either completely in the crystalline or the liquid phase (Fig. 6C). The Deep-TICA CV, other than classifying the states, also reflects the transition dynamics. In fact, in Fig. 6D, we see that it describes more smoothly the transition between the two phases as Deep-TICA is linearly correlated with the number of crystalline atoms, which is a relevant quantity in the classical nucleation theory framework (60).
Conclusions
The extension of the variational principle of conformation dynamics to enhanced sampling data (29) represents a promising way to address the chicken-and-egg dilemma intrinsic to the determination of CVs. Here, we leverage the flexibility of NNs and recent developments in advanced sampling techniques to construct a general and robust protocol. The Deep-TICA method allows us to analyze a biased simulation trajectory, extract the slow modes that hinder its convergence, and subsequently, accelerate them. This can be used to extract CVs from generalized ensemble simulations and to complement approximate CVs constructed based on physical considerations or in a data-driven manner. Other than improving sampling, this method provides us with atomistic details on the rare events dynamics. Remarkably, our work underlines the fact that even a partial information about the transition pathways does go a long way to solve the rare event problem. In fact, the test on the alanine dipeptide benchmark shows that the procedure is applicable even when starting from a very poor initial enhanced sampling simulation. This promises to be of great help in the study of realistic systems, where the identification of appropriate CVs is challenging. Application of the method to the more complex examples of chignolin folding and material crystallization illustrates how this acceleration allows the FES to be reconstructed with high accuracy, with no need of physical or chemical insight into the transition dynamics. We are confident that our approach can be applied to even more complex systems and that it can be of great help to the broad molecular simulation community.
Materials and Methods
Time-Lagged Covariance Matrices
Given an enhanced sampling simulation, we first rescale the time according to Eq. 12. We then search for pairs of configurations distant a lag time τ in time . Due to time reweighting, the value of τ cannot be interpreted as a physical time. However, we found consistent results for a range of lag-time values such that all desired eigenvalues did not decay to zero (SI Appendix, Fig. S1). Note that, when Eq. 12 is discretized, time intervals become unevenly spaced in , and the calculation of the time-lagged covariance matrices requires some care. To deal with this numerical issue, we resort to the procedure proposed in ref. 45. These pairs of configurations are saved in a dataset and later used for the NN training. Furthermore, it should be noted that while in principle, the two correlation matrices are symmetric, this condition might not be satisfied when estimating them from MD simulations due to limited sampling. Here, we symmetrize the matrices to enforce detailed balance as . This choice is the simplest, although it introduces a bias (27).
Deep-TICA CVs Training
Deep-TICA CVs are trained using the machine learning library PyTorch (61). As previously done for Deep-LDA and other nonlinear VAC methods (33), we apply Cholesky decomposition to C(0) to convert Eq. 8 into a standard eigenvalue problem. This allows us to back propagate the gradients through the eigenvalue problem by using the automatic differentiation feature of the machine learning libraries. We use a feed-forward NN composed by two layers and the hyperbolic tangent as the activation function. The NN parameters are optimized using ADAM with a learning rate of 1e-3. To avoid overfitting, we split the dataset into training/validation and apply early stopping with a patience of 10 epochs. Furthermore, the inputs are scaled to have zero mean and variance equal to one. Also, the Deep-TICA CVs are scaled in order for their range of values to be between –1 and 1. The normalization factors are calculated over the training set and saved into the model for inference. After the training is performed, the model is serialized so that it can be used on the fly in an MD simulation.
PLUMED–PyTorch Interface
To use the transfer operator eigenfunctions as CVs for enhanced sampling simulations, we use a modified version of the open-source PLUMED2 (62) plug-in which we interfaced with the LibTorch C++ library, as in ref. 20. The model trained in Python is loaded by PLUMED to evaluate CV values and derivatives with respect to descriptors for configurations explored during the simulation and apply a bias potential along them.
Alanine Dipeptide Simulations
Alanine dipeptide (ACE-ALA-NME) simulations are carried out using GROMACS (63) patched with PLUMED. We use the Amber99-SB (64) force field with a time step of 2 fs. The isothermal–isochoric (NVT) ensemble is sampled using the velocity rescaling thermostat (65) with a temperature of 300 K. For the OPES multithermal simulation, we sample a range of temperatures from 300 to 600 K, updating the bias every PACE = 500 steps. We run a 50-ns simulation and use the last 35 ns where the bias is in a quasistatic regime. We then look for configurations separated by a lag time of 0.1. The input descriptors of the Deep-TICA CVs are the 45 distances between the heavy atoms, and the following NN architecture is used: 45-30(tanh)-30(tanh)-3. We optimize the first two eigenvalues in the loss function. After training the CVs, a new OPES simulation is performed in the multithermal ensemble with the same parameters as before, combined with the multiumbrellas OPES ensemble along Deep-TICA 1 CV with the parameters SIGMA = 0.1 and BARRIER = 40. Since in the simulation driven by Deep-TICA 1, the time needed to converge the multithermal bias is very short, we did not use the static bias from the previous simulation, but we optimized it together with the bias along the TICA CV.
The second example involves the OPES simulation in which the dihedral angle ψ is used as the CV. The parameters of OPES are PACE = 500, SIGMA = 0.15, and BARRIER = 40. The first 500 ns of a total simulation length of 5 µs are discarded, while the remaining is used to compute time correlation functions with a lag time equal to five. The NN details are the same as in the multithermal example. Next, an OPES simulation is performed using Deep-TICA 1 as the CV, with parameters PACE = 500, SIGMA = 0.025, and BARRIER = 30, along with the static bias from the previous simulation.
Chignolin Simulations
Simulations of the CLN025 peptide (sequence TYR-TYR-ASP-PRO-GLU-THR-GLY-THR-TRP-TYR) are performed using GROMACS patched with PLUMED. Computational setup is chosen to make a direct comparison with ref. 50. CHARMM22* force field (66) and TIP3P water model (67) are used, the integration time step is 2 fs, and the target temperature of the thermostat is set to 340 K. ASP, GLU residues as well as the N- and C-terminal amino acids are simulated in their charged states. The simulation box contains 1,906 water molecules, together with two sodium ions that neutralize the system. The linear constraint solver algorithm is applied to every bond involving H atoms, and electrostatic interactions are computed via the particle mesh Ewald scheme, with a cutoff of 1 nm for all nonbonded interactions.
The initial simulation is performed with OPES to simulate the multithermal ensemble in a range of temperatures from 270 to 700 K. We simulate eight replicas sharing the same bias potential to harvest more transitions. The simulation time is 250 ns, of which the first 50 ns are not used for the Deep-TICA training. A lag time equal to five is used. In order to compute the scaled time correlation functions, we reweight at the simulation temperature of 340 K. Note that when starting from a multithermal simulation, one could also reweight at different temperatures and extract the associated eigenfunctions. Initially, a larger NN is trained using as input all the heavy atom distances, with an architecture 4278-256(tanh)- 256(tanh)-5. After performing an analysis of the features’ relevance, based on the derivatives of the leading eigenfunction with respect to the inputs (20), a smaller NN is trained using a reduced set of 210 distances and architecture 210-50(tanh)-50(tanh)-5. The list of the distances used is available in the PLUMED-NEST repository. We observe very similar results in terms of the extracted eigenvalue when using between 100 and 300 inputs. The number of optimized eigenvalues in the loss function is equal to two. We also analyzed the effect of optimizing up to three eigenvalues. The second eigenfunction does not change, while we found additional nested states within the three folded states identified by Deep-TICA 2 when also including the third one in the analysis. Finally, we enhance the fluctuations of the Deep-TICA 1 CV via an OPES simulation with parameters PACE = 500, SIGMA = 0.1, and BARRIER = 30, together with the static multithermal potential from the initial simulation.
Silicon Simulations
Silicon simulations are carried out using LAMMPS (68) patched with PLUMED using the Stillinger–Weber interatomic potential (59). A 3 × 3 × 3 supercell (216 atoms) is simulated in the isothermal–isobaric (NPT) ensemble with a time step of 2 fs. A thermostat with a target temperature of 1,700 K is used with a relaxation time of 100 fs, while the values for the barostat are 1 atm and 1 ps.
First, two 5-ns-long simulations of standard MD in the solid and liquid states are performed. The values of the 95 three-dimensional structure factor peaks in these configurations are computed, and this information is used to construct a Deep-LDA CV using a two-layer NN with 30 nodes per layer. A 50-ns OPES simulation biasing this variable, with PACE = 500, adaptive sigma, and BARRIER = 1,000, is performed. The first 25 ns are not used for NN training. A lag time of 0.5 is used. The input descriptors and architecture of the NN are the same as those used for Deep-LDA. Only the principal eigenvalue is optimized in the loss function. We then run a new OPES simulation biasing the Deep-TICA CV using the same parameters as in the initial simulation, along with the static bias potential . The fraction of diamond-like atoms is computed in PLUMED with the Environment Similarity CV, with parameters SIGMA = 0.4 LATTICE_CONSTANTS = 5.43 MORE_THAN = R_0 = 0.5 NN = 12 MM = 24.
Acknowledgments
We thank Dr. Michele Invernizzi for several valuable discussions and Dr. Michele Invernizzi and Dr. Andrea Rizzi for carefully reading the paper. The calculations were carried out on the Euler cluster of ETH Zürich.
Footnotes
The authors declare no competing interest.
Published under the PNAS license.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2113533118/-/DCSupplemental.
Data Availability
The code for the training of the Deep-TICA CVs, a Jupyter notebook tutorial, and the instructions to employ them in PLUMED are available at GitHub at https://github.com/luigibonati/deep-learning-slow-modes. All the simulations are performed using open-source software as described in previous sections. Input files necessary to perform the simulations are available at GitHub and at the PLUMED-NEST (72) repository with plumID:21.039. MD trajectories are deposited in the Materials Cloud repository (DOI: 10.24435/materialscloud:3g-9x) (73).
References
- 1.Peters B., Reaction Rate Theory and Rare Events (Elsevier, 2017). [Google Scholar]
- 2.Valsson O., Tiwary P., Parrinello M., Enhancing important fluctuations: Rare events and metadynamics from a conceptual viewpoint. Annu. Rev. Phys. Chem. 67, 159–184 (2016). [DOI] [PubMed] [Google Scholar]
- 3.Torrie G. M., Valleau J. P., Nonphysical sampling distributions in Monte Carlo free-energy estimation: Umbrella sampling. J. Comput. Phys. 23, 187–199 (1977). [Google Scholar]
- 4.Mezei M., Adaptive umbrella sampling: Self-consistent determination of the non-Boltzmann bias. J. Comput. Phys. 68, 237–248 (1987). [Google Scholar]
- 5.Voter A. F., Accelerated molecular dynamics of infrequent events. Phys. Rev. Lett. 78, 3908–3911 (1997). [Google Scholar]
- 6.Laio A., Parrinello M., Escaping free-energy minima. Proc. Natl. Acad. Sci. U.S.A. 99, 12562–12566 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Valsson O., Parrinello M., Variational approach to enhanced sampling and free energy calculations. Phys. Rev. Lett. 113, 090601 (2014). [DOI] [PubMed] [Google Scholar]
- 8.Bonati L., Zhang Y. Y., Parrinello M., Neural networks-based variationally enhanced sampling. Proc. Natl. Acad. Sci. U.S.A. 116, 17641–17647 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Debnath J., Parrinello M., Gaussian mixture-based enhanced sampling for statics and dynamics. J. Phys. Chem. Lett. 11, 5076–5080 (2020). [DOI] [PubMed] [Google Scholar]
- 10.Invernizzi M., Parrinello M., Rethinking metadynamics: From bias potentials to probability distributions. J. Phys. Chem. Lett. 11, 2731–2736 (2020). [DOI] [PubMed] [Google Scholar]
- 11.Barducci A., Bonomi M., Parrinello M., Metadynamics. Wiley Interdiscip. Rev. Comput. Mol. Sci. 1, 826–843 (2011). [Google Scholar]
- 12.Bussi G., Laio A., Using metadynamics to explore complex free-energy landscapes. Nat. Rev. Phys 2, 200–212 (2020). [Google Scholar]
- 13.Sidky H., Chen W., Ferguson A. L., Machine learning for collective variable discovery and enhanced sampling in biomolecular simulation. Mol. Phys. 118, 1737742 (2020). [Google Scholar]
- 14.Wang Y., Lamim Ribeiro J. M., Tiwary P., Machine learning approaches for analyzing and enhancing molecular dynamics simulations. Curr. Opin. Struct. Biol. 61, 139–145 (2020). [DOI] [PubMed] [Google Scholar]
- 15.Noé F., Clementi C., Collective variables for the study of long-time kinetics from molecular trajectories: Theory and methods. Curr. Opin. Struct. Biol. 43, 141–147 (2017). [DOI] [PubMed] [Google Scholar]
- 16.Mendels D., Piccini G., Parrinello M., Collective variables from local fluctuations. J. Phys. Chem. Lett. 9, 2776–2781 (2018). [DOI] [PubMed] [Google Scholar]
- 17.Sultan M. M., Pande V. S., Automated design of collective variables using supervised machine learning. J. Chem. Phys. 149, 094106 (2018). [DOI] [PubMed] [Google Scholar]
- 18.Brandt S., Sittel F., Ernst M., Stock G., Machine learning of biomolecular reaction coordinates. J. Phys. Chem. Lett. 9, 2144–2150 (2018). [DOI] [PubMed] [Google Scholar]
- 19.Piccini G., Mendels D., Parrinello M., Metadynamics with discriminants: A tool for understanding chemistry. J. Chem. Theory Comput. 14, 5040–5044 (2018). [DOI] [PubMed] [Google Scholar]
- 20.Bonati L., Rizzi V., Parrinello M., Data-driven collective variables for enhanced sampling. J. Phys. Chem. Lett. 11, 2998–3004 (2020). [DOI] [PubMed] [Google Scholar]
- 21.Rizzi V., Bonati L., Ansari N., Parrinello M., The role of water in host-guest interaction. Nat. Commun. 12, 93 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Karmakar T., Invernizzi M., Rizzi V., Parrinello M., Collective variables for the study of crystallisation. Mol. Phys., 10.1080/00268976.2021.1893848 (2021). [DOI] [Google Scholar]
- 23.Naritomi Y., Fuchigami S., Slow dynamics in protein fluctuations revealed by time-structure based independent component analysis: The case of domain motions. J. Chem. Phys. 134, 065101 (2011). [DOI] [PubMed] [Google Scholar]
- 24.Prinz J. H., et al., Markov models of molecular kinetics: Generation and validation. J. Chem. Phys. 134, 174105 (2011). [DOI] [PubMed] [Google Scholar]
- 25.Pérez-Hernández G., Paul F., Giorgino T., Fabritiis G. De, Noé F., Identification of slow molecular order parameters for Markov model construction. J. Chem. Phys. 139, 015102 (2013). [DOI] [PubMed] [Google Scholar]
- 26.Schwantes C. R., Pande V. S., Improvements in Markov State Model construction reveal many non-native interactions in the folding of NTL9. J. Chem. Theory Comput. 9, 2000–2009 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Wu H., et al., Variational Koopman models: Slow collective variables and molecular kinetics from short off-equilibrium simulations. J. Chem. Phys. 146, 154104 (2017). [DOI] [PubMed] [Google Scholar]
- 28.Sultan M. M, Pande V. S., tICA-metadynamics: Accelerating metadynamics by using kinetically selected collective variables. J. Chem. Theory Comput. 13, 2440–2447 (2017). [DOI] [PubMed] [Google Scholar]
- 29.McCarty J., Parrinello M., A variational conformational dynamics approach to the selection of collective variables in metadynamics. J. Chem. Phys. 147, 204109 (2017). [DOI] [PubMed] [Google Scholar]
- 30.Hernández C. X., Wayment-Steele H. K., Sultan M. M., Husic B. E., Pande V. S., Variational encoding of complex dynamics. Phys. Rev. E 97, 062412 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Wehmeyer C., Noé F., Time-lagged autoencoders: Deep learning of slow collective variables for molecular kinetics. J. Chem. Phys. 148, 241703 (2018). [DOI] [PubMed] [Google Scholar]
- 32.Mardt A., Pasquali L., Wu H., Noé F., VAMPnets for deep learning of molecular kinetics. Nat. Commun. 9, 5 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Chen W., Sidky H., Ferguson A. L., Nonlinear discovery of slow molecular modes using state-free reversible VAMPnets. J. Chem. Phys. 150, 214114 (2019). [DOI] [PubMed] [Google Scholar]
- 34.McGibbon R. T., Husic B. E., Pande V. S., Identification of simple reaction coordinates from complex dynamics. J. Chem. Phys. 146, 044109 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Rohrdanz M. A., Zheng W., Clementi C., Discovering mountain passes via torchlight: Methods for the definition of reaction coordinates and pathways in complex macromolecular reactions. Annu. Rev. Phys. Chem. 64, 295–316 (2013). [DOI] [PubMed] [Google Scholar]
- 36.Tiwary P., Berne B. J., Spectral gap optimization of order parameters for sampling complex molecular systems. Proc. Natl. Acad. Sci. U.S.A. 113, 2839–2844 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Chen W., Ferguson A. L., Molecular enhanced sampling with autoencoders: On-the-fly collective variable discovery and accelerated free energy landscape exploration. J. Comput. Chem. 39, 2079–2102 (2018). [DOI] [PubMed] [Google Scholar]
- 38.Demuynck R., et al., Protocol for identifying accurate collective variables in enhanced molecular dynamics simulations for the description of structural transformations in flexible metal-organic frameworks. J. Chem. Theory Comput. 14, 5511–5526 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Ribeiro J. M. L., Bravo P., Wang Y., Tiwary P., Reweighted autoencoded variational Bayes for enhanced sampling (RAVE). J. Chem. Phys. 149, 072301 (2018). [DOI] [PubMed] [Google Scholar]
- 40.Zhang J., Chen M., Unfolding hidden barriers by active enhanced sampling. Phys. Rev. Lett. 121, 010601 (2018). [DOI] [PubMed] [Google Scholar]
- 41.Wang Y., Ribeiro J. M. L., Tiwary P., Past-future information bottleneck for sampling molecular reaction coordinate simultaneously with thermodynamics and kinetics. Nat. Commun. 10, 3573 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Rydzewski J., Valsson O., Multiscale reweighted stochastic embedding: Deep learning of collective variables for enhanced sampling. J. Phys. Chem. A 125, 6286–6302 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Tsai S. T., Smith Z., Tiwary P., SGOOP-d: Estimating kinetic distances and reaction coordinate dimensionality for rare event systems from biased/unbiased simulations. arXiv [Preprint] (2021). https://arxiv.org/abs/2104.13560 (Accessed 15 July 2021). [DOI] [PubMed]
- 44.Belkacemi Z., Gkeka P., Lelièvre T., Stoltz G., Chasing collective variables using autoencoders and biased trajectories. arXiv [Preprint] (2021). https://arxiv.org/abs/2104.11061v1 (Accessed 15 July 2021). [DOI] [PubMed]
- 45.Yang Y. I., Parrinello M., Refining collective coordinates and improving free energy representation in variational enhanced sampling. J. Chem. Theory Comput. 14, 2889–2894 (2018). [DOI] [PubMed] [Google Scholar]
- 46.Noé F., Nüske F., A variational approach to modeling slow processes in stochastic dynamical systems. Multiscale Model. Simul. 11, 635–655 (2013). [Google Scholar]
- 47.Invernizzi M., Piaggi P. M., Parrinello M., Unified approach to enhanced sampling. Phys. Rev. X 10, 041034 (2020). [Google Scholar]
- 48.Barducci A., Bussi G., Parrinello M., Well-tempered metadynamics: A smoothly converging and tunable free-energy method. Phys. Rev. Lett. 100, 020603 (2008). [DOI] [PubMed] [Google Scholar]
- 49.Invernizzi M., Parrinello M., Making the best of a bad situation: A multiscale approach to free energy calculation. J. Chem. Theory Comput. 15, 2187–2194 (2019). [DOI] [PubMed] [Google Scholar]
- 50.Lindorff-Larsen K., Piana S., Dror R. O., Shaw D. E., How fast-folding proteins fold. Science 334, 517–520 (2011). [DOI] [PubMed] [Google Scholar]
- 51.Okumura H., Temperature and pressure denaturation of chignolin: Folding and unfolding simulation by multibaric-multithermal molecular dynamics method. Proteins 80, 2397–2416 (2012). [DOI] [PubMed] [Google Scholar]
- 52.Shaffer P., Valsson O., Parrinello M., Enhanced, targeted sampling of high-dimensional free-energy landscapes using variationally enhanced sampling, with an application to chignolin. Proc. Natl. Acad. Sci. U.S.A. 113, 1150–1155 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.McKiernan K. A., Husic B. E., Pande V. S., Modeling the mechanism of CLN025 beta-hairpin formation. J. Chem. Phys. 147, 104107 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Mendels D., Piccini G., Brotzakis Z. F., Yang Y. I., Parrinello M., Folding a small protein using harmonic linear discriminant analysis. J. Chem. Phys. 149, 194113 (2018). [DOI] [PubMed] [Google Scholar]
- 55.Kührová P., De Simone A., Otyepka M., Best R. B., Force-field dependence of chignolin folding and misfolding: Comparison with experiment and redesign. Biophys. J. 102, 1897–1906 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Maruyama Y., Mitsutake A., Analysis of structural stability of chignolin. J. Phys. Chem. B 122, 3801–3814 (2018). [DOI] [PubMed] [Google Scholar]
- 57.Zhang Y. Y., Niu H., Piccini G., Mendels D., Parrinello M., Improving collective variables: The case of crystallization. J. Chem. Phys. 150, 094509 (2019). [DOI] [PubMed] [Google Scholar]
- 58.Bonati L., Parrinello M., Silicon liquid structure and crystal nucleation from ab-initio deep metadynamics. Phys. Rev. Lett. 121, 265701 (2018). [DOI] [PubMed] [Google Scholar]
- 59.Stillinger F. H., Weber T. A., Computer simulation of local order in condensed phases of silicon. Phys. Rev. B Condens. Matter 31, 5262–5271 (1985). [DOI] [PubMed] [Google Scholar]
- 60.Kelton K. F., Greer A., Nucleation in Condensed Matter: Applications in Materials and Biology (Pergamon, 2010), vol. 15. [Google Scholar]
- 61.Paszke A., et al., “Automatic differentiation in PyTorch” in Advances in Neural Information Processing Systems 32, Wallach H., et al., Eds. (NeurIPS, 2019), pp. 8024–8035. [Google Scholar]
- 62.Tribello G. A., Bonomi M., Branduardi D., Camilloni C., Bussi G., PLUMED 2: New feathers for an old bird. Comput. Phys. Commun. 185, 604–613 (2014). [Google Scholar]
- 63.Van Der Spoel D., et al., GROMACS: Fast, flexible, and free. J. Comput. Chem. 26, 1701–1718 (2005). [DOI] [PubMed] [Google Scholar]
- 64.Hornak V., et al., Comparison of multiple Amber force fields and development of improved protein backbone parameters. Proteins 65, 712–725 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Bussi G., Donadio D., Parrinello M., Canonical sampling through velocity rescaling. J. Chem. Phys. 126, 014101 (2007). [DOI] [PubMed] [Google Scholar]
- 66.Piana S., Lindorff-Larsen K., Shaw D. E., How robust are protein folding simulations with respect to force field parameterization? Biophys. J. 100, L47–L49 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Jorgensen W. L., Chandrasekhar J., Madura J. D., Impey R. W., Klein M. L., Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 79, 926–935 (1983). [Google Scholar]
- 68.Plimpton S., Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 117, 1–19 (1995). [Google Scholar]
- 69.Humphrey W., Dalke A., Schulten K., VMD: Visual molecular dynamics. J. Mol. Graph. 14, 33–38 (1996). [DOI] [PubMed] [Google Scholar]
- 70.Piaggi P. M., Parrinello M., Calculation of phase diagrams in the multithermal-multibaric ensemble. J. Chem. Phys. 150, 244119 (2019). [DOI] [PubMed] [Google Scholar]
- 71.Stukowski A., Visualization and analysis of atomistic simulation data with OVITO-the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 18, 015012 (2009). [Google Scholar]
- 72.Bonomi M., et al.; PLUMED consortium, Promoting transparency and reproducibility in enhanced molecular simulations. Nat. Methods 16, 670–673 (2019). [DOI] [PubMed] [Google Scholar]
- 73.Bonati L., Piccini G., Parrinello M., Deep learning the slow modes for rare events sampling. Materials Cloud Archive. 10.24435/materialscloud:3g-9x. Deposited 16 September 2021. [DOI] [PMC free article] [PubMed]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The code for the training of the Deep-TICA CVs, a Jupyter notebook tutorial, and the instructions to employ them in PLUMED are available at GitHub at https://github.com/luigibonati/deep-learning-slow-modes. All the simulations are performed using open-source software as described in previous sections. Input files necessary to perform the simulations are available at GitHub and at the PLUMED-NEST (72) repository with plumID:21.039. MD trajectories are deposited in the Materials Cloud repository (DOI: 10.24435/materialscloud:3g-9x) (73).