On the global time evolution of the Covid-19 pandemic: Logistic modeling

Abstract

In this article it is presented a multi-logistic model to describe the time evolution of the Covid-19 pandemics. The model is not intended as paragon for the accurate prediction of the future number of people infected, but instead as a useful phenomenological approach for a comprehensive understanding of the pandemic development, able to uncover some hidden aspects of its unfolding. Our results, using OWID data of total cases and daily cases of Covid-19 from March 12, 2020, up to September 27, 2021, brought to light that the pandemic has unfolded globally as a multi-step logistic, namely six logistic phases, each with its own characteristic duration and intensity. Moreover, it is demonstrated how differently the pandemics spread among different countries and continents. The methodology is tested regarding its ability of forecasting, and is demonstrated that it works well in the range of circa 30 days within a margin of less than 3% error while a given phase is still in development. The case study of Portugal demonstrates the benefit of preventive sanitary measures, as well as shows how disastrous it may be the absence of such measures due to hesitations and/or political positions. Completing the article, a qualitative analysis is presented to scrutinize the possible causes of the asymmetry observed in the diffusion of Covid-19 among the different continents and countries.

1. Introduction

Along the first half of the eighteenth century, there was a great debate, notably in French and British societies, regarding the inoculation technique as a form of treatment for smallpox. Lady Montague, wife of the British ambassador in the Ottoman Empire, introduced this technique in England in 1718. By the middle of that century, the debate over inoculation spread over the continent. It ultimately attracted the attention of many scientists like, Daniel Bernoulli, Euler, and D'Alembert.

The outcome of this debate was that by 1760 Bernoulli published in Mem. Math. Phys. Acad. Roy. Sci. on a mathematical modeling of the deaths from smallpox, aiming at influencing public policy towards variolation, the technique of injecting a mild stain of the smallpox virus to induce immunity against the full disease. Sally Blower in Reviews in Medical Virology (Blower, 2004) has republished Bernoulli's work and its historical and current significance.

After that, more systematic work on modeling disease was carried out only by the early 20th century by Hamer (1906), Ross (1913), among others. Hamer formulated and analyzed a discrete time model in his attempt to understand the recurrence of measles epidemics. Hamer's model may have been the first to assume that the incidence (number of new cases per unit time) depends on the product of the densities of the susceptible and infective. Ross, on the other hand, was interested in the incidence and control of malaria, so he developed differential equation models for malaria as a host-vector disease. For his work on the malaria transmission Ross had won the 1902 Nobel Prize in Medicine.

Based on these previous works, Kermack and McKendrick (1927) published a classical paper revealing a threshold condition for the spread of a disease and providing means of predicting the ultimate size of an epidemic. Since then, epidemiologic modeling experienced an exponential growth. We refer to Bailey (1975) and Anderson and May (1991) for detailed discussions and further references on the subject.

Regarding the disease status, an individual in a given population is in one of the following categories: susceptible (S), infected (I), or recovered (R). In the simplest epidemic case, the population consists only of susceptible and infected individuals, that is:

$$S\left(t\right)+I\left(t\right)=N$$ (1)

where N represents the constant population size, and S(t) and I(t) are, respectively, the numbers of susceptible and infected individuals at time t. The time evolution of these individuals is governed by the following equations:

$$dS/dt=-f\left(S,I\right),dI/dt=f\left(S,I\right)$$ (2)

Here, f (S, I) designates the incidence of the disease, i.e., the rate at which infection occurs. This function is clearly an increasing function of both S and I, and its simplest form is:

$$f\left(S,I\right)=\lambda \left(I\right)S=\beta IS$$ (3)

The function λ(I) is called the “force of infection”. It is defined as the probability density of a given susceptible contracting the disease in the next time interval, whereas the parameter β is called the “infectious contact rate”, i.e., the rate of infection per susceptible per infected.

Substituting S in Eq. (2) by (N – I) one gets:

$$dI/dt=\beta I\left(N-I\right)=rI(1-I/K)$$ (4)

Eq. (4) is the usual logistic equation with a growth rate parameter r equal to βN and a carrying capacity K = N. In order words, the evolution of the number of infect individuals in a typical epidemic should exhibit an S-shaped curve. This case, usually designated as ‘SI epidemic’, does not include recovery. It describes a situation that will always spread and will eventually infect all susceptible.

There are many other more models with varying degree of complexity. The so-called SIS (susceptible-infected-susceptible) model considers the case of recovered individuals. It assumes that the individuals leaving the infective class are considered again as susceptible, while in the SIR (susceptible-infected-recovered) epidemic the individuals leaving the infective class play no further role in the epidemics. They may be immune, dead, or removed by an isolation policy. We find it interesting for future analysis to proceed with the discussion of these basic epidemiologic models. Accordingly, let us consider the SIR model.

The governing equations for the SIS epidemics are the same as those of Eq. (2) to which we add a term denoted by g(I) representing recovery from the disease, namely:

$$dS/dt=-\beta IS+g\left(I\right),dI/dt=\beta IS-g\left(I\right)$$ (5)

The simplest form for g (I) is a linear expression of the type:

$$g\left(I\right)=\gamma I$$ (6)

Substituting in Eq. (5) S and I by uN and vN, respectively, and the time variable by x = γt, the governing equations reduces to:

$$du/dx=-\left(R_{0}u-1\right)v;dv/dx=(R_{0}u-1)v$$ (7)

where the parameter R₀ = β Ν / γ  is known as the ‘reproductive ratio’.

This interpretation of R₀ (also known as ‘R naught’) is as follows. The numerator βΝ  represents the rate at which a single infected introduced into a susceptible population of size N makes infectious contacts, and γ⁻¹ is the expected length of time such infected remains so. That is, R₀ is the expected number of infectious contacts made by an infected individual.

Noting that according to the above definitions u + v = 1, the equation for the infected individuals (v) may be finally written as:

$$dv/dx=\left(R_0--1\right)\mathrm{v}[1--(R_0/\left(1-R_0\right)v]=rv\left(1-v/K\right)$$ (8)

In other words, the equation governing the time evolution of the fraction of infected individuals in a population of size N is again a logistic equation with a growth rate parameter equal to (R ₀ −1), and a carrying capacity equal to K = R ₀ −1)/ R ₀. It differs from the SI epidemic case (c.f., Eq. (5)) by the fact that in this case the parameters r and K are both always positive. In the SIS epidemics case, in contrast, these two parameters can be either positive or negative depending whether the reproductive ratio R ₀ is less or greater than unity. For R ₀〈 1 the disease dies out, while for R ₀〉 1 the disease become endemic. This can be seen by recalling that the generic form of the solution to the logistic equation can be written as:

$$f\left(t\right)=\frac{K\exp \left(r\left(t-t_c\right)\right)}{1+\text{exp}\left(r\left(t-t_c\right)\right)}$$ (9)

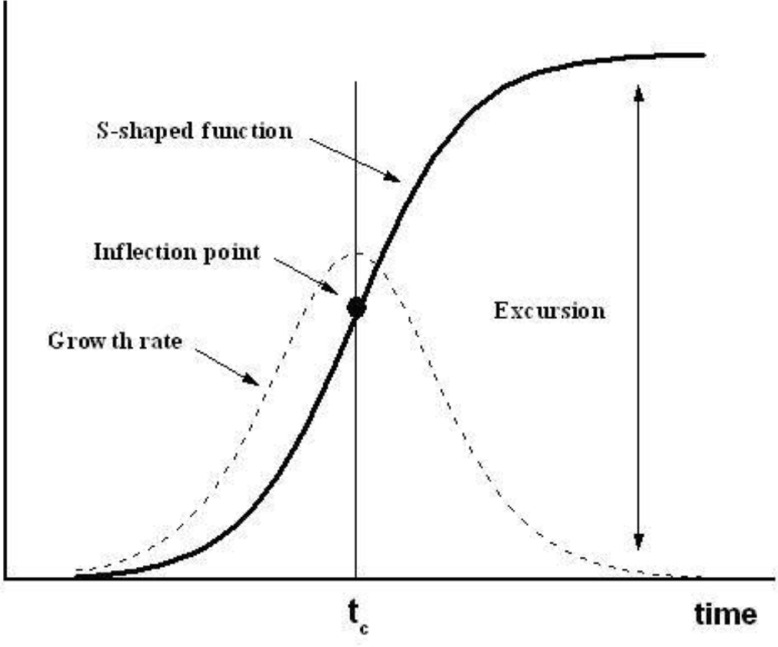
This means that for r〈 0, as in the case of R ₀ < 1, the fraction of infected population vanishes as time increases. For R ₀〉 1, the fraction of infected individuals tends to a steady-state regime around the carrying capacity value, that is, the disease becomes endemic. In other words, a typical epidemiological growth process described by some cumulative indicator (e.g., number of infected individuals) evolves in time following an S-shaped or sigmoid curve, as shown schematically in Fig. 1 . After reaching a maximum growth rate, somewhere along its evolutionary trajectory, it eventually saturates. The dynamics of such process is determined by the way it grows in its early stages and declines at later times, that is, it results from the specific relationship between its amplitude and its growth rate, or growth frequency, at a given time.

Fig. 1.

Schematic plot of a typical S-shaped curve, characterized by three parameters, namely, its excursion towards saturation, the point tc at which the inflection from the initial growth stage to the final saturation occurs, and a characteristic growth time telling us how sharp its growth rate curve profile is. The dashed curve is the time derivative of the S-shaped curve, representing its growth rate, and exhibits a characteristic “bell” shape.

This overall logistic trend used to describe epidemics is a common feature of a considerable number of biological and manmade systems. Nevertheless, in many of these complex systems, the hypothesis of a single carrying capacity is not a realistic one. For instance, in biological systems the carrying capacity is essentially dependent on the fact that the species can expand or shrink their niches. In manmade or man controlled systems, such as energy sources, transportation, communications, just to mention a few, the carrying capacity at a given period of time is frequently limited by the relevant technological development attained at that period. As scientific knowledge and technology advances, new products and processes are introduced in society which will ultimately alter the dynamics of a specific sector. For instance, wood has been gradually substituted by coal, as a primary energy source, which, in its turn, has been partially replaced by oil and gas. Eventually, the latter will yield space to coexist with fuel cells, wind energy, nuclear plants, and other alternative sources within the energy mix in the near future. At each stage of a technological substitution process, the relative dominance of a given primary energy source over another changes and the carrying capacity of an energy supply system becomes different.

These are some examples of systems where several different factors conjugate to change the system carrying capacity, requiring, accordingly a multi-step logistic approach to describe their time evolution. The worldwide Covid-19 pandemic is not an exception to this reasoning, as we shall see in this paper. A large number of factors involved in an epidemic demands a multi-logistic approach for the analysis of its time evolution analysis. These include the readiness of local health authorities to impose some preventing and prophylactic measures (like the use of equipment of individual protection, social distance recommendations, and so on) as well as availability of diagnosis tests and vaccine. All these intervening factors do not take place simultaneously and have their own time response, thereby contributing to the buildup of different phases along with the epidemics.

The data used in this study were taken from the Covid-19 data collection presented in “Our World in Data” (OWID, 2021). The primary data source comes from the Covid-19 Data Repository by the Center for Systems Science and Engineering (CSSE) at the Johns Hopkins University. Our analysis in this paper covers the time period spanning from January 22, 2020, to September 27, 2021, consisting of 565 data records of accumulated and daily number of confirmed Covid-19 cases.

Closing this introductory section, it is worth to address some words about the above chosen dates framing our analysis. By epidemic we mean the situation in which more than normal number of an illness or other health-related events affects a given community or region, whereas a pandemic refers to the situation in which the disease responsible for an epidemic experiences a worldwide spread. China has reported the first cases in early December 2019, but soon, as of January 31st, 2020, the disease has spread for 27 other countries in all continents (USA, Canada, 8 European countries, 15 Asian countries, and the United Arab Emirates), infecting about 10,000 people. By this time the World Health Organization (WHO) declared the outbreak as a ‘Public Health Emergency of International Concern’. On March 2nd, 2020, when the first case was reported in Portugal (a case study to be considered in this paper), the number of countries reporting infection cases jumped to about 90 countries and on March 11th, 2020, WHO finally declared the disease as pandemic, when the number of infected people surpassed 126,000, having caused the death of about 4600 people.

Accordingly, our counting starts on January 22nd, 2020, when the disease was spread for more than 20 countries1 and closes on September 27, 2021, covering then a time span of about 20 months. Our choice for September 27, 2021, as the closing date of our analysis was based on two major aspects, namely, the fact that by September 21, 2021, 6 billion doses of Covid-19 vaccine had already been administered across the world and, secondly, on the ongoing international commitment that every country would have vaccinated at least 40% of its population with at least one dose by the end of 2021. These two points suggest that, if the pandemics end is not close, any subsequent rise in the number of infected cases is expected to be limited in numbers and geographic regions.

2. - Logistic Modeling

The modeling of the Covid-19 pandemic spreading attracted the attention of several authors since its early stages. Among these, we mention the works by Komarova and collaborators (Komarova et al., 2020), (Aviv-Sharon et al., 2020) and of Utsunomiya and collaborators (Utsunomiya et al., 2020). They all focused their studies on the spreading and acceleration of the covid-19 infections along the first 3 to 4 months of the pandemic evolution. The work by Komarova and collaborators is based on use of computer simulations of a metapopulation model that considers both local spread and spread across geographic space. Their analysis provided evidence for exponential growth in early phase of the epidemics which is followed by a power law behavior in the long-term. Similar conclusions were also found by the other above mentioned authors. Due to the reduced number of records and diversity of the data at the early stages of the epidemics evolution, they all fail to describe quantitatively the dynamics of the several phases the epidemics passed through. Nevertheless, they pointed, at that time, to the complexity of such endeavor.

It is important to point out that one of the earliest proposed actions to control the current epidemics aimed slowing down the rate of the virus diffusion. This became popular in the media by the slogan “flattening the curve”. In this way, one of the first attempts on the logistic modeling of the Covid-19 pandemics focused on the discussion of this important question (Debecker and Modis, 2021). These authors used their earlier finding (Debecker and Modis, 1994) regarding a negative correlation between the final ceiling of the logistic equation and its growth rate to discuss the proposed flattening of the curve. They showed that flattening the curve by reducing its growth rate induces the prolongation of the pandemics, which, in turn, results in a greater number of infections. That is, the actual problem is not as simple as that (“flattening the curve”); it turns out to be a rather complicated optimization problem to be solved. We refer to these worth reading works for further details on this important issue.

A new methodology to improve the multi-logistic analysis of evolutionary time series has been presented in previous publications, (Miranda and Lima, 2010, Miranda and Lima, 2012) and Miranda et al. (2016). The primary aim in those papers was the modeling to deal with any extended series, especially those corresponding to a sequence of manmade events that involve a complex blending of social, economic, technological, and political interests. The proposed methodology was used to evaluate and disclose the onset of eventual periodic structures that can be attributed to the interplay among these components. By associating these aspects, the methodology was also checked as to its potential to improve the quality of short-term logistic forecasts.

In general, the complexity of factors affecting the evolutionary character of a time series entails that the relative influence of these components cannot be expected to be homogeneously distributed in time. Each of them has its own characteristic evolution time. One component may predominate over another during a certain period, or even over the entire time lapse considered. As a result, it would seem natural not to expect the entire process to be represented by a smooth single evolutionary logistic, or learning, curve, but rather to encompass a sequence of learning phases reflecting the interplay of these components in a way that corresponds to their relative importance along the process.

In other words, in general, the analysis of extended time series calls for a multi-logistic description. The multi-logistic description of a given time series uses a series of either logistic growth functions, when dealing with a cumulative indicator, such as the automobile fleet of a given country, or the derivatives of the logistic functions, the so-called logistic pulses, when the indicator refers to a given rate of events per unit of time, that is, to an event frequency time series.

Another important aspect of this new methodology regards the data fitting procedure. Should the chosen model function be a good ansatz the data fitting procedure provides us a set of fitting parameters that yields the best least square fit to the data. The model function so calculated represents the data tendency curve and is taken as an optimized phenomenological description of the time behavior of the quantity expressed by the empirical time series. However, the results from this data fitting procedure go far beyond exposing the overall tendency curve. In fact, the procedure also generates a data-to-model residuals time series associated to the original data series. In general, the residuals in a data fitting procedure will consist of random fluctuations, normally associated with random errors. They are not expected a priori to exhibit any kind of structured behavior, but rather they consist of a set of uncorrelated components. This is, for instance, the usual case of the noise observed in typical electrical circuits.

In some systems, however, the residuals series do not appear as a set of purely random fluctuations. On the contrary, they exhibit a structured oscillatory behavior. Accordingly, one may assume an existing cause-and-effect relationship among their components and associate this correlation to some intrinsic properties of the system represented by the original time series under consideration. In any event, the important point here is that if the residuals pattern can be described, say, by some harmonic sine series, its fundamental frequency will directly reflect the actual system parameters.

Thus, a methodology to deal with modeling complex evolutionary systems demands not only finding out a good model function to fitting the data, thereby ensuring a good description of the trend exhibited by the events, but also a thorough analysis of the resulting data fitting residuals. The residuals or deviations respond to the influences of the events or processes that decisively drive the initiatives represented by the data set.

Accordingly, the proposed methodology consists in modeling the trend of a given series of events by a multi-logistic function or multi-logistic pulses, whose model functions are written either as:

$$F\left(t\right)=\sum _i{K}_i\frac{\exp (\left(t-t_{ci}\right)/{\tau }_i)}{1+\exp (\left(t-t_{ci}\right)/{\tau }_i)}$$ (10)

in the case of a cumulative series of events, or,

$$F\left(t\right)=\sum _i{A}_i\frac{\exp \left(\left(t-t_{ci}\right)/{\tau }_i\right)}{1+\exp {\left(\left(t-t_{ci}\right)/{\tau }_i\right)}^2}$$ (11)

in the case the time series refers to the rate of events per unit time. In Eqs. (10) and (11), the parameter K_i denotes the excursion towards saturation during the i th growth sequence, in the case of cumulative events, and A_i the rate of change of the amplitude in the case of a time series of events frequency. The parameter t_{c i} is the inflection point of maximum rate of change of F(t) in the sequence i and τ _i ⁻¹ is its growth rate, or the growth capacity of respective i th growth sequence (it corresponds to r introduced in Eq. (9)).

The parameter τ in Eqs. (10) and (11) allows to determine the characteristic duration of the process to reach saturation, also known as ‘take-over time’ Δt. The characteristic duration Δt is defined as the time required for the system to complete 80% of its excursion, corresponding to the system evolution from 10% to 90% of the total excursion. It can be demonstrated that this lapse of time is equal to ln 81 (4.39) times the value of τ, that is Δt = 4.39τ.

As for the residuals analysis two aspects are relevant. The first one regards finding out repeating patterns in the residuals time series, such as the presence of periodic structures obscured by noise. This is usually carried out by the cross-correlation of the events with itself at different points in time. The conventional estimator for the correlation between observations separated by k time steps, the so-called autocorrelation coefficient at lag k, is given by Box et al. (2008) as:

$$r_k=\frac{{\sum }_{i=1}^{N-k}\left(x_i-\overline{x}\right)\left(x_{i+k}-\overline{x}\right)}{{\sum }_{i=1}^N\left(x_i-\overline{x}\right)\left(x_i-\overline{x}\right)}$$ (12)

where $\overline{x}$ is the overall mean value of the time series consisting of N observations x_i.

The plot of the so obtained autocorrelation coefficients of the residuals data as a function of the varying time lags provides the answer to this question. If random, such autocorrelations should be near zero for any and all time-lag separations, alternating between positive and negative spikes. If non-random, then one or more of the autocorrelations will be significantly non-zero.

Once the periodic structures are disclosed from the residuals time series, we may then carry on a spectral analysis of it (using Fourier techniques for instance) in order to find out the characteristic periods of the driving events.

3. - Time evolution of the worldwide Covid-19 cases

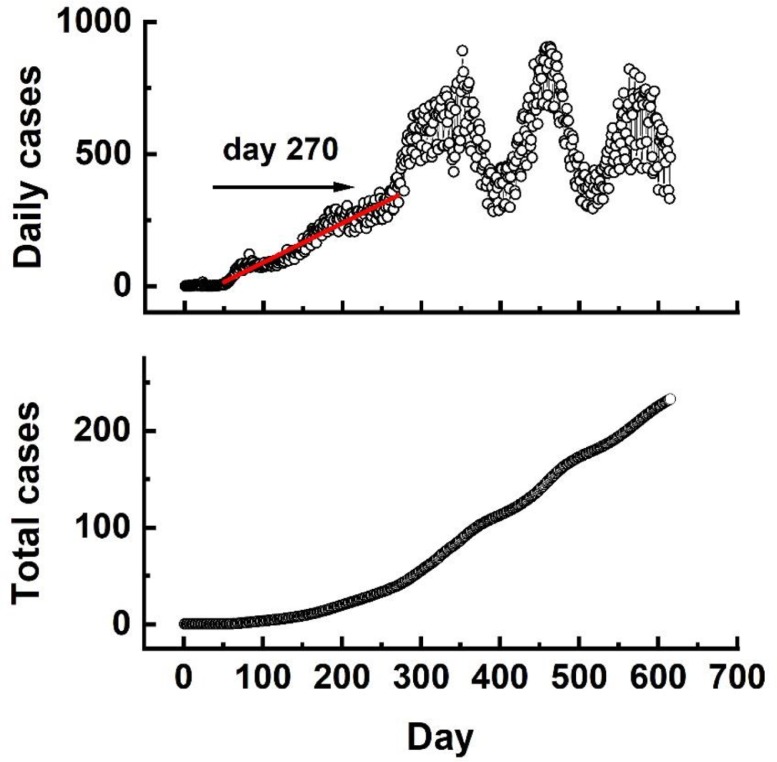
Our study of the time evolution of the Covid-19 pandemics was based on the analysis of the two major indicators, namely, the total and the daily number of confirmed cases. These are two complementary indicators, according to their major characteristics. The daily number of cases is a rate parameter indicating the pandemics build-up, while the total (or the accumulated) number of cases, inform us about the tendency of its evolutionary trajectory. The overall picture of the time evolution of these two indicators from Jan 22, 2020, up to Sep 27, 2021, is shown in Fig. 2 .

Fig. 2.

Time evolution of the worldwide daily and total number of Covid-19 cases since January 22, 2020, up to September 27, 2021. The daily number of cases are expressed in thousand units while the total number in million units. The red line in the plot of the daily cases was inset just to emphasize the pandemic fast build up along the 220 days after the first 50 days since January 22, 2020.

The pandemic build-up, as described by the evolution of the worldwide daily number of cases, may be summarized as follows. After an initial stage lasting for roughly 50 days, the daily number of cases entered a fast growing phase emphasized in Fig. 2 by the red line. This phase comprises 220 days from day 50 up to day 270, along which it grew roughly at an average rate of 1500 cases per day, accompanied, however, by some regular bursts. After this fast rising phase, Fig. 2 indicates that it entered another oscillating phase looking, however, as a ceiling phase. In other words, the overall picture coming out of Fig. 2 is that the Covid-19 build-up consisted of a sequence of pulses of cases having different intensities and durations. As a help to better understanding the pandemics time evolution discussed in this paper, we present in Table 1 the listing of the days numbered after January 22, 2020, and the corresponding calendar days.

Table 1.

Comparison between the day number used in this work, counted after January 22, 2020, and the calendar day.

Day number	Calendar day	Day number	Calendar day
1	22/01/2020	346	01/01/2021
11	01/02/2020	377	01/02/2021
40	01/03/2020	405	01/03/2021
71	01/04/2020	436	01/04/2021
101	01/05/2020	466	01/05/2021
132	01/06/2020	497	01/06/2021
162	01/07/2020	527	01/07/2021
193	01/08/2020	558	01/08/2021
224	01/09/2020	589	01/09/2021
254	01/10/2020	619	01/10/2021
285	01/11/2020	650	01/11/2021
315	01/12/2020	680	01/12/2021

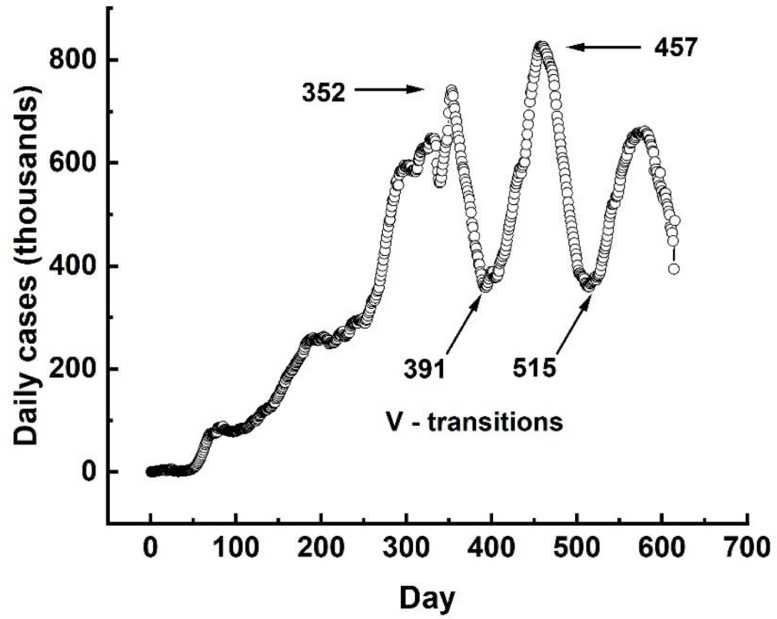
To get further insights regarding the oscillatory behavior of the noisy daily cases data we smoothed it using a 7 adjacent days averaging procedure. This is shown in Fig. 3 .

Fig. 3.

Time evolution of the seven adjacent days averaging of the number of worldwide daily Covid-19 cases from January 22, 2020, until September 27, 2021.

Fig. 3 clearly shows that up to day 391 (February 15th, 2021), the build-up of the Covid-19 pandemics experienced at least four major bursts and it also shows two new pulses starting at the turning points at days 391 and 515 (June 19th, 2021). These turning points occur when the downward trends that followed days 352 (January 7th, 2021) and 457 (April 22nd, 2021), suddenly turned into upward turns at a staggering rates. These turning points, which we coined as the V-transitions, happened along a period of large-scale worldwide vaccination effort.

Using the OWID data on the daily number of Covid-19 cases in the major world regions (Asia, Europe, Americas and Africa) we find that the peak following the first V-transition was dominated by Asian and Europeans countries. In contrast, the peak following the second V-transition may be attributed to the added contribution of North America to the contributions of the Asian and European countries.

The qualitative appraisal presented until now suggests that we should adopt a multi-logistic approach for the quantitative analysis of the Covid-19 time evolution. In order to accomplish this goal a quantitative analysis of the Covid-19 time evolution was thus carried out by considering the total number of cases evolution. The reason for this choice lies on the fact that this type of indicator is more adequate for getting information regarding the pandemic tendency. In addition, we restricted our quantitative analysis as starting on March 12, 2020, which coincides with the time of the WHO's pandemic declaration and ignore the initial 50 days stage mentioned above, encompassing then a set of 565 OWID data points.

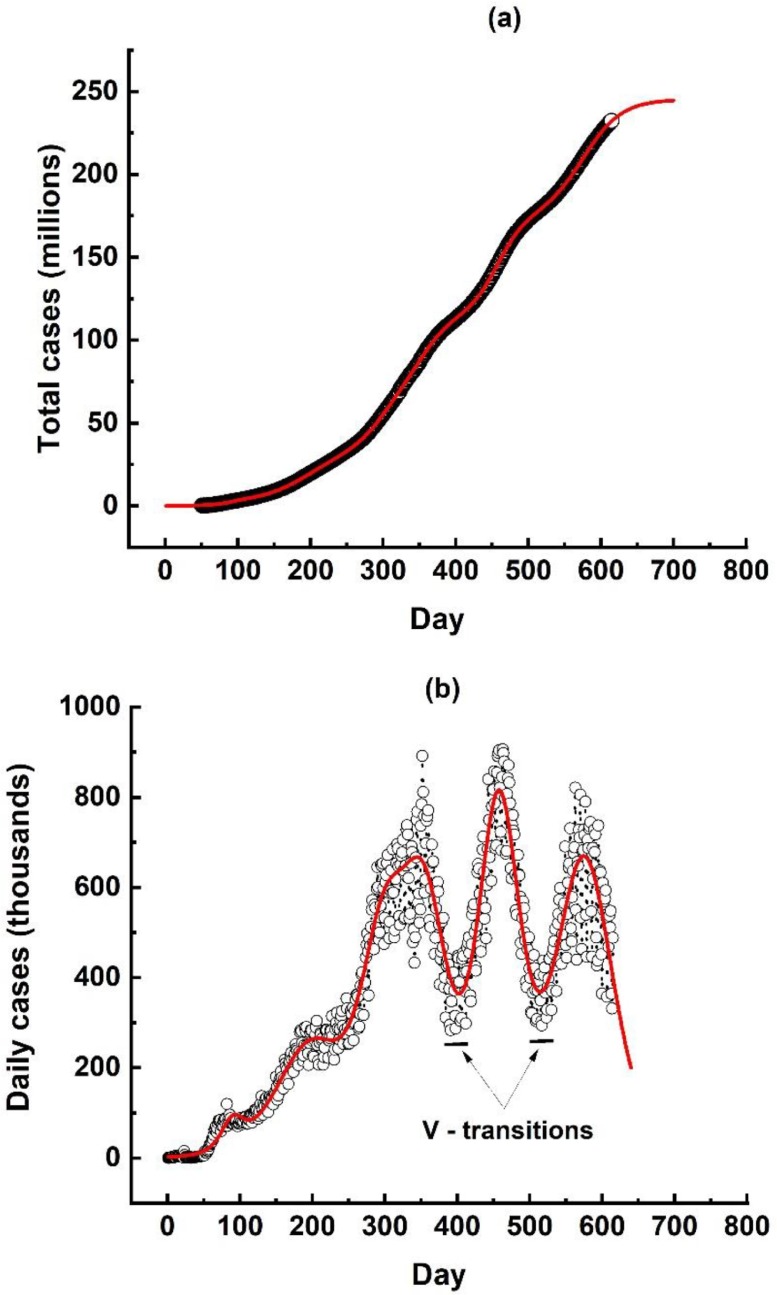
Fig. 4a shows the time evolution of the worldwide confirmed total number of Covid-19 cases form March 12, 2020 (day 51) up to Sep 27, 2021 (day 615), while Fig. 4b shows the time evolution of the corresponding daily number of cases. The continuous red line in Fig. 4a corresponds to the result of the total number of cases data fitting to a six logistic growth function model, as given by Eq. (10), while the red line in Fig. 4b represents its time derivative. A reflection on the meaning of this extrapolation is presented in the final remark section. The values found for the fitting parameters as well as of the major statistics indicator are listed in Table 2.

Fig. 4.

(a) Time evolution of the total number of Covid-19 cases since March 12, 2020, up to Sep 27, 2021, and (b) daily number of cases for the same time span. The red line in (a) represents the results from our six logistic growth modeling extrapolated to the entire time range from day 1 (January 22, 2020) up to day 700 (Dec 21, 2021), while in (b) it corresponds to the time derivative of the six logistic growth model displayed in (a).

Table 2.

Values of the adjusted parameters as obtained from the least square data fitting of the worldwide total number of Covid-19 cases to a six logistic modeling. The parameter K_i represents the total number of cases in million units, whereas t_ci refers to the center position of phase i in number of days since January 22, 2020, τ_i denotes the time constant, in days, of phase i, and Δt_i the time duration of phase i. It is also included in this table the average error of the parameters evaluations as well as the calendar days corresponding to the center positions of each phase.

Parameters	Phase 1	Phase 2	Phase 3	Phase 4	Phase 5	Phase 6
Ki (cases)	2447	32,031	35,764	44,993	59,268	70,748
t ci (day) calendar day	89.631 Apr 19, 2020	197.008 Aug 05, 2020	298.102 Nov 14, 2020	354.909 Jan 10, 2021	457.366 Apr 22, 2021	575.470 Aug 18, 2021
τi (days)	10.140	32.525	21.323	21.482	19.337	26.693
τi − 1 (day−1)	0.099	0.031	0.047	0.047	0.052	0.037
Δti (days)	44.515	142.785	93.608	95.886	84.889	117.682
Statistics	Number of records	Degrees of freedom	Reduced Chi-Sqr	Residual Sum of Squares	R2 (COD)	Average parameter error (%)
	565	547	0.034	18.630	0.99999	3.85
Parameter	Value
< Ki>	6.4%
<tci>	0.5%
<τι>	4.7%

These results indicate that along the considered 565 days, from March 12, 2020, to September 27, 2021, the evolution of the worldwide daily number of Covid-19 infected cases progressed through a sequence of six major phases, for which our procedure allowed to retrieve their time location, duration, and intensity of contamination.

The first three phases occurred along the year 2020, centered, respectively, around the days April 19, August 05, and November 14, while the last three phases, taking place along the current year, are centered on January 10, April 22, and August 18, 2021. The first three phases, lying along the year 2020, present lower intensities, while phases 4 to 6, along year 2021, are the most intense ones.

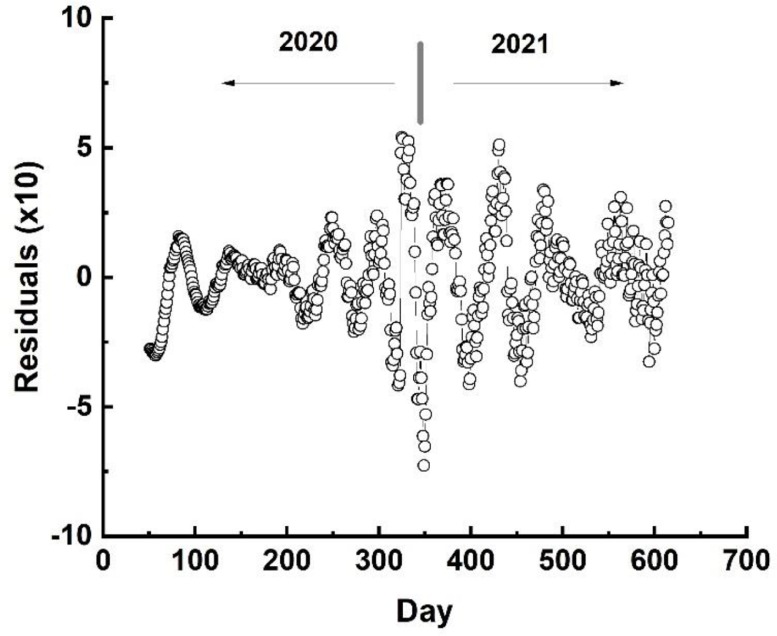
We next consider the second aspect of our methodology, namely, the analysis of the residuals of the total number of cases data fitting, representing the local mismatch between the trend curve, represented by our logistic modeling, and the empirical data. The data-to-model residuals from the six logistic growth modeling of the total number of cases, from March 12, 2020, to September 27, 2021, are shown in Fig. 5 .

Fig. 5.

Residuals from the total worldwide number of Covid-19 cases fitting to a six logistic growth functions model.

This figure clearly shows that there are some hidden oscillatory mechanisms driving the pandemics data collection. Furthermore, it also suggests that these eventual mechanisms are not homogeneously distributed along the observed time period, as indicated by the average amplitude weighted time lags between the successive peaks.

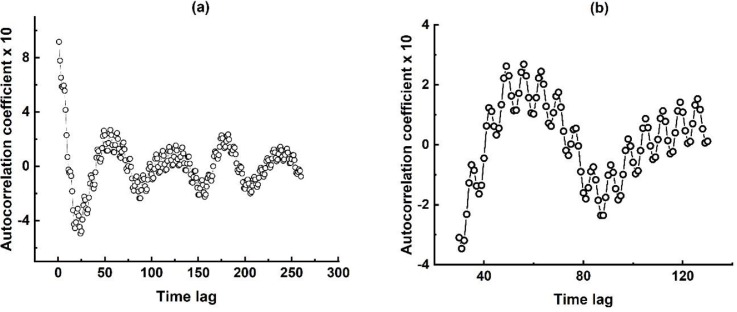
According to our previous methodological remarks, the first procedure adopted was to check whether these residuals represent a sequence of random or auto-correlated events. That was done by performing an autocorrelation analysis of the residuals displayed in Fig. 6 . The result of this autocorrelation analysis indicated that, indeed, the residuals from our logistic modeling of the total worldwide number of Covid-19 cases are not exclusively due to random errors but also to some underlying oscillatory mechanisms driving the time evolution of the pandemics, as clearly displayed in Fig. 6

Fig. 6.

(a) Plot of the autocorrelation coefficient of the residuals from the total worldwide number of Covid-19 cases fitting to the six logistic growth functions model as a function of their time lags. (b) expanded view the autocorrelation coefficient between time lags of 30 through 130 days.

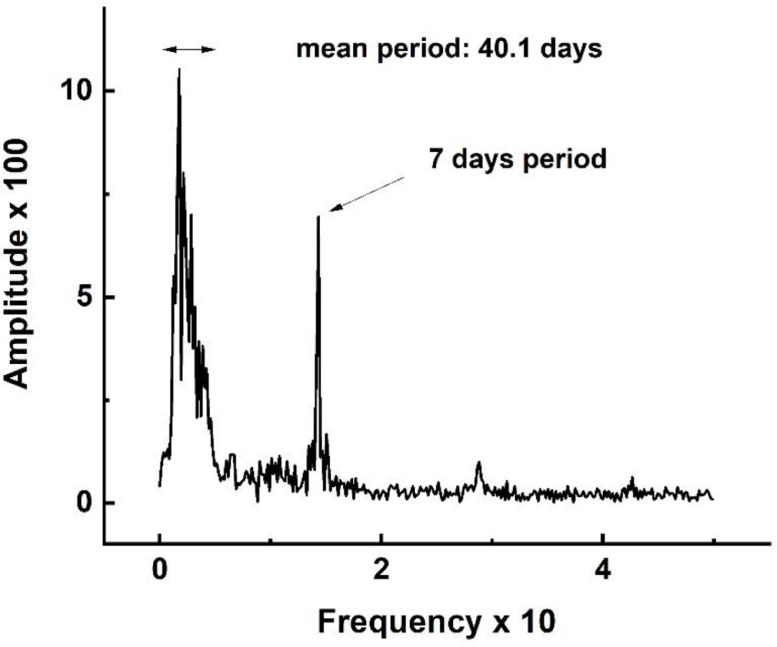
Fig. 6 exhibits two characteristic oscillatory behaviors. Some long term oscillations to which, higher frequency oscillations are superimposed, as displayed in Fig. 6b. A straightforward visual inspection of Fig. 6b suggests that this secondary oscillatory regime operates with a period of the order of 7 days. This conclusion is also confirmed by a straightforward FFT (Fast-Fourier Transform) spectral analysis of the residuals, which is shown in Fig. 7 .

Fig. 7.

Amplitude of the FFT spectral analysis of the residuals of the six logistic growth modeling of the time evolution of the total worldwide number of Covid-19 cases.

Fig. 7 consists of two major frequency bands. One, sharper, centered around a period of 7 days, and a broad lower frequency band consisting of successive neighboring peaks with periods ranging from 22 to 94 days. The amplitude weighted average period of this low frequency band is of the order of 40.1 days. The first five majors peaks within this low-frequency band correspond to modes with periods of the order of 62,8, 56,.5, 47.1, 35.3 and 43.3 days, all close to some harmonics of the 7 days period mode. This leads us to consider the time interval of 7 days as the natural clock of the Covid-19 pandemics. We shall return to these aspects in the next section.

4. – Discussion on the results

During the course of the entire pandemic, successive ‘waves’ of infection were mentioned, and depending on the country or region of the planet, different interpretations about the arrival of a second or third wave occurred. But the results presented above reveal that in fact, when globally analyzed, the daily registered number of cases has unfolded as a succession of at least six logistic spurts or phases, each with its own characteristic duration and intensity. In other words, we can say, using then an informal language, that we actually had a succession of six waves on a global scale in which the pandemic spread across borders, overcoming unsuccessful attempts at restrictions and/or sanitary measures.

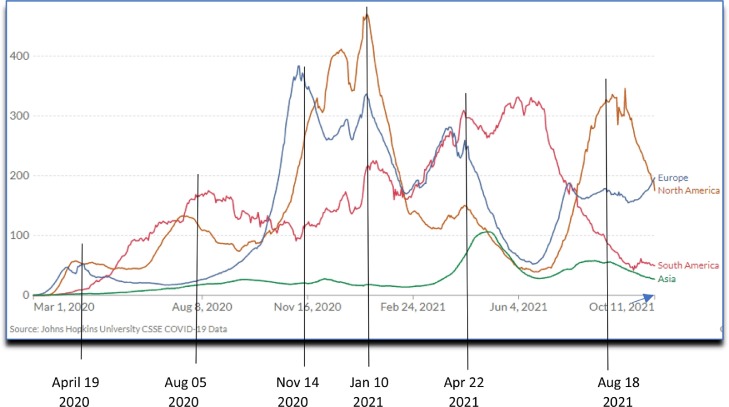
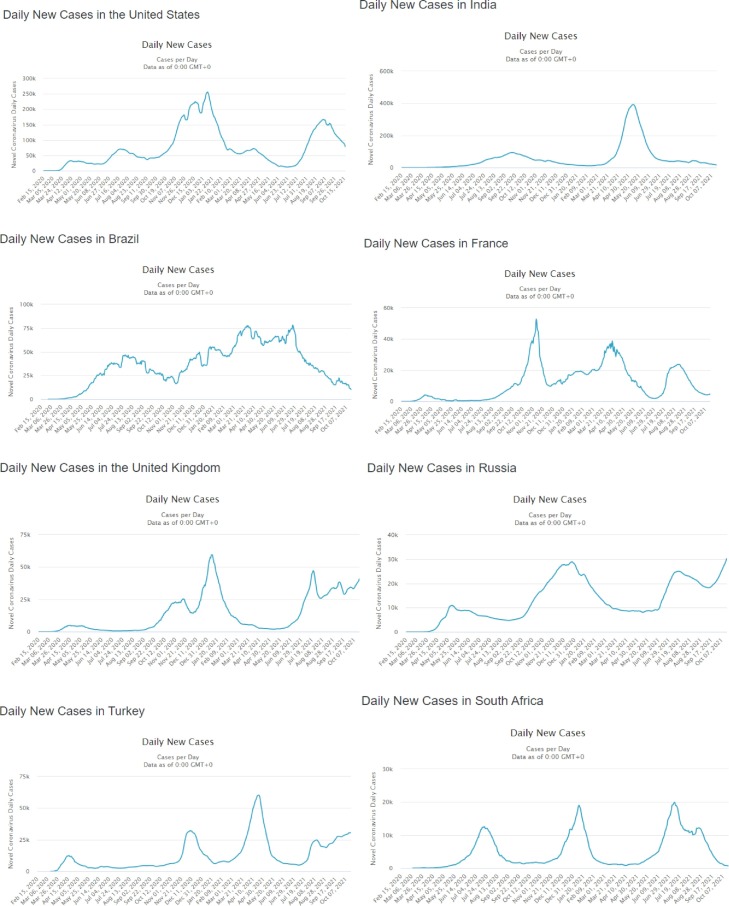
Important to keep on mind that the above results regard the consideration of the pandemic on a planetary scale, and the distribution of the daily number of registered cases varies significantly from country to country or from continent to continent, a point that can be easily visualized in the graphs presented in Figs. 8 e 9, retrieved directly from OWID data base, in which we can discern clearly how differently the pandemic has hit the different continents and countries. In Fig. 8 the curves refer to the daily new confirmed Covid-19 cases (7-day rolling average) per million people for Asia, Europe, North and South America. The straight lines indicate the dates of the six peaks (t_ci) resulting from the multilogistic data fitting presented in Table 2. As we know, after emerging in the Wuhan province in China by the end of 2019, the new Corona virus spread quickly to Europe (mainly Italy and Spain) and to North America (mainly USA), regions that undoubtedly contributed in force to the further worldwide dissemination of the virus.

Fig. 8.

Daily new confirmed Covid-19 cases (7-day rolling average) per million people for Asia (green), Europe (blue), North (brown) and South America (red). The straight lines indicate the dates of the six peaks (tci) resulting from the multilogistic data fitting and presented in table 2.

Now let's compare our fitting results with some details of the graph in Fig. 8. The first peak occurred on April 19, 2020, was due to the average daily number of infections observed in Europe and North America (USA). It is worth to note that t_ci of phase 1 (April 19) coincides with the peaks of daily cases presented by Debecker and Modis (2021) for most European countries and New York (figures presented in the Appendix of their paper). After this date the pandemic was reasonably controlled in Europe but continued to grow in North America and grew substantially in South America (with significant contribution from Brazil), an increase that is translated by the second peak observed on August 05. During the three last months of 2020 it was observed a huge increase of daily cases in Europe and North America, which average is translated by the peak identified on November 14, while in South America was observed a slight downward trend. At this time the USA assumed the global leadership in the number of cases, and deaths as well. It is interesting to observe the almost constant (and low, considering the measure by million people) rate of contaminations in Asia. At the onset of 2021 things got significantly worse in the three continents – Europe, North and South America, which resulted in the short period between the 3rd and 4th phase, peaking in January 10 as the result of the average of the numbers of these three continents. In the following months it could be observed a strong downward trend in the USA, but on the other hand a renewed growth again in Europe (but soon followed by a decreasing rate of daily cases) and an accentuated growth in South America (still leaded by Brazil). At this time (April 2021) it could be observed an increase in Asia due to the explosion of daily cases in India. The fifth peak identified on April 22 clearly translates the average of cases observed in Brazil, USA, and India. Closing the picture we have the sixth peak on August 18, translating the average of daily cases of the observed four continents, but undoubtedly leaded by the USA.

In the analysis above we spoke about the average of the individual peaks observed in the different continents as the explanation for the peaks of the successive phases resulting from our multi-logistic fitting. But it is worth to call the attention to the fact that the mean distance between the individual peaks for each continent is of about 30 to 50 days, a fact that will be considered ahead in our discussion on the results of the frequency analysis.

Still regarding the discussion on the successive waves announced by different countries it is important to give a look at the next Fig. 9 , which exhibits an overview of the pandemic diffusion for 8 selected nations: USA, India, Brazil, France, UK, Russia, Turkey and South Africa. In these graphs, retrieved directly from Worldometer Coronavirus, we can perceive how disparately the pandemic affected these countries. Some present a succession of at least 4 waves (USA, France, UK, Turkey), but in very different moments of the timespan considered, while other like Russia, and South Africa present three waves separated by a larger timespan. Important to point out the cases of India and Brazil (second and third place in the world rank in number of cases and deaths), which present each just two waves, but while in the former (India) both waves are well defined and separate by a very large time span, in the latter (Brazil) the two waves appear as a very large oscillation, as if expressing an almost continuous spread of the disease. The pattern is very similar (with at least 4 waves) for the most continental European countries, as in the case of Portugal that will be considered ahead in this paper as a case study. In a nutshell, the multilogistic fit presented in Fig. 4 is the summed mix of all these different peaks, which resulted in the six distinct phases of the global pandemic diffusion.

Fig. 9.

Overview of the pandemic diffusion for 8 selected nations: USA, India, Brazil, France, Russia, UK, South Africa, and Turkey (7-day moving average graphs retrieved directly from Worldometer Coronavirus on October 17th).

Following the sequence of the results presented in the previous section, let's give a closer look at our spectral analysis of residuals as a function of frequency as obtained from the FFT calculations shown in Fig. 7, which deserve some further considerations.

As seen, two major frequency bands could be identified. One, sharper, centered around a period of 7 days, and a broad lower frequency band consisting of successive neighboring peaks, whose weighted average period is of the order of 40 days.

Regarding the lower frequency band is very difficult to correlate it with some specific mechanism linked to the pandemic diffusion. On one hand, the center of the successive peaks contributing to the building-up of this band have periods which are close to harmonics of the 7 day very intense high frequency peak. But, on the other hand, it is not to disclose that the found weighted average of about 40 days, or even the mean spacing of 55 days resulting from the data-to-model residuals from the six logistic growth modeling presented in Fig. 6a, might be related to the mean distance between the individual peaks for each continent as exhibited in Fig. 9. This being the case, we can speculate that these low frequencies are a consequence of the movement of people and the resulting spread of the pandemic between nations and continents, even though other effects such patient recovery influence may not be ruled out.

An interesting result of the present analysis is related with the intense 7-day frequency identified in Fig. 7, which consists undoubtedly in a natural clock of the worldwide pandemic diffusion. Initially we were inclined to relate it with the virus incubation time, as indicated by most studies on the characteristics of SARS-CoV-2, as for instance (Lauer et al., 2020), Qun Li et al. (2020), and Backer et al. (2020). But, on the other hand, the same studies mention in fact a relatively broader timespan for the incubation time, between 7 and 14 days, which then implies some trouble in explaining why the so intense peak in just 7 days. Looking then more closely at the day-to-day sequence of data we can see that the lows invariably occurred on weekends and the highs in the middle of the week, which in this way explains without a doubt the cadence of 7 days found in the spectral analysis. This pattern is easily observed in the daily rate of infections in almost all countries, evidencing quite clearly the existence of a weekend effect. In other words, this clock is not related directly with any property related with the disease diffusion, but instead with the pandemics data collection.

The obvious explanation for this weekend effect may be related to at least two important facts: a lower number of tests carried out on weekends, as well as the reduced communications by the entities in charge for disseminating the statistics reporting the actual number of occurrences, which can accumulate for the following days.

But in any case, we should not rule out the hypothesis that a possible predominant incubation time of about 7 days may have some influence on this effect. At weekends there is much less movement of people going to and coming from their workplaces and therefore much less crowds at stations and means of transport, in short, much less movement of people. Thus, if an incubation time of about a week is the predominant mode of manifestation of the symptoms of the disease, there would consequently be a lower number of infected people in the following weekend.7

5. – A case study: Portugal

Modeling the spread of the novel coronavirus has brought to evidence the limitations of the existing epidemiological models that had led to disparate divergences about possible measures to control the worldwide contagion. Scientists came to realize how unprepared they were to present suggestions for possible preventive measures.

Such divergences were attributed to a wide assortment of reasons, ranging from ignorance about the properties of the new virus to the contingency and unpredictability linked to human behavior. Both factors combined paved a terribly difficult terrain to move on, let alone to make predictions about future events.

In a recent article, Devezas (2020) pondered about the reasons for the surprise that shook the planet at the dawn of 2020. One of the reasons pointed out by the author is related to the very peculiar and unknown properties (and contagious capacity) of the new virus SARS-CoV-2. The models advanced then by epidemiologists and other scientists failed by far when making assumptions not only about the virus biology, which remains far from fully understood, but also about human actions, which are even more unpredictable. As highlighted by Devezas, the longer incubation time, to which adds the ability to infect other people asymptomatically during this period, wiped out in a few months the capacity for hospital assistance even in the most advanced economies. But many other socioeconomic factors linked to the fragility of our globalized institutions led to rapidly cascading effects on governmental and financial systems, which were prone to blow.

These aspects lead us to adopt a phenomenological instead of a first principles approach to modeling the Covid-19 pandemic. Despite of that, in the treatment of the global infection data presented in the previous section describing the planetary unfolding of the disease among some 200 countries, it is impossible to discern how decisions and policies, both for shutting down parts of society, as well as for opening then back up, have influenced the aspect of the resulting multiple logistic curves. The implicit complexity of the two hundreds countries taking completely different measures and at different times completely hide the possible signs of the consequences of the best procedures for preventing the uncontrolled spread of the pandemic.

For this reason, it was chosen to give a close look to the contagious unfolding in just one small country. The elected country was Portugal (residence country of one of the authors), which has two important characteristics: a relatively homogeneous small population (∼10 million people) and, because located at the far western Europe, it borders just one country (Spain). Knowing in detail all the types and dates of the decisions made by the government regarding sanitary measures, one can probably discern their positive or negative effects.

Moreover, the analysis of this case study will serve to demonstrate how the spread of a pandemic is strongly dependent of human behavior in modern society. The idea of human behavior in this context must be understood in a very broad and overwhelming sense, encompassing movement of people, political positions, social attitudes, psychological reactions in situation of stress, economic pressures, and much more, characterizing what can be considered a very complex socioeconomic system subject to the iron rules of self-organized criticality (SOC) (Devezas, 2020).

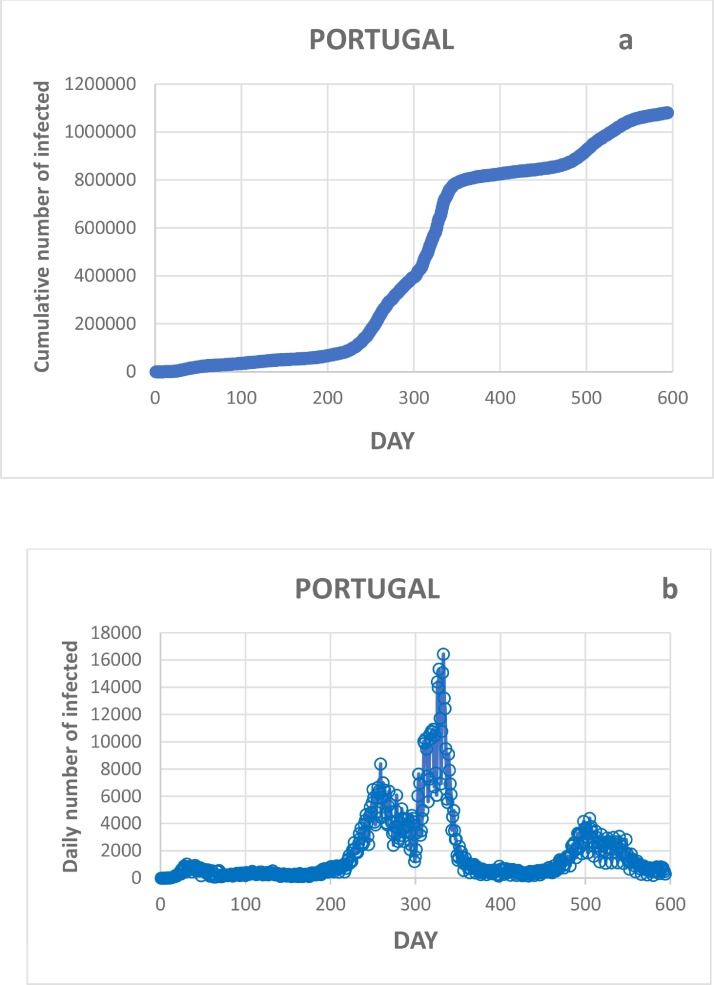
Fig. 10 below presents the unfolding of the Covid-19 pandemic in Portugal, from March 2nd, 2020 (day 1 for Portugal, when was observed the first case) until October 20th, 2021. A first visual inspection tells us that after day 350 (February 24th, 2021) the number of daily infected declined substantially, signalizing some degree of control over the pandemic. During the time interval March – May 2021 it was observed an almost constant and low number of daily infections (between 300 – 500), but after June 2021 a renewed upward trend in the number of cases was observed to form, with a clear spike observed on day 505 (July 23rd, 4376 cases). This was followed by a gradual decrease in the number of cases, which returned in September to the levels of daily case numbers observed between March and May.

Fig. 10.

Unfolding of the Covid-19 pandemic in Portugal from March 2nd, 2020, up to October 20th, 2021, (a) cumulative number of infected (b) daily number of infected.

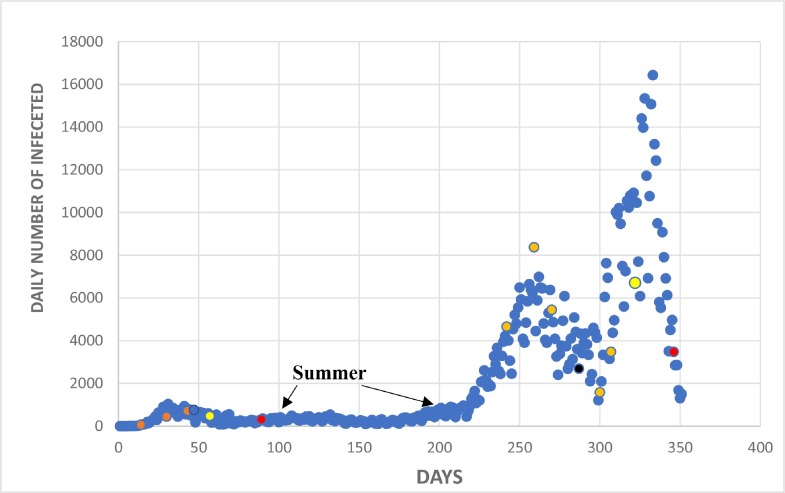
Our analysis of the Portuguese case should be divided into two distinct periods - from the outbreak to the 350th day (end of February 2021), when two waves of great intensity were observed, and from this date to the end of October 2021, when we finished this work. The following Fig. 11 , embracing the first period, will be used to demonstrating the effect of successive sanitary and confinement rules applied by the Portuguese government in order to control the spread of Covid-19 disease. The graph exhibits the number of daily cases from March 2nd, 2020, up to February 24th, 2021(day 350) in order to allow an expanded view of the x-axis with better definition of the individual day points.

Fig. 11.

Time evolution of the daily number of Covid-19 in Portugal since its outbreak on March 02, 2020, up to February 24, 2021. The colored points indicate the dates on which important mitigation and prevention decisions were taken by the Portuguese government, as commented on in the text.

Soon after the outbreak of the pandemic, the Portuguese government declared three successive “Estados de Emergência” (Emergency States), on March 18th (for 2 weeks), April 2nd (1 week), and April 16th (2 weeks), respectively, marked with orange points in the graph. The most important characteristics of the then imposed rules were the closure of non-essential activities (mainly shopping malls, hairdressers, restaurants limited to take-away, etc.), restrictions on the movement of people between districts or counties, schools and universities were shut down (activities restricted to online classes), and also some constraints on the entry of travelers from abroad. In addition, the use of masks and hand disinfection became strongly recommended and even mandatory to enter the few commercial spaces open to the public.

On May 2nd (yellow point at day 57 in the graph) the Emergency State was replaced by another public edict named as “Estado de Calamidade” (Calamity State), whereby a progressive lifting of the most radical restrictions was observed. On June 1st (red point at day 89 in the graph) there happened a general relaxation of all restrictive measures and there was a return to what was coined then as the ‘new normal’. The main sanitary measures were maintained, teleworking became commonplace, schools and universities were reopened, restaurants and many other public spaces were able to resume their activities, but with limitations on the occupation of their respective spaces and attending some specific sanitary conditions to prevent contamination.

It can be appreciated from the data shown in figure 11 that the various measures taken in a timely manner since the onset of the pandemic in Portugal worked quite well, resulting with the daily number of infected cases kept under control and almost constant (of about 2 to 3 hundred daily cases) up to the end of summer, around day 200. The media at this time spoke about a Portuguese miracle, considering that in neighboring Spain and some other European countries the pandemic had much more significant figures of daily contamination.

Nevertheless, as lengthy discussed in Devezas’ paper (2020), human society consists of a highly complex system, and as happens in all nonlinear systems, small causes may manifest itself as great effects, carrying on seemingly uncontrolled and chaotic consequences. The absence of preventive actions all along the summertime triggered the escalation of new cases as early as the middle of autumn. New restrictive measures were delayed and, consequently, by the end of autumn the number of new contaminations and fatalities skyrocketed.

There were several reasons for the above mentioned delay in taking preventions and/or mitigations measures. Some negationist movements certainly have their share in this attitude, but above all, Government's hesitation was related to the huge crisis in the service sector, mainly catering and tourism, responsible for a significant share of the Portuguese GDP. Only on November 06 the government made the announcement of a new Emergency State act (valid for 2 weeks), later renewed twice on November 20 and December 02 valid for 2 weeks each. These are indicated in figure 13 by the three orange points around day 250.The effects of these renewed Emergency States were soon felt as manifested by the drastic drop in the number of new daily infection cases.

But the good news did not last long. When renewing the Emergency State acts short before Christmas (black point at day 287 in figure 13), Portuguese legislators, probably in response to the wishes of a society already saturated with so many periods of confinement, allowed the free movement of people for family celebrations during Christmas holydays. Huge mistake immediately reflected in the new and serious pandemic worsening, as can be seen in figure 13, which could not be stopped by two successive renovations of the Emergency States (two orange points following day 300). But yet other hesitation contributed further to the worsening of the contamination rate: in all these Emergency State acts imposed since November, schools and universities were not shut down, what probably contributed to spreading further the virus asymptomatically through the young population. Only on January 28th the 10th Emergency State act was finally issued, including the decision of a renewed lockdown, shutting down all school activities, further limiting the movement of people, and forbidding the entry of travelers (yellow point on day 322).

However, by this time the big damage was already done, and the worst consequences were not long to come. Portugal was soon entering into the worst worldwide statistics with the highest rate of contaminations and fatalities per million inhabitants. But quickly, after the 11th Emergency State act issued on February 15 (last red point at day 346), the positive effect of the new measures was felt – numbers dropped significantly. All along the following months (March, April, May), successive Emergency State acts were issued.

On May 10th universities and schools reopened, as well as restaurants and shopping malls, but still with severe limitations regarding occupation of spaces and opening hours. At the time, there was also an important change in the implementation of the new ‘State of Emergency’ or ‘Calamity State’: it was established a new criterion for the application of preventive sanitary restrictions and punctuated lockdowns in different regions of the country, depending on the local number of infected people per 100,000 people (red light at 120 cases per 100k).

We can then conclude that the new measures worked well for a while (ca. 3 months), the situation was maintained under control, with a number of daily infections in the range of 300 to 500. However, after June 2021, corresponding to second period mentioned above, things worsened again, in despite of the Portuguese starting effort in the vaccination process. But this time the cause was not directly related with the absence of control measures, but mainly related to two disparate causes: firstly, the appearance of an unexpected virus variant (coined as ‘delta’ variant), with a much higher contagious capacity (about two times as contagious as previous variants), and secondly, the entrenching summertime 2021. The latter was certainly responsible for the easier spread of the new variant.

The tourism sector, responsible for a significant share of the Portuguese GDP, was in fact under great pressure, many hotels and restaurants going bankrupt, and demanding from the Portuguese State a definitive opening of the summer season, even if under restrictive measures (certificates of vaccination and/or negative Covid-19 tests). This was done in June 2021, the tourism season was allowed, and there was a flood of tourists, mainly from the UK, where, as we know, a significant increase of the delta variant strain was being observed at this time, and the result could not have been other than a renewed increase in the number of infections in Portugal. Across Europe the movement of people at airports was recovering the level observed in 2019, and in despite of controlled restriction measures, the spread of the new strain could not be avoided in a time when the numbers of the vaccinated population had not yet reached the share of 75% that is considered safe to guarantee collective immunity.

But the effort of the Portuguese state to advance in a very well organized manner with the entire process of applying the two doses of vaccines proved to be very efficient, and by the end of September Portugal presented itself as the world leader in vaccination, with 85% of its population fully immunized. As we can infer from Fig. 10b, after the spike of infections on July 23rd (point 505), the number of daily infections presented in fact a steady decreasing trend. Moreover, it should be stressed the fact that the last observed wave was not as damaging as the previous ones, what means that vaccination, while not guaranteed 100% immunity, works. The Portuguese case should serve as a good example to trigger an international effort to stop (or at least to fight against) the antivaccine nonsense.

The above exposed picture of the events in Portugal allows some important inductions: there is no other way to fight a pandemic but through stringent preventive health measures, there is no room for the discussion between damage to the economy and population health protection. Hesitation and politicization of decisions only favor the vector of infection (in this case the virus SARS-CoV-2) to fulfill the goal of its biological existence, that is, its replication. This theme will be further discussed in the next section.

6. – Why some countries have done better with Covid 19?

The results of our multilogistic analysis help to shed new light on the complexity of Covid-19′s meteoric expansion from its origin in a highly localized point in the Chinese province of Wuhan to being reported in more than 200 nations across the globe in about one year. The found six phases of the worldwide pandemic's diffusion translate well how asymmetrically the disease hit the different continents and countries.

The world on which Covid-19 unleashed its destructive power was one excessively globalized, endowed with multilateral structures with declining authority, and prone to blow as pointed out by Devezas (2020). The combination of the devastating economic impact of extensive lockdowns with local social and political trends was disastrous in some nations, but it is worth noting that this effect was not so pronounced in certain regions of the planet. In this context, there is then a relevant question: why some countries have done better with Covid-19?

Despite the excessively globalized world we live in today, there is an important aspect of societies that has been fortunately preserved: cultural diversity. Although it is also historically the cause of ethnic conflicts and wars, it is an important driving force of social development and consists in a positive aspect still present in our globalized society, because it is our motivation to contact people from other cultures – what a dull world would be one without the filigree of contrasts in customs or social manifestations. This same cultural diversity may, however, constitute a possible reason to explain the differences observed between nations in their response to the shock caused by Covid-19, according to a study recently published in the periodic The Lancet (Gelfand et al., 2021) by an international team of scientists leaded by Michelle Gelfand, eminent cultural psychologist at the University of Maryland, who also published a worth to read book on the theme (Gelfand, 2018).

The authors collected data on cultural tightness-looseness for 57 countries, available online (Center for Open Science, OSF, 2020), and compared them with data from OWID about Covid-19 cases and deaths per million citizens for the same 57 countries. The methodology used by the authors is a very complex one, fitting a series of stepwise models to capture whether cultural tightness-looseness variation in counting Covid-19 daily cases and deaths may be influenced by under-reporting, demographics, geopolitical factors, other cultural dimensions, and even climate. It would be out of place to describe the methodology here in detail, and so we suggest the reader a detailed reading of the work with its various tables and graphs.

The results of this study indicated that, compared with nations with high levels of cultural tightness, nations with high levels of cultural looseness are estimated to have had 4•99 times the number of cases and 8•71 times the number of deaths, in other words, nations that are tight and abide by strict norms have had more success in controlling the spread of the disease than those that are looser. The authors also use a formal evolutionary game model to demonstrate that tight groups cooperate much faster under threat and have higher survival rates than loose groups. The results suggest that tightening social norms might confer an evolutionary advantage in times of collective threat. In the two graphs presented in the paper (Fig. 1 for daily cases, and Fig. 2 for deaths, both log-transformed so that they were normally distributed) we can easily observe that cultures that had tighter norms like Japan, China, Singapore, Poland, South Korea, and Vietnam performed far well in fighting the pandemic than cultures that had looser norms like Italy, Spain, Brazil, the USA, and most South American countries. The authors argue that variation in tightness–looseness is related to cultures’ histories of social and ecological threat. As compared with loose cultures, tight cultures generally have higher historical rates of natural disasters, disease prevalence, resource scarcity, and invasions.

As a matter of fact, we can make stand out the case that several European countries, like France, Germany, or even Portugal, who were successful in flattening the curve of daily cases at beginning of 2020, but people got tired of following rules in the summer and there were several protest demonstrations from the services and tourism sectors, facts not observed in most Asian countries.

7. – Final remark – what comes next?

As highlighted earlier, the presented model is not intended as paragon for the accurate forecast of the entire unfolding of a pandemic, and as such it is not capable to answer this hard-to-foreseen question. Our results point to a succession of six waves that did unfold very differently in distinct countries and continents, presenting moments of intense trend reversion (V-transitions), and moments of decreasing trend, as if indicating the end of the pandemic.

In Fig. 4a we presented the multilogistic fit of data points from March 12th, 2020, to September 27th, 2021. In the same graph it is shown a red line, which represents the corresponding extrapolation until day 700 (December 21st, 2021). This extrapolation does not mean that our model is forecasting the ceiling of the pandemic at this date, but only that, with conditions in place until the peak of the developing wave, this will be the most likely trend. But as we can infer from the observed wave sequence, it is not possible to predict when (and if) the boundary conditions will change, and a new trend prevails. It is of paramount importance to keep on mind that such extrapolation only considers the unfolding of a given phase that is reaching its ceiling and does not allow to foresee if a new phase might develop.

Apparently, we are currently witnessing a worldwide decreasing trend of the total number of cases, even though some countries have experienced some recent and worrying rises. On a worldwide basis, these localized rises have not yet affected the global trend. Furthermore, the increasing vaccination rate at the global scale is a strong point in supporting the worldwide decreasing trend.

In order to check the forecasting capability of the presented model, we have tried two other fitting attempts, varying the dates considered for the end of the analysis, namely September 6th and October 25th (the graph in Fig. 4a considers the data until September 27th). Using the extrapolation of the results from our data fitting up to day 700 (December 21, 2021), and comparing it with the current OWID data up to October 25, 2021 (day 643) we found a date-to-model error of the order of 1.6%. That is, 28 days after the limiting date used in our data modeling, the forecasted error of our multi-logistic modeling for the Covid-19 pandemics is less than 2%. If, however, we had limited our data modeling up to September 06, 2021, the date-to-model error one would get by October 25, 2021, would be of about 3%. That is, our modeling forecasts an error of about 3% for the total number of cases 49 days after the last day ending the data modeling. In view of this, we may say that, at least 28 days ahead, our multi-logistic approach is supposed to forecast the evolution of the total number of cases within a maximum 3% error.

Returning then to the question of what comes next, we have to stay in the arena of speculation. As already pointed out, we are now noticing the appearance of new strains of the SARS-CoV-2 virus, and the effectiveness of the existing vaccine pool against these new variants is still uncertain. Uncertain is also the duration of the immunization of this or that vaccine. Add to this level of uncertainty our very important observation in the previous section that it is evident that the dynamics of propagation of this pandemic has much more to do with socio-political attitudes, so that it cannot be ruled out that a renewed wave of infection may happen in the near future. Let's hope that the worldwide effort in vaccination works towards obtaining the expected group immunity.

In this case, even if new surges of the infection do happen, their effect will be less and less intense, and a very likely scenario will be one of a damped oscillatory movement type effect. But whatever the scenario, it can be stated with certainty that many of the socio-cultural effects of this pandemic are here to stay, a topic that we strongly suggest being targeted by a forward-looking scientific analysis to be published in the future on the pages of TF&SC.

Biographies

Luiz Carlos M. Miranda got his D.Phil. in Physics from Oxford University, UK, in 1972. Along his scientific career he has published over three hundred papers in international scientific journals. He was a John Simon Guggenheim Fellow at the University of Arizona during 1975–76 and has exerted several administrative positions in different Brazilian academic and scientific institutions, such as Dean of Undergraduates at the University of Brasilia, Vice-Director of the Institute of Advanced Studies of the Aerospace Technical Center, Scientific Director of the Rio de Janeiro Polytechnic Institute, and director of the National Space Research Institute (INPE). He is currently a retired senior researcher of the National Space Research Institute acting as an independent consultant.

Tessaleno Campos Devezas got his PhD in Materials Engineering from the Friedrich-Alexander University Erlangen-Nürnberg, Germany (1981), and is currently Associate Professor with habilitation at the Atlântica Instituto Universitário, Lisbon (Portugal), teaching and researching in the field of Materials and Aeronautical Engineering and Technological Forecasting, and is associate researcher of the Research Unit C-MAST (center for Mechanical Aerospace Science and Technologies, FCT Portugal). He belongs to the Advisory Board of the journal Technological Forecasting & Social Change (Elsevier), Editorial Manager of the Periodical Fractals (World Scientific Publishing Co), member of the International Kondratieff Foundation (Moscow, Russia), Member of the Scientific Committee – Simon Kuznets Institute for Self-Organization and Development (Kiev, Ukraine), and full member of the International Research Academy (Moscow, Russia). Prof. Devezas has published more than 60 scientific papers in several international scientific periodicals and authored/co-authored 10 books and is co-editor of the Springer Series “Studies on Entrepreneurship, Structural Change and Industrial Dynamics”.