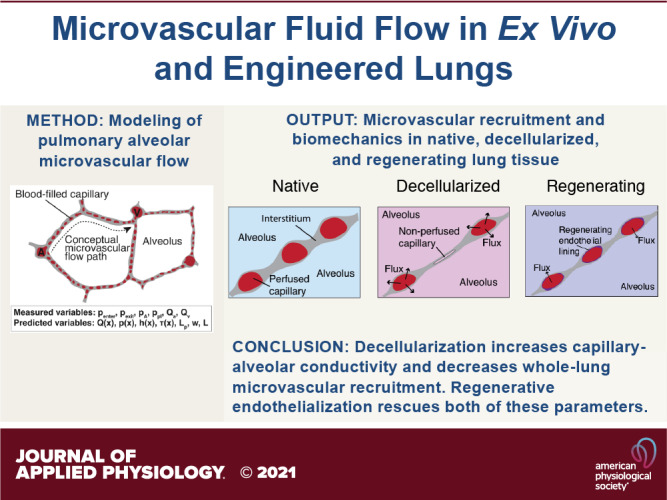
Keywords: alveolar barrier, decellularized, lung physiology, microvasculature, Starling coefficient
Abstract
In recent years, it has become common to experiment with ex vivo perfused lungs for organ transplantation and to attempt regenerative pulmonary engineering using decellularized lung matrices. However, our understanding of the physiology of ex vivo organ perfusion is imperfect; it is not currently well understood how decreasing microvascular barrier affects the perfusion of pulmonary parenchyma. In addition, protocols for lung perfusion and organ culture fluid-handling are far from standardized, with widespread variation on both basic methods and on ideally controlled parameters. To address both of these deficits, a robust, noninvasive, and mechanistic model is needed which is able to predict microvascular resistance and permeability in perfused lungs while providing insight into capillary recruitment. Although validated mathematical models exist for fluid flow in native pulmonary tissue, previous models generally assume minimal intravascular leak from artery to vein and do not assess capillary bed recruitment. Such models are difficult to apply to both ex vivo lung perfusions, in which edema can develop over time and microvessels can become blocked, and to decellularized ex vivo organomimetic cultures, in which microvascular recruitment is variable and arterially perfused fluid enters into the alveolar space. Here, we develop a mathematical model of pulmonary microvascular fluid flow which is applicable in both instances, and we apply our model to data from native, decellularized, and regenerating lungs under ex vivo perfusion. The results provide substantial insight into microvascular pressure-flow mechanics, while producing previously unknown output values for tissue-specific capillary-alveolar hydraulic conductivity, microvascular recruitment, and total organ barrier resistance.
NEW & NOTEWORTHY We present a validated model of pulmonary microvascular fluid mechanics and apply this model to study the effects of increased capillary permeability in decellularized and regenerating lungs. We find that decellularization alters microvascular steady-state mechanics and that re-endothelialization partially rescues key biologic parameters. The described model provides powerful insight into intraorgan microvascular dynamics and may be used to guide regenerative engineering experiments. We include all data and derivations necessary to replicate this work.
INTRODUCTION
Over the past decade, whole organ engineering has often employed approaches of decellularization of a native organ, followed by cellular repopulation of that organ within biomimetic bioreactors. Decellularization is a process in which intact organs are washed of all cellular material, leaving only the proteinous extracellular matrix behind (1–3). In acellular lung, the remaining extracellular matrix preserves the major histologic architecture, including an intact capillary-alveolar basement membrane and patent microvascular flow pathways from artery to vein via the intervening capillary bed (4–6). Procedures to recellularize such organ matrix scaffolds, and to subsequently condition the regenerating tissue in ex vivo bioreactor culture, have not yet been optimized. Progress is significantly hampered by an incomplete understanding of the structural, fluidic, and mechanical conditions of the capillary bed in the alveolar regions of decellularized scaffolds. An accurate and functional tool that is capable of predicting steady-state flow mechanics in decellularized organ parenchyma will be useful for the design of repeatable experimental procedures.
Recent studies have also shown the clinical potential of ex vivo organ perfusion, in which lungs, livers, and kidneys are removed from cadaveric donors and reconditioned or therapeutically modified in perfusion bioreactors (7–12). Across each of these organs, vascular integrity is a key metric of tissue health and can be seen as an essential criterion for transplantation. Measuring vascular integrity in whole organ perfusions is therefore of paramount importance in both the clinical and research setting. Since many ex vivo perfusion studies also seek to selectively modify tissue regions or deliver therapeutic agents (13–15), a robust understanding of tissue fluid mechanics during perfusion is also key. Metrics must be devised to assess whether therapeutic interventions are reaching all desired regions of a tissue and with appropriate fluidic forces.
Although microvascular fluid dynamics have been well-characterized in normal lung tissue (16), no similar investigations have been published regarding decellularized lungs or ex vivo perfused lungs experiencing barrier breakdown. The loss of epithelium in the alveolus, and of endothelium in the pulmonary capillaries, compromises plasma membrane- and tight-junction-mediated barrier function. This means that during arterial perfusion of a decellularized lung, substantial fluid crosses the capillary-alveolar barrier, manifesting macroscopically as both tracheal and transpleural efflux (17). A similar event also occurs, manifesting as edema, in perfused native lungs that are treated with ex vivo lung perfusion or regenerative cross-circulation (18–20). In the present study, we sought to build a theoretical model that could calculate quantitative values for both capillary recruitment and barrier hydraulic conductivity in native (i.e., cellular), decellularized, and in regenerating lungs.
Fluid flow in the pulmonary microvasculature is best modeled as a thin inter-septal “sheet” of blood flowing from arteriolar sources to venular sinks (21). This model is appropriate because the dense and interlocking nature of the pulmonary capillary bed (Fig. 1A) leads to distinctly non-Poisellian flow patterns and greatly reduced arteriole-to-venule capillary resistance (23, 24). The dimensions of this sheet of blood, however, are highly dynamic (Fig. 1B). Greater arteriolar or venular pressure corresponds to recruitment of additional recruitment of capillary segments and a greater percentage of the alveolar septae being perfused with blood (w in Fig. 1B) (25, 26). Furthermore, the sheet itself is elastic: capillary segments radially expand and contract in diameter (h in Fig. 1B) in response to transmural pressure (23, 27, 28). Since the lung parenchyma is elastic, changes to alveolar inflation also affect mean flow path length from arteriole to venule (Fig. 1C). Any model of fluid flow in the pulmonary microvasculature must therefore account for each of these principles.
Figure 1.
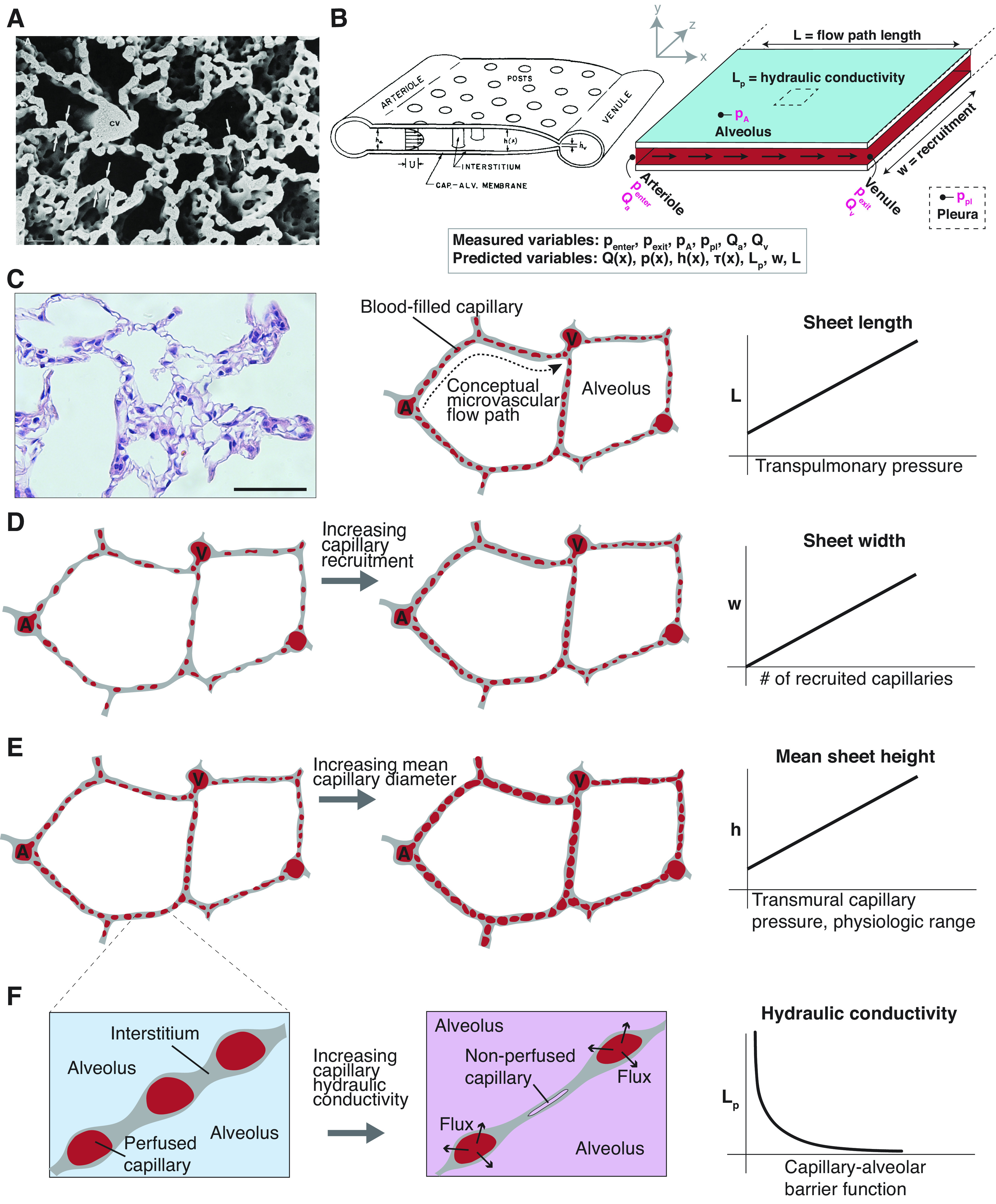
Permeable sheet-flow setup and schema of vascular cast of the alveolar capillary network in adult rat lung (A), reproduced with permission from Caduff et al. (22). The dense, intersecting nature of the pulmonary microvascular makes it appropriately modeled as a continuous “sheet” of blood flowing from many arteriolar sources to many venular sinks. B: schema of pulmonary sheet flow, from Fung 1974, and adaptation showing measurable and solvable variables, including the capillary pressure p(x), diameter/capillary sheet height h(x), flow Q(x), shear stress τ(x), length (L), sheet width (w), and barrier hydraulic conductivity (Lp). Directly measurable parameters , , pA, ppl, Qa, and Qv are emphasized in magenta. C: rat pulmonary histology (H&E) and schematic articulating arteriole (A) to venule (V) flow path. Scale bar = 50 µm. The mean distance between arteriolar sources and venular sinks changes slightly with increasing transpulmonary pressure. D: capillaries with intramural flow are recruited while those with no flow are not. Increasing capillary recruitment is reflected by an increase in the output parameter w. E: capillaries are highly elastic and can distend in diameter in response to increased arteriolar and/or venular pressure. The height h(x) of the pulmonary blood sheet is the mathematical representation of capillary diameter along flow path length L. F: increased barrier hydraulic conductivity causes an increase in transmural flux which must be accounted for in fluidic model. We hypothesized that an increase in Lp would cause a decrease in steady-state capillary diameters and might affect parenchymal recruitment. Lp is a permeability metric and, all else being equal, is inversely related to total organ barrier resistance.
The pulmonary sheet-flow model was pioneered in the latter third of the 20th century by the laboratory of Y. C. Fung, culminating in a predictive model for intravascular flow in the cat which was validated experimentally (29, 30). As originally described, the capillary was assumed to display zero permeability, thereby maintaining constant flow across the capillary bed from arteriole to venule. This was a reasonable assumption given that native tissue displays extremely low hydraulic conductivity (often represented as a Starling coefficient, commonly abbreviated as Lp), which has been measured directly by a variety of techniques to be between 1.32 × 10−9 and 5.20 × 10−9 cm/Pa·s (see Model Constants and Literature Lp.xlsx, dataset available at https://doi.org/10.6084/m9.figshare.12126342.v2) (31–35). Later work explored the theoretical effects of alveolar exudate and lymphatic drainage, finding that under physiologic conditions, the biomechanical effects of this flux on the capillary bed are minimal (36). However, when cells are completely removed from the lung, as in modern-day decellularized scaffolds that are used for tissue engineering, the hydraulic conductivity of the capillary wall substantially increases, manifesting macroscopically as reduced venous outflow coupled with substantial airway/alveolar outflow and transpleural fluid flux. For decellularized and engineered/recellularized lungs, the elevated hydraulic conductivity of the capillary-alveolar barrier must be taken into account during fluidic modeling. Since hydraulic conductivity values for decellularized pulmonary microvasculature have not been previously reported, any applicable model of fluid flow must also be able to solve for an unknown value of Lp in the native, decellularized, or repopulated organ.
In prior reports, we have described experimental approaches that allow the quantification of key pressure values from the alveolar region of ex vivo lungs, and to estimate the total alveolar basement membrane barrier resistance of an entire perfused organ (17). The recruitable nature of the pulmonary microvascular bed (Fig. 1D), however, can obscure the meaning of a calculated, total barrier resistance value: increased capillary leak in a perfused organ can mean either worsening inherent barrier function, or an increased total number of perfused capillaries across which leak may occur. Furthermore, observed fluctuations in capillary arterio-venous resistance can be due to either recruitment of greater or fewer capillary segments (Fig. 1D), or to dimensional changes to the elastic capillaries themselves (Fig. 1E). In tissues with compromised barrier function, this mechanical system is even more complicated, with intravascular pressures varying as fluid flows along the length of the capillary and partially crosses into the alveolar compartment. We hypothesized that the loss of barrier function in lung would lead to alterations in both capillary steady-state mechanics and in pulmonary parenchymal recruitment (Fig. 1F).
We sought a computational model which could utilize benchtop measurements obtained from perfused native, decellularized, and engineered organs and reveal microvascular steady-state mechanics. The goals of the model development were to provide pressure-flow mechanical solutions for recruited portions of the network, to solve for an unknown barrier hydraulic conductivity, and to estimate the degree of capillary bed recruitment. Here, we present a model which is capable of providing a numerical solution to all three of these unknowns simultaneously, when combined with appropriate boundary conditions derived from basic physical assumptions about the perfused organ.
In this report, we apply this model to data derived from cultured lungs to describe pressure-flow conditions for the capillary flow path in native, decellularized, and engineered lungs. We are able to measure and compute, with high confidence, the values for native capillary hydraulic conductivity in various types of cultured lung samples. Further application to data from decellularized constructs allows us to provide, for the first time, estimates of both microvascular hydraulic conductivity and capillary bed recruitment in decellularized lung matrix scaffolds. Comparison of steady-state capillary dimensions and pressure-flow contours in native and decellularized lungs demonstrates notable differences in capillary morphometry and applied fluidic stresses, both of which are critical for the design and implementation of cell seeding and bioreactor culture paradigms for organ engineering. Finally, by applying this tool to data from engineered ex vivo lung cultures that are undergoing vascular bed re-cellularization, we gain insight into cell-mediated shifts in microvascular fluid dynamics. Our model provides answers to an interlocking set of previously unapproachable questions regarding microvascular architecture and fluid dynamics in regenerative pulmonary experiments.
METHODS
Governing Equations for Permeable Sheet-Flow
The pulmonary capillary bed is highly elastic and is best modeled as an interrupted sheet of fluid connecting many arteriolar inputs to many venular outputs (Fig. 1B). The radial and longitudinal elastic properties of a given capillary segment affect both the flow-path dimensions and the intravascular pressure-flow mechanics, through storage of potential energy in the pulmonary capillary walls. The model we describe here accounts for the sheet-like nature of the pulmonary capillary bed, the biaxial elastic properties of the microvasculature in the lung, and the elastic properties of bulk lung parenchyma.
The concept of sheet flow in lung microvasculature is well established (16). The dense and elastic nature of the pulmonary capillaries causes bulk microvascular flow to be distinctly non-Poisellian, with the fundamental one-dimensional governing equation describing the arterio-venular velocity of flow U:
| (1) |
where p is the pressure inside the capillary sheet, x is the distance from the arteriole in the direction of the venule, h is the height of capillary sheet (equivalent to the diameter of a single capillary), µ is the fluid viscosity, f is a dimensionless geometric friction factor which is a function of the ratio of sheet thickness to intercapillary post diameter (37, 38), and k is a theoretical dimensionless constant (16, 38). The volumetric flow rate Q for a portion of the sheet of unit width is then given by:
| (2) |
Due to the elasticity of the capillary bed, h changes with the transmural pressure ptm according to
| (3) |
where h0 is the height of the capillary sheet at zero transmural pressure, α is an experimentally determined elasticity constant, p(x) is the pressure within the capillary lumen at position x, and pA is the pressure in the alveolus. For a capillary with non-negligible hydraulic conductivity, and assuming no osmotic driving force but only pressure as a driving force for fluid flow across the alveolar barrier, then Starling’s equation states that the transmural velocity of fluid flow from the capillary into the alveolus, uσ, is related to the transmural pressure by (39):
| (4) |
where Lp is the hydraulic conductivity, or Starling coefficient. The physical structure of the capillary sheet requires that for an infinitesimal distance along the length of the sheet dx in the direction of fluid flow, the loss of fluid across the wall of the sheet is:
where S is the experimentally determined vascular-space-tissue-ratio, which is the fraction of alveolar wall surface area that directly overlies a capillary; and L is the average capillary blood pathway distance between an arteriole and a venule. A, in this instance, is the perfused area of the capillary sheet and is equal to the cumulative perfused width across all alveoli in the lung, w, multiplied by the mean arteriolar-venular length L.
Mass conservation then requires that, for a rectangular strip of the pulmonary capillary sheet of unit width:
| (5) |
Equations 2, 3, and 5 combine to yield
| (6) |
which simplifies to the second-order differential equation:
| (7) |
This model takes as inputs a number of constant values that can be deduced from literature (h0, α, S, µ, k, f). The Model Constants and Literature Lp.xlsx dataset (https://doi.org/10.6084/m9.figshare.12126342.v2) shows the values of these constants that are used in this manuscript, along with associated references (16, 30, 40–42).
Definition of Permeable Sheet-Flow Boundary Conditions
To solve the second-order differentiation equation in Eq. 7, we applied specific boundary conditions. First-order boundary conditions were derived for the entry and exit pressures to the capillary sheet:
| (8) |
and
| (9) |
respectively. Both and are directly measurable by experiment—see Application to Benchtop Measurements from Ex Vivo and Engineered Lungs. These two boundary conditions are sufficient to provide a solution if there are no other unknowns in Eq. 7. However, since there are two unknowns, Lp and A, two additional boundary conditions must be applied. We derived second-order boundary conditions for Eq. 7 from the slope of the capillary pressure curve at the entrance and exit of the alveolar capillary, which are, respectively
| (10) |
and
| (11) |
where w is the width of the perfused capillary sheet and is equal to A/L. Equations 10 and 11 can be derived from Eq. 2, assuming that the width of the total perfused capillary sheet is equal to the sum of the widths of all the perfused rectangular strips of unit width, and assuming that flow is evenly distributed among arteriolar sources and venular sinks.
From Eq. 8–11, we may derive four boundary conditions. It follows that if five key empiric parameters, all measurable by experiment, are known—, , pA, Qa, and Qv—then we have enough information to solve Eq. 7 and to provide solutions for the two unknown parameters: the capillary-alveolar hydraulic conductivity Lp, and the width of the recruited capillary bed w. Assuming negligible transmural permeability of noncapillary blood vessels, Qa and Qv are simply the arterial and venous flow rates and can be measured directly from perfused organs ex vivo. As described in detail by Engler et al. (17), direct measurement of , , and pA are feasible in ex vivo platforms. Equation 7 may then be solved with the aforementioned four boundary conditions and an empirical estimation of the typical flow-path length L from arteriole to venule. Such a solution simultaneously estimates the capillary pressure-flow profile, the degree of capillary recruitment in the whole organ, and the per-unit-area Starling coefficient (hydraulic conductivity) of the recruited microvascular bed.
Estimation of Mean Capillary Length as a Function of ptp
Solutions to the model require a defined value for L, which is the average length between arteriole and venule and depends upon the degree of expansion of the alveoli. Due to the elasticity of the lung parenchyma, these values are expected to vary slightly in proportion to the transpulmonary pressure ptp. To build a reasonable model, therefore, we incorporate data from Tschumperlin and Margulies (28) that describe the variation in alveolar surface area in rat with respect to ptp as:
where Aalv is in units of cm2 and ptp is in centimeters water column pressure. From this, we calculate L(ptp) by assuming the capillary sheet to be a rectangle of width w and length L. Then, we assume isometric expansion of this sheet (uniform along both axes) during pulmonary inflation. This allows
and
for two alveolar areas at different transpulmonary pressures where . Simplifying, we find that
| (12) |
Combined with data from Sobin et al. (42), which reports a mean capillary length of 556 ± 286 μm at a transpulmonary pressure of 10 cmH2O, this equation allows us to calculate a reasonable capillary length L over which to solve Eq. 7 for a given measured ptp.
Conversion between Sheet-Flow and Circuit-Resistance Model
We designed the permeable sheet-flow model to provide output values for total alveolar membrane barrier resistance, and we compared the resulting theoretical calculations to those derived from prior empirical work which calculated barrier resistance using a circuit analog model (17). Although the data inputs to the empirically based circuit model and the theoretical permeable-sheet flow model described here are the same, the permeable-sheet flow model involves empiric parameters including morphometric measurements and elasticity coefficients. Because of the inclusion of morphometric coefficients, the permeable-sheet flow model provides as output a detailed view of the mechano-fluidic steady state of the capillary bed. To assess the reliability of the outputs of the permeable-sheet theoretical flow model, relevant outputs were compared with bulk measurements of whole-organ pulmonary barrier from previous studies (17). In the circuit analog model that incorporated direct measures of flow rates and pressures, the total lung barrier resistance is calculated by
| (13) |
where Qbarrier is the total flow leaving the vasculature of the lung (exiting via the airway or pleural spaces), and
To compare values for with commensurate values from the present permeable sheet-flow model, we combine output values for Lp (the per-unit-area hydraulic conductivity) and w (the hypothetical width of the recruited capillary bed) with L (the length of the flow path from arteriolar source to venular sink), S (the vascular space tissue ratio), and a units conversion factor, to yield:
| (14) |
Lp and w are unique outputs satisfying Eq. 7. This equation relates outputs from the permeable sheet-flow model (Lp, w) to outputs from the resistance circuit model () in the same units of mmHg/(mL/min). Unit conversion is only applicable in this specific equation, because we need to convert between Rbarrier_sheet-flow, which is derived from (Lp), (w), (L), and (S) and therefore has units of (Pa·s)/cm3, and Rbarrier_circuit, which is defined by Engler et al. in 2019 (17) as having units of mmHg/(mL/min).
Estimation of Microvascular Wall Shear Stress
For understanding of endothelial cell biology and for tissue engineering applications, the applied wall shear stress is of particular interest. Although the tortuous flow paths present in alveolar parenchyma make modeling complex, for a discreet sample of capillary blood flux it is reasonable to assume laminar flow. For an infinitesimal portion of the length of the capillary sheet along the flow path, for a rectangular strip of sheet of unit width, we may assume Hele-Shaw flow between parallel plates, and estimate wall shear stress in this system as follows (43):
| (15) |
This equation allows estimation of wall shear stress in the capillary bed along the flow path from arteriole to venule.
Tables 1, 2, 3, 4, and 5 summarize all model parameters, measured variables, and dependent variables used in this manuscript.
Table 1.
Literature parameters
| Symbol | Descriptor | Value | Units | References |
|---|---|---|---|---|
| α | Elasticity constant of capillary | 2.2332 e−7 | cm/Pa | Zhuang (30) |
| µ | Fluid viscosity | 7.8 e−4 | Pa·s | Bacabac (40) |
| k | Theoretical dimensionless constant | 12 | Fung (16) | |
| f | Dimensionless geometric friction factor | 3.5 | Fung (16) | |
| L 0 | Mean path length between arteriole and venule, measured at ptp of 10 cmH2O | 0.0556 | cm | Sobin (42) |
| S | Vascular-space-tissue-ratio | 0.91 | Fung (16) | |
| h 0 | Mean height of capillary bed (mean capillary diameter) under zero transmural pressure | 3 e−4 | cm | Glazier (41) |
Table 2.
Measured variables
| Symbol | Descriptor | Units |
|---|---|---|
| p tp | Transpulmonary pressure | Pa |
| p A | Mean pressure in the alveoli | Pa |
| p enter_cap | Mean luminal pressure of recruited capillary bed at x = 0 | Pa |
| p exit_cap | Mean luminal pressure of recruited capillary bed at x = L | Pa |
| Q a | Total flow entering recruited capillary bed at x = 0 | mL/s |
| Q v | Total flow exiting recruited capillary bed at x = L | mL/s |
Table 3.
Dependent variables (analytically solved)
Table 4.
Dependent variables (numerically solved)
Table 5.
Dependent variables (derived)
| Symbol | Descriptor | Derived from | Units | Definition |
|---|---|---|---|---|
| h(x) | Height of capillary bed (mean capillary diameter) along x | p(x) | cm | Eq. 3 |
| Q(x) | Axial flow in capillary bed, along dimension x, per unit width | h(x), p(x) | cm2/s | Eq. 2 |
| U(x) | Axial velocity in capillary along x | h(x), p(x) | cm/s | Eq. 1 |
| τ(x) | Capillary wall shear stress, along x | U(x) | Pa | Eq. 15 |
| Fluidic resistance of total recruited capillary-alveolar barrier | Lp, w, L | mmHg/(mL/min) | Eq. 14 |
Application to Benchtop Measurements from Ex Vivo and Engineered Lungs
To test this model, we applied the aforementioned formalism to empirical benchtop data from freshly explanted and fluid-inflated rat lungs (n = 3, hereafter referred to as “native”), decellularized lungs (n = 3), and decellularized pulmonary constructs undergoing short-term re-endothelialization (n = 2). All data were acquired as part of a previous study by Engler et al. (17); the data were acquired as follows.
All animal work was performed in accordance with AAALAC guidelines and was approved by the Yale Institutional Animal Care and Use Committee (IACUC). Lungs were harvested from adult Sprague–Dawley male rats as previously described (44), and cannulae were sutured into the trachea, the pulmonary artery via the right ventricle, and the pulmonary vein via the left atrium. Lungs were then either decellularized (45) or were mounted into a custom bioreactor system (17) with 37°C Dulbecco’s modified Eagle’s medium (DMEM). Native lungs, not decellularized, were perfused continuously through the pulmonary artery for ∼15 min, at perfusion rates ranging from 10 to 60 mL/min, which corresponds to 16.6%–100% of normal rat cardiac output. The lungs were submerged in DMEM and oriented to mimic the supine position in vivo. Effluent from the pulmonary vein, in addition to any tracheal or pleural leak, was collected in the bioreactor to be pumped back into the pulmonary artery, ensuring the total fluid volume in the bioreactor chamber remained constant. The airways were fluid-filled with DMEM and a tracheal pressure of 1 mmHg was applied to the nonventilated lung.
The six key empiric parameters , , pA, ppl, Qa, and Qv were measured after ∼45 s of flow at each perfusion rate, once the cultured lung had reached steady state (mean values were no longer changing) following any perfusion perturbation. Arterial flow rate (Qa) was set by the speed of the peristaltic pump, whereas venous flow (Qv) was directly measured. Arterial, venous, tracheal, and pleural (ppl) pressures were all directly measured. As detailed further in prior work (17), the precapillary (), postcapillary (), and alveolar (pA) pressures were measured by briefly (<0.5 s) blocking the artery, vein, and trachea, respectively, allowing pressure sensors at those external locations to read the pressures at each corresponding internal location. This methodology is similar to the principles used in a pulmonary arterial catheter to measure capillary wedge pressures, where the pressure measured immediately after the cessation of flow represents internal pressures right before flow is stopped. The empirical measurements of both internal and external pressures enable the calculation of lumped resistances throughout the vascular tree, including capillary resistances, as detailed in previous reports (17).
Decellularized lungs were characterized in a similar manner using PBS as perfusate. Lungs were decellularized as previously described (45) by perfusing the pulmonary artery with Triton X-100, sodium deoxycholate, benzonase endonuclease, and extensive PBS rinses. Decellularized lungs were stored at 4°C for no longer than 2 wk until characterization or reseeding. The decellularized lungs were similarly submerged in PBS and oriented to mimic the supine position, with the airways filled with PBS and a tracheal pressure of 1 mmHg applied to the nonventilated lungs.
Primary rat lung microvascular endothelial cells (RLMVECs) isolated from 6- to 8-wk-old Sprague–Dawley male rats were purchased (VEC Technologies) and cultured in MCDB-131 Complete media (VEC-technologies) on fibronectin-coated tissue culture flasks (1 μg/cm2). Cells were routinely passaged at 90% confluence every 5–6 days with culture medium changed every 2–3 days, and cells were seeded onto two decellularized scaffolds at passage 5 as previously described (46). Fifty million cells were seeded into the pulmonary vein and allowed to attach for 1 h, which was then repeated on the pulmonary artery. After seeding, perfusion was initiated at 2 mL/min with MCDB-131 medium, then ramped up over the course of 90 min to 33% of normal rat cardiac output (20 mL/min) and perfused for a total of 96 h. All five key empiric parameters were directly measured at regular intervals throughout culture. A numerical boundary value problem solver (“bvp4c”) was used in MATLAB to calculate model solutions (47). Raw data and codes to produce outputs are provided in the Raw Data—Microvascular Flow (Native, Decell, Engineered) (https://doi.org/10.6084/m9.figshare.12126675.v2) and MATLAB Model Scripts (https://doi.org/10.6084/m9.figshare.13583006.v2), respectively.
RESULTS
Steady-State Solutions for Freshly Explanted Lungs
We investigated the effects of variable perfusion rate on microvascular fluid mechanics in native ex vivo tissue, directly measuring , , pA, ppl, Qa, and Qv and then solving Eq. 7 with boundary conditions from Eqs. 8–11. Solutions to Eq. 7 show that increasing perfusion rate in freshly explanted lung tissue causes a nonlinear increase in computed mean capillary pressure across the entire length of the capillary (Fig. 2A). For all perfusion rates, computed luminal capillary pressure shows a linear decline from arteriolar source to venular sink. Calculated capillary segment diameter [h(x), Fig. 2B] increases with increasing applied perfusion rate. The mean capillary segment diameter in tissue perfused at 100% of theoretical rat cardiac output (60 mL/min) is calculated to be ∼8 μm, which is in alignment with histological and morphometric analyses (28). Capillary axial flow, while nearly constant from arteriole to venule at lower perfusion rates, begins to fall along the length of the capillary as perfusion rate is increased (Fig. 2C). Our model predicts shear stress levels in native tissue to be ∼5 dyn/cm2, which is in agreement with previous empiric experiments estimating shear stress in the pulmonary microvasculature between 5 and 20 dyn/cm2 (48).
Figure 2.
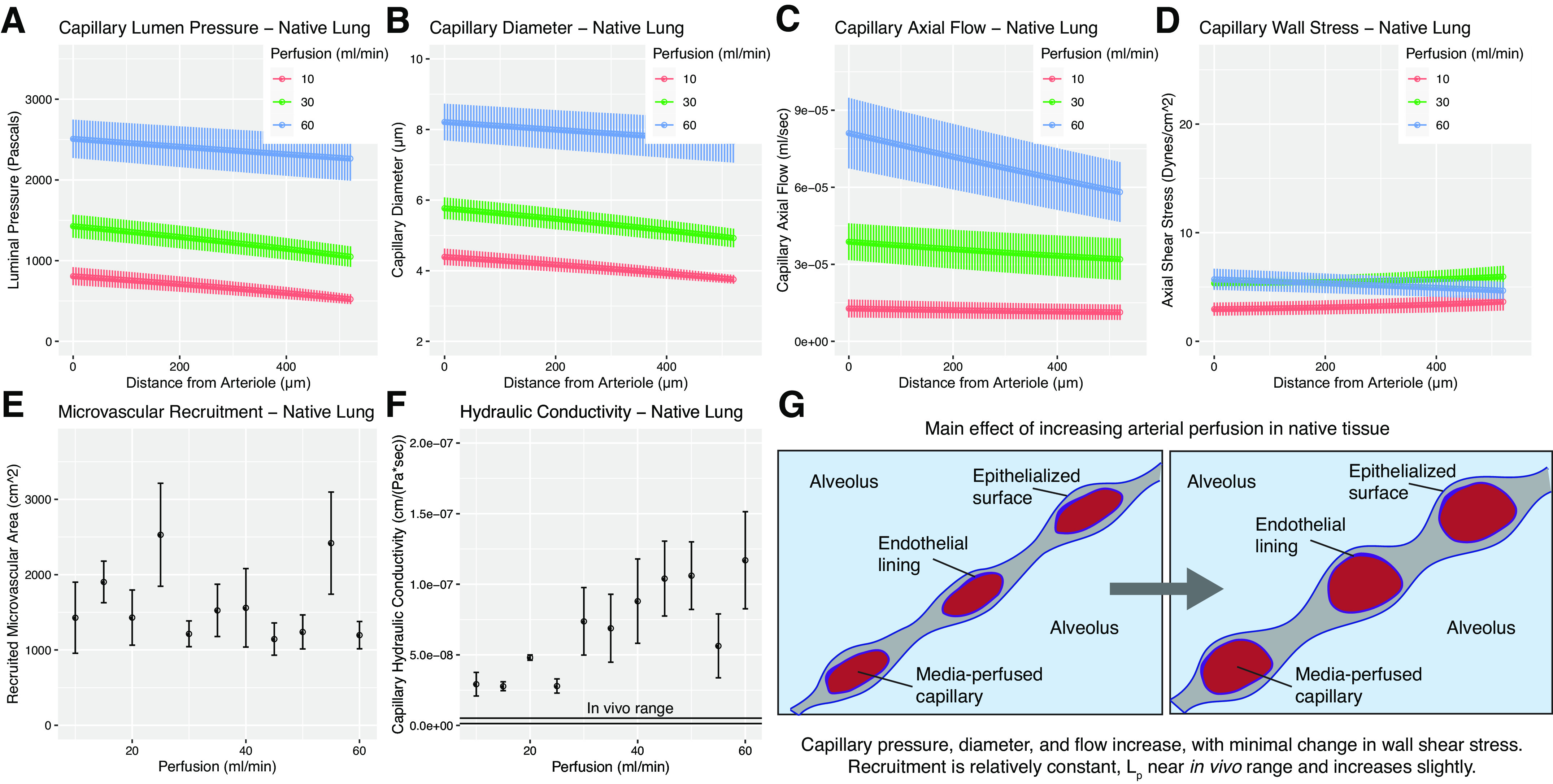
Model solutions for native tissues. A–F: represent model outputs for native lungs. A: microvascular pressure in native tissue. Increasing arterial perfusion is predicted to substantially increase intramural pressure. B: capillary diameter in native tissue. Increasing arterial perfusion increases capillary diameter. C: capillary flow in native tissue. Increasing arterial perfusion is found to increase the flow experienced by a given recruited capillary. D: wall shear stress predictions in native microvasculature. Values are in agreement with previous literature (48). Shear stress is predicted to be nearly constant along the axis of flow, with slight increases at the venular end. Increasing perfusion is predicted to have negligible effect on the shear forces present in a given capillary, which can be explained by the opposing effects of increasing flow and increasing diameter. E: microvascular recruitment in native rat tissue is predicted to be relatively constant from 16.6% to 100% cardiac output. F: capillary hydraulic conductivity in fluid-filled ex vivo lungs is found to be slightly higher than literature-reference in vivo range (black lines), and increases marginally with increasing perfusion rate. G: schematic visualizing tissue-level changes due to increasing perfusion. Benchtop experiments yielding input values for modeling were performed using n = 3 tissues. Model solutions for each experimental run were then averaged to yield mean values, shown here. Error bars in all graphs represent ± standard error of the mean across experiments.
In native lungs not subject to decellularization, modeling shows that capillary recruitment is relatively constant over a physiological range of perfusion rates (Fig. 2E). In combination with Fig. 2B, we see from these data that in healthy pulmonary tissue, an increase in arterial perfusion from 16.6% to 100% of theoretical cardiac output manifests predominantly as an increase in mean capillary diameter, rather than as an increase in capillary microvascular recruitment from a previously collapsed or no-flow state.
Figure 2F reports the Starling coefficient (Lp) values calculated for ex vivo perfused lungs when Eq. 7 is solved using the boundary conditions in Eqs. 8–11 and the aforementioned directly measured parameters. Starling coefficient values increase very slightly with increasing perfusion rates, an observation that is relevant in our later calculation of total organ barrier function (Fig. 5A). All Starling coefficient values approach the known range for hydraulic conductivity of native pulmonary parenchyma (dual solid lines in Fig. 2F) but are nonetheless larger than reported in vivo values. Mean output value for Lp across all perfusion rates for ex vivo normal tissue is 6.79 × 10−8 cm/(Pa·s) ± 9.92 × 10−9 (SE).
Steady-State Solutions for Decellularized Lungs
An additional goal of this study was to model the fluid mechanics in decellularized lung tissue and to estimate the hydraulic conductivity of the capillary-alveolar barrier in decellularized lung. To do so, we applied the permeable sheet-flow model to decellularized lung tissue. Using our model, we find that increasing arterial perfusion in decellularized lung tissue provides only a modest increase in capillary luminal pressure (Fig. 3A). Furthermore, increasing perfusion rate has a negligible effect on transmural pressure and capillary diameter (Fig. 3B). The capillary diameter in decellularized lung, across all perfusion rates, is calculated to be between 3 and 4 μm (Fig. 3B), which is smaller than the capillary diameter found in native lung tissue during even very low arterial perfusion (Fig. 2B, red data points). Axial flows—those along the arteriolar-to-venular flow path—in decellularized tissue are revealed to be both nonlinear and lower than in native tissue (Fig. 3C). Increasing perfusion rate in this context has a minimal effect on axial flow rates traversing the vasculature, with flow profiles looking quite similar from 10 to 60 mL/min perfusion. Strikingly, the capillary wall shear stresses calculated for decellularized tissue (Fig. 3D) are higher at the arteriolar inlet to the microvascular bed than in native lung, and vary nonlinearly with distance along the flow path.
Figure 3.
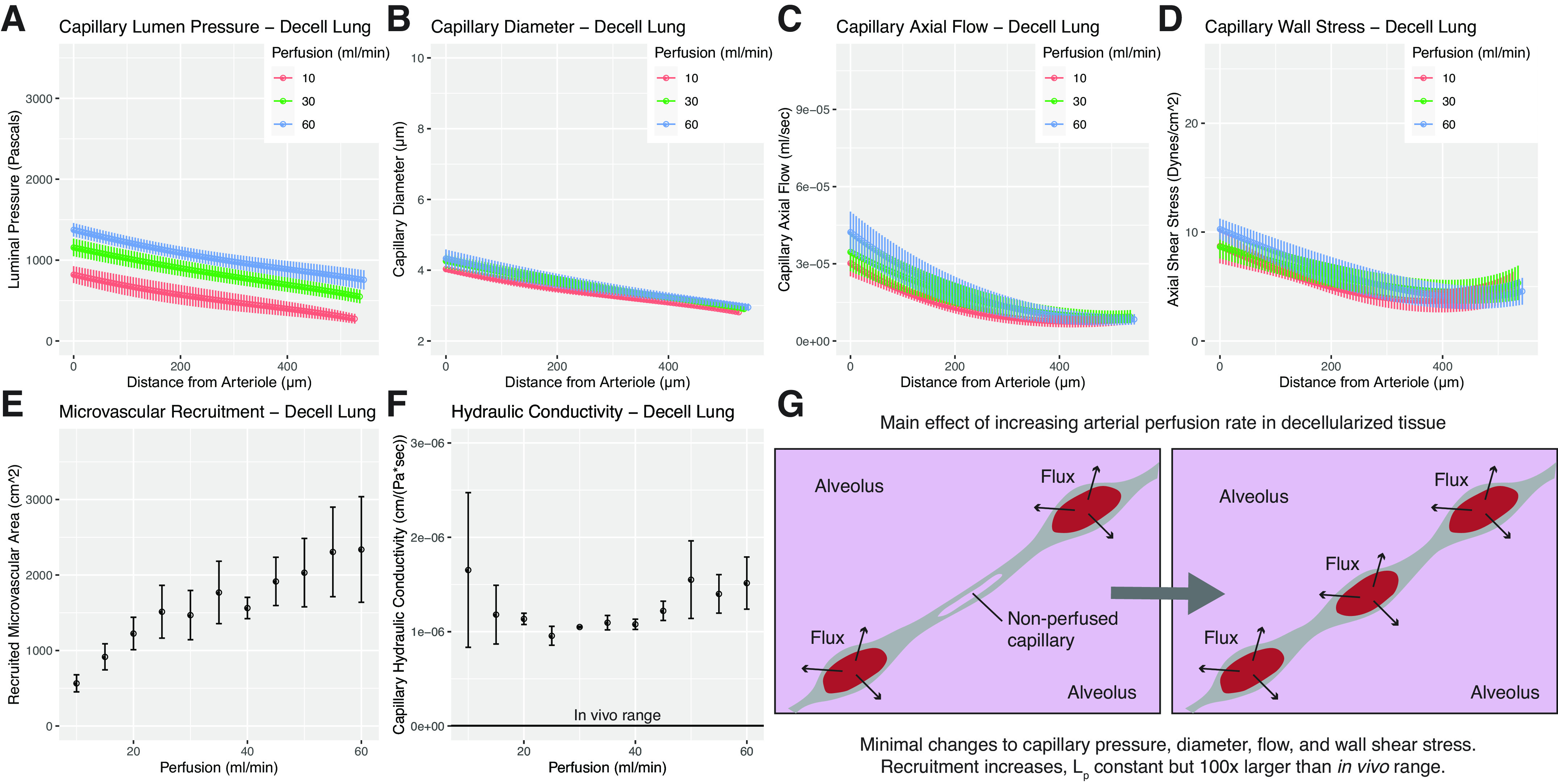
Model solutions for decellularized tissues. A–F: represent model outputs for decellularized lungs. A: microvascular pressure in decellularized lung. Increasing arterial perfusion is found to only marginally increase intramural pressures. B: fluid readily passes into the alveolus in decellularized tissue, and our model predicts that capillary diameter in decellularized tissue is independent of perfusion rate in the range tested. C: axial flow in decellularized lung is found to be nonlinear and substantially lower than in native lung. D: microvascular wall shear stress in decellularized lung is predicted to be higher than that of native at the arteriolar inlet, while approaching more comparable values at the venule. E: recruitment is found to increase steadily with increasing perfusion rate. F: hydraulic conductivity in decellularized lung is found to be two orders of magnitude larger than in native tissue. In vivo range shown for reference. G: visual schematic showing changes in decellularized lung microvascular steady state due to increased perfusion. Benchtop experiments yielding input values for modeling were performed using n = 3 tissues. Model solutions for each experimental run were then averaged to yield mean values, shown here. Error bars in all graphs represent ± standard error of the mean across experiments.
Recruitment of decellularized lung capillaries rises steadily in decellularized tissue as perfusion is increased (Fig. 3E), which is in contrast to the behavior calculated for native lung. Hydraulic conductivity of the capillary-alveolar barrier in decellularized lung (Fig. 3F) is found to be largely constant over the range of perfusion rates. Of note, however, model solutions for Lp in decellularized lung matrix are roughly three orders of magnitude larger than the literature-reported range for native lung tissue, and roughly two orders of magnitude larger than the values we calculated with the same model for ex vivo perfused tissue. The average hydraulic conductivity across all perfusion rates for decellularized tissue is found to be 1.25 × 10−6 cm/(Pa·s) ± 7.03 × 10−8 (SE).
Steady-State Solutions for Organ-Based Endothelial Monoculture
To determine the microvascular effects of recellularizing lung matrix with endothelium, we studied two rat lungs that were seeded with 100 × 106 endothelial cells and then cultured for 4 days. In brief, during this process a decellularized lung is seeded with endothelial cells via both the pulmonary artery and vein, leading to local vascular regions of dense endothelial repopulation (Fig. 4A). This tissue is then cultured in a bioreactor for 4 days under 20 mL/min arterial perfusion (1/3 normal cardiac output) (Fig. 4B). After 4 days of culture, the microvascular compartment of the lung became densely and uniformly populated with endothelial cells (Fig. 4C). We were interested in seeing how microvascular fluid mechanics changed in this system over time, as compared with both acellular lung matrix and to native lung. A caveat to interpreting the outputs of the mathematical model for this condition is the unknown effects of matrix remodeling during re-endothelialization, which may change the permeability, elasticity, and composition of the alveolar basement membrane.
Figure 4.
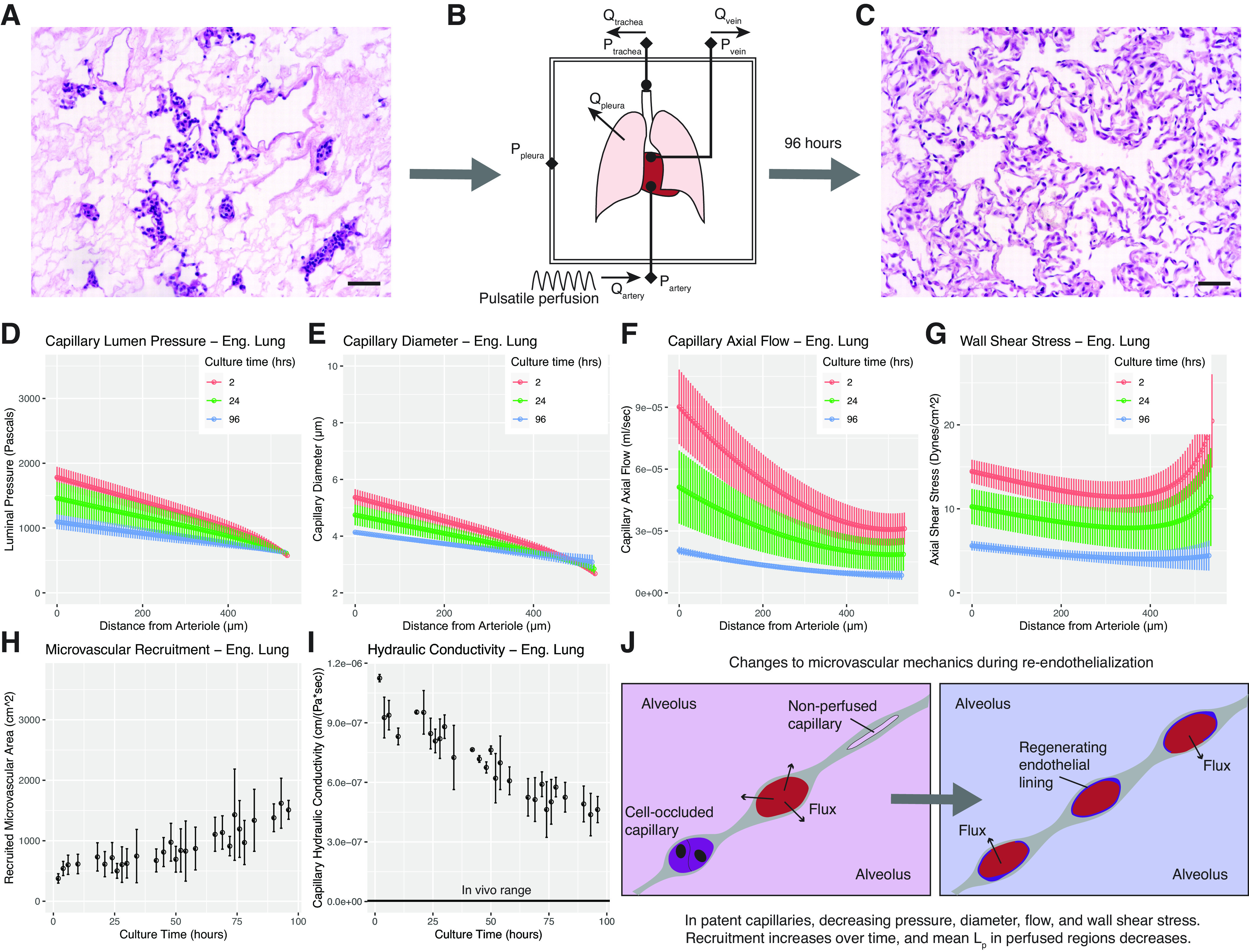
Model application to engineered tissues over time. A: histology (H&E) of lung construct immediately after seeding. Cells are concentrated around arteriolar sources and venular sinks. B: schematic of bioreactor culture providing arterial media perfusion and allowing real-time pressure-flow measurements. C: histology of construct after 4 days of culture. Parenchyma is now nearly completely re-endothelialized. Scale bars = 50 µm. D–I: represent model outputs for engineered lungs over culture time. D: capillary pressures over time during re-endothelialization. Intramural pressures decrease over time and the arterio-venous drop flattens. E: diameters follow a similar trend, approaching a native profile after four days of culture. F: initial flow rates in the perfused capillaries are very high. Over time, these rates both decrease and smooth in character. G: wall shear stress is high at the beginning of culture and decreases over time. H: recruitment of microvascular flow paths steadily increases as the organ undergoes re-endothelialization. I: hydraulic conductivity of the capillary-alveolar wall steadily decreases over time. J: visual schematic of changes to microvascular fluid mechanics due to re-endothelialization. Recruitment increases, Lp decreases, and mean capillary diameter decreases. Benchtop experiments yielding input values for modeling were performed using n = 2 tissues. Model solutions for each experimental run were then averaged to yield mean values, shown here. Error bars in all graphs represent ± standard error of the mean across experiments.
At the beginning of culture, cells are densely packed in arterioles and venules (Fig. 4A). Solutions to the model at this point in the culture show that the average perfused capillary displays a steep luminal pressure drop from arteriolar source to venular sink (Fig. 4D, red data points: each color corresponds to a different point in the culture, rather than a different flow rate as in earlier figures). However, capillary pressures decrease over time in culture, with a mean flow profile at four days (Fig. 4D, blue data points) that is similar to that seen in native lung perfused at the same arterial flow rate.
Calculated capillary diameters and flow rates mirror this trend (Fig. 4, E and F); they are both much higher immediately after seeding than in a similarly perfused decellularized lung. By day 4 of culture, capillary diameter and flow rate approach values seen in the original decellularized scaffold (Fig. 4, E and F, blue data points). Wall shear stress is as expected given the diameter and flow data: very high and nonlinear values at the start of culture, and much lower and more linear values after 4 days of culture (Fig. 4G). Correlating with this overall picture, capillary recruitment is found to be low immediately after seeding, and found to increase over time during biomimetic culture (Fig. 4H).
Intriguingly, we calculate that Lp, the hydraulic conductivity per unit area of the capillary-alveolar wall, decreases over time during endothelial cell culture (Fig. 4I). This suggests a decrease in capillary-alveolar wall permeability: regardless of how many pathways are recruited, capillaries at the conclusion of culture exhibit better barrier function than those at the start. Although the permeabilities at 4 days are still orders of magnitude larger than native tissue [4.63 × 10−7 cm/(Pa·s) ± 6.59 × 10–8], we do calculate a nearly twofold reduction in alveolar barrier permeability when compared with values from perfusion in decellularized lung matrix.
Permeable Sheet-Flow Solutions Explain Trends in Total Organ Barrier Resistance
We have previously reported calculations of lung alveolar barrier that were based upon experimental measurements and a simpler model of flow in the lung as a resistive electronic circuit (17). This measure of whole organ barrier treats all recruited microvascular parenchyma as a single resistive element. The two models—electrical resistance and permeable sheet—take the same empiric inputs , , pA, ppl, Qa, and Qv), but use wholly different conceptual approaches to calculate outputs and yield different insights. To check that the permeable sheet flow model could be used to explain previously observed trends in whole organ circuit resistance, the two mathematical models had to empirically align across all observations, i.e., had to roughly equal for all measurements:
| (16) |
For a given set of measured inputs , , pA, ppl, Qa, and Qv, the permeable sheet-flow model provides a unique set of outputs for Lp and w which solves Eq. 7 and simultaneously satisfies the boundary conditions in Eqs. 8–11. By combining these output values to yield , we were able to compare the solution presented by permeable sheet-flow modeling to the values of calculated by the circuit modeling described by Engler et al. (17). If we found agreement between these two models, it would support the fluid-mechanical portrait of the microvascular bed described by the permeable sheet-flow model. If these two models proved not to agree, then we would have to consider the outputs from permeable sheet-flow modeling to be trivial, and could not use the solutions to explain previously observed trends.
Figure 5 shows the results of this comparison for each tissue type tested in this study. In native lung (Fig. 5A), we see that the models agree very tightly. We find that the very slight increase in Lp shown earlier (Fig. 2F) explains the previously observed (17) decrease in whole organ barrier with increasing perfusion rate. When coupled with relatively constant recruitment (Fig. 2E), the observed small increase in hydraulic conductivity over this perfusion change manifests as a substantial decrease in whole organ barrier function. Values for agree with ±7.97%. The two models across all perfusion rates have a Pearson correlation of 0.9867, where 1 is perfect correlation.
Figure 5.
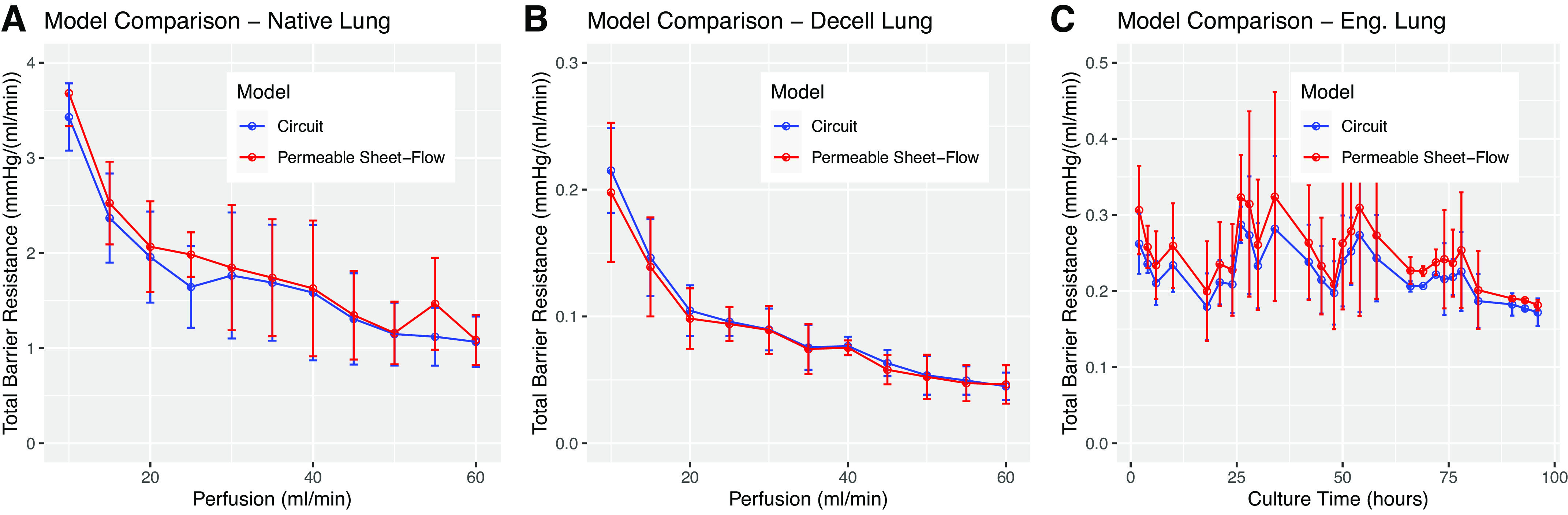
Permeable sheet flow solutions predict total organ barrier resistance. A: comparison of total organ barrier resistance in native tissue calculated using Ohm’s law (blue) and permeable sheet-flow incorporating microvascular dimension and recruitment estimates (red). High agreement between the models supports the accuracy of permeable sheet-flow modeling against previously published methods (17). The decreasing trend is a consequence of steady recruitment coupled with marginally increasing hydraulic conductivity as perfusion is increased. B: commensurate graphs for decellularized lung tissue. C: time-course data for engineered lung constructs undergoing re-endothelialization. The combination of increasing recruitment and decreasing hydraulic conductivity leads to a relatively flat output for total organ barrier resistance.
When applied to decellularized tissues (Fig. 5B), the models again agree well, but in this case we see that an increase in recruitment (Fig. 3E), rather than hydraulic conductivity, is predicted to be the variable responsible for decreasing in whole organ barrier over perfusion rate. Lp does not change substantially over perfusion rate in decellularized tissue (Fig. 3F), but recruitment increases (Fig. 3E), which causes slightly decreasing total organ barrier resistance. In decellularized tissue, agrees with previously reported values of . The two models correlate with a Pearson coefficient of 0.9988.
In re-endothelializing tissue, we hypothesized that a combination of increasing recruitment and decreasing conductivity would offset each other and yield a relatively flat trend in total organ barrier over time. Our model suggests that this is indeed the case. We find total organ barrier resistance to be roughly constant over time in both models (Fig. 5C). Due to the permeable sheet-flow model, we see that this trend is a combined effect of increasing recruitment w and decreasing barrier hydraulic conductivity Lp. For engineered tissue across all time points, agrees with measures of , and the two models correlate with a Pearson coefficient of 0.9945.
DISCUSSION
A key goal of this study was to compare fluid flow steady-states in decellularized, native, and engineered tissues. A selection of outputs comparing conditions are shown in Fig. 6. In Fig. 6, A–D, we reproduce together the results from native and decellularized tissues when perfused at full cardiac output (60 mL/min.) Substantial differences are readily observable in steady-state capillary pressure profiles, dimensions, axial flow rates, shear mechanics, and recruitment, all of which can be attributed to increased capillary-alveolar hydraulic conductivity due to decellularization.
Figure 6.
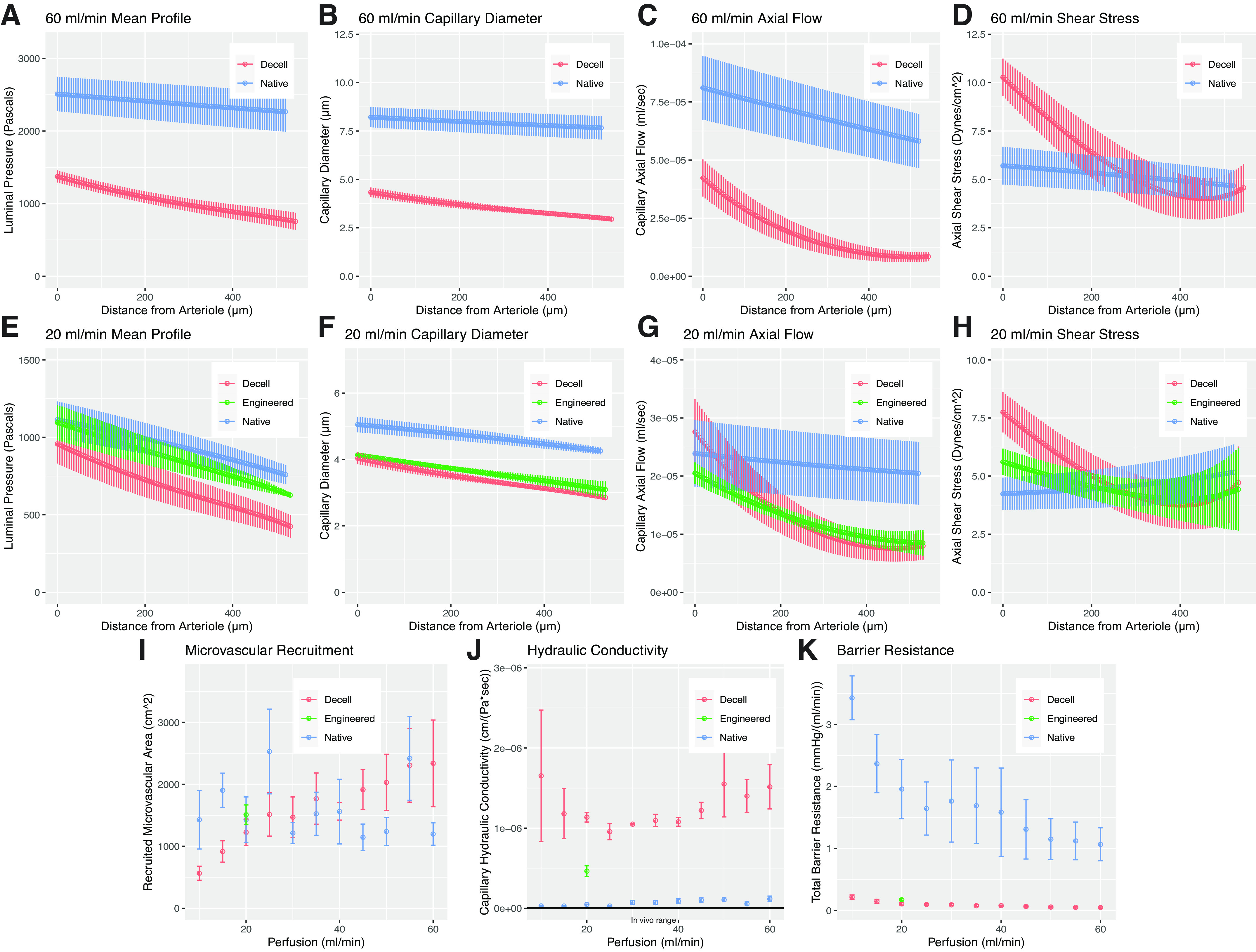
Selected comparisons between model outputs for native, decellularized, and engineered tissue. Decellularized lungs, when compared to native, display substantial differences in capillary pressure (A), diameter (B), flow rate (C), and wall shear stress (D) even when perfused at full cardiac output. Four days of re-endothelialization improves microvascular pressure profiles (E) and diameters (F), while smoothing arteriolar-venular gradients in axial flow (G) and wall shear stress (H). By the end of culture, recruitment at 20 mL/min is similar to native tissue (I), and capillary-alveolar hydraulic conductivity is reduced nearly twofold (J). This improvement only marginally increases total organ barrier resistance (K); the achievement of native levels will require hydraulic conductivity to be reduced by two additional orders of magnitude.
Conclusions regarding Microvascular Fluid Mechanics in Native versus Decellularized Tissue
In native tissue, our model shows that increasing perfusion rate causes an increase in mean capillary diameter (Fig. 2, A and B). This makes sense because alveolar pressure is constant in a healthy organ displaying intact barrier. In decellularized tissue, however, hydraulic conductivity is so low that pressure equalizes between the capillary and the alveolus along the flow path, causing increased perfusion to have little effect on capillary diameter (Fig. 3, A and B). The net effect of this is that perfused capillaries in decellularized tissue are much smaller in diameter than in native tissue (Fig. 6, A and B).
The change in hydraulic conductivity also affects axial flow in the capillary: Fig. 6C shows that arterio-venous flow rates in decellularized tissue are much lower than in native lung. Furthermore, perfusion rate has a very different effect in the two tissues: while in native lung, increasing perfusion from 10 mL/min to 60 mL/min causes an increase in axial flow rate (Fig. 2C), whereas in decellularized tissue there is almost no change (Fig. 3C).
Predicted microvascular wall shear stress, which in our model is directly dependent on both capillary dimensions and on axial flow rate, is also shown to be radically different in decellularized tissue as compared with native. In native tissue, capillary wall shear stress is ∼5 dyn/cm2 across all perfusion rates tested and is nearly constant from arteriole to venule (Fig. 2D). This is a remarkable demonstration of the ability of healthy pulmonary vasculature to maintain a crucial endothelial cell-sensed homeostatic parameter: wall shear stress does not change, even though pressures, diameters, and flows increase substantially with increasing pulmonary artery flow rate. In decellularized tissue, however, we predict a peak wall shear stress of ∼10 dyn/cm2 (Fig. 3D) and we observe highly nonlinear shear along the arterio-venous path (Fig. 6D).
In native tissue, we find that the expansion of height h of the capillary sheet occurs more readily than the recruitment of new pulmonary capillary flow paths. This makes sense for two reasons: 1) in healthy tissue alveoli, distal airway pressure is constant despite increasing perfusion rate, thereby allowing the thickness of the capillary sheet height h to increase easily. In addition, the opening of new capillary flow paths (i.e., increasing w) requires overcoming an energy barrier associated with the “opening pressure” of each zero-flow capillary region, due to surface energy effects that are present in closed capillaries (16). In decellularized lung tissue, conversely, the increasing input energy from increasing arterial perfusion causes increasing microvessel recruitment rather than altering mean capillary diameter/pressure-flow dynamics. This is likely due to equilibration between mean capillary pressure and that of the alveolus, and because the high hydraulic conductivity of the capillary-alveolar barrier lowers the energy barrier for new vessel recruitment.
It should be noted that in native tissue, we find that increasing arterial perfusion causes a slight increase in wall hydraulic conductivity (Fig. 2F), an effect not seen in decellularized tissue.
This difference may be reflective of short-term barrier breakdown that is sometimes observed in ex vivo native perfusion experiments. Since these ex vivo perfusion studies took ∼40 min from incision to completion, some degree of barrier breakdown is expected.
Fundamentally, we find a distinct difference in microvascular steady-state in native and decellularized lungs during arterial perfusion. In native tissue, increasing pulmonary artery perfusion toward normal cardiac output is found to cause an increase in mean capillary pressure and diameter rather than an increase in microvascular/capillary recruitment. In decellularized tissue, conversely, increasing perfusion rate is found to increase microvascular recruitment without affecting the dimensions and fluid mechanics of a single given capillary flow path, at least for the perfusion rates tested. Our model therefore demonstrates major, important changes in microvascular steady-state mechanics due to decellularization.
Conclusions regarding Engineered Lung Culture
The model solutions for native and decellularized lung provide critical benchmarks and desired functional endpoints for regenerative pulmonary engineering. Figure 6, E–K shows how engineered lungs, seeded with endothelium and at the end of a 4-day culture, compared with both the original decellularized tissue and to native tissue when perfused at 20 mL/min. Our model demonstrates the effects of re-endothelialization in context and shows definitive progress in the recapitulation of native microvascular fluid mechanics by day 4 of organomimetic culture.
Immediately following cell seeding, occlusion blocks flow through many regions of the microvascular sheet. This can be seen histologically (Fig. 4A, note endothelium-filled arterioles and venules). Since arterial perfusion is maintained at 20 mL/min but there are fewer microvascular flow paths than in bare decellularized tissue, the average perfused capillary displays a steeper pressure drop from arteriolar source to venular sink (Fig. 4D). Over time, however, cells come to populate the microvasculature and no longer clog end-arterioles and venules (Fig. 4C). Correlating with this histologic shift, pressures, flows, and shear stresses in individual capillaries all decrease over time in culture (Fig. 4, A–G).
The calculated trend in capillary recruitment aligns with histological and fluidic findings. At the beginning of culture, many capillaries are not perfused because their respective arterioles and venules are blocked with seeded endothelium (Fig. 4H, left-most point). The remaining parenchyma therefore receives the totality of arterial flow, leading to high perfusion pressures, and larger capillary diameters (Fig. 4, D–G, red data points), though not as large as those calculated for native lung (Fig. 6F.) By the end of culture, the organ is largely re-endothelialized and most arterioles and venules are patent. Much more of the parenchyma is found to be recruited (Fig. 4H, right-most point) and, since the pulmonary arterial flow rate is still the same, microvascular pressures, diameters, and calculated wall shear all decrease, approaching native lung values and trends though not fully matching native curves (Fig. 4, D–G, blue data points, and Fig. 6, E–H).
The predicted increase in recruitment is tied to a notable decrease in microvascular hydraulic conductivity of the recruited pathways (Fig. 4J). Although there is little change in the overall barrier resistance of the engineered organ, our model shows that there is a nonetheless a substantial decrease in capillary-alveolar hydraulic conductivity (Fig. 6, J and K). Our model therefore shows that achieving native total organ barrier function will require engineering of exquisitely small values of capillary-alveolar hydraulic conductivity (note the inverse relationship schematized in Fig. 1F). Even with a high degree of cellularity, native levels of hydraulic conductivity require both endothelial lumenization and organized tight junction formation, and these design criteria are thus far difficult to achieve in vitro (46).
Drawbacks and Limitations
There are some unavoidable limitations to the model as presented. Elasticity constants for the pulmonary vasculature are not known for rat, and to calculate solutions we have adapted values reported from cat lungs. For more accurate results, direct measurements should be made from the exact species being considered, and these placeholder values should be corrected.
Furthermore, there are a few assumptions in the model. First, we assume that with removal of all cells, the walls of the large vessels in decellularized lung are negligibly permeable to flow as compared with the microvasculature, inverting the relationship present in normal, cellularized tissue (49–51). We consider this to be a reasonable modeling assumption given that the capillary-alveolar basement membrane is on the order of 5–10 nm in thickness (52), which is nearly 100 times thinner than the walls of the smallest arterioles. Coupled with the immense surface area of the pulmonary capillary bed as compared with the alveolar-bordering surface area of the large vessels, it is reasonable to assume that the majority of measured vascular-airway flux in decellularized tissue occurs at the capillary-alveolar barrier. Second, we do not consider possible changes to elasticity constants due to decellularization and recellularization. This is because previous papers have found decellularization to only minimally affect tissue mechanical properties (53, 54). Third, the blood vessels and capillaries are currently modeled as having a linear elasticity, but they likely have a maximum diameter that they asymptotically approach with increasing transmural pressure. The derivation of sheet-flow mechanics requires a number of assumptions regarding both pulmonary architecture and continuum mechanics that are detailed by Fung (16). Fourth, we do not here consider the effects of the pulsatile flow applied to the organ in reality, but treat the pressures/flows in the supplying vasculature as constant at the capillary bed so that Eq. 7 applies and is solvable. Pulmonary artery pulsatility is known to increase lung capillary recruitment for a given mean pressure (55), and this literature precedent should be taken into account when interpreting results. And finally, here we assume Lp to be constant along the length of the capillary, when in reality Lp is likely a function of the material distension of the capillary-alveolar basement membrane, which would make it a complex function of both ptp and ptm(x).
Summary Conclusions
In this study, we show that permeable sheet-flow modeling provides quantitative metrics for functional assessments of native, decellularized, and engineered lung tissues. We find that the described model predicts values for total organ barrier resistance which agree across all observations with the lumped circuit resistance model previously described by Engler et al. in 2019. Most importantly, the model in this manuscript makes these predictions in terms of independent values for microvascular recruitment and microvascular wall hydraulic conductivity. This reveals a much clearer portrait of microvascular fluid flow. By taking into account the biomechanics of the pulmonary microvasculature, permeable sheet-flow modeling is able to differentiate between two hypothetical tissues which have the same total organ barrier resistance but distinct microvascular recruitments and wall conductivities. Such a model has been needed in the field of pulmonary regeneration for many years, both to inform engineering experiments and to define quantitative design criteria for clinical translation. We present it here, along with all scripts necessary to apply the method, in the hopes that it may aid the larger community.
In native tissues that are perfused ex vivo, we find the microvascular hydraulic conductivities to be similar to values measured in vivo. Furthermore, we find that microvascular recruitment in native tissues is minimally affected by increasing arterial perfusion rate between 10 and 60 mL/min, with the effects of flow manifesting instead as increasing intramural pressures and consequent increases in capillary diameter. This trend, which contrasts with other physiologic studies of capillary recruitment (26, 27, 56), may be due to the fact that all of our experiments were performed at or below normal cardiac output, without supraphysiological pressures or flows. In decellularized tissues, we find the opposite to be true: increasing arterial perfusion at the rates tested minimally affects capillary intramural pressures and diameters, but has a pronounced effect on microvascular recruitment.
In addition, we are able to compute hydraulic conductivity values for the capillary-alveolar barrier in decellularized lung, finding these values to be two orders of magnitude larger than native ex vivo cultures, and nearly three orders of magnitude higher than in vivo. Finally, we show that application of this model to developing engineered tissues is a means to derive quantitative metrics reflective of changing microvascular character, over time, during recellularization and organ culture.
The removal of cells from the lung causes a profound increase in capillary-alveolar hydraulic conductivity. All experimental parameters being equal, this permeability increase causes capillary steady-state diameters to shrink substantially, and axial flow in the capillary lumen to be reduced and to become nonlinear over distance from the arteriole to the venule. Consequently, wall shear stress is, in general, elevated at the arteriolar end of the microvascular flow path and decreased at the venular end, as compared with native.
Lung re-endothelialization begins to rectify each of these changes in microvascular function, though only partially. Capillary-alveolar hydraulic conductivity is decreased, microvascular intramural pressures and diameters increase, arterio-venular flow becomes more linear, and shear begins to approach the native profile. These changes in the mean microvascular flow are strongly associated with the recruitment of additional flow paths within the organ. The observed reduction in mean hydraulic conductivity is likely due to the recruitment of re-endothelialized flow paths combined with the development of nascent barrier function by cultured endothelium.
Importantly, this study dissects previously published findings (17) showing that total organ barrier resistance changes minimally during re-endothelization, despite widespread cell growth. We demonstrate here that in engineered lung, parenchymal recruitment increases toward native levels and barrier conductivity decreases toward native levels with progressive endothelialization of the vascular compartment. The combination of these two shifting variables causes total barrier resistance to remain nearly constant over time. Permeable sheet-flow modeling can decouple these two interacting changes in a way that provides greater insight into organ physiology in a noninvasive manner. The resulting portrait of change in the engineered lung barrier is more favorable than would otherwise be understood. As this model is able to provide a metric for capillary barrier function decoupled from recruitment, it can be applied equally to ex vivo perfusions with different flow rates, back pressures, or levels of patent microvasculature.
Given the results of this study, we conclude that lung re-endothelialization is an effective first step in the engineering of pulmonary barrier in decellularized matrix. However, the hydraulic conductivity of the resulting capillary-alveolar barrier needs to be reduced much further—by at least two orders of magnitude—to yield a construct with barrier function comparable with that of native tissue. Achieving this goal will likely require the addition of appropriate epithelial and supporting cells, as well as the modulation of bioreactor conditions. From this body of experimental and modeling work, we present permeable sheet-flow modeling as a way to establish common standards for the engineering of pulmonary barrier ex vivo.
DATA AVAILABILITY
All raw data, MatLab scripts, model outputs, and R scripts are publicly available on FigShare at the following links:
Raredon, Micha Sam (2020): Supplementary Data 1—Model Constants and Literature Lp.xlsx. figshare. Data set. https://doi.org/10.6084/m9.figshare.12126342.v2.
Raredon, Micha Sam (2020): Supplementary Data 2—Raw Data—Microvascular Flow (Native, Decell, Engineered). figshare. Data set. https://doi.org/10.6084/m9.figshare.12126675.v2.
Raredon, Micha Sam (2021): Supplementary Data 3—MATLAB Model Scripts. figshare. Software. https://doi.org/10.6084/m9.figshare.13583006.v2.
Raredon, Micha Sam (2021): Supplementary Data 4—Model Outputs. figshare. Data set. https://doi.org/10.6084/m9.figshare.13582967.v2.
Raredon, Micha Sam (2020): Supplementary Data 5—R Plotting Scripts. figshare. Software. https://doi.org/10.6084/m9.figshare.12126693.v2.
GRANTS
This work was funded by NIH Medical Scientist Training Program Training Grant T32GM007205 (to M. S. B. Raredon), F30HL143906 (to M. S. B. Raredon), R21 EB024889 (to L. E. Niklason), R01 HL138540 (to L. E. Niklason), and an unrestricted research gift from Humacyte Inc. (to L. E. Niklason).
DISCLOSURES
L. E. Niklason is a founder and shareholder in Humacyte, Inc., which is a regenerative medicine company. Humacyte produces engineered blood vessels from allogeneic smooth muscle cells for vascular surgery. L. E. Niklason’s spouse has equity in Humacyte, and L. E. Niklason serves on Humacyte’s Board of Directors as CEO. L. E. Niklason is an inventor on patents that are licensed to Humacyte and that produce royalties for L. E. Niklason. L. E. Niklason has received an unrestricted research gift to support research in her laboratory at Yale. A.J. Engler is employed by Humacyte, Inc. None of the other authors has any conflicts of interest, financial or otherwise, to disclose.
DISCLAIMERS
Humacyte did not fund these studies, and Humacyte did not influence the conduct, description, or interpretation of the findings in this report.
AUTHOR CONTRIBUTIONS
M.S.B.R. and A.J.E. conceived and designed research; M.S.B.R., A.J.E., Y.Y., and A.M.G. performed experiments; M.S.B.R. and A.J.E. analyzed data; M.S.B.R., A.J.E., and L.E.N. interpreted results of experiments; M.S.B.R., A.J.E., and L.E.N. prepared figures; M.S.B.R. and L.E.N. drafted manuscript; M.S.B.R., A.J.E., Y.Y., A.M.G., and L.E.N. edited and revised manuscript; M.S.B.R. and L.E.N. approved final version of manuscript.
ENDNOTE
At the request of the authors, readers are herein alerted to the fact that additional materials related to this manuscript may be found at https://doi.org/10.6084/m9.figshare.12126342.v2, https://doi.org/10.6084/m9.figshare.12126675.v2, https://doi.org/10.6084/m9.figshare.13583006.v2, https://doi.org/10.6084/m9.figshare.13582967.v2, and https://doi.org/10.6084/m9.figshare.12126693.v2. These materials are not a part of this manuscript and have not undergone peer review by the American Physiological Society (APS). APS and the journal editors take no responsibility for these materials, for the website address, or for any links to or from it.
ACKNOWLEDGMENTS
The authors thank Katherine L. Leiby for participation in helpful discussions informing this work and for assistance in proofreading the mathematical derivations published here. We additionally thank Pavlina Baevova for help as lab manager and Daryl Smith for constructing the glass bioreactors used in these studies.
REFERENCES
- 1.Badylak SF, Taylor D, Uygun K. Whole-organ tissue engineering: decellularization and recellularization of three-dimensional matrix scaffolds. Annu Rev Biomed Eng 13: 27–53, 2011. doi: 10.1146/annurev-bioeng-071910-124743. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Crapo PM, Gilbert TW, Badylak SF. An overview of tissue and whole organ decellularization processes. Biomaterials 32: 3233–3243, 2011. doi: 10.1016/j.biomaterials.2011.01.057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Petersen TH, Calle EA, Colehour MB, Niklason LE. Matrix composition and mechanics of decellularized lung scaffolds. Cells Tissues Organs 195: 222–231, 2012. doi: 10.1159/000324896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Nichols JE, Niles J, Riddle M, Vargas G, Schilagard T, Ma L, Edward K, La Francesca S, Sakamoto J, Vega S, Ogadegbe M, Mlcak R, Deyo D, Woodson L, McQuitty C, Lick S, Beckles D, Melo E, Cortiella J. Production and assessment of decellularized pig and human lung scaffolds. Tissue Eng Part A 19: 2045–2062, 2013. doi: 10.1089/ten.TEA.2012.0250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ott HC, Clippinger B, Conrad C, Schuetz C, Pomerantseva I, Ikonomou L, Kotton D, Vacanti JP. Regeneration and orthotopic transplantation of a bioartificial lung. Nat Med 16: 927–933, 2010. doi: 10.1038/nm.2193. [DOI] [PubMed] [Google Scholar]
- 6.Petersen TH, Calle EA, Zhao L, Lee EJ, Gui L, Raredon MB, Gavrilov K, Yi T, Zhuang ZW, Breuer C, Herzog E, Niklason LE. Tissue-engineered lungs for in vivo implantation. Science 329: 538–541, 2010. doi: 10.1126/science.1189345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Boehnert MU, Yeung JC, Bazerbachi F, Knaak JM, Selzner N, McGilvray ID, Rotstein OD, Adeyi OA, Kandel SM, Rogalla P, Yip PM, Levy GA, Keshavjee S, Grant DR, Selzner M. Normothermic acellular ex vivo liver perfusion reduces liver and bile duct injury of pig livers retrieved after cardiac death. Am J Transplant 13: 1441–1449, 2013. doi: 10.1111/ajt.12224. [DOI] [PubMed] [Google Scholar]
- 8.Bral M, Gala-Lopez B, Bigam D, Kneteman N, Malcolm A, Livingstone S, Andres A, Emamaullee J, Russell L, Coussios C, West LJ, Friend PJ, Shapiro AMJ. Preliminary single‐center Canadian experience of human normothermic ex vivo liver perfusion: results of a clinical trial. Am J Transplant 17: 1071–1080, 2017. doi: 10.1111/ajt.14049. [DOI] [PubMed] [Google Scholar]
- 9.Cypel M, Yeung JC, Hirayama S, Rubacha M, Fischer S, Anraku M, Sato M, Harwood S, Pierre A, Waddell TK, de Perrot M, Liu M, Keshavjee S. Technique for prolonged normothermic ex vivo lung perfusion. J Heart Lung Transplant 27: 1319–1325, 2008. doi: 10.1016/j.healun.2008.09.003. [DOI] [PubMed] [Google Scholar]
- 10.Cypel M, Yeung JC, Liu M, Anraku M, Chen F, Karolak W, Sato M, Laratta J, Azad S, Madonik M, Chow C-W, Chaparro C, Hutcheon M, Singer LG, Slutsky AS, Yasufuku K, de Perrot M, Pierre AF, Waddell TK, Keshavjee S. Normothermic ex vivo lung perfusion in clinical lung transplantation. N Engl J Med 364: 1431–1440, 2011. doi: 10.1056/NEJMoa1014597. [DOI] [PubMed] [Google Scholar]
- 11.Kaths JM, Cen JY, Chun YM, Echeverri J, Linares I, Ganesh S, Yip P, John R, Bagli D, Mucsi I, Ghanekar A, Grant DR, Robinson LA, Selzner M. Continuous normothermic ex vivo kidney perfusion is superior to brief normothermic perfusion following static cold storage in donation after circulatory death pig kidney transplantation. Am J Transplant 17: 957–969, 2017. doi: 10.1111/ajt.14059. [DOI] [PubMed] [Google Scholar]
- 12.Kaths JM, Hamar M, Echeverri J, Linares I, Urbanellis P, Cen JY, Ganesh S, Dingwell LS, Yip P, John R, Bagli D, Mucsi I, Ghanekar A, Grant D, Robinson LA, Selzner M. Normothermic ex vivo kidney perfusion for graft quality assessment prior to transplantation. Am J Transplant 18: 580–589, 2018. doi: 10.1111/ajt.14491. [DOI] [PubMed] [Google Scholar]
- 13.Heikkila P, Parpala T, Lukkarinen O, Weber M, Tryggvason K. Adenovirus-mediated gene transfer into kidney glomeruli using an ex vivo and in vivo kidney perfusion system-first steps towards gene therapy of Alport syndrome. Gene Ther 3: 21–27, 1996. [PubMed] [Google Scholar]
- 14.Nakajima D, Cypel M, Bonato R, Machuca TN, Iskender I, Hashimoto K, Linacre V, Chen M, Coutinho R, Azad S, Martinu T, Waddell TK, Hwang DM, Husain S, Liu M, Keshavjee S. Ex vivo perfusion treatment of infection in human donor lungs. Am J Transplant 16: 1229–1237, 2016. doi: 10.1111/ajt.13562. [DOI] [PubMed] [Google Scholar]
- 15.Tietjen GT, Hosgood SA, DiRito J, Cui J, Deep D, Song E, Kraehling JR, Piotrowski-Daspit AS, Kirkiles-Smith NC, Al-Lamki R, Thiru S, Bradley JA, Saeb-Parsy K, Bradley JR, Nicholson ML, Saltzman WM, Pober JS. Nanoparticle targeting to the endothelium during normothermic machine perfusion of human kidneys. Sci Transl Med 9: eaam6764, 2017. doi: 10.1126/scitranslmed.aam6764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Fung Y. Blood flow in the lung. In: Biomechanics. New York: Springer, 1997, p. 333–445. doi: 10.1007/978-1-4757-2696-1_6. [DOI] [Google Scholar]
- 17.Engler AJ, Raredon MSB, Le AV, Yuan Y, Oczkowicz YA, Kan EL, Baevova P, Niklason LE. Non-invasive and real-time measurement of microvascular barrier in intact lungs. Biomaterials 217: 119313, 2019. doi: 10.1016/j.biomaterials.2019.119313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Aboelnazar NS, Himmat S, Hatami S, White CW, Burhani MS, Dromparis P, Matsumura N, Tian G, Dyck JRB, Mengel M, Freed DH, Nagendran J. Negative pressure ventilation decreases inflammation and lung edema during normothermic ex-vivo lung perfusion. J Heart Lung Transplant 37: 520–530, 2018. doi: 10.1016/j.healun.2017.09.007. [DOI] [PubMed] [Google Scholar]
- 19.O’Neill JD, Guenthart BA, Kim J, Chicotka S, Queen D, Fung K, Marboe C, Romanov A, Huang SXL, Chen Y-W, Snoeck H-W, Bacchetta M, Vunjak-Novakovic G. Cross-circulation for extracorporeal support and recovery of the lung. Nat Biomed Eng 1: 0037, 2017. doi: 10.1038/s41551-017-0037. [DOI] [Google Scholar]
- 20.Valenza F, Rosso L, Pizzocri M, Salice V, Umbrello M, Conte G, Stanzi A, Colombo J, Gatti S, Santambrogio L, Iapichino G, Gattinoni L. The consumption of glucose during ex vivo lung perfusion correlates with lung edema. Transplant Proc 43: 993–996, 2011. doi: 10.1016/j.transproceed.2011.01.122. [DOI] [PubMed] [Google Scholar]
- 21.Fung Y, Sobin S. Theory of sheet flow in lung alveoli. J Appl Physiol 26: 472–488, 1969. doi: 10.1152/jappl.1969.26.4.472. [DOI] [PubMed] [Google Scholar]
- 22.Caduff JH, Fischer LC, Burri PH. Scanning electron microscope study of the developing microvasculature in the postnatal rat lung. Anat Rec 216: 154–164, 1986. doi: 10.1002/ar.1092160207. [DOI] [PubMed] [Google Scholar]
- 23.Fung Y, Sobin S. Pulmonary alveolar blood flow. Circ Res 30: 470–490, 1972. doi: 10.1161/01.res.30.4.470. [DOI] [PubMed] [Google Scholar]
- 24.Sobin SS, Tremer HM, Fung Y. Morphometric basis of the sheet-flow concept of the pulmonary alveolar microcirculation in the cat. Circ Res 26: 397–414, 1970. doi: 10.1161/01.res.26.3.397. [DOI] [PubMed] [Google Scholar]
- 25.Presson RG Jr, Todoran TM, De Witt BJ, McMurtry IF, Wagner WW Jr.. Capillary recruitment and transit time in the rat lung. J Appl Physiol (1985) 83: 543–549, 1997. doi: 10.1152/jappl.1997.83.2.543. [DOI] [PubMed] [Google Scholar]
- 26.Wagner WW Jr, Latham LP, Capen RL. Capillary recruitment during airway hypoxia: role of pulmonary artery pressure. J Appl Physiol Respir Environ Exerc Physiol 47: 383–387, 1979. doi: 10.1152/jappl.1979.47.2.383. [DOI] [PubMed] [Google Scholar]
- 27.Short AC, Montoya ML, Gebb SA, Presson RG Jr, Wagner WW Jr, Capen RL. Pulmonary capillary diameters and recruitment characteristics in subpleural and interior networks. J Appl Physiol (1985) 80: 1568–1573, 1996. doi: 10.1152/jappl.1996.80.5.1568. [DOI] [PubMed] [Google Scholar]
- 28.Tschumperlin DJ, Margulies SS. Alveolar epithelial surface area-volume relationship in isolated rat lungs. J Appl Physiol (1985) 86: 2026–2033, 1999. doi: 10.1152/jappl.1999.86.6.2026. [DOI] [PubMed] [Google Scholar]
- 29.Yen R, Sobin S. Pulmonary blood flow in the cat: correlation between theory and experiment. In: Frontiers in Biomechanics, edited by Schmid-Schönbein GW, Woo SL-Y, Zweifach BW. New York: Springer, 1986, p. 365–376. [Google Scholar]
- 30.Zhuang F, Fung Y, Yen R. Analysis of blood flow in cat's lung with detailed anatomical and elasticity data. J Appl Physiol Respir Environ Exerc Physiol 55: 1341–1348, 1983. doi: 10.1152/jappl.1983.55.4.1341. [DOI] [PubMed] [Google Scholar]
- 31.Dull RO, Mecham I, McJames S. Heparan sulfates mediate pressure-induced increase in lung endothelial hydraulic conductivity via nitric oxide/reactive oxygen species. Am J Physiol Lung Cell Mol Physiol 292: L1452–L1458, 2007. doi: 10.1152/ajplung.00376.2006. [DOI] [PubMed] [Google Scholar]
- 32.Parker JC, Stevens T, Randall J, Weber DS, King JA. Hydraulic conductance of pulmonary microvascular and macrovascular endothelial cell monolayers. Am J Physiol Lung Cell Mol Physiol 291: L30–L37, 2006. doi: 10.1152/ajplung.00317.2005. [DOI] [PubMed] [Google Scholar]
- 33.Ragette R, Fu C, Bhattacharya J. Barrier effects of hyperosmolar signaling in microvascular endothelium of rat lung. J Clin Invest 100: 685–692, 1997. doi: 10.1172/JCI119581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Rumbaut RE, McKay MK, Huxley VH. Capillary hydraulic conductivity is decreased by nitric oxide synthase inhibition. Am J Physiol Heart Circ Physiol 268: H1856–H1861, 1995. doi: 10.1152/ajpheart.1995.268.5.H1856. [DOI] [PubMed] [Google Scholar]
- 35.Tsukada H, Ying X, Fu C, Ishikawa S, McKeown-Longo P, Albelda S, Bhattacharya S, Bray BA, Bhattacharya J. Ligation of endothelial αvβ3 integrin increases capillary hydraulic conductivity of rat lung. Circ Res 77: 651–659, 1995. doi: 10.1161/01.res.77.4.651. [DOI] [PubMed] [Google Scholar]
- 36.Fung Y. Fluid in the interstitial space of the pulmonary alveolar sheet. Microvasc Res 7: 89–113, 1974. doi: 10.1016/0026-2862(74)90040-5. [DOI] [PubMed] [Google Scholar]
- 37.Lee JS. Slow viscous flow in a lung alveoli model. J Biomech 2: 187–198, 1969. doi: 10.1016/0021-9290(69)90030-X. [DOI] [PubMed] [Google Scholar]
- 38.Yen R-T, Fung Y-C. Model experiments on apparent blood viscosity and hematocrit in pulmonary alveoli. J Appl Physiol 35: 510–517, 1973. doi: 10.1152/jappl.1973.35.4.510. [DOI] [PubMed] [Google Scholar]
- 39.Pozrikidis C. Stokes flow through a permeable tube. Arch Appl Mech 80: 323–333, 2010. doi: 10.1007/s00419-009-0319-9. [DOI] [Google Scholar]
- 40.Bacabac RG, Smit TH, Cowin SC, Van Loon JJ, Nieuwstadt FT, Heethaar R, Klein-Nulend J. Dynamic shear stress in parallel-plate flow chambers. J Biomech 38: 159–167, 2005. doi: 10.1016/j.jbiomech.2004.03.020. [DOI] [PubMed] [Google Scholar]
- 41.Glazier J, Hughes J, Maloney J, West J. Measurements of capillary dimensions and blood volume in rapidly frozen lungs. J Appl Physiol 26: 65–76, 1969. doi: 10.1152/jappl.1969.26.1.65. [DOI] [PubMed] [Google Scholar]
- 42.Sobin SS, Fung Y-C, Lindal RG, Tremer HM, Clark L. Topology of pulmonary arterioles, capillaries, and venules in the cat. Microvasc Res 19: 217–233, 1980. doi: 10.1016/0026-2862(80)90042-4. [DOI] [PubMed] [Google Scholar]
- 43.Usami S, Chen H-H, Zhao Y, Chien S, Skalak R. Design and construction of a linear shear stress flow chamber. Ann Biomed Eng 21: 77–83, 1993. doi: 10.1007/BF02368167. [DOI] [PubMed] [Google Scholar]
- 44.Calle EA, Petersen TH, Niklason LE. Procedure for lung engineering. J Vis Exp 49: 2651, 2011. doi: 10.3791/2651. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Calle EA, Hill RC, Leiby KL, Le AV, Gard AL, Madri JA, Hansen KC, Niklason LE. Targeted proteomics effectively quantifies differences between native lung and detergent-decellularized lung extracellular matrices. Acta Biomater 46: 91–100, 2016. doi: 10.1016/j.actbio.2016.09.043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Le AV, Hatachi G, Beloiartsev A, Ghaedi M, Engler AJ, Baevova P, Niklason LE, Calle EA. Efficient and functional endothelial repopulation of whole lung organ scaffolds. ACS Biomater Sci Eng 3: 2000–2010, 2017. doi: 10.1021/acsbiomaterials.6b00784. [DOI] [PubMed] [Google Scholar]
- 47.Kierzenka J, Shampine LF. A BVP solver based on residual control and the Maltab PSE. ACM Trans Math Softw 27: 299–316, 2001. doi: 10.1145/502800.502801. [DOI] [Google Scholar]
- 48.Wu D, Birukov K. Endothelial cell mechano-metabolomic coupling to disease states in the lung microvasculature. Front Bioeng Biotechnol 7: 172, 2019. doi: 10.3389/fbioe.2019.00172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Effros RM, Parker JC. Pulmonary vascular heterogeneity and the Starling hypothesis. Microvasc Res 78: 71–77, 2009. doi: 10.1016/j.mvr.2009.03.004. [DOI] [PubMed] [Google Scholar]
- 50.Gebb S, Stevens T. On lung endothelial cell heterogeneity. Microvasc Res 68: 1–12, 2004. doi: 10.1016/j.mvr.2004.02.002. [DOI] [PubMed] [Google Scholar]
- 51.Ochoa CD, Stevens T. Studies on the cell biology of interendothelial cell gaps. Am J Physiol Lung Cell Mol Physiol 302: L275–L286, 2012. doi: 10.1152/ajplung.00215.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Vaccaro CA, Brody JS. Structural features of alveolar wall basement membrane in the adult rat lung. J Cell Biol 91: 427–437, 1981. doi: 10.1083/jcb.91.2.427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Melo E, Garreta E, Luque T, Cortiella J, Nichols J, Navajas D, Farré R. Effects of the decellularization method on the local stiffness of acellular lungs. Tissue Eng Part C Methods 20: 412–422, 2014. doi: 10.1089/ten.tec.2013.0325. [DOI] [PubMed] [Google Scholar]
- 54.Nonaka PN, Uriarte JJ, Campillo N, Melo E, Navajas D, Farré R, Oliveira LV. Mechanical properties of mouse lungs along organ decellularization by sodium dodecyl sulfate. Respir Physiol Neurobiol 200: 1–5, 2014. doi: 10.1016/j.resp.2014.04.008. [DOI] [PubMed] [Google Scholar]
- 55.Presson RG, Baumgartner WA, Peterson AJ, Glenny RW, Wagner WW. Pulmonary capillaries are recruited during pulsatile flow. J Appl Physiol 92: 1183–1190, 2002. doi: 10.1152/japplphysiol.00845.2001. [DOI] [PubMed] [Google Scholar]
- 56.Hanson WL, Emhardt JD, Bartek JP, Latham LP, Checkley L, Capen R, Wagner W Jr.. Site of recruitment in the pulmonary microcirculation. J Appl Physiol (1985) 66: 2079–2083, 1989. doi: 10.1152/jappl.1989.66.5.2079. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
All raw data, MatLab scripts, model outputs, and R scripts are publicly available on FigShare at the following links:
Raredon, Micha Sam (2020): Supplementary Data 1—Model Constants and Literature Lp.xlsx. figshare. Data set. https://doi.org/10.6084/m9.figshare.12126342.v2.
Raredon, Micha Sam (2020): Supplementary Data 2—Raw Data—Microvascular Flow (Native, Decell, Engineered). figshare. Data set. https://doi.org/10.6084/m9.figshare.12126675.v2.
Raredon, Micha Sam (2021): Supplementary Data 3—MATLAB Model Scripts. figshare. Software. https://doi.org/10.6084/m9.figshare.13583006.v2.
Raredon, Micha Sam (2021): Supplementary Data 4—Model Outputs. figshare. Data set. https://doi.org/10.6084/m9.figshare.13582967.v2.
Raredon, Micha Sam (2020): Supplementary Data 5—R Plotting Scripts. figshare. Software. https://doi.org/10.6084/m9.figshare.12126693.v2.


