Abstract
Purpose:
To develop a deep learning-based method to quantify multiple parameters in the brain from conventional contrast-weighted images.
Methods:
Eighteen subjects were imaged using an MR Multitasking sequence to generate reference T1 and T2 maps in the brain. Conventional contrast-weighted images consisting of T1 MPRAGE, T1 GRE and T2 FLAIR were acquired as input images. A U-Net-based neural network was trained to estimate T1 and T2 maps simultaneously from the contrast-weighted images. 6-fold cross-validation was performed to compare the network outputs with the MR Multitasking references.
Results:
The deep learning T1/T2 maps were comparable with the references, and brain tissue structures and image contrasts were well preserved. Peak signal-to-noise ratio > 32 dB and structural-similarity-index > 0.97 were achieved for both parameter maps. Calculated on brain parenchyma (excluding CSF), the mean absolute errors (and mean percentage errors) for T1 and T2 maps were 52.7 ms (5.1%) and 5.4 ms (7.1%), respectively. ROI measurements on four tissue compartments (cortical gray matter, white matter, putamen, and thalamus) showed that T1 and T2 values provided by the network outputs were in agreement with the MR Multitasking reference maps. The mean differences were smaller than ±1%, and limits of agreement were within ±5% for T1 and within ±10% for T2 after taking the mean differences into account.
Conclusion:
A deep learning-based technique was developed to estimate T1 and T2 maps from conventional contrast-weighted images in the brain, enabling simultaneous qualitative and quantitative MRI without modifying clinical protocols.
Keywords: MR imaging, brain, deep learning, quantitative imaging, multi-parametric mapping
1. Introduction
Quantitative MRI is promising for tissue characterization and detection of various diseases, such as brain tumor1, multiple sclerosis (MS)2-4 and Parkinson’s disease5,6. Compared with conventional contrast-weighted images, quantitative parametric maps have the benefits of improved sensitivity to subtle tissue alterations7 and higher reproducibility8. Traditionally, quantitative MRI acquires multiple sets of images with different time parameters (TI, TE, TR, etc.), from which quantitative tissue parameters are obtained through pixel-wise nonlinear fitting of the desired signal model (e.g., Bloch equations). The prolonged scan time required by this process poses challenges to the wide application of quantitative MRI. Although advanced multi-parametric mapping techniques have been developed for more efficient quantitative MRI, such as MR fingerprinting (MRF)9 and MR Multitasking10, they still require specialized sequences which are not currently part of standardized clinical protocols nor widely available, limiting the clinical availability and impact of quantitative MRI.
In recent years, deep learning (DL) methods have emerged as a powerful tool for various applications in the field of biomedical imaging. For quantitative MRI, DL-based techniques have been developed to extract relaxometry information from various inputs. A number of approaches used end-to-end DL mapping to directly derive parameter maps from undersampled dynamic relaxometry-weighted images or accelerated MRF data.11 Cheng et al12 applied a multilayer perceptron to generate quantitative maps and qualitative weighted images from images acquired by a versatile multi-pathway multi-echo sequence. These methods showed neural networks’ capability to quantify relaxation parameters, but additional specialized acquisitions are still required.
Recently Wu et al13 proposed to estimate T1, proton density, and B1 maps separately from a single T1-weighted image using a self-attention convolutional neural network (CNN) and validated the method in cartilage MRI, demonstrating the feasibility of direct DL-quantification of parametric maps from conventional weighted images used in standard clinical protocols. However, this work was limited to T1 contrast only, lacking the clinically important T2 contrast.
In this study, we trained a CNN to simultaneously quantify multi-parametric maps (T1 and T2 maps) from three contrast-weighted images (T1-MPRAGE, T1-GRE, and T2-FLAIR) that are commonly used in clinical practice. The network was trained to learn the inverse transformation of the Bloch equations (without explicit knowledge of these equations) to extract relaxation parameters from these three contrast-weighted images. With the proposed method, existing clinical imaging protocols can directly produce both qualitative contrast-weighted images and multiple quantitative relaxation parameter maps. Retrospective estimation of parameter maps can also be performed on previously acquired clinical contrast-weighted images. The approach was validated with in vivo brain imaging in MS patients and healthy volunteers.
2. Methods
2.1. Data acquisition
In vivo studies were approved by the institutional review board of Cedars-Sinai Medical Center. All subjects gave written informed consent. Eighteen subjects were scanned on a 3T clinical scanner (Biograph mMR, Siemens Healthineers, Erlangen, Germany), including 9 diagnosed MS patients, 6 suspected MS patients, and 3 healthy volunteers. For each subject, conventional contrast-weighted images were acquired, including T1 MPRAGE, T1 GRE and T2 FLAIR images (T1 MPRAGE: FOV = 256×256×160 mm3, resolution = 1.0×1.0×1.0 mm3, TR = 1900 ms, TI = 900 ms, TE = 2.93 ms, flip angle = 9°; T1 GRE: FOV = 256×256×176 mm3, resolution = 1.0×1.0×1.0 mm3, TR = 7.8 ms, TE = 3.00 ms, flip angle = 18°; T2 FLAIR: FOV = 256×256×176 mm3, resolution = 1.0×1.0×1.0 mm3, TR = 4800 ms, TI = 1800 ms, TE = 352 ms). The reference T1 and T2 maps were obtained using a whole-brain T1-T2-T1ρ MR Multitasking sequence14, with FOV = 240×240×112 mm3, resolution = 1.0×1.0×3.5 mm3. The T1ρ maps generated by MR Multitasking were ignored in this study since there were no corresponding T1ρ-weighted images to use as input.
2.2. Data preprocessing
All the contrast-weighted images and quantitative maps were co-registered using a rigid transformation in ANTsPy15, with T1 MPRAGE as the target. Skull stripping was performed using BET16 and applied for all the images and maps. Contrast-weighted images were normalized by dividing by the 95th percentile of intensity within the brain region slice by slice. Quantitative maps were normalized by dividing by 3 s; most brain tissues have T1 and T2 values < 3 s17,18, so this normalization ensured that most voxels were in the range of 0–1, a common range for neural networks12. After excluding extreme superior or inferior slices with low SNR or aliasing artifacts due to imperfect slab profile, 75-110 slices were available for each subject and a total of 1802 slices for the whole dataset.
2.3. Training the DL model
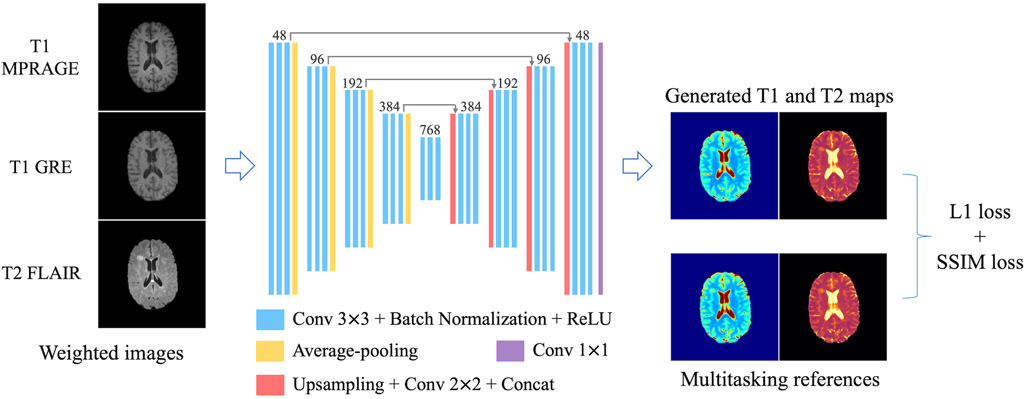
After testing several network architectures, a 2D U-Net19-based structure was selected as the DL model. The specific architecture design is shown in Figure 1. It had four down-sampling steps and four up-sampling steps to extract information from different scales. 2×2 average pooling was used in the down-sampling track and accordingly a bilinear interpolation-based up-sampling layer followed by 2×2 convolution in the up-sampling track. Three convolutional groups (i.e., 3×3 convolution + batch normalization + rectified linear unit) were sequentially applied to extract features at each spatial scale. Long skip connections were added to recover fine-grained details in the up-sampling track. Slices of the three conventional contrasts (i.e., T1 MPRAGE, T1 GRE and T2 FLAIR) were concatenated as the 3-channel input. Slices of T1 and T2 maps formed the 2-channel target.
FIGURE 1.
Network design. A 2D U-Net-based architecture with four down-sampling steps and four up-sampling steps was used. 2×2 average pooling layers were used in the down-sampling track. Bilinear interpolation-based up-sampling layers followed by 2×2 convolution were used in the up-sampling track. At each resolution scale, 3 convolutional groups were sequentially applied, each consisting of 3×3 convolution followed by batch normalization and rectified linear unit (ReLU). Long skip connections were added to recover fine details in the up-sampling track. Slices of the three conventional weighted images (i.e., T1 MPRAGE, T1 GRE and T2 FLAIR) were concatenated as the 3-channel input. Slices of T1 and T2 maps formed the 2-channel target. A combination of L1 loss and SSIM loss was used as the loss function.
The loss function was a combination of L1 loss and structural-similarity-index (SSIM) loss: Ltotal = L1 + λLSSIM. Compared with L2 loss, L1 loss is more robust to artifacts, noise and misregistration errors. The introduction of SSIM loss helps to preserve local structures and generate less-blurred results. The weighting factor λ was empirically determined to be 0.1, which achieved a good balance between mean absolute error and sharpness.
The ADAM optimizer20 was used to minimize the loss function. A learning rate of 0.0001 was used for the first 300 epochs and then exponentially decayed with a rate of exp(−0.02) for the following 200 epochs. Patch-based training was used, with a patch size of 160×128 and batch size of 16. Random cropping and flipping were employed for data augmentation. We implemented the models in Tensorflow21 and trained them from scratch on a Linux workstation with an Nvidia GTX 1080 TI GPU. It took 3.7 hours to train for 500 epochs on a dataset with about 1500 slices. Once the network has been trained, making predictions on 1 subject (100 slices) took about 1.6 seconds.
2.4. Performance evaluation and statistical analysis
6-fold cross-validation was implemented to evaluate the performance of the proposed DL method. Specifically, the 18 subjects were divided into 6 groups, each with 3 subjects, resulting in 276-317 slices within each group. At each time, 5 groups were used to train the model and the remaining one group was used for validation. The quantitative analysis was performed using the results from all the subjects.
Mean absolute error (MAE), mean percentage error (MPE), peak signal-to-noise ratio (PSNR) and SSIM were calculated for each slice between the deep learning T1/T2 maps and the reference T1/T2 maps obtained from MR Multitasking. Because cerebrospinal fluid (CSF) has much larger T1/T2 values than the other parts of the brain and is of little interest to clinical diagnosis, the metrics were also calculated excluding CSF regions. More specifically, to reduce the impact of segmentation error and partial volume effects, image dilation with a spherical structuring element of 1-pixel radius was performed on the CSF segmentation obtained using FAST22, and the remaining region of the brain was evaluated in this calculation.
In addition to global analysis of the deep learning T1/T2 maps, regions of interest (ROIs) analyses were also performed on four brain tissue compartments: cortical gray matter (GM), white matter (WM), putamen and thalamus. ROIs for putamen and thalamus were manually drawn on a slice at similar locations for all the subjects. For these two compartments, two ROIs were drawn on the left and right sides, respectively, which were combined to calculate mean T1/T2 values. For GM and WM, twenty slices centered at a fixed distance (25 mm) apart from the slice where the putamen/thalamus ROIs locate were picked. GM and WM segmentations were obtained using FAST22. Similar to the previously mentioned operation on CSF masks, image erosion with a spherical structuring element of 1-pixel radius was performed on the segmentations to get cleaner GM/WM ROIs. For either GM or WM, the eroded segmentations across the twenty slices were combined, resulting in one ROI for each subject.
For each tissue compartment of each subject, the mean T1/T2 values were calculated over the corresponding ROI and comparisons were made between the network outputs and the MR Multitasking references. Paired t-tests with a significance level of P = 0.05 were performed to evaluate the difference between the DL maps and the references. Bland-Altman analysis was also performed to evaluate the bias and limits of agreement.
To investigate how the network’s performance depends on the input contrasts, we also trained the network using only subsets of the weighted input images and quantitative metrics were calculated.
3. Results
3.1. Image Analysis
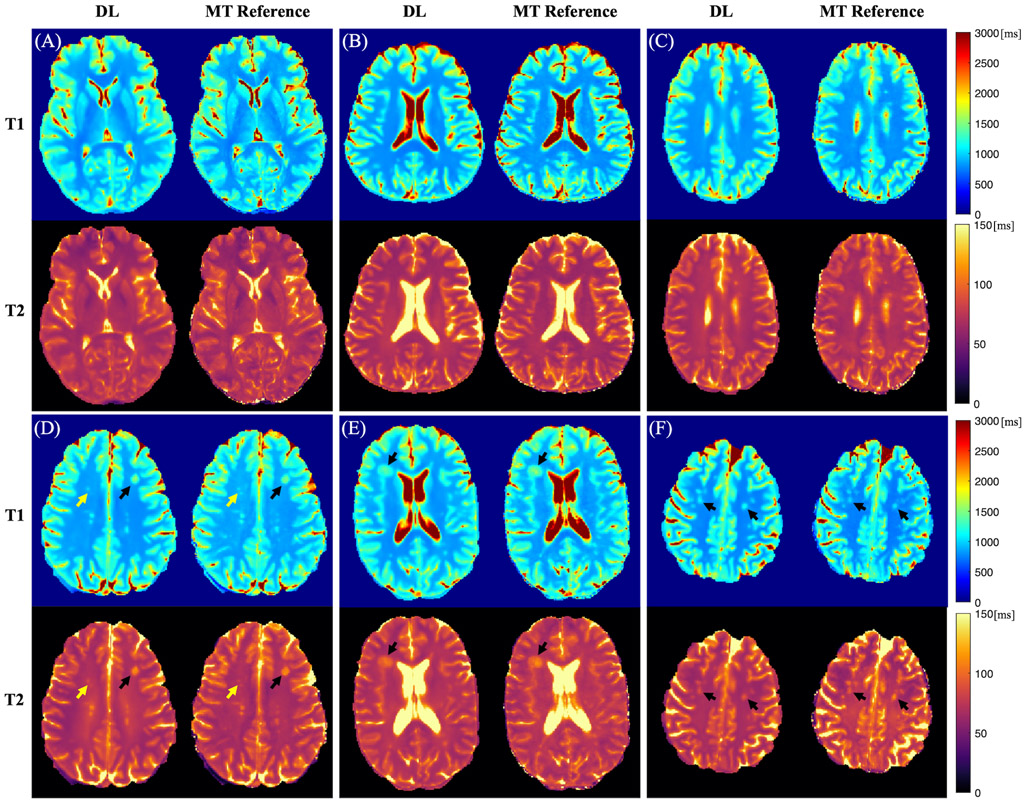
Representative cases of the deep learning T1 and T2 maps from MS patients are shown in Figure 2. The deep learning maps showed high quality and were comparable with the MR Multitasking references. Although some blurring was observed, most of the brain tissue structure and contrasts were well preserved. Figure 2 (D)-(F) show representative cases with hyperintense lesions. Deep learning T1 and T2 maps were able to delineate these lesions. However, for some cases, slight overestimation or underestimation of T1/T2 values of lesions was observed on the network outputs (Figure 2 (F)).
FIGURE 2.
Representative cases of the deep learning (DL) T1/T2 maps and the MR Multitasking (MT) references from 6 different MS patients (A-F). The black arrows show hyperintense lesions. The yellow arrows indicate some small white matter hyperintensities affected by the blurring.
Table 1 lists the quantitative metrics obtained from the 6-fold cross-validation. High PSNR (32.5 dB and 37.1 dB for T1 and T2, respectively) and SSIM (0.973 and 0.978 for T1 and T2, respectively) were achieved. The MAE (and the MPE) for T1 and T2 maps were 120.3 ms (8.6%) and 21.5 ms (13.0%), respectively. Excluding CSF, the MAE (and the MPE) for T1 and T2 maps were 52.7 ms (5.1%) and 5.4 ms (7.1%), respectively, indicating that CSF made a large contribution to the error metrics.
TABLE 1.
Quantitative metrics for the deep learning T1/T2 maps.
| Full brain region | Excluding CSF | ||
|---|---|---|---|
| MAE (ms) | T1 | 120.3±26.3 | 52.7±11.5 |
| T2 | 21.5±15.2 | 5.4±1.8 | |
| MPE (%) | T1 | 8.6±1.5 | 5.1±1.0 |
| T2 | 13.0±4.5 | 7.1±2.6 | |
| PSNR (dB) | T1 | 32.5±1.9 | 38.4±2.8 |
| T2 | 37.1±3.2 | 38.7±4.4 | |
| SSIM | T1 | 0.973±0.009 | 0.992±0.004 |
| T2 | 0.978±0.011 | 0.991±0.005 |
MAE: mean absolute error, MPE: mean percentage error, PSNR: peak signal-to-noise ratio, SSIM: structural-similarity-index.
The network’s performance using only a subset of the weighted input images is shown in the Supporting Information. Larger errors were observed when fewer input contrasts were used (Supporting Information Tables S1, S2). The inclusion of T2 FLAIR improved the delineation of lesions (Supporting Information Figures S1, S2).
3.2. T1/T2 measurements
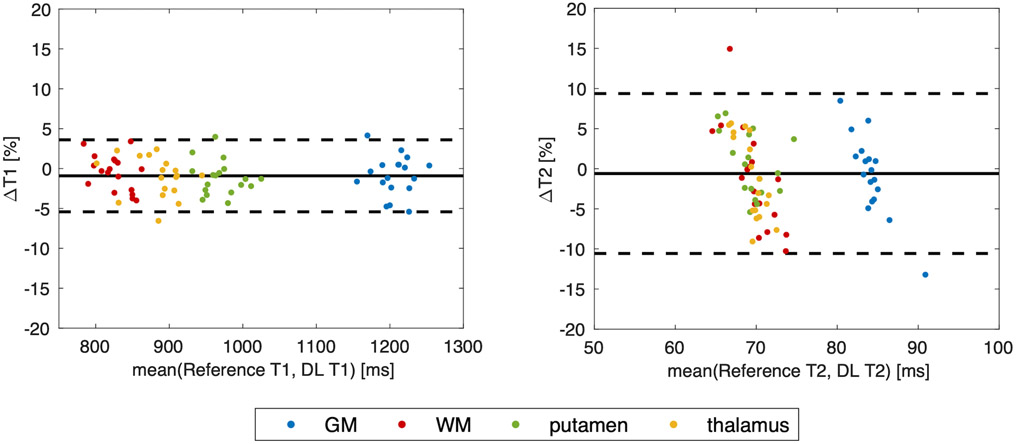
The T1 and T2 measurements obtained on the four tissue compartments for the deep learning maps and the MR Multitasking reference are listed in Table 2. A statistically significant bias between the network output and the MR Multitasking reference was found only for T1 in the putamen (P=0.027). For this compartment, a small bias of 11.6 ms (i.e., 1.2% of the reference value) was observed. No other significant differences were observed for the T1 values of the other three tissue types (i.e., GM, WM and thalamus) or for the T2 values of any of the four tissue compartments. Figure 3 shows the Bland-Altman plots for combined T1 and T2 measurements of all the tissues. The mean differences were smaller than ±1%, and limits of agreement were within ±5% for T1 and within ±10% for T2 after taking the mean differences into account.
TABLE 2.
T1/T2 ROI measurements on the four tissue compartments from the network outputs and the MR Multitasking references. P values obtained from the paired t-tests are also listed. The asterisk indicates a statistically significant difference (i.e., P<0.05).
| DL | MT reference | P value | ||
|---|---|---|---|---|
| T1 (ms) | GM | 1199.8±27.0 | 1210.7±32.9 | 0.14 |
| WM | 823.5±20.8 | 823.3±30.0 | 0.32 | |
| putamen | 964.4±25.7 | 976.0±29.3 | 0.027* | |
| thalamus | 879.4±32.8 | 888.9±38.0 | 0.084 | |
| T2 (ms) | GM | 83.8±1.0 | 84.7±3.9 | 0.51 |
| WM | 69.3±1.5 | 69.9±4.2 | 0.39 | |
| putamen | 69.5±2.2 | 69.2±3.2 | 0.64 | |
| thalamus | 69.0±1.1 | 69.8±3.1 | 0.36 |
FIGURE 3.
Bland-Altman plots for T1/T2 measurements on the four types of tissues. Each color represents one tissue compartment.
4. Discussion
In this study, a deep learning-based approach was developed to quantify T1 and T2 maps from conventional contrast-weighted images. This method allows the simultaneous acquisition of qualitative contrast-weighted images and quantitative parametric maps with a conventional clinical imaging protocol. The method was validated on in vivo brain data from healthy volunteers and confirmed/suspected MS patients. Global error metrics for image quality evaluation as well as T1/T2 ROI analyses on different brain tissues demonstrate that the proposed method provided T1 and T2 maps comparable with the reference.
Our results show that the proposed method achieved excellent accuracy on T1 and T2 maps when CSF regions were excluded. When CSF was included, both mean absolute error and mean percentage error were increased. There are several possible reasons. First, CSF T2 error was expected because CSF signals were nulled on T2 FLAIR, resulting in low SNR for T2 information in CSF. Second, the reference MR Multitasking method was designed for mapping soft tissues with shorter T1 and T2 values than CSF, so the label values for CSF from MR Multitasking may already be inaccurate or imprecise, potentially posing an additional challenge for network prediction. We consider the substandard calculation of CSF values of only minor concern in potential clinical applications, as the T1/T2 values of CSF region are of little clinical value in diagnosis and prognosis.
The T1/T2 ROI measurements on the four types of tissues showed that our network outputs generally provided T1/T2 values in agreement with the MR Multitasking reference, with no statistically significant difference observed in 7 out of the 8 paired t-tests and very small biases (<1%) in the overall Bland-Altman analyses. The statistical tests showed a significant difference in T1 measurements of putamen between the network outputs and the references. Despite the statistical significance, the measured mean difference was small, which was 1.2% of the reference value. This small bias could potentially result from factors such as the partial volume effect and the blurring effect observed on the DL results, but further investigation with a larger dataset is desirable to make any conclusions regarding this issue.
In the evaluation, we primarily focused on the proposed method’s capability to estimate the overall T1 and T2 maps on soft brain tissues. In addition, in Figure 2 (D)-(F), we also presented some example cases of the lesions on the DL maps. While generally the lesions were preserved in the DL maps, for some cases overestimation or underestimation may be present. Compared with the normal-appearing brain tissue, estimation on the lesions is more vulnerable to factors like misregistration errors, mismatching resolution between the source and target images, deficiency of diversity of subjects included in the dataset, and the blurring effects commonly presented in DL methods. Evaluation of performance on lesions requires more careful clinical labeling and scoring of the maps, which will be investigated in our future work.
In this study, a U-Net-based architecture was selected for deep learning. In the results, certain blurring in the deep learning T1/T2 maps was observed. To make improvements on this, with a larger dataset in the future, we will explore some more complex network architectures and modules, such as generative adversarial network (GAN)23 and networks equipped with attention mechanisms24, which have been shown to be better at preserving high-frequency details.
MR Multitasking was employed to acquire reference T1/T2 maps in this work due to time constraints in patient studies. The whole-brain T1-T2-T1ρ MR Multitasking took 9 min to acquire multi-parametric maps with high quality and accuracy as previously validated,14 while traditional quantification methods require much longer scan time (e.g., about 17 min). Also, MR Multitasking provides inherently co-registered T1 and T2 maps, which avoids errors in additional registration and requires less label preprocessing. The Multitasking-trained network serves as a proof of concept of our approach; however, the network could also be trained using reference maps provided by other quantification methods if desired, such as conventional mapping or MRF.
There are several limitations in this study. First, due to the imaging time limit, our MR Multitasking maps had a 3.5 mm slice thickness, which did not match that of the conventional weighted images (1.0 mm) used in the source domain. With the acceleration of MR Multitasking imaging underway, we plan to collect datasets with matched spatial resolution in the future. Also, in this work our dataset consisted of 1802 slices from only 18 subjects, including MS patients and healthy volunteers. We performed cross-validation to reduce the impact of dataset splitting on the results. A larger dataset with a more diverse cohort would be preferable to further validate the approach. Furthermore, this work was trained on input images acquired with specific imaging parameters (e.g., TE, TR). To use images with different parameters as inputs, the network may require retraining. An alternative solution to enhance generalizability is to incorporate imaging parameters as additional inputs to the network, which will be explored in future work. Finally, although examples of lesion detection are presented, a systematic evaluation of the approach for disease diagnosis needs to be conducted.
5. Conclusions
A CNN-based technique was developed to quantify both T1 and T2 maps directly from conventional multiple contrast-weighted images acquired in clinical practice. The deep learning T1/T2 maps preserved the brain tissue structures and image contrasts well, produced satisfactory error metrics, and provided T1/T2 measurements in agreement with the references. The proposed method provides both qualitative and quantitative MRI without modifications to standard clinical imaging protocols. A clinical study is warranted to evaluate the diagnostic value of this approach.
Supplementary Material
Supporting Information Table S1. Quantitative metrics for deep learning T1 maps when the networks were retrained with different input contrasts.
Supporting Information Table S2. Quantitative metrics for deep learning T2 maps when the networks were retrained with different input contrasts.
Supporting Information Figure S1. An example case of the deep learning T1 maps when the networks were retrained with different input contrasts. The arrows show a lesion. (M: T1 MPRAGE, G: T1 GRE, F: T2 FLAIR.)
Supporting Information Figure S2. An example case of the deep learning T2 maps when the networks were retrained with different input contrasts. The arrows show a lesion. The inclusion of T2 FLAIR in the input made the lesion better delineated in the generated T2 map. (M: T1 MPRAGE, G: T1 GRE, F: T2 FLAIR.)
ACKNOWLEDGEMENTS
This work was supported by NIH R01EB028146. We acknowledge Nancy L. Sicotte and Marwa Kaisey for patient recruitment.
REFERENCES
- 1.Lescher S, Jurcoane A, Veit A, Bahr O, Deichmann R, Hattingen E. Quantitative T1 and T2 mapping in recurrent glioblastomas under bevacizumab: Earlier detection of tumor progression compared to conventional MRI. Neuroradiology. 2015;57:11–20. [DOI] [PubMed] [Google Scholar]
- 2.Blystad I, Haåkansson I, Tisell A, et al. Quantitative MRI for analysis of active multiple sclerosis lesions without gadolinium-based contrast agent. AJNR Am J Neuroradiol. 2016;37:94–100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Gracien RM, Reitz SC, Hof SM, et al. Changes and variability of proton density and T1 relaxation times in early multiple sclerosis: MRI markers of neuronal damage in the cerebral cortex. Eur Radiol. 2016;26(8):2578–2586. [DOI] [PubMed] [Google Scholar]
- 4.Reitz SC, Hof SM, Fleischer V, et al. Multi-parametric quantitative MRI of normal appearing white matter in multiple sclerosis, and the effect of disease activity on T2. Brain Imaging Behav. 2017;11(3):744–753. [DOI] [PubMed] [Google Scholar]
- 5.Baudrexel S, Nuürnberger L, Ruüb U, et al. Quantitative mapping of T1 and T2* discloses nigral and brainstem pathology in early Parkinson's disease. Neuroimage. 2010;51:512–520. [DOI] [PubMed] [Google Scholar]
- 6.Nurnberger L, Gracien RM, Hok P, et al. Longitudinal changes of cortical microstructure in Parkinson's disease assessed with T1 relaxometry. Neuroimage Clin. 2017;13:405–414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Cheng HLM, Stikov N, Ghugre NR, Wright GA. Practical medical applications of quantitative MR relaxometry. J Magn Reson Imaging. 2012;36:805–824. 10.1002/jmri.23718. [DOI] [PubMed] [Google Scholar]
- 8.Roujol S, Weingaärtner S, Foppa M, Chow K, Kawaji K, Ngo LH, et al. Accuracy, precision, and reproducibility of four T1 mapping sequences: a head-to-head comparison of MOLLI, ShMOLLI, SASHA, and SAPPHIRE. Radiology. 2014. September;272(3):683–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Ma D, Gulani V, Seiberlich N, et al. Magnetic resonance fingerprinting. Nature. 2013;495:187–192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Christodoulou AG, Shaw JL, Nguyen C, Yang Q, Xie Y, Wang N, et al. Magnetic resonance multitasking for motion-resolved quantitative cardiovascular imaging. Nat Biomed Eng. 2018;2(4):215–226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Feng L, Ma D, Liu F. Rapid MR relaxometry using deep learning: An overview of current techniques and emerging trends. NMR in Biomedicine. 2020;e4416. doi: 10.1002/nbm.4416. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Cheng CC, Preiswerk F, Madore B. Multi-pathway multi-echo acquisition and neural contrast translation to generate a variety of quantitative and qualitative image contrasts. Magn Reson Med. 2020;83(6):2310–2321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Wu Y, Ma YJ, Du J, Xing L. Deciphering tissue relaxation parameters from a single MR image using deep learning. In Proceedings of SPIE. 2020;11314. [Google Scholar]
- 14.Ma S, Wang N, Fan Z, et al. Three-dimensional whole-brain simultaneous T1, T2, and T1ρ quantification using MR Multitasking: Method and initial clinical experience in tissue characterization of multiple sclerosis. Magn Reson Med. 2021;85:1938–1952. doi: 10.1002/mrm.28553. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Avants BB, Tustison N, Song G. Advanced normalization tools (ANTS). Insight j. 2009;2(365):1–35. [Google Scholar]
- 16.Smith SM. Fast robust automated brain extraction. Hum Brain Mapp. 2002;17(3):143–155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Wansapura JP, Holland SK, Dunn RS, Ball WS. NMR relaxation times in the human brain at 3.0 tesla. J Magn Reson Im. 1999;9(4):531–538. [DOI] [PubMed] [Google Scholar]
- 18.Bojorquez JZ, Bricq S, Acquitter C, Brunotte F, Walker PM, Lalande A. What are normal relaxation times of tissues at 3 T? Magn Reson Imaging. 2017;35:69–80. [DOI] [PubMed] [Google Scholar]
- 19.Ronneberger O, Fischer P, Brox T. U-Net: convolutional networks for biomedical image segmentation. In Proceedings of Medical Image Computing and Computer-Assisted Intervention. Vol. 9351. Berlin, Germany: Springer; 2015. p. 234–241. [Google Scholar]
- 20.Kingma DP, Ba J. Adam: a method for stochastic optimization. In Proceedings of the International Conference on Learning Representations (ICLR), Banff, Canada, 2014. p. 1–15. [Google Scholar]
- 21.Abadi M TensorFlow: Learning Functions at Scale. Acm Sigplan Notices. 2016;51(9):1–1. [Google Scholar]
- 22.Zhang YY, Brady M, Smith S. Segmentation of brain MR images through a hidden Markov random field model and the expectation-maximization algorithm. IEEE Trans Med Imaging. 2001;20(1):45–57. [DOI] [PubMed] [Google Scholar]
- 23.Isola P, Zhu JY, Zhou TH, Efros AA. Image-to-Image Translation with Conditional Adversarial Networks. In Proceedings of the IEEE conference on computer vision and pattern recognition. 2017:5967–5976. [Google Scholar]
- 24.Vaswani A, Shazeer N, Parmar N, et al. Attention Is All You Need. Adv Neur In. 2017;30. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Information Table S1. Quantitative metrics for deep learning T1 maps when the networks were retrained with different input contrasts.
Supporting Information Table S2. Quantitative metrics for deep learning T2 maps when the networks were retrained with different input contrasts.
Supporting Information Figure S1. An example case of the deep learning T1 maps when the networks were retrained with different input contrasts. The arrows show a lesion. (M: T1 MPRAGE, G: T1 GRE, F: T2 FLAIR.)
Supporting Information Figure S2. An example case of the deep learning T2 maps when the networks were retrained with different input contrasts. The arrows show a lesion. The inclusion of T2 FLAIR in the input made the lesion better delineated in the generated T2 map. (M: T1 MPRAGE, G: T1 GRE, F: T2 FLAIR.)