Physics-Based Protein Structure Refinement in the Era of Artificial Intelligence

Abstract

Protein structure refinement is the last step in protein structure prediction pipelines. Physics-based refinement via molecular dynamics (MD) simulations has made significant progress during recent years. During CASP14, we tested a new refinement protocol based on an improved sampling strategy via MD simulations. MD simulations were carried out at an elevated temperature (360 K). An optimized use of biasing restraints and the use of multiple starting models led to enhanced sampling. The new protocol generally improved the model quality. In comparison with our previous protocols, the CASP14 protocol showed clear improvements. Our approach was successful with most initial models, many based on deep learning methods. However, we found that our approach was not able to refine machine-learning models from the AlphaFold2 group, often decreasing already high initial qualities. To better understand the role of refinement given new types of models based on machine-learning, a detailed analysis via MD simulations and Markov state modeling is presented here. We continue to find that MD-based refinement has the potential to improve AI predictions. We also identified several practical issues that make it difficult to realize that potential. Increasingly important is the consideration of inter-domain and oligomeric contacts in simulations; the presence of large kinetic barriers in refinement pathways also continues to present challenges. Finally, we provide a perspective on how physics-based refinement could continue to play a role in the future for improving initial predictions based on machine learning-based methods.

INTRODUCTION

Knowledge about protein structures is a key step for understanding the biological function of proteins at the molecular level. There have been numerous efforts to predict protein structure in atomistic detail using in silico methods.^1,2 Template-based modeling became the first successful approach with the growth of protein structure databases by relying on homologous protein structures.³ In the meantime, the number of protein sequences has exploded as sequencing techniques advanced.⁴ This progress enabled the identification of co-evolutionary relationships between residues from multiple sequence alignments of protein homologs.⁵ At the beginning co-evolutionary information was most helpful for proteins for which abundant homologous sequences could be found.^6–8 However, with the emergence of the deep neural networks and extensive training on existing sequence and structure databases, it became possible to extract co-evolutionary information from much fewer closely related homologous sequences and reliably predict inter-residue geometries.^9–13 The predicted geometries were then sufficient to build high-accuracy protein structures via protein modeling tools such as Rosetta.¹² This approach has now been adopted by many protein structure prediction servers as an independent protocol or as a hybrid protocol in combination with traditional template-based modeling. Recently, a new deep learning-based method, AlphaFold2 (AF2) from DeepMind, was proposed during the CASP14 experiment. The method is designed to directly predict a protein tertiary structure from its sequence or multiple sequence alignment, rather than building a protein model using predicted inter-residue geometries via protein modeling tools. This advance led to substantial progress over previous approaches with many predictions reaching quasi-experimental accuracy.

Protein model refinement methods have been developed to improve the quality of predicted protein models further.^14,15 Structure refinement is usually based on orthogonal approaches to initial protein structure prediction methods. More specifically, physics-based methods have been successful for improving protein models that were built initially via information-driven modeling methods.^16–19 A good template-based model often has the highest accuracy at its core where structure is more conserved among proteins in a homologous relationship. On the other hand, template-based modeling is not as well suited for accurately predicting regions of a protein where there is greater structural variation within a protein family such as loops. Ab initio protein loop modeling methods are helpful for improving the model quality at these regions by predicting structures based on physical chemistry principles.^20,21 However, template-based modeling methods have also increasingly been applied to predict correctly folded structures using remote homologs. Such models predicted using structure templates with low sequence identities may display greater inaccuracies throughout the entire structure. For example, residue packing may be incorrect, or the orientation and extent of secondary structure elements may deviate from the true native structure, thus requiring more extensive structure refinement. Molecular dynamics (MD) simulation-based refinement methods have successfully addressed such problems.^22,23 The idea is that simulations started from an incorrect model will fold to a physically more reasonable, lower free energy, structure under the guidance of a force field. In addition, MD simulations generate dynamic ensembles of low-energy snapshots that can be averaged to better approximate how experimental structures are determined. MD simulation-based refinement methods have become successful for consistently improving model qualities although full refinement to a native-like structure is not always achieved. The main limitation is the presence of significant kinetic energy barriers that have to be overcome on a relatively flat energy landscape via conformational sampling to reach the native state from an initially misfolded model.^24,25 Another issue is that even if sampling is sufficient, e.g., by using accelerated sampling techniques, it may be just as likely or easier to further unfold an initially misfolded structure than to find conformational transitions that lead to the native state. This has resulted in the need for restraints during sampling that have to be chosen such that unfolding is prevented yet the native state can still be reached.²⁶

Carefully tuned MD-based refinement sampling protocols are now expected to consistently improve the accuracy of initial models generated by other approaches.²⁷ In general, residue packing is improved via refinement and incorrect secondary structure elements may be adjusted. Typical model refinement now results in improvements in both global and local quality metrics by several units. In some cases, more substantial improvements have been documented. Refinement methods have remained relevant as ML-based models emerged in recent years. In fact, initial tests suggested that there may be more success in refining ML-based models than traditional template-based models via physics-based methods, presumably since the data-driven residue-level predictions resulted in poor structure packing that could be improved relatively easily via MD-based refinement.^24,28 However, the emergence of a new class of ML-based predictions with much greater accuracy during the last round of CASP is posing renewed challenges to the need and utility of refinement methods. At the same time, there have also been attempts to use deep learning techniques to guide refinement, such as the DeepAccNet method²⁹.

Here, we are reviewing the performance of physics-based protein structure refinement via MD simulations in the face of changing approaches in ML-based protein structure prediction. The focus is on the performance of the refinement methods from the Feig group during CASP14. The results are analyzed in the context of advances over earlier methods, continuing challenges, and opportunities for further improvements. A particular emphasis is placed on the potential for refinement of a new class of ML-based predictions as exemplified by the highly accurate AF2 predictions during CASP14. To address this point, we are including an in-depth analysis of selected targets where we constructed Markov state models from extensive sampling following an approach taken earlier²⁵. The goal was to map out the energy landscape between initial models and native states and address the key questions of whether the native state according to experiment could be found in principle based on energetics, how the AF2 models mapped onto the MD-generated landscapes, and what kind of kinetic barriers needed to be overcome to reach the native state. The insights from this analysis allowed us to better understand the future role of MD-based refinement and identify remaining challenges towards high-accuracy structure prediction going forward.

METHODS

Overview of refinement protocol

The overall refinement protocol used in CASP14 consisted of three major components as illustrated in Figure 1A. For an initial model, information about its protein contexts was gathered to construct a simulation system. The oligomeric state, putative binding ligands, and the possibility of membrane interactions were predicted manually based on its homologous structures searched by HHsearch³⁰. To limit computational cost, the predicted oligomer structure was only considered in cases where the oligomerization appeared to be crucial for its structure stabilization. We regarded an oligomerization to be important for stabilization if some residues had little contacts within the protein but extensive interactions with other proteins in the predicted complex structure. For a homo-oligomeric complex, the initial model was replicated and superposed to each chain in the homologous complex to construct a homo-oligomeric initial model. For a hetero-oligomeric complex, bound protein structures in the homologous complex were used. Putative bound ligands and their binding sites were inferred based on homologous structures.²⁴ Stereochemical errors were corrected prior to the equilibration of the simulation system by applying locPREFMD³¹.

Figure 1.

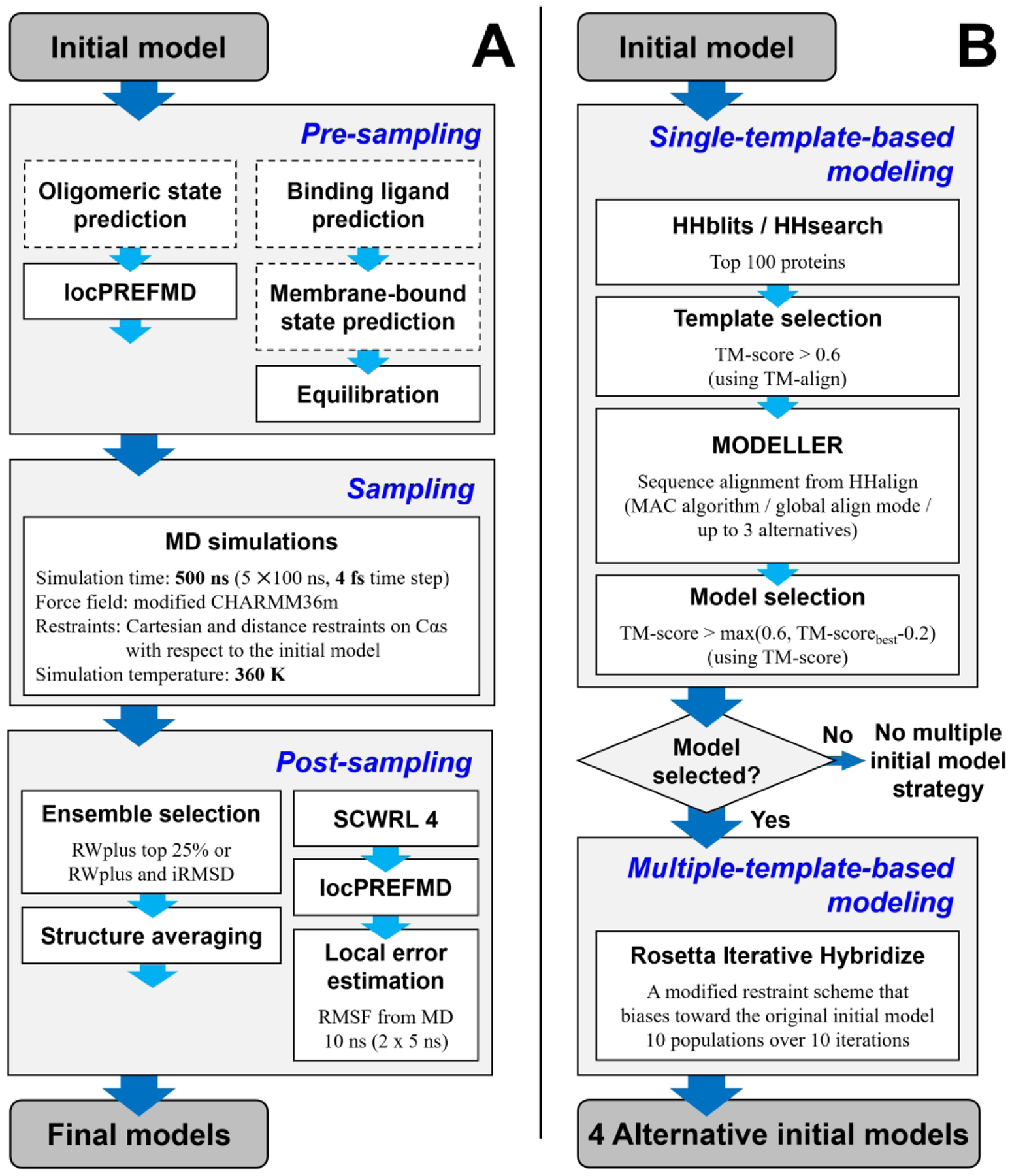
Overview of the refinement protocol used during CASP14. The standard refinement protocol for a single initial model (A). Steps that were manually performed are shown in dashed boxes. Multiple alternative initial model building procedure (B).

Simulation systems for non-membrane-bound proteins were constructed in an explicit water box. The principal component axes of the modeling protein were aligned to the X, Y, and Z axes. A periodic rectangular box was constructed with a minimal distance from any protein atom to the closest box edge of 9 Å. Empty spaces in the box were filled with the CHARMM version of TIP3P water molecules³². Either sodium or chloride ions replaced randomly selected water molecules to neutralize the simulation system. The protein was described with a modified CHARMM 36m force field³³. When ligands were included, they were modeled using CGenFF^34,35. Lennard-Jones and direct electrostatic interactions were turned off between 8 and 10 Å using a switching function. To calculate the full electrostatic energy in a periodic system, particle-mesh Ewald summation³⁶ was used. The SHAKE algorithm³⁷ was applied to keep bonds involving hydrogen atoms rigid. In addition, the protein structure was restrained throughout the equilibration step with harmonic restraints that were applied to every Cɑ atoms with a force constant of 0.5 kcal/mol/Ų. The constructed systems were then locally minimized for up to 500 steps with the l-BFGS-b algorithm. The energy-minimized system was gradually heated to 360 K and equilibrated via Langevin dynamics simulation with a friction coefficient of 0.01/ps for 1 ns using a 2 fs integration time step. The NVT ensemble was applied during the heating stage followed by simulations in the NpT ensemble at 1 bar with a Monte Carlo barostat. Proteins predicted to be membrane-bound were modeled in a lipid bilayer consisting of POPC (1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine) using CHARMM-GUI.³⁸ Membrane-bound protein systems were equilibrated like non-membrane protein systems. The CHARMM 36 lipid force field³⁹ was used for the POPC molecules.

Protein conformations were sampled via molecular dynamics simulations. The sampling step utilized our recent improved sampling strategy for protein model refinement. Langevin dynamics simulations were carried out at 360 K in the NVT ensemble starting from the equilibrated system. Five independent replicas of simulations were conducted for 100 ns, and simulation snapshots were recorded at every 50 ps. Hydrogen mass repartitioning⁴⁰ was used to allow simulations with a 4 fs integration time step along with the SHAKE algorithm³⁷. To focus sampling on the vicinity of the initial structure and prevent it from unfolding, restraints were applied on every Cɑ atoms in the functional form of Eq. 1. Restraints were gradually switched from Cartesian restraints (Eq. 2) to distance restraints (Eq. 3) throughout the simulation by changing λ from 0 to 1. The Cartesian restraints biased every Cɑ atoms to their Cartesian coordinates. For the Cartesian restraint parameters, we used k₀ = 0.025 kcal/mol/Ų and b_flat = 4 Å. The distance restraints were applied to Cɑ atom pairs that had distances below 10 Å in the initial model and separated by four or more residues. For distance restraints, we used k₀ = 0.05 kcal/mol/Ų and b_flat = 2 Å.

$$E_{\text{combined}}(\lambda )=(1-\lambda ){\sum }_i{E}_{\text{Cartesian}}\left(r_i;r_i^0\right)+\lambda {\sum }_{j-i\ge 3}{E}_{\text{distance}}\left(d_{ij};d_{ij}^0\right)$$ (1)

$$E_{\text{Cartesian}}\left(r_i;r_i^0\right)=k_{0}max{\left(0,\left|r_i-r_i^0\right|-b_{\mathit{\text{flat}}}\right)}^2$$ (2)

$$E_{\text{distance}}\left(d_{ij};d_{ij}^0\right)=k_{0}max{\left(0,|d_{ij}-d_{ij}^0|-b_{\mathit{\text{flat}}}\right)}^2$$ (3)

Restraints were based on a flat-bottom harmonic function to allow transitions between conformational states via “restraint-free” regions. The use of both restraint types allowed more diverse sampling than either one restraint type.²⁷

The sampled conformations were subsequently processed to generate a refined model. Simulation snapshots were initially scored using RWplus.⁴¹ A subset of structures was then selected for the further structure averaging. We used slightly different ensemble selection methods depending on the number of initial model structures. When a single initial model was used for the sampling, the 25% lowest-scoring structures were selected.²⁷ The deviation from the original initial model was additionally considered for selection^23,42 when multiple initial models were used for the sampling. The selected structures were superimposed onto the initial model and averaged based on Cartesian coordinates. To finish, the stereochemical quality of the averaged structure was improved via local relaxation by short MD simulation, sidechain rebuilding using SCWRL4⁴³, and the application of locPREFMD.³¹ Sidechain rebuilding was added over our previous CASP13 protocol to improve sidechain packing and increase lDDT scores. Finally, residue-wise errors were estimated from root mean square fluctuations (RMSF) from short unrestrained MD simulations.

For some targets, alternative initial models were generated to enhance the conformational sampling for refinement. (Figure 1B) Sampling from multiple initial models allowed much broader sampling in conformational space.²⁷ We used template-based modeling to predict the alternative initial models. Homologous structures in the PDB were searched using HHsearch³⁰ with a sequence profile that was generated by sequence search against the UniClust30 database⁴⁴ using HHblits⁴⁵. To generate models that are comparable to the original initial model, the top 100 searched proteins were compared with the original initial model using TM-align⁴⁶, and structures that were close to the initial model (TM-score > 0.6) were selected for further modeling steps. Single-template-based models were built using MODELLER⁴⁷ for each selected protein with sequence alignments generated by HHalign^30,48 with the MAC algorithm, the global alignment mode, and allowing up to three alternative alignments. From the generated models, up to ten models were selected that had higher structural similarities to the original initial model than a TM-score cutoff, either 0.6 or the best TM-score minus 0.2, whichever was greater. We did not use the alternative initial model strategy if none of the built models satisfied the selection criterion. We built hybrid models by recombining structural information from the original initial model and the selected single-template-based models to take advantages of multiple-template-based modeling. Because the hybridization step combines the original model to be refined with other models, we believe that this protocol is still what is typically considered refinement of a given initial model, but with a more aggressive approach towards broader conformational sampling by taking advantage of alternative structures. The hybridization was carried out by a modified Rosetta “iterative hybridize” protocol⁴⁹. We chose the Rosetta hybridize protocol to perform multiple-template-based modeling rather than running MODELLER with multiple templates. MODELLER occasionally resulted in a frustrated model because of conflicting information between templates.⁵⁰ In addition, the Rosetta hybridize protocol can generate reasonable structures for residues for which template information is not available by relying on fragment assembly.⁵¹ Different from the original Rosetta “iterative hybridize” protocol, sampling was limited to the vicinity of the original initial model through only ten iterations, fewer than in the original protocol. The detailed modifications are described in Heo et al.²⁷ Among the hybridized models, the four models with the lowest Rosetta scores were selected as alternative initial models. Simulations for the alternative initial models were carried out in the exact same way as for the original initial model. When the multiple initial model strategy was used, the aggregated simulation time was 2.5 μs.

CASP14 predictors from the Feig group

The predictors from the Feig group are summarized in Table S1. In the refinement (TR) category, we participated with two predictors: FEIG-S for server predictions and FEIG for “human” predictions. There was no human intervention for FEIG-S, except for two targets, R1056 and R1057, where putatively bound ligands were included manually in the simulation systems. (Table S2) Since the CASP14 refinement targets were not straightforward to be predicted by template-based modeling, we used alternative initial models only for six out of 37 regular refinement targets for the FEIG-S predictions. For the FEIG predictions, we applied a different multiple alternative initial model strategy: instead of using in-house template-based modeling, we used other models from the same predictor group for a given target protein (e.g., Zhang-server_TS2–5 for a target that was originally Zhang-server_TS1) as inputs of the hybridization for the alternative initial model building protocol. This may be a practical procedure even outside CASP, because most structure prediction methods usually give multiple models. We only included similar models for the alternative initial model building by visual inspection, excluding models where any part deviated significantly, such as different or reoriented secondary structure elements, or models that were virtually identical to the initial model. As a consequence, the multiple initial model building with other submitted models in the FEIG predictor was used only for 14 regular refinement targets. For the other targets, we simulated much longer than the FEIG-S predictions to take advantage of the longer time allowed for human predictions. We simulated 10 μs in total for a target using ten replicas over 1 μs. (vs. 500 ns in total from five replicas each over 100 ns simulation time for the FEIG-S predictions)

For the regular tertiary structure prediction (TS) category, we participated with one predictor for server prediction and four predictors for human predictions. These predictors combined state-of-the-art protein structure prediction methods—they used machine learning models for initial predictions—followed by our refinement protocol. FEIG-S was a server predictor that used an in-house modeling pipeline based on trRosetta,¹² followed by refinement. FEIG-R1, 2, and 3 were human predictors that refined “model 1” structures of RaptorX, Zhang-Server, and BAKER-ROSETTASERVER using our refinement protocol, respectively. For simplicity, the multiple initial model strategy was not used for these predictors. FEIG was another human predictor that functioned as a meta predictor where sampled structures from the FEIG-R1, 2, 3, and FEIG-S refinement protocols were combined in the post-sampling ensemble selection and averaging step of our refinement protocol. After the CASP14 meeting, we also refined AF2 models with our refinement protocol; the resulting models are named here as FEIG-AF. Since this paper focuses on the effect of the refinement protocol, we mainly analyzed the effect of refinement of other predictors’ models, FEIG-R1, 2, 3, and FEIG-AF to complement the analysis of our performance in the refinement category with a more systematic view of refinement as a function of initial model generation.

Comparison with previous refinement protocols

Two additional refinement protocols were applied to directly measure the progress over previous MD refinement protocols (see Table S3). These refinement protocols were based on our previous refinement protocols that were used during CASP12⁴² and CASP13.²⁴ They were simplified and optimized to match the computational cost for the MD sampling with the latest refinement protocol, while key components of each protocol were maintained.²⁷ The CASP12 refinement protocol involved various numbers of various lengths of MD simulations. MD simulations were performed at 298.15 K with the original CHARMM36m force field³³ and harmonic restraints on Cartesian coordinates of every Cα atoms. We found that MD sampling with harmonic restraints saturates quickly so that more and longer replicas of MD simulations provided marginal improvements over shorter and fewer simulations.⁴² Thus, the simplified CASP12 protocol ran five trajectories of 50 ns-long MD simulations using the same simulation parameters. During CASP13, we applied two refinement protocols: an iterative and a conservative protocol. The conservative protocol is identical to the simplified CASP12 protocol, and we selected final models among the models from both protocols based on protocol selection rules. The iterative protocol iteratively carried out MD simulations and clustering for three iterations. MD simulations for the protocol were carried out at 298.15 K with a modified CHARMM36m force field²⁴, hydrogen mass repartitioning, and flat-bottom harmonic restraints on Cartesian coordinates of every Cα atoms. The number of MD simulation trajectories and their lengths varied for each iteration. We previously found that the iterative sampling did not provide additional gains over just one iteration.²⁴ Thus, the CASP13 protocol was simplified to perform five trajectories of 100 ns-long MD simulations with the same simulation parameters and without iterations.

Markov state modeling

In order to provide further insights into the refinability of AF2 models, we built Markov state models (MSM)⁵² for six domains during post-CASP analysis. We selected these domains to span different initial AF2 modeling qualities, to cover domains extracted from both single-domain and multi-domain proteins, and to consider target structures determined via different experimental methodologies (see Table 1). As an input to the MSM generation, we ran unrestrained MD simulations with a similar protocol as the one that was used for the refinement protocol where restraints were applied. The simulations were carried out with the original CHARMM 36m force field³³ with a 2 fs time step at 298.15 K in the NVT ensemble. The strategy for building MSMs was similar to the one reported previously²⁵. For each domain, starting from the experimental structure and from model 1 generated by AF2, ten unrestrained 200 ns MD simulations were launched for each. Snapshots were collected every 100 ps. The MD trajectories were featurized using Cα-Cα distances. Time-lagged independent components analysis (tICA)⁵³ was employed to reduce the dimensionality of these input features and k-means clustering was then used to cluster the MD snapshots in the tICA space. Preliminary MSMs were constructed, and snapshots located in clusters between the experimental and AF2 structures were selected as starting points for successive MD runs. For each selected snapshot, ten unrestrained 200 ns MD simulations were again carried out. This sampling strategy was continued until an MSM connecting the experimental and AF2 states could be obtained and validated. Our goal was to explore as much as possible of the conformational landscape of the domains around these two states; therefore, we removed from the analysis those trajectories that were clearly driven off-pathway or those that resulted in partial unfolding of the domains. More specifically, trajectories that drifted away significantly from both the experimental and AF2 conformations by Cα RMSD of around 6 Å or greater were removed. The total sampling time used for MSM analyses amounted to 99.8–350.0 μs depending on the domain (see Table S4). The lag times used for constructing the final MSMs were found by inspection of the implied timescales plots of the domains. Time scale convergence was determined at 20 to 30 ns depending on the domain (see Figure S1). To identify the optimal tICA parameters and the number of microstates for building the final MSMs, we employed a variational scoring approach based on the rank-10 VAMP-2 score combined with cross-validation⁵⁴. The microstate-based MSMs were further coarse-grained into a smaller number of kinetically metastable states (macrostates) using the Perron cluster cluster analysis (PCCA++) algorithm⁵⁵ to aid further interpretation. The “experimental” and “AF2” macrostates were defined as the states closest to the experimental and AF2 structures, respectively. In order to help with the structural interpretation of a MSM state, we randomly picked 1,000 snapshots assigned to a given macrostate based on the probability proportional to the equilibrium probability of the corresponding microstate, selected the best 25% snapshots according to RWplus scores and averaged them using the same protocol described above as used for MD-based refinement. The number of macrostates used for each domain (from 6 to 20, see Table S4) was selected to achieve a balance between model interpretability (having a small number of kinetically separated states) and structural homogeneity of states. More specifically, we tested increasing numbers of macrostates and for each we scored the GDT-HA of the experimental structure with the averaged model of its macrostate. We selected a macrostate number where this score was less than 5 units away from the GDT-HA of the experimental structure with the averaged model of its microstate, as microstates represent the finest level of clustering in MSMs. Macrostate discretization and MSMs were validated using the Chapman-Kolmogorov test (see Figure S1). Once we had applied PCCA++, we derived the equilibrium probabilities (and free energies) of macrostates and mean first passage times (MFPTs) for transitions between them. To assess the uncertainties in these quantities, we employed bootstrap analysis without replacement (with ten iterations), in which 90% of the original trajectories were used to re-build a MSM and re-compute these values. Refinement pathways from the AF2 state to the experimental one were identified by transition path theory (TPT) analysis. Every step of MSM building, validation and analysis was performed with the PyEMMA software⁵⁶.

Table 1.

Structural, energetic, kinetic comparison between experimental and AF2 macrostates in the MSMs of six selected domains.

	T1029-D1	T1031-D1	T1055-D1	T1070-D3	T1074-D1	T1093-D1
Domain from a multi-domain target	No	Yes	No	Yes	No	Yes
Experimental technique 1	NMR	X-ray (3.50 Å)	NMR	X-ray	X-ray	Cryo-EM
AF2 error(s)	Packing of multiple secondary structure elements	Register error in the N-term. tail	N-term. tail modeled as an helix	N-and C-termini; hinges connecting to other domains in the full structure	Two loops stemming from β-strands	Loop contacting other domains in the full structure
AF2 vs2 exp	26.2/47.3/7.12	70.5/71.4/2.97	68.2/73.7/2.27	74.0/73.6/5.05	78.2/83.6/1.87	65.1/76.6/3.24
refined vs2 exp	26.0/46.1/7.123	65.8/68.3/2.95	66.0/69.2/2.27	69.1/69.7/5.41	62.3/72.6/2.56	66.5/76.0/3.21
A vs2 exp	25.4/46.2/7.06	64.5/69.0/2.80	67.0/70.6/2.59	71.1/69.9/4.72	67.8/73.5/2.21	65.3/75.4/3.26
E vs2 exp	40.4/58.9/4.07	67.6/73.8/1.47	65.6/71.7/1.70	79.0/78.9/1.97	83.0/80.9/1.30	66.3/75.2/2.05
M vs2 exp	21.4/45.2/7.61	52.6/62.2/4.12	63.7/70.4/2.42	-	50.8/64.8/3.87	-
M vs2 AF2	56.8/67.4/2.3	54.5/59.9/4.74	82.6/83.6/2.06	-	53.2/66.2/3.21	-
ΔΔG3 (E – A) [kcal/mol]	2.48 (±0.10)	−0.27 (± 0.03)	−1.76 (±0.11)	−2.31 (±0.16)	2.39 (±0.14)	−0.34 (± 0.05)
ΔΔG3 (E – M) [kcal/mol]	3.18 (±0.11)	−0.81 (±0.03)	0.61 (± 0.09)	-	2.98 (± 0.09)	-
MFPT4 (A→E) [μs]	2478.8 (±300.6)	41.9 (±1.9)	1.9 (±0.2)	36.3 (± 2.9)	136.1 (± 16.1)	17.5 (± 3.6)

AF2: original AF2 model 1, exp: experimental structure, refined: AF2 model refined using our CASP14 protocol, A: averaged model of the AF2 macrostate, E: averaged model of the experimental macrostate, M: averaged model of the minimum energy macrostate.

¹The resolution of X-ray structure is reported in brackets where its value is known.

²Comparison between two structures in terms of GDT-HA, lDDT and Cα RMSD [Å]. For all comparisons with exp, the value of the structure closest to it is marked in bold for each metric. When the E state coincides with the M state, an empty value is present in the table.

³Free energy difference between two macrostates. Standard errors (reported in brackets) were evaluated through a bootstrap strategy with 10 iterations and 90% trajectory subsets.

⁴Mean first passage time for transitions between two macrostates. Standard errors were evaluated as for free energy differences.

Relaxation of experimental structures

In addition to the MSM construction, we also relaxed the experimental structures to establish the ‘native’ state conformations for all targets according to the MD simulations and the force field. The resulting models can be considered as an ideal-case maximum performance of our current MD simulation-based refinement protocol. As for the Markov state modeling, we carried out unrestrained MD simulations starting from the experimental structures using the same protocol (see Table S3). Because the identification of the native state conformation did not require significant conformational state transitions from the experimental structure via extensive simulations, we ran only five trajectories of 50 ns-long MD simulations, enough to achieve local relaxation. To define the native state conformations, the same post-sampling steps of the refinement protocol were applied. The resulting models were referred to as “MD-native”. For the input of the experimental structure refinement, we used experimental structures after parsing domains based on the CASP14 domain definition, to follow the procedure by which targets were selected as refinement targets.

In addition to the domain-based refinement, we also used the experimental structures with the whole domains for multi-domain targets and the whole proteins for targets that form oligomers if the interaction information was available and the whole system consisted of less than 5,000 residues. By refining the experimental structures in this manner, we could determine not only the effect of the force field and simulation methodology, but also the effect of including or excluding other interacting proteins or domains during refinement.

RESULTS

CASP14 refinement category performance

The CASP14 refinement performance by FEIG-S (server predictor) and FEIG (human predictor) are summarized in Figure 2, Figure S2, and Table 2. FEIG-S was a fully automatic refinement server except for two targets, R1056 and R1057, where putatively bound ligands were added manually before beginning conformational sampling. FEIG was a human group that used other predictions from the same group of the initial model or simulated longer than the server predictions. Both predictors refined the initial models on average in terms of both global and local accuracy measures. All the following analysis is based on model 1 predictions.

Figure 2.

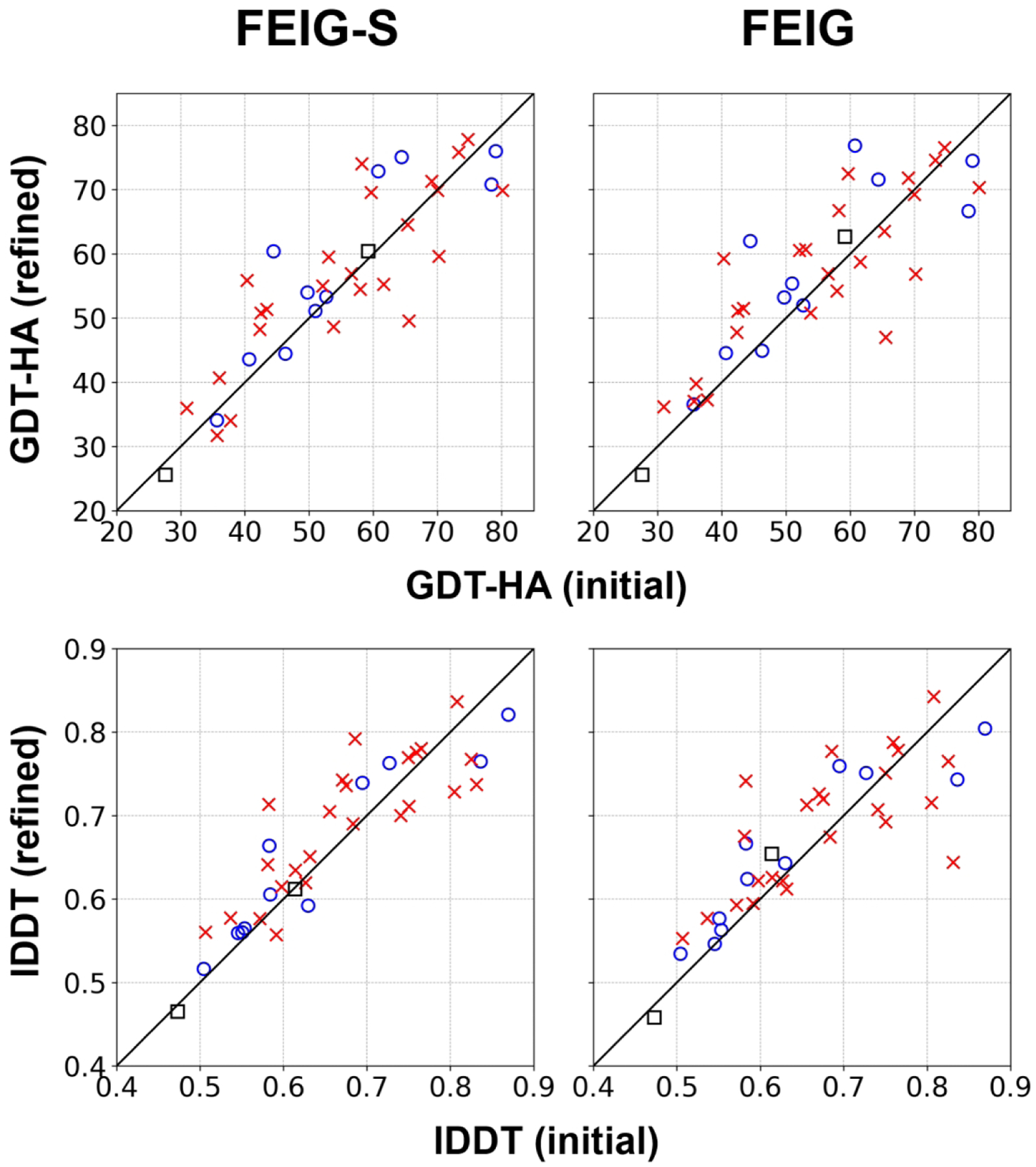
Overall performance for FEIG-S (server) and FEIG (human) on TR targets. Targets from multimeric or multi-domain proteins are shown as red Xs, while targets from monomeric and single-domain proteins are depicted in blue circles. Targets for which the native structure was determined by NMR experiments are shown as black squares.

Table 2.

Refinement performance on TR targets

Method	ΔMeasure1
	GDT-HA	Ca-RMSD [Å]	lDDT	SphGr
FEIG-S	+1.67 (59%)	−0.06 (56%)	+1.16% (67%)	−0.47 (27%)
FEIG	+2.08 (62%)	+0.16 (54%)	+1.13% (70%)	−0.14 (43%)
CASP13 2	+0.27 (51%)	−0.01 (56%)	−0.15% (51%)	−1.35 (29%)
CASP12 2	+1.02 (51%)	+0.01 (51%)	−0.10% (51%)	−0.73 (24%)

¹Mean changes of each measure. Percentage of improved targets are shown in the parentheses.

²Simplified version of our refinement protocol used during CASP13 and CASP12.

For 37 regular refinement targets, which excludes the CASP-COVID and the extended time targets, FEIG-S improved GDT-HA⁵⁷ and IDDT⁵⁸ scores on average by +1.67 and +1.16%, respectively. However, performance varied depending on targets. First of all, better performance was achieved for single-domain proteins and proteins that are not in extensive contact with other biological molecules such as oligomers. (for the list of multiple-domain and oligomeric targets, see Table S5) For monomeric and single-domain targets, GDT-HA scores were improved by +2.85. On the other hand, for targets that form complexes or that are part of multi-domain proteins, GDT-HA scores were improved less, by +1.24 on average. Moreover, some multi-domain or oligomeric targets also became significantly worse after refinement. The refinement of oligomeric and multi-domain targets will be discussed further below.

The FEIG predictor improved GDT-HA and IDDT scores on average by +2.08 and +1.13%, respectively. In comparison between FEIG-S and FEIG, there was little overall difference in terms of performance measured via GDT-HA, lDDT, Cɑ-RMSD, and SphereGrinder scores⁵⁹ (Figure S3). Again, we found a tendency towards better refinement of monomeric and single-domain targets.

We also refined the targets with the refinement protocols that were used by us during CASP12 and CASP13 to directly measure methodological progress. (Figure S4 and S5). In comparison between the previous methods^24,42 and the latest refinement protocol²⁷ used for FEIG-S, there has been clear progress after CASP13. The latest protocol outperformed the previous protocols both in global and local accuracy measures. Previously, our refinement protocols did not improve local structural accuracy as much,²⁴ but this was addressed in the latest protocol by introducing an improved MD sampling strategy and by using multiple initial models.²⁷ Improved MD sampling resulted from simulations at a higher temperature than room temperature, so that conformational space could be explored more rapidly. The new protocol also utilized an improved restraint scheme that gradually switches from one restraint scheme to another one. This scheme allowed for better sampling of more diverse conformations. Despite the progress, some targets became significantly worse with the FEIG-S predictor. For example, GDT-HA scores decreased from 65.6 to 49.6 (−16.0) for R1042v2. Interestingly, the previous CASP12 protocol did not result in significant deterioration of this target as the GDT-HA decreased only slightly to a value of 64.5 (−1.1). The reason is that the CASP12 protocol⁴² used more conservative harmonic restraints vs. flat-bottom harmonic restraints in the CASP13²⁴ and CASP14²⁷ FEIG-S protocols. The stronger bias toward the initial model in the CASP12 protocol prevented significant deterioration.

We further analyzed refinement performance as a function of how the initial model was generated. (Figure 3 and S6) Clearly, both FEIG-S and FEIG failed to improve AF2 models. On the other hand, models from the other groups such as tFold, Zhang, and Baker groups could be improved significantly. 73% and 76% of the targets of those were improved in terms of GDT-HA by FEIG-S and FEIG, respectively. Refinement targets with initial models from AF2 had very high initial accuracies with an average GDT-HA score of 70.4. Models from other groups had lower GDT-HA scores of 50.9 on average, suggesting that there was more room for improvement during refinement. We found that AF2 models were not just more difficult to improve, but the model quality actually deteriorated significantly with the FEIG-S protocol. This will be discussed in more detail in the following sections. Among non-AF2 models, we found that models from the tFold and Zhang groups were more refinable than models from the Baker group. These differences may reflect the degree to which models were already refined during the initial model generation since many prediction protocols now include a final refinement stage based on a similar physics-based simulation protocol as used by us.

Figure 3.

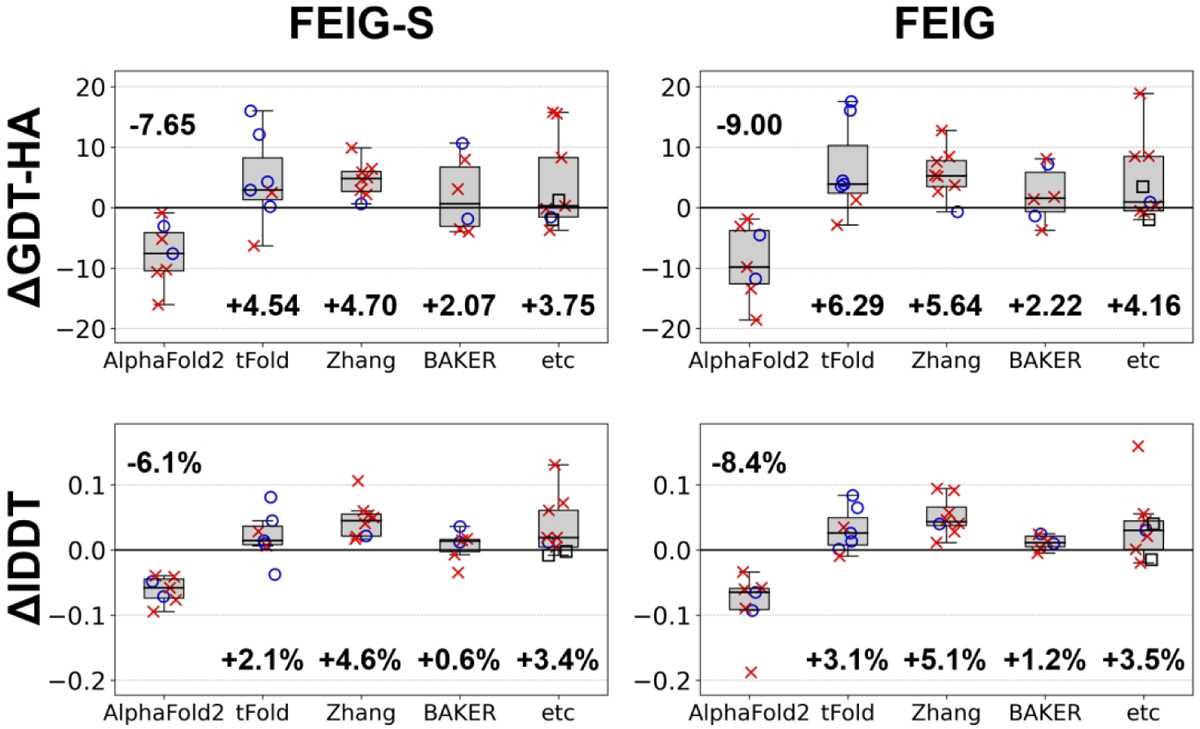
Performance on TR targets as a function of initial model predictor. Performance for each predictor is shown as a boxplot. Individual target quality changes are overlaid onto the markers (for their definitions, see Figure 2).

When we compared the performance by FEIG-S and FEIG on non-AF2 targets, FEIG appeared to perform better than FEIG-S (+4.67 for FEIG vs. +3.85 for FEIG-S in GDT-HA on average), but with low statistical significance (p=0.052 according to Student’s paired t-test, n=30). The key differences between FEIG and FEIG-S were more extensive sampling and the use of multiple initial models. The idea of multiple initial models was benchmarked before on previous CASP refinement targets and found to result in significantly better performance than with the single initial model-based protocol. However, in CASP14, alternative initial models could be built via homology modeling only for a few targets. Instead, we used other models from the same group of the initial model as alternative initial models for the FEIG protocol. We expected that the use of these alternative models may provide benefits in a similar way to homology models, but from the CASP14 results it is unclear whether this modified strategy was beneficial due to poor statistics given the limited number of targets (+4.97 vs. +4.35 in GDT-HA on average for FEIG with and without the multiple initial model strategy, respectively, with the difference not being significant according to p=0.21 from Student’s paired t-test, n=14). Longer simulations for the FEIG predictions were likely to provide additional progress over the FEIG-S predictions, but the statistical significance was low due to the small number of targets. (+4.40 for FEIG with longer simulations vs. +3.49 for FEIG-S in GDT-HA on average; p=0.061 from Student’s paired t-test, n=16). When we performed a post-analysis to use a subset of sampled conformations for the FEIG predictions with longer simulations, there was a clear trend that the refinement performance improved with additional sampling. (Figure S7) Refinement with more independent simulations resulted in better performance, but there was not significant gain beyond running more than five trajectories.

Refinement of TS models

To test our refinement protocol more broadly, we also refined regular tertiary structure (TS) models generated by different methods during the prediction season (FEIG-R1/2/3) and after the CASP14 conference (FEIG-AF). The results are summarized in Table 3, Figure 4, and Figure S8. The main conclusions based on the refinement of TS models were similar as for TR targets: It was generally possible to improve models built by top-performing methods - except for AF2. As for TR targets, the extent of refinement varied depending on the prediction methods. For example, models from the Zhang group (FEIG-R2) were refined more than models generated by the Baker group (FEIG-R3). Again, it was very difficult to improve AF2 models, and although modest refinement was possible in some cases, it was more common that AF2 models deteriorated significantly after refinement.

Table 3.

Refinement performance on TS targets

Predictor	Mean initial model quality				ΔMeasure1
	GDT-HA	Cα-RMSD [Å]	lDDT	SphGr	GDT-HA	Co-RMSD [Å]	lDDT	SphGr
FEIG-R1	41.89	7.91	55.85%	65.16	+1.17 (52%)	−0.04 (43%)	+0.71% (54%)	−0.04 (40%)
FEIG-R2	44.46	6.48	58.72%	72.21	+2.78 (66%)	−0.10 (57%)	+1.77% (65%)	−0.26 (40%)
FEIG-R3	42.17	7.71	57.11%	68.08	+1.09 (50%)	−0.02 (45%)	−0.14% (37%)	−1.07 (29%)
FEIG-AF 2	74.37	2.44	82.10%	94.11	−6.75 (13%)	+0.25 (22%)	−6.38% (1%)	−2.24 (10%)

¹Mean changes of each measure. Percentage of improved targets are shown in the parentheses.

²Refinement of AlphaFold2 (group TS427) models. It was performed after the CASP14 conference.

Figure 4.

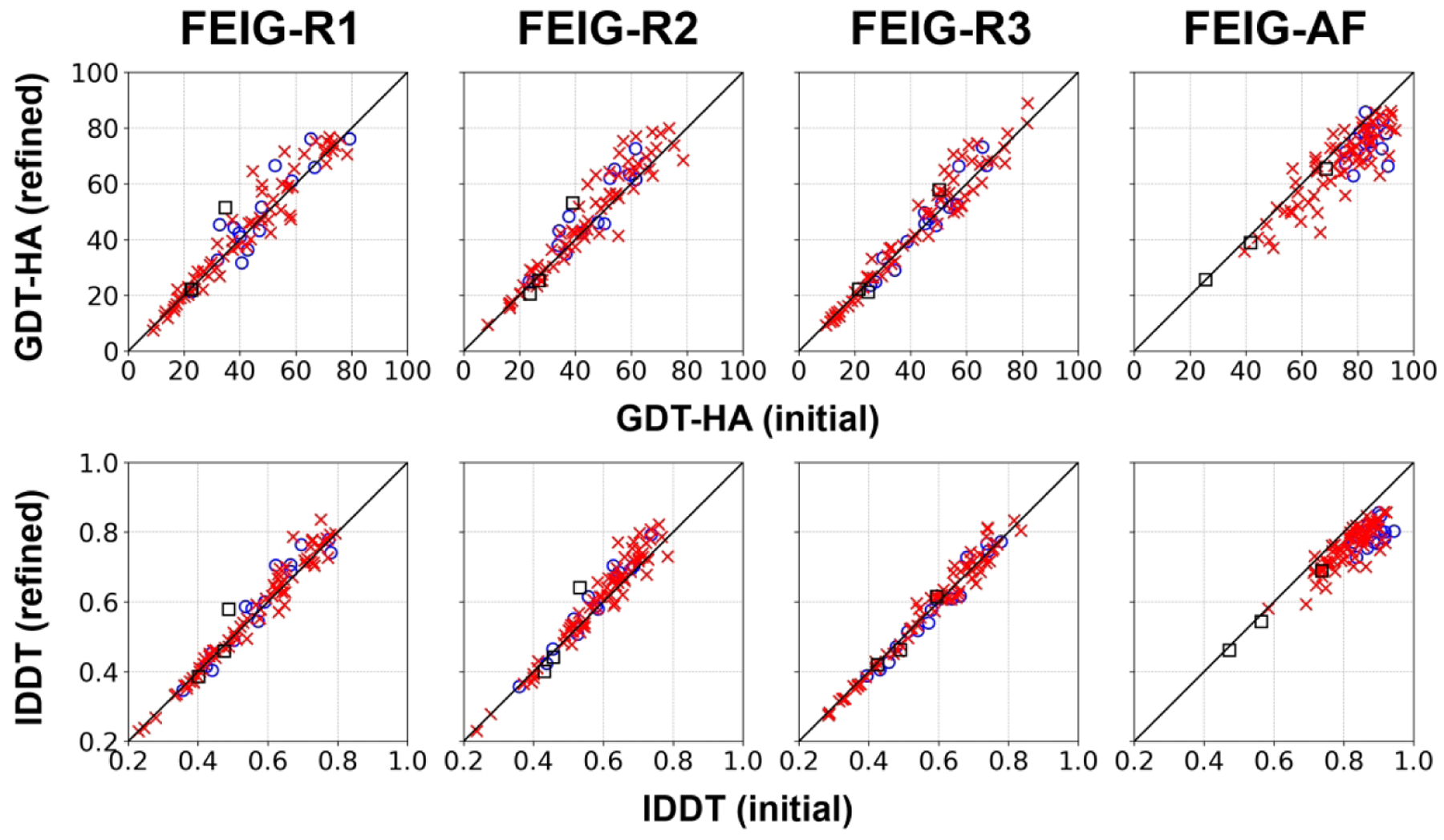
Overall performance in GDT-HA for FEIG-R1/2/3 (refinement of RaptorX, Zhang-server, BAKER-ROSETTASERVER model 1 structures) and FEIG-AF (refinement of AF2 model 1 structures, post-CASP14 analysis) on TS targets. For marker definitions, see Figure 2.

We found that the refinement protocol works well with moderately accurate models (GDT-HA scores between 40 and 70).²⁴ This may partially explain why models from the Zhang group could be refined more than the others because most of their models (47) were in that range. There were fewer models in that range with other methods: 34 for RaptorX models (FEIG-R1), 45 for Baker models (FEIG-R3) and 24 for AF2 models (FEIG-AF). In addition, we expect that the extent of refinement that was already applied to the initial models played a role as well although this point is difficult to assess without knowing the exact details of each prediction method and without access to possibly unrefined final models. 69 out of 87 TS domains had inter-protein or inter-domain contacts, and those were harder to improve as for TR targets. When measuring the refinement performance only on monomeric and single-domain targets, average improvements in GDT-HA were +2.55, +3.61, +0.74, and −7.53 for FEIG-R1, 2, 3, and FEIG-AF, respectively.

Detailed conformational landscapes via MSM analysis

In order to better understand the limits of our refinement protocol, especially in the context of seemingly unrefinable AF2 models, we carried out in-depth conformational landscape analysis for six domains (see Table 1). The domains were selected to focus on different types of situations where AF2 produced models with large to moderate deviations from the experimental structure (GDT-HA scores from 26.20 to 78.22, see Figure 5) and where our CASP14 protocol was unable to successfully refine those models (with a GDT-HA deterioration in five out of six cases and a small increase in the remaining case). We applied extensive MD sampling to each system (ranging from 99.8 to 350.0 μs) and subsequently combined simulation snapshots via MSM analysis.

Figure 5.

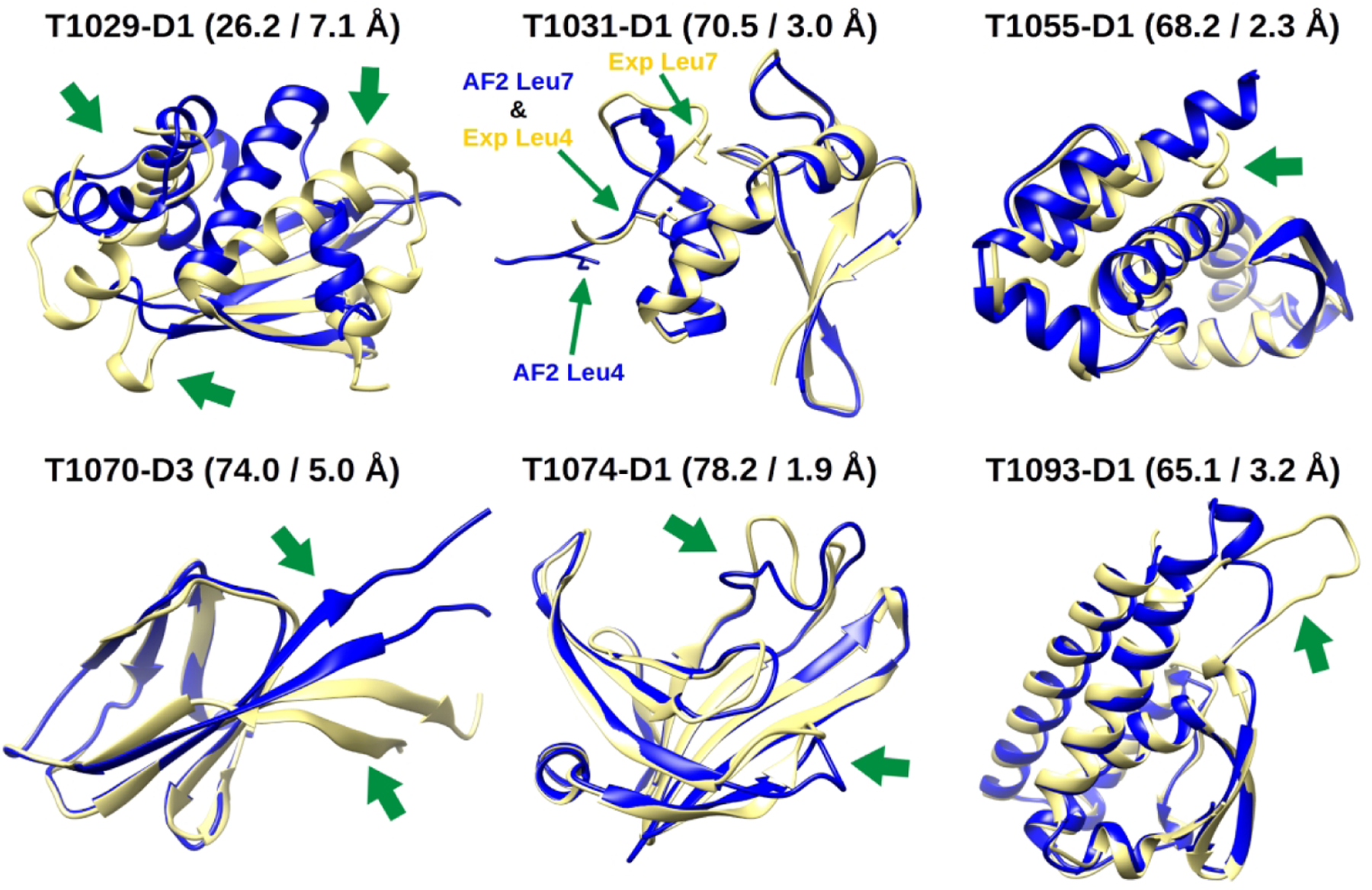
Superpositions between the experimental structures (yellow) and AF2 models (blue) of the CASP14 domains we selected for MSM analysis. Beside the names of the domains, the GDT-HA and Cα RMSD of the AF2 models with the experimental reference are reported. Green arrows point to the major errors in the AF2 models. For T1031-D1, residues Ile4 and Ile7 (which are discussed in the main text) are additionally highlighted.

Figure 6 shows the free energy landscapes of each domain projected along the first two independent components from tICA. The experimental structures and models 1 from AF2 are mapped onto them. AF2 models 2 to 5 almost always map very close to model 1 (see Figure S9). For this reason, we will concentrate our discussion on model 1 of each domain. The main result emerging from the MSM analysis is that, for all systems, the experimental structure and the AF2 model map onto different macrostates and these states are often separated by large kinetic barriers (see the MFPTs values in Table 1). The importance of this finding is that although the AF2 models for the targets discussed here are very good, there is at least in principle room for further refinement.

Figure 6.

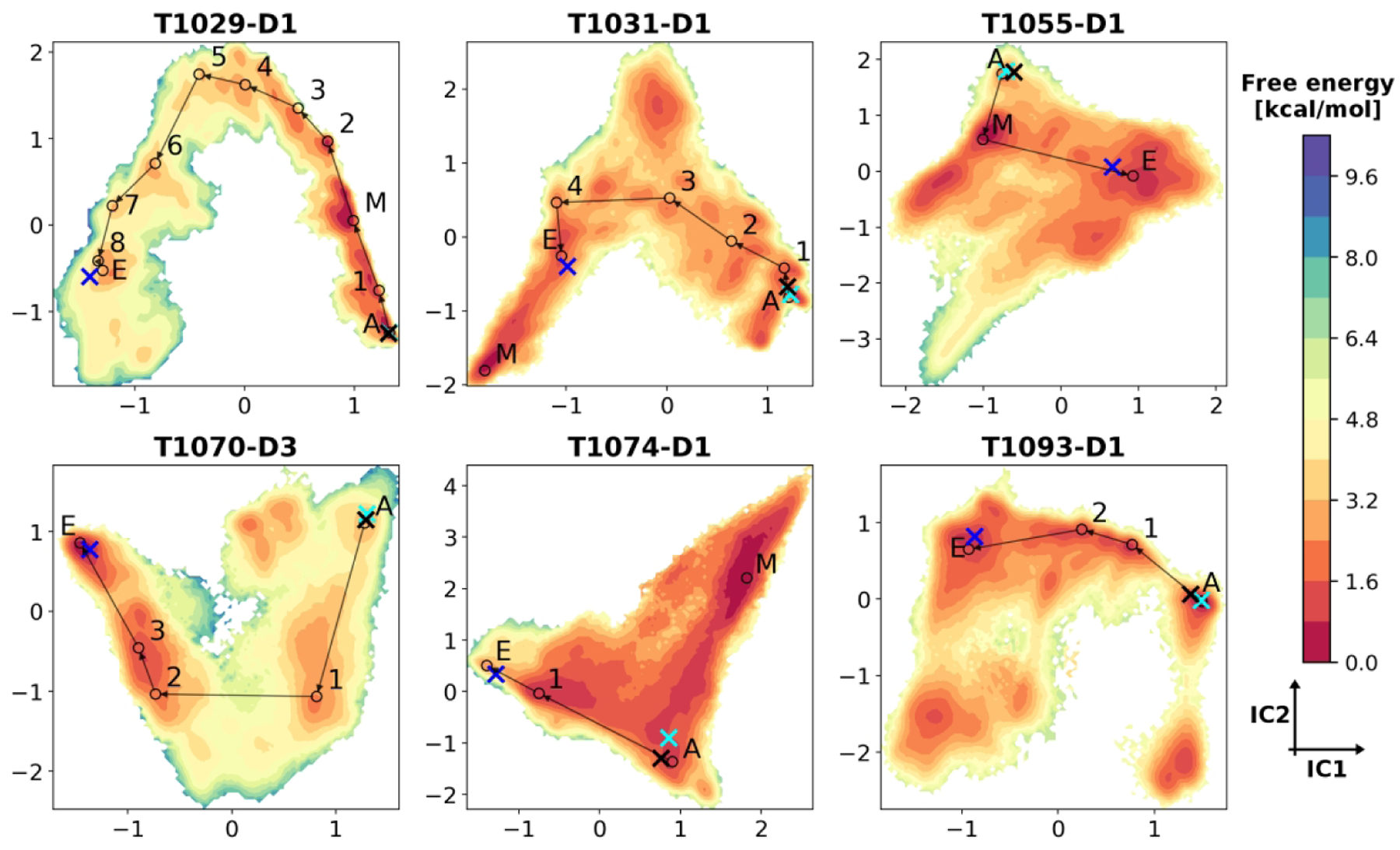
Free energy landscapes for selected domains from MSM analysis. MSM-reweighted free energy values are projected on the first two independent components (ICs) from tICA. Energy levels are reported in units of kcal/mol. Projected structures are indicated as follows: blue X, experimental structure; black X, AF2 model 1; cyan X, MD-refined model; circles, macrostate averaged structures. Macrostates are denoted as: E, experimental state; A, AF2 state; M, minimum energy state if not E or A. Representative high-flux refinement pathways identified by TPT are shown with lines connecting the averaged macrostate models. Intermediate macrostates found in these pathways are labeled with numbers.

From an energetic point of view, for four out of six domains (T1031-D1, T1055-D1, T1070-D3 and T1093-D1), the experimental state has a lower free energy with respect to the AF2 one, with ΔG values ranging from −2.31 to −0.27 kcal/mol. However, we also find that for four domains (T1029-D1, T1031-D1, T1055-D1 and T1074-D1) there is another macrostate that is different from the AF2 and experimental states and that has an even lower free energy than the experimental one. For two domains (T1031-D1 and T1055-D1) this lowest energy state is kinetically near the experimental one, i.e. both states interconvert rapidly despite structural differences, but for the other two (T1029-D1 and T1074-D1) it is far from it, i.e. in addition to structural differences there are significant kinetic barriers between the lowest energy and experimental states. This means that the application of MD-based refinement to the AF2 models for the targets analyzed here should move the initial structures to different conformations based on the energetic driving force due to the force field, and in four out of six cases, the structures favored by the force field would be more native like than the initial AF2 models. However, the MSM and MD data also suggests that a major reason for why we could not actually refine these models is the existence of high kinetic barriers along the refinement pathways that are difficult to overcome in blind refinement. Another factor appears to be the presence of highly dynamical regions in some of these domains that may require extensive sampling to generate conformational averages matching experimental ones.

Relaxation of experimental structures

We relaxed the experimental structures for all targets to determine the best-case native state models that could be expected with our simulation setup. This tested certain methodological aspects such as the force field, but also the validity of a protocol focused on single domains without considering any additional factors or uncertainties that may be present during experimental structure determination. Experimental structures are not expected to require any structural transition to reach the native state. Therefore, only local relaxation via MD simulations was needed to generate the MD-native structures via ‘refinement’ of the experimental structures.

The MD-native structures were first compared with the experimental states identified by the MSM analysis from extensive MD simulations for the selected domains. (Figure S10 and Table S6) We found that the MD-native structures were generally in the same state of the experimental states with little structure difference for most of the domains. For T1029-D1, the MD-native structure was intermediate between the experimental structure and the MSM experimental state. This may be because the simulation time for the MD-native structure generation was less extensive than the sampling applied during the MSM model generation. However, the MD-native structure changed in a similar direction as the MSM experimental state, i.e., it resulted in significant deviation from the experimental structure. Therefore, we believe that the approach of applying short MD relaxation to all of the experimental structures at least approximates what would otherwise be obtained by a full MSM analysis with respect to the experimental state according to the force field we used and given the other assumptions we applied during the refinement MD simulations.

The structural similarity between the true experimental structures and the MD-native structures is summarized in Figure 7 and Figure S11 for the TR and the TS targets, respectively. Again, the MD-native structures resulting from relaxation of the experimental structures have to be considered as the maximum ideal-case performance of our MD simulation-based refinement given our current protocol simulation setup. This maximum performance would be attained only if the experimental macrostate were the lowest energy state for every domain. For some domains, this condition may hold true (see Table 1 and our previous work). For others, the experimental state is expected to be the lowest energy one only if simulating the domains in their full experimental contexts (see discussion below). Nevertheless, the analysis suggests that many tertiary structure models could theoretically be expected to be refined to near-atomistic accuracy (Cɑ-RMSD ~ 1 Å). Among the refinement targets, 12 out of 31 unique domains had lower than 1 Å accuracy in Cɑ-RMSD. Similarly, 27 out of 87 TS domains achieved such high near-atomistic accuracy. On the other hand, even although we started from the experimental structure, some of the MD-native structures ended up with significant deviations from the experimental structures. We found that there was a big gap between monomeric single-domain targets and oligomeric or multi-domain targets in the maximum performance. On average, monomeric, single-domain targets can reach up to 81.0 GDT-HA units, while targets that were simulated without the interaction contexts showed less similarity with an average GDT-HA score of 71.7. When we compared the MD-native structures with the AF2 models, they had lower GDT-HA scores than the AF2 models for 55 out of 87 domains (63%).

Figure 7.

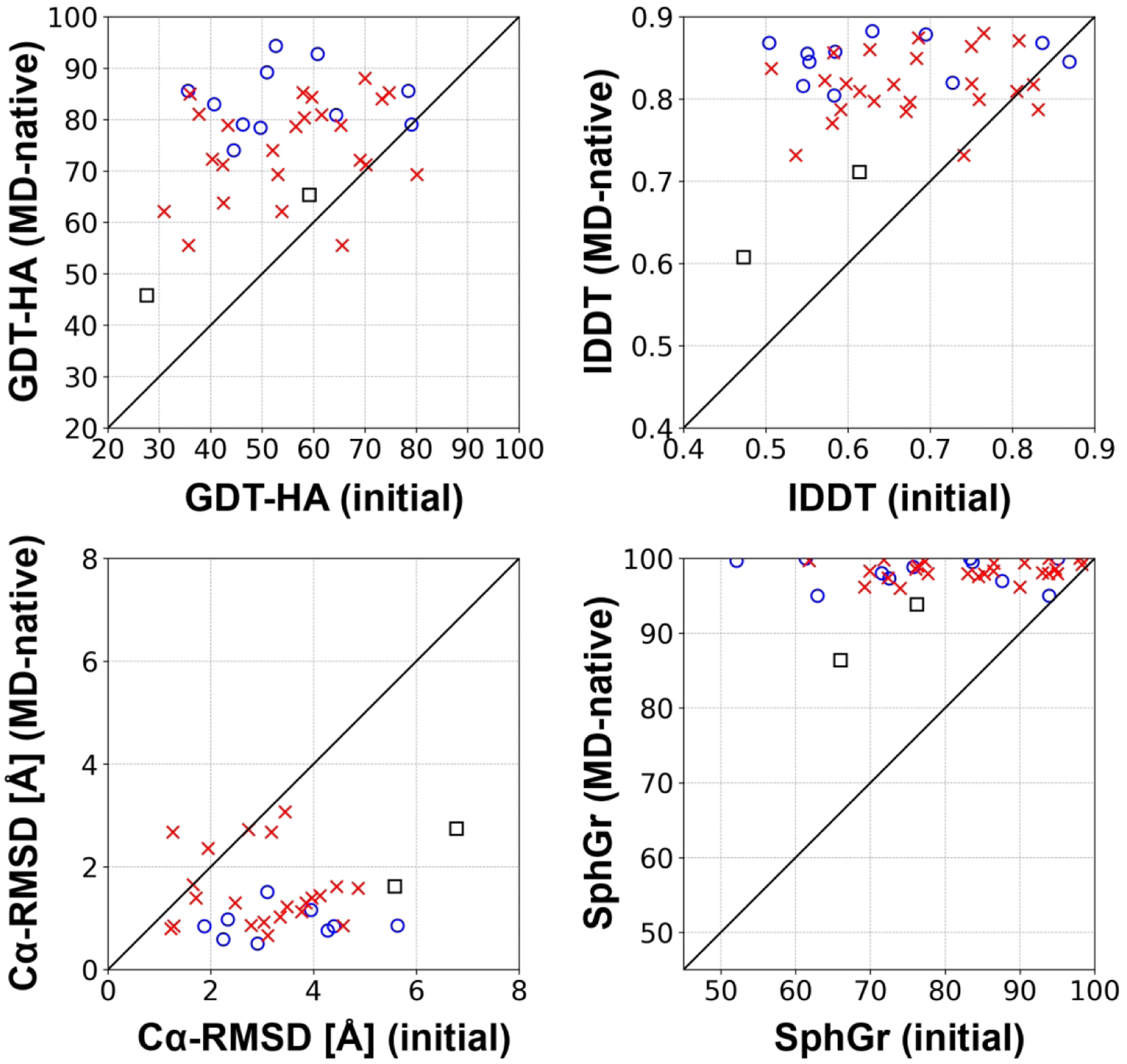
Maximum refinement performance that could be achieved by MD-based refinement with the CHARMM36m force field and the TIP3P water model when starting from the actual experimental structure. For marker definitions, see Figure 2.

DISCUSSION AND CONCLUSIONS

Conformational sampling is still a major obstacle for refinement

Based on what we found from relaxing the experimental structures via MD, it seems that we could in principle reach near-atomistic accuracy for many targets. However, this requires long enough simulations to sample the native state with an assumption that the native state remains the lowest free energy state as other non-native conformations are being explored. It appears that this assumption is usually valid. The native states for proteins described in Heo et al.²⁵ had lowest free energies. Among the domains analyzed here via MSM analysis, the experimental macrostate is the global energy minimum for two domains, T1070-D3 and T1093-D1. For other domains, where the experimental macrostate is not the global energy minimum, the discrepancies could be rationalized by specific reasons such as the absence of crystal contacts. This will be discussed more below. Therefore, unless the experimental macrostate is not at the lowest free energy, the ideal-case relaxation of the experimental structures suggests that MD simulation-based refinement should be able to improve many models to near-atomistic accuracy.

The theoretical expectation of reaching near-atomistic accuracy for many models, was, however, not fulfilled by our actual refinement performance during CASP14. This suggests that insufficient sampling remains a significant challenge for actually realizing what may be the best-case scenario for MD-based refinement. The fundamental reason for the significant difficulties in achieving sufficient conformational sampling is the presence of sizable kinetic barriers that have to be overcome during refinement.²⁵ This remains true even when the starting model is very close already to the experimental structure. The MSM analysis presented here shows that even although the structural divergences between the AF2 and experimental structures are small (the starting AF2 model’s GDT-HA scores range from 65 to 74), there were still significant kinetic distances separating the AF2 and experimental macrostates because non-trivial structural transitions were needed to reach the native state. For five out of six analyzed domains, the estimated MFPT from the AF2 to experimental states is greater than 10 μs, 20 times the aggregated MD simulation time used in our refinement protocol, with refinement pathways progressing through series of slow transitions (see Figure S12). T1031-D1 gives a clear example for the sampling challenge encountered during refinement. In the AF2 model, there is a register error (see Figure 5) at the N-terminal tail (residues 1–13); the pocket where the sidechain of Ile7 is positioned in the experimental structure is occupied by Ile4 in the initial model. In the refinement pathway identified via simulation, the N-terminal tail has to lose contacts with the rest of the domain, followed by partial unfolding (from state A to 1 with an MFPT of 12.6 μs), sliding to the correct register (from state 2 to 3 with an MFPT of 11.1 μs) and, finally, refolding. (see Figure S13D)

Meanwhile, the MD sampling during the actual refinement protocol rarely transited to other conformational states from the initial states as demonstrated in detail for the targets subjected to the extensive MSM analysis. Figure S14 shows how the sampled conformations for the refinement mapped onto the free energy landscapes obtained from the MSM analysis. The mapped trajectories show that the MD sampling never diverged too far from the initial AF2 models. As a result, the refined AF2 models remained structurally similar to the unrefined AF2 structures (see Table S6). Moreover, when the refined AF2 models were mapped onto the energy landscape, they are very near to the starting AF2 models and they are always included in the AF2 macrostates.

The sampling challenge during MD-based refinement is not new and although we did see some progress in CASP14 due to improvements in our sampling strategy, insufficient sampling is still the major bottleneck. Increasing computer time may provide some relief, but more effective strategies that selectively employ enhanced sampling techniques to enhance progress towards refinement without resulting in unfolding remain to be identified.

Inter-protein and domain interactions are important for high-accuracy refinement

We found that the performance of FEIG-S for multi-domain and oligomeric targets was clearly lower than for single-domain and monomeric targets. There may be various reasons for that observation, but the main factor was likely because we simulated incomplete system configurations where experimental structures could not be stabilized due to missing domain or crystal contacts. This was also seen when we relaxed the experimental structures: monomeric and single-domain targets reached much higher accuracy as they could be stabilized by themselves. On the other hand, for domains that form oligomeric complexes or that are part of multi-domain proteins, the MD-native states deviated much more from their experimental structures after relaxation without considering such contacts. (Figure 7 and Figure S11)

In previous rounds of CASP the impact of domain or inter-protein interactions was not as obvious, perhaps because of different sets of targets and higher initial model accuracy during CASP14. However, it is perhaps not surprising that inter-protein or inter-domain interactions can be important for stabilizing protein structures. For example, such interactions are highly important for stabilizing intertwined beta strands or proteins with swapped domains. As perhaps extreme examples, among the refinement targets, the MD-native structures for R1042v2 and R1053v2 were less similar to the experimental structures in terms of GDT-HA than the initial model given as refinement targets. (Figure S15) The experimental structures for those domains suggest extensive interactions with other domains that appear to be essential for stabilizing their native structures. This means that refinement without considering the larger domain context is probably not very meaningful. Or to turn the argument around, it appears likely that these proteins may possess different structures in the absence of their interacting domains. Therefore, it seems to be an ill-posed challenge to expect refinement of a model given without the interaction context and evaluate the resulting model based on an experimental structure obtained in that context.

When the native states defined by MD simulations were simulated together with other domains or proteins that are in the experimental structures, the maximum performance of the refinement reached much higher values than that of the refinement without the interaction contexts with an average GDT-HA score of 77.5. (Figure S16) Among the AF2 models for TS targets, 50 out of 87 domains (57%) had room for improvement based on the MD-native models obtained in the presence of the interaction contexts. In particular, for 24 moderately accurate AF2 models that had GDT-HA scores between 40 and 70, most of the models (21 domains) could be refined when interaction contexts were provided by up to an average of 11.6 GDT-HA units. However, without the domain context, only half of the models could theoretically be improved and the average maximum improvement in GDT-HA, from comparing MD-native models with AF2 models, was only 0.4.

We further analyzed the impact of interactions by relating refinement progress to the buried interfacial solvent accessible surface area (SASA), which is the percentage of buried SASA of a domain upon inter-domain or inter-protein interactions. (Figure S17) As one may expect, domain contacts had more impact when a domain had a larger interfacial surface fraction. This direct comparison clearly shows that inter-domain or inter-protein interactions are important for stabilizing protein structures especially when the interface region comprises a large fraction of their solvent accessible surface. Again, we reiterate the perhaps by now obvious statement that interactions within the large protein context should be considered for successful refinement of protein models that are in contact with other domains or proteins.

Most of the TS targets had some inter-protein or inter-domain interactions. When we carried out BLAST searches for those multi-domain or oligomeric targets, close homologs that were identified possessed very similar arrangements of domains⁶⁰ or proteins.^61,62 This may imply that the ML model underlying AF2 might have been able to implicitly learn not just about intra-domain interactions but also about possible arrangements within a larger multi-domain or oligomeric context. On the other hand, not including such interactions with other domains or proteins clearly emerged as a major obstacle within the context of physics-based refinement methods, which are not designed to ‘learn’ or otherwise infer knowledge about domain contacts unless explicitly considered as part of the system.

Experimental factors affecting structure prediction accuracy

In addition to biologically relevant interactions, experimental artefacts can also alter the energy landscape and thus affect the ability to refine successfully towards the experimental structures. In the lowest free energy macrostate identified by the MSM analysis for T1031-D1, the N-terminal tail was positioned in the correct register, but a loop segment (residues 48–59) lost contact with the tail and acquired a more extended conformation. In the X-ray structure of this domain⁶³, the space, where this loop is positioned in the lowest energy conformer, is populated by another protein in a neighboring crystal lattice (see Figure S13A). This implies that the experimental macrostate would not be energetically favored unless the crystal contact is present. Another example where crystal contacts alter the energy landscape and protein structure is T1064 (PDB ID: 7JTL),⁶⁴ the SARS-CoV-2 ORF8 protein, for which there is another crystal structure independently determined by another group (PDB ID: 7JX6). Both structures are very similar for most of the residues. However, the two experimental structures significantly differ at residues 62–78, due to different crystal contacts with other molecules. (Figure S18) The CASP reference structure for this target has several hydrogen bonds with residues in another molecule in the crystal lattice. On the other hand, the other crystal structure has fewer interaction across its crystal lattice. Therefore, that structure would have been a more attainable target for prediction and high-resolution refinement in the absence of crystal contacts. Furthermore, these analyses revisit the question about how reliable the crystal structure near crystal lattice interface is because crystal contacts can distort the structure.⁶⁵

A more significant issue appears to pertain to experimental structures obtained via NMR experiments. Generally, the MD-native state conformations had low similarity to the experimental structures that were determined by NMR experiments. There were three targets among the TS targets: T1027, T1029, and T1055. Structure similarity measured in GDT-HA was only 44.2, 45.8, and 65.4, respectively.

For T1055-D1, the minimum energy macrostate is a refinement intermediate between the AF2 and the experimental states. The AF2 error for this domain is located in its N-terminal tail (residues 3–12). In the prediction, these residues are modeled as an α-helix, while in the NMR snapshot, they are found in a coiled conformation. In the minimum energy macrostate, the full AF2 α-helix is partly unwound, but residues 7–11 still form a helical turn (see Figure S13B). As the NMR restraints for this domain are not currently publicly available, it is not possible to check which conformation better agrees with the experimental data.

For T1029-D1, the AF2 model substantially deviates from the experimental snapshot (see Table 1). The MSM shows that the AF2 macrostate has a much lower energy with respect to the experimental one (the ΔΔG is 2.48 kcal/mol). The AF2 state is closer to the minimum energy state in structural and energetics terms. The experimental and AF2 macrostates are also separated by a large kinetic barrier (see Table 1 and Table S4). The amount of sampling required to refine the AF2 model towards the experimental snapshot would be prohibitively large. The estimated MFPT between the AF2 and experimental states is ~2.5 ms. The experimental state appears to be much more dynamic than the AF2 one (see Figure S19) and trajectories initiated from the NMR snapshot tend to largely deviate from this starting conformation, while those initiated from the AF2 model are comparatively more stable (see Figure S20). This is a surprising result, given the generally consistent performance of AF2 and MD-based approaches in identifying native states as low-energy conformations, at least in the absence of domain or inter-protein interactions. On the other hand, it is well-known that NMR data interpretation can be challenging. Since experimental data is available for T0129-D1, we could evaluate experimental observables directly between the different models generated for this target. The two main quantities available for comparison are residual dipolar couplings (RDCs) and nuclear Overhauser effect (NOE) restraints. We found that all of the models were in good agreement with the experimental data with respect to the RDCs (see Table S7), there were a significant number of large NOE violations for all of the computationally generated models (see Table S8). This suggests that that the experimental structure is clearly in much better agreement with the reported NOE restraints, however, that comparison could also be affected by misassigned NOEs, which is difficult to assess without full access to all of the experimental data.

Additional challenges to refinement at highly dynamic regions

For some domains, even if the experimental macrostates could be reached, it would still be difficult to obtain refined models that match exactly the experimental structures due to the presence of highly dynamic regions. From the MSM analysis for T1031-D1 and T1055-D1, there is significant dynamics due to flexible N-terminal tails, and there is a long loop that is stabilized by contacts with a neighboring domain in the original structure for T1093-D1. (see Figure S13C) In unrestrained MD simulations initiated from the experimental structures, the Cα RMSF values show large values in those regions (see Figure S20, upper panels). Such local high-amplitude fluctuations give rise to experimental macrostates that contain kinetically-proximate conformations but with a high degree of structural variability (see Figure S19). The high structural variability is a particularly challenging issue. Although we relaxed the experimental structures with all available biological system information such as inter-domain and inter-protein contacts, the relaxed structures still had imperfect structures with respect to the experimental structure, i.e. 77.5 in GDT-HA and 1.36 Å in Cɑ-RMSD on average. When we analyzed the MD-native structures of all TS domains, there was a clear correlation between thermal fluctuations of a residue and its error with an R² value of 0.40. (Figure S21) In general, some deviations may be expected due to force field inaccuracies, but the dynamic nature of protein structures poses an additional challenge. In the macrostates of these three domains, snapshots with high GDT-HA scores (above 70) are extremely rare and the RWplus potential that we use for filtering cannot identify them with high specificity (see Figure S22, right panels). This may be expected because experimental structures should capture the ensemble and time average of native-like conformations rather than any specific snapshot that may exist in a single molecule at a single time. The ensemble-averaging protocol employed here addresses this issue in principle. However, it means that in order to make highly accurate structure predictions of average structures for systems with significant dynamics, it is necessary not just to find the native state but correctly and completely sample the entire set of conformations corresponding to the native basin. This is, of course, a formidable challenge for the simulations because it requires complete sampling and a force field that is accurate enough to reproduce the entire native state ensemble for systems with significant conformational heterogeneity.

Why was it so difficult to refine AF2 models?

Our refinement protocol continued to be able to refine models from other predictors, including many models generated based on machine-learning methods. However, we experienced significant difficulty in improving AF2 models. A simple explanation may be that AF2 models already had very high accuracy to begin with. In terms of GDT-HA, only 26 out of 87 TS domains had lower than 70 GDT-HA units. Thus, not many models required refinement. However, even for models that had significant errors that should have been fixed, refinement was not very successful.

The MSM analysis and relaxation of the experimental structures revealed several issues with the current refinement protocol. First, there is still a sampling problem with the MD-refinement protocol. To reach the native state from the initial model state via MD simulations, it has to overcome several kinetic energy barriers for partial unfolding and refolding.²⁵ However, time required for the transitions were much longer than our simulations for refinement, and also, state transitions were prohibited by the restraints. As a result, the sampled structures during the refinement simulations hardly deviated from the initial AF2 models, despite improvements in our sampling protocol.

However, even though the structures did not deviate much from the AF2 models, they appeared to be consistently worse in terms of standard accuracy metrics. This is an interesting observation and likely reflects that the AF2 method was trained to directly predict ensemble-averaged experimental structures at very high accuracy. On the other hand, MD refinement protocols have to sample conformations via MD simulations and obtain an ensemble-averaged structure using the sampled conformations. MD simulations sample conformations around the energy minimum basin for a state, however, the sampled ensemble may be incomplete, slightly inaccurate, or weighted incorrectly, all of which would affect the accuracy of the ensemble average even though sampled conformations belong to the experimental macrostate. (Figure S20 bottom panels and Figure S21) We observed that the experimental structures deteriorated as much as 77.5 in GDT-HA and 1.36 Å in Cɑ-RMSD on average as a cumulative result of minor fluctuations across the experimental ensemble averaged structures. In other words, just like MD simulations of any experimental structures do not exactly recover the experimental ensemble averages, any simulations of the AF2 models are likely to lead to a deterioration of accuracy in the parts of the model that were predicted correctly, while the refinement simulations could not cross kinetic barriers needed to improve actual errors in the initial AF2 models.

Second, protein domains in contact with other domains or proteins clearly emerged as a major challenge. The relaxation of the experimental structures demonstrates that some of the domains cannot be stabilized by themselves and need other domains or proteins to maintain their experimentally determined structures. Indeed, the MSM analysis also showed that the energy landscape can be altered by interactions with other proteins in the system. The inclusion of other biomolecules is in principle possible during refinement, but in practice there may not be enough information about such contacts, and it increases the computational costs during the MD simulations. Previously, inter-protein and -domain contacts were not so critical for refinement because most models had easily refinable errors, while interface regions were often not modeled with high-accuracy. However, now, AF2 models apparently learned not only intra-domain interactions but also biologically relevant domain-domain and inter-protein interactions which made it extremely challenging to then ‘refine’ such models without considering such interactions.

Role of MD-based refinement in the future

Physics-based refinement has served its purpose as an orthogonal approach for improving the quality of protein models that were predicted by informatics-based approaches. The emergence of highly accurate structure prediction by machine learning is now raising questions about the limitations and the future role of physics-based refinement. The machine learning based models still have deficiencies, but further refinement has become much harder. As the current refinement protocols rely on MD simulations, the sampling problem continues to be a major challenge as it continues to be difficult to reach different conformational states from a given initial model. It may be possible, however, to eventually address this problem by applying enhanced sampling methods. One could imagine, for example, that MD simulations could be assisted or guided by machine learning methods.^29,66 However, the larger issue that has emerged from this round of CASP is the importance of the larger environment and the experimental conditions under which structures are determined. Going forward, it appears that any attempts at structure refinement without inclusion of such interaction contexts are increasingly becoming a futile effort. Finally, there is probably also room for better force fields, such as polarizable force fields⁶⁷ or force fields parameterized directly against quantum-mechanical energy functions.⁶⁸ Considering such approaches may be necessary to go further towards true atomistic accuracy.

Another view may be that the role of protein model refinement will change in the future. Previously, the purpose of refinement was to improve protein model quality. As predicted models are clearly becoming much more accurate with respect to experimentally obtained structures, the focus on accuracy improvements may not be as critical anymore. However, physics-based refinement can be re-defined as a tool for predicting models under various environmental conditions starting from an initial model. For example, a protein structure may adopt different conformations upon transient protein-protein interaction, but structure prediction for a monomer would not be expected to consider interacting proteins, or even alternative conformations based on different interaction partners. Physics-based refinement also can be used to generate multiple distinct structures with comparable free energies. Since proteins are inherently flexible molecules, dynamics is a feature, and many proteins feature not just one but multiple functionally relevant conformations. Indeed, an ensemble of structures often captured by cryo-EM⁶⁹ or X-ray crystallography⁷⁰ for a protein, albeit the resulting structures usually only report on the ensemble average. MD-based approaches can be utilized to generate the ensemble of structures by simulating from an initial model. Finally, MD-based approaches can be applied for predicting conformations in a biological environment rather than under in vitro or structure determination conditions. In a cell, a protein is in a crowded environment,⁷¹ which consists of other biomolecules. All of these environmental factors may be hard to consider during structure prediction, and it may be a long time before suitable machine learned models can be trained to capture all of these facets that are encountered by proteins in real physical environments.