Significance
Understanding the principles underlying microbial growth is paramount to the cycle of carbon and nutrients in the biosphere, bioremediation technologies, and biochemical engineering, as well as to natural selection and evolution. Yet, fundamental questions remain on the links between mass and energy balances in microbial metabolism and growth. Guided by a nonequilibrium thermodynamics framework, we interpret extensive literature data on microbial growth. The analysis reveals how mass and energy conversion are tightly coupled by scaling laws relating the thermodynamic efficiency to the electron donor uptake rate and the growth yield. Most importantly, these results appear to be universal, in that they apply across microbial species and metabolic pathways, and pave the way for a general thermodynamic theory of microbiological systems.
Keywords: microbial growth, thermodynamics, energy dissipation, energy scaling, thermodynamic efficiency
Abstract
Microbial growth is a clear example of organization and structure arising in nonequilibrium conditions. Due to the complexity of the microbial metabolic network, elucidating the fundamental principles governing microbial growth remains a challenge. Here, we present a systematic analysis of microbial growth thermodynamics, leveraging an extensive dataset on energy-limited monoculture growth. A consistent thermodynamic framework based on reaction stoichiometry allows us to quantify how much of the available energy microbes can efficiently convert into new biomass while dissipating the remaining energy into the environment and producing entropy. We show that dissipation mechanisms can be linked to the electron donor uptake rate, a fact leading to the central result that the thermodynamic efficiency is related to the electron donor uptake rate by the scaling law and to the growth yield by . These findings allow us to rederive the Pirt equation from a thermodynamic perspective, providing a means to compute its coefficients, as well as a deeper understanding of the relationship between growth rate and yield. Our results provide rather general insights into the relation between mass and energy conversion in microbial growth with potentially wide application, especially in ecology and biotechnology.
Microbial metabolism and growth are the result of complex interactions between constituents and reactions organized in a metabolic network that regulates the transfer of mass and energy (1). While effort is being devoted to genome-scale reconstruction of such biochemical networks (2), so that emerging phenotypes could be predicted by solving mass and energy balance for each link of the network (e.g., flux and energy balance analysis) (3, 4), its complexity still makes it hard to translate such predictions into a mechanistic understanding of microbial metabolism (5). As a result, microbial growth is often studied through macroscopic approaches that analyze the microbial cell or community as a whole (6). At this scale, key descriptive parameters are the growth rate, the yield, and the thermodynamic efficiency, which reflect the internal regulation of the metabolic network in response to environmental conditions and structural constraints naturally imposed by evolution (7–9).
Growth rate, yield, and thermodynamic efficiency are intrinsically related by the fundamental interconnection between mass and energy balances (10–14). A microbe, or a microbial community, can be considered an open thermodynamic system that dissipates energy to maintain and operate under nonequilibrium conditions (14–16). Specifically, a microbe is conceptually similar to a chemical engine transducing free energy (12, 17–20), in which a thermodynamically favorable catabolic reaction (e.g., oxidation of an electron donor [ED]) fuels a set of anabolic reactions (thermodynamically unfavorable generally), leading ultimately to cell replication. Similarly to heat engines, biomass growth reaches maximum thermodynamic efficiency (i.e., the efficiency of this energy conversion) only if it proceeds infinitesimally slow (i.e., a quasistatic process). As the microbial engine runs faster, some energy must be necessarily dissipated, and entropy is produced, resulting in reduced thermodynamic efficiencies. In other words, biosynthesis, strictly a nonequilibrium process, necessarily carries an energetic cost: free energy dissipation (14). As a result, in addition to trade-offs in nutrient allocation, microorganisms face important trade-offs in energy allocation.
These microbial engines drive and regulate biogeochemical cycles, and their abundance in the Earth’s biosphere and the rate at which they operate have profound impacts on ecosystem functioning (21, 22). Yet, due to the difficulty of describing biological systems (such as microorganisms) from basic principles, fundamental questions remain on the relation between energy (thermodynamic) efficiency and microbial growth parameters. Key examples include the relationship between growth rate and yield (23–25) and the observed variability in maintenance requirements (26), which reflect trade-offs in both nutrient and energy allocation. While these questions are commonly addressed from a mass balance perspective [e.g., the Pirt equation (27)] and thus, only address the issue of nutrient allocation, a nonequilibrium thermodynamics approach may shed new light on energy generation and transfer from catabolism to anabolism and in turn, on the relation with growth parameters (i.e., growth rate and yield) (28–30).
Along the lines of finite-time thermodynamics (31–33), some studies have analyzed the relation between growth and energy efficiency to explore possible underlying optimality principles governing metabolic regulation and growth (17, 34–36). These were based on the assumption of linear nonequilibrium thermodynamics (for a system not too far from equilibrium), in which a coupling coefficient expressing the degree of coupling between the anabolic and catabolic reactions was interpreted as a parameter that microbes regulate to satisfy some optimization criteria (e.g., power output, growth rate, and so on). Given the low thermodynamic efficiencies, however, it is not so clear whether microbial growth is truly a close to equilibrium phenomenon, hence questioning whether linear thermodynamics applies. More general Gibbs free energy frameworks have also been developed but with the specific goal of estimating growth yields from typical energy dissipation rates observed experimentally (18, 29, 37, 38). It remains to be explored which macroscopic parameters are closely related to the speed of the microbial machinery and its dissipation mechanisms, thereby regulating the energy trade-off.
Here, we present a comprehensive analysis of the nonequilibrium thermodynamics of microbial growth. In particular, we analyze an extensive dataset on monoculture growth guided by a detailed formulation of the governing energy balance equations. By placing particular emphasis on the relationships between energy dissipation and macroscopic growth parameters, we obtain relations for the thermodynamic efficiency, of general validity across microbial species and metabolic pathways, which uniquely link mass and energy balances. In light of our results, we provide an energetic perspective on the Pirt equation and the trade-offs between rates and yield and conclude by highlighting the importance of the results for microbial growth modeling.
Theory
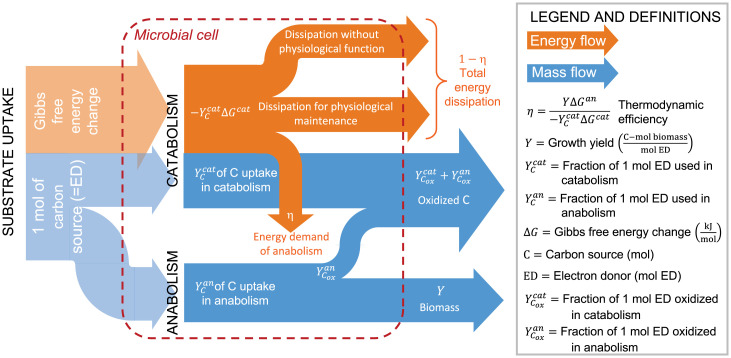
Whether at steady state (continuous cultures) or growing in batch, microbial growth is a nonequilibrium thermodynamic process. In contrast to isolated systems, which always relax to equilibrium, microbes are open thermodynamic systems, which exchange matter and energy with the environment to store energy and maintain an out-of-equilibrium state (14, 15). In fact, microbial isolates effectively operate as thermodynamic machines, specifically as free energy converters; they harvest energy from highly energetic but kinetically stable compounds (catabolic reaction) and use it to synthesize new biomass (anabolic reaction) or to perform basic metabolic functions (Fig. 1). Being open thermodynamic systems operating at a finite rate out of equilibrium, microbes continuously dissipate some of the energy they harvest and produce entropy, in accordance with the second law of thermodynamics (19).
Fig. 1.
Schematics of ED and energy partitioning for a metabolism in which the carbon source C is also used as the ED. After being taken up, a fraction of the ED is directed to the catabolic reaction to produce energy, . The remaining ED is utilized in the anabolic reaction to create new biomass. Of the catabolic energy , the anabolic reaction uses only an amount equal to , while the remaining is dissipated. The energy partitioning is characterized by the thermodynamic efficiency .
Coupling Catabolic and Anabolic Reactions
To establish our notation and explicitly derive the energy fluxes during microbial growth, it is instructive to briefly describe the catabolic and anabolic reactions through which microbes obtain and then utilize energy, respectively. When necessary (e.g., in the stoichiometric coefficients), we use the superscript to relate quantities to the catabolic (cat) or anabolic (an) reaction. For brevity, here we discuss the case in which the carbon source (C) is also the ED, while the derivation of the equations for a more general case is presented in Materials and Methods.
The input of energy for microbial growth derives from a catabolic reaction, involving an ED (C in this case) and an electron acceptor A (e.g., O2). As illustrated in Fig. 1, for a mole of C entering the microbial cell, a fraction is utilized in the catabolic reaction (39),
| (1) |
where C is the oxidized form of C, A is the reduced form of the electron acceptor, and the Y’s are the corresponding stoichiometric coefficients. As the reaction proceeds, for constant pressure and temperature the reaction releases an amount of energy per mole C oxidized equal to the Gibbs free energy of the reaction (i.e., ), a part of which as we discuss below is needed for growth.
In parallel, the synthesis of new biomass can be represented by a corresponding anabolic reaction, where the carbon source C is converted into biomass B. In this case, given a nitrogen source N, the anabolic reaction can be written as (39)
| (2) |
where Y is the growth yield, the C mole of biomass produced per mole ED taken up (Fig. 1). Eq. 2 is for a C that is more oxidized than B, so that to reduce its oxidation state, a fraction of C is used as ED and is oxidized to to generate the necessary electrons (e.g., Table 1). As we discuss later, this situation is more relevant from a thermodynamic perspective, but for completeness, the case of C more reduced than B is also presented in Materials and Methods. The Gibbs free energy change per C mole biomass associated with the anabolic reaction, , is positive and indicates the amount of energy that is necessary to carry out the reaction.
Table 1.
Example derivation of the macrochemical equation for the growth of S. lothica (strain PV-4) with C = ED = acetate and A = NO
| Reaction | YA | YC | Y | |||
| Catabolism | 1.32 | 0.66 | 0.66 | 1.32 | — | |
| Anabolism | — | — | 0.34 | 0.03 | 0.65 | |
| Overall* | ||||||
| 1.32 | 0.66 | 1 | 1.35 | 0.65 |
*The macrochemical equation expressed per unit mole of C is obtained by summing up the catabolic and anabolic reactions, as discussed in Coupling Catabolic and Anabolic Reactions.
At this point, the macrochemical growth equation, expressing the overall stoichiometry of microbial growth, is obtained by summing up Eqs. 1 and 2 (29, 39),
| (3) |
in which the stoichiometric coefficient of C is equal to one because we expressed the mass balances per one mole of C taken up by the microbial cell (Fig. 1) (so that ). To characterize the reaction kinetics of Eq. 3, we also need to define the microbial growth rate. The specific growth rate (growth rate per unit biomass) is referred to as μ (hours– 1), while the ED uptake rate (moles ED C mole biomass– 1 hour– 1). As an example, we derive in Table 1 the macrochemical equation for the growth of Shewanella lothica (strain PV-4) using acetate as both C and ED and nitrate as A.
The Energy Balance of Growth
The energy balance can then be derived by combining the Gibbs free energies of the catabolic and anabolic reactions. According to the maximum work (40) and Gouy–Stodola (41, 42) theorems, however, the energy balance also reflects the fact that only a fraction of the energy released by the catabolic reaction can effectively be utilized in the anabolic reaction, while the remaining is dissipated into the environment, producing entropy (Fig. 1). Accordingly, if is the catabolic energy and is the anabolic energy (both in kilojoules mole ED– 1), then the microbial energy balance can be written as
| (4) |
where the energy dissipated , with being the entropy production. Eq. 4 can also be formulated in terms of energy fluxes by multiplying both sides by the ED uptake rate, μED.
The thermodynamic efficiency of microbial growth (i.e., the ratio of anabolic to catabolic energies) (Materials and Methods) then is
| (5) |
where λ () links the stoichiometry of the catabolic and anabolic reactions and corresponds to the number of moles of ED used in the catabolic reaction to produce one C mole of biomass. Intuitively, Eqs. 4 and 5 depend on the speed of the energy conversion (i.e., how fast the microbial machinery operates), although such a dependence is not explicit. Indeed, virtually all the energy terms in Eq. 4 depend on this speed. As we show below, in analogy with heat engines, the efficiency η will be at its maximum for quasistatic transformations and will decrease as the microbial engine runs faster. While in heat engines the maximum efficiency is the Carnot efficiency (, with TC and TH being the cold and hot temperatures, respectively), which is lower than one, in chemical engines maximum efficiency can theoretically reach one. However, energy dissipation includes both energy requirements for physiological maintenance and energy waste due to inefficiencies (26, 35, 43) (Fig. 1). As we show in Materials and Methods, since the energetic cost for physiological maintenance is inevitable, the maximum thermodynamic efficiency of microbial communities is also lower than one. Note also that here we expressed the energy balance per mole ED consumed, in contrast to previous investigations that analyzed the energy balance per C mole biomass produced (18, 29, 39). This unit conversion will unveil a general pattern in the energy conversion (Results) that was not previously observed.
Lastly, the definition of thermodynamic efficiency (5) applies only to the case . In fact, when B is more oxidized than C it is possible that the anabolic reaction is itself a thermodynamically spontaneous reaction (). In this case, by synthesizing biomass the system actually moves toward thermodynamic equilibrium. Even in these energetically favorable conditions, microorganisms still run the catabolic reaction and obtain energy for basic metabolic functions. Therefore, both catabolic and anabolic reactions are sources of energy; however, all the energy is dissipated, and η = 0.
Results
Guided by the theory outlined above, we analyzed existing data on growth of bacterial isolates (44). We relied on an extensive dataset in ref. 29, which mostly includes data originally compiled in ref. 45. Overall, the dataset contains data on 132 growth experiments, with EDs including carbon sources with one to six C atoms and H2. Data provide growth yields (per mole ED and per C mole ED), stoichiometry of the anabolic and catabolic reactions, standard- and nonstandard-state Gibbs free energies, temperature, and specific growth rate. The reaction and calculations of thermodynamic data are based on microbial biomass formula C5H9ON (molecular weight 24.6 g C mol biomass– 1). Throughout the dataset, temperature is about 300 K. As we mentioned in The Energy Balance of Growth, the thermodynamic efficiency for , while η = 0 for . Accordingly, we do not consider those experiments for which , ending up with data on 100 experiments. Furthermore, the specific growth rate μ was not always provided, so in those analyses requiring μ, 65 experiments are considered.
Thermodynamic Efficiency
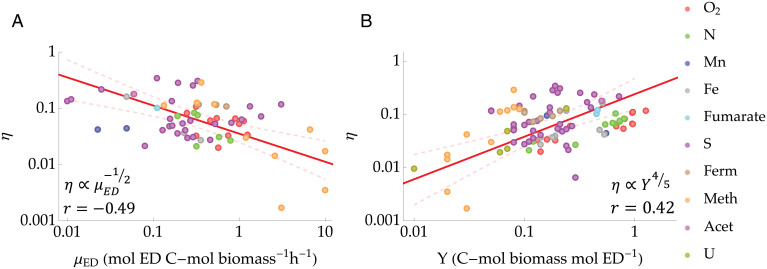
We began by computing the energy terms in Eq. 4 to explore the variability in thermodynamic efficiency (Eq. 5) across the experiments. In the dataset, the thermodynamic efficiencies are rather low, spanning from to and with an average of . However, given that microbes likely operate far from equilibrium (i.e., outside of the linear regime) (14, 46, 47), it is not surprising to observe such low efficiencies. We then searched for a relation between the efficiency of energy and mass conversions, which led us to the first central result that the thermodynamic efficiency decreases with μED following a power law scaling (Fig. 2),
| (6) |
where the empirical exponent (Table 2 shows a summary of the regressions). Interestingly, such relation agrees with the expectation that η increases as (i.e., quasistatic transformation). It also suggests that η may be related exclusively to the speed of the cellular engine and not (at least directly) to the size of the population or whether the latter is in steady state or not. The importance of such a relation is paramount, in that it provides an explicit link between mass and energy balances. The direct implications of this relation are discussed in Discussion.
Fig. 2.
Thermodynamic efficiency across different metabolic pathways. (A) Power law relation between thermodynamic efficiency, η, and ED uptake rate, μED. (B) Power law relation between thermodynamic efficiency, η, and growth yield, Y. Red lines indicate the observed regression lines, while dashed light red lines indicate the 95% confidence bands. The data points are plotted using different colors depending on the specific electron accepting metabolic pathway (O2, N, Mn, Fe, fumarate, S, and U; fermentation [Ferm], methanogenic [Meth], and acetanogenic [Acet]). The power laws and the corresponding Pearson’s r values are shown. Table 2 shows a summary of the regressions.
Table 2.
Scaling of thermodynamic efficiency and energy fluxes in microbial growth
| Y | X | Slope (CI) | Intercept (CI) | Pearson’s r | P value | n | Fig. |
| η | μED | –0.476 (–0.719, –0.271) | –1.443 (–1.579, –1.306) | –0.486 | <0.001 | 65 | Fig. 2A |
| η | Y | 0.804 (0.491, 1.257) | –0.621 (–0.888, –0.353) | 0.416 | <0.001 | 100 | Fig. 2B |
| μED | –0.309 (–0.753, 0.046) | 1.685 (1.490, 1.881) | –0.217 | >0.050 | 65 | Fig. 3A | |
| μED | –0.871 (–1.324, –0.559) | 0.203 (–0.007, 0.414) | –0.526 | <0.001 | 65 | Fig. 3B | |
| Y | 0.720 (0.271, 1.502) | –0.766 (–1.137, –0.394) | 0.277 | <0.01 | 100 | Fig. 3C | |
| λ | Y | –1.137 (–1.167, –1.108) | –0.183 (–0.208, –0.158) | –0.992 | <0.001 | 100 | Fig. 3D |
| μ | Y | 2.750 (1.043, 4.932) | 0.873 (–1.558, 3.304) | 0.214 | >0.05 | 65 | Fig. 4A |
| Y | –2.021 (–3.450, –1.352) | –2.005 (–2.705, –1.305) | –0.449 | <0.001 | 65 | Fig. 4B |
All the scaling relations, , were fitted through a major axis regression in a log–log scale. Here, we report the exponent b (i.e., slope in the log–log plot) and the Pearson’s coefficient r. We also report the number n of observations.
Next, as a direct consequence of the above relation we investigated whether variations in thermodynamic efficiency are linked to variations in the mass conversion efficiency, namely to the growth yield. As shown in Fig. 2, η indeed scales with the growth yield as
| (7) |
where the exponent . These two results establish a fundamental relationship between mass and energy conversion in microbial growth, which remarkably, applies across different microbial species and metabolic pathways for most of the explored range of μED and Y (Fig. 2). Interestingly, the relation seems to also apply within each individual metabolic pathway, as suggested by their efficiencies aligning well with the regression lines. This is especially visible in Fig. 2B, for which more data (on Y) were available. However, more experimental data for each metabolic pathway and wider ranges of μED and Y are needed to test this properly.
Although the relations are highly significant (P < 0.001), observations still scatter around the regression lines (i.e., ). An important source of uncertainty here is the use of a constant biomass formula (i.e., C5H9ON) and the corresponding Gibbs free energy of formation. The latter in fact can vary substantially (at least by a factor of two) due to variations in the biomass formula, as recently shown in ref. 48. Additionally, since the dataset is a compilation of various experiments from different laboratories and performed over a window of at least 50 y (29), some uncertainty also inevitably arises from methodological differences in the laboratory measurements across the experiments.
Origin of the Energy Scaling
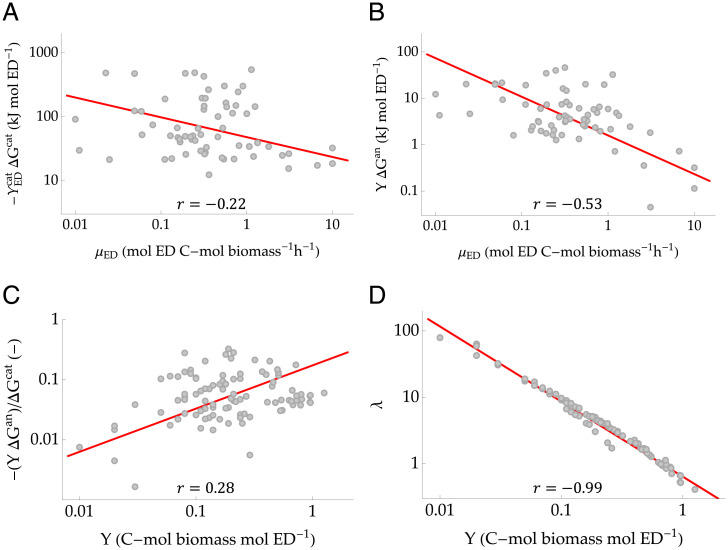
To understand the origin of the above relations, we further explored how the energy terms in Eq. 4 vary as a function of μED and Y. We noticed that the decrease of η with the ED uptake rate is the result of two contrasting trends in the catabolic and anabolic energies. On the one hand, when the catabolic energy that can be obtained from the ED () is low, microbes direct more ED to the catabolic reaction (hence, and μED increase) but are only partly successful in balancing the production of energy. As a result, as μED increases, the catabolic energy per unit ED () decreases in absolute value (Fig. 3A). This mechanism tends to increase η. On the other hand, the anabolic energy, , also decreases with μED (Fig. 3B), but its decay is faster than the decay of the catabolic energy, suggesting that due to energy dissipation, more energy does not make it to the anabolic reaction as μED increases. This fact would decrease η. The ratio of these two trends yields the power law in Eq. 6.
Fig. 3.
(A) Decrease of catabolic energy per unit ED with respect to the ED uptake rate, μED. (B) Decrease of anabolic energy per unit ED with respect to μED. (C) Relation between the dimensionless ratio and growth yield, Y. (D) Relation between the fraction of ED used in the catabolic reaction, λ, and Y. Red lines and gray points indicate the observed regression lines and experimental values, respectively. The Pearson’s r values are shown, while the regressions are summarized in Table 2.
Independently, we observed that the dimensionless ratio of the anabolic energy to the catabolic energy, , scales with the growth yield Y (Fig. 3C) with an exponent . Accordingly, η (Eq. 5) can be expressed as
| (8) |
The thermodynamic efficiency thus depends on λ and its relationship with Y. Recall that λ expresses the number of times the catabolic reaction proceeds in order to meet the energy demand for the growth of one C mole of biomass. By definition, higher values of λ imply that more ED needs to be consumed to produce one C mole of biomass, hence reducing the growth yield. Fig. 3D shows that across metabolic pathways, λ decreases with Y also following a power law. It can be readily seen that substituting this power law into Eq. 8 yields Eq. 7.
Discussion
Even if microbes are complex biological structures operating in thermodynamic nonequilibrium, we found fundamental relations (Eqs. 6 and 7) at the macroscopic level linking the thermodynamic efficiency η to commonly measured microbial parameters (ED uptake rate, μED, and growth yield, Y), thus strongly coupling mass and energy balances. Accordingly, knowing only one microbial growth parameter (e.g., μED) is sufficient to estimate the thermodynamic efficiency and interpret the energy balance in Eq. 4, at least under energy-limited conditions. As we discuss below, these findings have important theoretical and practical implications, from explaining the relationship between growth rate and yield under energy-limited conditions to providing mathematical expressions for improving biogeochemical modeling.
Energy Interpretation of the Pirt Equation
Our results on the scaling of the thermodynamic efficiency provide a direct thermodynamic interpretation to the dependence of microbial growth on maintenance requirements (26, 27, 49), generally described by the Pirt equation (27):
| (9) |
where the maintenance coefficient, m, represents the substrate utilized for all functions other than growth and Ymax is a hypothetical maximum growth yield for m = 0. In fact, the Pirt equation takes into account all the energetic and carbon requirements other than growth in terms of the substrate uptake rate but not in terms of the energy flow from catabolism to anabolism. Additionally, it has been challenging to understand variations in the coefficients m and Ymax (26).
Here, we can derive the Pirt equation directly from the metabolic balance (Eq. 4). Multiplying Eq. 4 by μED and dividing by , one obtains
| (10) |
where we have introduced the thermodynamic efficiency. By comparing Eqs. 9 and 10, one can readily see that
| (11) |
which link the maximum yield, Ymax, and the maintenance coefficient, m, to the thermodynamic efficiency. Additionally, the observed scaling relationships allow direct quantification of Ymax and m as a function of the uptake rate (Eq. 6) or of the growth yield (Eq. 7) across microbial species and metabolic pathways.
Interestingly, Roels (10, p. 2,480, equation 32) more than four decades ago defined the thermodynamic efficiency using Eq. 11 (), although not in the context of the Pirt equation. η and Ymax were then calculated based on the assumption that the thermodynamic efficiency could reach one (i.e., limit imposed by the second law of thermodynamics). As we show in Materials and Methods, however, because microbes are themselves the result of nonequilibrium conditions, the maximum thermodynamic efficiency is always lower than one. This energetic perspective on the Pirt equation also clarifies that the maintenance coefficient m accounts for both physiological (e.g., macromolecules turnover) and nonphysiological (i.e., inefficiencies, waste) requirements.
The Rate–Yield Trade-Off
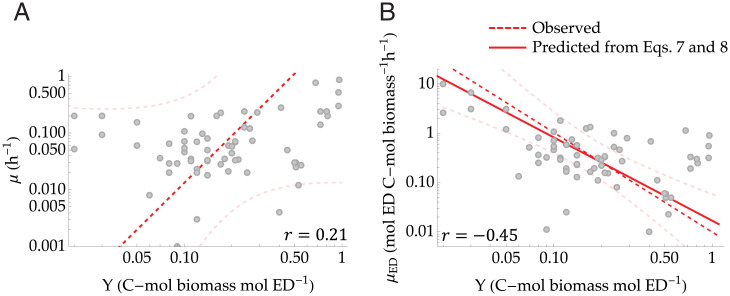
The above results also led us to important considerations on the rate–yield trade-off. The existence of a trade-off between growth rate and yield has often been reported (24, 25, 50), and its origin has been attributed to the second law of thermodynamics, and hence Eq. 4, in that higher energy dissipation is due to faster growth, which comes at the expense of the growth yield (e.g., refs. 23, 24, 51, and 52). However, while Eq. 4 suggests a relation between yield and dissipation, the equation per se does not explicitly show the dependence on the growth rate because it does not show how the various terms (e.g., Gibbs free energies, Y) may covary. In fact, the growth rate and the yield in energy-limited growth do not show such a trade-off (Fig. 4A), suggesting that this does not emerge from constraints on energy allocation. The growth rate–yield trade-off thus is likely the result of other mechanisms, such as within-species resource investment in stress resistance (53) or overflow metabolism (25), or at the community level due to ecological interactions leading to the prevalence of species with contrasting resource investment strategies (54).
Fig. 4.
Relations between (A) growth rate, μ, and yield, Y, and (B) ED uptake rate, μED, and Y. B shows that there is a trade-off between the ED uptake rate and yield, which follows a power law relation. The solid red line indicates the prediction based on Eqs. 6. and 7, while dashed red lines indicate the observed regression (dark red) and confidence bands (light red). Gray points indicate the experimental values. The Pearson’s r values are given, and the regressions are summarized in Table 2.
By contrast, as we discussed in the previous section, energy dissipation is related to the rate of ED uptake, μED, and to the growth yield, Y. Indeed, combining Eqs. 6 and 7 yields a power law relationship between μED and Y with exponent , hence suggesting a trade-off between the two. As illustrated in Fig. 4B, this trade-off is confirmed by the experimental data. The predicted slope falls within the 95% CI of the observed slope of (Table 2), where the small discrepancy may be due to limited sample size and data uncertainty. Recently, this trade-off was also observed in adaptive evolution experiments and numerical results from genome-scale models of Escherichia coli (55).
Importance for Biogeochemical Modeling
Lastly, relating the energy and mass balances of microbial growth (e.g., Eq. 6 linking the thermodynamic efficiency and ED uptake rate) allows integration of thermodynamics into biogeochemical models of microbial growth (29, 56–60), so as to effectively take into account the amount of energy available for growth. While a number of methods have been developed to compute the energy dissipation based on the composition of the carbon source (e.g., number of carbon atoms) when the specific carbon source is known (18, 29, 37–39), our results may be particularly useful when the exact carbon source or metabolic pathway is not known, such as in soil carbon modeling where the microbial carbon use efficiency (C mole biomass C mole substrate– 1) is calculated based on carbon (and energy) allocation to maintenance requirements (49, 61–63). A theoretical approach to account for metabolic constraints on growth related to body size (i.e., maintenance energy) leveraging the Pirt equation has been proposed in ref. 64. Based on the energy interpretation of the Pirt equation (Energy Interpretation of the Pirt Equation), this approach could be generalized by introducing the thermodynamic constraints (e.g., Eq. 6) related to the speed of the microbial machinery (i.e., the substrate uptake rate). This may have an impact in fields as diverse as ecosystem modeling (e.g., soil carbon cycling modeling) and biochemical engineering (e.g., water treatment, fermentation processes), in which it is important to accurately predict microbial growth (19).
Conclusions
The thermodynamics of microbial growth has received considerable attention for decades (10, 17, 34, 64). Understanding how microbes process energy may in fact elucidate the underlying fundamental principles governing the ecology and evolution of living systems at large, explain the success of empirical laws, such as the Monod equation (65), and guide research in nanotechnology inspired by biological systems (66). Here, we provided a comprehensive analysis of the nonequilibrium thermodynamics of microbial growth based on a large dataset on energy-limited growth. Our analysis showed that the thermodynamic efficiency is related by scaling laws to commonly measured macroscopic parameters (growth yield, ED uptake rate). These findings add to our understanding of mass and energy conversion in microbial growth (e.g., the Pirt equation, the rate–yield trade-off) and underline the importance of the thermodynamic efficiency in microbial growth and microbially mediated processes. Furthermore, the scaling laws can be readily integrated into biogeochemical modeling to account for thermodynamic constraints on microbial growth. In the light of these results, future investigations will explore the microscopic origin of the power laws [e.g., by analyzing the scaling properties of metabolic networks (1)] and whether similar thermodynamic scaling laws apply across evolutionary transitions (prokaryotes to metazoans), in which the demand for C and energy to maintain the biological structure tends to increase, resulting in a decrease in growth yields (67) and in shifts in metabolic scaling (68).
Materials and Methods
Coupling Catabolic and Anabolic Reactions
Here, we report a more general derivation than in the text, accounting for carbon sources either more oxidized or more reduced than biomass and also considering the case of a carbon source that is not the ED. As microorganisms take up substrates, energy is obtained from the catabolic reaction, which can be written generically as (Eq. 1)
| (12) |
where ED is the ED (the energy source), A is the electron acceptor, A is the reduced form of A, ED is the oxidized form of ED, and Y’s are the stoichiometric coefficients. As the reaction proceeds, an amount of energy equal to (at constant pressure and temperature) is released per mole of ED consumed. The energy released by the catabolic reaction is then used to drive the anabolic reaction. For carbon sources more oxidized than the biomass, this can be written as
| (13) |
where the ED is needed to reduce the oxidation state of C and form biomass. When the carbon source is more reduced than the biomass, electrons required for biosynthesis are already met, so the anabolic reaction needs an electron acceptor and can be written as
| (14) |
where for the compound participating in both catabolic and anabolic reactions, we used superscripts to distinguish the different yields between the two reactions. The Gibbs free energy change per unit biomass associated with the anabolic reaction [13] or [14] is .
To obtain the overall macrochemical equation, the catabolic and anabolic reactions need to be summed up. Then, for C more oxidized than B, one obtains
| (15) |
where since Y is the C mole biomass per one mole ED, we used the fact that , whereas for B more oxidized than C, we have
| (16) |
where we now used .
A common situation is one in which the ED is also the carbon source (i.e., ED = C). In this case, for C more oxidized than B, the overall growth equation reduces to
| (17) |
while for B more oxidized than C it reduces to
| (18) |
Metabolic Energy Balance
As mentioned in the text, the metabolic energy balance, Eq. 4, derives from the maximum work (40) and Gouy–Stodola (41, 42) theorems, which combine the first and second laws of thermodynamics. In other words, the metabolic energy balance is an exergy balance, according to which available energy (maximum work) can be utilized to do work (i.e., chemical work) or is dissipated into the environment,
| (19) |
where is the available energy, W is the chemical work, T is the temperature of the environment, and is the entropy production. For chemical reactions at constant temperature and pressure, the exergy is expressed in terms of Gibbs free energy. The available work is provided by the catabolic reaction, , while chemical work is done to drive the anabolic reaction, . The remaining energy that is not used by the anabolic reaction is dissipated into the environment:
| (20) |
Eq. 20 is essentially the starting point for the thermodynamics of microbial growth. The efficiency of this energy conversion is quantified by the thermodynamic efficiency, which can be generically defined as
| (21) |
Theoretically, η can vary between zero and one. If the conversion of energy occurred at an infinitesimally slow rate, then thermodynamic dissipation would tend to decrease, but as we show below, it is important to also take into account the physiological energy requirements to maintain the nonequilibrium state.
Maximum Thermodynamic Efficiency
An important goal of thermodynamics is also the estimation of maximum efficiencies of energy conversion (69). Generally, these are computed assuming quasistatic transformations (infinitesimally slow). In the case of microbial growth, however, microbes reside in a nonequilibrium state that requires a constant influx of energy (physiological maintenance requirements) to be maintained (70). The quasistatic condition is thus somewhat unrealistic for microbes, in that for slow transformations (small rate of energy production), these energy requirements would not be met and microbes would decay.
For microbial growth, a different definition of maximum thermodynamic efficiency that is more suitable for the nonequilibrium condition is needed. Rather than assuming quasistatic conditions, the maximum thermodynamic efficiency can be computed by assuming that the energy released by the catabolic reaction equals the amount of energy utilized for growth plus the energy needed for physiological maintenance, excluding inefficiencies (i.e., energy waste). Under these ideal conditions, the energy produced in the catabolic reaction, at rate , is equal to the energy needed by the anabolic reaction () plus the energy required for physiological maintenance, with mp being the portion of the total maintenance m (the Pirt equation) used for physiological functions (, mw being linked to energy dissipated via inefficiencies). Introducing these catabolic and anabolic energies in Eq. 21, the maximum thermodynamic efficiency can be expressed as
| (22) |
where the second equality was obtained through algebraic manipulation. If (i.e., energy is used for turnover of macromolecules), then Eq. 22 reduces to
| (23) |
Eqs. 22 and 23 readily show that, as long as , ηmax is always lower than one for microbial growth. This originates from the fact that microbial engines are the result of and operate under nonequilibrium conditions. Such an insight likely applies to any biological system. The equations above also demonstrate that the thermodynamic efficiency is a dynamic property of the microbial community, which is controlled by growth conditions. Maximum thermodynamic efficiencies tend to be higher under fast growth conditions (i.e., and ), while under slow growth conditions, maintenance requirements can prevail, such that and . This approach extends previous studies, in which only the condition is considered, so that the thermodynamic efficiency could virtually reach one.
Acknowledgments
This work was supported by the Department of Biological and Agricultural Engineering and AgriLife Research at Texas A&M University and US Department of Agriculture National Institute of Food and Agriculture Hatch Project 1023954. S.M. has received funding from the European Research Council under the European Union’s Horizon 2020 Research and Innovation Programme Grant 101001608.
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
Data Availability
Experimental data and Mathematica code used to draw the figures have been deposited in Texas Data Repository (https://dataverse.tdl.org/dataset.xhtml?persistentId=doi:10.18738/T8/4UGXZV). Experimental data were retrieved from ref. 29.
References
- 1.Jeong H., Tombor B., Albert R., Oltvai Z. N., Barabási A. L., The large-scale organization of metabolic networks. Nature 407, 651–654 (2000). [DOI] [PubMed] [Google Scholar]
- 2.Oberhardt M. A., Palsson B. Ø., Papin J. A., Applications of genome-scale metabolic reconstructions. Mol. Syst. Biol. 5, 320 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Edwards J. S., Covert M., Palsson B., Metabolic modelling of microbes: The flux-balance approach. Environ. Microbiol. 4, 133–140 (2002). [DOI] [PubMed] [Google Scholar]
- 4.Gianchandani E. P., Chavali A. K., Papin J. A., The application of flux balance analysis in systems biology. Wiley Interdiscip. Rev. Syst. Biol. Med. 2, 372–382 (2010). [DOI] [PubMed] [Google Scholar]
- 5.Lopatkin A. J., Collins J. J., Predictive biology: Modelling, understanding and harnessing microbial complexity. Nat. Rev. Microbiol. 18, 507–520 (2020). [DOI] [PubMed] [Google Scholar]
- 6.Scott M., Hwa T., Bacterial growth laws and their applications. Curr. Opin. Biotechnol. 22, 559–565 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Torres J., Natural selection and thermodynamic optimality. Il Nuovo Cimento D 13, 177–185 (1991). [Google Scholar]
- 8.Bachmann H., Bruggeman F. J., Molenaar D., Branco Dos Santos F., Teusink B., Public goods and metabolic strategies. Curr. Opin. Microbiol. 31, 109–115 (2016). [DOI] [PubMed] [Google Scholar]
- 9.Saadat N. P., Nies T., Rousset Y., Ebenhöh O., Thermodynamic limits and optimality of microbial growth. Entropy (Basel) 22, 277 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Roels J., Application of macroscopic principles to microbial metabolism. Biotechnol. Bioeng. 22, 2457–2514 (1980). [DOI] [PubMed] [Google Scholar]
- 11.Qian H., Beard D. A., Thermodynamics of stoichiometric biochemical networks in living systems far from equilibrium. Biophys. Chem. 114, 213–220 (2005). [DOI] [PubMed] [Google Scholar]
- 12.Carlson C. A., Del Giorgio P. A., Herndl G. J., Microbes and the dissipation of energy and respiration: From cells to ecosystems. Oceanography (Wash. D.C.) 20, 89–100 (2007). [Google Scholar]
- 13.von Stockar U., Biothermodynamics of live cells: A tool for biotechnology and biochemical engineering. J. Non-Equilib. Thermodyn. 35, 415–475 (2010). [Google Scholar]
- 14.Penocchio E., Rao R., Esposito M., Thermodynamic efficiency in dissipative chemistry. Nat. Commun. 10, 3865 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Ragazzon G., Prins L. J., Energy consumption in chemical fuel-driven self-assembly. Nat. Nanotechnol. 13, 882–889 (2018). [DOI] [PubMed] [Google Scholar]
- 16.Tafoya S., Large S. J., Liu S., Bustamante C., Sivak D. A., Using a system’s equilibrium behavior to reduce its energy dissipation in nonequilibrium processes. Proc. Natl. Acad. Sci. U.S.A. 116, 5920–5924 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Westerhoff H. V., Hellingwerf K. J., Van Dam K., Thermodynamic efficiency of microbial growth is low but optimal for maximal growth rate. Proc. Natl. Acad. Sci. U.S.A. 80, 305–309 (1983). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.von Stockar U., Maskow T., Liu J., Marison I. W., Patiño R., Thermodynamics of microbial growth and metabolism: An analysis of the current situation. J. Biotechnol. 121, 517–533 (2006). [DOI] [PubMed] [Google Scholar]
- 19.von Stockar U., Biothermodynamics: The Role of Thermodynamics in Biochemical Engineering (PPUR Presses Polytechniques, 2013). [Google Scholar]
- 20.Niebel B., Leupold S., Heinemann M., An upper limit on Gibbs energy dissipation governs cellular metabolism. Nat. Metab. 1, 125–132 (2019). [DOI] [PubMed] [Google Scholar]
- 21.Falkowski P. G., Fenchel T., Delong E. F., The microbial engines that drive Earth’s biogeochemical cycles. Science 320, 1034–1039 (2008). [DOI] [PubMed] [Google Scholar]
- 22.Stumm W., Morgan J. J., Aquatic Chemistry: Chemical Equilibria and Rates in Natural Waters (John Wiley & Sons, 2012), vol. 126. [Google Scholar]
- 23.Pfeiffer T., Schuster S., Bonhoeffer S., Cooperation and competition in the evolution of ATP-producing pathways. Science 292, 504–507 (2001). [DOI] [PubMed] [Google Scholar]
- 24.Bachmann H., et al., Availability of public goods shapes the evolution of competing metabolic strategies. Proc. Natl. Acad. Sci. U.S.A. 110, 14302–14307 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Lipson D. A., The complex relationship between microbial growth rate and yield and its implications for ecosystem processes. Front. Microbiol. 6, 615 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.van Bodegom P., Microbial maintenance: A critical review on its quantification. Microb. Ecol. 53, 513–523 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Pirt S. J., The maintenance energy of bacteria in growing cultures. Proc. R. Soc. Lond. B Biol. Sci. 163, 224–231 (1965). [DOI] [PubMed] [Google Scholar]
- 28.Maitra A., Dill K. A., Bacterial growth laws reflect the evolutionary importance of energy efficiency. Proc. Natl. Acad. Sci. U.S.A. 112, 406–411 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Smeaton C. M., Van Cappellen P., Gibbs energy dynamic yield method (GEDYM): Predicting microbial growth yields under energy-limiting conditions. Geochim. Cosmochim. Acta 241, 1–16 (2018). [Google Scholar]
- 30.Chakrawal A., Herrmann A. M., Šantrůčková H., Manzoni S., Quantifying microbial metabolism in soils using calorespirometry—a bioenergetics perspective. Soil Biol. Biochem. 148, 107945 (2020). [Google Scholar]
- 31.Mironova V. A., Tsirlin A. M., Kazakov V. A., Berry R. S., Finite-time thermodynamics: Exergy and optimization of time-constrained processes. J. Appl. Phys. 76, 629–636 (1994). [Google Scholar]
- 32.Bejan A., Entropy generation minimization: The new thermodynamics of finite-size devices and finite-time processes. J. Appl. Phys. 79, 1191–1218 (1996). [Google Scholar]
- 33.Andresen B., Current trends in finite-time thermodynamics. Angew. Chem. Int. Ed. Engl. 50, 2690–2704 (2011). [DOI] [PubMed] [Google Scholar]
- 34.Lems S., Van der Kooi H., de Swaan Arons J., Thermodynamic optimization of energy transfer in (bio) chemical reaction systems. Chem. Eng. Sci. 58, 2001–2009 (2003). [Google Scholar]
- 35.Von Stockar U., Optimal energy dissipation in growing microorganisms and rectification columns. J. Non-Equilib. Thermodyn. 39, 3–11 (2014). [Google Scholar]
- 36.Nath S., Optimality principle for the coupled chemical reactions of ATP synthesis and its molecular interpretation. Chem. Phys. Lett. 699, 212–217 (2018). [Google Scholar]
- 37.Hoijnen J. J., van Loosdrecht M. C., Tijhuis L., A black box mathematical model to calculate auto- and heterotrophic biomass yields based on Gibbs energy dissipation. Biotechnol. Bioeng. 40, 1139–1154 (1992). [DOI] [PubMed] [Google Scholar]
- 38.Heijnen S. J., Thermodynamics of microbial growth and its implications for process design. Trends Biotechnol. 12, 483–492 (1994). [Google Scholar]
- 39.Kleerebezem R., Van Loosdrecht M. C., A generalized method for thermodynamic state analysis of environmental systems. Crit. Rev. Environ. Sci. Technol. 40, 1–54 (2010). [Google Scholar]
- 40.Callen H. B., Thermodynamics and an Introduction to Thermostatistics (Wiley, New York, NY, 1998). [Google Scholar]
- 41.Lucia U., The Gouy-Stodola theorem in bioenergetic analysis of living systems (irreversibility in bioenergetics of living systems). Energies 7, 5717–5739 (2014). [Google Scholar]
- 42.Pal R., On the Gouy–Stodola theorem of thermodynamics for open systems. Int. J. Mech. Eng. Educ. 45, 194–206 (2017). [Google Scholar]
- 43.Tijhuis L., Van Loosdrecht M. C., Heijnen J. J., A thermodynamically based correlation for maintenance Gibbs energy requirements in aerobic and anaerobic chemotrophic growth. Biotechnol. Bioeng. 42, 509–519 (1993). [DOI] [PubMed] [Google Scholar]
- 44.Calabrese S., Chakwral A., Manzoni S., Van Cappellen P., Energetic scaling in microbial growth_data. Texas Data Repository. 10.18738/T8/4UGXZV. Deposited 28 May 2021. [DOI]
- 45.Roden E. E., Jin Q., Thermodynamics of microbial growth coupled to metabolism of glucose, ethanol, short-chain organic acids, and hydrogen. Appl. Environ. Microbiol. 77, 1907–1909 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.De Groot S. R., Mazur P., Non-Equilibrium Thermodynamics (Courier Corporation, 2013). [Google Scholar]
- 47.van der Zwaag D., Meijer E. W., Fueling connections between chemistry and biology. Science 349, 1056–1057 (2015). [DOI] [PubMed] [Google Scholar]
- 48.Popovic M., Thermodynamic properties of microorganisms: Determination and analysis of enthalpy, entropy, and Gibbs free energy of biomass, cells and colonies of 32 microorganism species. Heliyon 5, e01950 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Wang G., Post W. M., A theoretical reassessment of microbial maintenance and implications for microbial ecology modeling. FEMS Microbiol. Ecol. 81, 610–617 (2012). [DOI] [PubMed] [Google Scholar]
- 50.Ferenci T., Trade-off mechanisms shaping the diversity of bacteria. Trends Microbiol. 24, 209–223 (2016). [DOI] [PubMed] [Google Scholar]
- 51.Novak M., Pfeiffer T., Lenski R. E., Sauer U., Bonhoeffer S., Experimental tests for an evolutionary trade-off between growth rate and yield in E. coli. Am. Nat. 168, 242–251 (2006). [DOI] [PubMed] [Google Scholar]
- 52.Stettner A. I., Segrè D., The cost of efficiency in energy metabolism. Proc. Natl. Acad. Sci. U.S.A. 110, 9629–9630 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Maharjan R., et al., The form of a trade-off determines the response to competition. Ecol. Lett. 16, 1267–1276 (2013). [DOI] [PubMed] [Google Scholar]
- 54.Malik A. A., et al., Defining trait-based microbial strategies with consequences for soil carbon cycling under climate change. ISME J. 14, 1–9 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Cheng C., et al., Laboratory evolution reveals a two-dimensional rate-yield tradeoff in microbial metabolism. PLOS Comput. Biol. 15, e1007066 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Jin Q., Bethke C. M., The thermodynamics and kinetics of microbial metabolism. Am. J. Sci. 307, 643–677 (2007). [Google Scholar]
- 57.LaRowe D. E., Van Cappellen P., Degradation of natural organic matter: A thermodynamic analysis. Geochim. Cosmochim. Acta 75, 2030–2042 (2011). [Google Scholar]
- 58.Desmond-Le Quéméner E., Bouchez T., A thermodynamic theory of microbial growth. ISME J. 8, 1747–1751 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Song H. S., et al., Representing organic matter thermodynamics in biogeochemical reactions via substrate-explicit modeling. Front. Microbiol. 11, 531756 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.González-Cabaleiro R., Martinez-Rabert E., Argiz L., van Kessel M. A., Smith C. J., A framework based on fundamental biochemical principles to engineer microbial community dynamics. Curr. Opin. Biotechnol. 67, 111–118 (2021). [DOI] [PubMed] [Google Scholar]
- 61.Manzoni S., Taylor P., Richter A., Porporato A., Ågren G. I., Environmental and stoichiometric controls on microbial carbon-use efficiency in soils. New Phytol. 196, 79–91 (2012). [DOI] [PubMed] [Google Scholar]
- 62.Allison S. D., Modeling adaptation of carbon use efficiency in microbial communities. Front. Microbiol. 5, 571 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Hagerty S. B., Allison S. D., Schimel J. P., Evaluating soil microbial carbon use efficiency explicitly as a function of cellular processes: Implications for measurements and models. Biogeochemistry 140, 269–283 (2018). [Google Scholar]
- 64.Kempes C. P., Dutkiewicz S., Follows M. J., Growth, metabolic partitioning, and the size of microorganisms. Proc. Natl. Acad. Sci. U.S.A. 109, 495–500 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Monod J., The growth of bacterial cultures. Annu. Rev. Microbiol. 3, 371–394 (1949). [Google Scholar]
- 66.Grzybowski B. A., Huck W. T., The nanotechnology of life-inspired systems. Nat. Nanotechnol. 11, 585–592 (2016). [DOI] [PubMed] [Google Scholar]
- 67.Manzoni S., et al., Reviews and syntheses: Carbon use efficiency from organisms to ecosystems-definitions, theories, and empirical evidence. Biogeosciences 15, 5929–5949 (2018). [Google Scholar]
- 68.DeLong J. P., Okie J. G., Moses M. E., Sibly R. M., Brown J. H., Shifts in metabolic scaling, production, and efficiency across major evolutionary transitions of life. Proc. Natl. Acad. Sci. U.S.A. 107, 12941–12945 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Kestin J., A Course in Thermodynamics (CRC Press, 1979), vol. 1. [Google Scholar]
- 70.Horowitz J. M., Zhou K., England J. L., Minimum energetic cost to maintain a target nonequilibrium state. Phys. Rev. E 95, 042102 (2017). [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Experimental data and Mathematica code used to draw the figures have been deposited in Texas Data Repository (https://dataverse.tdl.org/dataset.xhtml?persistentId=doi:10.18738/T8/4UGXZV). Experimental data were retrieved from ref. 29.