Significance
Larger ecosystems support more species; this ubiquitous pattern is the foundation of current conservation schemes. However, many ecosystems possess a complex spatial structure that cannot be represented by area, and the role of such complexity in regulating biodiversity patterns is largely unknown. Here, we use theory and extensive fish community data to show that ecosystem size and complexity dictate riverine biodiversity. We found that larger and more branched “complex” river networks harbored greater species richness due to increased space and environmental heterogeneity. The complexity effect was comparable to the size effect, and this pattern has emerged regardless of ecological contexts. Our discovery illustrates a fundamental ecological law in complex ecosystems, laying the groundwork for future research exploring macroecological patterns.
Keywords: metacommunity, species diversity, scaling law, network theory, freshwater
Abstract
A prevailing paradigm suggests that species richness increases with area in a decelerating way. This ubiquitous power law scaling, the species–area relationship, has formed the foundation of many conservation strategies. In spatially complex ecosystems, however, the area may not be the sole dimension to scale biodiversity patterns because the scale-invariant complexity of fractal ecosystem structure may drive ecological dynamics in space. Here, we use theory and analysis of extensive fish community data from two distinct geographic regions to show that riverine biodiversity follows a robust scaling law along the two orthogonal dimensions of ecosystem size and complexity (i.e., the dual scaling law). In river networks, the recurrent merging of various tributaries forms fractal branching systems, where the prevalence of branching (ecosystem complexity) represents a macroscale control of the ecosystem’s habitat heterogeneity. In the meantime, ecosystem size dictates metacommunity size and total habitat diversity, two factors regulating biodiversity in nature. Our theory predicted that, regardless of simulated species’ traits, larger and more branched “complex” networks support greater species richness due to increased space and environmental heterogeneity. The relationships were linear on logarithmic axes, indicating power law scaling by ecosystem size and complexity. In support of this theoretical prediction, the power laws have consistently emerged in riverine fish communities across the study regions (Hokkaido Island in Japan and the midwestern United States) despite hosting different fauna with distinct evolutionary histories. The emergence of dual scaling law may be a pervasive property of branching networks with important implications for biodiversity conservation.
Ecologists have long sought to understand the general drivers of biodiversity. One of the most robust empirical generalizations in ecology is the positive relationship between species richness and area, that is, the species–area relationship (the SAR) (1). In 1921, Arrhenius (2) formulated the SAR as a power law , an equation currently known as the Arrhenius SAR ( is the number of species observed in a given geographic area , the constant, and the scaling exponent). Since then, the spatial scaling of species richness has been observed in many taxonomic groups (3). The SAR is ubiquitous because multiple mechanisms produce an apparently similar pattern. Larger ecosystems typically support more diverse metacommunities due to increased habitat diversity (4), larger metacommunity size (5), and/or enhanced colonization dynamics (6). Importantly, the SAR provides the foundation for global conservation efforts (7–9). For example, conservation ecologists have used SAR estimates to design marine and terrestrial protected areas (7, 8), which currently encompass more than 30 million km2 globally (10).
Many ecosystems, however, possess a complex spatial structure that cannot be represented by area—a dimension referred to as scale-invariant complexity (11, 12). Such complexity is evident in branching ecosystems, including rivers, trees, and mountain ranges, to name just a few (12). Geomorphic or biological processes generate a pronounced self-similarity in complex branching patterns such that the part and the whole look alike (12). Even though the branching structure is independent of spatial scale, it forms a physical template that dictates habitat diversity and dispersal corridors for living organisms (13). Limited but accumulating evidence suggests that classical metapopulation and metacommunity theories cannot predict ecological dynamics driven by branching structure (14–16), and this recognition has led to recent developments of spatial theories devoted to complex branching ecosystems (17). For example, these studies have highlighted key roles of branching structure in driving local biodiversity patterns, such as increased species richness at merging points of branches (18). However, most research has explored the consequences of branching complexity for local community structure (19) or has relied solely on theoretical arguments with limited replications of branching architecture (20). At present, we lack a comprehensive evaluation of how branching complexity scales biodiversity patterns at the metacommunity level. Filling this knowledge gap may provide common ground for achieving successful conservation in spatially complex ecosystems, where accelerated species loss threatens the delivery of ecosystem services (21).
Here, we propose a unified framework of ecosystem size and complexity in scaling biodiversity patterns in rivers—a prime example of complex branching ecosystems. Individual streams and rivers flow through different landscapes with distinct geological and climatic backgrounds, serving as a spatial unit of unique in-stream environments (16, 22–27). The recurrent merging of diverse tributaries ultimately forms a fluvial network with fractal branching patterns (12). As such, the complexity of branching structure, which we define here as the probability of branching per unit river distance (24, 28), may represent a macroscale control of the ecosystem’s habitat heterogeneity (habitat diversity per unit area) (13, 23, 24). Meanwhile, ecosystem size (watershed area) should determine the metacommunity size and total habitat diversity (area times heterogeneity), two factors that regulate biodiversity at the metacommunity level (4, 5). Hence, riverine biodiversity may manifest scaling laws along the two orthogonal dimensions of branching networks. We call this the dual scaling hypothesis of biodiversity.
The present study combines theory and analysis of extensive community data from two different regions of the globe to show that multiple ecological pathways converge to the emergence of dual diversity scaling. Specifically, watershed-scale species richness ( diversity) followed power laws with ecosystem size and branching probability as ( and are the scaling exponents) regardless of ecological contexts. However, contributing factors of increased diversity—either enhanced local species richness ( diversity) and/or spatial variation of species composition ( diversity)—depended on constituent species’ characteristics. Our findings suggest that the dual scaling law is a pervasive yet overlooked feature of complex ecosystems with important implications for biodiversity conservation.
Results and Discussion
Theoretical Synthesis of Ecosystem Size and Complexity Influences.
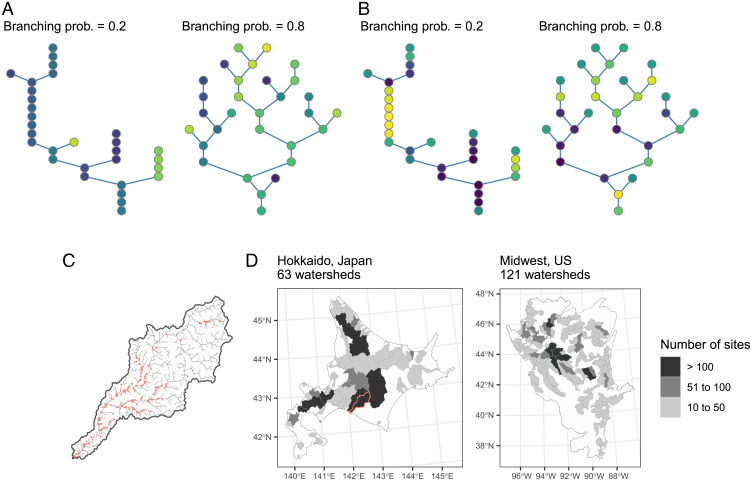
We developed a theoretical framework synthesizing the influences of ecosystem size and complexity on biodiversity patterns in branching ecosystems. We depicted branching ecosystems as a spatial network of connected habitat patches which local communities inhabit (24, 28) (Fig. 1 A and B). In this network, the number of habitat patches (a theoretical proxy for ecosystem size ) and branching probability (ecosystem complexity) shape the spatial structure (Materials and Methods). We introduced two factors determining the temporal mean of environmental condition at each habitat patch : headwater environments (the most upstream habitat patch) and local environmental noise. Environmental values at headwaters are drawn randomly from a normal distribution with a mean of zero and an SD of and propagate downstream. We modeled the downstream propagation as a spatial autoregressive process, in which local noise is added to the adjacent upstream environment as ( is the network distance from the outlet patch; at the outlet). The environmental values recurrently “mix” at confluences considering the relative size of joining tributaries (Materials and Methods). Therefore, our network-generation procedure resembles natural processes of how branching river networks create diverse habitats in a metacommunity (26).
Fig. 1.
(A and B) Theoretical branching networks generated under contrasting landscape scenarios. Branching river networks are depicted as a network of connected habitat patches, in which the number of habitat patches and branching probability dictate the ecosystem size and complexity ( and in this example). Environmental conditions at headwaters (i.e., the most upstream patches) are drawn randomly from a normal distribution and propagate downstream with local environmental noise (Materials and Methods). Habitat patches are colored in proportion to environmental values (similar colors have similar environmental values). A and B show distinct landscape scenarios. Environmental variation at headwaters exceeds the degree of local environmental noise in A (), while the opposite is true in B (). (C) Example of intensively surveyed watersheds in Hokkaido, Japan (the red-colored watershed in D). Red dots indicate sampling sites for fish surveys. (D) Map of study regions (Left, Hokkaido, Japan; Right, Midwest, United States). Watersheds (i.e., metacommunities) are gray shaded in proportion to the number of sampling sites.
Metacommunity dynamics were then simulated in the theoretical branching networks using a general metacommunity model (29). In this model, the realized species’ population growth is regulated by local abiotic environments, competition, and dispersal. Specifically, the number of individuals for species at patch and time was given as follows:
where is the expected number of individuals given the local community dynamics at time , the expected number of immigrants to patch , and the expected number of emigrants from patch . We assumed the Beverton–Holt equation to simulate local community dynamics (30):
is the site- and time-specific reproductive rate of species , the maximum reproductive rate, the site-specific carrying capacity, the competition coefficient between species and , and the number of species in a metacommunity (). Interspecific competition coefficients are random draws from a uniform distribution as while keeping intraspecific competition coefficients constant (). Here, the reproductive rate was related to local abiotic environments through a Gaussian function with species’ niche optimum and width . That is, decreases as the temporally variable abiotic environment deviates from ( is drawn randomly from a multivariate normal distribution with the mean environment of the patch ; Materials and Methods). Species’ reproductive performance has therefore an explicit linkage with local abiotic environments, which can be driven largely by branching structure. After local community dynamics, species emigrate from the local habitat patch with probability and disperse through the branching network following an exponential dispersal kernel with the rate parameter (the reciprocal represents an expected dispersal distance). These dispersal parameters affect the number of immigrants and emigrants .
Prior to the main simulation analysis, we performed a systematic sensitivity analysis to identify simulation parameters that strongly influence the relationships between biodiversity metrics (, , and diversity) and ecosystem properties (size and complexity). Our analysis revealed that the following parameters were particularly influential: environmental variation at headwaters , local environmental noise , maximum value of interspecific competition coefficient , dispersal probability , and dispersal rate parameter (SI Appendix). Therefore, we considered 32 combinations of these parameters as primary simulation scenarios, which include a combination of four landscape and eight ecological scenarios.
The four landscape scenarios represent distinct patterns of spatial environmental heterogeneity, which were produced by different combinations of environmental variation at headwaters ( 0.01, 1) and the degree of local environmental noise ( 0.01, 1). When , branching produces greater habitat heterogeneity because headwaters are the primary source of environmental variation (Fig. 1A). This landscape scenario reproduces natural patterns of habitat heterogeneity, in which environmental conditions differ greatly among tributaries but are highly correlated within a tributary (22, 26). In the meantime, when , local environmental noise masks environmental variation among tributaries, leading to limited influences of branching on habitat heterogeneity (Fig. 1B). This scenario may reflect human-modified landscapes, in which human activities may reduce the headwater diversity by homogenizing in-stream processes (e.g., dams) (31) and/or may increase the local environmental noise through localized habitat degradation (e.g., removal of riparian forests) (32). Thus, the inequality between and defines the contrasting scenarios of natural and human-dominated landscapes. The eight ecological scenarios distinguish ecological characteristics of constituent species in a metacommunity. Among the ecological scenarios, we changed dispersal distance (), dispersal probability (), and the maximum value of interspecific competition strength (). This setup enables us to examine how ecological traits of constituent species mediate biodiversity relationships. The combinations of landscape and ecological scenarios were capable of reproducing common spatial patterns of local species richness in rivers, corroborating the appropriateness of our choice in parameter combinations (SI Appendix). Under each simulation scenario, we simulated 1,400 time steps of metacommunity dynamics (including 400 time steps of initialization and burn-in periods) in 1,000 branching networks with the gradients of ecosystem size (the number of habitat patches: 10 to 150) and complexity (branching probability: 0.01 to 0.99).
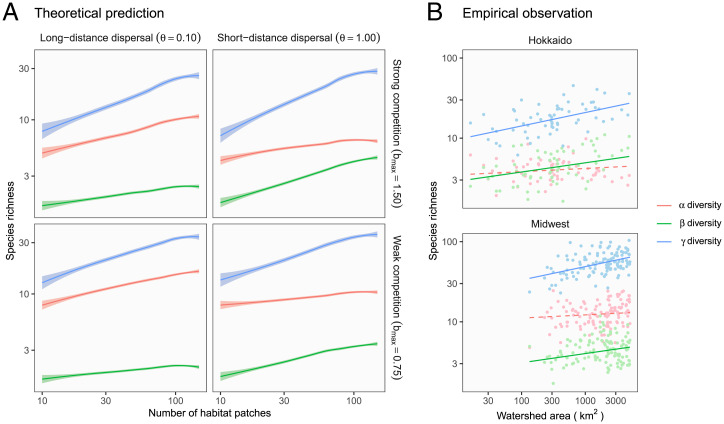
Our simulation predicted the emergence of dual scaling law under a realistic landscape scenario, where the environmental variation at headwaters is greater than the degree of local environmental noise (Fig. 1A). Ecosystem size and complexity both increased diversity (Figs. 2A and 3A) with a signature of power law (i.e., linear in a log–log scale), and these relationships were consistent across ecological scenarios (compare panels in Figs. 2A and 3A). Importantly, the impact of ecosystem complexity was comparable to that of ecosystem size. Hence, regardless of ecological scenarios, ecosystem size and complexity are likely to be equally important in scaling diversity. Our results contrast with predictions from neutral models, in which the enhanced connectivity of highly branched networks reduced diversity by facilitating the further expansion of an already widespread species (33). Nonneutral components of our model should therefore have played a central role in generating the predicted patterns. Indeed, the robustness of the scaling law stemmed from the convergence of niche and dispersal assembly processes as described in the next two paragraphs.
Fig. 2.
Qualitative match between theoretical predictions and empirical patterns in power law scaling of biodiversity. (A) Theoretical predictions. Ecosystem size (the number of habitat patches) scales diversity through increased or diversity across ecological scenarios. Lines and shades are loess curves fitted to simulated data and their 95% CIs. Each panel represents different ecological scenarios under which metacommunity dynamics were simulated. Rows represent different competition strength. Competition coefficients () were varied randomly from 0 to 1.5 (Top, strong competition) or 0.75 (Bottom, weak competition). Columns represent different dispersal scenarios. Two dispersal parameters were chosen to simulate scenarios with long-distance (the rate parameter of an exponential dispersal kernel ) and short-distance dispersal (). In this simulation, environmental variability among headwaters (i.e., the most upstream patches), which is expressed as the SD of a normal distribution (), was greater than that of local environmental noise occurring at each habitat patch (). Dispersal probability was 0.01 for all the scenarios. (B) Empirical observations. Observed biodiversity patterns match theoretical predictions of power law scaling along the axis of ecosystem size. Dots represent watershed replicates (i.e., metacommunities), and lines are predicted values from the robust regression models (solid: siginificant relationships; dashed: insignificant). The estimated slopes (i.e., the scaling exponents) were consistent across geographically distant regions with distinct fish fauna (Top: Hokkaido, Japan; Bottom: Midwest, United States).
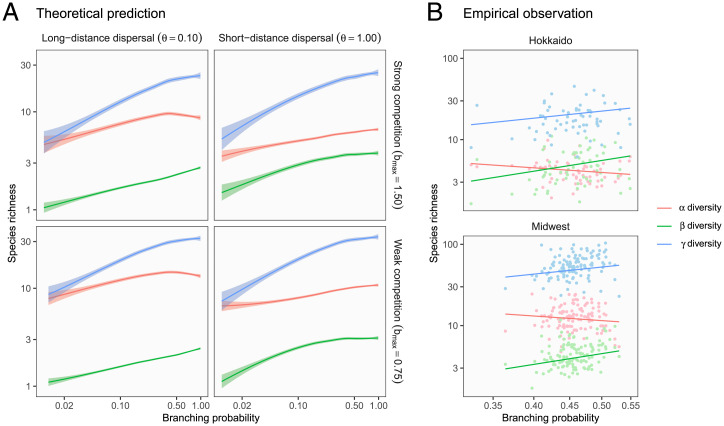
Fig. 3.
Qualitative match between theoretical predictions and empirical patterns in power law scaling of biodiversity. (A) Theoretical predictions. Ecosystem complexity (branching probability) scales diversity through increased or diversity across ecological scenarios. Lines and shades are loess curves fitted to simulated data and their 95% CIs. Each panel represents different ecological scenarios under which metacommunity dynamics were simulated. Refer to Fig. 2 for details. (B) Empirical observations. Observed biodiversity patterns match theoretical predictions of power law scaling along the axis of ecosystem complexity. Dots represent watershed replicates (i.e., metacommunities), and solid lines are predicted values from the robust regression models. The estimated slopes (i.e., the scaling exponents) were consistent across geographically distant regions with distinct fish fauna (Top: Hokkaido, Japan; Bottom: Midwest, United States).
Dispersal strength regulated the relative importance of ecological mechanisms that underlie the scaling relationships of diversity (compare Left and Right columns in Figs. 2A and 3A). We observed a greater contribution of diversity (defined as ) to increased diversity when dispersal limitation existed (i.e., species travel short distances). This result reflected significant spatial variation in species composition over the branching network and was likely driven by the local association of species’ niche and abiotic environments (i.e., species sorting) (29, 34). In contrast, when the dispersal limitation was relaxed (species travel long distances), a clear increase in diversity underpinned the positive relationships between diversity and ecosystem properties. The results agree with previous predictions that increased dispersal homogenizes community composition while enhancing local diversity through increased immigrants from suitable habitat patches (i.e., mass effects) (29, 34, 35). Therefore, ecosystem size and complexity can increase diversity via enhanced species sorting (niche assembly) or mass effects (dispersal assembly) and which takes primacy is dependent on the degree of dispersal limitation. These patterns were qualitatively similar across different levels of dispersal probabilities (SI Appendix, Figs. S5 and S12).
Interspecific competition had minimal influences on the underlying mechanisms (compare Top and Bottom rows in Figs. 2A and 3A). Strong competition reduced diversity as observed in former studies (29). Yet, it did not change the qualitative relationships between biodiversity and ecosystem properties (Figs. 2A and 3A). Accordingly, macroecological patterns are expected to be robust to variation in species interaction networks. This result deserves attention given the long-lasting debate on how species interactions change the dynamics of ecological communities (36, 37). Collectively, our theoretical analysis highlights how apparently similar scaling in diversity emerges through different ecological pathways by explicitly modeling niche and dispersal assembly processes.
It should be borne in mind that influences of ecosystem size and complexity differed significantly in their dependence on landscape scenarios. Ecosystem size had positive effects on diversity regardless of landscape scenarios, although the slopes were steeper with greater environmental variation (higher and/or ) (Fig. 2A and SI Appendix, Figs. S5–S11). This result is attributable to the fact that larger ecosystems can hold more individuals in a metacommunity (5). In contrast, we observed limited or no influences of branching complexity when local environmental noise was equal to or exceeded environmental variation at headwaters (; SI Appendix, Figs. S13–S18). Under this scenario, branching has a minor influence on the ecosystem’s habitat heterogeneity because patch-level environmental variation is equivalent to or greater than environmental differences between tributaries (Fig. 1B). Therefore, this landscape scenario eliminates the positive effect of branching complexity on diversity. This theoretical prediction may not apply to pristine or seminatural river networks where individual streams show distinct and spatially correlated environmental conditions, including water temperature, water chemistry, and flow/sediment regimes (22, 23, 26). Instead, it may be most relevant to severely altered landscapes where human disturbance disrupts the environmental distinctiveness of branches through, for example, flow regulations by dams (31). Hence, our theory has important implications for riverine biodiversity conservation by pointing to the crucial role of habitat diversity produced by branching structure.
Empirical Evidence from Distinct Geographic Regions.
The proposed theory provided important insights into how ecological communities are structured in branching networks; however, empirically testing the predictions is extremely difficult because it requires metacommunity-level replications. To confront this logistical challenge, we compiled fish community data across two geographic regions: Hokkaido Island in Japan and the midwestern United States (Midwest). These regions are located in comparable latitude ranges (Fig. 1D) but support distinct fish communities (SI Appendix, Tables S5 and S6). Therefore, this data set provides an excellent opportunity to examine the generality of our theoretical predictions. After careful data selection (Materials and Methods and SI Appendix), we estimated , , and diversity (asymptotic species richness; Materials and Methods) at 184 watersheds (63 in Hokkaido and 121 in the Midwest), each of which comprised 10 sites of presence–absence fish community data (a total of 6,649 sites). These watersheds are small enough (16 to 5,008 km2) to assume that fishes can disperse therein at a multigeneration time scale (38), while posing challenges to traverse across watersheds (the ocean or lentic habitats; refer to Materials and Methods for watershed definition). We combined this data set with geospatial information, including watershed characteristics (watershed area and branching probability), climates (annual mean temperature and annual cumulative precipitation), and land-use patterns (the fraction of agricultural land use and dam density) to evaluate potential influences of macroscale factors.
Using this data set, we were able to ask the following questions that have never been addressed in tandem: Is there a dual scaling law in riverine biodiversity? If so, is the dual scaling consistent across different geographic regions despite hosting drastically different fauna with distinct evolutionary histories? To test these questions, we developed global and region-specific models of robust linear regression in log–log space (Materials and Methods). In the global model, we assumed that slopes of ecosystem size (watershed area) and complexity (branching probability) are constant across the two regions (i.e., fixed scaling exponents). Meanwhile, the region-specific model assumes different slopes of ecosystem size and complexity between the regions (i.e., varied scaling exponents). We compared the support of these competing models using the Bayes factor, a measure of the strength of evidence in favor of one model over the alternative. In our definition (Materials and Methods), the Bayes factor of indicates the support for the global model over the region-specific model.
Surprisingly, we found decisive support for the global model in explaining diversity (Bayes factor = 188.9). The estimated diversity linearly increased with increasing watershed area (ecosystem size) and branching probability (ecosystem complexity) on a log–log scale, and the estimated scaling exponents were consistent across the study regions (0.17 for watershed area and 0.90 for branching probability; Table 1 and Figs. 2B and 3B). Thus, watershed-scale riverine biodiversity likely obeys a general scaling law along the two independent axes of ecosystem size and complexity. The regional consistency implies that ecological traits of constituent species have a minor effect on the scaling relationships, as our theory predicts (Figs. 2A and 3A). It is also important to note that the effect of ecosystem complexity was striking in its magnitude. Average predictive comparisons (39) revealed that an expected increase of diversity per 0.1 branching probability was 8.37 2.74 species (Materials and Methods and SI Appendix); this level of increase in diversity requires 1,497 km2 in the watershed area (reference SI Appendix, Table S7 for the estimated average predictive comparisons). Overall, the observed patterns were reasonable because numerous studies have shown that tributaries are the primary source of environmental heterogeneity in river networks (16, 22–27)—the sole theoretical assumption required for the dual scaling of diversity to emerge.
Table 1.
Estimated parameters of robust regression models explaining fish species richness in Hokkaido (Japan) and the Midwest (United States)
| Parameter | Effect | diversity | diversity | diversity |
| Intercept | 0.81 (0.14)* | 1.12 (0.11)* | 0.30 (0.11)* | |
| Watershed area | 0.04 (0.02) | 0.11 (0.03)* | 0.17 (0.02)* | |
| Branching probability | −0.59 (0.28)* | 1.37 (0.36)* | 0.90 (0.27)* | |
| Region (Midwest versus Hokkaido) | 0.46 (0.02)* | −0.09 (0.03)* | 0.37 (0.02)* | |
| Air temperature | 0.09 (0.01)* | −0.07 (0.02)* | 0.03 (0.01)* | |
| Precipitation | −0.03 (0.01) | 0.05 (0.02)* | 0.02 (0.01) | |
| Fraction of agriculture | 0.01 (0.01) | −0.01 (0.01) | −0.01 (0.01) | |
| Dam density | 0.00 (0.01) | −0.01 (0.01) | 0.00 (0.01) |
The SEs are shown in parentheses. Response variables were log-10 transformed. Climate and land-use variables (air temperature, precipitation, fraction of agriculture, and dam density) are deviations from the regional averages and were standardized to a mean of zero and an SD of one prior to the analysis.
*Parameter estimates whose 95% confidence intervals (approximately ) do not include 0.
Similarly, there were weak to moderate supports for the global models of and diversity (Bayes factor = 3.1 and 6.7, respectively). In both regions, diversity responded significantly to ecosystem size and complexity while diversity showed a weaker or a vague response to these ecosystem properties (Table 1 and Figs. 2B and 3B). In our simulations, this pattern has emerged under the scenarios with dispersal limitation, which elegantly matches the previous observations of stream fish movement. Field studies (e.g., mark-recapture) recurrently revealed the restricted movement of stream fish, typically limited to several hundreds of meters at an annual time scale (40). The reciprocal agreement of theoretical and empirical patterns provides indirect but convincing evidence that dispersal limitation, which results in the increasing importance of species sorting process (Figs. 2 and 3), plays a key role in driving the associations between diversity and ecosystem properties in rivers.
The consistent effect of branching probability on diversity across the study regions is noteworthy because many watersheds in the Midwest have been altered by agricultural land use (mean % agricultural land use: 55% in the Midwest and 6% in Hokkaido). If the intensive land use by humans impairs biological or physical distinctiveness among tributaries, our theory predicts a weakened effect of branching probability on diversity (SI Appendix, Figs. S13–S18). However, diversity increased significantly with increasing branching probability in this highly modified landscape, suggesting that tributaries still sustain unique environmental conditions to support high spatial variation in species composition. Indeed, diversity increased with increasing branching probability in both regions (Fig. 3B). It is conceivable that local geological and geomorphological differences, such as slope, aspect, and soil porosity, persist in human-dominated landscapes to maintain the diversity of in-stream processes. The lack of land-use effects (the fraction of agricultural land use and dam density) further corroborates our interpretation (Table 1). Although our analysis is correlative, the finding is encouraging because the branching complexity of river networks may serve as a natural defense system to human-induced environmental changes.
While our empirical results showed an excellent match with the predictions of our niche-based model (Figs. 2 and 3), we must note that a neutral model developed by Muneepeerakul et al. (41) was also capable of reproducing fish diversity patterns in the Mississippi–Missouri River Basin. This apparent contradiction is perhaps not a surprise when considering the difference in the spatial resolution of interest. Their neutral model used subbasins (ca. 5,000 km2 in the watershed area) as a unit of local communities (metacommunities in our study) and modeled variation in habitat capacity and dispersal among those units. At this coarse resolution, stochastic immigration processes coupled with random speciation, a core of the Unified Neutral Theory of Biodiversity (5), are critical to forming biogeographic patterns (42). Meanwhile, we defined local communities at much finer resolutions (several tens to hundred meters) at which species’ niche should interact with environments to determine community structure (43). It is therefore necessary for our theoretical model to assume niche-based processes. This interpretation is supported by the fact that a neutral model could not reproduce the positive complexity–diversity relationship observed in our empirical data (33). As such, our research is uniquely significant in showing the qualitative agreement of theoretical and empirical results at this level of biological organization.
A potential criticism is that our results are driven by spurious correlations; however, this is very unlikely. We have statistically controlled the potential influences of climates and land-use patterns (Table 1). Moreover, our empirical results were qualitatively consistent with theoretical predictions, which are free from any confounding factors. Thus, we are confident in our statistical inference.
Implications.
Our unified framework unveiled the surprising consistency of dual scaling across ecological contexts or geographic regions, suggesting the universality of our findings. In particular, the emerging complexity–diversity relationship points to several important avenues for riverine biodiversity conservation. First and foremost, any simplification of complex river networks may result in regional biodiversity loss via reduced environmental heterogeneity. Human-induced habitat alterations, including flow regulation (31), habitat fragmentation (44), and stream burial (45), may compromise or restrict access to the diverse habitats that complex branching networks may support. Our findings underscore the importance of preserving the structural complexity of ecosystems and support the modern conservation initiative that seeks to protect a diverse habitat portfolio (46). Second, the complexity perspective may provide insights into the spatial planning of conservation efforts. Riverine reserves and local restoration are increasingly recognized as an effective management tool, and the spatial prioritization of conservation sites in rivers is an area of active research (47). While the old “single large or several small” debate has led to a principle prioritizing a single large habitat (48), emerging perspectives posit the potential of coordinated networks of small habitats in protecting biodiversity (49). Understanding the role of branching complexity helps design such networks. For example, synergies of multiple small reserves may emerge at the watershed scale when ecologically distinct tributaries are involved in the design, as evidenced by the recent successful conservation of tropical fishes in Thailand’s Salween basin (47).
Although the foundational concepts in ecology emphasize the importance of ecosystem size in biodiversity relationships (3, 5, 50, 51), ecosystem complexity has not received the attention it deserves. However, the ubiquity of scale-invariant complexity across terrestrial (11) and aquatic ecosystems (12) calls for more research embracing the two orthogonal dimensions of the ecosystem’s geometric structure. In this context, the present study substantially advanced our understanding of how biodiversity is organized in spatially complex ecosystems, offering a conceptual pillar for future research. For example, the proposed framework may be extended to explore how these ecosystem properties regulate functional diversity (52) and shifts in stochastic/deterministic community assembly (53). Recognizing the dual control of biodiversity broadens viable options for spatial planning of protected areas or restoration sites, thereby helping conserve biodiversity from societal demands that threaten it. The generalization of our discovery should therefore bring paradigm shifts in macroecological science with far-reaching implications for biodiversity conservation.
Materials and Methods
Theory.
Network generation.
We depicted branching ecosystems as a bifurcating network of connected habitat patches (24, 28) (Fig. 1). Habitat patches, or local communities, can be either nonbranching or branching river sections with a unit length , which defines the scale of local species interactions. Two parameters determine the geometric properties of simulated branching networks: the number of habitat patches (ecosystem size) and branching probability (ecosystem complexity). Each habitat patch is assigned to be a branching patch (including upstream terminals) with probability or a nonbranching patch with probability . In this framework, an individual branch is a consecutive series of nonbranching patches terminated at a branching patch; therefore, the number of habitat patches in branch , , is a realization of a random variable drawn from a geometric distribution (24) but conditional on ( is the number of branches in a network). The number of branches is identical to the number of branching habitat patches in a network or the number of “success” out of trials. This leads to an assumption that is a realization of a random variable drawn from a binomial distribution as . This framework has two merits. First, it reflects observed patterns of branch length distribution, which is known to follow an exponential distribution (a continuous version of a geometric distribution) (12). Second, it preserves the fractal nature of branching patterns (54). An alternative approach is the use of optimal channel networks (55). However, we employed our framework because branching probability is quantifiable in natural river networks, enabling us to compare theoretical predictions with empirical observations.
In our network generation, we first drew from the binomial distribution but selected an odd number to constitute a bifurcating branching network. We then determined as random draws from the geometric distribution with the constraint of . The generated branches were organized randomly into a bifurcating branching network.
Two sources of variation characterize the long-term average of the abiotic environment at each habitat patch: environmental variation at headwaters () and local environmental noise (). We drew random values from a normal distribution with a mean of zero and an SD of and assigned them to headwater patches (i.e., the most upstream patches). These environmental values at headwaters propagate downstream through a spatial autoregressive process defined as follows:
| [1] |
where is the mean environmental value at longitudinal position ( is the network distance from the outlet patch; at the outlet), the strength of spatial autocorrelation, and the local environmental noise that follows a normal distribution with a mean of zero and an SD of . The parameter can take values of 0 to 1 with larger values indicating greater spatial autocorrelation. In this study, we set to mimic strong spatial autocorrelation in riverine environments. At confluences, we took a weighted mean of environmental values given the relative size of upstream contributing area of joining tributaries:
| [2] |
where and denote “right” and “left” branches, respectively, and is the number of upstream habitat patches at longitudinal position (akin to the upstream watershed area; at the most upstream patch). The parameter takes values of 0 to 1 and represents the relative influence of the right tributary given the relative size of joining tributaries. With this expression, larger tributaries have a greater influence on the downstream environment, as observed in natural river networks (56).
Metacommunity model.
We simulated metacommunity dynamics in branching river networks following the metacommunity framework proposed by Thompson et al. (29). In this framework, abiotic environmental conditions (density-independent), intra- and interspecific competition (density-dependent), and dispersal regulate a species’ realized population growth. Below, we describe the details of our metacommunity model.
The realized number of individuals (species at patch and time ) is given as follows:
| [3] |
where is the expected number of individuals given the local community dynamics at time , the expected number of immigrants to patch , and the expected number of emigrants from patch . The realized discrete number of individuals is drawn from a Poisson distribution to account for stochasticity in demographic and dispersal processes (29, 57). Local community dynamics are simulated based on the Beverton–Holt equation (30):
| [4] |
where is the reproductive rate of species given the environmental condition at patch and time , the maximum reproductive rate of species , the carrying capacity at patch , the competition coefficient between species and , and the number of species in a metacommunity. was expressed as a function of the number of upstream habitat patches () to represent increasing habitat size with increasing upstream watershed area (58, 59). The parameter represents the strength of interspecific competition relative to that of intraspecific competition: interspecific competition is greater than intraspecific competition if > 1 (intraspecific competition coefficient was set constant as ). was drawn randomly from a uniform distribution as . The density-independent reproductive rate is affected by abiotic environments (nonconsumable) and determined by the following Gaussian function:
| [5] |
where is the optimal environmental value for species , the environmental value at patch and time , and the niche width of species . We introduced the cost of a wide niche by multiplying (60):
| [6] |
Smaller values of imply greater costs of having a wider niche (i.e., decreased maximum reproductive rate) and reduce the realized reproductive rate near the niche optimum.
The environmental value at patch and time , , is assumed to follow a multivariate normal distribution as , where is the vector of mean environmental conditions of habitat patches and is the variance–covariance matrix. The diagonal elements of the variance–covariance matrix represent the degree of temporal environmental variation. The off-diagonal elements represent the spatial autocorrelation in temporal environmental variation as follows:
| [7] |
denotes the temporal covariance of environmental conditions between patch and , which is assumed to decay exponentially with increasing distance between the patches (the shortest network path measured as the number of habitat patches). The parameter determines the degree of the distance decay of environmental correlates.
The expected number of emigrants at time is the product of dispersal probability and : . The immigration probability at patch for species , , is calculated using the following equation that accounts for separation distance among habitat patches and dispersal capability of a species:
| [8] |
The parameter regulates the dispersal distance of a species that follows an exponential distribution ( corresponds to the expected dispersal distance). The expected number of immigrants is calculated as .
Simulation.
We used 32 sets of parameter combinations (i.e., simulation scenarios) based on the results of extensive sensitivity analysis (SI Appendix). The parameter combinations comprise four landscape and eight ecological scenarios. Landscape scenarios distinguish spatial patterns of habitat heterogeneity, while ecological scenarios change ecological traits of simulated species. For landscape scenarios, we used four combinations of environmental variation at headwaters () and the degree of local environmental noise (). The inequality of and controls the relationship between branching complexity and habitat heterogeneity (Fig. 1 A and B). For ecological scenarios, we varied three ecological parameters that are relevant for dispersal and interspecific competition: dispersal distance (), dispersal probability (), and the maximum value of competition coefficients ( 0.75, 1.5). This setup results in eight ecological scenarios with different levels of dispersal and competition.
We allowed interspecific variation in niche optimum and width, which were drawn from uniform distributions as and . We used fixed values for the following parameters: maximum reproductive rate (), niche cost (), the degree of temporal environmental variation (), and the extent of spatial autocorrelation in temporal environmental dynamics ().
Under each simulation scenario, we introduced 50 species () and simulated 1,400 time steps of metacommunity dynamics (including 200 time steps for initialization and 200 time steps for burn-in) in 1,000 branching networks with the gradients of ecosystem size (the number of habitat patches: 10 to 150) and complexity (branching probability: 0.01 to 0.99). During the first 200 time steps (an initialization period), we initialized the simulation by seeding each habitat patch with populations of each species drawn from a Poisson distribution with a mean of 0.5. We repeated the seeding every 10 time steps during the initialization to allow species to establish their populations if they can grow from low abundances. After the initialization period, we ran 200 time steps as a burn-in period with no seeding to minimize influences of initial conditions. We saved the last 1,000 time steps to estimate the temporal averages of , , and diversity. diversity was defined as . We removed simulation replicates in which no species established populations over the initial 400 time steps (13 replicates out of 32,000 replicates). Ecosystem size and complexity were drawn randomly from uniform distributions as follows: and ( was rounded to the nearest integer before running simulations). Values of simulation parameters were summarized in SI Appendix, Table S2. We performed simulations using R version 4.1.0 (61).
Empirical Data.
Fish community data.
We compiled fish data at two geographic regions: Hokkaido Island in Japan and the midwestern United States (Midwest). For Hokkaido, we used data from the Hokkaido Freshwater Fish Database HFish (62, 63), monitoring data at protected watersheds (24, 64), and primary data collected by the authors (58, 65), which collectively cover the entire island. For the Midwest, we assembled fish community data collected by the Iowa Department of Natural Resources (66), Illinois Environmental Protection Agency and Illinois Department of Natural Resources (67), Minnesota Pollution Control Agency (68), and Wisconsin Department of Natural Resources (69). We detailed procedures for initial data selection in SI Appendix.
We considered watersheds as independent replicates of metacommunities if the river network flows into one of the following: the ocean, a large lake/reservoir ( 10 km2 in the areal area), or a large river that may represent lentic habitats ( 5,000 km2 in the watershed area). We estimated , , and diversity at each watershed. diversity is the total species richness at each watershed. Since it is impossible to sample all species present in each watershed, we used asymptotic species richness as a proxy for diversity. Asymptotic species richness can be interpreted as the estimated true species richness in a given area when estimated using spatial replicates of local community data within a metacommunity (70). We estimated asymptotic species richness using sampling sites located in the same watershed (i.e., spatial replicates within a metacommunity) via the R package “iNEXT” (71). Metacommunities with ≥10 sampling sites were used in our analysis because a small sample size inflates statistical uncertainties in estimating asymptotic species richness (SI Appendix). We assessed the completeness of the observed species richness based on sample coverage, which is the total proportional abundances of observed species to the whole metacommunity (70). We excluded watersheds whose sample coverage was below 0.9 because the estimates of asymptotic species richness may contain nonnegligible statistical uncertainty. diversity was estimated by taking an average of local species richness at each site. diversity was estimated by dividing the estimated diversity by diversity (72).
After the data selection procedure, we obtained diversity estimates from 184 watersheds (Hokkaido: 63; Midwest: 121), which encompassed a total of 6,649 sites (Hokkaido: 2,650; Midwest: 3,999). Observations ranged from 1990 to 2013 in Hokkaido and from 1994 to 2015 in the Midwest. Fish species observed in the final data set were listed in SI Appendix, Tables S5 and S6.
Environmental data.
We collected data for watershed characteristics (watershed area [km2], branching probability, and mean elevation [m]), climatic variables (mean annual air temperature [degree Celsius] and cumulative precipitation [mm]), and land use (the fractions of forest, urban, and agriculture and dam density per watershed area [km−2]). We used MERIT Hydro (73) to delineate watershed polygons and river lines (defined as ≥1 km2 in the watershed area), which were separated by either the ocean, large lakes/reservoirs (≥10 km2 in the areal area), or large rivers (≥ 5,000 km2 in the watershed area). The ocean and large lakes/reservoirs were extracted from Global 1-second Water Body Map version 1.0 (74). Watershed area was estimated based on the delineated watershed polygons. We estimated branching probability by fitting exponential distributions to histograms of branch length as (unit: kilometer, river segment between successive confluences or a confluence and the outlet/upstream terminal). A derived statistical quantity corresponds to the theoretical branching probability .
We estimated the spatial averages of elevation, mean annual air temperature, and cumulative precipitation for each watershed polygon, which were extracted from Hydrologically Adjusted Elevations of MERIT Hydro (73) and WorldClim 1.4 (75). The fractions of forest, urban, and agriculture were calculated based on land-use data in 2015 from Copernicus Global Land Service (100-m resolution) (76). The Global Reservoir and Dam Database, Version 1 (77) was used to estimate dam density per unit watershed area (km−2). We used ArcMap 10.7 and the following R packages to perform geospatial analysis: “sf” (78), “raster” (79), “stars” (80), and “exactextractr” (81).
Statistical analysis.
We developed robust regression models with an M-estimation method to examine power laws of riverine biodiversity. The robust regression analysis is insensitive to outliers of a response variable; therefore, this method allows us to account for uncertainties of our diversity estimates (Fish community data). Log-transformed diversity metrics (, , and diversity) at watershed , , were assumed to follow a normal distribution as . The parameter was related to linear predictors, including log-transformed watershed area (ecosystem size; ), log-transformed branching probability (ecosystem complexity; ), region (coded as Hokkaido = 0, Midwest = 1; ), air temperature, precipitation, the fraction of agricultural land use, and dam density. Although our primary focus of this analysis is to assess the effects of watershed area and branching probability, we included climate and land-use variables to control their effects statistically. We did not include the fractions of urban and forest land use in the statistical models because these variables were strongly correlated with the fraction of agricultural land use (SI Appendix, Fig. S19) or had a very limited range of values. Similarly, we did not use mean elevation in the statistical models because it showed a moderate correlation with air temperature (SI Appendix, Fig. S19). Correlations for other combinations of explanatory variables were weak to moderate.
Climate (air temperature and precipitation) and land use (the fraction of agricultural land use and dam density) differed clearly between the regions. Therefore, we used residuals of the simple linear regressions between the climate or land-use variable (response variable) and region (explanatory variable). The residuals represent deviations from the regional averages; positive values indicate values greater than the regional average while negative values indicate values smaller than the regional average.
We constructed two models for each of the diversity metrics: global and region-specific models. The global model assumes that the effects of watershed area and branching probability are consistent across geographic regions (i.e., no interactive effects of the region with other linear predictors).
| [9] |
where are the intercept and regression coefficients for linear predictors. In an ordinary scale, the global model represents a dual scaling law as , where . Meanwhile, the region-specific model assumes the effects of watershed area and branching probability differ between regions (i.e., interactions between region and watershed area/branching probability).
| [10] |
This is equivalent to:
| [11] |
Therefore, in an ordinary scale, the model assumes different scaling exponents between regions as . All explanatory variables except watershed area, branching probability, and region were standardized to a mean of zero and an SD of one before the analysis.
We compared the performance of these competing models using the Bayes factor (82), which gives the relative strength of evidence in favor of the global model (M0) over the region-specific model (M1). We used Bayesian Information Criteria of the linear models to approximate the Bayes factor (82):
| [12] |
where .
For the supported model of diversity, we estimated average predictive comparisons of watershed area and branching probability to compare their effect sizes. The average predictive comparison is an expected change of the response variable per a unit difference of the explanatory variable of interest (39). Unlike other common metrics of effect size (e.g., standardized regression coefficients), this method provides intuitive yet rigorous estimates of effect size in models with nonlinear variable transformations (reference SI Appendix for further details). We performed statistical analysis using R version 4.1.0 (61).
Supplementary Material
Acknowledgments
We are grateful to numerous people who have been involved in the collection of fish community data. We thank the Illinois Environmental Protection Agency, Minnesota Pollution Control Agency, Iowa Department of Natural Resources, Wisconsin Department of Natural Resources, Michio Fukushima and Hirokazu Urabe for providing data for our empirical analysis. We thank Jacques Finlay for his constructive comments on the earlier version of the manuscript and Tatsuya Amano, Nobuo Ishiyama, and Masashi Soga for their technical support. This material is based upon work supported by the NSF through the Water Sustainability and Climate Program Observatory grant (EAR‐1209402) Resilience under Accelerated Change and through the Division of Environmental Biology (DEB 2015634), the Environmental Protection Agency through the Water Quality Benefits grant (EPA-G2015-STAR-A1), the University of North Carolina at Greensboro through start-up funds, and the Japan Society for the Promotion of Science through the Grants-in-Aid for Scientific Research (20H03010).
Footnotes
The authors declare no competing interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at https://www.pnas.org/lookup/suppl/doi:10.1073/pnas.2105574118/-/DCSupplemental.
Data Availability
R functions for the generation of branching networks and the metacommunity simulation are provided as the R package “mcbrnet,” version 1.1.0 (available at https://github.com/aterui/mcbrnet and mirrored on Zenodo at https://doi.org/10.5281/zenodo.5644009) (83). Codes for simulations, statistical analysis, figures, and tables are available at Zenodo at https://doi.org/10.5281/zenodo.5570593 (84). The fish data provided by third parties (63, 66–69) cannot be shared due to licensing issues. Previously published data used for this work are available at the RivFishTIME database (64) and Zenodo at https://doi.org/10.5281/zenodo.5640132 (85). Environmental data are available at MERIT Hydro (http://hydro.iis.u-tokyo.ac.jp/~yamadai/MERIT_Hydro/) (73), Global 3-second/1-second Water Body Map (http://hydro.iis.u-tokyo.ac.jp/~yamadai/G3WBM/index.html) (74), WorldClim (https://www.worldclim.org/data/v1.4/worldclim14.html) (75), Copernicus Global Land Service (https://doi.org/10.5281/zenodo.3939038) (76), and Global Reservoir and Dam database (https://sedac.ciesin.columbia.edu/data/set/grand-v1-dams-rev01) (77).
References
- 1.Lomolino M. V., Ecology’s most general, yet protean pattern: The species-area relationship. J. Biogeogr. 27, 17–26 (2000). [Google Scholar]
- 2.Arrhenius O., Species and area. J. Ecol. 9, 95–99 (1921). [Google Scholar]
- 3.Triantis K. A., Guilhaumon F., Whittaker R. J., The island species-area relationship: Biology and statistics. J. Biogeogr. 39, 215–231 (2012). [Google Scholar]
- 4.Kallimanis A. S., et al. , How does habitat diversity affect the species-area relationship? Glob. Ecol. Biogeogr. 17, 532–538 (2008). [Google Scholar]
- 5.Hubbell S. P., The Unified Neutral Theory of Biodiversity and Biogeography (Princeton University Press, 2001). [Google Scholar]
- 6.Losos J. B., Ricklefs R. E., The Theory of Island Biogeography Revisited (Princeton University Press, 2009). [Google Scholar]
- 7.Neigel J. E., Species-area relationships and marine conservation. Ecol. Appl. 13, 138–145 (2003). [Google Scholar]
- 8.Desmet P., Cowling R., Using the species-area relationship to set baseline targets for conservation. Ecol. Soc. 9, art11 (2004). [Google Scholar]
- 9.Myers N., Mittermeier R. A., Mittermeier C. G., da Fonseca G. A. B., Kent J., Biodiversity hotspots for conservation priorities. Nature 403, 853–858 (2000). [DOI] [PubMed] [Google Scholar]
- 10.Deguignet M., et al. , 2014 United Nations List of Protected Areas (UNEP-WCMC, Cambridge, UK, 2014). [Google Scholar]
- 11.Turner M. G., Gardner R. H., O’Neill R. V., Landscape Ecology in Theory and Practice: Pattern and Process (Springer, New York, 2015). [Google Scholar]
- 12.Rodríguez-Iturbe I., Rinaldo A., Fractal River Basins: Chance and Self-Organization (Cambridge University Press, 2001). [Google Scholar]
- 13.Campbell Grant E. H., Lowe W. H., Fagan W. F., Living in the branches: Population dynamics and ecological processes in dendritic networks. Ecol. Lett. 10, 165–175 (2007). [DOI] [PubMed] [Google Scholar]
- 14.Fagan W. F., Connectivity, fragmentation, and extinction risk in dendritic metapopulations. Ecology 83, 3243–3249 (2002). [Google Scholar]
- 15.Campbell Grant E. H., Nichols J. D., Lowe W. H., Fagan W. F., Use of multiple dispersal pathways facilitates amphibian persistence in stream networks. Proc. Natl. Acad. Sci. U.S.A. 107, 6936–6940 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Brown B. L., Swan C. M., Dendritic network structure constrains metacommunity properties in riverine ecosystems. J. Anim. Ecol. 79, 571–580 (2010). [DOI] [PubMed] [Google Scholar]
- 17.Rinaldo A., Gatto M., Rodriguez-Iturbe I., River networks as ecological corridors: A coherent ecohydrological perspective. Adv. Water Resour. 112, 27–58 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Carrara F., Altermatt F., Rodriguez-Iturbe I., Rinaldo A., Dendritic connectivity controls biodiversity patterns in experimental metacommunities. Proc. Natl. Acad. Sci. U.S.A. 109, 5761–5766 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Erős T., Lowe W. H., The landscape ecology of rivers: From patch-based to spatial network analyses. Current Landscape Ecology Reports 4, 103–112 (2019). [Google Scholar]
- 20.Holt G., Chesson P., The role of branching in the maintenance of diversity in watersheds. Freshw. Sci. 37, 712–730 (2018). [Google Scholar]
- 21.Reid A. J., et al. , Emerging threats and persistent conservation challenges for freshwater biodiversity. Biol. Rev. Camb. Philos. Soc. 94, 849–873 (2019). [DOI] [PubMed] [Google Scholar]
- 22.Peterson E. E., et al. , Modelling dendritic ecological networks in space: An integrated network perspective. Ecol. Lett. 16, 707–719 (2013). [DOI] [PubMed] [Google Scholar]
- 23.Moore J. W., et al. , Emergent stability in a large, free-flowing watershed. Ecology 96, 340–347 (2015). [DOI] [PubMed] [Google Scholar]
- 24.Terui A., et al. , Metapopulation stability in branching river networks. Proc. Natl. Acad. Sci. U.S.A. 115, E5963–E5969 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Isaak D. J., et al. , Slow climate velocities of mountain streams portend their role as refugia for cold-water biodiversity. Proc. Natl. Acad. Sci. U.S.A. 113, 4374–4379 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.McGuire K. J., et al. , Network analysis reveals multiscale controls on streamwater chemistry. Proc. Natl. Acad. Sci. U.S.A. 111, 7030–7035 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Abbott B. W., et al. , Unexpected spatial stability of water chemistry in headwater stream networks. Ecol. Lett. 21, 296–308 (2018). [DOI] [PubMed] [Google Scholar]
- 28.Yeakel J. D., Moore J. W., Guimarães P. R. Jr., de Aguiar M. A. M., Synchronisation and stability in river metapopulation networks. Ecol. Lett. 17, 273–283 (2014). [DOI] [PubMed] [Google Scholar]
- 29.Thompson P. L., et al. , A process-based metacommunity framework linking local and regional scale community ecology. Ecol. Lett. 23, 1314–1329 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Beverton R. J., Holt S. J., On the Dynamics of Exploited Fish Populations (Chapman and Hall, 1957). [Google Scholar]
- 31.Poff N. L., Olden J. D., Merritt D. M., Pepin D. M., Homogenization of regional river dynamics by dams and global biodiversity implications. Proc. Natl. Acad. Sci. U.S.A. 104, 5732–5737 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Dala-Corte R. B., et al. , Thresholds of freshwater biodiversity in response to riparian vegetation loss in the Neotropical region. J. Appl. Ecol. 57, 1391–1402 (2020). [Google Scholar]
- 33.Muneepeerakul R., Bertuzzo E., Rinaldo A., Rodriguez-Iturbe I., Evolving biodiversity patterns in changing river networks. J. Theor. Biol. 462, 418–424 (2019). [DOI] [PubMed] [Google Scholar]
- 34.Leibold M. A., et al. , The metacommunity concept: A framework for multi-scale community ecology. Ecol. Lett. 7, 601–613 (2004). [Google Scholar]
- 35.Economo E. P., Keitt T. H., Species diversity in neutral metacommunities: A network approach. Ecol. Lett. 11, 52–62 (2008). [DOI] [PubMed] [Google Scholar]
- 36.Kadoya T., Gellner G., McCann K. S., Potential oscillators and keystone modules in food webs. Ecol. Lett. 21, 1330–1340 (2018). [DOI] [PubMed] [Google Scholar]
- 37.Ushio M., et al. , Fluctuating interaction network and time-varying stability of a natural fish community. Nature 554, 360–363 (2018). [DOI] [PubMed] [Google Scholar]
- 38.Comte L., Olden J. D., Fish dispersal in flowing waters: A synthesis of movement- and genetic-based studies. Fish Fish. 19, 1063–1077 (2018). [Google Scholar]
- 39.Gelman A., Pardoe I., Average predictive comparisons for models with nonlinearity, interactions, and variance components. Sociol. Methodol. 37, 23–51 (2007). [Google Scholar]
- 40.Radinger J., Wolter C., Patterns and predictors of fish dispersal in rivers. Fish Fish. 15, 456–473 (2014). [Google Scholar]
- 41.Muneepeerakul R., et al. , Neutral metacommunity models predict fish diversity patterns in Mississippi-Missouri basin. Nature 453, 220–222 (2008). [DOI] [PubMed] [Google Scholar]
- 42.Carvajal-Quintero J., et al. , Drainage network position and historical connectivity explain global patterns in freshwater fishes’ range size. Proc. Nat. Acad. Sci. U.S.A. 116, 201902484 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Jackson D. A., Peres-Neto P. R., Olden J. D., What controls who is where in freshwater fish communities the roles of biotic, abiotic, and spatial factors. Can. J. Fish. Aquat. Sci. 58, 157–170 (2001). [Google Scholar]
- 44.Grill G., et al. , Mapping the world’s free-flowing rivers. Nature 569, 215–221 (2019). [DOI] [PubMed] [Google Scholar]
- 45.Elmore A. J., Kaushal S. S., Disappearing headwaters: Patterns of stream burial due to urbanization. Front. Ecol. Environ. 6, 308–312 (2008). [Google Scholar]
- 46.Schindler D. E., Armstrong J. B., Reed T. E., The portfolio concept in ecology and evolution. Front. Ecol. Environ. 13, 257–263 (2015). [Google Scholar]
- 47.Koning A. A., Perales K. M., Fluet-Chouinard E., McIntyre P. B., A network of grassroots reserves protects tropical river fish diversity. Nature 588, 631–635 (2020). [DOI] [PubMed] [Google Scholar]
- 48.Diamond J. M., The island dilemma: Lessons of modern biogeographic studies for the design of natural reserves. Biol. Conserv. 7, 129–146 (1975). [Google Scholar]
- 49.Fahrig L., Why do several small patches hold more species than few large patches? Glob. Ecol. Biogeogr. 29, 615–628 (2020). [Google Scholar]
- 50.Iwasaki Y., Ryo M., Sui P., Yoshimura C., Evaluating the relationship between basin-scale fish species richness and ecologically relevant flow characteristics in rivers worldwide. Freshw. Biol. 57, 2173–2180 (2012). [Google Scholar]
- 51.Sabo J. L., Finlay J. C., Kennedy T., Post D. M., The role of discharge variation in scaling of drainage area and food chain length in rivers. Science 330, 965–967 (2010). [DOI] [PubMed] [Google Scholar]
- 52.Petchey O. L., Gaston K. J., Functional diversity (FD), species richness and community composition. Ecol. Lett. 5, 402–411 (2002). [Google Scholar]
- 53.Chase J. M., Stochastic community assembly causes higher biodiversity in more productive environments. Science 328, 1388–1391 (2010). [DOI] [PubMed] [Google Scholar]
- 54.Peckham S. D., Gupta V. K., A reformulation of Horton’s laws for large river networks in terms of statistical self-similarity. Water Resour. Res. 35, 2763–2777 (1999). [Google Scholar]
- 55.Carraro L., et al. , Generation and application of river network analogues for use in ecology and evolution. Ecol. Evol. 10, 7537–7550 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Benda L. E. E., et al. , The network dynamics hypothesis: How channel networks structure riverine habitats. Bioscience 54, 413–427 (2004). [Google Scholar]
- 57.Fronhofer E. A., Altermatt F., Classical metapopulation dynamics and eco-evolutionary feedbacks in dendritic networks. Ecography 40, 1455–1466 (2017). [Google Scholar]
- 58.Terui A., Miyazaki Y., Three ecological factors influencing riverine fish diversity in the Shubuto River system, Japan: Habitat capacity, habitat heterogeneity and immigration. Limnology 17, 143–149 (2016). [Google Scholar]
- 59.Rahel F. J., Hubert W. A., Fish assemblages and habitat gradients in a Rocky Mountain-Great Plains stream: Biotic zonation and additive patterns of community change. Trans. Am. Fish. Soc. 120, 319–332 (1991). [Google Scholar]
- 60.Chaianunporn T., Hovestadt T., Evolutionary responses to climate change in parasitic systems. Glob. Change Biol. 21, 2905–2916 (2015). [DOI] [PubMed] [Google Scholar]
- 61.R Core Team, R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna, Austria: (2021). [Google Scholar]
- 62.Fukushima M., Kameyama S., Kaneko M., Nakao K., Ashley Steel E., Modelling the effects of dams on freshwater fish distributions in Hokkaido, Japan. Freshw. Biol. 52, 1511–1524 (2007). [Google Scholar]
- 63.Fukushima M., Hokkaido freshwater fish database HFish. Center for Environmental Biology and Ecosystem Studies, National Institute for Environmental Studies (2011). http://www.nies.go.jp/biology/data/hfish.html. Accessed 12 November 2021.
- 64.Comte L., et al. , RivFishTIME: A global database of fish time-series to study global change ecology in riverine systems. Glob. Ecol. Biogeogr. 30, 38–50 (2021). [Google Scholar]
- 65.Miyazaki Y., Terui A., Temporal dynamics of fluvial fish community caused by marine amphidromous species in the Shubuto River, southwestern Hokkaido, Japan. Ichthyol. Res. 63, 173–179 (2016). [Google Scholar]
- 66.Iowa Department of Natural Resources, Biological assessment of Iowa’s wadeable streams (2004).
- 67.Illinois Environmental Protection Agency, Illinois water monitoring strategy 2015-2020 (2014).
- 68.Minnesota Pollution Control Agency, Development of a fish-based index of biological integrity for Minnesota’s rivers and streams. Document number wq-Bsm2-03 (2014).
- 69.Wisconsin Department of Natural Resources, Guidelines for assessing fish communities of wadeable streams in Wisconsin v2.0 (2018).
- 70.Chao A., et al. , Rarefaction and extrapolation with Hill numbers: A framework for sampling and estimation in species diversity studies. Ecol. Monogr. 84, 45–67 (2014). [Google Scholar]
- 71.Hsieh T. C., Ma K. H., Chao A., iNEXT: An R package for rarefaction and extrapolation of species diversity (Hill numbers). Methods Ecol. Evol. 7, 1451–1456 (2016). [Google Scholar]
- 72.Whittaker R. H., Vegetation of the Siskiyou Mountains, Oregon and California. Ecol. Monogr. 30, 279–338 (1960). [Google Scholar]
- 73.Yamazaki D., et al. , MERIT hydro: A high-resolution global hydrography map based on latest topography dataset. Water Resour. Res. 55, 5053–5073 (2019). [Google Scholar]
- 74.Yamazaki D., Trigg M. A., Ikeshima D., Development of a global ∼90m water body map using multi-temporal Landsat images. Remote Sens. Environ. 171, 337–351 (2015). [Google Scholar]
- 75.Hijmans R. J., Cameron S. E., Parra J. L., Jones P. G., Jarvis A., Very high resolution interpolated climate surfaces for global land areas. Int. J. Climatol. 25, 1965–1978 (2005). [Google Scholar]
- 76.Buchhorn M., et al. , Copernicus global land service: Land cover 100m: Collection 3: Epoch 2015: Globe (2020). 10.5281/zenodo.3939038.
- 77.Lehner B., et al. , Global reservoir and dam database, version 1 (GRanDv1): Dams, revision 01. Palisades, NY: NASA Socioeconomic Data and Applications Center (SEDAC). https://sedac.ciesin.columbia.edu/data/set/grand-v1-dams-rev01. Accessed 25 January 2021.
- 78.Pebesma E., Simple features for R: Standardized support for spatial vector data. R J. 10, 439–446 (2018). [Google Scholar]
- 79.Hijmans R. J., raster: Geographic data analysis and modeling. R package version 3.3-13 (2020).
- 80.Pebesma E., stars: Spatiotemporal arrays, raster and vector data cubes. R package version 0.4-3 (2020).
- 81.Baston D., exactextractr: Fast extraction from raster datasets using polygons. R package version 0.5.0 (2020).
- 82.Wagenmakers E. J., A practical solution to the pervasive problems of p values. Psychon. Bull. Rev. 14, 779–804 (2007). [DOI] [PubMed] [Google Scholar]
- 83.Terui A., mcbrnet: metacommunity simulation in a branching network (1.1.0). Zenodo. 10.5281/zenodo.5644009. Deposited 3 November 2021. [DOI]
- 84.Terui A., Kim S., Dolph C. L., Kadoya T., Miyazaki Y., Code for: Emergent dual scaling of riverine biodiversity (v1.0). Zenodo. 10.5281/zenodo.5570593. Deposited 14 October 2021. [DOI] [PMC free article] [PubMed]
- 85.Terui A., Miyazaki Y., Fish community data in the Shubuto River system, Japan (v1.0). Zenodo. 10.5281/zenodo.5640132. Deposited 2 November, 2021. [DOI]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
R functions for the generation of branching networks and the metacommunity simulation are provided as the R package “mcbrnet,” version 1.1.0 (available at https://github.com/aterui/mcbrnet and mirrored on Zenodo at https://doi.org/10.5281/zenodo.5644009) (83). Codes for simulations, statistical analysis, figures, and tables are available at Zenodo at https://doi.org/10.5281/zenodo.5570593 (84). The fish data provided by third parties (63, 66–69) cannot be shared due to licensing issues. Previously published data used for this work are available at the RivFishTIME database (64) and Zenodo at https://doi.org/10.5281/zenodo.5640132 (85). Environmental data are available at MERIT Hydro (http://hydro.iis.u-tokyo.ac.jp/~yamadai/MERIT_Hydro/) (73), Global 3-second/1-second Water Body Map (http://hydro.iis.u-tokyo.ac.jp/~yamadai/G3WBM/index.html) (74), WorldClim (https://www.worldclim.org/data/v1.4/worldclim14.html) (75), Copernicus Global Land Service (https://doi.org/10.5281/zenodo.3939038) (76), and Global Reservoir and Dam database (https://sedac.ciesin.columbia.edu/data/set/grand-v1-dams-rev01) (77).