Abstract
Purpose of Review
To introduce readers to policy modeling, a multidisciplinary field of quantitative analysis, primarily used to help guide decision-making. This review focuses on the choices facing educational administrators, from K-12 to universities in the USA, as they confronted the COVID-19 pandemic. We survey three key model-based approaches to mitigation of SARS-CoV-2 spread in schools and on university campuses.
Recent Findings
Frequent testing, coupled with strict attention to behavioral interventions to prevent further transmission can avoid large outbreaks on college campuses. K-12 administrators can greatly reduce the risks of severe outbreaks of COVID-19 in schools through various mitigation measures including classroom infection control, scheduling and cohorting strategies, staff and teacher vaccination, and asymptomatic screening.
Summary
Safer re-opening of college and university campuses as well as in-person instruction for K-12 students is possible, under many though not all epidemic scenarios if rigorous disease control and screening programs are in place.
Keywords: Policy modeling, COVID-19, Schools, Universities, SARS-CoV-2 screening
Introduction
Mathematical models of the spread of SARS-CoV-2 proliferated in the scientific literature, on pre-print servers and on data science blogs, many being described in the popular press to offer the general public information on the possible trajectories of the pandemic. Using traditional statistical and epidemiological approaches, these efforts have focused largely on predicting the future course of the pandemic. The Centers for Disease Control and Prevention (CDC) combines many of these models in an ensemble forecast that predicts outcomes 4 weeks into the future [1]. Some forecasting models have been adapted to include intervention scenarios evaluating the impact of various tools to mitigate disease transmission, morbidity and mortality, and in this way offer a general-purpose platform to assess policies such as school closures, social distancing, mask-wearing and vaccines [2]. These kinds of epidemiological models have been discussed and reviewed elsewhere [3]. In this review, we will focus on a different type of analytic endeavor in which specific policy questions are the fundamental basis for the initial inquiry, with simple disease models being used to provide the epidemiological context for this research. Rather than focusing on disease dynamics, these policy models put “attention on decisions that must be made and their operational consequences [4].” In the use of policy models, the first-order task is to provide a “sufficient basis for policy decision-making,” where the data may be uncertain or unobtainable, but the need to make a decision is pressing nonetheless [5].
What Is Policy Modeling?
Epidemiological models of SARS-CoV-2 are primarily designed with the goal of capturing disease dynamics over time. Short-term predictive accuracy is paramount in these models—can they reliably predict the path of the pandemic out into the near or not-so-near future?
Policy models come with a different approach and look to portray the same disease processes, their interactions, and dynamics, but explicitly in the context of imminent and critical decisions needing to be made. Many of the methods of policy modeling are based in the tenets of decision science, in which the primary goal is representing the uncertainty inherent in given scenarios facing decision-makers, articulating objectives, and the trade-offs represented by choices facing them in reaching their objectives [6]. Sensitivity analyses are used to manage this uncertainty and value of information methods are used to quantify the benefits of gathering more evidence that can reduce this uncertainty in a way that leads to more optimal decisions.
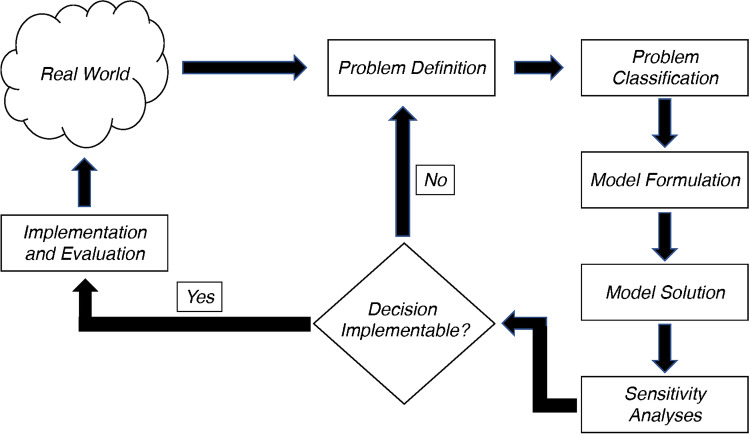
In the context of COVID-19, these models are less concerned with precise predictions of the most likely epidemic trajectory than with the robustness of the analysis of policy choices under a wide range of assumptions about key parameters in the underlying disease model. Policy modeling also tends to follow an operations research framework, in which the policy problem is first defined, the problem classified, the model formulated and solved, sensitivity analyses performed and then if the decision is implementable, it is evaluated with real-world data [7]. If all the decisions in a policy model are impractical—or if plausible data for the key inputs to the model cannot be assembled—the policy modeling process begins again with the reformulation of the problem at hand (see Fig. 1).
Fig. 1.
The policy modeling process
Policy models also tend to balance precision versus tractability, prizing first-strike models that can articulate the key features of policy problems with simplicity, moving towards more complexity as needed—as questions evolve, as new evidence and insights into the problem emerge, and as long as the model is still tractable, solvable with these new components. Because policy models are often developed to address a current policy issue, the default is to often distill models down to the bare essential considerations that matter most in answering the policy question, bounding best- and worst-case scenarios, using what-if sensitivity analysis and even-if, a fortiori, arguments to ground simple models. This specificity to a particular question or questions facing decision-makers distinguishes policy models from many more complex systems dynamics models, which often aim to serve as a general purpose representation of a phenomenon like an epidemic, and to serve multiple, conflicting objectives, where presenting specific alternatives and trade-offs for decision-makers are not the primary goal of the exercise [8]. Finally, policy modeling encourages an interdisciplinary, team-based approach in which those with experience in decision science, operations research or other quantitative disciplines (e.g., epidemiology, statistics) often pair up with those with domain knowledge to work through the policy modeling process together [9]. This is because the details of how the decisions will get made, the kinds of information decision-makers require, the nature of the trade-offs, and their acceptability need specific knowledge that only domain experts can provide.
During the COVID-19 pandemic, many disease models have emerged, but far fewer policy models have been published or discussed. This review will describe in detail several key policy models developed during the pandemic, meant to answer policy questions, assist decision-makers in the difficult choices they faced in 2020 and in 2021, on a key issue that was a priority for politicians across the country: when, if, and how to open educational institutions from K-12 through universities.
Preventing SARS-CoV-2 Outbreaks in Educational Settings
Who Are the Decision-Makers?
In the three papers discussed here, the decision-makers were university and/or primary and secondary school administrators [10–12]. In fact, in Chang et al. (2020), the policy model was specifically developed to assist Yale University’s plan to resume on-campus instruction, while Paltiel et al.’s (2020) work was used to advise a set of Boston-area universities and colleges in their return to campus decision-making [13]. In Bilinski et al. (2021), the model was developed in discussions with primary and secondary school administrators in Massachusetts, Maryland, and California to ensure that model structure and parameters were realistic, and that strategies and scenarios in the analysis captured policy alternatives most salient to ongoing decisions. Bilinski et al. interviewed administrators, teachers, and other school staff as they developed their model, and the comments received from many underscored the urgent need for policy advice even in the absence of definitive on-the-ground data to guide decisions.
What Is the Problem Definition?
In the two papers looking at COVID-19 on university campuses, the problem definitions overlap in part, diverge in others. Both Chang et al. and Paltiel et al. defined the problem as preventing large outbreaks of SARS-COV-2 on residential campuses through repeated testing and isolation of those receiving a positive screening test. Paltiel et al.’s work extends the problem definition to ask which testing and isolation strategies are more cost-effective and examines the budget impact of choices facing decision-makers. Bilinski et al. assessed safe school-reopening strategies in different settings, primary and secondary schools, and looked at a broader set of interventions than Chang et al. and Paltiel et al., including reducing class sizes, alternative scheduling of in-person instruction, staff vaccination, quarantine of contacts of infected individuals, as well as regular testing and isolation of those infected.
The differences in the problem formulations here are important to consider. In the case of Chang et al., decision-makers have almost certainly made a decision to test and the model is built to assess the specific strategies that will avoid a large outbreak with the objective of keeping cumulative infections below some defined ceiling. However, in Paltiel et al., the objective is to maximize return on investment for decision-makers. Thus, the authors highlight both the epidemiological and economic impact of the available policy choices in their model. Importantly, Paltiel et al. offers a policy choice, not included in Chang et al., where there is an option to forgo regular testing and rely on symptom-based screening alone. This makes their model part persuasion, particularly for those administrators who may be considering no proactive testing at all on campus, focusing on the impact of this decision for their universities. Finally, Bilinski et al. are wading into a national policy debate rather than advising specific school districts. While the authors consider a broader range of interventions than either Chang et al. or Paltiel et al., the overall problem to be addressed here is less about the relative merits of specific programmatic interventions than about the feasibility of re-opening schools at all under various levels of ongoing community transmission, a much more basic question for decision-makers. Taken together, these three studies offer three variations on a similar theme: one offers choices of strategies for testing and isolation in the context of a decision to establish such a program; another weighs these kinds of choices, but also makes the case for the need for such programs rather than relying on symptom-based screening; and the last posits that safe re-opening of schools is possible under a variety of scenarios with different disease control strategies, based on a range of choices a decision-maker might pursue.
What Are the Problem Classification and Model Formulation?
All three of these studies approach the problem of preventing or ameliorating large outbreaks in educational settings using dynamic disease models of varying complexity and distinguish themselves from each other by approach, by what they include and exclude from the models themselves. They also make concessions to simplicity as described above, which would usually not be done in an epidemiological forecasting model of SARS-CoV-2 but are suitable for answering the policy problem facing decision-makers. For instance, Chang et al. and Paltiel et al. assume homogeneous mixing without age-dependent transmission in their models. The reason this kind of assumption may be suitable for decision-making but not forecasting is because work by Kaplan and others has shown that one is very often assuming the worst-case transmission scenario when one assumes homogeneous mixing [14]. So, if one can show that the intervention of interest is sufficient to control matters under worst-case conditions, one can argue with confidence that the intervention will be sufficient to control matters under less extreme circumstances. This is a fortiori (i.e., “even if”) argumentation and is a hallmark of policy modeling.
The model formulation in these papers reflects the audience of decision-makers for each of them and the ensuing problem definition based on decision-makers’ needs. In the case of Chang et al., the model was developed to guide a testing program, which was all but certain to be put in place, most likely with a PCR-based assay. Thus, the model formulation beyond the basic structure to recapitulate disease dynamics includes a unique feature that does not appear in the other two studies: age-of-infection-dependent sensitivity, which is important in this case because PCR based assays cannot detect infection immediately following a transmission event. The key decisions to be made here are how often to test and with a PCR-based assay, with given sensitivity and specificity. The age of infection-dependent sensitivity’s impact on the test’s performance is key to the model, as no detection can happen in the window period and can substantially reduce the efficiency of repeated testing. Paltiel et al. do not include this feature in their model but provide a range of test sensitivities and specificities to interrogate, along with the economic features (i.e., cost-effectiveness and budget impact) of strategies described above based on two test costs. This model formulation does not assume a testing program will happen, it’s explicitly designed to show the outcomes over a range of test sensitivities and specificities, test costs in contrast with symptom-based screening alone.
Chang et al. use a generalized representation of common epidemic models described by Kaplan, while Paltiel et al. use a traditional SEIR (susceptible-exposed-infected-recovered) framework for their study [15]. The set-up of the two models either explicitly requires a recovered/removed compartment (Paltiel et al.) or addresses this through other means (Chang et al.). In Chang et al., the transmission intensity as a function of age of infection, λ, which accounts for the distribution of infectiousness over time and allows for individuals to simply stop transmitting according to this parameter. However, both studies rely on a set of common inputs and parameters including: the initial number of susceptible and infected students; the time horizon or number of days over which the simulation will be conducted; R0 or effective Rt; the influx of exogenous infections from off campus, and of course, the frequency of screening of students. Both university models have similar performance measures, including number of total infections, total true positive infections, total false positive infections, average number of students in isolation, and for Paltiel et al., incremental cost-effectiveness and budget impact.
Bilinski et al.’s model is the most complex of the three discussed here. Given the bias towards simplicity in policy modeling, it was important to understand the rationale for the use of an individual-based stochastic network simulation (i.e., an ‘agent-based’ model) in this study. In discussions with authors, again the perspective of the decision-maker was forefronted in their model development:
In talking to stakeholders, we realized how important it was to make sure that the diversity of interactions in the model felt realistic -- that we considered rotating teachers for music, art, special education, etc., and teacher-teacher interactions in staff rooms, and random kids interactions like busses, and out-of-school interactions when kids were out of school and less likely to be masked. Of course, it became clear over time in the modeling process that some of these were more important than others, but it was very useful to a) have a framework that could easily adapt to test the implications of different movement patterns and b) that incorporated a rich set of realistic interactions (A. Bilinski, personal communication).
The agent-based approach was also taken to ensure that the stochasticity in outcomes in the real world could be mirrored in the simulations, in particular because of the wide variety in existing policy approaches to school closures in the primary and secondary setting globally and conflicting reports on the impact of transmission in schools in these places. The motivating idea of this study and for the model choice was that the same set of parameters can produce a wide range of outcomes (e.g., usually no onward transmission but sometimes an outbreak), but that the risk of severe ones can be controlled by a variety of mitigation strategies.
For the agent-based model deployed by Bilinski et al. a set of synthetic households of students, staff and other resident adults was constructed. Then, an elementary and a high school were simulated, with teachers and other adult staff (representing administrators, counselors, custodians, “specials” or teachers of subjects like art and music) assigned rotating in-classroom roles or out-of-classroom roles. In the simulation, families interact outside of school settings to represent social interactions and other interpersonal ones such as childcare for non-school-aged children. Dyadic interactions were modeled between individuals of all ages, according to relationships in the school, household, or childcare setting. Transmission occurred in these interactions based on setting and duration of contact, infectiousness, and susceptibility, which differed for adults and children. The secondary attack rate—the probability that an infected individual transmits SARS-CoV-2 to a contact—was defined for adult-adult interactions in both household and school-based interactions, and distinct attack rates allowed for elementary and high school students. The chance of transmission was also modified in the model by duration of contact, symptomatic status, and interventions such as mask wearing. Transmission was set up to vary by symptomatic status, but adult transmissibility was also allowed to be heterogeneous in the model to represent the overdispersion common with this infection.
Bilinski et al. are evaluating a far larger set of interventions in their study, including isolation of symptomatic individuals, quarantine of an infected individual’s contacts, reduced class sizes, alternative schedules, staff vaccination, and weekly asymptomatic screening, defined in three broad categories, general infection control in schools, COVID-19-specific countermeasures, and scheduling/cohorting. The performance measure here was the ability of a mitigation strategy to control transmission among students, educators, school staff, or families, where control was defined by the strategy’s ability to confer on average, less than a 1 percentage point increase in infections in the specific group under consideration, compared with remote learning.
What Are the Model Solutions and Sensitivity Analyses?
Despite the differences in their construction, assumptions, parameter estimates, Chang et al. and Paltiel et al.’s models demonstrate results that largely agree with each other in terms of the broad implications of the work, suggesting repeated testing of students greater than once weekly followed by isolation of infected individuals is required to contain campus outbreaks of COVID-19. Both studies evaluate different testing frequencies in an 80-day simulation and in sensitivity analyses vary the R0 and test sensitivity as well. In fact, both papers also arrive at the same principal observation: frequency of testing is by far the most powerful variable that university administrators have at their disposal. In Chang et al., with 10,000 students using a 2-day non-detection window and then a constant 80% sensitivity and 99.8% specificity along with a 2.5 R0 recommended by the CDC for base case modeling values (CDC recommends between 2.0-3.0) weekly testing could not contain an outbreak (i.e., results in > 5% of initial population infected) on campus. Chang et al. also show that minimizing the time from detection to isolation was key to outbreak mitigation. In Paltiel et al., in 5000 students with an R0 of 2.5, a test with a constant 70% sensitivity and 98% specificity, weekly testing leads to cumulative infections totaling over 1/3 of the student body only exceeded by symptomatic screening in which almost the entire student body is infected. With additional numbers of imported infections into the campus community, this ability of weekly testing to prevent large outbreaks continues to deteriorate in both studies.
In Chang et al., weekly testing is juxtaposed against testing once every 3 days and a Shiny app lets readers modify the parameters in the model to provide a greater range of scenarios to consider than what is offered in the paper. In Paltiel et al., testing every day, every 2 days, every 3 days, testing weekly or simply screening for symptoms were compared against each other. As with Chang et al., multiple scenarios are considered, and a Google sheet was provided to readers to allow a broader set of choices to be interrogated (an independent research group developed an associated webapp after the paper was published and is available at https://data-viz.it.wisc.edu/covid-19-screening/). What is critical about Paltiel et al.’s analysis is that it uses cost-effectiveness analysis to identify the preferred screening strategy at a set of different willingness to pay thresholds based on incremental cost-effectiveness ratios. In both Chang et al. and Paltiel et al., testing more frequently reduces the number of infections by identifying and isolating cases more rapidly, though screening with a more sensitive test less frequently can achieve similar goals. However, there are trade-offs associated with increased case detection and increased number of false positives when one elects to increase the frequency with less sensitive tests. What Paltiel et al. offer in addition is a way to understand if the incremental benefit in infections averted is worth the incremental cost of investing in more frequent testing.
In addition to the wide range of sensitivity analyses in both papers, both studies also use best- and worst-case scenarios to identify upper and lower bounds for their key outcome estimates. In Chang et al., the best- and worst-case scenarios are determined by whether the set-up includes early versus late transmission of infections and one of three accompanying time-dependent sensitivity functions. In the worst-case, pessimistic scenario, infections are happening early under a test sensitivity function derived from a Bayesian hierarchical model by Kucirka and a weekly PCR assay-based screening strategy cannot contain an outbreak with an R0 of greater than 1.4 [16]. The best-case, optimistic scenario, with late transmission and a step function test sensitivity, can only contain an outbreak under R0 < 2.25. With testing three times a week, an outbreak can be contained in the worst-case scenario (early transmission; Kucirka) if R0 < 1.75, and in the best-scenario (late transmission; step function) with R0 as high as 4.8. However, there are also perfectly plausible modeling assumptions and data scenarios under which the very same testing and isolation strategy can contain an outbreak successfully or see one run out of control. The message here for decision-makers is that these containment strategies are fragile, require everything to go as planned (e.g., testing turn-around, masking and social distancing on campus) and administrators have to be ready to adapt to changing circumstances.
The best- and worst-case scenarios in Paltiel et al. are more straight-forward, and thus perhaps more understandable to decision-makers, based on R0, test specificity and exogenous infections from off-campus. With the use of cost-effectiveness and ICERs, the best- and worst-case scenarios also include preferred scenarios based on willingness to pay thresholds. In the worst-case scenario, with R0 at 3.5, test sensitivity at 98% and 25 exogenous infections per week, daily screening was preferred at WTP thresholds above $4400 per infection averted; under the best-case scenario with R0 at 1.5, test sensitivity at 99.7% and 5 exogenous infections per week, weekly screening was preferred with WTP thresholds under $5500 per infection averted. Test costs and sensitivity, the probability of progressing from infections to symptoms changed preferred status of different scenarios as well. Finally, Paltiel et al., provide an 80-day-semester per student cost of each of their preferred screening strategies, with $120, $470, and $910, representing implementation costs of the best-, base and worst-case scenarios.
Bilinski et al.’s work examines a number of interventions, in combination, at various levels of stringency in implementation in the K-12 setting. The primary insight the model offers decision-makers is that elementary schools—in the context of controlled community transmission and moderate levels of interventions to mitigate transmission—can safely re-open, while high schools require a higher level of intervention to block transmission. In the context of more significant community spread of SARS-CoV-2, asymptomatic testing can offer a way to still (re)open schools and contain outbreaks. General mitigation strategies such as mask wearing and social distancing were the foundation of disease control strategies in Bilinski et al.
In elementary schools, outbreaks could be contained through successful combination of more than one prevention and screening program, including (a) splitting the student population into two cohorts attending on alternating days; (b) achieving high adherence to masking and distancing; (c) conducting symptomatic screening; (d) rapidly following up the detection of symptomatic cases with contact tracing, isolation, and asymptomatic testing. In high schools, it was more difficult to contain outbreaks without high adherence to masking and distancing, even with classroom quarantine (i.e., symptomatic screening of classes, testing and isolation of infected students and contacts). With low adherence to masking and social distancing in elementary schools with classroom quarantine, 1.7 secondary infections emerged over 30 days as compared with 23 in high schools with the same strategies in place. Interestingly, teacher vaccination did not substantially affect outbreak size, but did reduce transmission among teachers themselves. Asymptomatic testing on a weekly basis was useful in containing outbreaks, particularly in conjunction with other interventions (i.e., classroom quarantine).
Bilinski et al. also looked at the probability of outbreaks in 2000 simulations with each set of parameters. What is important to note is that the chance of seeing no secondary infections occurred in 79% (and more than 5 secondary infections in 0.3%) of the simulations with high mask wearing and social distancing and classroom quarantines, dropping to 52% (and more than 5 secondary infections rising to 8.4%) when mask wearing and social distancing were at their lowest levels. In high schools, with classroom quarantine zero secondary cases were seen in 18% to 51% of the simulations in the context of a range of other interventions, while the frequency of outbreaks of at least 5 secondary cases ranged from 12 to 61%. That the tail risk of large outbreaks was disrupted with any intervention is probably the key take-home point for decision-makers reading this work. A sensitivity analyses in Bilinski et al., assuming that elementary school children were as infectious as adults (rather than half as infectious as in the base case) resulted in 1.9 times the number of secondary infections as in the base case; assuming that adolescents were half as infectious as adults (rather than equally infectious as in the base case) led to a reduction in cases in high schools by a factor of 0.3.
Were These Decisions Implementable?
Both Chang et al. and Paltiel et al. were akin to users’ guides for testing on campuses, with Chang et al. advising Yale University and Paltiel et al. advising a larger group of universities in New England. Thus, in fact, the insights derived from these policy models were put to use in real time. As was mentioned above, Paltiel et al.’s paper was also a useful persuasive tool, suggesting to university administrators who thought that symptomatic screening alone might allow for safe (re-)opening of campuses to re-evaluate their assumptions and decisions. Bilinski et al.’s study was not commissioned or used by any specific school district, but the strategies discussed and evaluated in the model were used all over the country over the course of the 2020–2021 school year. The debates on (re-)opening of elementary and high schools in the USA were contentious and heated. As is the case with many policy models, Bilinski et al. weighed in on a topic where evidence was contradictory and incomplete, attempting to make crude, but critical insights based on their research to guide educators and families with school-aged children. The key insight of their study—that the tail risk of serious outbreaks was largely alleviated by any intervention—was a crucial signal that schools could open safely with proper precautions and that schools that decided to open without these in place risked outbreaks that they could not control.
Conclusions
Policy modeling is not disease forecasting. While in the context of COVID-19, the work described here all used disease models, their primary purpose was to interrogate competing policy and programmatic choices for educators around the country. In a way, each of these models was designed for a decision-maker, either explicitly or implicitly, who was asking how do I continue our students’ education and keep them safe? In all cases, these models were built with the input and advice of the decision-makers themselves, about what mattered to them: the administrators at Yale, those at colleges and universities around New England, the school leaders in Massachusetts, Maryland, and California. Policy-modeling is inherently a team-sport, not just the province of those with quantitative expertise whether they be epidemiologists, decision scientists or statisticians. These models range from the simple SEIR set-up to complicated agent-based designs, but again, constructed with an audience in mind. The audience here could be a university president who wants to know do I have to test, how often and how much will it cost me or a larger group of stakeholders in cities and towns around the country facing competing information on the dangers of COVID-19 in K-12 settings and who wants to see the world reflected back to them in more detail than a compartmental model can provide. Policy models also offers up choices, not necessarily answers; in each of these studies you can design your own scenario, in Chang et al. with a web app that lets you modify the entire world of the model yourself, to Paltiel et al.’s smorgasbord of choices of screening strategies based on the kinds of testing you use, your willingness to pay more for fewer infections on campus, to the variety of mitigation strategies layered on top of mask wearing and social distancing in Bilinski et al. In addition, through sensitivity analyses, policy models ask you to work through your assumptions, the best-case and worst-case scenarios, which strive to tell you how good it might be or how bad it can get, with the idea that the actual outcome is bounded between these extremes. At the end of the policy modeling process, decision-makers act on the choices presented to them. In the case of the COVID-19 pandemic, educators across the USA acted on insights from these models (i.e., Chang et al. and Paltiel et al.) or could take solace from their bottom line (i.e., Bilinski et al.).
Footnotes
This article is part of the Topical Collection on The Global Epidemic
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.CDC. COVID-19 mathematical modeling [Internet]. Centers for Disease Control and Prevention. 2020 [cited 2021 Jul 5]. Available from: https://www.cdc.gov/coronavirus/2019-ncov/science/forecasting/mathematical-modeling.html
- 2.Borchering RK. Modeling of future COVID-19 cases, hospitalizations, and deaths, by vaccination rates and nonpharmaceutical intervention scenarios — United States, April–September 2021. MMWR Morb Mortal Wkly Rep [Internet]. 2021 [cited 2021 Jul 5];70. Available from: https://www.cdc.gov/mmwr/volumes/70/wr/mm7019e3.htm [DOI] [PMC free article] [PubMed]
- 3.James LP, Salomon JA, Buckee CO, Menzies NA. The use and misuse of mathematical modeling for infectious disease Policymaking: lessons for the COVID-19 pandemic. Med Decis Making. 2021;41(4):379–385. doi: 10.1177/0272989X21990391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Kaplan EH. Adventures in policy modeling! Operations research in the community and beyond. Omega. 2008;36(1):1–9. doi: 10.1016/j.omega.2005.07.012. [DOI] [Google Scholar]
- 5.Kaplan EH. OM forum—perspectives on policy modeling: 2018 MSOM Fellow Award. Manuf Serv Oper Manag. 2021;23(2):267–273. [Google Scholar]
- 6.Clemen RT. Making hard decisions: an introduction to decision analysis. Brooks/Cole Publishing Company; 1996.
- 7.Hillier FS. Introduction to operations research. Tata McGraw-Hill Education; 2012.
- 8.Murdock CA. Defense policy formation: a comparative analysis of the McNamara era. Suny Press; 1974.
- 9.Brandeau ML. Creating impact with operations research in health: making room for practice in academia. Health Care Manag Sci. 2016;19(4):305–312. doi: 10.1007/s10729-015-9328-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Chang JT, Crawford FW, Kaplan EH. Repeat SARS-CoV-2 testing models for residential college populations. Health care management science. 2020;1–14. [DOI] [PMC free article] [PubMed]
- 11.Paltiel AD, Zheng A, Walensky RP. Assessment of SARS-CoV-2 Screening Strategies to Permit the Safe Reopening of College Campuses in the United States. JAMA Netw Open. 2020;3(7):e2016818–e2016818. doi: 10.1001/jamanetworkopen.2020.16818. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Bilinski A, Salomon JA, Giardina J, Ciaranello A, Fitzpatrick MC. Passing the Test: a model-based analysis of safe school-reopening strategies. Ann Intern Med. 2021 Aug;174(8):1090–1100. [DOI] [PMC free article] [PubMed]
- 13.Massachusetts Higher Education Testing Group. Developing an integrated COVID-19 testing strategy: considerations for institutions of higher education in Massachusetts. https://www.wellesley.edu/sites/default/files/assets/departments/publicaffairs/files/final_report_of_the_ma_higher_education_covid-19_testing_group_1.pdf.
- 14.Kaplan EH, Lee YS. How bad can it get? bounding worst case endemic heterogenous mixing models of HIV/AIDS. Math Biosci. 1990;99(2):157–180. doi: 10.1016/0025-5564(90)90002-G. [DOI] [PubMed] [Google Scholar]
- 15.Kaplan EH. OM Forum—COVID-19 scratch models to support local decisions. M&SOM. 2020;22(4):645–655. doi: 10.1287/msom.2020.0891. [DOI] [Google Scholar]
- 16.Kucirka LM, Lauer SA, Laeyendecker O, Boon D, Lessler J. Variation in false-negative rate of reverse transcriptase polymerase chain reaction–based SARS-CoV-2 tests by time since exposure. Ann Intern Med. 2020;173(4):262–267. doi: 10.7326/M20-1495. [DOI] [PMC free article] [PubMed] [Google Scholar]