Estimating the decision curve and its precision from three study designs

Abstract

The decision curve plots the net benefit (NB) of a risk model for making decisions over a range of risk thresholds, corresponding to different ratios of misclassification costs. We discuss three methods to estimate the decision curve, together with corresponding methods of inference and methods to compare two risk models at a given risk threshold. One method uses risks (R) and a binary event indicator (Y) on the entire validation cohort. This method makes no assumptions on how well-calibrated the risk model is nor on the incidence of disease in the population and is comparatively robust to model miscalibration. If one assumes that the model is well-calibrated, one can compute a much more precise estimate of NB based on risks R alone. However, if the risk model is miscalibrated, serious bias can result. Case–control data can also be used to estimate NB if the incidence (or prevalence) of the event (Y = 1) is known. This strategy has comparable efficiency to using the full (R, Y) data, and its efficiency is only modestly less than that for the full (R, Y) data if the incidence is estimated from the mean of Y. We estimate variances using influence functions and propose a bootstrap procedure to obtain simultaneous confidence bands around the decision curve for a range of thresholds. The influence function approach to estimate variances can also be applied to cohorts derived from complex survey samples instead of simple random samples.

1 |. INTRODUCTION

Statistical risk prediction models for disease incidence (e.g., Pfeiffer et al., 2013) or, following disease onset, disease recurrence (e.g., Stephenson et al., 2006) or mortality (e.g., Albertsen, Hanley, & Fine, 2005), are used to inform choices for preventive intervention or treatment. For public health applications, they can be used to target preventive interventions to those with high enough risks to justify an intervention that has adverse effects and to identify high-risk individuals for intensive screening for early detection of disease.

Before a risk prediction model can be recommended for clinical or public health applications, one needs to assess how valid and useful the predictions are. General criteria such as calibration and discriminatory accuracy are recommended (see, e.g., Gail & Pfeiffer, 2005; Gerds, Cai, & Schumacher, 2008). However, it is preferable to assess model utility in the context of a specific clinical decision, whenever possible. Suppose one must decide whether or not to intervene, and suppose there are two health states (such as diseased or not diseased). If one can define “costs” (or “losses”) for each of the four combinations of intervention decision and health state, there is an optimal risk threshold, which is independent of the risk model, above which one should intervene to minimize expected losses (Gail & Pfeiffer, 2005; Pauker & Kassirer, 1975). For that application, a figure of merit for a given risk model is the expected cost at that optimal threshold. In comparing two risk models, the preferred model is the one with smaller expected cost. (Instead of costs or losses, some investigators equivalently specify “utilities” and the preferred risk model is the one that yields the larger expected utility.)

A problem with this paradigm for model evaluation is defining the “costs,” which determine the optimal threshold. Vickers and Elkin (2006) proposed instead to examine the “net benefit” at threshold t, which is the probability of a true positive (the event that a case has risk > t), minus the product of the probability of a false positive (the event that a noncase has risk > t) times the threshold odds {t/(1 − t)}. The “decision curve” (Vickers & Elkin, 2006), a plot of the net benefit (NB) over a range of thresholds, covers decision problems for a range of cost ratios. If one model had a higher NB curve over a range of relevant thresholds than a second model, the first model would be preferred. The paper by Vickers and Elkin (2006) has been cited over 800 times, and decision curves are popular in the literature (e.g., Vienot et al., 2017), but we have not seen analytical statistical methods for putting confidence intervals (CIs) on the NB at a given threshold or on the difference in NBs between two models evaluated on the same data at that threshold.

In this paper, we assume that a previously developed risk model R(x) is assessed in independent external “test” or “validation” data. The model is fixed, and statistical variability arises from estimation in the validation sample. The validation data may be cohort data, case–control data, if the incidence rate of disease is also known, or simply a random sample of projected risks, if the model is assumed to be well-calibrated. We develop pointwise CIs for the NBs at a given threshold and for the difference in two NBs from different models at that threshold. We also discuss the decision curve as a stochastic process in t and propose a bootstrap procedure to produce simultaneous confidence bands for the entire curve.

We assume thatR(x) models the probability that an individual with risk factors x will have a dichotomous event, Y = 1. Although this is a simple formulation, it applies to several important problems in clinical medicine and public health. The event Y = 1 could denote developing a specific disease in a defined time interval in the presence of competing risks. Then all subjects who were potentially at risk for the duration of the time interval, regardless of whether they had a competing event, contribute complete information on Y. Following diagnosis, Y could represent death from the diagnosed disease in a defined time interval in the presence of competing causes of death. If R predicts the prevalence of a disease, then Y could indicate whether or not the disease was found by a medical evaluation, such as a biopsy.

In Section 2, we formalize model assessment based on expected costs. In Section 3, we define the NB and the decision curve, show how to estimate it from various types of data and provide tests for comparing two models. We illustrate the methods using simulations (Section 4) and data from an external validation study of two absolute risk models for invasive breast cancer in Section 5, before closing with a discussion (Section 6). As far as we know, this paper is the first to provide variance estimates and formal methods of inference for the decision curve.

2 |. BACKGROUND: MODEL ASSESSMENT BASED ON EXPECTED COSTS

We are interested in predicting the probability of a binary event, Y = 1 or Y = 0 given the vector of baseline predictors, X. This event could denote incidence of a particular disease over a given time period, for example 5 years, or of dying before the end of a defined time interval after disease onset. Given a set of baseline predictors X, a risk prediction model $R(\mathbf{x})=P(Y=1\mid \mathbf{X}=\mathbf{x})$ is a mapping from the set of possible values of X to [0,1]. In a specific population, the distribution of the covariates F_X(x) induces the distribution F of risk R that has support on [0,1] through

$$F(r)=P(R\le r)=\underset{\{x:R(x)\le r\}}{\int }d{F}_{\mathbf{X}}(\mathbf{x}).$$ (1)

We define G, the distribution of risk in those who experience the event (cases, Y = 1), as

$$G(r)=P(R\le r\mid Y=1),$$ (2)

and K, the distribution of risk in noncases or controls (Y = 0) as

$$K(r)=P(R\le r\mid Y=0).$$ (3)

We denote risk realizations from F by r^F, and risk realizations from cases and noncases by r^G and r^K, respectively.

We assume that a risk estimate r is used to decide to intervene or not, according to some risk threshold, t. The rule is to intervene if r > t and not to intervene if r ≤ t. Costs (or losses) for the various combinations of intervention choice and disease state are shown in Table 1. Letting $\mu \equiv P(Y=1)$ denote the true probability of disease or of an adverse health outcome, sens(t) = 1 − G(t), the sensitivity of the risk model at threshold t, and spec(t) = K(t), the corresponding specificity, one can express the joint probability of being diseased and having the intervention as μ × sens(t). Other joint probabilities are shown in Table 1.

TABLE 1.

Definitions for a decision problem with two health states and two intervention options

Intervention	Disease state	Costs	Risk criterion at threshold t	Outcome probability
Yes	Diseased	CTP	r > t	μ × sens(t)
No	Diseased	CFN	r ≤ t	μ × {1 − sens(t)}
Yes	Not Diseased	CFP	r > t	(1 − μ){1 − spec(t)}
No	Not Diseased	CTN	r ≤ t	(1 − μ)spec(t)

Abbreviations: C, cost; r, risk; t, threshold; μ, probability of disease or adverse outcome; sens, sensitivity; spec, specificity.

If there is a cost, C_test, associated with assessing risk, the total expected cost is

$$\overline{C}(t)=-\mu \times \text{sens}(t)B_{\mathit{\text{case}}}-(1-\mu )\text{spec}(t)B_{\mathit{\text{noncase}}}+\mu C_{FN}+(1-\mu )C_{FP}+C_{\mathit{\text{test}}},$$ (4)

where $B_{\mathit{\text{case}}}=C_{FN}-C_{TP}\ge 0$ is the NB of (or reduction in cost from) intervening on a case and $B_{\mathit{\text{noncase}}}=C_{FP}-C_{TN}\ge 0$ is the net cost from intervening on a noncase (Pfeiffer & Gail, 2017, chapter 6). The risk threshold t* that minimizes $\overline{C}(t)$ is

$$t^{\ast }=B_{\mathit{\text{noncase}}}/\left(B_{\mathit{\text{noncase}}}+B_{\mathit{\text{case}}}\right)={\left(1+B_{\mathit{\text{case}}}/B_{\mathit{\text{noncase}}}\right)}^{-1},$$ (5)

and the corresponding minimum expected cost is

$${\overline{C}}_{\min }=-\mu \times \text{sens}\left(t^{\ast }\right)B_{\mathit{\text{case}}}-(1-\mu )\left\{spec\left(t^{\ast }\right)\right\}{B}_{\mathit{\text{noncase}}}+\mu C_{FN}+(1-\mu )C_{FP}+C_{\mathit{\text{test}}}.$$ (6)

Equation (5), first derived by Pauker and Kassirer (1975), is remarkable because the optimal threshold depends only on the costs and not on which risk model is used. This important result shows that specifying a threshold is equivalent to specifying the cost ratio B_case/B_noncase.

3 |. THE NB: ESTIMATION AND INFERENCE

3.1 |. Definition of NB

Vickers and Elkin (2006) defined the “net benefit” at a risk threshold t as

$$\text{NB}(t)=\mu \times \text{sens}(t)-(1-\mu )\{1-\text{spec}(t)\}\{t/(1-t)\}.$$ (7)

One can obtain NB(t) from Equation (4) by discarding terms that do not depend on t, dividing by − B_case, and recognizing from Equation (5) that $t/(1-t)=B_{\mathit{\text{noncase}}}/B_{\mathit{\text{case}}}$. Vickers and Elkin (2006) recommended a “decision curve,” which is a plot of NB(t) against t. By varying t between 0 and 1, one is implicitly examining NB for a range of values of implied cost ratios B_noncase/B_case. If none receive the intervention, NB(t) = 0. If all receive the intervention, $\text{NB}(t)=\mu -(1-\mu )t/(1-t)$, which is very nearly linear with slope −(1 − μ) for small t. The decision curve can be compared with these two loci to see whether using the risk model is preferable to intervening on all or intervening on none, without a risk model.

3.2 |. Estimation of NB(t) from three study designs

We now discuss estimating NB in (7) nonparametrically from three types of data and derive the corresponding asymptotic distributions. First, we estimate NB when only a random sample of risk estimates $r_i^F$, i = 1, …, N is observed. Such data might be obtained from a cross-sectional sample of a population, or from baseline information in a cohort study before the outcome information is available. In order to estimate NB with this design, we need to assume that the risk model is perfectly calibrated, which we formally define in the next section. A second design is based on a case–control sample. We estimate NB using random samples of risks in cases, $r_i^G\sim G$, i = 1, …, m, and controls, $r_j^K\sim K$, j = 1, …, n, provided that the event probability $\mu =P(Y=1)$ in the population is known. If the case–control data are nested within an identified cohort, we may be able to use the disease risk in the cohort to estimate μ. Otherwise, we would need to estimate μ from external sources. The third design is a cohort study that provides not only baseline risk estimates but also outcome data. Then, without assumptions concerning μ or model calibration, we can estimate NB based on a random sample of risks in the population and their associated binary outcomes $\left(r_i^F,Y_i\right)$, i = 1, …, N.

3.2.1 |. Estimating NB using observed risks when the risk model is well-calibrated

A risk model R is well-calibrated if $P(Y=1\mid R=r)=r$, that is, among individuals with R = r the expected proportion with Y = 1 is r. If R is well-calibrated, then $\mu =P(Y=1)=E(R)={\int }_0^{1}rdF(r)$, and the quantities 1 − G and 1 − K in cases and noncases, respectively, can be derived from the population distribution F(Gail & Pfeiffer, 2005) as

$$1-G(r)=P(R>r\mid Y=1)=\frac{1}{\mu }{\int }_r^{1}tdF(t),\text{and}1-K(r)=P(R>r\mid Y=0)=\frac{1}{1-\mu }{\int }_r^1(1-t)dF(t).$$ (8)

Using the expressions in (8) in Equation (7) yields

$$\text{NB}(t)=\mu \{1-G(t)\}-(1-\mu )\{1-K(t)\}\{t/(1-t)\}=\{1/(1-t)\}{\int }_t^{1}sdF(s)-\{t/(1-t)\}(1-F(t)).$$ (9)

Thus if the risk model is well-calibrated, NB can be estimated from a random sample $r_1^F,\dots ,r_N^F$ of risks from the continuous distribution F in a given population. Let $r_{(1)}^F\le \dots \le r_{(N)}^F$ denote the order statistics of the estimated risks, and [x] be the largest integer less or equal to x. For $0\le t\le 1$, let $S_{[t]}={\sum }_{k=1}^{[Nt]}{r}_{(k)}$, and let F_N denote the empirical distribution function of F. Then an estimate of NB is

$${\widehat{\text{NB}}}_R(t)=\left\{S_{[N]}-S_{[t]}\right\}/N+\{t/(1-t)\}\left\{1-F_N(t)\right\}.$$ (10)

3.2.2 |. Estimation using risks in a case–control sample when μ = P(Y = 1) is known

We assume that risks $r_i^G\sim G$, i = 1, …, m, are available from a random sample of cases and risks $r_j^K\sim K$, j = 1, …, n, are available from a random sample of noncases from the validation population, and that the event probability $\mu =P(Y=1)$ in that population is known. This might be a reasonable assumption if cases and controls are sampled from a large cohort with known disease incidence, for example. We then can estimate NB(t) using the empirical distribution functions

$$G_m\left(r^{\ast }\right)=\frac{1}{m}\sum _{i=1}^{m}I\left(r_i^G\le r^{\ast }\right)\text{and}{K}_n\left(r^{\ast }\right)=\frac{1}{n}\sum _{i=1}^{n}I\left(r_i^K\le r^{\ast }\right),$$

where $I(\mathit{arg})=1$ if arg is true and 0 otherwise. Plugging μ, G_m, and K_n into (7) yields

$${\widehat{\text{NB}}}_{cc}(t)=\mu \times \left\{1-G_m(t)\right\}-(1-\mu )\left\{1-K_n(t)\right\}\{t/(1-t)\}.$$ (11)

3.2.3 |. Estimation using risks and outcomes in a population

Here, we observe the i.i.d. samples $\left(r_i^F,Y_i\right)$, i = 1, …, N. For a model that predicts disease incidence, these data would be comprised of risk estimates at baseline and observed outcomes at the end of the follow-up period, and for a model that predicts prevalence of a disease, the risks and outcomes could be based on a cross-sectional sample. Then an estimate of NB is

$${\widehat{\text{NB}}}_{RY}(t)=N^{-1}\sum _{i=1}^N\left[I\left(r_i>t,Y_i=1\right)-\{t/(1-t)\}I\left(r_i>t,Y_i=0\right)\right].$$ (12)

3.3 |. Variance estimates, asymptotic distributions, and pointwise CIs for $\widehat{\text{NB}}$

For all estimates of NB, we obtain influence function-based variance estimates, by treating the estimate $\widehat{\text{NB}}(t)$ as a functional of empirical distribution functions for the different study designs. For $\widehat{\text{NB}}$ estimated from any of the three designs mentioned above, we use a first-order approximation of the statistic $T=\text{NB}(t)$ in terms of the empirical distribution function F_N of the observed risks,

$$T\left(F_N\right)\approx T(F)+\frac{1}{N}\sum _1^N{\psi }_i(t),$$ (13)

where Ψ is an influence function and Ψ_i are independent with E_Ψ = 0 (Huber, 2004). Under regularity conditions that assure that the remainder term in the linearization is of the order o(N⁻¹), which are satisfied if T is Fréchet or Hadamard differentiable (van der Vaart, 1998), the variance is

$$\mathrm{var}\left\{T\left(F_N\right)\right\}=\frac{1}{N}E{\psi }^2(t).$$ (14)

The influence functions ${\psi }^R$, ${\psi }^{cc}$, and ${\psi }^{RY}$, expressions for $E{\left({\psi }^R\right)}^2$, $E{\left({\psi }^{cc}\right)}^2$, and $E{\left({\psi }^{RY}\right)}^2$ and further details on the derivations for case–control data and observed outcomes and risks in a population are given in the Online Appendix.

The asymptotic normality of $N^{1/2}\{\widehat{\text{NB}}(t)-\text{NB}(t)\}$ for fixed t follows from (13), (14) and the application of the central limit theorem for all the estimates $\widehat{\text{NB}}(t)$ defined in the previous sections. The covariance matrix of the multivariate Gaussian distribution for $N^{1/2}\{\widehat{\text{NB}}(t)-\text{NB}(t)\}$ for any finite set of points t_s, s = 1, …, S can be estimated based on the influence functions. For example, an estimate of $N^{1/2}\mathrm{cov}\left\{\widehat{\text{NB}}\left(t_1\right),\widehat{\text{NB}}\left(t_2\right)\right\}$, is $N^{-1}\sum _{i=1}^N{\psi }_i\left(t_1\right){\psi }_i\left(t_2\right)$.

Using asymptotic normality, pointwise CIs can be obtained as [$\widehat{\text{NB}}(t)-1.96{\{\widehat{\mathrm{var}}(\widehat{\text{NB}}(t))\}}^{1/2}$, $\widehat{\text{NB}}(t)+1.96{\{\widehat{\mathrm{var}}(\widehat{\text{NB}}(t))\}}^{1/2}$], where $\widehat{\mathrm{var}}(\widehat{\text{NB}}(t))=\frac{1}{N}{\sum }_1^N{\psi }_i^2$. As an alternative to the influence functions, the bootstrap or jackknife could be used to estimate $\widehat{\mathrm{var}}(\widehat{\text{NB}}(t))$.

3.4 |. Confidence bands for NB

NB(t) can also be regarded as a stochastic process in t and it may be desirable to provide confidence bands over the whole or a partial range of thresholds.

Using results by Csörgo and Yu (1999), who showed that, under mild conditions, the process $N^{1/2}\left\{S_{[Nt]}-S_F(t)\right\}$, termed the “unscaled empirical Lorenz process,” converges to a Gaussian process, and the fact that $N^{1/2}\left\{F_N(t)-F(t)\right\}$, converges to a Gaussian process with a Brownian bridge covariance structure, it follows that the process $N^{1/2}\left\{{\widehat{\text{NB}}}_R(t)-\text{NB}(t)\right\}$ is Gaussian. Similarly, as ${\widehat{\text{NB}}}_{cc}$ is a linear combination of two independent empirical distribution functions G_m(t) and K_n(t), it follows that $N^{1/2}\left\{{\widehat{\text{NB}}}_{cc}(t)-\text{NB}(t)\right\}$ converges to a Gaussian process with covariance function ${\mu }^2\{G(s\wedge t)-G(s)G(t)\}+{(1-\mu )}^2\{t/(1-t)\}\{s/(1-s)\}\{K(s\wedge t)-K(s)K(t)\}$. For ${\widehat{\text{NB}}}_{RY}$, the theoretical foundation is less clear and we have not proven that $N^{-1/2}\left\{{\widehat{\text{NB}}}_{RY}(t)-\text{NB}(t)\right\}$ converges to a Gaussian process. Nonetheless, we assume that it does.

We propose to estimate simultaneous confidence bounds for all estimates $\widehat{\text{NB}}(t)$ using the following bootstrap method for constructing a simultaneous confidence bound, that builds upon work of Bickel and Krieger (1989).

1. Define the vector of thresholds t = (0.001, 0.002…, 0.999)′ and compute $\widehat{\text{NB}}(t)$

2. Draw B, for example, B = 500 or B = 1,000 bootstrap samples with replacement from the observed risks, risks and outcomes, or separately from cases and controls.

3. For bootstrap sample b, compute ${\widehat{\text{NB}}}_b(t)$ and $D_b={\sup }_t\left|{\widehat{\text{NB}}}_b(t)-\widehat{\text{NB}}(t)\right|$, b = 1, …, B.

4. Let K_B(d) denote the empirical distribution function of the D_b and find its 1 − α quantile, $q_B=\inf \left\{d:K_b(d)\ge 1-\alpha \right\}$.

5. 5. The 95% confidence band is then given by $\widehat{\text{NB}}(t)\pm q_N$.

3.5 |. Comparing two risk models

Here, we compare NB₁ and NB₂ from two risk models, R₁ and R₂, evaluated on the same validation data. For example, the risk model R₁ might be compared to a model R₂ that additionally includes a new molecular marker.

The risk model with larger NB over a relevant range of values of t might be preferred to another, that is if ${\text{NB}}_2(t)>{\text{NB}}_1(t)$ for t ∈ [t₀, t₁], then model 2 is preferred to model 1.

For fixed t, we propose tests based on the estimates in Section 3.2 to assess whether, ${\text{NB}}_1(t)={\text{NB}}_2(t)$,

$$T_{\text{NB}}(t)=\frac{N{\left\{{\widehat{\text{NB}}}_1(t)-{\widehat{\text{NB}}}_2(t)\right\}}^2}{{\widehat{V}}_T}.$$ (15)

${\widehat{V}}_T$ is a consistent estimate of the variance of the difference of the estimates that can be computed based on the respective influence functions Ψ_R1 and Ψ_R2 for models 1 and 2 as $V_T=\mathrm{var}\left({\psi }_{R_1}-{\psi }_{R_2}\right)$, or alternatively, by using a bootstrap variance estimate. Asymptotically all test statistics, T_NB have a central ${\chi }_1^2$ distribution under H₀. Under the alternative, the noncentrality parameters for the test statistics are ${\delta }_{\text{NB}}=N{\left({\text{NB}}_1-{\text{NB}}_2\right)}^2/V_T$. For case–control data, N = n + m in these expressions.

4 |. SIMULATIONS

4.1 |. Efficiency comparison

We use simulations to investigate the properties of the estimates of NB defined in Section 3.2 and to compare their efficiency. We assume that the population distribution of risk is a beta distribution with parameters α and β, Beta(α, β). In this setting, the distributions of risk in cases and noncases are also beta distributions, given by $G(r)=\text{Beta}(\alpha +1,\beta )$ and $K(r)=\text{Beta}(\alpha ,\beta +1)$, and $\mu =\alpha /(\alpha +\beta )$. Thus, NB(t) in (7) is easily computed theoretically.

To create data for each of the study designs, we first simulated individual risks $r_i^F$, i = 1, …, N, and then generated the binary outcomes Y_i from a binomial distribution with probability r_i. For the estimates using the population-based risks and the risks and outcomes, we used all the observations of $r_i^F$ or ($r_i^F$), respectively. To simulate a case–control study, we sampled all the cases that arise in the population and three controls for each case, yielding on average m = 500 cases and n = 1,500 controls with μ = .05 and N = 10,000. The subscripts R, CC, and RY refer to estimates based on the population risks only, on risks observed for a case–control sample with known disease prevalence μ, and on risks and observed outcomes in the population, respectively.

For each simulated data set, we estimated variances estimated from Equation (14), with $E{\psi }^2$ replaced by (1/N) ${\sum }_i{\psi }_i^2$. We present the square root of the means of these variance estimates over all simulations in Tables 2 and 3, labeled as standard deviations. We compared the efficiency of the various estimates using the ratios of the mean influence function-based variances estimates (VarRatio).

TABLE 2.

Mean values of 100 * NB(t) estimated using observed risks R in a population assuming that the model is well-calibrated; risk estimates in a case–control sampling when the disease prevalence μ is known, and based on observations of (R, Y) in the population

					Standard deviation of 100 * $\widehat{\text{NB}}$
		100 * $\widehat{\text{NB}}$			R		CC		(R, Y)		VarRatio
t	true	R	CC	(R, Y)	emp	infl	emp (emp($\widehat{\mu }$)a)	infl	emp	infl	CC/R	RY/R	RY/CC
α = 6.55, β = 124.45*
0.02	3.07	3.07	3.07	3.07	0.02	0.02	0.02 (0.23)	0.02	0.23	0.22	1.39	132.94	95.83
0.03	2.15	2.15	2.14	2.15	0.02	0.02	0.06 (0.22)	0.06	0.22	0.22	11.08	139.15	12.56
0.04	1.36	1.37	1.37	1.37	0.02	0.02	0.1 (0.21)	0.10	0.20	0.20	38.98	153.73	3.94
0.05	0.79	0.79	0.79	0.79	0.01	0.01	0.13 (0.19)	0.13	0.18	0.18	92.49	178.79	1.93
0.06	0.42	0.42	0.43	0.42	0.01	0.01	0.12 (0.15)	0.13	0.14	0.15	170.31	214.02	1.26
0.07	0.21	0.21	0.20	0.21	0.01	0.01	0.12 (0.13)	0.12	0.11	0.11	270.05	262.23	0.97
0.08	0.09	0.09	0.10	0.10	0.00	0.00	0.09 (0.1)	0.09	0.08	0.08	390.57	321.22	0.82
0.09	0.04	0.04	0.04	0.04	0.00	0.00	0.07 (0.07)	0.07	0.06	0.06	513.47	381.24	0.74
α = 1, β = 19**
0.02	3.41	3.41	3.41	3.42	0.04	0.05	0.06 (0.22)	0.06	0.22	0.21	1.60	22.20	13.84
0.03	2.80	2.81	2.81	2.82	0.04	0.04	0.08 (0.21)	0.08	0.21	0.21	3.52	23.28	6.61
0.04	2.30	2.30	2.29	2.30	0.04	0.04	0.10 (0.22)	0.10	0.22	0.20	6.21	24.45	3.94
0.05	1.89	1.89	1.89	1.88	0.04	0.04	0.11 (0.20)	0.12	0.19	0.19	9.40	25.91	2.76
0.06	1.54	1.54	1.54	1.54	0.04	0.04	0.12 (0.19)	0.13	0.19	0.18	13.24	27.59	2.08
0.07	1.26	1.26	1.26	1.27	0.03	0.03	0.13 (0.19)	0.13	0.17	0.17	17.52	29.34	1.68
0.08	1.03	1.02	1.02	1.02	0.03	0.03	0.14 (0.19)	0.14	0.17	0.16	22.34	31.04	1.39
0.09	0.83	0.83	0.84	0.83	0.03	0.03	0.13 (0.17)	0.14	0.15	0.15	27.72	33.13	1.20
α = 3, β = 5.7***
0.02	3.95	3.95	3.94	3.95	0.08	0.08	0.05 (0.21)	0.05	0.21	0.21	0.47	7.33	15.46
0.03	3.57	3.56	3.57	3.55	0.08	0.08	0.07 (0.22)	0.07	0.21	0.21	0.86	7.53	8.76
0.04	3.24	3.24	3.24	3.23	0.07	0.07	0.09 (0.22)	0.09	0.22	0.21	1.31	7.75	5.93
0.05	2.95	2.95	2.95	2.95	0.08	0.07	0.10(0.2)	0.10	0.19	0.21	1.82	8.00	4.40
0.06	2.69	2.69	2.68	2.70	0.07	0.07	0.11 (0.21)	0.11	0.20	0.20	2.39	8.22	3.44
0.07	2.46	2.46	2.46	2.46	0.07	0.07	0.11 (0.20)	0.12	0.19	0.20	3.03	8.47	2.79
0.08	2.25	2.25	2.25	2.25	0.07	0.07	0.13 (0.20)	0.13	0.20	0.19	3.73	8.72	2.34
0.09	2.06	2.07	2.06	2.06	0.07	0.06	0.14 (0.22)	0.13	0.20	0.19	4.47	8.97	2.01

Note. Results are based on 500 simulations for each set of parameters (α, β) for the beta distribution and values of threshold t. Each simulation has N = 10, 000 samples with μ =.05. For the case–control design, three controls were sampled for each case. Variance ratios (VarRatios) are computed as the ratio of the influence function-based variances.

^*AUC = 0.61;

^**AUC = 0.76;

^***AUC = 0.88.

Abbreviations: emp, empirical; infl, influence function-based; CC/R, var(NB_CC)/var(NB_R); RY/R, var(NB_RY)/var(NB_R); RY/CC, var(NB_RY)/var(NB_CC).

^aStandard deviations of ${\widehat{\text{NB}}}_{CC}$ with $\widehat{\mu }=\overline{Y}$ substituted for μ.

TABLE 3.

Mean values of $\widehat{\text{NB}}(t)$ estimated from different study designs under model miscalibration

					Standard deviation of 100 * $\widehat{\text{NB}}$
		100 * $\widehat{\text{NB}}$			R		CC		(R, Y)
t	true NB	R	CC	(R, Y)	emp	infl	emp	infl	emp	infl
α = 6.55, β = 124.45*
0.02	3.07	6.68	3.06	3.06	0.03	0.03	0.00	0.00	0.22	0.22
0.03	2.15	5.72	2.07	2.06	0.03	0.03	0.01	0.01	0.23	0.22
0.04	1.36	4.74	1.09	1.10	0.03	0.03	0.02	0.02	0.23	0.23
0.05	0.79	3.78	0.20	0.21	0.02	0.03	0.05	0.05	0.25	0.23
α = 1, β = 19**
0.02	3.41	6.24	3.29	3.29	0.06	0.06	0.03	0.03	0.21	0.22
0.03	2.80	5.46	2.60	2.61	0.06	0.06	0.05	0.05	0.22	0.22
0.04	2.30	4.74	2.01	2.01	0.05	0.06	0.07	0.07	0.22	0.22
0.05	1.89	4.09	1.54	1.54	0.06	0.05	0.09	0.09	0.23	0.22
0.06	1.54	3.51	1.14	1.14	0.05	0.05	0.11	0.11	0.21	0.21
0.07	1.26	3.00	0.83	0.84	0.05	0.05	0.13	0.13	0.21	0.21
0.08	1.03	2.54	0.59	0.59	0.05	0.05	0.14	0.14	0.20	0.20
0.09	0.83	2.15	0.38	0.38	0.04	0.04	0.16	0.15	0.20	0.20
α = 0.3, β = 5.7***
0.02	3.95	5.80	3.85	3.86	0.09	0.09	0.04	0.04	0.23	0.22
0.03	3.57	5.32	3.43	3.43	0.09	0.09	0.05	0.05	0.22	0.22
0.04	3.24	4.87	3.08	3.08	0.09	0.09	0.07	0.07	0.23	0.22
0.05	2.95	4.46	2.77	2.77	0.08	0.08	0.08	0.08	0.22	0.22
0.06	2.69	4.10	2.50	2.50	0.08	0.08	0.09	0.10	0.21	0.22
0.07	2.46	3.77	2.25	2.27	0.08	0.08	0.11	0.11	0.22	0.21
0.08	2.25	3.46	2.04	2.05	0.08	0.08	0.12	0.12	0.21	0.21
0.09	2.06	3.17	1.85	1.84	0.08	0.07	0.13	0.13	0.21	0.21

Note. Results are based on 500 separate simulations for each set of parameters (α, β) for the beta distribution and values of threshold t. Each simulation has N = 10,000. For the case–control design, three controls were sampled for each case. Miscalibrated risks used to estimate NB were derived from true risks r via exp{0.8 * logit(r)} + 1]⁻¹.

^*AUC = 0.61;

^**AUC = 0.76;

^***AUC = 0.88.

emp, empirical; infl, influence function-based.

Table 2 gives results for 500 simulations each based on a random sample of size N=10,000 for a rare disease. The parameters of the beta distribution were (α, β) = (6.55, 124.45), (1, 19.0) and (3, 5.7) with expected risk μ = E(R) = .05 for each (α, β) pair. The values of the AUC, the area under the receiver operating characteristic (ROC) curve, that can be expressed as the probability that the risk r for a randomly selected case exceeds that for a randomly selected control (Pepe, 2003, p. 67), for these parameter choices are 0.61, 0.76, and 0.88, respectively, corresponding to models with moderate to high discriminatory ability. The mean estimates of NB were virtually identical to the theoretical values for all estimators and risk thresholds. $\widehat{\text{NB}}$ decreased as t increased.

The standard deviations estimated using the influence functions agreed very well with the empirical standard deviations of $\widehat{\text{NB}}$ for all designs. As indicated by the VarRatios, ${\widehat{\text{NB}}}_{RY}$ was much less precise than ${\widehat{\text{NB}}}_R$. For example, for (α, β) = (6.55, 124.45) the VarRatio for ${\widehat{\text{NB}}}_{RY}$ compared to ${\widehat{\text{NB}}}_R$ ranged from 132.73 to 388.07. ${\widehat{\text{NB}}}_{RY}$ was usually somewhat less precise than ${\widehat{\text{NB}}}_{cc}$. Estimates ${\widehat{\text{NB}}}_{CC}$ were less precise than ${\widehat{\text{NB}}}_R$ except for t ≤ 0.03 and AUC = 0.88 (α, β) = (.3, 5.7). These results for ${\widehat{\text{NB}}}_{CC}$ assumed μ = .05 was known. When instead we substituted $\widehat{\mu }=\overline{Y}$, ${\widehat{\text{NB}}}_{CC}$ was slightly less precise than ${\widehat{\text{NB}}}_{RY}$, as shown in the column labeled “emp ($\widehat{\mu }$)” of Table 2. The corresponding empirical variance ratios RY/CC were near 0.8.

We conducted simulation studies for the three beta distributions of risk in Table 1 to assess coverage of our proposed bootstrap procedure to obtain confidence bands. In each simulation, we generated 500 data sets to estimate the proportion of times that the confidence bands covered the entire true NB curve. For ${\widehat{\text{NB}}}_R$, one minus the coverage was 0.074 (95%CI: 0.0526, 0.100) for (α = 6.55, β = 124.45), 0.052 (0.0342, 0.0753) for (α = 1, β = 19), and 0.042 (0.0262, 0.0635) for (α = .3, β = 5.7). For ${\widehat{\text{NB}}}_{cc}$, one minus the coverage was 0.034 (95%CI: 0.0199, 0.0539) for (α = 6.55, β = 124.45), 0.032 (0.0184, 0.0514) for (α = 1, β = 19), and 0.040 (0.0246, 0.0611) for (α = .3, β = 5.7). For ${\widehat{\text{NB}}}_{RY}$, one minus the coverage was 0.06 (95%CI: 0.0408, 0.0846) for (α = 6.55, β = 124.45), 0.048 (0.031, 0.0706) for (α = 1, β = 19), and 0.044 (0.0278, 0.0659) for (α = .3, β = 5.7), respectively. Thus this algorithm provides near nominal simultaneous coverage of the NB curve for all types of estimates.

4.2 |. Impact of model miscalibration

Here, we again assumed that the population distribution of true risk is a beta distribution with parameters α and β, but obtained estimates $\widehat{\text{NB}}(t)$ based on miscalibrated risks ${\tilde{r}}_1,\dots ,{\tilde{r}}_n$ obtained from the true risks r_i, i = 1, …, N as ${\tilde{r}}_i=\exp [{\gamma }_1\text{log}\{r_i/(1-r_i)\}]/[1+\exp \left[{\gamma }_1\log \left\{r_i/\left(1-r_i\right)\right\}\right]$. The results in Table 3 are based on ${\gamma }_1$ = .8, resulting in overdispersion of the misspecified risks, with mean miscalibrated risks of 0.07 to 0.09, instead of μ = .05. We used the correct μ = .05 in Equation (11) to obtain ${\widehat{\text{NB}}}_{cc}$.

Estimates ${\widehat{\text{NB}}}_R$ were much larger than the true values of NB, regardless of AUC(Table 3). ${\widehat{\text{NB}}}_{RY}$ and ${\widehat{\text{NB}}}_{CC}$ were very similar and were on average slightly lower than the true NB, with very small biases for AUC = 0.61 but slightly larger biases for higher AUC. Influence function-based variances agreed with empirical variances, and ${\widehat{\text{NB}}}_{RY}$ was less precise than ${\widehat{\text{NB}}}_R$ and ${\widehat{\text{NB}}}_{CC}$.

4.3 |. Comparing two risk models

We examined the size and power of a test (15) for comparing risk models 1 and 2 when $N{B}_i(t)$, i = 1, 2 are estimated from the three types of validation data. To simulate bivariate risks with outcome data, we first drew a random number m of cases (Y = 1) in a population of size N from a binomial distribution with parameter μ, and assigned the remaining n = N − m individuals to be controls (Y = 0). To obtain correlated risk estimates from the two models that have marginal beta distributions, we first generated bivariate normal random variables $\left(X_{i1},X_{i2}\right)\sim MVN((0,0),\text{Σ})i=1,\dots ,N$, where ${\text{Σ}}_{11}={\text{Σ}}_{22}=1$ and ${\text{Σ}}_{12}={\text{Σ}}_{21}=\rho$. We then separately computed risks for the m cases and n controls from $r_{i1}=F_1^{-1}\circ \text{Φ}\left(X_{i1}\right)$ and $r_{i2}=F_2^{-1}\circ \text{Φ}\left(X_{i2}\right)$, where $F_k^{-1}$, k = 1, 2, denotes the inverse of the beta distribution function with parameters $\left({\alpha }_k+1,{\beta }_k\right)$ for cases and parameters $({\alpha }_k,{\beta }_k+\text{1)}$ for controls, and $\text{Φ}$ is the standard normal distribution. This yielded a random sample (r_i1, r_i2, Y_i), i = 1, …, N. We fixed (α₁, β₁) = (6.55, 124.45) and let (α₂, β₂) vary to assess the performance of the tests for risk models with different AUC values. The parameters were chosen so that μ = .05 for all settings for both models.

We computed T_NB in Equation (15) with the variance estimated by the empirical variance of the differences of the paired influences for the two risk models. Size and power were estimated based on 500 simulations for each choice of parameter values, each based on N=10,000 bivariate risks, or bivariate risks and outcomes, or on a case–control study with bivariate risks from cases and from three controls per case.

All tests had the correct 0.05 type one error level, when the risk models were generated from the same parameters for the beta distributions (Table 4). Table 4 highlights that estimates computed under the assumption of a well-calibrated model have better power than those relying on risks and outcome data. For example, for (α₂, β₂) = (4, 76), corresponding to an AUC = 0.64 for model R₂ compared to AUC = 0.61 for model R₁, the power was 0.906 for t = 0.03 for T_R, but only 0.176 for T_CC and 0.218 for T_RY, and did not increase noticeably with larger values of t. Only for (α₂, β₂) = (42, 38), corresponding to an AUC = 0.69 for model R₂, was the power high for T_CC and T_RY, with respective values 0.683 and 0.690 for t = 0.02 and respective values 0.882 and 0.932 for t = 0.03.

TABLE 4.

Proportion of rejections of the null hypothesis H₀: NB₁(t) = NB₂(t) based on 500 simulations for comparing estimates of NB for two risk models evaluated on the same validation data, when NB(t) is estimated, using observed risks R in a population assuming that the model is well-calibrated; using risk estimates from a case–control sample when the disease prevalence μ is known; and using observations of (R, Y) in the population

					Proportion rejected H0 for
(α1, β1)	(α2, β2)	AUC 1	AUC 2	t	TR	TCC	TRY
(6.55,124.45)	(6.55,124.45)	0.61	0.61	0.02	0.050	0.036	0.034
				0.03	0.046	0.054	0.054
				0.04	0.054	0.044	0.042
				0.05	0.044	0.062	0.070
				0.06	0.052	0.052	0.050
(6.55,124.45)	(4,76)	0.61	0.64	0.02	0.150	0.108	0.116
				0.03	0.906	0.176	0.218
				0.04	1.000	0.192	0.266
				0.05	1.000	0.240	0.272
				0.06	1.000	0.208	0.234
(6.55,124.45)	(3,57)	0.61	0.66	0.02	0.418	0.286	0.306
				0.03	1.000	0.442	0.524
				0.04	1.000	0.570	0.648
				0.05	1.000	0.560	0.640
				0.06	1.000	0.424	0.522
(6.55,124.45)	(2,38)	0.61	0.69	0.02	0.946	0.684	0.69
				0.03	1	0.882	0.932
				0.04	1	0.934	0.974
				0.05	1	0.924	0.978
				0.06	1	0.872	0.944

Note. Results are based on data sets with N = 10, 000 and 500 simulations for each set of parameters and values of threshold t. For the case–control design, three controls were sampled for each case.

The test T_RY had higher power than T_CC. For both tests, the power decreased slightly for large values of t.

5 |. DATA EXAMPLE

To illustrate the estimation methods, we used a subset of the data from the external validation study, derived from the Nurses’ Health Study (NHS) cohort, that was used to evaluate an absolute risk model for invasive breast cancer with potentially modifiable risk factors (BC2013) (Pfeiffer et al., 2013). The predictors in the BC2013 model are age and race/ethnicity of a woman, her family history of breast or ovarian cancer, personal history of benign breast disease/breast biopsies, estrogen and progestin menopausal hormone therapy (MHT) use, other MHT use, age at first live birth, menopausal status, age at menopause, alcohol consumption, and body mass index (BMI).

We also compared the BC2013 model to another absolute breast cancer risk model, the National Cancer Institute’s Breast Cancer Risk Assessment Tool (BCRAT), which includes modifications of the original “Gail model” (Gail et al., 1989), as described previously (Costantino et al., 1999). BCRAT predicts a woman’s breast cancer risk based on her age and race/ethnicity, family history of breast cancer, personal history of breast biopsy and diagnosis of atypical hyperplasia, her age at her first live birth of a child and age at menarche. BMI, MHT, and alcohol use are not included as predictors in BCRAT, and age at menarche and a diagnosis of atypical hyperplasia are not included in BC2013.

All examples and comparisons were based on 5-year absolute risk estimates from BC2013 and BCRAT for the 17,085 women aged 50–55 years at baseline in the NHS cohort, so R can be interpreted as a 5-year absolute risk of breast cancer. In this population, 252 incident breast cancers were observed. For both models, the estimate of the AUC was 0.62. The Hosmer–Lemeshow goodness-of-fit statistic was 16.9 for BC2013, with corresponding p = .03, and 13.6 for BCRAT, with p = .09, indicating some of lack of fit for BC2013, when compared to ${\chi }_8^2$(.95) = 15.507.

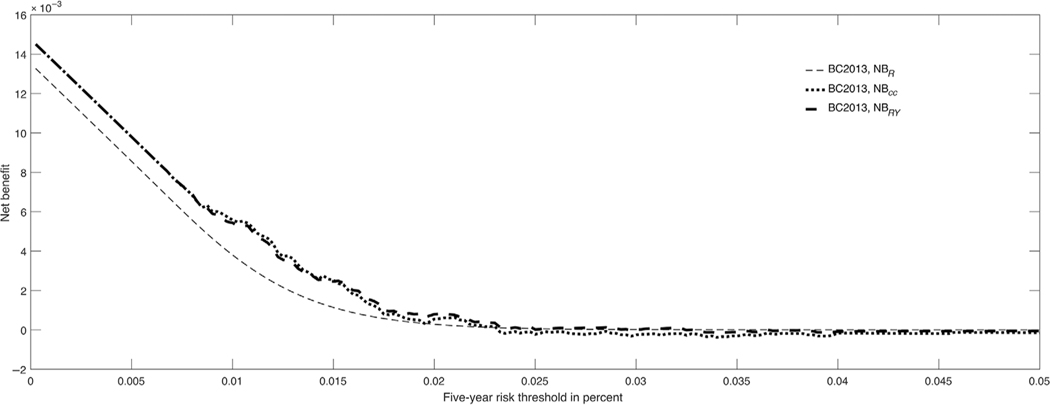
${\widehat{\text{NB}}}_{cc}$ was estimated using the observed disease incidence $\widehat{\mu }=\overline{Y}$ in the population. Figure 1 shows the estimated NB plots for BC2013 from different study designs. There were only small differences between the three curves. For example, for t = 0.0166, a threshold on the drug label for the use of tamoxifen to prevent breast cancer, the estimated NBs were ${\widehat{\text{NB}}}_{RY}$ = 0.0016 (95%CI: 0.0006 to 0.0027), ${\widehat{\text{NB}}}_R$ = 0.0007 (95%CI: 0.00069 to 0.0008), and ${\widehat{\text{NB}}}_{cc}$ = 0.0015 (95%CI: 0.0005 to 0.0025). The lower estimate of ${\widehat{\text{NB}}}_R$ reflects some lack of calibration of the model.

FIGURE 1.

Decision curves for BC2013 for 50–55-year-old women from the Nurses’ Health Study validation study

The 5-year risk threshold for the tamoxifen drug label, 1.66%, is too low for many women in view of adverse effects of tamoxifen (Gail et al., 1999). In fact, for women in their 50s, the 5-year risk threshold above which the benefits of tamoxifen of reducing from breast cancer incidence outweigh the risks is 4.5% (Freedman et al., 2011). Figure 1 shows that there is negligible benefit from using tamoxifen and treating the very small portion of the population with risks above this threshold. With safer interventions, lower thresholds could be used, and there might be positive net benefits, even with a model that had low discriminatory accuracy like BC2013 (Figure 1).

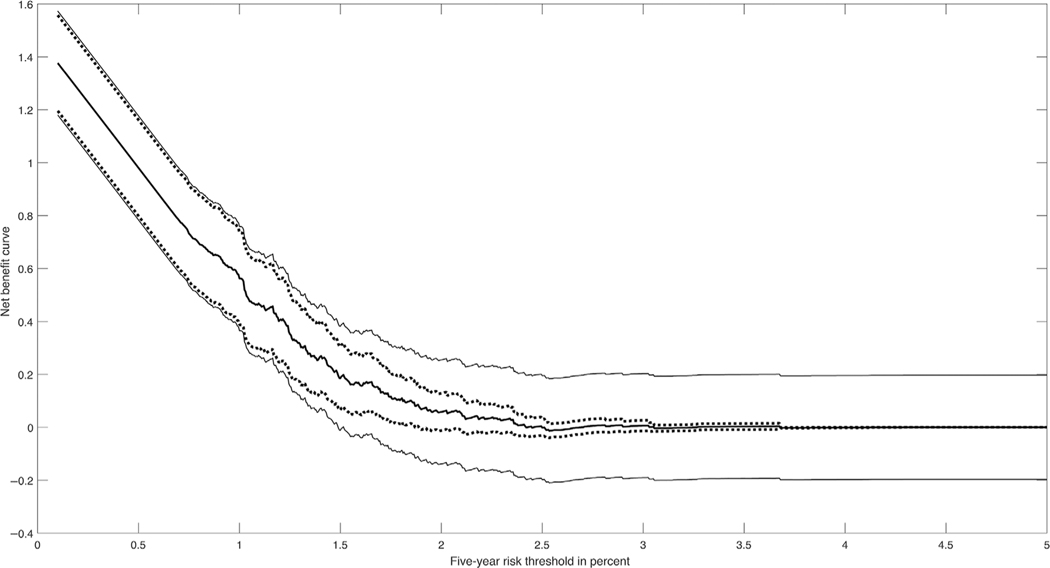
Figure 2 shows the NB curve estimated using ${\widehat{\text{NB}}}_{RY}$ for BC2013 with 95% pointwise CIs and with the bootstrap based confidence bands for t ∈ [0, 0.05]. It can be seen that for t < 0.01 the pointwise CIs and the confidence bands are very close, but for t > 0.01 the confidence bands are much wider.

FIGURE 2.

Decision curves for BC2013 for 50–55-year-old women from the Nurses’ Health Study validation study with 95% pointwise confidence intervals (dotted lines) and 95% confidence bands (solid lines)

When we compared the two models, the estimated NBs were identical, with ${\widehat{\text{NB}}}_{RY}$ (0.0016) for BCRAT and BC2013. None of the tests based on the three designs yielded statistically significant differences in NB values for the two models.

6 |. DISCUSSION

We have given three methods to estimate the NB curve, together with corresponding methods of inference and methods to compare two risk models at a given risk threshold. Estimation based on risk and outcome data (R, Y) was proposed by Vickers and Elkin (2006). It makes no assumptions on how well-calibrated the risk model is nor on the incidence of disease in the population. It is therefore robust to model miscalibration, but, as our calculations showed, the standard errors of the estimates can be large. If one is willing to assume that the model is well-calibrated, we have shown how to compute a much more precise estimate of NB based on risks R alone. However, if the risk model is miscalibrated, large bias can result. Van Calster and Vickers (2015) showed that miscalibrated models lead to smaller NB than the correct model, but they did not investigate the estimation of NB under a miscalibrated model. Case–control data can also be used to estimate NB if the incidence (or prevalence) μ of the outcome Y = 1 is known. This strategy has greater efficiency than using the full (R, Y) data but relies on knowing μ, for which reliable information may not be available. If one has data on Y for all members of a cohort, however, and if the case–control sample is nested within the cohort, our simulations show that by using $\widehat{\mu }=\overline{Y}$, the incidence in the cohort in place of μ, the case–control approach with three controls per case is nearly as precise (VarRatio ≈ 0.8) as using the full (R, Y) data. In this setting, ${\widehat{\text{NB}}}_{cc}$ requires risk data only on a small fraction of the cohort if the disease is rare. If the case–control sample is nested within a cohort and if the risk information is obtained from stored baseline cohort data, the case–control approach should be quite reliable. In other settings, the case–control data may be subject to selection bias and mismeasurement of risk factors.

We also present methods for testing for a difference in NB between two risk models evaluated on the same validation data at a given threshold. Unless one is certain that both models are well-calibrated, one should avoid the comparison based on R alone. Likewise, one should not use the case–control method unless one has good data on prevalence in the source population. If one knows the outcomes for all members of the validation cohort, however, one can rely on the (R, Y) method or on a properly conducted case–control study within the cohort. The power to demonstrate superiority of one model over another can be limited, which adds a useful perspective on informal graphical assessment.

Using the influence function method, we can also derive covariances of the NB estimates at different thresholds. Such procedures could allow us to put confidence ellipsoids around the NB at several thresholds and to compare two tests at several thresholds using a test with multiple degrees of freedom. We showed that ${\widehat{\text{NB}}}_R$ and ${\widehat{\text{NB}}}_{cc}$ can be treated as Gaussian processes in t and conjectured this is also true for ${\widehat{\text{NB}}}_{RY}$. We proposed a bootstrap procedure that had proper coverage for simultaneous confidence bands based on ${\widehat{\text{NB}}}_R$, ${\widehat{\text{NB}}}_{cc}$, and ${\widehat{\text{NB}}}_{RY}$.

Some of the variance calculations we performed using influence functions could have been derived by simpler methods. However, the influences we gave can be used to compute the variance of ${\widehat{\text{NB}}}_{RY}(t)$, for example, if the cohort was obtained from a complex survey that might involve stratification and cluster sampling, such as the NHANES (National Health and Nutrition Examination Survey (Cox et al., 1992)).

We give pointwise CIs for a given t because certain risk thresholds are in medical use for specific risk models (e.g., the drug label for tamoxifen says that only women with 5-year breast cancer risk above 1.66% should take it). We also give simultaneous confidence bounds in case one wants to bound the NB over the entire range of thresholds.

In our examples, pointwise CIs nearly coincide with simultaneous CIs for small thresholds but were much narrower for large thresholds. Future research might attempt to develop simultaneous CIs that are proportional to the pointwise CIs.

We assumed that the risk model was evaluated in an independent validation data set, which allows the most rigorous and unbiased assessment of model performance. Ideally, such validation data arise from the relevant target population. However, sometimes independent validation data may not be available. If one uses the same data, both to estimate the model and compute the decision curve, then, depending on the size of the data set, five or 10-fold cross-validation could be used to avoid overestimation of performance.

There are many criteria that can be used to evaluate the validity and potential usefulness of a risk model (see, for example, Gail & Pfeiffer, 2005; Pfeiffer & Gail, 2017; Steyerberg, 2009). Few of these criteria directly address the value of a risk model for making a specific dichotomous medical decision, however. The decision curve (Vickers & Elkin, 2006) and the EUROC plot (Hilden, 1991) address this problem by combining information on sensitivity, specificity, disease prevalence, benefits of true positive tests, and costs of false negative tests, all of which are needed to estimate expected losses when using the model. The paper on the decision curve (Vickers & Elkin, 2006) has already been cited extensively. Vickers, Cronin, Elkin, and Gonen (2008) and Kerr, Brown, Zhu, and Janes (2016) proposed pointwise CIs for the decision curve based on a bootstrap, but our paper is the first to provide analytic variance estimates and formal analytic methods for inference for this important curve.