Incorporating non-linear alignment and multi-compartmental modeling for improved human optic nerve diffusion imaging

Abstract

In vivo human optic nerve diffusion magnetic resonance imaging (dMRI) is technically challenging with two outstanding issues not yet well addressed: (i) non-linear optic nerve movement, independent of head motion, and (ii) effect from partial-volumed cerebrospinal fluid or interstitial fluid such as in edema. In this work, we developed a non-linear optic nerve registration algorithm for improved volume alignment in axial high resolution optic nerve dMRI. During eyes-closed dMRI data acquisition, optic nerve dMRI measurements by diffusion tensor imaging (DTI) with and without free water elimination (FWE), and by diffusion basis spectrum imaging (DBSI), as well as optic nerve motion, were characterized in healthy adults at various locations along the posterior-to-anterior dimension. Optic nerve DTI results showed consistent trends in microstructural parametric measurements along the posterior-to-anterior direction of the entire intraorbital optic nerve, while the anterior portion of the intraorbital optic nerve exhibited the largest spatial displacement. Multi-compartmental dMRI modeling, such as DTI with FWE and DBSI, were less subject to spatially dependent biases in diffusivity and anisotropy measurements in the optic nerve that corresponded to similar spatial distributions of the estimated fraction of isotropic diffusion components. DBSI results derived from our clinically feasible (~10 min) optic nerve dMRI protocol in this study are consistent with those from small animal studies, which provides the basis for evaluating the utility of multi-compartmental dMRI modeling in characterizing coexisting pathophysiology in human optic neuropathies.

Graphical Abstract

1. Introduction

The optic nerves are a pair of white matter fiber bundles in the anterior visual pathway. They connect the retinal ganglion cells (RGC) in the retinal nerve fiber layer (RNFL) to the visual system regions in the brain through the optic chiasm and optic tract. Optic neuritis and glaucoma are two common disorders that involve the optic nerve. Optic neuritis, often the initial presentation of multiple sclerosis, can lead to demyelination and/or axonal injury in the optic nerve (Petzold et al., 2014; Toosy et al., 2014). Glaucoma, a group of progressive eye disorders characterized by eventual RGC death, can cause concomitant degenerative axonal damage in the optic nerve (Nuschke et al., 2015; Weinreb et al., 2014). Quantifying neurodegeneration in the anterior visual pathway, as a model system, in optic neuritis or glaucoma provides a unique opportunity for developing neuroprotective therapies (Bessero and Clarke, 2010; Frohman et al., 2008).

Optical coherence tomography (OCT) is an established and easily accessible imaging method to evaluate the structural integrity of the retina, macula, and optic nerve head. OCT has been widely used to measure the unmyelinated RNFL thickness as an effective RGC axon loss marker in several optic neuropathies (Adhi and Duker, 2013; Dong et al., 2016; Petzold et al., 2010). OCT and/or visual evoked potential are usually the primary outcomes in clinical trials of optic neuritis (Cadavid et al., 2017; Raftopoulos et al., 2016). However, OCT cannot directly assess retrolaminar optic nerve tissue integrity. In addition, OCT does not assess myelin content, can be confounded by edema, and may be susceptible to other ocular pathologies. For monitoring ongoing neurodegeneration along the optic nerve or assessing the effects of neuroprotective or neuroregenerative therapies (Barkhof et al., 2009; Henderson et al., 2010), complementary non-invasive imaging methods that can directly measure retrolaminar optic nerve tissue damage are desirable.

Conventional structural optic nerve magnetic resonance imaging (MRI) with or without contrast is routinely performed to facilitate differential diagnosis of optic neuropathies in association with other systemic or neurological conditions (Becker et al., 2010). In addition, high resolution structural MRI with both fat- and cerebrospinal fluid (CSF)-suppression offers a way to quantify optic nerve atrophy and optic nerve sheath dilation (Hickman et al., 2005a, 2001). Hence, structural MRI, either brain atrophy or optic nerve cross-sectional area, has been used as secondary outcomes in clinical trials of optic neuritis (McKee et al., 2015; Raftopoulos et al., 2016). However, structural MRI cannot measure tissue microstructure critical for differentiating the underlying pathophysiology in various optic neuropathies. Quantitative diffusion MRI (dMRI), such as diffusion tensor imaging (DTI) (Basser et al., 1994) or diffusion basis spectrum imaging (DBSI) (Wang et al., 2011, 2015), holds promise to provide metrics describing tissue microstructural changes related to demyelination, axonal injury, or possible remyelination in the optic nerve (Brusa et al., 2001; Mallik et al., 2014). Applying these quantitative dMRI to the optic nerve would provide imaging biomarkers more directly related to the primary injury site than brain dMRI in clinical trials of optic neuropathies.

Over the past fifteen years, in vivo human optic nerve dMRI has been under active development and refinement (Chabert et al., 2005; Dowell et al., 2009; Jeong et al., 2015; Samson et al., 2013; Wheeler-Kingshott et al., 2006, 2002; Xu et al., 2008) to overcome many acquisition challenges - small size of the optic nerve (3.5 – 4 mm in diameter in healthy adults (Karim et al., 2004) ), surrounding CSF and orbital fat, movement of the globe and nerve, and severe field inhomogeneity (Barker, 2001; Wheeler-Kingshott et al., 2002). The requirements of high spatial resolution, motion insensitivity, and spatial distortion minimization have led the field of high resolution optic nerve dMRI to the convergence on reduced field-of-view (rFOV) or inner-volume-imaging (IVI) single-shot echo-planar imaging (EPI) acquisitions, either in the oblique coronal imaging plane with high in-plane resolution (e.g., 1.25 mm × 1.25 mm) but thick slices (e.g., 4 – 5 mm) (Dowell et al., 2009; Li et al., 2014; Samson et al., 2013; Wheeler-Kingshott et al., 2006) or in the axial imaging plane with isotropic high resolution (e.g., 1.3 mm) (Xu et al., 2008).

By applying these technical developments in rFOV optic nerve dMRI, we and others have successfully conducted imaging studies in optic neuritis (Hickman et al., 2005b; Naismith et al., 2009, 2010, 2012; Trip et al., 2006) and glaucoma (Chang et al., 2014) over the last decade. Nevertheless, challenges in optic nerve dMRI remain, among which optic nerve motion and effect from partial-volumed CSF or interstitial fluid such as in edema are recognized but remain unresolved and under-investigated.

The globe moves as the extraocular recti muscles contract, which can lead to substantial intraorbital optic nerve movement (Fig. 1A). Such optic nerve motion is non-linear and independent of head movement (Sengupta et al., 2017), with restricted posterior motion at the tendinous ring and the largest displacement close to the globe like a pendulum with a bendable string under lateral load (from the surrounding meninges, CSF, and fat). This non-linear optic nerve movement further couples with image distortions in EPI diffusion acquisitions due to both static and dynamic field inhomogeneity around the orbital sinus and eddy currents following strong diffusion encoding gradients (Andersson et al., 2018; Graham et al., 2017). Although visual fixation during optic nerve dMRI acquisition can reduce eye movement (Fanea and Fagan, 2012), prolonged fixation during typically lengthy dMRI acquisition introduces discomfort and is often not achievable in patients with optic neuropathies. Existing distortion correction schemes routinely used for brain dMRI fail to adequately correct for these non-linear distortions specific to optic nerve diffusion imaging. In studies employing optic nerve dMRI in the coronal plane, such eye movement-induced optic nerve misalignment among volumes was typically mitigated by simple signal averaging without effective ways of image space correction (Trip et al., 2006). In our previous studies employing optic nerve dMRI in the oblique axial plane, we had applied rigid-body affine registration (Naismith et al., 2009; Xu et al., 2008; Chang et al., 2014), which did not fully account for the non-linear optic nerve displacement.

Figure 1.

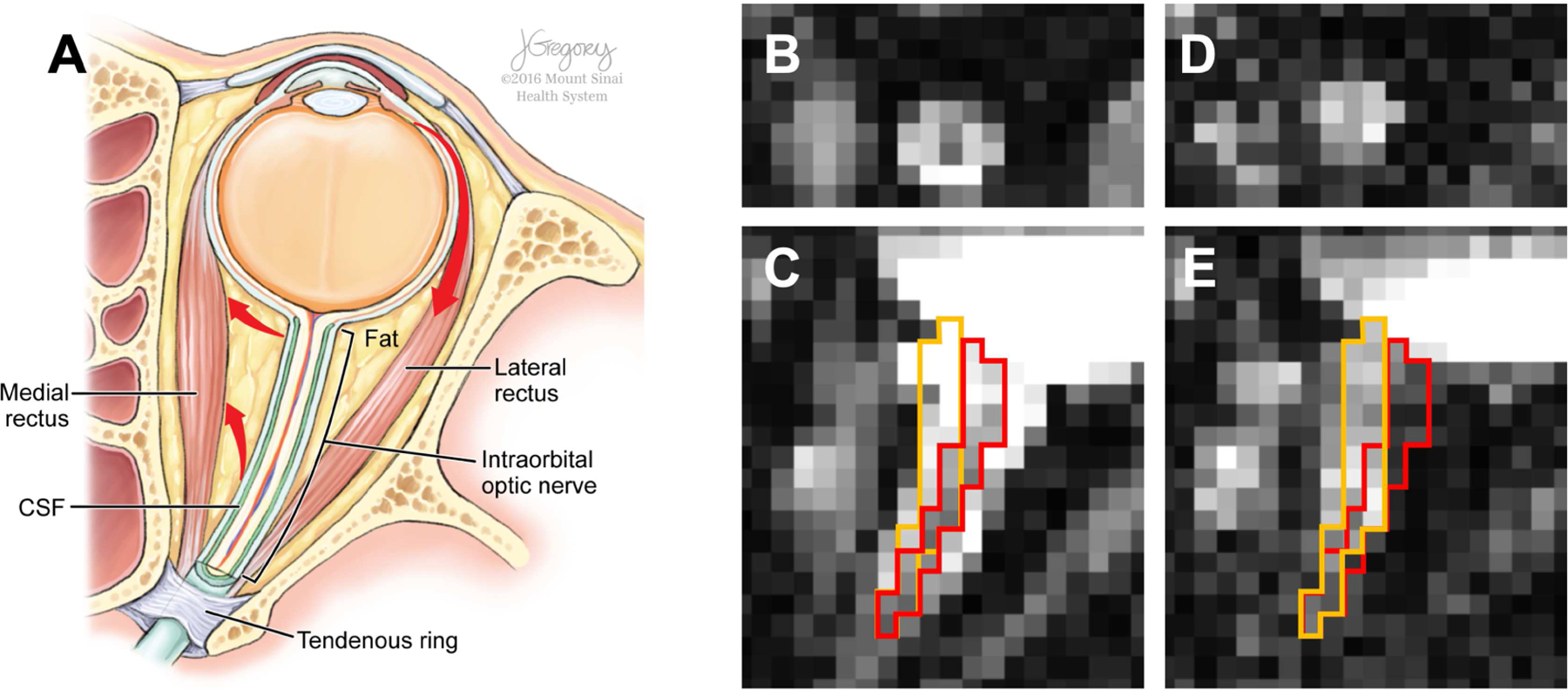
Illustration of anatomical structures around the human optic nerve on the axial plane (A) and optic nerve misalignment on dMRI b₀ (B and C) and diffusion-weighted (D and E) volumes of oblique axial rFOV EPI dMRI acquisition in coronal (B and D) and axial (C and E) views. Red arrows (A) indicate the directions of globe and optic nerve movement resulting from lateral rectus contraction. Red and orange boundaries in C and E delineate the optic nerve location in C and E, respectively, and demonstrate the apparent optic nerve displacement between these two image volumes. Illustration (A) by Jill Gregory, printed with permission from ©Mount Sinai Health System.

In addition, the effect from partial-volumed CSF or interstitial fluid on in vivo human optic nerve DTI metrics is apparent. For example, the reported radial diffusivities in healthy human optic nerve (e.g., see Table 1 in Xu et al., 2008), even for acquisitions employing CSF-suppression techniques (Trip et al., 2006; Wheeler-Kingshott et al., 2006), are typically much higher than those in healthy small animal optic nerve, which were measured with high enough signal-to-noise ratio (SNR) and resolution to avoid partial volume effect, and no eye movement-induced confounds (Song et al., 2003; Sun et al., 2008). Recognizing the inadequacy in addressing optic nerve movement and CSF contamination, well-planned high resolution optic nerve dMRI studies have either avoided acquiring anterior slices close to the globe in coronal acquisitions or excluded the anterior optic nerve voxels from region-of-interest (ROI) analysis in axial acquisitions. Nevertheless, such compromises further limit the number of analyzable optic nerve image slices or voxels, which negatively affects optic nerve dMRI quantification.

Table 1.

Summary dMRI measurements (mean ± standard deviation) of the intraorbital optic nerve in healthy volunteers (n = 7 subjects × 2 nerves) from this study and those of Naismith et al. 2009 (n = 12) and Chang et al. 2014 (n = 22), as well as age distribution, mean (range) or mean ± standard deviation years. Diffusivity values are in unit of µm²/ms and FA and anisotropic fraction values are unitless.

Age		This study (n = 7) 31 (23–41)		Naismith 2009 (n = 12) 37 (21–49)	Chang 2014 (n = 22) 59 ± 10
	DTI	DTI (FWE)	DBSI (fiber compartment)	DTI	DTI
AD	1.45 ± 0.23	1.38 ± 0.15	1.79 ± 0.11	1.66 ± 0.18	1.42 ± 0.5
RD	0.60 ± 0.15	0.33 ± 0.06	0.22 ± 0.06	0.81 ± 0.26	0.71 ±0.5
MD	0.82 ± 0.16	0.68 ± 0.07	N/A	1.09 ± 0.21	0.91 ± 0.3
FA	0.60 ± 0.08	0.73 ± 0.06	0.86 ± 0.04	0.43 ± 0.15	0.44 ± 0.2
anisotropic fraction	N/A	0.77 ± 0.05	0.64 ± 0.10	N/A	N/A

To address these issues, in this study of high resolution oblique axial optic nerve dMRI, we (i) incorporated and evaluated non-linear distortion correction in optic nerve dMRI volume alignment; and (ii) evaluated the feasibility of multi-compartmental dMRI signal modeling, such as DTI with free water elimination (FWE) (Pasternak et al., 2009) or DBSI (Wang et al., 2011) in the non-linearly aligned optic nerve.

2. Methods

2.1. Subjects

From a larger institutional review board (IRB)-approved study of optic neuritis at Washington University School of Medicine, in which about 85% of the recruited subjects had usable optic nerve dMRI data (i.e., artifact-free, both optic nerves covered in the FOV, and adequate SNR), we randomly chose 7 healthy volunteers with usable data (3 females, mean age 31 yrs, range 23 – 41 yrs) for this study.

2.2. MRI acquisition

MRI data were acquired on a 3 T scanner (Trio, Siemens, Germany) with a body coil for radiofrequency (RF) transmission, a 32-channel head coil (Siemens, Germany) for RF signal reception, of which 12 anterior channels were activated. Imaging gradients were capable of 40 mT/m maximum amplitude and 200 T/m/s maximum slew rate.

Diffusion MRI:

Oblique axial optic nerve dMRI data (Fig. 2) were acquired with an IVI spin echo EPI diffusion sequence (Jeong et al., 2005) at 1.3 mm isotropic resolution similar (notable differences are explained in detail in the following paragraph) to our previous study (Xu et al., 2008, pulse sequence binary available at labs.icahn.mssm.edu/junqianxulab/resources/c2p), with the following parameters: TR/TE = 5000/56.4 ms, 10 interleaved slices with 1.3 mm slice thickness, FOV = 166 × 41.5 mm, matrix = 128 × 32, 6/8 partial Fourier, bandwidth = 1396 Hz/pixel, echo spacing = 0.86 ms, echo train length = 24 (echo train duration = 20.6 ms), phase-encoding (PE) in the posterior-to-anterior (PA) dimension, chemical-shift fat saturation with gradient spoiling, monopolar diffusion encoding (δ/∆ = 15.9/26.3 ms) with a pre-inversion pulse before excitation (both inversion and refocusing pulses were implemented as hyperbolic secant pulses), optimized 25 multi-b_val (linearly-spaced) multi-b_vec (uniform over a sphere) diffusion scheme (See Inline Supplementary Table 1) with b_max=1000 s/mm², SENSE1 coil combination (Sotiropoulos et al., 2013), eyes closed for the entire dMRI acquisition, T_acq=10 min (5 min acquisition with polarity reversed gradients repeated twice within each acquisition, two acquisitions including a total of 108 dMRI volumes with 8 interleaved b₀ images). Additional b₀ images with reversed PE direction (anterior-to-posterior, AP) were acquired for field map estimation.

Figure 2.

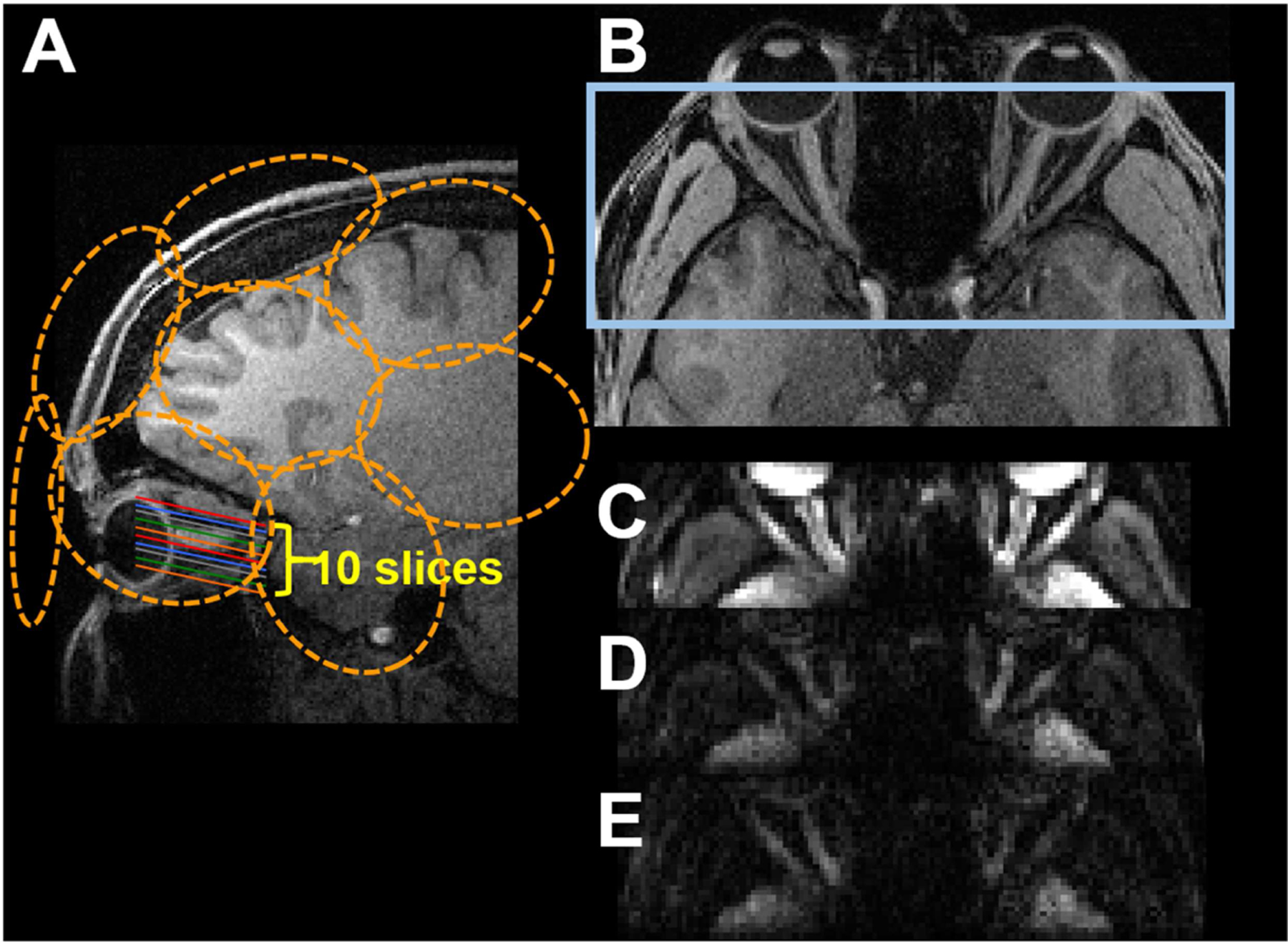
Illustration of the rFOV optic nerve dMRI acquisition (A and B) and representative b₀ (C) and diffusion weighted images with b values of 680 (D) and 1000 (E) s/mm². Orange circles (A) illustrate the approximate location of the receive coil elements. Blue rectangle in (B) illustrates the optic nerve dMRI FOV.

With the advance of MRI technology, we have applied a few notable changes to our rFOV optic nerve dMRI acquisition in this study as compared to our previous studies (Chang et al., 2014; Naismith et al., 2009; Xu et al., 2008) in order to improve SNR per unit time and make the protocol more clinically feasible: (i) Monopolar (i.e., Stejskal-Tanner) diffusion encoding (Stejskal and Tanner, 1965) was used in this study to reduce TE by 22.2 ms as compared to twice-refocused spin-echo diffusion encoding (Reese et al., 2003). (ii) A pair of hyperbolic secant inversion/refocusing pulses was used to improve the IVI slab profile in the PE direction, instead of sinc pulses. (iii) A 25 directional diffusion encoding table with different b values was used, which has been shown through simulation and small animal studies to provide reliable DBSI modeling results for single coherent fiber bundle, such as the optic nerve or spinal cord white matter (Chiang et al., 2014). The diffusion encoding table was optimized for gradient efficiency, as follows: First, a single-shell containing 25 direction vectors uniformly covering the sphere were generated from http://www.emmanuelcaruyer.com/q-space-sampling.php (Caruyer et al., 2013). Second, the magnitude of each vector was scaled according to the linear b_value spacing. Third, the maximum value in any of the physical gradient axis (i.e. X, Y, Z) of any vector was minimized by iteratively exchanging the b_value between the vectors, which resulted in ~ 30% more gradient efficiency (~ 15 ms TE reduction) than the original table. Lastly, the vector with the largest magnitude was normalized (conforming to the vendor’s “Normalization = none” DiffusionVector file scheme) and the other vectors were scaled accordingly. With these sequence and diffusion vector table optimizations, we achieved a relatively short TE = 56.2 ms on a whole-body clinical scanner with a typical b_max = 1000 s/mm² (commonly used in in vivo brain dMRI), as compared to b = ~ 600 s/mm² in our and others’ previous optic nerve dMRI studies. (iv) Finally, the 12 anterior elements of a commercial 32-channel coil in this study provide respectable receive sensitivity in the optic nerve region as compared to a custom-built 4-channel phased-array coil used in our previous studies. To avoid the inflation of noise floor associated with magnitude image reconstruction from high-density channel arrays, we used a sensitivity encoding-based multichannel coil combination (i.e., SENSE1) (Sotiropoulos et al., 2013) in this study. The combination of these approaches has reduced our optic nerve dMRI protocol from 30–40 min in our previous studies to ~ 10 min, which is more clinically applicable using a commercially available head coil.

2.3. Initial pre-processing

To establish a baseline correction for motion and distortion, we pre-processed the dMRI data first using the FMRIB Software Library (FSL) topup and eddy. In cases of unsatisfactory topup or eddy results (e.g., exaggerated distortion or artifacts due to failed topup step), rigid-body registration was used to simply correct for bulk motion between the two dMRI acquisitions (See Supplementary materials for details).

2.4. Non-linear registration

The resulting 4D volumes from topup/eddy or rigid-body registration contained residual misalignments due to the non-linear optic nerve movement and distortion. To correct these misalignments, we applied a non-linear registration scheme which consists of four main steps – (i) manual definition of landmarks, (ii) initial optic nerve estimation, (iii) optic nerve center estimation, and (iv) optic nerve segmentation and registration (Fig. 3). Software implementation of steps ii - iv can be found at github.com/junqianxulab/optic_nerve_dMRI_registration. Processed imaging data will be available upon request.

Figure 3.

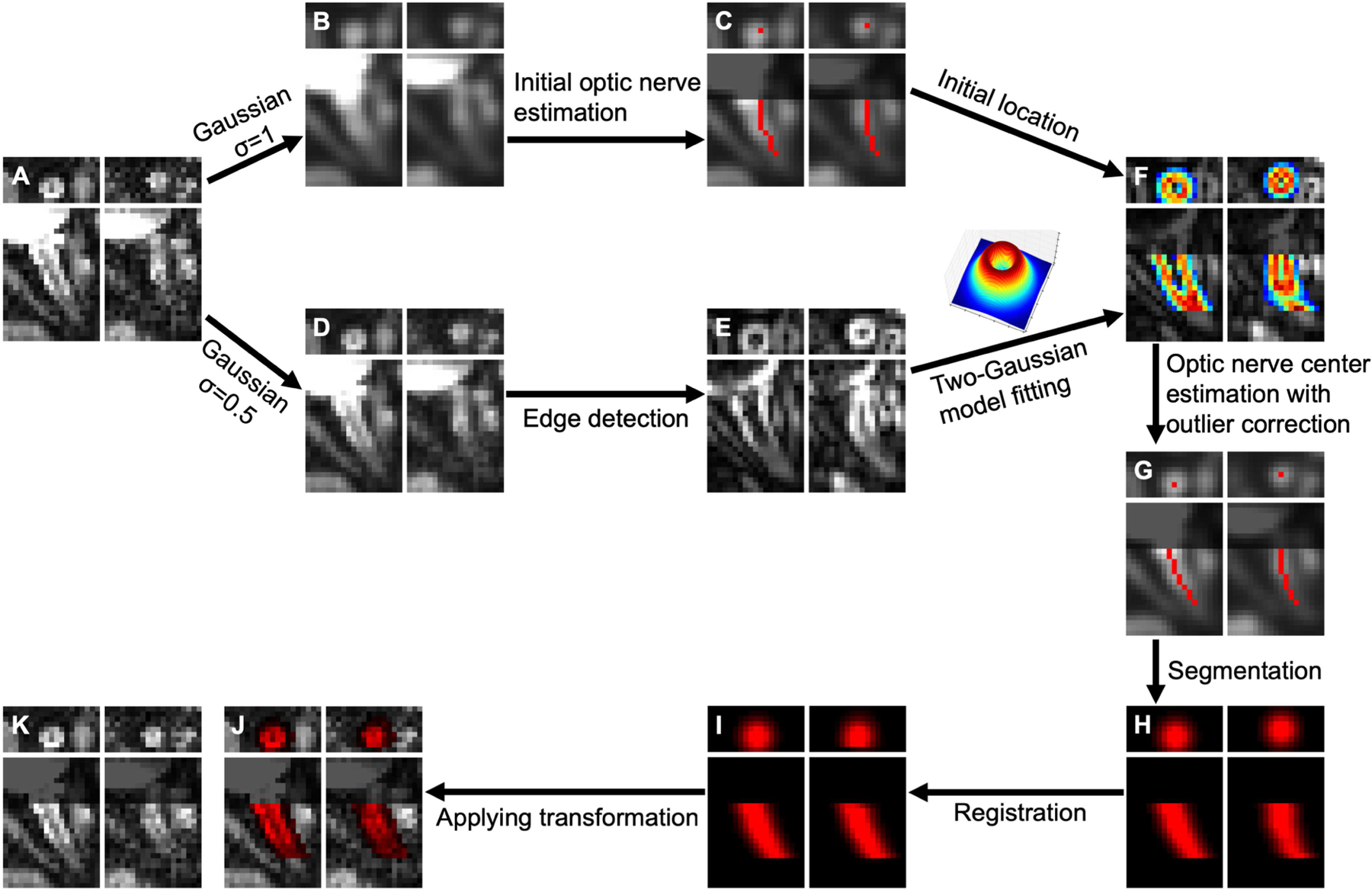
Non-linear optic nerve registration scheme with representative results. Each plot consists of coronal (top row) and axial (bottom row) views of a b₀ volume (left column) and a diffusion-weighted volume (right column). A: image before registration, B: Gaussian-filtered (σ = 1 voxel) image, C: initial optic nerve estimation (red curves) on B, D: Gaussian-filtered (σ = 0.5 voxel) image, E: edge detection using a Sobel filter on D, F: two-Gaussian model fitting on C and E, G: optic nerve center (red dots and curves), H: non-binary optic nerve segmentation using a Gaussian function center at the optic nerve center, I: registration of optic nerve segmentation, J: registration result of A with registered optic nerve segmentation (red overlay), K: final registration result. Note that the grayed regions (C, F, G, J, K) near the globe in the axial views were for illustration purpose to avoid distraction from misalignment beyond the anterior end of the optic nerve estimation.

2.4.1. Manual landmarks

Manual definition of the rigid structures surrounding the optic nerve is an important first step for robust optic nerve segmentation. Since the locations of the globes, extraocular recti muscles, and the optic nerve near the tendinous ring (i.e., annulus of Zinn) remain visible and spatially invariant across dMRI volumes as compared to the rest of the orbital part of the optic nerve, we defined three landmarks (see Supplementary materials) based on the mean b₀ image and the mean high-b-value (> 400 s/mm²) diffusion-weighted image.

2.4.2. Initial optic nerve estimation

The initial optic nerve estimation was performed on each volume and in each eye to find a path from the posterior optic nerve point to the optic nerve head defined in §2.4.1 (See Supplementary Figure 1). We defined a graph, on which the Dijkstra shortest path algorithm (Dijkstra, 1959) was used to generate the path, consisting of voxels as nodes, voxel neighbors sharing a vertex as edges, and intensity-difference-weighted distance function values as edge weights. The optic nerve was hyperintense in high b-value volumes regardless of b-vector directions when the surrounding CSF signal was attenuated and was hypointense in low b-value volumes compared to the surrounding CSF. In order to consistently identify the optic nerve across dMRI volumes, a Gaussian filter with a high sigma value (σ = 1 voxel) was applied to merge the optic nerve with the surrounding CSF in low b-value volumes. On the defined graph (Appendix A) in this filtered image, starting from the posterior optic nerve point, the Dijkstra shortest path algorithm finds a path to a voxel in the optic nerve head region without passing through the extraocular recti muscles defined as the exclusion region (§2.4.1).

2.4.3. Optic nerve center estimation

To locate the optic nerve center in the initial optic nerve estimation from the previous step, we applied an optic nerve image intensity model in the coronal view based on the difference of two Gaussian functions (Appendix B). One of the difficulties in finding the optic nerve center is that diffusion-weighted images with different diffusion encodings produce different CSF-to-optic nerve contrasts. To make the model independent of the applied diffusion encoding, an edge detection (Sobel) filter was applied on Gaussian-filtered images with a low sigma (σ = 0.5 voxel) for denoising. We assigned 0 to the intensity of the exclusion region (§2.4.1) in the Sobel-filtered image and reduced the intensity of the neighboring voxels of the exclusion region by a half in order to exclude the nearby extraocular recti muscles from optic nerve model fitting. The optic nerves in the modified Sobel-filtered image were hypointense with hyperintense circular boundary (Fig. 3E). In coronal slices, this resembles the difference of two Gaussian functions of different widths (Fig. 3F and Appendix B), similar to the method proposed for optic nerve segmentation from high resolution T2-weighted coronal images (Harrigan et al., 2016). This two-Gaussian model was fitted to each of the left and right optic nerves on every coronal slice and volume, which resulted in optic nerve center estimations (Appendix B, (x₀,y₀) of the fitted model). Among these optic nerve centers in all volumes for each of left and right optic nerves on each slice, outliers were identified and replaced (Fig. 3G and Appendix C).

2.4.4. Optic nerve segmentation and registration

After defining all optic nerve centers, the optic nerve on each slice and volume was segmented by applying another Gaussian function with $G\left(x,y\right)=2\exp \left(-\frac{1}{8}\left({\left(x-x_0\right)}^2+{\left(y-y_0\right)}^2\right)\right)$, where (x₀,y₀) is the optic nerve center and ${\left(x-x_0\right)}^2+{\left(y-y_0\right)}^2<5^2$ voxels (6.42² mm)We used non-binary segmentation because it allows distinguishing an optic nerve center located in the center of a voxel from an optic nerve center located near the border of two neighboring voxels (Fig. 3H). The segmented optic nerve, a 3D structure, in each volume was non-linearly registered to the first volume, using symmetric diffeomorphic image normalization (SyN, Avants et al., 2008) from the Advanced Normalization Tools (ANTs v2.1, Avants et al., 2009) with mean square cost function (Fig. 3I-K).

2.5. Optic nerve center region of interest

The closest voxel to the optic nerve center coordinate defined in §2.4.3 was assigned as the automated optic nerve center voxel. In addition, to compare these automated optic nerve center voxels with our established manual procedures of defining optic nerve center ROI (Naismith et al., 2009), manual optic nerve center voxels were defined by consensus from two experienced optic neuritis researchers (CN and RTN, see Supplementary materials). The distances between the automated and manual optic nerve center voxels were calculated on the coronal slices for which optic nerve center voxels exist for both methods.

2.6. Registration evaluation

The optic nerve registration results were evaluated by comparing unprocessed, topup/eddy-corrected, and non-linear movement/distortion-corrected images at three locations (posterior, middle, and anterior slices). To visually compare the optic nerve edge alignment over volumes, the horizontal lines (Inline Supplementary Figure 2) or 8 voxels around the optic nerve on every horizontal line (Fig. 4) of a representative coronal slice were stacked along all volumes ordered by b values, similar to what was used to evaluate volume alignment in brain dMRI images (Figure 5 in Andersson and Sotiropoulos, 2016). In addition, we compared the average coronal slices of high b values zoomed around the optic nerve at three locations (Fig. 4D-F). On this averaged coronal slice, more spatially constrained higher image intensity represents better-registered optic nerve center.

Figure 4.

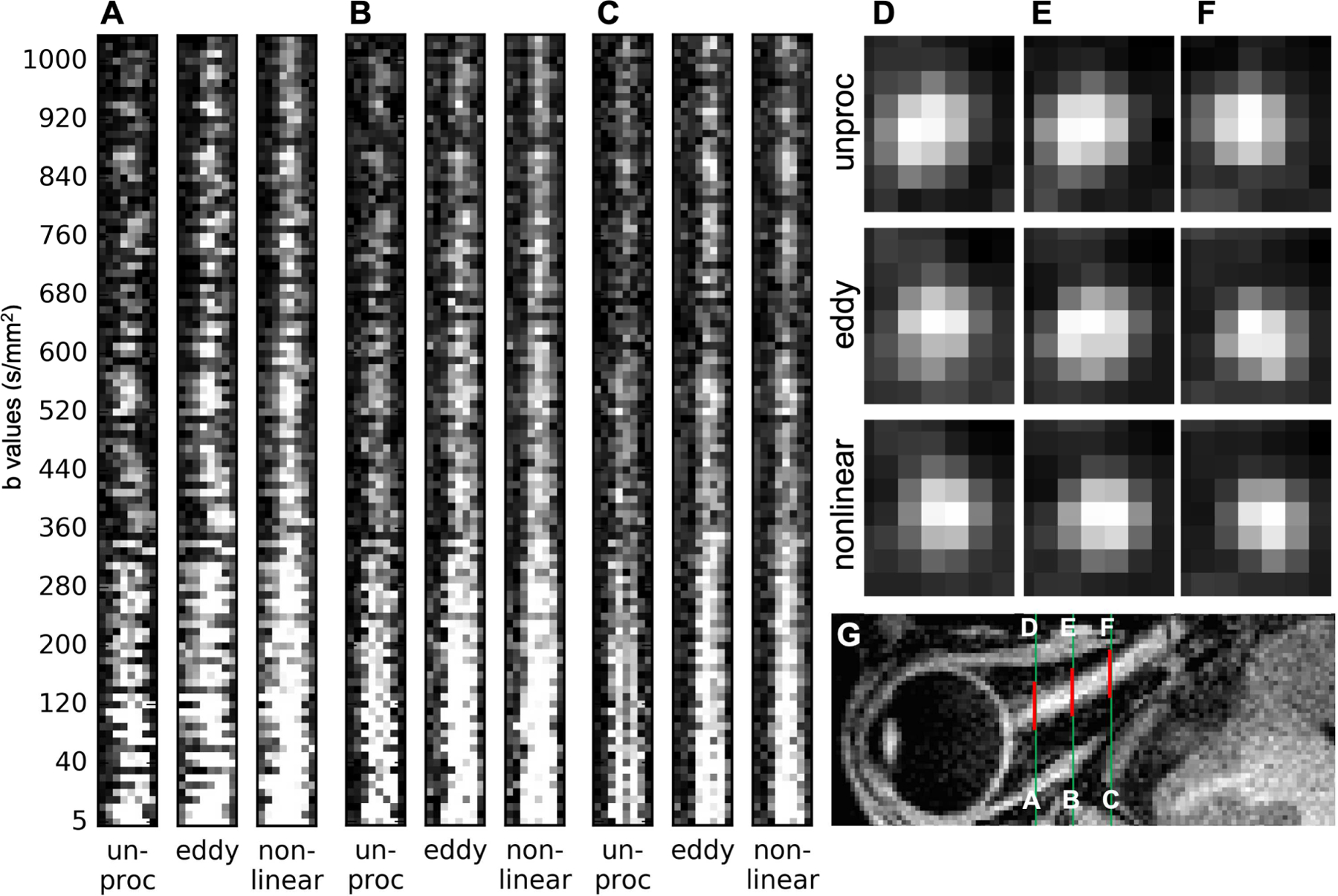
Representative registration comparison of unprocessed (unproc), after topup and eddy (eddy), and after non-linear registration (non-linear), at three optic nerve locations (A-F), using zoomed-in (Inline Supplementary Figure 2. A-C, yellow boxes) vertically stacked line profiles (left-right) of every volume ordered by b values (A-C) and representative average high-b-value (> 400 s/mm²) volumes in coronal views (D-F, the same locations as A-C), in which more spatially constrained higher image intensity represents better-registered optic nerve center. Slight image blurring can be appreciated after non-linear registration (A-C, non-linear). Green lines in the corresponding axial slice of T1w image (G) are the same locations as in Inline Supplementary Figure 2 and red lines (G) indicate the zoomed regions. Note that the apparently aligned CSF-to-optic nerve contrast in the low b value volumes in C (unproc) does not reflect the misalignment of the optic nerve in the other dimensions. Also, note that the low optic nerve signal intensity in many unprocessed volumes (A-C, unproc) was mainly due to the optic nerve movement out of the shown line profiles. The remaining low signal intensity volume after non-linear registration (A-C, non-linear) was either due to the applied diffusion encoding vector parallel to the optic nerve orientation or artifactual signal dropout.

Figure 5.

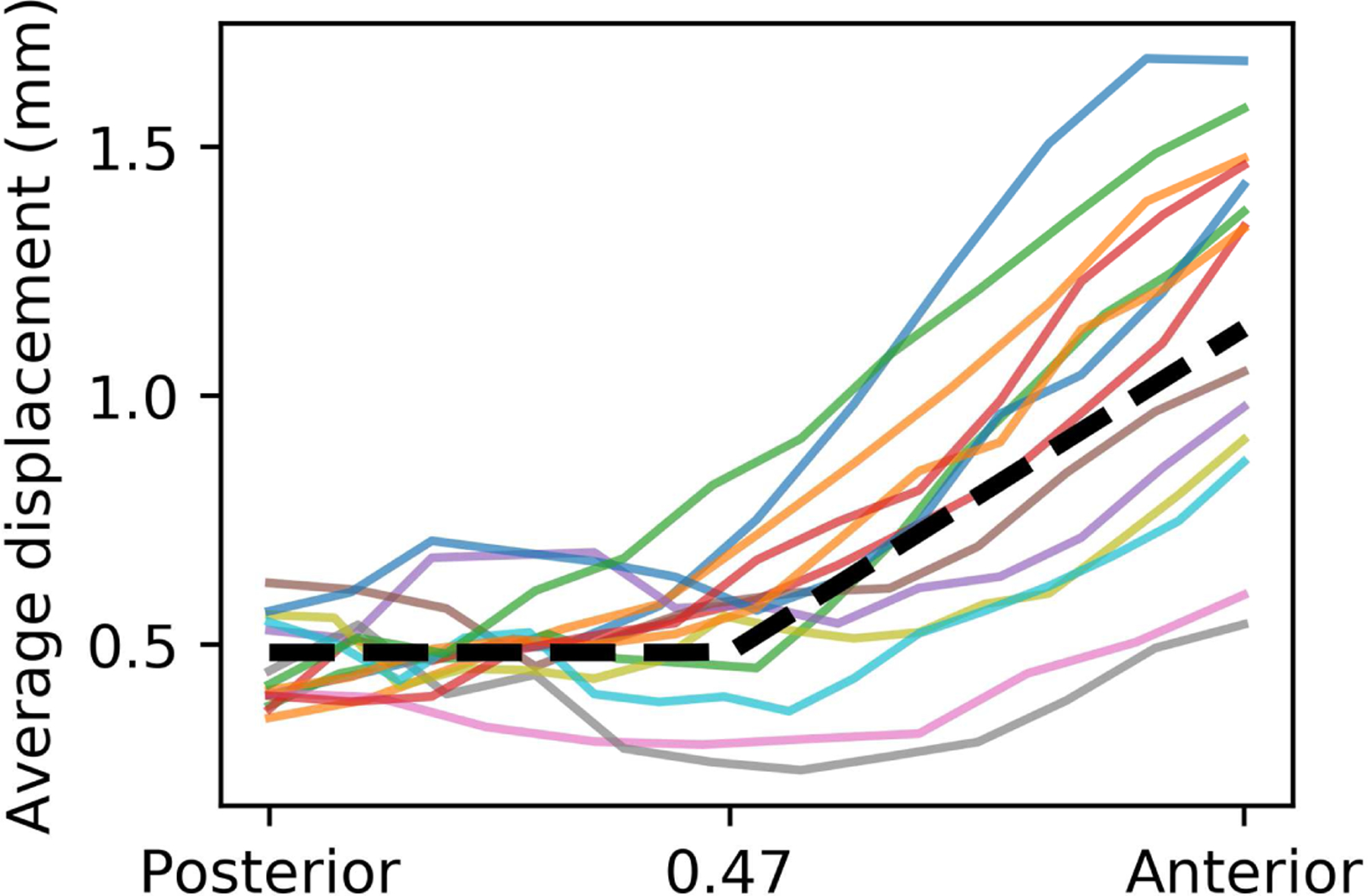
Average optic nerve displacement as a function of posterior-anterior location. Each solid curve represents one optic nerve’s displacement, averaged over all dMRI volumes (displacement in individual volume could be much larger). The axis ranges from 0 (posterior optic nerve point, near the tendinous ring) to 1 (optic nerve head). The dashed black line represents the step-wise fitting.

The total image processing took about 2 hours or less per data set, including topup and eddy (< 30 min.), registration with at most 4 iterations of exclusion mask modification (< 30 min.), and manual evaluation and ROI/mask drawing (about 1 hour).

2.7. Optic nerve center displacement along the nerve

To assess the spatial dependence of the optic nerve center displacement, as a surrogate measure of the severity of motion, we calculated the average optic nerve center displacement over dMRI volumes for each eye of each subject on each coronal slice along the intraorbital optic nerve location. A step-wise function m(x) was fitted to the mean optic nerve center displacement for all subjects as

$$m\left(x\right)=\left\{\begin{array}{c}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}b\hspace{1em}\hspace{1em}\left(x<c\right)\\ a\left(x-c\right)+b\hspace{0.33em}\left(x\ge c\right)\end{array}\right.$$ (1)

where is the coronal location (arbitrary unit) from the posterior end (x = 0) to the optic nerve head (x = 1). Here, is not distance (mm) but relative location from posterior end to the optic nerve head, for better inter-subject comparison.

2.8. Optic nerve dMRI signal modeling

We applied three dMRI signal models – DTI, DTI with FWE (i.e., a two-compartment tensor model with isotropic component estimation), and DBSI – to our diffusion-weighted data via a scheme of multiple b-vector and b-value. The DTI model, implemented in FSL dtifit (Jenkinson et al., 2012), provides axial (AD), radial (RD), and mean (MD) diffusivity, and FA maps. The DTI with FWE, implemented in diff_4dfp (ftp://imaging.wustl.edu/pub/raichlab/4dfp_tools) with -f option, models an extra isotropic diffusion term (in addition to the diffusion tensor), f × exp(−bD_iso) where D_iso, has diffusion characteristics of free water, which provides an additional anisotropic component fraction (1–f) map (Pasternak et al., 2009; Pierpaoli and Jones, 2004). DBSI uses a data-driven multiple-tensor modeling approach, implemented in an in-house MATLAB program, to treat dMRI data as a combination of multiple discrete anisotropic diffusion tensors representing fiber tracts (represented by fiber AD, fiber RD, fiber FA, fiber fraction maps), and a spectrum of isotropic diffusion tensors covering a range of apparent diffusion coefficients (ADC) including restricted diffusion (0 < ADC ≤ 0.3 µm²/ms, representing cells), hindered diffusion (0.3 < ADC < 3.0 µm²/ms, representing edema), and free diffusion (ADC ≥ 3.0 µm²/ms, representing extracellular water content due to tissue loss or CSF) (Wang et al., 2011). Because of the noisy nature of the in vivo human optic nerve dMRI data, which could lead to ill-conditioned dMRI signal modeling, we excluded optic nerve center voxels with the following physically non-sensible dMRI parameter values in respective signal modeling: negative values in any of the derived parameters, AD = 0, DBSI fiber fraction = 0, or FA/DBSI fiber FA > 1.

2.9. Optic nerve dMRI measurements along the nerve

We quantitatively evaluated the residual effect of the optic nerve movement on dMRI measurements after volume alignment. Similar to §2.7, the dMRI measurements were represented as discrete functions of coronal location from the posterior end (x = 0) to the optic nerve head (x = 1) for each eye of each subject. To summarize the dMRI measurements across all subjects, we linearly interpolated the discrete functions. We plotted the dMRI values (§3.5) of each eye as dots without connecting lines for visualization. In order to accentuate the spatial dependence of the dMRI measurements along the nerve, normalized values were calculated by dividing each map’s measurements by their mean (i.e., removing subject-level measurement variance).

3. Results

3.1. Common initial preprocessing

The topup and eddy adequately aligned 4 subjects’ data out of 7 with or without manual masking (e.g., exclusion of brain tissue appearing at the posterior end of the FOV) during the initial alignment step. For these 4 subjects, the dMRI volume alignment after topup and eddy was improved overall (Inline Supplementary Figure 2, 1D slice profiles), particularly at the edge of the brain (Inline Supplementary Figure 2, white arrows) as expected. Nevertheless, the improvement for the optic nerve alignment (Inline Supplementary Figure 2, yellow boxes) was not entirely satisfactory and inconsistent along the length of the nerve. For the other 3 subjects that topup or eddy failed to provide adequate initial alignment, rigid-body registration mostly corrected bulk head motion between the two acquisitions (data not shown).

3.2. Non-linear registration

Non-linear registration yielded consistently better volume alignment after the initial alignment step (Fig. 4 and Inline Supplementary Figure 2) and the non-linear registration performance was not affected by the choice of topup and eddy or rigid-body registration in the initial alignment step. With appropriate manual drawing of the optic nerve posterior points, globes and exclusion regions (§2.4.1), the initial optic nerve estimation and the following optic nerve center estimation were successful for all analyzed nerves. For images with low SNR or recti muscle very close to the optic nerves, the optimal exclusion region had to be revised several times empirically (2 out of 7 subjects).

3.3. Optic nerve center region of interest

The automated and manual optic nerve center voxels agreed well. The average distance between them in coronal slices was 0.53 ± 0.52 mm (n = 14, 2 eyes × 7 subjects), which is less than a half voxel difference in the acquisition space. For the subsequent analysis, we used the dMRI measurements in the automated optic nerve center voxels.

3.4. Optic nerve center displacement

The average optic nerve displacement was fitted as two distinct portions (Fig. 5, dashed curve), approximately separated at the middle (x = 0.47) of the intraorbital optic nerve. The posterior half of the nerve had, on average, minimal displacement: m(x) = 0.48 mm if x < 0.47; while the anterior half of the nerve shows increasing displacement towards the globe: m(x) = 1.2(x – 0.47) + 0.48 mm if x ≥ 0.47. The average displacement near the globes (1.15 ± 0.36 mm, n = 14) was almost twice of that near the middle of the ROI (0.56 ± 0.19 mm, n = 14). The optic nerve center could displace up to 2 mm (averaged over all dMRI volumes, displacement in individual volume could be much larger, up to 7.7 mm), near the globe, although large variations existed among the individual optic nerves.

3.5. Optic nerve dMRI measurements along the optic nerve

About 6, 10, and 3% optic nerve center voxels were excluded from dMRI measurements using DTI, DTI with FWE, and DBSI, respectively, by the voxel-wise exclusion criteria of physically non-sensible values in §2.8. If a voxel was excluded from any dMRI model, to be conservative on data quality in this study, we excluded the voxel from other dMRI models, too, in the subsequent analysis (Fig. 6 and 7).

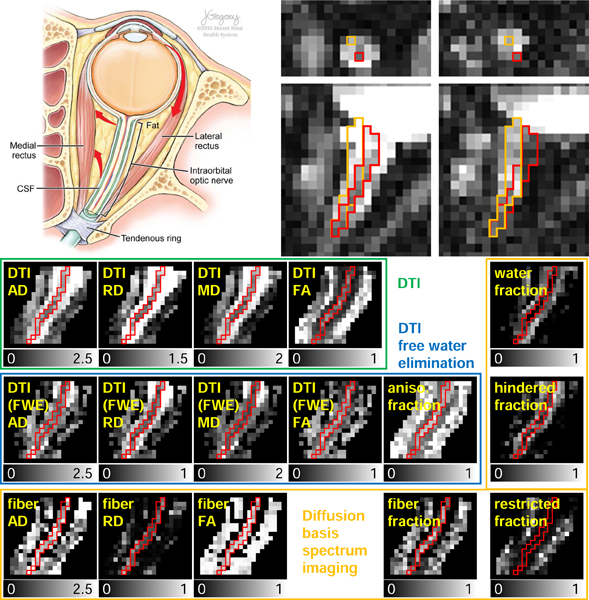
Figure 6.

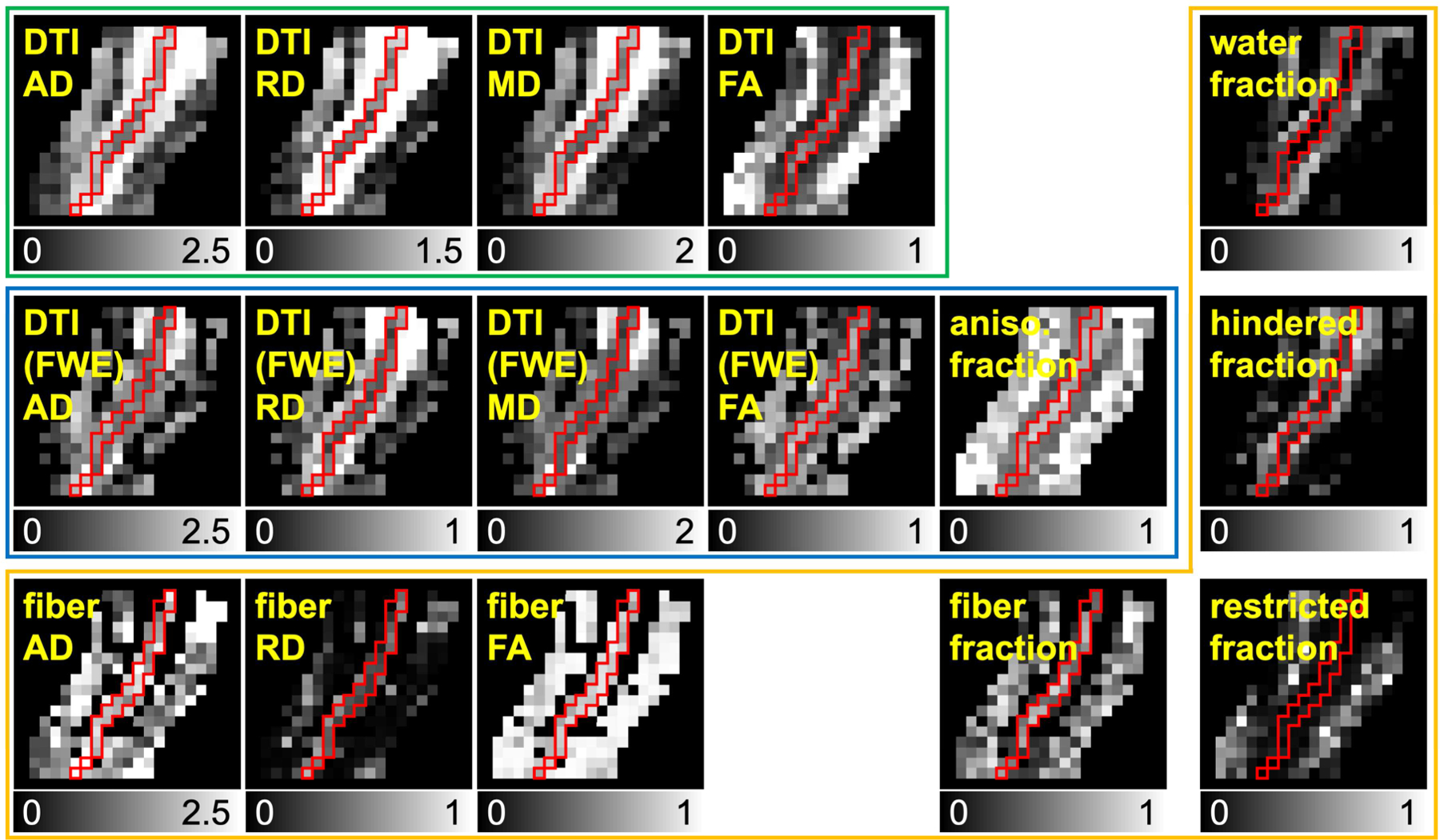
Representative dMRI metric maps derived from non-linearly aligned dMRI data. The maps inside green, blue, and orange boxes are from DTI, DTI with free water elimination (FWE), and DBSI, respectively. Red boundaries represent the optic nerve location. The grayscales range from 0 to 1 for fractional anisotropy and fraction (i.e., compartment ratio) maps, 0 to 2.5 µm²/ms for AD, 0 to 2 µm²/ms for MD, 0 to 1.5 µm²/ms for DTI RD, and 0 to 1 µm²/ms for DTI (FWE) and DBSI RD.

Figure 7.

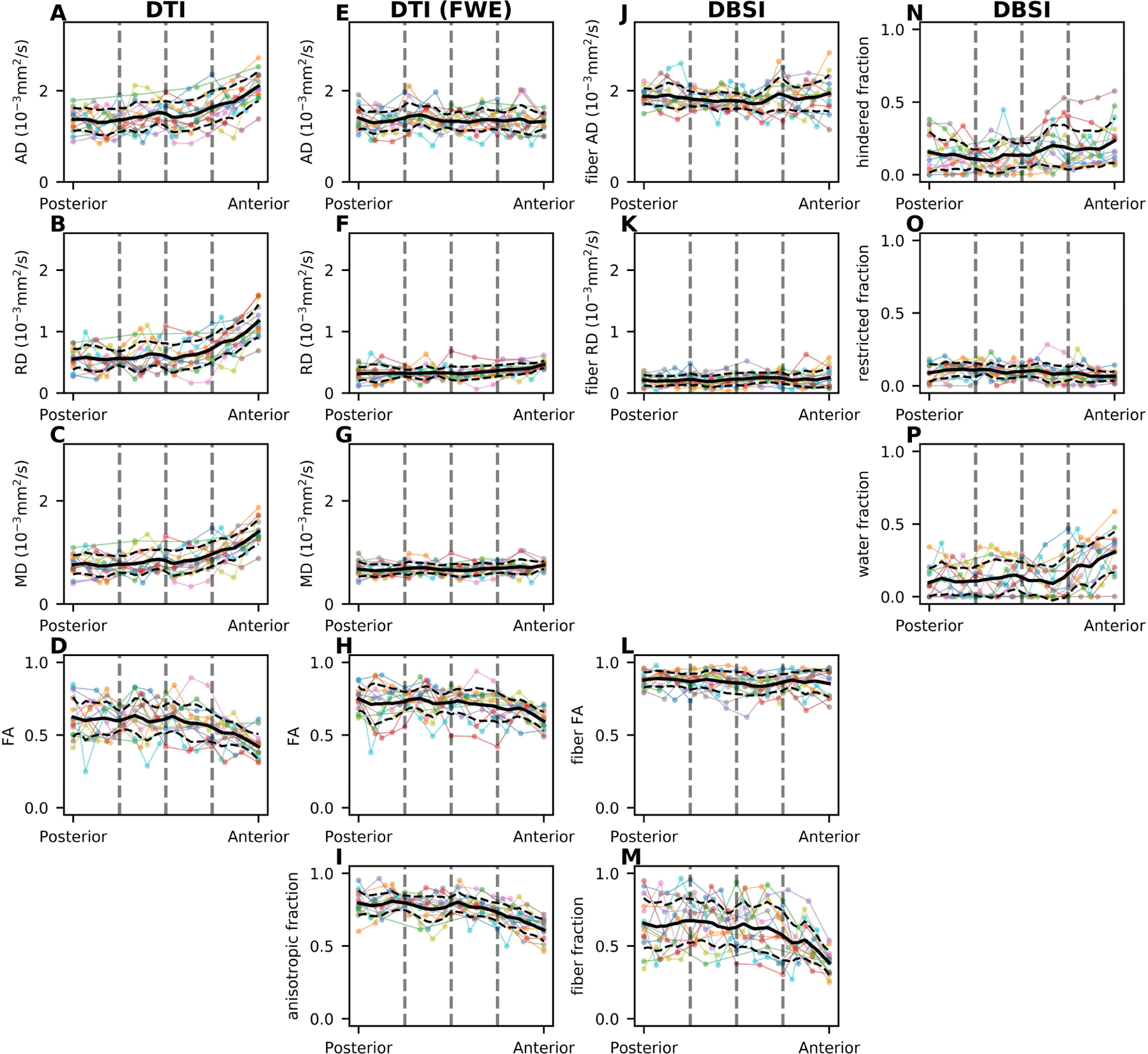
Spatial distribution of the DTI (A-D), DTI with free water elimination (FWE) (E-I), and DBSI (J-P) map values from posterior to anterior of the intraorbital optic nerve. Each colored line represents dMRI measurement in optic nerve center voxel from one eye. Solid and dashed black lines represent the mean and standard deviation, respectively, along the nerve location in the axis, ranging from the posterior optic nerve point (posterior) to the optic nerve head (anterior). The dashed gray vertical lines indicate quartiles of coronal location (see §2.7).

When modeled by DTI, all three diffusivity (i.e., AD, RD, and MD) measurements progressively increase (Fig. 7A-C), while FA measurements progressively decrease (Fig. 7D), from the posterior to the anterior optic nerve. These spatially dependent trends disappeared, except for the most anterior voxels, when applying DTI with FWE (Fig. 7E-H) or DBSI modeling (Fig. 7J-L), which can be explained by the associated progressively decreasing anisotropic component fraction (Fig. 7I) or DBSI fiber fraction (Fig. 7M). The estimated DBSI restricted isotropic diffusion fraction is small (< 0.3), followed by moderate free diffusion (i.e., water) fraction and hindered isotropic diffusion fraction, both of which show an increasing trend from the posterior to the anterior optic nerve, converse to the DBSI fiber fraction. These spatially dependent trends were more clearly visualized in the normalized plots (See Inline Supplementary Figure 3). These spatially dependent trends were quadratic; for example, a quadratic fitting of the normalized AD (y = 0.7x² − 0.4x + 0.9) yielded less mean squared error than a linear or exponential fitting.

To summarize the dMRI measurements (i.e., AD, RD, MD, and FA from DTI, AD, RD, MD, FA, and anisotropic fraction from DTI with FWE, and fiber AD, fiber RD, fiber FA, and fiber fraction from DBSI) in the middle of the intraorbital optic nerve (to be comparable to other studies), we averaged the values in the optic nerve center voxels for each nerve, excluding anterior and posterior quarters, and reported the mean ± standard deviation for the subjects (n = 7 subjects × 2 eyes) in this study (Table 1).

4. Discussions

Image volume alignment is crucially important to quantitative MRI, especially dMRI. Although substantial progress has been made recently in brain dMRI volume alignment (Andersson et al., 2018; Andersson and Sotiropoulos, 2016), achieving similar dMRI volume alignment for the optic nerve remains challenging. In this study, we demonstrated a non-linear optic nerve registration scheme to improve the volume alignment in high resolution optic nerve dMRI acquired in oblique axial view, outperforming conventional approaches such as topup and eddy. Building on the improved volume alignment, multi-compartmental dMRI signal modeling with estimation of isotropic diffusion compartment(s) allows less spatially biased microstructural quantification, especially for the anterior optic nerve center voxels close to the globe.

The substantially larger average optic nerve center displacement at the anterior location near the globe, compared to the middle and posterior locations, indirectly corroborated the pendulum-like optic nerve movement induced by eye movement. The much less optic nerve displacement at the posterior half of the intraorbital optic nerve likely reflected the detection limit of voxel displacement, independent of the mechanism of motion, which was limited by the image acquisition resolution and method (i.e., single-shot EPI) of this study. Note that the primary aim of this study was not optic nerve motion estimation, which could be better achieved using high-resolution, distortion-free, and high SNR MRI sequences, such as radial acquisition in (Sengupta et al., 2017). Approximately quadratic trends of decreasing DTI FA and increasing DTI diffusivities exist along the optic nerve (from posterior to anterior), which is at least partly attributable to the residual effects (i.e., additional attenuation of the diffusion-weighted signal) of optic nerve motion. Analogous trends have also been observed in the rostral-to-caudal direction along the cervical spinal cord (Smith et al., 2010; Xu et al., 2013), which are partly attributable to the effects of increasing respiration motion caudally (Verma and Cohen-Adad, 2014). These trends confirm the recognized best practice of optic nerve ROI definition for DTI quantification, with no additional isotropic component modeling, at least 1 cm away from the globe. Although the diameter of the intraorbital optic nerve progressively decreases from ~ 3.5 – 4 mm closely behind the globe to ~ 3.0 – 3.5 mm at about 10 mm behind the globe in adults (Harrigan et al., 2016; Karim et al., 2004; Yiannakas et al., 2010), we do not expect such systematic anatomical variation to explain the observed trends in optic nerve dMRI measurements. Neither was our diffusion encoding scheme sensitive to the reduced number of fascicles (Jeffery et al., 1995), possible systematic variation of collagen connective tissue in the extra-fascicular matrix (Karim et al., 2004), or increased axonal dispersion (Williams and Rakic, 1985) along the optic nerve. On the other hand, multi-compartmental dMRI modeling such as DTI with FWE or DBSI apparently removes this spatial bias in anisotropy and diffusivity measurements along the optic nerve, except for the very anterior end of the nerve. The estimated trend of increasing isotropic component (DTI-FWE, Fig. 7I) or DBSI water fraction (Fig. 7P) along the posterior-to-anterior dimension is consistent with the increasing CSF compartment size anteriorly towards the globe, which demonstrates that CSF contamination has a significant effect in the optic nerve DTI quantification, even for optic nerve center voxels at 1.3 mm isotropic resolution. The very anterior end of the optic nerve (i.e., retrolaminar region) was possibly affected by partial voluming with the lamina cribrosa, where the optic nerve begins to become unmyelinated (Hayreh, 2011). This mixture of myelinated and unmyelinated axons in the dMRI voxel is expected to result in increased RD and decreased FA, but unchanged AD in DTI-FWE or DBSI modeling.

In addition to the residual effects of motion and CSF contamination, there are two potential sources of dMRI quantification error related to the non-linear optic nerve motion: (1) spatially dependent orientation discrepancy between the optic nerve anatomy and the diffusion encoding vector and (2) bending (i.e., curvature change) and anteriad (toward anterior) motion of the optic nerve during eye movement (See Supplementary materials).

Our proposed image alignment algorithm registers the optic nerve segmentation, instead of a masked dMRI image including the optic nerve as we have previously done (Naismith et al., 2009), for better registration accuracy and robustness of this small structure in dMRI images with different SNR, contrast-to-noise ratio (CNR), and diffusion encoding. We proposed a two-Gaussian model on the Sobel-filtered images, in which the optic nerve image intensity was always lower than the surrounding image intensity. From this model, we segmented the optic nerve centers, which have the same shape for all volumes to avoid stretching or shrinking during registration. We speculate that the same logic, i.e., segmentation followed by registration, applies to dMRI volume alignment for other cranial nerves or peripheral nerves; and our algorithm could be adapted to isotropic high resolution dMRI acquisition of these other small nerves. Nevertheless, like any other dMRI studies, motion-induced artifactual signal dropout did occasionally occur in our optic nerve dMRI data, which would require manual identification and removal of these outlier volumes.

Besides the rFOV or IVI approach for high resolution optic nerve dMRI acquisition, other researchers have adapted axial or coronal whole brain dMRI protocols, using parallel imaging techniques, with high in-plane resolution (e.g., 1.2 – 1.5 mm), but thick (e.g., 3 – 4 mm) slices to study the optic nerve in clinical populations (Gerlach et al., 2017; Kolbe et al., 2009; Li et al., 2014; Smith et al., 2011; Techavipoo et al., 2009; Walt et al., 2013). We do not expect our proposed scheme to be applicable to facilitate the volume alignment of optic nerve dMRI images acquired from this type of optic nerve dMRI protocols, because our algorithm performs 3D non-linear registration, which assumes continuous identifiable optic nerve voxels between slices, while the relatively thick slices, as compared to the small optic nerve structure, from this type of protocol typically results in discontinuous optic nerve voxels between slices.

It is ideal to combine all processing, or image transformations, in a single step to minimize image blurring. In this study, we applied the non-linear registration on the resulting images of topup/eddy or rigid-body registration, which introduced a small amount of unnecessary blurring. For the same reason of avoiding further blurring, we used the native acquisition coordinate space for our evaluation, instead of making our evaluation plane perpendicular to the optic nerve, which requires resampling.

The optic nerves are close to the orbital sinus, where large magnetic field inhomogeneity exists. The associated large signal pile-up or dropout and optic nerve motion could lead to suboptimal distortion correction by using reversed PE direction methods (Andersson et al., 2003; Morgan et al., 2004). We used topup with a pair PE-reversed b0 images separately by only a single TR to minimize motion between the images in our initial preprocessing to establish a more robust initial condition than the unprocessed images for our non-linear dMRI volume alignment scheme. Although the field inhomogeneity estimated by topup is spatially smooth, misestimating optic nerve motion as field inhomogeneity is possible, which might lead to erroneous distortion correction. In addition, even the acceptable topup results in this study contained obvious residual distortion and should not be considered as distortion-free results. Nevertheless, these residual image space distortions, if present, are consistent across the dMRI volumes. Based on our pilot imaging data, in most adult subjects, the field inhomogeneity caused the optic nerves to appear stretched in PA images and compressed in AP images (Inline Supplementary Figure 4). Our initial piloting also demonstrated that the difference in image distortion due to eddy currents from diffusion gradients was marginal between monopolar and bipolar diffusion encoding (Inline Supplementary Figure 4) with the short EPI acquisition window (i.e., echo train duration = 20.6 ms) used in this study. Hence the much reduced TE by using monopolar diffusion encoding outweighed the slightly less distortion by using bipolar diffusion encoding.

The mean DTI AD / RD / MD (µm²/ms) / FA values of the healthy adult intraorbital optic nerve in this study (excluding the anterior optic nerve voxels) are comparable to our previous studies (Chang et al., 2014; Naismith et al., 2009). Notably, the present results exhibit less variability, which is likely attributable to the larger number of analyzable optic nerve voxels provided by the improved volume alignment. As expected, DTI with FWE leads to reduced diffusivity values and increased FA as compared to DTI without FWE, which is consistent with result from studies applying DTI with FWE to brain dMRI (Berlot et al., 2014; Chad et al., 2018). Also, as expected, DBSI modeling accentuates the anisotropic nature of the coherent fiber component in the optic nerve, yielding fiber AD / RD and FA values of the healthy adult optic nerve consistent with the DTI AD / RD and FA values measured from healthy small animal optic nerve (Song et al., 2003; Sun et al., 2008), where partial volume effects were minimal. Given the much higher dMRI data quality requirement of DBSI modeling, which is based on a data-driven optimization algorithm, the reasonable DBSI results obtained from this 10 min in vivo human optic nerve dMRI protocol with a b_max = 1000 s/mm² are encouraging. More importantly, the advantage of DBSI modeling is best shown when coexisting patholophysiological substrates, such as inflammation, demyelination, vasogenic edema, and axonal injury, are present (Lin et al., 2017; Shirani et al., 2018; Wang et al., 2014, 2015). Quantitative comparison of the different dMRI modeling presented in this study will be evaluated in a future analysis of all subject data in the larger clinical imaging study of optic neuritis, while keeping in mind that more complex modeling always puts a higher demand on data quality and a balance between model complexity and robustness, and interpretability of results is required for clinical utility.

5. Conclusions

We have developed a non-linear optic nerve registration scheme for improved volume alignment in high resolution axial optic nerve dMRI. The registration scheme corrected the optic nerve movement due to eye movement, which is non-linear and independent of head motion. The spatial trend of optic nerve displacement, during eyes-closed dMRI acquisiton, along the posterior-to-anterior dimension was characterized, as well as the dMRI measurements by DTI, DTI with FWE, and DBSI. Multi-compartmental dMRI modeling, such as DTI with FWE and DBSI, show less spatially biased dMRI parameter estimation. DBSI results derived from our clinically feasible (~10 min) optic nerve dMRI protocol in this study are consistent with those from small animal studies, which provides the basis for evaluating the utility of multi-compartmental dMRI modeling in characterizing coexisting pathophysiology in human optic neuropathies.

Appendix A. Weighted graph for the Dijkstra shortest path algorithm

We defined a graph, on which the Dijkstra shortest path algorithm (Dijkstra, 1959) was used to generate the path, consisting of voxels as nodes, voxel neighbors sharing a vertex as edges, and intensity-difference-weighted distance function values as edge weights. The nodes n_i,j of the graph were defined as voxels and the weight w_i,j of the edge e_i,j connecting nodes n_i and n_j, were defined as $w_{i,j}=d\left(n_i,n_j\right)\left(\frac{C_1\left|I_i-I_j\right|}{I_i+I_j}+\frac{C_2}{I_i}+\frac{C_2}{I_j}\right)$, where d(n_i,n_j) is the Euclidian distance between these two voxels, I_i,j is the voxel intensity of n_i,j and C_i,j are empirically defined constants (C₁ = 5 and C₂= 100). High intensity difference between two neighboring voxels results in high edge weight, which the Dijkstra shortest path algorithm avoids passing through.

Appendix B. Two Gaussian Model

The two-Gaussian model was defined as $I\left(x,y\right) =G_{out}\left(x,y\right)-G_{in}\left(x,y\right)$ where (x,y), is a voxel coordinate on a coronal slice, $G_{out\hspace{0.17em}or\hspace{0.17em}in}\left(x,y\right)=A\exp \left(-\left(a{\left(x-x_0\right)}^2-2b\left(x-x_0\right)\left(y-y_0\right)+c{\left(y-y_0\right)}^2\right)\right)$, $a=\raisebox{1ex}{${\cos }^2\theta $}\!\left/ \!\raisebox{-1ex}{$2\hspace{0.17em}{\sigma }_x^2$}\right.+\raisebox{1ex}{${\sin }^2\theta $}\!\left/ \!\raisebox{-1ex}{$2\hspace{0.17em}{\sigma }_y^2$}\right.$, $b=-\raisebox{1ex}{$\sin \hspace{0.17em}2\theta $}\!\left/ \!\raisebox{-1ex}{$4\hspace{0.17em}{\sigma }_x^2$}\right.+\raisebox{1ex}{$\sin \hspace{0.17em}2\theta $}\!\left/ \!\raisebox{-1ex}{$4\hspace{0.17em}{\sigma }_y^2$}\right.$ and $c=\raisebox{1ex}{${\sin }^2\theta $}\!\left/ \!\raisebox{-1ex}{$2\hspace{0.17em}{\sigma }_x^2$}\right.+\raisebox{1ex}{${\cos }^2\theta $}\!\left/ \!\raisebox{-1ex}{$2\hspace{0.17em}{\sigma }_y^2$}\right.$. After successful fitting, the voxel (x₀,y₀) is the center location of the Gaussian, which is the optic nerve center.

Appendix C. Outliers

The outliers were identified (Appendix C). if the x or y coordinate was less than Q1 – 1.5 × IQ or greater than Q3 + 1.5 × IQ, where Q1 and Q3 are the first and third quartiles of the x or y position, respectively, where inter-quartile (IQ) = Q3 – Q1. Each optic nerve center of the outliers was replaced by linear interpolation using the optic nerve centers on its adjacent slices from the adjacent volumes