Modeling the epidemic control measures in overcoming COVID-19 outbreaks: A fractional-order derivative approach

Mohammad Sharif Ullah; M Higazy; KM Ariful Kabir

doi:10.1016/j.chaos.2021.111636

. 2021 Nov 27;155:111636. doi: 10.1016/j.chaos.2021.111636

Modeling the epidemic control measures in overcoming COVID-19 outbreaks: A fractional-order derivative approach

Mohammad Sharif Ullah ^a,^b,^⁎, M Higazy ^c,^d, KM Ariful Kabir ^b

PMCID: PMC8626290 PMID: 34866811

Abstract

Novel coronavirus named SARS-CoV-2 is one of the global threads and uncertain challenges worldwide faced at present. It has stroke rapidly around the globe due to viral transmissibility, new variants (strains), and human unconsciousness. Lack of adequate and reliable vaccination and proper treatment, control measures such as self-protection, physical distancing, lockdown, quarantine, and isolation policy plays an essential role in controlling and reducing the pandemic. Decisions on enforcing various control measures should be determined based on a theoretical framework and real-data evidence. We deliberate a general mathematical control measures epidemic model consisting of lockdown, self-protection, physical distancing, quarantine, and isolation compartments. Then, we investigate the proposed model through Caputo fractional order derivative. Fixed point theory has been used to analyze the Caputo fractional-order derivative model's existence and uniqueness solutions, whereas the Adams-Bashforth-Moulton numerical scheme was applied for numerical simulation. Driven by extensive theoretical analysis and numerical simulation, this work further illuminates the substantial impact of various control measures.

Keywords: COVID-19, Control measures, Infectious diseases, Caputo fractional-order derivative

1. Introduction

COVID-19, a transmissible respiratory disease, first time reported in Wuhan of Hubei Province, Republic of China [1] in 2019. Furthermore, it has rapidly spread internationally; thus, WHO declared that COVID-19 is a global pandemic [2]. According to health experts, it has found a variety of COVID-19 symptoms [3], [4], [5], [6]. Enormous mainstream people experienced mild to moderate respiratory illnesses [7]. However, some of individuals would improve complexities of respiratory disappointment or severe respiratory suffering signs. Further, few studies emphasize that more than 80% of the individuals are asymptomatic infection carriers like they perceive no or mild side effects [8]. Thus, the recognition and control of SARS-CoV-2 disease become considerably more sophisticated. To this, various COVID-19 alleviation procedures have been adjusted so far, for example, self-protection, lockdown, quarantine, or isolation, with the end goal of decreasing community transmission of the disease.

One of the most commonly adopted mathematical epidemiological models is the SIR (Susceptible-Infected-Recovered) model. It characterizes the epidemic dynamics, predicts possible contagion scenarios, and simulates the time-histories of an epidemic phenomenon. The people who still can not seem to be contaminated by the virus represented by compartment S (susceptible). Infected individuals who showed symptoms and can spread the virus to the susceptible compartment. Finally, R (recovered), individuals who have recovered—beside, expected to have an immune acknowledgment to the virus [9], [10], [11], [12], [13], [14]. But SARS-CoV-2 is a novel virus as well as we have exceptionally constrained information about this disease. Many scholars of the entire world investigated this pandemic's control measures [15], [16], [17], [18]. The readers are requested to read some work of covid-19 [19], [20], [21], [22], [23], [24], [25]. Lacking proper treatment and vaccination, computational simulation with self-protection, physical distance, the lockdown situation, a great deal of testing, quarantine, and isolation would be played a significant role in analyzing and controlling the current pandemic. Considering such cases, we modified the usual SIR model to the SLTIA_dI_sndI_sdQJL_tRDP model.

Furthermore, many researchers from various disciplines have recently given deep concentration to the theory of fractional calculus and fractional differential equations [26], [27], [28], [29], [30], [31], [32]. As a measure of fact, it mentioned that fractional derivatives are beneficial for modeling many real-worlds problems due to memory and the universal properties [33], [34], [35], [36]. As a result, the importance and potential application enlarged day by day [37], [38], [39]. The fractional-order differential equations supplement new dimensions in the investigation of epidemiological models. Yadav and Rene's first time developed the Caputo–Fabrizio fractional derivative model of COVID-19 [40]. Subsequently, many studies [38], [41], [42], [43], [44] address the COVID-19 fractional-order differential model. In this work, we introduce Caputo fractional derivative [45] approach to our proposed epidemic model.

This research aims to model and analyze a modified SIR mathematical epidemic model by considering all possible control measures. Beside, we represent the proposed model through a Caputo fractional order derivative. Fixed point theory has been used to analyze the Caputo fractional-order derivative model's existence and uniqueness solutions. Also, for numerical simulation, we applied the Adams-Bashforth-Moulton numerical scheme. The analysis of thirteen compartments and the concentration of COVID-19 in the surrounding circumstances concerning time for several fractional-order derivative values have been theoretically investigated and graphically manifested.

The development of this work is as follows. The formulation of the model is elaborately discussed in Section 2. In Section 3, we present a fractional model using Caputo fractional derivatives, where the fractional order of differentiation is p. Calibration of the epidemic model is given in Section 4. In Section 5, we offer some numerical results through the graphs. The concluding words are given in Section 6.

2. Mathematical model formulation

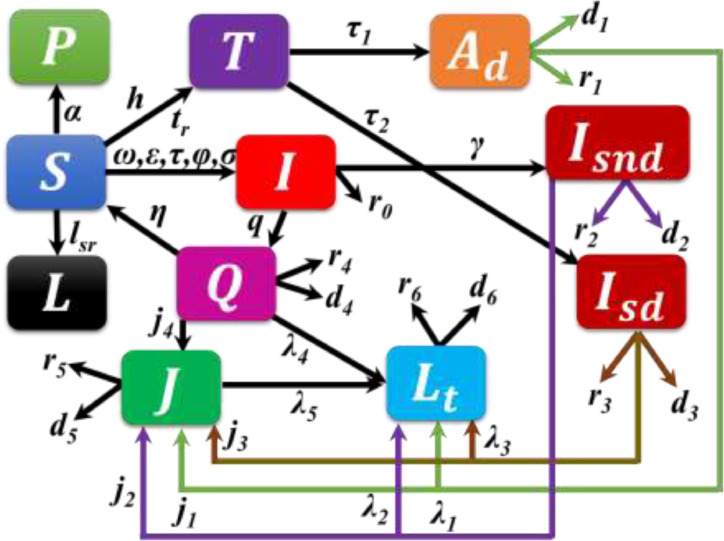
The proposed model displays the dynamics of thirteen compartments (Fig. 1 ), namely susceptible $(S (t))$ , lockdown $(L (t))$ , tested state $(T (t)),$ Infected $I (t)$ (asymptomatic, mild-symptomatic-infected, minor or moderate infection but not detected), asymptomatic infected with detected $A_{d} (t)$ , symptomatic infected with not detected $I_{s n d} (t)$ , symptomatic infected with detected $I_{s d} (t)$ , quarantine $(Q (t))$ , isolated or hospitalized $(J (t))$ , life-threatening condition $(L_{t} (t))$ , recovered $(R (t))$ $(R (t))$ , death $(D (t))$ , and self-protected $(P (t))$ individuals. The mean-field mathematical epidemiological dynamics are then modeled by the following system of ordinary differential equations.

\begin{matrix} \frac{d S (t)}{d t} \\ = - p_{d} β S (t) {ω I (t) + ε A_{d} (t) + τ I_{s n d} (t) + I_{s d} (t) + ϕ Q (t) + σ J (t)} \\ - l_{s r} S (t) + l_{d} L (t) - t_{r} S (t) T (t) + h T (t) + η Q (t) - α S (t), \end{matrix}

(1.1)

\frac{d L (t)}{d t} = l_{s r} S (t) - l_{d} L (t),

(1.2)

\frac{d T (t)}{d t} = t_{r} S (t) T (t) - (h + τ_{1} + τ_{2}) T (t),

(1.3)

\begin{matrix} \frac{d I (t)}{d t} & = & p_{d} β S (t) {ω I (t) + ε A_{d} (t) + τ I_{s n d} (t) + I_{s d} (t) \\ + ϕ Q (t) + σ J (t)} - (γ + q + r_{0}) I (t) \end{matrix}

(1.4)

\frac{d A_{d} (t)}{d t} = τ_{1} T (t) - (j_{1} + λ_{1} + r_{1} + d_{1}) A_{d} (t),

(1.5)

\frac{d I_{s n d} (t)}{d t} = γ I (t) - (j_{2} + λ_{2} + r_{2} + d_{2}) I_{s n d} (t),

(1.6)

\frac{d I_{s d} (t)}{d t} = τ_{2} T (t) - (j_{3} + λ_{3} + r_{3} + d_{3}) I_{s d} (t),

(1.7)

\frac{d Q (t)}{d t} = q I (t) - (η + j_{4} + λ_{4} + r_{4} + d_{4}) Q (t),

(1.8)

\frac{d J (t)}{d t} = j_{1} A_{d} (t) + j_{2} I_{s n d} (t) + j_{3} I_{s d} (t) + j_{4} Q (t) - (λ_{5} + r_{5} + d_{5}) J (t),

(1.9)

\frac{d L_{t} (t)}{d t} = λ_{1} A_{d} (t) + λ_{2} I_{s n d} (t) + λ_{3} I_{s d} (t) + λ_{4} Q (t) + λ_{5} J (t) - (r_{6} + d_{6}) L_{t} (t),

(1.10)

\frac{d R (t)}{d t} = r_{0} I (t) + r_{1} A_{d} (t) + r_{2} I_{s n d} (t) + r_{3} I_{s d} (t) + r_{4} Q (t) + r_{5} J (t) + r_{6} L_{t} (t),

(1.11)

\frac{d D (t)}{d t} = d_{1} A_{d} (t) + d_{2} I_{s n d} (t) + d_{3} I_{s d} (t) + d_{4} Q (t) + d_{5} J (t) + d_{6} L_{t} (t),

(1.12)

\frac{d P (t)}{d t} = α S (t),

(1.13)

Fig 1 — Schematic flow diagram for the epidemic SARS-CoV-2 models. In our epidemic model, we presumed total of 13 compartments as follows: susceptible $S (t)$ , lockdown $(L (t))$ , Tested state $(T (t)),$ infected $I (t)$ (asymptomatic, mild-symptomatic-infected, minor or moderate infection but not detected), asymptomatic infected with detected $A_{d} (t)$ , symptomatic infected with not detected $I_{s n d} (t)$ , symptomatic infected with detected $I_{s d} (t)$ , quarantine $(Q (t))$ , isolated or hospitalized $(J (t))$ , life-threatening condition $(L_{t} (t))$ , recovered $(R (t))$ , death $(D (t))$ , and self-protected $(P (t))$ ). [The proposed model has a lot of recovery and death parameters, and their determination is more complicated. As a result, the recovered and death compartments are absent in the Schematic flow diagram.]

The total population

N (t) = S (t) + L (t) + T (t) + I (t) + A_{d} (t) + I_{s n d} (t) + I_{s d} (t) + Q (t) + J (t) + L_{t} (t) + R (t) + D (t) + P (t) .

(1.14)

Now, if the vector of the state variable is,

x = {(S (t), L (t), T (t), I (t), A_{d} (t), I_{s n d} (t), I_{s d} (t), Q (t), J (t), L_{t} (t), R (t), D (t), P (t))}^{'}

and $f : R^{13} \to R^{13} .$

Then the right side of the proposed model (Eqs. (1.1)–(1.13)) is a continuously differentiable function on $R^{13}$ . Necessarily, a novel clarification of (1.1–1.14) exists in $Ω$ for any initial condition and remains for its maximal existence interval [46]. Therefore, the proposed model is well-defined in biological meaning. Also, according to Nabi et al. [43], the model's solution is positive for all $t \geq 0$ and bounded by the total population $N (t)$ (Eq. (1.14)). Thus, at any time, each compartment is considered to be in one of the following thirteen possible states.

(i) Susceptible individuals, $S (t)$ : Initially, the susceptible is the fraction of the total population subject to the infected individuals (Eq. (1.1)). The suspected susceptible population is increased by the net inflow of people from quarantine and other compartments and diminished by self-protected and natural death rates. The susceptible populations likewise decrease the following disease, obtained by contact between susceptible and infected people, who might be contacting asymptomatic, mild-symptomatic infected, minor or moderate infection but not detected, asymptomatic infected (detected), symptomatic infected (not detected), symptomatic infected (detected) and isolated individuals. The transmission coefficient for these classes of infected individuals is $β ω, β ε, β τ, β, β ϕ$ , and $β σ$ respectively. Here, the primary transmission coefficient of infectious and contact rates is $β .$ The change parameter $ϕ$ represents different levels of hygiene precautionary measures during quarantine.

(ii) Lockdown individuals, $L (t)$ : These are the people who have followed lockdown policies. The lockdown compartment refers to susceptible individuals staying at home and staying safe from the virus. Here, we quantify the lockdown open and close mechanism by using the Heaviside function.

l_{s r} [d_{1}, d_{2}] = {\begin{matrix} 0, t \notin [d_{1}, d_{2}] \\ 1, t \in [d_{1}, d_{2}] \end{matrix}

(2.1)

where, $d_{1} =$ lockdown starting time and $d_{2} =$ lockdown ending time.

(iii) Tested individuals, $T (t)$ : One of the powerful tactics to control the spread of the disease is testing the susceptible population. Lack of plethora of testing undetected infected people generously the asymptomatic individual who sustains the environment and spreads the epidemic. The people of this compartment that is healthy again is susceptible, and detected individuals tested positive at the rate $τ_{1}$ and $τ_{2} .$

(iv) Asymptomatic infected, mild-symptomatic infected, and minor or moderate infected but not detected individuals, $I (t)$ : The asymptomatic, mild-symptomatic infected, minor or moderate infection but not detected individuals are the entire populations. They are infected by the SARS-CoV-2 virus but have no apparent substantial clinical side effects yet. This period is known as the latent phase, and at this juncture, a disease can be infectious or partially infectious. This compartment population is lessened by an infected (symptomatic and asymptomatic, which is identified by the test), symptomatic infected (not detected), quarantine and recover at the rates $γ,$ $q$ and $r_{0} .$

(v) Asymptomatic infected, detected individuals, $A_{d} (t)$ : It is one of the most hazardous components of any transmissible disease. Generally, people are not apparent by the clinical symptoms of COVID-19. As a result, the disease spreads smoothly. Furthermore, one is confirmed by testing at the rate $τ_{1} .$ Finally, the isolation rate $j_{1}$ , life-threatening $λ_{1}$ , recovery rate $r_{2}$ , and disease-induced death $d_{1}$ decreased this compartment population.

(vi) Symptomatic infected, not detected individuals, $I_{s n d} (t)$ : These are the people of symptomatic infected but not detected. They have mild clinical symptoms of COVID-19 after the latent period. But did not detect due to scarcity of testing, financial crisis, and lack of knowledge of the disease. The isolation rate $j_{2},$ life-threatening $λ_{2}$ , recovery rate $r_{2}$ , and disease-induced death $d_{2}$ decreased this compartment population.

(vii) Symptomatic with detected individuals, $I_{s d} (t)$ : These are the people who have been apparent the growth of clinical symptoms of COVID 19 after the latent period and confirmed by testing at the rate $τ_{2} .$ The isolation rate $j_{3}$ , life-threatening $λ_{3}$ , recovery rate $r_{3}$ , and disease-induced death $d_{3}$ decreased this compartment population.

(viii) Quarantined individuals, $Q (t)$ : These are the people who have been contracting with a source of SARS-CoV-2 virus at rates $q$ asymptomatic, mild-symptomatic infected, minor or moderate infection but not detected. The practical reality is that sometimes a few uninfected characters also entered the quarantined compartment, which substantially lessens the model. The population of this class diminished by the improvement of clinical side effects at a rate $j_{5}$ with removal to the isolated compartment, recovery rate $r_{5}$ , life-threatening rate $λ_{4}$ , and disease-induced death $d_{4}$ .

(ix) Isolated individuals, $J (t)$ : The isolation or hospitalization compartment simply represents people who are self-isolated in-home, institute or occupy a bed in a hospital. These are the people who have been established clinical symptoms and isolated like hospitalization. These originate from asymptomatic infected (detected), symptomatic infected (not detected), symptomatic infected (detected), quarantine class at rates $j_{I}, j_{2}, j_{3}$ and $j_{4}$ respectively. Life-threatening rate $λ_{5}$ , recovery rate $r_{5}$ and disease-induced death rate $d_{5}$ decreased this compartment population.

(x) Life-threatening individuals, $L_{t} (t)$ : In the life-threatening compartment, $λ_{1}, λ_{2}, λ_{3}, λ_{4}$ and $λ_{5}$ respectively denote the rate at which asymptomatic infected (detected), symptomatic infected (not detected), symptomatic infected (detected), quarantine, isolated subjects develop life-threatening symptoms, respectively. Recovery rate $r_{6}$ and disease-induced death rate $d_{6}$ decreased this compartment population.

(xi) Recovered individuals, $R (t)$ : It is assumed that recovered people have permanent immunity against the SARS-CoV-2 virus. Asymptomatic, mild-symptomatic infected, minor or moderate infection but not detected, asymptomatic infected (detected), symptomatic infected (not detected), symptomatic infected (detected), quarantine, isolated, and life-threatening individuals are recovered from the disease at rates $r_{0}, r_{I}, r_{2}, r_{3}, r_{3}, r_{4}, r_{5}$ and $r_{6}$ respectively.

(xii) Dead individuals, $D (t)$ : Asymptomatic infected (detected), symptomatic infected (not detected), symptomatic infected (detected), quarantine, isolated, and life-threatening individuals are passing at rates $d_{I}, d_{2}, d_{3}, d_{3}, d_{4}, d_{5}$ and $d_{6}$ respectively.

(xiii) Self-protected individuals, $P (t)$ : In this compartment, individuals who have been conscious performed self-protection measures against viral diseases by using virus protecting tools at the rate $α .$

2.1. Basic reproduction number $R_{0}$

The disease-free equilibrium's local stability and instability depend on the value of the reproduction number $R_{0}$ . Also, it identifies the threshold for the disease-free equilibrium local stability. Furthermore, it plays an essential role in controlling the disease and leading epidemiological indicators of disease. When $R_{0} < 1$ , the disease-free equilibrium is locally asymptotically stable; a small amount of infection into the population may cause it to evolve into an endemic prevalence. On the other hand, when $R_{0} > 1$ , the disease-free equilibrium is locally unstable; a sufficiently small number of infected people will generate an outbreak. Here, $R_{0}$ is deduced from the system of non-linear ODE's (Eqs. (1.1)–(1.14)) by the next generation matrix approach [47].

Based on the above proposed system of non-linear ODE's model, the disease-free equilibrium point is $(0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0) .$

F = [\begin{matrix} r & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & p_{d} β ω & p_{d} β ε & p_{d} β τ & p_{d} β & p_{d} β ϕ & p_{d} β σ & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{matrix}]

(2.2)

V = [\begin{matrix} v_{1} & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & v_{2} & 0 & 0 & 0 & 0 & 0 & 0 \\ - τ_{1} & 0 & v_{3} & 0 & 0 & 0 & 0 & 0 \\ 0 & - γ & 0 & v_{4} & 0 & 0 & 0 & 0 \\ - τ_{2} & 0 & 0 & 0 & v_{5} & 0 & 0 & 0 \\ 0 & - q & 0 & 0 & 0 & v_{6} & 0 & 0 \\ 0 & 0 & - j_{1} & - j_{2} & - j_{3} & - j_{4} & v_{7} & 0 \\ 0 & 0 & - λ_{1} & - λ_{2} & - λ_{3} & - λ_{4} & - λ_{5} & v_{8} \end{matrix}]

(2.3)

F V^{- 1} = [\begin{matrix} a_{11} & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ a_{21} & a_{22} & a_{23} & a_{24} & a_{25} & a_{26} & a_{27} & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{matrix}]

(2.4)

where,

v_{1} = h + τ_{1} + τ_{2}, v_{2} = γ + q + r_{0}, v_{3} = j_{1} + λ_{1} + r_{1} + d_{1}, v_{4} = j_{2} + λ_{2} + r_{2} + d_{2}

v_{5} = j_{3} + λ_{3} + r_{3} + d_{3}, v_{6} = η + j_{4} + λ_{4} + r_{4} + d_{4}, v_{7} = λ_{5} + r_{5} + d_{5}, v_{8} = r_{6} + d_{6}

a_{11} = \frac{r}{v_{11}}

a_{21} = \frac{τ_{1} p_{d} β ε}{v_{11} v_{33}} + \frac{p_{d} β τ_{2}}{v_{11} v_{55}} + \frac{p_{d} β σ (τ_{2} j_{3} v_{2} v_{3} v_{4} v_{6} v_{8} + τ_{1} v_{2} v_{4} v_{5} v_{6} v_{8})}{v_{1} v_{2} v_{3} v_{4} v_{5} v_{6} v_{7} v_{8}}

a_{22} = \frac{p_{d} β ω}{v_{2}} + \frac{p_{d} β τ γ}{v_{2} v_{4}} + \frac{p_{d} β ϕ q}{v_{2} v_{6}} + \frac{p_{d} β σ (j_{4} q v_{1} v_{3} v_{4} v_{5} v_{8} + γ j_{2} v_{1} v_{3} v_{5} v_{6} v_{8})}{v_{1} v_{2} v_{3} v_{4} v_{5} v_{6} v_{7} v_{8}}

a_{23} = \frac{p_{d} β ε}{v_{3}} + \frac{p_{d} β σ j_{1}}{v_{3} v_{7}}

a_{24} = \frac{p_{d} β τ}{v_{4}} + \frac{p_{d} β σ j_{2}}{v_{4} v_{7}}

a_{25} = \frac{p_{d} β}{v_{5}} + \frac{p_{d} β σ j_{3}}{v_{5} v_{7}}

a_{26} = \frac{p_{d} β ϕ}{v_{6}} + \frac{p_{d} β σ j_{4}}{v_{6} v_{7}}

a_{27} = \frac{p_{d} β σ}{v_{7}}

According to the next-generation matrix approach, the basic reproduction number $R_{0}$ is the largest Eigenvalue of $| F V^{- 1} | .$

Thus, $R_{0} = ρ (F V^{- 1}),$ where $ρ$ is the spectral radius of $F V^{- 1}$ .

R_{0} = \frac{p_{d} β ω}{v_{2}} + \frac{p_{d} β τ γ}{v_{2} v_{4}} + \frac{p_{d} β ϕ q}{v_{2} v_{6}} + \frac{p_{d} β σ (j_{4} q v_{1} v_{3} v_{4} v_{5} v_{8} + γ j_{2} v_{1} v_{3} v_{5} v_{6} v_{8})}{v_{1} v_{2} v_{3} v_{4} v_{5} v_{6} v_{7} v_{8}}

(2.5)

2.2. Strength number

The concept of the reproduction number discussed above has been widely used in epidemiology for assessing whether or not the spread will exist. However, a reproduction number could not specify whether a model has formed the waves or not. To determine the complications in the epidemic spread and assist in detecting the waves, we consider a new number approach termed the strength number, derived using the next-generation matrix by taking the second derivative of infectious classes.

For determining the strength number (SN) of the proposed model, we assume the total population is finite (N). Then the mass and standard action incidence have no difference.

Thus,

p_{d} β ω S I = \frac{p_{d} β ω S I}{N}

(2.6)

Now, according to Atangana et al. [48,49]

\frac{\partial^{2}}{\partial I^{2}} (\frac{p_{d} β ω S I}{N}) = p_{d} β ω S \frac{\partial}{\partial I} (\frac{N - \dot{N} I}{N^{2}})

(2.7)

= - \frac{p_{d} β ω S}{N^{2}}

Similarly,

\frac{\partial^{2}}{\partial A_{d}^{2}} (\frac{p_{d} β ε S A_{d}}{N}) = - \frac{p_{d} β ε S}{N^{2}}

(2.8)

\frac{\partial^{2}}{\partial I_{s n d}^{2}} (\frac{p_{d} β τ S I_{s n d}}{N}) = - \frac{p_{d} β τ S}{N^{2}}

(2.9)

\frac{\partial^{2}}{\partial I_{s d}^{2}} (\frac{p_{d} β S I_{s d}}{N}) = - \frac{p_{d} β S}{N^{2}}

(2.10)

\frac{\partial^{2}}{\partial Q^{2}} (\frac{p_{d} β ϕ S Q}{N}) = - \frac{p_{d} β ϕ S}{N^{2}}

(2.11)

\frac{\partial^{2}}{\partial J^{2}} (\frac{p_{d} β σ S Q}{N}) = - \frac{p_{d} β σ S}{N^{2}}

(2.12)

In this case,

F_{S N} = [\begin{matrix} r & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & - \frac{p_{d} β ω}{N^{2}} & - \frac{p_{d} β ε}{N^{2}} & - \frac{p_{d} β τ}{N^{2}} & - \frac{p_{d} β}{N^{2}} & - \frac{p_{d} β ϕ}{N^{2}} & - \frac{p_{d} β σ}{N^{2}} & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{matrix}]

(2.13)

Then

D e t (F_{S N} V^{- 1} - λ I_{8}) = 0

(2.14)

Therefore, strength number,

S N = - [\frac{p_{d} β ω}{N^{2} v_{2}} + \frac{p_{d} β τ γ}{N^{2} v_{2} v_{4}} + \frac{p_{d} β ϕ q}{N^{2} v_{2} v_{6}} + \frac{p_{d} β σ (j_{4} q v_{1} v_{3} v_{4} v_{5} v_{8} + γ j_{2} v_{1} v_{3} v_{5} v_{6} v_{8})}{N^{2} v_{1} v_{2} v_{3} v_{4} v_{5} v_{6} v_{7} v_{8}}] < 0

(2.15)

$S N = 0$ indicates that the spread will not renew and will hence have a single magnitude and die out. $S N > 0$ suggests sufficient strength to initiate the renewal phase, implying that the spread will have more than one wave. On the other hand, biologists will offer a clear explanation of the quantity, as mentioned earlier, which will be proven when the second derivative of infectious classes is studied.

2.3. The first derivative of the Lyapunov function

The endemic equilibrium $E^{*}$ for the endemic Lyapunov function is ${S, L, T, I, A_{d}, I_{s n d}, I_{s d}, Q, J, L_{t}, R, D, P}, L_{f} < 0$ .

Theorem 1

The endemic equilibrium points $E^{*}$ in the SLTIA_dI_sndI_sdQJL_tRDP model are globally asymptotically stable when the reproductive number $R_{0} > 1$ .

Proof

For proof of the theorem, the Lyapunov function can be expressed as follows

$\begin{matrix} L_{f} (S, L, T, I, A_{d}, I_{s n d}, I_{s d}, Q, J, L_{t}, R, D, P) & = & (S - S^{*} - S^{*} l o g \frac{S^{*}}{S}) + (L - L^{*} - L^{*} l o g \frac{L^{*}}{L}) \\ + (T - T^{*} - T^{*} l o g \frac{T^{*}}{T}) + (I - I^{*} - I^{*} l o g \frac{I^{*}}{I}) + (A_{d} - A_{d}^{*} - A_{d}^{*} l o g \frac{A_{d}^{*}}{A_{d}}) \\ + (I_{s n d} - I_{s n d}^{*} - I_{s n d}^{*} l o g \frac{I_{s n d}^{*}}{I_{s n d}}) + (I_{s d} - I_{s d}^{*} - I_{s d}^{*} l o g \frac{I_{s d}^{*}}{I_{s d}}) \\ + (Q - Q^{*} - Q^{*} l o g \frac{Q^{*}}{Q}) + (J - J^{*} - J^{*} l o g \frac{J^{*}}{J}) + (L_{t} - L_{t}^{*} - L_{t}^{*} l o g \frac{L_{t}^{*}}{L_{t}}) \\ + (R - R^{*} - R^{*} l o g \frac{R^{*}}{R}) + (D - D^{*} - D^{*} l o g \frac{D^{*}}{D}) + (P - P^{*} - P^{*} l o g \frac{P^{*}}{P}) \end{matrix}$ (2.16)

Differentiating both sides concerning t yields

\begin{matrix} \frac{d L_{f}}{d t} & = & {\dot{L}}_{f} = (\frac{S - S^{*}}{S}) \dot{S} + (\frac{L - L^{*}}{L}) \dot{L} + (\frac{T - T^{*}}{T}) \dot{T} + (\frac{I - I^{*}}{I}) \dot{I} + (\frac{A_{d} - A_{d}^{*}}{A_{d}}) {\dot{A}}_{d} \\ + (\frac{I_{s n d} - I_{s n d}^{*}}{I_{s n d}}) I_{s n d} + (\frac{I_{s d} - I_{s d}^{*}}{I_{s d}}) {\dot{I}}_{s d} + (\frac{Q - Q^{*}}{Q}) \dot{Q} + (\frac{J - J^{*}}{J}) \dot{J} + (\frac{L_{t} - L_{t}^{*}}{L_{t}}) {\dot{L}}_{t} \\ + (\frac{R - R}{R}) \dot{R} + (\frac{D - D^{*}}{D}) \dot{D} + (\frac{P - P^{*}}{P}) \dot{P} \end{matrix}

(2.17)

Applying the values of $\dot{S}, \dot{L}, \dot{T}, \dot{I}, {\dot{A}}_{d}, {\dot{I}}_{s n d}, {\dot{I}}_{s d}, \dot{Q}, \dot{J}, {\dot{L}}_{t}, \dot{R}, \dot{D}, \dot{P}$ in Eq. (2.17), then we get,

\begin{matrix} \frac{d L_{f}}{d t} & = & (\frac{S - S^{*}}{S}) {- p_{d} β S (ω I + ε A_{d} + τ I_{s n d} + I_{s d} + ϕ Q + σ J) - l_{s r} S + l_{d} L - t_{r} S T + h T + η Q - α S} \\ + (\frac{L - L^{*}}{L}) (l_{s r} S - l_{d} L) + (\frac{T - T^{*}}{T}) {t_{r} S T - (h + τ_{1} + τ_{2}) T} \\ + (\frac{I - I^{*}}{I}) {p_{d} β S (ω I + ε A_{d} + τ I_{s n d} + I_{s d} + ϕ Q + σ J) - (γ + q + r_{0}) I} \\ + (\frac{A_{d} - A_{d}^{*}}{A_{d}}) {τ_{1} T - (j_{1} + λ_{1} + r_{1} + d_{1})} A_{d} \\ + (\frac{I_{s n d} - I_{s n d}^{*}}{I_{s n d}}) {γ I - (j_{2} + λ_{2} + r_{2} + d_{2}) I_{s n d}} \\ + (\frac{I_{s d} - I_{s d}^{*}}{I_{s d}}) {τ_{2} T - (j_{3} + λ_{3} + r_{3} + d_{3}) I_{s d}} \\ + (\frac{Q - Q^{*}}{Q}) {q I - (η + j_{4} + λ_{4} + r_{4} + d_{4}) Q} \\ + (\frac{J - J^{*}}{J}) {j_{1} A_{d} + j_{2} I_{s n d} + j_{3} I_{s d} + j_{4} Q - (λ_{5} + r_{5} + d_{5}) J} \\ + (\frac{L_{t} - L_{t}^{*}}{L_{t}}) {λ_{1} A_{d} + λ_{2} I_{s n d} + λ_{3} I_{s d} + λ_{4} Q + λ_{5} J - (r_{6} + d_{6}) L_{t}} \\ + (\frac{R - R^{*}}{R}) (r_{0} I + r_{1} A_{d} + r_{2} I_{s n d} + r_{3} I_{s d} + r_{4} Q + r_{5} J + r_{6} L_{t}) \\ + (\frac{D - D^{*}}{D}) (d_{1} A_{d} + d_{2} I_{s n d} + d_{3} I_{s d} + d_{4} Q + d_{5} J + d_{6} L_{t}) + (\frac{P - P^{*}}{P}) (α S) \end{matrix}

(2.18)

Putting $S = S - S^{*}, L = L - L^{*}, T = T - T^{*}, I = I - I^{*}, A_{d} = A_{d} - A_{d}^{*}, I_{s n d} = I_{s n d} - I_{s n d}^{*}, I_{s d} = I_{s d} - I_{s d}^{*}, Q = Q - Q^{*}, J = J - J^{*}, L_{t} = L_{t} - L_{t}^{*}, R = R - R^{*}, D = D - D^{*}, P = P - P^{*}$ in Eq. (2.18), then

\begin{matrix} \frac{d L_{f}}{d t} & = & (\frac{S - S^{*}}{S}) [- p_{d} β (S - S^{*}) {ω (I - I^{*}) + ε (A_{d} - A_{d}^{*}) + τ (I_{s n d} - I_{s n d}^{*}) + (I_{s d} - I_{s d}^{*}) + ϕ (Q - Q^{*}) + σ (J - J^{*})} \\ - l_{s r} (S - S^{*}) + l_{d} (L - L^{*}) - t_{r} (S - S^{*}) (T - T^{*}) + h (T - T^{*}) + η (Q - Q^{*}) - α (S - S^{*})] \\ + (\frac{L - L^{*}}{L}) {l_{s r} (S - S^{*}) - l_{d} (L - L^{*})} \\ + (\frac{T - T^{*}}{T}) {t_{r} (S - S^{*}) (T - T^{*}) - (h + τ_{1} + τ_{2}) (T - T^{*})} \\ + (\frac{I - I^{*}}{I}) [p_{d} β (S - S^{*}) {ω (I - I^{*}) + ε (A_{d} - A_{d}^{*}) + τ (I_{s n d} - I_{s n d}^{*}) + (I_{s d} - I_{s d}^{*}) + ϕ (Q - Q^{*}) + σ (J - J^{*})} - (γ + q + r_{0}) (I - I^{*})] \\ + (\frac{A_{d} - A_{d}^{*}}{A_{d}}) {τ_{1} (T - T^{*}) - (j_{1} + λ_{1} + r_{1} + d_{1}) (A_{d} - A_{d}^{*})} \\ + (\frac{I_{s n d} - I_{s n d}^{*}}{I_{s n d}}) {γ (I - I^{*}) - (j_{2} + λ_{2} + r_{2} + d_{2}) (I_{s n d} - I_{s n d}^{*})} \\ + (\frac{I_{s d} - I_{s d}^{*}}{I_{s d}}) {τ_{2} (T - T^{*}) - (j_{3} + λ_{3} + r_{3} + d_{3}) (I_{s d} - I_{s d}^{*})} \\ + (\frac{Q - Q^{*}}{Q}) {q (I - I^{*}) - (η + j_{4} + λ_{4} + r_{4} + d_{4}) (Q - Q^{*})} \\ + (\frac{J - J^{*}}{J}) {j_{1} (A_{d} - A_{d}^{*}) + j_{2} (I_{s n d} - I_{s n d}^{*}) + j_{3} (I_{s d} - I_{s d}^{*}) + j_{4} (Q - Q^{*}) - (λ_{5} + r_{5} + d_{5}) (J - J^{*})} \\ + (\frac{L_{t} - L_{t}^{*}}{L_{t}}) {λ_{1} (A_{d} - A_{d}^{*}) + λ_{2} (I_{s n d} - I_{s n d}^{*}) + λ_{3} I_{s d} + λ_{4} (Q - Q^{*}) + λ_{5} (J - J^{*}) - (r_{6} + d_{6}) (L_{t} - L_{t}^{*})} \\ + (\frac{R - R^{*}}{R}) {r_{0} (I - I^{*}) + r_{1} (A_{d} - A_{d}^{*}) + r_{2} (I_{s n d} - I_{s n d}^{*}) + r_{3} (I_{s d} - I_{s d}^{*}) + r_{4} (Q - Q^{*}) + r_{5} (J - J^{*}) + r_{6} (L_{t} - L_{t}^{*})} \\ + (\frac{D - D^{*}}{D}) {d_{1} (A_{d} - A_{d}^{*}) + d_{2} (I_{s n d} - I_{s n d}^{*}) + d_{3} (I_{s d} - I_{s d}^{*}) + d_{4} (Q - Q^{*}) + d_{5} (J - J^{*}) + d_{6} (L_{t} - L_{t}^{*})} \\ + (\frac{P - P^{*}}{P}) {α (S - S^{*})} \end{matrix}

(2.19)

For avoiding complexity, the above equation can be written in the following form

\frac{d L_{f}}{d t} = Π - Ω

(2.20)

where

\begin{matrix} Π & = & p_{d} β (ω I^{*} + ε A_{d}^{*} + τ I_{s n d}^{*} + I_{s d}^{*} + ϕ Q^{*} + σ J^{*}) \frac{{(S - S^{*})}^{2}}{S} + l_{d} L + l_{d} \frac{S^{*}}{S} L^{*} \\ + t_{r} \frac{{(S - S^{*})}^{2}}{S} T^{*} + h T + h \frac{S^{*}}{S} T^{*} + η Q + η \frac{S^{*}}{S} Q^{*} + l_{s r} S + l_{s r} \frac{L^{*}}{L} S^{*} + t_{r} \frac{{(T - T^{*})}^{2}}{T} S \\ + (p_{d} β S + p_{d} β \frac{I^{*}}{I} S^{*}) (ω I + ε A_{d} + τ I_{s n d} + I_{s d} + ϕ Q + σ J) + τ_{1} T \\ + τ_{1} \frac{A_{d}^{*}}{A_{d}} T^{*} + γ I + γ \frac{I_{s n d}^{*}}{I_{s n d}} I^{*} + τ_{2} T + τ_{2} \frac{I_{s d}^{*}}{I_{s d}} T^{*} + q I + q \frac{Q^{*}}{Q} I^{*} + j_{1} A_{d} + j_{2} I_{s n d} \\ + j_{3} I_{s d} + j_{4} Q + j_{1} \frac{J^{*}}{J} A_{d}^{*} + j_{2} \frac{J^{*}}{J} I_{s n d}^{*} + j_{3} \frac{J^{*}}{J} I_{s d}^{*} + j_{4} \frac{J^{*}}{J} Q^{*} + λ_{1} A_{d} + λ_{2} I_{s n d} \\ + λ_{3} I_{s d} + λ_{4} Q + λ_{5} J + λ_{1} \frac{L_{t}^{*}}{L_{t}} A_{d}^{*} + λ_{2} \frac{L_{t}^{*}}{L_{t}} I_{s n d}^{*} + λ_{3} \frac{L_{t}^{*}}{L_{t}} I_{s d}^{*} + λ_{4} \frac{L_{t}^{*}}{L_{t}} Q^{*} \\ + λ_{5} \frac{L_{t}^{*}}{L_{t}} J^{*} + r_{0} I + r_{1} A_{d} + r_{2} I_{s n d} + r_{3} I_{s d} + r_{4} Q + r_{5} J \\ + r_{6} L_{t} + r_{0} \frac{R^{*}}{R} I^{*} + r_{1} \frac{R^{*}}{R} A_{d}^{*} + r_{2} \frac{R^{*}}{R} I_{s n d}^{*} + r_{3} \frac{R^{*}}{R} I_{s d}^{*} + r_{4} \frac{R^{*}}{R} Q^{*} + r_{5} \frac{R^{*}}{R} J^{*} + r_{6} \frac{R^{*}}{R} L_{t}^{*} + d_{1} A_{d} + d_{2} I_{s n d} \\ + d_{3} I_{s d} + d_{4} Q + d_{5} J + d_{6} L_{t} + d_{1} \frac{D^{*}}{D} A_{d}^{*} + d_{2} \frac{D^{*}}{D} I_{s n d}^{*} + d_{3} \frac{D^{*}}{D} I_{s d}^{*} + d_{4} \frac{D^{*}}{D} Q^{*} \\ + d_{5} \frac{D^{*}}{D} J^{*} + d_{6} \frac{D^{*}}{D} L_{t}^{*} + α S + \frac{P^{*}}{P} α S^{*} \end{matrix}

and

\begin{matrix} Ω & = & p_{d} β (ω I + ε A_{d} + τ I_{s n d} + I_{s d} + ϕ Q + σ J) \frac{{(S - S^{*})}^{2}}{S} + l_{s r} \frac{{(S - S^{*})}^{2}}{S} + l_{d} L^{*} + l_{d} \frac{S^{*}}{S} L \\ + t_{r} \frac{{(S - S^{*})}^{2}}{S} T + h T^{*} + h \frac{S^{*}}{S} T + η Q^{*} + η \frac{S^{*}}{S} Q + α \frac{{(S - S^{*})}^{2}}{S} + l_{s r} S^{*} + l_{s r} \frac{L^{*}}{L} S \\ + l_{d} \frac{{(L - L^{*})}^{2}}{L} + t_{r} \frac{{(T - T^{*})}^{2}}{T} S^{*} + (h + τ_{1} + τ_{2}) \frac{{(T - T^{*})}^{2}}{T} \\ + (p_{d} β S^{*} + p_{d} β \frac{I^{*}}{I} S) (ω I^{*} + ε A_{d}^{*} + τ I_{s n d}^{*} + I_{s d}^{*} + ϕ Q^{*} + σ J^{*}) + (γ + q + r_{0}) \frac{{(I - I^{*})}^{2}}{I} \\ + τ_{1} T^{*} + τ_{1} \frac{A_{d}^{*}}{A_{d}} T + (j_{1} + λ_{1} + r_{1} + d_{1}) \frac{{(A_{d} - A_{d}^{*})}^{2}}{A_{d}} + γ I^{*} + γ \frac{I_{s n d}^{*}}{I_{s n d}} I \\ + (j_{2} + λ_{2} + r_{2} + d_{2}) \frac{{(I_{s n d} - I_{s n d}^{*})}^{2}}{I_{s n d}} + τ_{2} T^{*} + τ_{2} \frac{I_{s d}^{*}}{I_{s d}} T \\ + (j_{3} + λ_{3} + r_{3} + d_{3}) \frac{{(I_{s d} - I_{s d}^{*})}^{2}}{I_{s d}} + q I^{*} + q \frac{Q^{*}}{Q} I \\ + (η + j_{4} + λ_{4} + r_{4} + d_{4}) \frac{{(Q - Q^{*})}^{2}}{Q} + j_{1} A_{d}^{*} + j_{2} I_{s n d}^{*} + j_{3} I_{s d}^{*} + j_{4} Q^{*} \\ + j_{1} \frac{J^{*}}{J} A_{d} + j_{2} \frac{J^{*}}{J} I_{s n d} + j_{3} \frac{J^{*}}{J} I_{s d} + j_{4} \frac{J^{*}}{J} Q + (λ_{5} + r_{5} + d_{5}) \frac{{(J - J^{*})}^{2}}{J} \\ + λ_{1} A_{d}^{*} + λ_{2} I_{s n d}^{*} + λ_{3} I_{s d}^{*} + λ_{4} Q^{*} + λ_{5} J^{*} + λ_{1} \frac{L_{t}^{*}}{L_{t}} A_{d} + λ_{2} \frac{L_{t}^{*}}{L_{t}} I_{s n d} \\ + λ_{3} \frac{L_{t}^{*}}{L_{t}} I_{s d} + λ_{4} \frac{L_{t}^{*}}{L_{t}} Q + λ_{5} \frac{L_{t}^{*}}{L_{t}} J + (r_{6} + d_{6}) \frac{{(L_{t} - L_{t}^{*})}^{2}}{L_{t}} + r_{0} I^{*} + r_{1} A_{d}^{*} \\ + r_{2} I_{s n d}^{*} + r_{3} I_{s d}^{*} + r_{4} Q^{*} + r_{5} J^{*} + r_{6} L_{t}^{*} + r_{0} \frac{R^{*}}{R} + r_{1} \frac{R^{*}}{R} A_{d} + r_{2} \frac{R^{*}}{R} I_{s n d} \\ + r_{3} \frac{R^{*}}{R} I_{s d} + r_{4} \frac{R^{*}}{R} Q + r_{5} \frac{R^{*}}{R} J + r \frac{R^{*}}{R} L_{t} + d_{1} A_{d}^{*} + d_{2} I_{s n d}^{*} \\ + d_{3} I_{s d}^{*} + d_{4} Q^{*} + d_{5} J^{*} + d_{6} L_{t}^{*} + d_{1} \frac{D^{*}}{D} A_{d} + d_{2} \frac{D^{*}}{D} I_{s n d} \\ + d_{3} \frac{D^{*}}{D} I_{s d} + d_{4} \frac{D^{*}}{D} Q + d_{5} \frac{D^{*}}{D} J + d_{6} \frac{D^{*}}{D} L_{t} + α S^{*} + \frac{P^{*}}{P} α S \end{matrix}

Taking everything into consideration, if $Π < Ω,$ then $\frac{d L_{f}}{d t} < 0 .$ Therefore, when $S = S^{*}, L = L^{*}, T = T^{*}, I = I^{*}, A_{d} = A_{d}^{*}, I_{s n d} = I_{s n d}^{*}, I_{s d} = I_{s d}^{*}, Q = Q^{*}, J = J^{*}, L_{t} = L_{t}^{*}, R = R^{*}, D = D^{*}, P = P^{*}$ Eq. (2.20) can be written as

0 = Π - Ω

\Rightarrow \frac{d L_{f}}{d t} = 0

(2.21)

Thus, the most prominent compact invariant set for the proposed model

{(S^{*}, L^{*}, T^{*}, I^{*}, A_{d}^{*}, I_{s n d}^{*}, I_{s d}^{*}, Q^{*}, J^{*}, L_{t}^{*}, R^{*}, D^{*}, P^{*}) \in Γ : \frac{d L_{f}}{d t} = 0}

(2.22)

is the endemic equilibrium of the suggested model at the point ${E^{*}}$ . It follows that $E^{*}$ is globally asymptotically stable in $Γ$ if $Π < Ω$ according to Lasalle's invariance.

2.4. The second derivative of the Lyapunov function

The first derivative of the Lyapunov function is used to assess the global stability of endemic equilibrium points. The first derivative analysis provides essential information that the second derivative analysis may supplement without loss of generality. For example, the second derivative of these Lyapunov functions tells us the curvature according to its sign, but the first derivative offers us information on the disease's progress. We are confident that its second derivative will provide further insights.

\begin{matrix} \frac{d {\dot{L}}_{f}}{d t} & = & \frac{d}{d t} {(1 - \frac{S^{*}}{S}) \dot{S} + (1 - \frac{L^{*}}{L}) \dot{L} + (1 - \frac{T^{*}}{T}) \dot{T} + (1 - \frac{I^{*}}{I}) \dot{I} + (1 - \frac{A_{d}^{*}}{A_{d}}) {\dot{A}}_{d} + (1 - \frac{I_{s n d}^{*}}{I_{s n d}}) {\dot{I}}_{s n d} + (1 - \frac{I_{s d}^{*}}{I_{s d}}) {\dot{I}}_{s d} + (1 - \frac{Q^{*}}{Q}) \dot{Q} \\ + (1 - \frac{J^{*}}{J}) \dot{J} + (1 - \frac{L_{t}^{*}}{L_{t}}) {\dot{L}}_{t} + (1 - \frac{R^{*}}{R}) \dot{R} + (1 - \frac{D^{*}}{D}) \dot{D} + (1 - \frac{P^{*}}{P}) \dot{P}} \\ = & {(\frac{\dot{S}}{S})}^{2} S^{*} + {(\frac{\dot{L}}{L})}^{2} L^{*} + {(\frac{\dot{T}}{T})}^{2} T^{*} + {(\frac{\dot{I}}{I})}^{2} I^{*} + {(\frac{{\dot{A}}_{d}}{A_{d}})}^{2} A_{d}^{*} + {(\frac{{\dot{I}}_{s n d}}{I_{s n d}})}^{2} I_{s n d}^{*} + {(\frac{{\dot{I}}_{s d}}{I_{s d}})}^{2} I_{s d}^{*} \\ + {(\frac{\dot{Q}}{Q})}^{2} Q^{*} + {(\frac{\dot{J}}{J})}^{2} J^{*} + {(\frac{{\dot{L}}_{t}}{L_{t}})}^{2} L_{t}^{*} + {(\frac{\dot{R}}{R})}^{2} R^{*} + {(\frac{\dot{D}}{D})}^{2} D^{*} + {(\frac{\dot{P}}{P})}^{2} P^{*} + (1 - \frac{S^{*}}{S}) \ddot{S} \\ + (1 - \frac{L^{*}}{L}) \ddot{L} + (1 - \frac{T^{*}}{T}) \ddot{T} + (1 - \frac{I^{*}}{I}) \ddot{I} + (1 - \frac{A_{d}^{*}}{A_{d}}) {\ddot{A}}_{d} + (1 - \frac{I_{s n d}^{*}}{I_{s n d}}) {\ddot{I}}_{s n d} \\ + (1 - \frac{I_{s d}^{*}}{I_{s d}}) {\ddot{I}}_{s d} + (1 - \frac{Q^{*}}{Q}) \ddot{Q} + (1 - \frac{J^{*}}{J}) \ddot{J} + (1 - \frac{L_{t}^{*}}{L_{t}}) {\ddot{L}}_{t} \\ + (1 - \frac{R^{*}}{R}) \ddot{R} + (1 - \frac{D^{*}}{D}) \ddot{D} + (1 - \frac{P^{*}}{P}) \ddot{P} \end{matrix}

(2.23)

Here,

\ddot{S} = - p_{d} β \dot{S} (ω I + ε A_{d} + τ I_{s n d} + I_{s d} + ϕ Q + σ J) - p_{d} β S (ω \dot{I} + ε {\dot{A}}_{d} + τ {\dot{I}}_{s n d} + {\dot{I}}_{s d} + ϕ \dot{Q} + σ \dot{J}) - l_{s r} \dot{S} + l_{d} \dot{L} - t_{r} \dot{S} T - t_{r} S \dot{T} + h \dot{T} + η \dot{Q} - α \dot{S}

\ddot{L} = l_{s r} \dot{S} - l_{d} \dot{L}

\ddot{T} = t_{r} \dot{S} T + t_{r} S \dot{T} - (h + τ_{1} + τ_{2}) \dot{T}

\ddot{I} = p_{d} β \dot{S} (ω I + ε A_{d} + τ I_{s n d} + I_{s d} + ϕ Q + σ J) + p_{d} β S (ω \dot{I} + ε {\dot{A}}_{d} + τ {\dot{I}}_{s n d} + {\dot{I}}_{s d} + ϕ \dot{Q} + σ \dot{J}) - (γ + q + r_{0}) \dot{I}

{\ddot{A}}_{d} = τ_{1} \dot{T} - (j_{1} + λ_{1} + r_{1} + d_{1}) {\dot{A}}_{d}

{\ddot{I}}_{s n d} = γ \dot{I} - (j_{2} + λ_{2} + r_{2} + d_{2}) {\dot{I}}_{s n d}

{\ddot{I}}_{s d} = τ_{2} \dot{T} - (j_{3} + λ_{3} + r_{3} + d_{3}) {\dot{I}}_{s d}

\ddot{Q} = q \dot{I} - (η + j_{4} + λ_{4} + r_{4} + d_{4}) \dot{Q}

\ddot{J} = j_{1} {\dot{A}}_{d} + j_{2} {\dot{I}}_{s n d} + j_{3} {\dot{I}}_{s d} + j_{4} \dot{Q} - (λ_{5} + r_{5} + d_{5}) \dot{J}

{\ddot{L}}_{t} = λ_{1} {\dot{A}}_{d} + λ_{2} {\dot{I}}_{s n d} + λ_{3} {\dot{I}}_{s d} + λ_{4} \dot{Q} + λ_{5} \dot{J} - (r_{6} + d_{6}) {\dot{L}}_{t}

\ddot{R} = r_{0} \dot{I} + r_{1} {\dot{A}}_{d} + r_{2} {\dot{I}}_{s n d} + r_{3} {\dot{I}}_{s d} + r_{4} \dot{Q} + r_{5} \dot{J} + r_{6} {\dot{L}}_{t}

\ddot{D} = d_{1} {\dot{A}}_{d} + d_{2} {\dot{I}}_{s n d} + d_{3} {\dot{I}}_{s d} + d_{4} \dot{Q} + d_{5} \dot{J} + d_{6} {\dot{L}}_{t}

\ddot{P} = α \dot{S}

Thus,

\begin{matrix} \frac{d {\dot{L}}_{f}}{d t} & = & {(\frac{\dot{S}}{S})}^{2} S^{*} + {(\frac{\dot{L}}{L})}^{2} L^{*} + {(\frac{\dot{T}}{T})}^{2} T^{*} + {(\frac{\dot{I}}{I})}^{2} I^{*} + {(\frac{{\dot{A}}_{d}}{A_{d}})}^{2} A_{d}^{*} + {(\frac{{\dot{I}}_{s n d}}{I_{s n d}})}^{2} I_{s n d}^{*} + {(\frac{{\dot{I}}_{s d}}{I_{s d}})}^{2} I_{s d}^{*} \\ + {(\frac{\dot{Q}}{Q})}^{2} Q^{*} + {(\frac{\dot{J}}{J})}^{2} J^{*} + {(\frac{{\dot{L}}_{t}}{L_{t}})}^{2} L_{t}^{*} + {(\frac{\dot{R}}{R})}^{2} R^{*} + {(\frac{\dot{D}}{D})}^{2} D^{*} + {(\frac{\dot{P}}{P})}^{2} P^{*} \\ + (1 - \frac{S^{*}}{S}) {- p_{d} β \dot{S} (ω I + ε A_{d} + τ I_{s n d} + I_{s d} + ϕ Q + σ J) \\ - p_{d} β S (ω \dot{I} + ε {\dot{A}}_{d} + τ {\dot{I}}_{s n d} + {\dot{I}}_{s d} + ϕ \dot{Q} + σ \dot{J}) - l_{s r} \dot{S} + l_{d} \dot{L} - t_{r} \dot{S} T \\ - t_{r} S \dot{T} + h \dot{T} + η \dot{Q} - α \dot{S}} + (1 - \frac{L^{*}}{L}) (l_{s r} \dot{S} - l_{d} \dot{L}) \\ + (1 - \frac{T^{*}}{T}) (t_{r} \dot{S} T + t_{r} S \dot{T} - (h + τ_{1} + τ_{2}) \dot{T}) \\ + (1 - \frac{I^{*}}{I}) {p_{d} β \dot{S} (ω I + ε A_{d} + τ I_{s n d} + I_{s d} + ϕ Q + σ J) \\ + p_{d} β S (ω \dot{I} + ε {\dot{A}}_{d} + τ {\dot{I}}_{s n d} + {\dot{I}}_{s d} + ϕ \dot{Q} + σ \dot{J}) - (γ + q + r_{0}) \dot{I}} \\ + (1 - \frac{A_{d}^{*}}{A_{d}}) {τ_{1} \dot{T} - (j_{1} + λ_{1} + r_{1} + d_{1}) {\dot{A}}_{d}} \\ + (1 - \frac{I_{s n d}^{*}}{I_{s n d}}) {γ \dot{I} - (j_{2} + λ_{2} + r_{2} + d_{2}) {\dot{I}}_{s n d}} \\ + (1 - \frac{I_{s d}^{*}}{I_{s d}}) {τ_{2} \dot{T} - (j_{3} + λ_{3} + r_{3} + d_{3}) {\dot{I}}_{s d}} \\ + (1 - \frac{Q^{*}}{Q}) {q \dot{I} - (η + j_{4} + λ_{4} + r_{4} + d_{4}) \dot{Q}} \\ + (1 - \frac{J^{*}}{J}) {j_{1} {\dot{A}}_{d} + j_{2} {\dot{I}}_{s n d} + j_{3} {\dot{I}}_{s d} + j_{4} \dot{Q} - (λ_{5} + r_{5} + d_{5}) \dot{J}} \\ + (1 - \frac{L_{t}^{*}}{L_{t}}) {λ_{1} {\dot{A}}_{d} + λ_{2} {\dot{I}}_{s n d} + λ_{3} {\dot{I}}_{s d} + λ_{4} \dot{Q} + λ_{5} \dot{J} - (r_{6} + d_{6}) {\dot{L}}_{t}} \\ + (1 - \frac{R^{*}}{R}) {r_{0} \dot{I} + r_{1} {\dot{A}}_{d} + r_{2} {\dot{I}}_{s n d} + r_{3} {\dot{I}}_{s d} + r_{4} \dot{Q} + r_{5} \dot{J} + r_{6} {\dot{L}}_{t}} \\ + (1 - \frac{D^{*}}{D}) {d_{1} {\dot{A}}_{d} + d_{2} {\dot{I}}_{s n d} + d_{3} {\dot{I}}_{s d} + d_{4} \dot{Q} + d_{5} \dot{J} + d_{6} {\dot{L}}_{t}} + (1 - \frac{P^{*}}{P}) α \dot{S} \end{matrix}

(2.24)

and

\begin{matrix} \frac{d^{2} L_{f}}{d t^{2}} & = & \dot{Π} (S, L, T, I, A_{d}, I_{s n d}, I_{s d}, Q, J, L_{t}, R, D, P) \\ + (1 - \frac{S^{*}}{S}) {- p_{d} β \dot{S} (ω I + ε A_{d} + τ I_{s n d} + I_{s d} + ϕ Q + σ J) \\ - p_{d} β S (ω \dot{I} + ε {\dot{A}}_{d} + τ {\dot{I}}_{s n d} + {\dot{I}}_{s d} + ϕ \dot{Q} + σ \dot{J}) - l_{s r} \dot{S} + l_{d} \dot{L} - t_{r} \dot{S} T \\ - t_{r} S \dot{T} + h \dot{T} + η \dot{Q} - α \dot{S}} + (1 - \frac{L^{*}}{L}) (l_{s r} \dot{S} - l_{d} \dot{L}) \\ + (1 - \frac{T^{*}}{T}) (t_{r} \dot{S} T + t_{r} S \dot{T} - (h + τ_{1} + τ_{2}) \dot{T}) \\ + (1 - \frac{I^{*}}{I}) {p_{d} β \dot{S} (ω I + ε A_{d} + τ I_{s n d} + I_{s d} + ϕ Q + σ J) \\ + p_{d} β S (ω \dot{I} + ε {\dot{A}}_{d} + τ {\dot{I}}_{s n d} + {\dot{I}}_{s d} + ϕ \dot{Q} + σ \dot{J}) - (γ + q + r_{0}) \dot{I}} \\ + (1 - \frac{A_{d}^{*}}{A_{d}}) {τ_{1} \dot{T} - (j_{1} + λ_{1} + r_{1} + d_{1}) {\dot{A}}_{d}} \\ + (1 - \frac{I_{s n d}^{*}}{I_{s n d}}) {γ \dot{I} - (j_{2} + λ_{2} + r_{2} + d_{2}) {\dot{I}}_{s n d}} \\ + (1 - \frac{I_{s d}^{*}}{I_{s d}}) {τ_{2} \dot{T} - (j_{3} + λ_{3} + r_{3} + d_{3}) {\dot{I}}_{s d}} \\ + (1 - \frac{Q^{*}}{Q}) {q \dot{I} - (η + j_{4} + λ_{4} + r_{4} + d_{4}) \dot{Q}} \\ + (1 - \frac{J^{*}}{J}) {j_{1} {\dot{A}}_{d} + j_{2} {\dot{I}}_{s n d} + j_{3} {\dot{I}}_{s d} + j_{4} \dot{Q} - (λ_{5} + r_{5} + d_{5}) \dot{J}} \\ + (1 - \frac{L_{t}^{*}}{L_{t}}) {λ_{1} {\dot{A}}_{d} + λ_{2} {\dot{I}}_{s n d} + λ_{3} {\dot{I}}_{s d} + λ_{4} \dot{Q} + λ_{5} \dot{J} - (r_{6} + d_{6}) {\dot{L}}_{t}} \\ + (1 - \frac{R *}{R}) {r_{0} \dot{I} + r_{1} {\dot{A}}_{d} + r_{2} {\dot{I}}_{s n d} + r_{3} {\dot{I}}_{s d} + r_{4} \dot{Q} + r_{5} \dot{J} + r_{6} {\dot{L}}_{t}} \\ + (1 - \frac{D *}{D}) {d_{1} {\dot{A}}_{d} + d_{2} {\dot{I}}_{s n d} + d_{3} {\dot{I}}_{s d} + d_{4} \dot{Q} + d_{5} \dot{J} + d_{6} {\dot{L}}_{t}} + (1 - \frac{P *}{P}) α \dot{S} \end{matrix}

(2.25)

Now substitute $\dot{S}, \dot{L}, \dot{T}, \dot{I}, {\dot{A}}_{d}, {\dot{I}}_{s n d}, {\dot{I}}_{s d}, \dot{Q}, \dot{J}, {\dot{L}}_{t}, \dot{R}, \dot{D}, \dot{P}$ with their respective formulas and combine positive and negative components, we have

\frac{d^{2} L_{f}}{d t^{2}} = Σ_{1} - Σ_{2}

(2.26)

As a result, it is clear that, if $\sum_{1} > \sum_{2}$ then $\frac{d^{2} L_{f}}{d t^{2}} > 0$

if \sum_{1} < \sum_{2} then \frac{d^{2} L_{f}}{d t^{2}} < 0

(2.27)

if $\sum_{1} = \sum_{2}$ then $\frac{d^{2} L_{f}}{d t^{2}} = 0 .$

After that, the interpretation associated with the second-order sign is as follows.

2.5. Existence and uniqueness

This section presents a detailed analysis of the existence and uniqueness of the system of equations that describes classical calculus's survival. The following theorem must be proved to do this.

Theorem 2

Assume that there exists a positive constant $ϑ_{i}, {\bar{ϑ}}_{i}$ such that

(i)
$\forall i \in {1, 2, 3, . . ., 13}$
${| f_{i} (x_{i}, t) - f_{i} (x_{i}^{'}, t) |}^{2} \leq ϑ_{i} {| x_{i} - x_{i}^{'} |}^{2} .$ (2.28)

(ii)
$\forall (x, t) \in R^{13} \times (0, T)$
${| f_{i} (x_{i}, t) |}^{2} \leq {\bar{ϑ}}_{i} (1 + {| x_{i} |}^{2}) .$ (2.29)

The proposed model can be written as

\frac{d S (t)}{d t} = - p_{d} β S (t) {ω I (t) + ε A_{d} (t) + τ I_{s n d} (t) + I_{s d} (t) + ϕ Q (t) + σ J (t)} - l_{s r} S (t) + l_{d} L (t)

- t_{r} S (t) T (t) + h T (t) + η Q (t) - α S (t) = f_{1} (t, S, L, T, I, A_{d}, I_{s n d}, I_{s d}, Q, J, L_{t}, R, D, P)

\frac{d L (t)}{d t} = l_{s r} S (t) - l_{d} L (t) = f_{2} (t, S, L, T, I, A_{d}, I_{s n d}, I_{s d}, Q, J, L_{t}, R, D, P)

\frac{d T (t)}{d t} = t_{r} S (t) T (t) - (h + τ_{1} + τ_{2}) T (t) = f_{3} (t, S, L, T, I, A_{d}, I_{s n d}, I_{s d}, Q, J, L_{t}, R, D, P)

\frac{d I (t)}{d t} = p_{d} β S (t) {ω I (t) + ε A_{d} (t) + τ I_{s n d} (t) + I_{s d} (t) + ϕ Q (t) + σ J (t)} - (γ + q + r_{0}) I (t) = f_{4} (t, S, L, T, I, A_{d}, I_{s n d}, I_{s d}, Q, J, L_{t}, R, D, P)

\frac{d A_{d} (t)}{d t} = τ_{1} T (t) - (j_{1} + λ_{1} + r_{1} + d_{1}) A_{d} (t) = f_{5} (t, S, L, T, I, A_{d}, I_{s n d}, I_{s d}, Q, J, L_{t}, R, D, P)

\frac{d I_{s n d} (t)}{d t} = γ I (t) - (j_{2} + λ_{2} + r_{2} + d_{2}) I_{s n d} (t) = f_{6} (t, S, L, T, I, A_{d}, I_{s n d}, I_{s d}, Q, J, L_{t}, R, D, P)

\frac{d I_{s d} (t)}{d t} = τ_{2} T (t) - (j_{3} + λ_{3} + r_{3} + d_{3}) I_{s d} (t) = f_{7} (t, S, L, T, I, A_{d}, I_{s n d}, I_{s d}, Q, J, L_{t}, R, D, P)

\frac{d Q (t)}{d t} = q I (t) - (η + j_{4} + λ_{4} + r_{4} + d_{4}) Q (t) = f_{8} (t, S, L, T, I, A_{d}, I_{s n d}, I_{s d}, Q, J, L_{t}, R, D, P)

\frac{d J (t)}{d t} = j_{1} A_{d} (t) + j_{2} I_{s n d} (t) + j_{3} I_{s d} (t) + j_{4} Q (t) - (λ_{5} + r_{5} + d_{5}) J (t) = f_{9} (t, S, L, T, I, A_{d}, I_{s n d}, I_{s d}, Q, J, L_{t}, R, D, P)

\frac{d L_{t} (t)}{d t} = λ_{1} A_{d} (t) + λ_{2} I_{s n d} (t) + λ_{3} I_{s d} (t) + λ_{4} Q (t) + λ_{5} J (t) - (r_{6} + d_{6}) L_{t} (t) = f_{10} (t, S, L, T, I, A_{d}, I_{s n d}, I_{s d}, Q, J, L_{t}, R, D, P)

\frac{d R (t)}{d t} = r_{0} I (t) + r_{1} A_{d} (t) + r_{2} I_{s n d} (t) + r_{3} I_{s d} (t) + r_{4} Q (t) + r_{5} J (t) + r_{6} L_{t} (t) = f_{11} (t, S, L, T, I, A_{d}, I_{s n d}, I_{s d}, Q, J, L_{t}, R, D, P)

\frac{d D (t)}{d t} = d_{1} A_{d} (t) + d_{2} I_{s n d} (t) + d_{3} I_{s d} (t) + d_{4} Q (t) + d_{5} J (t) + d_{6} L_{t} (t) = f_{12} (t, S, L, T, I, A_{d}, I_{s n d}, I_{s d}, Q, J, L_{t}, R, D, P)

\frac{d P (t)}{d t} = α S (t) = f_{13} (t, S, L, T, I, A_{d}, I_{s n d}, I_{s d}, Q, J, L_{t}, R, D, P)

Firstly, for the function $f_{1} (t, S, L, T, I, A_{d}, I_{s n d}, I_{s d}, Q, J, L_{t}, R, D, P)$ we will prove that

| f_{1} (S_{1}, t) - f_{1} (S_{2}, t) |^{2} \leq ϑ_{1} {| S_{1} - S_{2} |}^{2} .

(2.30)

Now

| f_{1} (S_{1}, t) - f_{1} (S_{2}, t) |^{2} = | - p_{d} β (ω I + ε A_{d} + τ I_{s n d} + I_{s d} + ϕ Q + σ J) (S_{1} - S_{2}) - l_{s r} (S_{1} - S_{2}) - t_{r} T (S_{1} - S_{2}) - α (S_{1} - S_{2}) |^{2}

= | {- p_{d} β (ω I + ε A_{d} + τ I_{s n d} + I_{s d} + ϕ Q + σ J) - l_{s r} - t_{r} T - α} (S_{1} - S_{2}) |^{2}

\leq {2 p_{d}^{2} β^{2} (ω^{2} {| I |}^{2} + ε^{2} {| A_{d} |}^{2} + τ^{2} {| I_{s n d} |}^{2} + {| I_{s d} |}^{2} + ϕ^{2} {| Q |}^{2} + σ^{2} {| J |}^{2}) + 2 l_{s r}^{2} + 2 t_{r}^{2} {| T |}^{2} + 2 α^{2}} {| S_{1} - S_{2} |}^{2}

\begin{matrix} \leq & {2 p_{d}^{2} β^{2} (ω^{2} sup_{0 \leq t \leq T} {| I |}^{2} + ε^{2} sup_{0 \leq t \leq T} {| A_{d} |}^{2} + τ^{2} sup_{0 \leq t \leq T} {| I_{s n d} |}^{2} + sup_{0 \leq t \leq T} {| I_{s d} |}^{2} + ϕ^{2} sup_{0 \leq t \leq T} {| Q |}^{2} + σ^{2} sup_{0 \leq t \leq T} {| J |}^{2}) \\ + 2 l_{s r}^{2} + 2 t_{r}^{2} sup_{0 \leq t \leq T} {| T (t) |}^{2} + 2 α^{2}} {| S_{1} - S_{2} |}^{2} \end{matrix}

\leq {2 p_{d}^{2} β^{2} (ω^{2} {| | I (t) | |}_{\infty}^{2} + ε^{2} {| | A_{d} (t) | |}_{\infty}^{2} + τ^{2} {| | I_{s n d} (t) | |}_{\infty}^{2} + {| | I_{s d} (t) | |}_{\infty}^{2} + ϕ^{2} {| | Q (t) | |}_{\infty}^{2} + σ^{2} {| | J (t) | |}_{\infty}^{2}) + 2 l_{s r}^{2} + 2 t_{r}^{2} {| | T (t) | |}_{\infty}^{2} + 2 α^{2}} {| S_{1} - S_{2} |}^{2}

\leq ϑ_{1} {| S_{1} - S_{2} |}^{2} .

where, $ϑ_{1} = 2 p_{d}^{2} β^{2} (ω^{2} {| | I (t) | |}_{\infty}^{2} + ε^{2} | | A_{d} (t) | |_{\infty}^{2} + τ^{2} | | I_{s n d} (t) | |_{\infty}^{2} + | | I_{s d} (t) | |_{\infty}^{2} + ϕ^{2} {| | Q (t) | |}_{\infty}^{2} + σ^{2} {| | J (t) | |}_{\infty}^{2}) + 2 l_{s r}^{2} + 2 t_{r}^{2} {| | T (t) | |}_{\infty}^{2} + 2 α^{2} .$

Analogously we can prove that the remaining compartments hold the above inequality.

Secondly, we will prove that

| f_{1} (S, t) |^{2} \leq {\bar{ϑ}}_{1} (1 + {| S |}^{2}) .

(2.31)

Then

\begin{matrix} | f_{1} (S, t) |^{2} = | - p_{d} β (ω I + ε A_{d} + τ I_{s n d} + I_{s d} + ϕ Q + σ J) S - l_{s r} S - t_{r} T S - α S + l_{d} L + h T + η Q |^{2} \\ = & | {- p_{d} β (ω I + ε A_{d} + τ I_{s n d} + I_{s d} + ϕ Q + σ J) - l_{s r} - t_{r} T - α} S + l_{d} L + h T + η Q |^{2} \\ \leq & {2 p_{d}^{2} β^{2} (ω^{2} {| I |}^{2} + ε^{2} {| A_{d} |}^{2} + τ^{2} {| I_{s n d} |}^{2} + {| I_{s d} |}^{2} + ϕ^{2} {| Q |}^{2} + σ^{2} {| J |}^{2}) + 2 l_{s r}^{2} + 2 t_{r}^{2} {| T |}^{2} + 2 α^{2}} {| S |}^{2} + 2 l_{d}^{2} {| L |}^{2} + 2 h^{2} {| T |}^{2} + 2 η^{2} {| Q |}^{2} \\ \leq & {2 p_{d}^{2} β^{2} (ω^{2} sup_{0 \leq t \leq T} {| I |}^{2} + ε^{2} sup_{0 \leq t \leq T} {| A_{d} |}^{2} + τ^{2} sup_{0 \leq t \leq T} {| I_{s n d} |}^{2} + sup_{0 \leq t \leq T} {| I_{s d} |}^{2} + ϕ^{2} sup_{0 \leq t \leq T} {| Q |}^{2} + σ^{2} sup_{0 \leq t \leq T} {| J |}^{2}) + 2 l_{s r}^{2} + 2 t_{r}^{2} sup_{0 \leq t \leq T} {| T (t) |}^{2} + 2 α^{2}} {| S |}^{2} \\ + 2 l_{d}^{2} sup_{0 \leq t \leq T} {| L |}^{2} + 2 h^{2} sup_{0 \leq t \leq T} {| T |}^{2} + 2 η^{2} sup_{0 \leq t \leq T} {| Q |}^{2} \\ \leq & {2 p_{d}^{2} β^{2} (ω^{2} {| | I (t) | |}_{\infty}^{2} + ε^{2} {| | A_{d} (t) | |}_{\infty}^{2} + τ^{2} {| | I_{s n d} (t) | |}_{\infty}^{2} + {| | I_{s d} (t) | |}_{\infty}^{2} + ϕ^{2} {| | Q (t) | |}_{\infty}^{2} + σ^{2} {| | J (t) | |}_{\infty}^{2}) + 2 l_{s r}^{2} + 2 t_{r}^{2} {| | T (t) | |}_{\infty}^{2} + 2 α^{2}} {| S |}^{2} \\ + 2 l_{d}^{2} {| | L (t) | |}_{\infty}^{2} + 2 h^{2} {| | T (t) | |}_{\infty}^{2} + 2 η^{2} {| | Q (t) | |}_{\infty}^{2} \\ \leq & {\bar{ϑ}}_{1} (1 + {| S |}^{2}) . \end{matrix}

such that

\begin{matrix} {2 p_{d}^{2} β^{2} (ω^{2} {| | I (t) | |}_{\infty}^{2} + ε^{2} {| | A_{d} (t) | |}_{\infty}^{2} + τ^{2} {| | I_{s n d} (t) | |}_{\infty}^{2} + {| | I_{s d} (t) | |}_{\infty}^{2} + ϕ^{2} {| | Q (t) | |}_{\infty}^{2} + σ^{2} {| | J (t) | |}_{\infty}^{2}) + 2 l_{s r}^{2} + 2 t_{r}^{2} {| | T (t) | |}_{\infty}^{2} + 2 α^{2}} / \\ {l_{d}^{2} {| | L (t) | |}_{\infty}^{2} + h^{2} {| | T (t) | |}_{\infty}^{2} + η^{2} {| | Q (t) | |}_{\infty}^{2}} < 1 . \end{matrix}

where, ${\bar{ϑ}}_{1} = l_{d}^{2} {| | L (t) | |}_{\infty}^{2} + h^{2} {| | T (t) | |}_{\infty}^{2} + η^{2} {| | Q (t) | |}_{\infty}^{2} .$

Similarly, we can prove that the remaining compartments hold the above inequality.

In conclusion, the solution of our system exists and is unique under the maximality condition, detailed in [48].

3. Epidemic model based on Caputo fractional derivative

By implementing the well-known Caputo fractional-order derivative [45], we intend to modify our proposed epidemic dynamics as follows,

_{0}^{C} D_{t}^{p} f (t) = \frac{1}{Γ (n - p)} \int_{0}^{t} \frac{f^{(n)} (η)}{{(t - η)}^{p - n - 1}} d η, t > 0, p > 0, n - 1 < p \leq n, n \in N

(3)

where, $Γ$ is the well-known Gamma function, $p$ is the order of the Caputo fractional derivative operator ^CD^p.

Although integer derivative-based mathematical models have been implemented in the modern decades with tremendous progress, sometimes such models cannot perfectly replicate the real-world phenomenon due to the scarcity of information or exactness in transforming reality into a mathematical formula. Therefore, their use is essential to humanity for prediction, which helps humans understand what could happen soon, such that to avoid worst-case situations, they can take some control measures. Thus, in the current section, a Caputo fractional derivative-based mathematical model is devolved, predicting the outbreak of covid-19 for the Italian populations. In this regard, Caputo fractional derivative [50], [51], [52], [53], [54], [55] has been applied in the conventional proposed mathematical model (Eqs. (1.1)–(1.14)). Then the system of the nonlinear fractional-order differential equation is as follows:

_{0}^{C} D_{t}^{p} S (t) = - p_{d} β S (t) {ω I (t) + ε A_{d} (t) + τ I_{s n d} (t) + I_{s d} (t) + ϕ Q (t) + σ J (t)}

- l_{s r} S (t) + l_{d} L (t) - t_{r} S (t) T (t) + h T (t) + η Q (t) - α S (t)

(4.1)

_{0}^{C} D_{t}^{p} L (t) = l_{s r} S (t) - l_{d} L (t)

(4.2)

_{0}^{C} D_{t}^{p} T (t) = t_{r} S (t) T (t) - (h + τ_{1} + τ_{2}) T (t)

(4.3)

_{0}^{C} D_{t}^{p} I (t) = p_{d} β S (t) {ω I (t) + ε A_{d} (t) + τ I_{s n d} (t) + I_{s d} (t) + ϕ Q (t) + σ J (t)} - (γ + q + r_{0}) I (t)

_{0}^{C} D_{t}^{p} A_{d} (t) = τ_{1} T (t) - (j_{1} + λ_{1} + r_{1} + d_{1}) A_{d} (t)

(4.5)

_{0}^{C} D_{t}^{p} I_{s n d} (t) = γ I (t) - (j_{2} + λ_{2} + r_{2} + d_{2}) I_{s n d} (t)

(4.6)

_{0}^{C} D_{t}^{p} I_{s d} (t) = τ_{2} T (t) - (j_{3} + λ_{3} + r_{3} + d_{3}) I_{s d} (t)

(4.7)

_{0}^{C} D_{t}^{p} Q (t) = q I (t) - (η + j_{4} + λ_{4} + r_{4} + d_{4}) Q (t)

(4.8)

_{0}^{C} D_{t}^{p} J (t) = j_{1} A_{d} (t) + j_{2} I_{s n d} (t) + j_{3} I_{s d} (t) + j_{4} Q (t) - (λ_{5} + r_{5} + d_{5}) J (t)

(4.9)

_{0}^{C} D_{t}^{p} L_{t} (t) = λ_{1} A_{d} (t) + λ_{2} I_{s n d} (t) + λ_{3} I_{s d} (t) + λ_{4} Q (t) + λ_{5} J (t) - (r_{6} + d_{6}) L_{t} (t)

(4.10)

_{0}^{C} D_{t}^{p} R (t) = r_{0} I (t) + r_{1} A_{d} (t) + r_{2} I_{s n d} (t) + r_{3} I_{s d} (t) + r_{4} Q (t) + r_{5} J (t) + r_{6} L_{t} (t)

(4.11)

_{0}^{C} D_{t}^{p} D (t) = d_{1} A_{d} (t) + d_{2} I_{s n d} (t) + d_{3} I_{s d} (t) + d_{4} Q (t) + d_{5} J (t) + d_{6} L_{t} (t)

(4.12)

_{0}^{C} D_{t}^{p} P (t) = α S (t)

(4.13)

As the above mathematical model (Eqs. (4.1)–(4.13)) of covid-19 outbreak predicts a real-world problem's characteristic, [38] helps analyze the model's positivity. Then

R_{+}^{13} = {ζ \in R^{13} : ζ \geq 0},

$ζ (t) = {[S (t), L (t), T (t), I (t), A_{d} (t), I_{s n d} (t), I_{s d} (t), Q (t), J (t), L_{t} (t), R (t), D (t), P (t)]}^{T} .$

Since summation of all Eq. of the system (4.1–4.13) gives zero, the system is classified and exhibits the preservation characteristic of mass. Directly,

_{0}^{C} D_{t}^{p} {S (t) + L (t) + T (t) + I (t) + A_{d} (t) + I_{s n d} (t) + I_{s d} (t) + Q (t) + J (t)

+ L_{t} (t) + R (t) + D (t) + P (t)} = 0

which signifies that the total population is constant.

As the all-state variables imply the whole population portions, we can suppose that $\sum_{\forall i} ζ (i) = 1,$ where 1 denotes the total population $N (t)$ .

Lemma

The proposed model ( Eqs. (4.1) –( 4.13 )) solution $ζ (t)$ is positive, unique, and lies in $R_{+}^{13}$ .

Proof

Since the proposed model deals with the population model, all the ingredients are confined in the positive quadrant to analyze its positivity. Therefore, the vector field tends to $R_{+}^{13}$ , then

$_{0}^{C} D_{t}^{p} S (t) = l_{d} L (t) + h T (t) + η Q (t) \geq 0$ (5.1)

$_{0}^{C} D_{t}^{p} L (t) = l_{s r} S (t) \geq 0$ (5.2)

$_{0}^{C} D_{t}^{p} T (t) = 0$ (5.3)

$_{0}^{C} D_{t}^{p} I (t) = p_{d} β S (t) {ε A_{d} (t) + τ I_{s n d} (t) + I_{s d} (t) + ϕ Q (t) + σ J (t)} \geq 0$ (5.4)

$_{0}^{C} D_{t}^{p} A_{d} (t) = τ_{1} T (t) \geq 0$ (5.5)

$_{0}^{C} D_{t}^{p} I_{s n d} (t) = γ I (t) \geq 0$ (5.6)

$_{0}^{C} D_{t}^{p} I_{s d} (t) = τ_{2} T (t) \geq 0$ (5.7)

$_{0}^{C} D_{t}^{p} Q (t) = q I (t) \geq 0$ (5.8)

$_{0}^{C} D_{t}^{p} J (t) = j_{1} A_{d} (t) + j_{2} I_{s n d} (t) + j_{3} I_{s d} (t) + j_{4} Q (t) \geq 0$ (5.9)

$_{0}^{C} D_{t}^{p} L_{t} (t) = λ_{1} A_{d} (t) + λ_{2} I_{s n d} (t) + λ_{3} I_{s d} (t) + λ_{4} Q (t) + λ_{5} J (t) \geq 0$ (5.10)

$_{0}^{C} D_{t}^{p} R (t) = r_{0} I (t) + r_{1} A_{d} (t) + r_{2} I_{s n d} (t) + r_{3} I_{s d} (t) + r_{4} Q (t) + r_{5} J (t) + r_{6} L_{t} (t) \geq 0$ (5.11)

$_{0}^{C} D_{t}^{p} D (t) = d_{1} A_{d} (t) + d_{2} I_{s n d} (t) + d_{3} I_{s d} (t) + d_{4} Q (t) + d_{5} J (t) + d_{6} L_{t} (t) \geq 0$ (5.12)

$_{0}^{C} D_{t}^{p} P (t) = α S (t) \geq 0 .$ (5.13)

3.1. Existence of uniformly stable solution

Assume that

_{0}^{C} D_{t}^{p} S (t) = - p_{d} β S (t) {ω I (t) + ε A_{d} (t) + τ I_{s n d} (t) + I_{s d} (t) + ϕ Q (t) + σ J (t)} - l_{s r} S (t) + l_{d} L (t)

- t_{r} S (t) T (t) + h T (t) + η Q (t) - α S (t) = f_{1} (S, L, T, I, A_{d}, I_{s n d}, I_{s d}, Q, J, L_{t}, R, D, P)

_{0}^{C} D_{t}^{p} L (t) = l_{s r} S (t) - l_{d} L (t) = f_{2} (S, L, T, I, A_{d}, I_{s n d}, I_{s d}, Q, J, L_{t}, R, D, P)

_{0}^{C} D_{t}^{p} T (t) = t_{r} S (t) T (t) - (h + τ_{1} + τ_{2}) T (t) = f_{3} (S, L, T, I, A_{d}, I_{s n d}, I_{s d}, Q, J, L_{t}, R, D, P)

_{0}^{C} D_{t}^{p} I (t) = p_{d} β S (t) {ω I (t) + ε A_{d} (t) + τ I_{s n d} (t) + I_{s d} (t) + ϕ Q (t) + σ J (t)} - (γ + q + r_{0}) I (t) = f_{4} (S, L, T, I, A_{d}, I_{s n d}, I_{s d}, Q, J, L_{t}, R, D, P)

_{0}^{C} D_{t}^{p} A_{d} (t) = τ_{1} T (t) - (j_{1} + λ_{1} + r_{1} + d_{1}) A_{d} (t) = f_{5} (S, L, T, I, A_{d}, I_{s n d}, I_{s d}, Q, J, L_{t}, R, D, P)

_{0}^{C} D_{t}^{p} I_{s n d} (t) = γ I (t) - (j_{2} + λ_{2} + r_{2} + d_{2}) I_{s n d} (t) = f_{6} (S, L, T, I, A_{d}, I_{s n d}, I_{s d}, Q, J, L_{t}, R, D, P)

_{0}^{C} D_{t}^{p} I_{s d} (t) = τ_{2} T (t) - (j_{3} + λ_{3} + r_{3} + d_{3}) I_{s d} (t) = f_{7} (S, L, T, I, A_{d}, I_{s n d}, I_{s d}, Q, J, L_{t}, R, D, P)

_{0}^{C} D_{t}^{p} Q (t) = q I (t) - (η + j_{4} + λ_{4} + r_{4} + d_{4}) Q (t) = f_{8} (S, L, T, I, A_{d}, I_{s n d}, I_{s d}, Q, J, L_{t}, R, D, P)

_{0}^{C} D_{t}^{p} J (t) = j_{1} A_{d} (t) + j_{2} I_{s n d} (t) + j_{3} I_{s d} (t) + j_{4} Q (t) - (λ_{5} + r_{5} + d_{5}) J (t) = f_{9} (S, L, T, I, A_{d}, I_{s n d}, I_{s d}, Q, J, L_{t}, R, D, P)

_{0}^{C} D_{t}^{p} L_{t} (t) = λ_{1} A_{d} (t) + λ_{2} I_{s n d} (t) + λ_{3} I_{s d} (t) + λ_{4} Q (t) + λ_{5} J (t) - (r_{6} + d_{6}) L_{t} (t) = f_{10} (S, L, T, I, A_{d}, I_{s n d}, I_{s d}, Q, J, L_{t}, R, D, P)

_{0}^{C} D_{t}^{p} R (t) = r_{0} I (t) + r_{1} A_{d} (t) + r_{2} I_{s n d} (t) + r_{3} I_{s d} (t) + r_{4} Q (t) + r_{5} J (t) + r_{6} L_{t} (t) = f_{11} (S, L, T, I, A_{d}, I_{s n d}, I_{s d}, Q, J, L_{t}, R, D, P)

_{0}^{C} D_{t}^{p} D (t) = d_{1} A_{d} (t) + d_{2} I_{s n d} (t) + d_{3} I_{s d} (t) + d_{4} Q (t) + d_{5} J (t) + d_{6} L_{t} (t) = f_{12} (S, L, T, I, A_{d}, I_{s n d}, I_{s d}, Q, J, L_{t}, R, D, P)

_{0}^{C} D_{t}^{p} P (t) = α S (t) = f_{13} (S, L, T, I, A_{d}, I_{s n d}, I_{s d}, Q, J, L_{t}, R, D, P)

Assume for the total population $N (t)$ that

Φ = {(S (t) + L (t) + T (t) + I (t) + A_{d} (t) + I_{s n d} (t) + I_{s d} (t) + Q (t) + J (t) + L_{t} (t)

$+ R (t) + D (t) + P (t)) \in R^{13} : | ζ (i) | \leq N (t)$ and $t \in [0, T] .$

Then over $Φ$ , we have

\frac{\partial f_{1}}{\partial S} = - p_{d} β {ω I (t) + ε A_{d} (t) + τ I_{s n d} (t) + I_{s d} (t) + ϕ Q (t) + σ J (t)} - l_{s r} - t_{r} T (t) - α \Rightarrow | \frac{\partial f_{1}}{\partial S} | \leq a_{11};

\frac{\partial f_{1}}{\partial L} = l_{d} \Rightarrow | \frac{\partial f_{1}}{\partial L} | \leq a_{12}; \frac{\partial f_{1}}{\partial T} = h - t_{r} S (t) \Rightarrow | \frac{\partial f_{1}}{\partial T} | \leq a_{13}; \frac{\partial f_{1}}{\partial I} = - p_{d} β ω S (t) \Rightarrow | \frac{\partial f_{1}}{\partial I} | \leq a_{14};

\frac{\partial f_{1}}{\partial A_{d}} = - p_{d} β ε S (t) \Rightarrow | \frac{\partial f_{1}}{\partial A_{d}} | \leq a_{15}; \frac{\partial f_{1}}{\partial I_{s n d}} = - p_{d} β τ S (t) \Rightarrow | \frac{\partial f_{1}}{\partial I_{s n d}} | \leq a_{16};

\frac{\partial f_{1}}{\partial I_{s d}} = - p_{d} β S (t) \Rightarrow | \frac{\partial f_{1}}{\partial I_{s d}} | \leq a_{17}; \frac{\partial f_{1}}{\partial Q} = η - p_{d} β ϕ S (t) \Rightarrow | \frac{\partial f_{1}}{\partial Q} | \leq a_{18};

\frac{\partial f_{1}}{\partial J} = - p_{d} β σ S (t) \Rightarrow | \frac{\partial f_{1}}{\partial J} | \leq a_{19}; \frac{\partial f_{1}}{\partial L_{t}} = 0 \Rightarrow f_{1} (L_{t}) = a_{110}; \frac{\partial f_{1}}{\partial R} = 0 \Rightarrow f_{1} (R) = a_{111};

\frac{\partial f_{1}}{\partial D} = 0 \Rightarrow f_{1} (D) = a_{112}; \frac{\partial f_{1}}{\partial P} = 0 \Rightarrow f_{1} (P) = a_{113} .

\frac{\partial f_{2}}{\partial S} = l_{s r} \Rightarrow | \frac{\partial f_{2}}{\partial S} | \leq a_{21}; \frac{\partial f_{2}}{\partial L} = - l_{d} \Rightarrow | \frac{\partial f_{2}}{\partial L} | \leq a_{22}; \frac{\partial f_{2}}{\partial T} = 0 \Rightarrow f_{2} (T) = a_{23};

\frac{\partial f_{2}}{\partial I} = 0 \Rightarrow f_{2} (I) = a_{24}; \frac{\partial f_{2}}{\partial A_{d}} = 0 \Rightarrow f_{2} (A_{d}) = a_{25}; \frac{\partial f_{2}}{\partial I_{s n d}} = 0 \Rightarrow f_{2} (I_{s n d}) = a_{26}; \frac{\partial f_{2}}{\partial I_{s d}} = 0 \Rightarrow f_{2} (I_{s d}) = a_{27};

\frac{\partial f_{2}}{\partial Q} = 0 \Rightarrow f_{2} (Q) = a_{28}; \frac{\partial f_{2}}{\partial J} = 0 \Rightarrow f_{2} (J) = a_{29}; \frac{\partial f_{2}}{\partial L_{t}} = 0 \Rightarrow f_{2} (L_{t}) = a_{210};

\frac{\partial f_{2}}{\partial R} = 0 \Rightarrow f_{2} (R) = a_{211}; \frac{\partial f_{2}}{\partial D} = 0 \Rightarrow f_{2} (D) = a_{212}; \frac{\partial f_{2}}{\partial P} = 0 \Rightarrow f_{2} (P) = a_{213} .

\frac{\partial f_{3}}{\partial S} = t_{r} T (t) \Rightarrow | \frac{\partial f_{3}}{\partial S} | \leq a_{31}; \frac{\partial f_{3}}{\partial L} = 0 \Rightarrow f_{3} (L) = a_{32}; \frac{\partial f_{3}}{\partial T} = - h - τ_{1} - τ_{2} \Rightarrow | \frac{\partial f_{3}}{\partial T} | \leq a_{33};

\frac{\partial f_{3}}{\partial I} = 0 \Rightarrow f_{3} (I) = a_{34}; \frac{\partial f_{3}}{\partial A_{d}} = 0 \Rightarrow f_{3} (A_{d}) = a_{35}; \frac{\partial f_{3}}{\partial I_{s n d}} = 0 \Rightarrow f_{3} (I_{s n d}) = a_{36}; \frac{\partial f_{3}}{\partial I_{s d}} = 0 \Rightarrow f_{3} (I_{s d}) = a_{37};

\frac{\partial f_{3}}{\partial Q} = 0 \Rightarrow f_{3} (Q) = a_{38}; \frac{\partial f_{3}}{\partial J} = 0 \Rightarrow f_{3} (J) = a_{39}; \frac{\partial f_{3}}{\partial L_{t}} = 0 \Rightarrow f_{3} (L_{t}) = a_{310};

\frac{\partial f_{3}}{\partial R} = 0 \Rightarrow f_{3} (R) = a_{311}; \frac{\partial f_{3}}{\partial D} = 0 \Rightarrow f_{3} (D) = a_{312}; \frac{\partial f_{3}}{\partial P} = 0 \Rightarrow f_{3} (P) = a_{313} .

\frac{\partial f_{4}}{\partial S} = p_{d} β {ω I (t) + ε A_{d} (t) + τ I_{s n d} (t) + I_{s d} (t) + ϕ Q (t) + σ J (t)} \Rightarrow | \frac{\partial f_{4}}{\partial s} | \leq a_{41}; \frac{\partial f_{4}}{\partial L} = 0 \Rightarrow f_{4} (L) = a_{42};

\frac{\partial f_{4}}{\partial T} = 0 \Rightarrow f_{4} (T) = a_{43}; \frac{\partial f_{4}}{\partial I} = p_{d} β ω S (t) - γ - q - r_{0} \Rightarrow | \frac{\partial f_{4}}{\partial I} | \leq a_{44}; \frac{\partial f_{4}}{\partial A_{d}} = p_{d} β ε S (t) \Rightarrow | \frac{\partial f_{4}}{\partial A_{d}} | \leq a_{45};

\frac{\partial f_{4}}{\partial Q} = p_{d} β ϕ S (t) \Rightarrow | \frac{\partial f_{4}}{\partial Q} | \leq a_{48}; \frac{\partial f_{4}}{\partial J} = p_{d} β σ S (t) \Rightarrow | \frac{\partial f_{4}}{\partial J} | \leq a_{49}; \frac{\partial f_{4}}{\partial L_{t}} = 0 \Rightarrow f_{4} (L_{t}) = a_{410};

\frac{\partial f_{4}}{\partial R} = 0 \Rightarrow f_{4} (R) = a_{411}; \frac{\partial f_{4}}{\partial D} = 0 \Rightarrow f_{4} (D) = a_{412}; \frac{\partial f_{4}}{\partial P} = 0 \Rightarrow f_{4} (P) = a_{413} .

\frac{\partial f_{5}}{\partial S} = 0 \Rightarrow f_{5} (S) = a_{51}; \frac{\partial f_{5}}{\partial L} = 0 \Rightarrow f_{5} (L) = a_{52}; \frac{\partial f_{5}}{\partial T} = \inf A_{d} \Rightarrow | \frac{\partial f_{5}}{\partial T} | \leq a_{53}; \frac{\partial f_{5}}{\partial I} = γ \Rightarrow | \frac{\partial f_{5}}{\partial I} | \leq a_{54};

\frac{\partial f_{5}}{\partial A_{d}} = - j_{1} - λ_{1} - r_{1} - d_{1} \Rightarrow | \frac{\partial f_{5}}{\partial A_{d}} | \leq a_{55}; \frac{\partial f_{5}}{\partial I_{s n d}} = 0 \Rightarrow f_{5} (I_{s n d}) = a_{56}; \frac{\partial f_{5}}{\partial I_{s d}} = 0 \Rightarrow f_{5} (I_{s d}) = a_{57};

\frac{\partial f_{5}}{\partial Q} = 0 \Rightarrow f_{5} (Q) = a_{58}; \frac{\partial f_{5}}{\partial J} = 0 \Rightarrow f_{5} (J) = a_{59}; \frac{\partial f_{5}}{\partial L_{t}} = 0 \Rightarrow f_{5} (L_{t}) = a_{510};

\frac{\partial f_{5}}{\partial R} = 0 \Rightarrow f_{5} (R) = a_{511}; \frac{\partial f_{5}}{\partial D} = 0 \Rightarrow f_{5} (D) = a_{512}; \frac{\partial f_{5}}{\partial P} = 0 \Rightarrow f_{5} (P) = a_{513} .

\frac{\partial f_{6}}{\partial S} = 0 \Rightarrow f_{6} (S) = a_{61}; \frac{\partial f_{6}}{\partial L} = 0 \Rightarrow f_{6} (L) = a_{62}; \frac{\partial f_{6}}{\partial T} = 0 \Rightarrow f_{6} (T) = a_{63}; \frac{\partial f_{6}}{\partial I} = γ \Rightarrow | \frac{\partial f_{6}}{\partial I} | \leq a_{64};

\frac{\partial f_{6}}{\partial A_{d}} = 0 \Rightarrow f_{6} (A_{d}) = a_{65}; \frac{\partial f_{6}}{\partial I_{s n d}} = - j_{2} - λ_{2} - r_{2} - d_{2} \Rightarrow | \frac{\partial f_{6}}{\partial I_{s n d}} | \leq a_{66}; \frac{\partial f_{6}}{\partial I_{s d}} = 0 \Rightarrow f_{6} (I_{s d}) = a_{67};

\frac{\partial f_{6}}{\partial Q} = 0 \Rightarrow f_{6} (Q) = a_{68}; \frac{\partial f_{6}}{\partial J} = 0 \Rightarrow f_{6} (J) = a_{69}; \frac{\partial f_{6}}{\partial L_{t}} = 0 \Rightarrow f_{6} (L_{t}) = a_{610};

\frac{\partial f_{6}}{\partial R} = 0 \Rightarrow f_{6} (R) = a_{611}; \frac{\partial f_{6}}{\partial D} = 0 \Rightarrow f_{6} (D) = a_{612}; \frac{\partial f_{6}}{\partial P} = 0 \Rightarrow f_{6} (P) = a_{613} .

\frac{\partial f_{7}}{\partial S} = 0 \Rightarrow f_{7} (S) = a_{71}; \frac{\partial f_{7}}{\partial L} = 0 \Rightarrow f_{7} (L) = a_{72}; \frac{\partial f_{7}}{\partial T} = \inf I_{s d} \Rightarrow | \frac{\partial f_{7}}{\partial T} | \leq a_{73}; \frac{\partial f_{7}}{\partial I} = 0 \Rightarrow f_{7} (I) = a_{74};

\frac{\partial f_{7}}{\partial A_{d}} = 0 \Rightarrow f_{7} (A_{d}) = a_{75}; \frac{\partial f_{7}}{\partial I_{s n d}} = 0 \Rightarrow f_{7} (I_{s n d}) = a_{76}; \frac{\partial f_{7}}{\partial I_{s d}} = - j_{3} - λ_{3} - r_{3} - d_{3} \Rightarrow | \frac{\partial f_{7}}{\partial I_{s d}} | \leq a_{77};

\frac{\partial f_{7}}{\partial Q} = 0 \Rightarrow f_{7} (Q) = a_{78}; \frac{\partial f_{7}}{\partial J} = 0 \Rightarrow f_{7} (J) = a_{79}; \frac{\partial f_{7}}{\partial L_{t}} = 0 \Rightarrow f_{7} (L_{t}) = a_{710};

\frac{\partial f_{7}}{\partial R} = 0 \Rightarrow f_{7} (R) = a_{711}; \frac{\partial f_{7}}{\partial D} = 0 \Rightarrow f_{7} (D) = a_{712}; \frac{\partial f_{7}}{\partial P} = 0 \Rightarrow f_{7} (P) = a_{713} .

\frac{\partial f_{8}}{\partial S} = 0 \Rightarrow f_{8} (S) = a_{81}; \frac{\partial f_{8}}{\partial L} = 0 \Rightarrow f_{8} (L) = a_{82}; \frac{\partial f_{8}}{\partial T} = 0 \Rightarrow f_{8} (T) = a_{83}; \frac{\partial f_{8}}{\partial I} = q \Rightarrow | \frac{\partial f_{8}}{\partial I} | \leq a_{84};

\frac{\partial f_{8}}{\partial A_{d}} = 0 \Rightarrow f_{8} (A_{d}) = a_{85}; \frac{\partial f_{8}}{\partial I_{s n d}} = 0 \Rightarrow f_{8} (I_{s n d}) = a_{86}; \frac{\partial f_{8}}{\partial I_{s d}} = 0 \Rightarrow f_{8} (I_{s d}) = a_{87};

\frac{\partial f_{8}}{\partial Q} = - η - j_{4} - λ_{4} - r_{4} - d_{4} \Rightarrow | \frac{\partial f_{8}}{\partial Q} | \leq a_{88}; \frac{\partial f_{8}}{\partial J} = 0 \Rightarrow f_{8} (J) = a_{89}; \frac{\partial f_{8}}{\partial L_{t}} = 0 \Rightarrow f_{8} (L_{t}) = a_{810};

\frac{\partial f_{8}}{\partial R} = 0 \Rightarrow f_{8} (R) = a_{811}; \frac{\partial f_{8}}{\partial D} = 0 \Rightarrow f_{8} (D) = a_{812}; \frac{\partial f_{8}}{\partial P} = 0 \Rightarrow f_{8} (P) = a_{813} .

\frac{\partial f_{9}}{\partial S} = 0 \Rightarrow f_{9} (S) = a_{91}; \frac{\partial f_{9}}{\partial L} = 0 \Rightarrow f_{9} (L) = a_{92}; \frac{\partial f_{9}}{\partial T} = 0 \Rightarrow f_{9} (T) = a_{93}; \frac{\partial f_{9}}{\partial I} = 0 \Rightarrow f_{9} (I) = a_{94};

\frac{\partial f_{9}}{\partial A_{d}} = j_{1} \Rightarrow | \frac{\partial f_{9}}{\partial A_{d}} | \leq a_{95}; \frac{\partial f_{9}}{\partial I_{s n d}} = j_{2} \Rightarrow | \frac{\partial f_{9}}{\partial I_{s n d}} | \leq a_{96}; \frac{\partial f_{9}}{\partial I_{s d}} = j_{3} \Rightarrow | \frac{\partial f_{9}}{\partial I_{s d}} | \leq a_{97};

\frac{\partial f_{9}}{\partial Q} = j_{4} \Rightarrow | \frac{\partial f_{9}}{\partial Q} | \leq a_{98}; \frac{\partial f_{9}}{\partial J} = - λ_{5} - r_{5} - d_{5} \Rightarrow | \frac{\partial f_{9}}{\partial J} | \leq a_{99}; \frac{\partial f_{9}}{\partial L_{t}} = 0 \Rightarrow f_{9} (L_{t}) = a_{910};

\frac{\partial f_{9}}{\partial R} = 0 \Rightarrow f_{9} (R) = a_{911}; \frac{\partial f_{9}}{\partial D} = 0 \Rightarrow f_{9} (D) = a_{912}; \frac{\partial f_{9}}{\partial P} = 0 \Rightarrow f_{9} (P) = a_{913} .

\frac{\partial f_{10}}{\partial S} = 0 \Rightarrow f_{10} (S) = a_{101}; \frac{\partial f_{10}}{\partial L} = 0 \Rightarrow f_{10} (L) = a_{102}; \frac{\partial f_{10}}{\partial T} = 0 \Rightarrow f_{10} (T) = a_{103}; \frac{\partial f_{10}}{\partial I} = r_{0} \Rightarrow | \frac{\partial f_{10}}{\partial I} | \leq a_{104};

\frac{\partial f_{10}}{\partial A_{d}} = λ_{1} \Rightarrow | \frac{\partial f_{10}}{\partial A_{d}} | \leq a_{105}; \frac{\partial f_{10}}{\partial I_{s n d}} = λ_{2} \Rightarrow | \frac{\partial f_{10}}{\partial I_{s n d}} | \leq a_{106}; \frac{\partial f_{10}}{\partial I_{s d}} = λ_{3} \Rightarrow | \frac{\partial f_{10}}{\partial I_{s d}} | \leq a_{107};

\frac{\partial f_{10}}{\partial Q} = λ_{4} \Rightarrow | \frac{\partial f_{10}}{\partial Q} | \leq a_{108}; \frac{\partial f_{10}}{\partial J} = λ_{5} \Rightarrow | \frac{\partial f_{10}}{\partial J} | \leq a_{109}; \frac{\partial f_{10}}{\partial L_{t}} = - r_{6} - d_{6} \Rightarrow \frac{\partial f_{10}}{\partial L_{t}} \leq a_{1010};

\frac{\partial f_{10}}{\partial R} = 0 \Rightarrow f_{10} (R) = a_{1011}; \frac{\partial f_{10}}{\partial D} = 0 \Rightarrow f_{10} (D) = a_{1012}; \frac{\partial f_{10}}{\partial P} = 0 \Rightarrow f_{10} (P) = a_{1013} .

\frac{\partial f_{11}}{\partial S} = 0 \Rightarrow f_{11} (S) = a_{111}; \frac{\partial f_{11}}{\partial L} = 0 \Rightarrow f_{11} (L) = a_{112}; \frac{\partial f_{11}}{\partial T} = 0 \Rightarrow f_{11} (T) = a_{113}; \frac{\partial f_{11}}{\partial I} = r_{0} \Rightarrow f_{11} (I) = a_{114};

\frac{\partial f_{11}}{\partial A_{d}} = r_{1} \Rightarrow | \frac{\partial f_{11}}{\partial A_{d}} | \leq a_{115}; \frac{\partial f_{11}}{\partial I_{s n d}} = r_{2} \Rightarrow | \frac{\partial f_{11}}{\partial I_{s n d}} | \leq a_{116}; \frac{\partial f_{11}}{\partial I_{s d}} = r_{3} \Rightarrow | \frac{\partial f_{11}}{\partial I_{s d}} | \leq a_{117};

\frac{\partial f_{11}}{\partial Q} = r_{4} \Rightarrow | \frac{\partial f_{11}}{\partial Q} | \leq a_{118}; \frac{\partial f_{11}}{\partial J} = r_{5} \Rightarrow | \frac{\partial f_{11}}{\partial J} | \leq a_{119}; \frac{\partial f_{11}}{\partial L_{t}} = r_{6} \Rightarrow; | \frac{\partial f_{11}}{\partial L_{t}} | \leq a_{1110};

\frac{\partial f_{11}}{\partial R} = 0 \Rightarrow f_{11} (R) = a_{1111}; \frac{\partial f_{11}}{\partial D} = 0 \Rightarrow f_{11} (D) = a_{1112}; \frac{\partial f_{11}}{\partial P} = 0 \Rightarrow f_{11} (P) = a_{1113} .

\frac{\partial f_{12}}{\partial S} = 0 \Rightarrow f_{12} (S) = a_{121}; \frac{\partial f_{12}}{\partial L} = 0 \Rightarrow f_{12} (L) = a_{122}; \frac{\partial f_{12}}{\partial T} = 0 \Rightarrow f_{12} (T) = a_{123}; \frac{\partial f_{12}}{\partial I} = 0 \Rightarrow f_{12} (I) = a_{124};

\frac{\partial f_{12}}{\partial A_{d}} = d_{1} \Rightarrow | \frac{\partial f_{12}}{\partial A_{d}} | \leq a_{125}; \frac{\partial f_{12}}{\partial I_{s n d}} = d_{2} \Rightarrow | \frac{\partial f_{12}}{\partial I_{s n d}} | \leq a_{126}; \frac{\partial f_{12}}{\partial I_{s d}} = d_{3} \Rightarrow | \frac{\partial f_{12}}{\partial I_{s d}} | \leq a_{127};

\frac{\partial f_{12}}{\partial Q} = d_{4} \Rightarrow | \frac{\partial f_{12}}{\partial Q} | \leq a_{138}; \frac{\partial f_{12}}{\partial J} = d_{5} \Rightarrow | \frac{\partial f_{12}}{\partial J} | \leq a_{129}; \frac{\partial f_{12}}{\partial L_{t}} = d_{6} \Rightarrow | \frac{\partial f_{12}}{\partial L_{t}} | \leq a_{1210};

\frac{\partial f_{12}}{\partial R} = 0 \Rightarrow f_{12} (R) = a_{1211}; \frac{\partial f_{12}}{\partial D} = 0 \Rightarrow f_{12} (D) = a_{1212}; \frac{\partial f_{12}}{\partial P} = 0 \Rightarrow f_{12} (P) = a_{1213} .

\frac{\partial f_{13}}{\partial S} = α \Rightarrow | \frac{\partial f_{13}}{\partial S} | \leq a_{131}; \frac{\partial f_{13}}{\partial L} = 0 \Rightarrow f_{13} (L) = a_{132}; \frac{\partial f_{13}}{\partial T} = 0 \Rightarrow f_{13} (T) = a_{133}; \frac{\partial f_{13}}{\partial I} = 0 \Rightarrow f_{13} (I) = a_{134};

\frac{\partial f_{13}}{\partial A_{d}} = 0 \Rightarrow f_{13} (A_{d}) = a_{135}; \frac{\partial f_{13}}{\partial I_{s n d}} = 0 \Rightarrow f_{13} (I_{s n d}) = a_{136}; \frac{\partial f_{13}}{\partial I_{s d}} = 0 \Rightarrow f_{13} (I_{s d}) = a_{137};

\frac{\partial f_{13}}{\partial Q} = 0 \Rightarrow f_{13} (Q) = a_{138}; \frac{\partial f_{13}}{\partial J} = 0 \Rightarrow f_{13} (J) = a_{139}; \frac{\partial f_{13}}{\partial L_{t}} = 0 \Rightarrow f_{13} (L_{t}) = a_{1310};

\frac{\partial f_{13}}{\partial R} = 0 \Rightarrow f_{13} (R) = a_{1311}; \frac{\partial f_{13}}{\partial D} = 0 \Rightarrow f_{13} (D) = a_{1312}; \frac{\partial f_{13}}{\partial P} = 0 \Rightarrow f_{13} (P) = a_{1313} .

where $a_{i j} (i \geq 1 and j \leq 13)$ all are the positive constants. Then each of the thirteen functions $f_{1}, f_{2}, \dots, f_{13}$ agreed with the Lipchitz condition [56,57]. Concerning the above thirteen arguments, it is clear that all functions are absolutely continuous.

4. Numerical simulation

In this section, the proposed model is generalized via applying the fractional Caputo derivative and numerically simulated based on parameter values presented in Table 1 . Numerical simulations were carried out by the Adams-Bashforth-Moulton algorithm [58].

Table 1.

Parameter values of the proposed epidemic dynamics and their references.

Parameter	Value/Range	Current Model	Refs.
$N (t)$	60,403,693	60,403,693	[19]
$p_{d}$	$(1 / 6 - 1 / 3) f t^{- 1}$	$1 / 3$	[25]
$β$	$(0.2 - 1.5)$ days^–1	0.5	[59], [60], [61]
$ω$	0.57	0.57	[19]
$ε$	0.0114	0.0114	[19]
$τ$	0.456	0.456	[19]
$ϕ$	–	0.0114	Estimated
$σ$	–	0.0114	Estimated
$η$	$(1 / 14 - 1 / 3)$ days^–1	$1 / 13$	[[61],[62]]
$l_{s r}$	–	0.8	Estimated
$l_{d}$	16	16	[63]
$t_{r}$	0.0251	0.0251	[64]
h	0.9829	0.9829	[64]
$τ_{1}$	0.171	0.0171	[19]
$τ_{2}$	0.3705	0.03705	[19]
$γ$	0.264	0.264	[19]
$q$	–	0.5	Estimated
$j_{1}$	$(1 / 14 - 1 / 5)$ days^–1	0.1	[[65],[66]]
$j_{2}$	–	0.2	Estimated
$j_{3}$	0.2–0.9	0.3	[[65],[66]]
$j_{4}$	–	0.15	Estimated
$λ_{1}$	0.08–	0.08	Estimated
$λ_{2}$	0.0171	0.0171	[19]
$λ_{3}$	0.0274	0.0274	[19]
$λ_{4}$	–	0.05	Estimated
$λ_{5}$	–	0.08	Estimated
$r_{0}$	–	0.4	Estimated
$r_{1}$	0.0342	0.0342	[19]
$r_{2}$	0.0171	0.0171	[19]
$r_{3}$	0.02	0.02	[[61],[66],[67]]
$r_{4}$	0.0239	0.0239	[61]
$r_{5}$	$(1 / 30 - 1 / 3)$ days^–1	$1 / 30$	[[66],[67]]
$r_{6}$	0.0171	0.0171	[19]
$d_{1}$	–	0.05	Estimated
$d_{2}$	0.001–0.1	0.005	[65]
$d_{3}$	0.001–0.01	0.003	[[68],[69]]
$d_{4}$	0.001–0.01	0.001	[[68],[69]]
$d_{5}$	0.001–0.1	0.005	[65]
$d_{6}$	0.01	0.01	[19]
$α$	–	0.5	Estimated

Open in a new tab

First, let us recall the primary method produced to solve initial value problems with Caputo derivatives (Eqs. (4.1)–(4.13)). The technique extends the familiar Adams-Bashforth-Moulton integrator that is well known for the numerical simulation of first-order differential equations [56]. This method relies on the feature that the initial value problem is equal to the Volterra integral equation. The fractional Adams-Bashforth-Moulton method is fully described by the following Equations (all other states can be found same as $S$ ). Let [0, T] is the domain of the solution and, $n = 0, 1, 2, \dots, N$ , $h = T / N$ , $t_{n} = n h$ :

S (t_{n + 1}) = \sum_{k = 0}^{⌈ α ⌉ - 1} S_{0}^{(k)} \frac{{t_{n + 1}}^{k + 1}}{k!} + \frac{h^{α}}{Γ (α + 2)} f_{1} (t_{n + 1}, S^{p} (t_{n + 1})) + \frac{h^{α}}{Γ (α + 2)} \sum_{j = 0}^{n} A_{j, n + 1} f_{1} (t_{j}, S (t_{j})),

S^{p} (t_{n + 1}) = \sum_{k = 0}^{⌈ α ⌉ - 1} S_{0}^{(k)} \frac{{t_{n + 1}}^{k + 1}}{k!} + \frac{1}{Γ (α)} \sum_{j = 0}^{n} B_{j, n + 1} f_{1} (t_{j}, S (t_{j})),

where

A_{j, n + 1} = {\begin{matrix} n^{α + 1} - (n - α) {(n + 1)}^{α}, & if j = 0, \\ {(n - j + 2)}^{α + 1} + {(n - j)}^{α + 1} - 2 {(n - j + 1)}^{α + 1}, & if 1 \leq j \leq n, \\ 1 & if j = n + 1, \end{matrix}

and

B_{j, n + 1} = \frac{h^{α}}{α} ({(n + 1 - j)}^{α} - {(n - j)}^{α}) .

For more details about the method, the reader can see [56].

The initial values [19] of the thirteen compartments are taken as follows:

L (0) = 0, T (0) = \frac{200}{N (0)}, I (0) = \frac{200}{N (0)}, A_{s d} (0) = \frac{20}{N (0)}, I_{s n d} (0) = \frac{1}{N (0)}, I_{s d} = \frac{2}{N (0)},

Q (0) = 0, J (0) = 0, L_{t} (0) = 0, R (0) = 0, D (0) = 0, P (0) = 0

S (0) = N (0) - L (0) - T (0) - I (0) - A_{s d} (0) - I_{s n d} (0) - I_{s d} (0) - Q (0) - J (0) - L_{t} (0) - R (0) - D (0) - P (0) .

5. Results and discussion

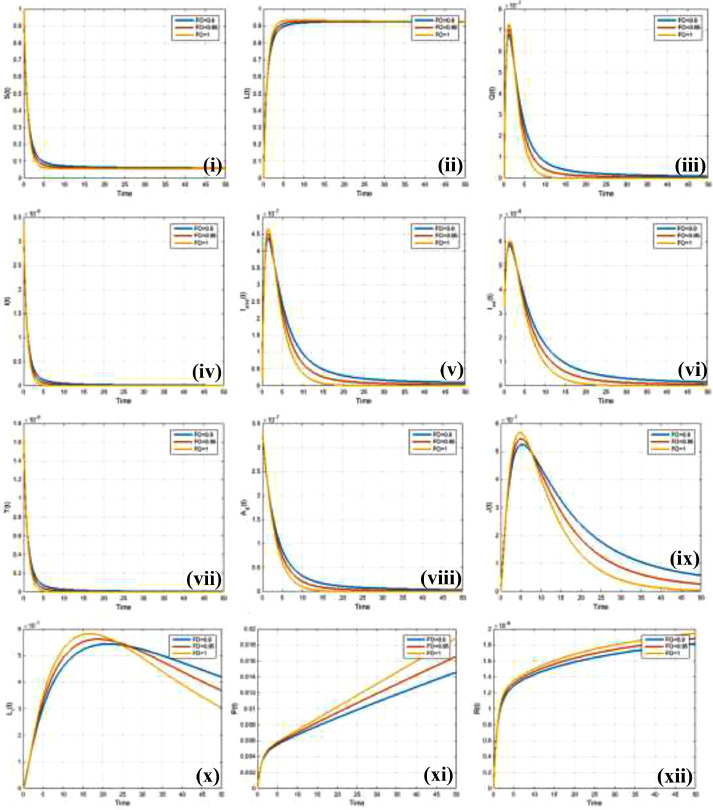
To study the sensitivity of fractional-order-based epidemic dynamics along time-elapsed around the steady-state situation called equilibrium, we present line graphs for $p \in {0.9, 0.95, 1.0}$ , depicted in Fig. 2 . It displays the fraction of susceptible, lockdown, quarantine, infected (asymptomatic, mild-symptomatic-infected, minor or moderate infection but not detected), symptomatic infected with not detected, symptomatic infected with detected, Tested, asymptomatic infected with detected, isolated or hospitalized, life-threatening condition, self-protected and recovered individuals from (i) to (xii), respectively. According to the simulated results, the fractional-order can significantly influence the changing pattern of different epidemic compartments. Thus, we can confer that the decreasing of the fractional-order $p$ , lessened the portion of susceptible, quarantined, infected, and tested individuals, as expected.

Fig 2 — Impact of different fractional order $p \in {0.9, 0.95, 1.0}$ on (i) susceptible $(S (t))$ , (ii) lock-down $(L (t))$ , (iii) quarantine, (iv) infected $I (t)$ (asymptomatic, mild-symptomatic-infected, minor or moderate infection but not detected), v) symptomatic infected with not detected $I_{s n d} (t)$ , (vi) symptomatic infected with detected $I_{s d} (t)$ , (vii) Tested state $(T (t))$ , (viii) asymptomatic infected with detected $A_{d} (t)$ , (ix) isolated or hospitalized $(J (t))$ (x) life threatening condition $(L_{t} (t))$ , (xi) self-protected $(P (t))$ ) (xii) recovered $(R (t))$ .

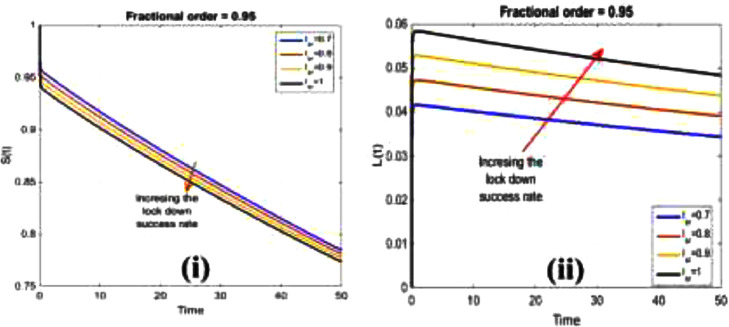
Fig. 3 displays the effect of $S (t)$ and $L (t)$ to illustrate the susceptibility and lockdown state concerning the lockdown success rate more profoundly. It seems that the increase of lockdown success rate lessens the amount of suspected susceptible individuals. However, the rise in lockdown rate increased the fraction of individuals in lockdown compartments, reducing infection risk.

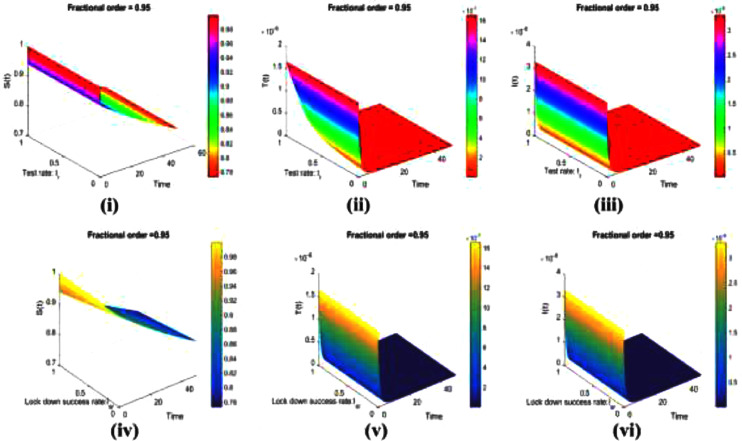
Next, we inspect the relation of test rate vs. time (i–iii) and lockdown success rate vs. time (iv–vi) for a fraction of $S (t)$ , $T (t)$ , and $I (t)$ individuals depicted in Fig. 4 . As a general tendency, we can confirm that the fraction of infected and tested individuals is lessened for increasing of both test rate and lockdown success rate.

Fig 4 — The impact of changing the test rate $t_{r}$ vs. time on susceptible $(S (t))$ , Tested state $(T (t)),$ infected $I (t)$ (asymptomatic, mild-symptomatic-infected, minor or moderate infection but not detected) are presented in (i), (ii) and (iii). Similarly, the impact of changing lockdown success rate $l_{s r}$ vs. time are depicted in (iv) susceptible $(S (t))$ , (v) Tested state $(T (t)),$ and (vi) infected $I (t)$ (asymptomatic, mild-symptomatic-infected, minor or moderate infection but not detected). Throughout, we used the fractional order of $p = 0.95$ .

6. Conclusion

Motivated by the current COVID-19 situation, we proposed the protecting measures-based epidemic models by incorporating the fractional-order approach to study the disease behavior. Model investigation and analysis are carried out by presuming the Caputo fractional-order derivative notion to generate the fractional-order mathematical epidemic model. Further, the numerical simulation of the suggested system is carried out by consuming the Adams-Bashforth-Moulton algorithm. It is observed that irrespective of introducing a vaccine policy, the combined effect of several self-protecting measures helps to reduce the disease risk.

Furthermore, because a first derivative analysis does not always offer an apparent indication of function change a priori, a second derivative analysis is necessary. The study of the second derivative discloses infection points, as well as local maximum and minimum values. These fundamental analyses may be employed in epidemiological modeling to understand dissemination patterns better. A new concept called Strength number was recently proposed. It is derived by taking the second derivative of the nonlinear section of a particular infectious disease model, then applying the next generation matrix approach to obtain the strength number. Such numbers, it was suggested, may aid in detecting waves or instability in a model. This paper uses a similar technique in conjunction with second derivative analysis in a complex $S L T I A_{d} I_{s n d} I_{s d} Q J L_{t} R D P$ problem. The computed strength number was negative, implying that the model with second derivatives could only produce one wave before dying out.

In the current work, we only developed and analyzed our proposed model theoretically. In practice and reality, the successful model should depend on actual data fitting and deliberate numerical analysis. Such a complex phenomenon and numerical analysis contain meaningful suggestions to develop health policy and public health measurement to explore future studies.

CRediT authorship contribution statement

Mohammad Sharif Ullah: Software, Formal analysis, Writing – original draft. M. Higazy: Methodology, numerical analysis. K.M. Ariful Kabir: Conceptualization, Supervision, Writing – original draft. All author's critically revised the manuscript and gave final approval.

Declaration of Competing Interest

We declare we have no competing interests.

References

1.COVID-19 Coronavirus Pandemic, https://www.worldometers.info/coronavirus/#repro, (accessed March 26, 2020).
2.HuiDS I.A.E., Madani T., Ntoumi F., Koch R., Dar O., et al. The continuing 2019-nCoV epidemicthreatof novel coronaviruses to global health: the latest 2019 novel coronavirus outbreak in Wuhan, China. Int J Infect Dis. 2020;91:264–266. doi: 10.1016/j.ijid.2020.01.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
3.Coronavirus and COVID-19: what you should know, https://coronavirus & COVID-19 overview: symptoms, risks, prevention, Treatment & More (webmd.com).
4.What are the typical symptoms, https://coronavirus incubation period: how long before symptoms appear? (healthline.com).
5.The epidemiology and pathogenesis of coronavirus disease (COVID-19) outbreak. [DOI] [PMC free article] [PubMed]
6.Wu D., Wu T., Liu Q., Yang Z. The SARS-CoV-2 outbreak: what we know. [DOI] [PMC free article] [PubMed]
7.Is it coronavirus? What we know about common and atypical COVID-19 symptoms – NBC connecticut.
8.About 80% of asymptomatic people with COVID-19 develop symptoms (medscape.com).
9.Martcheva M. Springer; 2015. An introduction to mathematical epidemiology. [Google Scholar]
10.Li MY. Springer; 2017. An introduction to mathematical modeling of infectious diseases. [Google Scholar]
11.Brauer F., Castillo-Chavez C., Castillo-Chavez C. Mathematical models in population biology and epidemiology, 2, 2012. doi: 10.1007/978-1-4614-1686-9. [DOI]
12.Raj Bhopal R. OXPORD University Press; 2002. Concepts of epidemiology: an integrated introduction to the ideas, theories, principles and methods of epidemiology. [Google Scholar]
13.Thomas J.C., Weber D.J. OXPORD University Press; 2001. Epidemiologic methods for the study of infectious diseases. [Google Scholar]
14.Population biology of infectious diseases: part I. NatureNature. 1979;280(5721):361–367. doi: 10.1038/280361a0. [DOI] [PubMed] [Google Scholar]
15.Bertolaccini L., Spaggiari L. The hearth of mathematical and statistical modelling during the Coronavirus pandemic, 2020, doi: 10.1093/icvts/ivaa076. [DOI] [PMC free article] [PubMed]
16.Kermack W.O., McKendrick A.G. A contribution to the mathematical theory of epidemics. Proc R Soc Lond Ser A Math Phys Eng Sci. 1927;115(772):700–721. [Google Scholar]
17.Kabir K.M.A., Tanimoto J. Analysis of epidemic outbreaks in two-layer networks with different structures for information spreading and disease diffusion. Commun Nonlinear Sci Numer Simul. 2019;72:565–574. [Google Scholar]
18.Kabir K.M.A., Tanimoto J. Vaccination strategies in a two-layer SIR/V-UA epidemic model with costly information and buzz effect. Commun Nonlinear Sci Numer Simul. 2019;76:92–108. [Google Scholar]
19.Giordano G., Blanchini F., Bruno R., Colaneri P., Filippo A.D., Matteo A.D., et al. Modelling the COVID-19 epidemic and implementation of population-wide interventions in Italy. Nat Med. 2020;22 doi: 10.1038/s41591-020-0883-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
20.Islam M.S., Ira J.I., Ariful Kabir K.M.A., Kamrujjaman M. Effect of lockdown and isolation to suppress the COVID-19 in Bangladesh: an epidemic compartments model. J Appl Math Comput. 2020;4(3):83–93. doi: 10.26855/jamc.2020.09.004. [DOI] [Google Scholar]
21.Alam M., Kabir K.M.A., Tanimoto J. Based on mathematical epidemiology and evolutionary game theory, which is more effective: quarantine or isolation policy? J Stat Mech. 2020:03350. [Google Scholar]
22.Kabir K.M.A., Chowdhury A., Tanimoto J. An evolutionary game modeling to assess the effect of border enforcement measures and socio-economic cost: export-importation epidemic dynamics. Chaos Solitons Fractals. 2021;146 doi: 10.1016/j.chaos.2021.110918. [DOI] [PMC free article] [PubMed] [Google Scholar]
23.Kucharski A.J., Russell T.W., Diamond C., Liu Y., Edmunds J., Funk S., Eggo R.M., Sun F., Jit M., Munday J.D., et al. Early dynamics of transmission and control of COVID-19: a mathematical modelling study. Lancet Infect Dis. 2020 doi: 10.1016/S1473-3099(20)30144-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
24.Prem K., Liu Y., Russell T.W., Kucharski A.J., Eggo R.M., Davies N., Flasche S., Clifford S., Pearson C.A., Munday J.D., et al. The effect of control strategies to reduce social mixing on outcomes of the COVID-19 epidemic in wuhan, China: a modelling study. Lancet Infect Dis. 2020 doi: 10.1016/S2468-2667(20)30073-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
25.Chowdhury, A, Kabir, KA, Tanimoto, J, How quarantine and social-distancing policy can suppress the outbreak of novel coronavirus in developing or under poverty level countries: a mathematical and statistical analysis, 2020. doi: 10.21203/rs.3.rs-20294/v1. [DOI]
26.Ge F., Chen Y.Q., Kou C. Springer; Cham: 2018. Regional analysis of time-fractional diffusion processes. [Google Scholar]
27.Hilfer R. World Scientific Publishing Co, Inc; River Edge, NJ: 2000. Applications of fractional calculus in physics. [DOI] [Google Scholar]
28.Kilbas A.A., Srivastava H.M., Trujillo J.J. Elsevier Science; Amsterdam: 2006. Theory and applications of fractional differential equations. [Google Scholar]
29.Samko S.G., Kilbas A.A., Marichev O.I. Fractional integrals and derivatives. Theory and applications. Amsterdam: gordon and Breach; 1993.
30.Tarasov V.E. Higher Education Press; Beijing: 2010. Fractional dynamics: application of fractional calculus to dynamics of particles, fields and media. Springer, Heidelberg. [Google Scholar]
31.Valério D., Sá da Costa J. Institution of Engineering and Technology (IET); London: 2013. An introduction to fractional control. [Google Scholar]
32.Zhou Y. World Scientific; Singapore: 2014. Basic theory of fractional differential equations. [Google Scholar]
33.Baleanu D., Tenreiro Machado J.A., Luo A.C.J. Springer; New York: 2012. Fractional dynamics and control. URL. [DOI] [Google Scholar]
34.Diethelm K. An application-oriented exposition using differential operators of Caputo type. Springer-Verlag; Berlin: 2010. The analysis of fractional differential equations. [DOI] [Google Scholar]
35.Podlubny I. Academic Press, Inc.; San Diego, CA: 1999. Fractional differential equations. volume 198 of Mathematics in science and engineeringAn introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications. [Google Scholar]
36.Tarasov VE. Applications of fractional calculus to dynamics of particles, fields and media. Higher Education Press; Beijing: 2010. Fractional dynamics. [DOI] [Google Scholar]
37.Alshabanat A., Jleli M., Kumar S., Samet B. Generalization of Caputo-Fabrizio fractional derivative and applications to electrical circuits. Front Phys. 2020;8 doi: 10.3389/fphy.2020.00064. Art. 64, 10 pp. [DOI] [Google Scholar]
38.Nisar K.S. Generalized Mittag-Leffler type function: fractional integrations and application to fractional kinetic equations. Front Phys. 2020;8 doi: 10.3389/fphy.2020.00033. Art. 33, 7 pp. [DOI] [Google Scholar]
39.Yıldız T.A. Optimal control problem of a non-integer order waterborne pathogen model in case of environmental stressors. Front Phys. 2019;7 doi: 10.3389/fphy.2019.00095. Art.10 pp. [DOI] [Google Scholar]
40.Yadav R.P., Verma R. A numerical simulation of fractional order mathematical modeling of COVID-19 disease in case of Wuhan China. Chaos Solitons Fractals. 2020;140 doi: 10.1016/j.chaos.2020.110124. [DOI] [PMC free article] [PubMed] [Google Scholar]
41.Ndaïrou F., Area I., Nieto J.J., Torres D.F.M. Mathematical modeling of COVID-19 transmission dynamics with a case study of Wuhan. Chaos Solitons Fractals. 2020;141 doi: 10.1016/j.chaos.2020.109846. 2020;1 35:1 09846Corrigendum Chaos Solitons Fractals[10.1016/j.chaos.2020.110311] [DOI] [PMC free article] [PubMed] [Google Scholar]
42.Khan M.A., Atangana A. Modeling the dynamics of novel coronavirus (2019- nCov) with fractional derivative. Alex Eng J. 2020:1–11. doi: 10.1016/j.aej.2020.02.033. [DOI] [Google Scholar]
43.Nabi K.N., Abboubakar H., Kumar P. Forecasting of covid-19 pandemic: from integer derivatives to fractional derivatives. Chaos Solitons Fractals. 2020;141 doi: 10.1016/j.chaos.2020.110283. [DOI] [PMC free article] [PubMed] [Google Scholar]
44.Nabi K.N., Kumar P., Erturk V.S. Projections and fractional dynamics of COVID-19 with optimal control strategies. Chaos Solitons Fractals. 2021;145 doi: 10.1016/j.chaos.2021.110689. [DOI] [PMC free article] [PubMed] [Google Scholar]
45.Caputo M. Linear model of dissipation whose Q is almost frequency independent. II. Geophys J Int. 1967;13(5):529–539. doi: 10.1111/j.1365-246x.1967.tb02303.x. [DOI] [Google Scholar]
46.Walter W. Springer; 1998. Ordinary differential equations. [Google Scholar]
47.Diekmann O., Heesterbeek J.A.P., Metz J.A. On the definition and the 580 computation of the basic reproduction ratio R0 in models for infectious diseases in 581 heterogeneous populations. J Math Biol. 1990;28(4):365–382. doi: 10.1007/BF00178324. [DOI] [PubMed] [Google Scholar]
48.Atangana A. Mathematical model of survival of fractional calculus, critics and their impact: how singular is our world? Adv Differ Equ. 2021;403 doi: 10.1186/s13662-021-03494-7. 2021. [DOI] [Google Scholar]
49.Atangana, A., ARAZ, S.I., (2021). Advanced analysis in epidemiological modeling: detection of wave, medRxiv preprint. doi: 10.1101/2021.09.02.21263016. [DOI]
50.Naik P.A., Zu J., Owolabi K.M. Modeling the mechanics of viral kinetics under immune control during primary infection of HIV-1 with treatment in fractional order. Phys A Stat Mech Appl. 2020;545 [Google Scholar]
51.Owolabi K.M. Behavioural study of symbiosis dynamics via the Caputo and Atangana Baleanu fractional derivatives. Chaos Solitons Fractals. 2019;122:89–101. [Google Scholar]
52.Higazy M., Alyami M.A. New Caputo-Fabrizio fractional order SEIASqEqHR model for COVID-19 epidemic transmission with genetic algorithm based control strategy. Alex Eng J. 2020 doi: 10.1016/j.aej.2020.08.034. Available online 31st August. [DOI] [Google Scholar]
53.Higazy M. Novel fractional order SIDARTHE mathematical model of COVID-19 pandemic. Chaos Solitons Fractals. 2020;138 doi: 10.1016/j.chaos.2020.110007. [DOI] [PMC free article] [PubMed] [Google Scholar]
54.Higazy M., Allehiany F.M., Mahmoud E.E. Numerical study of fractional order COVID-19 pandemic transmission model in context of ABO blood group. Results Phys. 2021;22 doi: 10.1016/j.rinp.2021.103852. [DOI] [PMC free article] [PubMed] [Google Scholar]
55.Inc M., Acay B., Berhe H.W., Yusuf A., Khan A., Yao S.-.W. Analysis of novel fractional COVID-19 model with real-life data application. Results Phys. 2021;23 doi: 10.1016/j.rinp.2021.103968. [DOI] [PMC free article] [PubMed] [Google Scholar]
56.El-Shahed M., Alsaedi A. The fractional SIRC model and influenza A. Math Probl Eng. 2011;2011:1–9. [Google Scholar]
57.Mahdy A.M.S., Sweilam N.H., Higazy M. Approximate solutions for solving nonlinear fractional order smoking model. Alex Eng J. 2020;59(2):739–752. [Google Scholar]
58.Diethelm K., Freed A.D. In: Research and scientific computing 1998. Heinzel S., Plesser T., editors. Society for Scientific data Processing; Göttingen: 1999. The FracPECE subroutine for the numerical solution of differential equations of fractional order; pp. 57–71. [Google Scholar]
59.Shen M., Peng Z., Xiao Y., Zhang L. Modelling the epidemic trend of the 2019 novel coronavirus outbreak in China, 2020, bioRxiv. [DOI] [PMC free article] [PubMed]
60.Read J.M., Bridgen J.R., Cummings D.A., Ho A., Jewell C.P. Novel coronavirus 2019-nCoV: early estimation of epidemiological parameters and epidemic predictions, 2020, MedRxiv. [DOI] [PMC free article] [PubMed]
61.Li R., Pei S., Chen B., Song Y., Zhang T., Yang W., Shaman J. Substantial undocumented infection facilitates the rapid dissemination of novel coronavirus (SARS-CoV2) Science. 2020;368(6490):489–493. doi: 10.1126/science.abb3221. [DOI] [PMC free article] [PubMed] [Google Scholar]
62.Lauer S.A., Grantz K.H., Bi Q., Jones F.K., Zheng Q., Meredith H.R., Lessler J. The incubation period of coronavirus disease 2019 (COVID-19) from publicly reported confirmed cases: estimation and application. Ann Intern Med. 2020;172(9):577–582. doi: 10.7326/M20-0504. [DOI] [PMC free article] [PubMed] [Google Scholar]
63.Chronology of main steps and legal acts taken by the Italian Government for the containment of the COVID-19 epidemiological emergency. http://www.protezionecivile.gov.it/documents/20182/1227694/Summary+of+measures+taken+against+the+spread+of+C-19/c16459ad-4e52-4e90-90f3-c6a2b30c17eb (accessed 12 March 2020).
64.New testing guidelines have been released on behalf of the Ministry of Health. https://www.covid19healthsystem.org/countries/italy/livinghit.aspx?Section=1.3%20Isolation%20and%20quarantine&Type=Section (accessed, 23rd October 2020).
65.Ferguson N., Laydon D., Gilani N.G., Imai N., Ainslie K., Baguelin M., Dighe A.. Report 9: impact of non-pharmaceutical interventions (NPIs) to reduce COVID19 mortality and healthcare demand, 2020.
66.Zhou F., Yu T., Du R., Fan G., Liu Y., Liu Z., Guan L. Clinical course and risk factors for mortality of adult inpatients with COVID-19 in Wuhan, China: a retrospective cohort study. Lancet. 2020;395(10229):1054–1062. doi: 10.1016/S0140-6736(20)30566-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
67.Tang B., Bragazzi N.L., Li Q., Tang S., Xiao Y., Wu J. An updated estimation of the risk of transmission of the novel coronavirus (2019-nCov) Infect Dis Model. 2020;5:248–255. doi: 10.1016/j.idm.2020.02.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
68.Liu P.Y., He S., Rong L.B., Tang S.Y. The effect of control measures on COVID-19 transmission in Italy: comparison with Guangdong province in China. Infect Dis Poverty. 2020;9 doi: 10.1186/s40249-020-00730-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
69.Tang B., Wang X., Li Q., Bragazzi N., Tang S., Xiao Y., Wu J. Estimation of the transmission risk of the 2019-nCoV and its implication for public health interventions. J Clin Med. 2020;9:462. doi: 10.3390/jcm9020462. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib0001] 1.COVID-19 Coronavirus Pandemic, https://www.worldometers.info/coronavirus/#repro, (accessed March 26, 2020).

[bib0002] 2.HuiDS I.A.E., Madani T., Ntoumi F., Koch R., Dar O., et al. The continuing 2019-nCoV epidemicthreatof novel coronaviruses to global health: the latest 2019 novel coronavirus outbreak in Wuhan, China. Int J Infect Dis. 2020;91:264–266. doi: 10.1016/j.ijid.2020.01.009. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib0003] 3.Coronavirus and COVID-19: what you should know, https://coronavirus & COVID-19 overview: symptoms, risks, prevention, Treatment & More (webmd.com).

[bib0004] 4.What are the typical symptoms, https://coronavirus incubation period: how long before symptoms appear? (healthline.com).

[bib0005] 5.The epidemiology and pathogenesis of coronavirus disease (COVID-19) outbreak. [DOI] [PMC free article] [PubMed]

[bib0006] 6.Wu D., Wu T., Liu Q., Yang Z. The SARS-CoV-2 outbreak: what we know. [DOI] [PMC free article] [PubMed]

[bib0007] 7.Is it coronavirus? What we know about common and atypical COVID-19 symptoms – NBC connecticut.

[bib0008] 8.About 80% of asymptomatic people with COVID-19 develop symptoms (medscape.com).

[bib0009] 9.Martcheva M. Springer; 2015. An introduction to mathematical epidemiology. [Google Scholar]

[bib0010] 10.Li MY. Springer; 2017. An introduction to mathematical modeling of infectious diseases. [Google Scholar]

[bib0011] 11.Brauer F., Castillo-Chavez C., Castillo-Chavez C. Mathematical models in population biology and epidemiology, 2, 2012. doi: 10.1007/978-1-4614-1686-9. [DOI]

[bib0012] 12.Raj Bhopal R. OXPORD University Press; 2002. Concepts of epidemiology: an integrated introduction to the ideas, theories, principles and methods of epidemiology. [Google Scholar]

[bib0013] 13.Thomas J.C., Weber D.J. OXPORD University Press; 2001. Epidemiologic methods for the study of infectious diseases. [Google Scholar]

[bib0014] 14.Population biology of infectious diseases: part I. NatureNature. 1979;280(5721):361–367. doi: 10.1038/280361a0. [DOI] [PubMed] [Google Scholar]

[bib0015] 15.Bertolaccini L., Spaggiari L. The hearth of mathematical and statistical modelling during the Coronavirus pandemic, 2020, doi: 10.1093/icvts/ivaa076. [DOI] [PMC free article] [PubMed]

[bib0016] 16.Kermack W.O., McKendrick A.G. A contribution to the mathematical theory of epidemics. Proc R Soc Lond Ser A Math Phys Eng Sci. 1927;115(772):700–721. [Google Scholar]

[bib0017] 17.Kabir K.M.A., Tanimoto J. Analysis of epidemic outbreaks in two-layer networks with different structures for information spreading and disease diffusion. Commun Nonlinear Sci Numer Simul. 2019;72:565–574. [Google Scholar]

[bib0018] 18.Kabir K.M.A., Tanimoto J. Vaccination strategies in a two-layer SIR/V-UA epidemic model with costly information and buzz effect. Commun Nonlinear Sci Numer Simul. 2019;76:92–108. [Google Scholar]

[bib0019] 19.Giordano G., Blanchini F., Bruno R., Colaneri P., Filippo A.D., Matteo A.D., et al. Modelling the COVID-19 epidemic and implementation of population-wide interventions in Italy. Nat Med. 2020;22 doi: 10.1038/s41591-020-0883-7. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib0020] 20.Islam M.S., Ira J.I., Ariful Kabir K.M.A., Kamrujjaman M. Effect of lockdown and isolation to suppress the COVID-19 in Bangladesh: an epidemic compartments model. J Appl Math Comput. 2020;4(3):83–93. doi: 10.26855/jamc.2020.09.004. [DOI] [Google Scholar]

[bib0021] 21.Alam M., Kabir K.M.A., Tanimoto J. Based on mathematical epidemiology and evolutionary game theory, which is more effective: quarantine or isolation policy? J Stat Mech. 2020:03350. [Google Scholar]

[bib0022] 22.Kabir K.M.A., Chowdhury A., Tanimoto J. An evolutionary game modeling to assess the effect of border enforcement measures and socio-economic cost: export-importation epidemic dynamics. Chaos Solitons Fractals. 2021;146 doi: 10.1016/j.chaos.2021.110918. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib0023] 23.Kucharski A.J., Russell T.W., Diamond C., Liu Y., Edmunds J., Funk S., Eggo R.M., Sun F., Jit M., Munday J.D., et al. Early dynamics of transmission and control of COVID-19: a mathematical modelling study. Lancet Infect Dis. 2020 doi: 10.1016/S1473-3099(20)30144-4. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib0024] 24.Prem K., Liu Y., Russell T.W., Kucharski A.J., Eggo R.M., Davies N., Flasche S., Clifford S., Pearson C.A., Munday J.D., et al. The effect of control strategies to reduce social mixing on outcomes of the COVID-19 epidemic in wuhan, China: a modelling study. Lancet Infect Dis. 2020 doi: 10.1016/S2468-2667(20)30073-6. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib0025] 25.Chowdhury, A, Kabir, KA, Tanimoto, J, How quarantine and social-distancing policy can suppress the outbreak of novel coronavirus in developing or under poverty level countries: a mathematical and statistical analysis, 2020. doi: 10.21203/rs.3.rs-20294/v1. [DOI]

[bib0026] 26.Ge F., Chen Y.Q., Kou C. Springer; Cham: 2018. Regional analysis of time-fractional diffusion processes. [Google Scholar]

[bib0027] 27.Hilfer R. World Scientific Publishing Co, Inc; River Edge, NJ: 2000. Applications of fractional calculus in physics. [DOI] [Google Scholar]

[bib0028] 28.Kilbas A.A., Srivastava H.M., Trujillo J.J. Elsevier Science; Amsterdam: 2006. Theory and applications of fractional differential equations. [Google Scholar]

[bib0029] 29.Samko S.G., Kilbas A.A., Marichev O.I. Fractional integrals and derivatives. Theory and applications. Amsterdam: gordon and Breach; 1993.

[bib0030] 30.Tarasov V.E. Higher Education Press; Beijing: 2010. Fractional dynamics: application of fractional calculus to dynamics of particles, fields and media. Springer, Heidelberg. [Google Scholar]

[bib0031] 31.Valério D., Sá da Costa J. Institution of Engineering and Technology (IET); London: 2013. An introduction to fractional control. [Google Scholar]

[bib0032] 32.Zhou Y. World Scientific; Singapore: 2014. Basic theory of fractional differential equations. [Google Scholar]

[bib0033] 33.Baleanu D., Tenreiro Machado J.A., Luo A.C.J. Springer; New York: 2012. Fractional dynamics and control. URL. [DOI] [Google Scholar]

[bib0034] 34.Diethelm K. An application-oriented exposition using differential operators of Caputo type. Springer-Verlag; Berlin: 2010. The analysis of fractional differential equations. [DOI] [Google Scholar]

[bib0035] 35.Podlubny I. Academic Press, Inc.; San Diego, CA: 1999. Fractional differential equations. volume 198 of Mathematics in science and engineeringAn introduction to fractional derivatives, fractional differential equations, to methods of their solution and some of their applications. [Google Scholar]

[bib0036] 36.Tarasov VE. Applications of fractional calculus to dynamics of particles, fields and media. Higher Education Press; Beijing: 2010. Fractional dynamics. [DOI] [Google Scholar]

[bib0037] 37.Alshabanat A., Jleli M., Kumar S., Samet B. Generalization of Caputo-Fabrizio fractional derivative and applications to electrical circuits. Front Phys. 2020;8 doi: 10.3389/fphy.2020.00064. Art. 64, 10 pp. [DOI] [Google Scholar]

[bib0038] 38.Nisar K.S. Generalized Mittag-Leffler type function: fractional integrations and application to fractional kinetic equations. Front Phys. 2020;8 doi: 10.3389/fphy.2020.00033. Art. 33, 7 pp. [DOI] [Google Scholar]

[bib0039] 39.Yıldız T.A. Optimal control problem of a non-integer order waterborne pathogen model in case of environmental stressors. Front Phys. 2019;7 doi: 10.3389/fphy.2019.00095. Art.10 pp. [DOI] [Google Scholar]

[bib0040] 40.Yadav R.P., Verma R. A numerical simulation of fractional order mathematical modeling of COVID-19 disease in case of Wuhan China. Chaos Solitons Fractals. 2020;140 doi: 10.1016/j.chaos.2020.110124. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib0041] 41.Ndaïrou F., Area I., Nieto J.J., Torres D.F.M. Mathematical modeling of COVID-19 transmission dynamics with a case study of Wuhan. Chaos Solitons Fractals. 2020;141 doi: 10.1016/j.chaos.2020.109846. 2020;1 35:1 09846Corrigendum Chaos Solitons Fractals[10.1016/j.chaos.2020.110311] [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib0043] 42.Khan M.A., Atangana A. Modeling the dynamics of novel coronavirus (2019- nCov) with fractional derivative. Alex Eng J. 2020:1–11. doi: 10.1016/j.aej.2020.02.033. [DOI] [Google Scholar]

[bib0044] 43.Nabi K.N., Abboubakar H., Kumar P. Forecasting of covid-19 pandemic: from integer derivatives to fractional derivatives. Chaos Solitons Fractals. 2020;141 doi: 10.1016/j.chaos.2020.110283. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib0045] 44.Nabi K.N., Kumar P., Erturk V.S. Projections and fractional dynamics of COVID-19 with optimal control strategies. Chaos Solitons Fractals. 2021;145 doi: 10.1016/j.chaos.2021.110689. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib0046] 45.Caputo M. Linear model of dissipation whose Q is almost frequency independent. II. Geophys J Int. 1967;13(5):529–539. doi: 10.1111/j.1365-246x.1967.tb02303.x. [DOI] [Google Scholar]

[bib0047] 46.Walter W. Springer; 1998. Ordinary differential equations. [Google Scholar]

[bib0048] 47.Diekmann O., Heesterbeek J.A.P., Metz J.A. On the definition and the 580 computation of the basic reproduction ratio R0 in models for infectious diseases in 581 heterogeneous populations. J Math Biol. 1990;28(4):365–382. doi: 10.1007/BF00178324. [DOI] [PubMed] [Google Scholar]

[bib0049] 48.Atangana A. Mathematical model of survival of fractional calculus, critics and their impact: how singular is our world? Adv Differ Equ. 2021;403 doi: 10.1186/s13662-021-03494-7. 2021. [DOI] [Google Scholar]

[bib0050] 49.Atangana, A., ARAZ, S.I., (2021). Advanced analysis in epidemiological modeling: detection of wave, medRxiv preprint. doi: 10.1101/2021.09.02.21263016. [DOI]

[bib0051] 50.Naik P.A., Zu J., Owolabi K.M. Modeling the mechanics of viral kinetics under immune control during primary infection of HIV-1 with treatment in fractional order. Phys A Stat Mech Appl. 2020;545 [Google Scholar]

[bib0052] 51.Owolabi K.M. Behavioural study of symbiosis dynamics via the Caputo and Atangana Baleanu fractional derivatives. Chaos Solitons Fractals. 2019;122:89–101. [Google Scholar]

[bib0053] 52.Higazy M., Alyami M.A. New Caputo-Fabrizio fractional order SEIASqEqHR model for COVID-19 epidemic transmission with genetic algorithm based control strategy. Alex Eng J. 2020 doi: 10.1016/j.aej.2020.08.034. Available online 31st August. [DOI] [Google Scholar]

[bib0054] 53.Higazy M. Novel fractional order SIDARTHE mathematical model of COVID-19 pandemic. Chaos Solitons Fractals. 2020;138 doi: 10.1016/j.chaos.2020.110007. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib0055] 54.Higazy M., Allehiany F.M., Mahmoud E.E. Numerical study of fractional order COVID-19 pandemic transmission model in context of ABO blood group. Results Phys. 2021;22 doi: 10.1016/j.rinp.2021.103852. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib0056] 55.Inc M., Acay B., Berhe H.W., Yusuf A., Khan A., Yao S.-.W. Analysis of novel fractional COVID-19 model with real-life data application. Results Phys. 2021;23 doi: 10.1016/j.rinp.2021.103968. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib0057] 56.El-Shahed M., Alsaedi A. The fractional SIRC model and influenza A. Math Probl Eng. 2011;2011:1–9. [Google Scholar]

[bib0058] 57.Mahdy A.M.S., Sweilam N.H., Higazy M. Approximate solutions for solving nonlinear fractional order smoking model. Alex Eng J. 2020;59(2):739–752. [Google Scholar]

[bib0059] 58.Diethelm K., Freed A.D. In: Research and scientific computing 1998. Heinzel S., Plesser T., editors. Society for Scientific data Processing; Göttingen: 1999. The FracPECE subroutine for the numerical solution of differential equations of fractional order; pp. 57–71. [Google Scholar]

[bib0060] 59.Shen M., Peng Z., Xiao Y., Zhang L. Modelling the epidemic trend of the 2019 novel coronavirus outbreak in China, 2020, bioRxiv. [DOI] [PMC free article] [PubMed]

[bib0061] 60.Read J.M., Bridgen J.R., Cummings D.A., Ho A., Jewell C.P. Novel coronavirus 2019-nCoV: early estimation of epidemiological parameters and epidemic predictions, 2020, MedRxiv. [DOI] [PMC free article] [PubMed]

[bib0062] 61.Li R., Pei S., Chen B., Song Y., Zhang T., Yang W., Shaman J. Substantial undocumented infection facilitates the rapid dissemination of novel coronavirus (SARS-CoV2) Science. 2020;368(6490):489–493. doi: 10.1126/science.abb3221. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib0063] 62.Lauer S.A., Grantz K.H., Bi Q., Jones F.K., Zheng Q., Meredith H.R., Lessler J. The incubation period of coronavirus disease 2019 (COVID-19) from publicly reported confirmed cases: estimation and application. Ann Intern Med. 2020;172(9):577–582. doi: 10.7326/M20-0504. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib0064] 63.Chronology of main steps and legal acts taken by the Italian Government for the containment of the COVID-19 epidemiological emergency. http://www.protezionecivile.gov.it/documents/20182/1227694/Summary+of+measures+taken+against+the+spread+of+C-19/c16459ad-4e52-4e90-90f3-c6a2b30c17eb (accessed 12 March 2020).

[bib0065] 64.New testing guidelines have been released on behalf of the Ministry of Health. https://www.covid19healthsystem.org/countries/italy/livinghit.aspx?Section=1.3%20Isolation%20and%20quarantine&Type=Section (accessed, 23rd October 2020).

[bib0066] 65.Ferguson N., Laydon D., Gilani N.G., Imai N., Ainslie K., Baguelin M., Dighe A.. Report 9: impact of non-pharmaceutical interventions (NPIs) to reduce COVID19 mortality and healthcare demand, 2020.

[bib0067] 66.Zhou F., Yu T., Du R., Fan G., Liu Y., Liu Z., Guan L. Clinical course and risk factors for mortality of adult inpatients with COVID-19 in Wuhan, China: a retrospective cohort study. Lancet. 2020;395(10229):1054–1062. doi: 10.1016/S0140-6736(20)30566-3. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib0068] 67.Tang B., Bragazzi N.L., Li Q., Tang S., Xiao Y., Wu J. An updated estimation of the risk of transmission of the novel coronavirus (2019-nCov) Infect Dis Model. 2020;5:248–255. doi: 10.1016/j.idm.2020.02.001. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib0069] 68.Liu P.Y., He S., Rong L.B., Tang S.Y. The effect of control measures on COVID-19 transmission in Italy: comparison with Guangdong province in China. Infect Dis Poverty. 2020;9 doi: 10.1186/s40249-020-00730-2. [DOI] [PMC free article] [PubMed] [Google Scholar]

[bib0070] 69.Tang B., Wang X., Li Q., Bragazzi N., Tang S., Xiao Y., Wu J. Estimation of the transmission risk of the 2019-nCoV and its implication for public health interventions. J Clin Med. 2020;9:462. doi: 10.3390/jcm9020462. [DOI] [PMC free article] [PubMed] [Google Scholar]

PERMALINK

Modeling the epidemic control measures in overcoming COVID-19 outbreaks: A fractional-order derivative approach

Mohammad Sharif Ullah

M Higazy

KM Ariful Kabir

Abstract

1. Introduction

2. Mathematical model formulation

Fig. 1.

2.1. Basic reproduction number $R_{0}$

2.2. Strength number

2.3. The first derivative of the Lyapunov function

Theorem 1

Proof

2.4. The second derivative of the Lyapunov function

2.5. Existence and uniqueness

Theorem 2

3. Epidemic model based on Caputo fractional derivative

Lemma

Proof

3.1. Existence of uniformly stable solution

4. Numerical simulation

Table 1.

5. Results and discussion

Fig. 2.

Fig. 3.

Fig. 4.

6. Conclusion

CRediT authorship contribution statement

Declaration of Competing Interest

References

ACTIONS

PERMALINK

RESOURCES

Cite

Add to Collections

PERMALINK

Modeling the epidemic control measures in overcoming COVID-19 outbreaks: A fractional-order derivative approach

Mohammad Sharif Ullah

M Higazy

KM Ariful Kabir

Abstract

1. Introduction

2. Mathematical model formulation

Fig. 1.

2.1. Basic reproduction number R0

2.2. Strength number

2.3. The first derivative of the Lyapunov function

Theorem 1

Proof

2.4. The second derivative of the Lyapunov function

2.5. Existence and uniqueness

Theorem 2

3. Epidemic model based on Caputo fractional derivative

Lemma

Proof

3.1. Existence of uniformly stable solution

4. Numerical simulation

Table 1.

5. Results and discussion

Fig. 2.

Fig. 3.

Fig. 4.

6. Conclusion

CRediT authorship contribution statement

Declaration of Competing Interest

References

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases

2.1. Basic reproduction number $R_{0}$