Effect of ruptured cavitated bubble cluster on the extent of the cell deformation by ultrasound

Highlights

• •Cell deformation visualized using simulated graphs.
• •Effect of bubble radius change on cell deformation.
• •Investigation of the effect of change of bubble medium on cell deformation from a physical point of view.

Abstract

In this paper, the bubble-cell model is presented. The effects of the spacing between the bubble population and the cell, the radius of the bubble and the bubble medium on the degree of cell deformation were investigated by solving the Helmholtz equation and the equilibrium of motion equation using COMSOL Multiphysis@ software. The ultrasonic transducer is applied in a round bottom flask with the bubble-cell model on the side of the ultrasonic transducer. When the distance between the bubble cluster and the cell gradually increases, the extent of deformation of the cell is reflected as first increasing and then decreasing, reaching the maximum deformation at D = 2. When the radius of the bubble is changed, there is a “constant frequency” at low frequency ultrasound in any distance case, at which the cell deformation will be violent. However, when the bubble medium is changed, there is no significant change in the degree of deformation of the cells. In other words, changes in the structure of the bubble-cell model affect the degree of cell deformation, but without structural changes, the degree of cell deformation changes very little.

1. Introduction

The renal cortex is the outer nephron layer consisting of renal tubules and convoluted tubules. Since glomerular filtration is an important clinical assessment of renal function and is the primary function of the renal cortex, there is considerable research value in accurately assessing the size, volume, and composition of the contents of the renal cortex [17]. Several renal diseases progress to the final stages of fibrosis, in which highly specialized structures are replaced by fibroblasts and collagen, while progressive loss of renal function occurs [18]. For example, the inflammatory process in the renal cortical tubulointerstitium is caused by exposure of tubular cells to glomerular filtration proteins. The reabsorption of these molecules by tubular cells can lead to the accumulation of macrophages and lymphocytes into the tubulointerstitial region [19], [20], [21], [22]. Therefore, the study of the properties of the intracellular substances in the renal cortex is important for the study of renal diseases.

Ultrasound technology is widely used in the fields of biology and cytology. The most common applications in biological cytology include cell disruption and extraction of intracellular substances [11]. Ultrasonic (US) waves are mechanical waves with a frequency range of 20 kHz–10 MHz. The mechanical effects they produce increase the modification properties of certain solids [12], [13]. In particular, high-energy US, characterized by low frequencies (20 kHz−100 kHz), is associated with cavitation phenomena due to the wave mechanics effect. The effect of US (when the frequency is close to 20 kHz) is based on the formation, growth and rupture of small bubbles in liquids; this mechanism is called “cavitation” [11]. During several oscillations, the bubble grows larger by absorbing gas or vapor from the medium. The newly formed bubbles collapse in the second stage of cavitation oscillation, releasing the absorbed energy and producing mechanical effects such as local heat and high pressure [14], [15], [16]. The resulting stress and repeated collapse of the bubbles can cause damage to the cell membrane and cell surface. It would be of great benefit to study the pressure required for cell rupture.

In previous studies we have concluded that the round bottom flask environment is most suitable for ultrasonic experiments because the reflection effect of the spherical bottom surface on the acoustic waves will minimize the interference of external factors, such as the probe depth length [23].

In this study, the bubble-cell model is presented. The effects of the spacing between the bubble population and the cell, the radius of the bubble and the bubble medium on the degree of cell deformation were investigated by solving the Helmholtz equation and the equilibrium of motion equation using COMSOL Multiphysis@ software.

2. Numerical study

In this paper, a bubble-cell model is constructed in a vessel with an ultrasound probe. This section will elucidate the equations and methods used in the bubble-cell model. Simulation calculation domain, acoustic pressure simulation, solid mechanics simulation, and boundary conditions will be presented in this section.

2.1. Simulation calculation domain

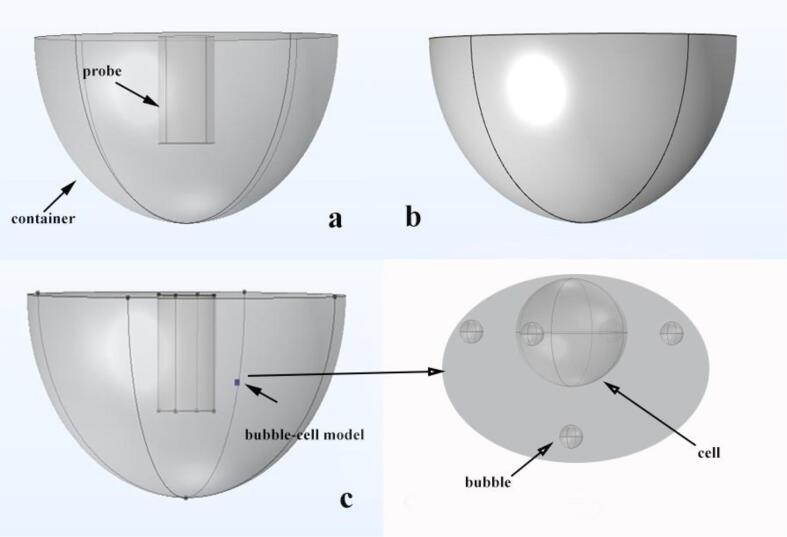
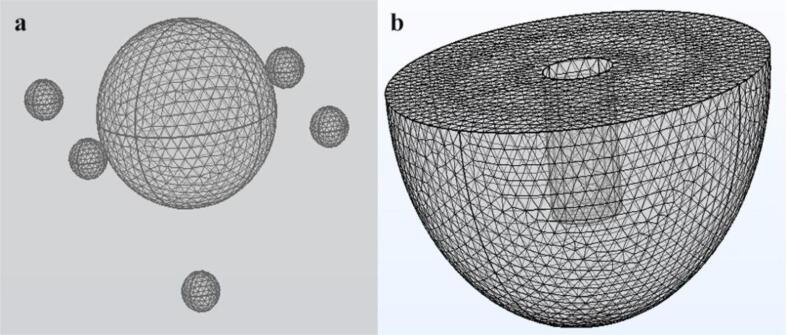
In order to ensure that the simulated bubble-cell model is modeled in an optimal environment, a round-bottom flask inserted with an ultrasonic probe is used as the reaction vessel for the experiment. The model consists of a glassy round-bottom flask and an iron ultrasound probe. Since the reaction area of the bubble-cell model is in the attachment of the ultrasonic probe, which means that the main reaction area of the model is in the lower half of the round bottom flask, the simulation calculation area of this article is located in the lower half of the round bottom flask. In order to reduce the complexity of the calculation, the two geometric parts are combined in this article, and the accuracy of the calculation is ensured by defining different materials for the boundary parts. The radius of the round bottom flask is R_f = 70 mm, the depth is H_f = 70 mm, the radius of the ultrasonic probe is R_p = 13 mm, and the depth of the probe into the round bottom flask is H_p = 40 mm. Fig. 1(a) and (b) show the geometry of the probe deep into the round bottom flask, and the material properties to be used for the simulation are shown in Table 1.

Fig. 1.

Geometry of the model.

Table 1.

Density and sound velocity of the material.

Material	Density (kg/m3)	sound velocity (m/s)
Air	1.2	343
Water	998	1500
Iron	787	5930
Glass	2500	5100
Nitrogen	1.25	351
Oxygen	1.329	328
Hydrogen	0.089	1310

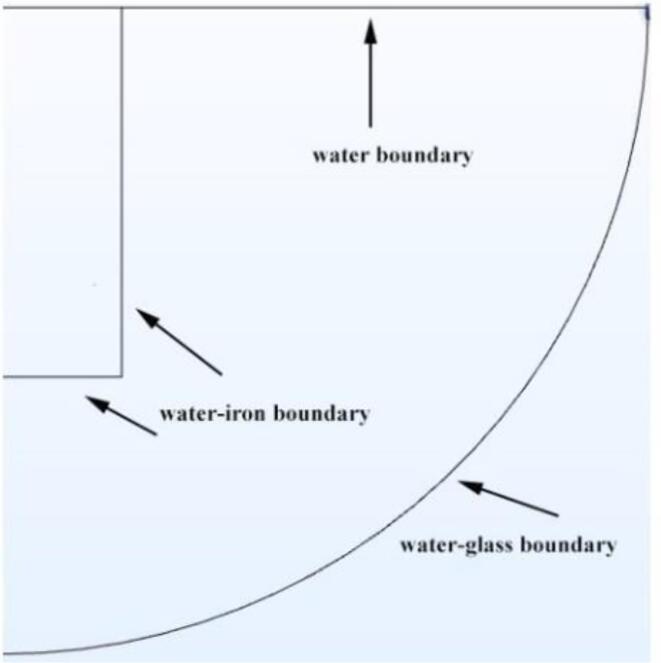
The acoustic impedance boundary is a key constraint in the simulation. Since the model is axisymmetric, a 2D geometry is used to demonstrate the acoustic impedance boundary of the model, as shown in Fig. 2. Since the model is axisymmetric, a 2D geometry is used to demonstrate the acoustic impedance boundary of the model as shown in Fig. 2. The acoustic impedance boundaries are the water boundary, the water-iron boundary, and the water–glass boundary Fig. 3.

Fig. 2.

Boundary conditions of the model (2D).

Fig. 3.

Kinetic response of bubbles under the action of positive and negative sound pressure.

The bubble-cell model is located next to the ultrasound probe. If the center point of the ultrasound probe located at the water surface of the round bottom flask is used as the coordinate origin, the cell is located at x_c = 20 mm, y_c = 10 mm and z_c = −30 mm, as shown in Fig. 1(c). The geometry of the cell in the model is a sphere with a radius of R_c = 0.007 mm, and the cell is surrounded by five bubbles located in the ± x direction, ±y direction and −z direction of the bubble, respectively. Fig. 1(d) shows the structural diagram of the bubble-cell model. The properties of Renal cortex cells and the parameters calculated by the model are shown in Table 2.

Table 2.

Data used for simulation experiments.

f	Ultrasound frequency [kHz]	1–100
Pu	Input power [W]	32
ρc	Density of cell [kg/m3]	1058.6
Ec	Young's modulus [Pa]	10
nu	Poisson's ratio [1]	0.45

2.2. Acoustic pressure simulation

COMSOL Multiphysics 5.5 ® is a finite element method software that is used in this part to simulate the physical field of pressure acoustics. This study is computed using the linear Euler equation in the frequency domain, which contains the sound propagation problem controlled by partial differential equations (PDEs). The linear Navier-Stokes equation is

$$\frac{\partial \rho }{\partial t}+\mathrm{\nabla }·({\rho }_{0}u+\rho u_0)=M$$

$${\rho }_0(\frac{\partial u}{\partial t}+(u·\mathrm{\nabla })u_0+(u_0·\mathrm{\nabla })u)+\rho (u_0·\mathrm{\nabla })u_0=\mathrm{\nabla }·\sigma +F-u_{0}M$$

$${\rho }_0{C}_p(\frac{\partial T}{\partial t}+u·\mathrm{\nabla }{T}_0+u_0·\mathrm{\nabla }T)+\rho C_p(u_0·\mathrm{\nabla }{T}_0)-{\alpha }_p{T}_0(\frac{\partial p}{\partial t}+u·\mathrm{\nabla }{p}_0+u_0·\mathrm{\nabla }p)$$

$$-{\alpha }_{P}T(u_0·\mathrm{\nabla }{p}_0)=\mathrm{\nabla }·(k\mathrm{\nabla }T)+\mathrm{\Phi }+Q$$

Where

$$\sigma =-pI+\mu (\mathrm{\nabla }u+{(\mathrm{\nabla }u)}^T)+({\mu }_B-\frac{2}{3}\mu )(\mathrm{\nabla }·u)I$$

$$\rho ={\rho }_0({\beta }_{T}p-{\alpha }_{p}T)$$

In the equation, p is the sound pressure change, T is the temperature, u is the velocity field, ρ is the density, and μ is the gas viscosity.

The model used in this study is one without viscosity and heat loss and without flow, which means

$$\mu =0,u_0=0$$

Thus the Helmholtz equation in the frequency domain can be obtained as

$$\mathrm{\nabla }·(-\frac{1}{{\rho }_0}\mathrm{\nabla }p)-\frac{1}{{\rho }_0}{(\frac{\omega }{c})}^{2}p=0$$

Where

$$\omega =2\pi f$$

$$\mathrm{\nabla }=\frac{{\partial }^{2}p}{\partial x^2}+\frac{{\partial }^{2}p}{\partial y^2}+\frac{{\partial }^{2}p}{\partial z^2}$$

ρ₀ is the liquid density (m/s), p is scattered pressure field (N/m²), c₀ is sound velocity of liquid, and k refers to the wave number (rad/m), defined by the angular frequency ω(rad/s).

In the process of acoustic pressure vibration, when the acoustic pressure reaches its maximum value, the acceleration of the local area of the medium is expressed as

$$a_n=\omega \sqrt{\frac{2I}{{\rho }_0{c}_0}}$$

and I refers to the sound intensity, defined by Eq. (10)

$$I=\frac{P_U}{A}=\frac{P_u}{\pi r^2}$$

Substitution of Eq. (10) into Eq. (9) gives the acoustic excitation acceleration of the ultrasound probe as

$$a_n=\omega \sqrt{\frac{8P_u}{\pi {\rho }_0{c}_0{D}_p}}$$

Where D_p = 26 mm refers to the diameter of the probe.

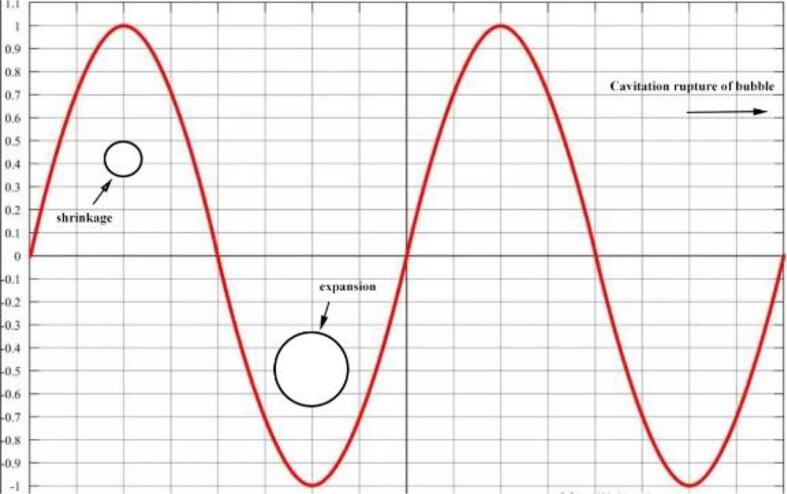
High ultrasound intensity will let the bubbles in the liquid produce inertial cavitation effect, that is, generally inactive and difficult to detect the cavitation nucleus into an active cavity, so that the bubbles in the alternating excitation of positive and negative ultrasound sound pressure to produce the corresponding kinetic response, when the negative ultrasound pressure continues to rise to and reach a certain threshold, the bubbles collapse and rupture due to excessive vibration amplitude. The ultrasonic intensity causes the ruptured bubble to be in a transient cavitation state at the moment of rupture, and this process generates a large amount of broadband noise. In addition, the cavitation bubble in this study ruptures in the presence of a solid wall around the bubble, which leads to the generation of a jet, the intensity of which is defined by Eq. (12)

$$\gamma =\frac{d}{R_{max}}$$

where d is the distance from the center of the bubble to the solid wall, and R_max is the maximum bubble radius.

The model in this study is calculated by considering that the instant of bubble rupture generates a jet acting on the surface of the cell membrane. The point on the surface of the bubble near the cell is defined as a unipolar source, due to the large amount of noise generated when the bubble bursts. The computational equation of the unipolar point source in the model is

$$\mathrm{\nabla }·\left(-\frac{1}{{\rho }_c}(\mathrm{\nabla }{p}_t-q_d)\right)-\frac{k_{\mathit{eq}}^2{p}_t}{{\rho }_c}=\frac{4\pi }{{\rho }_c}S\delta \left(x-x_0\right)$$

where

$$k_{\mathit{eq}}=\frac{\omega }{c_0},S=e^{i\varphi }\frac{i\omega {\rho }_c{Q}_s}{4\pi }$$

Ф is the phase and Q_s is the volume flow rate from the source, calculated from the jet velocity v = 11.4 m/s [3].

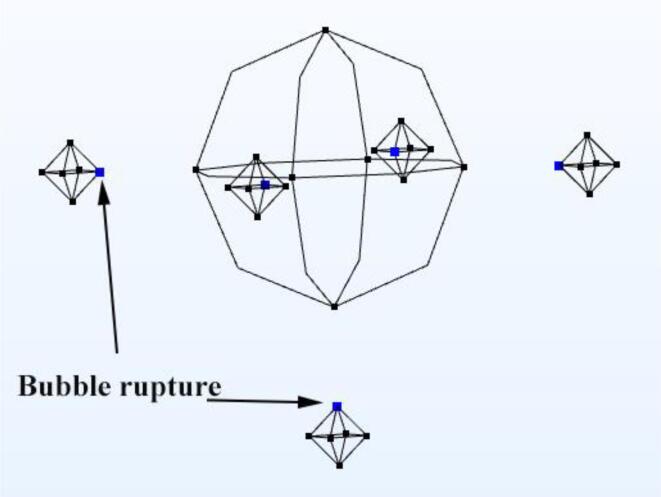
In order to more significantly demonstrate the relationship between the location of the bubble rupture generating jet and the cell, the 2D model was used to describe the jet generation point in this model. As shown in Fig. 4, the jet generation locations in this model are all located on the side of the bubble near the cell.

Fig. 4.

Position of the jet generation site in relation to the cell.

2.3. Solid mechanics simulation

Stress and strain in cells affected by bubble jets and ultrasound are modeled and calculated using a solid mechanics approach. The equilibrium equation of motion is

$$\rho \frac{{\partial }^2\overrightarrow{u}}{\partial t^2}+d_a\frac{\partial \overrightarrow{u}}{\partial t}-\mathrm{\nabla }\stackrel{\sim }{\sigma }=\overrightarrow{f}$$

where ρ is the solid density, d_a is the damping factor, u is the displacement, σ is the stress, and f is the volume force. Besides the duhamel-hooke law is

$$\stackrel{\sim }{\sigma }=C{\stackrel{\sim }{\epsilon }}_{\mathit{el}}+{\stackrel{\sim }{\sigma }}_0=C(\stackrel{\sim }{\epsilon }-{\stackrel{\sim }{\epsilon }}_0-{\stackrel{\sim }{\epsilon }}_{\mathit{th}})+{\stackrel{\sim }{\sigma }}_0$$

where

$$\stackrel{\sim }{\epsilon }=\frac{1}{2}[{(\mathrm{\nabla }\overrightarrow{u})}^T+\mathrm{\nabla }\overrightarrow{u}]$$

In the equation, C is the isotropic elastic matrix, ε_el is the elastic strain, ε is the total strain, ε₀ is the pre-strain, ε_th is the thermal strain, and σ₀ is the pre-stress. The simple harmonic-frequency domain equation of comsol can be obtained from the type of study as

$$-\rho {\omega }^2{\overrightarrow{U}}_0+d_{a}j\omega {\overrightarrow{U}}_0-\mathrm{\nabla }·\stackrel{\sim }{\sigma }={\overrightarrow{F}}_0$$

From Eqs. (14)–(16), the force generated by the jet on the cell when the bubble bursts can be calculated for the bubble-cell model.

2.4. Boundary conditions

Acoustic impedance is the complex ratio of the acoustic pressure of the medium in an area of the wave front surface to the volume velocity through this area, which reflects the damping characteristics of a location in the medium to the mass vibration caused by acoustic perturbation. The boundary conditions of the pressure acoustics are shown in Fig. 2, where the governing equations are as follow:

$$n·(-\frac{1}{\rho }·\mathrm{\nabla }{p}_u)=p_u\frac{i\omega }{Z_i},Z_i={\rho }_i{c}_i$$

where Z_i is resistivity. Fig. 5 shows the meshing of the simulation computational domain. The maximum size of bubble, cell and ultrasonic reactor is 0.0005 mm, 0.001 mm and 5 mm respectively.

Fig. 5.

Mesh distribution of the model.

3. Results and discussion

Due to the strong inaccuracy of Comsol for the calculation of nm magnitude values and the radius of the cell is R_c = 0.007 mm, the radius of the cavitation bubble considered in the model of this paper is R_b = 0.1–5 µm and the cavitation bubble-cell spacing is D = 0.5–5 µm. It is worth mentioning that only the case of 100% bubble rupture is considered in this paper, and the case where the bubble only oscillates and deforms without rupture is not considered.

3.1. Effect of bubble-cell distance

Cell surface acoustic pressure and cell volume strain are important indicators of the degree of cell deformation used in this paper. Ultrasound propagates through the medium and the vibrations produce a change in pressure. The bubbles and cells in the medium are excited by the alternating positive and negative sound pressure to produce kinetic effects. Fig. 6 illustrates the relationship between cell surface acoustic pressure and cell deformation. Volume strain is defined as the amount of change per unit volume of an object, when the volume V increases or decreases by ΔV, the volume strain can be expressed by the following equation

$$\theta =\frac{V^{\prime }-V}{V}={\epsilon }_x+{\epsilon }_y+{\epsilon }_z$$

where ε_i refers to the positive strain in direction i(i = x,y,z), that is, the first strain invariant.

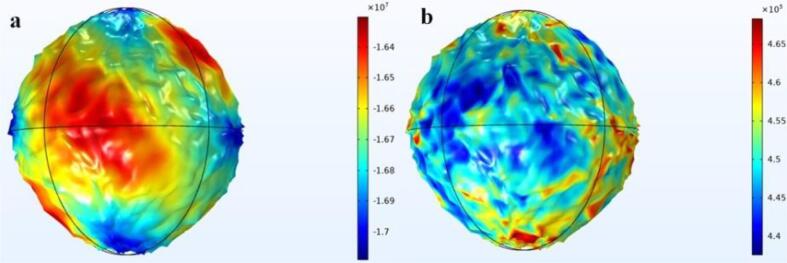
Fig. 6.

a) Cell surface acoustic pressure; b) Volume strain.

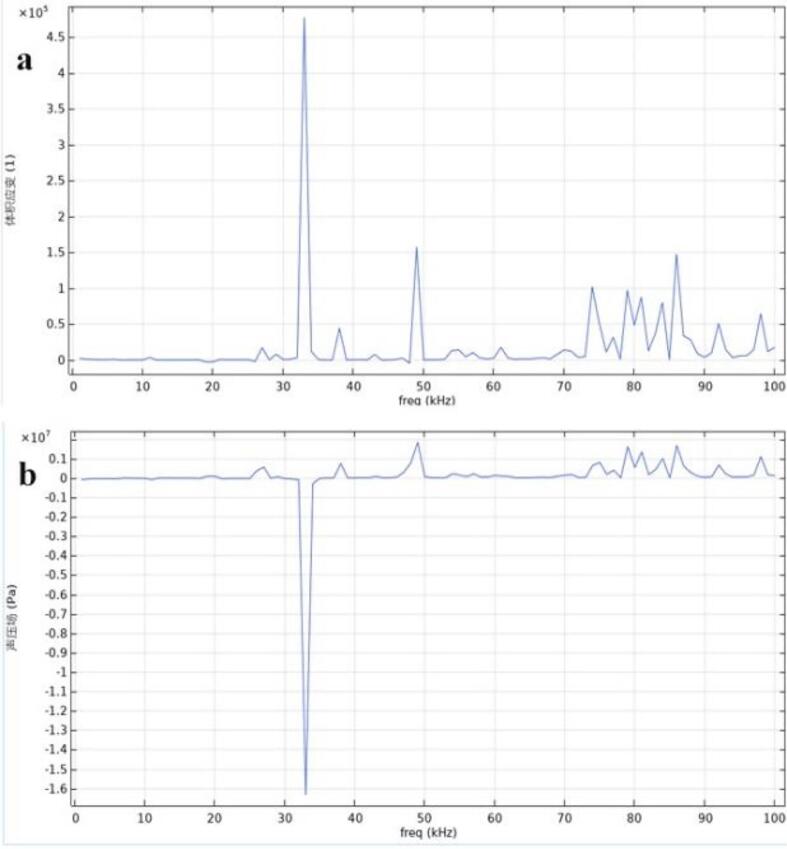
When the cell surface acoustic pressure is a minimum, as in the blue region of Fig. 6(a), the corresponding cell volume strain reaches a maximum, as in the red region of Fig. 6(b); conversely, when the cell surface acoustic pressure is a maximum, as in the red region of Fig. 6(a), the corresponding cell volume strain reaches a minimum, as in the blue region of Fig. 6(b). This phenomenon indicates that the elevated negative acoustic pressure of ultrasound causes drastic changes in vibration and deformation, and it matches the phenomenon described in other articles [1], [2], [3], [4], which indicates that the model established in this paper is reliable. In addition, the curve in Fig. 7 also shows that the maximum negative acoustic pressure corresponds to the maximum deformation.

Fig. 7.

(a) Volumetric strain; (b) curve of acoustic pressure at the cell surface with frequency.

Under ultrasonic excitation, the bubbles in a multi-bubble system are subjected to not only the incident ultrasonic waves, but also the inter-bubble forces, forming a complex kinetic motion process [1]. Therefore, a complex mechanical effect on the cells in the system occurs when the cavitated bubbles in the bubble-cell model are all ruptured.

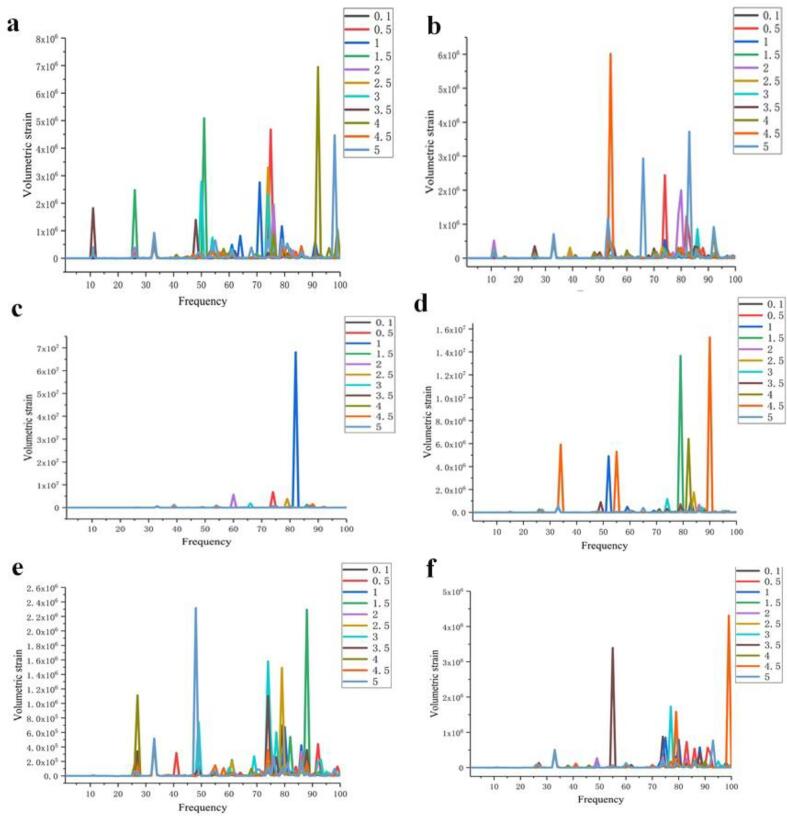
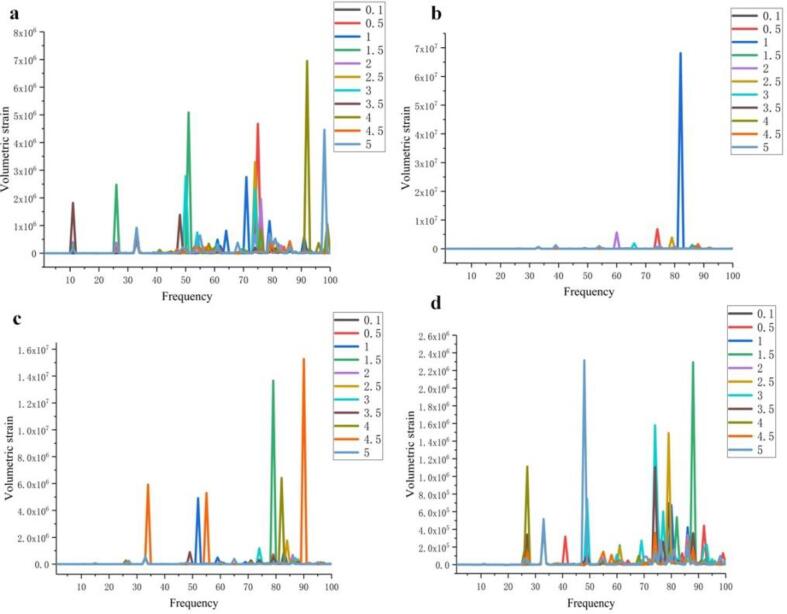
The model in this paper has a frequency interval in the range of 1–100 kHz as shown in Fig. 8 and Fig. S1-S66. It can be seen from Fig. 8(a)-(f) that the degree of deformation of the cells showed a trend of increasing and then decreasing. The deformation amplitude of the cells gradually increased in the intervals of D = 0.5, 1, 2 μm and reached the maximum value at D = 2 μm, however, the deformation amplitude of the cells gradually decreased in the intervals of D = 2, 3, 4 μm, and the cells had smaller deformation at D = 4 μm. When the bubble-cell distance was 5 μm, the cell deformation in the rest of the cases was smaller than that of D = 4 μm, although there was a larger cell deformation at R_b = 3.5, 4.5 μm.

Fig. 8.

Effect of bubble radius on cell volume strain at different spacing. a) 0.5 μm; b) 1 μm c) 2 μm; d) 3 μm; e) 4 μm; f) 5 μm.

The action of ultrasound on cells is caused by cavitation bubbles [5]. The resonant frequency of bubble oscillation and the large amount of broadband noise generated by cavitation promote cell deformation, and cell damage is caused by the shear stress generated by bubble rupture acting as a local force on the cell surface. In the case where the bubble-cell distance is small, the bubbles are also spaced less apart from each other, and the broadband noise and shear forces generated by bubble rupture are eliminated more between each other. Conversely, when the bubble-cell distance increases, the force and sound pressure field generated by bubble rupture will be influenced by the background sound pressure field, and thus the force acting on the cell surface is reduced. With a bubble-cell distance of 2 μm, the interaction between multiple bubbles is not too violent, and the cavitated bubble ruptures with just the right amount of force on the cell to ensure that the cell produces a violent deformation.

3.2. Effect of bubble radius

The bubbles affected by ultrasound oscillate. At very low acoustic pressure, the bubble oscillates in a linear and symmetric manner, and this cavitation is called steady-state cavitation. When the net gas flows into the bubble, the bubble will keep expanding and growing to the resonance size, at which time it will exhibit stable low-amplitude oscillations, and the stable low-amplitude oscillations will generate micro-flow around the bubble. Cavitation at higher ultrasonic intensities is called inertial cavitation. The inactive and undetectable cavitation nuclei in the liquid transform into active cavities and bubbles, which in turn generate oscillations that may eventually lead to bubble rupture. Bubble oscillation and rupture to generate jets is one of the causes of cell rupture. In distinction from most simulations of continuous bubble oscillations, this paper focuses on the kinetic effects of multiple bubbles on cells for ten cases with discrete bubble radius R_b = 0.1, 0.5, 1, 1.5, 2, 2.5, 3, 3.5, 4, 4.5, 5 μm.

From the study in section 3.1, it can be seen that the degree of influence of bubble-cell distance on cell deformation tends to increase first and then decrease. Therefore, in this section, D = 0.5, 2, 3 and 4 μm were chosen as fixed spacing to investigate the effect of bubble radius on cell deformation when the distance is fixed. The radius of the bubble with the greatest effect on the cell is found to be Rb = 4 μm for D = 0.5 μm, Rb = 4.5 μm for D = 3 μm, and Rb = 5 μm for D = 4 μm. However, the radius of the bubble with the greatest effect on the cell is Rb = 1 μm in the case of D = 2 μm, which has the most significant effect, as observed in Fig. 9.

Fig. 9.

Effect of bubble radius on cell volume strain at different spacing. a) 0.5 μm; b) 2 μm; c) 3 μm; d) 4 μm.

As can be found in Fig. 9(a), although the maximum deformation of the cell occurs at R_b = 4 μm, the effect of bubbles on the cell in these cases of R_b < 3 μm is evident at both low (f < 40 kHz) and high frequencies. In particular, at f = 11, 26, and 33 kHz, bubbles of different radius cause drastic deformation of the cells under the action of ultrasound at this frequency. This means that there is some fixed frequency in low-frequency ultrasound at which the cells are violently deformed by ultrasound, regardless of the radius of the bubbles. Whereas in medium and high frequency ultrasound, the larger the radius of the bubble, the higher the frequency at which the deformation of the cell will be affected. When D = 2 μm, the bubble cluster with R_b = 1 μm has the most pronounced effect on cell deformation. In addition to bubbles of this radius, the bubble cluster with R_b = 0.5 μm also has a very pronounced mechanical effect on cells. The frequency of the effect of bubble cluster on cell deformation is concentrated with f = 60–100 kHz, that is the middle and high frequency stage. The effect of the change in bubble cluster radius on the degree of cell deformation at D = 3 μm was similar to that at D = 0.5 μm, but it is noteworthy that the change in bubble radius had almost no effect on cell deformation under the action of low-frequency ultrasound. In the f = 1–30 kHz interval, as seen in Fig. 9(c), the ten curves almost coincide tightly, which indicates that the change in bubble radius is not the main factor for the change in cell deformation occurring in these frequency ranges. At middle and high frequency, the cell deformation by the action of the bubble cluster with R_b = 4.5 μm appears many times drastically deformed, while R_b = 4,5μm does not have a very obvious effect. The case of D = 4 μm is very similar to that of D = 3 μm, but since the force of bubble cluster rupture on the cell is much less pronounced in this spacing case than in the previous cases, the change in cell deformation reflected by the change in bubble radius is more chaotic. However, Fig. 9(d) still demonstrates the presence of a fixed frequency of the bubble-cell model species, which is better found in the range of f = 10–50 kHz.

Therefore, the effect of bubble radius change on cell deformation under the action of low frequency ultrasound is not obvious, and their forces on cells are similar regardless of bubble radius change. On the other hand, the change of bubble radius during high-frequency ultrasound action is an important influencing factor for the different deformation of cells, and the radius of bubble that causes significant cell deformation is larger as the bubble-cell model distance increased.

3.3. Effect of bubble media

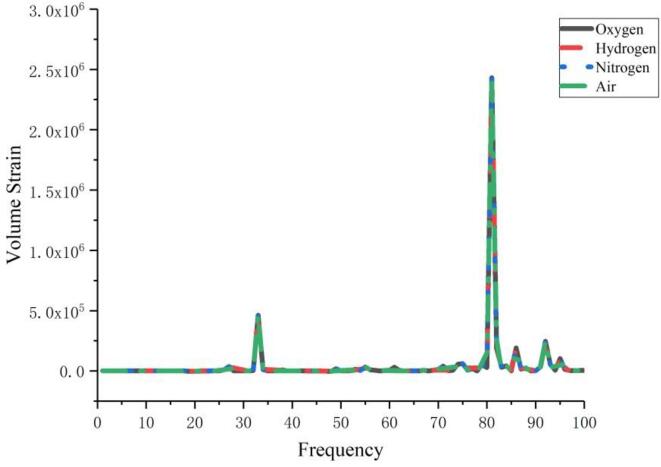
Anaerobic bacteria have a pivotal role in human health and can also be used to produce high-value industrial products, thus anaerobic bacteria have a wide range of research interests [6], [7], [8], [9], [10]. In contrast to aerobic cells, oxygen or air, gases rich in oxygen ions, should not be introduced into the liquid when studying the deformation of anaerobic cells. Therefore, in this paper, it was investigated whether changing the gas properties, which means introducing different classes of gases into the liquid, would have an effect on cell deformation. Oxygen, air, hydrogen and nitrogen are the gases studied, and the properties of the gases are presented in Table 1.

From Fig. 10, it can be found that the change in the properties of the gas introduced into the liquid has almost no effect on the cell deformation, and the cell deformation curves almost overlap under the action of the four common gas bubble populations. This implies that the passage of any type of gas into pure liquid, a gas-free and nucleation-free liquid, has no effect on the experimental results in kHz-scale ultrasound cell experiments.

Fig. 10.

Effect of bubble properties on cell deformation.

From the perspective of physics, changes in the bubble medium do not affect the deformation of the cells. However, in response to the claim of many studies that the introduction of different gases affects the experimental results, this study suggests that the change of bubble medium may cause the change of chemical ions in the solution, which in turn affects the deformation and permeability of the cells.

4. Conclusion

The bubble rupture of ultrasound-induced cavitation has a clear effect on cell deformation. The change in the structure of the bubble-cell model implies a change in the shear force of the microjets generated by the bubbles acting on the cell surface during rupture, thus causing deformation of the cells in the bubble-cell model. However, when the structure of the bubble-cell model does not change, but only the bubble medium changes, there is no significant difference in the deformation of cells. Therefore the structure of the bubble-cell model is the decisive factor affecting the cell deformation.

CRediT authorship contribution statement

Peilin Cao: Conceptualization, Investigation, Software, Validation, Writing – original draft. Changchun Hao: Writing – review & editing, Project administration, Funding acquisition. Binbin Li: Methodology, Data curation. Hao Jiang: Formal analysis, Methodology. Yongfeng Liu: Resources, Supervision.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.