Abstract
Accurate rotational correlation times (τc) are critical for quantitative analysis of fast timescale NMR dynamics. As molecular weights increase, the classic derivation of τc using transverse and longitudinal relaxation rates becomes increasingly unsuitable due to the non-trivial contribution of remote dipole-dipole interactions to longitudinal relaxation. Derivations using cross-correlated relaxation experiments, such as TRACT, overcome these limitations but are erroneously calculated in 65% of the citing literature. Herein, we developed an algebraic solutions to the Goldman relationship that facilitate rapid, point-by-point calculations for straightforward identification of appropriate spectral regions where global tumbling is likely to be dominant. The rigid-body approximation of the Goldman relationship has been previously shown to underestimate TRACT-based rotational correlation time estimates. This motivated us to develop a second algebraic solution that employs a simplified model-free spectral density function including an order parameter term that could, in principle, be set to an average backbone S2 ≈ 0.9 to further improve the accuracy of τc estimation. These solutions enabled us to explore the boundaries of the Goldman relationship as a function of the H-N internuclear distance ( r ), difference of the two principal components of the axially-symmetric 15N CSA tensor (ΔδN), and angle of the CSA tensor relative to the N-H bond vector (θ). We hope our algebraic solutions and analytical strategies will increase the accuracy and application of the TRACT experiment.
Keywords: Model-free, order parameters, TROSY, NMR, dipole-dipole (DD), chemical shift anisotropy (CSA)
Introduction
A particle’s rotational Brownian diffusion is characterized by the average time to rotate one radian, also known as the rotational correlation time (τc). It is related to the size and shape of a molecule, and in the case of a rigid, spherical particle, can be estimated from the Stokes-Einstein relation1. The rotational correlation time is frequently used in biophysics to gauge molecular aggregation and solvent viscosity. In protein NMR, rotational correlation time estimates are used to optimize interscan recycling delays, magnetization transfer delays in correlation experiments, and indirect dimension evolution times in multidimensional experiments2. Perhaps most significantly, τc is the critical parameter for quantitative dynamics analyses, such as ‘model-free’ formalism, in which separation of overall and internal motion are required3,4.
The 1989 seminal work by Kay, Torchia and Bax5 showed τc can be estimated from 15N longitudinal (R1) and transverse (R2) relaxation rates using equations established by Abragam6. These equations assume there is no rapid internal motion of the internuclear bond vector (i.e. motion faster than the rate of molecular tumbling), and that relaxation only results from i) dipole coupling with the covalently bonded nucleus and ii) the chemical shift anisotropy of the relaxing nucleus. In the original model free formalism, the amplitude and time parameter for this fast internal motion are referred to as the order parameter (S2) and the effective correlation time (τe), respectively, where it is assumed that τe ≪ τc3,4. Note that τm is frequently used in the literature to refer to overall molecular tumbling time, where 1/τm = 1/τe + 1/τc. In this present work, unless stated otherwise, we assume fast motions on the time scale of τe ≪ τc do not exist and thus τc is synonymous with τm. In the absence of τe, the S2 order parameter essentially cancels out when R2 is divided by R15. Thus, the R2/R1 ratio can be used to estimate τc by using the approximate formula in Eqn. 1, where vN is the 15N resonance frequency (in Hz).
| (1) |
Although this is a common approach for estimating the rotational correlation time, there are several important considerations. First, R1 values are susceptible to rapid internal motions of the spin system bond vector; Kay and co-workers established that this could be resolved by excluding all spin systems with 15N{1H}-NOE values < 0.65. Second, substantial chemical exchange contributions can potentiate the observed R2 rates7. Again, Kay et al. established a precedence for manually inspecting each 15N rate constant for indications of fast internal motions and chemical exchange5. This method of excluding spin systems from τc estimates was subsequently automated by Clore et al8, who first suggested determination of the mean R2/R1 ratio and exclusion of all values outside one standard deviation. Implicit in this model is that the tumbling is isotropic5,8; Barbato et al9 expanded application to anisotropic biomolecular systems. Anisotropic tumbling deviates R2 and R1 values, independent of chemical exchange or fast internal motions, but in opposing directions. Therefore, exchanging residues in which the R2/R1 model does not apply can be detected by considering R2 values that deviate more than one standard deviation from the mean, but without an associated decrease in R1 relaxation 9. Again, spin systems with 15N{1H}-NOE < 0.6 (indicating significant fast time scale motion) were excluded from τc estimation. The remaining R2/R1 values are then used to calculate τc using Eqn 1. Statistical selection of spin systems for τc calculation is generally appropriate but does have the potential for mishandling by an inexperienced user. For example, a protein with significant regions undergoing chemical exchange will report high R2 or R2/R1 standard deviations from inclusion of unsuitable spin systems. It is also not hard to imagine systems with significant regions of high internal motions, but not complete random coil, which would skew the distribution of R1 values and lead to the inclusion of spin systems where the R2/R1 model is a poor approximation. Lastly, the R2/R1 method does not account for the effects of dipolar couplings to remote (non-covalently bonded) protons on R1, which increase near exponentially as a function of molecular weight10,11; although perdeuteration largely ameliorates this problem. Nonetheless, there are clear advantages to approaches that can estimate τc from a measurable relaxation parameter that is insensitive to the effects of remote dipolar couplings and chemical exchange.
One such quantifiable phenomenon is transverse cross-correlated relaxation (CCR, ηxy). CCR results from the coordinated rotation of two nuclei in a magnetic field12 and is primarily a function of dipole-dipole (DD) coupling, the chemical shift anisotropy (CSA) of the observed relaxing nucleus, and the molecular rotational correlation time. Measurements of CCR exploit the fact that the sign (±) of ηxy depends on the spin states of the coupled nuclei. Cross-correlated relaxation only contributes to R2 and R1 in coupled systems because the opposing (opposite sign) contributions to relaxation cancel for decoupled spins12. 1H-15N and 1H-13C aromatic TROSY experiments exploit this property by only selecting signals from the spin state with relaxation interference13,14. Several methods have been developed to measure ηxy in the 1H-15N spin system15–18 where the most common approach is a pair of spectra that record the transverse relaxation rates of 15N alpha (Rα) and beta (Rβ) spin states. These rates are the sum of the auto-relaxation rate (Rauto), remote 1H dipolar interactions (RD), chemical exchange (Rex), and ηxy (Eqns. 2 and 3); where ηxy is derived from subtraction of Rα and Rβ11,16,17 (Eqns. 4 and 5).
| (2) |
| (3) |
| (4) |
| (5) |
Using this method, the contributions to relaxation from remote protons and chemical exchange are cancelled and extraction of ηxy is possible. Goldman12 showed that ηxy can be estimated given τc, via the spectral density function, using Eqn. 6.
| (6) |
where:
| (7) |
| (8) |
| (9) |
and:
Goldman’s relationship between ηxy and τc was first exploited experimentally by Lee and colleagues in the [15N,1H]-TRACT (TROSY for rotational correlation times) pulse sequence11; although, the manuscript does not explicitly detail how the Goldman relationship was solved. There are three important assumptions when applying the Goldman approach to TRACT data: i) the region analyzed is free of fast internal motions, which is rarely known a priori, ii) the system is a rigid body (i.e. S2 ~ 1.0), and iii) the spin pair is isolated from remote DD/CSA relaxation interference. When pursuing our own TRACT analyses, we noted our τc calculations were inconsistent with the original manuscript despite using identical physical and geometric constants.
Herein, we report an algebraic solution to the Goldman approach for straightforward calculation of τc from measured Rα and Rβ relaxation rate. Using this solution, we show that a numerical error in the original TRACT report has propagated into a high proportion of the citing literature. We use our algebraic solution to investigate complications from fast internal motions and propose analytical strategies to exclude unsuitable spin systems. The impact of order parameters motivated us to develop a second algebraic solution that includes S2 as a parameter. We also noted that little attention has been paid to distributions of the difference of the two principal components of the axially-symmetric CSA tensor (ΔδN), the CSA tensor angle relative to the internuclear bond vector (θ), and the internuclear distance (r). We show that the chosen value can have a non-negligible effect on τc calculations but, as the relationship is near linear, a symmetrical random distribution around an average value would cancel out over many spin systems. Finally, we discuss how relaxation interference between remote 1H DD and local CSA affects the observed CCR rate; a phenomenon that is independent of RD above but is generally negligible compared to other factors discussed in this paper.
Experimental
Uniformly-labeled [U-15N,2H]-OmpX was expressed, purified, and solubilized into 0.5% (w/v) dodecylphosphocholine (DPC) micelles as previously described19. Final buffer conditions were: 20 mM NaPi (pH 6.8), 100 mM NaCl, 5 mM EDTA, and 10% D2O. NMR experiments were performed at 303.15 K on Varian 800 MHz spectrometer equipped with Agilent 5 mm PFG 1H{13C,15N} triple resonance salt tolerant cold probes. 1D TRACT experiments were collected with 4096 complex points and 1.5 s relaxation delay. A series of experiments were collected with eight variable relaxation delays: 1, 2, 4, 8, 16, 32, 64, and 128 ms. Relaxation rates were determined by fitting to a two-parameter exponential function.
Results and Discussion
An algebraic solution to the Goldman relationship
While validating our own numerical solution to the Goldman relationship, we noted a 6.6% overestimation of ηxy in Lee et al11. Specifically, Figures 3 and 4 in their paper present τc = 21 ns and 24 ns, respectively, from which we calculate ηxy = 27.1 Hz and 30.9 Hz, respectively, using Eqns. 6–9 and the quoted physical constants. This is inconsistent with the reported Rα and Rβ which yield ηxy rates of (64–13)/2 = 25.5 Hz and (80–22)/2 = 29 Hz, respectively, using Eqns. 4–5. Hypothesizing that this discrepancy may be the result of poor numerical minimization, we generated an exact solution to Eqn. 6 with respect to τc, given B0 and ηxy.
Figure 3:
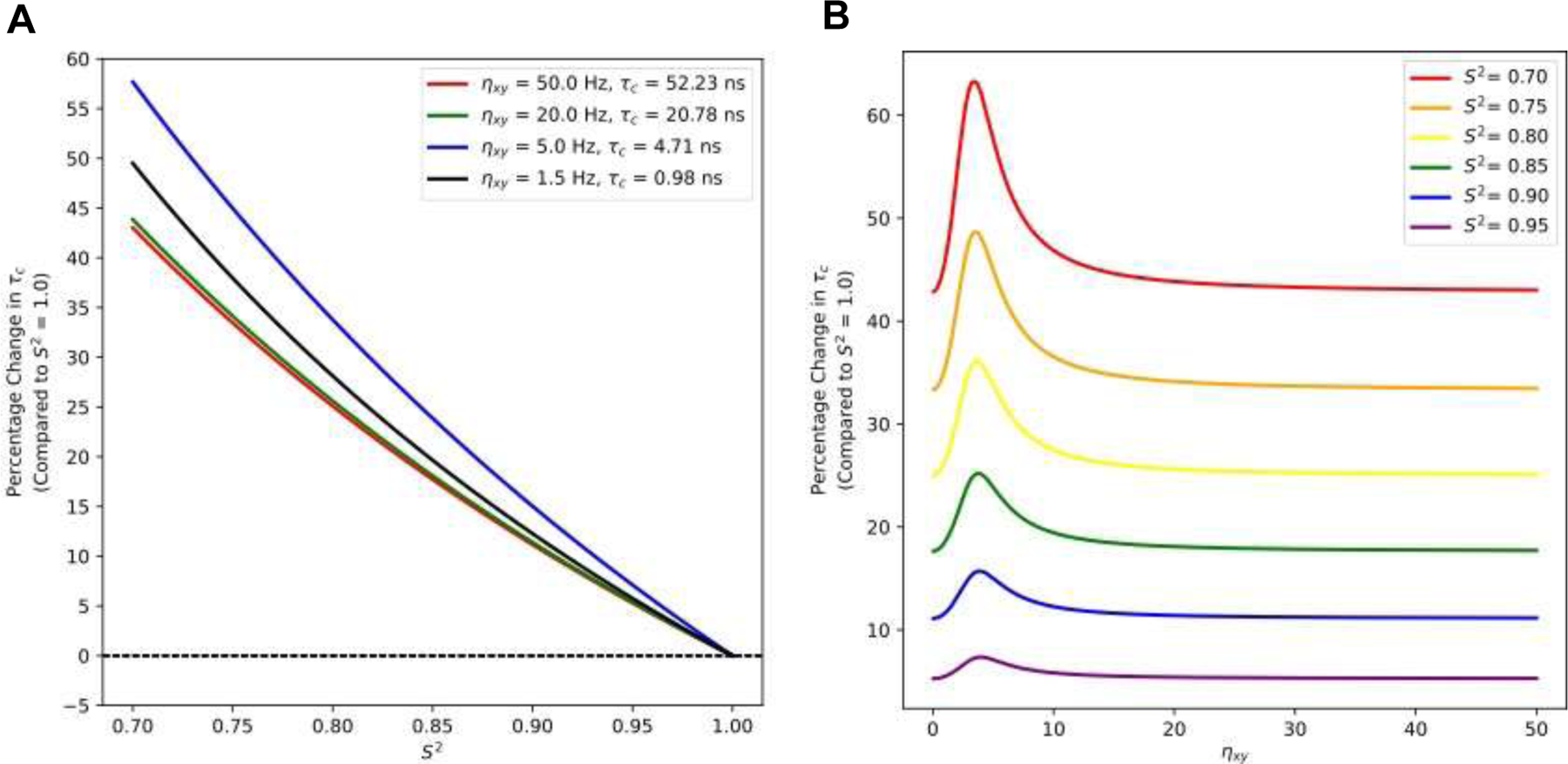
Effect of rigid-body approximation on rotational correlation time estimates derived from modified Goldman relationship. A) Plot of percentage change in τc estimation, relative to rigid body approximation, as a function of S2 order parameter. Relative to the rigid body assumption, typical backbone order parameters (0.85 ≤ S2 ≤ 0.95)23,24 increase the rotational correlation time 5–25% depending on the CCR rate; this error increases to ≥45% at an S2 ≈ 0.7. B) Plot of percentage change in τc estimation, relative to rigid body approximation, versus ηxy for select S2 values from 0.7 to 0.95. A sharp, biphasic rise in error is observed for ηxy≈ 4 Hz.
Figure 4:

Effect of the internuclear distance (r), difference of the two principal components of the axially-symmetric CSA tensor (ΔδN), and angle of the CSA tensor relative to the N-H bond vector (θ) on rotational correlation time τc estimation. The relative values simulated are taken from the original TRACT manuscript11; as discussed in the text, other values for these parameters may be more accurate. A) Percentage change in τc estimation versus τ (relative to τ = 1.02 Å) for ηxy ranging from 10 – 40 Hz. B) Percentage change in τc estimation versus ΔδΝ (relative to ΔδΝ = −160 ppm) for ηxy ranging from 10 – 40 Hz. C) Percentage change in τc estimation versus θ (relative to θ = 17°) for ηxy ranging from 10 – 40 Hz. The error for each parameter is negatively symmetric around the chosen value with little variation over the range of simulated ηxy from 10 to 40 Hz. When integrated over many spins, any deviations around the mean would tend to average out the error in τc estimation.
We start by expanding the spectral density function (J) in Eqn. 6 and substituting ηxywith (Rβ − Rα)/2 to give Eqn. 10, where ωN is the 15N Larmor frequency (in radians per second):
| (10) |
The right-hand side of Eqn. 10 is a constant once the relaxation rates have been measured. We therefore replace this side with the symbol ‘c’.
| (11) |
Solving Eqn. 11 for τc gives20,
| (12) |
where,
| (13) |
Using Eqns. 12 and 13, we recalculated τc = 19.8 and 22.5 ns, respectively, which are again approximately 6.5% less than the reported values. We concluded that Lee et al. contains an inadvertent error, and note that using a 700 MHz field (instead of the quoted 750 MHz) does reproduce the reported τc values.
We next surveyed the citing literature with the hypothesis that subsequent TRACT users may have similar miscalculations. As of early 2021, the original manuscript had been cited 120 times in PubMed. Half of all citing publications appeared in the years 2015–2020, indicating an increasing interest in this methodology 10–15 years after its’ original publication. We focused our analysis on manuscripts with sufficient data to validate calculations using our algebraic solution (Eq. 12). Table 1 shows that out of 120 manuscripts, three referenced the original TRACT paper without performing any cross-correlated relaxation experiments, six were methodological reviews, and seventy-eight used the TRACT methodology but did not provide enough experimental information to confirm their calculations. Thirty-three papers (30%) reported sufficient data to authenticate 65 total calculations.
Table 1:
Published manuscripts that cite the TRACT paper7 categorized by: papers that reference the TRACT paper but provided no τc calculations; NMR methodological reviews that detail the TRACT experiment; papers that determined τc using the TRACT method but did not provide sufficient data for τc verification; and papers that did provide enough data for verification of τc calculations.
| Paper Category | Number of Articles | Percentage of Articles (%) |
|---|---|---|
| Only Referenced | 3 | 2.5 |
| Reviews | 6 | 5.0 |
| Insufficient Data for Analysis | 78 | 65.0 |
| Sufficient Data for Analysis | 33 | 27.5 |
We defined an error measure by dividing the published τc by our algebraically determined value. For example, the original paper reported τc = 21 and 24 ns, while we calculated values of 19.8 and 22.5 ns, giving error ratios of 1.061 and 1.067, respectively. There are several features of this analysis worthy of report (Fig. 1A). First, 35% (23/65) of results are accurate (error ratio 1.0), clustering to within a 2% error interval of 0.99 and 1.01 and validating our algebraic approach. Second, 23% (15/65) of results cluster around 1.067 ± 0.03 (dotted line); this strongly suggests an error from the original TRACT report11 was propagated into the NMR literature. Finally, we note that 29% (19/65) of calculations have error ratios greater than 1.1 (>10% error). Extrapolating our results implies that ~65% of all citing literature (over 70 calculations) incorrectly estimate the rotational correlation time using the TRACT methodology. We also noted that researchers are more likely to overestimate the rotational correlation time, especially for low τc values. A scatter plot of τc versus error ratio demonstrates an inverse trend with highly erroneous values when τc < 2 ns (Fig. 1B). Plotting τc errors by year of publication underscores the persistence of these miscalculations in contemporary literature (Fig. 1C).
Figure 1:
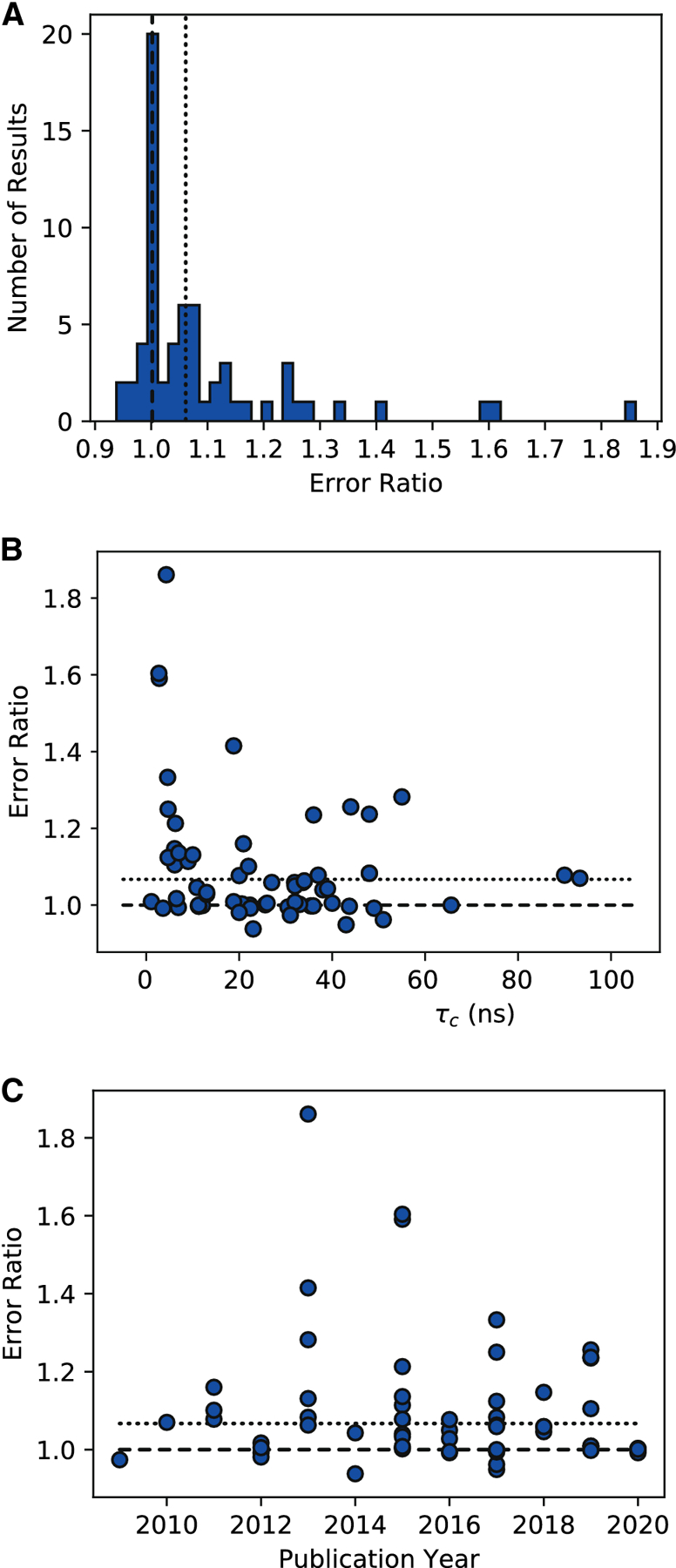
Error analysis of 65 published TRACT-derived rotational correlation times (τc). The error ratio is defined as the published τc divided by the algebraically-determined value using Eqn 12. In all panels, the dashed line (−) and dotted line (…) denote error ratios of 1.0 and 1.067, respectively. A) Histogram of error ratios reveals two clusters: 35% (23/65) of results are narrowly distributed around the accurate result at 1.0 (dashed line), and 23% (15/65) of results are centered at an error ratio of ~1.067 (dotted line) with a slightly wider distribution. The remaining 29% (19/65) of results tend to be overestimates and do not cluster. B) Scatter plot of errors versus year of publication indicate no clear trend that calculation errors are diminishing. C) A scatter plot of τc versus error ratio demonstrating there is generally no trend between τc and error ratio, apart from a group of large errors for small τc values.
Evaluation and analysis using experimental data
While the CCR experiments eliminate complications from chemical exchange and remote dipolar couplings (Eqns. 2 and 3), the existence of fast internal motions cannot be established from these data alone. Spin systems possessing non-negligible τe would artificially reduce τc values using Goldman’s relationship (Eqns. 6 and 12)12. This concern is especially relevant to the TRACT approach because spectra are often only collected in the directly-acquired 1H dimension, and then analyzed by integration over a chosen 1HN region (typically 1HN δ > 8 ppm) to improve S/N. This leads to significant signal overlap, especially in the high molecular weight target proteins for which these experiments were designed10,11. Overlap itself can be mitigated by acquiring 2D versions with indirect 15N evolution (although at a significant time expense), but confirmation of fast timescale motions still requires 15N{1H}-NOE data which are especially problematic in perdeuterated, high molecular weight systems21.
Our algebraic solution enables rapid point-by-point τc calculation, which we used to explore the signal overlap problem using [U-15N,2H]-OmpX prepared in DPC micelles (Fig. 2). The 1D 1HN TROSY (i.e. Nα spin state) spectrum at a relaxation delay = 1 ms is well dispersed with high intensity from 8.5 – 8.0 ppm indicative of many overlapped spin systems and/or rapid local motions (Fig. 2A). As expected, regions with weak signal intensity (e.g. 9.8 ppm ≥ 1H δ ≤ 8.0 ppm) give wildly variable τc estimates (Fig. 2B). There is sufficient signal intensity between 9.5 – 8.8 ppm to calculate reasonable τc values of 30–50 ns. A significant drop in τc is observed as data approaches the center of the amide region (~8.5 ppm; Fig. 2C), which reflects OmpX’s unstructured loops 3 and 519 that resonate at random coil chemical shifts22. Together, this demonstrates that arbitrary selection of a region for integration, without knowledge of underlying dynamic processes, is problematic. Even estimations from relatively invariable regions, such as 9.5 – 8.8 ppm, still possess high variance on a point-by-point basis. We applying a 200 point (5% of 4096 point amide region) sliding window as an optimal compromise for both sensitivity (via integration) and variability (region selection). The 200 points in the window are integrated and a τc prediction generated (Fig. 2C). As illustrated in Figure 2, the sliding window approach narrows the standard deviation for straight-forward identification of regions with consistent τc values. For example, calculations from 9.5 – 9.17 ppm, with and without a sliding window, result in τc of 37.92 ± 4.25 ns and 37.17 ± 0.59 ns, respectively (Fig. 2C,D). While commonly-applied assumptions about dispersed signals and global tumbling are useful when analyzing overlapped signals, point-by-point calculations coupled with the sliding window approach enable data-driven verification of consistent properties across the region of interest.
Figure 2:
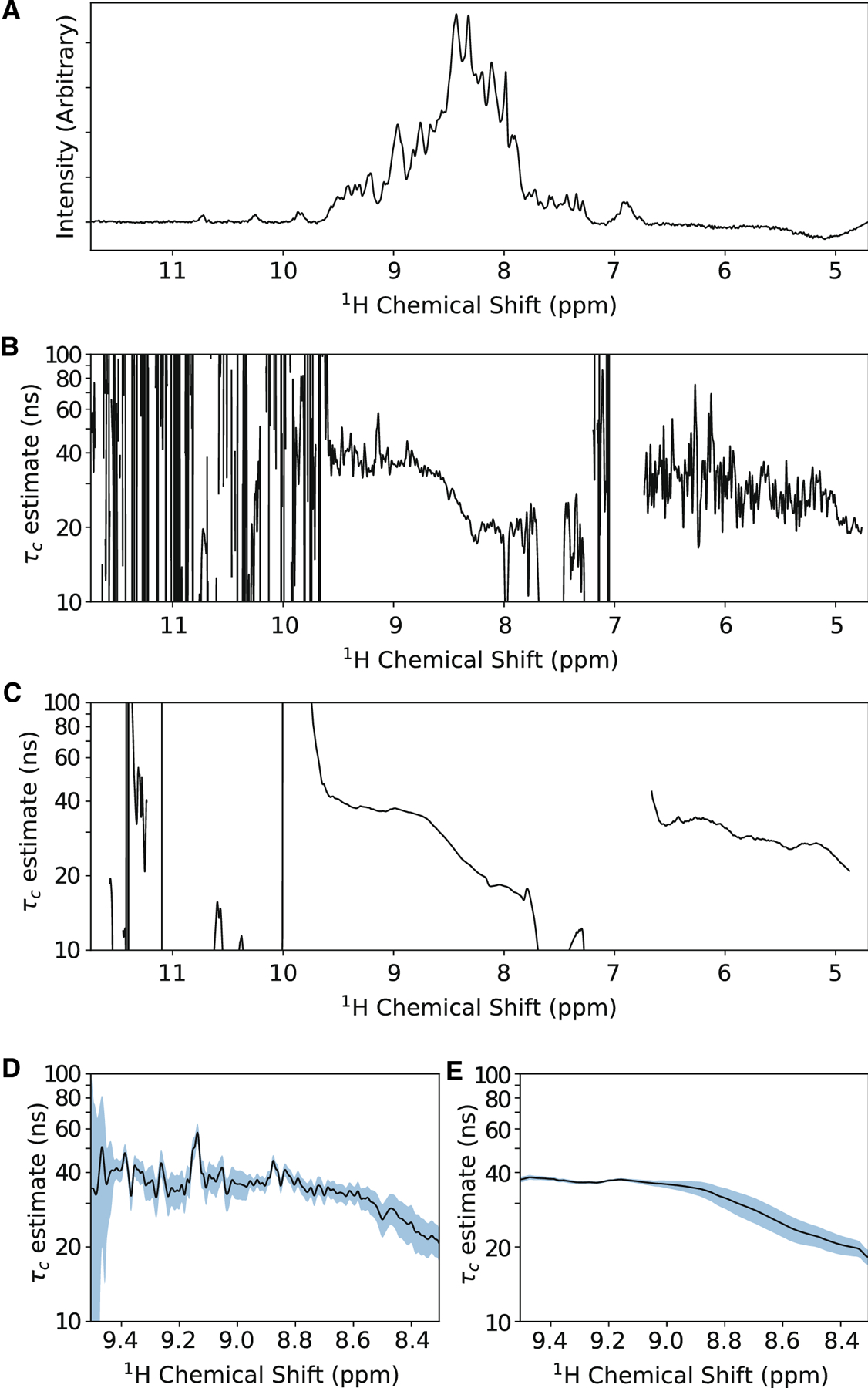
Analysis of TRACT data on OmpX in DPC micelles. A) The amide region (4.70 – 11.74 ppm; 4096 complex points) of the 15N-filtered 1D 1HN TRACT spectrum for [15N,2H]-OmpX is reproduced. The spectrum represents the first relaxation delay (1 ms) for the TROSY component (i.e. Nα spin state). B) Point-by-point estimations of the rotational correlation time. Calculated values vary wildly even where signals are intense and dispersed (e.g. 9.5 – 8.8 ppm). C) Estimation of τc based on a 200 point sliding window (~5% of 4096 complex points). A region of dispersed signals with consistent τc calculations can now be seen from approximately 8.8 – 9.5 ppm. D,E) Expansion of 8.3 – 9.5 ppm region from panels B and C, respectively. The blue regions represent one standard deviation based on a sampling of 200 points around a given point in the spectrum. Application of the sliding window improves τc estimates over the 9.17 – 9.5 ppm region from 37.92 ± 4.25 ns to 37.17 ± 0.59 ns.
Rigid-body approximation as source of systematic error
In its current form, the Goldman relation (Eqn. 6) and our algebraic solution (Eqn. 12) do not account for bond motions. As well-ordered protein regions generally possess backbone 15NH 0.85 ≤ S2 ≤ 0.9523,24, we hypothesize the rigid-body assumption results in an underestimate of rotational correlation times estimated from TRACT experiments. We modified the spectral density function in Goldman’s relationship (Eqn. 6) to include an order parameter (Eqn. 14) and solved for τc as a function of B0, Rα, Rβ, and S2 (Eqn. 15). Note, we use a simplified form of the model-free spectral density function3 that excludes fast timescale motions (τe) which TRACT data alone is insufficient to estimate. Therefore, Eqns. 14 and 15 are only applicable to spin systems where τe has been established to be negligible through the process above.
| (14) |
| (15) |
Where O is intended to stand for the S2 order parameter, and
| (16) |
We then modelled the effect of S2 order parameters on τc estimation using Eqn. 15 (Fig. 3). Relative to the rigid body assumption, typical backbone order parameters (0.85 ≤ S2 ≤ 0.95) increase the rotational correlation time 5–25% depending on the CCR rate; this error increases to ≥45% at an S2 ≈ 0.7. Plotting errors in τc as a function of ηxy for various order parameters reveals a pronounced biphasic character centered ≈ 4 Hz that becomes largely invariant at ηxy > 10 ns (Fig. 3B). This simulation was performed with B0 = 800 MHz where ηxy= 4 Hz gives a τc of ~ 4 ns (assuming S2 = 1.0). There is insufficient data to estimate S2 from TRACT data alone; however, as shown, the rigid body assumption leads to significant underestimation of the rotational correlation time. This problem has been previously discussed by Wand and coworkers25 who found TRACT underestimated τc by an ≈ 20% for five different proteins, with errors ranging from 15–35%, when compared to more rigorous methods. Here we show that, in principle, these errors could be substantially-reduced by inclusion of an order parameter to the Goldman relationship.
Potential sources of systematic error
The internuclear distance (r), difference of the two principal components of the axially-symmetric CSA tensor (ΔδN), and angle of the CSA tensor relative to the N-H bond vector (θ) are three additional parameters assumed constant in the equations above. These values are typically applied uniformly across the protein in 15N relaxation analyses although they’re well documented to be dependent on local structure26,27. Further, there are multiple commonly-employed values used throughout the literature, which are, themselves, interdependent and likely sources of systematic error26,27. For example, a static N-H τ = 1.02 Å was used across NMR dynamics analyses until Ottiger and Bax calculated a vibrationally-corrected τ = 1.041 ± 0.006 Å28. A much wider range of ΔδN values have been reported, including −157 ± 19 ppm29, −172 ± 13 ppm30, and between −173.9 and −177.2 ppm31. Several studies demonstrate the CSA tensor is dependent on secondary structure26,27,32 with solid-state NMR experiments reporting average 15N CSA values = −187.9, −166.0, and −161.1 ppm for helices, strands, and turns, respectively; Ramamoorthy and colleagues go on to show that a change of 10−2 Å in N-H bond length or 1° deviation in θ could alter the calculated CSA tensor27. Recent values for θ include 15.7 ± 5°Fushman, 1998 #21}, 19.9°31, and 21.4 ± 2.3°33. To explore the effect of each parameter on the Goldman relationship, we calculated rotational correlation times as a function of each parameter individually and plotted the percentage error relative to τ = 1.02 Å, θ = 17° and ΔδN = −160 ppm (Fig. 4). While τ and θ deviations generally effect rotational correlation time estimates within a ±5% error, variations of ΔδN can result in errors up to ±15% (Fig. 4). It is important to note, however, that these errors approximate a mathematically-odd function centered around the elected value. That is, integration over many spin systems would cancel out small deviations around the average value for these three parameters, regardless of the parameter’s chosen magnitude. Although, this characteristic would have little benefit in situations when the geometric constant is obviously inappropriate, such as using a helical CSA tensor to evaluate a beta-stranded protein.
Finally, we consider the contribution of remote dipole-dipole interference with local CSA on measured transverse cross-correlated relaxation rates. These interactions are distinct from the RD contributions in Eqns. 2 and 3 and do not cancel out when subtracting Rβ from Rα. Generally, remote protons are not found within 2.2 Å of a given 1H-15N spin system, regardless of secondary structure, due to steric exclusion34. Given the τ−3 dependence of the dipole effect, protons at a distance of 2.2 Å contribute approximately 10 times less than protons at 1.02 Å to dipole relaxation. Liu and Prestegard have previously simulated the contributions of remote dipole/local CSA interference on measured CCR rates for the yARF1 protein18. They demonstrate that the average error in the CCR rate is 0.75% with an upper limit of ~3.5%{Liu, 2008 #17. In the perdeuterated case, which is essential for the study of proteins > 30 kDa, this effect would be even further minimized. Moreover, if the structure is known, the method described by Lui and Prestegard could be used to determine the error contribution.
Conclusion
All NMR methods for estimating the rotational correlation time depend on a number of assumptions concerning how molecules behave in solution. The most comprehensive, and time-consuming, approach involves the collection of multidimensional T2, T1 and heteronuclear 15N{1H}-NOE experiments. Establishing which spin systems have suitable behavior is not trivial and difficult to automate; nonetheless, this strategy is independent of order parameters. This advantage is significant and enables site-specific τc estimation. Two major drawbacks are the difficulties associated with applying these experiments to high molecular weight systems, and the significant effect of remote dipolar couplings on measured longitudinal relaxation rates. In an attempt to circumvent complications from chemical exchange and remote protons, Lee and coworkers developed the TRACT experiment to estimate rotational correlation times from cross-correlated relaxation rates using the Goldman relationship.
Herein, we developed two algebraic solutions to the Goldman relationship for accurate calculations assuming the rigid-body approximation or a specific order parameter. These solutions enabled us to explore the boundaries of the Goldman relationship without relying on numerical minimization, which is computationally slow and potentially inaccurate. However, as we have discussed in this paper, accurate analysis of TRACT data also requires careful consideration. First, there is no way to directly detect spin systems with fast internal motions that would undervalue τc estimates. Second, experiments are frequently collected in a one-dimensional mode that is quite fast, but sensitive to signal overlap. The algebraic solutions facilitate rapid, point-by-point calculations for straightforward identification of appropriate spectral regions where global tumbling is likely to be dominant. Combining this approach with a sliding window simulates the advantages of integration while minimizing the inclusion of inappropriate spin systems. We also demonstrate that the rigid-body approximation can substantially underestimate TRACT-based rotational correlation time estimates. Our algebraic solution incorporates a simplified model-free spectral density function with order parameter that could, in principle, be set to an average backbone S2 ≈ 0.9 to further improve the accuracy of τc estimation. This has not been considered previously. Deviations in τ, θ and ΔδN contribute modest errors to τc estimation, although these would be expected to cancel out over a large number of spin systems. We hope our algebraic solutions and analytical strategies will increase the accuracy and application of the TRACT experiment.
Supplementary Material
Acknowledgements
This study was supported by National Institutes of Health grant R00GM115814 (J.J.Z.), Indiana University start-ups (J.J.Z.), and the Indiana Precision Health Initiative (J.J.Z.). The 800 MHz NMR spectrometer used in this research was generously supported by a grant from the Lilly Endowment.
Funding:
National Institutes of Health (R00GM115814 to J.J.Z.)
Footnotes
Publisher's Disclaimer: This AM is a PDF file of the manuscript accepted for publication after peer review, when applicable, but does not reflect post-acceptance improvements, or any corrections. Use of this AM is subject to the publisher’s embargo period and AM terms of use.
Conflicts of Interest/Competing interests: None
Declarations
Availability of data and material: Available from Authors upon request
Code Availability: Published in SI and available at https://github.com/nomadiq/TRACT_analysis/blob/master/tract_algebraic_analysis.py
Ethics approval: N/A
Consent to participate: N/A
Consent for publication: All of the authors have approved the contents of this paper and have agreed to the Journal of Biomolecular NMR’s submission policies.
References
- 1.Einstein A Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen. Annalen der Physik 322, 549–560 (1905). [Google Scholar]
- 2.Rovnyak D, Hoch JC, Stern AS & Wagner G Resolution and sensitivity of high field nuclear magnetic resonance spectroscopy. J Biomol NMR 30, 1–10 (2004). [DOI] [PubMed] [Google Scholar]
- 3.Lipari G & Szabo A Model-free approach to the interpretation of nuclear magnetic resonance relaxation in macromolecules. 1. Theory and range of validity. Journal of the American Chemical Society 104, 4546–4559 (1982). [Google Scholar]
- 4.Lipari G & Szabo A Model-free approach to the interpretation of nuclear magnetic resonance relaxation in macromolecules. 2. Analysis of experimental results. Journal of the American Chemical Society 104, 4559–4570 (1982). [Google Scholar]
- 5.Kay LE, Torchia DA & Bax A Backbone dynamics of proteins as studied by 15N inverse detected heteronuclear NMR spectroscopy: application to staphylococcal nuclease. Biochemistry 28, 8972–9 (1989). [DOI] [PubMed] [Google Scholar]
- 6.Abragam A The Principles of Nuclear Magnetism. American Journal of Physics 29, 860–861 (1961). [Google Scholar]
- 7.Kaplan JI & Fraenkel G Chapter IV - RELAXATION. in NMR of Chemically Exchanging Systems (eds. Kaplan JI & Fraenkel G) 27–56 (Academic Press, 1980). [Google Scholar]
- 8.Clore GM, Driscoll PC, Wingfield PT & Gronenborn AM Analysis of the backbone dynamics of interleukin-1.beta. using two-dimensional inverse detected heteronuclear nitrogen-15-proton NMR spectroscopy. Biochemistry 29, 7387–7401 (1990). [DOI] [PubMed] [Google Scholar]
- 9.Barbato G, Ikura M, Kay LE, Pastor RW & Bax A Backbone dynamics of calmodulin studied by nitrogen-15 relaxation using inverse detected two-dimensional NMR spectroscopy: the central helix is flexible. Biochemistry 31, 5269–5278 (1992). [DOI] [PubMed] [Google Scholar]
- 10.Luginbühl P & Wüthrich K Semi-classical nuclear spin relaxation theory revisited for use with biological macromolecules. Progress in Nuclear Magnetic Resonance Spectroscopy 40, 199–247 (2002). [Google Scholar]
- 11.Lee D, Hilty C, Wider G & Wuthrich K Effective rotational correlation times of proteins from NMR relaxation interference. J Magn Reson 178, 72–6 (2006). [DOI] [PubMed] [Google Scholar]
- 12.Goldman M Interference effects in the relaxation of a pair of unlike spin-12 nuclei. Journal of Magnetic Resonance (1969) 60, 437–452 (1984). [Google Scholar]
- 13.Pervushin K, Riek R, Wider G & Wuthrich K Attenuated T2 relaxation by mutual cancellation of dipole-dipole coupling and chemical shift anisotropy indicates an avenue to NMR structures of very large biological macromolecules in solution. Proc Natl Acad Sci U S A 94, 12366–71 (1997). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Pervushin K, Riek R, Wider G & Wüthrich K Transverse Relaxation-Optimized Spectroscopy (TROSY) for NMR Studies of Aromatic Spin Systems in 13C-Labeled Proteins. Journal of the American Chemical Society 120, 6394–6400 (1998). [Google Scholar]
- 15.Tjandra N, Szabo A & Bax A Protein Backbone Dynamics and 15N Chemical Shift Anisotropy from Quantitative Measurement of Relaxation Interference Effects. Journal of the American Chemical Society 118, 6986–6991 (1996). [Google Scholar]
- 16.Hall JB, Dayie KT & Fushman D Direct measurement of the 15N CSA/dipolar relaxation interference from coupled HSQC spectra. J Biomol NMR 26, 181–6 (2003). [DOI] [PubMed] [Google Scholar]
- 17.Vasos PR, Hall JB & Fushman D Spin-state selection for increased confidence in cross-correlation rates measurements. J Biomol NMR 31, 149–54 (2005). [DOI] [PubMed] [Google Scholar]
- 18.Liu Y & Prestegard JH Direct measurement of dipole-dipole/CSA cross-correlated relaxation by a constant-time experiment. J Magn Reson 193, 23–31 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Hagn F, Etzkorn M, Raschle T & Wagner G Optimized phospholipid bilayer nanodiscs facilitate high-resolution structure determination of membrane proteins. Journal of the American Chemical Society 135, 1919–25 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Wolfram|Alpha. (Wolfram Alpha LLC, 2009). [Google Scholar]
- 21.Lakomek NA, Ying J & Bax A Measurement of (1)(5)N relaxation rates in perdeuterated proteins by TROSY-based methods. J Biomol NMR 53, 209–21 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Wishart DS, Bigam CG, Holm A, Hodges RS & Sykes BD 1H, 13C and 15N random coil NMR chemical shifts of the common amino acids. I. Investigations of nearest-neighbor effects. J Biomol NMR 5, 67–81 (1995). [DOI] [PubMed] [Google Scholar]
- 23.Jarymowycz VA & Stone MJ Fast time scale dynamics of protein backbones: NMR relaxation methods, applications, and functional consequences. Chem Rev 106, 1624–71 (2006). [DOI] [PubMed] [Google Scholar]
- 24.Sharp KA, O’Brien E, Kasinath V & Wand AJ On the relationship between NMR-derived amide order parameters and protein backbone entropy changes. Proteins 83, 922–30 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Nucci NV et al. Optimization of NMR spectroscopy of encapsulated proteins dissolved in low viscosity fluids. J Biomol NMR 50, 421–30 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Cornilescu G & Bax A Measurement of Proton, Nitrogen, and Carbonyl Chemical Shielding Anisotropies in a Protein Dissolved in a Dilute Liquid Crystalline Phase. Journal of the American Chemical Society 122, 10143–10154 (2000). [Google Scholar]
- 27.Pandey MK et al. Determination of 15N chemical shift anisotropy from a membrane-bound protein by NMR spectroscopy. J Phys Chem B 116, 7181–9 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Ottiger M & Bax A Determination of Relative N−HN, N−C’, Cα−C’, and Cα−Hα Effective Bond Lengths in a Protein by NMR in a Dilute Liquid Crystalline Phase. Journal of the American Chemical Society 120, 12334–12341 (1998). [Google Scholar]
- 29.Fushman D, Tjandra N & Cowburn D Direct Measurement of 15N Chemical Shift Anisotropy in Solution. Journal of the American Chemical Society 120, 10947–10952 (1998). [Google Scholar]
- 30.Kroenke CD, Rance M & Palmer AG Variability of the 15N Chemical Shift Anisotropy in Escherichia coli Ribonuclease H in Solution. Journal of the American Chemical Society 121, 10119–10125 (1999). [Google Scholar]
- 31.Hall JB & Fushman D Variability of the 15N Chemical Shielding Tensors in the B3 Domain of Protein G from 15N Relaxation Measurements at Several Fields. Implications for Backbone Order Parameters. Journal of the American Chemical Society 128, 7855–7870 (2006). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Yao L, Vogeli B, Ying J & Bax A NMR determination of amide N-H equilibrium bond length from concerted dipolar coupling measurements. J Am Chem Soc 130, 16518–20 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Damberg P, Jarvet J & Graslund A Limited variations in 15N CSA magnitudes and orientations in ubiquitin are revealed by joint analysis of longitudinal and transverse NMR relaxation. J Am Chem Soc 127, 1995–2005 (2005). [DOI] [PubMed] [Google Scholar]
- 34.Wüthrich K NMR of proteins and nucleic acids, xv, 292 (Wiley, New York, 1986). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


