Strength, Deformability and Toughness of Uncrosslinked Fibrin Fibers from Theoretical Reconstruction of Stress-Strain Curves

Abstract

Structural mechanisms underlying the mechanical properties of fibrin fibers are elusive. We combined tensile testing of uncrosslinked fibrin polymers in vitro and in silico to explore their material properties. The experimental stress (σ) – strain (ε) curves for fibrin fibers are characterized by elastic deformations with a weaker elastic response for ε<160% due to unraveling of αC tethers and straightening of fibrin protofibrils, and a stronger response for ε>160% owing to unfolding of the coiled coils and γ nodules in fibrin monomers. Fiber rupture for strains ε>212% is due to dissociation of the knob-hole bonds and rupture of D:D interfaces. We developed the Fluctuating Bilinear Spring model to interpret the σ – ε profiles in terms of the free energy for protofibril alignment ΔG₀ = 10.1–11.5 k_BT, Young’s moduli for protofibril alignment Y_u = 1.9–3.2 MPa and stretching Y_a = 5.7–9.7 MPa, strain scale $\tilde{\epsilon }\approx 12–40\text{\%}$ for fiber rupture, and protofibril cooperativity m = 3.6–8. We applied the model to characterize the fiber strength σ_cr = 12–13 MPa, deformability ε_cr ≈ 222%, and rupture toughness U ≈ 9 MJ/m³, and to resolve thermodynamic state functions, 96.9 GJ/mol entropy change for protofibril alignment (at room temperature) and 113.6 GJ/mol enthalpy change for protofibril stretching, which add up to 210.5 GJ/mol free-energy change. Fiber elongation is associated with protofibril dehydration and sliding mechanism to create an ordered protofibril array. Fibrin fibers behave like a hydrogel; protofibril dehydration and water expulsion account for ~94–98% of the total free-energy changes for fiber elongation and rupture.

Graphical Abstract

INTRODUCTION

Fibrinogen (MW, 340 kDa) is a highly abundant protein in blood (1.5–4 mg/ml). One of its key physiological roles is to form a mesh of fibrin fibers – the main structural and mechanical component of a blood clot. Fibrinogen has a cylindrical, trinodular shape; it is 45 nm in length, several nanometers in diameter and consists of two sets of three polypeptide chains denoted Aα (610 amino acids), Bβ (461 amino acids), and γ (411 amino acids). Upon damage to a blood vessel, the coagulation cascade is activated. The final enzymatic step of this cascade is the proteolytic cleavage of fibrinopeptides A (16 amino acids) and fibrinopeptides B (14 amino acids) from the N-termini of the fibrinogen α-chains and β-chains by the enzyme thrombin, thereby converting fibrinogen to fibrin. Thrombin initially cleaves fibrinopeptide A from the two α-chains, exposing knob ‘A’ (key residues, Gly-Pro-Arg [1,2]) in the central, nodular E region of fibrinogen. Knob ‘A’ binds to a complementary binding pocket (hole ‘a’) located in the γ chain of the distal D region on a different fibrin molecule [3]. Fibrin monomers assemble via these A:a knob-hole interactions into half-staggered, double-stranded protofibrils of about 15 to 20 monomers in length (11). The key interaction for protofibril assembly is the non-covalent A:a knob-hole bond [4–7]; when the A:a interaction is blocked with a knob ‘A’ mimic or disrupted by a mutation in hole ‘a’ sequence, protofibril formation is severely impaired [2,7]. Additionally, a favorable D:D interface between abutting fibrin molecules is formed during protofibril formation, but this interaction does not drive the assembly process. After the protofibrils have been formed, thrombin proteolytically removes fibrinopeptide B, thus exposing knob ‘B’ (key residues, Gly-His-Arg-Pro), which binds to a corresponding binding pocket (hole ‘b’) located in the β chain of the distal D region. The B:b knob-hole interactions might aid, but are not required for protofibril assembly [8–10]. Finally, the two-stranded protofibrils coalesce by lateral (radial) aggregation into fibrin fibers ~100–130 nm in diameter, which branch out to form a mesh of fibrin fibers (2,17). At least two types of non-covalent interactions are important for the lateral aggregation of fibrin protofibrils: the B:b knob-hole interactions [6,8,11–16] and interactions between the αC regions [17–20].

Blood clots perform the mechanical task of stemming the outflow of blood when damage to a blood vessel occurs. The clots undergo large deformations under physiological conditions due to the shear stress from blood flow and platelet contraction. In addition, blood clots can rupture, which results in dangerous embolisms. This explains a longstanding research interest to investigate the mechanical properties of blood clots and their main structural constituents – fibrin meshes and single fibers making up these meshes [21–25]. The mechanical and structural properties of blood clots have been related to pathological conditions, such as heart attack and strokes [26–28]; yet, resolving how the clot structure, fibrinogen concentration, properties of fibrin fibers, and other factors affect clot mechanical properties remains an active area of research. Because fibrin fibers are building blocks of the fibrin network, elucidating the mechanical properties of fibrin fibers can provide a better understanding of hemostasis and thrombosis. In the last fifteen years, advances in nanotechnology have enabled researchers to perform mechanical manipulations with single protein fibrils, and experimental data on the mechanical properties of single fibrin fibers have been gradually accumulating [19,29,38,30–37]. These experiments revealed that fibrin fibers are: extraordinarily extensible (capable of sustaining ~150–230% strain before breaking), elastic (accommodating ~50–70% strain without incurring irreversible damage), and soft (with a Young’s modulus on the order of a few megapascals). Furthermore, the stress-strain curves collected for single fibrin fibers exhibit strain stiffening, which is reflected in a threefold increase in the Young’s modulus beyond the 100%-strain level [33].

The large extensibility, low stiffness, and strain stiffening appear to be at odds with the ordered, paracrystalline structure of fibrin fibers. Indeed, biological fibrils that have an ordered structure, such as collagen, keratin, actin, or microtubules, are not very extensible (with breaking strains of less than 30%), and stiff (with a Young’s modulus of the order of 1 GPa). On the other hand, soft and extensible protein fibrils, like elastin, spider catching thread, or fibronectin, have amorphous or unstructured domains [39]. The crystal structures of chicken fibrinogen [40] and human fibrinogen [41] have provided researchers with structural insights into fibrin molecules at the atomic level of detail. Dynamic force spectroscopy experiments in vitro and in silico revealed that an applied pulling force triggers unfolding transitions in the coiled coils and in the γ-nodule of the D region [42]. Furthermore, the triple-helical coiled coils unwind and undergo a force-induced phase transition to form three-stranded parallel β-sheets [43,44]. Using Fourier transform infrared spectroscopy (FTIR) on strained clots, Litvinov et al. obtained evidence that at high strains, there is an alpha helical to beta sheet conversion in fibrin molecules, which likely corresponds to the alpha-helical coiled coils being converted to beta strands [45]. Using coherent anti-Stokes Raman scattering (CARS), Fleissner et al. obtained similar results [46]. Moreover, the A:a knob-hole interactions undergo a tension-induced transition from “catch” bonds, which are characterized by an increasing bond lifetime with increasing force, to “slip” bonds, in which bond lifetimes decreases with force [47]. However, these studies were carried out on single fibrinogen molecules and single-stranded fibrinogen oligomers, not protofibrils, and so the interaction between fibrin protofibrils, mediated by the B:b knob-hole bonds and flexible αC connectors, has not yet been explored. The αC region, which consists of the unstructured αC connector (residues α221-391) and the αC-domain (residues α392-610) extending from residue α221 to the C-terminus (residue α610), is 390 amino acid residues long. The N-termini of the β-chain in the crystal structure of human fibrinogen, up to the disulfide-bonded residue Cys 65, is attached to a 51 amino acid residue long, flexible tether forming knob ‘B’ [41]. Since a fully extended knob ‘B’ is ~17 nm long, this gives it enough length to connect different protofibrils within a fiber. Although AFM imaging studies show that αC-domain interactions and B:b knob-hole bonds might be capable of linking protofibrils together [17], the role of these structural determinants in mediating the mechanical response of fibrin on several spatial scales, from fibrin protofibrils to fibers and to the fibrin network, is not understood.

The following findings provide evidence that interactions between the αC regions play an important role [18,19]. A fibrinogen variant, in which the αC region is truncated beyond residue α251, forms clots with thinner, denser fibers; these clots are less stiff and lyse more rapidly [20]. Human fibrinogen in which the αC region is substituted with the αC region from chicken fibrinogen shows severely impaired lateral aggregation [48]. Extensibility of single fibrin fibers scales with the length of the αC connector [37]. Diffusivity of fibrinogen variant I-9 with truncated C-terminal portions of the Aα chains is much less concentration-dependent, as compared to wild-type fibrinogen [49]. The following results provide evidence that the B:b knob-hole interactions play a role in protofibril interactions. Selective release of fibrinopeptides A or B results in differences in the dynamics of clot formation and in clot structure [6,8,11–16]. Blocking hole ‘b’ with knob ‘B’ (or its derivatives) influences fibrin formation and fibrin structure [50–52]. Naturally occurring or recombinant mutations in knob ‘B’ or hole ‘b’ affect fibrin formation [53]. The extensibility of single fibrin fibers is drastically reduced from 180% to 100% when the B:b interactions are blocked with ‘B’ knob mimics [31]. A composite fibrin fiber model in which protofibrils are connected only by flexible αC connectors was able to explain the small-angle X-ray scattering (SAXS) measurements on stretched fibers [54]. The 22.5-nm repeat spacing of fibrin monomers in a protofibril changed only minimally, but the diffraction peak lost intensity upon stretching, which is indicative of a loss of repeat units caused most likely by fibrin forced unfolding.

Notwithstanding the large body of accumulated experimental evidence summarized above, which suggests important roles played by various fibrin structural determinants, the structural mechanisms underlying the unique mechanical properties of fibrin fibers remain elusive, mainly due to the unresolved dynamic changes in molecular packing of fibrin protofibrils within fibrin fibers. Although atomic models of fibrin oligomers and protofibrils have been reported [51,52], which include the α chains, A:a and B:b knob-hole bonds and γ-γ crosslinking and which take into account proper spacing between fibrin monomers, structures of fibrin fibers do not exist. To understand how fibrin protofibrils pack together to form fibers, here we carried out combined mechanical testing experiments on single uncrosslinked fibrin fibers in vitro and on single uncrosslinked fibrin protofibrils in silico. By directly comparing the results of simulations of forced unfolding and rupture of fibrin protofibrils with the experimental data for fibrin fibers, we have resolved the structural mechanisms of elongation and rupture of uncrosslinked fibrin fibers and illuminated the dynamic remodeling of the tension-transducing network of fibrin protofibrils.

To interpret the experimental stress-strain curves for single fibrin fibers, we developed the Fluctuating Bilinear Spring (FBS) model. The model considers the initial, intrafiber alignment of fibrin fibers due to simultaneous elongation of long αC connectors and straightening of protofibrils at small mechanical loads, followed by fiber elongation at intermediate loads due to forced unfolding of fibrin protofibrils, and subsequent rupture of fibrin fibers at mechanical loads above the critical threshold. The synergy from combining AFM-based mechanical testing assays on single uncrosslinked fibrin fibers with computational molecular modeling of protofibrils and Fluctuating Bilinear Spring theory has enabled us to explore the mechanics, thermodynamics, and material properties of fibrin fibers, and to resolve the structural underpinnings of the mechanical deformation and rupture of fibrin fibers. These combined experimental and computational efforts have enabled us to clarify the role of structural alterations in γ-nodules and αC regions at the fibrin monomer level, reveal dynamic remodeling of the tension-transducing network of fibrin protofibrils at the whole fiber level, and highlight the importance of structural rearrangements in the water matrix. This study provides valuable insights into the mechanisms of fibrin clot rupture and further advance our understanding of the structural biomechanics that underlie the stability and structural integrity of blood clots and thrombi.

MATERIALS AND METHODS

Experimental Methods:

Striated substrate:

To prepare the substrate with ridges and grooves, a drop of optical adhesive ((Norland Optical Adhesive NOA 81, Norland Products, Cranbury, NJ, USA) was placed in a petri dish (5 cm diameter). A 1 cm × 1 cm rectangular PDMS (Polydimethylsiloxane, Sylgard® 184, Sigma-Aldrich, St. Louis, MO, USA) stamp with imprinted ridges and grooves was pressed into the optical adhesive and exposed to UV light ((UPV, Upland, CA) and cured for 2 minutes before being peeled off. The PDMS stamp was prepared by pouring the PDMS onto a silicon master to a height of about 5 mm in a petri dish (10 cm diameter), letting it cure, and excising a 1 cm × 1 cm stamp with a scalpel. The grooves (spacing between ridges) and the lateral dimension of the ridges were both 12 μm.

Suspended fibrin fibers:

0.75 μl of fibrinogen stock (concentration 13.3 mg/ml; final concentration in reaction, 0.5 mg/ml; Enzyme Research Laboratories, South Bend, IN) and 17.25 μl of fibrin buffer (140 mM NaCl, 10 mM Hepes, 5 mM CaCl2, pH 7.4) were mixed to make 18 μl of fibrinogen solution. The final fibrinogen concentration was 0.5 mg/ml, which is below the physiological concentration of 1.5 to 4.0 mg/ml. We used this lower concentration to obtain somewhat diluted clots and fewer fibers on the substrate. Higher concentrations result in too many fibers on the substrate, which does not leave enough room to manipulate individual fibers. This 18 μl of fibrinogen solution and 2 μl of thrombin (final concentration: 0.1 NIH units/ml, Enzyme Research Laboratories, South Bend, IN) were then placed on the striated substrate in the petri dish and incubated in a wet atmosphere at room temperature for 2 h. The substrate, now covered by fibrin fibers, was rinsed three times with fibrin buffer and fluorescently labeled by adding 100 μl of 20 nm carboxyl coated fluorospheres (5 μl of fluorospheres in 95 μl of deionized water; Invitrogen, Carlsbad, CA). The sample was finally rinsed and kept in fibrin buffer. An Atomic Force Microscope (MFP-3D-BIO; Oxford Instruments, Abingdon, UK) combined with an inverted optical microscope (IX73; Olympus, Tokyo, Japan) were used to obtain the stress-strain curves of single fibrin fibers suspended over grooves (Figure 1). An AFM probe (normal spring constant 2 N/m; resonance frequency 79 kHz; coated with Cr/Au; AC240TS-R3, Oxford Instruments) was used for the manipulation and imaging of fibrin fibers. The spring constant 1.2 N/m is calculated by thermal tune. Videos of the fiber manipulations were taken from underneath the sample with the inverted optical microscope. Fibrin fibers are naturally ‘sticky’ and they remain attached to the substrate even at large extensions, as can be seen in videos and images that are taken from underneath the sample as fibers are stretched [30,33,34]. Slipping between the fibrin fiber and the AFM tip or slipping of the fibrin fibers at the ridges was rare; in case slipping was observed, the data for that fiber were discarded. The majority of rupture events occurred at the location on the fibrin fibers where the tip contacted the fiber. The rupture points were located near the middle part of the fibers. A smaller portion of rupture events occurred in the space between the cantilever tip and the ridges.

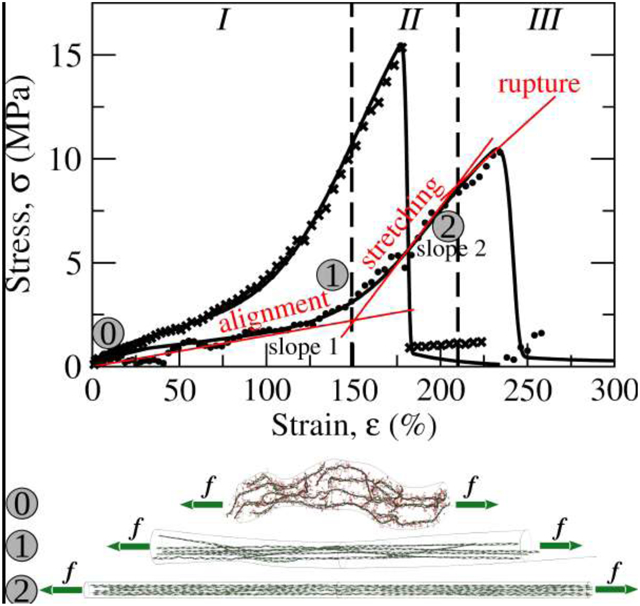
Figure 1. Mechanical testing experiments on single, uncrosslinked fibrin fibers:

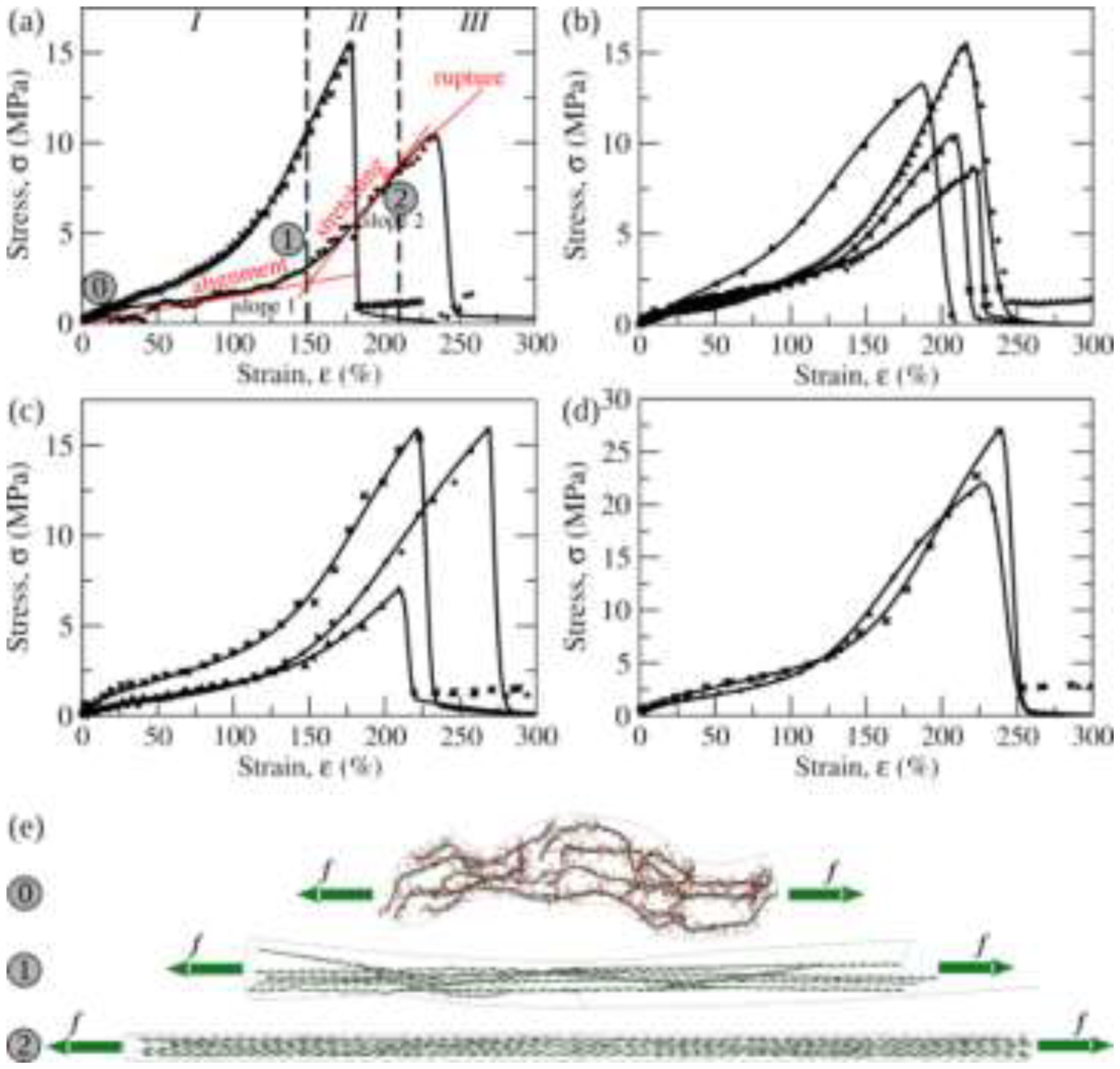
(a) Schematic of the setup used in the AFM-based experiments. (b) The initially unstretched fibrin fiber and stretched fiber are shown schematically in dotted gray and solid black, respectively. (c) 48 experimental stress (σ) - strain (ε) spectra (shown for clarity in different colors). The σ – ε profiles are collected for the pulling speeds: v_f = 0.2–1.1 μm/s (shown in black), 1.8–2.5 μm/s (red), 2.5–5.0 μm/s (green), 6–7 μm/s (violet), and 9–10 μm/s (blue). The inset displays a representative stress-strain profile showing elastic extension in regime I with the smaller slope at lower strains (ε < ~130%) and in regime II with a larger slope for higher strain (ε < 180–200%); and the rupture regime III for the strains above the critical threshold (ε > ε* ≈ 220%).

Mechanical testing experiments:

In these experiments on single uncrosslinked fibrin fibers, we used a 0.2 – 10-μm/s range of pulling speeds, which translated to a 40 – 2000 μN/s range of the force-loading rate. All experiments were carried out in fibrin buffer; details of AFM nanomechanical fiber pulling experiments can be found in [55]. There are technical limitations to the range of pulling speeds. The main limitation for high speeds is the electronic feedback speed of the AFM. When inputting higher pulling speeds, the feedback cannot keep up any longer, so the tip is not moving any faster than a certain threshold value. Therefore, our highest speeds are at this threshold value. The main limitation for low speeds is thermal drift; below a certain speed, thermal drift may be faster than the pulling speed. Also, as Fig. 1 shows, the force drops down to zero after the fiber ruptures. However, occasionally it does not drop down to zero, which might be due to a small misalignment of the cantilever system that can occur during these dynamic force measurements.

Error considerations:

The strain of the fiber, ε, is defined as the change in the fiber length, X, divided by the initial fiber length, L_init; $\epsilon =\frac{\left(L_{\mathit{\text{final}}}-L_{\mathit{\text{init}}}\right)}{L_i}$ . L_final, the final length of the fiber, can be found using the Pythagorean Theorem (Fig. 1) as $L_{\mathit{\text{final}}}=\sqrt{L_{\mathit{\text{init}}}{}^2+s^2}$ , where s is the travel distance of the AFM probe during pulling. The error in L_init (size of gap between ridges) and of L_final is about 5% (600 nm), yielding an overall error in ε (and the extensibility) of 10%. The stress, σ, on a fiber with cross-sectional area, A, is defined as $\sigma =\frac{F_{\mathit{\text{fiber}}}}{A}$ , where F_fiber is the force exerted on the fiber. Cantilevers were calibrated before each experiment, according to the bent beam method. The error in the force measurement is estimated to be 50%, as described in detail in [55,56]. The error in the diameter measurement (determined by imaging the fiber with the AFM on top of the ridge, or via SEM) is estimated to be 20%, thus the area has an error of 40%. Therefore, the stress has an error of 50% + 40% = 90% (error in force plus error in area). The modulus corresponds to the slope of a stress-strain curve, and therefore has an error of 90% + 10% = 100% (stress error plus strain error). It should be noted that these are the absolute instrumental errors in the measurements. The average value can be determined much more accurately when many measurements are taken, as was the case in our study. The precision of the average of multiple measurements μ is given by $\sigma /\sqrt{N}$ , where σ is the standard deviation and N is the number of measurements. The standard deviations of the measurements, as derived from the statistics of the measurements, is $\sqrt{\frac{\sum x_i-\mu }{N}}$ , were μ is the average. For the experimental measurements, the modulus of uncrosslinked fibers is 3.0 ± 1.3 MPa; and the extensibility of uncrosslinked fibers is 210 ± 46%. The standard deviations are a combination of sample variability and instrumentation error.

Self-Organized Polymer model of uncrosslinked fibrin protofibrils:

We used the native topology-based Self-Organized Polymer (SOP) model to describe the mechanical properties of uncrosslinked fibrin protofibrils at the C_α-atom-based amino-acid level of detail. The SOP model was described in detail in Ref. [57], and was used with success to model large biomolecular assemblies, including fibrin oligomers [58], microtubule filaments [59], virus shells [60,61], and cell organelles [62]. Briefly, in the SOP model, an amino acid is represented by the C_α-atom (C_α-particle). Therefore, the polypeptide chains representing two strands in the all-atom structure of double-stranded fibrin protofibrils [58,63] are replaced by a collection of the C_α-C_α covalent bonds. To make the uncrosslinked fibrin oligomer and protofibrils, we removed the covalent bond connecting the crosslinking sites (residues γLys399 and γLys406) in abutting fibrin monomers [58,63]. The potential energy function of protein conformation U_SOP is specified in terms of the coordinates of the C_α-particles {r_i} = r₁, r₂, …, r_p (p is the total number of particles): $U_{\mathit{\text{SOP}}}=U_{\mathit{\text{FENE}}}+U_{\mathit{\text{ANG}}}+U_{\mathit{\text{NB}}}^{\mathit{\text{ATT}}}+U_{\mathit{\text{NB}}}^{\mathit{\text{REP}}}$ . The first term is the finite extensible nonlinear elastic (FENE) potential $U_{\mathit{\text{FENE}}}=-{\sum }_{b=1}^{N_{\mathit{\text{bond}}}}\frac{k}{2}{R}_0^2\text{log}\left[1-\frac{{\left(r_b-r_b^0\right)}^2}{R_0^2}\right]$ with a spring constant k = 14 N/m, which is the average value for stretching deformations of proteins, and a tolerance for the change of covalent bond distance R₀ = 2Å. This potential energy term (U_FENE) describes the extensibility of polypeptide chains forming the two-stranded fibrin protofibrils. In U_FENE, the summation is performed over all covalently linked C_α-particles and disulfide bonds, N_bond is the total number of covalent bonds in a polypeptide chain, r_b is the distance between the covalently linked particles, and $r_b^0$ is the equilibrium distance between these atoms in the atomic structure (reference structure). An additional constraint is imposed on the bond angle, formed by a triplet of covalently linked residues, by adding the repulsive Lennard-Jones potential for the beads separated by two covalent bonds (1–3 interactions) $U_{\mathit{\text{ANG}}}={\sum }_{a=1}^{N_{\mathit{\text{ANG}}}}{\epsilon }_{\mathit{\text{ang}}}{\left({\sigma }_{\mathit{\text{ang }}}/r_{\mathit{\text{ij}}}\right)}^6$ , where ε_ang = 4.2 kJ/mol is the energy scale for bending, and σ_ang = 3.8 Å is the range. In the bending potential U_ANG, the summation is performed over N_ANG bond angles. This potential energy term (U_ANG) describes the bending propensity of the polypeptide chains forming the fibrin protofibrils. To account for the non-covalent interactions between residues reinforcing the native structure, we use the Lennard-Jones potential $U_{\mathit{\text{NB}}}^{\mathit{\text{ATT}}}={\sum }_{n=1}^{N_{\mathit{\text{att}}}}{\epsilon }_n\left[{\left(r_n^0/r_n\right)}^{12}-2{\left(r_n^0/r_n\right)}^6\right]$ [64]. Here ε_n is the energy associated with the strength of non-covalent bonds. This potential energy term ($U_{\mathit{\text{NB}}}^{\mathit{\text{ATT}}}$) describes the energetics of residue-residue interactions stabilizing the native folded state (native contacts) of fibrin protofibrils. Typical values of ε_n are between 2.5 kJ/mol and 5.4 kJ/mol, depending on the nature of the residue-residue contact (e.g. hydrophobic vs. electrostatic). A pair of residues, out of a total of N_att pairs, forms a native contact if the distance between their C_α-atoms are in the cutoff distance r_c = 8Å in the reference structure. The non-native contacts are treated using the potential $U_{\mathit{\text{NB}}}^{\mathit{\text{REP}}}={\sum }_{n=1}^{N_{\mathit{\text{REP}}}}{\epsilon }_l{\left({\sigma }_l/r_n\right)}^6$ , where the summation runs over all N_REP pairs of C_α-particles that are neither covalently linked nor form a native contact. In $U_{\mathit{\text{NB}}}^{\mathit{\text{REP}}}$ , we set ε_l = 4.2 kJ/mol (strength) and σ_l = 3.8Å (range).

Dynamic force spectroscopy in silico:

We used the SOP model of fibrin protofibrils FP9/9, comprised by 18 fibrin monomers, to carry out GPU-accelerated Langevin Dynamics simulations of their forced alignment, unfolding, and rupture [65–67]. We used the parameterization of the SOP model for fibrin protofibrils from our previous studies [42,58,63,67]. In short, the binary contacts between amino acids in fibrin protofibrils were divided into two groups. In group 1, there are residue-residue contacts stabilizing the native state of the α-helical regions of the coiled-coil connectors (residues α45–210, β76–197 and γ19–139). In group 2, there are the contacts in the β-nodules (residues β198–461), in the γ-nodules (residues γ140–394), and the contacts forming the A:a knob-hole bonds (residues α17–45) and the B:b knob-hole bonds (residues β15–76). We set ε_h = 5.0 kJ/mol and 6.3 kJ/mol as the energy scale for all residue-residue contacts in group 1 and group 2, respectively. To mimic the experimental measurements, in the pulling simulations we constrained one end of a polypeptide chain (the N-terminal) and applied the pulling force to the other end (the C-terminal). Residues αAsp114, βSer144, γSer86 in the upper strand and αGln131, βAsn164, γSer105 in the lower strand in the leftmost monomers in FP9/9, were constrained. The pulling force was applied to residues αArg118, βLys148, γLeu90 in the upper strand and αIle127, βAsn160 and γLeu101 in the lower strand in the rightmost monomers. We utilized the time-dependent pulling force f(t) = r_ft ramped up in time t with the force-loading rate r_f = k_spv_f = 3 μN/s, where v_f = 5 μm/s is the pulling speed and k_sp = 600 pN/nm is the cantilever spring constant. In the pulling simulations, the value of the spring constant for the virtual cantilever tip (k_sp) was set equal to one half the values of the cantilever spring used in the experiment on single fibrin fiber, because fibrin protofibrils are softer than fibrin fibers. A schematic of tensile testing experiments in silico is displayed in Fig. 2c.

Figure 2. Dynamic mechanical transitions in uncrosslinked fibrin protofibrils:

(a): Structure of fibrin protofibril FP9/9 in the bent free energy-minimum conformation (native state). FP9/9 has a 410 nm contour length and ~360 nm end-to-end distance in the bent conformation. (b): Force-extension profiles (F – X curves; left y-axis, rising blue and black curves), obtained using a pulling speed of v_f = 5 μm/s (3 μN/s force-loading rate), and the number of native contacts (right y-axis, smoother blue and black curves in lower third of plot) for fibrin protofibril from the simulations for FP9/9. Also shown in the blue F – X curve is lower slope 1 (protofibril straightening), and higher slope 2 (protofibril unfolding). Theoretical F – X curve for the forced unraveling of an αC tether modeled as WLC springs is shown in red color. The slopes (spring constants) for FP9/9 (k_u and k_a) from simulations and for αC tether ($k_u^{\alpha C}$ and $k_a^{\alpha C}$) from WLC-based modeling are represented by solid and dashed lines, respectively. The horizontal line at 50 pN is the force per protofibril strand corresponding to a protofibril transitioning from state u to state a; the line at 190 pN is the average critical force for fibrin protofibril FP9/9 from simulations. (c) Setup used in the pulling simulations on FP9/9 and selected conformations (snapshots 0 to 4), which correspond to the accordingly numbered regions in the F – X-profile (black F – X curve in panel b). The left end of FP9/9 is constrained and the time-dependent pulling force f(t) is applied to the other end of FP9/9. Initially, the protofibril is in the bent conformation with the end-to-end distance of ~360 nm (snapshot 0). Tension results in protofibril elongation due to straightening (snapshot 1) and unraveling of the coiled coils (snapshot 2), which are followed by the disruption of D:D interfaces in both strand (snapshots 3 and 4).

RESULTS

Dynamic regimes of forced elongation and rupture of uncrosslinked fibrin fibers:

A technique based on a combined Atomic Force Microscope (AFM) and an inverted optical microscope was used to mechanically manipulate single, uncrosslinked fibrin fibers suspended over 12 μm wide grooves in a striated substrate (see Fig. 1a and b) [29,33]. For mechanical testing experiments, we only selected fibrin fibers that ran perpendicularly across grooves. Single fibrin fibers were pulled laterally with the AFM cantilever until they ruptured, and the stress-strain curves were obtained from the data provided by the AFM. In these stress-strain measurements, the AFM tip positioned above the sample pulls on the fiber while the inverted optical microscope (40X lens), located below the sample, acquires images and movies of the manipulation (Fig. 1a). A top-view schematic of the dynamic force measurement is displayed in Fig. 1b. Here, L_init is half the resting length of the fiber, L_final is half the length of the stretched fiber, and s is the distance traveled by the tip. L_final can be found trigonometrically from and L_init and s the strain ε can be calculated using these quantities. The collected stress (σ)-strain (ε) profiles are displayed in Fig. 1c. A detailed description of the geometry and the force calculations is given in [55].

Visual inspection of the experimental σ – ε-profiles shows that the mechanical response of single fibrin fibers is characterized by three different, dynamic, mechanical regimes (displayed in the inset to Fig. 1c): the fiber’s elastic deformation both in regime I with a lower constant slope $\raisebox{1ex}{$d\sigma $}\!\left/ \!\raisebox{-1ex}{$d\epsilon $}\right.$ for small strains ε < 130% and in regime II with higher slope for large strains 150% < ε < 180% (from 130% to 150% the slope is transitioning), and rupture regime III of the fiber rupture for very large strains (ε_cr = 210–222 %) above the critical threshold ε > ε* = 180% with a rapidly decreasing slope after reaching the stress maximum. These dynamic mechanical regimes exist due to different structural transitions in fibrin protofibrils forming the fiber. We hypothesized that the initial portion of σ – ε profiles with the lower slope (ε < 130%) is due to tension-induced straightening of fibrin protofibrils spanning the fiber structure, which results in their alignment in the direction of applied stress (regime I). This is the lower-energy mechanical excitation characterized by the lower slope $\raisebox{1ex}{$d\sigma $}\!\left/ \!\raisebox{-1ex}{$d\epsilon $}\right.$ . The middle range of the stress-strain curves with the higher slope (ε < 150 – 180%) is due to stress-induced stretching and unraveling of entire bundles of fibrin protofibrils (regime II). These occur only after the protofibrils have aligned and have bundled together. At the critical strains (average value is ε_cr ≈ 222%), the mechanical rupture of fibrin protofibrils forming the fiber occurs. The rupture transitions in fibrin protofibrils correspond to ~6–21 MPa values of the critical stress, and a subsequent stress drop to zero (regime III). This is likely due to the irreversible rupture of the D:D interfaces in two-stranded fibrin protofibrils (Fig. 1c).

To test these hypotheses, we first performed tensile testing measurements in silico on single fibrin protofibrils (not the whole fiber), in which we used the C_α-atom-based coarse-grained SOP model of fibrin protofibril FP9/9 (see Materials and Methods). This model has been derived from the full atomic structures of fibrin protofibrils [58,63]. Fibrin protofibril FP9/9 has a contour length of 410 nm, but 360 nm equilibrium end-to-end distance due to its partially bent structure. A bundle of protofibrils FP9/9 in their bent native conformations is displayed in Fig. 2a. A schematic of mechanical testing in silico is displayed in Fig. 2c, which also shows the energy-minimum bent conformations (native state; snapshot 0) and straight conformation of FP9/9 (snapshots 1 and 2). The simulated force (F) - extension (Y) curves for FP9/9 are displayed in Fig. 2b. The F – X-curves for FP9/9 revealed the existence of the same dynamic mechanical regimes: the elastic extensions with a lower slope for shorter ~7–100 nm elongation (regime I) and with a higher slope for longer 100–180 nm extension (regime II), and plastic deformation and rupture for the protofibril extension above the critical ~170 nm threshold (regime III; snapshots 3 and 4 in Fig. 2c). The initial force response of fibrin protofibrils is due to the elongation of the coiled-coil portions of the fibrin structure without disruption of residue-residue contacts reinforcing the native state (see Fig. 2b). This initial force response has a lower slope $\raisebox{1ex}{$dF$}\!\left/ \!\raisebox{-1ex}{$dX$}\right.~0.4-0.5\text{pN}/\text{nm}$ (X < 80–100 nm; regime I). A ramping up of tension in the γ-nodules of abutting fibrin monomers results in a steeper force increase with a higher slope of ~1.5–1.7 nN/nm (100 nm < X < 180 nm; regime II). When the tension exceeds the mechanical stability of the γ-nodules, these portions of fibrin structure undergo partial unfolding, which results in the rupture of D:D interfaces, and dissociation of the A:a and B:b knob-hole bonds in both protofibril strands (X > 180 nm; regime III).

Motivation for Fluctuating Bilinear Spring model:

The results of the mechanical testing in silico on a protofibril FP9/9 suggest that the origin of dynamic mechanical regimes I-III for fibrin fibers (Fig. 1) is rooted in conformational transitions in fibrin protofibrils. In the pulling simulations on single protofibril FP9/9, the αC regions of the α chains emanating from the protofibril do not extend because tension does not propagate through the αC regions (see Fig. 2). However, at the fibrin fiber level, the force-induced stretching of the αC regions, which couple protofibrils within a fibrin fiber, plays an important role in mechanical unraveling of fibrin fibers. There is experimental evidence suggesting that forced stretching of αC regions [19] occurs at pulling forces of 5–20 pN, which also agrees with predictions of the WLC model (Fig. 2b). Because in the simulations protofibrils straighten in the 10–50 pN force range (Fig. 2b), we concluded that in regime I the forced unfolding of αC regions and straightening of fibrin protofibrils occur simultaneously. Indeed, a fibrin fiber of initial (not stretched) length L_init = 6 μm is spanned by a total of 17 fibrin protofibrils FP9/9, each 360-nm long (end-to-end distance of intact FP9/9). From the experimental stress-strain profiles (Fig. 1c), the transition of fibrin fiber from regime I to regime II in the strain range of ε ≈ 130–180% translates to X = L_final − L_init = 7.8–10.8 μm fiber extension. This extension corresponds to X/17 ≈ 460–635 nm elongation per protofibril FP9/9. However, in the simulations a single protofibril extends only by X ≈ 85 nm in regime I (Fig. 2b and Fig. S2). Therefore, straightening of 17 protofibrils can account only for ~10–20% of fiber extension. Hence, forced unraveling of the αC regions contributes significantly to the elongation of fibrin fibers in regime I.

Furthermore, in silico mechanical testing of a protofibril FP9/9 shows that fibrin protofibrils exist in state u (unaligned) in which the protofibrils are bent and the αC regions are in the random coil conformation, and state a (aligned) in which protofibrils are straightened and the αC regions are extended in the direction of the pulling force. In state u, fiber elongation is due to straightening of protofibrils and full extension of the unstructured αC regions (red curve in Fig. 2b) at lower forces, whereas in state a, fiber elongation is due to unfolding of the coiled-coil regions and the γ-nodules at higher forces. In both states, the mechanical response is elastic with the lower elastic constant for state u (regime I), and with the higher elastic constant for state a (regime II; Fig. 1c). This bi-linear elastic deformation persists until the irreversible rupture of the fiber occurs (regime III; Fig. 1c). Hence, at the minimal model level, mechanical deformation of single fibrin fibers in the elastic deformation regimes I and II can be described by considering only two types of mechanical excitations – the bending (protofibril straightening and unraveling of the αC regions) and stretching (protofibril unfolding).

To investigate if bending and stretching can account for the elastic deformation, we constructed a bead-spring model of the fibrin fiber (Fig. S1). The potential energy function of fiber conformation is defined by the harmonic potentials for bending and stretching with the elastic constants for bending k_b and k_s stretching (see Supplementary Material (SM)). We performed Langevin simulations of forced elongation of the bead-spring model of the fiber chain. By fitting the simulated σ – ε-curves to the average experimental stress-strain profile, we obtained the best fit for k_b = 1.1 nN/μm and k_s = 21.9 nN/μm. Very good agreement between the experimental and simulated σ – ε-curves demonstrates that protofibril alignment and stretching are sufficient to develop a minimal model of deformation of single fibrin fibers. These findings have provided a foundation for the Fluctuating Bilinear Spring model described below.

Fluctuating Bilinear Spring model of uncrosslinked fibrin fibers:

Mechanical excitations –

The Fluctuating Bilinear Spring (FBS) model treats a single fibrin fiber as a collection of fibrin protofibrils (Fig. 3a) mechanically coupled both longitudinally and laterally (Fig. 3b and 3c). The protofibrils are linked together by highly extendable αC regions (Fig. 3a), which connect protofibrils in series (n_l protofibrils are linked together in the longitudinal direction) and in parallel (n_r protofibrils are assembled radially) [19]. In state u, the protofibrils are bent (Fig. 3d); an applied force f(t) gradually straightens protofibrils and unravels the αC regions (Fig. 3e), which results in the stress σ_u = Y_uε for small strain ε. Here, Y_u = n_rK_u/n_l is the fiber Young’s modulus due to n_r protofibril strands and αC regions with the stiffness in state u, K_u/n_l, where K_u is the average stiffness of protofibril and αC regions in state u. A pulling force triggers the transition to state a, in which the protofibrils are straightened and αC regions are unraveled (Fig. 3f). In state a, the pulling force stretches the protofibrils, and the mechanical response is elastic, σ_a = Y_aε, albeit with the larger Young’s modulus, n_rK_a/n_l = Y_a > Y_u, where K_a (> K_u) is the average stiffness in state a.

Figure 3. Structure of fibrin protofibrils and Fluctuating Bilinear Spring model:

(a) Structure of short fibrin oligomer FO4/4 formed by 8 fibrin monomers each with the αC region shown in red (top) and its cartoon representation (bottom). (b) Mechanical mapping of the fibrin protofibril. The harmonic spring represents elastic extension of stiff structural parts of the protofibril (shown in black) and random coils denote the unstructured portions formed by the αC regions (shown in red) described with the worm-like chain (WLC) model. (c) Mechanical model of fibrin fiber. There are n_l fibrin protofibril fragments spanning the 6-μm fiber longitudinally along the fiber axis (arranged in series) and n_r structure elements formed by fibrin protofibrils combined together laterally (arranged in parallel). (d) Simplified structure of a short fibrin fiber fragment formed by fibrin protofibrils in the unaligned state. The protofibrils are interconnected both longitudinally and laterally through the non-covalent αC-αC interactions. The direction of force application (f) is indicated by the green arrow. (e) Stretching of fibrin fiber under applied tensile force. Shown are the fibrin protofibrils in the aligned state at small strains. (f) Shown are the aligned fibrin protofibrils with extended αC regions at intermediate strains.

The unstructured αC regions can be modeled as worm-like chains (see Fig. 3b). A worm-like chain model of the αC connector was used to account for the very short recoil time (< 4 ms) [36] and to describe the shape of experimental stress-strain curves for fibrin fibers [68]. Results from molecular modeling studies suggest that refolding γ-nodules is too slow to account for rapid recoil [42,43]. Therefore, in the FBS model, the extension of fibrin protofibrils in the native state u is due to simultaneous straightening of protofibrils and their alignment owing to unfolding of αC regions. In state a, the protofibrils’ elongation is due to extension of the coiled coils and unfolding of the γ-nodules. The average stiffness in state u (K_u) and in state a (K_a) are functions of the average stiffness of the αC region (K^αC) and the average stiffness of the protofibrils in state u (k_u) and in state a (k_a), $K_u=g\left(k_u,k_u^{\alpha C}\right)$ and $K_a=g\left(k_a,k_a^{\alpha C}\right)$ (Fig. 3c). The precise form of these functions is not known because how these structure elements are connected in a fiber is not understood. Here, we used pulling simulations to resolve the contributions from the protofibril elements and the αC regions to the average stiffness of fibrin fibers.

The population of aligned protofibrils p_a increases with increasing strain ε, i.e. p_a = p_a(ε). When σ = 0 the free energy difference between states u and a is ΔG₀; the pulling force lowers the energy difference for transition u → a, i.e. ΔG(ε) = ΔG₀ − g₀ε. Here, g₀ = vσ₀ is the characteristic free energy and σ₀ is characteristic stress for protofibril alignment (v is protofibril volume). From the simulations for FP9/9, g₀ can be estimated as g₀ = f₀l_init, where l_init = 360 nm is the average length of FP9/9 and f₀ ≈ 0.06–0.08 pN is average force for the 5–6 nm extension of FP9/9 due to alignment. Therefore, the average value of g₀ = 7.0 k_BT was used in theoretical modeling of the experimental σ – ε-curves for fibrin fibers. The probability for transition u → a is given by the Boltzmann factor, p_a(ε)/p_u(ε) = exp[−ΔG(ε)/k_BT], where p_u(ε) is the population of aligned protofibrils (T is temperature and k_B is Boltzmann’s constant). The average stress in a fibrin fiber, σ(ε), is given by the sum of contributions from states u and a,

$$\sigma (\epsilon )=p_u(\epsilon )Y_u\epsilon +p_a(\epsilon )Y_a\epsilon$$ (1)

Damage probability:

When the stress exceeds the critical value σ_cr(ε_cr), where ε_cr is the critical strain, the protofibrils begin to rupture (regime III). There are n protofibril strands and that have failed ((N − n) strands have survived) as ε increases, and so the mechanical response in state a is given by σ_a(ε) = y_a(N − n)ε = y_aε(1 − n/N), where y_a is the Young’s modulus of a protofibril strand in state a. When N is large, the discrete survival probability s = 1 − n/N can be replaced by the continuous probability function. The longest-lasting protofibril element determines the onset of rupture, and so the statistics of extremes determines the fiber failure. For this reason, we use the two-parameter Weibull distribution [69]:

$$s=\text{exp}\left[-{(\epsilon /\tilde{\epsilon })}^m\right]$$ (2)

where $\tilde{\epsilon }$ is the fiber strain scale (range of strains for fibrin fibers values in which the protofibrils fail; see Fig. 4a) and m is the mechanical cooperativity. The strain scale correlates with the width of stress peaks; larger $\tilde{\epsilon }$ imply broader stress peaks. In state u, s(ε) = 1; in state a, s(ε) decreases to zero as ε approaches the strain threshold ε*, above which the fiber begins to rupture. Because fibrin protofibrils are coupled through highly extensible αC regions [18–20,70,71], the FBS model treats protofibrils as mechanically coupled (Fig. 3). The inter-protofibril coupling is described by the cooperativity parameter m. The larger m > 1, the more cooperative is the protofibrils’ breakage.

Figure 4. FBS model based interpretation of experimental stress-strain profiles for single uncrosslinked fibrin fibers:

Experimental stress-strain profiles for single fibrin fibers from 48 experimental curves (Fig. 1) collected for the following ranges of pulling speed: v_f = 0.25–0.5 μm/s (panel a), 1.5–2.5 μm/s (panel b), 6–7 μm/s (panel c), and 9–10 μm/s (panel d). Also shown in panel a are the linear regime I of fiber elastic elongation (protofibrils’ alignment), linear regime II of fiber elastic elongation (protofibrils’ stretching) and rupture regime III. The borders of the regimes are shown for the bottom curve. The experimental stress-strain profiles are compared with the theoretical stress-strain curves constructed with Eq. (3). The FBS model parameters obtained from the least-squares fit of the theoretical curves to the experimental spectra are in Table I. e) Schematic of a short fibrin fiber fragment with unaligned protofibrils (state u; snapshot 0), aligned protofibrils (state a; snapshot 1), and stretched protofibrils (state a; snapshot 2). Snapshots 0–2 correspond to the accordingly numbered regions in a σ – ε-profile in panel a (lower theoretical curve and experimental data points).

Dynamic mechanical response:

The master equation for the total mechanical response from a single uncrosslinked fibrin fiber σ reads:

$$\sigma (\epsilon )=p_u(\epsilon )Y_u\epsilon +p_a(\epsilon )Y_a\epsilon \mathit{\text{exp}}\left[-\theta \left(\epsilon -{\epsilon }^{*}\right){\left(\frac{\left(\epsilon -\epsilon *\right)}{\tilde{\epsilon }}\right)}^m\right]$$ (3)

where θ(ε) is the Heaviside step function. In Eq. (3), the first term p_u(ε)Y_uε is the elastic mechanical response in state u with lower modulus Y_u. The second term proportional to p_a(ε)Y_aε represents the elastic response in state a with a higher modulus Y_a > Y_u. In Eq. (3), s(ε) describes the survival probability of fibrin protofibrils in state a and a gradual decrease of σ to zero due to the mechanical failure of all protofibrils (Fig. 1); since protofibrils break only when ε > ε*, s(ε) is shifted by ε* along the ε –axis.

Mechanical strength and extensibility of uncrosslinked fibrin fibers:

We used Eq. (3) to interpret 48 experimental stress-strain spectra collected for different pulling speeds: v_f = 0.2–1.1, 1.8–2.5, 2.5–5.0, 6.0–7.0, and 9.0–10 μm/s. The strain threshold ε* was set to be equal to the smallest experimental critical strain for fiber rupture, ε* = 212%. Representative experimental and theoretical stress-strain profiles are compared in Fig. 4. Numerical values of the FBS model parameters, i.e. the equilibrium free energy difference between state u (unaligned protofibrils) and state a (aligned protofibrils with extended αC regions) ΔG₀, the Young’s moduli Y_u (for alignment) and Y_a (for stretching), the strain scale $\tilde{\epsilon }$ and the cooperativity parameter m, are listed in Table I.

Table I. Parameters of Fluctuating Bilinear Spring (FBS) model for mechanical deformation and rupture of uncrosslinked fibrin fibers:

The equilibrium free energy difference between state u (unaligned protofibrils) and state a (aligned protofibrils) ΔG₀, the Young’s moduli Y_u and Y_a, the strain scale $\tilde{\epsilon }$ , and the cooperativity parameter m. The values of these quantities (averages and standard deviations) are obtained from the numerical fit of Eq. (3) to 48 experimental stress-strain curves (Figs. 1 and 4) collected using different ranges of the pulling speed v_f (M is the number of the experimental curves). The strain threshold ε* was estimated by finding the minimum value of critical strain ε_cr from experimental stress-strain profiles. The stress scale $\tilde{\sigma }$ was obtained using the formula: $\tilde{\sigma }=Y_a\tilde{\epsilon }$.

	Pulling speed Vf, μm/s
Parameter	0.2–1.1 (M = 17)	1.8–2.5 (M = 11)	2.5–5.0 (M = 13)	6.0–7.0 (M = 5)	9.0–10.0 (M = 3)
ΔG0, kBT	11.5 ± 1.1	10.1 ± 0.7	10.2 ± 1.5	10.4 ± 0.8	10.9 ± 1.7
Yu, MPa	2.6 ± 0.9	1.9 ± 0.9	2 ± 0.9	2.4 ± 0.5	3.2 ± 0.23
Ya, MPa	6.3 ± 2.2	5.7 ± 1.8	6 ± 2.2	7.5 ± 2.9	9.7 ± 0.9
$\tilde{\epsilon }$, %	11.8 ± 6.5	22 ± 7.8	23 ± 7.1	18.8 ± 9.8	41.3 ± 14.4
m	5.2 ± 2	5 ± 1.1	3.6 ± 0.7	5.2 ± 0.5	8 ± 3.5
ε*, %	212 ± 34	212 ± 28	215 ± 38	220 ± 38	175 ± 26
$\tilde{\sigma }$, MPa	0.7 ± 0.3	1.2 ± 0.5	1.3 ± 0.4	1.4 ± 0.9	4.0 ± 1.2

The values of model parameters are statistically the same for all ranges of pulling speed v_f (Table I). We estimated the free-energy difference between states u and a to be ΔG₀≈11.5k_BT (v_f = 0.2–1.1 μm/s). The free energy change for protofibril FP9/9 straightening, which can be estimated by integrating the simulated F – X - spectra over the 5–6 nm extension, is 7–9 k_BT. This value is smaller than the value of ΔG₀ by 2.5–4.5 k_BT. Therefore, the 2.5–4.5 k_BT free energy difference is due to the unraveling of the αC regions. By equating the populations of the unaligned and aligned states, i.e. p_u = p_a (see Eq. (1)), we estimated the fiber strain, which corresponds to the transition of the protofibrils from state u to state a, to be 160%. The Young’s modulus for protofibril alignment, Y_u = 1.9–3.2 MPa, is about three-to-six-fold smaller than the Young’s modulus for protofibril stretching Y_a = 5.7–9.7 MPa (Table I). The strain scale is very broad, $\tilde{\epsilon }=11.8–41.3\text{\%}$. This points to large stochasticity in the mechanics of rupture of fibrin fibers. Indeed, the standard deviations of $\tilde{\epsilon }(6.5–14.4\text{\%})$ are quite comparable with the average values of strain (Table I). This translates to a large variability in the stress scale $\tilde{\sigma }=Y_a\tilde{\epsilon }=0.7–4.0$ MPa, a range in which the rupture of fibrin fibers occurs, and large standard deviations of 0.3–1.2 MPa (Table I). The large cooperativity parameter m = 3.6–5.2 points to strong mechanical cross-communication among fibrin protofibrils due to interactions through the αC regions (Table I).

We applied the FBS theory to probe the limits of mechanical strength and extensibility of fibrin fibers measured by the average critical stress σ_cr and average critical strain ε_cr. In the rupture regime III, when ε > ε* (and p_u(ε) = 0) the mechanical response becomes:

$$\sigma (\epsilon )=Y_a\epsilon \mathit{\text{exp}}\left[-{\left(\frac{\left(\epsilon -\epsilon *\right)}{\tilde{\epsilon }}\right)}^m\right]$$ (4)

By taking the derivative of σ(ε) with respect to and setting it equal to zero, we obtain

$$\frac{m}{\tilde{\epsilon }}{\left(\frac{\left({\epsilon }_{\mathit{\text{cr}}}-\epsilon *\right)}{\tilde{\epsilon }}\right)}^{m-1}{\epsilon }_{\mathit{\text{cr}}}=1$$ (5)

Eq. (5) cannot be solved for ε_cr in closed form for arbitrary m, and so we solved Eq. (5) numerically. The obtained values of ε_cr were then substituted back into Eq. (4), which enabled us to estimate σ_cr. The estimated and experimental values of σ_cr and ε_cr are compared in Table II.

Table II. Limits of extensibility and mechanical stability of uncrosslinked fibrin fibers:

The average critical stress σ_cr and average critical strain ε_cr obtained using Eqs. (4) and (5), respectively. These are compared with the same quantities extracted from the experimental stress-strain profiles collected for the pulling speeds v_f = 0.2–1.1 and 1.8–2.5 μm/s (separated by a slash).

Critical stress/strain	Pulling speed Vf, μm/s		Average value
	0.2–1.1 (M = 17)	1.5–2.5 (M = 11)
σcr, MPa	13.4/12.2	12.4/10.7	12.9/11.5
εcr, %	218/221	221/224	219/222

Statistics of mechanical strength and extensibility of uncrosslinked fibrin fibers:

Although σ_cr and ε_cr carry the information about the average stress and extension, the stress-strain spectra show large variability in the mechanical response of fibrin fibers (Figs. 1 and 4). Because the standard deviations are quite comparable with the averages, i.e., $\tilde{\sigma }=0.7\pm 0.3$ MPa for v_f = 0.2–1.1 μm/s vs. $\tilde{\sigma }=4.0\pm 1.2$ MPa for v_f = 9.0–10.0 μm/s, which correlates with the experimental results, the information obtained from the average stress-strain curves is not sufficient to understand the statistics of critical stresses and critical strains. Therefore, we used the FBS model to derive analytical expressions for the probability distributions of critical stresses p(σ) and critical strains p(ε) (see SM for more detail). The probability distribution of critical stresses p(σ) is given by

$$p(\sigma )=\left\{\begin{array}{c}0,\sigma \le \sigma *\\ \frac{m}{\tilde{\sigma }}{\left(\frac{\sigma -\sigma *}{\tilde{\sigma }}\right)}^{m-1}\text{exp}\left[-{\left(\frac{\sigma -\sigma *}{\tilde{\sigma }}\right)}^m\right],\sigma >\sigma *\end{array}\right.$$ (6)

where σ* = p_u(ε*)Y_uε* + p_a(ε*)Y_aε* is the stress threshold below which the fibers’ rupture does not occur. The probability distribution of critical strains p(ε) reads

$$p(\epsilon )=\left\{\begin{array}{c}0,\epsilon \le \epsilon *\\ \frac{m}{\tilde{\epsilon }}{\left(\frac{\epsilon -\epsilon *}{\tilde{\epsilon }}\right)}^{m-1}\text{exp}\left[-{\left(\frac{\epsilon -\epsilon *}{\tilde{\epsilon }}\right)}^m\right],\epsilon >\epsilon *\end{array}\right.$$ (7)

Using the experimental σ – ε-curves, we constructed the histograms of critical stresses and critical strains and compared them with the theoretical curves of p(σ) and p(ε) obtained with Eqs. (6) and (7) above. Both p(σ) and p(ε) are broad distributions (Fig. 5). This implies that strong stochasticity is a prominent feature of the dynamics of elongation of fibrin fibers. Also, p(σ) has a long right tail (Fig. 5a). The most probable critical stress at rupture is ~9 MPa and the standard deviation is ~11.1 MPa. Similar findings are observed for p(ε) with the most probable critical strain at rupture ~220% (see the inset in Fig. 5a).

Figure 5. Statistics of critical stresses, critical strains, and rupture toughness for single uncrosslinked fibrin fibers:

(a) The experimental histograms and theoretical curves of the probability density functions of critical stresses p(σ) and critical strains p(ε) (in the inset). The histograms are obtained by combining M = 28 values of the critical stress and critical strain extracted from the experimental stress-strain profiles (v_f = 0.2–2.5 μm/s; see Fig. 1c). Theoretical curves of p(σ) and p(ε) are obtained with Eqs. (6) and (7), respectively, and model parameters from Table I. (b) Experimental histogram and theoretical curves of the probability density function of the values of rupture toughness p(U). The histogram of p(U) is obtained by numerical integration of the stress-strain-spectra (M = 28); the theoretical curve of p(U) is generated using Eq. (12) and model parameters (Table I).

Thermodynamics of mechanical deformation and rupture of uncrosslinked fibrin fibers:

We used the experimental σ – ε-curves to extract the thermodynamic state functions of fibrin fiber stretching. The area under the average stress-strain curve is the total work, $w\left({\epsilon }_{\mathit{\text{cr}}}\right)=V{\int }_0^{{\epsilon }_{\mathit{\text{cr}}}}\sigma \left({\epsilon }^{\prime }\right)d{\epsilon }^{\prime }$ , which is equal to the equilibrium free energy change for fiber strain and rupture, w(ε_cr) = ΔG_eq. We assumed that the fibrin fibers remain roughly cylindrical in the course of mechanical testing, i.e. V = AL_init, where A = 7,854 nm² is the average cross-sectional area for a fiber with 100 nm diameter (L_init = 6 μm). From the simulations, straightening of fibrin protofibrils (in state u) does not result in the disruption of native residue-residue contacts that reinforce their native structure (Fig. 2). Also, forced unraveling of the αC regions is an entropic process. These findings suggest that protofibrils alignment in state u (regime I) is mostly an entropy-driven process. By performing the integration over ε in the first term in Eq. (3), we obtain the entropy change for fibrin fiber elongation due to alignment of protofibrils in regime I (see SM for more detail):

$$T\Delta S_I=-V{\int }_0^{{\epsilon }_{\mathit{\text{cr}}}}{p}_u(\epsilon )Y_u\epsilon d\epsilon$$ (8)

Tension-induced stretching of fibrin protofibrils in state a leads to the disruption of native contacts that reinforce the native structure (Fig. 2). Hence, protofibril unfolding in regime II is mostly an enthalpy-driven process. By performing the integration in the second term in Eq. (3), we obtain the enthalpy change for fibrin fiber elongation in regime II (see SM),

$$\Delta H_{II}=V{\int }_0^{\epsilon *}{p}_a(\epsilon )Y_a\epsilon d\epsilon +V{\int }_{\epsilon *}^{{\epsilon }_{\mathit{\text{cr}}}}{p}_a(\epsilon )Y_a\epsilon \text{ exp}\left[-{\left(\frac{\left(\epsilon -\epsilon *\right)}{\tilde{\epsilon }}\right)}^m\right]d\epsilon$$ (9)

By adding Eqs. (8) and (9), we obtain the free-energy change:

$$\begin{gathered} \Delta G_{I,II}=\Delta H_{II}-T\Delta S_I \\ =V{\int }_0^{\epsilon *}{p}_a(\epsilon )Y_a\epsilon d\epsilon +V{\int }_{\epsilon *}^{{\epsilon }_{\mathit{\text{cr}}}}{p}_a(\epsilon )Y_a\epsilon \text{ exp}\left[-{\left(\frac{\left(\epsilon -{\epsilon }^{*}\right)}{\tilde{\epsilon }}\right)}^m\right]+V{\int }_0^{{\epsilon }_{\mathit{\text{cr}}}}{p}_u(\epsilon )Y_u\epsilon d\epsilon \end{gathered}$$ (10)

We used Eqs. (8)–(10) and parameters of the FBS model (Table I) to calculate TΔS_I, ΔH_II, and ΔG_I,II summarized in Table III: TΔS_I ≈ −(82−112) GJ/mol is large and negative, whereas ΔH_II ≈ 107−120 GJ/mol is large and positive, which results in large and positive values of ΔG_I,II ≈ 202−219 GJ/mol. Not unexpectedly, because |TΔS_I| < |ΔH_II| the protofibrils align first at lower strains before they stretch at higher strains.

Table III. Thermodynamic state functions and material toughness for uncrosslinked fibrin fibers:

The entropy part of the free energy change for protofibrils’ alignment in state u (TΔS_I), enthalpy change for fiber stretching in state a (ΔH_II), free energy change (ΔG_I,II), and rupture toughness U obtained with Eqs. (8), (9), (10), and (11), respectively, and model parameters from Table I for pulling speeds v_f = 0.2–1.1 and 1.8–2.5 μm/s. ΔG_I,II and U obtained with the FBS model and by performing the numerical integration of the average experimental stress-strain spectra are separated by a slash.

		Pulling speed Vf, μm/s		Average value
		0.2–1.1	1.8–2.5
Thermodynamic state functions	TΔSI, GJ/mol	−112.2	−81.6	−96.9
	ΔHII, GJ/mol	106.8	120.4	113.6
	ΔGI,II, GJ/mol	219.0/216.6	202.0/206.7	210.5/211.7
Toughness	U, MJ/m3	7.6/7.6	7.1/7.3	7.4/7.5

Material toughness of uncrosslinked fibrin fibers:

We used the FBS theory to estimate the material toughness of fibrin fibers. Starting with Eq. (3), the average toughness U – the free energy density for fiber elongation and rupture – can be obtained by performing the integration over the stress-strain function, i.e.

$$U\left({\sigma }_{\mathit{\text{cr}}}\right)={\int }_0^{{\epsilon }_{\mathit{\text{cr}}}}\sigma (\epsilon )d\epsilon$$ (11)

We used Eq. (11) to calculate the average toughness of fibrin fibers. The results accumulated in Table III indicate that the toughness of single fibrin fibers is in the megajoule range (U ≈ 7.1−7.6 MJ/m³). We also modeled the probability distribution of the values of fiber toughness p(U) using the same analytical form (Weibull distribution) (see SM),

$$p(U)=\left\{\begin{array}{c}0,U\le U*\\ \frac{m}{\tilde{U}}{\left(\frac{U-U*}{\tilde{U}}\right)}^m\text{exp}\left[-{\left(\frac{U-U*}{\tilde{U}}\right)}^m\right],U>U^{*}\end{array}\right.$$ (12)

with the toughness scale parameter $\tilde{U}$. We estimated the toughness threshold U* = 3 MJ/m³ by finding the smallest experimental values of toughness (Fig. 5b). We used Eq. (12) to model the experimental histogram of toughness values for fibrin fibers, which were reconstructed by integrating the experimental σ – ε-curves (Fig. 1). The histogram and theoretical curve of p(U) are compared in Fig. 5b, which shows a broad profile of p(U). The toughness scale parameter $\tilde{U}=8.1$ MJ/m³ is comparable with the most probable toughness for rupture ~ 8.5 MJ/m³ (Fig. 5b).

DISCUSSION

Understanding of blood clots, including their physiological function (hemostasis) and thrombotic disease [26,27], requires a fundamental understanding of the mechanical properties of a blood clot. Blood clots are exposed to the forces of blood flow and the contraction of platelets, but the response of blood clots to these forces may be different for patients with thrombotic diseases, compared to healthy individuals [29–32]. The main structural feature of a blood clot that determines its mechanical behavior is a mesh of fibrin fibers. Recent experimental work has shown that fibrin fibers are very extensible (180–220% rupture strain), elastic (up to 70% strain), and that they have a modulus on the order of a few MPa, which increases about three-fold at strains larger than 100% [19,29–36] (Fig. 1). In addition to the important roles played by fibrin in blood clots, it is also a unique biomaterial [72–75]. However, the molecular mechanisms, which endow fibrin fibers with these mechanical properties, are not understood. While physiological fibrin fibers are ultimately crosslinked by factor FXIII, this study on uncrosslinked fibrin fibers is physiologically relevant to understand the early stages of fibrin fiber formation of fibrin fibers, when fibers (and blood clots) are not yet crosslinked. At a fundamental level, the work presented helps understand in molecular detail protein-protein interactions involved in fibrin fiber assembly.

We carried out a combination of experimental work, computer simulations, and theoretical modeling in order to illuminate the physical picture underlying dynamic structural changes in single uncrosslinked fibrin fibers and to understand their mechanical and material properties. Although fibrin protofibrils are structure elements of fibrin fibers, the physical properties of fibers is not the sum of properties of protofibrils, because the uncrosslinked protofibrils are mechanically coupled both longitudinally (along the fiber axis) and in the radial direction through an intricate network of non-covalent interactions, which includes the D:D interfaces, the A:a and B:b knob-hole bonds, and interactions between the αC domains in αC tethers. Furthermore, while the atomic structures of fibrin monomer and its various portions were solved (reviewed in Ref. [63,76,77]) and were used to construct the atomic models of fibrin oligomers [63] and protofibril [58], the structure of fibrin fiber is not known. This makes a purely experimental exploration of the structure-mechanics relationship for fibrin fibers difficult. We have overcome this problem by coupling the mechanical testing experiments on single uncrosslinked fibers with the pulling simulations on single uncrosslinked protofibrils. By directly correlating the results of simulations on single protofibril FP9/9 (force-distance curves, energies, structures; Figs. 2 and 3; see also Fig. S2) with the experimental stress-strain profiles for single fiber (Figs. 1 and 4), and by using information about the structure of fibrin fibers, we were able to resolve the structural mechanisms of force-induced elongation of uncrosslinked fibrin fibers and to explain the existence of different regimes of their dynamic mechanical deformation and rupture. The structural insights from the simulations on protofibrils were used to formulate the analytically tractable Fluctuating Bilinear Spring theory, which was then used to provide meaningful interpretation of the experimental stress-strain profiles for fibrin fibers.

Theoretical model development:

The FBS theory (Eq. (3)) treats a fibrin fiber as a collection of coupled, staggered fibrin protofibrils, and it maps the structural changes observed in protofibrils, i.e. straightening, unfolding, unraveling of αC tethers, dissociation of D:D interfaces and knob-hole bonds, into the dynamics of fiber elongation and rupture (Figs. 1 and 4). Wang et al. studied fibrin fibers under shear and tensile loads using fluorescence and vibrational microscopy. As in FBS theory, in their model, extension of the αC regions occurs in parallel with the structural transition from α-helices to β-sheets in coiled-coil regions of fibrin monomers, which happens at larger strains [78]. Applying the FBS theory to the experimental stress-strain spectra for fibrin fibers (Fig. 1) yields information not only about their average mechanical and material properties, but also about the distributions of these properties (Fig. 5). We applied the FBS theory to estimate: i) the elastic constants due to protofibril alignment (Y_u) and protofibril elongation (Y_a); ii) the critical strain range, $\tilde{\epsilon }$; iii) the cooperativity parameter, m; and iv) the equilibrium free-energy difference ΔG₀ for the transition from state u of unaligned protofibrils to state a of aligned protofibrils (Table I). The FBS model also provides access to the following quantities: v) the average critical stress σ_cr (Eq. (4)) and the average critical strain ε_cr (Eq. (5)); and vi) the distributions p(σ) (Eq. (6)) and p(ε) (Eq. (7)). Furthermore, using the stress-strain spectra collected under slow, near-equilibrium force-loading conditions, the FBS theory enables one to calculate the following thermodynamic state functions: vii) the entropy change for protofibrils’ alignment ΔS_I (Eq. (8)); viii) the enthalpy change for protofibrils’ stretching ΔH_II (Eq. (9)); and ix) the free-energy ΔG_I,II (Eq. (10)). Moreover, using ΔG_I,II, one can obtain: x) the average toughness for rupture of fibrin fibers U (Eq. (11)) and xi) the distribution of toughness values (Eq. (12)).

Dynamic mechanical regimes of elongation of uncrosslinked fibrin fibers:

Dynamic force measurements in silico on uncrosslinked fibrin protofibrils helped us to identify the relevant mechanical excitations for forced elongation and rupture of fibrin fibers. These findings provided the structural foundation of the Fluctuating Bilinear Spring (FBS) model. The FBS model considers: 1) straightening of protofibrils and unraveling of the αC tethers at lower loads; 2) elongation of the α-helical coiled coils and partial unfolding of γ-nodules in fibrin monomers at higher loads; and 3) rupture of the D:D interfaces and dissociation of the A:a and B:b knob-hole bonds in both protofibril strands for loads above the critical level (Fig. 2c). These structural transitions in fibrin protofibrils give rise to the following dynamic mechanical regimes (Fig. 1): elastic deformation of fibrin fibers with a lower slope $\raisebox{1ex}{$d\sigma $}\!\left/ \!\raisebox{-1ex}{$d\epsilon $}\right.$ at small strains (regime I) and with a higher slope at large strains (regime II); and fiber rupture for strains above the critical threshold (regime III). The rupture regime III is very short lasting only 2–10% of strain, and so the fiber rupture is an all-or-none process due to mechanical cooperativity among fibrin protofibrils.

The FBS model focuses on the protofibrils (γ-nodules, α-helical coiled coils, D:D interfaces, knob-hole bonds and αC regions in fibrin monomers), while not explicitly treating the contributions from the B:b tethers; but this is not because we consider the B:b knob-hole bonds to be unimportant. Protofibrils, the αC regions, and the B:b knob-hole bonds are all part of a connected network (see Fig. 3). Some of these connections (αC regions and B:b knob-hole bonds) are in series whereas others (e.g. protofibrils) are in parallel, and, thus, the stress propagates through all structure elements. When mechanical springs are connected in series, the force applied to the endpoint of the structure is applied equally to all elements, and the elements extend inversely proportionally to their spring constant (Hooke’s law: Δx_i = F/k_i). When the elements are connected in parallel, they all extend by the same amount Δx, but the force experienced by the i-th element is F_i = k_iΔx. Fibrin protofibrils are likely connected together in series (longitudinally) and in parallel (radially) in a complex way by the network of αC region interactions and B:b knob-hole bonds. There are typically n_r = 60 protofibril strands in a 100 nm fiber diameter and the tension on the fiber is of the order of 100 nN at the largest extensions. The protofibrils experience a force of the order of 1–2 nN at the largest extensions and 100–200 pN at 100% strain, at which stiffness changes. These are in the range of forces necessary to induce structural changes in the protofibrils (Fig. 2). Hence, unraveling of the αC regions and protofibril elongation define the mechanical properties of fibrin fibers. Within the experimental range of pulling speeds used in this study, we did not see any speed-dependence of the rupture force or stiffness of the fibers, as would be expected for viscous materials. There are several reasons that can explain this behavior. Fibers may experience mainly elastic deformations, which would not show a pulling speed-dependence of their stiffness. The range of pulling speeds may not have been large enough to detect any speed-dependent mechanisms.

Structural mechanisms of deformation and rupture of uncrosslinked fibrin fibers:

We employed the native topology based SOP modeling of a polypeptide chain to describe the mechanical properties of large protein assemblies, such as a ~360 nm long fibrin protofibril FP9/9 (~36,000 amino acid residues) [57]. This type of modeling was applied to describe fibrin oligomers [58], microtubule filaments [59], virus shells [60,61], and cell organelles [62]. Here, we employed the SOP model of uncrosslinked fibrin protofibril FP9/9, as a structural unit of fibrin fiber (Fig. 3), in conjunction with the pulling simulations, accelerated on a GPU [65,66], to uncover the mechanisms of elongation and rupture of fibrin fiber. The initial straightening of protofibril FP9/9 in the 0–0.05 nN force range results in a ~70–100 nm elongation, and subsequent stretching of the coiled coils in the 0.05–0.2-nN force range results in an additional ~70–90 nm elongation. The disruption of the D:D interface at the ~0.2 nN critical force is preceded by the partial unraveling of the γ-nodules (Fig. 2c). While the N- and C-terminal portions were found to unravel in single-stranded fibrin oligomers [42], in the uncrosslinked protofibrils analyzed here the N- and C-terminal portions remain intact, because the D:D interface is mechanically weaker than the N- and C-terminal parts of the D regions. Whether the A:a knob-hole bonds are intact or dissociated does not affect the strength of the D:D interface. This is because the A:a knob-hole bonds hold the two strands in a protofibril together, and so the pulling force creates roughly equal tension in both strands. The dissociation of B:b knob-hole bonds weakens the D:E:D interface. In the simulations, the D:D interfaces, in which the B:b knob-hole bonds were dissociated, ruptured more easily.

Fibrin Fiber Rupture is a Complex Process:

By directly correlating the results of mechanical testing in silico on the uncrosslinked fibrin protofibril PF9/9 with the experimental σ – ε curves for uncrosslinked fibrin fibers, we were able to gather the following quantitative information:

1) Simultaneous unraveling of αC regions and straightening of protofibrils results in protofibril alignment.

From the simulations, we estimated that the initial straightening of protofibrils corresponds to a small ~5–6 nm protofibril extension. The free-energy change associated with protofibril FP9/9 straightening, as calculated by integrating the simulated F − X-spectra in the 5–6 nm extension range, comes to ~7–9 k_BT. This value is lower than the equilibrium free energy difference between state u (unaligned protofibrils) and state a (aligned protofibrils), ΔG₀ ≈ 11.5 (v_f = 0.2–1.1 μm/s), as obtained from a fit of the FBS model to the experimental stress-strain curves for fibrin fibers (Figs. 1 and 4; Table I). Therefore, the remaining 2.5–4.5k_BT energy difference is due to the 20–25-nm unraveling of the αC regions. This conclusion correlates with our finding that unraveling of the αC regions accounts for ~80% of the fiber extension at 160% strain.

2) Protofibril network remodeling results in increased strength and extensibility of fibrin fiber.

The equilibrium length of unstretched fibrin fiber (half the fiber length in Fig. 1) is L_init = 6 μm, which is spanned by n_l = L_init/l_init ≈ 17 protofibrils FP9/9 connected in the longitudinal direction by 17 αC tethers. Here, l_init = 360 nm is the equilibrium end-to-end distance of intact protofibril FP9/9 from simulations (Fig. 2a). The contribution to the 6 μm fiber length from the αC regions in the random coil conformation in state u is negligible. In regime I, the native contacts reinforcing the protofibril structure remain intact until the characteristic extension of x_a = 85 nm is reached, which corresponds to a 50 pN force. Hence, in regime I, the protofibrils straighten but do not stretch, and the transition from state u (unaligned protofibrils) to state a (aligned protofibrils) occurs. We modeled the force (F^αC)-induced extension of an αC tether (x^αC) using the WLC model [19]: F^αC(x^αC) = k_BT/l_p(1/4(1 − x^αC/l_c)⁻²) – 1/4 + x^αC/l_c, where l_p = 0.38 nm is the persistence length and l_c is the contour length of the αC tether. One αC connector has 170 amino acids, and so l_c = 2×170×0.35 nm = 119 nm (0.35 nm is the length of one amino acid). From the WLC model, the average extension of the αC tether, which corresponds to a 50 pN force, is $x_a^{\alpha C}\approx 90$ nm (Fig. 2b). We converted the experimental σ – ε curves for fibrin fibers (Fig. 1) to the force (F)-extension (X) profiles and estimated the average fiber extension X_a ≈ 10 μm, which corresponds to the protofibrils transitioning from state u to state a. By dividing X_a by $x_a^{\alpha C}+x_a$, we obtained n_l = 57 mechanically engaged protofibrils connected by 57 αC tethers to account for the X_a = 10 μm experimental fiber extension.

These results show that in the unstretched fiber (at zero extension) there are n_l = 17 mechanically engaged protofibrils PF9/9 connected by 17 αC tethers, and that at X_a ≈ 10 μm fiber extension, this number is increased to n_l = 57 protofibrils and ~57 αC tethers. This apparent increase in the number of protofibrils in the longitudinal direction can be explained by considering dynamic remodeling of the network of tension-transducing protofibrils at lower strains (in regime I). In a fiber, fibrin protofibrils are spatially separated by ~13–14 nm [40,79], and ~80% of the fiber volume is occupied by water [79]. This implies that the internal structure of fibrin fibers consists of a dispersed, staggered, somewhat disordered array of loosely bound protofibrils that are capable of sliding past each other. Tension induces dynamic structural changes within the protofibrils (protofibril straightening) and between the protofibrils (unraveling of αC tethers), as well as in the space occupied by water [79]. The protofibrils slide past each other, thereby joining the tension-transducing network of fibrin protofibrils, and tension-induced bundling of fibrin protofibrils brings them closer together (thereby expelling water molecules from the water matrix, as we detail below), which results in the increase of the number of mechanically engaged protofibrils.

We interrogated whether a similar dynamic remodeling takes place at higher strains. We estimated the number of protofibrils in the protofibril network at the critical strain for fibrin rupture (ε_cr ≈ 220%). From the simulations, the average critical extension for rupture of protofibril FP9/9 is x_cr ≈ 170 nm, which corresponds to the 190 pN average critical force for FP9/9 rupture (Fig. 2b). Using the F − X-profiles derived from the experimental σ – ε curves (Fig. 1), we extracted the average critical fiber extension X_cr = 13.2 μm. The critical extension of the αC tether corresponding to 190 pN force is $x_{\mathit{\text{cr}}}^{\alpha C}\approx 105$ nm. The total number of protofibrils which accounts for the 13.2-μm critical fiber extension is $n_l=X_{\mathit{\text{cr}}}/\left(x_{\mathit{\text{cr}}}^{\alpha C}+x_{\mathit{\text{cr}}}\right)\approx 48$. We also estimated this number using the experimental stress-strain curves but for fibrin fibers without the αC regions (unpublished data). In this case, X_cr ≈ 7.9 μm and dividing 7.9 μm by x_cr ≈ 170 nm we arrive at n_l = 47 protofibrils. Hence, there is no dynamic remodeling of the protofibril network at higher strains. In the calculations below, we set the number of protofibrils in one protofibril strand (i.e. longitudinal connections) to be equal to n_l = 52 (arithmetic average from two independent estimates 57 and 47 obtained above). Because the total number of protofibril strands in a fiber (17×60=1020) is conserved, sliding of staggered protofibrils past each other leads to an increase (decrease) in the number of protofibrils in longitudinal direction n_l (in cross-sectional area n_r ). In regime I, n_l increases 52/17 ≈ 3-fold, whereas n_r decreases 3-fold, i.e. n_r = 60/3 = 20.

3) Structural rearrangements in aqueous environment dominate thermodynamics of fibrin fiber rupture.

We compared the contributions to the thermodynamic state functions from the protein component (fibrin protofibrils plus αC tethers) and water component by analyzing the FX-profiles for the αC tethers (WLC model; Fig. 2b), fibrin protofibril FP9/9 (simulations; Fig. 2b) and fibrin fiber (experimental FX-curves; Figs. 1 and 4). The free-energy changes for FP9/9 elongation and unraveling of the αC tethers in state u and state a come to ~1.0 MJ/mol and ~6.0 MJ/mol, and 0.6 MJ/mol and 0.9 MJ/mol, respectively. Summing over n_l = 52 protofibril strands connected by 52 αC tethers spanning the X_a = 10-μm fiber extension, and taking into account n_r = 20 of 10 μm long such strands (per fiber diameter), we obtain the free-energy changes for elongation of the protein component of fibrin fiber in state u (entropy-driven process) to be ~1.7 GJ/mol and in state a (enthalpy-driven process) to be ~7.2 GJ/mol. These values account for ~1.8% of the entropy change, TΔS_I = −96.9 GJ/mol, and for ~6.3 % of the enthalpy change, ΔH_II = 113.6 GJ/mol, extracted from the experimental stress (σ)-strain (ε) profiles for fibrin fiber (Table III). Hence, ~95.2 GJ/mol (for state u) and 106.4 GJ/mol (for state a) of the free energy change correspond to structural rearrangements in the aqueous environment, which accounts for ~94–98% of the total free energy change per fibrin fiber. Interestingly, ~2–6% energy change from the protein component (fibrin protofibrils plus αC tethers) and 94–98% energy due to water correlate with the ~20% protein content and ~80% water content of fibrin fibers (by volume) [79]. Thermodynamic state functions (extensive quantities) scale with the amount of substance. Because the protein density (~1.2–1.3 g/ml) is close to the water density (~1.0 g/ml), the free-energy changes for the protein and water components scale with the volumes occupied by protein and water, respectively.

4) Structural rearrangements in aqueous environment control fibrin fiber elasticity.

We compared the contributions to the fibrin fiber elasticity from the protein and water components. The average stiffness of αC tether in state u and state a is $k_u^{\alpha C}\approx 0.16$ pN/nm and $k_a^{\alpha C}\approx 9.5$ pN/nm (Fig. 2b). The average stiffness of fibrin protofibril in state u and state a is k_u = 0.45 pN/nm and k_a = 1.63 pN/nm. Using the experimental values of Young’s modulus for fibrin fiber (Table I), the fiber stiffness in state u and state a is K_u = 3.40 pN/nm and K_a = 10 pN/nm. The spring constant for one 6 μm long protofibril strand of n_l = 52 fibrin protofibrils connected by 52 αC tethers, treated as a collection of harmonic springs arranged in series, can be calculated as $k_i^{st}={\left(\frac{n_{l,i}}{k_i}+\frac{n_{l,i^{-1}}}{k_i^{\alpha C}}\right)}^{-1}$. The spring constant for the protein component can be estimated by multiplying $k_i^{st}$ by the total number of stands n_r , each containing 52 protofibrils and 52 αC tethers, arranged in parallel (per fiber diameter), i.e. $20\times k_u^{st}\approx 0.05$ pN/nm for state u and $20\times k_a^{st}\approx 0.54$ pN/nm for state a. Comparing 0.05 pN/nm and 0.54 pN/nm (protein component) with the experimental values of K_u = 3.4 pN/nm and K_a = 10 pN/nm (protein and water components), we find that the stiffness of the protein component of fibrin fiber (protofibrils) accounts for ~1.5–5.5% of the total fiber stiffness in state u and state a. Hence, the stiffness of fibrin fibers is largely dominated by structural rearrangements in the aqueous environment.

5) Fibrin fibers exhibit hydrogel-like hydration behavior.

These findings described above have some similarity to the behavior of hydrogels, where the relative amounts of surface-bound water (i.e. water surrounding a protein) versus bulk water, with different measured enthalpies and entropies, helps to understand the different physical properties and thermodynamics for different states of the hydrogel [76]. Similarly, in a fibrin fiber ~80% of the volume is occupied by the surface-bound and bulk water, and so the dynamic structural changes characterized in this work clearly involve rearrangement of the protein surface-bound water (protofibrils’ dehydration) and transfer of surface-bound water to the bulk solvent (water expulsion). Given the large contribution of water to the free energy of fibrin fiber stretching we determined in this study, we felt a need to provide the reader with some idea of how this may be achieved, even in the absence of definitive evidence. In that spirit, we estimated the free energy of dehydration of 52 – 17 = 35 protofibrils, which corresponds to sliding-driven remodeling of the tension-transducing network of protofibrils transforming from unaligned in state u to aligned in state a at lower strains discussed above. The average hydration free energy per amino acid is ~20–30 kJ/mol [82]. Excluding the αC tethers, which are expected to be hydrated both in the random coil and in extended conformations, there are ~2,000 residues per fibrin monomer, of which ~150 residues are water exposed. There are 18 fibrin monomers in protofibril FP9/9, and a total of 20 of 6 μm long protofibril strands per 100 nm fiber diameter. Therefore, the free energy cost for fibrin monomer dehydration within fibrin protofibrils is ~(20–30) kJ/mol ×150×18×35×20 = (37–56) GJ/mol. The remaining free-energy cost (from ~95 GJ/mol for state u), i.e. ~39–58 GJ/mol, is due to water expulsion. Hence, a protofibril dehydration and sliding mechanism operates during the dynamic remodeling of the tension-transducing network of fibrin protofibrils at lower strains (regime I). This results in the recruitment of ~35×20 = 700 additional protofibrils to create an ordered and closer packed protofibril array.

CONCLUSION

We explored the biomechanics and thermodynamics of the tensile deformation of single, uncrosslinked fibrin fibers, and characterized different dynamic mechanical regimes of their forced elongation and rupture. Mechanical testing in silico was employed to interrogate the mechanical, material, and thermodynamic properties of the uncrosslinked fibrin protofibrils, the building blocks of fibrin fibers, and to uncover the mechanisms of their elongation and rupture. The elastic deformation of fibrin fiber with a lower elastic modulus of 0.5–4 MPa for small strains below 160% (regime I) is due to simultaneous protofibril straightening and unraveling of the regions, and the elastic deformation with a higher elastic modulus of 2.4 – 11 MPa for larger strains above 160% (regime II) is due to forced unfolding transitions in coiled coils and γ nodules in fibrin monomers. The rupture of fibrin fibers at the critical 13 MPa stress and the critical 220% strain is due to forced dissociation of the D:D interfaces and the knob-hole bonds in two-stranded fibrin protofibrils. We proposed the Fluctuating Bilinear Spring theory, which was applied to interpret the experimental stress-strain profiles for single fibrin fibers in all three regimes I-III of their elastic deformation and rupture. Previous models were not able to capture these different regimes of mechanical behavior of fibrin fibers, including fiber rupture [19,68,83]. The FBS theory can be applied more widely to interpret the results of tensile testing experiments for other biologically important protein fibrils. Extending the FBS theory to modeling crosslinked fibrin fibers will be the subject of future work. Experimentally, crosslinked fibrin fibers show increased stiffness (modulus) by a factor of 2–3, reduced extensibility by a factor of 0.6–0.8, and reduced strain hardening, compared to the uncrosslinked fibers.

We arrived at the following main conclusions. 1) Dynamic remodeling of the protofibril network at lower strains (<160%) extends the limits of strength and deformability of fibrin fiber; we found that tension-induced straightening and sliding of staggered protofibrils results in an increased number of mechanically engaged protofibrils (strength) and prolonged extension range (deformability). 2) Structural rearrangements in the aqueous environment control fibrin fiber stiffness; the stiffness of the tension-transducing network of fibrin protofibrils was found to accounts for ~1.5–5.5% of the total fiber stiffness. 3) Structural rearrangements in the aqueous environment dominate the thermodynamics of fibrin fiber rupture; indeed, ~94–98% of the total free energy change for fibrin fiber elongation and rupture was found to be due to structural rearrangements in the water matrix. The main conclusion: 4) A fibrin fiber behavior is somewhat similar to a hydrogel; our results highlight the approximately equal energetic roles played by protein surface-bound water (~37–56 GJ/mol free energy change for protein dehydration) and transfer of surface-bound water to the bulk water (~39–58 GJ/mol free energy change associated with water expulsion). These results reveal the operation of a protofibril dehydration and sliding mechanism that engages additional protofibrils to create a closer packed protofibril array.

Statement of significance.

Structural mechanisms underlying the mechanical properties of fibrin fibers, major components of blood clots and obstructive thrombi, are elusive. We performed tensile testing of uncrosslinked fibrin polymers in vitro and in silico to explore their material properties. Fluctuating Bilinear Spring theory was developed to interpret the stress-strain profiles in terms of the energy for protofibril alignment, elastic moduli for protofibril alignment and stretching, and strain scale for fiber rupture, and to probe the limits of fiber strength, extensibility and toughness. Fibrin fibers behave like a hydrogel. Fiber elongation is defined by the protofibril dehydration and sliding. Structural rearrangements in water matrix control fiber elasticity. These results contribute to fundamental understanding of blood clot breakage that underlies thrombotic embolization.