Multimodal neural recordings with Neuro-FITM uncover diverse patterns of cortical-hippocampal interactions

Summary/Abstract

Many cognitive processes require communication between neocortex and hippocampus. However, coordinations between large-scale cortical dynamics and hippocampal activity are not well-understood, partially due to the difficulty to simultaneously record from those regions. Here we developed a Flexible, Insertable, and Transparent Microelectrode array (‘Neuro-FITM’) that enables investigation of cortical-hippocampal coordinations during hippocampal sharp-wave ripples (SWRs). Flexibility and transparency of Neuro-FITM allow simultaneous recordings of local field potentials and neural spiking from hippocampus during wide-field calcium imaging. These experiments revealed that diverse cortical activity patterns accompanied SWRs, and in most cases, cortical activation preceded hippocampal SWRs. We demonstrated that, during SWRs, different hippocampal neural population activity was associated with distinct cortical activity patterns. These results suggest that hippocampus and large-scale cortical activity interact in a selective and diverse manner during SWRs underlying various cognitive functions. Our technology can be broadly applied to comprehensive investigations of interactions between cortex and other subcortical structures.

Introduction

Brain computations often require interactions between different cortical and subcortical structures. Understanding these long-range interactions in the brain requires monitoring of simultaneous activity patterns across these areas. That could be achieved by simultaneous multimodal recordings combining electrophysiological recordings and large-scale functional optical imaging. However, seamless integration of optical imaging with electrophysiology is difficult with conventional microelectrodes since large probe shanks made of rigid and opaque materials can prevent lowering the microscope objective and block the field of view of imaging. To address this issue, we developed ‘Neuro-FITM’, a Flexible, Insertable, and Transparent Microelectrode array which can be implanted into deep cortical layers and subcortical structures. The flexible probe shank of Neuro-FITM can be bent to the side to allow lowering the microscope objective. Optical transparency of the shank provides a clear field of view and prevents optical shadows or additional noise in optical signals. Low impedance of Neuro-FITM provides reliable recordings of local field potentials (LFPs), high frequency oscillations and single units with high signal-to-noise ratio (SNR).

Here we performed multimodal experiments with Neuro-FITM to investigate the coupling between the hippocampus and the cortex during sharp wave-ripples (SWRs). Hippocampal SWRs have been suggested to coordinate activity between the hippocampus and cortex^1–4. Experiments with closed-loop manipulations have shown the indispensable role of SWRs in learning and memory^5–7. However, most studies only focused on a single or a few cortical regions^8–12 and thus little is known about the simultaneous interaction between multiple cortical regions and hippocampus during SWRs. Furthermore, it is unclear whether the cortex is passively activated by hippocampal SWRs or whether certain cortical activity patterns can precede SWRs. Importantly, simultaneous variations across SWRs in hippocampal population activity and cortical activity patterns have not been studied. These questions could be addressed by simultaneous multimodal recordings that include electrophysiological recordings of the hippocampus and functional imaging of the cortex across large areas. We implanted Neuro-FITM to the hippocampus and performed simultaneous electrophysiological recordings of SWRs and single units during wide-field calcium imaging of most of the dorsal cortex in awake, head-fixed mice. Empowered by the multimodal recording capability, we investigated the large-scale cortical activity patterns associated with SWRs on single-event basis using tensor component analysis (TCA)¹³ and found a rich spatiotemporal diversity. Furthermore, by performing decoding analysis with support vector machine (SVM)¹⁴, we found that different cortical activity patterns relate to distinct activity of hippocampal neurons. Our results reveal that SWRs accompany diverse and specific interactions between the activity of hippocampus and cortex and support the model that SWRs mediate diverse cortical-hippocampal interactions depending on the behavioral context and demand.

Results

Neuro-FITM Fabrication and Characterization

Neuro-FITM arrays developed in this study combine three key advantages: flexibility, transparency and shuttle-free implantation in a single probe. They were fabricated on transparent and flexible Parylene-C substrate (Fig. 1a–c). Briefly; PMGI sacrificial layer was spin-coated on a silicon wafer. A 14 μm-thick Parylene-C layer was deposited with the chemical-vapor-deposition (CVD) method. 5 nm Cr and 100 nm Au were deposited with sputtering and patterned with photo-lithography and wet-etching. 2 μm-thick Parylene-C was deposited as the encapsulation layer (Fig. 1c). Electrode openings were patterned with photo-lithography and oxygen plasma etching. The profile of the probe was defined with photo-lithography and oxygen reactive ion etching (Fig. 1d–f). Neuro-FITM arrays can be fabricated in various configurations depending on specific needs of the experiments. Neuro-FITM probe shown in Fig. 1 is designed to record hippocampal LFPs and units during optical imaging. The width of the array is 50 μm at the tip, whereas the shank is tapered up to a maximum width of 170 μm at the top. The array consists of 32 circular recording electrodes, each with 10 μm diameter connected to 2 μm-wide wires. The scanning electron microscope (SEM) images show the profile of the probe and well-defined electrode openings (Fig. 1d–f). We fabricated several different configurations of Neuro-FITM including probes with smaller electrode spacing (20 μm) for potential use in tetrode configuration (Extended Data Fig. 1a), probes with higher channel count (64 channels per shank) (Extended Data Fig. 1b), and probes with longer shanks to allow recording from deeper structures of the brain or to use in rats (Extended Data Fig. 1c) and primates (Extended Data Fig. 1d).

Fig. 1 |. Characterization of Neuro-FITM.

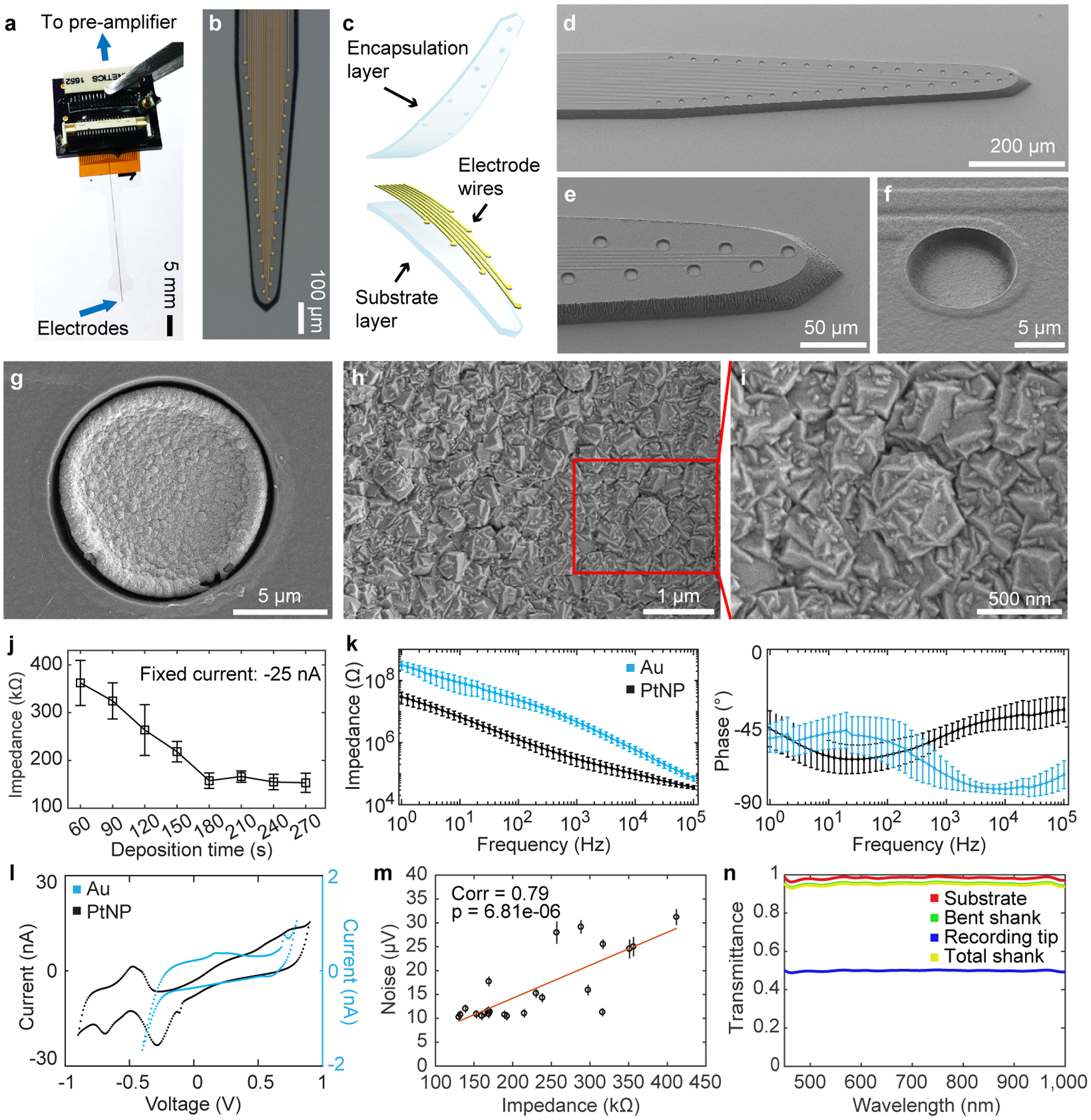
a, Neuro-FITM connected to the custom PCB board.

b, Microscope image showing the layout of the microelectrode array.

c, Schematic showing exploded view of 3-layered structure of Neuro-FITM.

d-f, Scanning electron microscope (SEM) images of the array showing 10 μm-diameter microelectrode openings and 2 μm-wide wires connecting to the microelectrodes.

g-I, SEM images showing PtNPs deposited onto the Au microelectrodes.

j, Electrode impedance as a function of deposition time during Platinum nanoparticle (PtNP) deposition (mean ± s.d., n = 3 electrodes for 60, 90, 180, 210, and 270 s deposition time, n = 4 electrodes for 120, 150, 240 s deposition time).

k, Electrochemical impedance spectroscopy magnitude (left) and phase (right) are compared between Au and PtNP-deposited Au electrodes. PtNPs reduced the impedance of Au electrodes. The phase plot shows that PtNP electrodes are more resistive at higher frequency ranges than Au electrodes, consistent with the reduction in the impedance magnitude (mean ± s.d., n = 26 electrodes for Au and n = 21 electrodes for PtNP).

l, Cyclic voltammetry characteristics of PtNP-deposited electrodes showing redox peaks corresponding to electrochemical reactions of Pt, indicating an active engagement of PtNPs in the redox processes at the electrochemical interface.

m, Noise level for electrodes with different impedances measured in 0.1 M PBS solution. Recorded signals were first high-pass filtered at 5Hz and chunked into non-overlapping 1 s segments. The noise level for each segment was defined as its root-mean-square value. Each dot marks the mean noise level for each recording channel. The error bar marks the s.e.m. n = 87 measurements. The noise levels are higher for electrodes with higher impedance (two-sided Student’s T-test, P = 6.81E-6, n = 23, degree of freedom = 21).

n, Transmittance of the substrate, the bent shank, the recording tip, and the total shank as a function of wavelength.

Reducing the electrode impedance is important to minimize the electrical noise, particularly for single unit recordings^15–17. To achieve low impedance, platinum nanoparticles (PtNPs) were deposited onto 10 μm Au electrodes of Neuro-FITM probes (Fig. 1g–i)¹⁷. The electrode impedance can be controlled as a function of PtNP deposition time (Fig. 1j) and the size of the PtNP increases as the deposition time increases¹⁷. The largest grains of PtNPs are about 500 nm in diameter for 180 s deposition time. Electrochemical impedance spectroscopy (EIS) results show that the impedance of the Neuro-FITM electrodes was reduced by ~16x (Fig. 1k) as a result of PtNP deposition. Cyclic voltammetry (CV) measurements confirm that the PtNPs are actively engaged in the redox processes at the electrochemical interface (Fig. 1l). The impedance of our 10 μm diameter electrodes is ~150 kΩ at 1 kHz, similar to those of the Neuropixel probes (~150 kΩ)¹⁸ even though the surface area (78.5 μm²) is half the size (Neuropixel = 144 μm²). Considering the impedance is inversely proportional to the electrode area, the impedance of Neuro-FITM electrodes is effectively 2 times smaller than the Neuropixel probes. We investigated the effect of impedance reduction on recording noise. Fig. 1m shows recorded electrical noise as a function of electrode impedance, varied by controlling PtNP deposition time. Neuro-FITM electrodes exhibit sufficiently low noise (10 μV) for reliable detection and sorting of single units.

Optical transparency is important for seamless integration of electrophysiological recordings and optical imaging in multimodal experiments^16,19. We characterized the optical transparency of Neuro-FITM. The transmittance of the bent shank is ~95.7% and the recording tip with dense Au electrodes and interconnects shows a transmittance of ~50% (Fig. 1n). It is important to point out that although the Au electrodes and Au wires are not transparent, the functional imaging would not be affected since 1) Neuro-FITM is vertically implanted so that the penetrating tip of the probe does not directly block the light pathway, and 2) the bent shank in the light pathway has thin Au wires resulting in a high transmittance of ~95.7%. In order to better clarify the advantages of Neuro-FITM in multimodal configurations involving two-photon microscopy or wide-field imaging, we compared Neuro-FITM to commercially available Neuronexus and Neuropixel probes (Extended Data Fig. 2). The high flexibility of Neuro-FITM allows bending the probe shank away to lower the microscope objective for two-photon imaging (Extended Data Fig. 2b), while rigid shanks of the Neuropixel and Neuronexus probes prevent lowering the microscope objective to its working distance. Wide-field microscope images (Extended Data Fig. 2c) show that Neuronexus and Neuropixel probes block the field of view and generate shadows. In addition, large probe shanks can also result in out-of-focus images (Extended Data Fig. 2c, Neuropixel probe). Transparency of Neuro-FITM prevents blocking the field of view and the formation of optical shadows which can obscure imaging. In addition to multiphoton imaging and wide-field imaging, Neuro-FITM array is also compatible with other optical imaging techniques commonly used in neuroscience, including near-infrared spectroscopy, and diffuse optical tomography.

In vivo Multimodal Recordings with Neuro-FITM

Vertical implantation of Neuro-FITM arrays is critical for not blocking the light pathway during optical imaging and minimizing implantation damage. In order to implant Neuro-FITM arrays vertically without using a rigid shuttle or adding a bioresorbable stiffening layer, we carefully engineered the geometry and the length of the microelectrode array by performing mechanical analysis to prevent buckling during insertion. Furthermore, the probe was designed to include additional micromanipulator pads to maximize insertion force against buckling (Fig. 2a, see Methods). Note that, implantation of Neuro-FITM arrays with very long probe lengths designed for primate use (Extended Data Fig. 1d) will require the aid of shuttles during the insertion step. After the insertion and successful targeting of hippocampus (Fig. 2b), the shank of the array was bent away to the side to allow lowering the microscope objective to its working distance and to clear the field of view of the microscope (Fig. 2a, and Extended Data Fig. 3a). 2 μm-wide wires are confined to a narrow width to increase transparency of the shank and to minimize formation of shadows during imaging (Fig. 2c). In order to investigate the use of Neuro-FITM in in vivo multimodal experiments, we implanted it into the CA1 layer of hippocampus (Fig. 2b, Extended Data Fig. 3b) of transgenic mice expressing GCaMP6s in most cortical excitatory neurons²⁰ (CaMK2-tTA::tetO-GCaMP6s, methods). We performed simultaneous electrophysiological recordings of CA1 and wide-field calcium imaging of the dorsal cortex²¹. Hippocampal SWRs were detected in multiple channels located near the CA1 pyramidal layer (Fig. 2d) with concurrent large-scale cortical dynamics monitored using wide-field calcium imaging. Fig. 2e shows representative examples of various spatial patterns of cortical activation during individual SWRs. In addition to recordings of high frequency SWR events, Neuro-FITM electrodes also detected spikes from multiple hippocampal neurons (12 ± 2 (mean ± s.e.m.) neurons in each animal). Most neurons could be detected in multiple adjacent channels, each exhibiting different spike amplitudes (Extended Data Fig. 3c). Fig. 3a shows spike waveforms of 21 neurons recorded across different channels in three recording sessions from one animal. Fig. 3b shows the spike waveforms of all 21 neurons from the channel with largest amplitude. Recorded neurons show stable spike waveforms across the sessions. Signal-to-noise ratio of the electrical recordings is critical for spike detection and sorting as well as reliable detection of SWRs across different sessions. Therefore, we investigated SNR for both unit (Fig. 4a) and LFP recordings adopting the method used for measuring spike SNR of Neuropixel probes¹⁸. The SNR is computed as A/(0.6457*B), where A is the maximum signal amplitude and B is the baseline taken as the median absolute deviation (MAD). The mean SNR of detected spikes is between 6 and 15 (Fig. 4b), similar to the SNR recorded by Neuropixel and other Si probes^18,22. To quantify the SNR of the LFP recordings, we measured the SNR for ripples and sharp-wave events using the same method¹⁸. The LFP signals recorded from the channels located in the pyramidal layer were band-pass filtered at the ripple frequency range (120 Hz – 250 Hz) and sharp-wave frequency range (5 Hz – 50 Hz) respectively. The baseline was then chosen as MAD of the filtered signal from each channel. For each ripple event, the maximum signal amplitude is taken. The distribution of the detected amplitude and the SNR for ripples and sharp-waves are shown in Fig. 4c, d and Fig. 4e, f, respectively. These results confirm that Neuro-FITM achieves high SNR for both single-unit and LFP recordings in all animals. Another important question is how SNR of fluorescence response in wide-field imaging would be affected by the presence of Neuro-FITM electrodes. We characterized the SNR of the ΔF/F to quantify whether the implanted array affects imaging quality following the procedure in a previous study²³. Briefly, we first identified the onset and offset time points of each cortical activation events. The SNR of each event is computed as the ratio between the maximum ΔF/F amplitude during activation and the standard deviation of the ΔF/F fluctuation during [−1s, 0s] before onset. We found similar SNR for the fluorescence activity from the area covered by Neuro-FITM shank and the corresponding area in the contralateral hemisphere (Fig. 4g), showing that Neuro-FITM does not significantly change the SNR of fluorescence signals during wide-field calcium imaging.

Fig. 2 |. Simultaneous multimodal recordings from the hippocampus and cortex.

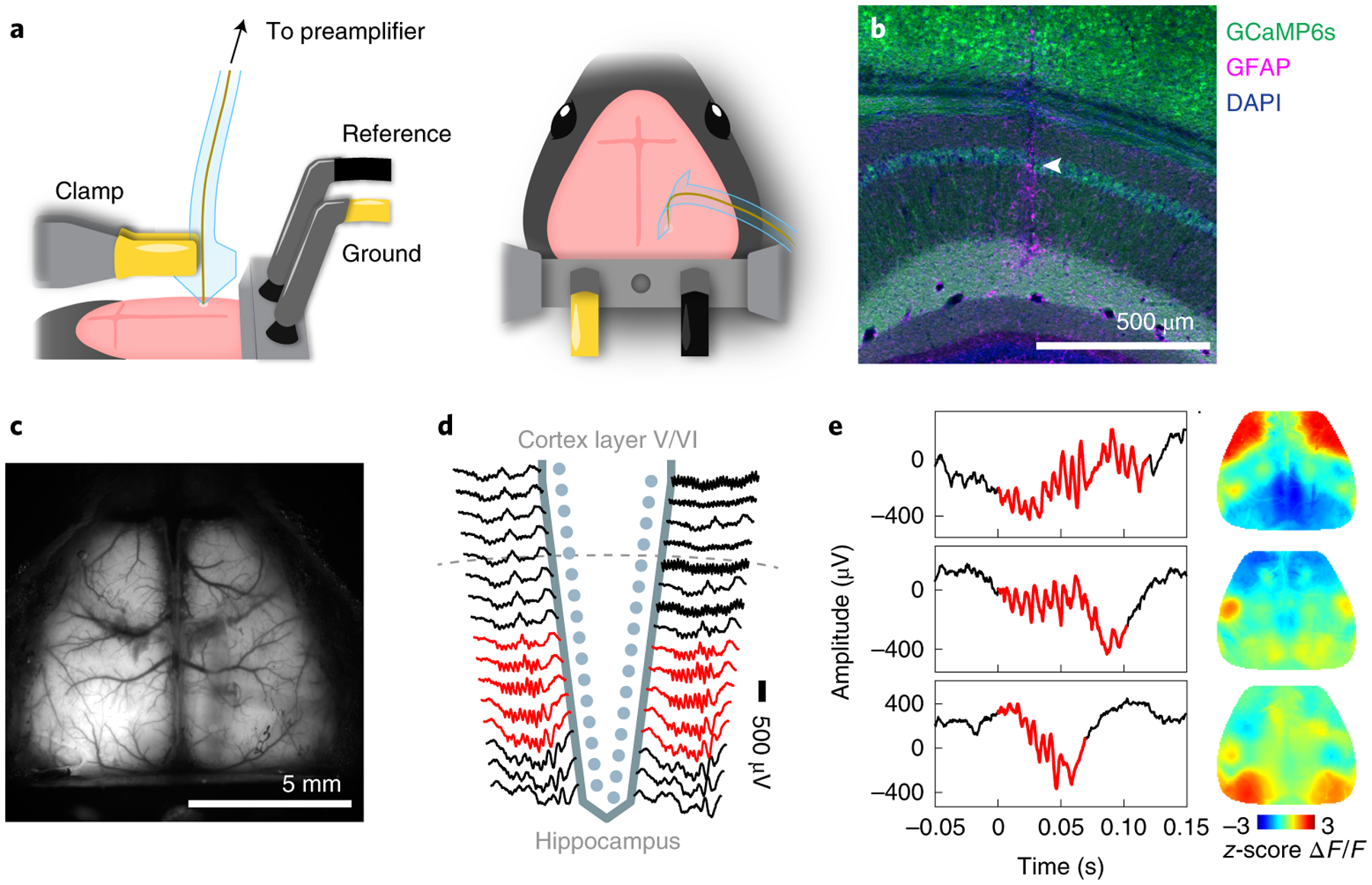
a, Surgical setup. Neuro-FITM was first inserted into the hippocampus (left) and then the shank was bent down to the right side to allow lowering the microscope objective and clearing the field of view for imaging (right).

b, Penetrating trajectory of Neuro-FITM in the hippocampus visualized by immunostaining against glia acidic protein (GFAP). Arrowhead: trajectory in CA1 pyramidal layer.

c, Field of view of wide-field calcium imaging during experiment. Note that the array shank was largely invisible and generated minimal shadows on the overlaying cortex.

d, Representative LFP recordings from the channels of the Neuro-FIRM probe in one recording session. Multiple channels adjacent (red) to the pyramidal layer of CA1 detected SWRs.

e, Examples of simultaneously recorded hippocampal SWRs (left column) and cortical activity (right column, single image frames at SWR onset). Cortical activity shows diverse spatial patterns during SWRs.

Fig. 3 |. The neuron spike waveforms in different recording sessions from one mouse.

a, Spatial profiles of spike waveforms of all 21 neurons recorded across 32 channels in three recording sessions marked by three different colors. Many neurons exhibit stable waveforms that are most prominent in adjacent channels.

b, Spike waveforms of all 21 neurons from the channel with the largest amplitude recorded in 3 sessions. Different colors indicate different recording sessions, as in a. The waveforms of the same neuron recorded at different sessions are highly similar.

Fig. 4 |. SNR for the spikes, the LFP, and the wide-field fluorescence.

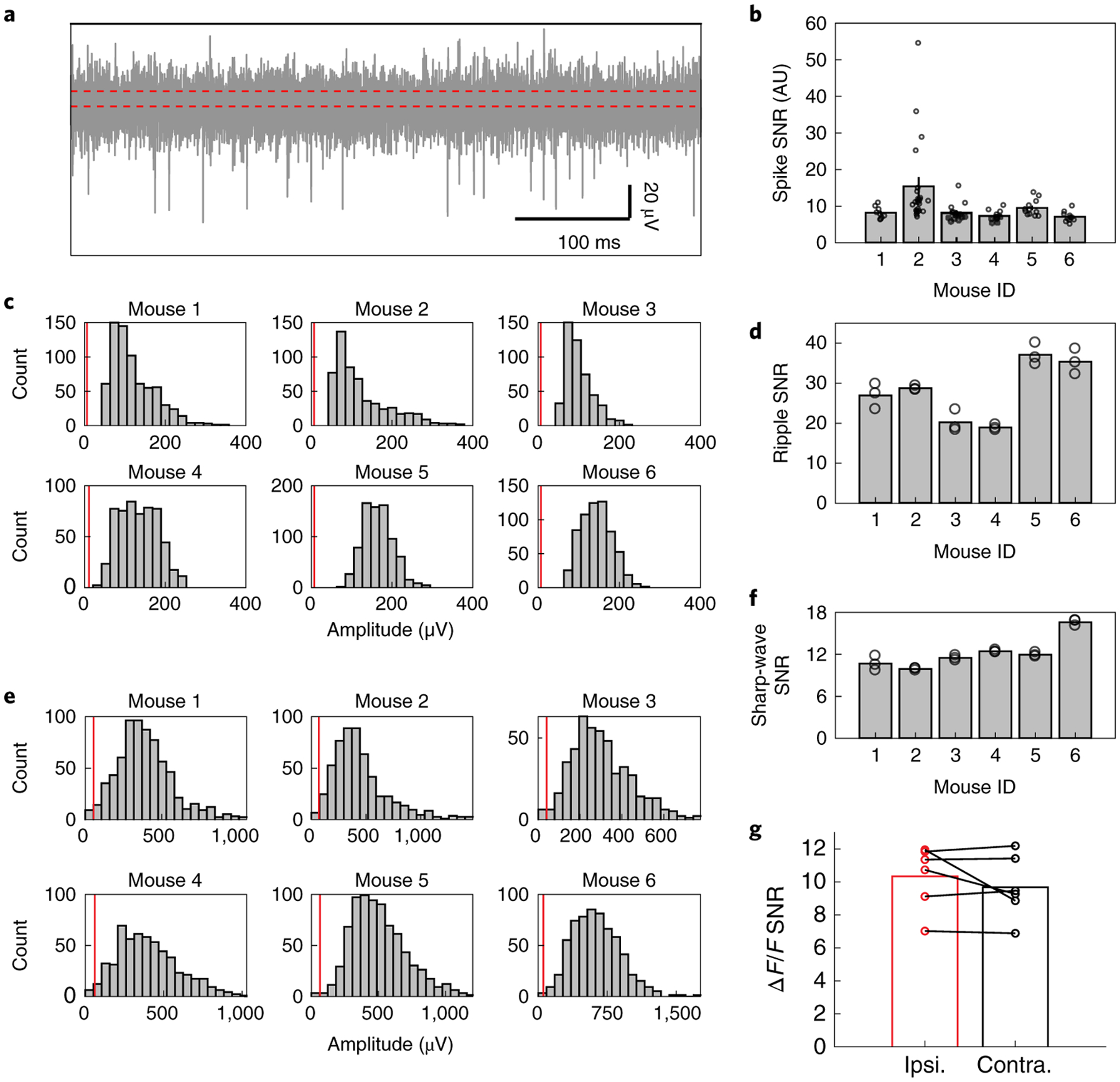
a, Representative example of high-pass filtered data from one channel showing the detection of multiple spikes and the median absolute deviation (MAD) denoted by the width between two red dashed lines.

b, SNR of the recorded spikes in all 6 mice. Bar shows the mean SNR averaged over all the neurons and the error bar denotes the s.e.m. Each dot represents the spike SNR for one neuron.

c, Histogram of amplitude of the detected ripples. The red line shows the MAD of the ripple range LFP (120 Hz – 250 Hz).

d, Mean SNR for the ripples detected in all 6 mice. Each dot represents the mean SNR of the ripples recorded in one recording channel.

e, Histogram of amplitude of the sharp-waves during SWR. The red line shows the MAD of the sharp-wave range LFP (5 Hz – 50 Hz).

f, Mean SNR for the sharp-waves detected in all 6 mice. Each dot represents the mean SNR of the sharp-waves recorded in one recording channel.

g, Signal-to-noise ratio of the ΔF/F for the cortical regions covered by the array shank (ipsilateral) vs. the symmetric cortical regions on the contralateral side, showing similar SNR for both cases.

Cortical activation onset tends to precede hippocampal SWRs

Our multimodal recording setup with Neuro-FITM provides an ideal platform to investigate the spatiotemporal properties of cortical-hippocampal interactions during SWRs. We first examined the large-scale cortical activity patterns averaged across all SWRs. To analyze the onsets of cortical activity and SWR accurately without contamination from prior SWR events, we focused on SWRs that did not have other SWRs for at least the preceding 3 s (4290 ‘well-separated SWRs’ out of 8643 SWRs). We found that the onset of cortical activation averaged across SWRs preceded SWR onset by 1.33 ± 0.15 s (mean ± s.d., Fig. 5a, Extended Data Fig. 4a) while the peak of cortical activation occurred 0.67 ± 0.18 s (mean ± s.d.) after the SWR onset. To investigate whether different cortical regions have different activation timing relative to SWR onset, we parcellated the dorsal cortex into 16 individual regions based on Allen Brain Atlas (Fig. 5b) and examined the activity of each cortical region around SWR onset. On average all the cortical regions increased their activity around SWRs (Fig. 5c, Extended Data Fig. 4b). Furthermore, the activation onset timing of cortical regions relative to the SWR onset exhibited an anterior-posterior gradient, with the earlier activation of posterior cortical regions such as visual cortex, retrosplenial cortex, and posterior parietal cortex (Fig. 5d, Extended Data Fig. 5). Similarly, the fraction of SWR events with the activation of the cortical region leading SWR onset increased from anterior to posterior cortical regions (Fig. 5e). 93.78 % of SWRs had at least one cortical region whose activity onset preceded the SWR onset. Taken together, in a majority of SWR events, the cortical activation started before hippocampal SWRs, especially in posterior cortical regions.

Fig. 5 |. Cortical activity onset tends to precede SWRs.

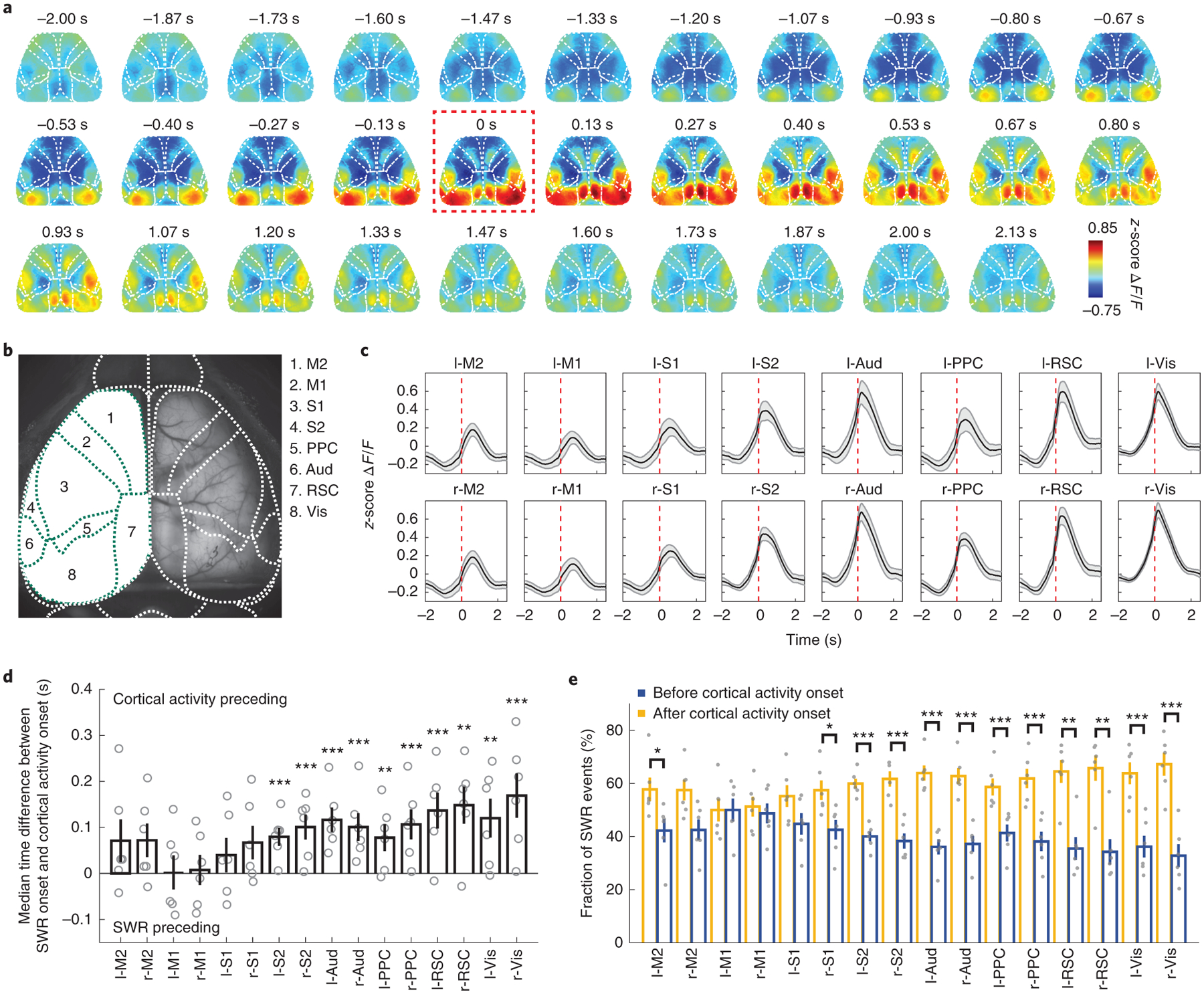
a, Average cortical activity aligned to SWR onset from one example mouse. The cortex exhibited broad activation around SWRs with the cortical activity rising before SWR onset. Red dashed box: SWR onset.

b, Identified cortical regions based on Allen Brain Atlas. M2: secondary motor cortex; M1: primary motor cortex; S1: primary somatosensory cortex; S2: secondary somatosensory cortex; Aud: auditory cortex; PPC: posterior parietal cortex; RSC: retrosplenial cortex; Vis: visual cortex.

c, Average activity in 16 cortical regions aligned to SWR onset (mean ± s.e.m., across 6 animals). All cortical regions increased activity around SWRs. Red dashed lines: SWR onset.

d, Time difference of SWR onset relative to cortical activity onset (two-tailed bootstrap test, 10000 times, Benjamini–Hochberg adjusted for FDR = 0.05, *P < 0.05, **P < 0.01,***P < 0.001). Gray circles: median time difference for each mouse. The time difference exhibited an anterior-posterior gradient with earlier activity onset in posterior regions. All error bars are s.e.m., n = 6 mice. The adjusted p-values are 0.123, 0.050, 1.656, 1.493, 0.420, 0.050, 0, 0, 0, 0, 0.005, 0, 0, 0.001, 0, 0.

e, Fraction of SWR events with cortical activity onset before or after SWR onset (two-tailed bootstrap test, 10000 times, Benjamini–Hochberg adjusted for FDR = 0.05, *P < 0.05, **P < 0.01,***P < 0.001). Gray dots: fraction of SWR events before or after cortical activity onset for each mouse. From anterior to posterior regions, the fraction of SWR events with cortical activity onset leading SWRs increased. All error bars are s.e.m., n = 6 mice. The adjusted p-values are 0.016, 0.047, 1.601, 1.317, 0.319, 0.007, 0, 0, 0, 0, 0, 0, 0.003, 0.002, 0, 0.

Distinct patterns of cortical activity around SWRs

Given that multimodal recordings with Neuro-FITM showed spatiotemporal variations in cortical activity from SWR events to SWR events (Fig. 2e), we next asked whether there were distinct cortical activation patterns that were reproducibly observed across subsets of the SWRs. Simultaneous wide-field imaging of the dorsal cortex and SWR recordings from hippocampus with Neuro-FITM across many sessions generated large-scale neural datasets that can be analyzed to answer this question. To that end, we performed a two-stage tensor component analysis (TCA)¹³ on the activity from all the recorded cortical regions during all SWR events, including well-separated and non-well-separated SWRs. TCA is an unsupervised dimensionality reduction method that extracts recurring patterns in high-dimensional data (Extended Data Fig. 6) by decomposing the data into 3 factors (Fig. 6a). The region factors and time factors describe the spatial and temporal dynamics of cortical patterns respectively, and the event factors measure the weighting of a given SWR event on the established set of patterns. By multiplying the region factors and time factors, we identified 8 distinct cortical activity pattern templates that were common across all animals (Fig. 6b, Extended Data Fig. 7a). The patterns exhibited distinct activated regions focusing on either the anterior or the posterior cortices, with patterns 1, 2, and 3 dominated by anterior regions (‘anterior patterns’) and patterns 4, 5, and 6 dominated by posterior regions (‘posterior patterns’) with different time courses relative to the SWR onset. Besides patterns 1–6 showing transient and spatially-discrete activity patterns, pattern 7 was dominated by an extended activation in visual cortex and pattern 8 showed periodic and oscillatory activation in all cortical regions. The cortical activity pattern in each SWR event could be well reconstructed as a linear sum of the 8 templates weighted by the event factors (Extended Data Fig. 6b).

Fig. 6 |. Diverse SWR-associated cortical activity patterns.

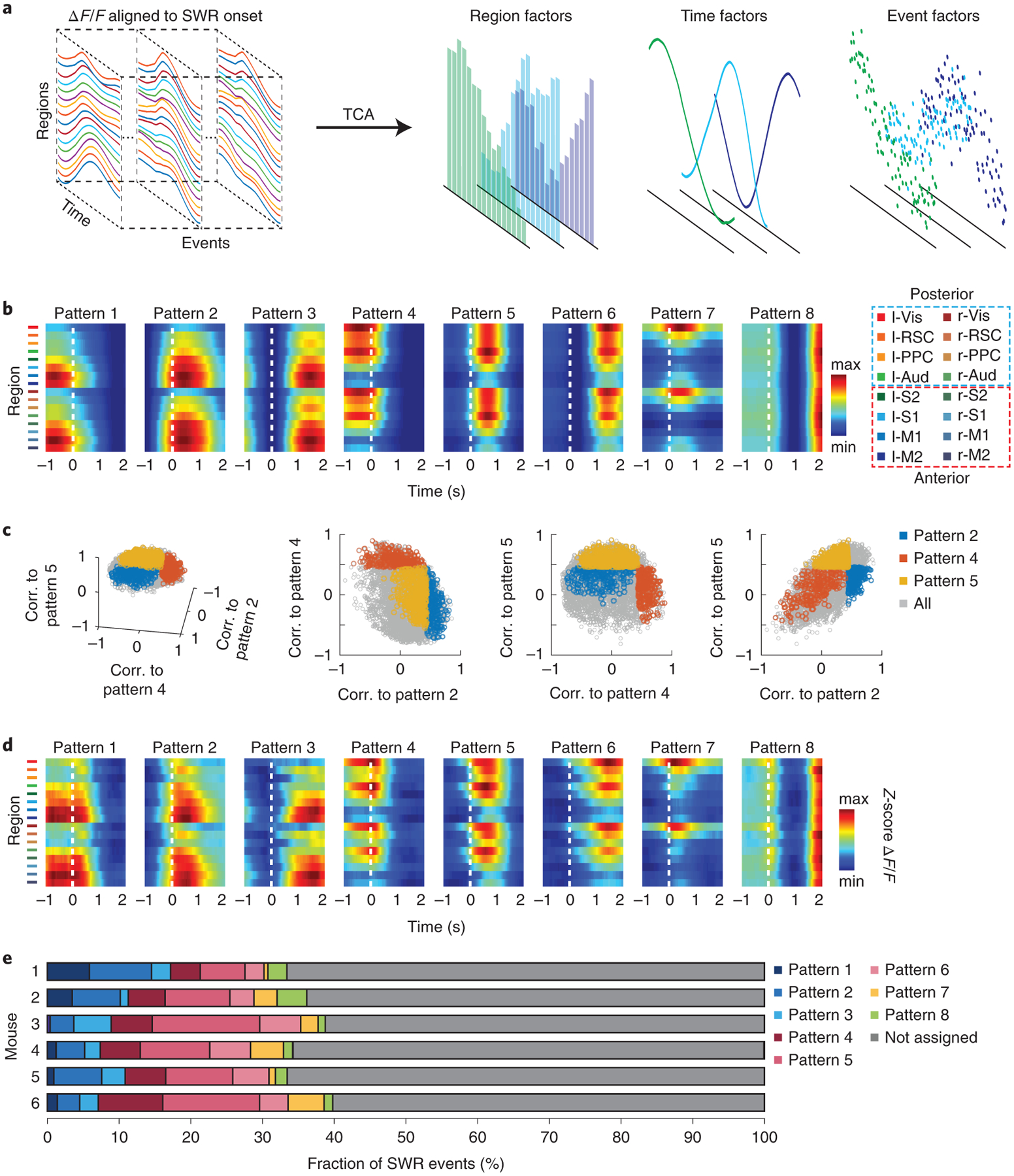
a, Schematic of the TCA algorithm. The activity of 16 cortical regions during SWR events formed 3D tensors that were concatenated across mice. Using the two-stage TCA algorithm, the original data were decomposed into region, time, and event factors to capture the spatiotemporal dynamics of single SWR events.

b, Common SWR-associated cortical activity pattern templates identified across animals by the TCA algorithm. Note that patterns 1–6 exhibited activation of anterior or posterior cortical regions with 3 different time courses around SWR onsets. We defined patterns 1–3 as ‘anterior patterns’ and patterns 4–6 as ‘posterior patterns’ based on the activated cortical regions. Pattern 7 was dominated by an extended activation in visual cortex, and pattern 8 showed periodic activation in all cortical regions.

c, Correlations (corr.) of cortical activity from single SWR events with 3 of the cortical activity templates. Cortical activity during single SWR events showed a continuous distribution.

d, SWR events whose cortical activity was dominated by single cortical pattern templates were grouped separately (see text). The figure shows the average cortical activity during SWR events assigned to each template, which closely resembled the identified cortical activity templates shown in b.

e, Fraction of SWR events assigned to each cortical pattern template for all 6 animals. More SWR events were assigned to posterior patterns (patterns 4–6) than anterior patterns (patterns 1–3), suggesting the posterior regions associate with SWRs more frequently than anterior regions.

To explore the diversity of SWR-associated cortical activity, we first measured the 2D correlation between the cortical activity during individual well-separated SWR events and each of the cortical pattern templates. The correlations for SWR events followed a continuous distribution instead of aggregating into isolated clusters (Fig. 6c), indicating that broadly distributed diverse cortical activity patterns were associated with SWRs. To examine the SWR events with divergent associated cortical activity, we next focused our analysis on groups of SWR events whose cortical activity was mainly dominated by one of the cortical pattern templates (Fig. 6c, colored dots, 2D correlation > 0.45). In total, ~36 % of all the well-separated SWR events were assigned to one of the cortical pattern templates. The cortical activity averaged across the SWR events assigned to each cortical pattern template highly resembled the corresponding template (Fig. 6d, compare to 6b). Thus, many SWR events accompany diverse sets of reproducible cortical activity patterns. For the SWR events assigned to the two patterns with peak activity immediately after ripple onset (pattern 2 and pattern 5), we also found the activity onset of most cortical regions preceded ripple onset by 0.16–0.6 s (Extended Data Fig. 7b). Fig. 6e shows the fraction of SWR events assigned to each pattern for all the mice. Overall, there were more SWR events associated with the posterior cortical patterns than the anterior patterns, suggesting a more frequent coupling between the hippocampus and posterior cortical regions during SWRs.

Different cortical patterns associate with distinct hippocampal activity

Considering that SWR-associated cortical activity exhibited distinct patterns, we explored whether hippocampal neuronal activity during individual SWR events is differentially modulated depending on the concurrent cortical patterns. In addition to SWRs, Neuro-FITM electrodes also detect spikes from the nearby hippocampal neurons in multimodal experiments. Fig. 7a shows 3 representative hippocampal neurons exhibiting selective (Neurons 1 and 2) or non-selective (Neuron 3) firing rates at the onsets of SWRs associated with different cortical patterns. To study the distinct modulation of hippocampal neurons during different cortical activity patterns, we performed SVM decoding analysis to examine whether cortical patterns could be discriminated based on the hippocampal population activity. SVM is a decoding technique that looks for a hyperplane to best separate the data according to their classes while maximizing the margin between the data samples and the hyperplane. SVM has been shown to give robust decoding performance for high dimensional data, especially when the size of dataset is limited. Because of this advantage, it has been commonly used to decode stimuli and choices using neuronal activity^24–28. In this study, we built a SVM decoder that performs pairwise discrimination of cortical patterns based on hippocampal population activity. The SWR events associated with two cortical patterns were selected, and the decoder attempted to discriminate the cortical patterns using the spiking activity of the simultaneously recorded hippocampal neurons (12 ± 2 neurons in each animal, Fig. 7b). We used the recursive feature elimination algorithm²⁹, which selected the subset of neurons in each decoder whose activity was significantly informative about the cortical activity patterns (‘discriminant neurons’). This process was repeated for all pairs of cortical patterns. For many cortical pattern pairs, the cortical patterns could be discriminated significantly above chance based on the activity of hippocampal neurons during SWRs. Fig. 7c shows the decoding accuracy for each cortical pattern pair from one example mouse. In all 6 mice, a large fraction of cortical pattern pairs was distinguishable (Fig. 7d, Extended Data Fig. 8). By examining the decodable cortical pattern pairs, we found that different subsets of hippocampal neurons were discriminant for different cortical pattern pairs (Extended Data Fig. 9a), and all hippocampal neurons were discriminant in at least one of the pairs. These results suggest that all hippocampal neurons are modulated differently depending on cortical activity patterns during SWRs. We also repeated the decoding analysis using hippocampal pyramidal cells and interneurons separately. We found that both hippocampal pyramidal cells and interneurons can decode the cortical activity pattern, indicating that both neuron types were modulated specifically during SWRs (Extended Data Fig. 9b).

Fig. 7 |. Different cortical activity patterns associated with distinct hippocampal neuronal activity patterns during SWRs.

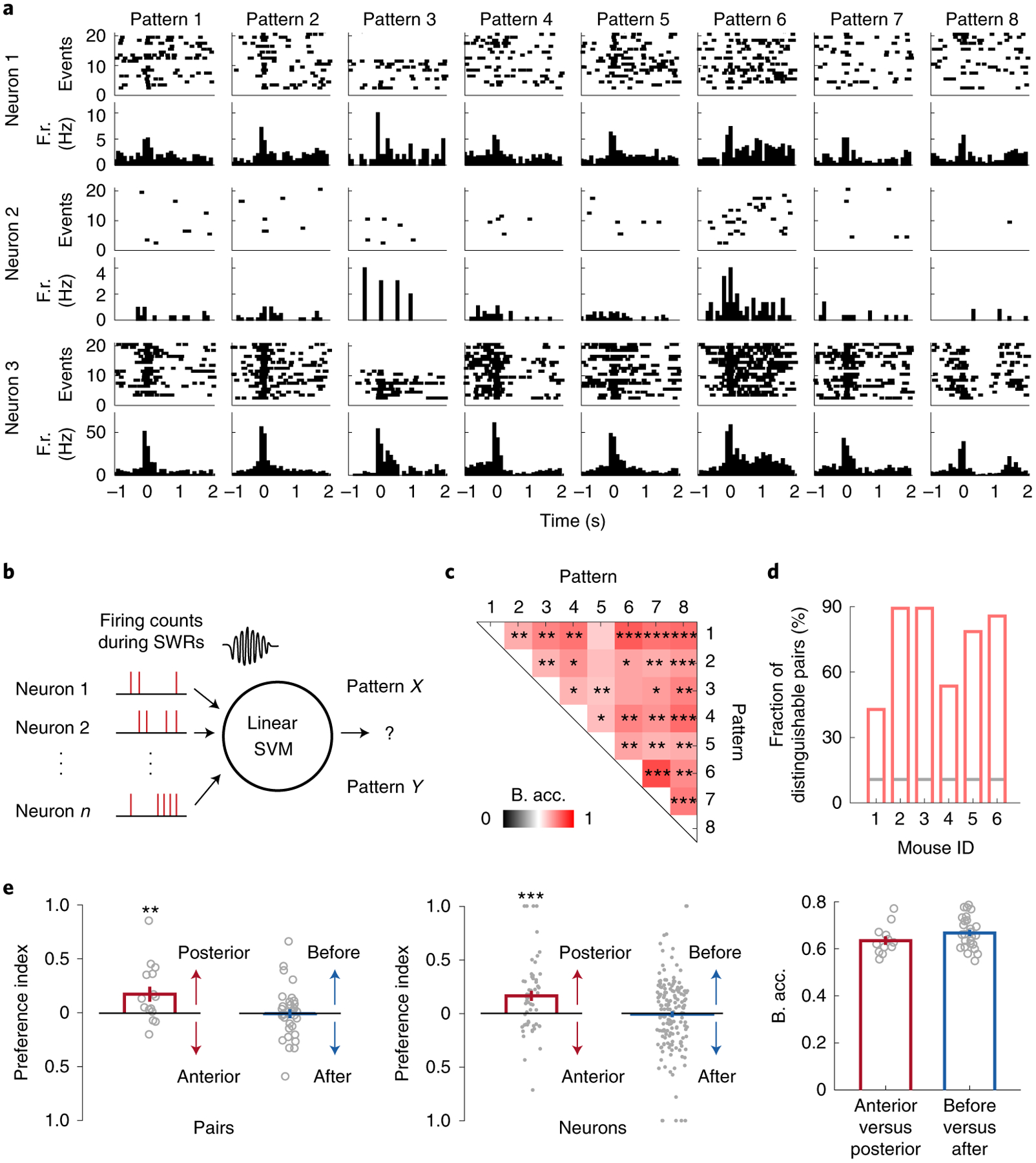
a, Raster plots (spikes) and the peri-event time histograms of example hippocampal neurons, showing different (Neurons 1 and 2) and similar (Neuron 3) firing rates at SWR onset under different cortical activity patterns. F.r.: firing rate.

b, Schematic of the decoding model. The firing counts of each hippocampal neuron during 0–100 ms relative to SWR onset were used as input features for the linear SVM to decode the cortical patterns.

c, Decoding accuracy of all cortical pattern pairs from one example animal (Mouse 2). Cortical pattern pairs that are significantly distinguishable based on hippocampal activity are marked by asterisks (shuffled 2000 times, one-tailed, *P < 0.05, **P < 0.01, ***P < 0.001, see Methods for exact p values). B. acc.: balanced accuracy.

d, Fraction of distinguishable cortical pattern pairs in each animal. Across 6 animals, many cortical pattern pairs were distinguishable based on the hippocampal neuron activity. Gray lines: the chance level fraction with P < 0.05 (one-sided binomial test, n = 28 pattern pairs). The p-values for mouse 1–6 are 2.24E-10, 5.10E-32, 5.10E-32, 2.60E-14, 9.17E-26, 8.42E-30

e, Preference index and decoding accuracy between anterior(A)-posterior(P) and early(E)-late(L) pattern pairs. Left: preference index of discriminant hippocampal neurons between A-P pairs (pattern 1 vs. 4, 2 vs. 5, and 3 vs. 6) or between E-L patterns (pattern 1 vs. 2, 1 vs. 3, 2 vs. 3, 4 vs. 5, 4 vs. 6, and 5 vs. 6). Posterior patterns were associated with higher firing counts of discriminant neurons than the anterior patterns (two-tailed bootstrap test, 10000 times, **P(A-P) = 0.0017, n = 15 pattern pairs) while no significant differences were detected between early and late patterns (P(E-L) = 0.4646, n = 33 pattern pairs). Gray circles: preference index averaged over all neurons for each pair within each animal. Middle: same as Left but for individual discriminant neurons (two-tailed bootstrap test, 10000 times, ***P(A-P) = 0.0001, n = 56 neurons, P(E-L) = 0.3802, n = 160 neurons). Gray dots: preference index of individual discriminant neurons. Right: Decoding accuracy between A-P and E-L pairs was similar (two-tailed bootstrap test, 10000 times, P = 0.0656, n = 15 pattern pairs for A-P, n = 33 pattern pairs for E-L). All error bars are s.e.m. Gray circles: decoding accuracy for each pair.

Given that many cortical pattern pairs could be decoded, we further investigated whether hippocampal neuron activity exhibited consistent modulations based on the different features of cortical activity patterns. To address this issue, we analyzed two groups of pattern pairs. One included pattern pairs with the same activation time course but different activated regions (anterior vs. posterior, pattern 1 vs. 4, 2 vs. 5, and 3 vs. 6), whereas the other included pattern pairs with the same activated regions but different time courses (early vs. late, e.g. pattern 1 vs. 2, or 4 vs. 5). To compare the activation levels of discriminant neurons determined by the recursive feature elimination algorithm for cortical pattern pairs (Extended Data Fig. 9a), we defined the ‘preference index’ for each neuron as the difference in the spike counts during one pattern vs. the other, divided by the sum of the two (see Methods). When comparing posterior with anterior patterns activated at similar timing, we found that posterior patterns were associated with higher firing in a majority of discriminant neurons than the anterior patterns, which was evident in a significantly positive preference index (Fig. 7e). In contrast, when comparing cortical activation of similar areas but with different timing, the general activity level of discriminant neurons did not show a significant preference for earlier vs. later activation (Fig. 7e). Despite the lack of consistent difference in the general hippocampal activation level for early-late pattern pairs, their decoding accuracy was similar to that for anterior-posterior pattern pairs (Fig. 7e). We also repeated the same decoding analysis and preference index analysis for all the ripple events, including the non-well-separated SWRs (Extended Data Fig. 10). The results are qualitatively similar compared to Fig. 7, indicating that the conclusions are generalizable across heterogeneous ripples. Taken together, these results reveal diverse associations between cortical activity patterns and hippocampal neuronal activity during SWRs. The posterior cortical activation is associated with stronger hippocampal activation in most of the hippocampal neurons. The relative timing between cortex and SWRs is associated with heterogeneous modulation of individual hippocampal neurons.

Discussion

We developed a mostly-transparent, bendable microelectrode array (Neuro-FITM) to enable cortex-wide simultaneous optical imaging during electrophysiological recordings. To achieve the same goal, conventional silicon probes will have to be inserted contralaterally or horizontally, which would inevitably lead to long insertion trajectories causing additional implantation damage to the brain tissue. Furthermore, horizontal implantation will cause increased mechanical stress applied onto the thin silicon shank at the clamping point which can lead to premature fracture of the probe. Instead, our flexible array could be inserted vertically to the hippocampus with the shortest trajectory, minimizing brain tissue damage. In addition, our Neuro-FITM has up to 64 recording electrodes per shank, providing a higher spatial resolution for electrophysiology compared to other polymer-based microelectrodes used for hippocampal recordings^30,31. Given the high flexibility and small dimensions of the insertable shank of the array, we anticipate that our flexible microelectrode array will improve the stability of unit recordings in chronic studies.

Our Neuro-FITM array could potentially be combined with other neural technologies that further expands its applications into various neuroscience studies. For example, Neuro-FITM array could be integrated with wireless electrophysiological recording platforms for wireless data transmission^32–34, which are ideal for recordings in freely moving animals. Neuro-FITM array could also be augmented to allow simultaneous electrophysiological recordings and manipulations of neural activity. This could be achieved by optimizing the charge injection capacity of the electrodes for electrical stimulation³⁵, or by incorporating the μLEDs³⁶ or waveguides³⁷ into the device to form optoelectronic neural interfaces.

The simultaneous multimodal recordings of the hippocampal and cortical activity allowed us to characterize the cortical-hippocampal interactions during individual SWRs. In contrast to the conventional notion that cortical activity is mainly triggered by hippocampal SWRs^{11,12,38–41}(but see^8–10,42), our findings suggest that the hippocampus and cortex exhibit bidirectional communications with the cortical activation frequently preceding SWR onset. Furthermore, the relative timing between cortical activation and SWRs is area-specific. The cortical activation could start before or after SWRs in both anterior and posterior cortical regions, while the activation of posterior cortical regions precedes SWRs more frequently than that of anterior regions. A previous study in non-human primates performed simultaneous fMRI recordings of the whole brain and electrophysiological recordings of the hippocampus and showed that the activation of several cortical regions can on average precede hippocampal SWRs. However, the signal-to-noise ratio of fMRI limited their analysis to the average activity across SWRs and prevented the analysis of the diversity of cortical activity during individual SWRs⁴. The approach adopted in the current study achieved a sufficient signal-to-noise ratio to perform single-event analyses across large recording areas to uncover the remarkable and coordinated diversity of cortical and hippocampal activity during SWRs. The activation of different cortical regions with different timing relative to SWR onset forms distinct cortical activity patterns from SWR to SWR. Importantly, these cortical activity patterns differentially associate with the hippocampal neuronal activity which indicated that these patterns are not merely random fluctuation but that there is rather a predictable relation of cortical activity patterns with hippocampal neuron populations, indicative of large-scale neuron assemblies that span the hippocampus and cortex.

The interaction between hippocampus and single brain regions under different behavioral states has been extensively studied. For example, it has been reported that awake SWRs were accompanied by the reactivation of neurons in the prefrontal cortex, suggesting that the awake SWRs played important roles in memory retrieval^11,43. On the other hand, the existence of a bidirectional loop between the hippocampus and auditory cortex, which could play a role in memory consolidation, was also demonstrated⁹. A recent study showed that at a larger scale, the coupling between hippocampal ripples and ripples in association cortices becomes stronger after spatial learning, suggesting a closer communication between the hippocampus and association cortices during memory transfer⁴⁴. Hippocampus encodes a variety of information including spatial, sensory, and reward^45–49. The broad and diverse activation of cortical regions we observed during hippocampal SWRs may reflect a specific binding of distinct types of information encoded in hippocampus and the relevant cortical regions through different anatomical connections. The diversity of cortical-hippocampal interactions around SWRs suggests that the hippocampus and cortex can communicate through multiple information streams based on contexts and cognitive processes. Future studies should uncover how such cortical-hippocampal interaction is dynamically shaped when the animals are experiencing different task contexts or under different behavioral states.

Online methods

- Array design and measurement

The Neuro-FITM array has 32 or 64 electrodes with a flexible shank (Fig. 1a–b, Extended Data Fig. 1). The electrodes are aligned in two rows that are 20 μm apart from either edge of the probe. The diameter of each electrode is 10 μm and the spacing between adjacent electrodes is 50 or 20 μm. For the electrode designed to record in mouse hippocampus, the distance between the top and bottom electrodes is 750 μm, which is long enough to record from multiple depths of CA1 region in the dorsal-ventral axis. The microelectrode array consists of a 1.55 mm probe and a 1.9 cm transparent flexible shank, connecting the electrodes to the ZIF connector. To determine the optimal length of the shank for shuttle-free insertion, we performed mechanical analysis as shown in Equation 1, where w = 170 μm, t = 16 μm, L, and E = 3.2 GPa are the width, thickness, length, and the Young’s modulus of the shank. The maximum force a probe can uphold without buckling is inversely proportional to the square of its length. Since the insertion force F required to penetrate brain tissue was commonly accepted to be 1 mN⁵⁰, we estimated the length of the probe must be shorter than 1.9 mm. Therefore, we chose the length of the probe to be 1.8 mm, which was long enough to target the CA1 region of the mouse hippocampus, yet short enough to prevent buckling during insertion.

$$F_{BF}=\frac{{\pi }^{2}Ew{t}^3}{5.88L^2}$$ (Equation 1)

All electrochemical characterizations were performed with Gamry 600 Plus in 0.01 M phosphate-buffered saline (Sigma-Aldrich P3813 dry powder dissolved in deionized water). To measure the EIS and CV, we adopted a three-electrode configuration, where the Ag/AgCl (gauge 25) served as the reference electrode, and Pt (gauge 25) served as the counter electrode. During EIS, the applied AC voltage was 20 mV with frequency ranging from 100 kHz to 1 Hz at open circuit potential. We performed EIS of one representative array and the mean and s.d. were shown in Fig. 1k. During CV, the applied voltage between the PtNP/Au electrodes and the Ag/AgCl ranged from −0.9 V to 1 V (Fig. 1l). To stabilize the electrode/electrolyte interface, we performed CV of a representative channel. During the measurement of CV and EIS, we used a custom-made Faraday cage to shield from the 60 Hz powerline contamination and other electromagnetic noises.

- Animals

All procedures were performed in accordance with protocols approved by the UCSD Institutional Animal Care and Use Committee and guidelines of the National Institute of Health. Mice (cross between CaMKIIa-tTA:B6;CBA-Tg(Camk2a-tTA)1Mmay/J [JAX 003010] and tetO-GCaMP6s: B6;DBA-Tg(tetO-GCaMP6s)2Niell/J [JAX 024742], Jackson laboratories) were group-housed in disposable plastic cages with standard bedding in a room with a reversed light cycle (12 h-12 h). Temperatures and humidity ranged from 18–23 °C and 40–60%, respectively. Experiments were performed during the dark period. Both male and female healthy adult mice (6 weeks or older) were used. Mice had no prior history of experimental procedures that could affect the results.

- Surgery, multimodal experiments, and data acquisition

Adult mice (6 weeks or older) were anesthetized with 1–2% isoflurane and injected with baytril (10 mg/kg) and buprenorphine (0.1 mg/kg) subcutaneously. A circular piece of scalp was removed to expose the skull. After cleaning the underlying bone using a surgical blade, a custom-built head-bar was implanted onto the exposed skull over the cerebellum (~1 mm posterior to lambda) with cyanoacrylate glue and cemented with dental acrylic (Lang Dental). Two stainless-steel wires (791900, A-M Systems) were implanted into the cerebellum as ground/reference. The exposed skull was covered with cyanoacrylate glue applied several times. After cyanoacrylate glue formed a solid layer, a craniotomy (~0.5 mm in diameter, ~1.5–1.7 mm lateral, and ~2.1–2.3 mm posterior to bregma) was made at the right hemisphere for microelectrode array insertion and the dura over the exposed brain surface was carefully removed. The microelectrode array was connected to the amplifier board first and held by a custom-made electrode holder attached to a micromanipulator (MP-285, Sutter Instrument). The array was inserted at ~45 μm/s. Once inserted, the array was secured to the skull with Vetbond (3M). After the Vetbond became solid, the array was carefully released from the electrode holder and the exposed part of the array shank was bent to the right side of the animal. The amplifier board was fixed onto the right head-bar clamp arm on the stage (Fig. 2a, Extended Data Fig. 3a). Animals were fully awake before recordings. In 6 out of 8 animals, we successfully recorded SWRs and spikes in multiple recording channels. To quantify the accuracy of array implantation, we measured the distance between the target location and the actual location of the tip of the array based on the staining results (Extended Data Fig. 3b). We find that the distance is 100 ± 33 μm in medial-lateral direction, 113 ± 18 μm in anterior-posterior direction, and 87± 24 μm in vertical direction.

The wide-field calcium imaging was performed using a commercial fluorescence microscope (Axio Zoom.V16, Zeiss, objective lens (1x, 0.25 NA)) and a CMOS camera (ORCA-Flash4.0 V2, Hamamatsu) through the intact skull as previously described²¹. Images were acquired using HCImage Live (Hamamatsu) at 29.98 Hz, 512 × 512 pixels (field of view: 11 mm × 11 mm, binning: 4, 16 bit).

The microelectrode array was attached to a custom-made connector board that routed the electrical signals to the Intan RHD2132 amplifier boards (Intan Technologies, USA). Electrophysiological recordings were performed using Intan RHD 2000 system. The sampling rate was 30 kHz. For each animal, all recording sessions are on the same day with 5–10 min interval between sessions. In total, 6 mice were recorded, each having 2–3 sessions. The length of each session was 1 h.

- Immunohistochemistry

The microelectrode array was left in the brain for 4–5 weeks before perfusion to allow glial scar formation, which is a good indication of the array location. The mice were anesthetized (ketamine/xylazine, 150 mg/kg, 12 mg/kg body weight) and perfused transcardially with 4% paraformaldehyde. Brains were then cryoprotected in a 30% sucrose solution overnight. 50 mm coronal sections were cut with a microtome (Microm HM 430, Thermo Scientific) and blocked in a solution consisting of 4% normal donkey serum, 1% BSA and 0.3% Triton X-100 in PBS for 1 h at room temperature. They were then incubated overnight at 4°C with primary antibodies (1:1000 chicken anti-GFP, Aves Labs; 1:400 goat anti-GFAP, Santa Cruz) diluted in the blocking solution. After washing, sections were then incubated in Alexa Fluor–conjugated secondary antibodies (1:1000 anti-chicken 488; 1:1000 anti-goat 594, Jackson Immuno Research) for 2 h at room temperature. Slices were then mounted with a mounting medium for DAPI staining (Vector Laboratories) and imaged using a fluorescence microscope (ApoTome.2, Zeiss, Fig. 2b, and Extended Data Fig. 3b).

- SWR detection, spike sorting, ΔF/F processing

The detection of SWRs was performed by the following procedures. The raw LFP signals from the channels near CA1 pyramidal layers were band-pass filtered at 100–200 Hz (8th order Butterworth filter) in both forward and reverse directions to prevent phase distortion. The Hilbert transform was then used to obtain the envelope of the ripple-band signals. To detect the potential SWR events, we set a threshold to 2–3 standard deviations above the mean. Once the ripple-band envelope crossed the threshold, one candidate SWR event was labeled. The start and end time of this candidate SWR event was then defined as the time when the envelope just passed or returned back to the mean level. Between the start and end time, if the peak amplitude of the signal envelope further exceeded 4–6 standard deviations above the mean, then a SWR event was finally identified. Note that similar to other studies^51,52, we only considered SWR events with a duration longer than 20 ms.

The spike sorting was performed with Kilosort 2⁵³ and the output results were followed by manual curation. The recording sessions from the same day were pooled together before the spike sorting to identify the same neurons across sessions. The LFP data were first high-pass filtered at 250 Hz (3rd order Butterworth filter) and whitened to remove the correlation between nearby channels. Then the Kilosort algorithm identified the best templates and the putative clusters of neurons along with their spike timing and amplitudes. These preliminary results were further manually refined by merging the same neurons, splitting different neurons, and labeling low amplitude inseparable spikes as multi-unit activities. Finally, the hippocampus pyramidal cells and interneurons were classified based on the firing rates and the asymmetry of the spike waveforms⁵⁴.

To obtain the ΔF/F time series from the wide-field calcium imaging data, 512 × 512 pixel images were first down-sampled to 128 × 128 pixels. For each pixel, time-varying baseline fluorescence (F) was estimated for a given time point as the 10th percentile value over 180 s around it. For the beginning and end of each imaging block, the following and preceding 90-s window was used to determine the baseline, respectively. The raw ΔF/F of each pixel was z-score normalized. We corrected for hemodynamic contamination following published procedures²¹. Briefly, we performed principal component analysis (PCA) followed by independent component analysis (ICA)²¹ on z-score normalized ΔF/F to extract hemodynamic components from total signal. We first performed PCA and preserved the top 50 principal components, which explained ~95% variance of the data. Then the spatial ICA was performed over the top 50 PCs to generate 50 spatially independent modules. Finally, the modules containing the vasculature activities were excluded and the reconstruction of cortical activity was done with the remaining modules. We screened different numbers of components (20, 40, 50, 150, and 200) preserved in PCA/ICA analysis and using 50 components gave the best separation of hemodynamic and neural signal. To obtain the ΔF/F of each cortical region, the dorsal cortex was manually parcellated into individual regions based on Allen Brain Atlas (Fig. 5b) and ΔF/F time series was computed as the mean of the pixel values within each cortical region.

- The time delay between cortical activation and SWRs

For the analysis of the timing of SWR onset and the onset of dorsal cortex activity averaged across SWR events (Fig. 5a, Extended Data Fig. 4), we only included the ‘well-separated SWRs’ which did not have any preceding SWR events for at least 3 seconds. This was to prevent potential contamination from the tail of cortical activity associated with preceding SWRs. The onset timing of the event-averaged cortical activity was defined as the earliest activity onset among 16 cortical regions. For each region, using the ΔF/F at −2 s relative to SWR onset as the baseline, we performed rank-sum tests at each frame between [−2 s, 2 s] relative to SWR onset. The activity onset time for each cortical region was defined as the time when its ΔF/F was significantly higher (P < 0.05) than the baseline for at least 3 consecutive frames. The mean onset time was computed by first averaging across sessions within animals and later averaging across animals. The peak time of event-averaged cortical activity was defined as the time when cortical activity averaged across 16 regions reached the maximum value. The mean peak time was computed by first averaging across sessions within animals and then averaging across animals.

For the analysis of timing between SWR onset and the activity onset of each cortical region during individual SWRs (Fig. 5d–e, Extended Data Fig. 5), we also focused on well-separated SWR events. The activity onset of each cortical region was identified as previously described²¹. In brief, we first computed the derivative of the smoothed ΔF/F traces (loess, 1-s window) and defined the inactive segments as the periods with the derivative within 1 standard deviation of the whole derivative trace. Then we defined ΔF/F events as the periods when the derivative exceeded the 1 standard deviation of the inactive period. For each event, the onset time was first estimated as the time when the derivative exceeded the 1 standard deviation criterion, and the offset time was estimated as the time when the derivative dropped below zero for the first time after the onset. To further refine the onset time, for each event, the baseline ΔF/F was defined as the value at the first time point when the derivative was above zero before the offset time, and ΔF/F noise level was defined as the mean of the absolute difference between the raw and smoothed ΔF/F traces. The onset was further refined as the last time point before the offset time when the ΔF/F value is within the noise level from the baseline ΔF/F.

After identifying the activity onset of each cortical region, we determined the timing of each SWR onset relative to the activity onset of each region using the following procedures. For each SWR onset, we first examined the slope of the instantaneous ΔF/F traces of one region. If the ΔF/F was rising, we looped backward in time frame by frame until reaching −1 s before the SWR onset. If a cortical activity onset was detected within this time interval, we labeled this SWR event as occurring after the cortical activity onset. On the other hand, if the ΔF/F was not rising, we looped forward in time frame by frame until reaching +1 s after the SWR onset. If a cortical activity onset was detected within this time interval, we labeled this SWR event as occurring before the cortical activity onset. The above procedure was done for every well-separated SWR and all the cortical regions.

- Two-stage TCA algorithm

To prepare the data for the TCA algorithm, we performed below preprocessing procedures. The ΔF/F traces in each cortical region were z-score normalized within each recording session. For each SWR event, we used the 3-s ΔF/F traces (1 s before SWR onset, 2 s after) from 16 cortical regions to construct a 2D data matrix (region × time). Then we concatenated the 2D data matrices from all the SWR events to form a 3D data tensor (region × time × event). Finally, the data tensors from all the 6 mice were concatenated along the event dimension to form a big data tensor (Fig. 6a).

The tensor component analysis (TCA) has been demonstrated to be effective in discovering the low-dimensional dynamics of neural activity¹³. However, since the original algorithm did not guarantee to achieve the global optimum, the results could vary from run to run. To achieve reliable results, we devised a two-stage TCA algorithm, which includes a pre-clustering step to alleviate the variations from individual runs. The detailed procedure is shown in Extended Data Fig. 6a. The first stage of the algorithm consisted of fitting a TCA model with a sufficiently high rank order. The tensor toolbox v3.0 (https://www.tensortoolbox.org/) was used to perform TCA decomposition. To determine this rank order, we fitted multiple TCA models with rank 2 to 15 and examined the reconstruction error of each TCA model. The reconstruction error started to show diminishing returns towards rank 15 (Extended Data Fig. 6b). Therefore, we chose rank 15 for the initial TCA and ran it 100 times. Each result gave a slightly different decomposition of the original high dimensional data. To capture the underlying dynamics that were common and consistent in most TCA results, we performed clustering of the 1500 TCA spatiotemporal patterns by computing the similarity matrix using 2D correlation. Then the community detection algorithm was performed with the community detection toolbox (http://netwiki.amath.unc.edu/GenLouvain/GenLouvain) to identify the clusters. As shown in the sorted similarity matrix (Extended Data Fig. 6c), we identified 8 different clusters of TCA patterns. The number of patterns assigned to each cluster is shown in Extended Data Fig. 6d. Examples of randomly chosen patterns assigned to each cluster are shown in Extended Data Fig. 6f. The second stage of the TCA algorithm used the centroids of 8 clusters identified from the first stage to initialize the region and time factors, leaving all the event factors randomly initialized. Then we ran the TCA optimization algorithm as before until it converged to obtain the final set of TCA factors (Extended Data Fig. 7a). Compared with the original TCA algorithm, our two-stage TCA algorithm gave significantly lower reconstruction error (p = 1.38E-11, Extended Data Fig. 6e).

- Cortical pattern assignment

To assign the cortical activity pattern of each SWR event to one of the 8 spatiotemporal templates (Fig. 6b), we computed the 2D correlation between the z-score normalized ΔF/F traces and each template. If the correlation value for one pattern was higher than a threshold (0.45, Fig. 6c–e), we assigned the SWR event to that pattern. If one SWR event was assigned to multiple patterns, we excluded that SWR event.

- The algorithm for pairwise discrimination of the cortical patterns

To discriminate the cortical patterns based on hippocampal activity, we used the support vector machine (SVM). The hippocampal neuron firing counts during 0–100 ms relative to SWR onset were used as input features for the SVM algorithm. Since the numbers of SWR events assigned to each cortical pattern templates were often unbalanced (Fig. 6e), we modified the misclassification costs to be inversely proportional to the sample frequencies of the two pattern types in each pair, N1 and N2. Therefore, misclassifying pattern type 1 as pattern type 2 had cost N2 / (N1+N2), whereas misclassifying pattern type 2 as pattern type 1 had cost N1 / (N1+N2). Also, to measure the decoding performance, we used balanced accuracy instead of the accuracy, which could be misleading in the unbalanced datasets. The balanced accuracy was defined as the average of the correct proportion for each class (i.e. cortical pattern). We performed the recursive feature elimination^29,55 to identify the discriminant neurons for each cortical pattern pair (Extended Data Fig. 9). This was done by choosing the subset of neurons that give the highest balanced accuracy in the leave-one-out cross-validation. To evaluate whether the decoding performance for each cortical pattern pair was significantly better than chance, we randomly shuffled the cortical pattern identities 2000 times, performed SVM using the identified discriminant neurons, and computed the balanced accuracy in each shuffle to obtain a null distribution of it. Then we computed the p-value based on the balanced accuracy from the original data set and the distribution of the balanced accuracy from the shuffled data set (Fig. 7c, Extended Data Fig. 10b, and Extended Data Fig. 8). The exact p values associated with Fig. 7c are as follows: Mouse 1: P(1–2)=0.086, P(1–3)=0.2815, P(1–4)=0.1415, P(1–5)=0.153, P(1–6)=0.0035, P(1–7)=0.094, P(1–8)=0.0965, P(2–3)=0.3365, P(2–4)=0.0315, P(2–5)=0.036, P(2–6)=0.0535, P(2–7)=0.0245, P(2–8)=0.0425, P(3–4)=0.5235, P(3–5)=0.28, P(3–6)=0.052, P(3–7)=0.037, P(3–8)=0.3795, P(4–5)=0.13, P(4–6)=0.0695, P(4–7)=0.005, P(4–8)=0.016, P(5–6)=0.153, P(5–7)=0.017, P(5–8)=0.062, P(6–7)=0.0205, P(6–8)=0.0025, P(7–8)=0.0275; Mouse 2: P(1–2)=0.0035, P(1–3)=0.0045, P(1–4)=0.004, P(1–5)=0.0665, P(1–6)=0, P(1–7)=0, P(1–8)=0, P(2–3)=0.009, P(2–4)=0.017, P(2–5)=0.0525, P(2–6)=0.0375, P(2–7)=0.0055, P(2–8)=0.0005, P(3–4)=0.039, P(3–5)=0.007, P(3–6)=0.0545, P(3–7)=0.035, P(3–8)=0.0025, P(4–5)=0.0125, P(4–6)=0.001, P(4–7)=0.002, P(4–8)=0, P(5–6)=0.0085, P(5–7)=0.006, P(5–8)=0.0015, P(6–7)=0, P(6–8)=0.001, P(7–8)=0; Mouse 3: P(1–2)=0.0105, P(1–3)=0.015, P(1–4)=0.024, P(1–5)=0.0275, P(1–6)=0.0035, P(1–7)=0, P(1–8)=0.0295, P(2–3)=0.008, P(2–4)=0.006, P(2–5)=0.017, P(2–6)=0.2245, P(2–7)=0.0015, P(2–8)=0.0135, P(3–4)=0.0005, P(3–5)=0.017, P(3–6)=0.1865, P(3–7)=0.001, P(3–8)=0.015, P(4–5)=0.047, P(4–6)=0.001, P(4–7)=0.0035, P(4–8)=0.041, P(5–6)=0.0035, P(5–7)=0, P(5–8)=0.0165, P(6–7)=0.0295, P(6–8)=0.034, P(7–8)=0.2295; Mouse 4: P(1–2)=0.0055, P(1–3)=0.0085, P(1–4)=0.023, P(1–5)=0.0135, P(1–6)=0.054, P(1–7)=0.0135, P(1–8)=0.167, P(2–3)=0.073, P(2–4)=0.013, P(2–5)=0.037, P(2–6)=0.0765, P(2–7)=0.3305, P(2–8)=0.1825, P(3–4)=0.25, P(3–5)=0.0675, P(3–6)=0.0175, P(3–7)=0.03, P(3–8)=0.029, P(4–5)=0.034, P(4–6)=0.0905, P(4–7)=0.0375, P(4–8)=0.0675, P(5–6)=0.0015, P(5–7)=0.0775, P(5–8)=0.0285, P(6–7)=0.046, P(6–8)=0.094, P(7–8)=0.39; Mouse 5: P(1–2)=0.0335, P(1–3)=0.0755, P(1–4)=0.009, P(1–5)=0.0075, P(1–6)=0.013, P(1–7)=0, P(1–8)=0.0055, P(2–3)=0.0295, P(2–4)=0.0145, P(2–5)=0.0495, P(2–6)=0.057, P(2–7)=0.0215, P(2–8)=0.1255, P(3–4)=0.0875, P(3–5)=0.0195, P(3–6)=0.015, P(3–7)=0.0095, P(3–8)=0.0535, P(4–5)=0.0155, P(4–6)=0.009, P(4–7)=0.0325, P(4–8)=0.0245, P(5–6)=0.0145, P(5–7)=0.0415, P(5–8)=0.026, P(6–7)=0.007, P(6–8)=0.0065, P(7–8)=0.1315; Mouse 6: P(1–2)=0.018, P(1–3)=0.0175, P(1–4)=0.017, P(1–5)=0.0065, P(1–6)=0.046, P(1–7)=0.013, P(1–8)=0.001, P(2–3)=0.007, P(2–4)=0.0105, P(2–5)=0.108, P(2–6)=0.0115, P(2–7)=0.1615, P(2–8)=0.0025, P(3–4)=0.0345, P(3–5)=0.0025, P(3–6)=0.008, P(3–7)=0.001, P(3–8)=0.0045, P(4–5)=0.0835, P(4–6)=0.0015, P(4–7)=0.062, P(4–8)=0.017, P(5–6)=0.0315, P(5–7)=0.03, P(5–8)=0.0065, P(6–7)=0.0055, P(6–8)=0.0025, P(7–8)=0.0125. The exact p-values associated with Extended Fig. 10b are as follows: Mouse 1: P(1–2)=0.0645, P(1–3)=0.1735, P(1–4)=0.0315, P(1–5)=0.057, P(1–6)=0.128, P(1–7)=0.008, P(1–8)=0.027, P(2–3)=0.1735, P(2–4)=0.0375, P(2–5)=0.0025, P(2–6)=0.0205, P(2–7)=0.0135, P(2–8)=0.345, P(3–4)=0.1685, P(3–5)=0.0225, P(3–6)=0.012, P(3–7)=0.04, P(3–8)=0.3775, P(4–5)=0.01, P(4–6)=0.3415, P(4–7)=0.0415, P(4–8)=0.289, P(5–6)=0.042, P(5–7)=0.1595, P(5–8)=0.066, P(6–7)=0.473, P(6–8)=0.01, P(7–8)=0.07; Mouse 2: P(1–2)=0.018, P(1–3)=0.034, P(1–4)=0.007, P(1–5)=0.114, P(1–6)=0.0065, P(1–7)=0.0245, P(1–8)=0, P(2–3)=0.0135, P(2–4)=0.012, P(2–5)=0.0115, P(2–6)=0.037, P(2–7)=0.0205, P(2–8)=0, P(3–4)=0.058, P(3–5)=0, P(3–6)=0.02, P(3–7)=0.0345, P(3–8)=0.0035, P(4–5)=0.0115, P(4–6)=0.0015, P(4–7)=0, P(4–8)=0, P(5–6)=0.0465, P(5–7)=0.009, P(5–8)=0, P(6–7)=0, P(6–8)=0, P(7–8)=0; Mouse 3: P(1–2)=0, P(1–3)=0.001, P(1–4)=0.0135, P(1–5)=0.035, P(1–6)=0.011, P(1–7)=0.0935, P(1–8)=0.001, P(2–3)=0.0575, P(2–4)=0.0015, P(2–5)=0.003, P(2–6)=0.0515, P(2–7)=0.0045, P(2–8)=0.0015, P(3–4)=0.0025, P(3–5)=0.0225, P(3–6)=0.2895, P(3–7)=0.0045, P(3–8)=0.0025, P(4–5)=0.002, P(4–6)=0.0295, P(4–7)=0.002, P(4–8)=0.0205, P(5–6)=0.023, P(5–7)=0.0055, P(5–8)=0.01, P(6–7)=0.088, P(6–8)=0.002, P(7–8)=0.0355; Mouse 4: P(1–2)=0.221, P(1–3)=0.177, P(1–4)=0.111, P(1–5)=0.0335, P(1–6)=0.011, P(1–7)=0.0175, P(1–8)=0.0435, P(2–3)=0.0765, P(2–4)=0.0025, P(2–5)=0.0205, P(2–6)=0.0615, P(2–7)=0.001, P(2–8)=0.143, P(3–4)=0.2925, P(3–5)=0.0335, P(3–6)=0.009, P(3–7)=0.049, P(3–8)=0.0335, P(4–5)=0.0105, P(4–6)=0.123, P(4–7)=0.022, P(4–8)=0.1275, P(5–6)=0.0195, P(5–7)=0.105, P(5–8)=0.1305, P(6–7)=0.0875, P(6–8)=0.0255, P(7–8)=0.11; Mouse 5: P(1–2)=0.085, P(1–3)=0.627, P(1–4)=0.1625, P(1–5)=0.4755, P(1–6)=0.024, P(1–7)=0.259, P(1–8)=0.009, P(2–3)=0.105, P(2–4)=0.052, P(2–5)=0.1565, P(2–6)=0, P(2–7)=0.0065, P(2–8)=0.09, P(3–4)=0.142, P(3–5)=0.0705, P(3–6)=0.176, P(3–7)=0.014, P(3–8)=0.12, P(4–5)=0.0705, P(4–6)=0.0015, P(4–7)=0.2375, P(4–8)=0.007, P(5–6)=0.001, P(5–7)=0.185, P(5–8)=0.0995, P(6–7)=0.0075, P(6–8)=0.0105, P(7–8)=0.115; Mouse 6: P(1–2)=0.063, P(1–3)=0.021, P(1–4)=0.023, P(1–5)=0.0065, P(1–6)=0.0995, P(1–7)=0.013, P(1–8)=0.1085, P(2–3)=0.01, P(2–4)=0.0105, P(2–5)=0.004, P(2–6)=0.0455, P(2–7)=0.0925, P(2–8)=0.0005, P(3–4)=0.008, P(3–5)=0.004, P(3–6)=0.044, P(3–7)=0.003, P(3–8)=0.0165, P(4–5)=0.0105, P(4–6)=0.034, P(4–7)=0.2415, P(4–8)=0.077, P(5–6)=0.011, P(5–7)=0.0035, P(5–8)=0.045, P(6–7)=0.0035, P(6–8)=0.033, P(7–8)=0.012. Finally, to further quantify the overall decoding performance for each mouse, we computed the fraction of distinguishable cortical pattern pairs (P < 0.05) over the cortical pattern pairs included in the analysis within each animal (Fig. 7d, Extended Data Fig. 10c). To examine whether the fraction of distinguishable cortical pattern pairs in each animal is significant, we test against the null hypothesis that the fraction is obtained out of chance. Since the probability of each pattern pair being mislabeled as distinguishable is 0.05, under the null hypothesis, the number of distinguishable pairs in each mouse follows a binomial distribution where the parameter p equals 0.05 and N equals the number of pattern pairs included in analysis within each animal. Therefore, the critical number of pattern pairs Nc is determined as the smallest integer that makes the binomial cumulative density function larger than 0.95. Finally, the chance level fraction is obtained as the ratio between Nc and N.

- Hippocampal neuron firing rates under different cortical patterns during SWRs

To obtain the instantaneous firing rates between −1 s and 2 s relative to SWR onset for each hippocampal neuron, we used 100-ms time bins without overlap for each SWR event (Fig. 7a, Extended Data Fig. 10a). We defined the preference index (P.I.) to measure whether one neuron showed higher activity for one pattern than the other (Fig. 7e, Extended Data Fig. 10d). For each pattern pair (e.g. pattern X and pattern Y), the preference index of one neuron was calculated using its mean firing count between 0–100 ms relative to SWR onset under each pattern, as shown in Equation 2.

$$P.I.(X)=\frac{\mathit{\text{Firing}}\mathit{\text{Count}}(X)-\mathit{\text{Firing}}\mathit{\text{Count}}(Y)}{\mathit{\text{Firing}}\mathit{\text{Count}}(X)+\mathit{\text{Firing}}\mathit{\text{Count}}(Y)}$$ (Equation 2)

The early vs. late group included pattern pairs of pattern 1 vs. 2, 1 vs. 3, 2 vs. 3, 4 vs. 5, 4 vs. 6, and 5 vs. 6. The anterior vs. posterior group included pattern pairs of pattern 1 vs. 4, 2 vs. 5, and 3 vs. 6. For each cortical pattern pair, the preference index at population level was calculated by averaging across discriminant hippocampal neurons (Fig. 7e, Extended Data Fig. 10d).

- Statistics and Reproducibility

For electrode arrays designed for recordings in mice, rats, and monkeys, four electrode arrays were imaged respectively and example images are shown in Fig. 1 and Extended Fig. 1. Two animals were excluded from 8 animals from recordings and analyses due to unsuccessful implantations. The 6 animals with successful implantations went through the same recording procedures and were all included in analyses. All statistical analyses were performed in MATLAB. Statistical tests were two-tailed and significance was defined by alpha pre-set to 0.05. Error bars and shaded regions surrounding line-plots indicate ± standard error of the mean (s.e.m.) unless otherwise noted. All the statistical tests are described in the figure legends and each test was selected based on data distributions using histograms. For Fig. 1m, a two-sided Student’s T-test was used to test the correlation between the electrode impedance and the recording noise level. For Fig. 5d and 5e, a two-tailed bootstrap test (10000 times) was used to test the median time difference between SWR and cortical activity onset and the fraction of SWR events occurring before or after cortical activity onset. For Fig. 7c, the decodable pattern pair was determined by a one-tailed shuffling test, which randomly permuted the labels of cortical patterns. For Fig. 7d, the chance level number of decodable pattern pairs (nc) was computed from the inverse of binomial cumulative distribution with probability 0.95 and the chance level fraction was obtained by dividing nc with n = 28, the number of pattern pairs on which decoding was performed. For Fig. 7e, a two-tailed bootstrap test (10000 times) was used to determine the significance of preference index and the balanced accuracy. Multiple comparisons were corrected for by Benjamini-Hochberg corrections. Sample sizes (n) are as follows where applicable. Recording sessions per animal: 2, 3, 3, 3, 2, 2. Well-separated SWRs / all SWRs per animal: 530/1245, 896/1785, 787/1440, 826/1618, 673/1365, 578/1190. Hippocampal neurons per animal: 8, 21, 14, 11, 10, 10. No statistical methods were used to predetermine sample size but our sample sizes are similar to those reported in previous publications from our lab²¹ and others using wide-field calcium imaging^56,57 and electrophysiological recordings⁵⁸. No randomization was performed. Randomization is not necessary to our study as all animals underwent the same surgical and recording procedures. Data collection and analysis were not performed blind to the conditions of the experiments.

Life Sciences Reporting Summary

Further information on research design is available in the Nature Research Reporting Summary linked to this article.

Extended Data

Extended Data Fig. 1. Microscope pictures of different Neuro-FITM probe designs.

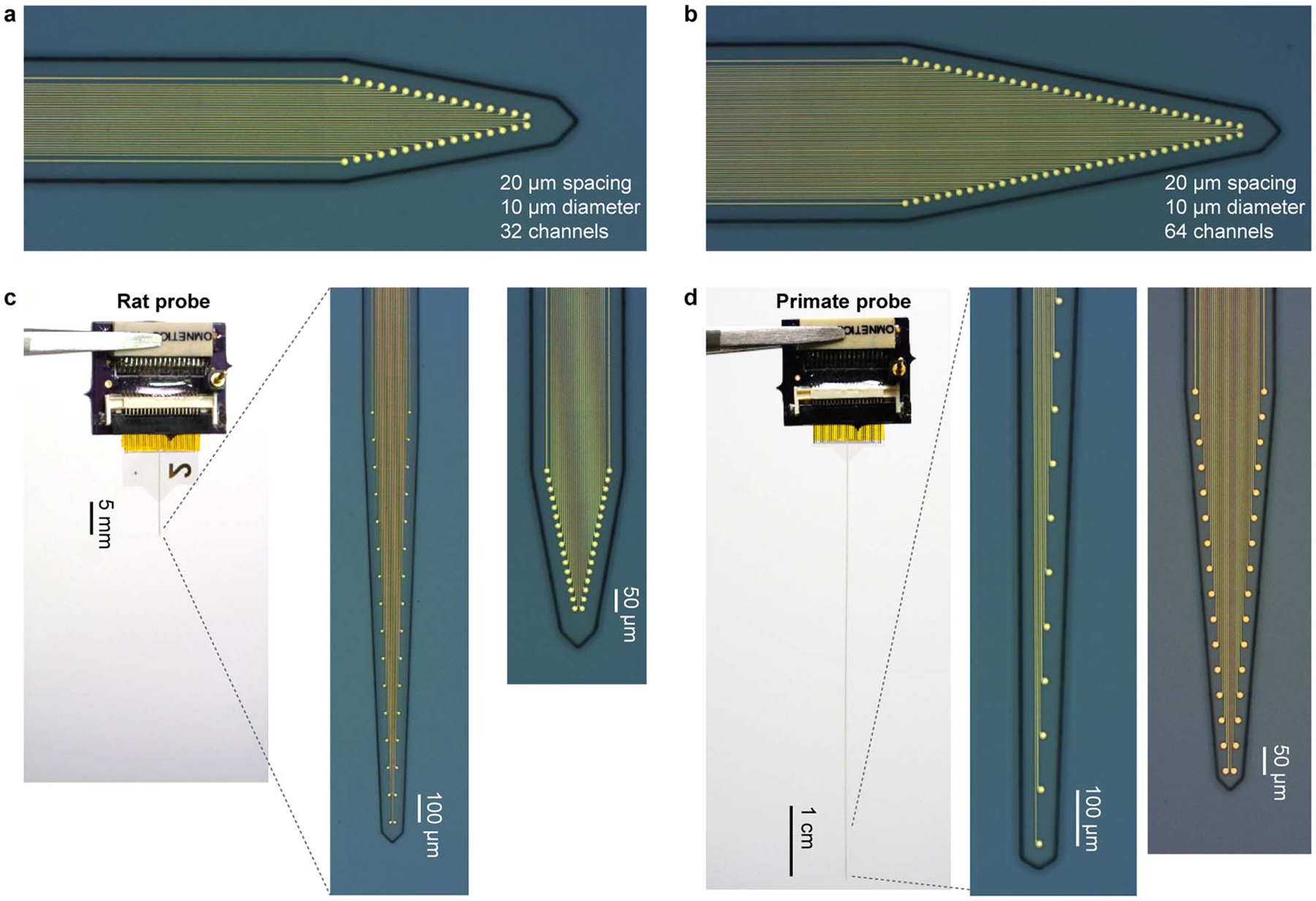
a, Microscope image of the recording tip of 32 channel Neuro-FITM array with 20 μm spacing. b, Same as (a), but for 64 channel Neuro-FITM array with 20 μm spacing. c, Picture of the whole probe (left), the microscope pictures of the recording tip of 32 channel Neuro-FITM array with 100 μm spacing (middle) and 20 μm spacing (right) for recording in rats. d, Same as c, but for 32 channel Neuro-FITM array with 100 μm spacing and 50 μm spacing for recording in primates.

Extended Data Fig. 2. Testing the multimodal recording setup using Neuro-FITM and standard silicon probes under both the wide-field and 2-photon imaging systems.

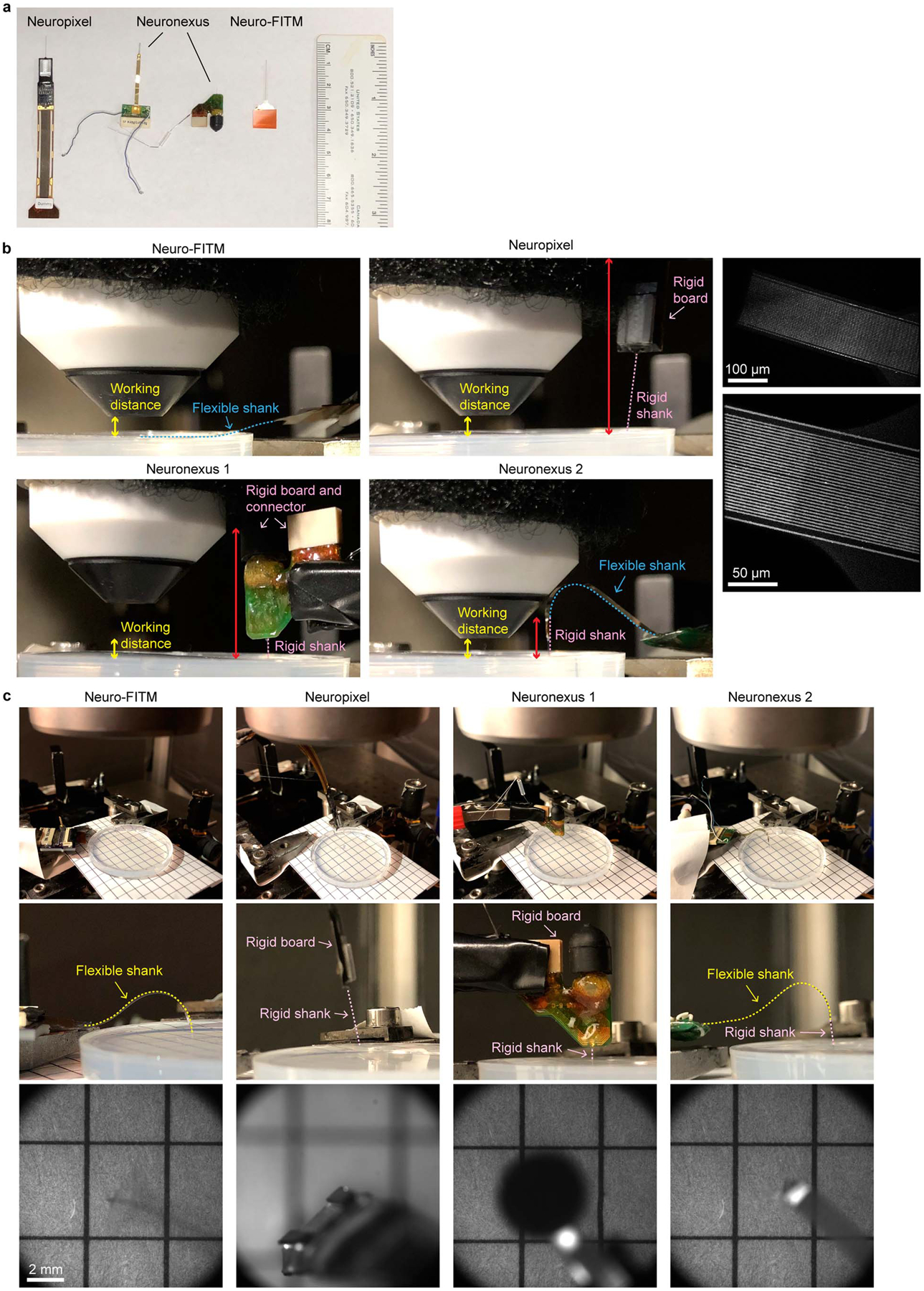
a, A picture of the probes tested in the multimodal recording setup. b, Pictures of the side view under the 2-photon imaging system. Neuro-FITM can be completely bent to the side as shown with the blue dashed line. Both the Neuronexus probes and the Neuropixel probe prevent the lowering of microscope objective (total rigid part indicated by red double arrow). The right column are the 2-photon images of the array surface, showing the thin Au wires, the boundary of the array substrate, and the penetration point. c, Pictures of the experimental setup (top), the zoom-in side view (middle), and the field of view (bottom) under wide-field imaging system, showing the blocking of field of view (Neuronexus probes) and preventing the lowering of microscope objective (Neuropixel probe). Wide-field image shows that mostly transparent Neuro-FITM does not block the field of view or generate shadows.

Extended Data Fig. 3. Implantation of Neuro-FITM array to HPC in in vivo experiments and the spike waveforms of example neurons.

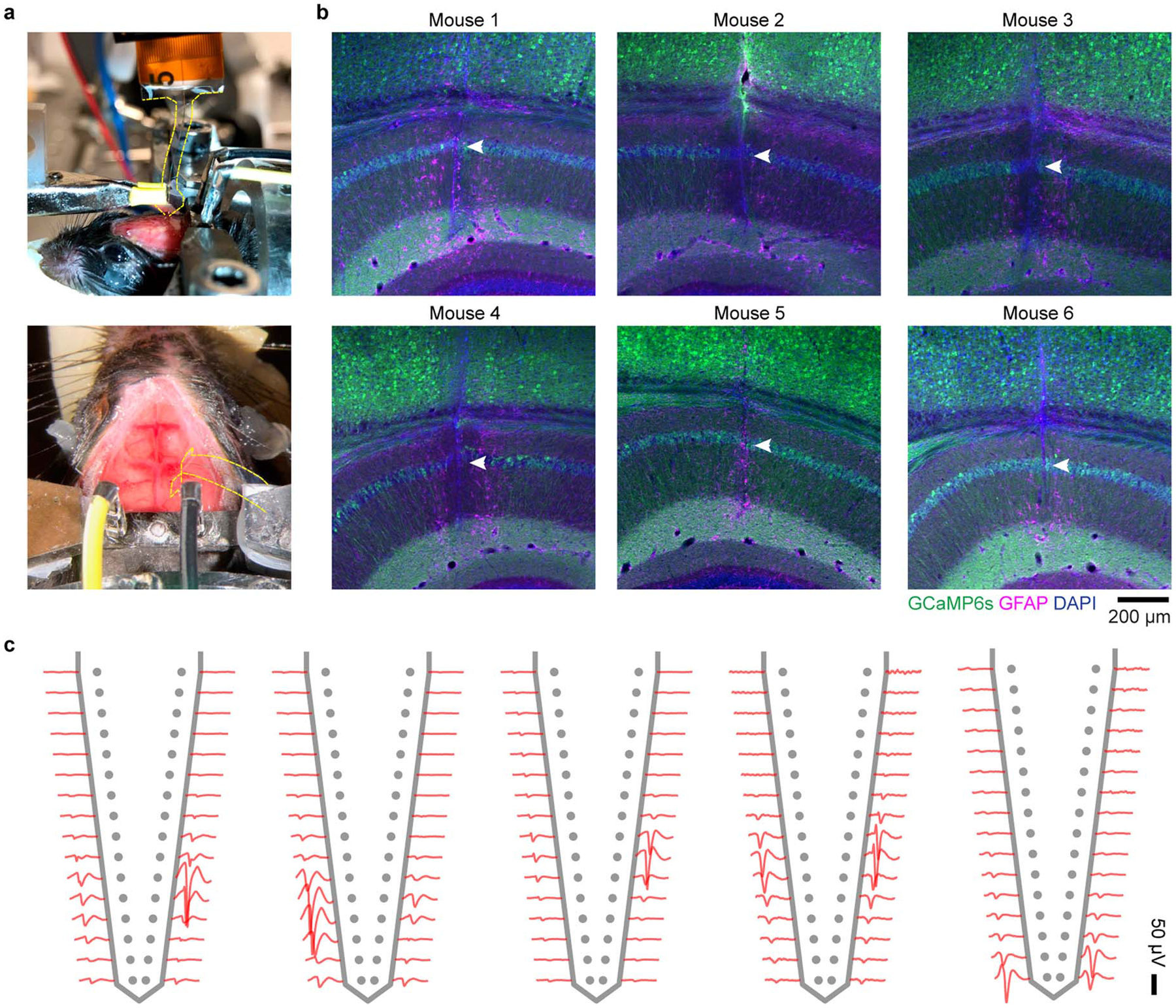
a, Surgical setup of array implantation in actual experiments. Note that the array shank is largely invisible. The edge of the shank is marked by yellow dashed lines. b, The staining results of 6 mice, showing the successful penetration to the CA1 pyramidal layer. Arrowheads: trajectory in CA1 pyramidal layer. c, The spike waveforms of a few example neurons recorded from different animals. Single neurons can be detected in multiple adjacent channels, each exhibiting different waveform amplitudes.

Extended Data Fig. 4. SWR-associated large-scale cortical activity.

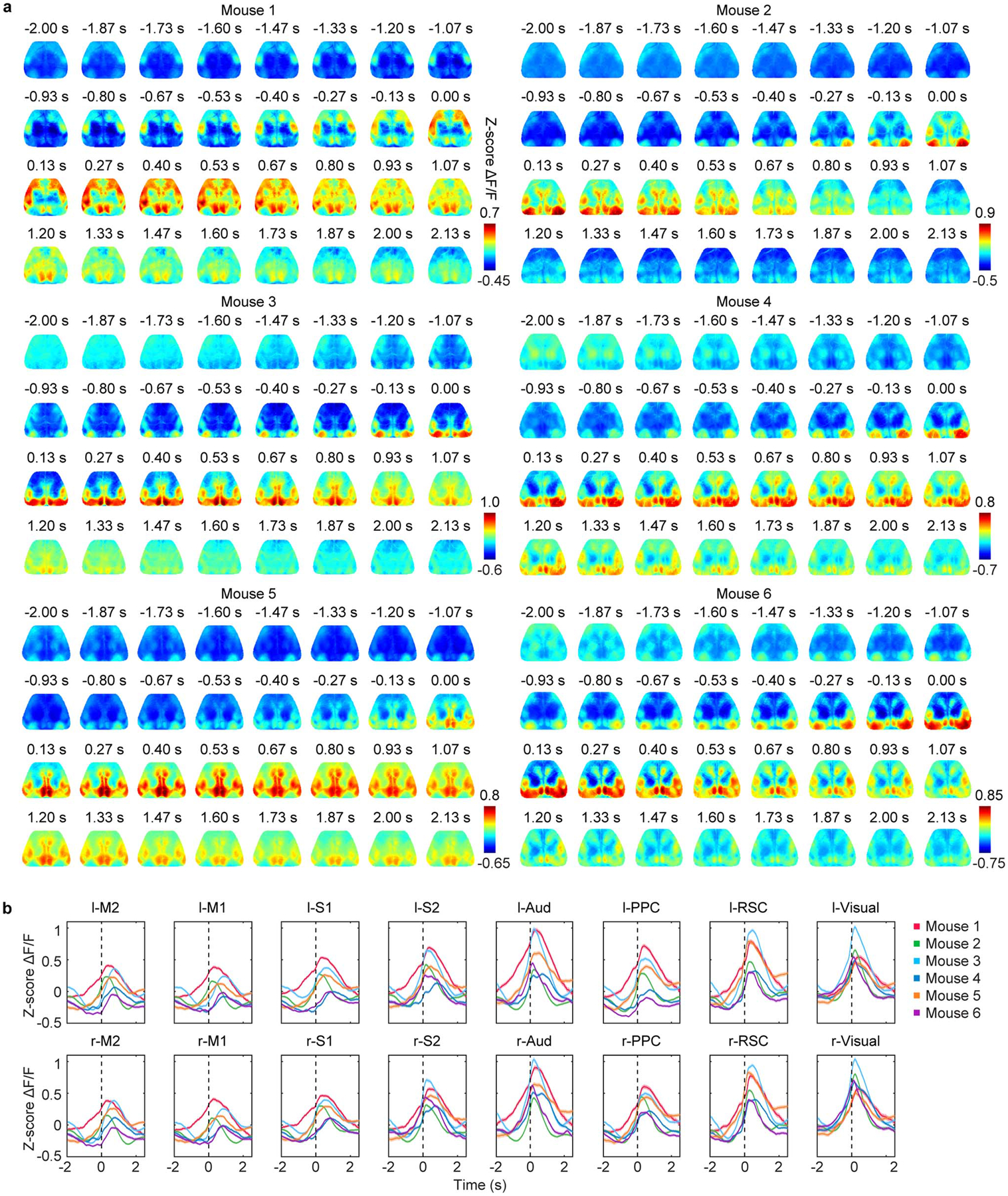
a, Averaged cortical activity aligned to SWR onset in each animal. In all animals, the cortex exhibited broad activation around SWRs with the cortical activity rising before SWR onset. b, Mean activity in each cortical region aligned to SWR onset (mean ± s.e.m., across SWR events). Black dashed lines: SWR onset.

Extended Data Fig. 5. The distribution of time differences between SWR onset and activity onset in each cortical region.

The time differences (SWR onset-cortical activity onset: positive = cortex precedes SWR) formed a continuum around cortical activity onset. Note that the distribution was skewed to positive side in posterior cortical regions, suggesting cortical activity onset in posterior regions preceded SWR onset in a larger fraction of SWR events. Black lines: cortical activity onset.

Extended Data Fig. 6. Two-stage TCA algorithm.

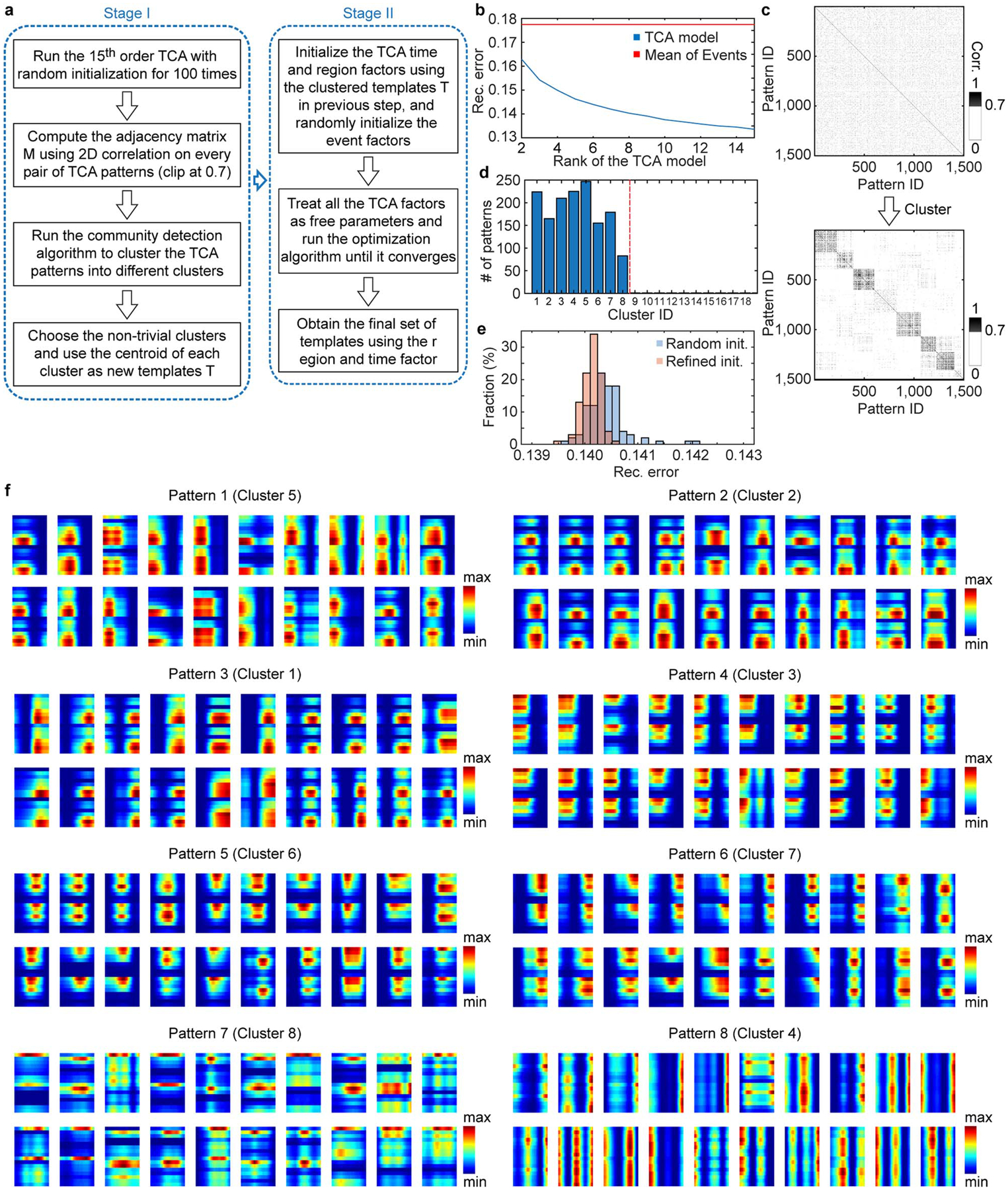
a, Schematic of algorithm flow. b, Reconstruction error (rec. error) under different ranks of TCA model. c, The adjacency matrix before and after clustering. The 1500 TCA patterns were obtained by the 100 runs of 15th order TCA with random initialization. Corr.: correlation. d, Number of assigned patterns in each cluster. Note that only the first 8 clusters had number of assigned patterns > 1. e, Reconstruction error (rec. error) of the original TCA algorithm with random initialization and the two-stage TCA algorithm with refined initialization (rank = 8). The reconstruction error given by the two-stage TCA model is smaller than that of the original TCA algorithm with random initialization (two-tailed rank-sum test, P=1.38E-11, n = 100 repetitions for each algorithm), indicating that our two-stage TCA better captured the dynamics of cortical activity. f, Randomly selected 20 TCA patterns in each cluster for clusters 1–8. Patterns within each cluster exhibited similar spatiotemporal properties.

Extended Data Fig. 7. The two-stage TCA result and the cortical activation timing analysis for two patterns.

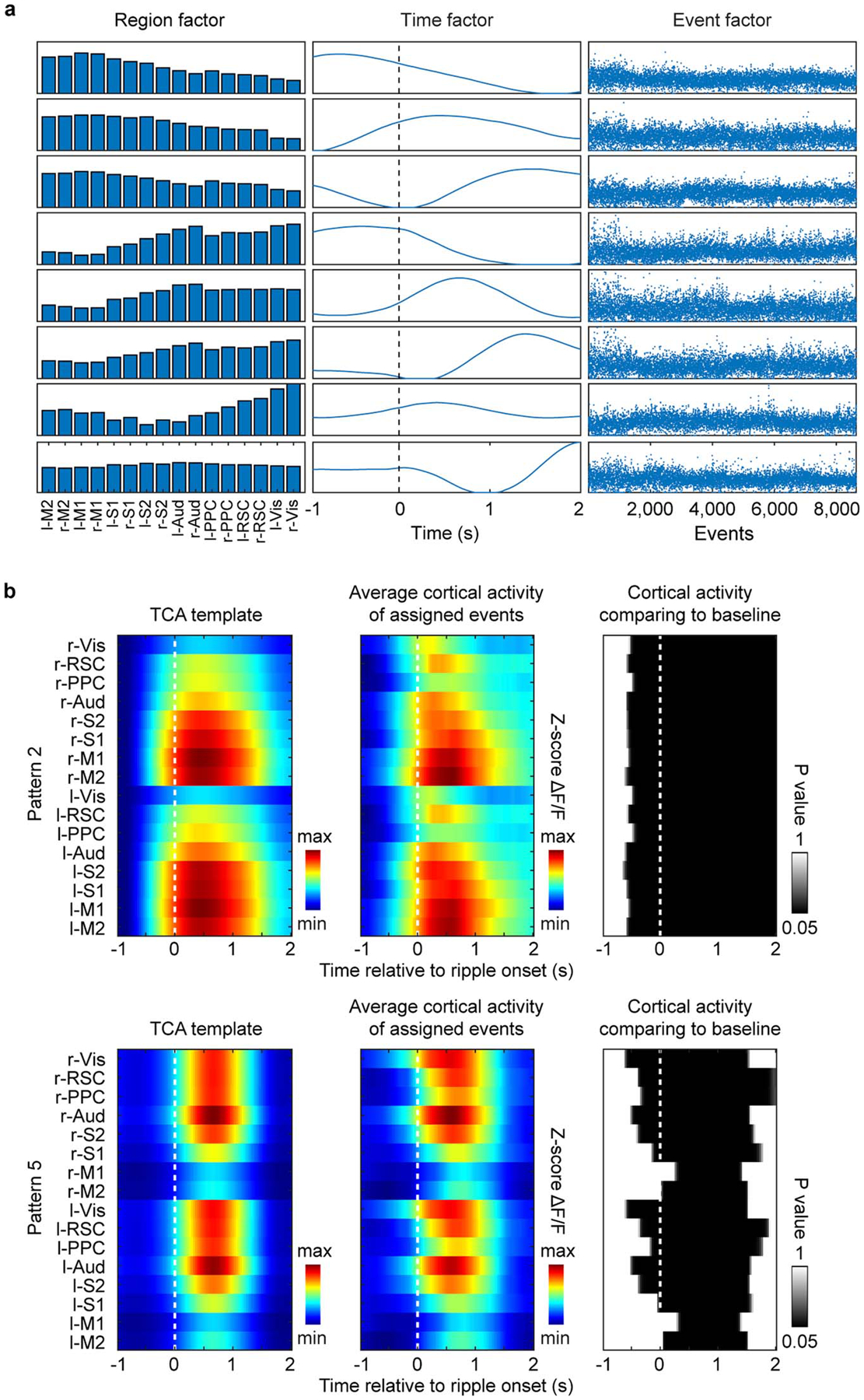
a, Factors generated by two-stage TCA algorithm. The high-dimensional data of SWR-associated activity from 16 cortical regions was decomposed into 3 factors. The region factors and time factors describe the spatial and temporal dynamics of cortical patterns respectively and the event factors measure the weighting of a given SWR event on the established set of patterns. b, Cortical activation timing for pattern 2 and pattern 5. Shown in each row are the pattern template (left), the average cortical activity for the events assigned to the pattern (middle), and the P-value maps (right) for all the cortical regions at [−1 s, 2 s] time interval aligned to SWR onset, showing significantly higher activity than baseline (−1 s) for most cortical regions.

Extended Data Fig. 8. The decoding accuracy of all cortical pattern pairs in each animal.

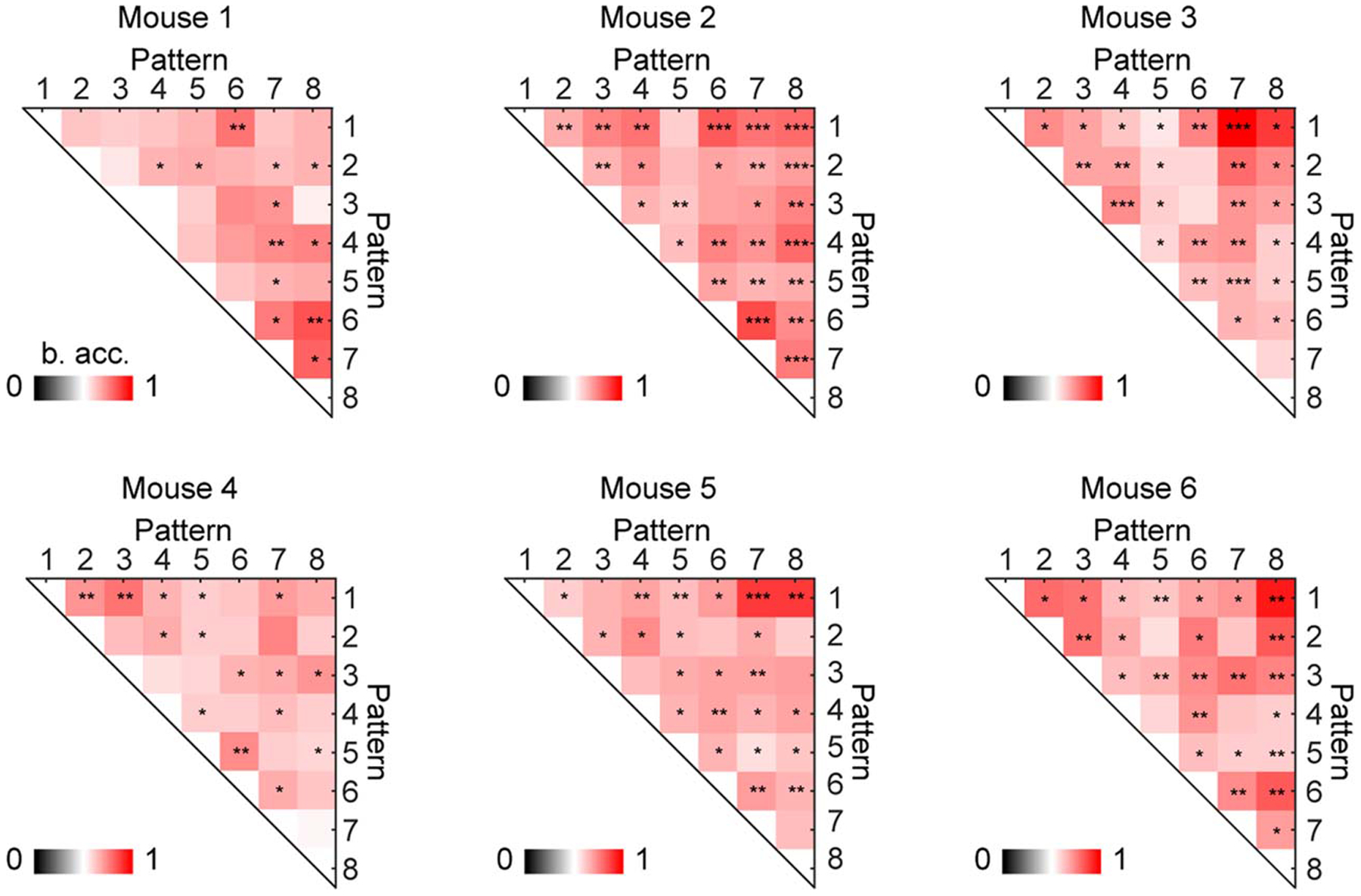
Many cortical pattern pairs can be distinguished from each other in each animal. The distinguishable pattern pairs are marked by asterisks (shuffling 2000 times, one-tailed, *P < 0.05, **P < 0.01, ***P < 0.001, see Methods for exact p values). B. acc.: balanced accuracy.

Extended Data Fig. 9. Discriminant neurons in decoding cortical pattern identity and the fraction of distinguishable pairs using different neuron populations.

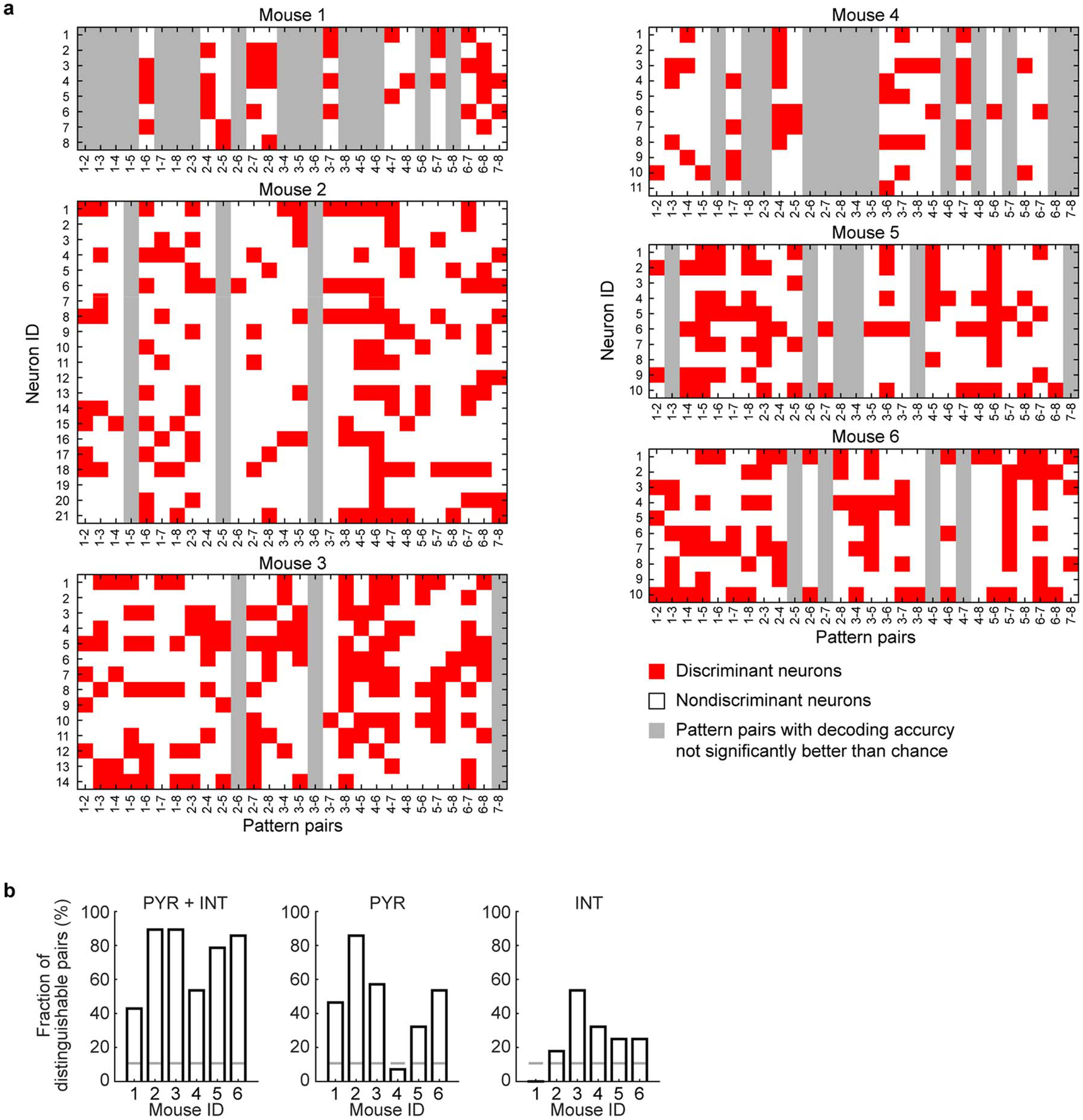
a, Discriminant neurons selected by feature elimination algorithm in decoding for each pattern pair. Note that the decoding often requires information from multiple HPC neurons, and all HPC neurons contributed to the decoding of some pattern pairs. b, The decoding results of cortical patterns using both the PYR and INT, the PYR only, and the INT only. Gray lines: the chance level fraction with P < 0.05. The chance level number of decodable pattern pairs (nc) was computed from the inverse of binomial cumulative distribution with probability 0.95 (one-sided binomial test, n = 28 pattern pairs). The chance level fraction was obtained by dividing nc with n = 28, the number of pattern pairs on which decoding was performed. PYR: pyramidal neurons, INT: interneurons. For PYR + INT, the p-values for mouse 1–6 are 2.24E-10, 5.10E-32, 5.10E-32, 2.60E-14, 9.17E-26, 8.42E-30. For PYR only, the p-values for mouse 1–6 are 1.26E-11, 8.42E-30, 9.63E-16, 0.16, 5.56E-7, 2.60E-14. For INT only, the p-values for mouse 1–6 are 0.76, 0.0023, 2.60E-14, 5.56E-7, 4.92E-5, 4.92E-5.

Extended Data Fig. 10. Different cortical activity patterns associated with distinct HPC neuronal activity patterns during all SWRs.

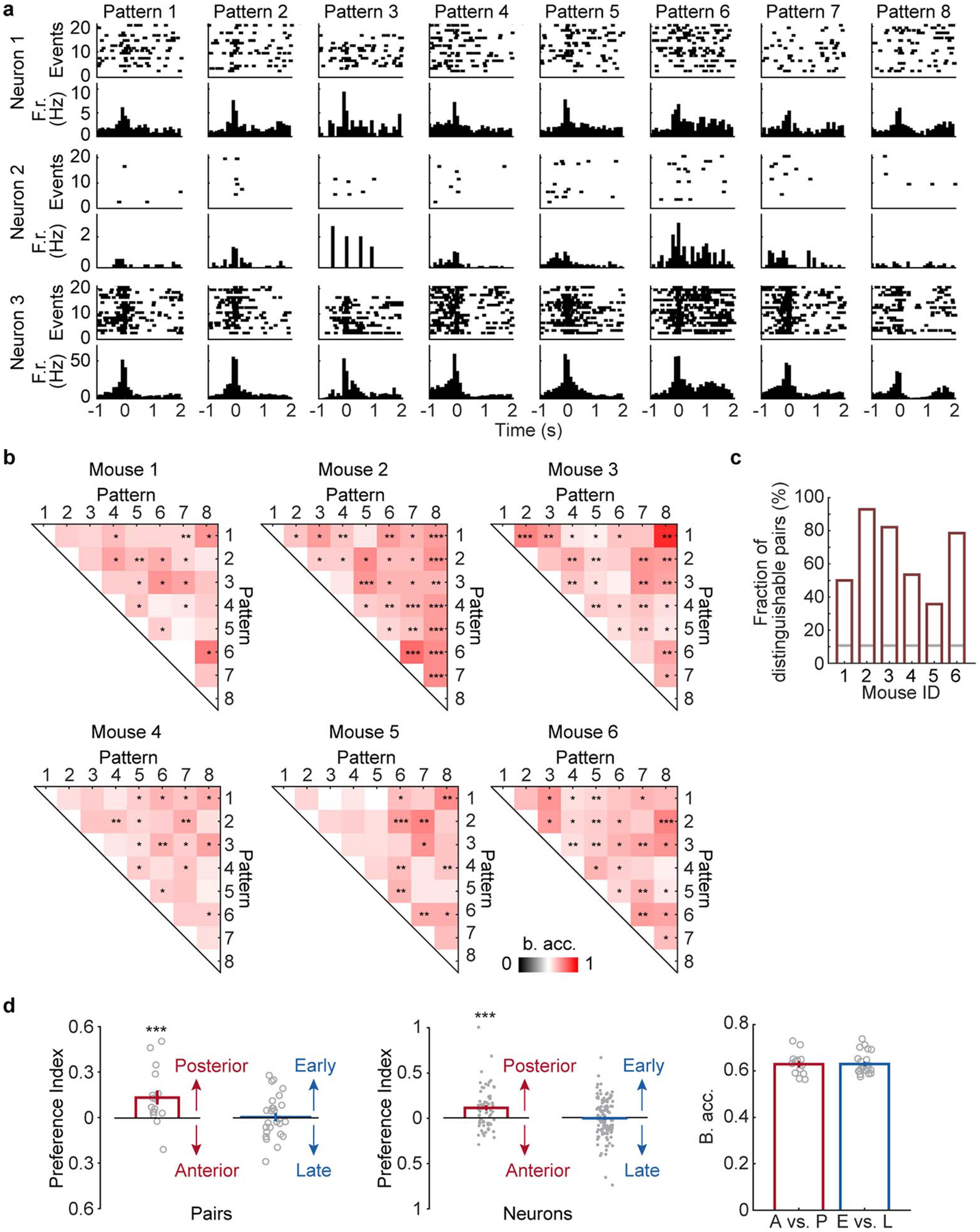
a, Raster plots (spikes) and the peri-event time histograms of example HPC neurons. b, Decoding accuracy of all cortical pattern pairs from all 6 animals. Cortical pattern pairs that are significantly distinguishable based on hippocampus activity are marked by asterisks (shuffled 2000 times, one-tailed, *P < 0.05, **P < 0.01, ***P < 0.001, see Methods for exact p values). B. acc.: balanced accuracy. c, Fraction of distinguishable cortical pattern pairs in each animal. Gray lines: the chance level fraction with P < 0.05. The p-values for mouse 1–6 are 6.13E-13, 1.99E-34, 1.00E-27, 2.60E-14, 4.73E-8, 9.17E-26, n = 28 pattern pairs. d, Preference index and decoding accuracy between anterior (A)-posterior (P) and early (E) - late (L) pattern pairs. Left: preference index of discriminant hippocampus neurons between A-P pairs (pattern 1 vs. 4, 2 vs. 5, and 3 vs. 6) or between E-L patterns (pattern 1 vs. 2, 1 vs. 3, 2 vs. 3, 4 vs. 5, 4 vs. 6, and 5 vs. 6). Posterior patterns were associated with higher firing counts of discriminant neurons than the anterior patterns (two-tailed bootstrap test, 10000 times, *** P(A-P)= 0.0005, n = 16 pattern pairs) while no significant differences were detected between early and late patterns (P(E-L) = 0.4380, n = 27 pattern pairs). Gray circles: preference index averaged over all neurons for each pair within each animal. Middle: same as Left but for individual discriminant neurons (two-tailed bootstrap test, 10000 times, *** P(A-P) = 0, n = 71 neurons, P(E-L) = 0.3591, n = 129 neurons). Gray dots: preference index of individual discriminant neurons. Right: Decoding accuracy between A-P and E-L pairs was similar (two-tailed bootstrap test, 10000 times, P = 0.4745, n = 16 pattern pairs for A-P, n = 27 pattern pairs for E-L). All error bars are s.e.m. Gray circles: decoding accuracy for each pair.

Data availability

Data available on request from the authors. The Allen Brain Atlas could be accessed through Brain Explorer 2: http://mouse.brain-map.org/static/brainexplorer