Host life-history traits influence the distribution of prophages and the genes they carry

Abstract

Bacterial strains with a short minimal doubling time—‘fast-growing’ hosts—are more likely to contain prophages than their slow-growing counterparts. Pathogenic bacterial species are likewise more likely to carry prophages. We develop a bioinformatics pipeline to examine the distribution of prophages in fast- and slow-growing lysogens, and pathogenic and non-pathogenic lysogens, analysing both prophage length and gene content for each class. By fitting these results to a mathematical model of the evolutionary forces acting on prophages, we predict whether the observed differences can be attributed to different rates of lysogeny among the host classes, or other evolutionary pressures. We also test for significant differences in gene content among prophages, identifying genes that are preferentially lost or maintained in each class. We find that fast-growing hosts and pathogens have a greater fraction of full-length prophages, and our analysis predicts that induction rates are significantly reduced in slow-growing hosts and non-pathogenic hosts. Consistent with previous results, we find that several proteins involved in the packaging of new phage particles and lysis are preferentially lost in cryptic prophages.

This article is part of the theme issue ‘The secret lives of microbial mobile genetic elements’.

1. Introduction

Bacteriophages (phages) are viral particles that infect bacteria, and are the most abundant organism in the biosphere [1,2]. After attaching to a receptor on a bacterial host’s surface, the phage injects its genome into the host. The injected viral genome has multiple avenues for reproduction [3]. However, there are two prominent reproductive strategies: lysis and lysogeny [4]. In lytic reproduction, the phage uses the molecular machinery of the host to produce and release a number of progeny phage into the environment, killing the host in the process [4,5]. By contrast, lysogeny involves the viral genome integrating into the host’s genome and reproducing through vertical transmission to daughter host cells, without killing the host [1,4,6]. Phages that are able to use either of these strategies are classified as temperate phages [4].

A prophage is the viral DNA of a temperate phage that has integrated into a host bacterium's genome [4]. As well as being transmitted to daughter cells during bacterial fission, prophages can also reproduce by re-entering the lytic cycle, thus killing the host and releasing progeny phage. This spontaneous initiation of the lytic life cycle by a prophage is called induction, a process that requires specific prophage genes for lysis and re-infection [7,8]. Prophages capable of inducing lysis are referred to as ‘intact’ or ‘functional’ [8]. By contrast, a cryptic or incomplete prophage has lost the ability to induce lysis [9], typically through the process of mutational degradation of prophage genes. Finally, we note that both intact and cryptic prophage sequences can confer fitness benefits to bacterial hosts (see [10–12] for discussion).

Recently, a number of independent investigations of the length distributions of chromosomal prophages have revealed that these distributions are often multimodal, exhibiting a large peak at lengths that are shorter than known active phage genomes [13–16]. In [17], the authors examined the underlying evolutionary processes that might explain this multimodal length distribution. Their model predicts that large prophages are primarily maintained though lysogeny, while small prophages, which may have lost genes necessary for induction but retained genes of benefit to the host, are primarily maintained through selection [17].

The frequency at which a temperate phage initiates lysogeny likely depends on a multitude of factors; the most common explanation for an increase in lysogeny is that this strategy may be favoured in conditions where susceptible bacteria are at low densities, possibly due to low temperature or resource concentrations [18–25]. In addition, it has been suggested that characteristics of the bacterial host may play a pivotal role in the propensity for a temperate phage to initiate lysogeny, notably the minimal doubling time of the bacterial host [26,27] and bacterial pathogenicity [28,29]. Motivated by this suggestion that host characteristics may play an important role in the lysis–lysogeny decision, Touchon et al. [30] investigated possible correlations between life-history traits of the host and lysogeny. The most significant association observed was between the minimal doubling time of the host and the presence of integrated prophages [30]: the minimal doubling time was on average five times shorter in lysogens [30]. The authors also identified a weak positive correlation between the pathogenicity of the host species and the presence of prophages [30].

Thus, while previous work has established a correlation between minimal doubling times, pathogenicity and prophage content, here we extend those results by comparing the functionality, length and gene repertoire of prophages carried in different host classes. Specifically, we compare the fraction of prophages that are intact (functional) or incomplete (cryptic) in fast- and slow-growing hosts, as well as pathogens and non-pathogens. We then apply the model developed by [17] to test for differences in the evolutionary forces acting on temperate phages infecting hosts of different types. Finally, we ask whether the gene repertoire of cryptic prophages differs across these host types. That is, we determine whether specific phage gene classes have been enriched or preferentially lost in the cryptic prophages of pathogens, or of fast- or slow-growing hosts.

2. Methods

(a) . Bioinformatics

In [30], the prophage content and life-history traits of 2110 complete bacterial genomes were studied. The minimal doubling times used to classify the bacteria were determined through Vieira-Silva and Rocha’s experimental work on bacterial species [31]. Bacterial species were classified as fast growers if their minimal doubling time under optimal conditions was less than 2.5 h, otherwise they were considered slow growers [30,31]. In addition, [30] used criteria developed by [32] to classify bacterial species as pathogenic and non-pathogenic. As noted in [30], the classification of pathogens and non-pathogens is not clean cut. Pathogenicity varies widely between strains, and often depends on the physiological state of the host. In addition, some species will opportunistically become pathogenic [33]. Thus, this coarse-grained classification may be thought of as species that do or do not include pathogenic strains.

We passed the complete list of accession numbers (unique genome identifiers) for hosts identified by [30] as either fast- or slow-growing, pathogenic or non-pathogenic into the PHASTER web interface for rapid prophage identification and gene annotation [34]. We note that not all host genomes are readily available through the automated PHASTER URL API interface; of the 2359 accession numbers we submitted, results for a reduced dataset of 374 genomes were returned through the URL API. To ensure that this subset of genomes was unbiased, we then submitted further randomly chosen accession numbers in small batches, with the aim of achieving at least 50% coverage across all four host classes. We also verified that the species retained in our dataset were broadly representative of the species composition of the full list of accession numbers (see figures S1–S4 in the electronic supplementary material) and that the distributions of bacterial genome lengths were roughly similar across classes (see figure S5 in the electronic supplementary material). This procedure yielded results for 684 genomes for the fast-growing hosts and 305 genomes for the slow-growing hosts, 523 genomes for pathogenic hosts, and 281 genomes for non-pathogenic hosts. Of the bacterial genomes investigated, 758 genomes appeared in both the fast/slow dataset and the pathogenic/non-pathogenic dataset. We also note a degree of overlap between classes: of the 758 genomes that appear in both classes, 399 are fast-growing and pathogenic, while 134 are slow-growing and non-pathogenic (e.g. Escherichia coli was classified as a fast-growing pathogen).

PHASTER results include the number of putative prophages in the genome and the length of each prophage; these datasets are summarized in table 1. Overall this yielded 3.6 prophages per bacterial genome in fast-growing hosts and 2.9 in slow-growing hosts, 4.0 in pathogenic hosts and 3.1 in non-pathogenic hosts. The PHASTER algorithm classifies each putative prophage sequence as an ‘intact’, ‘questionable’ or ‘incomplete’ prophage.

Table 1.

Data summary. Bacterial classifications as provided in [30]. The minimum, maximum and average lengths of prophages in each class are provided.

bacterial class	genomes: in [30]	this study	prophages	min (kb)	max (kb)	average (kb)
fast	938	684	2477	3.1	142.0	29.9
slow	420	305	871	5.1	74.2	22.9
overall	1358	989	3348	3.1	142.0	26.6
pathogen	596	523	2094	3.1	134.2	27.1
non-pathogen	405	281	881	4.7	141.6	24.1
overall	1001	804	3175	3.1	141.6	25.5

For each coding sequence within a putative prophage, PHASTER also provides an output of gene annotations identified as BLAST hits for that sequence. We recorded all annotations for all coding sequences within prophages, and then searched these annotations for phage gene keywords as previously described [35]. For these phage gene classes, we counted the number of prophages identified as containing at least one gene of that class; gene classes that constituted less than one per cent of the data (in this study, flippase and injection proteins) were excluded due to small numbers. We further partitioned these data based on host class and prophage completeness (intact, questionable or incomplete). For each host class, we then identified genes that were under- or over-represented in incomplete prophages by calculating the per cent change in gene frequency between incomplete (inc) and intact (int) prophages, that is:

$$\text{\%}\hspace{0.17em}\text{change}=\frac{100(f_{\mathrm{inc}}-f_{\mathrm{int}})}{f_{\mathrm{int}}}.$$

To evaluate the statistical significance of these results, for each gene type and host class, we randomly assigned the same total number of genes to one of the three prophage classes. Because intact prophages in the dataset contain more genes than incomplete prophages, we also preserved the proportion of genes assigned to each class [35]. We computed the per cent change in gene frequency for these bootstrapped data as described above, and repeated this procedure 10 000 times to build a bootstrapped distribution of gene frequencies and their per cent change.

To test whether these results might be biased by genes preferentially recognized by PHASTER, we re-analysed the prophage genomes from both the fast-growing host and slow-growing host datasets in a parallel bioinformatics pipeline. In this approach, we submitted accession numbers to PATRIC (Pathosystems Resource Integration Center, patricbrc.org [36]) and downloaded all the gene annotations for these genomes from the PATRIC database. Since PHASTER has been developed and calibrated to specifically identify prophage genomes, we used the positions of prophage sequences identified by PHASTER and isolated all PATRIC annotations that occurred within these sequences. We then re-ran the phage gene frequency and bootstrapping procedure described above, using the PATRIC annotations, as a comparison. Details regarding this comparison can be found in Section S3 in the electronic supplementary material.

(b) . Mathematical model

To fit the distribution of prophage lengths, we adapt the model developed by [17]. We fit data from each host class separately using a model comprised of functions describing lysogeny, selection, induction and degradation.

In brief, the partial differential equation

$$\begin{array}{rl}\frac{\mathrm{\partial }Q(x,t)}{\mathrm{\partial }t}& =\alpha f\hspace{0.17em}(x)+\frac{\mathrm{\partial }}{\mathrm{\partial }x}[r_D\hspace{0.17em}x\hspace{0.17em}Q(x,t)]+[r_{S}S(x)\\ & -r_{I}I(x)]Q(x,t)-\tilde{\delta }(t)Q(x,t),\end{array}$$ 2.1

describes the time evolution of the prophage length distribution in a given bacterial population. Here, Q(x, t) is the density of prophages of length x (kb) at time t, α represents the rate of lysogeny, while f(x) is the length distribution of active phages entering bacterial genomes via lysogeny. The parameter r_D is the mutational degradation rate, that is, the rate at which prophage sequences decay in length over evolutionary timescales, due to the deletion-biased mutation spectrum of bacteria [37]. We do not assume that all prophage genes are lost or retained at the same rate (figure 5), but we do assume that before the action of selection and induction, mutation acts at a constant and uniform rate across the prophage genome.

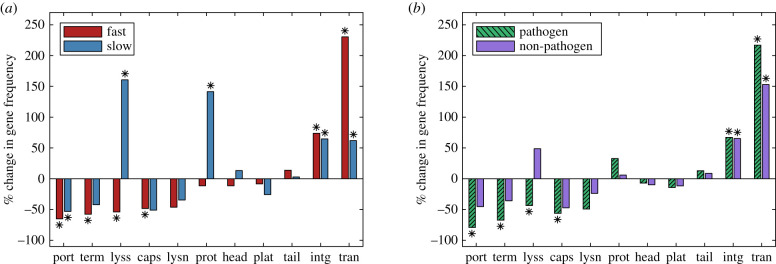
Figure 5.

The per cent change in gene frequency for prophages in fast- and slow-growing hosts (a), and pathogens and non-pathogens (b); the gene frequency in incomplete prophages is compared to intact prophages in the hosts of the same class. Frequencies that were significantly lower or higher than expected by chance with a two-sided 5% significance threshold are indicated by stars (Bonferroni-corrected for 11 simultaneous comparisons). Thus stars indicate gene classes that are preferentially lost or enriched in cryptic prophages. Gene classes are ordered from left to right by degree of enrichment in fast-growing hosts; phage gene keywords in the annotation search were: portal, terminase, lysis, capsid, lysin, protease, head, plate, tail, integrase and transposase. (Online version in colour.)

The parameter r_S is the selection coefficient conferred to the host by an intact prophage; since the deleterious effects of prophages are captured by induction (see below), in this study r_S was constrained to be positive; S(x) is the expected fraction of this benefit that is conferred by a prophage of length x. The parameter r_I represents the rate of induction, while I(x) is the probability that a prophage of length x may be lost by induction. I(x) itself depends on the parameter n_I, which is the number of genes required to facilitate the loss of the prophage via induction; for example, n_I might correspond to the number of genes necessary for the prophage to excise from the cellular genome as the first step in induction. For brevity, we omit the derivation of each of these terms but refer the interested reader to [17]. The parameter $\tilde{\delta }(t)$ is simply a normalizing factor, which is set to ensure that $\int Q(x,t)\hspace{0.17em}\mathrm{d}x=1$. A summary of model parameters and parameter fitting constraints can be found in table S1 and Section S5 in the electronic supplementary material.

The distribution that will be fit to the data, P(x), is the steady-state solution of Q(x, t), which is

$$P(x)=\underset{t\to \mathrm{\infty }}{lim}Q(x,t),$$

which itself depends on $\delta =\underset{t\to \mathrm{\infty }}{lim}\tilde{\delta }(t)$. When it exists, this steady-state solution gives the predicted long-term distribution of prophages of length x, and is given by

$$\begin{array}{r}P(x)=-(\alpha /r_D)\frac{{\mathrm{e}}^{-{\int }_m^x\mathcal{F}(y)\hspace{0.17em}\mathrm{d}y}}{x^{1-K}}{\int }_m^x\frac{\hspace{0.17em}f\hspace{0.17em}(y)}{y^K}\hspace{0.17em}{\mathrm{e}}^{{\int }_m^y\mathcal{F}(z)\hspace{0.17em}\mathrm{d}z}\mathrm{d}y+C{x}^{K-1}\hspace{0.17em}{\mathrm{e}}^{-{\int }_m^x\mathcal{F}(y)\hspace{0.17em}\mathrm{d}y},\end{array}$$ 2.2

where m is the minimum prophage length in the dataset, C is a constant of integration, K = δ/r_D and

$$\mathcal{F}(x)=\frac{1}{x}(\frac{r_S}{r_D}S(x)-\frac{r_I}{r_D}I(x)).$$ 2.3

To fit each dataset, we use numerical integration to obtain the steady-state solution (equation (2.2) and compare this steady-state solution to the data, optimizing the log-likelihood to identify the best-fit parameter values. The log-likelihood is defined as

$$\log (L)=\sum _{i=1}^n\log P(x_i),$$

where x_i are the n observed lengths of prophage genomes in the dataset, and P(x_i) is the numerically obtained steady-state solution. As described in [17], we used the Akaike information criterion (AIC) to determine which parameters should be included in the best-fit solution (see Section S5 in the electronic supplementary material).

To determine the uncertainty associated with each best fit parameter, we used a bootstrapping approach. We analysed 1000 bootstrap samples for each dataset by sampling with replacement to obtain samples of the same size as the original datasets (or the same size plus one when the size was odd) but with half the bootstrap prophage lengths chosen from the fast dataset and half from slow, or half from the pathogen dataset and half from non-pathogen (this condition is necessary because otherwise the vast majority of the bootstrap samples would be, for example, from fast-growing hosts). Each bootstrap sample was then fit to the model that best fit the corresponding true dataset (as described above). This approach allowed us to identify parameters for which the fast dataset, for example, differed significantly from a random sample of the pool of fast and slow datasets.

3. Results and discussion

(a) . Fast-growing hosts and pathogens have a higher fraction of intact prophages

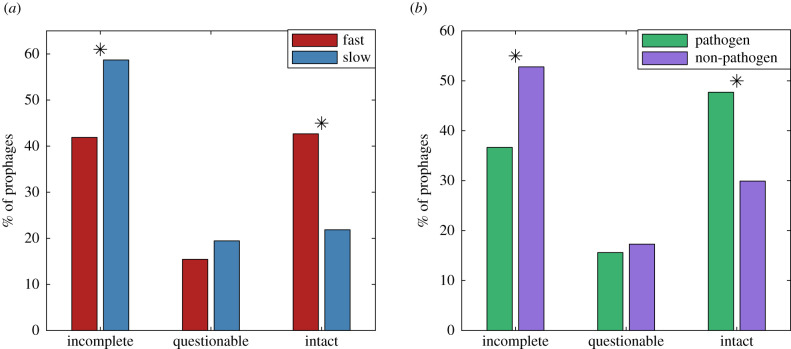
Figure 1 shows the distribution of incomplete, questionable and intact prophages in fast- and slow-growing hosts (a) and in pathogenic and non-pathogenic hosts (b). Bootstrapping to test for significance, we find that fast-growing hosts and pathogens have a higher fraction of intact prophages. In particular, fast-growing hosts have nearly double the frequency of intact prophages as compared to their slow-growing counterparts. This is in contrast to previous expectations; based in part on the observation that cryptic prophages may confer the ability to grow rapidly, [12] suggested that fast-growing bacteria may be more likely to harbour cryptic prophages. This initial finding motivated our more detailed study of the prophage length distribution.

Figure 1.

Percentage of prophages in each PHASTER classification [34] for fast- and slow-growing hosts (a) and pathogenic and non-pathogenic hosts (b). In (a), significance was assessed by drawing 10 000 bootstrapped samples of the same size as the fast and slow datasets from a pooled dataset (fast/slow); in (b), the pooled dataset contained the pathogenic and non-pathogenic data. Stars indicate significant differences between the two host types at the 5% significance level, two-sided test, Bonferroni correction for three comparisons in each case.

(b) . Prophage length distributions are left-skewed for slow-growing hosts and non-pathogens, but bimodal for fast-growing hosts and pathogens

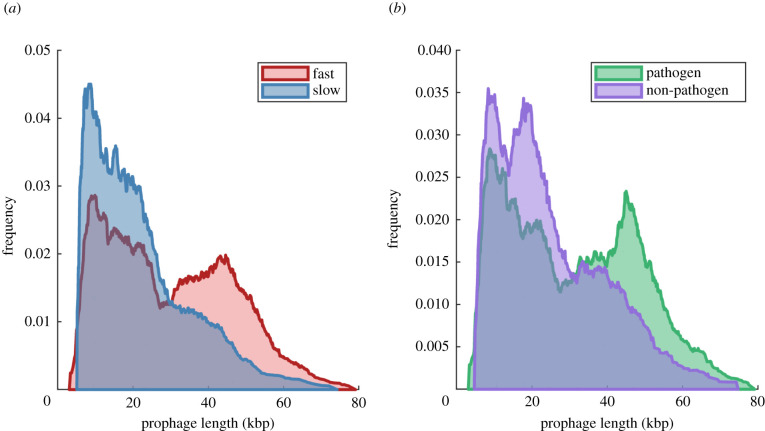
Figure 2 shows the length distributions for prophages in each host class. For fast-growing hosts and pathogens, we see clear bimodal distributions, similar to the prophage length distributions previously reported in E. coli and Salmonella enterica [13], in Desulfovibrio [15] and in Pneumococci [14]. In our dataset, however, prophages identified within slow-growing or non-pathogenic hosts are less clearly bimodal, and show strong positive skewness. Again, this result contrasted our naive expectation that lysogeny (the input of long, active-phage genomes), followed by gradual mutational degradation, would result in a negatively skewed length distribution in prophages. The observed distributions are, however, consistent with our observation that both slow-growing and non-pathogenic hosts carry more incomplete than intact prophages. The length distributions for each host class, stratified for intact, questionable or incomplete prophages, are shown in figure S8 in the electronic supplementary material.

Figure 2.

Length distributions of prophages found in fast- and slow-growing bacterial hosts (a), and pathogenic and non-pathogenic hosts (b). For a dataset of n prophages with lengths x_i, the cumulative distribution function (CDF) is constructed as CDF$(x)=\sum _{x_i<x}1/n$. For visualization, we show here a smoothed estimate of the probability density function, obtained by numerically differentiating this CDF.

The best-fit parameters for each dataset are given in table 2, relative to the rate of degradation, r_D. This normalization is necessary because the steady state solution does not depend independently on the rates but only on the ratio of the rates—α/r_D, r_S/r_D, r_I/r_D and δ/r_D—as shown in equations (2.2) and (2.3). In other words, because we fit the steady-state solution to the data, only four of the five rate constants in the model are identifiable. While in principle we could provide these rates relative to any of the rate parameters in the model, normalizing by the degradation rate has the additional advantage that the rate of degradation, a mutational rate, is not expected to differ between host classes, and as such allows for a more transparent comparison [37].

Table 2.

Parameter values for the best fits for each bacterial class: fast-growing hosts, slow-growing hosts, pathogenic hosts (path.) and non-pathogenic hosts (non-path.). Relative rates have been normalized by the degradation rate, r_D, and are unitless. The parameter n_I gives the estimated number of genes required to initiate the induction process. Dashes indicate parameters that were not included in the model that was the best fit to the data.

parameter		fast	slow	path.	non-path.
α/rD	lysogeny	38.4	10.8	16.2	17.5
rS/rD	selection	6.2	5.6	1.9	5.2
rI/rD	induction	16.8	—	9.5	—
nI	excision genes	3.4	—	4.2	—
δ/rD	turnover	2.3	1.7	1.1	1.9

As shown in table 2, the model that provided the best fit to the slow and non-pathogenic datasets did not include induction; in other words, including this process in the model did not give a statistically significant improvement in the fits to the data. We will discuss this result in greater detail below.

Figure 3 shows the best-fit distributions obtained for the parameters given in table 2. We note that the model was fit to the raw data (871–2477 prophage lengths), not the smoothed histograms that are presented in figures 2 and 3 for visualization only. Parameters defining f(x) are given in table S2 in the electronic supplementary material.

Figure 3.

(a,b) Data and best-fit distributions, P(x), for each of the four classes of hosts. (Online version in colour.)

To assess whether and to what extent best-fit parameter values differed between host classes, we further analysed 1000 bootstrap samples from pooled datasets. Figures S9 through S12 in the electronic supplementary material show examples of bootstrapped samples and their associated best fits. These figures give an intuitive feel for variation induced by sampling and its effect on the best-fit curves. Notably, several of the datasets (most clearly, non-pathogens) have the suggestion of two peaks in the cryptic phage distribution, i.e. separate peaks at 10 kb and 25 kb, which are somewhat robust to sampling. While our model includes multimodel distributions of active prophages (which could capture the impact of phage geometries, for example), none of the processes we include explains a second peak in cryptic prophages. An understanding of whether these apparent peaks are indeed sampling artefacts, or reflect something more interesting about prophages, is a clear avenue for future work.

Figure 4 shows the results of sensitivity analysis, comparing best-fit parameter values from the true data (circles) to the mean and standard deviation observed in fitting bootstrap samples of the pooled data (squares, error bars). After applying the Bonferroni correction for 20 comparisons (p < 0.0025), only the lack of induction in the slow and non-pathogenic datasets retained significance (the rate of induction, r_I/r_D varied substantially in best fits to the pooled data, such that the zero values in the true datasets were not significantly different from the bootstrap results, however fits with n_I = 0 were significantly different). In the paragraphs to follow, we will discuss both this result and two additional results that were not significant after Bonferroni correction: our data suggest that lysogeny may be lower in slow-growing hosts (p < 0.02), and that prophage turnover may be lower in pathogens (p < 0.015).

Figure 4.

Sensitivity analysis: best-fit parameter values in the full datasets (circles) and in 1000 bootstrapped datasets (squares); parameters as indicated on y-axis. Error bars give ±1 s.d. Double stars indicate best-fit parameters that differed from the corresponding bootstrap distribution at the Bonferroni-corrected significance value p < 0.0025. (Online version in colour.)

(c) . Prophages have significantly lower induction rates in slow-growing hosts and non-pathogenic hosts

The models that best described the slow-growing and non-pathogenic datasets did not include induction. This does not imply that prophages in these host classes never induce, but rather that the loss of prophages via induction is negligible compared to other evolutionary processes, and is not statistically justified in fitting the data. This result is not unexpected given the very high frequency of short, and thus presumably non-functional, prophages carried in these host classes.

In our previous investigation of three independent datasets describing bimodal prophage length distributions [17], we predicted that lysogeny maintains the peak corresponding to active prophage lengths, while the balance between positive selection (on genes that benefit the host) and induction maintains the peak at shorter prophage lengths. In particular, the ‘dip’ in these bimodal distributions can be attributed to degraded prophages that are no longer full length, but have retained the handful of genes necessary to instigate the induction process (i.e. to excise from the bacterial genome). By contrast, the results in table 2 suggest that when the prophage length distribution is unimodal and skewed left, both lysogeny and selection still play important roles, but induction is less important in maintaining the prophage distribution.

To put this result in context, recall that ‘slow-growing’ does not necessarily imply a longer generation time on average, but rather refers to bacterial strains with longer minimal doubling times. By contrast, strains with short minimal doubling times are able to grow quickly when resources are plentiful. It is expected therefore that fast-growing hosts are able to thrive in ‘boom or bust’ cycles of growth, whereas slow-growing hosts may experience less variable growth cycles. Pathogens, likewise, presumably experience ‘boom or bust’ cycles as they colonize new hosts, and as mentioned previously there is a high degree of overlap between the pathogen and fast-growing datasets. This suggests that both slow-growing hosts and non-pathogens may experience less variable growth conditions and, in particular, are more rarely in stress. Thus our model prediction—that slow-growing hosts and non-pathogens have substantially lower induction rates—is consistent with the long-standing observation that prophages initiate induction when the host cell experiences stressful conditions [38–41]. In summary, we predict that a unimodal, left-skewed length distribution may be a signature of prophage populations that are maintained in relatively stable host populations, and are therefore less likely to undergo induction.

(d) . Rates of lysogeny may be lower in slow-growing hosts

While not significant, the results of data fitting suggest that the relative rate of lysogeny, α/r_D, may be lower in slow-growing hosts. Previous work has found a strong positive association between minimal doubling times and lysogeny, in particular, slow-growing species carry fewer prophages [30]. In addition, as seen in both figures 1 and 2, the prophages carried by slow-growing hosts are more likely to be incomplete. Our model fitting results suggest that the underlying reason for these differences could be lower rates of lysogeny for phages infecting this host class. The suggestion that the relative rate of lysogeny is lower in slow-growing hosts is therefore consistent with the conclusions of [30], i.e. that a lysogenic strategy may be less favourable to the phage when encountering a host in a more constant environment. Taken together with our results for induction, this suggests a picture in which phages that infect slow-growing hosts are less likely to lysogenize the host, but once they do, induction is likewise rare. Thus slow-growing hosts carry a relatively ‘old’ distribution of prophages, including many cryptic, degraded sequences.

(e) . The rate of turnover of the prophage population may be lower in pathogens

Our results also suggest that the rate of population turnover (mathematically: loss of prophages independent of their length) may be lower in pathogenic bacteria. While not significant, this trend is puzzling, since lower rates of turnover would be associated with mechanisms such as lower death rates in the host species, or lower rates of horizontal gene transfer.

Finally, we returned to the bioinformatics results to assess the gene content of prophages in the four host classes. Figure 5 plots the per cent change in gene frequency in incomplete prophages, when compared with intact prophages, in hosts of the same class, as determined through gene content analysis via PHASTER. Positive values of per cent change thus indicate genes that are preferentially maintained in incomplete prophages, while negative values indicate genes that are preferentially lost; stars indicate significant differences. Although potentially of interest, we did not compare gene frequencies across host classes due to strong potential biases in phage gene identification across different classes of host and phage. We also note that some large per cent changes (e.g. loss of lysins in pathogens) are not significant due to the small absolute numbers of phage genes identified in some classes.

Phage protein annotations in PHASTER and PATRIC showed a high degree of correspondence, as illustrated in figures S6 and S7 in the electronic supplementary material. Averaged over the fast and slow datasets, PHASTER annotations identified 24.7% more phage proteins than PATRIC annotations (9015 versus 7232), and also identified fewer protein sequences as hypothetical, with an average of 8.96 hypothetical protein annotations per prophage in PHASTER, when compared with 14.0 hypothetical proteins per prophage in PATRIC. Bootstrapping analysis of the PATRIC annotations revealed fewer changes in gene frequency that were statistically significant (nine versus eleven), as expected due to the reduced number of annotations in total. Nonetheless, seven of the nine significant changes identified by PATRIC confirmed changes that were also identified as significant using the PHASTER annotations (see section S3 in the electronic supplementary material).

Figure 5 confirms the recent observation that integrase and transposase genes are over-represented in cryptic prophages; possible explanations and further predictions of the effects of transposases are presented in [35].

A number of proteins involved in packaging of progeny phage (portal, terminase, capsid) and lysis proteins are under-represented in cryptic prophages. These changes were significant for fast-growing and pathogenic hosts, while changes for the two smaller datasets were in the same direction, but did not reach significance. Again, this result is consistent with previous observations [35], for datasets describing enterobacteria [13] or phylogenetically diverse bacterial genomes [16].

(f) . In slow-growing hosts, protease and lysis genes are enriched in cryptic prophages

An unexpected result of this study is that both protease genes and genes associated with lysis are enriched in the cryptic prophages found in slow-growing hosts. In other words, as prophage sequences degrade and become cryptic in these hosts, proteases and lysis genes are preferentially maintained while other genes are lost; by contrast, in pathogens or fast-growers, these genes are lost at a higher rate than other phage genes.

This result could reflect sampling or detection biases. As mentioned previously, we excluded from analysis protein classes that accounted for less than 1% of the raw counts for each host class; proteases and lysis genes accounted for 2.14 and 1.35% of counts in slow-growing hosts, and were in fact the smallest protein classes that were included in the analysis. The results could also reflect subtle mutational biases such as ‘deletion shielding’ (genes that are at the borders of prophages or adjacent to selectively beneficial genes may be protected from deletion through selection on adjacent genes) [35]. Alternatively, protease and/or lysis genes could be co-opted and confer some benefit that is particularly advantageous for slow-growing hosts. We suggest that further analysis of prophage gene repertoires in well-studied phage/host systems will be necessary to offer insight into this unexpected observation.

Despite the inescapable limitations of sampling and detection bias in the bioinformatics work, as well as the broad simplifying assumptions that are necessary to mathematical modelling, we believe that the overall qualitative conclusions presented here merit further examination. For example, our work suggests that prophages are common in fast-growing hosts due to higher rates of lysogeny, relative to their slow-growing counterparts. By contrast, prophages may be more common in pathogens due to lower rates of population turnover. It is our hope that these novel observations and predictions will enrich our understanding of the intricate and sometimes baffling relationship between temperate phages and their hosts.

Data accessibility

Data are available from the Dryad Digital Repository: https://doi.org/10.5061/dryad.fn2z34tt2 [42].

Authors' contributions

T.P. and C.E. collated and developed the initial model fits. L.M.W. completed the model fits. T.P. and L.M.W. developed and wrote the manuscript.

Competing interests

We declare that we have no competing interests.

Funding

The Natural Sciences and Engineering Research Council of Canada is gratefully acknowledged for funding.