Abstract
As the national reference laboratory for febrile illness in Madagascar, we processed samples from the first epidemic wave of COVID-19, between March and September 2020. We fit generalized additive models to cycle threshold (Ct) value data from our RT-qPCR platform, demonstrating a peak in high viral load, low-Ct value infections temporally coincident with peak epidemic growth rates estimated in real time from publicly-reported incidence data and retrospectively from our own laboratory testing data across three administrative regions. We additionally demonstrate a statistically significant effect of duration of time since infection onset on Ct value, suggesting that Ct value can be used as a biomarker of the stage at which an individual is sampled in the course of an infection trajectory. As an extension, the population-level Ct distribution at a given timepoint can be used to estimate population-level epidemiological dynamics. We illustrate this concept by adopting a recently-developed, nested modeling approach, embedding a within-host viral kinetics model within a population-level Susceptible-Exposed-Infectious-Recovered (SEIR) framework, to mechanistically estimate epidemic growth rates from cross-sectional Ct distributions across three regions in Madagascar. We find that Ct-derived epidemic growth estimates slightly precede those derived from incidence data across the first epidemic wave, suggesting delays in surveillance and case reporting. Our findings indicate that public reporting of Ct values could offer an important resource for epidemiological inference in low surveillance settings, enabling forecasts of impending incidence peaks in regions with limited case reporting.
Keywords: COVID-19, LMIC, Madagascar, Africa, Cycle threshold value, Cross-sectional data
1. Introduction
Madagascar reported its first case of coronavirus disease 2019 (COVID-19) on 19 March 2020, in part with a government-sponsored surveillance platform testing all incoming international travelers (Randremanana et al., 2021). Subsequent to this introduction, the first wave of the COVID-19 epidemic was geographically staggered, with early cases in May 2020 largely concentrated in the eastern city of Toamasina, part of the Atsinanana administrative region, followed by a more severe outbreak which peaked in July 2020 in the capital city of Antananarivo, part of the Analamanga administrative region. Test positive rates exceeded 50% at the epidemic peak for both regions and at the national level, indicating widespread underreporting (Chitwood et al., 2020), a common feature of COVID-19, for which some 20–40% of infections are thought to be entirely asymptomatic (Oran and Topol, 2020, Mizumoto et al., 2020, Nishiura et al., 2020, Treibel et al., 2020). Early reporting on the first epidemic wave in Madagascar indicated an extremely high (56.6%) proportion of asymptomatic cases, based on targeted surveillance of symptomatic patients and their contacts (Randremanana et al., 2021).
Madagascar closed its borders to international air travel on 20 March 2020 and, subsequent to identification of the first case, implemented several non-pharmaceutical interventions aimed at curbing epidemic spread, including non-essential business closures, curfews, stay-at-home orders, and mandates for social distancing. These restrictions were relaxed after the first epidemic subsided in September 2020 but have since been re-implemented in the face of a second epidemic wave. In other regions of the globe, widespread efforts to estimate the effective reproduction number, R t, for COVID-19 at national, regional, and local levels (Abbott et al., 2020b) have been used to inform public health interventions and retrospectively assess their effectiveness (Gostic et al., 2020): disease transmission rates are increasing at R t > 1 and decreasing at R t < 1. Estimation of R t, or its related counterpart, r, the epidemic growth rate (Wallinga and Lipsitch, 2007, Park et al., 2020), from available case count data is challenged by limitations or variability in surveillance, uncertainty surrounding the shape of disease parameter distributions, and delays in reporting (Gostic et al., 2020). Despite the enormity of these challenges in the limited surveillance settings common to many lower- and middle-income countries (LMICs), real-time estimation of R t from COVID-19 case-counts has been attempted for most regions of the globe (Abbott et al., 2020b) and has been implemented locally in Madagascar (Rasambainarivo et al., 2020, Raherinirina et al., 2021b, Raherinirina et al., 2021a, Narison and Maltezos, 2021).
Recent methodological advances have introduced a new resource to the epidemiological toolkit by which to conduct real time estimation of epidemic trajectories (Hay et al., 2021), one that leverages the often-discarded cycle threshold, or Ct, value, that is returned as an-inverse log-10 measure of viral load from all RT-qPCR-based platforms (Tom and Mina, 2020). After observing that SARS-CoV-2 viral loads—and, as a consequence RT-qPCR Ct values—demonstrate a predictable trajectory following the onset of infection (Chen and Li, 2020, Jacot et al., 2020, Borremans et al., 2020), Hay et al., 2021 showed that the Ct value can be used as a biomarker of time since infection and, consequently, be leveraged to back-calculate infection incidence, in a manner analogous to previous work leveraging serological titer information in other systems (Borremans et al., 2016, Hay et al., 2020, Salje et al., 2018). Probabilistically, a randomly-selected infection is more likely to be early in its infection trajectory when identified during a growing epidemic and later in its trajectory in a declining epidemic (Rydevik et al., 2016, Wallinga and Lipsitch, 2007), and as a consequence, the population-level distribution of Ct values for any viral infection is expected to shift across the duration of an epidemic. Indeed, low-Ct-high-viral-load infections have been observed to coincide with growing COVID-19 epidemics and high-Ct-low-viral-load infections with declining epidemics in several settings (Jacot et al., 2020, Moraz et al., 2020, Walker et al., 2020). Exploiting this phenomenon, Hay et al. developed a method that embeds a within-host, viral kinetics model in a population-level disease transmission model to derive epidemic trajectories from cross-sectional Ct samples. Because this method depends on quantitative information captured in the biological sample itself, rather than the relationship between case count and reporting date, Ct value estimation more accurately predicts true epidemic trajectories than traditional incidence estimation in settings with uneven surveillance (Hay et al., 2021).
During the early phase of the COVID-19 epidemic in Madagascar, the Virology Unit laboratory (National Influenza Centre) at the Institut Pasteur of Madagascar (IPM) processed the majority of all SARS-CoV-2 testing samples derived from 114 districts across 6 major provinces in the country. Consistent with findings reported elsewhere (Jacot et al., 2020, Moraz et al., 2020, Walker et al., 2020), we observed a population-level decline in Ct values derived from RT-qPCR-testing in our laboratory, coincident with the epidemic peak across the first wave of COVID-19 in Madagascar. We here adopt the methods presented by Hay et al. (2021) to estimate COVID-19 epidemic growth rates at the national level (2018 population ~ 26 million (INSTAT Madagascar., 2018)) and in two major administrative regions of Madagascar: Atsinanana (east coast of Madagascar; 2018 population ~ 1.5 million (INSTAT Madagascar., 2018)) and Analamanga (including Antananarivo, capital city; 2018 population ~ 3.6 million (INSTAT Madagascar., 2018)). We evaluate the robustness of this Ct-based method in comparison with epidemic growth rates derived from more traditional case-count methods applied to the same regions and at the national level. Atsinanana and Analamanga comprised the geographic epicenter of the first COVID-19 wave in Madagascar but also the source of the majority of samples sent for testing. Given that vast majority of testing resources across the duration of the Madagascar pandemic have been concentrated in Antananarivo (Rakotonanahary et al., 2021), ‘national’ reported trends may belie temporally lagged disease dynamics in more rural regions of the country. We advocate for more widespread Ct reporting from rural areas, as our analysis indicates that Ct-based Rt estimation could be a particularly robust method of inferring epidemiological trajectories in low-surveillance settings.
2. Materials and methods
2.1. IPM SARS-CoV-2 Ct data
Methods for collection, transport, and processing of SARS-CoV-2 testing samples at IPM have been previously described (Randremanana et al., 2021). Briefly, nasopharyngeal and oropharyngeal swabs were collected at local administrative hospitals in viral transport medium and transported at 4 oC to our laboratory for testing. Between 18 March and 30 September 2020, we conducted 34,563 RT-qPCR tests targeting the E, N, Orf1a/b, or S gene of SARS-CoV-2. These tests were carried out across 20,326 discrete samples (many of which were tested across multiple platforms targeting multiple genes), and 17,499 discrete patients, a subset of whom were tested at multiple timepoints. Earlier in March 2020, the Madagascar Ministry of Public Health screened all travelers entering the country in an effort to prevent the introduction of COVID-19 to Madagascar (Randremanana et al., 2021). Despite these efforts, the first infection with SARS-CoV-2 was first confirmed in Madagascar on 19 March 2020, after which testing efforts were refocused to screen contacts of confirmed cases, as well as any patients reporting to clinics or hospitals with symptoms aligned with pre-existing surveillance systems for influenza-like illness (ILI) and severe acute respiratory infection (SARI), following guidelines from WHO (WHO, 2020). IPM has processed samples from ILI and SARI surveillance platforms in Madagascar for over a decade; in April 2020, we added SARS-CoV-2 to the routine screening of incoming specimens (Randremanana et al., 2021, Rakotoarisoa et al., 2017, Guillebaud et al., 2018).
Due to a dearth of available reagents in the early stages of the epidemic, our lab used seven different WHO-recommended kits and corresponding protocols (The World Health Organization (WHO), 2020) to assay infection in these samples (Randremanana et al., 2021): Charity Berlin (Corman et al., 2020), Hong Kong University (Chu et al., 2020), Da An gene (Da An Gene Co., Ltd. Sun Yatsen University, Guangzhou, China), LightMix® SarbeCoV E-gene plus EAV control (TIB Biolmol, Berlin, Germany), SarbeCoV TibMolBiol (TIB Biolmol, Berlin, Germany), TaqPath™ COVID- 19 Combo kit (Life Technologies Ltd, Paisley, UK), and GeneXpert (Cepheid, Sunnyvale, CA, USA).
Some 9493 of those tests, corresponding to 5310 individuals, were RT-qPCR positive for SARS-CoV-2 infection based on the cut-off positive value for the test in question (Charity Berlin: <= 38; Hong Kong: <= 40; Da An: <= 40; LightMix SarbeCoV/SarbeCoV TibMolBiol <= 38; TaqPath <= 37 for 2 of 3 targets; GeneXpert :<= 40). All analyses presented in this paper are derived from these positive test results, as Ct-values were not reliably recorded following negative results. We further subset our data as appropriate for each analysis of interest.
2.2. Estimating growth rates from IPM case data
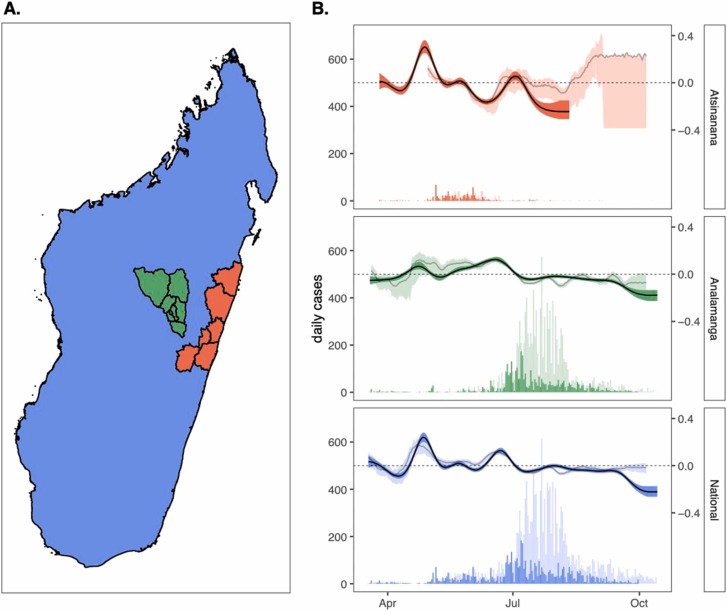
We first sought to obtain an estimate of new daily cases reported from our laboratory to the Malagasy government between 18 March and 30 September 2020. To this end, we reduced our dataset to include only sampling from the first reported positive test date for each unique patient; we assumed that reinfection was unlikely within the short duration of our study and that any subsequent positive tests were reflective of longer-duration infections in repeatedly sampled individuals. A patient was considered “positive” for SARS-CoV-2 infection if any test for any SARS-CoV-2 target was positive, and the results of the other samples were not inconsistent with this finding. We then summed cases by date at the national level and for two administrative regions (Atsinanana and Analamanga) that reported the majority of total cases across the study period overall. In total, 5276 cases were reported from our laboratory across the study period at the national level, 3505 in Analamanga region and 758 in Atsinanana. Daily cases for the two target regions and for the nation at large are summarized in Fig. 1.
Fig. 1.
Epidemic growth rate estimates from case count data across the first wave of COVID-19 in Madagascar. (A.) Map of Madagascar, colored by regions of case count tabulation, showing the Atsinanana region (orange), the Analamanga region (green), and the National region (blue); note that data analyzed at the National level includes data from both Atsinanana and Analamanga regions, as well as the rest of Madagascar. (B.) Time series of new case incidence lefthand y-axis) across the first wave of COVID-19 in Madagascar (18 March – 30 September 2020), across three focal regions. Darker shading shows data derived from the IPM RT-qPCR platform, while lighter shading depicts data nationally reported and consolidated on (Rasambainarivo et al., 2020). Righthand y-axis shows corresponding epidemic growth rate computed from case count data in EpiNow2 (Abbott et al., 2020a), with darker line corresponding to computation from IPM data and lighter line to computation from publicly reported data; background shading around each line depicts the corresponding 50% quantile by EpiNow2 (Abbott et al., 2020a). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
We applied the opensource R-package EpiNow2 (Abbott et al., 2020a) to the daily incidence data to estimate the epidemic growth rate for COVID-19 across the study period. EpiNow2 builds on previous R t estimation packages (Cori et al., 2013), using a non-stationary Gaussian process model to estimate the instantaneous time-varying reproduction number, R t, and the corresponding time-varying epidemic growth rate, r, while incorporating uncertainty in the generation interval. Following best recommended practices (Gostic et al., 2020), we modeled the SARS-CoV-2 incubation period as a log-normal distribution with a mean of 1.621 days (sd = 0.064) and a standard deviation of 0.418 days (sd = 0.061) (Lauer et al., 2020) and the generation time interval as a gamma distribution with a mean of 3.635 (sd = 0.71) and a standard deviation of 3.075 (0.77) (Ganyani et al., 2020). Since the IPM testing data reported the actual date of sample collection, no reporting delay was incorporated in our growth rate estimation.
2.3. Epidemic trajectories from publicly reported data
To compare our laboratory-derived epidemic growth estimates with those undertaken in real time in Madagascar, we collaborated with colleagues who recorded data on the number of new PCR-confirmed cases reported daily on national television by the Ministry of Health of the Government of Madagascar across the duration of the first epidemic wave. From these daily case estimates, we used the EpiNow2 package (Abbott et al., 2020a) to again estimate the epidemic growth rate across the same study period, assuming the same incubation period and general time interval referenced above (Lauer et al., 2020, Ganyani et al., 2020). For these estimates, we followed methods outlined in (Abbott et al., 2021), to additionally model a reporting delay from a log-normal distribution fit to 100 subsamples with 1000 bootstraps from a publicly available linelist that collates data globally for COVID-19 cases for which both infection onset and notification dates are available (Xu et al., 2020).
2.4. Standardizing Ct values across tests and targets
In our next series of analyses, we leveraged information captured in the individual Ct value returned from each positive test. To control for extensive variation in qPCR test and target (each of which reported varying thresholds for positivity), we carried out in vitro experiments using SARS-CoV-2 isolates from infected patients reporting similar Ct values on the TaqPath platform at the time of sampling. Briefly, three SARS-CoV-2 isolates (designated hCoV-19/Madagascar/IPM-00754/2021, hCoV-19/Madagascar/IPM-01263/2021 and hCoV-19/Madagascar/IPM-01315/2021) were obtained and cultured in Vero cells as previously described (Auerswald et al., 2021). Upon infection with SARS-CoV-2, the culture medium was replaced by infection medium containing DMEM, 5% FBS, antibiotics, 2.5 μg/ml Amphotericin B (Gibco) and 16 μg/ml TPCK-trypsin (Gibco). Virus-containing supernatants, as determined by the presence of cytopathic effect (CPE), were harvested 7 days after infection by centrifugation at 1500 r.p.m. for 10 min. RNA was subsequently extracted from supernatant and subjected to serial dilutions and subsequent testing on six of the seven RT-qPCR platforms used in our population-level dataset (LightMix SarbeCoV and SarbeCoV TibMolBiol were considered equivalent and tested only using the current version of the kit: SarbeCoV TibMolBiol). We fit linear mixed effect regression models in the lme4 (Bates et al., 2015) package in R to the resulting Ct curves returned from each testing platform across the dilution series and used the fitted slope and y-intercept of each regression equation to reproject all Ct values in our dataset to correspond to results returned from the TaqPath N gene test. We report, analyze, and visualize these TaqPath N-corrected Ct values in all analyses. We selected the TaqPath N gene Ct as the basis for reporting because our laboratory adopted the TaqPath assay for exclusive use after supply chains stabilized nine months into the pandemic; of the three targets returned from the TaqPath assay, the N-gene is the most common target across other SARS-CoV-2 diagnostic platforms (Kubina and Dziedzic, 2020).
2.5. Generalized additive modeling of the longitudinal Ct distribution by region
After observing a population-level dip in the average Ct value recovered from our testing platform, roughly coincident with the epidemic peak in the three regions of interest, we asked the broad question, what is the population level time-trend of SARS-CoV-2 C t values across these three regions? To address this question, we compiled all positive tests from the first date of positive testing for each patient, recording the date, region, test, and target that corresponded to each corrected Ct value, in addition to the numerical ID and the symptom status (asymptomatic, symptomatic, or unknown) of the patient from which it was derived. Symptom statuses were recorded by medical staff at the timepoint of sampling and merely indicated whether or not the patient presented with symptoms; thus, ‘asymptomatic’ classification did exclude the possibility that the same patient reported symptoms at later or earlier timepoints across the course of infection. The resulting data consisted of 8055 discrete Ct values, corresponding to 5280 patients, most of whom were tested using multiple tests and/or gene targets of interest. Ct values for these positive test results ranged from 6.36 to 39.91. When reprojected to TaqPath N levels, the range shifted from 7.82 to 39.99, such that 507Ct values classed as “positive” by the cutoff thresholds on other platforms exceeded the Ct <= 37 threshold for positivity on the TaqPath platform. These samples were nonetheless retained for generalized additive modeling (GAM) of longitudinal Ct trends but GAM-projected Ct values still exceeding the TaqPath cutoff were later excluded in mechanistic modeling of transmission trends fitted to positive data.
Using the mgcv package (Wood, 2001) in the R statistical program, we next fit a GAM in the gaussian family to the response variable of corrected Ct value, incorporating a numerical thinplate smoothing predictor of date, and random effects on the categorical variables of test (Charity Berlin, Hong Kong, Da An, LightMix SarbeCoV, SarbeCoV TibMolBio, TaqPath, or GeneXpert), target (E,N,Orf1a/b, or S), and individual patient ID. We refit the model to three different subsets of the data, encompassing the Atsinanana and Analamanga regions, as well as the entire National data as a whole. We then used the resulting fitted GAMs to simulate population-level Ct distributions for each date in our dataset, excluding the effects of test and target in the predict.gam function from mgcv. This produced a test- and target-controlled average Ct estimate for each positive patient at the timepoint of sampling. We used these GAM-simulated Ct distributions to carry out mechanistic model fitting in subsequent analyses, as described below, excluding 15 patients with Ct projections > 37, which exceeded the positive threshold for the TaqPath N gene assay.
2.6. Generalized additive modeling of Ct value since time of infection onset
To validate observations from the literature which indicate that the viral load and corresponding Ct value follow a predictable trajectory after the onset of SARS-CoV-2 infection (Chen and Li, 2020, Jacot et al., 2020) within our own study system, we next concentrated analyses on a subset of 4822 Ct values (corresponding to 2842 unique samples derived from 2404 unique patients), for which the timing of symptom onset was also recorded. For each of these samples, we randomly drew a corresponding incubation time from the literature-derived log-normal distribution above (Lauer et al., 2020) to approximate the timing of infection onset. To answer the question, how does C t vary with time since symptom onset?, we fit a GAM in the gaussian family to the resulting data with a response variable of Ct and a numerical thinplate smoothing predictor of days since infection onset, as well as random effects of test, target, and patient ID. After fitting, we used the predict.gam function from the mgcv package, excluding the effects of target and test, to produce a distribution of Ct values corresponding to times since symptom onset (one per each unique patient ID). We used these Ct trajectories to estimate parameters for the within-host viral kinetics model described in final methods section below.
2.7. Generalized additive modeling of the relationship between Ct value and symptom status
We next asked the question, does C t value vary in symptomatic vs. asymptomatic cases?
Our first investigation of this question required only reconsideration of the individual trajectory GAM described above to include additional predictor variables of age and symptom status, in addition to days since infection onset, target, and test. Since symptom status was recorded only at the first timepoint of sampling for each individual, we limited our individual trajectory dataset to a 4072 datapoint subset of Ct values from 2404 discrete patients reporting both date of symptom/infection onset and symptom status at the timepoint of sampling; as mentioned previously, ‘asymptomatic’ classification in our dataset included patients reporting symptoms from earlier or later timepoints prior to or following the sampling date. Thus, this GAM tested whether symptom status and Ct value interacted merely as a function of the timing since symptom onset (e.g. high Ct values were recovered from patients either very early or late in their infection trajectory), or whether independent interactions between symptomatic vs. asymptomatic infections and Ct were also present, while also controlling for age.
After observing results, we extended this analysis by applying another GAM in the gaussian family to a 7937 datapoint subset of the data used to model longitudinal Ct trajectories at the National level, which additionally reported symptom status (symptomatic vs. asymptomatic) at the timepoint of first sampling for 5202 unique patients. Corrected Ct values in this data subset ranged between 7.82 and 39.99. This GAM incorporated a response variable of Ct and random effects predictor smoothing terms of symptom status, test, target, and patient ID, as well as a numerical smoothing predictor for age of the infected patient.
2.8. Estimating epidemic growth rates from cross-sectional Ct values
Finally, following newly-developed methods (Hay et al., 2021), we sought to estimate the epidemic growth rate across our three regions of interest using cross-sectional Ct distributions and compare these results against estimates derived from the case count methods described above. In their original paper, Hay et al. (2021) applied two population-level models (a Susceptible-Exposed-Infectious-Recovered [SEIR] model and a more flexible Gaussian process [GP] model) to a time-series of infected cases from the Brigham and Women’s Hospital, Boston, MA, each reporting a quantitative estimate of viral load by Ct value. Rather than assuming all infectious (“I” class) individuals contributed equally to onward transmission, as is standard in compartmental modeling, Hay et al. (2021) nested a separate within-host viral kinetics model describing the mean trajectory a SARS-CoV-2-infected patient’s viral load (as indicated by Ct-value) across the timecourse of infection within their infectious (I) class. By fitting this within-host model to the quantitative data encapsulated in a Ct-value datapoint, the authors were able to back-infer the duration of time since the original infection occurred and the trajectory of viral load-dependent infectiousness for each positive patient, allowing for accurate estimation of epidemic trajectories independent of delays and biases in reporting (Hay et al., 2021).
To this end, we adopted the method developed in Hay et al. (2021), first fitting the within-host viral kinetics model to the test- and target-controlled Ct values produced from the above GAM describing Ct as a function of time since infection. We used the resulting parameter estimates as informed priors (Table S1) which we next incorporated into the same two population-level SARS-CoV-2 transmission models defined by Hay et al (2021), here applied to our time series data across the three Madagascar regions: a compartmental SEIR model and a GP model, which makes no assumptions about the specific mechanisms underlying an epidemic trajectory beyond the correlation of cases from one timestep to the next. Given uncertainty in the epidemiology underlying COVID-19 dynamics in Madagascar and other parts of Africa (Evans et al., 2020), we anticipated that the GP model would offer the most flexible fit to the data. Beyond the viral kinetics parameters, we adopted less-constrained priors from the original paper (Hay et al., 2021) for other epidemiological parameters included in both population-level models (Table S1), then re-fit both transmission models in turn to cross-sectional weekly Ct distributions derived from the Atsinanana, Analamanga, and National-level datasets. We fit both models to each dataset using an MCMC algorithm derived from lazymcmc R-package (Hay, 2020), as described in the original paper (Hay et al., 2021), applying the default algorithm to the GP fit and a parallel tempering algorithm able to accurately parse multimodal posterior distributions to the SEIR fit. Four MCMC chains were run for 500,000 iterations in the case of the GP model and three MCMC chains for 80,000 iterations each in the case of the SEIR model, then evaluated for convergence via manual inspection of the resulting trace plots and verification that, the potential scale reduction factor, had a value < 1.1 and the effective population size had a value > 200 for all parameters estimated.
After confirming chain convergence, we computed epidemic growth rates from the resulting estimated infection time series and compared results with those derived using more traditional case count methods outlined above. Code and supporting datasets needed to reproduce all analyses are available for download on our opensource GitHub repository at: github.com/carabrook/Mada-Ct-Distribute.
3. Results
3.1. Epidemic trajectories from case count data
The first wave of COVID-19 infections in Madagascar, between March and September 2020, was characterized by two subsequent outbreaks: one early, May 2020 peak centered in the eastern port city of Toamasina (region Atsinanana), followed by a second peak in July centered in the capital city of Antananarivo (region Analamanga) (Fig. 1) (Randremanana et al., 2021). Estimation of the epidemic growth rate showed broad agreement in trends at both the national and regional levels, whether computed from IPM testing data assuming perfect reporting of testing date, or from publicly reported national data, including a reporting delay parameterized from a global opensource database (Fig. 1) (Xu et al., 2020). Since IPM data comprised just over 30% of nationally reported data throughout the first six months of the Madagascar epidemic, this concurrence in growth rates was unsurprising but nonetheless validates the applicability of the globally parameterized reporting delay for use in Madagascar. In both datasets, we estimated the national level epidemic growth rate to be increasing in the months preceding the two epidemic sub-peaks (in April and in June) and declining beginning in mid-July after the last peak in national case counts (Fig. 1). When IPM data were considered at the regional level, we discovered the April peak to be concentrated in Atsinanana, preceding the Toamasina outbreak and the June peak to be concentrated in Analamanga preceding the Antananarivo outbreak. Growth rate estimation from publicly reported data confirmed this pattern for Analamanga but was not possible for the Atsinanana region due to a lack of clarity in regional reporting; indeed, nearly 70% of nationally reported data in the public dataset were derived from the Analamanga region.
3.2. Standardizing Ct values across tests and targets
All RT-qPCR platforms used in our laboratory demonstrated increases in Ct value corresponding to 10-fold dilutions of RNA extracted from the original virus isolate (Table S2), though the estimated slope and y-intercept of each regression varied across the tests and targets considered, with the steepest slope recovered from GeneXpert N-gene tests and the shallowest from the Hong Kong ORF1a/b kits (Fig. S1, Table S3). We used the corresponding slope and y-intercept for each test and platform to transform Ct values in all subsequent analyses into values predicted for a TaqPath N-gene platform.
3.3. Longitudinal population-level trends in SARS-CoV-2 Ct values across the epidemic wave
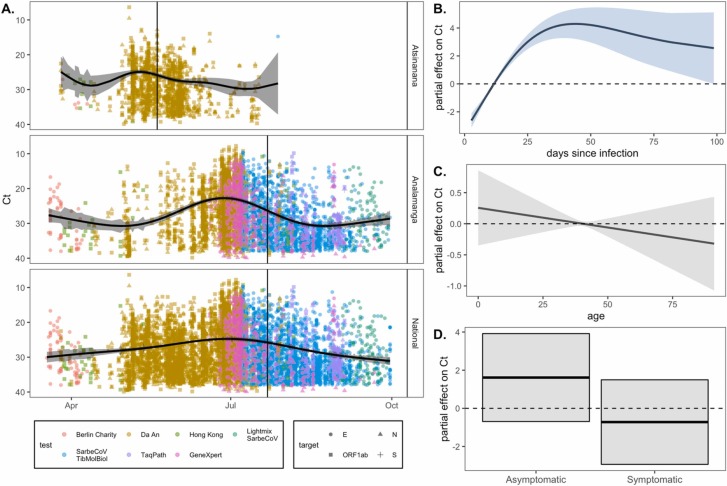
We observed a population-level dip in Ct values obtained from our SARS-CoV-2 RT-qPCR platform concurrent with the regional peak in cases in May for Atsinanana and June for Analamanga, with both peaks observable in the National data ( Fig. 2A). GAMs fit to Atsinanana, Analamanga, and National data subsets explained, respectively, 98.8%, 98.9%, and 98.9% of the deviation in the data (Table S4). All three GAMs demonstrated statistically significant effects of date, test, and individual patient ID, which contributed to the total deviance capture by each model. GAMs fit to the Analamanga and National data subsets showed an additional significant effect of target on the Ct value. Partial effects plots were computed from the resulting GAMs (Fig. S2) following methods described in (Mollentze and Streicker, 2020) and demonstrated no significant effects of any particular test or target gene. In general, most variation in Ct value beyond that of the individual patient was driven by the significant effect of date across all regions (Table S4).
Fig. 2.
RT-qPCR SARS-CoV-2 Ct value as a biomarker of population-level epidemic pace and individual infection trajectory. (A.) Population-level SARS-CoV-2 corrected Ct values from IPM RT-qPCR platform across three Madagascar regions from March-September 2020. Ct values are colored by the test and shaped by the target from which they were derived (legend), though note that all Ct values were first corrected to TaqPath N gene range. The vertical, black line gives the date of peak case counts per region in the IPM dataset, from which these Ct values were derived (May 20, 2020 for Atsinanana and July 22, 2020 for both Analamanga and National). The black, horizontal curve gives the output from a gaussian GAM fit to these data (Table S4), excluding the effects of target and test, which were also included as predictors in the model; 95% confidence intervals by standard error are shown in translucent shading. Partial effects of each predictor are visualized in Fig. S2. Righthand plots visualize partial effects of (B.) days since infection, (C.) patient age, and (D.) patient symptom status on Ct value from our individual trajectory GAM (Table S5). Significant predictors are depicted in light blue and non-significant in gray (Table S5). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
3.4. Individual trends in SARS-CoV-2 Ct values across the trajectory of infection
The SARS-CoV-2 Ct value also demonstrated a predictable trajectory from the timing of onset of infection. Our GAM fit to data reporting a date of symptom onset (which we converted to a date of infection onset) and incorporating a predictor smoothing term of days since infection onset, and random effects of test, target, and patient ID explained 92.7% of the deviance in the data and demonstrated statistically significant effects of all predictor variables, including days since infection onset (Table S5). These findings confirmed that Ct value can be used as a biomarker of time since infection, validating the applicability of methods outlined in (Hay et al., 2021) for our Madagascar data.
3.5. Relationship between symptom status and SARS-CoV-2 Ct value
As an extension of the individual trajectory analysis, we hypothesized that Ct value would likely be linked to symptom status, since many infection trajectories begin with a brief presymptomatic phase, progress to symptom presentation, then become asymptomatic during recovery (Chen and Li, 2020, Jacot et al., 2020). The first GAM we employed to address this question considered age and symptom status as additional predictor variables in our individual trajectory analysis. This final GAM explained 98.5% of the deviation in the data and included significant effects of days since infection onset, symptom status, test, target, and patient ID (Table S5). Despite the significance of symptom status as a predictor variable in the GAM overall, partial effects plots demonstrated no significant association between asymptomatic status and high Ct values or symptomatic status and low Ct values, while controlling for age (Fig. 2B–D). These results suggest that, in our dataset, Ct value varies predictably with an individual’s infection trajectory regardless of symptom classification or age of the patient, further validating its adoption as a robust biomarker of time since infection (Table S5).
We additionally extended this analysis to our National-level Ct dataset, including a predictor variable of symptom status, in addition to test, target, patient age, and patient ID in longitudinal GAMs. This model explained 98.9% of the deviation witnessed in the data, including significant effects of test, target, patient ID, and symptom status (Table S6). Test and target were here included as control variates only and cannot be considered for prediction, as both co-varied with date, which was not used as a predictor in this model. In this model, partial effects plots indicated a significant association of asymptomatic status with high Ct values and symptomatic status with low Ct values (Fig. S3), even when controlling for effects of age; as this larger dataset did not report date of symptom/infection onset, it is likely that this association co-varied with the timing of infection onset, suggesting that previous reports of a high proportion of asymptomatic infections in Madagascar (Randremanana et al., 2021) could reflect a high proportion of pre- or post-symptomatic infections.
3.6. Epidemiological dynamics inferred from cross-sectional Ct distributions
After confirming the predictable pattern of Ct value across an individual’s infection trajectory, and the predictable decline in population-level Ct in conjunction with the epidemic peak, we used our individual trajectory GAM to simulate a distribution of Ct values across a 50-day duration of infection and fit the within-host viral kinetics model described in (Hay et al., 2021) to the resulting data (Fig. S4). The model demonstrated a good fit to the data, and estimated posterior distributions for viral kinetics parameters were largely on par with those used previously in models of SARS-CoV-2 dynamics in Massachusetts, though the modal Ct value at peak viral load was slightly lower in our Madagascar dataset (Fig S4; Table S1).
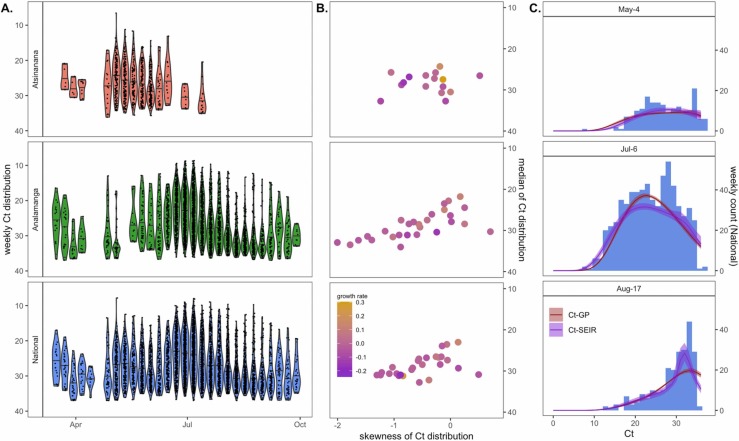
After fitting the within-host model, we next used longitudinal population-level GAMs (Fig. S2) to generate weekly cross-sectional Ct distributions, controlled for test and target, across our three regions of interest. As expected, weekly cross-sectional Ct distributions demonstrated a shift across the duration of the epidemic wave; with lower Ct values temporally correlated with high growth rates estimated from case count data ( Fig. 3).
Fig. 3.
Population-level Ct distribution reflects epidemic dynamics of the first wave of COVID-19 across three Madagascar regions. (A.) Simulated weekly Ct distributions by Madagascar region, derived from population-level longitudinal GAMs (Fig. 2A), excluding random effects of test and target. (B.) Higher skew and lower median Ct from each cross-sectional Ct distribution in (A.) were loosely associated with higher epidemic growth rates from the corresponding week, here derived from EpiNow2 estimation from IPM case count data (Fig. 1B.) (C.) Cross-sectional Ct distributions from Analamanga time series in (A.) were fit via Gaussian process (GP) and SEIR mechanistic models incorporating a within-host viral kinetics model. Modeled Ct distributions are shown as solid lines (GP = red; SEIR = purple), with 95% quantiles in surrounding sheer shading. Both models effectively recapture the shape of the Ct histogram as it changes (skews left) across the duration of the first epidemic wave. Model fits to the full time series of Ct histograms across all three regions are visualized in Figs. S7–S9. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
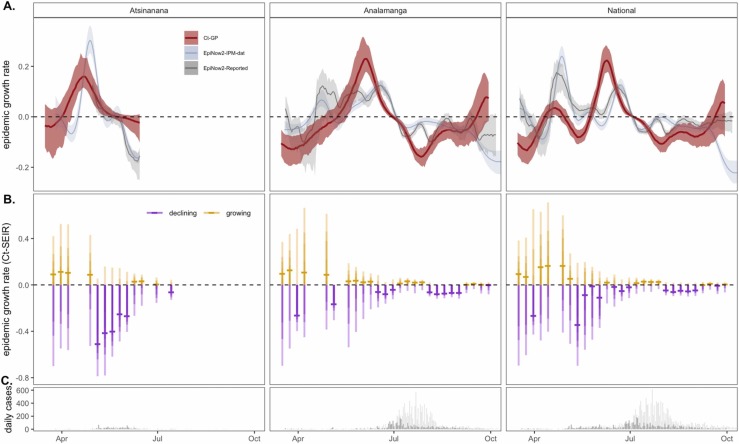
Finally, we used the viral kinetics posterior distributions resulting from the within-host viral kinetics model fit as prior inputs into SEIR and GP population-level epidemiological models, which we fit to the weekly cross-sectional Ct data. MCMC chains generated in the fitting process demonstrated good convergence (Fig. S5, Tables S7 and S8) and produced posterior distributions for all parameters on par with those estimated in previous work (Table S1, Fig. S6), which effectively recaptured cross-sectional Ct value histograms across the target timeseries in all three regions (Figs. 3, S7–S9) (Hay et al., 2021). From the resulting fitted models, we simulated epidemic incidence curves, which we used to compute growth rate estimates across the duration of the first epidemic wave in each of the three regions ( Fig. 4). We compared these estimates to growth rates inferred from case count data; patterns from both SEIR and GP models were largely complementary, though, as expected, the more flexible GP model demonstrated less extreme variation in epidemic growth rate. Both Ct-model fits demonstrated similar patterns to epidemic trajectories estimated from incidence data, with increasing growth rates in the months preceding both epidemic sub-peaks (April and June) and decreasing growth rates beginning in July. Nonetheless, growth rate estimates derived from the Ct model slightly preceded those estimated from case count data. The Ct model fits further predicted uncertainty in growth rate directionality towards the end of the study period for the Analamanga and National-level data, while incidence estimation projected decreasing cases at this time. This finding suggests that cross-sectional Ct distributions indicated a possible epidemic resurgence which was overlooked by growth rates estimated from declining incidence. If incidence declined in part due to declining surveillance, as was the reality at the end of Madagascar’s first epidemic wave (Randremanana et al., 2021), only the Ct method remained robust to the possibility of epidemic renewal.
Fig. 4.
Epidemic growth rate estimates from mechanistic model fits to population-level Ct distributions across the first wave of COVID-19 in three Madagascar regions. (A.) Comparison of COVID-19 epidemic growth rates from March-September 2020, estimated from IPM (blue) and publicly reported (gray) case count data using EpiNow2 (Abbott et al., 2020a) with estimates derived from Gaussian process (GP; red) mechanistic model fit to the time series of Ct distributions (Fig. 3A). Median growth rates are shown as solid lines, with 50% quantile on case-based estimates and 95% quantile of the posterior distributions from Ct-based estimates in corresponding sheer shading. (B.) Growth rate estimates from individual SEIR Ct-model fits to each Ct-distribution shown in Fig. 3A; median growth rates are given as horizontal dashes, with the 95%, 70%, 50%, and 20% of the posterior distribution indicated by progressively darker coloring. Estimates > 0 (indicating growing epidemics) are depicted in gold and < 0 (indicating declining epidemics) in purples. (C.) Raw case count data from the time series (dark = IPM data; light = publicly reported data) is shown for reference. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
4. Conclusions
Real-time estimation of epidemiological parameters, including the time-varying effective reproduction number, R t , and the related instantaneous epidemic growth rate, r, has played an important role in guiding public health interventions and policies across many epidemic outbreaks, including COVID-19 (Cauchemez et al., 2006, Kucharski et al., 2020, Pan et al., 2020). In Madagascar, an opensource platform (Rasambainarivo et al., 2020) was developed shortly after the introduction of COVID-19 in March 2020, to collate and visualize publicly reported data and estimate R t using traditional methods applied to daily reported incidence (Abbott et al., 2020a, Cori et al., 2013). We here compare the results from this platform applied to the first epidemic wave in Madagascar, with new estimates of the time-varying epidemic growth rate applied to our own laboratory data across the first epidemic wave—including those derived using a novel method based on the cross-sectional Ct value distribution at the time of sampling (Hay et al., 2021).
We find our new estimates to be largely congruent with those predicted from publicly reported data, demonstrating a pattern of increasing epidemic growth rates prior to a peak in cases, which occurred first in May 2020 in the Atsinanana region, followed by a second outbreak in July 2020 in the Analamanga region. Critically, our growth rate estimates derived using novel methods applied to the Ct distribution over time slightly precede those estimated from incidence data. As previous work has demonstrated Ct estimation to offer a more robust approximation of true dynamics under limited surveillance scenarios (Hay et al., 2021), these findings suggest that incidence-based methods to estimate epidemic trajectories in Madagascar may be underestimating the true pace of the epidemic, likely as a result of underreporting. Additionally, Ct-based methods adopted by a single laboratory allow for estimation of epidemic growth rates even in the absence of publicly reported case counts: in October 2020, the Malagasy Ministry of Health shifted its daily COVID-19 case notifications to weekly, interfering with incidence-based approaches to estimate epidemic trajectories (Rasambainarivo et al., 2020). Ct-based approaches, instead, should be robust to this variation in reporting, offering a powerful tool for public health efforts in low surveillance settings. Indeed, our analysis demonstrates that Ct-based epidemic growth rates show uncertain directionality towards the end of the first wave of COVID-19 in Madagascar, presaging eventual epidemic resurgence, while incidence-based rates categorically declined due to both truly declining cases and declining surveillance. Incidence-based growth rate estimation ceased during the continued limited surveillance period from October 2020 through March 2021 (Rasambainarivo et al., 2020); had Ct-based methods been available at the time, it is possible that the current second wave could have been predicted and mitigated by earlier rollout of public health interventions.
Statistical analysis of our Ct data indicates that Ct values vary predictably with days since onset of infection, allowing viral kinetics data to be leveraged for population-level estimation of epidemiological patterns. In our system, this pattern held even after controlling for the effects of age and symptom status on the Ct trajectory, further validating the applicability of Ct value as an indicator of time since infection. Nonetheless, in future work, it may be possible to fit unique viral kinetics trajectories for different classes of people; for example, older age cohorts or cohorts of people infected with more transmissible variants may be better represented by lower average Ct trajectories than the population as a whole (Jacot et al., 2020, Kidd et al., 2021). Our application of generalized additive models to both individual infection trajectory and population-level Ct distributions offers an effective means by which to control for variation in test and target across diverse RT-qPCR platforms to generate Ct values for epidemiological inference which represent a reliable average of population-level patterns overall.
We acknowledge the limitations of our current method, especially as it relates to testing biases. Nearly two-thirds of both case data and Ct-value data were derived from Madagascar’s Analamanga region, including the capital city of Antananarivo; as such, national trends are strongly influenced by the Antananarivo epidemic and may belie more time-lagged dynamics in more rural, less connected regions of the country. Nonetheless, these biases are unlikely to seriously impact inference from the early stages of the Madagascar epidemic, which began with an introduction event in Antananarivo (Randremanana et al., 2021), and despite the concentration of testing resources in the Analamanga (Rakotonanahary et al., 2021), our Ct-based estimation methods applied to the national dataset were nonetheless able to detect the epidemic in the Atsinanana region, too. During the earliest phases of the epidemic in Madagascar, testing resources were limited in our laboratory, which may have additionally biased sample intake towards high-viral-load, low-Ct-value cases that could bias epidemiological inference towards increasing growth rates even after the epidemic has, in reality, already begun to decline. As the epidemic ensued, however, the Madagascar Ministry of Health focused sampling on symptomatic patients and their suspected contacts, leading to a high proportion (56.6%) of reported asymptomatic infections in our dataset (Randremanana et al., 2021), which may have instead prematurely biased inference towards a declining epidemic. Nonetheless, our Ct-based projections of epidemic trajectories do not appear to underestimate realized trends, suggesting that our method was robust to these inconsistencies.
We apply a novel method leveraging within-host viral load data that is currently largely overlooked in the epidemiological literature to describe the dynamics of the first wave of COVID-19 in Madagascar. Our approach validates an important new tool for epidemiological inference of ongoing epidemics, particularly applicable to limited surveillance settings characteristic of many lower- and middle- income countries. We advocate for public release of real time data describing the Ct value distribution, in addition to daily case counts, to improve epidemiological inference to guide public health response and intervention.
CRediT authorship contribution statement
Soa Fy Andriamandimby: Conceptualization, Validation, Formal analysis, Investigation, Resources, Data curation, Writing – review and editing, Supervision, Project administration. Cara E. Brook: Conceptualization, Methodology, Software, Formal analysis, Writing – original draft, Visualization. Norosoa Razanajatovo: Investigation, Validation, Resources, Supervision, Project administration. Tsiry H. Randriambolamanantsoa: Investigation, Resources. Jean-Marius Rakotondramanga: Data curation, Supervision. Fidisoa Rasambainarivo: Resources. Vaomalala Raharimanga: Data curation, Supervision. Iony Manitra Razanajatovo: Investigation, Validation, Resources, Supervision, Project administration. Reziky Mangahasimbola: Data curation, Supervision. Richter Razafindratsimandresy: Investigation, Validation, Resources, Supervision, Project administration. Santatra Randrianarisoa: Resources. Barivola Bernardson, Data curation, Supervision. Joelinotahiana Hasina Rabarison: Investigation, Validation, Resources, Supervision, Project administration. Mirella Randrianarisoa: Data curation, Supervision. Frédéric Stanley Nasolo: Data curation. Roger Mario Rabetombosoa: Data curation, Supervision. Anne-Marie Ratsimbazafy: Investigation. Vololoniaina Raharinosy: Investigation. Aina H. Rabemananjara: Investigation. Christian H. Ranaivoson: Investigation. Helisoa Razafimanjato: Investigation. Rindra Randremanana: Supervision. Jean-Michel Héraud: Funding acquisition, Supervision, Validation, Resources, Project administration. Philippe Dussart: Supervision, Resources, Project administration.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
This work was supported by the US National Institutes of Health [1R01AI29822-01] United States; the Bill & Melinda Gates Foundation, Seattle, WA [GCE OPP1211841] - United States; the Innovative Genomics Institute at UC Berkeley, Berkeley, CA [COVID-19 Rapid Response Grant] and the Chan Zuckerberg Biohub (gift for COVID-19 response efforts). The authors thank Malavika Rajeev, Tanjona Ramiadantsoa, and Benjamin Rice for help in establishing the Madagascar COVID-19 dashboard.
Footnotes
Supplementary data associated with this article can be found in the online version at doi:10.1016/j.epidem.2021.100533.
Appendix A. Supplementary material
Supplementary material
.
Supplementary material
.
References
- Abbott, S., Hellewell, J., Sherratt, K., Gostic, K., Hickson, J., Badr, H.S., DeWitt, M., Thompson, R., EpiForecasts, Funk, S., 2020a. EpiNow2: Estimate Real-Time Case Counts and Time-varying Epidemiological Parameters.
- Abbott, S., Hellewell, J., Thompson, R.N., Sherratt, K., Gibbs, H.P., Bosse, N.I., Munday, J.D., Meakin, S., Doughty, E.L., Chun, J.Y., Chan, Y.-W.D., Finger, F., Campbell, P., Endo, A., Pearson, C.A.B., Gimma, A., Russell, T., Modelling Group, C.C., Flasche, S., Kucharski, A.J., Eggo, R.M., Funk, S.,. 2020b. Temporal Variation in Transmission During the COVID-19 Outbreak.
- Abbott S., Hellewell J., Thompson R.N., Sherratt K., Gibbs H.P., Bosse N.I., Munday J.D., Meakin S., Doughty E.L., Chun J.Y., Chan Y.D., Finger F., Campbell P., Endo A., Pearson C.A.B., Gimma A., Russell T., Covid C., Flasche S., Kucharski A.J., Eggo R.M., Funk S. Estimating the time-varying reproduction number of SARS-CoV-2 using national and subnational case counts. Wellcome Open Res. 2021:1–10. [Google Scholar]
- Auerswald H., Yann S., Dul S., In S., Dussart P., Martin N.J., Karlsson E.A., Garcia-Rivera J.A. Assessment of inactivation procedures for SARS-CoV-2. J. Gen. Virol. 2021;102:1–5. doi: 10.1099/JGV.0.001539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bates D., Mächler M., Bolker B.M., Walker S.C. Fitting linear mixed-effects models using lme4. J. Stat. Softw. 2015;67:1–48. doi: 10.18637/jss.v067.i01. [DOI] [Google Scholar]
- Borremans B., Gamble A., Prager K.C., Helman S.K., McClain A.M., Cox C., Savage V., Lloyd-Smith J.O. Quantifying antibody kinetics and rna detection during early-phase SARS-CoV-2 infection by time since symptom onset. ELife. 2020;9:1–27. doi: 10.7554/ELIFE.60122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Borremans B., Hens N., Beutels P., Leirs H., Reijniers J. Estimating time of infection using prior serological and individual information can greatly improve incidence estimation of human and wildlife infections. PLoS Comput. Biol. 2016;12 doi: 10.1371/journal.pcbi.1004882. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cauchemez S., Boëlle P.Y., Donnelly C.A., Ferguson N.M., Thomas G., Leung G.M., Hedley A.J., Anderson R.M., Valleron A.J. Real-time estimates in early detection of SARS. Emerg. Infect. Dis. 2006;12:110–113. doi: 10.3201/eid1201.050593. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen Y., Li L. SARS-CoV-2: virus dynamics and host response. Lancet Infect. Dis. 2020;2019(2019–2020) doi: 10.1016/S1473-3099(20)30235-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chitwood M.H., Russi M., Gunasekera K., Havumaki J., Pitzer V.E., Warren J.L., Weinberger D.M., Cohen T., Menzies N.A. Menzies3, Bayesian nowcasting with adjustment for delayed and incomplete reporting to estimate COVID-19 infections in the United States. MedRxiv. 2020;20:1–6. doi: 10.18907/jjsre.20.7_624_5. [DOI] [Google Scholar]
- Chu D.K.W., Pan Y., Cheng S.M.S., Hui K.P.Y., Krishnan P., Liu Y., Ng D.Y.M., Wan C.K.C., Yang P., Wang Q., Peiris M., Poon L.L.M. Molecular diagnosis of a novel coronavirus (2019-nCoV) causing an outbreak of pneumonia. Clin. Chem. 2020;66:549–555. doi: 10.1093/clinchem/hvaa029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cori A., Ferguson N.M., Fraser C., Cauchemez S. A new framework and software to estimate time-varying reproduction numbers during epidemics. Am. J. Epidemiol. 2013;178:1505–1512. doi: 10.1093/aje/kwt133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corman V.M., Landt O., Kaiser M., Molenkamp R., Meijer A., Chu D.K.W., Bleicker T., Brünink S., Schneider J., Schmidt M.L., Mulders D.G.J.C., Haagmans B.L., Van Der Veer B., Van Den Brink S., Wijsman L., Goderski G., Romette J.L., Ellis J., Zambon M., Peiris M., Goossens H., Reusken C., Koopmans M.P.G., Drosten C. Detection of 2019 novel coronavirus (2019-nCoV) by real-time RT-PCR. Eurosurveillance. 2020;25 doi: 10.2807/1560-7917.ES.2020.25.3.2000045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Evans M.V., Garchitorena A., Rakotonanahary R.J.L., Drake J.M., Andriamihaja B., Rajaonarifara E., Ngonghala C.N., Roche B., Bonds M.H., Rakotonirina J. Reconciling model predictions with low reported cases of COVID-19 in Sub-Saharan Africa: insights from Madagascar. Glob. Health Action. 2020;13 doi: 10.1080/16549716.2020.1816044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ganyani T., Kremer C., Chen D., Torneri A., Faes C., Wallinga J., Hens N. Estimating the generation interval for coronavirus disease (COVID-19) based on symptom onset data, March 2020. Eurosurveillance. 2020;25:1–8. doi: 10.2807/1560-7917.ES.2020.25.17.2000257. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gostic K.M., McGough L., Baskerville E.B., Abbott S., Joshi K., Tedijanto C., Kahn R., Niehus R., Hay A., De Salazar P.M., Hellewell J., Meakin S., Munday J.D., Bosse N.I., Sherrat K., Thompson R.N., White L.F., Huisman J.S., Scire J., Bonhoeffer S., Stadler T., Wallinga J., Funk S., Lipsitch M., Cobey S. Practical considerations for measuring the effective reproductive number, Rt. PLoS Comput. Biol. 2020;16 doi: 10.1371/journal.pcbi.1008409. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guillebaud J., Bernardson B., Randriambolamanantsoa T.H., Randrianasolo L., Randriamampionona J.L., Marino C.A., Rasolofo V., Randrianarivelojosia M., Vigan-Womas I., Stivaktas V., Venter M., Piola P., Héraud J.M. Study on causes of fever in primary healthcare center uncovers pathogens of public health concern in Madagascar. PLoS Negl. Trop. Dis. 2018;12:1–15. doi: 10.1371/journal.pntd.0006642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hay J.A., Kennedy-Shaffer L., Kanjilal S., Lennon N.J., Gabriel S.B., Lipsitch M., Mina M.J. Estimating epidemiologic dynamics from cross-sectional viral load distributions. Science. 2021 doi: 10.1126/science.abh0635. (80-.) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hay J.A., Minter A., Ainslie K.E.C., Lessler J., Yang B., Cummings D.A.T., Kucharski A.J., Riley S. An open source tool to infer epidemiological and immunological dynamics from serological data: serosolver. PLoS Comput. Biol. 2020;16:1–24. doi: 10.1371/journal.pcbi.1007840. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hay, J., 2020. lazymcmc. 〈https://github.com/jameshay218/lazymcmc〉.
- Jacot D., Greub G., Jaton K., Opota O. Viral load of SARS-CoV-2 across patients and compared to other respiratory viruses. Microbes Infect. 2020;22:617–621. doi: 10.1016/j.micinf.2020.08.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kidd M., Richter A., Best A., Cumley N., Mirza J., Percival B., Mayhew M., Megram O., Ashford F., White T., Moles-Garcia E., Crawford L., Bosworth A., Atabani S.F., Plant T., McNally A. S-Variant SARS-CoV-2 lineage B1.1.7 is associated with significantly higher viral load in samples tested by TaqPath Polymerase Chain Reaction. J. Infect. Dis. 2021;223 doi: 10.1093/infdis/jiab082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kubina R., Dziedzic A. Molecular and serological tests for COVID-19. A comparative review of SARS-CoV-2 coronavirus laboratory and point-of-care diagnostics. Diagnostics. 2020;10 doi: 10.3390/diagnostics10060434. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kucharski A.J., Russell T.W., Diamond C., Liu Y., Edmunds J., Funk S., Eggo R.M., Sun F., Jit M., Munday J.D., Davies N., Gimma A., van Zandvoort K., Gibbs H., Hellewell J., Jarvis C.I., Clifford S., Quilty B.J., Bosse N.I., Abbott S., Klepac P., Flasche S. Early dynamics of transmission and control of COVID-19: a mathematical modelling study. Lancet Infect. Dis. 2020;20:553–558. doi: 10.1016/S1473-3099(20)30144-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lauer S.A., Grantz K.H., Bi Q., Jones F.K., Zheng Q., Meredith H.R., Azman A.S., Reich N.G., Lessler J. The incubation period of coronavirus disease 2019 (CoVID-19) from publicly reported confirmed cases: estimation and application. Ann. Intern. Med. 2020;172:577–582. doi: 10.7326/M20-0504. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mizumoto K., Kagaya K., Zarebski A., Chowell G. Estimating the asymptomatic proportion of coronavirus disease 2019 (COVID-19) cases on board the Diamond Princess cruise ship, Yokohama, Japan, 2020. Eurosurveillance. 2020;25:1–5. doi: 10.2807/1560-7917.ES.2020.25.10.2000180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mollentze N., Streicker D.G. Viral zoonotic risk is homogenous among taxonomic orders of mammalian and avian reservoir hosts. Proc. Natl. Acad. Sci. 2020:1–8. doi: 10.1073/pnas.1919176117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moraz M., Jacot D., Papadimitriou-Olivgeris M., Senn L., Greub G., Jaton K., Opota O. Universal admission screening strategy for COVID-19 highlighted the clinical importance of reporting SARS-CoV-2 viral loads. New Microbes New Infect. 2020;38 doi: 10.1016/j.nmni.2020.100820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Narison S., Maltezos S. Scrutinizing the spread of COVID-19 in Madagascar. Infect. Genet. Evol. 2021;87 doi: 10.1016/j.meegid.2020.104668. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nishiura H., Kobayashi T., Miyama T., Suzuki A., Jung S. mok, Hayashi K., Kinoshita R., Yang Y., Yuan B., Akhmetzhanov A.R., Linton N.M. Estimation of the asymptomatic ratio of novel coronavirus infections (COVID-19) Int. J. Infect. Dis. 2020;94:154–155. doi: 10.1016/j.ijid.2020.03.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oran D.P., Topol E.J. Prevalence of asymptomatic SARS-CoV-2 infection: a narrative review. Ann. Intern. Med. Med. 2020;173:362–367. doi: 10.7326/M20-3012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pan A., Liu L., Wang C., Guo H., Hao X., Wang Q., Huang J., He N., Yu H., Lin X., Wei S., Wu T. Association of public health interventions with the epidemiology of the COVID-19 outbreak in Wuhan, China. JAMA J. Am. Med. Assoc. 2020;323:1915–1923. doi: 10.1001/jama.2020.6130. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park S.W., Bolker B.M., Champredon D., Earn D.J.D., Li M., Weitz J.S., Grenfell B.T., Dushoff J. Reconciling early-outbreak estimates of the basic reproductive number and its uncertainty: framework and applications to the novel coronavirus (SARS-CoV-2) outbreak. J. R. Soc. Interface. 2020;17 doi: 10.1098/rsif.2020.0144. 20200144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raherinirina A., Fandresena T.S., Hajalalaina A.R., Rabetafika H., Rakotoarivelo R.A., Rafamatanantsoa F. Probabilistic modelling of COVID-19 dynamic in the context of Madagascar. Open J. Model. Simul. 2021;09:211–230. doi: 10.4236/ojmsi.2021.93014. [DOI] [Google Scholar]
- Raherinirina A., Rafamatanantsoa F., Fandresena T.S., Rakotoarivelo R.A. Mathematical model and non-pharmaceutical control of the coronavirus 2019 disease in Madagascar. Open J. Model. Simul. 2021;09:259–274. doi: 10.4236/ojmsi.2021.93017. [DOI] [Google Scholar]
- Rakotoarisoa A., Randrianasolo L., Tempia S., Guillebaud J., Razanajatovo N., Randriamampionona L., Piola P., Halm A., Heraud J.-M. Evaluation of the influenza sentinel surveillance system in Madagascar, 2009-2014. Bull. World Health Organ. 2017;95:375–381. doi: 10.2471/BLT.16.171280. 〈http://www.who.int/entity/bulletin/volumes/95/5/16-171280.pdf%0Ahttp://ovidsp.ovid.com/ovidweb.cgi?T=JS&PAGE=reference&D=emex&NEWS=N&AN=615951962〉 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rakotonanahary R.J.L., Andriambolamanana H., Razafinjato B., Raza-Fanomezanjanahary E.M., Ramanandraitsiory V., Ralaivavikoa F., Tsirinomen’ny Aina A., Rahajatiana L., Rakotonirina L., Haruna J., Cordier L.F., Murray M.B., Cowley G., Jordan D., Krasnow M.A., Wright P.C., Gillespie T.R., Docherty M., Loyd T., Evans M.V., Drake J.M., Ngonghala C.N., Rich M.L., Popper S.J., Miller A.C., Ihantamalala F.A., Randrianambinina A., Ramiandrisoa B., Rakotozafy E., Rasolofomanana A., Rakotozafy G., Andriamahatana Vololoniaina M.C., Andriamihaja B., Garchitorena A., Rakotonirina J., Mayfield A., Finnegan K.E., Bonds M.H. Integrating health systems and science to respond to COVID-19 in a model district of rural Madagascar. Front. Public Health. 2021;9:1–10. doi: 10.3389/fpubh.2021.654299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Randremanana, R., Andriamandimby, S., Rakotondramanga, J.M., Razanajatovo, N., Mangahasimbola, R., Randriambolamanantsoa, T., Ranaivoson, H., Rabemananjara, H., Razanajatovo, I., Rabarison, J., Brook, C., Rakotomanana, F., Rabetombosoa, R., Razafimanjato, H., Ahyong, V., Raharinosy, V., Raharimanga, V., Raharinantoanina, S., Randrianarisoa, M., Bernardson, B., Randrianasolo, L., Randriamanantany, Z., Heraud, J., Biohub, C.Z., 2021. The COVID-19 Epidemic in Madagascar: Clinical Description and Laboratory Results of the First Wave, March-September 2020, Influenza Other Respiratory Viruses, 00, pp. 1–12. [DOI] [PMC free article] [PubMed]
- Rasambainarivo, F., Ramiadantsoa, T., Randrianarisoa, S., Rajeev, M., Rice, B., Metcalf, C.J., 2020. COVID-19 Madagascar Dashboard.
- Rydevik G., Innocent G.T., Marion G., Davidson R.S., White P.C.L., Billinis C., Barrow P., Mertens P.P.C., Gavier-Widén D., Hutchings M.R. Using combined diagnostic test results to hindcast trends of infection from cross-sectional data. PLoS Comput. Biol. 2016;12:1–19. doi: 10.1371/journal.pcbi.1004901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salje H., Cummings D.A.T., Rodriguez-Barraquer I., Katzelnick L.C., Lessler J., Klungthong C., Thaisomboonsuk B., Nisalak A., Weg A., Ellison D., Macareo L. Reconstruction of antibody dynamics and infection histories to evaluate dengue risk. Nature. 2018;557:719–723. doi: 10.1038/s41586-018-0157-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- The World Health Organization (WHO), 2020. Molecular Assays to Diagnose COVID-19: Summary Table of Available Protocols, (n.d.). 〈https://www.who.int/publications/m/item/molecular-assays-to-diagnose-covid-19-summary-table-of-available-protocols〉.
- Tom M.R., Mina M.J. To interpret the SARS-CoV-2 test, consider the cycle threshold value. Clin. Infect. Dis. 2020;71:2252–2254. doi: 10.1093/cid/ciaa619. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Treibel T.A., Manisty C., Burton M., McKnight Á., Lambourne J., Augusto J.B., Couto-Parada X., Cutino-Moguel T., Noursadeghi M., Moon J.C. COVID-19: PCR screening of asymptomatic health-care workers at London hospital. Lancet. 2020;395:1608–1610. doi: 10.1016/S0140-6736(20)31100-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walker, A.S., Pritchard, E., House, T., Robotham, J.V., Birrell, P.J., Bell, J.I., Newton, J.N., Farrar, J., Diamond, I., Studley, R., Hay, J., 2020. Viral Load in Community SARS-CoV-2 Cases Varies Widely and Temporally. [DOI] [PMC free article] [PubMed]
- Wallinga J., Lipsitch M. How generation intervals shape the relationship between growth rates and reproductive numbers. Proc. R. Soc. B Biol. Sci. 2007;274:599–604. doi: 10.1098/rspb.2006.3754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- T.W.H.O. (WHO), 2020. Maintaining Surveillance of Influenza and Monitoring SARS-CoV-2 – Adapting Global Influenza Surveillance and Response System (GISRS) and Sentinel Systems during the COVID-19 Pandemic: Interim Guidance, Geneva.
- Wood S.N. mgcv: GAMs and generalized ridge regression for R. R News. 2001;1/2:20–24. [Google Scholar]
- Xu B., Gutierrez B., Mekaru S., Sewalk K., Goodwin L., Loskill A., Cohn E.L., Hswen Y., Hill S.C., Cobo M.M., Zarebski A.E., Li S., Wu C.H., Hulland E., Morgan J.D., Wang L., O’Brien K., Scarpino S.V.V., Brownstein J.S., Pybus O.G., Pigott D.M., Kraemer M.U.G. Epidemiological data from the COVID-19 outbreak, real-time case information. Sci. Data. 2020;7:1–6. doi: 10.1038/s41597-020-0448-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- https://madagascar.unfpa.org/sites/default/files/pub-pdf/resultat_globaux_rgph3_tome_01.pdf. (2018). (Accessed 03 Dec 2021).
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary material
Supplementary material