Abstract
In the native vasculature, flowing blood produces a frictional force on vessel walls that affects endothelial cell function and phenotype. In the arterial system, the vasculature's local geometry directly influences variations in flow profiles and shear stress magnitudes. Straight arterial sections with pulsatile shear stress have been shown to promote an athero-protective endothelial phenotype. Conversely, areas with more complex geometry, such as arterial bifurcations and branch points with disturbed flow patterns and lower, oscillatory shear stress, typically lead to endothelial dysfunction and the pathogenesis of cardiovascular diseases. Many studies have investigated the regulation of endothelial responses to various shear stress environments. Importantly, the accurate in vitro simulation of in vivo hemodynamics is critical to the deeper understanding of mechanotransduction through the proper design and use of flow chamber devices. In this review, we describe several flow chamber apparatuses and their fluid mechanics design parameters, including parallel-plate flow chambers, cone-and-plate devices, and microfluidic devices. In addition, chamber-specific design criteria and relevant equations are defined in detail for the accurate simulation of shear stress environments to study endothelial cell responses.
1 Introduction
The vascular endothelium is the cellular monolayer located at the interface between flowing blood and the vessel wall. Playing a dynamic role, the endothelium actively adapts to preserve structural and functional homeostasis through the maintenance of anticoagulant properties, regulation of vessel permeability and vasomotion, and response to pathological disease processes associated with inflammation, wound healing, and cardiovascular diseases [1]. All of these properties are known to be influenced by biochemical and biomechanical stimuli that determine the pathology within the hemodynamic environment of the vasculature [2]. Endothelial cells (ECs) respond to tangential fluid shear stress and circumferential wall stretch forces via a variety of mechano-receptors and mechano-transducers, regulating various pathways that maintain vascular tone and homeostatic function [3,4]. Thus, the flow-sensitive mechanisms through which ECs respond to various (patho)physiological flow environments have been a continuous area of study within the field [5,6].
Wall fluid shear stress is defined as the frictional force blood (fluid) flow exerts on vessel walls and is expressed in units of force per area (dynes/cm2, where 1 dyne/cm2 = 0.1 Pa) [7]. Flow patterns in the human arterial system, as described in Table 1, are complex and can vary both spatially and temporally, causing variations in wall shear stress. Overall, the mean physiological shear stress level is normally maintained by instantaneous vasomotor changes to average between 10 and 20 dynes/cm2 but is highly dependent on the local fluid dynamics of the vessel [8–11]. In general, flow patterns in the arterial system can be categorized as either laminar unidirectional pulsatile or oscillatory shear flow. Unidirectional pulsatile shear stress occurs in straight arterial regions at 10–60 dynes/cm2. These regions experience flow in ordered, laminar patterns (fluid flows in parallel streamlines with no disruption between layers) of a pulsatile function that is dependent on the cardiac cycle, yielding mean positive shear stress [12]. Regions with fully developed (the velocity profile is not dependent on the axial location) unidirectional pulsatile flow with sufficiently high mean fluid shear stresses are known to induce an athero-protective EC phenotype and protect against the localization of cardiovascular disease [13,14]. This physiological flow is frequently simplified to steady laminar flow for in vitro EC flow experiments [12]. ECs exposed to steady laminar flow become elongated and align parallel to the direction of fluid flow (Fig. 1(b)), which is mediated by integrins [15], the cytoskeleton, primary cilia [16], and glycocalyx components, such as syndecan-1 and heparan sulfate [17,18]. Shear stress for fully developed steady Poiseuille flow in straight, circular vessels of constant cross-sectional area is directly proportional to the velocity of blood flow ( ) and inversely proportional to the vessel radius ( ) to the third power
| (1) |
Table 1.
Description of flow patterns within various in vivo locations
| Flow description | Velocity | Wall shear stress | In vivo locations | ||
|---|---|---|---|---|---|
| Laminar < 1400 | Steady | Positive or negative (directional) | Constant, unidirectional | Constant | Rare–capillary |
| Pulsatile | Unidirectional | Transient, mean positive flow–frequency ranges generally below 10 Hz | Low, transiently changing between positive and negative | Arteries, arterioles | |
| Oscillatory | Reversing | Low, positive and negative | Branching, bends | ||
| Turbulent > 1400 | Chaotic | Unpredictable | >95% stenosis | ||
Fig. 1.
![Representative images of endothelial cell morphology under static and laminar flow conditions. Immunofluorescent images are stained for microtubules and nuclei. (a) Endothelial cells under 24 h of static culture exhibit a nonaligned, cobblestone morphology. (b) Endothelial cells exposed to 24 h of 12.5 dynes/cm2 unidirectional laminar wall shear stress exhibit an aligned and elongated morphology. The flow study [14] was performed in a PPFC with dimensions of 7.62 cm × 2.54 cm × 250 μm. Fluid viscosity was 1 cP. Flow direction is horizontal. Scale bars indicate 50 μm.](https://cdn.ncbi.nlm.nih.gov/pmc/blobs/25cf/8628846/ecede2f1f0bd/bio-20-1480_020801_g001.jpg)
Representative images of endothelial cell morphology under static and laminar flow conditions. Immunofluorescent images are stained for microtubules and nuclei. (a) Endothelial cells under 24 h of static culture exhibit a nonaligned, cobblestone morphology. (b) Endothelial cells exposed to 24 h of 12.5 dynes/cm2 unidirectional laminar wall shear stress exhibit an aligned and elongated morphology. The flow study [14] was performed in a PPFC with dimensions of 7.62 cm × 2.54 cm × 250 μm. Fluid viscosity was 1 cP. Flow direction is horizontal. Scale bars indicate 50 μm.
where is the viscosity of blood [19]. Thus, small changes in greatly influence the magnitude of shear stress which ECs experience.
In contrast, oscillatory shear stress, which occurs with forward and reversing flow patterns, is found at arterial bifurcations, branch points, regions of high curvature (±4 dynes/cm2), and within stenotic arteries (30–40 dynes/cm2) [20]. These regions are characterized by a low shear stress magnitude and complex changes in the flow direction. These disturbed flow conditions fail to align and elongate ECs, which is seen in athero-protective hemodynamic conditions, and result in a cobblestone morphology (Fig. 1(a)). ECs experiencing disturbed flow, which is associated with low, oscillatory shear stress, have a pro-inflammatory phenotype and contribute to the pathogenesis of cardiovascular diseases [21,22].
Gaining insight into the direct effects of flow patterns, fluid shear stress magnitudes, and blood vessel geometry can deepen the understanding of EC responses to mechanical forces. Many flow chamber models have been designed to study these factors independently in vitro, including parallel-plate flow chambers, cone-and-plate viscometers, and microfluidic devices. Flow chamber device design is critical in shaping flow patterns, inducing the correct shear stress magnitude, and other flow parameters to accurately simulate in vivo (patho)physiology of ECs. This review discusses design criteria and device modifications for in vitro flow devices for the study of hemodynamic forces on vascular EC structures and functions.
2 Parallel-Plate Flow Chambers
The most commonly used in vitro device to study the combined effects of physical and chemical stimuli to advance the understanding of mechanical cues on ECs is the parallel-plate flow chamber (PPFC) [23]. Simple in design and operation, PPFCs have several advantages in their use over other flow chamber applications. Wall shear stress (SS) over a cell monolayer is well-defined due to the uncomplicated rectangular geometry of the chamber, allowing for the application of constant SS in physiological ranges for a defined time period (Fig. 2(a)). Different flow patterns can also be induced to study various physiological effects on an EC monolayer, including elongation and alignment [24], adhesion [25], and gene and protein expression [26]. This versatile tool enables researchers to grow cells under flow conditions, recover cells after a flow study for further experiments or subsequent data analyses, continually sample the fluid medium for secreted metabolites [27], study real-time cellular interactions and changes using live imaging apparatuses, and to directly fix cells once experiments are concluded, making studies easily reproducible. While the fluid can be continuously sampled for secreted molecules, fresh media can also be circulated to control cytokine influences. However, one limitation of PPFC devices used for experiments with downstream sampling is that the temporal resolution of the measurement depends on the flow rate and sampling frequency, which limits the sensitivity for detecting molecules that are produced in small quantities or have short half-lives. Representative optical images of PPFCs within literature can be viewed within references [28–31].
Fig. 2.
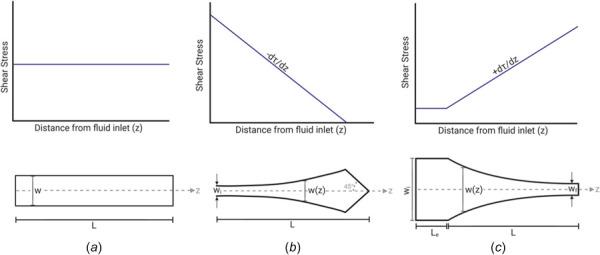
Characterization of PPFCs with variable width modifications. (a) The plain PPFC has a constant width (w) along the length of the chamber. This produces a constant shear stress for the entire chamber length (L). (b) As the width of the fluid channel increases from the inlet to the outlet, a constant, negative SSG is generated along the center axis of the channel. At the chamber inlet of width wi, the shear stress is at its maximum and linearly decreases to zero at the outlet of the chamber. (c) As the width of the fluid channel decreases from the inlet to the outlet, a constant, positive SSG is generated along the center axis of the channel. The entrance region of length Le and width wi produces a constant shear stress with fully developed laminar flow. As the width decreases along length L, a positive, uniform SSG is produced along the center axis of the channel. The width of the channel outlet is defined as wf.
2.1 Steady Laminar Flow in Parallel-Plate Flow Chambers.
Wall shear stress at the cellular monolayer within a PPFC can be derived through the simplification and rearrangement of the Navier–Stokes equations and continuity equations [32–34]. Given the assumptions of an incompressible, Newtonian fluid in fully developed laminar flow, shear stress (SS) between two stationary parallel-plates can be described as
| (2) |
where is the pressure gradient parallel along with the plates, is the fluid viscosity, is the fluid velocity, and is the height position with respect to the bottom plate ( ) [33]. After integrating with respect to the chamber height position twice and applying the no-slip boundary condition, the velocity profile between plates can be described as a parabolic function of the height position [33,35,36]
| (3) |
In two-dimensional Poiseuille flow, SS can be expressed as a function of PPFC geometry and flow rate ( ) of the fluid by integrating over the total height ( ) and width of the chamber [23,33,35,37–41]
| (4) |
in which is the wall SS at the EC monolayer. This equation is valid for Newtonian fluid in fully developed laminar flow within a chamber with a high aspect ratio ( ), where ; therefore, a chamber must be designed with a wide fluid channel with a short distance between the top plate and ECs. To ensure at least 85% of the monolayer is exposed to a homogeneous SS, the aspect ratio must be a value equal to or greater than 20 [33,36]. The initial design of a PPFC can be achieved by defining the required SS for the study, the fluid (media) viscosity, and chamber width and height to calculate the volumetric fluid flow rate required for the study.
To ensure ECs are experiencing purely laminar flow, one must consider the values of the Reynolds number ( ) and entry length ( ) at the monolayer. Physiologic arterial flow is typically between one hundred and several thousand, and, generally, a < 1400 is considered laminar [33,42,43]
| (5) |
In the equation above, is defined as fluid density. This equation can also be expressed in terms of the hydraulic diameter of the chamber [44]
| (6) |
To eliminate any possible entry effects of the flow profile, the EC monolayer must be placed beyond the entrance length of the flow. The entrance length is the length from the fluid inlet into the chamber to fully developed laminar flow and is a function of [37,44]
| (7) |
The criteria of Eqs. (5)–(7) must be met for the in vitro device to accurately simulate steady-state laminar flow. PPFCs can be initially designed using the equations in this section to estimate design criteria. Chamber specifications can be further refined through computational fluid dynamic (CFD) simulations to validate that the monolayer is experiencing fully developed, steady-state laminar flow. CFD models can also be used to calculate and/or confirm fluid velocity, pressure, SS, and other hemodynamic phenomena [45]. Generally, dimensions determined by numerical solutions should fall within 5% of CFD values for an optimal chamber design.
2.2 Linear Shear Stress Modifications
2.2.1 Variable Width PPFCs.
While plain PPFCs expose cells to a constant, homogeneous SS, many studies have modified the chambers to generate a varying SS along the length of the fluid channel [46]. Using the standard rectangular cell seeding area, the generation of different SS values is done by changing either the flow rate, the fluid viscosity, or the chamber height between the two plates, which require separate experiments and can require disassembling of the device [37]. One PPFC modification to enable the study of multiple SS values for a single cell source within a single experiment is to create a PPFC with tapered channel width. This PPFC design adaptation has a uniform height (h w,L) across the channel with an increasing, variable width, which is typically created by modifying the lower gasket (Fig. 2(b)). Based on Hele–Shaw stagnation flow theory, as the channel width increases along the chamber length from the fluid inlet to the outlet, a constant SS gradient of a linearly decreasing magnitude is generated [47]. In a tapered channel, SS is a function of axial distance (z) from the inlet and creates a stagnation point proximal to the fluid outlet. The increasing width of the channel along the centerline (z-axis) can be determined by
| (8) |
where is the total length of the fluid channel and is the width of the fluid inlet [48]. Thus, for a constant flow rate and height, SS diverges linearly along the center of the channel with respect to distance from the inlet [49]
| (9) |
Pressure drop ( ) across the channel can be calculated using [46]
| (10) |
Therefore, chamber designs with an increasingly tapered channel allow for the time-efficient study of a single cell source under a wide SS range for each experimental run.
Conversely, channels can also be inversely tapered by decreasing the width in the flow direction from the fluid inlet to the outlet, creating a converging PPFC [50]. As the channel width decreases along the chamber length from the fluid inlet to the outlet, a constant SS gradient (SSG = ) of a linearly increasing magnitude is generated (Fig. 2(c)). Both the SS and the shape of the variable side walls are a function of axial distance from the inlet and have been derived from the plane-Poiseuille solution by Lu et al. [23].
In a PPFC with a constant height, the variable decreasing width of the channel can be determined by
| (11) |
where is the width of the fluid outlet [23]. Thus, for a constant flow rate and negligible wall effects, SS increases linearly along the center of the channel with respect to distance from the inlet
| (12) |
The constant positive SSG across the channel can then be determined by
| (13) |
2.2.2 Variable Height PPFCs.
Another modification of the PPFC to generate a uniform SSG is made by tapering the top plate to have a variable height along the channel length [39]. Tapering of the top plate allows for the generation of three distinct experimental regions: (1) an entrance region with a minimum SS along the length L0, (2) a positive, constant SSG region of length Lg, and (3) an exit region with a maximum SS of length Lf (Fig. 3(b)). Because the chamber is variable in height, the constant heights at the inlet and outlet are denoted as h0 and hf, respectively, and the channel height along the gradient region is defined as a function along the chamber length
| (14) |
Fig. 3.
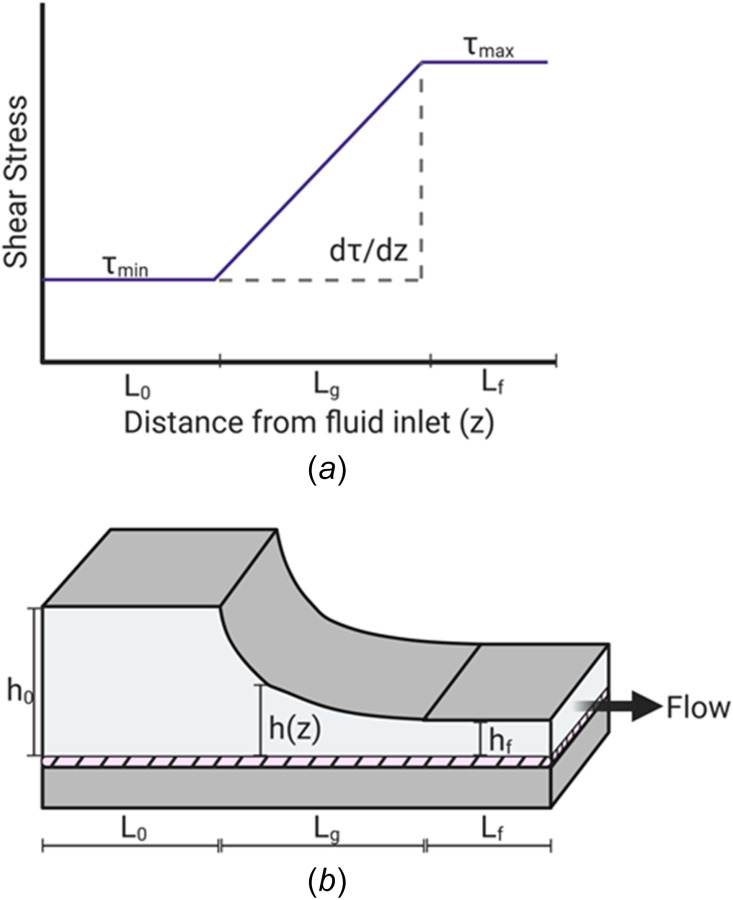
Characterization of the modification of tapering of the top plate. (a) The modification of producing a variable height of the PPFC by tapering the top plate forms three distinct experimental regions along the distance from the fluid inlet. As the fluid flows into the entrance, the height of the chamber is at its maximum, h0. This generates a constant, minimum shear stress along the entrance length, L0. As the height decreases, a positive, uniform SSG is generated for the gradient length of Lg. Shear stress reaches its maximum along the exit region of Lf at the minimum height of hf. (b) Schematic diagram of the modification of the tapering of the top plate. The hatched region represents the endothelial monolayer.
This flow chamber generates a uniform linear increase in SS along the constant gradient region (Fig. 3(a)) where SS and the SSG are, respectively, given by
| (15) |
| (16) |
Minimum and maximum SS values depending on the chamber design can be calculated as follows:
| (17) |
| (18) |
Another way to design a chamber with a uniform linear SS range is by defining the required values for minimum SS, maximum SS, and the SSG. Using the experimental criteria, the dimensions of the chamber can be designed using the equations below:
| (19) |
| (20) |
2.3 Parallel-Plate Flow Chamber Modifications for High Shear Stress Gradients.
It is speculated that low SS magnitudes and high SSGs play an important role in the pathogenesis of atherosclerosis due to the localization of atherosclerotic plaques in regions where ECs are exposed to low, disturbed flow, which creates temporal and spatial SSGs [23]. Flow separation (divided fluid streamlines due to adverse pressure gradients) and reattachment (divided streamline attaches to forward flow) cause SSGs large in magnitude, resulting in distinct regions of confluent EC monolayers mimicking both disturbed and physiologic flow regions in vivo [22]. Large positive SSGs with low SS magnitudes have also been shown to lower EC density, which promotes cell dysfunction in regions prominently located to arterial blockages and at vessel bifurcations and results in areas of atherogenesis, arteriovenous fistulae, stenoses, and collateral arteries [51,52]. While these areas of complex flow have been highly studied, areas of high SS magnitudes (>30 dynes/cm2) and high SSGs have been studied much less [53]. These hemodynamic conditions are located in areas with the complex flow that stimulate outward remodeling due to an increase in flow rate, such as aneurysm initiation, proximal to stenoses or other arterial blockages, and arteries upstream of arteriovenous fistulae [53]. These complex geometries induce flow impingement, generating both large positive and negative SSGs. Even though these regions are much less studied, their clinical relevance remains of interest. This section will briefly touch on the design of (1) high SSG chambers for the generation of high SS magnitudes, (2) the design of a vertical backward-facing step, and (3) radial impinging flow for the study of high SSGs with low SS magnitudes.
2.3.1 High SSG Chambers.
High SSG chambers (Fig. 4(b)) can be designed to produce a gradient along the channel through the variation in height of the top plate [40]
| (21) |
Fig. 4.
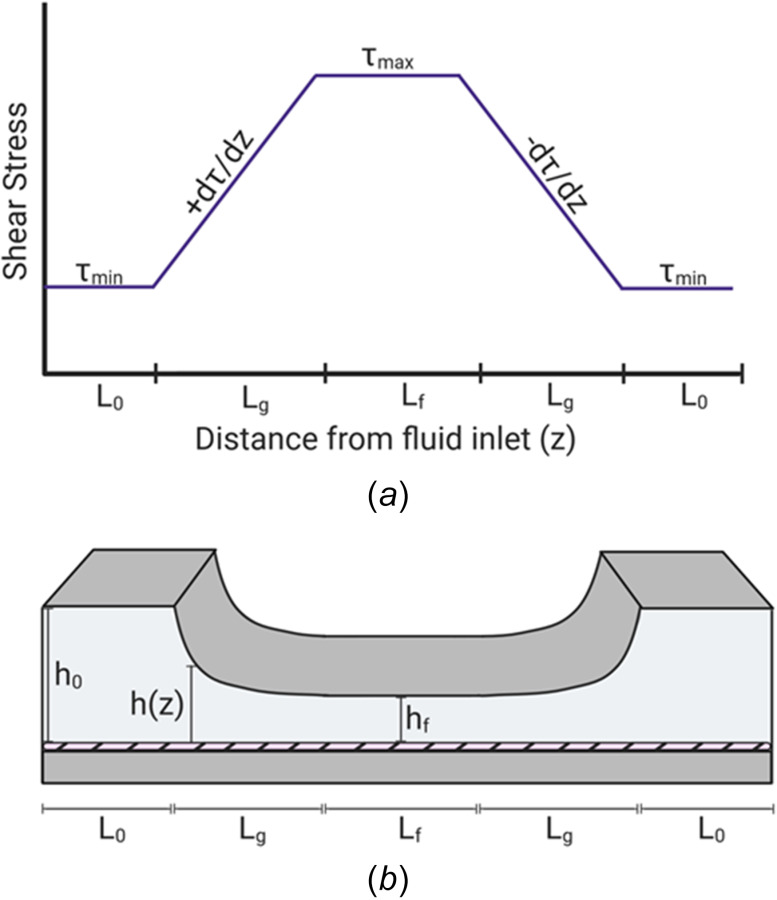
Characterization of the SSG chamber. (a) The modification of a variable height of the top plate of the PPFC forms four distinct experimental regions. Shear stress is either at its minimum or maximum values when the top plate is at its maximum height along the entrance length L0 or at its minimum height along the length Lf, respectively. Constant SSGs are formed along the varying height of the converging or diverging regions of equal lengths of Lg. The converging and diverging regions will generate either a uniform, positive SSG or a uniform, negative SSG, respectively. (b) Schematic diagram of a SSG chamber. As the fluid flows from the entrance region of height h0 and length L0, the shear stress at the monolayer is at a constant minimum. As the height of the top plate decreases, a converging region with a uniform, positive SSG is generated along the length Lg. As the height reaches a constant minimum of height hf, the shear stress at the monolayer is a constant maximum along the length Lf. As the height of the top plate increases, a diverging region with a uniform, negative SSG is generated along the length Lg.
where the channel height profile is a function of distance along the channel length, beginning at the initial height, at
| (22) |
Equation (22) allows the chamber to produce two regions with a constant SSG of opposite signs. In total, this chamber forms four regions of SSG values: two regions of SSG absence, a region of SSG convergence, and a region of SSG divergence. The ECs will be exposed to two uniform SS values of different magnitudes in the SSG absent regions, while the converging and diverging regions will generate SS ranges for one positive, uniform SSG and one negative, uniform SSG (Fig. 4(a)). In addition, the SSGs in these sections are constant and of similar magnitude but opposite in sign. This allows the two gradient regions to be directly compared to study shear effects attributed to only the sign of the SSG. The SS values in these regions of variable height will range directly between the maximum and minimum SS values. Modifications of PPFCs to produce a constant SSG are useful for distinguishing between the effects of an SSG from other aspects of disturbed flow patterns that also produce SSGs, such as flow separation, recirculation, and reattachment. However, it is important to note that results from constant SSG devices are not strictly dependent on the magnitude of SS values. ECs within a monolayer transmit force to neighboring cells via intercellular junctions and paracrine signaling. SSG devices cause these shear differences between neighboring cells, and studies have raised the possibility that SS differences between two cells might induce changes in gene expression due to intercellular junction interactions [50,54]. Therefore, the interpretation of results found from SSG devices should be further verified by experiments with single SS values.
2.3.2 Vertical Backward-Facing Step Modification.
ECs exposed to disturbed flow with a low, oscillatory SS coupled with a large SSG generally exhibit disease-prone phenotypes [55,56]. Disturbed flow conditions have been shown to increase cell loss, migration, proliferation, and monocyte adhesion [40,57]. These disturbed flow regions also reduce responses of cell morphology, orientation, cytoskeletal orientation, and anti-infammatory gene expression, often resulting in EC dysfunction [40]. The flow patterns exhibited in these environments are similar to those at arterial bifurcations and bends, e.g., flow separation, recirculation, and reattachment [42]. This complex flow system can be replicated in vitro with a vertical backward-facing step (Fig. 5(a)) [23]. Able to model inhomogeneous flow dynamics, an adequate vertical backward-facing step expansion chamber design can provide a well-defined laminar recirculation region downstream of the step without transitioning to turbulent flow (irregular flow patterns of individual fluid particles resulting in chaotic eddies and flow instabilities).
Fig. 5.
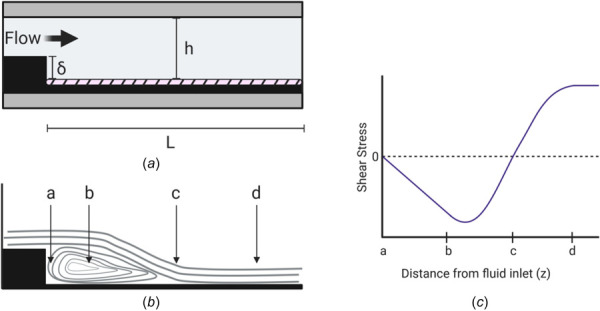
Characterization of the vertical backward-facing step PPFC modification. (a) Schematic diagram of the vertical backward-facing step modification where δ is the vertical height of the step, h is the total height between plates, and L is the total length distal to the step. (b) Schematic of the flow patterns induced by the vertical backward-facing step. Distal to the step, four regions along the length of the chamber are formed: a, the stagnant area with impinging flow; b, the laminar recirculation eddy; c, the flow reattachment point; and d, fully developed laminar flow. (c) Wall shear stress characterization in each of the four regions along the lower plate of the chamber. No shear stress occurs within the stagnation area or reattachment point. Negative values correspond to fluid flowing back toward the step within the recirculation eddy in the retrograde direction.
A vertical step expansion (i.e., 90 deg alignment to the channel axis) forms four specific flow regions along the length of the chamber: a stagnant flow area, a recirculation eddy, a point of flow reattachment, and a fully developed laminar flow area (Fig. 5(b)) [58]. The recirculation eddy causes an increasing velocity in the retrograde direction, which progressively decreases near the wall of the step. Approaching the step, upward curved streamlines carry fluid away from the lower surface of the chamber and toward the reattachment area. Thus, the eddy is characterized by negative SS values between the step and reattachment point (Fig. 5(c)). At the reattachment region (stagnation point), SS is approximately zero with steady flow fluctuating between the forward and retrograde directions with a large magnitude SSG [59,60]. This type of flow is also defined as “impinging flow.” At the initiation of experiments, the sudden onset of flow moves the reattachment point away from the vertical step in a developmental phase, lasting approximately a few hundred milliseconds [61,62]. If the flow is pulsatile, the reattachment point will shift forward and backward with each cycle [63]. Downstream of the reattachment point, SS becomes increasingly positive along the length of the chamber with constant, steady flow [64]. Disturbed flow occurs in both the stagnant flow and reattachment regions (Fig. 5(b), points a and c, respectively), whereas ECs are exposed to laminar flow in opposite directions within the recirculation eddy and the fully developed laminar flow regions (Fig. 5(b), points b and d, respectively). ECs in each region can be studied to determine the differential effects of each flow profile.
A well-defined, two-dimensional laminar recirculation eddy is highly reliant on adequate design of the vertical expansion step because the flow dynamics are dependent on the dimensions of the chamber. Two gaskets can be used to easily form the vertical step in the standard PPFC. The first gasket will help develop laminar flow before the step, which will aid in the characterization of the step-induced recirculation. The second gasket will form the step itself. Vertical height ( ) can be altered by using various gasket material thicknesses or multiple gaskets. It is imperative that the height is large enough to sufficiently generate disturbed flow in the region close to the step, but that the chamber can still develop laminar flow farther along the channel for direct comparisons. Thus, the vertical step height can be designed by the knowledge that the length of the recirculation region increases nonlinearly with an increasing expansion ratio ( ) [65]. For a two-dimensional laminar recirculation eddy with , an expansion ratio ranging between 1.25 and 4 is recommended [66]. It is important to note that sidewall effects are more prominent for smaller expansion ratios [67]. In addition to a vertical step, the effects of flow separation and recirculation eddies on ECs can also be designed with a gradual change in hydraulic diameter of the fluid channel [68]. This design alteration is capable of modeling the recirculation region directly downstream of an eccentric stenosis and can aid in accurately simulating physiological stenosis-induced blood flow conditions and their effect at the apex on ECs [69]. In general, because of the design of either the 90 deg backward-facing step or gradual change in hydraulic diameter, these PPFC expansion modifications are considered to have two-dimensional recirculation eddies.
Three-dimensional flow profiles can be generated with a backward-facing step expansion chamber where the step is aligned oblique (i.e., < 90 deg) to the chamber axis. Step angle characterization of the resulting flow pattern has been performed through dye visualization methods. Watkins et al. have demonstrated direct effects of the angle, flow velocity, and Reynolds number on the pitch on the newly generated eddy, width of the stagnant flow area, and clearance time of the fluid medium [70]. The design of an oblique backward step can allow for the study of higher dimensional, complex flows that are commonly found in large vessels, nonplanar bifurcations, and fluid interactions with vessel walls. Vertical backward-facing step chambers can also be combined with pulsatile and oscillatory flows to further study ECs under (patho)physiologically relevant flow patterns.
2.3.3 Radial Impinging Flow Chambers.
Hemodynamics at apices of arterial bifurcations are also subjected to disturbed flow. At these regions, blood flow impinges at the apex and locally accelerates downstream, forming a region at the center of the impingement that experiences flow stagnation characterized by a low SS and high SSG [71]. ECs in vitro can be studied under these circumstances by use of a radial impinging flow chamber, in which an incoming fluid impinges on the opposite wall of the chamber and flows radially outward. This device consists of two stationary, parallel disks separated by a small height . A central pipe (typically tubing or a blunt needle) forms a T-shaped inlet to the center of the top plate and directs flow outward from the center at a constant flow rate to flow radially over a substrate seeded with ECs (Fig. 6(a)). Radial impinging flow chambers offer several advantages to study ECs under disturbed flow: (1) this axisymmetric flow technique applies a large range of SSs (typically 10–200 dynes/cm2) to a monolayer in a single experiment due to the geometry of the device, (2) sterility issues are largely decreased due to no moving parts within the device, and (3) direct visualization and monitoring of cells by live imaging is possible if disks are made of transparent materials. These devices are commonly utilized to experimentally study cellular adhesion [72], EC migration [73,74], local heat and mass transfer principles [75,76], and ligand-receptor bond affinities [77].
Fig. 6.
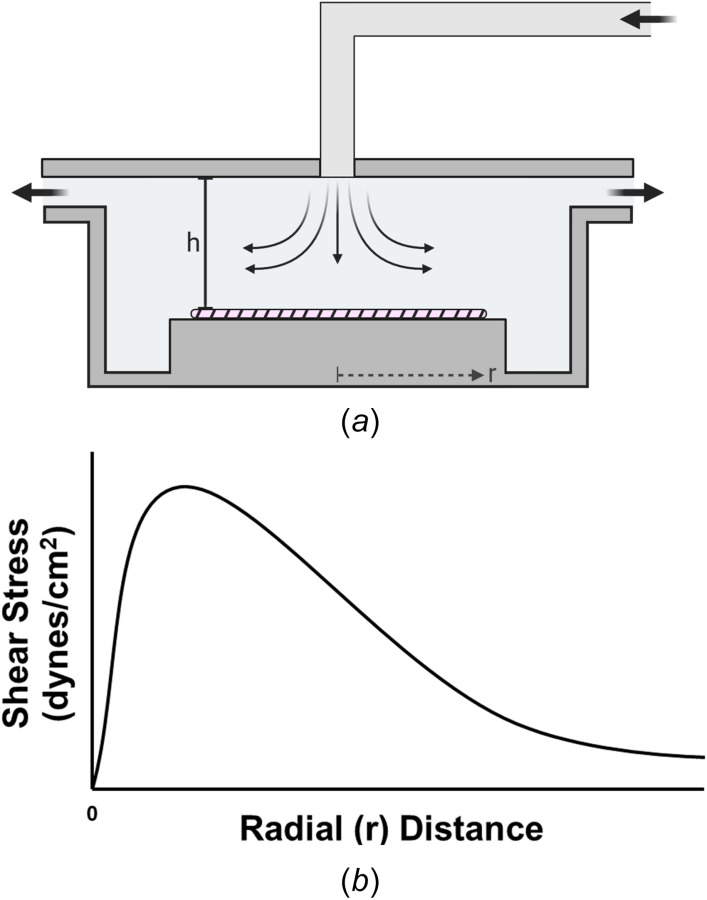
Characterization of the radial impinging flow chamber. (a) Schematic diagram of the radial impinging flow chamber. Disturbed flow is created by fluid flowing downward from a height onto the surface of the cellular monolayer, shown by the hatched region. (b) Schematic of the wall shear stress profile at the monolayer. Wall shear stress is spatially dependent on both the initial height/geometry of the inlet and the radial distance from the stagnation point of the impinging flow. For each flow system, the exact magnitude and values of the SS produced beyond the stagnation point should be computed with CFD simulations.
Wall SS generated in a radial impinging flow chamber can be modeled as a nonlinear function
| (23) |
where viscous SS generated by axisymmetric flow at the center of the chamber is accounted for in the first term. The second term is a correction to account for inertial effects that are formed near the sharp-edged inlet and will decrease with an increasing radial position. The design of these flow chambers should minimize the inertial effects to be less than 5% of the viscous forces by either modifying the geometry of the inlet [78] or adjusting the volumetric flow rate [79]. The radius of the inlet should be a function of the chamber height of to minimize flow disturbances [80,81]. One also needs to ensure that the tubing that forms the inlet is sufficiently rigid and long to produce fully developed flow before entering the chamber.
If one assumes laminar axisymmetric flow and neglects any entrance effects, the SS equation reduces to only the first viscous term [82]
| (24) |
From this equation, average fluid velocity and, therefore, wall SS decrease radially with distance from the stagnation point as the cross-sectional area increases. Most radial flow configurations operate under laminar flow , for If one goes above the critical Reynolds number, turbulence can form. This effect usually occurs at small radii or with an incorrectly set volumetric flow rate
| (25) |
Because these inertial effects will always be present, investigators should decrease parameters, such as , to minimize entry effects [83]
| (26) |
This equation shows that at larger radial positions, an increased volumetric flow rate, or increased gap height, the inertial effects become significant. However, the exact flow patterns and SS values around the stagnation point will depend on the Reynolds number and the specific geometry of the inlet and chamber height. Therefore, for regions not accurately described by the approximate numerical solution, CFD simulations must be performed to determine the SS values of the flow system as a function of radial distance from the inlet [83,84]. A schematic of the overall wall SS profile produced by impinging flow chambers is shown in Fig. 6(b).
2.4 Unsteady Flow in Parallel-Plate Flow Chambers.
While the majority of experimental studies have been performed under steady, unidirectional (nonreversing) flow in PPFCs, it is critical to expand in vitro studies to include more physiologic flow conditions. In their native environment, ECs experience unsteady, pulsatile flow due to the rhythmic nature of pressure applied by the cardiac cycle. In long, straight arterial sections of the vessel wall, blood flows in ordered, laminar patterns of pulsatile fashion where the flow rate is time-variant but always forward in direction [12]. In this hemodynamic environment, ECs experience pulsatile SS with fluctuations in magnitude that yield a positive mean SS. In vitro studies have shown that both nonreversing and reversing pulsatile flow with positive mean SS stimulates many of the same EC responses as steady flow, but there can be some modulation effects [85–87]. Conversely to a steady flow, nonreversing pulsatile SS with mean SS above 10 dynes/cm2 has been shown to elongate EC morphology, increase cellular stiffness, and decrease EC proliferation [88], while others have shown that a frequency of 1 Hz enhances prostacyclin (PGI2) by 2.5 fold [89], suppresses monocyte chemoattractant protein-1 expression [90], increases histamine metabolism [91], and transiently increases the proto-oncogene mRNA level of c-fos [86]. These studies collectively suggest pulsatile flow causes changes in EC functions due to the basic mechano-sensory interactions induced by flow rather than the transient elevation of SS magnitude during the cardiac cycle.
Arterial branches and bifurcations are subject to periodic flow recirculation zones, which expose ECs to time-reversing, oscillatory flow. These flow patterns can result in periodic flow reversal with a time-averaged SS of approximately zero [92–94]. It has been shown that the regulation of EC function can either be identical to or different than a steady flow, depending on the mean SS value, due to the dynamic ability of ECs to discriminate among and respond to different forms of unsteady flow. Immediately after the onset of flow, unidirectional, steady flow induces pro-inflammatory and proliferative regulation pathways, such as nuclear factor-κB, reactive oxygen species production, and monocyte chemoattractant protein-1 expression [90,95]. However, with prolonged exposure to steady or pulsatile SS, as the cells align, these pathways are transiently downregulated [96]. In contrast, oscillatory flow patterns sustain the activation of these pathways, and ECs do not undergo cytoskeletal remodeling, retaining a cobblestone morphology in response to the dynamic nature of the fluid behavior [97]. Compared to an elongated morphology, cobblestone ECs are more permeable to macromolecules and have increased monocyte adhesion. Importantly, the degree of intimal wall thickening has been correlated to hemodynamic characteristics of low shear, as seen in oscillatory regimes [98,99]. These studies suggest that oscillatory flow regimes have higher inflammatory responses and can ultimately result in atherogenesis due to the continuous changes in flow magnitude and direction [96,100–102]. Therefore, PPFCs have been modified to further produce pulsatile, oscillatory, and disturbed flow patterns.
Blood behaves in a Newtonian fashion in arteries with shear rates greater than 100 s−1 [103]. In vivo, blood pressure and flow are unsteady due to the cyclic nature of the heart alternating between systole and diastole. Acting as a natural physiologic pump, the cardiac output from the heart drives blood in the same direction as the decreasing pressure gradient within the cardiovascular system. Thus, flow and, therefore, SS are subjected to unsteady, pulsatile conditions with each cardiac cycle [104]. While the nature of the physiologic waveform differs at various regions of the vasculature, many experimental and computational studies have modeled in vivo blood flow profiles as a simple sinusoidal waveform [105,106]. For this arterial model, the hemodynamic conditions of the fluid velocity, rate of flow, and the viscous drag can be calculated if the pressure gradient is known for a cylindrical geometry with a rigid wall by using the Womersley theory [94], which also determines the unsteadiness of the flow profile.
The nature of unsteady flow can be described by the Womersley number ( ). This dimensionless parameter describes the ratio between the pulsation flow frequency with respect to viscous effects, where larger values correspond to increased unsteadiness [107]
| (27) |
In the equation above, is the angular frequency defined as , and is the kinematic viscosity of the fluid. When unsteady flow effects are negligible, i.e., inertial forces are small compared to viscous forces and the fluid velocity responds instantaneously to changes in the pressure gradient ( 1), the fluid behaves in a quasi-steady manner, and, thus, the steady equations in Sec. 2.1 can be used to approximate chamber design specifications for pulsatile and oscillatory SS when the following conditions are met:
| (28) |
| (29) |
where is the oscillating boundary layer thickness, and is the flow frequency [108]. The Poiseuille relationship has been shown to be 97% accurate for quasi-steady regimes [109]. When the Womersley number is equal to or greater than one, the quasi-steady approximation for the flow profile becomes ineligible due to the relationship between the volumetric flow rate and SS becoming time-dependent. At , the velocity profile maintains Poiseuille shape, but the oscillatory phase lag with respect to the pressure gradient begins to develop. As 1, both the phase lag and the deviation in the fluidic behavior from the quasi-steady behavior increase and become more unsteady. The amplitude of the oscillations will also vary with an increasing [110]. SS has further been derived for unsteady flow in a rigid tube with an approach similar to Womersley's solution [111] and by the use of heat transfer principles [112]. However, many investigators do not report the methods used to calculate SS under unsteady flow regimes for studies performed in PPFCs [113].
For quasi-steady flow of an incompressible, Newtonian fluid through a narrow rectangular channel, as such in a PPFC, SS can generally be derived from the Navier–Stokes equation for fluid under sinusoidal oscillating conditions
| (30) |
where and are the steady component and the oscillating component, respectively [108]. The fluid velocity is of the form
| (31) |
where A and B are real functions of further defined by Loudon et al. [110]. The integration of Eq. (31) over the interval results in the induced average velocity as a function of the amplitude and the phase lag of the average velocity
| (32) |
Oscillatory SS is directly proportional to the local velocity gradient at the cellular monolayer
| (33) |
where . Therefore, a dynamic velocity will result in a changing SS at the bottom plate. SS on the ECs will also vary sinusoidally with time at the same frequency as the oscillating pressure gradient
| (34) |
Here, is the relative amplitude of the wall SS, and is the phase lag with respect to the imposed pressure oscillation. Both of these constants are functions dependent upon the distance from the EC monolayer [114].
Stability of oscillations in the fluid profile can be determined by the Reynolds number based on the Stokes thickness . For , the oscillating flow will remain stable. At the range , the flow transitions between laminar and turbulent states over a single period. Above a value of , the flow regime becomes fully turbulent [115,116]. In addition to determining the stability of the unsteady flow, studies have shown that pulsatile flow in a PPFC can increase the entrance length of the fluid by 15% or more [117]. Therefore, it is important to fully characterize the flow in the channel using CFD simulations to either validate or determine the experimental conditions the cellular monolayer is experiencing.
While many studies investigate endothelial responses to unsteady flow, typically only sinusoidal oscillations at fundamental frequencies are studied. However, these simplified models do not fully mimic realistic physiological flow profiles, and results may not be representative of in vivo responses. While mean SS influences endothelial signaling and flow topology, the rate of shear development has been shown to affect endothelial responses, such as nitric oxide production [118]. Therefore, the reproduction of realistic arterial waveforms is recommended to fully investigate EC responses in vivo. The reproduction of arterial waveforms requires four or more harmonics and can be formed by a computer-controlled pump. The flow loop parameters, such as wall displacement (compliance in tubing), pressure, and velocity of the pulse wave, must also be considered when designing each study and require an understanding of the individual role of each of these parameters to the unsteady flow profile [119]. Literature device designs for PPFCs under multiple flow conditions and modifications and the studies' data analysis methods can be found in Tables 2 and 3, respectively.
Table 2.
Summary of designs for literature PPFC systems
| System | Type of flow | Type of cell | Time (hr) | Shear stress (dynes/cm2) | Length (mm) | (mm) | Width (mm) | Height (mm) | Aspect ratio | Pump type | Ref. | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Plain | Steady | HUVECs | 15 | 8 | 13.5 | 75.18 | 0.07 | 25.15 | 0.13 | 198 | Peristaltic | [33] |
| 2 | 8.4 | n.s.b | 85 | n.s.b | 25 | 0.3 | 83.3a | Constant Flow | [120] | |||
| 6 | 12 | n.s.b | 80 | n.s.b | 38 | 0.5 | 76a | n.s.b | [121] | |||
| BAECs | 24 | 10, 30, and 85 | 60 | 50 | 0.75 | 13 | 0.25 | 52 | Peristaltic | [36] | ||
| HMEC-1 | 24 | n.s.b | n.s.b | 75 | n.s.b | 38 | Variant | Variant | Peristaltic | [122] | ||
| HSVECs | 6 | 0.2–40 | 363a | 32 | 7 | 27 | 0.5 | 54a | Peristaltic | [123] | ||
| Rat aortic ECs | 6 | 10.4 | 0.133 | 75.3 | 0.238a | 35.2 | 0.330 | 106.67a | Peristaltic | [124] | ||
| Human aortic ECs | n.s.b | 120 | 2000 | 150 | 100 | 4 | 1 | 4a | Pulsatile | [125] | ||
| Porcine aortic ECs | 6 | 1.13 and 11.5 | 100 and 900 | 22.5 | 94 | 17.5 | 1.8 | 9.72 | Peristaltic | [126] | ||
| Rat EPCs | 24 | 5–20 | 0.0317–0.127 | 57.5 | 25.36 × 10−5–10.16 × 10−4 | 12.4 | 0.2 | 62a | Peristaltic | [127] | ||
| Human and Porcine EPCs | 48 | 15 and 100 | 13.9–234 | 70 | 0.1–2.5 | 19 | 0.166–0.267 | 114.5–71.2a | Peristaltic | [44] | ||
| Oscillatory | HUVECs | 6 | −195 to 70.19 | 1 | 50 | n.s.b | 12 | 0.5 | 24a | Peristaltic | [28] | |
| Porcine aortic ECs | 6 | 39.1–40.3 | 2750 | 22.5 | 198 | 17.5 | 1.8 | 9.72 | Peristaltic | [126] | ||
| Pulsatile | Human aortic ECs | n.s.b | 3.1–107 | 1000 | 150 | 100 | 4 | 1 | 4a | Pulsatile | [125] | |
| Porcine aortic ECs | 6 | 10.7 | 230–1260 | 22.5 | 94 | 17.5 | 1.8 | 9.72 | Peristaltic | [126] | ||
| Vertical-Step | Disturbed | HUVECs | 0.083 | −3 to 6 | 24–60 | 8 | n.s.b | 19 | 1.399 | 13.6 | Syringe | [128] |
| 0.333 | 1–7 | 100 | 45 | 15 | 10 | 0.5 | 20a | Double Syringe | [129] | |||
| BAECs | 0.083–0.05 | 0–13.5 | n.s.b | 30 | n.s.b | 22 | 1 | 22a | Peristaltic | [130] | ||
| 24 | 167 | 267 | 76.2 | 30 | 19.05 | 0.635 | 30a | Peristaltic | [131] | |||
| SSG | Steady | BAECs | 24 and 36 | 35–284 | 780–848 | 100 | n.s.b | 22 | 1–3 | 7.33–22a | Peristaltic | [40] |
| HCtAECs | 24 | 20–60 | 1510 | 16 | n.s.b | 12 | 0.20–1.11 | 10.8–60a | Peristaltic | [39] |
Values that have been calculated by the author with the information presented within the reference article listed.
Values were not stated (n.s.) in the reference article listed and were unable to be calculated by the author.
Table 3.
Analysis methods of various PPFC studies
| System | Type of flow | Type of cell | Analysis method |
|---|---|---|---|
| Plain | Steady | BAECs [36] | Atomic force microscopy [33] |
| HMEC-1 [122] | |||
| HSVECs [123] | |||
| Human aortic ECs [125] | |||
| Human & Porcine EPCs [44] | |||
| HUVECs [33,120,121] | |||
| Porcine aortic ECs [126] | |||
| Rat aortic ECs [124] | |||
| Rat EPCs [127] | |||
| Chemiluminescence [44] | |||
| Fluorescent microscopy [33,44,121,123] | |||
| MTT assay [127] | |||
| Nitric oxide assay [127] | |||
| Phase contrast microscopy [36,123,126,127] | |||
| Reverse transcription polymerase chain reaction (RT-PCR) [121,122,124] | |||
| Western blot [120] | |||
| μ-PIV [124,125] | |||
| Oscillatory | HUVECs [28] | Fluorescent microscopy [28] | |
| Pulsatile | Human aortic ECs [125] | μ-PIV [125] | |
| Vertical-step | Disturbed | BAECs [130,131] | Dye injections [130] |
| ELISA [131] | |||
| HUVECs [128,129] | Flow cytometry [129] | ||
| Fluorescent microscopy | |||
| Immunocytochemistry [130] | |||
| Phase contrast microscopy [128–131] | |||
| RT-PCR [129] | |||
| Western blot [129] | |||
| SSG | Steady | BAECs [40] | Fluorescent microscopy [39,40] |
| Phase contrast microscopy [40] | |||
| HCtAECs [39] |
3 Cone-and-Plate Devices
Cone-and-plate apparatuses are another way to induce wall SS on endothelial monolayers. Initially, these Couette flow devices were introduced to solve the limitation of the PPFC's inability to study SS on suspended cells [132]. In more recent studies, these devices have been used to study SS influence without the hydrostatic pressure gradient effects introduced by fluidic pumps on the seeded monolayer. For these purposes, cone-and-plate devices (CPDs) position an inverted, rotating cone above a stationary flat plate. The flat plate can be designed to either house several coverslips or directly be a replaceable tissue culture dish (Fig. 7). Representative optical images of CPDs have been included in many literature articles [133–135]. The rotation of the cone forces the fluid medium between the cone and plate to flow azimuthally in concentric circles and, thus, produce SS on the flat, bottom plate seeded with ECs [17,136]. This apparatus is able to achieve a laminar SS range between 0.01 and 100 dynes/cm2 and a turbulent SS range from 2 to 200 dynes/cm2, with the minimum values dependent upon the fluid's physical properties and the physical chamber parameters [17]. CPDs have several advantages over PPFCs: (1) entrance and exit length effects are nonexistent, (2) the laminar, homogeneous flow profile is independent of hydrostatic pressure gradients, (3) small dimensional changes of the device do not have large effects on the SS produced, (4) the operating fluid volume is small, making the detection of metabolites easier, and (5) they have the ability to produce both laminar and turbulent flow in a single device. However, these systems have their own limitations: (1) continuous sampling of the fluid requires further modifications, (2) accumulation of secreted molecules can occur within the operating fluid and could affect cell behavior if there are autocrine effects, (3) significant fluid evaporation can occur due to exposure to the open environment, requiring the continuous addition of fresh medium for long-term studies, and (4) live visualization of cells during the study is not possible unless transparent materials are used in device fabrication.
Fig. 7.
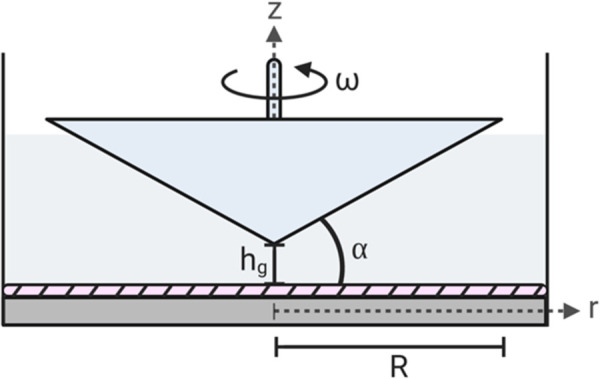
Schematic diagram of a cone-and-plate device depicting the flow domain and critical design parameters. The hatched region is the endothelial monolayer. As shown, α is the angle between the cone's surface and bottom plate, ω is the angular velocity of the cone, hg is the height gap, R is the total radius of the cone, r is the radial distance from the apex of the cone, and z is the coordinate orthogonal to the bottom plate, typically the cone's axis.
3.1 Shear Stress Calculations.
Assuming a constant, low angular velocity , the radial flow caused by centrifugal forces (secondary flow) is negligible, and SS across the surface of the bottom plate is defined as [137]
| (35) |
where is the coordinate normal to the plate and is the radial distance from the cone's apex. With a sufficiently small cone angle ( = 0.5–3 deg), the tangent function may be replaced solely by , resulting in a constant SS along the stationary plate [17]
| (36) |
If a gap exists between the cone apex and the bottom plate , the SS becomes spatially dependent (Fig. 8(a)) [138]
| (37) |
Fig. 8.
![Characterization of shear stress effects in a cone-and-plate device. (a) Wall shear stress at the monolayer is spatially dependent on the gap height between the cone and plate. With a gap height of zero, the plate experiences a constant shear stress along the radial distance from the apex of the cone, as calculated by Eq. (36) from Sdougos et al. [137]. As the gap height increases, the magnitude of the spatially dependent shear stress decreases, as calculated by Eq. (37) from Sucosky et al. [138] for the gap heights of 0.001 cm, 0.010 cm, and 0.100 cm. (b) Effect of the effective Reynolds number on wall shear stress at the monolayer as calculated by Eq. 38. When Rẽ < 1, the flow is primary and produces no secondary flow effects. An Rẽ between 1 and 4 develops secondary flow effects and becomes fully turbulent at values greater than 4. All equations were calculated with μ = 3.5 cP, ω = 2.49 rad/s, and α = 0.5 deg.](https://cdn.ncbi.nlm.nih.gov/pmc/blobs/25cf/8628846/0e55550f813f/bio-20-1480_020801_g008.jpg)
Characterization of shear stress effects in a cone-and-plate device. (a) Wall shear stress at the monolayer is spatially dependent on the gap height between the cone and plate. With a gap height of zero, the plate experiences a constant shear stress along the radial distance from the apex of the cone, as calculated by Eq. (36) from Sdougos et al. [137]. As the gap height increases, the magnitude of the spatially dependent shear stress decreases, as calculated by Eq. (37) from Sucosky et al. [138] for the gap heights of 0.001 cm, 0.010 cm, and 0.100 cm. (b) Effect of the effective Reynolds number on wall shear stress at the monolayer as calculated by Eq. 38. When < 1, the flow is primary and produces no secondary flow effects. An between 1 and 4 develops secondary flow effects and becomes fully turbulent at values greater than 4. All equations were calculated with μ = 3.5 cP, ω = 2.49 rad/s, and α = 0.5 deg.
SS can also generally be defined by the ratio of the viscous and inertial forces within the system, as shown by Fig. 8(b) [64,137,139]
| (38) |
where is the effective Reynolds number. This unitless parameter describes the flow regime induced by the system and is defined through the -theorem as
| (39) |
where is the total radius of the cone, is the gap height between the cone and plate, and a correction factor of 1/12 is included to coincide with literature values [139–141]. It is important to note that is locally dependent and ranges from 0 at the cone apex to a maximum at . Thus, it is possible to have laminar, transitional, and turbulent flows within the fluid at a single steady rotational rate. When , the flow is governed solely by viscous forces, and the radial flow velocity of the secondary flow is zero everywhere, inducing uniform SS over the entire plate surface. The flow produced is essentially axisymmetric, laminar, and tangential, which is termed primary flow. As becomes larger, the centrifugal forces become more significant, and secondary flow begins to develop in the range of . Here, the laminar fluid no longer flows in concentric circles and becomes three-dimensional. Turbulence first forms at the outer boundary and spreads inward with an increasing rotational speed. These secondary flow effects were first observed by Cox through the use of a dye visualization technique [141]. At these larger values of the effective Reynolds number (but still within the laminar flow range), SS at the surfaces of the plate and cone , respectively, become [137]
| (40) |
| (41) |
Regions with turbulence do not have a uniform SS. At , the flow is fully turbulent [138,143,144]. It is important to note that two values of and have been reported as the transition from laminar to turbulent flow due to the development of secondary effects.
3.2 Experimental Device Design.
Devices to produce primary laminar flow require minimal with a small cone angle. The use of a minimal produces a uniform SS on the cellular monolayer at a lower angular velocity. However, the requirement of a small cone angle magnifies the error in the cone positioning [33]. Literature values of are usually of the order of deg. Typical commercial devices are designed with and deg and cm, approximately [137]. In addition to a small cone angle, the cone axis (z-axis) must be closely aligned so that it is perpendicular to the plate, otherwise eccentric and pulsatile effects can form. Another aspect to consider is that the fluid must only fill the space between the plate and the cone or else an additional torque from fluid shearing can be developed [132]. Surfaces exposed to the study must also be biocompatible to reduce cell activation or damage. Importantly, these devices have a nonideal flow pattern near the outer boundary, and one should organize subsequent data analyses with this in mind. Literature designs of CPDs and their associated data analysis methods can be found in Table 4.
Table 4.
Cone-and-plate device designs
| Type of flow | Type of cell | Time (hr) | Shear stress (dynes/cm2) | Cone angle (deg) | Motor type | Analysis methods | References |
|---|---|---|---|---|---|---|---|
| Steady | HUVECs | 2 and 6 | 2.2 | 2.5 | Stepper | RT-PCR Immunoblot Fluorescent microscopy |
[145] |
| 48 | 8–10 | 0.5 | Brushless | Phase contrast microscopy | [134] | ||
| 0.5 | 12 | 1 | n.s.a | Fluorescent microscopy | [146] | ||
| 1–24 | 2–20 | 1 | n.s.a | RT-PCR ELISA Immunoblot |
[147] | ||
| 1 | 0–20 | 2 | DC Servo | Fluorescent microscopy | [148] | ||
| 12–36 | 5–20 | 0.5 | n.s.a | Western blot Phase contrast microscopy Flow cytometry |
[149] | ||
| 0.5–4 | 30 | 0.5 | n.s.a | Northern blot | [150] | ||
| BAECs | 1 | 15 | 0.5 | n.s.a | Western blot | [151] | |
| Pulsatile | HUVECs | 24 | −8.9 to 3.7 | 1 | n.s.a | RT-PCR ELISA Immunoblot |
[147] |
| 24 | 13.3–43.7 | 1 | n.s.a | RT-PCR ELISA Immunoblot |
[147] | ||
| 48 | 12–23 | 0.5 | Brushless | RT-PCR Phase contrast microscopy Fluorescent microscopy |
[133] | ||
| Oscillatory | HUVECs | 2 and 6 | 2.2–3.4 | 2.5 | Stepper | RT-PCR Immunoblot Fluorescent microscopy |
[145] |
| Human and rat aortic ECs | 24 | ±5 | 0.5 | Stepper | RT-PCR Western blot Phase contrast microscopy |
[152] | |
| Disturbed | HUVECs | 0.5 | −5 to 12 | 1 | n.s.a | Fluorescent microscopy | [146] |
Specifications were not stated (n.s.) in the reference article listed.
3.3 Device Modifications.
CPDs can undergo several modifications to induce various flow regimes. Production of turbulent flow or the alteration of SS magnitude can be accomplished by either increasing the rotational speed of the cone, increasing , or by increasing the viscosity of the fluid medium by adding dextran, gelatin, or polyvinylpyrrolidone. The device itself can be also altered for the ability to induce various flow regimes. CPDs used for studying the effect of mechanotransduction on cellular signaling generally fail to quantify and/or control the unsteady portion of the flow. For example, at the onset of flow, a lack of consideration of the time-dependent development of the flow profile could potentially lead to a mischaracterization of the effects of imposed flow regimes on cellular responses. Blackman et al. described the use of a microstepper motor modification to establish control of the dynamic fluid environment, allowing for quantification and control of the unsteady portion of the flow [153]. They later utilize this modification in a dynamic flow system to reproduce arterial waveforms segmented into discrete time steps [154]. In addition, the disturbed flow has been shown to be induced through a simple modification of the bottom plate similar to a vertical facing step for PPFCs by DePaola et al. [22]. Pulsatile and oscillatory flows can be induced by either positioning the cone oblique to the plate (i.e., not perpendicular) [155,156] or by bidirectional rotation of the cone [145], respectively. CPDs can also be modified for direct flow or cell visualization by using transparent materials, such as plexiglass [139,157].
4 Microfluidic Devices
While conventional macroscale devices have been widely used to generate mechanical forces, they require a large fluidic volume and many cells for culture. Additionally, these systems produce unstable SSGs [158] and lack the capacity to capture the full range of effects of complex in vivo models. To account for these insufficiencies, microfluidic devices have recently become an essential tool to study microcirculation systems at diameters comparable to human arterioles (∼90 μm) [159]. These devices can replicate physiologically relevant dimensions and lengths while holding the advantages of requiring minimal reagents (1–10−12 μL), shortened residence times, higher throughput, the ability for in situ quantification, and highly customizable geometries. Various micromodels of endothelial processes can also be developed at the microscale, with previous literature including devices for cell adhesion and detachment kinetics [160], blood-brain barrier function [161,162], tumor angiogenesis [163], nanoparticle permeability [164], and vascular permeability [165,166]. While microfluidic devices are highly customizable, representative optical pictures can be viewed within literature articles [167–171].
Due to scaling law effects, fluid behavior at the micron-level widely differs from behavior at the macroscale. It is imperative that the dimensions of microfluidic devices are not scaled-down from a conventional system design, making the appropriate construction and design of microfluidic devices essential to perform effective experiments. Dominant forces to leverage in device design due to the micron-length scale include laminar flow, diffusion, fluidic resistance, a large surface area to volume ratio, and surface tension [172]. By utilizing scaling laws, these devices provide the opportunity to integrate multiple mechanical cues and enable precise environmental control to accurately simulate physiologically relevant characteristics.
4.1 Shear Stress Calculations.
SS in a microchannel can range between 0.7 and 130 dynes/cm2 and is calculated as [173,174]
| (42) |
Therefore, given the same average velocity, SS will increase as the height of the channel decreases [175]. The exact equation will depend largely on the channel geometry and will need to be calibrated if there are various microdevices of differing height dimensions used in a study [158]. The simplest method to calculate SS in a microfluidic device is by using the planar Poiseuille model. For a parallel-plate configuration with an infinite aspect ratio, the wall SS and pressure drop across the channel, respectively, are
| (43) |
| (44) |
This method was adopted by Lu et al. for the design of two microfluidic devices with a large aspect ratio to simultaneously study cell detachment dynamics under multiple flow conditions [176]. In addition to Eq. (43), the Purday approximation can be used to calculate SS in the center of a microchamber [177,178]
| (45) |
In the equation above, and are empirical parameters related to the channel's aspect ratio. The empirical parameters were calculated by Young et al. for an aspect ratio less than three using , and [179]. Purday's approximation is valid for a fully developed laminar flow regime within a rectangular microchannel and has been shown to strongly correlate with experimental results [179]. The flow rate in a microchannel is given by where is the fluidic resistance within the channel. Resistance for a circular geometry can be calculated by the equation [172]
| (46) |
while a rectangular microchannel geometry with low or high aspect ratios have resistances, respectively, of
| (47) |
| (48) |
On the microscale, resistance can be a vital design parameter for the automatic modulation of the flow rate, and, therefore, SS, through individual parts of the device [180].
The Reynolds number for flows in long, straight microchannels of a constant cross section can be calculated with [181]
| (49) |
Because of the small scale of the chamber dimensions, flow within a microfluidic device will be exclusively laminar. The length of entrance effects in microchannels is approximated below. For a low Reynolds number approaching zero , it is predicted that the entrance length will be approximately 0.6 in length [182,183]
| (50) |
However, many microfluidic devices do not have a constant cross-sectional geometry, and, therefore, fluid dynamic parameters cannot be easily calculated by the methods described in this section. Because many microfluidic devices can easily be custom built for specific applications, the majority of experimental studies model the flow behavior using CFD analyses [184–186].
4.2 Device Design Considerations.
While many advantages come with the utilization of microfluidic devices, there are several design considerations that need to be accounted for with the initial fabrication. One needs to consider: (1) the choice of the device material, (2) the geometry and dimensions of the microchannels for the intended study, (3) pumping techniques and the method of controlling the fluid flow rate, and (4) external connections and their implications. The majority of devices are fabricated through soft lithography methods and use polydimethyl siloxane (PDMS) as the bulk material. PDMS is an excellent substrate material for experimental cell studies because the surface can easily be modified [187], and the geometry it uptakes can be specifically designed according to the intended application. In addition to the ease of fabrication, the material is characterized by a high gas permeability and optical transparency, giving the ability for real-time visualization. However, because of the hydrophobic nature of PDMS, the surface may cause unwanted adsorption of hydrophobic proteins or particles [188]. This can result in the loss of molecules or a significant decrease in molecule concentration during long-term recirculation of the fluid. While PDMS is highly utilized for device fabrication, microfluidic devices have been increasingly used by multiple groups to house three-dimensional (3D) hydrogels with more physiologic substrates, such as 3D extracellular matrices [189–192]. By designing 3D platforms to study cellular behavior on the micron-scale, both the 3D effects of flow are accounted for, and a more representative physiological environment can be utilized. Other microfluidic device fabrication methods and surface materials have been reviewed extensively elsewhere [163,193,194].
Due to the scale, the small hydraulic diameter used in microfluidic devices results in a significant pressure loss across the channel. This effect can be reduced by the use of a super hydrophobic surface as a coating or acting as the channel wall. The hydrophobicity introduced produces a mixed no-slip no-shear condition at the wall, comparatively reducing the pressure drop [195]. In addition to affecting the pressure drop, the inner surface of the fluid channel also provides the area for cell adhesion. Therefore, the fabrication material needs to be biocompatible. Cell seeding in micro-environments has been reviewed previously by Young et al. [196]. An important factor for data collection after applied SS is because the amount of cells cultured within the device is small, analysis of mRNA or proteins by either RT-PCR, enzyme-linked immunosorbent assay (ELISA), immunohistochemistry, or immunoblotting methods is difficult. New methods, such as single cell RNAseq, hold promise for these devices. Current major analysis approaches coupled with microfluidics can be broadly categorized as optical, electrochemical, or mass spectrometry [197].
The microscale also prohibits mixing within the fluid due to the low Reynolds number, enabling the study of responses to chemical gradients. Compared to macroscale devices that have the ability to produce mixing from turbulence, the laminar flows present in microchannels will not mix except by diffusion, which is governed by Brownian motion. Because diffusion is a dominant force, cells within the device may be inadvertently exposed to varying concentrations of nutrients, growth factors, or cell signaling molecules. Thus, microfluidic geometries may result in differing cellular responses depending on the position, and this mechanism has been widely used to study chemotactic, durotactic, and haptotactic responses to steady chemical gradients that cannot be captured in conventional macroscale devices [198].
The precise control of fluidic pumping is a critical consideration in device functionality, and much progress has been made in recent years to refine pumping techniques for microfluidic applications. Broadly, microfluidic pumps can be categorized as nonmechanically (i.e., electric field driven or passive flow [199]) or mechanically (e.g., Braille pins [200], syringe pumps [201,202], piezoelectric pumps [203], etc.) controlled. These methods have been extensively reviewed elsewhere for microdevices [204–208]. The method of pumping and controlling the fluid flow rate also influences how the device is externally connected to other components needed for operation. By increasing the number of connections, the potential for fluid leakage and contamination also becomes greater. In addition to the technique of media delivery to the cells, the consistent operation of pumps can lead to the formation of bubbles within the system. The development of bubbles can cause several consequences including inadequate supply of media, damage of cells at the gas–liquid interface, or obstruct fluid flow to certain areas of the device. Therefore, the prevention of bubble formation is critical and can be accomplished by either flushing the device either at a high-pressure flow or with a liquid characterized by a low surface tension before studies, utilization of a bubble trap, or by operating the device under a high-pressure flow for the duration of the experiment. As an alternative to pump-driven flow in microfluidic devices, gravity-driven perfusion flow, which is driven by a hydraulic head, has been implemented in microfluidic devices to help circumvent pump limitations [209,210].
5 Commercial Devices
While many in vitro flow chambers have been custom designed, an increasing number of commercial flow devices have been made available, with PPFCs and microfluidic devices being the most common on the current market (Table 5). In selecting a commercial PPFC, several aspects should be considered, including but not limited to: ease of sterilization, size of cell seeding area, the range of applied SS, imaging and/or analysis considerations, sealing mechanisms of the chamber, and overall cost. Commercial PPFCs are frequently supplied with the top and bottom chamber plates, precut silicone gaskets of varying thicknesses, and a length of tubing to fit the inlet and outlet chamber ports. PPFCs have a wide variety of applications in replicating (patho)physiologic flow regimes to study cellular phenomena, ranging from cellular adhesion under flow to effects of different flow regimes on cellular junctional proteins [25,191]. The use of microfluidic devices has expanded rapidly, as recently reviewed by Volpatti and Yetissen [130], which presents the current commercial market for microfluidic devices, the challenges it faces, and future directions microfluidic commercialization may take. Miniaturization and 3D printing manufacturing have allowed the design of complex microfluidic devices for many applications [211].
Table 5.
Commercially available flow chamber devices
| Manufacturer | Product | Base model price (USD) | Flow width (mm) | Flow depth (μm) |
|---|---|---|---|---|
| Applied Bio-Physics | ECIS flow system-single channel | $329 | 5.00 | 360 |
| SCIS flow system- Y channel | $329 | 5.00 | 600 | |
| Ibidi | μ-Slide I Luer | $200 | 5.00 | 200 |
| 400 | ||||
| 600 | ||||
| 800 | ||||
| IBI Scientific | Convertible flow cell | $122 | 24.00 | 8000 |
| IBI 3-channel flow cell | $171 | 4.00 | 1000 | |
| Glycotech | 31-001 circular flow chamber | $675 | 2.50 | 127 |
| 254 | ||||
| 5.00 | 254 | |||
| 10.00 | 254 | |||
| 31-010 rectangular flow chamber | $625 | 10.00 | 127 | |
| 254 | ||||
| Warner Instruments | (PFC-1) Pro-flow shear flow chamber | $1098 | 10.40 | 250 |
| RC-30 or RC-31 | $1360–$1461 | 4.00 | 125 | |
| 250 | ||||
| 375 | ||||
| 17.00 | 125 | |||
| 250 | ||||
| 375 |
The use of commercial devices inherently carries several advantages. Experimental studies become more repeatable with a commonly available commercial device. This also gives investigators the ability to compare and contrast studies from other groups if the same device and flow environment are used, thereby enabling meta-analyses and the potential extraction of meaningful results from a larger dataset across repeated experiments. The major disadvantage to widely available commercial devices is that they are generally designed for simple flow environments across a wide variety of applications, which is in contrast to custom-made chambers whose design is modified to the specific requirements of a specific experimental study.
6 Fluid Driving Systems
The performance of the flow chamber device is also dependent upon the design of the flow loop system. Typically, systems consist of a pump as a mechanical driving force, a digital flowmeter placed distal to the chamber outlet, one or more pressure transducers, a computer and software to monitor the flow environment, and an adequate number of connector ports and length of tubing to link all components to the flow loop (Fig. 9). While the entire system loop is specific to the experiment, the most critical aspect one needs to consider is the pump as a fluidic driving force. When choosing a pump, several factors must be considered to meet experimental requirements: (1) fluid capacity, (2) control of the fluid profile and/or range of flow rates, (3) directionality, (4) size if needed to fit inside an incubator, and (5) overall cost [212]. Various types of pumps offer recirculating or single pass flow and the ability to be easily integrated with the device. The most common pumps are peristaltic and syringe pumps.
Fig. 9.
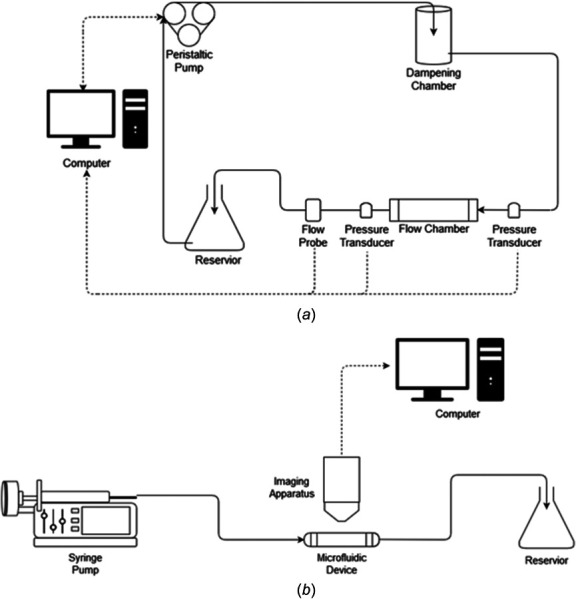
Process flow diagrams of fluid driving systems. (a) Process flow diagram for systems utilizing a peristaltic pump. Typically, fluid flow is driven from a reservoir by the pump. As the fluid exits the pump, it enters a dampening chamber, which minimizes pulsatile effects generated by the peristaltic pump. The fluid then flows through the flow chamber back to the reservoir, completing the flow system. Flow rate is monitored by a computer through a flow probe located downstream of the chamber. Pressure transducers can also be placed on either side of the flow chamber to monitor the pressure drop across the device. If changes are needed to the required flow rate, the computer will alter the angular velocity of the pump's rotor to produce the desired flow profile and shear stress for the study. (b) Process flow diagram of systems utilizing a syringe pump. Typically, a syringe loaded with fluid is mounted on a pump motor. The motor then pushes fluid from the syringe by a speed previously designated by the user. The fluid flows through the microfluidic device and into a discard reservoir. Real time imaging over the length of the study is collected by an imaging apparatus and is recorded by a computer.
6.1 Peristaltic Pumps.
The peristaltic pump, otherwise known as a roller pump, is the most common fluid driving system for both macro- and microdevices. This positive displacement pump drives fluid movement through the system loop by a process called peristalsis. This driving method utilizes flexible tubing placed on a rotor that houses multiple rollers (typically 3–4). As the rotor rotates, the tubing is alternatively compressed and released by the rollers, which actuates a fixed amount of fluid flow per rotation through mechanical action. However, because of the induced compression pattern, peristaltic pumps result in pulsatile flow. Pulsatility of the fluid can be minimized for studies requiring steady flow by the addition of a dampening chamber located downstream of the pump and proximal to the flow chamber. It is also important to note that for studies using whole blood as the recirculating fluid, the continued application of high shear stresses due to tube compression can result in the initiation of pump-induced platelet aggregation [213].
Peristaltic pumps offer several advantages over other types. Because of their size, they are able to generate high flow rates and handle large volumes of fluid. The rotor can also rotate either in a specified direction, producing pulsatile or steady flow, or in both directions, providing the ability to generate a more complex oscillatory flow. Their enclosed recirculation also reduces the volume of culture medium required. However, for long-term studies, the medium must be buffered with CO2 either within the chamber by the use of a gas-permeable material or by using a CO2-independent medium for a short time period [214]. In addition, systems are relatively inexpensive and have the ability to be sterilized, allowing them to be placed within an incubator. The likelihood of contamination is also minimal due to the fluid being in contact with only the inner surfaces of the tubing and not the pump itself.
When designing the flow system for use with a peristaltic pump, several factors should be considered. The first design parameter to be specified is the inner diameter of the tubing. For a given angular velocity of the rotor, as the inner diameter increases, the flow rate will also increase. Second, the flow rate is dependent on both the angular velocity of the pump's rotor and the inner diameter of the tubing. As the angular velocity increases for a given tube diameter, the flow rate will also increase. The last consideration is the pulsatility of the system. As the flow rate, length of tubing, the angular velocity of the rotor, and fluid density increase, more pulsation will occur. Therefore, for studies requiring steady flow, one should design the flow chamber to generate the required SS with a lower flow rate and include a dampening chamber to the flow loop, as described above, to reduce the pulsation. In addition, shorter lengths of tubing should be used, especially if the system needs to fit within an incubator.
In addition to a steady flow, this pump system is also used to simulate pulsatile and oscillatory flow conditions for the investigation of physiologic arterial pressure profile effects. For these unsteady flow conditions, two adjustments can be made to a peristaltic pump: (1) variation in the angular velocity of the stepping motor in one cycle, and (2) decreasing the gap size between the rollers and the roller bed of the pump head [215]. Generally, binary computer code will automatically vary the angular velocity. Flow pulsatility can also be simulated by adjusting the ratio of air to liquid in a compliance-adjustment chamber [216,217]. Setups using compliance-adjustment chambers usually place them after the flow probe within the system loop.
Systems with a peristaltic pump may be controlled by computer software systems, such as matlab or labview. These programable systems can monitor and record the flow rate and pressure over the time of the experiment by using flow probes and pressure transducers. Flow probes should be placed distal to the device to ensure the cellular monolayer is experiencing the correct flow rate. The software typically utilizes the flow probe to alter the pump's angular velocity to stabilize the flow rate to a user-defined value through a positive feedback loop (Fig. 9(a)).
6.2 Syringe Pumps.
Syringe pumps are most frequently used within microfluidic chambers due to the low volume requirements [201,202]. Syringe pump systems have two main components: the syringe and the motor that drives the fluid flow. Before studies, the syringe is loaded with a specific fluid input volume for the study, which only permits the system to pump a finite volume in a single direction. The pump can either drive fluid out of the syringe and through the chamber to a discard reservoir (Fig. 9(b)) or withdraw the fluid from a reservoir through the chamber. This latter configuration enables the pump to be placed outside the incubator. The flow is induced by a motor that the loaded syringe is placed upon. The motor can either push or pull the plunger of the syringe, depending on the setup of the system, and the flow rate can be changed by altering the motor speed. Various syringe diameters can be used to adapt the working range of the pump; however, smaller diameters enable better control of the flow rate at the cost of a smaller working volume. These systems can also be designed to hold multiple syringes. Commercially available motor systems are usually designed to accommodate one or two syringes but have recently been developed for up to 12 syringes (NE-1200, New Era Pump Systems, Inc., Farmingdale, NY). The addition of multiple syringes allows for studies to either use a larger fluid volume or run experiments in parallel with the same motor input conditions. Users can easily adapt the system to fit the experiment's needs.
Advantages of the syringe pump include little to no pulse of the fluid velocity, resulting in steady flow due to the constant motor speed. Multiple types of flow profiles can also be generated based on the system software. In addition, these systems give the user high flow precision while being easily programable. They are also able to be sterilized and usually allow for live imaging capabilities. However, they are typically more expensive than peristaltic pumps.
7 Conclusion
When choosing and designing a flow chamber, one needs to consider several vital criteria to accurately simulate the in vivo hemodynamic environment of interest. The chamber must be able to generate the flow profile and parameters that are to be considered, such as the magnitudes of the shear stress and the Reynolds number. Overall device size, between macro- and microdevices, is dependent on the analysis methods to be performed, such as RT-PCR or immunoblotting, and if one needs to either recover cells, detect metabolites, or have a continuous sampling of the fluid medium. Additionally, if the study requires direct visualization of the monolayer, the device materials must accommodate this need. The fluid driving system to actuate the fluid flow should deliver flow with optimal performance for the particular study. The chosen pump must easily handle the fluid capacity, be able to drive at the range of flow rates for the required SS magnitude(s), form the flow profile(s) of interest, and be able to fit within an incubator if needed. If multiple experiments are to be performed at various SS magnitudes and/or flow profiles, the system should be easily modified to switch between studies by either changing the pump's flow rate and/or directionality or by altering the cross-sectional geometry of the fluid channel within the flow chamber. By initially considering these aspects before designing the system, the choice of which flow chamber device design to use can be selected. Then, its dimensions can be optimized by using the equations and parameters provided throughout this review. It is important to note that the fluid analyses within this review assume the operating fluids are Newtonian. While this assumption is acceptable for cell culture media, it is limiting for in vitro systems studying hemodynamic effects using whole blood. While the assumption of blood as a Newtonian fluid is common for experimental studies, this is only applicable at shear rates greater than 100 s−1. At shear rates below this value, blood has a shear-thinning behavior where its apparent viscosity exponentially increases with decreasing shear rate. Therefore, this non-Newtonian behavior of blood, especially in the microvasculature and low shear flow conditions, can affect flow separation, velocity profile blunting, energy dissipation, and the magnitude and distribution of SS [218,219]. Thus, the Newtonian assumption for the fluid analyses within this review is applicable for cell culture media. Careful consideration of non-Newtonian effects must be made for whole blood studies.
While there are many studies focusing on endothelial responses under shear stress conditions within the literature, some articles do not include specifics about the flow chamber utilized to model the in vivo environments. As shown in this review, the design of the chamber's dimensions must accurately reproduce the specific in vivo shear stress environment through the design of the fluid channel's geometry. Investigators should include specifics detailing chamber dimensions, EC surface area coverage, and media components and properties, such as the density and viscosity, at the minimum. By neglecting to include this vital information for readers, the experiment cannot truly be accurately reproduced. Moving forward, investigators should clearly state the experimental design specifications in order to improve efficacy and for the validation of observations. The inclusion of chamber and flow loop design parameters will enable both the efficient design of new studies and the comparison to existing studies.
Acknowledgment
We appreciate Dr. Keri B. Vartanian for performing the flow experiments and contributing immunofluorescent images. The figures in this review were generated by the use of BioRender.com, a scientific illustration tool.
Funding Data
National Institutes of Health (NIH) (Grant Nos. R01HL130274 and R01HL144113; Funder ID: 10.13039/100000050).
Nomenclature
- =
hydraulic diameter of the fluid channel
- =
shear stress gradient
- EC =
endothelial cell
- =
frequency of flow
- =
total height of the fluid channel
- =
height at the fluid outlet
- =
gap height
- =
height at the fluid inlet
- =
total length of the fluid channel
- =
thickness of the oscillating boundary layer
- =
entrance length
- =
length of the gradient region
- =
length from the fluid inlet to the gradient region
- =
pressure
- =
fluid flow rate
- =
radial coordinate
- =
radius of cone
- =
fluidic resistance
- Re =
Reynolds number
- =
effective Reynolds number
- =
Reynolds number based on Stokes thickness
- SS =
wall shear stress
- SSG =
shear stress gradient
- =
time
- =
fluid velocity
- =
average fluid velocity
- =
width of the fluid channel
- =
width of the fluid outlet
- =
width of the fluid inlet
- W0 =
Womersley number
- =
vertical position with respect to the bottom plate
- z =
horizontal position along the length of the channel
- =
angle between the cone and bottom plate
- =
steady oscillatory component
- =
amplitude of average fluid velocity
- =
oscillatory component
- =
relative wall shear stress amplitude
- =
height of vertical step
- =
pressure drop across the fluid channel
- =
fluid viscosity
- =
kinematic viscosity of the fluid
- =
density of the fluid
- =
wall shear stress
- =
phase lag
- =
phase lag of average fluid velocity
- =
angular velocity of the cone or angular frequency
References
- [1]. Davies, P. F. , 1995, “ Flow-Mediated Endothelial Mechanotransduction,” Physiol. Rev., 75(3), pp. 519–560. 10.1152/physrev.1995.75.3.519 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2]. Natarajan, M. , Aravindan, N. , Sprague, E. A. , and Mohan, S. , 2016, “ Hemodynamic Flow-Induced Mechanotransduction Signaling Influences the Radiation Response of the Vascular Endothelium,” Radiat. Res., 186(2), pp. 175–188. 10.1667/RR14410.1 [DOI] [PubMed] [Google Scholar]
- [3]. Paszkowiak, J. J. , and Dardik, A. , 2003, “ Arterial Wall Shear Stress: Observations From the Bench to the Bedside,” Vasc. Endovascular Surg., 37(1), pp. 47–57. 10.1177/153857440303700107 [DOI] [PubMed] [Google Scholar]
- [4]. Chien, S. , 2007, “ Mechanotransduction and Endothelial Cell Homeostasis: The Wisdom of the Cell,” Am. J. Physiol. Circ. Physiol., 292(3), pp. H1209–H1224. 10.1152/ajpheart.01047.2006 [DOI] [PubMed] [Google Scholar]
- [5]. Chatterjee, S. , and Fisher, A. B. , 2014, “ Mechanotransduction in the Endothelium: Role of Membrane Proteins and Reactive Oxygen Species in Sensing, Transduction, and Transmission of the Signal With Altered Blood Flow,” Antioxid. Redox Signal., 20(6), pp. 899–913. 10.1089/ars.2013.5624 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [6]. Caligiuri, G. , 2019, “ Mechanotransduction, Immunoregulation, and Metabolic Functions of CD31 in Cardiovascular Pathophysiology,” Cardiovasc. Res., 115(9), pp. 1425–1434. 10.1093/cvr/cvz132 [DOI] [PubMed] [Google Scholar]
- [7]. Ballermann, B. J. , Dardik, A. , Eng, E. , and Liu, A. , 1998, “ Shear Stress and the Endothelium,” Kidney Int., 54, pp. S100–S108. 10.1046/j.1523-1755.1998.06720.x [DOI] [PubMed] [Google Scholar]
- [8]. Malek, A. M. , Alper, S. L. , and Izumo, S. , 1999, “ Hemodynamic Shear Stress and Its Role in Atherosclerosis,” JAMA, 282(21), pp. 2035–2042. 10.1001/jama.282.21.2035 [DOI] [PubMed] [Google Scholar]
- [9]. Giddens, D. P. , Zarins, C. K. , and Glagov, S. , 1993, “ The Role of Fluid Mechanics in the Localization and Detection of Atherosclerosis,” ASME J. Biomech. Eng., 115(4B), pp. 588–594. 10.1115/1.2895545 [DOI] [PubMed] [Google Scholar]
- [10]. Pohl, U. , Holtz, J. , Busse, R. , and Bassenge, E. , 1986, “ Crucial Role of Endothelium in the Vasodilator Response to Increased Flow In Vivo,” Hypertension, 8(1), pp. 37–44. 10.1161/01.HYP.8.1.37 [DOI] [PubMed] [Google Scholar]
- [11]. Kamiya, A. , Bukhari, R. , and Togawa, T. , 1984, “ Adaptive Regulation of Wall Shear Stress Optimizing Vascular Tree Function,” Bull. Math. Biol., 46(1), pp. 127–137. 10.1016/S0092-8240(84)80038-5 [DOI] [PubMed] [Google Scholar]
- [12]. Traub, O. , and Berk, B. C. , 1998, “ Laminar Shear Stress: Mechanisms by Which Endothelial Cells Transduce an Atheroprotective Force,” Arterioscler. Thromb. Vasc. Biol., 18(5), pp. 677–685. 10.1161/01.ATV.18.5.677 [DOI] [PubMed] [Google Scholar]
- [13]. Hagen, M. W. , and Hinds, M. T. , 2019, “ Static Spatial Growth Restriction Micropatterning of Endothelial Colony Forming Cells Influences Their Morphology and Gene Expression,” PLoS One, 14(6), p. e0218197. 10.1371/journal.pone.0218197 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [14]. Vartanian, K. B. , Kirkpatrick, S. J. , Hanson, S. R. , and Hinds, M. T. , 2008, “ Endothelial Cell Cytoskeletal Alignment Independent of Fluid Shear Stress on Micropatterned Surfaces,” Biochem. Biophys. Res. Commun., 371(4), pp. 787–792. 10.1016/j.bbrc.2008.04.167 [DOI] [PubMed] [Google Scholar]
- [15]. Shyy, J. Y. J. , and Chien, S. , 2002, “ Role of Integrins in Endothelial Mechanosensing of Shear Stress,” Circ. Res., 91(9), pp. 769–775. 10.1161/01.RES.0000038487.19924.18 [DOI] [PubMed] [Google Scholar]
- [16]. Rezgaoui, M. , Rodriguez, A. , Herlitz, K. , and Escudero, C. , 2018, “ Sensing Fluid-Shear Stress in the Endothelial System With a Special Emphasis on the Primary Cilium,” Endothelial Dysfunction—Old Concepts and New Challenges, IntechOpen, London, UK. [Google Scholar]
- [17]. Dewey, C. F. , Bussolari, S. R. , Gimbrone, M. A. , and Davies, P. F. , 1981, “ The Dynamic Response of Vascular Endothelial Cells to Fluid Shear Stress,” ASME J. Biomech. Eng., 103(3), pp. 177–185. 10.1115/1.3138276 [DOI] [PubMed] [Google Scholar]
- [18]. Ebong, E. E. , Lopez-Quintero, S. V. , Rizzo, V. , Spray, D. C. , and Tarbell, J. M. , 2014, “ Shear-Induced Endothelial NOS Activation and Remodeling Via Heparan Sulfate, Glypican-1, and Syndecan-1,” Integr. Biol., 6(3), pp. 338–347. 10.1039/C3IB40199E [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19]. Chatterjee, S. , 2018, “ Endothelial Mechanotransduction, Redox Signaling and the Regulation of Vascular Inflammatory Pathways,” Front. Physiol., 9, p. 524. 10.3389/fphys.2018.00524 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [20]. Flaherty, J. T. , Pierce, J. E. , Ferrans, V. , Patel, D. J. , Tucker, K. W. , and Fry, D. L. , 1972, “ Endothelial Nuclear Patterns in the Canine Arterial Tree With Particular Reference to Hemodynamic Events,” Circ. Res., 30(1), pp. 23–33. 10.1161/01.RES.30.1.23 [DOI] [PubMed] [Google Scholar]
- [21]. Wang, C. , Baker, B. M. , Chen, C. S. , and Schwartz, M. A. , 2013, “ Endothelial Cell Sensing of Flow Direction,” Arterioscler. Thromb. Vasc. Biol., 33(9), pp. 2130–2136. 10.1161/ATVBAHA.113.301826 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [22]. DePaola, N. , Gimbrone, M. A. , Davies, P. F. , and Dewey, C. F. , 1992, “ Vascular Endothelium Responds to Fluid Shear Stress Gradients,” Arterioscler. Thromb., 12(11), pp. 1254–1257. 10.1161/01.ATV.12.11.1254 [DOI] [PubMed] [Google Scholar]
- [23]. Lu, Y. , Li, W.-Q. , Oraifige, I. , and Wang, W. , 2014, “ Converging Parallel Plate Flow Chambers for Studies on the Effect of the Spatial Gradient of Wall Shear Stress on Endothelial Cells,” J. Biosci. Med., 02(02), pp. 50–56. 10.1115/1.4051765 [DOI] [Google Scholar]
- [24]. Wojciak-Stothard, B. , and Ridley, A. J. , 2003, “ Shear Stress–Induced Endothelial Cell Polarization is Mediated by Rho and Rac but Not Cdc42 or PI 3-Kinases,” J. Cell Biol., 161(2), pp. 429–439. 10.1083/jcb.200210135 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [25]. van Kooten, T. G. , Schakenraad, J. M. , Van der Mei, H. C. , and Busscher, H. J. , 1992, “ Development and Use of a Parallel-Plate Flow Chamber for Studying Cellular Adhesion to Solid Surfaces,” J. Biomed. Mater. Res., 26(6), pp. 725–738. 10.1002/jbm.820260604 [DOI] [PubMed] [Google Scholar]
- [26]. Dolan, J. M. , Sim, F. J. , Meng, H. , and Kolega, J. , 2012, “ Endothelial Cells Express a Unique Transcriptional Profile Under Very High Wall Shear Stress Known to Induce Expansive Arterial Remodeling,” Am. J. Physiol. Cell Physiol., 302(8), pp. C1109–C1118. 10.1152/ajpcell.00369.2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27]. Frangos, J. A. , McIntire, L. V. , and Eskin, S. G. , 1988, “ Shear Stress Induced Stimulation of Mammalian Cell Metabolism,” Biotechnol. Bioeng., 32(8), pp. 1053–1060. 10.1002/bit.260320812 [DOI] [PubMed] [Google Scholar]
- [28]. Wang, Y.-X. , Xiang, C. , Liu, B. , Zhu, Y. , Luan, Y. , Liu, S.-T. , and Qin, K.-R. , 2016, “ A Multi-Component Parallel-Plate Flow Chamber System for Studying the Effect of Exercise-Induced Wall Shear Stress on Endothelial Cells,” Biomed. Eng. Online, 15(Suppl 2), p. 154. 10.1186/s12938-016-0273-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- [29]. Balaguru, U. M. , Sundaresan, L. , Manivannan, J. , Majunathan, R. , Mani, K. , Swaminathan, A. , Venkatesan, S. , Kasiviswanathan, D. , and Chatterjee, S. , 2016, “ Disturbed Flow Mediated Modulation of Shear Forces on Endothelial Plane: A Proposed Model for Studying Endothelium Around Atherosclerotic Plaques,” Sci. Rep., 6(1), p. 27304. 10.1038/srep27304 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [30]. Erbeldinger, N. , Rapp, F. , Ktitareva, S. , Wendel, P. , Bothe, A. S. , Dettmering, T. , Durante, M. , Friedrich, T. , Bertulat, B. , Meyer, S. , Cardoso, M. C. , Hehlgans, S. , Rödel, F. , and Fournier, C. , 2017, “ Measuring Leukocyte Adhesion to (Primary) Endothelial Cells After Photon and Charged Particle Exposure With a Dedicated Laminar Flow Chamber,” Front. Immunol., 8(JUN), p. 627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31]. Koo, M.-A. , Kang, J. , Lee, M. , Seo, H. , Kwon, B.-J. , You, K. , Kim, M. , Kim, D. , and Park, J.-C. , 2014, “ Stimulated Migration and Penetration of Vascular Endothelial Cells Into Poly (L-Lactic Acid) Scaffolds Under Flow Conditions,” Biomater. Res., 18(1), p. 7. 10.1186/2055-7124-18-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32]. Qin, K. , Hu, X. , and Liu, Z. , 2007, “ Analysis of Pulsatile Flow in the Parallel-Plate Flow Chamber With Spatial Shear Stress Gradient,” J. Hydrodyn,., 19(1), pp. 113–120. 10.1016/S1001-6058(07)60036-5 [DOI] [Google Scholar]
- [33]. Wong, A. K. , LLanos, P. , Boroda, N. , Rosenberg, S. R. , and Rabbany, S. Y. , 2016, “ A Parallel-Plate Flow Chamber for Mechanical Characterization of Endothelial Cells Exposed to Laminar Shear Stress,” Cell. Mol. Bioeng., 9(1), pp. 127–138. 10.1007/s12195-015-0424-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34]. Kairong, Q. , Weiyuan, J. , Xixi, L. , and Zhaorong, L. , 1998, “ On Analysis of the Steady Flow in an Irrectangular Parallel-Plate Flow Chamber,” Appl. Math. Mech., 19(9), pp. 851–859. 10.1007/BF02458240 [DOI] [Google Scholar]
- [35]. Shen, L. , Qiao, A. , Ding, H. , Mo, G. , Xu, G. , Du, Y. , Li, M. , Chen, Z. , and Zeng, Y. , 2006, “ An Apparatus for Studying the Response of Cultured Endothelial Cells to Stresses,” Aust. Phys. Eng. Sci. Med., 29(2), pp. 196–202. 10.1007/BF03178893 [DOI] [PubMed] [Google Scholar]
- [36]. Levesque, M. J. , and Nerem, R. M. , 1985, “ The Elongation and Orientation of Cultured Endothelial Cells in Response to Shear Stress,” ASME J. Biomech. Eng., 107(4), pp. 341–347. 10.1115/1.3138567 [DOI] [PubMed] [Google Scholar]
- [37]. Nauman, E. A. , Risic, K. J. , Keaveny, T. M. , and Satcher, R. L. , 1999, “ Quantitative Assessment of Steady and Pulsatile Flow Fields in a Parallel Plate Flow Chamber,” Ann. Biomed. Eng., 27(2), pp. 194–199. 10.1114/1.173 [DOI] [PubMed] [Google Scholar]
- [38]. Rashad, S. , Han, X. , Saqr, K. , Tupin, S. , Ohta, M. , Niizuma, K. , and Tominaga, T. , 2020, “ Epigenetic Response of Endothelial Cells to Different Wall Shear Stress Magnitudes: A Report of New Mechano‐miRNAs,” J. Cell. Physiol., 235(11), pp. 7827–7839. 10.1002/jcp.29436 [DOI] [PubMed] [Google Scholar]
- [39]. Yoshino, D. , Sakamoto, N. , Takahashi, K. , Eri, I. , and Sato, M. , 2013, “ Development of Novel Flow Chamber to Study Endothelial Cell Morphology: Effects of Shear Flow With Uniform Spatial Gradient on Distribution of Focal Adhesion,” J. Biomech. Sci. Eng., 8(3), pp. 233–243. 10.1299/jbse.8.233 [DOI] [Google Scholar]
- [40]. Dolan, J. M. , Meng, H. , Singh, S. , Paluch, R. , and Kolega, J. , 2011, “ High Fluid Shear Stress and Spatial Shear Stress Gradients Affect Endothelial Proliferation, Survival, and Alignment,” Ann. Biomed. Eng., 39(6), pp. 1620–1631. 10.1007/s10439-011-0267-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41]. Uzarski, J. S. , Scott, E. W. , and McFetridge, P. S. , 2013, “ Adaptation of Endothelial Cells to Physiologically-Modeled, Variable Shear Stress,” PLoS One, 8(2), p. e57004. 10.1371/journal.pone.0057004 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [42]. McCormick, S. M. , Seil, J. T. , Smith, D. S. , Tan, F. , and Loth, F. , 2012, “ Transitional Flow in a Cylindrical Flow Chamber for Studies at the Cellular Level,” Cardiovasc. Eng. Technol., 3(4), pp. 439–449. 10.1007/s13239-012-0107-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Oertel, H. , ed., 2004, “ Biofluid Mechanics of Blood Circulation,” Prandtl's Essentials of Fluid Mechanics, Springer, New York, pp. 615–654. [Google Scholar]
- [44]. Lane, W. O. , Jantzen, A. E. , Carlon, T. A. , Jamiolkowski, R. M. , Grenet, J. E. , Ley, M. M. , Haseltine, J. M. , Galinat, L. J. , Lin, F.-H. , Allen, J. D. , Truskey, G. A. , and Achneck, H. E. , 2012, “ Parallel-Plate Flow Chamber and Continuous Flow Circuit to Evaluate Endothelial Progenitor Cells Under Laminar Flow Shear Stress,” J. Vis. Exp., 59, p. e3349. 10.3791/334 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45]. Putra, N. K. , Wang, Z. , Anzai, H. , and Ohta, M. , 2018, “ Computational Fluid Dynamics Analysis to Predict Endothelial Cells Migration During Flow Exposure Experiment With Placement of Two Stent Wires,” 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Honolulu, HI, July 18–21, pp. 5454–5457. 10.1109/EMBC.2018.8513517 [DOI] [PubMed] [Google Scholar]
- [46]. Usami, S. , Chen, H. H. , Zhao, Y. , Chien, S. , and Skalak, R. , 1993, “ Design and Construction of a Linear Shear Stress Flow Chamber,” Ann. Biomed. Eng., 21(1), pp. 77–83. 10.1007/BF02368167 [DOI] [PubMed] [Google Scholar]
- [47]. DeVerse, J. S. , Sandhu, A. S. , Mendoza, N. , Edwards, C. M. , Sun, C. , Simon, S. I. , and Passerini, A. G. , 2013, “ Shear Stress Modulates VCAM-1 Expression in Response to TNF-α and Dietary Lipids Via Interferon Regulatory Factor-1 in Cultured Endothelium,” Am. J. Physiol. Circ. Physiol., 305(8), pp. H1149–H1157. 10.1152/ajpheart.00311.2013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [48]. Tsou, J. K. , Gower, R. M. , Ting, H. J. , Schaff, U. Y. , Insana, M. F. , Passerini, A. G. , and Simon, S. I. , 2008, “ Spatial Regulation of Inflammation by Human Aortic Endothelial Cells in a Linear Gradient of Shear Stress,” Microcirculation, 15(4), pp. 311–323. 10.1080/10739680701724359 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [49]. Bailey, K. A. , Moreno, E. , Haj, F. G. , Simon, S. I. , and Passerini, A. G. , 2019, “ Mechanoregulation of P38 Activity Enhances Endoplasmic Reticulum Stress‐Mediated Inflammation by Arterial Endothelium,” FASEB J., 33(11), pp. 12888–12899. 10.1096/fj.201900236R [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50]. LaMack, J. A. , and Friedman, M. H. , 2007, “ Individual and Combined Effects of Shear Stress Magnitude and Spatial Gradient on Endothelial Cell Gene Expression,” Am. J. Physiol. Circ. Physiol., 293(5), pp. H2853–H2859. 10.1152/ajpheart.00244.2007 [DOI] [PubMed] [Google Scholar]
- [51]. Franzoni, M. , O'Connor, D. T. , Marcar, L. , Power, D. , Moloney, M. A. , Kavanagh, E. G. , Leask, R. L. , Nolan, J. , Kiely, P. A. , and Walsh, M. T. , 2020, “ The Presence of a High Peak Feature Within Low-Average Shear Stimuli Induces Quiescence in Venous Endothelial Cells,” Ann. Biomed. Eng., 48(2), pp. 582–594. 10.1007/s10439-019-02371-5 [DOI] [PubMed] [Google Scholar]
- [52]. Ene-Iordache, B. , and Remuzzi, A. , 2012, “ Disturbed Flow in Radial-Cephalic Arteriovenous Fistulae for Haemodialysis: Low and Oscillating Shear Stress Locates the Sites of Stenosis,” Nephrol. Dial. Transplant., 27(1), pp. 358–368. 10.1093/ndt/gfr342 [DOI] [PubMed] [Google Scholar]
- [53]. Dolan, J. M. , Kolega, J. , and Meng, H. , 2013, “ High Wall Shear Stress and Spatial Gradients in Vascular Pathology: A Review,” Ann. Biomed. Eng., 41(7), pp. 1411–1427. 10.1007/s10439-012-0695-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [54]. Sakamoto, N. , Saito, N. , Han, X. , Ohashi, T. , and Sato, M. , 2010, “ Effect of Spatial Gradient in Fluid Shear Stress on Morphological Changes in Endothelial Cells in Response to Flow,” Biochem. Biophys. Res. Commun., 395(2), pp. 264–269. 10.1016/j.bbrc.2010.04.002 [DOI] [PubMed] [Google Scholar]
- [55]. Givens, C. , and Tzima, E. , 2016, “ Endothelial Mechanosignaling: Does One Sensor Fit All?,” Antioxid. Redox Signal., 25(7), pp. 373–388. 10.1089/ars.2015.6493 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [56]. Dai, G. , Kaazempur-Mofrad, M. R. , Kamm, R. D. , Zhang, Y. , Vaughn, S. , Garcia-Cardena, G. , and Gimbrone, M. A. , 2004, “ Distinct Endothelial Phenotypes Evoked by Arterial Waveforms Derived From Atherosclerosis-Prone and Atherosclerosis-Protected Regions of the Human Vasculature,” Cardiovasc. Pathol., 13(3), p. 26. 10.1016/j.carpath.2004.03.070 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [57]. Chiu, J.-J. , Chen, C.-N. , Lee, P.-L. , Tsair Yang, C. , Sheng Chuang, H. , Chien, S. , and Usami, S. , 2003, “ Analysis of the Effect of Disturbed Flow on Monocytic Adhesion to Endothelial Cells,” J. Biomech., 36(12), pp. 1883–1895. 10.1016/S0021-9290(03)00210-0 [DOI] [PubMed] [Google Scholar]
- [58]. Chiu, J.-J. , and Chien, S. , 2011, “ Effects of Disturbed Flow on Vascular Endothelium: Pathophysiological Basis and Clinical Perspectives,” Physiol. Rev., 91(1), pp. 327–387. 10.1152/physrev.00047.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [59]. Chien, S. , 2008, “ Effects of Disturbed Flow on Endothelial Cells,” Ann. Biomed. Eng., 36(4), pp. 554–562. 10.1007/s10439-007-9426-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [60]. White, C. R. , Haidekker, M. , Bao, X. , and Frangos, J. A. , 2001, “ Temporal Gradients in Shear, but Not Spatial Gradients, Stimulate Endothelial Cell Proliferation,” Circulation, 103(20), pp. 2508–2513. 10.1161/01.CIR.103.20.2508 [DOI] [PubMed] [Google Scholar]
- [61]. Durst, F. , and Pereira, J. C. F. , 1988, “ Time-Dependent Laminar Backward-Facing Step Flow in a Two-Dimensional Duct,” ASME J. Fluids Eng., 110(3), pp. 289–296. 10.1115/1.3243547 [DOI] [Google Scholar]
- [62]. Haidekker, M. A. , White, C. R. , and Frangos, J. A. , 2001, “ Analysis of Temporal Shear Stress Gradients During the Onset Phase of Flow Over a Backward-Facing Step,” ASME J. Biomech. Eng., 123(5), pp. 455–463. 10.1115/1.1389460 [DOI] [PubMed] [Google Scholar]
- [63]. White, C. R. , Stevens, H. Y. , Haidekker, M. , and Frangos, J. A. , 2005, “ Temporal Gradients in Shear, but Not Spatial Gradients, Stimulate ERK1/2 Activation in Human Endothelial Cells,” Am. J. Physiol. Circ. Physiol., 289(6), pp. H2350–H2355. 10.1152/ajpheart.01229.2004 [DOI] [PubMed] [Google Scholar]
- [64]. Arslan, N. , Isik, S. , and Uykan, Ö. , 2010, “ Steady and Disturbed Flow Effects on Human Umbilical Vein Endothelial Cells (HUVECs) in Vascular System: An Experimental Study,” Acta Bioeng. Biomech., 12(4), pp. 3–9.http://www.actabio.pwr.wroc.pl/Vol12No4/1.pdf [PubMed] [Google Scholar]
- [65]. Biswas, G. , Breuer, M. , and Durst, F. , 2004, “ Backward-Facing Step Flows for Various Expansion Ratios at Low and Moderate Reynolds Numbers,” ASME J. Fluids Eng., 126(3), pp. 362–374. 10.1115/1.1760532 [DOI] [Google Scholar]
- [66]. Abu-Mulaweh, H. I. , 2003, “ A Review of Research on Laminar Mixed Convection Flow Over Backward- and Forward-Facing Steps,” Int. J. Therm. Sci., 42(9), pp. 897–909. 10.1016/S1290-0729(03)00062-0 [DOI] [Google Scholar]
- [67]. Kitoh, A. , Sugawara, K. , Yoshikawa, H. , and Ota, T. , 2007, “ Expansion Ratio Effects on Three-Dimensional Separated Flow and Heat Transfer Around Backward-Facing Steps,” ASME J. Heat Transfer-Trans. ASME, 129(9), pp. 1141–1155. 10.1115/1.2739619 [DOI] [Google Scholar]
- [68]. Barstad, R. M. , Roald, H. E. , Cui, Y. , Turitto, V. T. , and Sakariassen, K. S. , 1994, “ A Perfusion Chamber Developed to Investigate Thrombus Formation and Shear Profiles in Flowing Native Human Blood at the Apex of Well-Defined Stenoses,” Arterioscler. Thromb., 14(12), pp. 1984–1991. 10.1161/01.ATV.14.12.1984 [DOI] [PubMed] [Google Scholar]
- [69]. Barstad, R. M. , Kierulf, P. , and Sakariassen, K. S. , 1996, “ Collagen Induced Thrombus Formation at the Apex of Eccentric Stenoses—A Time Course Study With Non-Anticoagulated Human Blood,” Thromb. Haemost., 75(04), pp. 685–692. 10.1055/s-0038-1650343 [DOI] [PubMed] [Google Scholar]
- [70]. Watkins, N. V. , Caro, C. G. , and Wang, W. , 2002, “ Parallel-Plate Flow Chamber for Studies of 3D Flow-Endothelium Interaction,” Biorheology, 39(3–4), pp. 337–342.https://content.iospress.com/journals/biorheology/39/3-4 [PubMed] [Google Scholar]
- [71]. Szymanski, M. P. , Metaxa, E. , Meng, H. , and Kolega, J. , 2008, “ Endothelial Cell Layer Subjected to Impinging Flow Mimicking the Apex of an Arterial Bifurcation,” Ann. Biomed. Eng., 36(10), pp. 1681–1689. 10.1007/s10439-008-9540-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- [72]. Crouch, C. F. , Fowler, H. W. , and Spier, R. E. , 1985, “ The Adhesion of Animal Cells to Surfaces: The Measurement of Critical Surface Shear Stress Permitting Attachment or Causing Detachment,” J. Chem. Technol. Biotechnol. Biotechnol., 35(4), pp. 273–281. 10.1002/jctb.280350408 [DOI] [Google Scholar]
- [73]. Nakayama, K. H. , Surya, V. N. , Gole, M. , Walker, T. W. , Yang, W. , Lai, E. S. , Ostrowski, M. A. , Fuller, G. G. , Dunn, A. R. , and Huang, N. F. , 2016, “ Nanoscale Patterning of Extracellular Matrix Alters Endothelial Function under Shear Stress,” Nano Lett., 16(1), pp. 410–419. 10.1021/acs.nanolett.5b04028 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [74]. Ostrowski, M. A. , Huang, E. Y. , Surya, V. N. , Poplawski, C. , Barakat, J. M. , Lin, G. L. , Fuller, G. G. , and Dunn, A. R. , 2016, “ Multiplexed Fluid Flow Device to Study Cellular Response to Tunable Shear Stress Gradients,” Ann. Biomed. Eng., 44(7), pp. 2261–2272. 10.1007/s10439-015-1500-7 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [75]. Yapici, S. , Kuslu, S. , Ozmetin, C. , Ersahan, H. , and Pekdemir, T. , 1999, “ Surface Shear Stress for a Submerged Jet Impingement Using Electrochemical Technique,” J. Appl. Electrochem., 29(2), pp. 185–190. 10.1023/A:1003464614715 [DOI] [Google Scholar]
- [76]. Behnia, M. , Parneix, S. , and Durbin, P. , 1997, “ Accurate Modeling of Impinging Jet Heat Transfer,” Cent. Turbul. Res. Annu. Res. Briefs, pp. 149–164https://web.stanford.edu/group/ctr/ResBriefs97/behnia.pdf. [Google Scholar]
- [77]. Saterbak, A. , and Lauffenburger, D. A. , 1996, “ Adhesion Mediated by Bonds in Series,” Biotechnol. Prog., 12(5), pp. 682–699. 10.1021/bp960061u [DOI] [PubMed] [Google Scholar]
- [78]. Koseoglu, M. F. , and Baskaya, S. , 2010, “ The Role of Jet Inlet Geometry in Impinging Jet Heat Transfer, Modeling and Experiments,” Int. J. Therm. Sci., 49(8), pp. 1417–1426. 10.1016/j.ijthermalsci.2010.02.009 [DOI] [Google Scholar]
- [79]. Christ, K. V. , and Turner, K. T. , 2010, “ Methods to Measure the Strength of Cell Adhesion to Substrates,” J. Adhes. Sci. Technol., 24(13–14), pp. 2027–2058. 10.1163/016942410X507911 [DOI] [Google Scholar]
- [80]. Vaishnav, R. N. , Patel, D. J. , Atabek, H. B. , Deshpande, M. D. , Plowman, F. , and Vossoughi, J. , 1983, “ Determination of the Local Erosion Stress of the Canine Endothelium Using a Jet Impingement Method,” ASME J. Biomech. Eng., 105(1), pp. 77–83. 10.1115/1.3138389 [DOI] [PubMed] [Google Scholar]
- [81]. Bouafsoun, A. , Othmane, A. , Kerkeni, A. , Jaffrézic, N. , and Ponsonnet, L. , 2006, “ Evaluation of Endothelial Cell Adherence Onto Collagen and Fibronectin: A Comparison Between Jet Impingement and Flow Chamber Techniques,” Mater. Sci. Eng. C, 26(2–3), pp. 260–266. 10.1016/j.msec.2005.10.051 [DOI] [Google Scholar]
- [82]. Papadaki, M. , and Mclntire, L. V. , 1999, “ Quantitative Measurement of Shear-Stress Effects on Endothelial Cells,” Tissue Engineering Methods and Protocols. Methods in Molecular Medicine, Morgan J. R., and Yarmush M. L., eds., Humana Press, Totowa, NJ, pp. 577–593. 10.1385/0-89603-516-6:577 [DOI] [PubMed] [Google Scholar]
- [83]. Goldstein, A. S. , and DiMilla, P. A. , 1998, “ Comparison of Converging and Diverging Radial Flow for Measuring Cell Adhesion,” AIChE J., 44(2), pp. 465–473. 10.1002/aic.690440222 [DOI] [Google Scholar]
- [84]. Ostrowski, M. A. , Huang, N. F. , Walker, T. W. , Verwijlen, T. , Poplawski, C. , Khoo, A. S. , Cooke, J. P. , Fuller, G. G. , and Dunn, A. R. , 2014, “ Microvascular Endothelial Cells Migrate Upstream and Align Against the Shear Stress Field Created by Impinging Flow,” Biophys. J., 106(2), pp. 366–374. 10.1016/j.bpj.2013.11.4502 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [85]. Diamond, S. L. , Eskin, S. G. , and McIntire, L. V. , 1989, “ Fluid Flow Stimulates Tissue Plasminogen Activator Secretion by Cultured Human Endothelial Cells,” Science, 243(4897), pp. 1483–1485. 10.1126/science.2467379 [DOI] [PubMed] [Google Scholar]
- [86]. Hsieh, H.-J. , Li, N.-Q. , and Frangos, J. A. , 1993, “ Pulsatile and Steady Flow Induces C-Fos Expression in Human Endothelial Cells,” J. Cell. Physiol., 154(1), pp. 143–151. 10.1002/jcp.1041540118 [DOI] [PubMed] [Google Scholar]
- [87]. Helmlinger, G. , Berk, B. C. , and Nerem, R. M. , 1995, “ Calcium Responses of Endothelial Cell Monolayers Subjected to Pulsatile and Steady Laminar Flow Differ,” Am. J. Physiol., 269(2 Pt 1), pp. C367–C375. 10.1152/ajpcell.1995.269.2.C367 [DOI] [PubMed] [Google Scholar]
- [88]. Levesque, M. J. , Sprague, E. A. , Schwartz, C. J. , and Nerem, R. M. , 1989, “ The Influence of Shear Stress on Cultured Vascular Endothelial Cells: The Stress Response of an Anchorage-Dependent Mammalian Cell,” Biotechnol. Prog., 5(1), pp. 1–8. 10.1002/btpr.5420050105 [DOI] [Google Scholar]
- [89]. Frangos, J. , Eskin, S. G. , McIntire, L. V. , and Ives, C. L. , 1985, “ Flow Effects on Prostacyclin Production by Cultured Human Endothelial Cells,” Science, 227(4693), pp. 1477–1479. 10.1126/science.3883488 [DOI] [PubMed] [Google Scholar]
- [90]. Shyy, J. Y. , Lin, M. C. , Han, J. , Lu, Y. , Petrime, M. , and Chien, S. , 1995, “ The Cis-Acting Phorbol Ester ‘12-O-Tetradecanoylphorbol 13-Acetate’-Responsive Element is Involved in Shear Stress-Induced Monocyte Chemotactic Protein 1 Gene Expression,” Proc. Natl. Acad. Sci., 92(17), pp. 8069–8073. 10.1073/pnas.92.17.8069 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [91]. Skarlatos, S. I. , and Hollis, T. M. , 1987, “ Cultured Bovine Aortic Endothelial Cells Show Increased Histamine Metabolism When Exposed to Oscillatory Shear Stress,” Atherosclerosis, 64(1), pp. 55–61. 10.1016/0021-9150(87)90054-2 [DOI] [PubMed] [Google Scholar]
- [92]. Barakat, A. I. , and Lieu, D. K. , 2003, “ Differential Responsiveness of Vascular Endothelial Cells to Different Types of Fluid Mechanical Shear Stress,” Cell Biochem. Biophys., 38(3), pp. 323–343. 10.1385/CBB:38:3:323 [DOI] [PubMed] [Google Scholar]
- [93]. Hwang, J. , Ing, M. H. , Salazar, A. , Lassègue, B. , Griendling, K. , Navab, M. , Sevanian, A. , and Hsiai, T. K. , 2003, “ Pulsatile Versus Oscillatory Shear Stress Regulates NADPH Oxidase Subunit Expression: Implication for Native LDL Oxidation,” Circ. Res., 93((12), pp. 1225–1232. 10.1161/01.RES.0000104087.29395.66 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [94]. Womersley, J. R. , 1955, “ Method for the Calculation of Velocity, Rate of Flow and Viscous Drag in Arteries When the Pressure Gradient is Known,” J. Physiol., 127(3), pp. 553–563. 10.1113/jphysiol.1955.sp005276 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [95]. Hahn, C. , and Schwartz, M. A. , 2009, “ Mechanotransduction in Vascular Physiology and Atherogenesis,” Nat. Rev. Mol. Cell Biol., 10(1), pp. 53–62. 10.1038/nrm2596 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [96]. Conway, D. E. , Eskin, S. G. , and McIntire, L. V. , 2013, “ Effects of Mechanical Forces on Cells and Tissues (the Liquid–Cell Interface),” An Introduction to Materials in Medicine, Academic Press, Waltham, MA, pp. 474–487. 10.1016/B978-0-08-087780-8.00040-1 [DOI] [Google Scholar]
- [97]. Berk, B. C. , 2008, “ Atheroprotective Signaling Mechanisms Activated by Steady Laminar Flow in Endothelial Cells,” Circulation, 117(8), pp. 1082–1089. 10.1161/CIRCULATIONAHA.107.720730 [DOI] [PubMed] [Google Scholar]
- [98]. Nerem, R. M. , 1992, “ Vascular Fluid Mechanics, the Arterial Wall, and Atherosclerosis,” ASME J. Biomech. Eng., 114(3), pp. 274–282. 10.1115/1.2891384 [DOI] [PubMed] [Google Scholar]
- [99]. Ku, D. N. , Giddens, D. P. , Zarins, C. K. , and Glagov, S. , 1985, “ Pulsatile Flow and Atherosclerosis in the Human Carotid Bifurcation. Positive Correlation Between Plaque Location and Low Oscillating Shear Stress,” Arteriosclerosis, 5(3), pp. 293–302. 10.1161/01.ATV.5.3.293 [DOI] [PubMed] [Google Scholar]
- [100]. Orr, A. W. , Stockton, R. , Simmers, M. B. , Sanders, J. M. , Sarembock, I. J. , Blackman, B. R. , and Schwartz, M. A. , 2007, “ Matrix-Specific P21-Activated Kinase Activation Regulates Vascular Permeability in Atherogenesis,” J. Cell Biol., 176(5), pp. 719–727. 10.1083/jcb.200609008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [101]. Thoumine, O. , Nerem, R. M. , and Girard, P. R. , 1995, “ Oscillatory Shear Stress and Hydrostatic Pressure Modulate Cell-Matrix Attachment Proteins in Cultured Endothelial Cells,” Vitr. Cell. Dev. Biol. Anim., 31(1), pp. 45–54. 10.1007/BF02631337 [DOI] [PubMed] [Google Scholar]
- [102]. Zarins, C. K. , Giddens, D. P. , Bharadvaj, B. K. , Sottiurai, V. S. , Mabon, R. F. , and Glagov, S. , 1983, “ Carotid Bifurcation Atherosclerosis. Quantitative Correlation of Plaque Localization With Flow Velocity Profiles and Wall Shear Stress,” Circ. Res., 53(4), pp. 502–514. 10.1161/01.RES.53.4.502 [DOI] [PubMed] [Google Scholar]
- [103]. Ku, D. N. , 1997, “ Blood Flow in Arteries,” Annu. Rev. Fluid Mech., 29(1), pp. 399–434. 10.1146/annurev.fluid.29.1.399 [DOI] [Google Scholar]
- [104]. Banerjee, M. K. , Ganguly, R. , and Datta, A. , 2012, “ Effect of Pulsatile Flow Waveform and Womersley Number on the Flow in Stenosed Arterial Geometry,” ISRN Biomath., 2012, pp. 1–17. 10.5402/2012/853056 [DOI] [Google Scholar]
- [105]. Wong, P. K. , Johnston, K. W. , Ethier, C. R. , and Cobbold, R. S. , 1991, “ Computer Simulation of Blood Flow Patterns in Arteries of Various Geometries,” J. Vasc. Surg., 14(5), pp. 658–667. 10.1016/0741-5214(91)90190-6 [DOI] [PubMed] [Google Scholar]
- [106]. Du, T. , Hu, D. , and Cai, D. , 2015, “ Outflow Boundary Conditions for Blood Flow in Arterial Trees,” PLoS One, 10(5), p. e0128597. 10.1371/journal.pone.0128597 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [107]. Avari, H. , Rogers, K. A. , and Savory, E. , 2018, “ Wall Shear Stress Determination in a Small-Scale Parallel Plate Flow Chamber Using Laser Doppler Velocimetry Under Laminar, Pulsatile and Low-Reynolds Number Turbulent Flows,” ASME J. Fluids Eng., 140(6), p. 061404. 10.1115/1.4039158 [DOI] [Google Scholar]
- [108]. Bacabac, R. G. , Smit, T. H. , Cowin, S. C. , Van Loon, J. J. W. A. , Nieuwstadt, F. T. M. , Heethaar, R. , and Klein-Nulend, J. , 2005, “ Dynamic Shear Stress in Parallel-Plate Flow Chambers,” J. Biomech., 38(1), pp. 159–167. 10.1016/j.jbiomech.2004.03.020 [DOI] [PubMed] [Google Scholar]
- [109]. Tefft, B. J. , Kopacz, A. M. , Liu, W. K. , and Liu, S. Q. , 2013, “ Experimental and Computational Validation of Hele-Shaw Stagnation Flow With Varying Shear Stress,” Comput. Mech., 52(6), pp. 1463–1473. 10.1007/s00466-013-0887-y [DOI] [Google Scholar]
- [110]. Loudon, C. , and Tordesillas, A. , 1998, “ The Use of the Dimensionless Womersley Number to Characterize the Unsteady Nature of Internal Flow,” J. Theor. Biol., 191(1), pp. 63–78. 10.1006/jtbi.1997.0564 [DOI] [PubMed] [Google Scholar]
- [111]. Hale, J. F. , McDonald, D. A. , and Womersley, J. R. , 1955, “ Velocity Profiles of Oscillating Arterial Flow, With Some Calculations of Viscous Drag and the Reynolds Number,” J. Physiol., 128(3), pp. 629–640. 10.1113/jphysiol.1955.sp005330 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [112]. Hsiai, T. K. , Cho, S. K. , Wong, P. K. , Ing, M. , Salazar, A. , Sevanian, A. , Navab, M. , Demer, L. L. , and Ho, C.-M. , 2003, “ Monocyte Recruitment to Endothelial Cells in Response to Oscillatory Shear Stress,” FASEB J., 17(12), pp. 1648–1657. 10.1096/fj.02-1064com [DOI] [PMC free article] [PubMed] [Google Scholar]
- [113]. Davis, C. A. , Zambrano, S. , Anumolu, P. , Allen, A. C. B. , Sonoqui, L. , and Moreno, M. R. , 2015, “ Device-Based In Vitro Techniques for Mechanical Stimulation of Vascular Cells: A Review,” ASME J. Biomech. Eng., 137(4), p. 040801. 10.1115/1.4029016 [DOI] [PubMed] [Google Scholar]
- [114]. Yakhot, A. , Arad, M. , and Ben-Dor, G. , 1999, “ Numerical Investigation of a Laminar Pulsating Flow in a Rectangular Duct,” Int. J. Numer. Methods Fluids, 29(8), pp. 935–950. [DOI] [Google Scholar]
- [115]. Hino, M. , Kashiwayanagi, M. , Nakayama, A. , and Hara, T. , 1983, “ Experiments on the Turbulence Statistics and the Structure of a Reciprocating Oscillatory Flow,” J. Fluid Mech., 131(1), pp. 363–400. 10.1017/S0022112083001378 [DOI] [Google Scholar]
- [116]. Scotti, A. , and Piomelli, U. , 2001, “ Numerical Simulation of Pulsating Turbulent Channel Flow,” Phys. Fluids, 13(5), pp. 1367–1384. 10.1063/1.1359766 [DOI] [Google Scholar]
- [117]. Ruel, J. , Lemay, J. , Dumas, G. , Doillon, C. , and Charara, J. , 1995, “ Development of a Parallel Plate Flow Chamber for Studying Cell Behavior Under Pulsatile Flow,” ASAIO J., 41(4), pp. 876–883. 10.1097/00002480-199541040-00011 [DOI] [PubMed] [Google Scholar]
- [118]. Canty, J. M. , and Schwartz, J. S. , 1994, “ Nitric Oxide Mediates Flow-Dependent Epicardial Coronary Vasodilation to Changes in Pulse Frequency but Not Mean Flow in Conscious Dogs,” Circulation, 89(1), pp. 375–384. 10.1161/01.CIR.89.1.375 [DOI] [PubMed] [Google Scholar]
- [119]. Alastruey, J. , Passerini, T. , Formaggia, L. , and Peiró, J. , 2012, “ Physical Determining Factors of the Arterial Pulse Waveform: Theoretical Analysis and Calculation Using the 1-D Formulation,” J. Eng. Math., 77(1), pp. 19–37. 10.1007/s10665-012-9555-z [DOI] [Google Scholar]
- [120]. Zhang, Y. , Dong, Y.-H. , Liao, B. , Nie, Y.-M. , Wan, J. , Xiong, L.-L. , Fu, Y. , Xie, X.-J. , and Yu, F.-X. , 2019, “ Shear Stress Regulates ENOS Signaling in Human Umbilical Vein Endothelial Cells Via SRB1-PI3KAP1 Pathway,” Clin. Pract., 16(4), pp. 1221–1230. 10.37532/fmcp.2019.16(4).1221-1230 [DOI] [Google Scholar]
- [121]. Chiu, J.-J. , Chen, L.-J. , Lee, P.-L. , Lee, C.-I. , Lo, L.-W. , Usami, S. , and Chien, S. , 2003, “ Shear Stress Inhibits Adhesion Molecule Expression in Vascular Endothelial Cells Induced by Coculture With Smooth Muscle Cells,” Blood, 101(7), pp. 2667–2674. 10.1182/blood-2002-08-2560 [DOI] [PubMed] [Google Scholar]
- [122]. Lee, W. H. , Kang, S. , Hirani, A. A. , and Lee, Y. W. , 2007, “ A Novel Double-Layer Parallel-Plate Flow Chamber,” IEEE 33rd Annual Northeast Bioengineering Conference, Long Island, NY, Mar. 10–11, pp. 309–310. 10.1109/NEBC.2007.4413400 [DOI] [Google Scholar]
- [123]. Hoesli, C. A. , Tremblay, C. , Juneau, P.-M. , Boulanger, M. D. , Beland, A. V. , Ling, S. D. , Gaillet, B. , Duchesne, C. , Ruel, J. , Laroche, G. , and Garnier, A. , 2018, “ Dynamics of Endothelial Cell Responses to Laminar Shear Stress on Surfaces Functionalized With Fibronectin-Derived Peptides,” ACS Biomater. Sci. Eng., 4(11), pp. 3779–3791. 10.1021/acsbiomaterials.8b00774 [DOI] [PubMed] [Google Scholar]
- [124]. McCann, J. A. , Peterson, S. D. , Plesniak, M. W. , Webster, T. J. , and Haberstroh, K. M. , 2005, “ Non-Uniform Flow Behavior in a Parallel Plate Flow Chamber Alters Endothelial Cell Responses,” Ann. Biomed. Eng., 33(3), pp. 328–336. 10.1007/s10439-005-1735-9 [DOI] [PubMed] [Google Scholar]
- [125]. Leong, C. M. , Voorhees, A. , Nackman, G. B. , and Wei, T. , 2013, “ Flow Bioreactor Design for Quantitative Measurements Over Endothelial Cells Using Micro-Particle Image Velocimetry,” Rev. Sci. Instrum., 84(4), p. 045109. 10.1063/1.4802681 [DOI] [PubMed] [Google Scholar]
- [126]. Avari, H. , Savory, E. , and Rogers, K. A. , 2016, “ An In Vitro Hemodynamic Flow System to Study the Effects of Quantified Shear Stresses on Endothelial Cells,” Cardiovasc. Eng. Technol., 7(1), pp. 44–57. 10.1007/s13239-015-0250-x [DOI] [PubMed] [Google Scholar]
- [127]. Xiao, L. , Wang, G. , Jiang, T. , Tang, C. , Wu, X. , and Sun, T. , 2011, “ Effects of Shear Stress on the Number and Function of Endothelial Progenitor Cells Adhered to Specific Matrices,” J. Appl. Biomater. Biomech., 9(3), pp. 193–198. 10.5301/JABB.2011.6475 [DOI] [PubMed] [Google Scholar]
- [128]. Barber, K. M. , Pinero, A. , and Truskey, G. A. , 1998, “ Effects of Recirculating Flow on U-937 Cell Adhesion to Human Umbilical Vein Endothelial Cells,” Am. J. Physiol. Circ. Physiol., 275(2), pp. H591–H599. 10.1152/ajpheart.1998.275.2.H591 [DOI] [PubMed] [Google Scholar]
- [129]. Chen, C.-N. , Chang, S.-F. , Lee, P.-L. , Chang, K. , Chen, L.-J. , Usami, S. , Chien, S. , and Chiu, J.-J. , 2006, “ Neutrophils, Lymphocytes, and Monocytes Exhibit Diverse Behaviors in Transendothelial and Subendothelial Migrations Under Coculture With Smooth Muscle Cells in Disturbed Flow,” Blood, 107(5), pp. 1933–1942. 10.1182/blood-2005-08-3137 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [130]. DePaola, N. , Davies, P. F. , Pritchard, W. F. , Florez, L. , Harbeck, N. , and Polacek, D. C. , 1999, “ Spatial and Temporal Regulation of Gap Junction Connexin43 in Vascular Endothelial Cells Exposed to Controlled Disturbed Flows In Vitro,” Proc. Natl. Acad. Sci., 96(6), pp. 3154–3159. 10.1073/pnas.96.6.3154 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [131]. Truskey, G. A. , Barber, K. M. , Robey, T. C. , Olivier, L. A. , and Combs, M. P. , 1995, “ Characterization of a Sudden Expansion Flow Chamber to Study the Response of Endothelium to Flow Recirculation,” ASME J. Biomech. Eng., 117(2), pp. 203–210. 10.1115/1.2796002 [DOI] [PubMed] [Google Scholar]
- [132]. Tran-Son-Tay, R. , 1993, “ Techniques for Studying the Effects of Physical Forces on Mammalian Cells and Measuring Cell Mechanical Properties,” Physical Forces and the Mammalian Cell, Frangos J. A., ed., Academic Press, San Diego, CA, pp. 1–59. [Google Scholar]
- [133]. Franzoni, M. , Cattaneo, I. , Longaretti, L. , Figliuzzi, M. , Ene-Iordache, B. , and Remuzzi, A. , 2016, “ Endothelial Cell Activation by Hemodynamic Shear Stress Derived From Arteriovenous Fistula for Hemodialysis Access,” Am. J. Physiol. Circ. Physiol., 310(1), pp. H49–H59. 10.1152/ajpheart.00098.2015 [DOI] [PubMed] [Google Scholar]
- [134]. Franzoni, M. , Cattaneo, I. , Ene-Iordache, B. , Oldani, A. , Righettini, P. , and Remuzzi, A. , 2016, “ Design of a Cone-and-Plate Device for Controlled Realistic Shear Stress Stimulation on Endothelial Cell Monolayers,” Cytotechnology, 68(5), pp. 1885–1896. 10.1007/s10616-015-9941-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [135]. Wang, L. , and Li, C. , 2020, “ A Brief Review of Pulp and Froth Rheology in Mineral Flotation,” J. Chem., 2020, pp. 1–16. 10.1155/2020/3894542 [DOI] [Google Scholar]
- [136]. Remuzzi, A. , Dewey, C. F. , Davies, P. F. , and Gimbrone, M. A. , 1984, “ Orientation of Endothelial Cells in Shear Fields In Vitro,” Biorheology, 21(4), pp. 617–630. 10.3233/BIR-1984-21419 [DOI] [PubMed] [Google Scholar]
- [137]. Sdougos, H. P. , Bussolari, S. R. , and Dewey, C. F. , 1984, “ Secondary Flow and Turbulence in a Cone-and-Plate Device,” J. Fluid Mech., 138, pp. 379–404. 10.1017/S0022112084000161 [DOI] [Google Scholar]
- [138]. Sucosky, P. , Padala, M. , Elhammali, A. , Balachandran, K. , Jo, H. , and Yoganathan, A. P. , 2008, “ Design of an Ex Vivo Culture System to Investigate the Effects of Shear Stress on Cardiovascular Tissue,” ASME J. Biomech. Eng., 130(3), p. 035001. 10.1115/1.2907753 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [139]. Malek, A. M. , Ahlquist, R. , Gibbons, G. H. , Dzau, V. J. , and Izumo, S. , 1995, “ A Cone-Plate Apparatus for the In Vitro Biochemical and Molecular Analysis of the Effect of Shear Stress on Adherent Cells,” Methods Cell Sci., 17(3), pp. 165–176. 10.1007/BF00996123 [DOI] [Google Scholar]
- [140]. Buschmann, M. H. , Dieterich, P. , Adams, N. A. , and Schnittler, H.-J. , 2005, “ Analysis of Flow in a Cone-and-Plate Apparatus With Respect to Spatial and Temporal Effects on Endothelial Cells,” Biotechnol. Bioeng., 89(5), pp. 493–502. 10.1002/bit.20165 [DOI] [PubMed] [Google Scholar]
- [141]. Ankeny, R. F. , Hinds, M. T. , and Nerem, R. M. , 2013, “ Dynamic Shear Stress Regulation of Inflammatory and Thrombotic Pathways in Baboon Endothelial Outgrowth Cells,” Tissue Eng. Part A, 19(13–14), pp. 1573–1582. 10.1089/ten.tea.2012.0300 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [142]. Cox, D. B. , 1962, “ Radial Flow in the Cone-Plate Viscometer,” Nature, 193(4816), pp. 670–670. 10.1038/193670a0 [DOI] [Google Scholar]
- [143]. Kohn, J. C. , Zhou, D. W. , Bordeleau, F. , Zhou, A. L. , Mason, B. N. , Mitchell, M. J. , King, M. R. , and Reinhart-King, C. A. , 2015, “ Cooperative Effects of Matrix Stiffness and Fluid Shear Stress on Endothelial Cell Behavior,” Biophys. J., 108(3), pp. 471–478. 10.1016/j.bpj.2014.12.023 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [144]. Dreyer, L. , Krolitzki, B. , Autschbach, R. , Vogt, P. , Welte, T. , Ngezahayo, A. , and Glasmacher, B. , 2011, “ An Advanced Cone-and-Plate Reactor for the In Vitro-Application of Shear Stress on Adherent Cells,” Clin. Hemorheol. Microcirc., 49(1–4), pp. 391–397. 10.3233/CH-2011-1488 [DOI] [PubMed] [Google Scholar]
- [145]. Kouzbari, K. , Hossan, M. R. , Arrizabalaga, J. H. , Varshney, R. , Simmons, A. D. , Gostynska, S. , Nollert, M. U. , and Ahamed, J. , 2019, “ Oscillatory Shear Potentiates Latent TGF-Β1 Activation More Than Steady Shear as Demonstrated by a Novel Force Generator,” Sci. Rep., 9(1), p. 6065. 10.1038/s41598-019-42302-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- [146]. Nagel, T. , Resnick, N. , Dewey, C. F. , and Gimbrone, M. A. , 1999, “ Vascular Endothelial Cells Respond to Spatial Gradients in Fluid Shear Stress by Enhanced Activation of Transcription Factors,” Arterioscler. Thromb. Vasc. Biol., 19(8), pp. 1825–1834. 10.1161/01.ATV.19.8.1825 [DOI] [PubMed] [Google Scholar]
- [147]. Maroski, J. , Vorderwülbecke, B. J. , Fiedorowicz, K. , Da Silva-Azevedo, L. , Siegel, G. , Marki, A. , Pries, A. R. , and Zakrzewicz, A. , 2011, “ Shear Stress Increases Endothelial Hyaluronan synthase 2 and Hyaluronan Synthesis Especially in Regard to an Atheroprotective Flow Profile,” Exp. Physiol., 96(9), pp. 977–986. 10.1113/expphysiol.2010.056051 [DOI] [PubMed] [Google Scholar]
- [148]. Feugier, P. , Black, R. A. , Hunt, J. A. , and How, T. V. , 2005, “ Attachment, Morphology and Adherence of Human Endothelial Cells to Vascular Prosthesis Materials Under the Action of Shear Stress,” Biomaterials, 26(13), pp. 1457–1466. 10.1016/j.biomaterials.2004.04.050 [DOI] [PubMed] [Google Scholar]
- [149]. Kim, J.-S. , and Park, J.-Y. , 2019, “ Effects of Resveratrol on Laminar Shear Stress-Induced Mitochondrial Biogenesis in Human Vascular Endothelial Cells,” J. Exerc. Nutr. Biochem., 23(1), pp. 7–12. 10.20463/jenb.2019.0002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [150]. Morawietz, H. , Wagner, A. H. , Hecker, M. , and Goettsch, W. , 2008, “ Endothelin Receptor B-Mediated Induction of c-Jun and AP-1 in Response to Shear Stress in Human Endothelial Cells,” Can,” J. Physiol. Pharmacol., 86(8), pp. 499–504. 10.1139/Y08-026 [DOI] [PubMed] [Google Scholar]
- [151]. Boo, Y. C. , Sorescu, G. , Boyd, N. , Shiojima, I. , Walsh, K. , Du, J. , and Jo, H. , 2002, “ Shear Stress Stimulates Phosphorylation of Endothelial Nitric-Oxide Synthase at Ser1179 by Akt-Independent Mechanisms: Role of Protein Kinase A,” J. Biol. Chem., 277(5), pp. 3388–3396. 10.1074/jbc.M108789200 [DOI] [PubMed] [Google Scholar]
- [152]. Sorescu, G. P. , Sykes, M. , Weiss, D. , Platt, M. O. , Saha, A. , Hwang, J. , Boyd, N. , Boo, Y. C. , Vega, J. D. , Taylor, W. R. , and Jo, H. , 2003, “ Bone Morphogenic Protein 4 Produced in Endothelial Cells by Oscillatory Shear Stress Stimulates an Inflammatory Response,” J. Biol. Chem., 278(33), pp. 31128–31135. 10.1074/jbc.M300703200 [DOI] [PubMed] [Google Scholar]
- [153]. Blackman, B. R. , Barbee, K. A. , and Thibault, L. E. , 2000, “ In Vitro Cell Shearing Device to Investigate the Dynamic Response of Cells in a Controlled Hydrodynamic Environment,” Ann. Biomed. Eng., 28(4), pp. 363–372. 10.1114/1.286 [DOI] [PubMed] [Google Scholar]
- [154]. Blackman, B. R. , Garcı’A-Cardeña, G. , and Gimbrone, M. A. , 2002, “ A New In Vitro Model to Evaluate Differential Responses of Endothelial Cells to Simulated Arterial Shear Stress Waveforms,” ASME J. Biomech. Eng., 124(4), pp. 397–407. 10.1115/1.1486468 [DOI] [PubMed] [Google Scholar]
- [155]. Davies, P. F. , Dewey, C. F. , Bussolari, S. R. , Gordon, E. J. , and Gimbrone, M. A. , 1984, “ Influence of Hemodynamic Forces on Vascular Endothelial Function. In Vitro Studies of Shear Stress and Pinocytosis in Bovine Aortic Cells,” J. Clin. Invest., 73(4), pp. 1121–1129. 10.1172/JCI111298 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [156]. Malek, A. , and Izumo, S. , 1992, “ Physiological Fluid Shear Stress Causes Downregulation of Endothelin-1 MRNA in Bovine Aortic Endothelium,” Am. J. Physiol. Physiol., 263(2), pp. C389–C396. 10.1152/ajpcell.1992.263.2.C389 [DOI] [PubMed] [Google Scholar]
- [157]. Furukawa, K. S. , Ushida, T. , Noguchi, T. , Tamaki, T. , and Tateishi, T. , 2003, “ Development of Cone and Plate-Type Rheometer for Quantitative Analysis of Endothelial Cell Detachment by Shear Stress,” Int. J. Artif. Organs, 26(5), pp. 436–441. 10.1177/039139880302600510 [DOI] [PubMed] [Google Scholar]
- [158]. Kim, T. H. , Lee, J. M. , Ahrberg, C. D. , and Chung, B. G. , 2018, “ Development of the Microfluidic Device to Regulate Shear Stress Gradients,” BioChip J., 12(4), pp. 294–303. 10.1007/s13206-018-2407-9 [DOI] [Google Scholar]
- [159]. Gilbert, R. J. , Park, H. , Rasponi, M. , Redaelli, A. , Gellman, B. , Dasse, K. A. , and Thorsen, T. , 2007, “ Computational and Functional Evaluation of a Microfluidic Blood Flow Device,” ASAIO J., 53(4), pp. 447–455. 10.1097/MAT.0b013e3180a5e8ab [DOI] [PubMed] [Google Scholar]
- [160]. Ponmozhi, J. , Moreira, J. M. R. , Mergulhão, F. J. , Campos, J. B. L. M. , and Miranda, J. M. , 2019, “ Fabrication and Hydrodynamic Characterization of a Microfluidic Device for Cell Adhesion Tests in Polymeric Surfaces,” Micromachines, 10(5), p. 303. 10.3390/mi10050303 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [161]. Jiang, L. , Li, S. , Zheng, J. , Li, Y. , and Huang, H. , 2019, “ Recent Progress in Microfluidic Models of the Blood-Brain Barrier,” Micromachines, 10(6), p. 375. 10.3390/mi10060375 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [162]. Sato, K. , and Sato, K. , 2018, “ Recent Progress in the Development of Microfluidic Vascular Models,” Anal. Sci., 34(7), pp. 755–764. 10.2116/analsci.17R006 [DOI] [PubMed] [Google Scholar]
- [163]. Haase, K. , and Kamm, R. D. , 2017, “ Advances in on-Chip Vascularization,” Regen. Med., 12(3), pp. 285–302. 10.2217/rme-2016-0152 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [164]. Ho, Y. T. , Adriani, G. , Beyer, S. , Nhan, P.-T. , Kamm, R. D. , and Kah, J. C. Y. , 2017, “ A Facile Method to Probe the Vascular Permeability of Nanoparticles in Nanomedicine Applications,” Sci. Rep., 7(1), p. 707. 10.1038/s41598-017-00750-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [165]. Akbari, E. , Spychalski, G. B. , Rangharajan, K. K. , Prakash, S. , and Song, J. W. , 2018, “ Flow Dynamics Control Endothelial Permeability in a Microfluidic Vessel Bifurcation Model,” Lab Chip, 18(7), pp. 1084–1093. 10.1039/C8LC00130H [DOI] [PMC free article] [PubMed] [Google Scholar]
- [166]. Thomas, A. , Wang, S. , Sohrabi, S. , Orr, C. , He, R. , Shi, W. , and Liu, Y. , 2017, “ Characterization of Vascular Permeability Using a Biomimetic Microfluidic Blood Vessel Model,” Biomicrofluidics, 11(2), p. 024102. 10.1063/1.4977584 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [167]. Sonmez, U. M. , Cheng, Y.-W. , Watkins, S. C. , Roman, B. L. , and Davidson, L. A. , 2020, “ Endothelial Cell Polarization and Orientation to Flow in a Novel Microfluidic Multimodal Shear Stress Generator,” Lab Chip, 20(23), pp. 4373–4390. 10.1039/D0LC00738B [DOI] [PMC free article] [PubMed] [Google Scholar]
- [168]. Shemesh, J. , Jalilian, I. , Shi, A. , Heng Yeoh, G. , Knothe Tate, M. L. , and Ebrahimi Warkiani, M. , 2015, “ Flow-Induced Stress on Adherent Cells in Microfluidic Devices,” Lab Chip, 15(21), pp. 4114–4127. 10.1039/C5LC00633C [DOI] [PubMed] [Google Scholar]
- [169]. Bertulli, C. , Gerigk, M. , Piano, N. , Liu, Y. , Zhang, D. , Müller, T. , Knowles, T. J. , and Huang, Y. Y. S. , 2018, “ Image-Assisted Microvessel-on-a-Chip Platform for Studying Cancer Cell Transendothelial Migration Dynamics,” Sci. Rep., 8(1), p. 12480. 10.1038/s41598-018-30776-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [170]. Manz, X. D. , Albers, H. J. , Symersky, P. , Aman, J. , van der Meer, A. D. , Bogaard, H. J. , and Szulcek, R. , 2020, “ In Vitro Microfluidic Disease Model to Study Whole Blood-Endothelial Interactions and Blood Clot Dynamics in Real-Time,” J. Vis. Exp., 2020(159), p. e61068. 10.3791/61068 [DOI] [PubMed] [Google Scholar]
- [171]. DeStefano, J. G. , Xu, Z. S. , Williams, A. J. , Yimam, N. , and Searson, P. C. , 2017, “ Effect of Shear Stress on IPSC-Derived Human Brain Microvascular Endothelial Cells (DhBMECs),” Fluids Barriers CNS, 14(1), p. 20. 10.1186/s12987-017-0068-z [DOI] [PMC free article] [PubMed] [Google Scholar]
- [172]. Beebe, D. J. , Mensing, G. A. , and Walker, G. M. , 2002, “ Physics and Applications of Microfluidics in Biology,” Annu. Rev. Biomed. Eng., 4(1), pp. 261–286. 10.1146/annurev.bioeng.4.112601.125916 [DOI] [PubMed] [Google Scholar]
- [173]. Wu, J. , Day, D. , and Gu, M. , 2010, “ Shear Stress Mapping in Microfluidic Devices by Optical Tweezers,” Opt. Exp., 18(8), pp. 7611–7616. 10.1364/OE.18.007611 [DOI] [PubMed] [Google Scholar]
- [174]. Polacheck, W. J. , Li, R. , Uzel, S. G. M. , and Kamm, R. D. , 2013, “ Microfluidic Platforms for Mechanobiology,” Lab Chip, 13(12), pp. 2252–2267. 10.1039/c3lc41393d [DOI] [PMC free article] [PubMed] [Google Scholar]
- [175]. Nahmias, Y. , and Bhatia, S. , 2009, Microdevices in Biology and Medicine, Artech House, Norwood, MA. [Google Scholar]
- [176]. Lu, H. , Koo, L. Y. , Wang, W. M. , Lauffenburger, D. A. , Griffith, L. G. , and Jensen, K. F. , 2004, “ Microfluidic Shear Devices for Quantitative Analysis of Cell Adhesion,” Anal. Chem., 76(18), pp. 5257–5264. 10.1021/ac049837t [DOI] [PubMed] [Google Scholar]
- [177]. Shah, R. K. , London, A. L. , and White, F. M. , 1980, “ Laminar Flow Forced Convection in Ducts,” ASME J. Fluids Eng., 102(2), pp. 256–257. 10.1115/1.3240677 [DOI] [Google Scholar]
- [178]. Zheng, W. , Jiang, B. , Wang, D. , Zhang, W. , Wang, Z. , and Jiang, X. , 2012, “ A Microfluidic Flow-Stretch Chip for Investigating Blood Vessel Biomechanics,” Lab Chip, 12(18), pp. 3441–3450. 10.1039/c2lc40173h [DOI] [PubMed] [Google Scholar]
- [179]. Young, E. W. K. , Wheeler, A. R. , and Simmons, C. A. , 2007, “ Matrix-Dependent Adhesion of Vascular and Valvular Endothelial Cells in Microfluidic Channels,” Lab Chip, 7(12), pp. 1759–1766. 10.1039/b712486d [DOI] [PubMed] [Google Scholar]
- [180]. Godwin, L. A. , Deal, K. S. , Hoepfner, L. D. , Jackson, L. A. , and Easley, C. J. , 2013, “ Measurement of Microchannel Fluidic Resistance With a Standard Voltage Meter,” Anal. Chim. Acta, 758, pp. 101–107. 10.1016/j.aca.2012.10.043 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [181]. Yildiz-Ozturk, E. , and Yesil-Celiktas, O. , 2015, “ Diffusion Phenomena of Cells and Biomolecules in Microfluidic Devices,” Biomicrofluidics, 9(5), p. 052606. 10.1063/1.4923263 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [182]. Nguyen, N. T. , and Wereley, S. , 2006, Fundamentals and Applications of Microfluidics, Artech House, Norwood, MA. [Google Scholar]
- [183]. Sharp, K. V. , Adrian, R. , Santiago, J. G. , and Molho, J. I. , 2005, “ Liquid Flows in Microchannels,” MEMS: Introduction and Fundamentals, CRC Press, Boca Raton, FL, pp. 1–46.http://microfluidics.stanford.edu/Publications/ElectrokineticFlows/Sharp%20Microfluidics%20Chapter%2010%20in%20CRC%20MEMS%20Handbook.pdf [Google Scholar]
- [184]. Weibull, E. , Matsui, S. , Andersson Svahn, H. , and Ohashi, T. , 2014, “ A Microfluidic Device Towards Shear Stress Analysis of Clonal Expanded Endothelial Cells,” J. Biomech. Sci. Eng., 9(1), pp. JBSE0006–JBSE0006. 10.1299/jbse.2014jbse0006 [DOI] [Google Scholar]
- [185]. Glatzel, T. , Litterst, C. , Cupelli, C. , Lindemann, T. , Moosmann, C. , Niekrawietz, R. , Streule, W. , Zengerle, R. , and Koltay, P. , 2008, “ Computational Fluid Dynamics (CFD) Software Tools for Microfluidic Applications—A Case Study,” Comput. Fluids, 37(3), pp. 218–235. 10.1016/j.compfluid.2007.07.014 [DOI] [Google Scholar]
- [186]. Huang, M. , Fan, S. , Xing, W. , and Liu, C. , 2010, “ Microfluidic Cell Culture System Studies and Computational Fluid Dynamics,” Math. Comput. Model., 52(11–12), pp. 2036–2042. 10.1016/j.mcm.2010.01.024 [DOI] [Google Scholar]
- [187]. Zhou, J. , Ellis, A. V. , and Voelcker, N. H. , 2010, “ Recent Developments in PDMS Surface Modification for Microfluidic Devices,” Electrophoresis, 31(1), pp. 2–16. 10.1002/elps.200900475 [DOI] [PubMed] [Google Scholar]
- [188]. Huang, T. T. , Mosier, N. S. , and Ladisch, M. R. , 2006, “ Surface Engineering of Microchannel Walls for Protein Separation and Directed Microfluidic Flow,” J. Sep. Sci., 29(12), pp. 1733–1742. 10.1002/jssc.200600150 [DOI] [PubMed] [Google Scholar]
- [189]. Funamoto, K. , Zervantonakis, I. K. , Liu, Y. , Ochs, C. J. , Kim, C. , and Kamm, R. D. , 2012, “ A Novel Microfluidic Platform for High-Resolution Imaging of a Three-Dimensional Cell Culture Under a Controlled Hypoxic Environment,” Lab Chip, 12(22), p. 4855. 10.1039/c2lc40306d [DOI] [PMC free article] [PubMed] [Google Scholar]
- [190]. Nguyen, D.-H. T. , Stapleton, S. C. , Yang, M. T. , Cha, S. S. , Choi, C. K. , Galie, P. A. , and Chen, C. S. , 2013, “ Biomimetic Model to Reconstitute Angiogenic Sprouting Morphogenesis In Vitro,” Proc. Natl. Acad. Sci., 110(17), pp. 6712–6717. 10.1073/pnas.1221526110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [191]. Moya, M. L. , Alonzo, L. F. , and George, S. C. , 2014, “ Microfluidic Device to Culture 3D In Vitro Human Capillary Networks,” Methods Mol. Biol., 1202, pp. 21–27. 10.1007/7651_2013_36 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [192]. Zilberman-Rudenko, J. , Sylman, J. L. , Garland, K. S. , Puy, C. , Wong, A. D. , Searson, P. C. , and McCarty, O. J. T. , 2017, “ Utility of Microfluidic Devices to Study the Platelet–Endothelium Interface,” Platelets, 28(5), pp. 449–456. 10.1080/09537104.2017.1280600 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [193]. Xia, Y. , Si, J. , and Li, Z. , 2016, “ Fabrication Techniques for Microfluidic Paper-Based Analytical Devices and Their Applications for Biological Testing: A Review,” Biosens. Bioelectron., 77, pp. 774–789. 10.1016/j.bios.2015.10.032 [DOI] [PubMed] [Google Scholar]
- [194]. Faustino, V. , Catarino, S. O. , Lima, R. , and Minas, G. , 2016, “ Biomedical Microfluidic Devices by Using Low-Cost Fabrication Techniques: A Review,” J. Biomech., 49(11), pp. 2280–2292. 10.1016/j.jbiomech.2015.11.031 [DOI] [PubMed] [Google Scholar]
- [195]. Kharati-Koopaee, M. , and Rezaee, M. , 2017, “ Investigation of Turbulent Flow Through Microchannels Consisting of Different Micropost Arrangements,” Eng. Comput., 34(5), pp. 1367–1392. 10.1108/EC-02-2016-0069 [DOI] [Google Scholar]
- [196]. Young, E. W. K. , and Beebe, D. J. , 2010, “ Fundamentals of Microfluidic Cell Culture in Controlled Microenvironments,” Chem. Soc. Rev., 39(3), pp. 1036–1048. 10.1039/b909900j [DOI] [PMC free article] [PubMed] [Google Scholar]
- [197]. Wu, J. , and Gu, M. , 2011, “ Microfluidic Sensing: State of the Art Fabrication and Detection Techniques,” J. Biomed. Opt., 16(8), p. 080901. 10.1117/1.3607430 [DOI] [PubMed] [Google Scholar]
- [198]. Shih, H.-C. , Lee, T.-A. , Wu, H.-M. , Ko, P.-L. , Liao, W.-H. , and Tung, Y.-C. , 2019, “ Microfluidic Collective Cell Migration Assay for Study of Endothelial Cell Proliferation and Migration Under Combinations of Oxygen Gradients, Tensions, and Drug Treatments,” Sci. Rep., 9(1), p. 8234. 10.1038/s41598-019-44594-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [199]. Jeong, G. S. , Oh, J. , Kim, S. B. , Dokmeci, M. R. , Bae, H. , Lee, S.-H. , and Khademhosseini, A. , 2014, “ Siphon-Driven Microfluidic Passive Pump With a Yarn Flow Resistance Controller,” Lab Chip, 14(21), pp. 4213–4219. 10.1039/C4LC00510D [DOI] [PubMed] [Google Scholar]
- [200]. Erickson, B. E. , 2005, “ Braille Pins Control Microfluidic Flow,” Anal. Chem., 77(5), p. 93. 10.1021/ac053348r15623283 [DOI] [Google Scholar]
- [201]. Myers, D. R. , Sakurai, Y. , Tran, R. , Ahn, B. , Hardy, E. T. , Mannino, R. , Kita, A. , Tsai, M. , and Lam, W. A. , 2012, “ Endothelialized Microfluidics for Studying Microvascular Interactions in Hematologic Diseases,” J. Vis. Exp., 64, p. 3958. 10.3791/3958 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [202]. Varma, S. , and Voldman, J. , 2015, “ A Cell-Based Sensor of Fluid Shear Stress for Microfluidics,” Lab Chip, 15(6), pp. 1563–1573. 10.1039/C4LC01369G [DOI] [PMC free article] [PubMed] [Google Scholar]
- [203]. Mohammed, M. , Thurgood, P. , Gilliam, C. , Nguyen, N. , Pirogova, E. , Peter, K. , Khoshmanesh, K. , and Baratchi, S. , 2019, “ Studying the Response of Aortic Endothelial Cells Under Pulsatile Flow Using a Compact Microfluidic System,” Anal. Chem., 91(18), pp. 12077–12084.. 10.1021/acs.analchem.9b03247 [DOI] [PubMed] [Google Scholar]
- [204]. Byun, C. K. , Abi-Samra, K. , Cho, Y.-K. , and Takayama, S. , 2014, “ Pumps for Microfluidic Cell Culture,” Electrophoresis, 35(2–3), pp. 245–257. 10.1002/elps.201300205 [DOI] [PubMed] [Google Scholar]
- [205]. Hossan, M. R. , Dutta, D. , Islam, N. , and Dutta, P. , 2018, “ Review: Electric Field Driven Pumping in Microfluidic Device,” Electrophoresis, 39(5–6), pp. 702–731. 10.1002/elps.201700375 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [206]. Zhu, P. , and Wang, L. , 2017, “ Passive and Active Droplet Generation With Microfluidics: A Review,” Lab Chip, 17(1), pp. 34–75. 10.1039/C6LC01018K [DOI] [PubMed] [Google Scholar]
- [207]. Clime, L. , Daoud, J. , Brassard, D. , Malic, L. , Geissler, M. , and Veres, T. , 2019, “ Active Pumping and Control of Flows in Centrifugal Microfluidics,” Microfluid. Nanofluid., 23(3), p. 29. 10.1007/s10404-019-2198-x [DOI] [Google Scholar]
- [208]. Laser, D. J. , and Santiago, J. G. , 2004, “ A Review of Micropumps,” J. Micromech. Microeng., 14(6), pp. R35–R64. 10.1088/0960-1317/14/6/R01 [DOI] [Google Scholar]
- [209]. Lee, D. W. , Choi, N. , and Sung, J. H. , 2019, “ A Microfluidic Chip With Gravity-Induced Unidirectional Flow for Perfusion Cell Culture,” Biotechnol. Prog., 35(1), p. e2701. 10.1002/btpr.2701 [DOI] [PubMed] [Google Scholar]
- [210]. Yang, Y. , Fathi, P. , Holland, G. , Pan, D. , Wang, N. S. , and Esch, M. B. , 2019, “ Pumpless Microfluidic Devices for Generating Healthy and Diseased Endothelia,” Lab Chip, 19(19), pp. 3212–3219. 10.1039/C9LC00446G [DOI] [PMC free article] [PubMed] [Google Scholar]
- [211]. Volpatti, L. R. , and Yetisen, A. K. , 2014, “ Commercialization of Microfluidic Devices,” Trends Biotechnol., 32(7), pp. 347–350. 10.1016/j.tibtech.2014.04.010 [DOI] [PubMed] [Google Scholar]
- [212]. Soenksen, L. R. , Kassis, T. , Noh, M. , Griffith, L. G. , and Trumper, D. L. , 2018, “ Closed-Loop Feedback Control for Microfluidic Systems Through Automated Capacitive Fluid Height Sensing,” Lab Chip, 18(6), pp. 902–914. 10.1039/C7LC01223C [DOI] [PMC free article] [PubMed] [Google Scholar]
- [213]. Borgdorff, P. , and Tangelder, G. J. , 2006, “ Pump-Induced Platelet Aggregation With Subsequent Hypotension: Its Mechanism and Prevention With Clopidogrel,” J. Thorac. Cardiovasc. Surg., 131(4), pp. 813–821. 10.1016/j.jtcvs.2005.10.021 [DOI] [PubMed] [Google Scholar]
- [214]. Kurth, F. , Györvary, E. , Heub, S. , Ledroit, D. , Paoletti, S. , Renggli, K. , Revol, V. , Verhulsel, M. , Weder, G. , and Loizeau, F. , 2020, “ Organs-on-a-Chip Engineering,” Organ-on-a-Chip, Hoeng J., Bovard D., and Peitsch M. C., eds., Academic Press, San Diego, CA, pp. 47–130. [Google Scholar]
- [215]. Hsiai, T. K. , Cho, S. K. , Honda, H. M. , Hama, S. , Navab, M. , Demer, L. L. , and Ho, C.-M. , 2002, “ Endothelial Cell Dynamics Under Pulsating Flows: Significance of High Versus Low Shear Stress Slew Rates,” Ann. Biomed. Eng., 30(5), pp. 646–656. 10.1114/1.1484222 [DOI] [PubMed] [Google Scholar]
- [216]. Li, M. , Scott, D. E. , Shandas, R. , Stenmark, K. R. , and Tan, W. , 2009, “ High Pulsatility Flow Induces Adhesion Molecule and Cytokine MRNA Expression in Distal Pulmonary Artery Endothelial Cells,” Ann. Biomed. Eng., 37(6), pp. 1082–1092. 10.1007/s10439-009-9684-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [217]. Li, M. , Tan, Y. , Stenmark, K. R. , and Tan, W. , 2013, “ High Pulsatility Flow Induces Acute Endothelial Inflammation Through Overpolarizing Cells to Activate NF-ΚB,” Cardiovasc. Eng. Technol., 4(1), pp. 26–38. 10.1007/s13239-012-0115-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [218]. Wei, H. , Cheng, A. L. , and Pahlevan, N. M. , 2020, “ On the Significance of Blood Flow Shear-Rate-Dependency in Modeling of Fontan Hemodynamics,” Eur. J. Mech. B/Fluids, 84, pp. 1–14. 10.1016/j.euromechflu.2020.05.011 [DOI] [Google Scholar]
- [219]. Cheng, A. L. , Pahlevan, N. M. , Rinderknecht, D. G. , Wood, J. C. , and Gharib, M. , 2018, “ Experimental Investigation of the Effect of Non-Newtonian Behavior of Blood Flow in the Fontan Circulation,” Eur. J. Mech. B/Fluids, 68, pp. 184–192. 10.1016/j.euromechflu.2017.12.009 [DOI] [PMC free article] [PubMed] [Google Scholar]


