Analytical and Functional Aspects of Protein-Ligand Interactions: Beyond Induced Fit and Conformational Selection

Abstract

Ligand-dependent changes in protein conformation are foundational to biology. Historical mechanistic models for substrate-specific proteins are induced fit (IF) and conformational selection (CS), which invoke a change in protein conformation after ligand binds or before ligand binds, respectively. These mechanisms have important, but rarely discussed, functional relevance because IF vs. CS can differentially affect a protein’s substrate specificity or promiscuity, and its regulatory properties. The modern view of proteins as conformational ensembles in both ligand free and bound states, together with the realization that most proteins exhibit some substrate promiscuity, demands a deeper interpretation of the historical models and provides an opportunity to improve mechanistic analyses. Here we describe alternative analytical strategies for distinguishing the historical models, including the more complex expanded versions of IF and CS. Functional implications of the different models are described. We provide an alternative perspective based on protein ensembles interacting with ligand ensembles that clarifies how a single protein can ‘apparently’ exploit different mechanisms for different ligands. Mechanistic information about protein ensembles can be optimized when they are probed with multiple ligands.

Introduction

The ensemble nature of proteins is well established, where an ‘ensemble’ is the set of discrete and interconvertible protein conformers that form a multidimensional conformational landscape [1–5]. The thermodynamic and kinetic properties of the landscape govern the relative distribution of the individual conformers and the rates of their interconversion, which may occur over a wide range of time scales at physiological temperatures [6,7]. The distribution of conformers may be perturbed by addition of ligand or substrate, and this behavior is the central defining feature of biological recognition and response. Ensembles of equilibrating conformers likely also exist to varying degrees for the ligand bound states and this may distinguish ligand types (e.g., substrate vs inhibitor). However, several ensemble behaviors have not been fully incorporated into mechanistic models for protein-ligand interactions. Despite the availability of several elegant theoretical analyses of protein-ligand interactions, they often omit many practical aspects of the interpretation of ligand binding experiments. Here we aim to extend the theoretical framework for kinetic models and summarize practical considerations for their interpretation in the context of protein ensembles.

Two widely used limiting case models that include ligand-dependent perturbation of the conformational landscape are induced fit (IF) and conformational selection (CS), which acknowledge ensembles in the ligand-bound state and ligand-free state, respectively (Figure 1). Binding via either mechanism alters the conformational landscape. The simplest description of each model contains three protein states which occupy three minima within the conformational landscape. Although the two mechanisms share the common features of two conformations and two ligation states, they differ in the order of events. As a result, the evolution of the conformational landscape along the reaction coordinate for either the IF or CS mechanism proceed by two opposing scenarios. Specifically, ligand binding via IF leads to an expansion of the conformational landscape and occupation of a previously inaccessible conformational subspace whereas binding via CS leads to a narrowing of the conformational landscape or disappearance of an initial protein conformer.

Figure 1. Cartoon depiction of the induced fit, conformational selection, and mixed binding mechanisms.

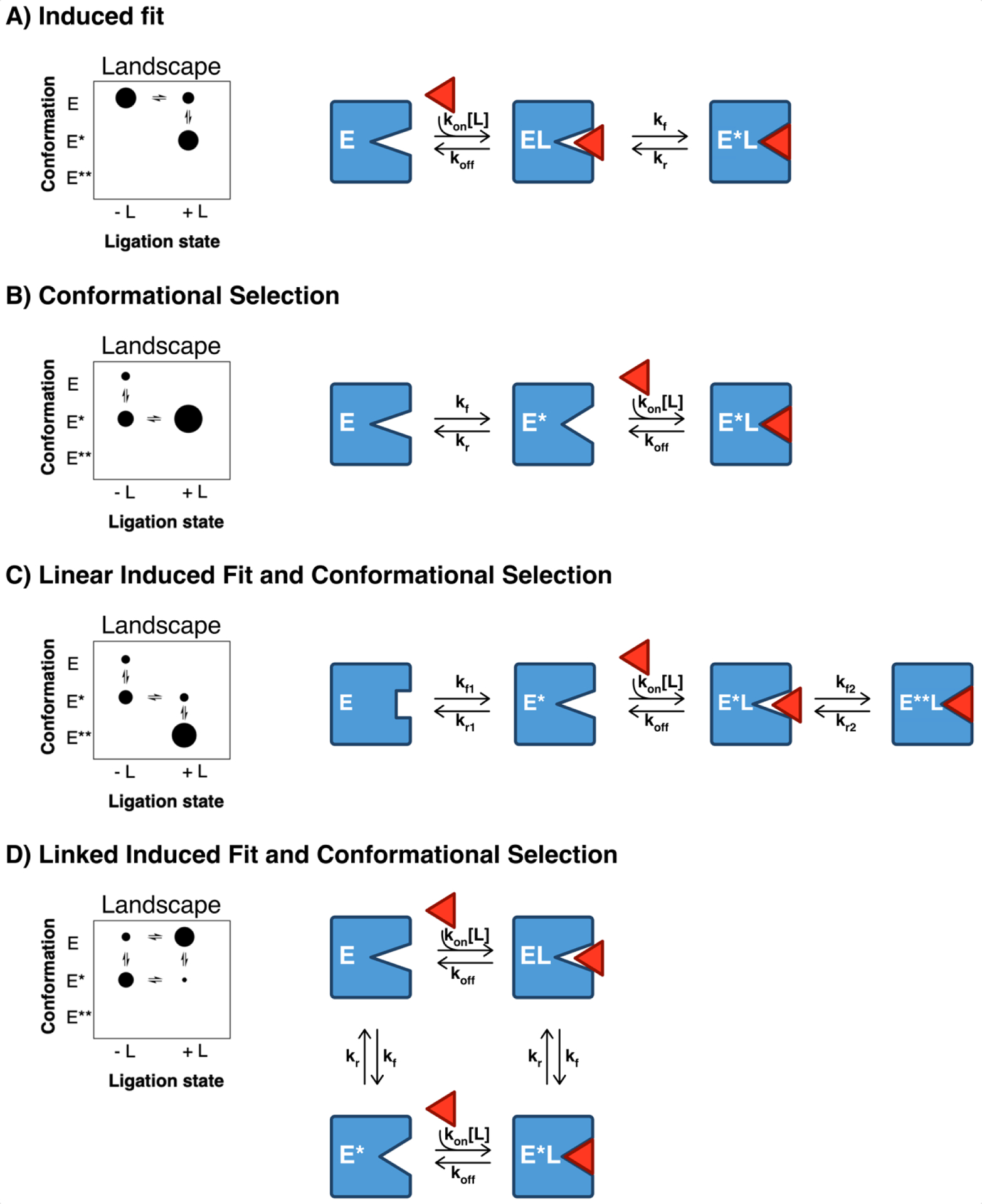
The simplest description of both models contains three enzyme states, and the two models share two common steps, ligand binding and conformational change, the order of which differentiates the models. For IF, ligand binding occurs prior to, and induces, a conformational change, yielding two distinct bound enzyme conformers (EL and E*L in figure 1). Notably, in the pure IF model, the ligand-induced conformer (E*L in figure 1) is only populated upon ligand binding and is otherwise inaccessible in the ligand-free ensemble. CS, on the other hand, occurs when ligand initially encounters an ensemble of unbound states and preferentially binds to (or selects) the ‘binding competent’ conformer (E*), resulting in a population shift to the ‘binding competent’ conformation. The diameter of the dots represents the relative amounts of each enzyme state within each ligation state to illustrate how addition of ligand results in a redistribution of the relative amounts of each enzyme conformer.

These historical models have provided a valuable conceptual framework for protein/ligand dynamics and descriptions of either mechanism have been discussed extensively [8–12]. However, the functional impact of the two mechanisms is rarely discussed. Different functional advantages and liabilities may be envisioned when either mechanism is operative. These outcomes are linked with the properties of the unbound state(s) (i.e. those poised for binding) and bound state(s) (i.e. those poised for functional outcomes - e.g. catalysis, signaling, etc) resulting from a binding interaction. Given the linkage between binding mechanism and functional outcome, there is a particular incentive to develop tools to distinguish mechanisms of ligand binding.

Despite their simplicity, it is surprisingly difficult to distinguish the IF and CS mechanisms. It is also important to note that the mechanisms are not mutually exclusive and linear and linked combinations of the two models are possible (Figure 1). Herein, we propose a deeper analysis and reconsideration of each model. Kinetic and thermodynamic signatures for different kinetic extremes of each mechanism are presented as a guide for experimental design and analysis. In addition, we discuss potential functional outcomes that may arise when either or both (mixed CS/IF) mechanisms are operative to highlight incentives for rigorous characterization of ligand binding mechanism. The reader should note that we use the terms ‘protein’ and ‘enzyme’ interchangeably, and we limit the analyses to ligand binding at equilibrium in the absence of catalysis, unless otherwise noted.

Analytic strategies to distinguish IF from CS: an overview of ‘universal’, ‘better’, and ‘best’ approaches

Traditional kinetic analyses aimed at distinguishing the IF and CS models rely on interpretation of the ligand concentration-dependent behavior of the observed rate of binding obtained by mixing unbound enzyme with varying concentrations of ligand, which are the conditions discussed in this review. Several publications have detailed this analytical approach or other experimental methods to distinguish IF from CS [13–17]. Herein, we expand on the analytical methods and we emphasize incorporation of amplitude analysis to help distinguish the mechanisms for kinetic cases that are indistinguishable when only the observed rate analysis is employed.

In most cases, binding kinetics for the IF and CS mechanism result in double exponential kinetics. The two relaxation processes in either mechanism are conveniently invoked when analyzing stopped flow data that fit to a ‘double exponential’ relaxation. This common analysis yields two observed rate constants (k_obs) and two amplitude terms (A_i) as in Equation 1, where the change is a function of time, t, A_n are the pre-exponential factors or amplitudes that describe the magnitude of change, k_obs,n are the observed rates of change, and the first term, A₀, is an offset that may represent either the initial or final signal, depending on the experimental setup.

$$f(t)=A_0+A_1{e}^{-k_{obs,1}t}+A_2{e}^{-k_{obs,2}t}$$ (Equation 1)

Generally, for the IF and CS mechanisms, one observed rate has a linear dependence while the other has a hyperbolic dependence with respect to ligand concentration. The pros and cons of this analysis are linked with its simplicity: equation 1 is ‘universal’ and may be used to describe any mechanism involving two relaxation processes. Therefore, the approach does not reveal rates of any actual binding or dissociation processes because equation 1 has no physical linkage to mechanism. Regardless, it is common to attempt to interpret the binding mechanism by considering the individual k_obs vs. [ligand] relationships. The amplitude results, which represent half of the data, are typically ignored in this approach.

For decades, kineticists interpreted a hyperbolic increase in observed rate as IF and a hyperbolic decrease as CS. Vogt and Di Cera recently demonstrated that the distinction is only valid if the conformational rearrangement step (k_f and k_r in Figure 1) is rate-limiting [8]. In their analysis, they showed that CS can also display a hyperbolic increase when the conformational rearrangements are not rate-limiting. Hence, a hyperbolic increase or even concentration independent observed rate behavior can result from either the IF or CS model.

A ‘better’ analytical approach provides a direct physical linkage to mechanism and uses k_obs expressions derived from the set of differential equations that are unique to each mechanism, see equation 1. The observed rate expressions, which are functions of ligand concentration, are shown below for each mechanism:

$$k_{obs,IF}(L)=\frac{-k_{on}[L]+k_{off}+k_f+k_r\pm \sqrt{{\left(k_{on}[L]+k_{off}+k_f+k_r\right)}^2-4\left(k_{on}[L]k_f+k_{on}[L]k_{off}+k_{off}{k}_r\right)}}{2}$$ (Equation 2)

$$k_{obs,CS}(L)=\frac{-k_{on}[L]+k_{off}+k_f+k_r\pm \sqrt{{\left(k_{on}[L]+k_{off}+k_f+k_r\right)}^2-4\left(k_{on}[L]k_f+k_f{k}_{off}+k_{off}{k}_r\right)}}{2}$$ (Equation 3)

In contrast to the ‘universal’ approach, which relies on local fits of individual data sets to equation 1, one may globally fit the k_obs expressions to data from multiple ligand concentrations. Due to the uniqueness of each expression, one may recover the individual rate constants for a given mechanism. Usually, one arrives at a mechanism by comparing goodness of fit and/or by comparing the recovered rate constants from the fits of k_obs expressions to kinetic data and the apparent binding affinity (K_Dapp) expression fits to equilibrium titration data (K_Dapp,IF = K_D*k_r/(k_f+k_r); K_Dapp,CS = K_D*(k_f+k_r)/k_f; K_D = k_off/k_on). For example, one might eliminate a mechanism on the basis of negative values for the recovered rate constant fits or inconsistencies between the rate constants defined by the k_obs and K_Dapp expressions. Note that for a true equilibrium affinity of ligand for the enzyme conformer that it binds to, E or E*, the apparent affinity, K_Dapp, will be different if the protein utilizes IF vs. CS, as the expressions above demand.

Of course, the ‘better’ analytical approach is not without limitations. Chakraborty and Di Cera recently discussed cases for which two different scenarios of IF and CS can yield equivalent k_obs and K_Dapp values despite differences in the intrinsic kinetic rate constants for either model [15]. To further complicate the matter, we must acknowledge the possibility of more complex mechanisms (larger than 3-state) producing the observed multi-exponential kinetics. The number of equilibration steps in a given binding model is equal to the theoretical maximum number of observable relaxation rates. Although the number of observed relaxation processes is closely linked to the number of equilibria in the binding model, there are several examples where multi-step binding processes result in less than the theoretical maximum number of kinetic processes. For example, the amplitude value for a given phase may be undetectably small and therefore ‘kinetically silent’ or perhaps two or more of the observed rates of change are indistinguishably similar. Thus, there is utility in understanding the amplitude behavior for each model.

The ‘best’ analytical approach involves using the k_obs and amplitude expressions obtained by solving the system of differential equations that define the mechanism [18–20]. In this approach, one obtains a unique expression for the time-dependent concentration of each enzyme state as shown below:

$$E1(L,t)=E{1}_{eq}+{\sum }_{i=1}^n{A}_{1i}exp\left(-k_{\mathit{\text{obsi}}}t\right)$$ (equation 4)

$$E2(L,t)=E{2}_{eq}+{\sum }_{i=1}^n{A}_{2i}exp\left(-k_{\mathit{\text{obsi}}}t\right)$$ (equation 5)

$$E3(L,t)=E{3}_{eq}+{\sum }_{i=1}^n{A}_{3i}exp\left(-k_{\mathit{\text{obsi}}}t\right)$$ (equation 6)

The individual amplitude expressions are defined for each mechanism in Tables 1 and 2. To derive these expressions ‘by hand’ for increasingly complex mechanisms becomes quite cumbersome and this once represented a computationally insurmountable hurdle. However, with modern computing and advances in mathematical platforms, the solutions are accessible with minimal effort.

Table 1.

Kinetic and thermodynamic signatures of the IF binding model. The K_D,app and K_D have units of concentration. The equilibrium concentrations, [C_eq], are expressed as a ratio of [E_total] where [E_total] = [E] + [EL] + [E*L]. The two observed rates, k_alow and k_fast, as well as their lower ([L] → 0) and upper ([L] →∞) limits have units of s⁻¹ Three unique expressions describe each enzyme state as a function of ligand concentration and time: [E](L,t) = [E_eq] + A_E,slowe^−kslow*t + A_E,faste^−kfast*t, [EL](L,t) = [EL_eq] + A_EL,slowe^−kslow*t + A_EL,faste^−kfast*t, and [E*L](L,t) = [E*L_eq] + A_E*_L,,slowe^−kslow*t + A_E*L,faste^−kfast*t

Induced fit: E⇄E*⇄E*L (solution: [C] = [Ceq]+Aslowe−kslow*t+Afaste−kfast*t
KD,app:	$K_D\left(\frac{k_r}{k_r+k_f}\right)\mathit{\text{where}}{K}_D=\frac{k_{off}}{k_{on}}$
[C eq ]:	$\begin{array}{ccc}\left[E_{eq}\right]=\frac{K_{D,app}\left[E_{max}\right]}{K_{D,app}+[L]}& \left[E{L}_{eq}\right]=\frac{[L]\left[E{L}_{max}\right]}{K_{D,app}+[L]}& \left[E^{*}{L}_{eq}\right]=\frac{[L]\left[E^{*}{L}_{max}\right]}{K_{D,app}+[L]}\\ \mathit{\text{where}}{E}_{max}=\left[E_{\mathit{\text{total}}}\right],& \left[E{L}_{max}\right]=\frac{k_r}{k_f+k_r}\left[E_{\mathit{\text{total}}}\right]& \left[E^{*}{L}_{max}\right]=\frac{k_f}{k_f+k_r}\left[E_{\mathit{\text{total}}}\right]\end{array}$
Aslow and Afast:	$$\begin{gathered} A_{E,i}=\frac{-k_{on}[L]\left(k_f+k_r-k_i\right)\left[E_0\right]+k_{off}\left(k_r-k_i\right)\left[E{L}_0\right]+k_{off}{k}_r\left[E^{*}{L}_0\right]}{k_i\left(k_i-k_j\right)} \\ {A}_{\text{E}L,i}=-A_{E,i}-A_{E^{*}L,i} \\ {A}_{E^{*}L,i}=\frac{k_{on}[L]k_f\left[E_0\right]-k_f\left(k_{on}[L]-k_i\right)\left[E{L}_0\right]-k_r\left(k_{on}[L]+k_{off}-k_i\right)\left[E^{*}{L}_0\right]}{k_i\left(k_i-k_j\right)} \\ \mathit{\text{when}}i=\mathit{\text{slow}},j=\mathit{\text{fast}}and\mathit{\text{vice}}\mathit{\text{versa}} \end{gathered}$$
kslow and kfast:	$$\begin{gathered} k_{\mathit{\text{slow}}}=\frac{b-\sqrt{b^2-4ac}}{2a}{k}_{\mathit{\text{fast}}}=\frac{b+\sqrt{b^2-4ac}}{2a} \\ \mathit{\text{where}}a=1,b=k_{on}[L]+k_{off}+k_f+k_r,c=k_{on}[L]k_f+k_{on}[L]k_r+k_{off}{k}_r \\ and\sum k_{obs}=b,\text{and }\prod k_{obs}=c \end{gathered}$$
$\underset{[\mathit{\text{L}}]\to 0}{lim}{\mathit{\text{k}}}_{\text{obs}1,2}:$	$$\begin{gathered} k_{\mathit{\text{slow}}}=\frac{b-\sqrt{b^2-4ac}}{2a}{k}_{\mathit{\text{fast}}}=\frac{b+\sqrt{b^2-4ac}}{2a} \\ \mathit{\text{where}}a=1,b=k_{off}+k_f+k_r,c=k_{off}{k}_r \end{gathered}$$
$\underset{[\mathit{\text{L}}]\to \infty }{lim}{\mathit{\text{k}}}_{\text{obs}1,2}:$	$k_{\mathit{\text{slow}}}=k_f+k_r{k}_{\mathit{\text{fast}}}=k_{on}\infty +k_{off}=\infty$

Table 2. Kinetic and thermodynamic signatures of the CS binding model.

The K_D,app and K_D have units of concentration. The equilibrium concentrations, [C_eq], are expressed as a ratio of [E_total] where [E_total] = [E] + [E*] + [E*L]. The two observed rates, k_slow and k_fast, as well as their lower ([L] →0) and upper ([L] →∞) limits have units of s⁻¹. Three unique expressions describe each enzyme state as a function of ligand concentration and time: [E](L,t)= [E_eq] + A_E,slowe^−kslow*t + A_E,faste^−kfast*t, [E*](L,t)= [E*eq] + A_E*,_slowe^−kslow*t + A_E*,faste^−kfast*t, and [E*L](L,t)= [E*L_eq] + A_E*L,slowe^−kslow*t + A_E*L,faste^−kfast*t.

Conformational selection: E⇄E*⇄E*L (solution: [C] = [Ceq]+Aslowe−kslow*t+Afaste−kfast*t
KD,app:	$K_D\left(\frac{k_f+k_r}{k_f}\right)\mathit{\text{where }}{K}_D=\frac{k_{off}}{k_{on}}$
[C eq ]:	$\begin{array}{ccc}\left[E_{eq}\right]=\frac{K_{D,app}\left[E_{max}\right]}{K_{D,app}+[L]}& \left[{E^{*}}_{eq}\right]=\frac{K_{D,app}\left[{E^{*}}_{max}\right]}{K_{D,app}+[L]}& \left[E^{*}{L}_{eq}\right]=\frac{[L]\left[E^{*}{L}_{max}\right]}{K_{D,app}+[L]}\\ \mathit{\text{where }}{E}_{max}=\frac{k_r}{k_f+k_r}\left[E_{\mathit{\text{total}}}\right],& \left[{E^{*}}_{max}\right]=\frac{k_f}{k_f+k_r}\left[E_{\mathit{\text{total}}}\right],& \left[E^{*}{L}_{max}\right]=\left[E_{\mathit{\text{total}}}\right]\end{array}$
Aslow and Afast:	$$\begin{gathered} A_{E,i}=\frac{-k_f\left(k_{on}[L]+k_{off}-k_i\right)\left[E_0\right]+k_r\left(k_{off}-k_i\right)\left[{E^{*}}_0\right]+k_r{k}_{off}\left[E^{*}{L}_0\right]}{k_i\left(k_i-k_j\right)} \\ {A}_{E^{*},i}=-A_{E,i}-A_{E^{*}L,i} \\ {A}_{E^{*}L,i}=\frac{k_f{k}_{on}[L]\left[E_0\right]+k_{on}[L]\left(k_f-k_i\right)\left[{E^{*}}_0\right]-k_{off}\left(k_f+k_r-k_i\right)\left[E^{*}{L}_0\right]}{k_i\left(k_i-k_j\right)} \\ \mathit{\text{when}}i=\mathit{\text{slow}},j=\mathit{\text{fast}}and\mathit{\text{vice}}\mathit{\text{versa}} \end{gathered}$$
kslow and kfast:	$$\begin{gathered} k_{\mathit{\text{slow}}}=\frac{b-\sqrt{b^2-4ac}}{2a}{k}_{\mathit{\text{fast}}}=\frac{b+\sqrt{b^2-4ac}}{2a} \\ \mathit{\text{where}}a=1,b=k_f+k_r+k_{on}[L]+k_{off},c=k_f{k}_{on}[L]+k_f{k}_{off}+k_r{k}_{off} \\ and\sum k_{obs}=b,\text{and }\prod k_{obs}=c \end{gathered}$$
$\underset{[\mathit{\text{L}}]\to 0}{lim}{\mathit{\text{k}}}_{\mathit{\text{obs}}1,2}:$	$\begin{array}{llll}{k}_{\mathit{\text{slow}}}=k_f+k_r\hfill & and\hfill & k_{\mathit{\text{fast}}}=k_{off}\hfill & \mathit{\text{when}}{k}_{off}>k_f+k_r\hfill \\ k_{\mathit{\text{slow}}}=k_{off}\hfill & and\hfill & k_{\mathit{\text{fast}}}=k_f+k_r\hfill & \mathit{\text{when}}{k}_{off}<k_f+k_r\hfill \end{array}$
$\underset{[\mathit{\text{L}}]\to \infty }{lim}{\mathit{\text{k}}}_{\mathit{\text{obs}}1,2}:$	$k_{\mathit{\text{slow}}}=k_f{\mathit{\text{k}}}_{\mathit{\text{fast}}}={\mathit{\text{k}}}_{on}\infty +k_{off}+k_r=\infty$

Given the uniqueness of the expressions for the individual enzyme states in each mechanism, one may easily discern the mechanism if the individual ligand-free species or the individual ligand-bound species in the reaction can be independently measured (see Figures S1 and S2). However, most kinetic studies of small molecule ligand binding utilize stopped-flow absorbance or fluorescence and the optical properties may only distinguish between bound vs. free, and not between individual states in either ensemble. Hence, the signal may represent a single species or a sum of the members in the ensemble. This is elaborated in later sections (see discussion of the k_obs equvalent cases).

As with the previous approaches, the ‘best’ analytical approach does not guarantee success. A potential reason that the amplitudes have been ignored in kinetic analyses is the possibility that different species in the binding mechanism differently contribute to the signal which could change the interpretation of the data. However, this limitation may be easily overcome provided there is a well-defined relationship between signal and concentration and the data across multiple ligand concentrations fit by global analysis. Another reason that the amplitudes may have been overlooked in the past is that the full expressions, which are quite long, exceed the character limits for simpler analytical platforms. Thus, one may need specialized (and sometimes expensive) software to analyze the data. However, the benefits of this approach far outweigh initial monetary setbacks. Finally, the possibility that multi-step binding processes yield fewer than the theoretical maximum number of kinetic processes needs to be addressed. The observation of multi-exponential binding kinetics requires careful examination of multi-step binding models or that have at least as many relaxation processes as the number of observed relaxation processes. Hence, one is limited purely by imagination (in terms of the tested mechanisms) and time (linked to computational power). Naturally, more complex mechanisms increase the likelihood for unnecessary overparameterization. Statistical analyses become critical to distinguish potential mechanisms and appropriate penalties should be applied to increasingly complex mechanisms [21, 22].

To summarize, the observation of double exponential processes requires interrogation of mechanisms with at least 3-states. The ‘best’ analytical approach involves global analysis of multiple data sets spanning a range of ligand concentrations wherein adequate observation of the mechanism-specific amplitude and observed rate expression behavior is achieved. More complex models, of course, require additional fitting parameters, which in turn demand strategies to distinguish between them. In addition to providing a quantitative description of thermodynamic and kinetic signatures for both the IF and CS mechanisms, we also describe situations where the ‘best’ approach is required to distinguish both mechanisms. Specifically, we demonstrate how incorporation of amplitude analysis (in the ‘best’ approach) can distinguish situations where ‘equivalent’ K_D,app and k_obs behavior are expected (i.e. when the ‘better’ analytical approach fails). Finally, we present a novel experimental approach, the ‘dilution’ experiment, to aid in mechanistic interrogation for situations where adequate characterization of the observed rate binding behavior is insufficient for one of the kinetic phases.

Quantitative descriptions of the IF and CS binding mechanisms

Here quantitative descriptions of the IF and CS mechanisms are presented using simulations from three kinetic extremes or ‘limiting cases’: rapid binding, rapid isomerization, and stationary intermediate. The goal is not to belabor each kinetic extreme (as they have been discussed extensively in the literature) but rather to show how varied the k_obs and amplitude behavior may be. We expect experimental data to fall somewhere between the kinetic extremes. Notably, we present cases where undetectably small amplitude contributions for one kinetic phase result in less than two observable rates.

A). Observed rate and amplitude behavior

The observed rate expressions simplify under the three ‘limiting cases.’ These simplified expressions have been discussed extensively in the literature for the rapid binding or rapid isomerization cases and we summarize them here for ease of reference (Table 3). Specifically, the k_fast expression simplifies to resemble the k_obs expression for the analogous 2-state system (E ⇄ EL where k_obs = k_on*[L] + k_off or E ⇄ E* where k_obs = k_f + k_r). The k_slow expression, on the other hand does not simplify to contain only the rate constants associated with the slower equilibrating step. This is because the slower step is coupled to the system by the intermediate enzyme state. Thus, an ‘equilibration factor’ that describes the relative buildup of the intermediate state (EL for IF and E* for CS) in terms of the faster equilibrating step is included. The rate constant associated with the depletion of the intermediate is scaled by the ‘equilibration factor’ (see Table 3). More specifically, the ‘equilibration factor’ represents: A) either the buildup of the bound state, E ⇄ EL, for IF or the depletion of the unbound state, E* ⇄ E*L, for CS case when binding is the faster step or B) the buildup of the initially bound state, EL ⇄ E*L, for IF or the depletion of the binding competent state, E ⇄ E*, for the CS case when the isomerization even is the faster step. For example, the equilibration factor when binding is rapid describes the buildup of EL ([L]/(K_D+[L])) for IF and the disappearance of E* (K_D/(K_D+[L])) for CS.

Table 3. Simplified observed rate expressions for the limiting cases.

The ‘equilibration’ factors in the k_slow expressions are bracketed by parentheses.

	Rapid binding (kon, koff >> kf, kr)	Rapid isomerization (kf, kr >> kon, koff)	Stationary Intermediate IF: koff, kf >> kon, kr CS: kr, kon >> kf, koff
IF: E⇄EL⇄E*L	$$\begin{gathered} k_{\mathit{\text{slow}}}=k_f\left(\frac{\left[L\right]}{\left[L\right]+K_D}\right)+k_r \\ {k}_f{}_{ast}=k_{on}\left[L\right]+k_{off} \end{gathered}$$	$$\begin{gathered} k_{\mathit{\text{slow}}}=k_{on}[L]+k_{off}\left(\frac{k_r}{k_f+k_r}\right) \\ {k}_{\mathit{\text{fast}}}=k_f+k_r \end{gathered}$$	$$\begin{gathered} k_{\mathit{\text{slow}}}=k_{on}[L]\left(\frac{k_f}{k_{off}+k_f}\right)+k_r\left(\frac{k_{off}}{k_{off}+k_f}\right) \\ {k}_{\mathit{\text{fast}}}=k_{off}+k_f \end{gathered}$$
CS: E⇄E*⇄E*L	$$\begin{gathered} k_{\mathit{\text{slow}}}=k_f+k_r\left(\frac{K_D}{[\text{L}]+K_D}\right) \\ {k}_{\mathit{\text{fast}}}=k_{on}[L]+k_{off} \end{gathered}$$	$$\begin{gathered} k_{\mathit{\text{slow}}}=k_{on}[L]\left(\frac{k_f}{k_f+k_r}\right)+k_{off} \\ {k}_{\mathit{\text{fast}}}=k_f+k_r \end{gathered}$$	$$\begin{gathered} k_{\mathit{\text{slow}}}=k_f\left(\frac{k_{on}[L]}{k_r+k_{on}[L]}\right)+k_{off}\left(\frac{k_r}{k_r+k_{on}[L]}\right) \\ {k}_{\mathit{\text{fast}}}=k_r+k_{on}[L] \end{gathered}$$

The same generalizations for k_fast may be made for the stationary intermediate case, wherein the two fastest rate constants are included. However, since the fastest rate constants are involved in the depletion of the intermediate, the k_slow expression contains much more complex equilibrating factors associated with both the slower rate constants. In this case, the intermediate (EL for IF and E* for CS) is converted to the terminal bound state (E*L for IF and CS) as quickly as it is generated. Hence, this kinetic case is often referred to as the ‘stationary intermediate’ or ‘steady state’ intermediate case. Under these conditions, the intermediate state remains fairly constant (at low amounts in either case) throughout the binding process (Figures S1C and S2C).

The lower and upper limits (as [L] approaches 0 and infinity) for k_fast and k_slow are summarized in Tables 1 and 2. A key ‘takeaway’ is that the observed rate behavior for kslow always increases with [L] for IF while it may increase, decrease, or remain constant for the CS mechanism, depending on the relative difference between k_off and k_f + k_r. Moreover, the CS mechanism has discrete upper and lower limits relating to a single rate constant or sum of constants. This is not true for the IF mechanism, which has a complex expression for the lower limit of k_slow. Where possible, the discrete k_obs limits are shown in Figure 2. Because of this, it should be noted that the rapid isomerization simplifications in the k_obs expressions do not hold across all ligand concentrations. This is because at increasing concentrations, the k_slow expression (which contains k_on*L) will eventually approach the lower limits of the k_fast expression.

Figure 2. Comparison of IF and CS kinetic cases.

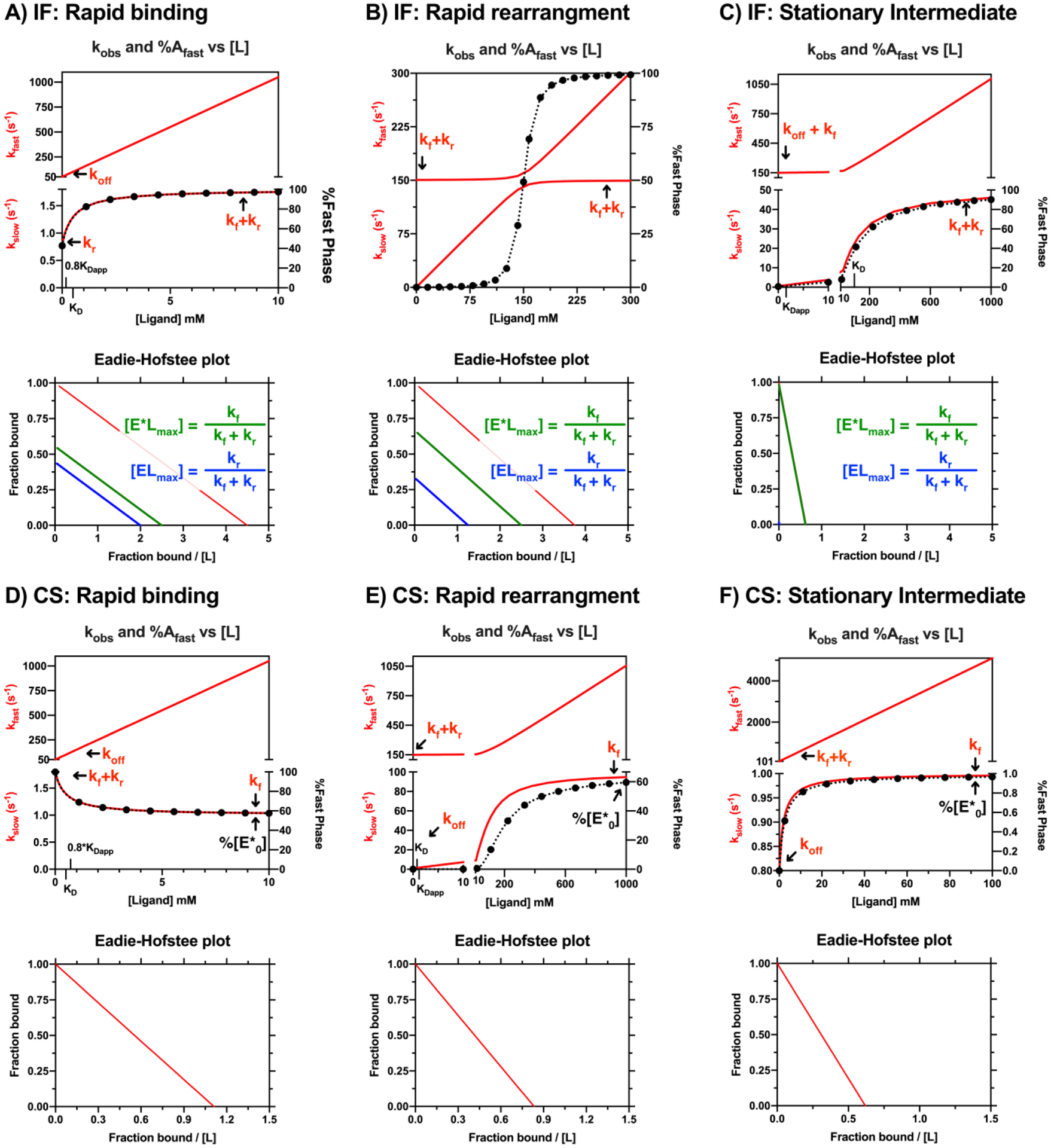
Summary of limiting kinetic cases for the IF and CS binding mechanisms. Rapid binding cases are in the left column (A, D), rapid rearrangement cases (isomerization) are in the middle (B, E), and stationary intermediate cases are in the right column (C,F). The k_obs vs [ligand] (red lines) and %fast phase vs [ligand] (black dots and red lines are overlaid with corresponding Eadie-Hofstee plots shown in the plot directly below. Three lines on the IF mechanism Eadie-Hofstee plots correspond to the total bound species (EL + E*L in red), the EL species (blue), and the E*L species (green) and the maximum values of each species are expressed relative to total enzyme. The Eadie-Hofstee plot for the IF case shows that the relative buildup of the bound states are parallel and depend on K_D,app, not K_D. The single line on the CS mechanism Eadie-Hofstee plot corresponds to the bound species, E*L (red). The rate constants for each binding mechanism are as follows: A and D) Rapid binding rate constants: k_on = 100 mM⁻¹ s¹, k_off = 50 s⁻¹,k_f = 1 s⁻¹,k_r = 0.8 s⁻¹, IF binding affinities: K_D,app,IF = 0.22 mM, K_D,IF = 0.5 mM. CS binding affinities: K_D,app,CS = 0.9 mM, K_D,IF = 0.5 mM. This case was used for the dilution experiment so 0.8*K_D,app and K_D are indicated on the x-axis. B and E) Rapid isomerization rate constants: k_on =1 mM⁻¹s⁻¹, k_off = 0.8 s⁻¹, k_f = 100 s⁻¹, k_r = 50 s⁻¹. IF binding affinities: K_D,app,IF = 0.27 mM, K_D,IF = 0.8 mM. CS binding affinities: K_D,app,CS = 1.2 mM, K_D,CS = 0.8 mM. C) IF Stationary intermediate rate constants: k_on = 1 mM⁻¹s⁻¹, k_off = 100 s⁻¹, k_f =50 s⁻¹, k_r =0.8 s⁻¹. IF binding affinities: K_D,app,IF =1.6 mM, K_D,IF = 100 mM. F) CS Stationary intermediate rate constants: k_on = 50 mM⁻¹s⁻¹, k_off = 0.8 s⁻¹, k_f = 1 s⁻¹, k_r = 100 s⁻¹. CS binding affinities: K_D,app,CS =1.62 mM, K_D,CS = 0.016 mM. Simulations were performed in MATLAB. See Figures S1 and S2 for the raw kinetic traces of the individual enzyme states.

The amplitude expressions are quite long and simplifications that were established for the observed rate expressions are difficult to achieve for the amplitude expressions. However, a few ‘takeaway’ conclusions are summarized here regarding their upper limits, which are indispensable in distinguishing the two mechanisms. The %fast phase always approaches the % of the binding competent species in the absence of ligand. The %fast phase behavior for the IF and CS are explained in detail below.

For IF, the %fast phase always approaches 100% at high ligand concentrations when both members in the ensemble of bound states contribute equally to the observed signal. In other words, ligand binds the entire population of the unbound state, i.e. %E₀ = 100%; Figure 1A). Hence at saturating ligand concentrations, the binding kinetics become monophasic wherein only the fast phase is observable; ligand binding at infinite ligand concentrations will likely occur within the mixing time or deadtime of the instrument. It is worth noting, however, that even though the observed signal appears to be fully equilibrated (See Figure S1A; EL + E*L vs Time plot), the isomerization process (EL ⇄ E*L) may still be approaching equilibrium (See Figure S1A, EL vs Time and E*L vs Time plots).

For CS, the %fast phase always approaches %E*₀ = 100*(k_f/(kf+k_r)); see Figure 1B. Thus, two kinetic phases are always observable at infinite ligand concentrations provided 0 ≪ E*₀ ≪ 100%. As with the IF mechanism, apparent “single exponential” kinetics may be observed when the %fast phase approaches 100% (in the case where k_f ⋙ k_r; i.e. %E*₀ approaches 100%), in which case the kinetics would be dominated by the fast phase at high ligand concentrations. Likewise, the opposite scenario may be expected when %fast phase approaches 0% (k_r ⋙ k_f; i.e. %E*₀ approaches 0%; see Figure 2F), in which case the kinetics are dominated by the slow phase (at high ligand concentrations). When k_f and k_r are not orders of magnitude apart (i.e. when 0 ≪ E*₀ ≪ 100%), then a persistent slow phase may be observed across several orders of magnitude (see discussion of amplitude analysis for the k_obs equivalent cases for further details).

Depending on the kinetic regime that a given ligand binding mechanism occupies (rapid binding, rapid isomerization, stationary intermediate, or somewhere in between), there is a potential for single exponential kinetics at low ligand concentrations (Figure 2B, 2C at low [L], 2E at low [L]). Examination of Figure 2 highlights how wide ranging the experimental ligand concentrations may need to be (note the concentration with respect to binding affinity).

B). Induced fit behavior

The limiting cases for the IF model are shown in Figure 2 (see Figure S1 for plots of the individual enzyme states over time) and the simplified k_obs expressions are presented in Table 3. In addition, the upper and lower limits for the k_obs expressions are presented in Table 1. A few general comments can be made upon examination of the limiting case behavior in Figure 2: 1) the lower limit of k_slow and k_fast varies depending on the relative magnitudes of k_off, k_f and k_r, 2) k_slow increases hyperbolically with an upper limit equal to k_f+k_r, 3) the build-up of the ensemble of bound enzyme states (EL and E*L) varies hyperbolically with respect to K_Dapp but are scaled by different maximum value expressions which are related to the isomerization step, 4) when EL and E*L contribute equally to the observed signal, the %fast phase always approaches 100% at high ligand concentrations, and 5) the simplified k_obs expressions only apply to all ligand concentration ranges in the rapid binding step example. To clarify, when k_on*[L] is in the simplified k_slow expression (as in the rapid isomerization or the stationary intermediate cases), the k_slow eventually approaches k_fast and the simplified k_obs expressions no longer describe the behavior.

C). Conformational selection behavior

The limiting cases for the CS model are shown in Figure 2 and the simplified k_obs expressions are presented in Table 3. A few general comments can be made upon examination of the limiting case behavior in Figure 2: 1) the lower limit of k_slow and k_fast varies depending on the relative magnitudes of k_off relative to the sum of k_f and k_r, where the lower limit of k_slow is equal to the lesser of k_off or k_f+k_r and the lower limit of k_fast is equal to the larger of k_off or k_f+k_r 2) k_slow has an upper limit equal to k_f, 3) a decrease in k_slow is unambiguous proof of CS, 4) k_slow only decreases under the following conditions: a) k_off > k_f+k_r or b) k_off < k_f+k_r and k_off < k_f 5) the depletion of the ensemble of unbound enzyme states (E and E*) varies hyperbolically with respect to K_Dapp but are scaled by different maximum value expressions related to the isomerization step, 6) when E*L contributes to the observed signal, the %fast phase always approaches %E*₀ (in the absence of ligand) at high ligand concentrations and two kinetic phases are always observable provided [E_total] ≫ [E*₀] ≫ 0, and 7) the simplified k_obs expressions only apply to all ligand concentration ranges in the rapid binding step example. To clarify, when k_on*[L] is in the simplified k_slow expression (as in the rapid isomerization or the stationary intermediate cases), the k_slow eventually approaches k_fast and the simplified kobs expressions no longer describe the behavior.

Special kinetic cases and experimental approaches to distinguish them

Two special cases are presented in the next two sections. The first set of simulations demonstrate the utility/requirement of amplitude analysis for distinguishing IF from CS. The second set of simulations demonstrate the utility/requirement of an additional experimental approach, the dilution experiment, to increase the kinetically observable experimental range.

A). The utility of amplitude terms when k_obs doesn’t differentiate IF from CS

Amplitude analysis is essential to distinguish cases where the IF and CS mechanisms are expected to have similar k_obs behavior. Two such examples were introduced by Chakraborty and Di Cera in [15] and we present kinetic simulations for the cases here (Figure 3 and Figures S3–S4). Analytical strategies that rely on differences in k_obs and K_Dapp as the sole mechanistic determinants are useless in these cases (see overlapping k_obs and Eadie-Hofstee plots). However, we note that the expressions that describe the individual enzymes states for each mechanism are not identical (see Tables 1 and 2). That is, although the observed rate expressions are similar, the amplitude values for the individual enzyme state expressions are distinct for each mechanism. The previous statement is obvious upon examination of the kinetic traces for the individual enzyme states (Figures S3 and S4; i.e. identical kinetic traces are not observed among the individual enzyme states for CS and IF mechanisms). Hence, amplitude analysis becomes critical to distinguishing the two mechanisms. Of course, experimental observation of the individual enzyme states is a luxury rarely afforded to researchers. Most often, the observed signal is from total fraction bound as shown in Figure 3 (see Bound vs Time and the resulting %Fast phase vs [Ligand] plots). The two k_obs equivalent cases present under two distinct physical scenarios. Both cases demonstrate the need to measure binding kinetics across a range of ligand concentrations, in order to distinguish the two mechanisms. We elaborate on each case below.

Figure 3. ‘Equivalent’ IF and CS cases: Amplitude analysis and across a range of ligand concentrations is critical to distinguish the mechanisms.

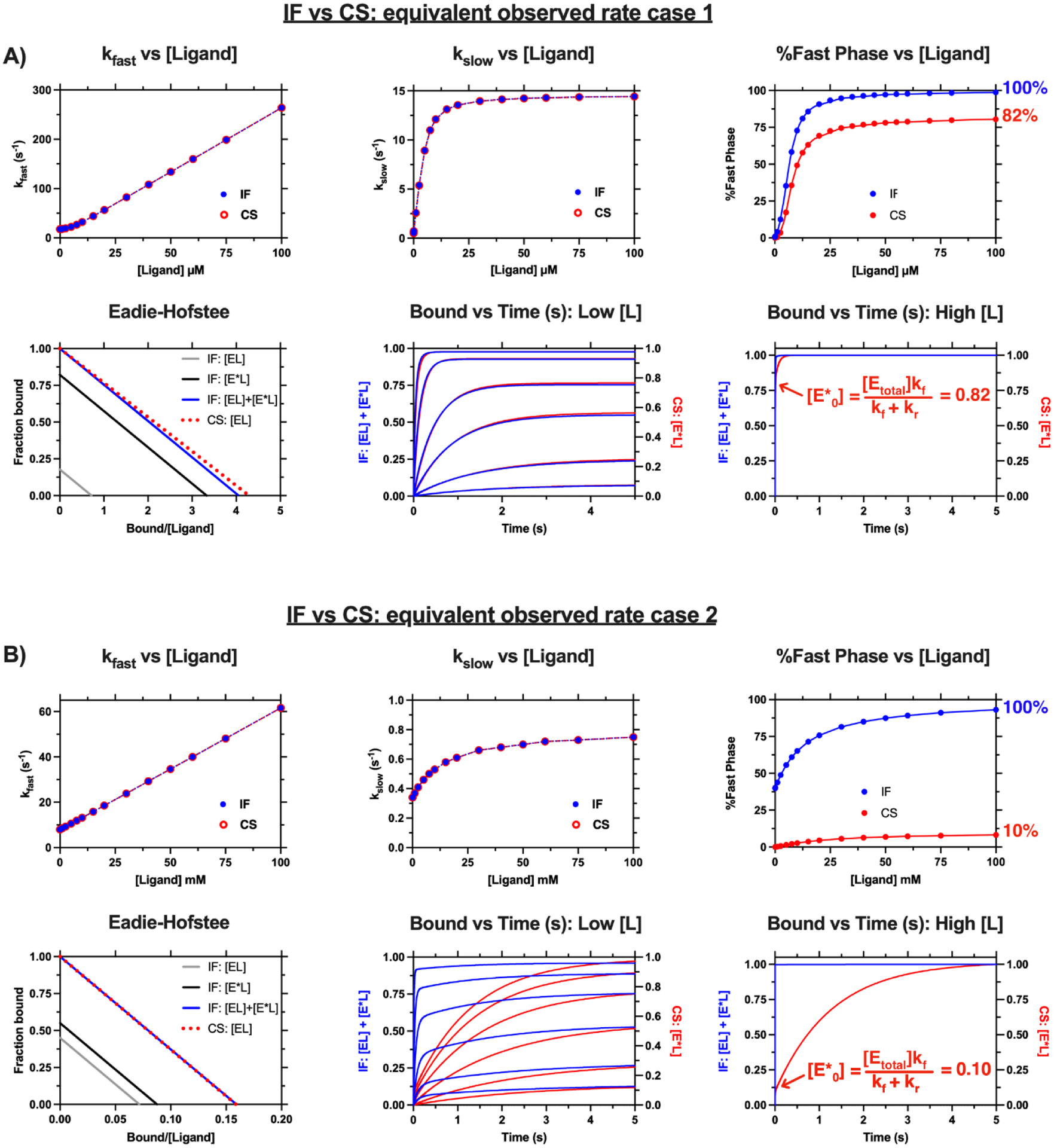
The two cases shown above have been discussed in [15]. The k_obs and Eadie-Hofstee plots for both mechanisms are superimposable for each case. The mechanisms are distinguishable when the amplitude contributions of the kinetic phases are compared (see the %Fast phase vs [Ligand]). A) Case 1: IF: k_on = 2.6 μM⁻¹ s⁻¹, k_off = 3.6 s⁻¹, k_f = 12 s⁻¹, k_r = 2.6 s⁻¹, K_D = 1.4 mM, K_D = 1.4 μM, K_D,app = 0.25 μM, CS: k_f = 14.6 s⁻¹, k_r = 3.1 s⁻¹, k_on = 2.6 μM⁻¹ s⁻¹, k_off = 0.50 s⁻¹, K_D = 0.19 μM, K_D,app = 0.23 μM. B) Case 2: IF: k_on = 0.54 mM⁻¹ s⁻¹, k_off = 7.54 s⁻¹, k_f = 0.44 s⁻¹, k_r = 0.36 s⁻¹, K_D = 14.0 mM, K_D,app = 6.28 mM, CS: k_f = 0.8 s⁻¹, k_r = 7.2 s⁻¹, k_on = 0.54 mM⁻¹ s⁻¹, k_off = 0.34 s⁻¹, K_D = 0.63 mM, K_D,app = 6.30 mM. The ligand concentrations at “high [L]” span several orders of magnitude illustrating the persistent and observable k_slow at high ligand concentration for the CS binding mechanism. Simulations were performed in MATLAB.

At first glance, the two mechanisms appear indistinguishable for case 1 (Figure 3A). Visual inspection of the Bound vs Time(s) plot at Low [L] and the resulting %Fast Phase vs [Ligand] plot below 12.5 μM reveal similar behavior between the two mechanisms. However, the two mechanisms begin to differ as [Ligand] increases, particularly as %Fast Phase approaches the upper limits for each mechanism. The %Fast Phase approaches 100% and 82% for the IF and CS mechanisms, respectively. Specifically, at concentrations above 25 μM, the %Fast phase for both mechanisms are near their upper limits. Examination of the Bound vs Time(s) plot at High [L] reveals a persistent slow phase for the CS mechanism (accounting for roughly 18% of the signal with k_obs equal to k_f or 14.6 s⁻¹) whereas the binding process appears to be complete within milliseconds for the IF mechanism. It is noteworthy that several kinetic profiles for ligand concentrations spanning 30 μM – 3000 μM are shown in the Bound vs Time (s) at High [L] plot yet they appear as a single kinetic trace. Thus, the two mechanisms may be experimentally distinguishable provided ligand is soluble above 30 μM and the kinetic instrument is able to measure kinetics with an observed rate of 14.6 s⁻¹ (note: this is feasible for most modern stopped flow instruments).

The differences between the mechanisms and the utility of amplitude analysis are obvious for Case 2 (Figure 3B). The Bound vs Time(s) plots and the resulting %Fast Phase vs [Ligand] plot are visibly different for each mechanism. This is because the %Fast Phase approaches 100% and 10% for the IF and CS mechanisms, respectively. In similar fashion to Case 1, several kinetic traces for ligands spanning several orders of magnitude are overlaid in the Bound vs. Time (s) at High [L] plot. Similarly to Case 1, a persistent slow phase is observed for the CS mechanism at High [L] (accounting for roughly 90% of the signal with k_obs equal to k_f or 0.8 s⁻¹) whereas the binding process appears to be complete within milliseconds for the IF mechanism. In contrast to Case 1, the two mechanisms are distinguishable across all ligand concentrations. This remains true for CS mechanisms where %E*₀, which is the upper limit of %Fast phase, is well below 100%.

A key ‘takeaway’ that distinguishes the binding mechanisms is the observation of a persistent slow phase in the case of the CS mechanism. However, we advise against concluding the presence of a CS component without a global analysis of kinetic data spanning a range of ligand concentrations using the full solutions of the enzyme states or the ‘best’ approach as described in the above section (e.g. Equations 4–6 for each mechanism; also see Tables 1 and 2). This is because the resulting %Fast phase behavior is related to the relative contributions of the members of the bound state to the signal. It is entirely possible for %Fast phase to approach a value below 100% for the IF mechanism if the two bound states differently contribute to the signal (i.e. when different extinction coefficients are expected for each bound state). However, due to the uniqueness of the individual expressions (see comparison of the kinetic traces of the individual enzyme states in Figures S3 and S4), a global analysis of the data with the full expressions of the enzyme states would strengthen confidence in distinguishing the mechanisms. Thus, utilization of the amplitude and k_obs expressions for the data analysis allows one to distinguish the models with a higher degree of confidence.

B). Expanding the experimental range by dilution

Here, a dilution experiment is presented as a method to expand the experimental range of [L]. The dilution experiment takes advantage of the fact that the observed rates of change are unaltered by the direction of change (binding vs. dilution). The experimental setup includes diluting ligand-bound enzyme into ligand-free buffer, which results in a re-equilibration of the system towards the unbound complex with kinetics defined by [L_final]. The amplitudes of change are maximal for the dilution experiment when the initial ligand concentration is equal to sqrt(D)*K_D,app (where D = dilution factor; see Supplementary file for derivation). Importantly, the change in signal for the dilution experiment exceeds that of the binding experiment for D>2 and [L_initial] < K_D,app*(D-2). Thus, the dilution experiment serves as a means of signal amplification at low ligand concentrations. This becomes useful for situations when the traditional binding experiment yields the following results: 1) no observable curvature in the k_slow, and 2) k_fast approaches the limits of detection. By lowering the experimental ligand concentration, the dilution experiment allows one to measure binding kinetics at near-zero ligand concentrations which: 1) increases the likelihood to observe curvature in k_slow and 2) increases the likelihood to capture the lower limits of k_fast (note: the lower limits of k_fast takes on different forms: k_off, k_f + k_r, or something more complex; see Tables 1–2 for the lower limits of k_fast).

The results from simulations for the comparison of the binding (black lines) and dilution (red lines, dilution factor = 10) are presented in Figure 4. Each row contains results for IF and CS and includes plots of the change in fraction bound, amplitude values, and %fast phase vs ligand concentration (scaled by K_D,app) in each column. Notably, the dilution experiment simulations were carried out on the ‘rapid binding’ kinetic case in Figure 2. The change in fraction bound display similar behavior between the different models (same dilution experiment maxima and point of intersection with the binding experiment results). In fact, identical plots are observed for both mechanisms. For the dilution factor of 10, the dilution experiment yields a higher change in fraction bound for the dilution experiment when the initial ligand concentration is less than 8*K_D,app. Thus, the dilution experiment will amplify the change in fraction bound for final ligand concentrations below 0.8*K_D,app ([L_final] = [L₀]/dilution factor). Examination of the k_obs and %fast phase plots for the relevant case in Figure 2 (rapid binding IF and CS cases) reveals that the dilution experiment range contains regions before either plot (kobs or %fast phase) plateaus, particularly for the CS (Figure 2). This is extremely useful for models where K_D < K_Dapp (e.g. CS) because the curvature in k_slow or %fast phase tends to vary around K_D. Strikingly, the %fast phase plots are identical for the binding and dilution experiments for both models. Global analysis of binding and dilution data takes the amplitude contribution into account and helps with model differentiation, particularly when data from both experiments are simultaneously fit.

Figure 4. The dilution experiment expands the experimental concentration range.

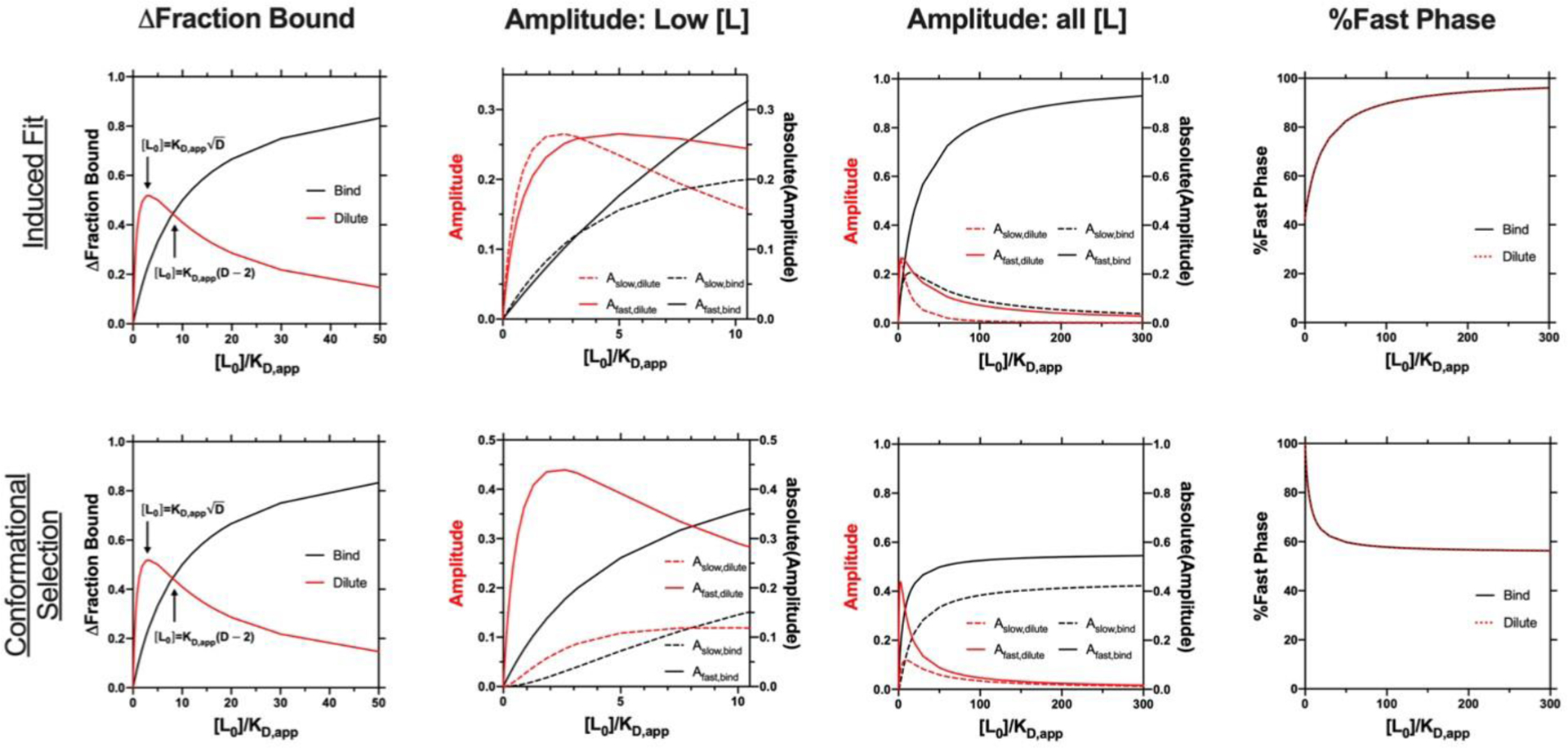
The dilution factor for all dilution simulations is equal to 10. Extinction coefficients for the bound species are equal to 1. IF: (Rapid binding example from Figure 2A) k_on = 100 mM⁻¹ s⁻¹, k_off = 50 s⁻¹, k_f = 1 s⁻¹, k_r = 0.8 s⁻¹, K_D,app = 0.22 mM, K_D = 0.5 mM, CS: (Rapid binding example from Figure 2D) k_f = 1 s⁻¹, k_r = 0.8 s⁻¹, k_on = 100 mM⁻¹ s⁻¹, k_off = 50 s⁻¹, K_D,app = 0.9 mM, K_D = 0.5 mM.

Functional Significance: IF vs CS

The formal analyses discussed above can be used to distinguish between IF vs. CS, but the distinction is most powerful when coupled to a consideration of its functional relevance. Whether IF or CS is advantageous or disadvantageous depends on the biological function of the protein. To illustrate this, effects that redistribute the conformational landscape are discussed below in terms of the initial ‘binding’ of ligand (Figure 5) vs the effects on catalysis or signaling subsequent to formation of the bound ensemble (Figure 6). Part of this distinction depends on whether the protein has evolved to be substrate specific or substrate promiscuous. We discuss potential functional outcomes that may arise from either binding mechanism, which are schematized in Figures 5 and 6.

Figure 5.

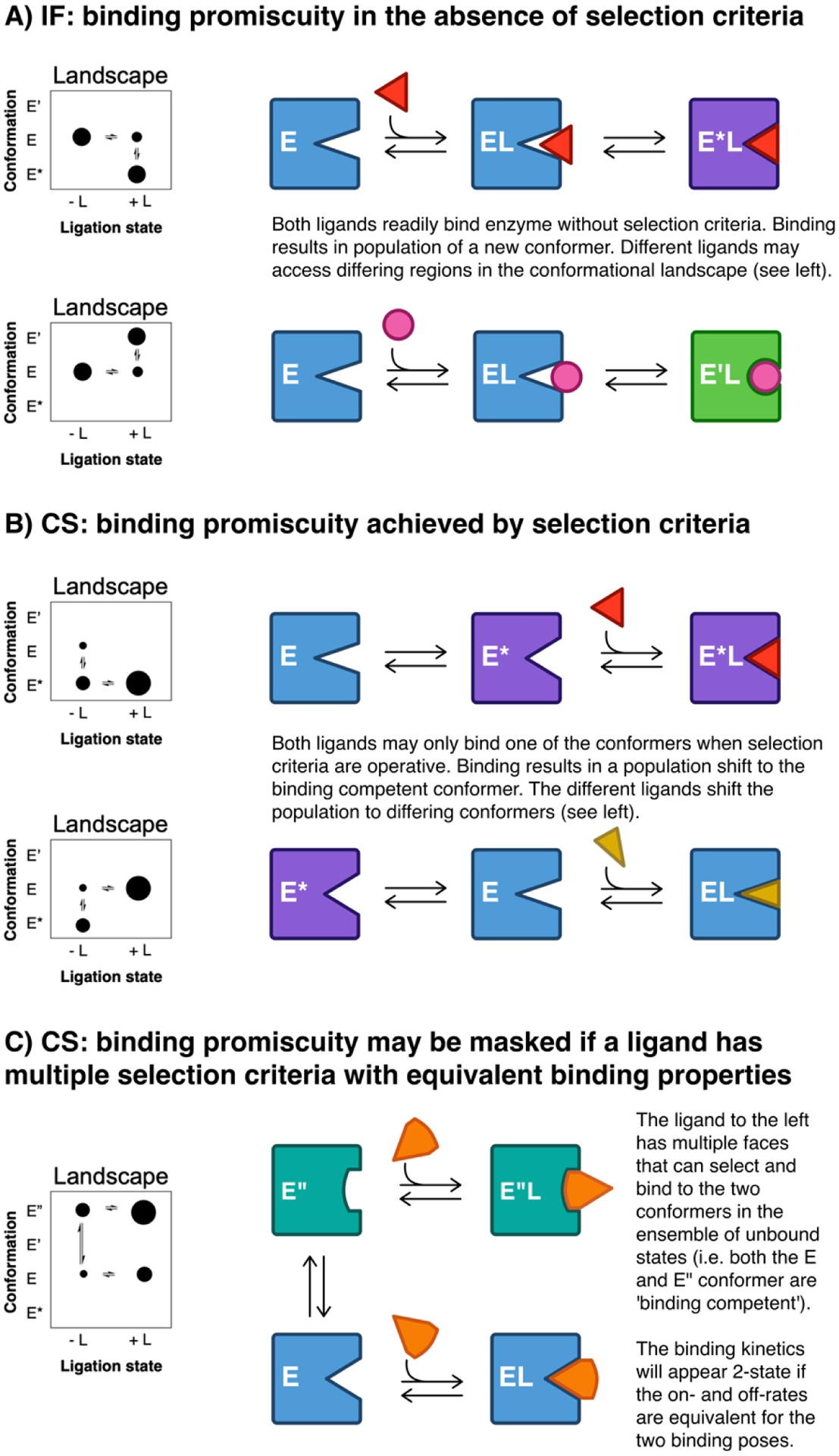
Binding promiscuity may be achieved with the IF and CS mechanisms. Four different conformers (E, E*, E’, E”) under different ligation states are shown in different scenarios. The different conformers are colored blue, purple, green and teal for E, E*, E’, and E”, respectively. The ‘binding competent’ or binding incompetent’ status differs for each ligand. A) Two IF binding scenarios are depicted wherein two unique ligands have no difference in selection criteria for initial binding. Binding promiscuity can be accomplished by IF when a single conformer binds multiple ligands. Each ligand induces different conformers (E*L or E’L for red and pink ligands, respectively). Potential functional implications are presented in Figure 6A. B) Two CS binding scenarios are depicted wherein two ligand-free conformers, E and E*, exist. E represents a ‘binding competent’ conformer for the red ligand and binding incompetent conformer for the gold ligand. The reverse is true for E*. Thus, binding promiscuity is achieved by CS when members of the ligand free ensemble bind to different ligands. Potential functional outcomes are depicted in Figure 6C. C) Binding promiscuity is achieved for the two conformers E” and E as depicted in Figure 5B, when a multiple ligands individually can bind to multiple conformers. This demonstrates how the functional binding promiscuity may be ‘kinetically’ masked; if the on- and off-rates governing the formation of E”L and EL are equal, then the binding kinetics will appear 2-state. The potential functional implications are presented in Figure 6C.”

Figure 6. Functional promiscuity and atypical (non-Michaelis-Menten) kinetics may be achieved with the IF and CS mechanisms.

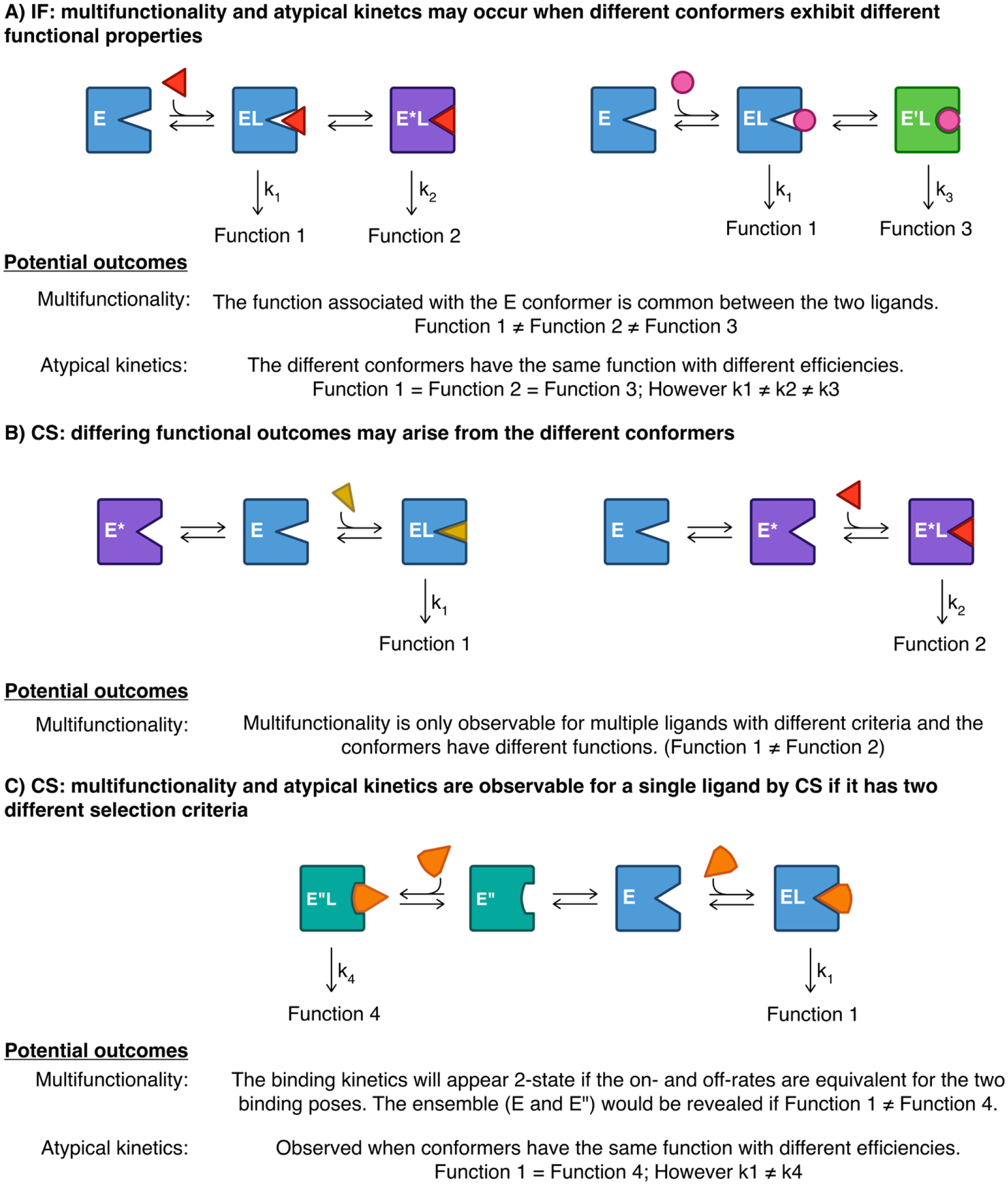
These are the same scenarios depicted in Figure 5 but emphasis is now placed on the resulting functional properties. Functionally competent or ‘functionally incompetent’ states may differ between ligands and potential outcomes are indicated for each. A) It is likely that the two ligand-induced conformers, E*L or E’L, have different functional properties and thus multifunctionality or atypical (non-Michaelis-Menten) kinetics are potential outcomes. However, it is also worth noting that the E conformer is still retained upon binding of ligand (i.e. EL remains in the ligated state for both the red and pink ligands) and thus the original function of the ground state conformer may be retained in both ligands though at different amounts. B). In this case, either ligand shifts the population in the bound state to approach 100% E*L or (red ligand) or EL (blue ligand). If the different conformers have different functional properties, different functional outcomes might be expected for either ligand. C). The ensemble of bound states is revealed if they have different functional properties (i.e. different functions or rate constants.

A). Binding properties: specificity vs promiscuity

‘Binding’ properties relate to how the ligand interacts initially with the ligand-free ensemble of protein states (Figure 5). Specificity is achieved by two mechanisms: 1) an enzyme exclusively binds to a single substrate or class of structurally related substrates without further discrimination based on conformational change. This has been referred to as the ‘rigid template’ model of recognition and, although examples exist [23, 24], this behavior is probably rare; 2) many different ligands may transiently bind, but only a single ‘specific’ substrate induces a conformational change to an active conformer, as in IF. The relationship between IF and ‘specificity’ has been appreciated adequately [25, 26]. Induced fit leads to longer ‘residence times’ for ligands on their cognate enzyme or receptor, facilitating forward flux of substrate to product for enzymes or increased downstream activation of the receptor. In contrast to the IF mechanism, whose ligand-free state is entirely comprised of the ‘binding competent/activity incompetent’ conformer, CS provides no advantage for substrate specific proteins or enzymes, unless it is used to provide conformers that bind to regulatory effectors that modulate activity in response to cellular status. The CS mechanism provides the potential to exploit regulatory or allosteric interactions at the expense of higher affinity for substrate and the possibility for noncognate ligands to bind and inhibit function. Regulatory molecules could be recruited to conformers that are present in the ligand free ensemble. In the absence of regulatory mechanisms, CS represents a ‘cost’ of the intrinsic dynamics of proteins that afford substrate specificity. It should be emphasized that conformational ensembles of the ligand-free protein are not a necessary condition to achieve allosteric regulation, but they provide states to which allosteric regulatory ligands can bind and, thus, are a sufficient condition for promiscuity.

Promiscuous or ‘multifunctional’ proteins may be considered from two perspectives. We refer to both types as ‘promiscuous’ in as much as they share the property of interacting with many different ligands. One type of promiscuity includes ‘substrate specific’ proteins whose biological function is to process a single substrate but binds other ‘noncognate’ substrates with some measurable affinity without having a useful functional result. Essentially all ‘substrate specific’ proteins exhibit this promiscuity to some degree and this is the basis for many therapeutic drugs that inhibit their targets. The second type of promiscuity occurs with multifunctional proteins whose function requires interaction with multiple substrates with different outcomes. These proteins deviate from the one protein-one ligand paradigm and the opposite advantages and liabilities described for specificity may be envisioned here. Here, the one protein-one ligand paradigm refers to the proteins that achieve their biological function through interactions with a single substrate. Examples of promiscuous proteins include detoxication enzymes that metabolize a wide range of structurally unrelated substrates such as cytochrome P450s and other drug metabolizing enzymes [27–29] or signaling proteins that are activated or inhibited by different ligands as part of their physiological function. These signaling proteins activate or inhibit multiple ‘downstream’ targets, such as GPCRs and their effectors [30–33].

For such systems, IF may represent a disadvantage if the single conformer present in the absence of ligand, E, is unable to recruit chemically diverse ligands or binding partners. Of course, this disadvantage is minimized if a single conformer can afford adequate promiscuity (Figure 5A). In contrast, ligand free ensembles of the CS mechanism can provide a mechanism of ligand promiscuity if members of the ensemble have orthogonal selectivity or if the distribution within an ensemble of overlapping but nonidentical ligand selectivity’s respond to different environmental cues and thus shift the ensemble selectivity (e.g. tissue dependence or in response to cellular status, Figure 5B and 5C). IF can also be advantageous for promiscuous proteins if the different ligands can each induce a conformation that increases the degree of saturation at equilibrium or steady state as with ligand specific proteins, via combined IF. Presumably, the combination of ensembles with distinct ligand selectivity’s in both free and bound states would maximize promiscuity, in a mixed IF-CS mechanism. These scenarios summarize the potential advantages or disadvantages of conformational ensembles in the ligand free state as they relate to substrate specificity or promiscuity. Importantly, the utility of the amplitude analysis discussed above is further increased when considering mechanisms of specificity or promiscuity, as elaborated below.

B). Catalytic properties: optimizing catalysis or signaling

Ensembles of ligand bound states also are important for function (Figure 6). For substrate specific enzymes whose function is to generate a specific reaction product, ensembles of bound species are advantageous to the extent that conversion to the E*L complex increases flux toward product, as noted above. However, if the ligand bound ensemble includes numerous states beyond EL and E*L, they could reduce the functional output (Figure 6A and 6C). That is, unless all bound states with a single ligand are catalytically equal, the IF mechanism can provide states that decrease the optimal function of the protein. This behavior has been historically referred to as ‘nonproductive binding’ [34, 35]. More generally, any ligand bound states created via IF that do not increase function relative to other bound states are disadvantageous for substrate specific proteins. From a catalytic perspective for enzyme/substrate pairs where a single product or single ‘output’ is desired, the CS binding mechanism represents a purely advantageous scenario while the IF binding mechanism, which contains an ensemble of bound states, represents a potential disadvantage.

In the context of promiscuous or multifunctional enzymes, an ensemble of bound states for a single ligand also is disadvantageous if some states have lower catalytic rates than others; the enzyme would be a better catalyst if a single ‘optimized’ E*L complex were formed without an ensemble of suboptimal complexes. However, ensemble behavior of the bound states for a single substrate is likely a cost that promiscuous enzymes must pay in order to form bound complexes with a wide range of substrates. For example, the detoxication CYPs noted above are among the most promiscuous enzymes known and they metabolize many unrelated substrates, with known differences in conformational ensembles of bound states with different substrates [36]. The ability to adapt conformation to many different substrates is an obvious advantage for their promiscuous function as noted above, but all of the resulting bound states for any single ligand may not be optimally active, and thus cause substrate inhibition. In fact, with CYPs, the substrate inhibition may occur with ‘uncoupling’ of the reaction cycle and wasteful expenditure of NADPH without substrate oxidation [37]. In this case, the ensemble of bound states allows for substrate promiscuity but at the cost of suboptimal catalysis for any specific substrate. Specifically, a substrate bound in a suboptimal orientation or conformation can lead to collapse of the quasi-stable enzyme intermediate that oxidizes the substrate, without successful substrate oxidation. This is a cost to the organism because it utilizes NADPH with productive metabolism. This is, in fact, a common behavior for some detoxication CYPs that nicely demonstrates induced fit conformations in the bound ensemble that decrease optimal activity. Obviously, the rates of interconversion between productive states and nonproductive states will determine how efficient the enzyme is for any substrate and these rates are, in principle, available from the analyses described above that utilize extended versions of IF or CS models.

Kinetically active vs kinetically silent transitions: experimental design matters

Despite the large number of literature examples, it is unlikely that a ‘pure’ IF mechanism (single unbound enzyme conformer) would be operative for many proteins given the ubiquity of conformational ensembles of ligand free proteins. Hence, the experimentally assigned mechanism and its implications require careful consideration of the experimental design. Specifically, a distinction between two kinetic processes must be made: ‘kinetically active’ vs ‘kinetically silent’. A ‘kinetically active’ process is one that is included in the measured binding mechanism (e.g., the IF and CS binding mechanisms contain isomerization and binding processes). A ‘kinetically silent’ process is one that is not included in the measured binding mechanism (e.g., a conformational change that has no bearing on the measured kinetic process). To clarify, the distinction between a ‘kinetically active’ vs a ‘kinetically silent’ process is dependent on the measured experimental output. Hence, the experimental design directly impacts the two ‘types’ of kinetic processes (i.e., the mechanism is only as informative as the experimental design allows it to be) and this is related to the measured experimental outcome (i.e., signal). The signal may differ with instrument and/or experimental setup, which are discussed below in the context of binding vs functional kinetic experimental setup.

The ensemble perspective can reconcile apparent mechanistic inconsistencies

Even when the same technique is used to determine the binding mechanism, it should be expected that the ‘apparent mechanism,’ IF vs. CS, will vary with different ligands for a single protein. If some ligands fit best to an IF model and others fit best to a CS model, this does not mean that some experiments are incorrect. In fact, interrogation with multiple ligands provides a powerful, and underappreciated, approach to understand the ensemble behavior of a protein.

For example, if an IF model clearly describes the kinetic data for a set of ligands this does not mean necessarily there is no conformational exchange in the ligand free state. There may be a conformational ensemble exchanging on a rapid time scale much faster than the on and off rates of ligand, the specific experimental method used may not report on time-dependent changes of the ligand free ensemble, or the conformational change may have no bearing on the binding event (e.g. distal from the binding site or ligand access/egress channels).

Similarly, if data fit well to a CS model with no improvement in the fit by inclusion of an IF component, this does not mean that no ensemble exists in the bound state(s). The exchange of conformations in the bound states may be too fast relative to binding and dissociation or the exchange may not be observed by the experimental method being chosen (e.g. SPR, BLI).

More interestingly, if different rate constants for conformational exchange, k_f, k_r, and A_i’s are recovered for a CS model with different ligands this is an experimental indication that different ligands bind to different conformers within the ligand free ensemble, as suggested above as a potential mechanism by which promiscuous proteins recruit different ligands. If a range of values is obtained, but a double exponential model fits in all cases, this would indicate that many ligand-free states are used to recruit different ligands, but their exchange properties are incompletely resolved kinetically. Alternatively, it would be expected that if multiple ligands bind to the same conformation and a CS model is the best fit, then each ligand would yield the same A_i’s, k_f and k_r. This could occur if a ligand free protein exists in an open state that binds ligands and a closed state that does not. Moreover, the amplitude, k_f and k_r terms obtained for the isomerization step would provide the equilibrium constant for the conformer interconversion. For a system that fits well to an IF behavior, interrogation by multiple ligands can also be useful for analogous reasons. If multiple ligands all drive the bound states to the same conformers, then the corresponding k_f, k_r and amplitude terms will be ligand independent. If different ligands drive the bound ensemble to different bound states, then k_f, k_r, and A_i’s will be ligand dependent.

Another interesting scenario may occur wherein multifunctionality is observed in a functional assay (e.g. multiple products detected) for a protein/ligand pair that had single-exponential or “apparently 2-state” kinetics (Figure 5C and 6C). In this example, the kinetically silent ensemble of bound states in the binding experiment are revealed in the functional assay. Hence, multiple techniques are strongly suggested to gain confidence in the most accurate description of a ligand/protein pair.

These examples highlight the potential utility of performing kinetic binding analyses for a single protein with multiple ligands. Mechanisms by which promiscuous proteins achieve their versatility or substrate specific proteins optimize their selectivity can be obtained from consideration of the ligand-dependent ensemble properties. However, the utility of this approach will be limited by the extent to which the experimental data can meaningfully resolve differences in k_f, k_r and corresponding amplitudes. This will be challenging and will likely require large data sets and very careful application of rigorous statistical tools. Regardless of these challenges, there are likely to be significant advances in our understanding of protein ensembles by considering more complex and realistic models by which they interact with ligands.

Abbreviations:

CS

conformational selection

IF

induced fit

k_obs

observed rate

k_f

forward rate constant

k_r

reverse rate constant’

K_D

equilibrium dissociation constant

K_Dapp

apparent equilibrium dissociation constant

E

enzyme

L

ligand

EL

enzyme ligand complex