Dental age assessment by the pulp/tooth area proportion in cone beam computed tomography: is medico-legal application for age estimation reliable?

Abstract

Introduction

Forensic dentistry has, as one of its main goals, the identification of living and/or deceased individuals, based on the individual features of the teeth. One of the identification criteria to be established is the chronological age. Several authors, including Kvaal, have developed age estimation methods based on secondary dentine deposition. Nowadays, three-dimensional imaging tests, such as Cone Beam Computed Tomography (CBCT), are used in age estimation.

Objective

The aims of this research project were to validate Kvaal’s method and its variables in age estimation and to create new linear regression formulae to better represent the study sample.

Methods

We selected 158 CBCT, with a total of 402 sound teeth (central incisors, lateral incisors and canines). The necessary measurements and ratios were calculated in both coronal and sagittal sections, with XelisDental^®. The formulae developed by Kvaal for age estimation calculation were applied. Subsequently, the results were statistically analyzed.

Results and Discussion

The intraclass correlation coefficients from the two measurements ranged from 0.918 to 0.997. The calculated age estimation had a mean error of -21.4years (coronal section) and -26.3years (sagittal section). The t test revealed statistically significant differences between chronological age and estimated age. The absolute values of Pearson’s correlation coefficient between age and the two Kvaal variables ranged from 0.06 to 0.38 and from 0.06 to 0.55. The coefficients of determination are lower than in the original study (between 0.03 and 0.39). In the linear regression formulae, the coefficients of determination ranged from 0.07 to 0.41.

Conclusion

This investigation concludes a non-reproducibility of Kvaal’s method in the Portuguese population when applied in CBCT, with statistically significant differences between the chronological age and the dental age, estimated by the pulp/tooth proportion method, based on the teeth analyzed in this study.

INTRODUCTION

Forensic odontology is a branch of dental medicine that deals with the examination of dental evidence for further evaluation and presentation of results to the court. One aspect involves the age estimation of individuals and using it in cases related to living or dead individuals. (1)

In post-mortem cases, the identification is based on the characteristics present in the teeth of different individuals due to enamel’s high resistance to environmental conditions. (2, 3) Age estimation can also be used in ante-mortem criminal investigation cases, such as physical assaults or cases related to illegal immigration, due to the gradual increase of people without any identification documentation when entering European countries. (4–6) Therefore, forensic odontology plays a key role in the implementation of the United Nations’ 16^th Sustainable Development Objective and the Portuguese laws no. 27/2008 (updated no. 26/2014) and no. 147/99 (7–10).

In order to estimate the age of adults, several authors created methods to estimate age taking into account secondary dentine deposition and consequent reduction of pulp size. (11, 12) Kvaal et al. developed a gender-dependent age estimation method, evaluating the pulp/tooth ratio on periapical radiographs and concluded that there are no differences between the right and left sides of the dental archs. Several authors successfully applied this method, (13, 14) while others refuted it. (15, 16)

Currently, complementary diagnostic tests such as CBCT can allow the visualization of oral tissues in three dimensions. Many authors used CBCT to understand whether this three-dimensional examination allows a more reliable age estimation than two-dimensional examinations (17–20), some of them applying Kvaal’s method. (21, 22)

AIM:

In this study, we estimated the age of a Portuguese population by dental means using the pulp/tooth ratio method initially proposed by Kvaal in the central incisors, lateral incisors and permanent canines, through CBCT.

The main aim of this investigation was to see if there were any statistically significant differences between the estimated and the chronological age of individuals.

As secondary objectives, it was intended to evaluate the correlation coefficients of the explanatory variables defined by Kvaal, when applied to this study, verifying the existence or not of statistically significant differences between the calculated and the original coefficients.

The final aim was, through CBCT analysis of tooth/pulp area proportions, to obtain a new regression formula for a more reliable calculation of age estimation with the three-dimensional method, verifying whether gender influenced age estimation.

MATERIAL AND METHODS

Experimental design

This study was conducted at a private medical dental clinic. The clinical and CBCT data of patients admitted to the Dental Medicine Clinic between 2016 and 2018 were retrospectively evaluated. The study protocol was approved by the Dental Medicine Faculty´s ethics committee.

Population sample

After the examination of medical records and CBCT data, the sample was selected based on several criteria: known gender; 21 years old or older; presence of fully visible permanent tooth of the anterior segment (central incisor, lateral incisor or canine, maxillary or mandibular), only one pulp canal, nil caries, restorations, rehabilitation, endodontic treatment, periapical/occlusal/periodontal pathology or anomalies that may cause morphological changes.

After selection, 158 CBCT where included, making a total of 402 teeth (central incisors, lateral incisors and canines, including in some cases several teeth from the same individual).

Data collection

Data from the patients referring to patient’s name, gender, date of birth and date of CBCT examination was collected in RayScan^® blindly to ensure anonymity and avoid bias.

In Kvaal’s original method, a set of measurements of tooth and pulp heights and widths were calculated on periapical radiographs, in order to calculate several ratios that would allow, when applied in an equation, an estimation of the individual's age. (11)

Since three-dimensional imaging was used in the present study, measurements were recorded on coronal (C) and sagittal (S) sections, parallel to the longitudinal axis of the tooth, using the cuts in which pulp dimensions were widest. The analyzed teeth were divided into 3 different image quality groups: G0 – poor quality due to root curvature/pulp cutting; G1 – poor quality due to poor image definition; G2 – good quality.

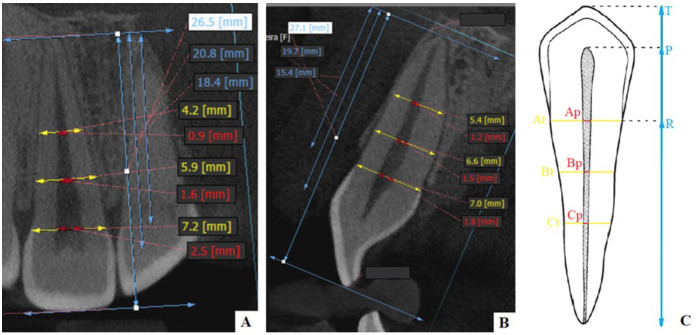
Measurements were recorded in XelisDental^® (as illustrated in Figure 1), using the “ruler” tool, in order to calculate age estimation based on Kvaal’s method:(11)

Figure 1.

Measurements made in CBCT

• ¾ Level A = tooth (At) and pulp (Ap) width at the cemento-enamel junction (CEJ) level;

• ¾ Level C = tooth (Ct) and pulp (Cp) width mid-root between CEJ and root apex;

• ¾ Level B = tooth (Bt) and pulp (Bp) width at the average distance between A and C;

• ¾ T = maximum tooth length;

• ¾ P = maximum pulp length;

• ¾ R = maximum root length.

Subsequently, the following Kvaal ratios were calculated:(11)

• ¾ Aind = Ap/At;

• ¾ Bind = Bp/Bt;

• ¾ Cind = Cp/Ct;

• ¾ RP = P/R;

• ¾ RT = T/R;

• ¾ RR = P/T;

• ¾ M = (RP+RR+Aind+Bind+Cind)/5

• ¾ W = (Bind+Cind)/2

• ¾ L = (RP+RR)/2

• ¾ Dif = W-L

Subsequently, the regression formulae defined by Kvaal were applied to the tooth groups 11/21, 12/22, 32/42 and 33/43 (dental nomenclature according to the FDI), to determine age estimation (Table 1). (11)

Table 1. Kvaal’s regression formulae to calculate age estimation. M and Dif are the age predictors defined by Kvaal (1995). G=Gender (0 female, 1 male).

Group of teeth	Kvaal’s regression formulae
11/21	Age = 110.2 – 201.4(M) – 31.3(Dif)
12/22	Age = 103.5 – 216.6(M) – 46.6(Dif)
32/42	Age = 106.6 – 251.7(M) – 61.2(Dif) – 6.0(G)
33/43	Age = 158.8 – 255.7(M)

Data validation

In order to evaluate the intra-observer variability, 10% of measurements were re-evaluated after 3 months without knowledge of the previous data. The agreement between the measurements of the observer was assessed using the Intraclass Correlation Coefficient (ICC).

Statistical data analysis

The Statistical Package for the Social Sciences (SPSS) software (version 25; IBM Corporation Armonk, NY, USA) was used for the statistical analyses. A level of significance of 5% was taken to perform all statistical tests.(23)

In the intra-observer validation, the ICC was used, based on Fleiss values. (24)

In order to confirm a normal distribution, the Kolmogorov-Smirnov test was applied (given the absolute frequency greater than 50). (23)

Student's t-test was used for paired samples to test the existence or not of statistically significant differences, between the chronological age and the dental age estimation.

Since there were different image qualities, the absolute estimation errors (AEE) were calculated for the different image quality groups: poor quality due to cutting (G0), poor quality due to poor definition (G1) and good quality (G2).

Pearson’s correlation coefficient was used to measure the correlation between chronological age and the variables used by Kvaal as predictors (M and Dif) in the original study. The same predictors were evaluated based on the ANOVA linear regression model, analyzing the existence of explanatory variables and verifying whether it is sufficiently explanatory by the determination coefficient (R²).

Finally, a multivariate linear regression was created by the ANOVA backward method in which only variables with p-value<0.1 in the Student’s t test were included, using the model that best described the relationship between the dependent variable (chronological age in years) and the independent variables included.

RESULTS

Descriptive analysis

In this study, we examined 158 patients with 402 teeth between 21 and 80 years of age, where 97 (61.4%) are females and 61 (38.6%) are males. The age distribution is shown in Table 2. Regarding the analyzed teeth (N=402), 235 (58.5%) belong to female individuals and 167 (41.5%) to male. The greatest number of teeth were maxillary canines (125 teeth) and the lowest mandibular central incisors (10 teeth).

Table 2. Age distribution of the patients for each type of tooth.

		Age
		< 30	30 - 39	40 - 49	50 - 59	60 - 69	70+	Total
Tooth	11	8	5	11	7	6	0	37
	12	10	9	10	6	5	1	41
	13	14	11	22	9	8	3	67
	21	7	4	6	6	5	0	28
	22	11	5	12	4	5	1	38
	23	13	12	20	5	7	1	58
	31	2	0	2	1	1	0	6
	32	2	1	5	5	3	2	18
	33	6	3	12	12	13	3	49
	41	2	1	0	0	0	1	4
	42	3	1	3	5	0	1	13
	43	3	5	11	14	8	2	43
	Total	81	57	114	74	61	15	402

Intra-observer variability

Intra-observer variability applied to measurements recalculated from 40 teeth observed twice. The lowest ICC value was 0.918 (variable RT, coronal section) and the highest was 0.997 (both variable Cp in the coronal section and variable Bp in the sagittal section).

Age estimation by Kvaal formulae

The age estimations were made by applying the formulae deduced by Kvaal (Table 1) and subsequently verifying any significant differences between our estimation (on each section, C or S) and chronological age. Only pairs 11/21, 12/22, 32/42 and 33/43 were included in this stage, totaling 267 teeth (since Kvaal did not use the pairs 31/41 or 13/23).

When we analyze the estimation errors (EE) (Table 3), a discrepancy between the age estimations calculated by Kvaal’s formulae and the chronological age is visible, with the mean of the calculated values negative, both for coronal and sagittal section. The most deviated estimations indicated a lower age than the real at about 75 years and a higher age between 24.15 (coronal) and 15.69 (sagittal) years.

Table 3. Estimation errors (EE) obtained, in years. (C=Coronal; S=Sagittal).

	EE (C)	EE (S)
Mean	-21.36	-26.28
Error Deviation	16.51	17.02
Minimum	-74.75	-75.38
Maximum	24.15	15.69

In the comparison of groups of images with different qualities, in the analysis of the good quality group, it was found that the AEE were higher than in the poor qualities (Table 4). The difference between the coronal and sagittal EE (C-S) was also evaluated for the good quality group.

Table 4. Absolute Estimation Errors (AEE), for the different groups of image quality.

	AEE (C, G0)	AEE (C, G1)	AEE (C, G2)	AEE (S, G0)	AEE (S, G1)	AEE (S, G2)	Difference between EE for G2 (C-S)
N	18	83	166	32	55	180	135
Mean	17.36	21.80	23.63	24.96	23.37	27.89	2.78
Error Deviation	10.19	14.52	15.11	21.63	13.84	16.14	12.57
Minimum	2.31	0.63	0.05	0.66	0.50	0.16	-24.55
Maximum	41.42	74.75	72.32	75.38	62.88	68.67	39.12

(G0 – poor quality due to root curvature and, consequently, pulp cutting; G1 – poor quality due to poor image definition; G2 – good quality; C=Coronal; S=Sagittal)

It was observed, based on the means presented in Tables 3 and 4, that coronal cutting was the better in the calculation of age estimation.

Statistical test of paired sampes

In this analysis, only pairs of teeth 11/21 (N=65), 12/22 (N=79) and 33/43 (N=92) were included since the N of the group 32/42 was insufficient in number. Three analyses for each group of teeth were made: comparison 1 – relation between age estimation in coronal section and age in years; comparison 2 – relation between age estimation in sagittal section and age in years; comparison 3 – relation between age estimation in coronal section and sagittal section (Table 5).The Pearson’s correlations between the variables analyzed in each pair are different from 0 (with values between 0.175 and 0.672) and all p-values lower than 0.05 (with only one exception occurring in teeth 33/43, coronal section and age in years).

Table 5. P-values of the Student’s t test for paired samples. (comparison 1 – relation between age estimation in coronal section and real age in years; comparison 2 – relation between age estimation in sagittal section and real age in years; comparison 3 – relation between age estimation in coronal section and sagittal section).

Groups of teeth	N	Comparison 1	Comparison 2	Comparison 3
11/21	65	0.00	0.00	0.05
12/22	79	0.00	0.00	0.28
33/43	82	0.00	0.00	0.00

When it comes to the t-test: first, it was applied to comparisons 1 and 2 to verify the existence or not of statistically significant differences between the mean age estimation (whether coronal or sagittal) and actual age; subsequently, the same test was applied to comparison 3 to assess whether there are statistical differences between the averages of the age estimations based on one section and on the other. All p-values were lower than 0.05, except for the comparison 3 in the 12/22 group.

Pearson’s correlation

As the coronal section revealed better results than the sagittal and, according to Kvaal,(11) M and Dif presented higher correlations, only the correlations of C_M and C_Dif (variables C and Dif in the coronal section) with age were analyzed with Pearson’s correlation coefficient, for the entire sample and the 6 pairs of teeth separately (Table 6).

Table 6. Pearson correlation coefficients, relating the chronological age with the variables M and Dif.

		Age
		Sample N=402	Teeth 11/21	Teeth 31/41	Teeth 12/22	Teeth 32/42	Teeth 13/23	Teeth 33/43
C_M	Correlation	-0.32**	-0.38**	-0.06	-0.34**	-0.24	-0.38**	-0.18
	p-value	0.00	0.00	0.87	0.00	0.20	0.00	0.09
C_Dif	Correlation	0.08	0.22	-0.55	0.19	-0.40*	0.06	0.10
	p-value	0.11	0.08	0.10	0.10	0.03	0.52	0.35

Regarding the correlation between C_M and age, all values were negative, with -0.32 (p-value < 0.05) in the entire sample and varying between -0.06 (teeth 31/41) and -0.38 (teeth 13/23). Pearson’s correlation for the mandibular pairs of teeth were not statistically significant, with p-values > 0,05. When it comes to the correlation between C_Dif and age, its value for the total sample was 0.08, ranging in absolute values from 0.06 (teeth 13/23) to -0.55 (teeth 31/41). Here, only the group of teeth 32/42 showed a statistically significant value (p-value = 0.03).

Evaluation of Kvaal’s linear regression coefficients

For each group of teeth and in each section, the linear regression between age (in years) and Kvaal’s explanatory variables M, Dif and G (gender) were estimated, the not significant variables were removed from the model.

As the pairs of teeth 31/41 and 32/42 have a small number of observations, only the remaining groups were evaluated (Table 7). The higher R² was found in the sagittal section, except for group 13/23. The highest coefficient belongs to the sagittal section of teeth 11/21, being the lowest value in the coronal section of teeth 33/43.

Table 7. Evaluation of Kvaal variables for selected teeth, in both cuts, in years (R²=determination coefficient; Standard Error of the Estimate=SEE).

Groups of teeth	Predictive variables	N	R2	SEE
11/21	C_M	65	0.15	12.64
	S_M	65	0.39	10.63
12/22	C_M	79	0.11	13.41
	S_M, S_Dif	79	0.24	12.47
13/23	C_M, C_Dif	125	0.17	12.60
	S_M	125	0.11	13.01
33/43	C_M	92	0.03	13.88
	G, S_M, S_Dif	92	0.15	13.14

Linear regression

In order to produce a formula that achieves more accurate age estimation, linear regressions between age (in years) and the remaining variables as predictors (G, RP, RT, RR, Aind, Bind and Cind) were also estimated for each group of teeth and in each section, removing all not significant variables. Table 8 presents the explanatory variables of the best model (R²) with the respective p-values for the ANOVA F test and the Standard Error of the Estimate (SEE). As in Table 7, the best R² values are obtained in the sagittal section (except in the tooth group 13/23). The highest and lowest coefficients were observed in the sagittal section of teeth 11/21 and in the coronal section of teeth 33/43, respectively. The obtained linear regression formulae are presented in the Table 9.

Table 8. Predictive variables of the best model, with the p-values, R² and SEE. (R²=determination coefficient; Standard Error of the Estimate=SEE).

Groups of teeth	Predictive variables	N	p-value	R2	SEE
11/21C	C_RR, C_RT, C_RP	65	0.01	0.18	12.55
11/21S	S_Cind, S_RP	65	0.00	0.41	10.57
12/22C	C_Cind, C_RR, C_Aind, C_Bind	79	0.00	0.23	12.74
12/22S	S_RP, S_Aind, S_RT, S_RR	79	0.00	0.30	12.12
13/23C	C_Cind, C_RP	125	0.00	0.17	12.59
13/23S	S_Bind, S_RR	125	0.00	0.12	12.98
33/43C	G, C_Aind	92	0.04	0.07	13.65
33/43S	G, S_Bind, S_RR	92	0.00	0.16	13.06

Table 9. Linear regression formulae created, based on the best models.

Group of teeth	Linear regression formulae
11/21CRR,RT,RP	- 484.166 - 526.419(C_RP) + 363.717(C_RT) + 764.473(C_RR)
11/21SCind,RP	122.790 - 45.001(S_RP) - 93.512(S_Cind)
12/22CCind,RR,Aind,Bind	84.756 - 41.578(C_RR) - 54.754(C_Aind) + 76.288(C_Bind) - 69.786(C_Cind)
12/22SRP,Aind,RT,RR	- 471.280 - 443.654(S_RP) + 326.338(S_RT) + 726.234(S_RR) - 75.834(S_Aind)
13/23CCind,RP	90.821 - 26.662(C_RP) - 85.065(C_Cind)
13/23SBind,RR	82.781 - 37.746(S_RR) - 43.978(S_Bind)
33/43CG,Aind	63.380 - 5.723(G) - 45.449(C_Aind)
33/43SG,Bind,RR	90.037 - 4.852(G) - 33.203(S_RR) - 43.764(S_Bind)

DISCUSSION

Intra-observer variability

In the intra-observer validation, no relationship was demonstrated between a specific section and a higher ICC value. Based on the presented values and on the Fleiss intervals, all ICC demonstrated an excellent level of agreement.(24) This calibration is in agreement with the existing literature: Li et al. (ICC between 0.837 and 0.855) and Erbudak et al. (highest ICC between 0.95 and 0.99). (25, 26) It is important to note that this only demonstrates a high precision and not exactly a high accuracy.

Age estimation by Kvaal formulae

Since the original article, applied to periapical radiographs, argues that there are no significant differences between the right and left sides of the archs, all teeth were grouped with those of the respective teeth on the contra-lateral side .(11) Additionally, since Kvaal only developed linear regression formulae to calculate the age estimation in specific pairs of teeth, only pairs of teeth 11/21, 12/22, 32/42 and 33/43 were analyzed.

The discrepancy between age estimation and chronological age indicates that estimations are, on average, lower than actual ages, by about 21 years in the coronal section and 26 years in the sagittal section (Table 3), These findings are similar to those of Mittal et al. and Kanchan-Talreja.(5,27) Li et al. presented higher estimations.(25) The wide interval between the minimum and maximum error values shown in Table 3 (difference of 100 and 90 years, in the coronal and sagittal sections, respectively) reveal a large margin of error in calculating the age estimation.

In what extent the different image qualities (Table 4), G2 presented not only higher AEE values than the overall average, but also the highest absolute estimation errors of the 3 image quality groups, refuting the idea that the best image quality would represent a better age estimation. Also, the fact that the average difference between the EE (C-S) of G2 was low does not indicate that the values are close to the actual ones, but rather that the estimations obtained from the different sections are close. Hence, there seems to be little difference between sections to the calculation of the age estimation.

Statistical test of paired samples

The Kolmogorov-Smirnov’s test confirmed that the sample followed a normal distribution. Also, for statistical purposes, the pair of teeth 32/42 was not included due to the low number available.

Pearson’s correlations between the variables of each analyzed pair indicate a correlation between the variables, from weakest (0.18) to strongest (0.67), and a p-value lower than 0.05 indicate that almost all correlations between estimated and chronological age were statistically significant, although far from the unit that denotes the perfect correlation.

Regarding the t test of paired samples for comparisons 1 and 2, due to the p-value lower than 0.05, we can affirm that there are statistically significant differences between the age estimation mean (either coronal or sagittal) and chronological age mean in years, in all groups of teeth. Thus, these results seem to reveal that this estimation methodology is biased. In comparison 3, the p-value lower than 0,05 obtained for teeth 11/21 and 33/43 indicates the existence of statistically significant differences. However, for the 12/22 group, the p-value was 0.28. Hence, no statistically significant differences were revealed between the age estimated by coronal or by sagittal section in this group of teeth (Table 5). Thus, it is unclear whether there are differences, on average, between the estimations based on the two sections.

Kvaal presented differences in age estimation and actual age between 8.6 and 11.5 years. (11) In the literature, several studies supported Kvaal's method, showing no statistically significant differences between estimated and actual age – like Paewinsky et al. and Bosmans et al., with an EE of 6.68 and between 0.37 and 7.21 years, respectively. (13, 14, 27–29) Although, some studies refuted this, presenting statistically significant differences between the age estimation and the actual age – like Kanchan-Talreja et al. and Meinl et al., with an EE of 18.1 years and between 31.4 and 47.1 years, respectively. Erbudak et al. showed the most closely resemble the differences observed in this study, with differences between 12.17 and 25.1 years. (5, 15, 25, 26, 30) Gopal et al. compared Kvaal’s method to Cameriere’s, concluding that the second presents better results of age estimation. (12, 31)

Pearson’s correlation coefficient

Pearson’s correlation coefficients between C_M and age presented only negative values, indicating a negative correlation. The values ranged from -0.06 (group 31/41) to -0.38 (group 13/23), revealing despicable to weak correlations. Regarding the variable C_Dif and age, correlation values went, considering absolutes values, from 0.06 (group 13/23) to -0.55 (group 31/41), resulting in despicable to moderate correlations. Table 6 emphasizes that only 5 coefficients are statistically significant (p-value < 0.05). All observed coefficients were lower than in the original study based on periapical radiographs (Table 10), concluding that the variables defined as predictors by Kvaal do not show a good correlation with age in this study based on CBCT.

Table 10. Pearson correlation coefficients from this study and original study (p-value<0.05).

Variable	Teeth group	Kvaal’s coefficients	Study’s coefficients
C_M (M)	11/21	-0.83*	-0.38*
	12/22	-0.80*	-0.34*
	32/42	-0.71*	-0.24
	33/43	-0.75*	-0.18
C_Dif (W-L)	11/21	0.66*	0.22
	12/22	0.54*	0.19
	32/42	0.30*	-0.40*
	33/43	0.35*	0.10

When observing the minimum and maximum values described in the literature (Table 11), a similarity of the values obtained in this study is visible. Yet, studies that applied Cameriere’s method in CBCT presented higher coefficients when compared to Kvaal's method in CBCT, supporting the idea that the variables analyzed by Cameriere et al. produced better correlations with age.(19–22)

Table 11. Pearson’s correlation coefficients (minimum and maximum, in absolute terms) described in the literature.

	Studies	Pearson’s coefficients
		Minimum	Maximum
Periapicais	Sharma et al. 34	-0.01	-0.44
	Gopal et al. (33)	-0.008	0.951
Panoramic	Erbudak et al. (28)	-0.187	0.36
	Chandramala et al. (30)	-0.07	0.54
	Mittal et al. (29)	0.238	0.68
	Maini et al. (31)	-0.01	-0.493
	Roh et al. (32)	-0.11	-0.7
	Li et al. (27)	-0.119	-0.518
CBCT	Penaloza et al. (23)	-0.21	-0.65
	Akay et al. (24)	-0.117	-0.551
CBCT Applying Cameriere’s method	Afify et al. (21)	-0.829	-0.959
	Haghandifar et al. (22)	-0.330	0.764

Evaluation of Kvaal’s linear regression coefficients

The groups of teeth 31/41 and 32/42 were excluded due to their small number in the sample under analysis. When applying the predictor variables of Kvaal to groups with higher N (Table 7), and considering the sections, there was an R² between 0.03 (group 33/43) and 0.39 (group 11/21). These values are much lower than Kvaal’s original study (between 0.56 and 0.76).(11)

Several studies presented lower coefficients than those determined in this study – Sharma et al. and Li et al., with R² between 0.011-0.198 and between 0.01-0.23, respectively^.25,32 Numerous articles showed higher values – Mittal et al. (between 0.240-0.453), Maini et al. (largest value of 0.517) and Akay et al. (values between 0.162 and 0.550 on CBCT).(22,27,29) Gopal et al., once again, supported the idea that Cameriere’s method presented better results, through its higher R² values (between 0.833 and 0.935). (31) Chandramala et al. presented results more similar to ours, with values between 0.014 and 0.385. (28)

As expected, the smaller SEE is found in the groups with a higher R² and vice versa. The SEE in this study ranged from 10.63 to 13.88 years (Table 7), which were higher than those described in the literature, including the range defined by Solheim et al. as acceptable for forensic application (10 years). (27, 31, 33) Li et al. presented similar SEE, between 11.4 and 12.9. (25)

Linear regression

All models used can explain part of the age variation, since p-value < 0.05 in the ANOVA F test in all cases (Table 8). Comparing the R² values of the original study with the values determined in this study (both for Kvaal predictor variables and for the new variables) (Table 12), all original values were higher than in this study (not only of the variables M and Dif, but also of the new established ones). However, and considering only this study values, R² of the new variables (between 0.07 and 0.41) is higher than that obtained with predictors defined by Kvaal (0.031 to 0.394), which may indicate a greater representativeness of the sample with the new variables, although the difference is always small.

Table 12. Comparative table between Kvaal’s variables in the original study, Kvaal’s variables in this study and the new variables.

Teeth	Kvaal’s R2	Study’s R2 Kvaal’s variables	Study’s R2	Kvaal’s SEE	Study’s SEE Kvaal’s variables	Study’s SEE
11/21C	0.70	0.15	0.18	9.50	12.64	12.55
11/21S		0.39	0.41		10.63	10.57
12/22C	0.67	0.11	0.23	10.0	13.41	12.74
12/22S		0.24	0.30		12.47	12.12
13/23C		0.17	0.17		12.60	12.59
13/23S		0.11	0.12		13.01	12.98
33/43C	0.56	0.03	0.07	11.5	13.88	13.65
33/43S		0.15	0.16		13.14	13.06

The existing literature supports our values – Paewisnky et al. with an R²=0.839 and Kanchan-Talreja et al., Erbudak et al. and Roh et al. with R² between 0.11-0.44, 0.035-0.345 and 0.14-0.49, respectively. (5, 13, 26, 30) Regarding studies in CBCT: the ones that applied Kvaal’s method reveal similarities with our study, like Penaloza et al. (R² between 0.01 and 0.56); Yang et al., on its pulp/tooth volume ratio, presented a lower value (R²=0.29); the ones that applied Cameriere’s method obtained not only similar values (Haghandifar et al. presented a R² between 0.109 and 0.583), but also higher values (Afify et al. had an interval between 0.687 and 0.919). (18–21)

When it comes to SEE (Table 12), the original study had the lowest values. Regarding this study SEE, the SEE of the new variables were slightly lower than the SEE obtained with the variables defined by Kvaal.

Despite having null mean estimation error, the estimations obtained by linear regression tend to underestimate in the lowest age groups and to overestimate in the highest age groups in all analysed models regardless of the section (coronal or sagittal) or the group of teeth used. Thus, the extreme age groups, namely the oldest, tend to have higher estimation errors. Nevertheless, there is no clear standard that distinguishes the precision of the estimations obtained by each group of teeth.

Kanchan-Talreja et al., Penaloza et al. and Roh et al. stipulated SEE values from 11 to 14, 10.58 to 15.4 and 10.4 to 14.2 years, all higher than the values defined by Solheim. (5, 21, 30, 33) The articles that applied Cameriere’s method in CBCT were the only ones that presented SEE within the interval established by Solheim. Haghandifar et al. established an interval between 7.1 and 10.5 and Afify et al. presented the lowest SEE interval, between 4.76 and 8.1 years. (19, 20)

CONCLUSIONS

Based on the obtained results, we can conclude that there are statistically significant differences between the chronological age and the dental age of individuals, estimated by the pulp/tooth ratio method evaluated on CBCT, based on any teeth analyzed in this study. In addition, there are statistically significant differences between the correlation coefficients of the explanatory variables defined by Kvaal on periapical radiographs and the correlation coefficients of the same variables calculated in this study on CBCT, that revealed much lower values. A regression formula was created with the aim to estimate age more accurately with the three-dimensional method, through CBCT analysis of the proportions of the tooth/pulp area – however, without practical application due the reduced explanatory capacity revealed.

For forensic age estimation, it is especially important to ensure the applicability of an unbiased method with high accuracy and precision, which can achieve reliable age estimations. The age estimation according to this dental biological parameter in the usual imaging diagnosis examination CBCT has limitations to be applied. Enlargement of the database with further multi-centre studies can help to improve the model.

In conclusion, Kvaal’s formulae for age estimation is not reproducible in the Portuguese population, when applied in CBCT.