A mobile isocentric C-arm for intraoperative cone-beam CT: Technical assessment of dose and 3D imaging performance

Abstract

Purpose:

To characterize the radiation dose and three-dimensional (3D) imaging performance of a recently developed mobile, isocentric C-arm equipped with a flat-panel detector (FPD) for intraoperative cone-beam computed tomography (CBCT) (Cios Spin 3D, Siemens Healthineers) and to identify potential improvements in 3D imaging protocols for pertinent imaging tasks.

Methods:

The C-arm features a 30 × 30 cm² FPD and isocentric gantry with computer-controlled motorization of rotation (0–195°), angulation (±220°), and height (0–45 cm). Geometric calibration was assessed in terms of 9 degrees of freedom of the x-ray source and detector in CBCT scans, and the reproducibility of geometric calibration was evaluated. Standard and custom scan protocols were evaluated, with variation in the number of projections (100–400) and mAs per view (0.05–1.65 mAs). Image reconstruction was based on 3D filtered backprojection using “smooth,” “normal,” and “sharp” reconstruction filters as well as a custom, two-dimensional 2D isotropic filter. Imaging performance was evaluated in terms of uniformity, gray value correspondence with Hounsfield units (HU), contrast, noise (noise-power spectrum, NPS), spatial resolution (modulation transfer function, MTF), and noise-equivalent quanta (NEQ). Performance tradeoffs among protocols were visualized in anthropomorphic phantoms for various anatomical sites and imaging tasks.

Results:

Geometric calibration showed a high degree of reproducibility despite ~19 mm gantry flex over a nominal semicircular orbit. The dose for a CBCT scan varied from ~0.8–4.7 mGy for head protocols to ~6–38 mGy for body protocols. The MTF was consistent with sub-mm spatial resolution, with f₁₀ (frequency at which MTF = 10%) equal to 0.64 mm⁻¹, 1.0 mm⁻¹, and 1.5 mm⁻¹ for smooth, standard, and sharp filters respectively. Implementation of a custom 2D isotropic filter improved CNR ~ 50–60% for both head and body protocols and provided more isotropic resolution and noise characteristics. The NPS and NEQ quantified the 3D noise performance and provided a guide to protocol selection, confirmed in images of anthropomorphic phantoms. Alternative scan protocols were identified according to body site and task — for example, lower-dose body protocols (<3 mGy) sufficient for visualization of bone structures.

Conclusion:

The studies provided objective assessment of the dose and 3D imaging performance of a new C-arm, offering an important basis for clinical deployment and a benchmark for quality assurance. Modifications to standard 3D imaging protocols were identified that may improve performance or reduce radiation dose for pertinent imaging tasks.

1. INTRODUCTION

Intraoperative cone-beam computed tomography (CBCT) provides visualization of structures that may be difficult to appreciate from two-dimensional (2D) projection imaging alone.^1,2 In orthopaedic/trauma surgery, CBCT can better depict challenging anatomical relationships, such as articular surfaces about the syndesmosis, spine, or sacroiliac joint.³ In spine surgery, CBCT integrated with real-time tracking is the basis for minimally invasive approaches with surgical navigation.^4,5 In vascular surgery, CBCT can better depict soft-tissue anatomy, abnormalities, and hemorrhage.⁶ In each of these areas, CBCT provides a basis for surgical planning, quality assurance (QA), and improved patient safety.^7–9 Integration with three-dimensional (3D)-3D image registration (CBCT to preoperative CT or MRI),¹⁰ 3D-2D image registration (CBCT to radiographs),¹¹ and surgical robotics are active areas of translational development.^12,13

Mobile C-arms with CBCT capability using x-ray image intensifiers (XRIIs) have been available for many years (e.g., Arcadis Orbic 3D, Siemens Healthcare) but exhibit major limitations in image quality owing to limited field of view, image distortion, spatial resolution, and noise. Many of these image quality limitations are remedied by systems employing a flat-panel detector (FPD) — for example, mobile systems such as the O-arm (Medtronic, Littleton MA) and Vision 3D C-arm (Ziehm, Nuremberg, Germany). Recent advances incorporate a complementary metal oxide semiconductor (CMOS) FPD to reduce electronic noise and improve spatial resolution.^14–17

Previous studies evaluated the performance characteristics of such systems. Phantom studies by Zhang et al.¹⁸ and Petrov et al.¹⁹ quantified the dose and image quality of the O-arm system, demonstrating performance consistent with applications emphasizing high-contrast visualization (bone and surgical instrumentation). Uneri et al.²⁰ demonstrated the boost in imaging performance for soft-tissue visualization and/or reduced radiation dose (e.g., ~90% increase in soft-tissue CNR at 50% dose) that could be achieved on the O-arm system (Medtronic, Littleton MA) using alternative reconstruction strategies. In Takao et al.,²¹ the performance of the Vision FD Vario 3D C-arm was assessed in terms of surgical navigation accuracy (<1.5 mm target registration error in all trials), noting improvements over XRII-based C-arms. Hassepass et al.²² investigated custom scan protocols on the Vision FD Vario 3D to optimize image quality of the skull base, reporting a significant improvement in image quality for elliptical scan modes. In a study by Ritschl et al.,²³ the Vision RFD 3D system (Ziehm, Nuremberg, Germany) was used to reduce artifacts and partial-orbit sampling effects using a modified scan trajectory (rotate, shift, and rotate) that allowed complete angular sampling.

Proceeding from a series of preclinical prototypes,^1,24–27 a new mobile C-arm (Cios Spin, Siemens Healthineers, Erlangen Germany) with 3D volumetric imaging capability has been recently introduced for clinical use. The C-arm features an isocentric gantry with motorized motion controls for ease of positioning and flexibility in 3D imaging. The system is equipped with a CMOS FPD and implements scan protocols offering various levels of view sampling and dose.

Rigorous technical assessment is important to characterize the imaging performance of such systems as they become available and to knowledgably guide their clinical deployment. Objective, observer-independent metrics of spatial resolution and noise quantify the performance tradeoffs among technique factors (e.g., tube voltage, tube current, exposure time, number of projections), provide a guide to technique selection in a manner that considers the imaging task, and gives a foundation for development of QA procedures. The C-arm reported in this work exhibits distinct differences in implementation from previous systems — including system geometry, technique protocols, and detector hardware — and warrants technical assessment as a prerequisite to clinical deployment.

The work reported below provides a technical assessment of 3D imaging performance and dose and identifies modifications that could improve performance. Custom scan protocols were designed to investigate performance beyond that of clinically available techniques. Modifications to the 3D image reconstruction method were evaluated to improve soft-tissue contrast resolution and the degree to which the system exhibits isotropic signal and noise characteristics. The reproducibility of geometric calibration was evaluated, along with the extent to which errors in calibration can affect imaging performance. Finally, the objective measures of imaging performance were related to visual image quality as evident in anthropomorphic phantoms that illustrate noise-resolution tradeoffs across a range of anatomical sites and imaging tasks.

2. MATERIALS AND METHODS

2.A. Isocentric C-arm for 2D and 3D intraoperative imaging

2.A.1. Mobile C-arm for intraoperative 2D and 3D imaging

The C-arm considered in this work (Cios Spin 3D, Siemens Healthineers, Forcheim, Germany) is shown in Figs. 1(a)–1(c). A summary of hardware components and technical specifications is in Table I. The system has an isocentric gantry and motorized motion control for positioning and CBCT imaging. The x-ray tube has a rotating tungsten anode (2.6 MHU) with a dual focal spot (0.3 and 0.5 FS) and inherent filtration of 0.1 mm Cu + 3.0 mm Al additional filtration. The x-ray generator provides a 40–125 kV range in tube potential with nominal 25 kW power (250 mA maximum at 100 kV) and optional energy storage unit (ESU, providing fluoroscopic pulses of up to 6.3 ms width and 126 mA maximum current at 125 kV). A lower-power (12 kW) option is also available. Motorized collimators allow symmetric variation of the field of view (FOV).

Fig. 1.

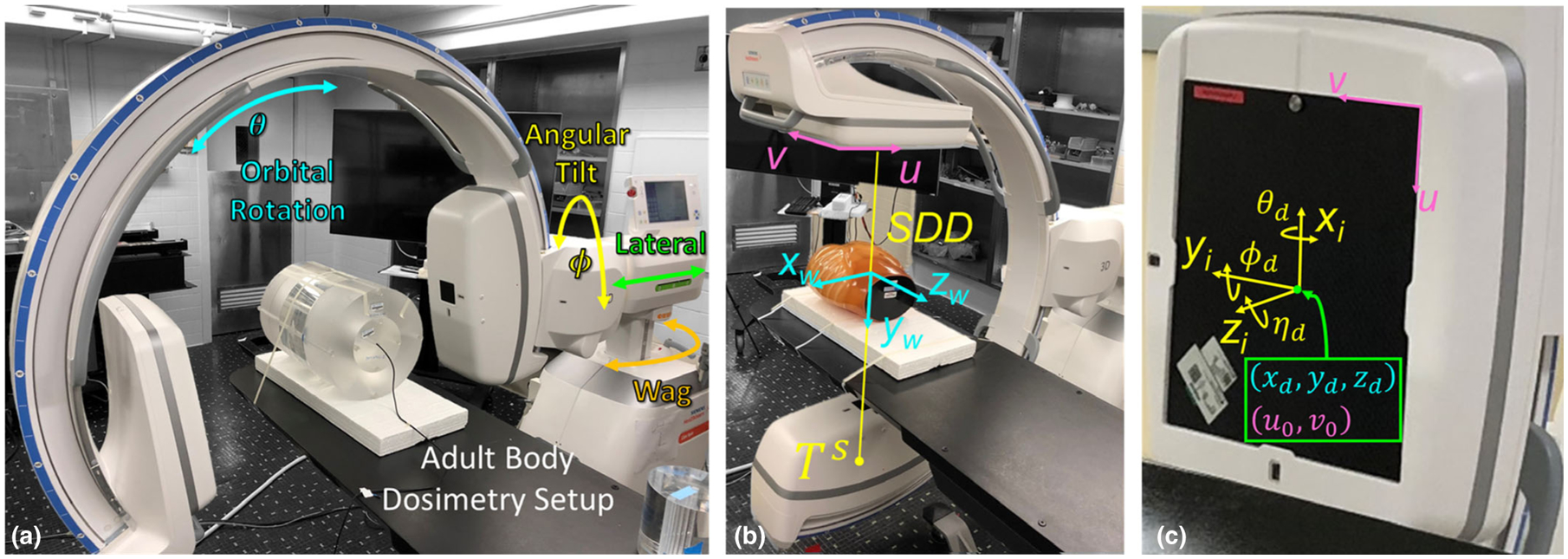
Experimental setup of the mobile C-arm for two-dimensional and three-dimensional imaging. (a) Dosimetry setup for adult body protocol (32 cm diameter phantom). (b)–(c) System geometry illustrating the world coordinate reference frame (w), virtual detector coordinate reference frame (i), and relevant geometric calibration parameters, as described in Cho et al.²⁸ The detector rotation (ϕ_d, θ_d, η_d) describe the orientation of the detector relative to the virtual coordinate frame (i).

Table I.

Summary of specifications and operating parameters for the mobile C-arm in this work.

System
Model name	Cios Spin 3D
Manufacturer	Siemens Healthineers
Software version	VA30B
X-ray tube/generator
X-ray generator	25 kW ESU (or 12 kWoption)
Tube kV	40–125 kV
Tube current	3–250 mA
Tube output	0.015–25 mAs
Focal spot size	0.3 or 0.5 FS
Inherent filtration	0.1 mm Cu + 3 mm A1
Detector
Detector	CMOS FPD (Xineos 3030HS)
Scintillator	600 μm thick CsI:Tl
Pixel pitch(1 × 1)	0.151 mm
Pixel pitch (2 × 2 Bin)	0.302 mm
Active area	1952 × 1952 pixels(295 × 295 mm2)
Frame rate (max)	14 fps (1 × 1) or 57 fps (2 × 2)
Geometry
SDD	116.4 cm
SAD	62.3 cm
CBCT scan arc	195°
Orbital range	±98° (motorized)
Angular range	±220° (motorized)
Vertical range	45 cm (motorized)
Lateral range	20 cm (manual)
Wag range	±10° (manual)
Image reconstruction
Algorithm	FBP
Filter types	Smooth, Normal, Sharp
Voxel size	0.313 × 0.313 × 0.313 mm3
FOV	512 × 512 × 512 voxels(16 × 16 × 16 cm3)

CBCT, cone-beam computed tomography; FOV, field of view; SAD, source-axis distance;SDD, source-detector distance.

The imaging chain is based on an indirect-detection, CMOS-based FPD (Xineos 3030HS, Teledyne Dalsa, Waterloo, ON, Canada) with a 600 μm CsI:Tl scintillator coupled to the CMOS sensor array via a fiber optic plate. The FPD contained 1952 × 1952 pixels at 0.15 mm pitch, giving an active area of ~30×30 cm². The detector can be read with 1 × 1 or 2 × 2 pixel binning and provides multiple sensitivity modes through switchable in-pixel capacitance. The maximum frame rate is 14 fps for 1 × 1 binning and 57 fps for 2 × 2 binning. The system includes a detachable one-dimensional (1D) focused antiscatter grid with 15:1 grid ratio and 80 lines/cm grid frequency (nominally in place for all studies reported below).

System geometry was determined from geometric calibration as detailed below. The source-detector distance (SDD) was 116.4 cm, and the source-axis distance (SAD) was 62.3 cm, corresponding to nominal magnification of ~1.8. For the 30 × 30 cm² detector, this corresponds to a 15° maximum cone angle in the lateral and longitudinal directions and a volumetric FOV of 16 × 16 × 16 cm³. The system geometry could be adjusted along 5 degrees of freedom for flexible positioning and/or tilted scan orbits. The C-arm orbital angle (θ) is motorized and computer-controlled over a 196° total arc. Gantry tilt (ϕ, ±220° range) and height (45 cm range along y_w) are motorized but not computer-controlled, with CBCT scanning permitted at tilt angle up to ±15°. The C-arm lateral position (20 cm range) and wag (±10° range) are manually adjusted.

2.A.2. Imaging protocols

For 2D radiographic/fluoroscopic imaging, standard 2D imaging protocols are defined by the manufacturer (e.g., general, interventional, gastro, vascular, urology, and orthopedic). Each protocol presents three dose levels (Low, Medium, and High) that vary in kV, mAs/ pulse, and pulse rate. Reference point air kerma is measured for each protocol and dose level as detailed in Section 2.B.1 to provide an assessment of dose for the system as deployed in 2D imaging applications. The 2D radiographic/fluoroscopic imaging performance characteristics for a system employing a CMOS detector were reported in previous work²⁹ and were not included in the results below.

Table II summarizes the 3D imaging protocols used in this work, including manufacturer-specified protocols and custom protocols. The four 3D imaging protocols specified by the manufacturer are collectively referred to below as the “clinical” protocols, denoted: Low Dose (L), Standard (S), High Quality (H), and Extra Power Obese (O). For the clinical protocols, the total mAs ranged from 5–32 mAs for head scans (16 cm diameter acrylic cylinder) and 101–660 mAs for body scans (32 cm diameter acrylic cylinder). Automatic exposure control (AEC) was enabled for both 2D and 3D imaging.

Table II.

Summary of three-dimensional (3D) imaging protocols for the mobile C-arm in this work. Clinical protocols are in white, and custom protocols are in gray. The mAs/view and mAs total values are set by automatic exposure control (AEC) (with values shown for 16 and 32 cm diameter head and body acrylic cylindrical phantoms).

Protocols	Tube voltage (kV)	Number of projections	Scan time (s)	Angular step (Δθ)	Pixel binning	Tube output (mAs/view)	Tube output (total) (mAs)
16 cm cylindrical phantom (head)
Low dose (L)	110	100	30	2°	2 × 2	0.05	5
Standard (S)	110	200	30	1°	2 × 2	0.05	10
High quality (H)	110	400	30	0.5°	2 × 2	0.08	32
Extra power obese (O)	110	400	60	0.5°	2 × 2	0.08	32
Custom head 1	110	100	30	2°	2 × 2	0.57	57
Custom head 2	110	200	30	1°	2 × 2	0.57	114
Custom head 3	110	400	30	0.5°	2 × 2	0.68	272
32 cm cylindrical phantom (body)
Custom body 1	110	100	30	2°	2 × 2	0.16	16
Custom body 2	110	200	30	1°	2 × 2	0.16	32
Custom body 3	110	400	30	0.5°	2 × 2	0.22	88
Low dose (L)	110	100	30	2°	2 × 2	1.01	101
Standard (S)	110	200	30	1°	2 × 2	1.02	204
High quality (H)	110	400	30	0.5°	2 × 2	1.47	588
Extra power obese (O)	110	400	60	0.5°	2 × 2	1.65	660

A variety of custom protocols were defined for both head and body setups to investigate alternative dose ranges that may be more suitable to some clinical tasks. For the head protocols, a range of higher dose protocols was investigated that may be suitable to imaging of low-contrast soft-tissue or intracranial hemorrhage — denoted Custom Head 1, 2, and 3. The hypothesis for such higher-dose protocols is that they would provide soft-tissue visualization while maintaining a clinically acceptable dose level (~10–50 mGy, recognizing ~50 mGy as a typical dose level for diagnostic CT of the head⁶), whereas the manufacturer-specified head protocols (all < 5 mGy) may only be suitable to bone visualization. To accomplish this, the internal system settings were modified to increase the dose per frame by 10×, resulting in ~57–272 mAs range for scans of a 16 cm diameter acrylic cylinder.

Custom protocols were similarly defined for body scans to investigate the alternative hypothesis stated above — namely, that a range of lower-dose custom body protocols would provide sufficient visualization of bone (e.g., in spine or pelvic trauma surgery) relative to the manufacturer-specified body protocols (all > 5 mGy). Custom body protocols were thus designed by modifying the internal system settings to reduce the mAs/frame by ¹/₆, resulting in ~16–88 mAs for scans of a 32 cm diameter acrylic cylinder.

2.A.3. Geometric calibration

Geometric calibration defines the source-detector pose (i.e., the position and orientation) with respect to a common coordinate system for each projection view in a CBCT scan (capturing deviations from a circular orbit) and is essential to 3D image reconstruction. The C-arm geometry is shown in Figs. 1(b)1(c). The nine degrees of freedom defining the pose of a point source (x_s, y_s, z_s) and area detector (x_d, y_d, z_d, θ_d, ϕ_d, η_d) for projection j are reflected by the system projection matrix^28,30,31 (P_j), which relates the 3D world coordinates of the CBCT volume (x_w, y_w, z_w) to the 2D coordinates on the detector (u, v) in homogenous coordinates:

$${\left(\begin{array}{l}u\hfill \\ v\hfill \\ 1\hfill \end{array}\right)}_j=P_j{\left(\begin{array}{c}{x}_w\\ y_w\\ z_w\\ 1\end{array}\right)}_j$$ (1)

For each projection j, this matrix can be written in terms of the system geometry intrinsics (I_j), the rotation matrix for the detector $\left(R_j^d\right)$, and translation matrix for the x-ray source $\left(T_j^S\right)$:

$$P_j=I_j\left[\begin{array}{ll}{R}_j^d\hfill & -R_j^d{T}_j^s\hfill \end{array}\right]$$ (2)

where

$$I_j=\left[\begin{array}{ccc}\mathit{\text{SDD}}& 0& u_0\\ 0& \mathit{\text{SDD}}& v_0\\ 0& 0& 1\end{array}\right],R_j^d=\left[\begin{array}{c}\widehat{u}\\ \widehat{v}\\ \widehat{u}\times \widehat{v}\end{array}\right],T_j^s=\left[\begin{array}{c}{x}_s\\ y_s\\ z_s\end{array}\right]$$ (3)

The piercing point is given by (u₀, v₀), which represents the projection of the origin of the world coordinate reference frame onto the detector. The detector rotation matrix is a 3 × 3 orthogonal matrix whose rows represent the directions (represented by the hat operator) of the detector axes as determined by the rotation angles (θ_d, ϕ_d, η_d), defined as in Cho et al.²⁸ and shown in Fig. 1(c).

A variety of methods have been reported for characterization of pose in projective geometries. The approach used by the manufacturer involves a phantom containing a helical pattern of metal ball bearings (BBs) that can be used to iteratively solve for the projection matrix at each projection angle.^32,33 In this work, we used the two-circle BB phantom and analytical solution described by Cho et al.²⁸ An important assumption in such methods is that the system geometry is reproducible from scan to scan. We evaluated the short-term reproducibility of the scan orbit in 10 repeat scans of the two-circle BB phantom. Each calibration was performed using the high quality (H) scan protocol, giving 400 pose estimations over the 195° orbit. The intrinsic (piercing point and source to detector distance) and extrinsic (source/detector positions and detector rotations) parameters were compared to quantify both the degree of departure from a circular orbit and the reproducibility of the orbit.

The two-circle BB phantom was augmented with a wire suspended along the z-axis, allowing evaluation of the axial plane point-spread function (PSF) from the same scan data as the geometric calibration, giving a best-case scenario of “self-calibrated” scan data. The reproducibility of geometric calibration was also assessed in terms of PSF broadening in scans reconstructed using projection matrices obtained from other (e.g., previous) scans.

2.A.4. 3D Image reconstruction

Projection data were corrected for variations in pixel offset, gain, and defects. Bare-beam (I₀) normalization was based on precalibration of detector output measured for various kV and mAs. Image reconstruction parameters are summarized in Table I. Two basic variations of the FDK algorithm for 3D filtered backprojection (FBP)³⁴ were investigated in this work. The first method (denoted FBP₁) was supplied by the manufacturer and represents imaging performance of the system in current clinical use. The FBP₁ algorithm used a Shepp-Logan apodization filter applied along the rows (u) of the projection data, tunable via three settings of a Gaussian width parameter, σ, to “Smooth,” “Normal,” or “Sharp” filters (σ = 3, 1.5, or 0.5 pixels, respectively). Irrespective of filter choice, CBCT images were reconstructed with 0.313 × 0.313 × 0.313 mm³ voxel size on a 512 × 512×512 grid (16 × 16×16 cm³ FOV).

The second method (referred to as FBP₂) was a custom FDK implementation modified to apply a 2D Hann apodization filter to the projection data (cf., the 1D Shepp-Logan in FBP₁; an illustration of these filters can be found in Buzug³⁵) and allow variable voxel size (ranging from 0.163 to 0.625 mm for sharp and smooth filters respectively). The purpose of the FBP₂ variant is to give more isotropic resolution and noise characteristics, noting that this simply means that the MTF and NPS are more symmetric in the x, y, and z directions (not that the resolution or noise are necessarily improved). Application of the 2D filter carries a concomitant reduction in noise associated with reduced z-direction MTF. The 2D Hann filter was implemented as the separable product of Hann functions along rows and columns of the projection data (with cutoff frequency in each direction held equal in the current work — that is, a roughly isotropic filter). The width of 2D Hann apodization was defined as a fraction (0.26–1.0) of the Nyquist frequency and set to match a particular FBP₁ filter by sweeping the width of the Hann filter and measuring the resulting MTF until the closest fit was found. The filter width was nominally set to match the “Normal” FBP₁ filter (corresponding to a width of 0.52 × Nyquist frequency). Projections were modified to handle truncation and were weighted³⁶ to handle data redundancy. Note that truncation correction between the FBP₁ algorithm (which is proprietary to the manufacturer) and the custom FBP₂ algorithm implemented in this work are believed to handle truncation effects somewhat differently. In the FBP₂ algorithm, truncation correction was performed by linearly extrapolating the detector signal laterally (i.e., along the u direction of detector rows) beyond the FOV of the detector. The (proprietary) FBP₁ algorithm appears to employ a different truncation correction — perhaps a nonlinear extrapolation or different method altogether. Consequently, information content outside the region of support of the reconstructed volume is expected to contribute differently between the two algorithms, giving a different appearance in residual truncation artifact at the edge of the FOV. However, the differences in truncation correction technique should not affect the performance of clinical tasks for which features of interest are fully within the FOV.

Recognizing the influence of x-ray scatter and lateral truncation, neither FBP₁ nor FBP₂ are expected to yield voxel values with accurate Hounsfield Units (HU). The manufacturer-specified algorithm (FBP₁) scales voxel values to “arbitrary units” (AU) using the rescale fields provided in the DICOM header. The relationship between AU and HU was investigated using a phantom containing materials of known HU values (Section 2.C.2, below), and FBP₂ reconstructions were linearly scaled to match the voxel values of FBP₁. Neither method employed corrections for x-ray scatter or beam hardening.

2.B. Dosimetry

2.B.1. 2D Fluoroscopy reference air Kerma

An air ionization chamber with 0.6 cm³ volume (10X6-0.6, Accu-Pro 9096, RadCal Corp., Monrovia, CA) was used to measure the reference point air kerma (RAK) and air kerma rate (units mGy/min) to represent patient surface exposure, as described in the AAPM Task Group Report 151.³⁷ The air chamber was calibrated by the manufacturer with a 70 kV beam (2.89 mm Al HVL) and tungsten target. The energy correction factor of the chamber is rated to within ±5% for energies ranging from 40 kV to 1.33 MV. The setup included a carbon-fiber fluoroscopy table and adult body phantom placed at isocenter as in Fig. 1(b). The presence of the phantom results in representative clinical techniques with the AEC and also contributes a realistic level of backscatter. The RAK was measured at a position ~15 cm above isocenter (i.e., toward the x-ray source) at the entrance surface of the phantom for each 2D imaging protocol described in Section 2.A.2.

2.B.2. 3D CBCT dose

The dose for CBCT scans was evaluated using the same ionization chamber placed within 16 and 32 cm diameter acrylic cylinders (“head” and “body” phantoms, Gammex RMI, Middleton WI). We characterized CBCT dose as described in Daly et al.,³⁸ Fahrig et al.,³⁹ and AAPM Task Group Report 238⁴⁰ in terms of air kerma that can be compared to standard CT dose measurements (e.g., CTDI_W). Three cylindrical phantoms were stacked longitudinally at isocenter on a carbon fiber table to give scatter conditions appropriate to a volumetric beam. All measurements were performed with half-scan (195°) orbits in which the x-ray tube traverses under the table. The weighted air kerma (D_w) was calculated as the weighted sum of the central (1/3 × D₀) and average peripheral $\left(2/3\times {\overline{D}}_P\right)$ dose, where ${\overline{D}}_P$ represents the average of the four peripheral locations about the cylindrical phantom. Note that air kerma measurements may be treated approximately equal to the absorbed dose at diagnostic x-ray energies and low atomic number material.⁴¹

2.C. 3D Imaging performance

2.C.1. Phantom for CBCT technical assessment

A modular phantom designed for CBCT imaging performance assessment⁴² was used in the measurements described below. The phantom consists of a stack of seven acrylic modules, each 13.5 cm in diameter and 3 cm in length (total of 21 cm) and designed to assess particular image quality metrics in CBCT.

2.C.2. Correspondence with HU

The correspondence of voxel values (AU) to HU was assessed for materials of manufacturer-specified HU. One of the phantom modules contained four inserts: low-density polyethylene (LDPE, −90 HU); polyamide (PA, +30 HU); polycarbonate (PC, +100 HU); and polyoxymethylene (POM, +390 HU). Another module containing Teflon (+950 HU), acrylic (+100 HU) as well as air (−1000 HU) were also included. Regions-of-interest (ROIs) were selected within each insert at the same distance from the center of reconstruction to reduce the influence of (radially symmetric) background nonuniformity caused by x-ray scatter and beam hardening.⁴³ Measurements are reported for the H protocol and Normal filter for FBP₁.

2.C.3. Uniformity

Image uniformity was assessed with a module presenting a uniform cylindrical slab of acrylic and characterized by the mean signal profile from seven rows extracted from axial slices near the center of reconstruction. The mean signal profile was assessed in terms of the extent of cupping artifact present due to x-ray scatter and beam hardening.⁴³ Cupping artifact magnitude was quantified in terms of t_cup:

$$t_{\mathit{\text{cup}}}=\frac{{\mu }_{\mathit{\text{edge}}}-{\mu }_{\mathit{\text{center}}}}{{\mu }_{\mathit{\text{edge}}}}$$ (4)

where μ_center and μ_edge represent the average voxel value at the center and edge of the line profile, respectively, with the “edge” defined at 90% of the module radius. Profiles were analyzed in 50 consecutive slices about the central slice. Uniformity was analyzed for all four clinical protocols (L, S, H, and O) for the Normal filter of FBP₁.

2.C.4. Spatial resolution

Spatial resolution was characterized in terms of the modulation transfer function (MTF) computed in the axial plane of CBCT reconstructions. MTF was measured using the line-spread function (LSF) module of the phantom, featuring an air slit (i.e., finely machined gap in acrylic) of width 0.1 mm. Line spread profiles were obtained using individual row-wise or column-wise LSF profiles along the length of the slit and shifting them to alignment based on the angle of the slit to obtain a finer sampling of the continuous line spread profile, often referred to as the oversampled LSF.⁴⁴ The oversampled LSF was then resampled to a uniform grid of 0.15 mm spacing, the background was detrended by subtraction of a linear fit to the LSF tails, and the LSF was normalized to an area of 1. The modulus of the discrete Fourier Transform of the oversampled LSF was computed to yield the presampling MTF. The presampling MTF describes resolution effects of the scintillator and aperture (without aliasing). The measured MTF was corrected by division of a sinc function corresponding to the 0.1 mm slit width. MTF measurements were computed as discrete data points for multiple sections along the length of the phantom (allowing for 50% overlap) and the average MTF is reported (N = 6 repeat measurements). The MTF was assumed to be radially symmetric (i.e., dominated by the MTF of the scintillator) such that the axial plane 2D MTF [MTF_2D(f_x, f_y)] was estimated by rotation of the 1D measured MTF with radial spatial frequency (f_r) given by $f_r=\sqrt{f_x^2+f_y^2}$. Measurements were performed for the H protocol and each reconstruction filter.

2.C.5. Contrast-to-noise ratio (CNR)

Contrast, noise, and CNR were obtained using the same module as in Section 2.C.2. Measurements were performed for all imaging protocols and reconstruction filters, focusing nominally on the LDPE insert (−90 HU contrast). Both head and body setups were evaluated – by inserting the modular phantom within a 16 and 32 cm diameter cylindrical annulus respectively. The contrast is simply the difference in mean signal between the insert and background $\left({\overline{\mathit{\text{ROI}}}}_{\mathit{\text{insert}}}-{\overline{\mathit{\text{ROI}}}}_{\mathit{\text{background}}}\right)$, and the noise (square root of the variance) is computed according to the pooled variance.⁴⁵ (The pooled variance can provide a more precise estimate than individual sample variances when the mean of each population may be different, but the variance of each population is the same.) The CNR is therefore:

$$\mathit{\text{CNR}}=\frac{\left|{\overline{\mathit{\text{ROI}}}}_{\mathit{\text{insert}}}-{\overline{\mathit{\text{ROI}}}}_{\mathit{\text{background}}}\right|}{\sqrt{1/2\left({\sigma }_{\mathit{\text{insert}}}^2+{\sigma }_{\mathit{\text{background}}}^2\right)}}$$ (5)

where ${\overline{\mathit{\text{ROI}}}}_{\mathit{\text{insert}}}$ and ${\overline{\mathit{\text{ROI}}}}_{\mathit{\text{background}}}$ are the average voxel value within ROIs of the insert and adjacent background, respectively, and σ_insert and σ_background are the standard deviation of voxel values within said ROIs. Note that the denominator in Eq. (5) reduces simply to the average noise under a small-signal-difference approximation (i.e., ${\overline{\mathit{\text{ROI}}}}_{\mathit{\text{insert}}}\approx {\overline{\mathit{\text{ROI}}}}_{\mathit{\text{background}}}$ and ${\sigma }_{\mathit{\text{insert}}}^2\approx {\sigma }_{\mathit{\text{background}}}^2$) with matched ROI size, or alternatively, simply the noise of the background.⁴⁶ ROI selection was performed as described in ICRU Report No.54 to reflect the large-area transfer characteristics of the system.⁴⁷ ROIs were sized greater than the correlation length (>> 10 voxels along each edge) and selected equidistantly about the center of reconstruction to satisfy stationarity between samples.

2.C.6. 3D noise-power spectrum (NPS)

The 3D NPS was measured using the uniform acrylic module, with two scans acquired in succession for each protocol and subtracted to yield a zero-mean, noise-only volume, Δ(x, y, z). An ensemble (>75) of 3D ROIs (64 × 64 × 64 voxels) were selected at a fixed distance from the center of reconstruction, and the 3D NPS was calculated as:⁴⁸

$$NPS\left(f_x,f_y,f_z\right)=\frac{1}{2N_{\mathit{\text{ROI}}}}\frac{a_x{a}_y{a}_z}{N_x{N}_y{N}_z}\sum _{\mathit{\text{ROI}}=1}^{N_{\mathit{\text{ROI}}}}{\left|\mathit{\text{DF}}{T}_{3D}\left\{{\Delta }_{\mathit{\text{ROI}}}(x,y,z)\right\}\right|}^2$$ (6)

where f_x, f_y, f_z are spatial frequencies corresponding to x, y, and z directions, respectively, N_ROI is the number of ROIs in the ensemble, a_x, a_y, and a_z are the voxel size in x, y, and z directions, N_x, N_y, and N_z are the ROI size in voxels in the x, y, and z directions, DFT_3D is the 3D discrete Fourier transform, and Δ_ROI is an ROI within the zero-mean image. The factor of 2 accounts for the doubling of variance from the subtraction of two images. The 3D NPS was radially averaged to yield a 1D representation of the axial NPS, denoted NPS(f_r), and a 1D representation of NPS(f_z) was taken as the circumferential average on a cylindrical shell parallel to the f_z axis at a radius given by the frequency at which the axial NPS peaks. The 3D NPS was evaluated for all imaging protocols and reconstruction filters.

2.C.7. 3D noise-equivalent quanta (NEQ)

The 3D NEQ is defined for all protocols and reconstruction filters according to:⁴⁹

$$\mathit{\text{NEQ}}\left(f_x,f_y,f_z\right)=\pi \left|f_r\right|\frac{\mathit{\text{MT}}{F}^2\left(f_x,f_y,f_z\right)}{\mathit{\text{NPS}}\left(f_x,f_y,f_z\right)}$$ (7)

where |f_r| is the magnitude of the spatial frequency vector (f_x, f_y, f_z). In this work, the axial NEQ(f_x, f_y) was computed using 2D representations of the MTF from Section 2.C.4 and the NPS from Section 2.C.6. Axial 1D representations of the 3D NEQ were computed as the radial average as described in Section 2.C.6 and are given by:

$$\mathit{\text{NEQ}}\left(f_r\right)=\pi \left|f_r\right|\frac{\mathit{\text{MT}}{F}^2\left(f_r\right)}{\mathit{\text{NPS}}\left(f_r\right)}$$ (8)

where |f_r| is the magnitude of the 2D spatial frequency vector (f_x, f_y), and the MTF and NPS refer to the radial average of the axial plane representations MTF(f_x, f_y) and NPS(f_x, f_y), respectively, assuming radial symmetry.

2.D. Anthropomorphic phantom study

Anthropomorphic phantoms were imaged to illustrate the image quality characteristics associated with the quantitative measures of noise and spatial resolution for various anatomical sites and imaging tasks. Cone-beam computed tomography volumes of an anthropomorphic head, abdomen, and pelvis were measured with the acquisition and reconstruction protocols described in Section 2.A, amounting to a total of 64 CBCT volumes. All images were acquired with 110 kV (6.7 mm Al HVL beam quality). Images were qualitatively assessed by a fellowship-trained orthopedic surgeon (~10 yr of experience) with respect to pertinent imaging tasks (e.g., visualization of bone trabeculae or simulated soft-tissue lesions) and interpreted relative to the observed trends in MTF, noise, CNR, NPS, and NEQ. Image evaluation was performed on monochrome, diagnostic-quality displays (MDCG-3210, Barco, Inc, Kortrijk, Belgium) and presented as orthogonal slices using the RadiANT DICOM viewer (Medixant, Poznan, Poland), allowing full control of slice selection and window-leveling.

2.D.1. Head phantom

An anthropomorphic head phantom (approximate lateral and AP extent = 15 and 20 cm, respectively) illustrated performance pertaining to imaging tasks of both high-frequency spatial resolution (trabecular bone and mastoid air cells in the temporal bone) and low-contrast visualization (simulated acute stage intracranial hemorrhage). The phantom consisted of natural human skeleton in tissue-equivalent plastic (Rando, The Phantom Lab, Greenwich NY) and included an array of 12.7 mm diameter spheres ranging in contrast from −120 to +900 HU.

2.D.2. Abdomen phantom

An anthropomorphic abdomen phantom (approximate lateral and AP extent = 25 and 18 cm, respectively) was used to evaluate imaging tasks related to low-contrast soft-tissue visualization — e.g., hepatic lesions. The phantom included a natural adult skeleton in tissue-equivalent (Rando) plastic with a variety of simulated soft-tissue structures, including a simulated liver containing 12.7 mm spheres ranging in contrast from −120 to +900 HU.

2.D.3. Pelvis phantom

An anthropomorphic pelvis phantom (approximate lateral and AP extent = 30 and 21 cm, respectively) presented imaging tasks relating to both high-contrast bone delineation (e.g., the femoral head, pelvis, and sacrioiliac joint) and low-contrast, soft-tissue visualization (e.g., the prostate, rectum, and bladder). The phantom consisted of a natural adult skeleton in tissue-equivalent (Rando) plastic with simulated bladder, prostate, colon, and rectum within the pelvic bowl. The phantom also included a QA test object located immediately superior to the simulated prostate that included an array of 18 mm diameter cylinders ranging in contrast from −1000 to +900 HU.

3. RESULTS

3.A. Dosimetry

3.A.1. Fluoroscopy reference-point air Kerma (RAK)

RAK measurements for each standard fluoroscopic protocol were performed, with techniques (variable kV, mA, and mAs/ pulse) set by the AEC. The techniques for the General, Vascular, Urology, and Orthopedic/Trauma protocols were the same and are represented in Table III by the General, Standard protocol, with air kerma rate ranging from 14 to 41 mGy/min (equivalent to an exposure rate of 1.6–4.7 R/min). The Gastro protocol ranged from 13 to 46 mGy/min (equivalent to an exposure rate of 1.5–5.2 R/min). The Interventional protocol ranged from 15 to 65 mGy/min (equivalent to an exposure rate of 1.7–7.4 R/min).

Table III.

Summary of reference point air kerma measurements for two-dimensional imaging protocols performed with an anthropomorphic abdominal phantom

Protocol	Dose level	Tube voltage (kV)	Tube current (mA)	Tube output (mAs/pulse)	Pulse rate (s−1)	Air Kerma rate (mGy/min)
General, standard	Low	64	60	0.35	7.5	13.9
	Medium	67	60	0.38	15	36.2
	High	68	58	0.63	10	40.9
Gastro, standard	Low	84	13	0.07	15	12.9
	Medium	87	16	0.08	30	33.6
	High	90	20	0.10	30	45.6
Interventional, standard	Low	64	67	0.36	7.5	14.5
	Medium	67	67	0.39	15	35.7
	High	63	173	0.87	15	64.7

3.A.2. 3D CBCT dose

Table IV summarizes CBCT dose measurements. For the head protocols, the dose for manufacturer-specified clinical protocols was 0.8–4.7 mGy (~0.15 mGy/mAs), and the dose for the custom protocols investigated for potential low-contrast visualization (e.g., intracranial hemorrhage) was 8.3–40 mGy. As points of reference, the dose reported for head scan protocols on other systems include: 1.3–6.8 mGy (Vision RFD 3D, Ziehm);⁵⁰ 6.7–67 mGy (O-arm, Medtronic);²⁰ and ~30–50 mGy (diagnostic MDCT),^41,51,52 recognizing that such dose values should not be interpreted in isolation, but in relation to the imaging task — for example, lower dose levels may correspond to fast, lower-quality protocols suitable to bone imaging, and higher dose protocols may correspond to tasks requiring low-contrast visualization (e.g., intracranial hemorrhage).

Table IV.

Summary of dose measurements for clinical and custom three-dimensional (3D) imaging protocols on the mobile C-arm for head and body protocols. Custom protocols are highlighted in gray. The terms D₀, ${\overline{D}}_P$, and D_W represent the central, average peripheral, and weighted dose, respectively, as defined in Section 2.B.2

Protocol	D0 (mGy)	${\overline{\mathit{D}}}_{\mathit{P}}$ (mGy)	Dw (mGy)
16 cm cylindrical phantom (head)
Low dose	0.7	0.8	0.8
Standard	1.4	1.6	1.5
High quality	4.2	4.9	4.6
Extra power: obese	4.2	4.9	4.7
Custom head 1	7.6	8.7	8.3
Custom head 2	15.1	17.4	16.6
Custom head 3	36.0	41.6	39.7
32 cm cylindrical phantom (body)
Custom body 1	0.6	1.1	0.9
Custom body 2	1.2	2.1	1.8
Custom body 3	3.2	5.8	4.9
Low dose	4.4	7.2	6.3
Standard	8.9	14.4	12.5
High quality	20.0	37.1	31.4
Extra power: obese	25.1	44.5	38.0

For the body protocols, the dose for manufacturer-specified clinical protocols was 6.3–38 mGy (~0.06 mGy/mAs), and the dose for the custom protocols investigated for lower-dose, high-contrast visualization (e.g., bone and surgical instrumentation) was 0.9–4.9 mGy. As points of reference, the dose reported for body scan protocols on other systems include: 14.8–36.7 mGy (Vision RFD 3D, Ziehm);⁵⁰ 6.7–27 mGy (O-arm, Medtronic);²⁰ and ~7–20 mGy (diagnostic MDCT),⁵² again recognizing that such dose values should not be interpreted in isolation, but in relation to the imaging task.

3.B. Geometric calibration

Figure 2(a) shows the variation in piercing point location over the course of the orbit, resulting from gantry flex over the course of the orbit, mechanical imperfection in the circularity of the C-arm gantry arm, vibration, and variation in BB centroid estimation owing to quantum noise. Displacement of the calibration phantom from isocenter introduces a low-frequency sinusoid with amplitude reflecting the distance between the center of the phantom and C-arm isocenter. Such sinusoidal trend (not shown) was subtracted from the measurement to better reflect sources of variation intrinsic to the system. The piercing point location varied from its mean position by 1.9 mm in u (detector rows) and 1.7 mm in v (detector columns). The reproducibility of the orbit is evident in the small variations in piercing point between the ten repeat scans overlaid in Fig. 2(a), with average standard deviation in u₀ and v₀ over the course of the orbit equal to (0.07 ± 0.03) mm and (0.09 ± 0.03) mm respectively. Variations were slightly higher at the start of the orbit, believed to be due to variability in the mechanical response to the acceleration curve.

Fig. 2.

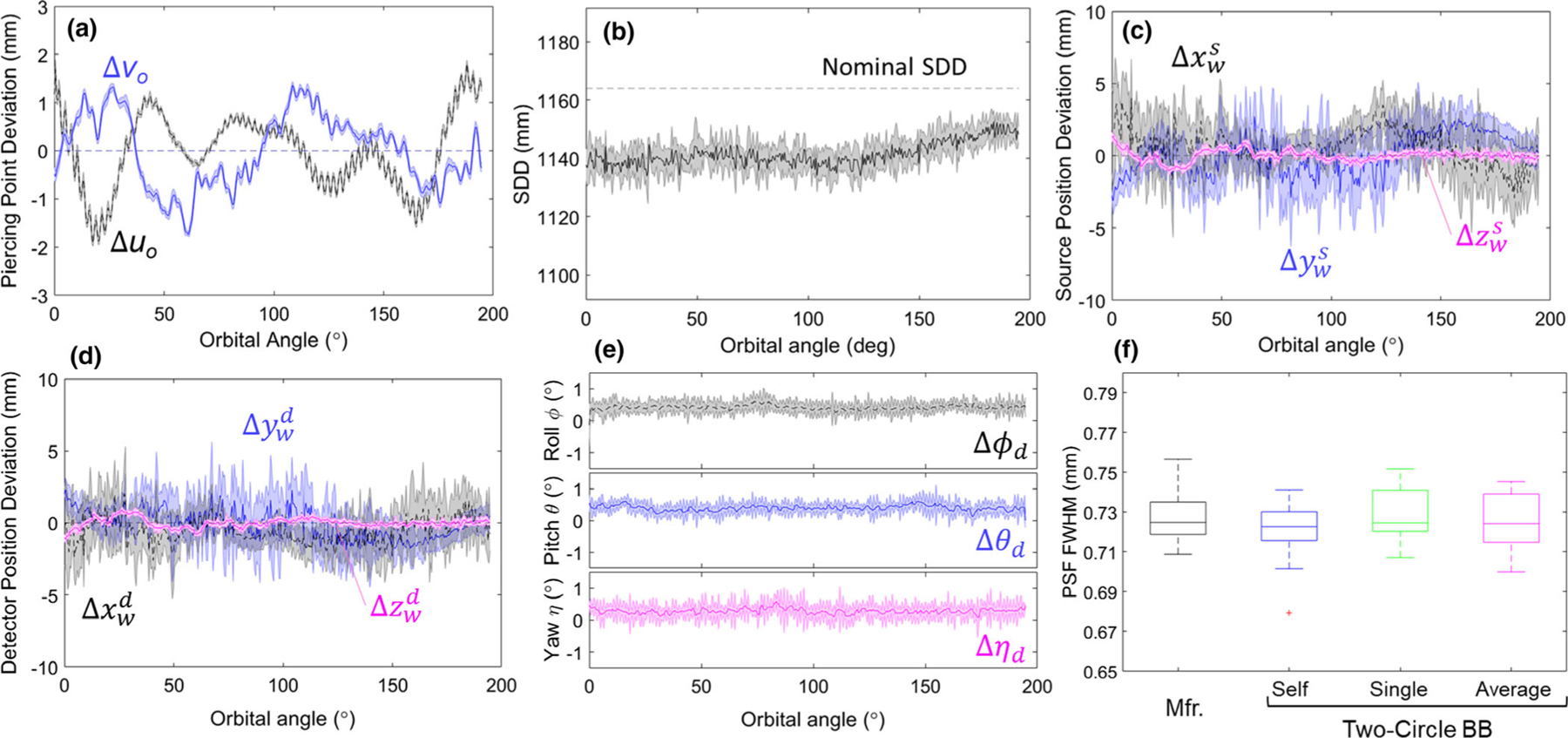
Geometric calibration and reproducibility for N = 10 orbits. Gantry (orbital) angles of 0° and 90° correspond to the x-ray beam directed along the x_w axis and y_w axis [Fig. 1(b)], respectively; for example, (for a patient laying supine on the OR table) a gantry angle of 0° corresponds to a lateral projection. Each orbit acquired 400 projections. (a) Variations in piercing point location on the detector. (b) Variations in source-detector distance over the course of the orbit. Deviations in (c) source position, (d) detector position, and (e) detector rotation over the course of a circular orbit. (f) Full width at half maximum of the point-spread function for various geometric calibration methods. All parameters prefixed with a “Δ” are plotted as the difference from a sinusoidal fit over the orbit. The shaded regions illustrate the variability (standard deviation) of the given parameter over the course of the orbit.

Figure 2(b) shows the variations in SDD over the course of the orbit, with gantry flex up to ~19 mm and an average SDD of 1141 mm (compared to the manufacturer specified SDD = 1164 mm). High-frequency variation in SDD between scans was ~0.4% error in SDD and was attributed primarily to the effects of quantum noise on BB centroid position. Figures 2(c)2(d) illustrate deviations in the source and detector position from an ideal circular orbit. For the source trajectory, the average variation in position was 1.7 ± 0.7 mm, 1.7 ± 0.7 mm, and 0.25 ± 0.09 mm in x, y, and z respectively. For the detector trajectory, the average variation in detector position was 1.5 ± 0.6 mm, 1.5 ± 0.7 mm, and 0.21 ± 0.08 mm in x, y, and z respectively. For both the source and detector, deviations were much smaller in the z direction compared to x and y, consistent with gravity/gantry flex. Figure 2(e) shows the detector angles over the course of the orbit, showing average variability over all angular views to be 0.20°, 0.19°, and 0.24° for roll (ϕ_d), pitch (θ_d), and yaw (η_d) respectively.

Figure 2(f) further illustrates the degree of geometric reproducibility in terms of the effect on PSF width in CBCT reconstructions. “Self-calibration” scans with no assumption on reproducibility of the orbit yielded PSF FWHM = 0.72 ± 0.01 mm (head scan protocol H with Normal reconstruction filter). Reconstructions using a single precalibration yielded the same (0.73 ± 0.01 mm) as did reconstructions using an average of 10 geometric calibrations (0.72 ± 0.01 mm) and reconstructions performed with the manufacturer-specified helical BB phantom calibration (0.73 ± 0.01 mm).

Overall, the results for the new system suggest a reasonably isocentric orbit (suitable to basic assumptions of a circular orbit for 3D FBP). This can be seen in Figs. 2(a), 2(c) and 2(d) where the piercing point (particularly along the row-wise direction, u) as well as the source and detector trajectory exhibit a relatively flat trend (within 5 mm deviation), indicative of an isocentric orbit. For a strongly non-isocentric orbit, the central ray (assuming a point source) would not pass through a common point and would exhibit large deviations in these curves. The results also suggest a high degree of reproducibility (a requirement for systems employing precalibration of system geometry) since the geometric parameters showed small variations across scans (for example, <0.1 mm variation in piercing point). Long-term reproducibility in routine clinical use is the subject of future work.

3.C. Uniformity and correspondence with HU

Figures 3(a) and 3(b) show example image uniformity in axial and sagittal slices (head protocol H with FBP₁ Normal filter). Figure 3(c) shows the degree of uniformity in image noise, increasing by ~35% from the lateral edge to center (due to attenuation) and by ~24% from the anterior to posterior (due to attenuation by the OR table). The line profiles in Fig. 3(d) show ~6.7% cupping and was the same for all protocols, as shown in Fig. 3(e). Figure 3(f) illustrates the correspondence of voxel value (AU) with HU, showing a strong linear relationship (solid line) between voxel value (AU) and specified HU values (r² = 0.99). Although the C-arm manufacturer does not claim HU calibration in 3D image reconstruction, for a small phantom without lateral truncation, the simple normalization described in Section 2.A.4 was found to give reasonable accuracy close to the identity line (dashed line).

Fig. 3.

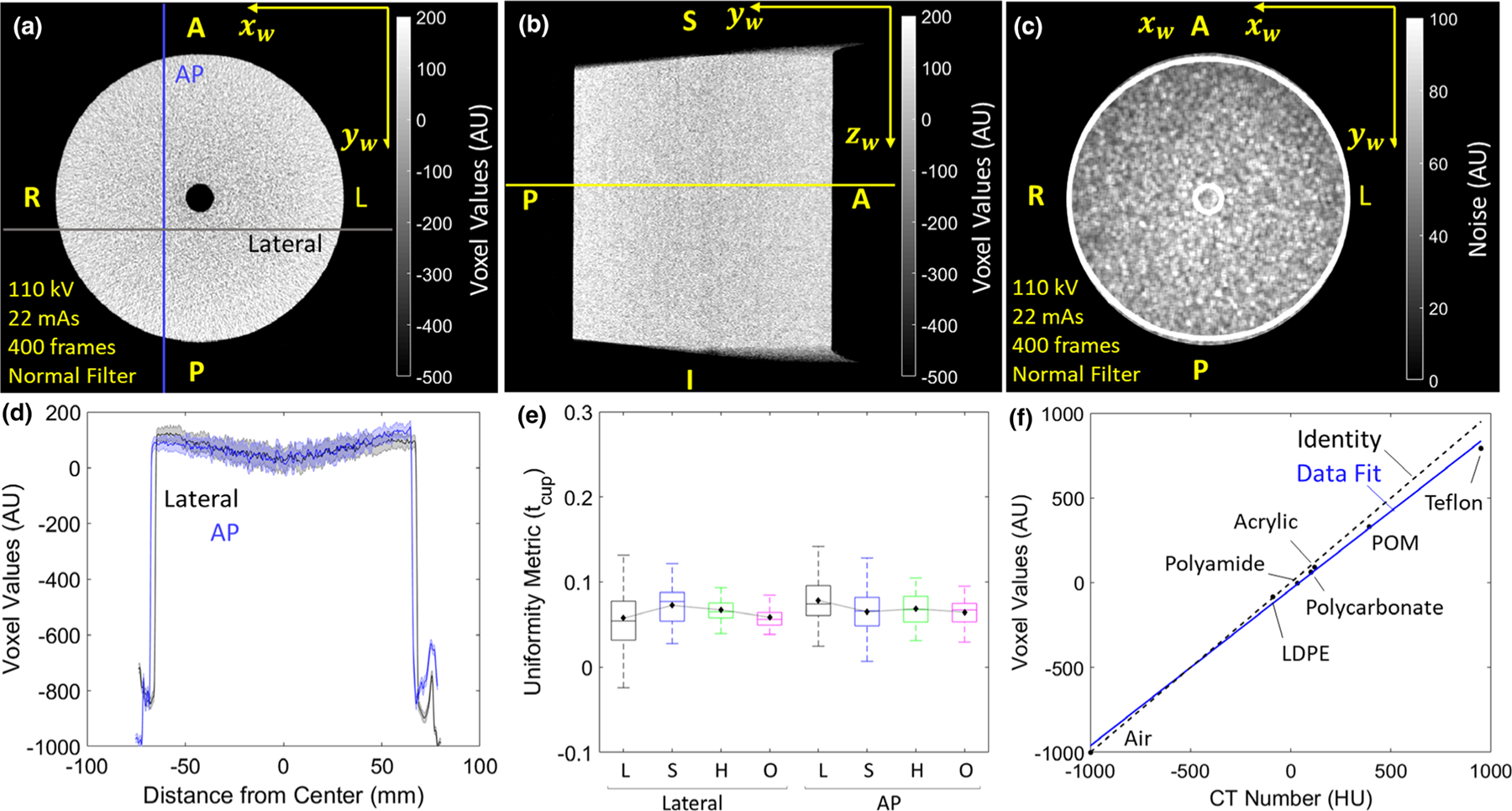
Uniformity and correspondence to Hounsfield units (HU). Slices of the uniform module in (a) axial and (b) sagittal planes (head protocol H with FBP₁ Normal filter). The yellow line in (b) corresponds to the axial slice shown in (a). (c) Noise map corresponding to (a). (d) AP and Lateral line profiles showing the magnitude of cupping artifact. (e) Uniformity (t_cup) for all clinical protocols in AP and LAT directions. (f) Correspondence of voxel value for various materials of known HU values. The dashed line represents the identity line.

3.D. Spatial resolution

Figure 4 shows the presampling MTF obtained for the head scan H protocol and each filter in the FBP₁ algorithm. The frequency (denoted f₁₀) at which MTF reduces to 10% was 0.64 mm⁻¹ for the Smooth filter, 1.0 mm⁻¹ for the Normal filter, and 1.5 mm⁻¹ for the Sharp filter. The FBP₂ algorithm gave equivalent axial plane MTF. The MTF did not depend on scan protocol (L, S, H, or O).

Fig. 4.

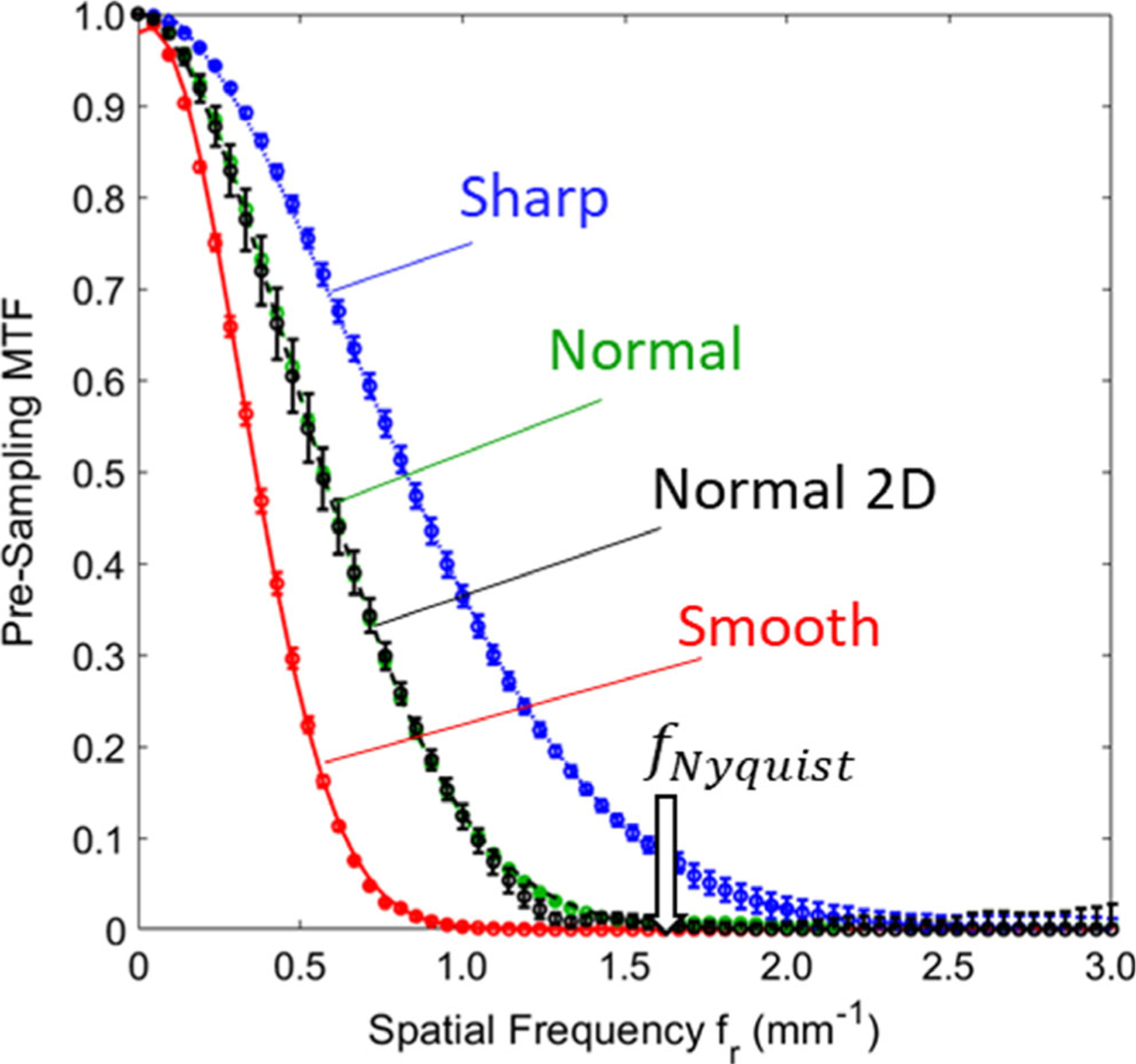
Pre-sampling modulation transfer function (MTF) for each reconstruction filter. Results were equivalent for each of the clinical protocols in Table II (H protocol shown). Error bars represent the standard deviation among multiple measurements (N = 6). The MTFs measured for Normal and Normal two-dimensional filters show small differences near the tails due to slight differences in the roll-off between the Shepp-Logan and Hann filters.

3.E. Noise, NPS, and NEQ

Figure 5 shows the CNR for each clinical protocol (horizontal axis L, S, H, and O) and reconstruction filter for a stimulus with −90 HU contrast (simulated intracranial hemorrhage in the head phantom) for FBP₁. As expected, the higher dose and smoother filter protocols monotonically improve CNR (noting that the H and O protocols are equivalent for the head protocols). The CNR for the FBP₂ algorithm with Normal filter (isotropic 2D Hann) is also shown, yielding a systematic improvement (~50–60%) compared to FBP₁ for both head and body setups and for all clinical protocols.

Fig. 5.

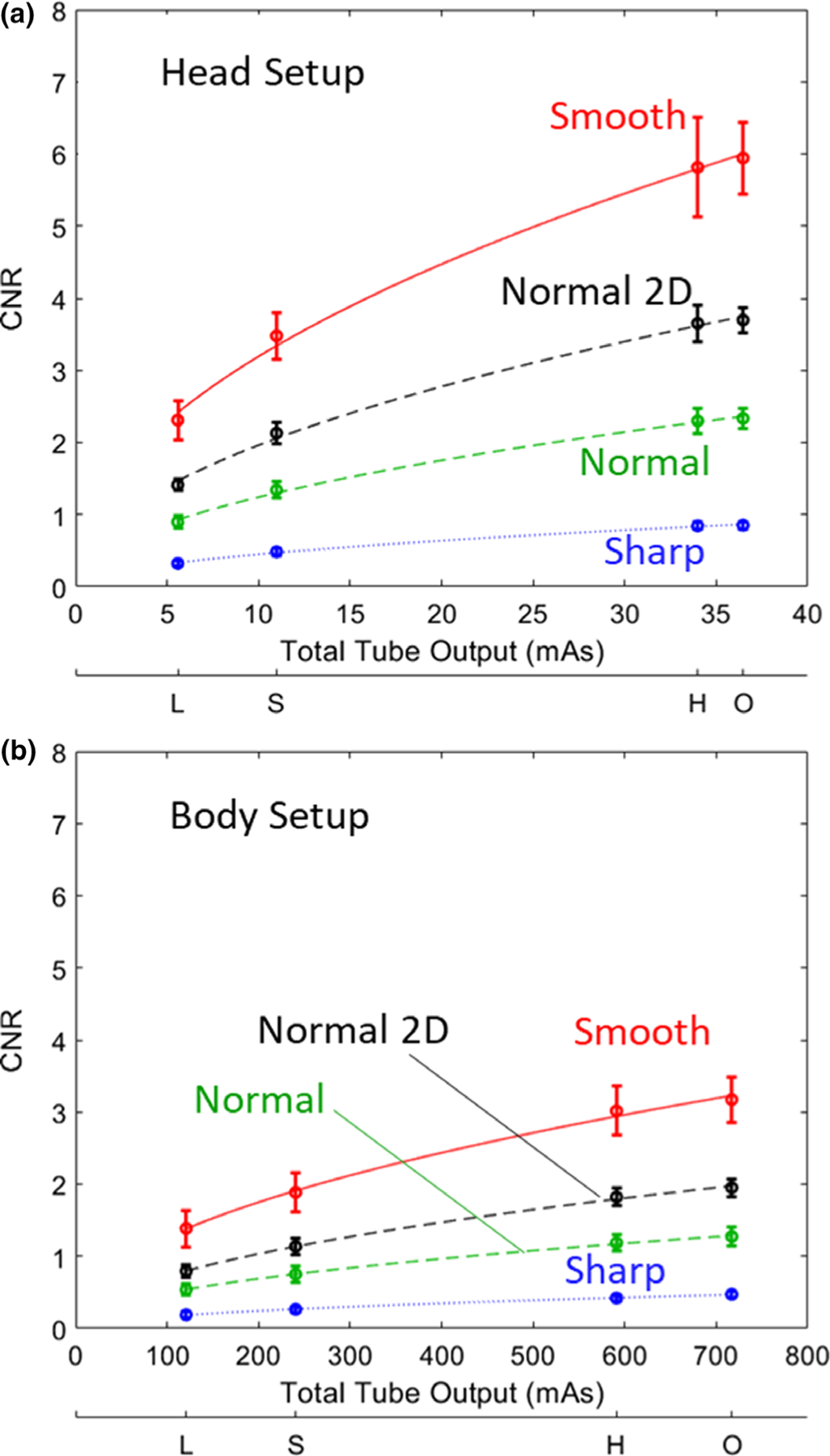
Contrast-to-noise ratio for a simulated soft-tissue stimulus (−90 HU contrast) imaged at each clinical protocol and filter choice. (a) Head setup. (b) Body setup. Results for the manufacturer-specified FBP₁ algorithm are shown in color, and those for the FBP₂ algorithm (Normal filter, labeled “Normal 2D”) are shown in black.

The axial and sagittal NPS for each clinical protocol and reconstruction filter are shown in Fig. 6. Consistent with the MTF measurements of Fig. 4, the axial NPS is bandlimited for the Smooth and Normal filters, while the Sharp filter carries a high degree of high-frequency noise, due in part to aliasing, since f₁₀ is nearly at the Nyquist frequency. For the relatively small phantom in these measurements, the AEC clamped x-ray tube output such that the O protocol matched the H protocol.

Fig. 6.

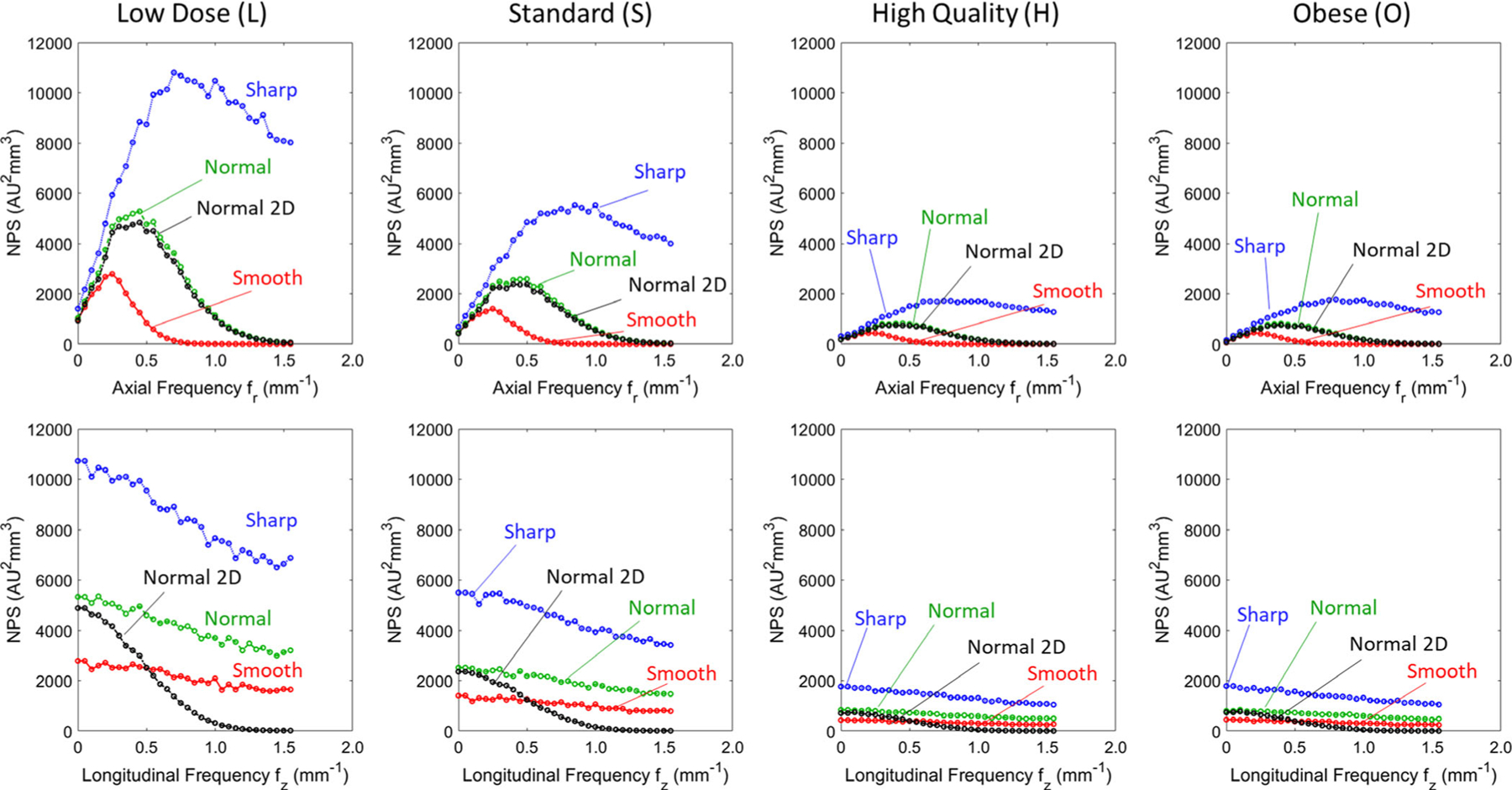
Noise-power spectrum (NPS). (Top) Axial and (Bottom) longitudinal NPS for each clinical protocol and reconstruction filter for FBP₁. The NPS for FBP₂ (Normal filter) is shown in black, denoted “Normal 2D.” The NPS is shown for frequencies up to the Nyquist (1.6 mm⁻¹).

The NPS for the FBP₂ algorithm is also shown in Fig. 6 (black curves) for the Normal filter (2D Hann filter). The main influence of the FBP₂ algorithm (i.e., of a more isotropic 2D filter) is evident in the sagittal (or coronal) NPS, where FBP₂ bandlimits the noise in the f_z direction, but FBP₁ carries increased high-frequency noise, since it is unfiltered in z. The effect was the same for all protocols (L, S, H, and O) and holds if the FBP₂ filter were set to match the Smooth or Sharp filters.

Figure 7 shows the 1D axial profile of the 3D NEQ (assuming radial symmetry about the f_z axis), which encapsulates the noise and resolution characteristics for each protocol. The boost in NEQ is immediately apparent for the H protocol compared to the L and S protocols — consistent with the findings of the anthropomorphic phantom studies reported below (Section 3.F) for bone and soft-tissue imaging tasks, respectively, where the H protocol was identified as preferable. To appreciate the relation to imaging task, it is useful to consider the H protocol further within low, middle, and high frequency bands for various filters (noting that trends in the H protocol extend to the other imaging protocols as well). At low to middle frequencies (in the range ~0.1–0.6 mm⁻¹), the Smooth filter demonstrates superior NEQ (as expected) and the NEQ increases by ~10% via the FBP₂ Normal 2D filter compared to FBP₁. This finding shows that an isotropic 2D filter benefits low-frequency imaging tasks. At higher frequencies (~1 mm⁻¹), the Smooth filter diminishes NEQ as expected, and there is little notable difference between the FBP₁ Normal and Sharp filters, suggesting that the latter suffers from high-frequency (aliased) noise to an extent that counters the improved spatial resolution. Given that the Normal filter has ~15% higher NEQ than the Sharp filter at low to middle frequencies (~0.1–0.6 mm⁻¹), and nearly equivalent performance at all other frequencies (within 6% at 0.5–1 mm⁻¹), there appears to be no suitable scenario (i.e., no imaging task) for the current implementation of the Sharp filter. This is confirmed qualitatively in anthropomorphic phantom images for various imaging tasks, below.

Fig. 7.

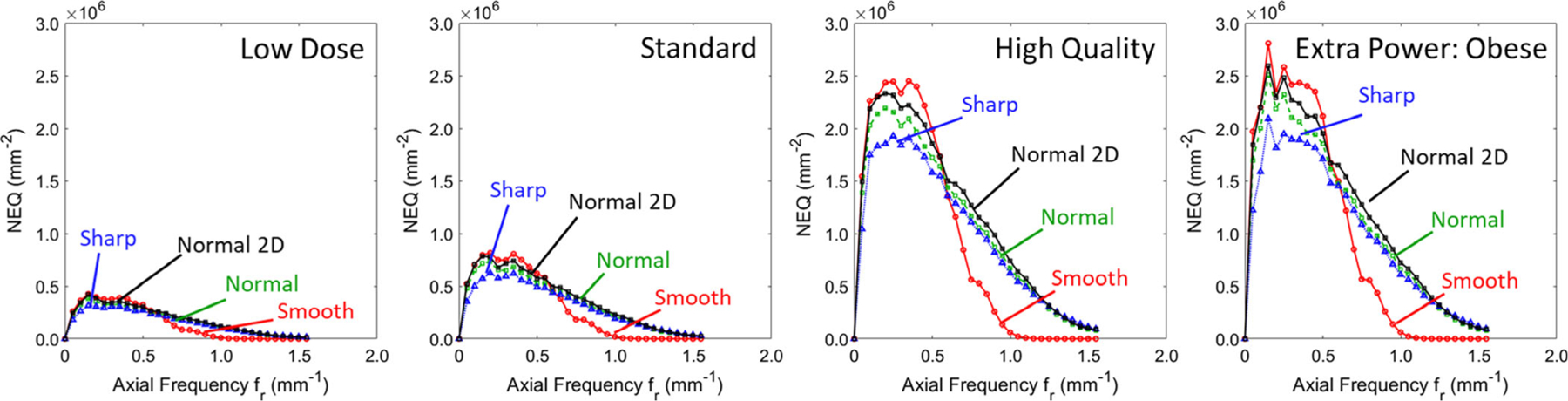
Axial noise-equivalent quanta for each various protocols and filters. Results for the FBP₁ algorithm various filters are in color, and for the FBP₂ algorithm (Normal 2D) are in black.

3.F. Anthropomorphic phantoms

Figure 8 illustrates the visual image quality associated with the MTF measurements of Fig. 4 with respect to high-contrast, high-frequency features in the temporal bone. The Normal and Sharp filters provided clearer visualization of mastoid air cells compared to the Smooth filter, consistent with the superior MTF (f₁₀ > 1.0 mm⁻¹). The Sharp filter provided minimal improvement in delineating high-frequency structures compared to the Normal filter due to the notable increase in high-frequency noise (e.g., ~3x higher noise than the Normal filter for the S protocol). The low dose (L) protocol also carried a noise increase that challenged visualization of mastoid air cells for any choice of filter.

Fig. 8.

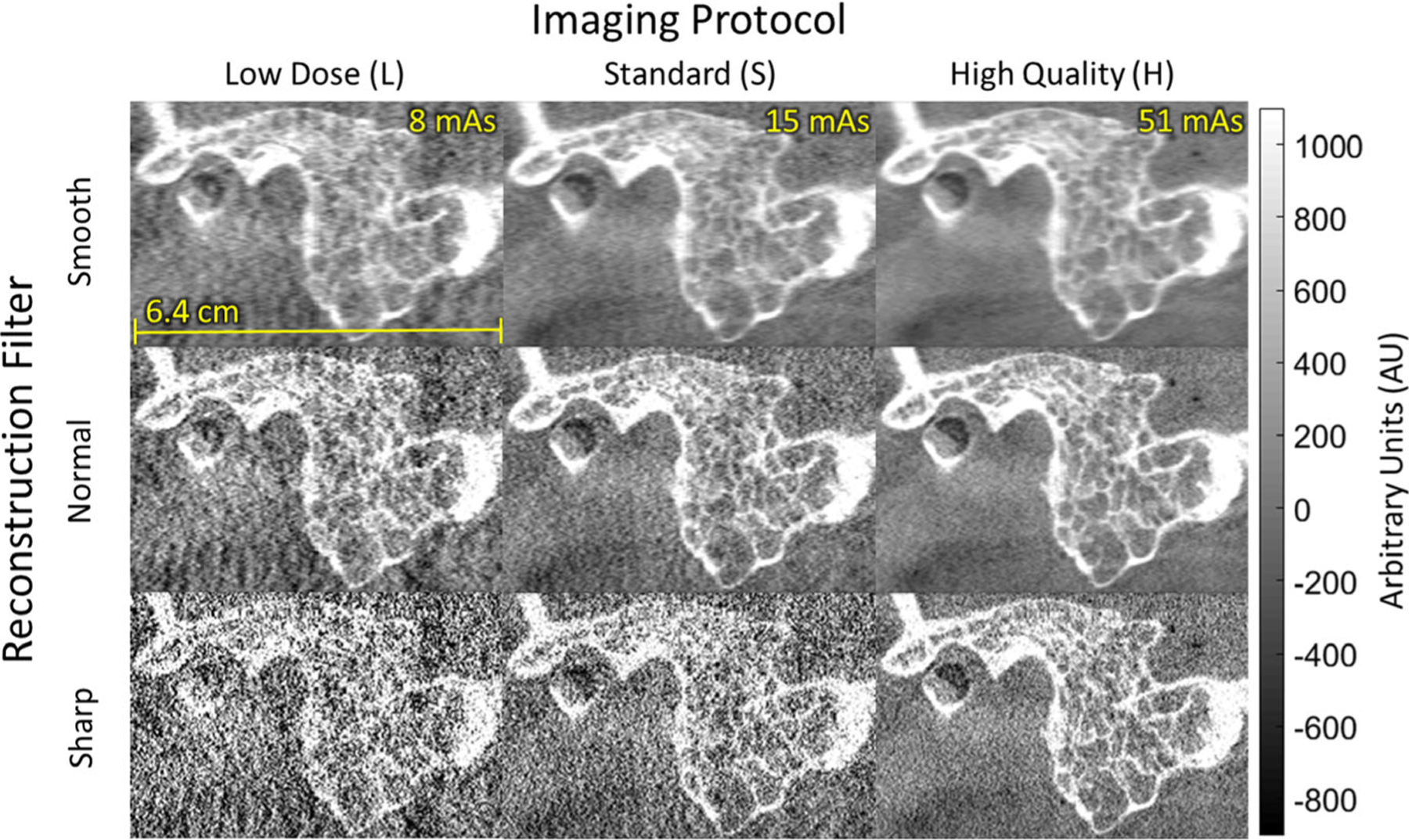
Cone-beam computed tomography images (sagittal) in the region of the temporal bone of an anthropomorphic head phantom. The visual image quality with respect to bone visualization reflects the modulation transfer function results in Fig. 4 and helped to guide technique chart definition — viz., head protocol H with Normal reconstruction filter for visualization of bone details.

The quantitative trends in CNR, NPS, and NEQ are illustrated in CBCT images of anthropomorphic head, body, and pelvis phantoms presenting various stimuli in Figs. 9–11. In Fig. 9, axial slices of the head phantom for each protocol are shown in a region containing simulated lesions in the brain parenchyma. Reliable visualization (e.g., the −80 HU contrast lesion marked by the yellow arrow) is fairly challenging for the L and S protocols. The H protocol with the Normal filter improved visibility (CNR ~ 1.1 for the marked lesion), and the FBP₂ algorithm boosted visibility further (CNR ~ 2.0 for the marked lesion). As expected, the Smooth filter showed the best CNR for all protocols.

Fig. 9.

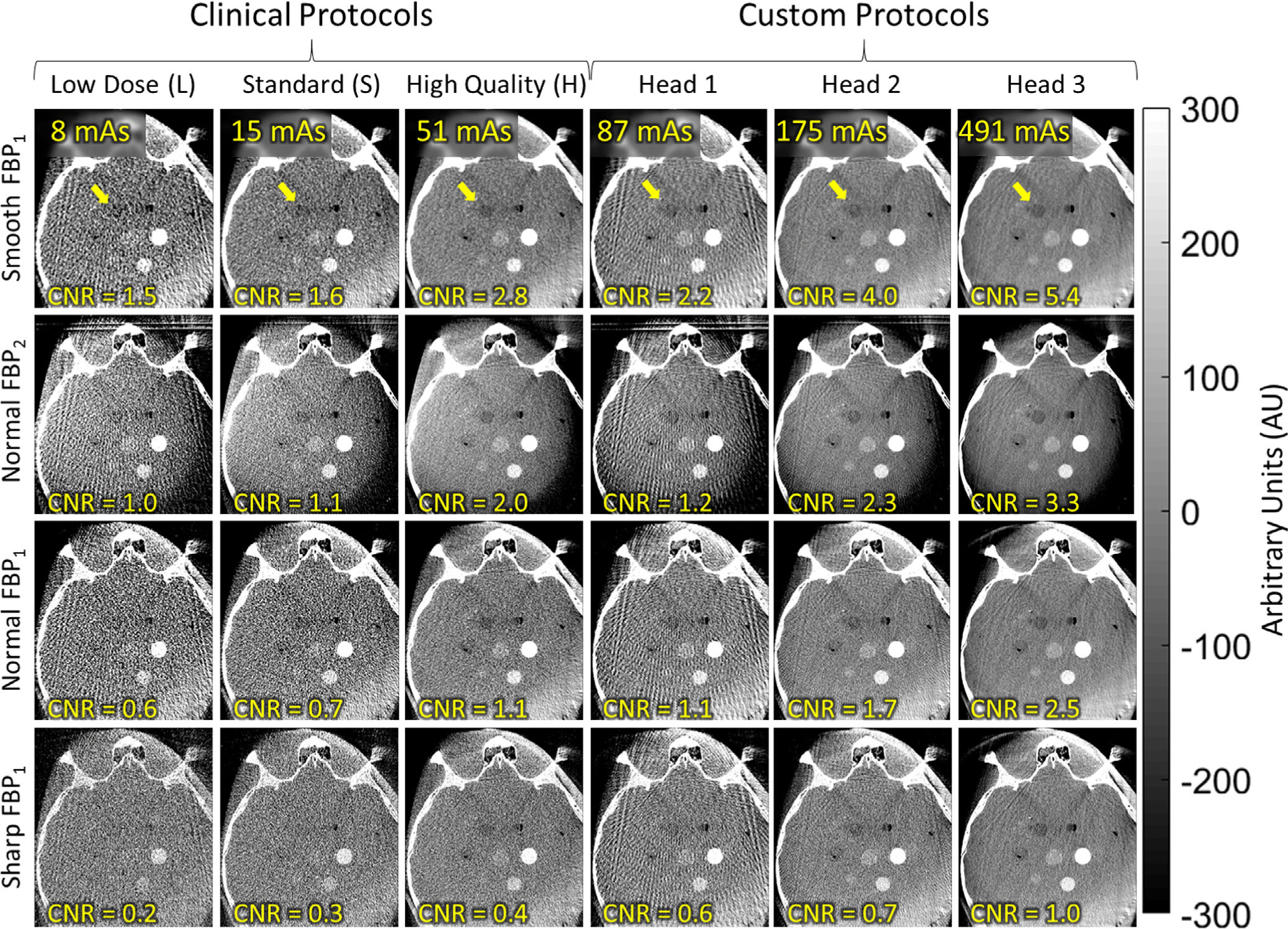
Axial images of the anthropomorphic head phantom, illustrating the visibility of low-contrast stimuli for various scan protocols and reconstruction filters. A relatively low-contrast stimulus (−80 HU) is marked by the arrow, with contrast-to-noise ratio noted in the lower-left of each panel. The results help to guide development of future protocols that may support soft-tissue visualization in head imaging — for example, Custom Head 2 with Smooth or Normal two-dimensional filters.

Fig. 11.

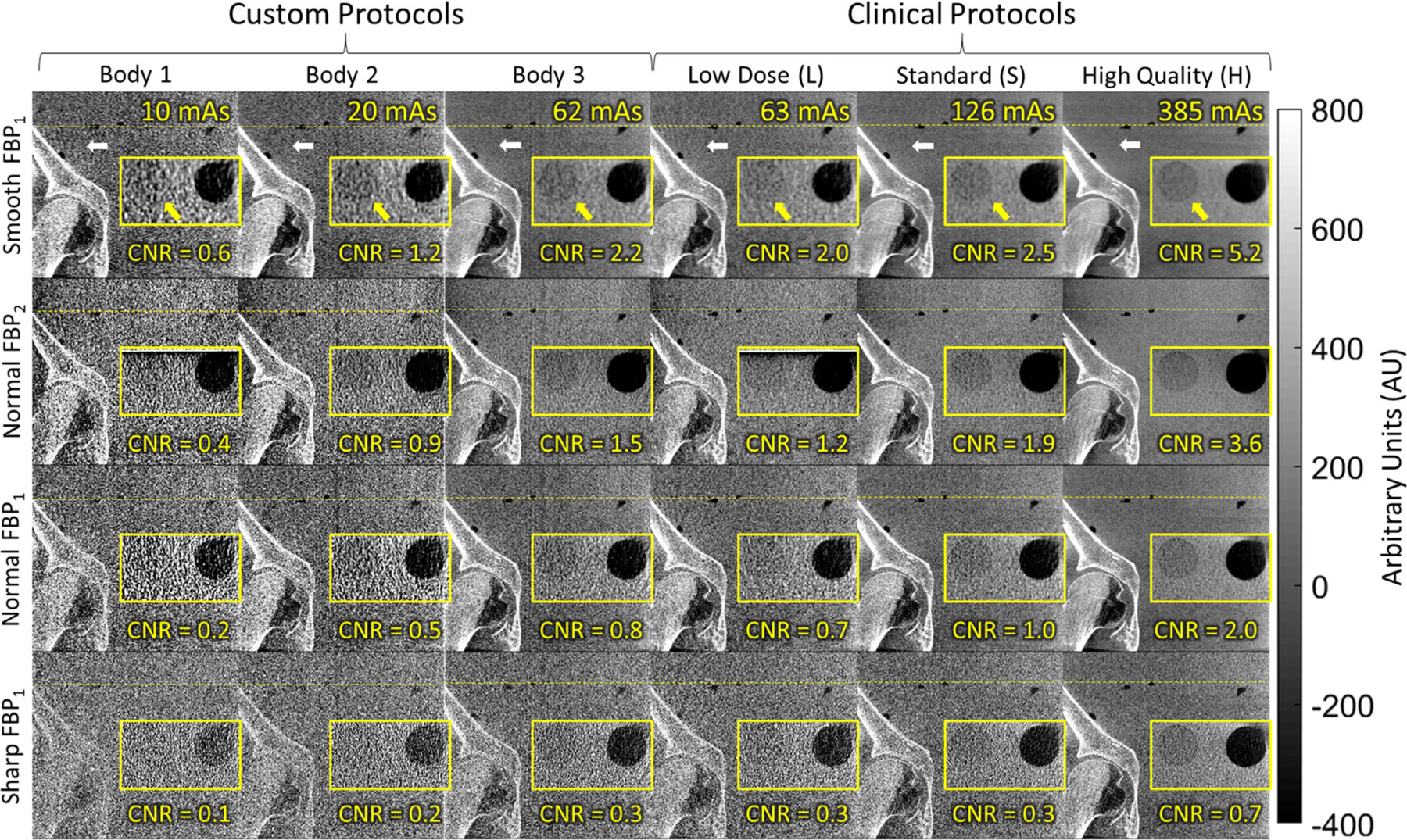
Imaging performance for body scan protocols visualized in cone-beam computed tomography images of a pelvis phantom: coronal views of the region about the acetabulum (white arrow) and zoomed-in axial views (yellow inset) of a low-contrast insert (yellow arrow). The clinical body protocols (right three columns) deliver relatively high mAs (potentially suitable to soft-tissue visualization—for example, the H protocol with Smooth or Normal two-dimensional filters) — and motivated the investigation of custom body protocols (left three columns) for bone visualization at reduced radiation dose.

The custom protocols (Custom Head 1, 2, and 3) were motivated by the challenge to soft-tissue visualization and recognizing the relatively modest dose of even the highest dose clinical head protocol (H, for which D_w = 4.6 mGy, compared to ~50 mGy for a diagnostic MDCT scan of the head). The Custom Head 1 protocol increases dose to 8.3 mGy but is seen to suffer view sampling artifacts due to the low number of projection views (N_proj = 100). The Custom Head 2 and 3 protocols increase the dose to 16.6 and 39.7 mGy, respectively, and demonstrate clearer visualization of the low-contrast lesion — for example, CNR improved to 4.0 for Custom Head 2 (Smooth) and to 5.4 for Custom Head 3 (Smooth); alternatively, CNR was improved to 2.3 for Custom Head 2 (Normal 2D) and to 3.3 for Custom Head 3 (Normal 2D).

Soft-tissue imaging performance is further illustrated in CBCT images of the body phantom in Fig. 10, which presents multiple inserts in the region of the liver emulating the contrast uptake of a hepatic lesion from −120 to +900 HU. For the relatively small abdomen phantom, the O protocol did not significantly boost x-ray tube output compared to the H protocol. The boundary of the liver and −95 HU lesion (marked by the yellow arrow) was observable for the H protocol. The FBP₂ algorithm again improved visualization of low-to-medium contrast structures, giving a ≥80% improvement in CNR for the marked lesion across all protocols (CNR ~ 2.6, H protocol). Images for the Smooth and Sharp FBP₁ filters (not shown for brevity) demonstrated trends in image quality similar to those shown in Fig. 9 — for example, (for the H protocol) the Smooth and Sharp FBP₁ filters showed CNR of 2.9 and 0.5 respectively.

Fig. 10.

Soft-tissue visibility in an anthropomorphic abdomen phantom. The higher x-ray tube output of the clinical body protocols provide improved soft-tissue visibility (e.g., the −95 HU contrast lesion marked by the arrow), with further improvement gained by the FBP₂ algorithm with isotropic two-dimensional filter.

Finally, Fig. 11 illustrates the trends quantified by the NPS and NEQ in relation to image quality for both high-contrast bone visualization tasks and low-contrast soft-tissue visualization tasks in a pelvis phantom. In each case, a coronal view of the hip joint is shown, with an inset showing a zoomed-in axial view of a low-contrast test object positioned roughly superior to the prostate. The benefit of the higher x-ray tube output for the body protocols is evident with respect to soft-tissue visualization (cf., the clinical head protocols in Fig. 9, limited to <~50 mAs). For example, the low-contrast insert (−80 HU) appears well-visualized for the H protocol and Normal filter (CNR ~ 2.0), and soft-tissue visibility was well-achieved using the lower dose S protocol with the FBP₂ algorithm and Normal 2D filter (CNR ~ 1.9).

For purposes of bone visualization, all of the clinical body protocols appeared nominally performant, with the exception of the L protocol and Sharp filter. This motivated the development and investigation of the Custom Body (1, 2, and 3) protocols that might maintain high-contrast bone visualization at a lower dose. For example, the Custom Body 2 protocol with Smooth or Normal filters (both FBP₁ and FBP₂) appears to maintain visualization of the femoral head and acetabulum, while delivering 1/3 the dose of the clinical L protocol.

A final point of comparison concerns the Custom Body 3 and L protocols, which deliver approximately the same total mAs. As shown in Table II, however, the Custom Body 3 protocol acquires a higher number of projections (each at proportionally reduced mAs/frame). Close inspection of Fig. 11 shows that this increase in the number of projection views reduces subtle view sampling effects seen in the region about the acetabulum (white arrow) in the L protocol, suggesting a potential improvement without an increase in scan time.

4. DISCUSSION

The short-term reproducibility of geometric calibration was validated. Departures from a circular orbit were evident (within ~19 mm) due to gantry flex, but the reproducibility of such variations was high — comparable to reports on previous prototype systems³¹ and sufficient to support accurate 3D image reconstruction. While not investigated in the current work, the long-term reproducibility of the system geometry in routine clinical use is important for QA. Assessment of long-term stability can help guide the QA process (e.g., the frequency of field service for calibration) and is the subject of future work.

Reconstruction protocols were investigated with respect to performance in pertinent imaging tasks. At matched axial-plane resolution, the FBP₂ algorithm exhibited ~50–60% improvement in CNR across all head and body protocols and a ~10% improvement in NEQ at low frequencies (~0.1 mm⁻¹) over the FBP₁ algorithm for the Normal reconstruction protocol. The noise reduction associated with application of an isotropic 2D linear filter is consistent with expectation — a result of smoothing the data in a more fully 3D sense (whereas a 1D filter smooths in axial planes). Such reduction in noise could also be accomplished with the FBP₁ algorithm via slice averaging; however, we note that the FBP₂ method (filtering in the projection domain, rather than slice-averaging in the reconstruction domain) carries an advantage with respect to 3D noise aliasing — that is, for equivalent MTF, the FBP₂ method exhibits slightly lower noise. For soft-tissue visualization tasks, the 2D filter may be particularly beneficial and imparts more isotropic noise and resolution characteristics, which may carry psychophysical benefits associated with a more natural, isotropic correlations in signal and noise — an interesting, if speculative, hypothesis that is beyond the scope of the current work.

Also of note was the performance of the Sharp FBP₁ filter, for which the NEQ was worse than or equal to the NEQ of the Normal FBP₁ filter at all spatial frequencies. This result could be qualitatively observed in images of the temporal bone where the sharp filter was seen to add little high-frequency information content and carried a visible increase in noise, in part due to aliased noise. An important observation that arises from this result involves the choice of voxel size according to the system magnification and filter cutoff frequency such that the system MTF is bandlimited at the Nyquist frequency. As noted above, voxel size is fixed at 0.313 mm for all of the manufacturer-specified reconstruction protocols. In the case of the Sharp filter, a finer voxel size would reduce the noise aliasing. Conversely, coarser voxel size for smoother filters could benefit low-frequency tasks. The FBP₂ implementation, which combined an adjustable 2D apodization filter and variable voxel size was found to reduce noise at matched axial spatial resolution compared to the FBP₁ implementation (giving ≥ 20% improvement in CNR across all three filter types).

Studies examining custom and clinical imaging protocols highlighted a number of important observations in technique selection for bone and soft-tissue imaging tasks. For procedures such as cochlear implantation or cranial-maxillofacial surgery for which the primary imaging task relates to bone structures and/or surgical implants, the findings helped to guide nominal technique chart definition using the head protocol H (D_w = 4.5 mGy) with Normal filter. In the body, visualization of large, bony structures were found to be achievable with lower dose, custom protocols with the Smooth and Normal filters (for both FBP₁ and FBP₂) indicating that clinical tasks requiring only coarse localization of bony structures and/or verification of device placement may be accomplished in a manner consistent with the lowest dose that can be reasonably achieved. The current head and body clinical protocols (L and S) were found to be challenged with respect to soft-tissue visualization, noting the possible exception of the H and/or O protocols with Smooth filter. The results suggest that comparable soft-tissue visibility could be achieved through the use of lower dose clinical protocols with the FBP₂ algorithm (isotropic Normal 2D or Smooth 2D filter) over corresponding protocols acquired at higher scan doses with the FBP₁ algorithm. Moreover, the combination of custom head scan protocols delivering higher dose (but still a fraction of the dose in diagnostic MDCT of the head) with an isotropic 2D filter may boost performance to a level supporting reliable visualization of soft-tissue structures in the head, such as intracranial hemorrhage.

5. CONCLUSIONS

The imaging performance and dose of a new isocentric mobile C-arm for intraoperative CBCT were evaluated, and the potential benefits of alternative technique protocols and reconstruction methods were investigated. Overall, the results conveyed three primary findings. First, modification of the standard FBP algorithm to implement a 2D isotropic filter yielded notable improvements in imaging performance, particularly for low-contrast tasks (≥20% improvement in CNR). Second, the current implementation of the Sharp reconstruction filter offered no suitable use case, partially due to noise aliasing. We propose an alternative approach by which the voxel size is varied with respect to the filter width to reduce noise aliasing effects. Third, custom scan protocols outside the set of clinically available protocols were shown to potentially offer improved performance or dose savings for pertinent imaging tasks. Finally, we note that the assessment reported here evaluates performance in the context of objective, observer-independent performance variables (viz. MTF, NPS, CNR, and NEQ) and does not fully assess task-based imaging performance — for example, a simple metric like CNR does not include the effects of noise correlation and can only be interpreted in the context of large-area tasks. Instead, the current work provides a guide by which the metrics reported may serve as a basis for evaluation of task-based image quality, for selection of appropriate imaging techniques, and for reference of benchmark QA. Future work includes more thorough investigation into task-driven design through which optimal imaging and reconstruction techniques can be defined for any given imaging task.