Estimate of the HOMA-IR Cut-off Value for Identifying Subjects at Risk of Insulin Resistance Using a Machine Learning Approach

Abstract

Objectives

This study describes an unsupervised machine learning approach used to estimate the homeostatic model assessment-insulin resistance (HOMA-IR) cut-off for identifying subjects at risk of IR in a given ethnic group based on the clinical data of a representative sample.

Methods

The approach was applied to analyse the clinical data of individuals with Arab ancestors, which was obtained from a family study conducted in Nizwa, Oman, between January 2000 and December 2004. First, HOMA-IR-correlated variables were identified to which a clustering algorithm was applied. Two clusters having the smallest overlap in their HOMA-IR values were retrieved. These clusters represented the samples of two populations, which are insulin-sensitive subjects and individuals at risk of IR. The cut-off value was estimated from intersections of the Gaussian functions, thereby modelling the HOMA-IR distributions of these populations.

Results

A HOMA-IR cut-off value of 1.62 ± 0.06 was identified. The validity of this cut-off was demonstrated by showing the following: 1) that the clinical characteristics of the identified groups matched the published research findings regarding IR; 2) that a strong relationship exists between the segmentations resulting from the proposed cut-off and those resulting from the two-hour glucose cut-off recommended by the World Health Organization for detecting prediabetes. Finally, the method was also able to identify the cut-off values for similar problems (e.g. fasting sugar cut-off for prediabetes).

Conclusion

The proposed method defines a HOMA-IR cut-off value for detecting individuals at risk of IR. Such methods can identify high-risk individuals at an early stage, which may prevent or delay the onset of chronic diseases such as type 2 diabetes.

Advances in Knowledge

• - A machine learning approach to estimate the homeostatic model assessment-insulin resistance (HOMA-IR) cut-off value for identifying individuals at risk of IR in a given ethnic group is described.

• - Identification of subjects at risk is fast and inexpensive since it consists of comparing an individual’s HOMA-IR value to the defined cut-off.

• - A HOMA-IR cut-off value of 1.62 is proposed to identify individuals at risk of IR among the Arab population living in Nizwa, Oman.

Applications to Patient Care

• - Identified at-risk individuals are recommended to undergo an additional investigation using the euglycaemic clamp test for confirming or rejecting the diagnosis.

• - This is of high importance for public health, as it identifies high-risk individuals at an early stage, which may prevent or at least delay the onset of chronic diseases such as type 2 diabetes and cardiovascular disease.

Insulin resistance (ir) is a synonym for impaired insulin action, such as inhibition of hepatic glucose production and insulin-mediated glucose disposal.1,2 IR increases the incidence of metabolic syndrome (MetS), which has emerged as a major pathophysiological factor in the development and progression of many common non-communicable diseases, including type 2 diabetes mellitus (T2DM), polycystic ovary syndrome, dyslipidaemia, hypertension, cardiovascular disease (CVD), obesity and cancer.2,3 Detecting this condition is, therefore, significantly important for public health. Several studies have illustrated a high prevalence of diabetes, impaired glucose tolerance, obesity and hypertension among Arab populations of the Middle East.4 In Oman, the first cause of premature death is CVD, and the fourth cause is T2DM.5 Therefore, there is a need to prevent and control CVD and T2DM in Oman. IR is an early marker of the development of these diseases; primary prevention requires the identification of high-risk individuals at an early stage. The gold standard for investigating and quantifying IR is the hyperinsulinaemic (euglycaemic) clamp.6 Given the complicated nature of the ‘clamp’ technique and potential dangers of hypoglycaemia in some patients, several surrogate estimates for IR have been proposed, such as the homeostatic model assessment (HOMA-IR), Quicki and Matsuda.6–8 HOMA-IR is the most popular among all of these indices due to the simplicity of the underlying mathematical model (HOMA-IR = fasting glucose (mM) × fasting insulin (mU/L)/22.5). HOMA-IR has been validated to be highly correlated with the hyperinsulinaemic (euglycaemic) clamp (r = 0.82; P <0.0001) as well as with the minimal model approximation of the metabolism of glucose (r = −0.66; P <0.001).9,10 Several studies have shown that the cut-off value for HOMA-IR depends on the ethnicity of the subjects.5,11 Therefore, this value has to be adapted for each ethnic group to reflect the prevailing normal glycaemic level.

Several statistical methods for estimating the HOMA-IR cut-off value have been reported in the literature. Most of these methods determine the cut-off values from reference ranges where percentiles or receiver operating characteristic (ROC) curves are applied.2 The use of the percentile method of analysis within a general population lacks the classification of subjects; therefore, it lacks sensitivity and specificity. Reported ROC curve analyses are limited, as they are based on healthy subjects and patients with T2DM or MetS, whereas IR is well established in an advanced disease state. Machine learning (ML) is a discipline of artificial intelligence that has proven to be very efficient in solving classification and prediction problems. The majority of ML algorithms can be categorised into two groups.12

The first category is supervised ML where a model is trained on a range of inputs (variables or features) that are associated with known outcomes (labels). In medicine, this might represent training a model to relate a person’s characteristics (e.g. height, weight and smoking status) to a certain outcome (e.g. onset of diabetes within five years). Once the algorithm is successfully trained, it becomes capable of making predictions when applied to new data. When the prediction is discrete (e.g. benign or malignant), the model is referred to as a classification. However, when it is of a continuous value (e.g. an individual’s life expectancy), the model is referred to as a regression. The most common supervised learning algorithms used in medicine are decision trees, logistic regression, support vector machines and artificial neural networks.

The second category is unsupervised learning, which does not involve predefined outcomes (labels) and does not need a training phase. This learning type is used to find hidden structures (or clusters) that occur within datasets. The most common methods used in this category are dimension reduction algorithms such as principal component analysis (PCA), association rules generation such as association rule mining and clustering algorithms such as k-means and a self-organising map.

Recently, several ML-based methods for defining HOMA-IR cut-off values have been proposed. Altuve et al.13 employed a k-means clustering algorithm to perform an unsupervised classification of subjects based on unidimensional observations (HOMA-IR and the Matsuda indexes separately) and multidimensional observations (insulin and glucose samples obtained from the oral glucose tolerance test). Their results indicated that when using the HOMA-IR index alone, the clusters are related to IR; however, when using HOMA-IR with other variables, the insulin-resistant cluster also contains normal samples. They argued that this could indicate that the normal samples either develop IR or already have the metabolic disorder. One of the drawbacks of this work was that it labelled subjects with HOMA-IR greater than 2.5 as insulin resistant, which is not necessarily true. Stern et al. developed three decision trees (decision rules) based on clinical and laboratory measurements of 2,321 individuals from 17 European sites, San Antonio, Texas and the Pima Indian reservation.14 The first model was based on both clinical and laboratory measurements; it achieved an area under curve (AUC) of 90%. The second model was developed from clinical variables only and achieved an AUC of 85%. The last one was developed from clinical and lipid measurements and achieved an AUC of 85%. These results indicated that IR can be defined using simple decision trees. Qu et al. proposed an ML approach to defining the HOMA-IR cut-off for Americans of Mexican descent.11 They first identified HOMA-IR-correlated variables using two classification methods (support vector machine and Bayesian logistic regression); then, they ran a clustering algorithm (k-means with k = 2) using the identified variables to obtain two reference groups representing insulin-resistant and normal individuals. Finally, the sensitivity and specificity of a series of HOMA-IR cut-off values were tested against the reference groups using Matthews’ correlation coefficient (MCC). A cut-off value of 3.80 corresponding to the highest MCC value was chosen.

In this study, an unsupervised ML method is proposed, which given a statistically representative sample of an ethnic group, automatically estimates a HOMA-IR cut-off value for identifying individuals at risk of IR. This approach was applied to an Omani population living in Nizwa, Oman, but it can be used to estimate the appropriate HOMA-IR cut-off value of any other population based on the clinical and biochemical variables of a statistically representative sample.

Methods

Data were obtained from the Oman Family Study, which was conducted during the period 2000–2004.15 The dataset was obtained from a previous study on 1,344 individuals of Arab ancestry as part of the Oman Family Study conducted in the Nizwa region of Oman.15–17 The data included measures of 26 variables representing anthropometric data, 24-hour systolic and diastolic blood pressures (SYST and DIAST, respectively), fasting and two-hour glucose and insulin, fasting lipid profile, hormone profile and liver function test. Study parameters were measured using a standard clinical biochemistry lab. Plasma insulin, growth hormone, free thyroxine (FT4) and triiodothyronine (FT3) were measured using the automated Beckman Coulter Access 2 immunoassay system (Beckman Coulter, California, USA). Plasma leptin (LEPT) levels were measured using a coated tube immuno-radiometric kit (Diagnostic Systems Laboratories, Texas, USA). For routine biochemical parameters, the automated Beckman Synchron CX7 (Beckman Coulter) was used to measure plasma glucose, glycated haemoglobin (HbA1c), total cholesterol (CHOL) and high-density lipoprotein (HDL) cholesterol, triglycerides (TG) and alanine transaminase (ALT). Very-low-density lipoprotein (VLDL) and LDL lipoprotein were calculated as follows: VLDL (mmol/L) = TG (mmol/L) / 2.2 and LDL (mmol/L) = CHOL – (VLDL + HDL). The 24-hour ambulatory blood pressure (BP) was also measured (Schiller AG, Baar, Switzerland). The percentage of total body fat was measured using the electro-impedance model. Further details on data collection have been described by Bayoumi et al. and Zadjali et al.16,18

A data cleaning operation was conducted to remove samples with missing data or outlier values. Details of this operation are provided in the results section. The final cleaned dataset included the measurements of 26 clinical variables collected from 798 individuals (338 males and 460 females).

To determine the HOMA-IR cut-off, a three-step approach was adopted, which was similar to the one adopted by Qu et al.11 for analysing the Americans of Mexican descent dataset; however, different techniques were used in this study. First, the HOMA-IR-correlated variables were identified. Then, this study’s own clustering algorithm was run to identify two reference groups representing samples of the two populations—individuals at risk of IR and those with normal insulin sensitivity (NIR), respectively. Based on the assumption that the HOMA-IR values of the two populations were normally distributed, the parameters of their Gaussian functions were estimated, and their intersections were used as an estimate of the sought cut-off value. A detailed description of this process is provided in subsequent sections. There were three major differences with Qu et al.’s approach. Firstly, Qu et al.’s feature selection method was based on two classification techniques (support vectors machine and Bayesian logistic regression) trained on a labelled dataset (where patients with HOMA-IR >2.6 were labelled as insulin resistant and the rest as normal, which was questionable since the objective was to precisely define this threshold).11 However, in the method adopted by the current researchers, the selection did not depend on any initial assumption about the HOMA-IR cut-off; instead, a statistical technique (Pearson correlation) was used to pre-select a subset of HOMA-IR-correlated variables. Secondly, Qu et al. used a k-means algorithm to determine the two reference groups, while a new clustering algorithm (minimum overlap k-means clustering algorithm) was developed for determining the two reference groups for the present work. Finally, Qu et al. tested several cut-off values in the range (minimum HOMA-IR value, maximum HOMA-IR value) and selected the value that best fit the reference groups. Their best fit was identified using MCC, while the cut-off in this study was defined by the intersection of the Gaussian functions that modelled the HOMA-IR distributions of the two populations—individuals at risk of IR and those with NIR.

The following subsections contain additional details about the proposed method, indicate the assumptions of the researchers and provide their justifications for making those assumptions.

As mentioned above, the first step in the method proposed in this study consisted of determining two reference groups representing the samples of two populations. Since IR is a complex metabolic disorder that may impact the levels of several correlated clinical variables, identifying and including those variables in the analysis process might lead to early detection of the disorder.19 For this reason, the researchers’ clustering operation included, in addition to HOMA-IR, a selected subset of variables that correlated with HOMA-IR. Moreover, it is known that feature selection is used to remove irrelevant, redundant and ‘noisy’ features. This process has several advantages.20 It speeds up the learning process and allows the building of a simpler and more accurate model, which leads to better predictors. The researchers’ feature selection algorithm consisted of ranking the variables according to their correlations with HOMA-IR and eliminating those with low correlation values. The relevance of a feature f to HOMA-IR was evaluated using the Pearson Correlation Coefficient defined in the following equation:

$$corr(f,HOMA-IR)=\frac{cov(f,HOMA-IR)}{\sigma f\sigma \hspace{0.17em}HOMA-IR}$$ [Equation 1]

where cov(x,y) is the covariance between features x and y, and σx is the standard deviation of feature x.

With the remaining features, all possible combinations (subsets) were generated and the one that produced the best binary clustering using the k-means++ algorithm was selected. The best clustering was defined as the one that minimised the overlap between the HOMA-IR values of the resulting clusters. This process was called the minimum overlap k-means clustering algorithm. Since k-means is known to minimise within-cluster variances, adding the minimum overlap between the HOMA-IR means constraint resulted in a clustering having a double property—samples from the same cluster had similar clinical characteristics (k-means property), and those in two different clusters had significantly different HOMA-IR values (minimum overlap property). Therefore, it was speculated that the two resulting clusters contained subjects with NIR and those at risk of IR, respectively.

The two identified clusters were simply samples of the two populations—individuals at risk of IR and those with NIR. Their respective HOMA-IR means (mean_IR, mean_NIR) and standard deviations (std_IR, std_NIR) were used to estimate the means and standard deviations of the populations they represented as well as the 95% confidence intervals [mean_IR1, mean_IR2] and [mean_NIR1, mean_NIR2] for the estimated means.21 The x-coordinate (cut-off 1) of the intersection point between the Gaussian functions modelled by the means of IR1 and NIR1 along with their standard deviations represented the lower value of the sought cut-off point. While the x-coordinate (cut-off 2) of the intersection point between the Gaussian functions modelled by the means of IR2 and NIR2 along with their standard deviations represented the upper value of the sought cut-off point. The HOMA-IR cut-off value was set to (cut-off 1 + cut-off 2)/2, and the confidence interval to [cut-off 1, cut-off 2]. The main assumption made in these calculations was the normality of the two populations based on the normality of large samples from these populations.

The major processes of the proposed method consisted of the following: first, a list L most correlated variables with HOMA-IR was selected using the Pearson correlation; then, the k-means++ algorithm (k set to 2) was applied to each subset of the list L. The subset producing clusters with the least overlap in terms of HOMA-IR values were selected and the two resulting clusters represented the samples of the two populations. Finally, the intersections of the Gaussian functions modelling the two populations’ HOMA-IR distributions were used to define the sought cut-off point and its confidence interval as explained earlier.

This study was approved by the Medical Research Committee at Sultan Qaboos University. Written and signed or thumb-printed and rubber-stamped informed consent was obtained from each participant or a parent and/or legal guardian if participants were under the age of 18 years.

Results

All calculations were performed using Python and related libraries, including the ML library sklearn (https://scikit-learn.org) and the statistics library scipy.stats (https://docs.scipy.org/doc/scipy/reference/stats.html).

As mentioned earlier, the initial dataset consisted of 1,344 samples. First, samples having missing data in any of the 26 variables were removed. This resulted in a new dataset of 1,003 samples. Then, the outliers (those samples with HOMA-IR values’ z-scores >3) were identified and removed, which resulted in a final dataset size of 798 samples that had valid values for 26 variables (338 males and 460 females).

Correlation values between HOMA-IR and the 26 variables were calculated. Variables with correlation values less than 0.1 were removed, which led to a subset of 16 variables: fasting plasma insulin (INSU0), fasting plasma glucose (SUG0), two-hour postprandial glucose concentration (SUG2), LEPT, waist circumference (WST), body mass index (BMI), VLDL, TG, percentage of fat (PERF), 24-hour DIAST and SYST, HbA1c, CHOL, ALT, human growth hormone (HGH) and FT4. SUG0 and INSU0 were also removed from the list to avoid having a clustering result dominated by these two variables, as they were redundant with the HOMA-IR variable that was included in the clustering process (HOMA-IR = [SUG0 × INSU0]/22.5). The main benefit of the preselection step was that it significantly reduced the search space in the feature selection stage (from 226 subsets to 214 subsets) as well as reduced the noise effect that the non-correlated (and weakly-correlated) variables with HOMA-IR would have created on the clustering results. Table 1 shows the correlation values between HOMA-IR and the 26 variables.

Table 1.

Correlation coefficients between the variables and HOMA-IR

Parameter	R	P value
INSU0 in mM	0.975	<0.0001
SUG0 in mM	0.442	<0.0001
LEPT in ng/mL	0.389	<0.0001
Waist circumference in cm	0.337	<0.0001
Body mass index in kg/m2	0.322	<0.0001
Percentage of fat	0.297	<0.0001
DIAST in mmHg	0.273	<0.0001
HbA1c in %	0.270	<0.0001
SUG2 in mM	0.250	<0.0001
SYST in mmHg	0.228	<0.0001
TG in mM	0.206	<0.0001
VLDL in mM	0.205	<0.0001
ALT in U/L	0.189	<0.0001
Total cholesterol in mM	0.145	<0.0001
Plasma cortisol in nmol/L	0.097	0.014
ALP in U/L	0.091	0.014
Age in years	0.076	0.0001
TSH in mU/L	0.057	0.091
Gender	0.012	0.800
HDL in mM	−0.060	0.002
Plasma albumin in g/dL	−0.060	0.023
IgE in U/mL	−0.066	0.043
Total plasma proteins in g/L	−0.079	0.087
Total bilirubin in μmol/L	−0.095	0.001
HGH in ng/mL	−0.108	0.066
FT4 in μg/dL	−0.147	<0.0001

HOMA-IR = homeostatic model assessment-insulin resistance; INSU0 = fasting plasma insulin; SUG0 = fasting blood glucose; LEPT = plasma leptin; DIAST = diastolic blood pressure; HbA1c = glycated haemoglobin; SUG2 = two-hour blood glucose; SYST = systolic blood pressure; TG = plasma triglycerides; VLDL = very-low-density lipoprotein; ALT = alanine aminotransferase; ALP = alkaline phosphatase; TSH = thyroid-stimulating hormone; HDL = high-density lipoprotein; Ig = immunoglobulin; HGH = human growth hormone; FT4 = free thyroxine.

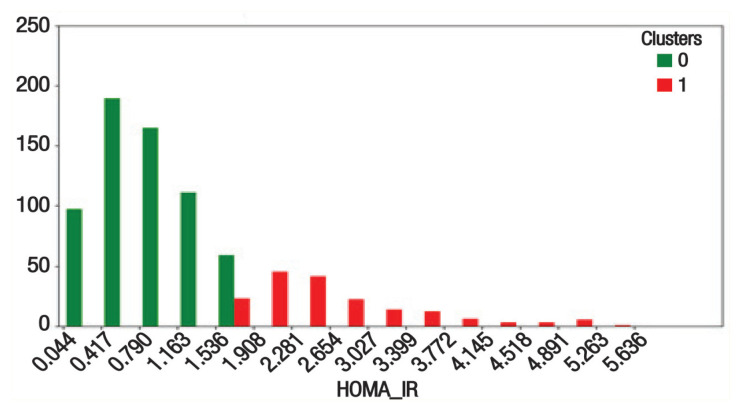
All possible subsets of the 14 variables (i.e. 16,383 subsets) were generated to which the proposed minimum overlap k-means clustering algorithm was applied. The variable values were codified using reference ranges that were consistent with the recommendations of the World Health Organization and the Omani Ministry of Health.22,23 Figure 1 shows the HOMA-IR histograms of the two reference groups, which were produced as a result of the clustering. The first group consisted of 621 individuals representing a sample of the non-insulin-resistant population; it had a HOMA-IR mean of 0.88 ± 0.43. The second group consisted of 177 individuals representing a sample of individuals at risk of IR; it had a HOMA-IR mean of 2.71 ± 0.88. The optimal subset of variables producing these groups consisted of HOMA-IR, VLDL, SYST and ALT.

Figure 1.

Homeostatic model assessment-insulin resistance histograms with insulin resistance (IR) reference group (red) and non-IR reference group (green).

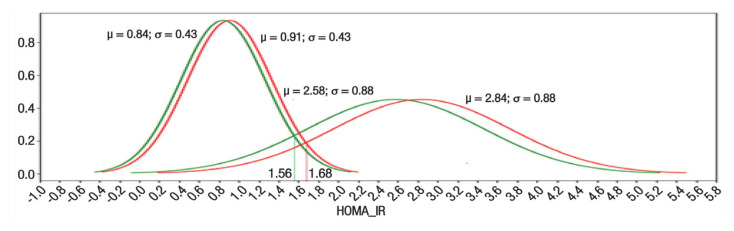
Normality tests on the HOMA-IR values of the two groups were conducted using the Python function (scipy.stats.normaltest) that implements D’Agostino and Pearson’s algorithm. This algorithm combines skew and kurtosis to produce an omnibus test of normality.24 The results obtained (P = 6.74e⁻¹⁴for the normal group and P = 2.06e⁻¹² for the IR group) confirmed the normality of the two samples’ HOMA-IR values. Their respective HOMA-IR means and standard deviations (0.88 ± 0.43, 2.71 ± 0.88) were used to estimate the 95% confidence intervals of the NIR and IR population’s means (0.84–0.91 and 2.58–2.84, respectively).21 The x-coordinate of the intersection of the Gaussian functions modelled by (0.84, 0.43), (2.58, 0.88) was equal to 1.56. It represented the lower value of the sought HOMA-IR cut off, and the x-coordinate of the intersection of the Gaussian functions modelled by (0.91, 0.43), (2.84, 0.88) was equal to 1.68. It represented the upper value of the sought HOMA-IR cut off. The HOMA-IR cut-off was set to (1.56 + 1.68)/2 = 1.62 and the confidence interval to (1.56–1.68). Figure 2 shows the Gaussians’ graphs that modelled the two populations and their intersections.

Figure 2.

Gaussian graphs modelling the two populations and used for estimating the homeostatic model assessment-insulin resistance cut-off value.

Ideally, such work should be evaluated either by testing its performance on a labelled dataset (dataset where the samples are labelled as insulin resistant or normal) or using a longitudinal study where the validity of the predictions made by the method is checked against the evolution of the health status of the subjects. Since none of these possibilities were available to the researchers, alternative means were adopted for the evaluation.

As an alternative way to quantitatively evaluate the performance of the method, it was used to solve a similar problem where labelled data were available. The chosen problem was related to the definition of the SUG0 cut-off for identifying prediabetes, since this study’s dataset could be used and the samples could be labelled based on the standard cut-off value of 5.6 mM. The SUG0-correlated variables were first identified, and the minimum overlap k-means clustering algorithm was applied to them. The SUG0 means and standard deviations of the resulting reference groups were used to estimate the means and standard deviations of the corresponding populations and to evaluate the cut-off value. The identified SUG0 cut-off was 5.89 mM and the 95% confidence interval was (5.83–5.95). This study’s dataset was then segmented using both cut-off points (5.6 mM and 5.89 mM) and the level of agreement between the two classifications was evaluated. Two agreement measures were used;25 the first was the percent agreement, which was defined as follows:

$$\frac{number\hspace{0.17em}of\hspace{0.17em}agreements}{number\hspace{0.17em}of\hspace{0.17em}total\hspace{0.17em}scores}$$ [Equation 2]

The second was the Kappa agreement, which was defined as follows:

$$K=\frac{Pr(a)-Pr(e)}{1-Pr(e)}$$ [Equation 3]

where Pr(a) is the observed agreement, and Pr(e) is the chance agreement. The percent agreement value was 0.89 and the Kappa agreement value was 0.72. These results demonstrated the suitability of the proposed method for defining the SUG0 cut-off for prediabetes identification.

A Chi-square test for independence shows how two sets of data are independent of each other. In this study, a Chi-square test was used to check the relationship between the segmentation resulting from the identified HOMA-IR cut-off value (1.62) and the segmentation produced by the standard SUG2 cut-off value (7.8 mM) for identifying pre-diabetes. Table 2 summarises the distribution of the samples among the four categories (Non-IR who are normal, Non-IR who are pre-diabetic or diabetic, IR who are normal and IR who are pre-diabetic or diabetic).

Table 2.

Distribution of this study’s dataset samples among the four categories defined by the HOMA-IR cut-off value of 1.62 and SUG2 cut-off value of 7.8 mM

	Two-hour Glucose
	Non-diabetic	Prediabetic and diabetic
NIR (below the cut-off value of 1.62)	523	63
IR (above the cut-off value of 1.62)	162	50

HOMA-IR = homeostatic model assessment-insulin resistance; SUG2 = two-hour postprandial glucose concentration; NIR = normal insulin sensitivity; IR = insulin resistance.

The Python function (scipy.stats.chi2_contingency) returned a Chi-square statistic of 21.10, and a P value of 4.37e^−6, which indicated a strong relationship between the two segmentations.

Table 3 shows the means and standard deviations of the clinical variable values for the two groups resulting from the segmentation by a HOMA-IR threshold of 1.62. The table shows that the mean values of almost all variables were higher for the IR group (i.e. group at risk of IR) than the NIR group (i.e. the normal group). The only variable that showed an opposite relationship was FT4.

Table 3.

Characteristics of the identified clusters

Variable*	Mean ± SD		P value
	IR	NIR
INSU0 in mM	9.82 ± 3.16	3.49 ± 1.61	<0.001
SUG0 in mM	5.84 ± 0.77	5.32 ± 0.54	<0.001
SUG2 in mM	6.89 ± 2.32	6.21 ± 1.52	<0.001
Plasma leptin in ng/mL	37.67 ± 25.66	22.56 ± 19.32	<0.001
Body mass index in kg/m2	26.96 ± 4.94	24.11 ± 4.59	<0.001
Waist circumference in cm	86.34 ± 14.47	78.20 ± 12.53	<0.001
VLDL in mM	0.52 ± 0.28	0.41 ± 0.23	<0.001
TG in mM	1.15 ± 0.62	0.91 ± 0.51	<0.001
Percentage of fat	26.89 ± 10.41	21.93 ± 9.65	<0.001
DIAST in mmHg	82.82 ± 8.61	77.58 ± 8.47	<0.001
SYST in mmHg	124.65 ± 11.73	118.87 ± 11.89	<0.001
HbA1c in %	5.47 ± 0.70	5.15 ± 0.63	<0.001
Total cholesterol in mM	4.96 ± 1.05	4.72 ± 1.03	<0.001
ALT in U/L	22.25 ± 12.43	17.97 ± 9.85	<0.001
FT4 in μg/dL	10.14 ± 1.64	10.48 ± 1.75	<0.001
HOMA-IR	2.54 ± 0.89	0.83 ± 0.39	<0.001

SD = standard deviation; IR = insulin resistance; NIR = normal insulin sensitivity; INSU0 = fasting plasma insulin; SUG0 = fasting blood glucose; SUG2 = two-hour blood glucose; VLDL = very-low-density lipoprotein; TG = plasma triglycerides; DIAST = diastolic blood pressure; SYST = systolic blood pressure; HbA1c = glycated haemoglobin; ALT = alanine aminotransferase; FT4 = free thyroxine; HOMA-IR = homeostatic model assessment-insulin resistance.

^*Only variables with a correlation with HOMA-IR ≥0.1 are shown.

Discussion

The proposed ML approach was adopted to define the HOMA-IR cut-off value for identifying individuals at risk of IR among an Omani Arab population living in Nizwa. A cut-off value of 1.62 was obtained as optimum. This value was within the range of literature-reported cut-off values (1.44–3.87) for different ethnic groups [Table 4].

Table 4.

Some HOMA-IR cut-offs reported in the literature2,11,32,33

Country	Subjects	Cut-off	Statistical Method
Sweden	Healthy population	2.00	75th percentile
France	Healthy population	3.80	75th percentile
Brazil	Healthy adult subjects	2.77	90th percentile
USA	Healthy adult subjects (Hispanic and non-Hispanic)	2.73	66th percentile
USA	Cross-sectional sample of adults	3.80	ML (clustering)
Portugal	Non-obese non-diabetic adults	2.33	90th percentile
Iran	Healthy adult subjects	3.87	ROC classified by MetS
Iran	Cross-sectional sample (healthy and diabetic adult women)	2.63	95th percentile
China	Healthy children and adolescents	3.00	95th percentile
Japan	Cross-sectional sample of non-diabetic adults	1.70	ROC classified by MetS
Caucasus	Rural population, non-diabetic	2.29	75th percentile
Thailand	Cross-sectional sample	1.55	90th percentile
China (Hong Kong)	Cross-sectional sample	1.44	75th percentile
		2.03	75th percentile 90th percentile

HOMA-IR = homeostatic model assessment-insulin resistance; ML = machine learning; ROC = receiver operating characteristic; MetS = metabolic syndrome.

The experiment described in this work demonstrated the validity of the proposed approach in identifying cut-off values in cases of problems similar to the one under investigation.

The result of the Chi-square test (P = 4.36e⁻⁶) indicated a strong relationship between the two segmentations: IR/NIR and normoglycaemia/hyperglycaemia. Table 2 shows that 89.25% of the NIR individuals (523 out of 586) were characterised as having normoglycaemia as expected from the NIR individuals. It also shows that there were 162 (23.65%) individuals with normoglycaemia who were included in the IR category. As in the case of Altuve et al., it was argued by the researchers that these might have been the subjects who were developing IR or already had the metabolic disorder.13 Such individuals should undergo a more thorough medical investigation starting with a euglycaemic clamp, which might help in identifying IR individuals at an early stage and, therefore, prevent or at least delay the onset of chronic disease.

The mean values in the IR group were larger than those in the NIR group for almost all variables [Table 3]. The only variable that showed an opposite relationship was FT4. A quick review of the literature indicated that these results aligned with the outputs of several research works. For example, a seven-year longitudinal study conducted on 1,734 subjects concluded that converters to T2DM had significantly higher BMI, WST, TG concentration and BP than non-converters.26 IR was found to be associated with increased TG and VLDL levels and decreased HDL levels.27,28 Liver function tests are frequently ordered for patients with MetS to monitor the development of non-alcoholic fatty liver disease. A study involving 1,309 non-diabetic individuals concluded that increased m-glutamyltransferase and ALT were biomarkers of both systemic and hepatic IR.29 Additionally, sub-clinical hypothyroidism is associated with higher insulin levels and IR, which correlates positively with thyroid-stimulating hormone (TSH) levels and negatively with FT3 and FT4.30 LEPT is a body fat biomarker that can play a major role as a predictor of IR syndrome; a study conducted on 80 individuals showed a positive relationship between LEPT and IR syndrome.31

The current study described an unsupervised ML approach for assessing the IR condition using the clinical data of a sample representing an ethnic group while taking into consideration the confounding variables. It allowed the researchers to estimate a cut-off HOMA-IR value that identifies individuals at risk of IR. This threshold can be used as a warning signal, suggesting that subjects with HOMA-IR greater than the identified threshold should undergo the hyperinsulinaemic (euglycaemic) clamp to confirm or reject the prognosis. It is the responsibility of the clinician to ensure that the health condition of the patient permits conducting the proposed test. To further validate this cut-off value, a longitudinal follow-up study on healthy subjects is warranted to study the prognostic power of the cut-off value in identifying subjects who develop T2DM. Moreover, it would be more informative to apply this approach to samples of the major ethnic groups living in different parts of Oman. The output of such research work is expected to define ethnicity-dependent HOMA-IR cut-off values.

Finally, it should be indicated that the proposed approach depends on three important factors: 1) at the data collection level, samples included in the dataset should be statistically representative of the ethnic group under investigation; 2) during the implementation of the code associated with the proposed approach, there is a need to properly tune two parameters—the one identifying the outliers that are to be removed and the one indicating the correlated variables that are to be kept; 3) the normality (or near normality) of the IR and NIR populations.

Conclusion

The HOMA-IR model is a good indicator of insulin sensitivity in population studies and displays ethnic variability in the cut-off values. In this study, a cut-off value of 1.62 ± 0.06 was identified in an Arab Omani population living in Nizwa. This approach will be helpful in future population studies concerning T2DM and MetS.