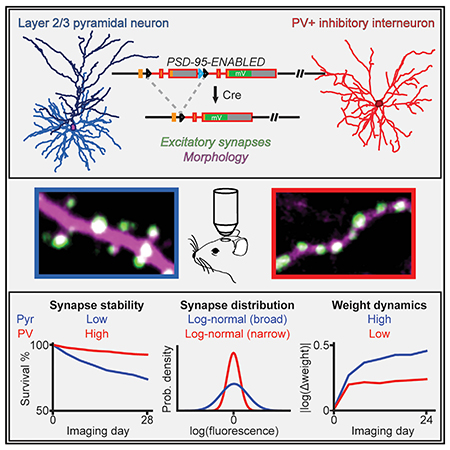
SUMMARY
Cortical function relies on the balanced activation of excitatory and inhibitory neurons. However, little is known about the organization and dynamics of shaft excitatory synapses onto cortical inhibitory interneurons. Here, we use the excitatory postsynaptic marker PSD-95, fluorescently labeled at endogenous levels, as a proxy for excitatory synapses onto layer 2/3 pyramidal neurons and parvalbumin-positive (PV+) interneurons in the barrel cortex of adult mice. Longitudinal in vivo imaging under baseline conditions reveals that, although synaptic weights in both neuronal types are log-normally distributed, synapses onto PV+ neurons are less heterogeneous and more stable. Markov model analyses suggest that the synaptic weight distribution is set intrinsically by ongoing cell-type-specific dynamics, and substantial changes are due to accumulated gradual changes. Synaptic weight dynamics are multiplicative, i.e., changes scale with weights, although PV+ synapses also exhibit an additive component. These results reveal that cell-type-specific processes govern cortical synaptic strengths and dynamics.
Graphical Abstract
In brief
Melander et al. use a genetic strategy to visualize excitatory neuronal connections that cannot be inferred from morphology, and they monitor how the connections change over weeks in mice. They find distinct characteristics between synapses onto cells that “suppress” brain activity and those onto cells that “excite” brain activity.
INTRODUCTION
The formation, plasticity, and rewiring of synaptic connections are fundamental to brain function. Toward understanding these processes, the organization and dynamics of excitatory synapses onto cortical pyramidal (Pyr) neurons have been studied extensively using dendritic spines as a proxy (Bhatt et al., 2009; Grutzendler et al., 2002; Holtmaat and Svoboda, 2009; Trachtenberg et al., 2002). In vivo two-photon imaging of morphologically identified dendritic spines has revealed several principles: their sizes are log normally distributed and change in a multiplicative manner (i.e., the magnitude of spine size change is proportional to the spine size) (Buzsáki and Mizuseki, 2014; Loewenstein et al., 2011; Ziv and Brenner, 2018). Furthermore, the addition and elimination of such spiny synapses correlate with the acquisition of certain learned behaviors (Hayashi-Takagi et al., 2015; Hofer et al., 2009; Holtmaat et al., 2006; Johnson et al., 2016; Xu et al., 2009; Zuo et al., 2005a). These observations are foundational to our current understanding of brain function (Buzsáki and Mizuseki, 2014).
In vivo imaging of spines, however, is limited in several aspects. First, the majority of excitatory synapses onto cortical inhibitory interneurons, such as parvalbumin-positive (PV+) interneurons, are shaft synapses (Harris and Shepherd, 2015; Huang, 2014; Kim et al., 2017; Lee et al., 2012), which cannot be identified using morphology under light microscopy (Goldberg et al., 2003; Keck et al., 2011; Sancho and Bloodgood, 2018). Even within Pyr neurons, not all excitatory synapses reside on dendritic spines (Knott et al., 2006; Santuy et al., 2018). Little is known about the distribution and dynamics of these synapses, particularly in vivo. Second, spines that protrude axially are difficult to distinguish under light microscopy. Third, although spine size is correlated with synaptic size and strength, such correlations are not perfect (Fortin et al., 2014; Harris and Stevens, 1989; Matsuzaki et al., 2001; see also Figure 1G).
Figure 1. Visualizing endogenous PSD-95 as a proxy for the presence and weight of excitatory synapses onto Pyr and PV+ dendrites.
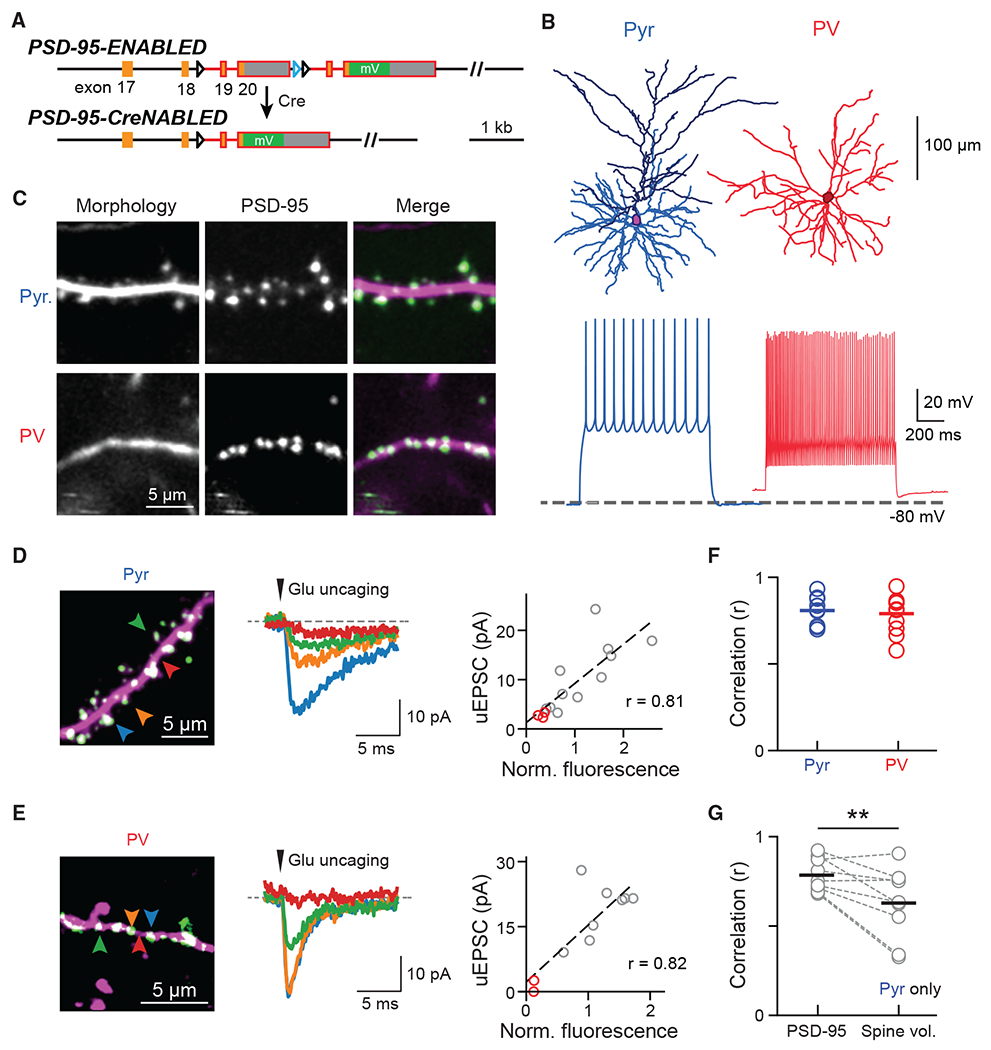
(A) Schematic of the ENABLED/CreNABLED strategy for tagging endogenous PSD-95 with mVenus in a Cre-dependent manner.
(B) Representative cellular reconstructions (top) and spike trains (bottom) elicited via supra-threshold current steps from Pyr (left) and PV+ (right) neurons.
(C) Representative two-photon images of dendritic segments from Pyr neurons (top) and PV+ interneurons (bottom). PSD-95 (green) and dendritic morphology (magenta) were labeled simultaneously.
(D and E) Two-photon glutamate uncaging experiment for Pyr (D) and PV+ (E) neurons in acute brain slices. Left: representative images; colored arrowheads correspond to the traces shown. Middle: Example uEPSCs (average of 5–10 trials). Right: correlation between integrated PSD-95mVenus fluorescence intensities with uEPSC of the example dendrite. Red circles indicate stimulations at locations without PSD-95mVenus.
(F) Correlation (Pearson’s r) between PSD-95mVenus fluorescence and uEPSC amplitude within individual dendrites. Averages are: 0.81 ± 0.03, n (dendrites/cells/animals) = 9/6/3 for Pyr neurons; and 0.79 ± 0.03, n = 11/8/3 for PV+ neurons.
(G) Correlation between uEPSC amplitudes and PSD-95mVenus fluorescence versus spine volume in Pyr neurons. Only clear, laterally protruding spines were included. Averages are 0.78 ± 0.03 for PSD-95mVenus and 0.63 ± 0.07 for spine volume, n (dendrites/animals) = 9/3. One-sided Wilcoxon signed-rank test: p = 0.009, W = 42.
See also Figure S1.
To overcome these limitations, several studies have overexpressed an essential postsynaptic scaffolding protein at excitatory synapses, PSD-95, tagged with a fluorescent protein (FP), to visualize synapses in vivo (Cane et al., 2014; Gray et al., 2006; Sheng and Kim, 2011; Sun et al., 2019; Villa et al., 2016). However, the overexpression of PSD-95 results in aberrant synaptic function and defective synaptic plasticity (Béïque and Andrade, 2003; Ehrlich and Malinow, 2004; Elias et al., 2008; Schnell et al., 2002).
Herein, we used a conditional knockin strategy called endogenous labeling via exon duplication (ENABLED) to label PSD-95 at its endogenous levels with the yellow FP mVenus (Fortin et al., 2014) in layer 2/3 (L23) cortical spiny Pyr neurons and aspiny PV+ inhibitory interneurons. We found that PSD-95 abundance provides an accurate assessment of synaptic weight in both cell types. Chronic in vivo two-photon imaging in the mouse barrel cortex revealed that the distribution and dynamics of excitatory synapses were cell type specific. Although excitatory synapses onto both neuronal types exhibited log-normal weight distributions, those onto PV+ dendrites were less heterogeneous and, on average, contained lower levels of PSD-95 than those onto Pyr neurons. PV+ synapses were also more stable than their Pyr counterparts. Furthermore, although synaptic weight changes were largely multiplicative, changes in PV+ neurons also exhibited a significant additive, weight-independent component. Notably, our results indicated that large, rapid changes in synaptic weights were rare, and substantial changes were primarily the accumulation of incremental changes over time. These results document the organization and dynamic properties of shaft excitatory synapses onto inhibitory interneurons in vivo and reveal that cell-type-specific processes govern cortical synaptic strengths and dynamics.
RESULTS
Cell-type-specific visualization of synapses via endogenous PSD-95 labeling
To visualize excitatory synapses onto different neuronal types, we employed the PSD-95-ENABLED mouse, in which PSD-95 is tagged at endogenous levels by mVenus in a Cre-dependent manner without altering synaptic function or plasticity (Figure 1A) (Fortin et al., 2014). To simultaneously visualize neuronal morphology, we crossed PSD-95-ENABLED mice with Ai9, a Cre-dependent tdTomato reporter line (Madisen et al., 2010). Cre was introduced into L23 Pyr neurons sparsely via in utero injection of adeno-associated virus (AAV) and into PV+ neurons by further crossing with the PV-IRES-Cre mouse (Hippenmeyer et al., 2005). Immunohistochemical experiments showed that PV-IRES-Cre mice reliably and specifically expressed Cre in PV+ neurons in the barrel cortex of adult mice (Figure S1A) (see also Pfeffer et al., 2013). Labeled neurons exhibited morphological and electrical properties characteristic of the corresponding neuronal type (Figure 1B). PSD-95mVenus was imaged in vivo via a cranial window in the mouse barrel cortex (Figure 1C). The cortical location was verified using functional intrinsic-signal imaging (Figure S1B).
PSD-95mVenus puncta represent excitatory synapses
To validate that PSD-95mVenus puncta represented functional excitatory synapses, we recorded labeled neurons in acute brain slices while performing two-photon focal glutamate uncaging. Uncaging adjacent to PSD-95mVenus puncta triggered excitatory postsynaptic currents (uEPSCs) in both L23 Pyr neurons and PV+ interneurons (Figures 1D and 1E), which were blocked by the AMPA (α-amino-3-hydroxy-5-methyl-4-isoxazolepropionic acid) receptor antagonist NBQX (Figure S1C). In contrast, uncaging at dendritic locations absent of PSD-95mVenus puncta gave little to no current (Figures 1D, 1E, and S1D). Importantly, the uEPSC amplitude correlated strongly with the fluorescence intensity of the corresponding PSD-95mVenus punctum for both neuronal types (Figures 1D–1F), indicating that PSD-95mVenus intensity at a given punctum is an accurate measurement of the “weight” of the synapse.
In Pyr neurons, synaptic weight has been shown to correlate with spine volume (Matsuzaki et al., 2001), and our data also indicated that PSD-95mVenus intensity correlated with spine volume (Figure S1E). However, it is difficult to measure the volume of spines overlapping with the dendritic shaft. In addition, the orientation of spines may change, which can result in errors when tracking the same spines (Figure S1F). Importantly, even for clear laterally protruding spines, uEPSCs were better correlated with integrated PSD-95mVenus fluorescence than spine volume (Figure 1G). Taken together, these data indicate that PSD-95mVenus puncta label functional glutamatergic synapses onto both L23 Pyr neurons and in PV+ interneurons, and that PSD-95mVenus fluorescence can be used to track synapses and estimate synaptic weights more precisely than the spine can.
The weight distribution of excitatory synapses is cell type specific
We asked whether the distribution of excitatory synaptic weights, as inferred from PSD-95mVenus intensity, differed between the two cell types in vivo. Segments of Pyr and PV+ dendrites residing in layer 1 (<100 μm from pia) of the barrel cortex of adult mice (~p70, both sexes) were imaged under anesthesia (Figure 1C). Twelve of 14 Pyr dendrites were traced back to their somas, all of which resided in L23 (125–300 μm from pia). Tracing of PV+ dendrites was not possible due to high dendritic density. Imaged dendritic stretches were manually scored to identify and classify each PSD-95mVenus puncta (Figure S2; see STAR Methods).
Pyr dendrites exhibited a higher synapse density than PV+ dendrites (Pyr: 1.02 ± 0.06 synapse/μm, PV+: 0.87 ± 0.02 synapse/μm; two-sided t test: t = 2.9, p < 0.01) (Figure 2A). In Pyr dendrites, PSD-95mVenus was nearly exclusively present as punctate signals, and most (~96%) spines contained PSD-95mVenus puncta. Importantly, about 1/3 of PSD-95mVenus puncta colocalized with the dendritic shaft in Pyr dendrites (Figures 1C and 2A). These puncta likely represented both axially protruding spines and shaft excitatory synapses, with the latter constituting approximately 20% of total excitatory synapses in cortical Pyr neurons (Fiala and Harris, 1999; Knott et al., 2006; Santuy et al., 2018). In contrast, excitatory synapses onto PV+ dendrites mostly (97.5%) resided on the dendritic shaft. Nevertheless, small spines containing PSD-95mVenus puncta can be occasionally found (Figures 2A and S1G) (see also Keck et al., 2011; Sancho and Bloodgood, 2018).
Figure 2. Population characteristics of the organization of synapses and their weights.
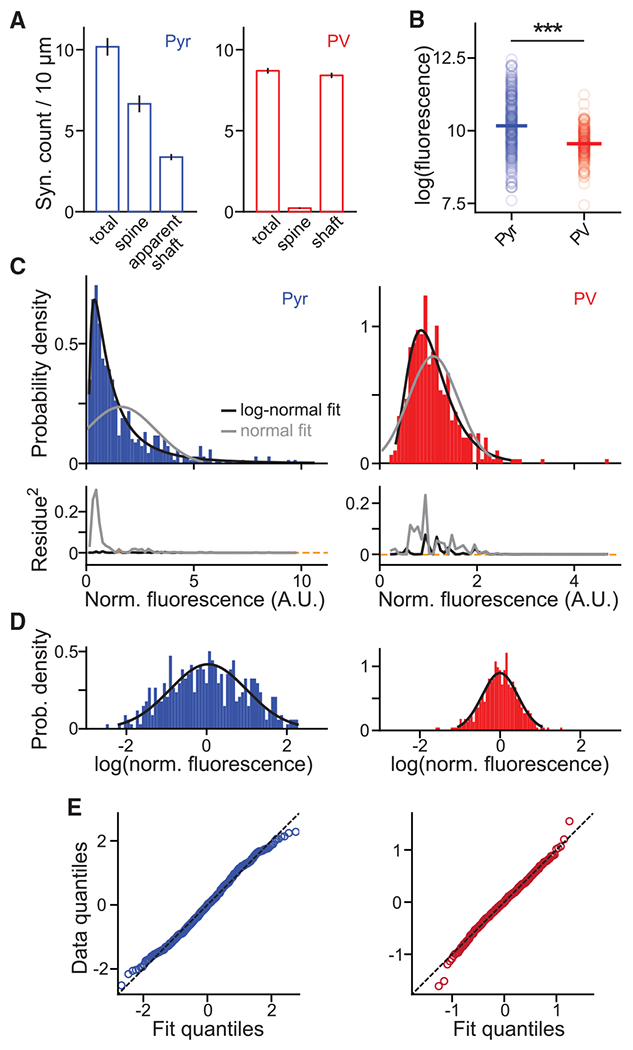
(A) The density of PSD-95mVenus puncta, and the fractions on laterally protruding spines and of those colocalized with dendritic shafts on Pyr (left) and PV+ (right) dendrites in vivo.
(B) Absolute integrated PSD-95mVenus fluorescence of Pyr and PV+ synapses in the logarithmic scale. Only synapses between 10 and 50 μm beneath the pia are included. Medians are 10.16 ± 0.05 (SEM), n (synapses/dendrites/animals) = 308/9/4 for Pyr, and 9.6 ± 0.04, n = 191/10/7 for PV+. Wilcoxon rank-sum test: p < 0.001, U = 8.28.
(C) Probability density histograms of normalized synaptic PSD-95mVenus fluorescence fitted by log-normal or normal distributions (top) and their squared residues (bottom). n (synapses/dendrites/animals) = 452/14/4 and 409/21/7 for Pyr and PV+, respectively.
(D and E) Histograms of the logarithm of synaptic PSD-95mVenus fluorescence plotted with the best-fit normal distribution (D) and their quantile-quantile plots (E).
All error bars are SEM. See also Figure S2.
We next compared the organization of synapses onto both neuronal types using integrated fluorescence of PSD-95mVenus puncta. Depth-matched synapses onto Pyr neurons were brighter than those onto PV+ neurons (Figures 2B and S1H), suggesting that Pyr excitatory synapses are more enriched for PSD-95 than PV+ synapses. Note that this result does not necessarily mean that PV+ synapses are weaker than Pyr synapses because, although PSD-95mVenus can be used to infer relative weights within a cell type (Figures 1D and 1E), the relationship between PSD-95 abundance and synaptic strength may differ across cell types. For both cell types, the distribution of normalized synaptic weights (see Figure S2) was well fit by a log-normal distribution but less so by a normal distribution (Figures 2C–2E). At the same time, the intensity distribution of Pyr synapses was much broader (full width half maximum of fit in log scale ± 95% confidence level: Pyr, 2.5 ± 0.8; PV+, 0.97 ± 0.08; Figure 2D). These results indicate that the composition and organization of excitatory synapses are cell type specific.
Excitatory synapses onto PV+ interneurons are stable at the month timescale
Previous studies found that a fraction of cortical spiny synapses are added or eliminated over behaviorally relevant timescales (Holtmaat et al., 2006; Xu et al., 2009; Zuo et al., 2005a), and aberrant spine dynamics are associated with certain neurological disorders and neurodegenerative diseases (Guo et al., 2015; He et al., 2017; Murmu et al., 2015; Spires et al., 2005; Tsai et al., 2004). We therefore performed longitudinal imaging in the barrel cortex every 4 days for seven to eight time points (2.5–4 months old, baseline home cage conditions) (Figures 3A and 3B), similar to those previously described (Holtmaat et al., 2006; Trachtenberg et al., 2002). To track synapses precisely, we developed software that permitted the side-by-side comparison and annotation of a given dendritic segment over all time points simultaneously (Figure S2). Each synapse was manually scored for its persistence, addition, or elimination across all time points.
Figure 3. Synapses onto PV+ dendrites are more stable compared to those onto pyramidal dendrites.
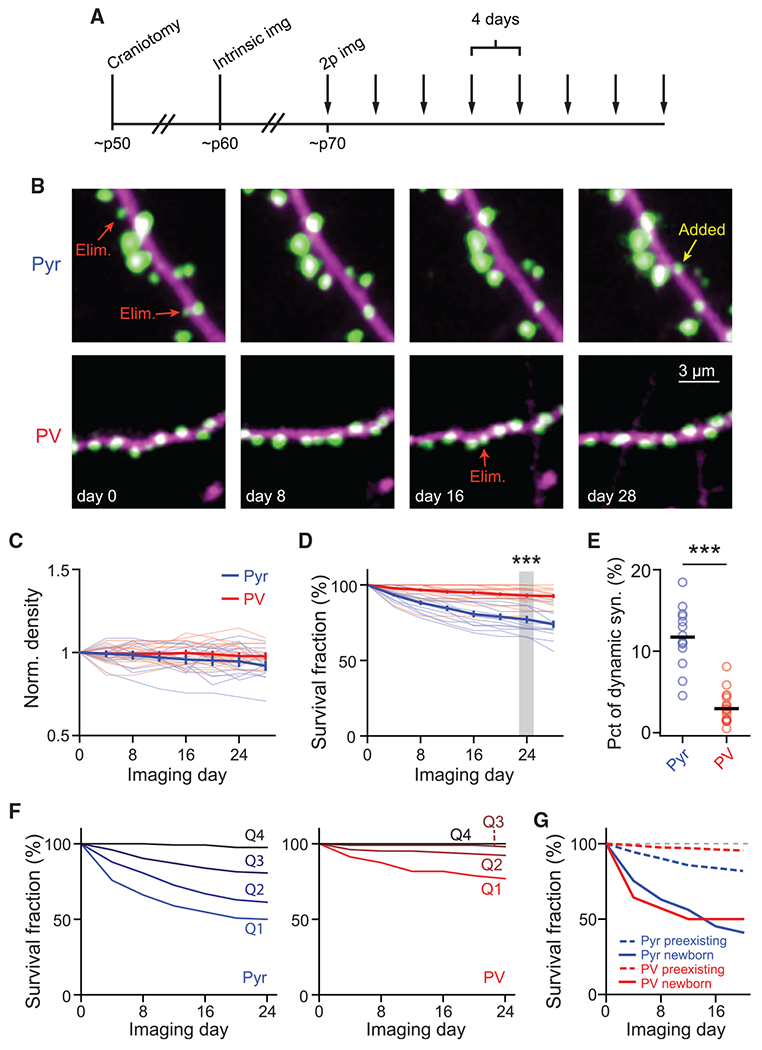
(A) Experimental protocol for longitudinal in vivo experiments.
(B) Representative images of Pyr (top) and PV+ (bottom) dendrites in layer 1 imaged over a month. Arrows indicate representative added and eliminated (Elim.) synapses.
(C) Time course of the synaptic density of Pyr and PV+ dendrites normalized to day 0.
(D) Survival fraction of synapses present on the first imaging session at subsequent time points. n (synapses/dendrites/animals) = 594/14/4 for Pyr and 683/21/7 for PV. Wilcoxon rank-sum test: p < 0.001, U = 4.09.
(E) Percentage of synapses on a dendritic segment that were added or eliminated during a 4-day interval. n (dendrites/animals) = 14/4 for Pyr and 21/7 for PV. Wilcoxon rank-sum test: p < 0.001, U = 4.8.
(F) Survival fractions of four quartiles (from weak to strong: Q1–Q4) of synapses sorted by weight on the first imaging day. n = 124 and 104 synapses/quartile for Pyr and PV+ dendrites, respectively.
(G) Survival fractions of newborn versus preexisting synapses onto Pyr and PV+ dendrites. n = 552, 441, 73, and 14, respectively, for Pyr preexisting, PV+ preexisting, Pyr newborn, and PV+ newborn.
All error bars are SEM. See also Figures S2 and S3.
Synapses on the two neuronal types exhibited distinct patterns of structural plasticity. The total number of synapses per dendritic segment was relatively stable, despite ongoing synaptic additions and eliminations (Figure 3C). Consistent with previous studies (Holtmaat et al., 2005; Ma et al., 2016; Sun et al., 2019; Tjia et al., 2017), Pyr dendrites exhibited a moderate level of synaptic turnover: 23% ± 2% of synapses observed at day 0 were lost at day 24 (Figure 3D), and 12% ± 1% of synapses were added or eliminated between adjacent time points (Figure 3E). In contrast, PV+ dendrites exhibited much lower levels of synaptic turnover (7% ± 1% of the synapses observed at day 0 were lost at day 24, p < 0.001, cf. Pyr dendrites; Figure 3D). The percentage of dynamic synapses onto PV+ dendrites per 4-day window was more than 3-fold lower than that of Pyr dendrites (Figure 3E).
It has been suggested that larger spines are more stable, and that newborn spines are more likely to be eliminated than preexisting spines (Holtmaat et al., 2005; Majewska et al., 2006; Xu et al., 2009; Zuo et al., 2005b). We therefore asked whether synapses with more PSD-95mVenus were more stable by grouping synapses into four quartiles based on their integrated PSD-95mVenus fluorescence on the first imaging day. As assayed using the survival function, smaller synapses were more dynamic than larger ones in both neuronal types (Figure 3F). Even for Pyr dendrites, synapses in the upper-most quartile exhibited little turnover over 24 days. In addition, we found that newborn synapses in both neuronal types were much more likely to be eliminated than preexisting synapses on the same dendrites (Figure 3G). Altogether, these results indicate that the dynamics of synaptic addition and elimination are cell type specific in vivo, with PV+ excitatory synapses being much more stable than those onto Pyr neurons. Furthermore, synaptic turnover in both neuronal types is dominated by smaller and newborn synapses, with stronger and preexisting synapses exhibiting a high degree of stability.
Synaptic weight dynamics are cell type specific
We next examined the evolution of synaptic weights over time, which has been less characterized in vivo. To do so, we pooled data of integrated PSD-95mVenus fluorescence from different dendrites and days together by normalizing individual synapses to the average fluorescence intensity of synapses within the 40th–60th percentile of the corresponding dendrite and time point (Figure S2). This normalization was necessary to correct for inevitable variations in imaging conditions across dendrites, animals, and days (e.g., see Figures S3A and S3B) and appeared more robust than an alternative approach that normalized mVenus intensity to the cytosolic reporter tdTomato due to the differential bleaching between PSD-95mVenus and tdTomato (Figures S3C and S3D).
We asked whether synaptic weight changes were cell type specific. Only synapses from the 25th–75th percentiles were analyzed to minimize the effect of low signal-to-noise ratios associated with the smallest synapses. For both neuronal types, the average weight of synapses that persisted throughout all imaging time points did not change over time (Figure 4A), presumably because of balanced weight increases and decreases across synapses. Indeed, when the absolute weight changes were analyzed (Figure 4B), the weights of individual synapses deviated from their original weight substantially. The degree of weight change, however, was cell type specific, with Pyr synapses exhibiting greater changes than PV+ synapses (Pyr: 0.46 ± 0.03 U on the natural log scale at day 24, corresponding to ~58% changes; PV+: 0.24 ± 0.02 U, corresponding to ~27% changes; Figure 4B).
Figure 4. Markov-chain model reveals cell-type-specific principles of synaptic weight dynamics.
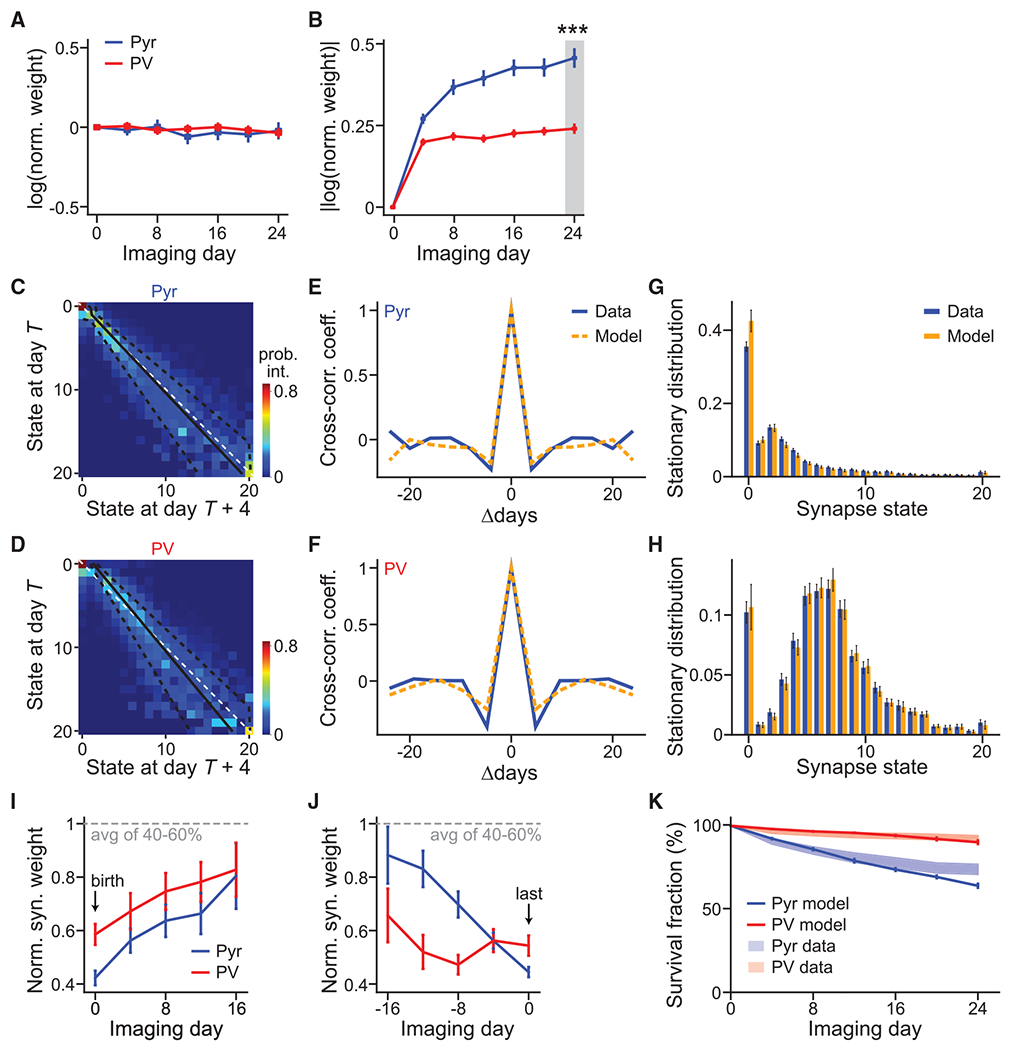
(A and B) Average of signed (A) and absolute (B) synaptic weight changes relative to day 1 in the natural log scale. n = 174 for Pyr and 190 for PV+.
(C and D) The Markov-state transition matrices of Pyr (C) and PV+ (D) synapses. The unity line (white dashed) and fitted Kesten process with its ± 1 standard deviation (solid and dashed black lines, respectively) are superimposed. The Markov process was fit using 678 and 451 high-quality synapses for Pyr and PV+ dendrites, respectively.
(E and F) Cross-correlation coefficient between synaptic weight changes from day T to day T+4 and those from day T+Δ to day T+Δ+4, averaged over all synapses and days.
(G and H) Steady-state distributions of synaptic weight for Pyr(G) and PV+ (H), as computed from experimental data (blue) or as predicted by the Markov model (orange). Error bars denote standard deviation across 30 bootstrap runs.
(I and J) Addition-triggered (I) and elimination-triggered (J) averages of weight trajectories, aligned to birth and death, respectively. n (synapses) = 225 (Pyr birth), 271 (PV+ birth), 45 (Pyr death), and 50 (PV+ death).
(K) The survival fraction as a function of time predicted by the Markovian transition model (solid lines) compared with experimental data (shades, SEM; same as Figure 3D) for both Pyr and PV+ synapses. n (synapses) = 721 (Pyr model), 468 (PV+ model), 496 (Pyr data), and 416 (PV+ data).
All error bars are SEM. See also Figures S2 and S4.
Markov model of weight dynamics predicts cell-type-specific stationary synaptic weight distributions
We then modeled the synaptic dynamics as a Markovian process. Synaptic weights were binned into 21 states, including one zero-strength state, to yield a Markov-state transition matrix (Figures 4C and 4D) between adjacent time points. Each row denoted the probability distribution of synaptic weights on the next observation day (T + 4) for synapses within a weight bin on the current day (T). To test the validity of our Markov assumption, we correlated changes in synaptic weights from day T to day T+4 with those from day T+Δ to day T+Δ+4. For both neuronal types, the cross-correlation of synaptic weight changes between two pairs of observation days dropped sharply as the separation Δ increased (Figures 4E and 4F), both in the data and in our model. In other words, knowledge of synaptic weights 8 days ago did not provide more information about the current weights, as measured via linear correlation, than did knowledge 4 days ago. These results indicate that the underlying dynamics of synaptic strengths can be modeled as a Markovian process on our experimental timescales.
Above, we found that synaptic weights adopted a cell-type-specific log-normal distribution (Figures 2C and 2D). However, the underlying mechanism was poorly understood. Our Markov models predicted steady-state distributions of synaptic weights that were specific to the corresponding cell type. Indeed, when drastically different starting distributions were evolved by iterating through the experimentally derived Markovian transition matrices, the distributions converged to the predicted stationary distribution of the corresponding neuronal type (Figures S4A and S4B). This predicted stationary distribution was very similar to the corresponding empirically measured distribution (Figures 4G and 4H). These results suggest that the synaptic weight distribution is intrinsically determined by the dynamics of synapses onto each neuronal type.
Gradual accumulative changes predict synapse addition and elimination
A noticeable feature of the Markov transition matrices was that synaptic changes were gradual, with very few large jumps, as evidenced by the concentration of higher transition probabilities near the diagonal (Figures 4C and 4D). One prediction of such Markovian dynamics is that synapses are both born into and die in states of weak strength. To test this prediction, we aligned synaptic weight dynamics by their addition or elimination day. For both cell types, new synapses were added with low synaptic weights, with those that survived gradually gaining strength over weeks (Figure 4I). At the same time, synapses were eliminated from a low synaptic weight state (Figure 4J). These results suggest that cortical synaptic changes, if they happen, are gradual, and large changes (e.g., the formation or loss of a strong synapse) arise primarily through the accumulation of multiple small events over the course of weeks.
To further test the ability of the Markov model to make predictions about synapse elimination over a prolonged period of time, we examined whether it could predict the survival function of synapses. Iterations through the model over multiple observation periods resulted in a survival function well matched with the experimental data for each neuronal type (Figure 4K). Overall, these and the above results indicate that our Markovian synaptic dynamics model accurately predicts fundamental cell-type-specific properties that emerge over a month-long timescale.
Synaptic weight changes are not always solely multiplicative
Our data provide the opportunity to test two opposing models of synaptic weight dynamics (Loewenstein et al., 2011). In the multiplicative model, unobserved synaptic activity leads to a synaptic change that is proportional to the synaptic weight. In contrast, the additive model hypothesizes that the magnitude of synaptic change is independent of the current weight. The Markov-state transition matrix of both Pyr and PV+ dendrites exhibited an increasingly widened central band as the previous day’s synaptic weights increased (Figures 4C and 4D). This indicates that the average magnitude of synaptic change grows with existing synaptic strength, suggesting a multiplicative component in both neuronal types. This conclusion is further supported by fitting the synaptic weights with a more constrained Kesten process consisting of both additive and multiplicative components (Hazan and Ziv, 2020; Statman et al., 2014; Ziv and Brenner, 2018). Under such a framework, the intercept of the linear fit to weight changes (wt+1 – wt) would indicate an additive component, whereas a linear correlation between the variance of synaptic weight changes with the square of the current synaptic weight indicates a multiplicative component. The fit Kesten process produced a widening central band structure with increasing state (overlaid black lines in Figures 4C and 4D), indicating consistency between the Kesten and the Markov transition models. Synapses onto both cell types have a clear multiplicative component (Figure S4D). Interestingly, the Kesten fit also revealed a significant additive component for PV+ synapses, as evidenced by deviation from the diagonal line in Figure 4D and the positive y-intercept in Figure S4C. Furthermore, removing the additive component from the Kesten model resulted in a poor fit for PV+ synapses (r2 = 0.03 and 0.89 without and with the additive component, respectively), but only moderately affected the fit for Pyr synapses (r2 = 0.53 and 0.62 without and with the additive component, respectively). Together, these analyses suggest that, although excitatory synaptic weight changes are multiplicative, synapses onto PV+ dendrites also have a significant additive component.
DISCUSSION
Here, we examined the in vivo dynamics of an understudied cortical synapse type, excitatory shaft synapses onto inhibitory interneurons, and compared them with L23 Pyr synapses by using endogenously labeled PSD-95mVenus as a marker for excitatory synapses. We found that synaptic organization and plasticity are cell type specific. Furthermore, we demonstrated several principles of synaptic dynamics that may have implications for both the experimental and computational understanding of synaptic plasticity. First, the stationary synaptic weight distribution is cell type specific and is intrinsically associated with the day-to-day synaptic dynamics. Second, the majority of synaptic weight changes in the cortex are incremental. Third, although synaptic weight changes follow multiplicative dynamics in both cell types, there is a cell-type-specific additive component present only in PV+ dendrites.
Synaptic marker proteins of both excitatory and inhibitory synapses, introduced via protein overexpression, have been previously imaged in vivo (Cane et al., 2014; Chen et al., 2012; Gray et al., 2006; van Versendaal et al., 2012; Villa et al., 2016). However, overexpression can cause undesirable effects, making results difficult to interpret at times. The ENABLED strategy provides a viable way to visualize endogenous proteins that is potentially expandable to other proteins. There are also parallel efforts to develop alternative strategies to label endogenous proteins for live imaging (Gross et al., 2013; Mikuni et al., 2016; Nishiyama et al., 2017; Rimbault et al.,2019, 2021; Suzuki et al., 2016; Zhong et al., 2021). Although each of these strategies has its own strengths and limitations, endogenous protein imaging will likely constitute an important research avenue in the future.
Previous studies of synaptic dynamics in vivo using spine imaging have generated important insights. However, axially protruding spines and shaft excitatory synapses are difficult to see. Our study overcame this by visualizing the synaptic molecular contents together with morphology. Our results confirm several previous conclusions from spine imaging, including the log-normal distribution and multiplicative dynamics of spiny synapses. A log-normal distribution of synaptic weights suggests that a small percentage of large synapses provide a critical ensemble of neuronal connections, while the smaller synapses provide fine adjustment to the circuit and repertoire for plasticity (Buzsáki and Mizuseki, 2014). Interestingly, the largest synapses in both neuronal types were rarely eliminated (Figure 3F), possibly reflecting that the critical neuronal circuit formed by strong synapses is highly stable. Furthermore, we found that there is rich information within the synaptic weight dynamics. Our results suggest that weight dynamics are well described by small, analog changes, and larger weight changes, including synaptic additions and eliminations, are the cumulative result of these smaller events. Overall, our results call for attention to such analog changes in future studies.
We found that shaft excitatory synapses onto PV+ interneurons exhibit markedly different characteristics compared with the spiny synapses onto Pyr neurons. Shaft excitatory synapses onto PV+ neurons are packed at a lower density, contain a lower PSD-95 content, and exhibit a narrower range of synaptic weights. They are also less dynamic than Pyr synapses. These cell-type-specific properties may be intrinsic to the geometric constraints of the synapse type. Spines effectively increase the cylindrical volume along the dendrite, allowing more synapses to be packed per unit dendritic length. Spiny synapses also enable the dendrite to sample a larger space and interact with more presynaptic partners. Regardless of the underlying mechanism, these observations add to the notion that the plasticity of cortical synapses is specific to the postsynaptic cell. The uniformity and stability of synapses onto PV+ neurons are consistent with their function as maintainers of stable excitation and inhibition (E/I) balance in the brain (Antoine et al., 2019; Xue et al., 2014; Zhou et al., 2014). In contrast, the larger range in synaptic weights and higher turnover of Pyr synapses may allow for the rewiring of cortical circuits when needed. Interestingly, the synaptic weight distribution is determined by the day-to-day dynamics of each synapse type. This may be the result of underlying homeostatic mechanisms (Turrigiano, 2012) and contribute to the cortical E/I balance.
Finally, classic models of synaptic plasticity often treat potentiation and depression events additively (Gerstner et al., 1996; Hopfield, 1982; Song et al., 2000). However, recent studies (Loewenstein et al., 2011) suggest that in vivo spine size changes in L23 Pyr neurons might be multiplicative. Here, by directly measuring the molecular content of the postsynaptic density and using it to assess synaptic weight, we And that both Pyr and PV+ neurons exhibit multiplicative dynamics, suggesting that multiplicative scaling may be a general rule of synaptic plasticity. Interestingly, PV+ synapses, but not Pyr synapses, also exhibited an additive component, providing in vivo evidence that additive and multiplicative mechanisms are not mutually exclusive (Ziv and Brenner, 2018), and the degree of their co-existence is cell type specific.
Limitations of the study
Our study is limited by the finite signal-to-noise ratio and resolution of imaging conditions. FP signals at endogenous PSD-95 levels are much lower than those achieved by overexpression. The finite resolution of two-photon microscopy makes it challenging to resolve synapses that are close to each other. These may result in an overestimation of synapse dynamics and an underestimation of synapse density. Future labeling with brighter and more photostable fluorophores, together with new microscopic tools with better resolutions, may overcome these limitations. It should be noted that our 4-day imaging interval may miss dynamic events happening at faster timescales. There are also many interneuron types other than PV+ neurons, which may exhibit different synapse organization and dynamics. These latter two points call for additional studies in the future.
STAR★METHODS
RESOURCE AVAILABILITY
Lead contact
Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Haining Zhong (zhong@ohsu.edu).
Materials availability
This study did not generate new unique reagents.
Data and code availability
The original longitudinal imaging data are available at the Brain Image Library (https://download.brainimagelibrary.org/87/f8/87f8546092155279/), and are publicly available as of the date of publication. The accession number is listed in the Key resources table.
Manual scoring software can be found at https://github.com/HZhongLab/synscore. All code necessary to perform the analyses within this paper can be found at https://github.com/HZhongLab/melander_nayebi_2021. These codes are publically available as of the date of publication. The DOI is listed in the Key resources table.
Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Antibodies | ||
| Monoclonal Anti-Parvalbumin Antibody | Millipore Sigma | P3088-100UL |
| Hoechst 33342 Solution | ThermoFisher | Cat#62249 |
| Bacterial and virus strains | ||
| AAV2/1-Syn-Cre | Custom preparation from Boris Zemelman | N/A |
| Chemicals, peptides, and recombinant proteins | ||
| Chlorprothixene hydrochloride | Sigma-Aldrich | Cat# C1671 |
| Isoflurane | Piramal | NDC# 66794-019 |
| MNI-Glutamate | Tocris | Cat# 1490 |
| Optical Adhesive NOA81 | Norland | Cat# 2018 |
| Deposited data | ||
| Longitudinal in vivo imaging data of PSD-95-CreNABLED dendrites of Pyr and PV+ neurons | This paper | Brain Image Library ID 87f8546092155279; https://download.brainimagelibrary.org/87/f8/87f8546092155279/ |
| Experimental models: Organisms/strains | ||
| C57BL/6 mouse | Charles River | C57BL/6NCrl; RRID: IMSR_CRL:27 |
| PV-IRES-Cre (B6.129P2-Pvalbtm1(cre) Arbr/J) | Jax | 008069; RRID: IMSR_JAX:008069 |
| Ai9 (B6.Cg-Gt(ROSA)26Sortm9 (CAG-TdTomato)Hze/J) | Jax | 012569; RRID: IMSR_JAX:012569 |
| Software and algorithms | ||
| MATLAB | MathWorks | RRID: SCR_001622; https://www.mathworks.com |
| ScanImage | Svoboda Lab, HHMI Janelia / Vidrio Technologies | RRID: SCR_014307 |
| synScore | This paper | https://github.com/HZhongLab/synscore |
| Custom analysis codes | This paper | https://zenodo.org/record/5553667#.YXI6BfrMItI |
| R | n/a | RRID:SCR_001905; https://cran.r-project.org |
| Python Programming Language (2.7 and 3.6) | n/a | RRID: SCR_008394; https://www.python.org |
EXPERIMENTAL MODEL AND SUBJECT DETAILS
Animal handling and experimental protocols were performed in accordance with the recommendations in the Guide for the Care and Use of Laboratory Animals of the National Institutes of Health and were approved by the Institutional Animal Care and Use Committee (IACUC) of the Oregon Health & Science University (#IS00002792).
Animals
Mice strains used in this study included: PSD-95-ENABLED (JAX #026092), parvalbumin-IRES-Cre (PV-IRES-Cre; JAX #008069), Ai9 (JAX #007909). All mice were backcrossed to C57BL/6J (Charles River) background for at least five generations. PSD-95-ENABLED;Ai9;PV-IRES-Cre triple heterozygous mice were bred for simultaneously visualizing PSD-95 and cell morphology in PV+ interneurons. PSD-95-ENABLED;Ai9 double heterozygous embryos were subjected to in utero injection of AAV to their lateral ventricles to broadly and sparsely label a subset of neurons throughout the brain, including L23 pyramidal neurons in the barrel cortex. All mice were housed in standard laboratory conditions in groups of 2 or more with ad libitum access to food and water at all times inside a vivarium with a 12-hour light/dark cycle. Experiments were performed during both the light and dark cycles. For longitudinal studies of synapse dynamics in vivo, a glass window was installed to the mouse skull at p45-p65 via craniotomy. In vivo two-photon imaging was performed at least two weeks post window installation in both male and female mice under isoflurane anesthesia. Some PV+ dendrites lacked PSD-95mVenus expression in their entirety, presumably due to incomplete Cre-recombination efficiency at the PSD-95-ENABLED allele (Fortin et al., 2014), and were not further examined.
Acute Slice
Preparation of acute slices for two-photon glutamate uncaging and whole-cell patch-clamp recording was performed as previously described (Fortin et al., 2014). Briefly, coronal brain slices (300 μm thick) were prepared from adult mice typically at p21-p28 using ice-cold cutting solution containing the following (in mM): 110 choline chloride, 25 NaHCO3, 25 glucose, 2.5 KCl, 7 MgCl2, 0.5 CaCl2, 1.25 NaH2PO4, 11.5 sodium ascorbate, and 3 sodium pyruvate and being gassed with 95% O2/5% CO2. For experiments involving the PV-IRES-Cre driver line P56 – P59 mice were used since parvalbumin (PV) expression turns on relatively late during development (Bergmann et al., 1991; Nitsch et al., 1990). Slices were incubated in a recovery chamber with gassed artificial cerebrospinal fluid (ACSF) containing (in mM): 127 NaCl, 25 NaHCO3, 25 D-glucose, 2.5 KCl, 1 MgCl2, 2 CaCl2, and 1.25 NaH2PO4at 34 – 36°C for 30 minutes and then at room temperature (RT) for up to 8 hours. Individual slices were subsequently transferred to a recording chamber mounted on an upright microscope (Olympus BX51WIF) that was circularly perfused with freshly oxygenated ACSF at RT.
METHOD DETAILS
Electrophysiology and Glutamate Uncaging
Whole-cell voltage-clamp recordings of uncaged excitatory post-synaptic currents (uEPSCs) from layer 2/3 neurons were carried out using an Axonpatch 200B amplifier (Molecular Devices) at RT. Electrophysiological signals were filtered at 2 kHz, and digitized and acquired at 20 kHz with custom software written in MATLAB. Borosilicate pipettes (2.8 – 6 MΩ; Warner Instruments) were filled with potassium gluconate-based internal solution containing (in mM): 120 potassium gluconate, 2 MgCl2, 0.1 CaCl2, 5 NaCl, 4 Na2-ATP, 0.3 Na-GTP, 15 Na-phosphocreatine. 10 HEPES, 1.1 EGTA, 0.01 Alexa-594 (Invitrogen), 3 mg/ml biocytin; pH 7.3; 290 mOsm. AMPA receptor mediated uEPSCs were isolated by addition of (in μM) 1 TTX, 10 SR 95531, 5 CPP in the ACSF to block voltage-gated Na channels, GABA-A receptors, and NMDA receptors, respectively. Cells were held at −70 mV throughout the course of the experiment.
In vitro two-photon imaging and uncaging were performed on a custom-built two-photon microscope controlled by ScanImage (Pologruto et al., 2003). Two Ti:sapphire lasers (MaiTai, Spectra Physics) were combined with polarized optics and passed through the same set of scan mirrors and objective for simultaneous imaging and uncaging. A water-immersion objective from Olympus (60X, 1.0 NA) was used. mVenus and tdTomato fluorescence were separated using a Chroma 565dcxr dichroic mirror and isolated using HQ510/70 (Chroma), and 630/92 (Semrock) or 635/90 (Chroma) emission filters, respectively.
For glutamate uncaging, 2.25 mM MNI-L-glutamate (Tocris Bioscience) was added to the ACSF. Glutamate uncaging was induced by applying 70 – 100 mW (measured at the back focal plane of the objective) light pulses of 0.2 – 0.5 ms duration at 720 nm. Approximately 60% of the power was transmitted though the objective. The power was held constant within the same field of view but was changed empirically depending on the tissue depth. The uncaging depth in the slice was restricted to 10 – 80 μm from tissue surface. To elicit uEPSCs the uncaging beam was positioned either at the tip of chosen spines or adjacent to the identified PSD-95mVenus puncta. uEPSC amplitudes were measured by averaging 5 – 10 trials per position elicited at a frequency of 0.1 Hz. To reliably determine uEPSC amplitudes, traces were smoothened using a sliding 2ms window. Peak uEPSC amplitude was calculated as the difference between the peak current amplitude and mean current amplitude over a 25 ms window prior to uncaging. Current amplitudes smaller than baseline + 3 times standard deviation were considered noise and were set to zero. To calculate charge transfer, a time window for integration was determined per dendrite. A mean onset time, time between 10% of the peak amplitude to peak, mean decay time, time between peak and 10% of the peak amplitude, and mean peak time were calculated based on all uEPSCs recorded within a given dendrite. The integration window was placed between the mean onset time and mean decay time, relative to the mean peak time. The charge transfer was corrected using a baseline charge transfer, calculated using the same time integration window placed before uncaging.
Cellular Reconstructions
For reconstruction of cell morphology, we performed intracellular recording with biocytin in the recording pipet. The slices were fixed overnight in 4% paraformaldehyde and 4% sucrose in 0.1 M phosphate buffer (PB, pH 7.4). Slices were washed in PB for 60 minutes followed by a 40-minute treatment with 3% peroxide, to reduce endogenous peroxidase activity, and a 20-minute wash in PB. Biocytin-filled cells were visualized using an avidin-biotinylated horseradish peroxidase complex reaction (Vectastain-Elite, Vector Laboratories). Slices were incubated in 1% Vectastain-Elite with 0.5% triton in PB, first for 30 minutes at room temperature followed by overnight at 4°C and 1.5 hours at room temperature. Slices were washed for 1 hour in PB and incubated in 1 mg/ml 3,3′-diaminobenzidine (DAB, Sigma-Aldrich) with 0.0002% CoCl2 and 0.0004% (NH4)2Ni(SO4)2 at 4°C. Chromogenic reaction was started by adding peroxide (0.0003% final concentration) and kept incubating until cell morphology was clearly visible. The chromogenic reaction was stopped by extensive washes in PB. Slices were mounted on gelatinized microscope slides and left to dry overnight, or until dry, in an 80% humidity chamber. Subsequently, slices were dehydrated in steps of 10% EtOH from 10% to 90%, twice in 100% EtOH, and xylenes, each step for 10 minutes. Slices were embedded and coverslipped in Eukitt. Cellular morphology was reconstructed using Neurolucida (MBF bioscience) at 1000x magnification. Reconstructions were not corrected for shrinkage.
In Utero Viral Transfection
For sparse labeling of layer 2/3 pyramidal neurons, we performed in utero viral transfection as previously described (Fortin et al., 2014). Briefly, 1 μl of AAV2/1 virus expressing Cre under the Synapsin promoter was diluted to an empirically-determined level (1:20 – 1:50) optimal for sparse labeling of dendrites in layer 1. The diluted virus was injected into the lateral ventricles of E15.5 pregnant mice.
Cranial Window Surgery
Surgical implantation of the cranial window was performed similarly to Fortin et al., 2014, with several exceptions. Briefly, adult mice were anesthetized with isoflurane (induction: 4 percent in 1.0 L/min medical grade oxygen, maintenance: 1.5 percent in 0.2 L/min medical grade oxygen) and given Dexamethasone (20 μl of 4 mg/ml solution) and Buprenorphine (80 μl of 0.03 mg/ml solution) to mitigate post-surgical inflammation and pain, respectively. Using sterile procedures, the scalp was retracted, and a craniotomy was performed over the left barrel cortex (from bregma, 1.2 mm posterior, 3.4 mm lateral). The drilling site was irrigated with sterile cortex buffer (in mM: NaCl 125, KCl 5, Glucose 10, HEPES 10, CaCl2 2, MgSO4 2, pH 7.4) to clear bone dust from the site and to prevent overheating of the neuropil. After removing the flap of bone, a customized glass window (laser cut by Potomac Photonics, assembled in-house) was gently pushed into the craniotomy. The glass window consisted of three layers of glass fused with Norland Optical Adhesive 61. These layers consisted of the following: a 3.5 mm circular coverslip on bottom, an inner ‘donut’ ring (ID: 3 mm, OD: 3.5 mm) in the middle, and an outer ‘donut’ ring (ID: 3mm, OD: 5 mm) on top. The ‘donut’ optical window assembly allows for high-resolution imaging through a single-piece of cover glass, and provides gentle pressure on the cerebral cortex to mitigate motion-induced artifacts during imaging. The glass window was sealed in place, along with a custom aluminum head-bar, using a mixture of cyanoacrylate glue and dental cement. The animal was allowed to recover from surgery in a heated cage and was monitored until anesthesia had worn off. A second dose of Buprenorphine and Dexamethasone was administered 24 hours after the cranial-window surgery.
Intrinsic-Signal Imaging
Approximately one week after cranial window implantation, experimental mice were sedated with chlorprothixene (50 μl of 100 μg/ml solution) and lightly anesthetized with isoflurane (1% in 0.2 l/min medical grade oxygen). Intrinsic signal imaging was performed as previously described (Ma et al., 2018; Masino et al., 1993), through the glass ‘donut’ apparatus. A piezo actuator coupled to a large vinyl surface was used to stimulate the majority of the subject’s whiskers. Controls were occasionally conducted by performing the experiment without stimulating the piezo actuator; in these experiments, no intrinsic signal responses were ever observed. Confirmatory experiments (Figure S1B) stimulated single barrels by loading a single whisker into a glass capillary tube coupled to the piezo.
Longitudinal in vivo Two-Photon Imaging
After allowing the animal to recover from the cranial window implantation surgery for at least two weeks, dendrites in layer I of barrel cortex (S1) were imaged using a custom-built two-photon microscope based on the MIMMS design (Janelia) for in vivo imaging. The time course of longitudinal two-photon imaging commenced at least 5-days after intrinsic signal imaging, to mitigate off-target effects of chlorprothixene and whisker stimulation. Throughout the experiment, the presence of barbering was monitored by imaging the whisker length of all animals; animals that were barbered during the course of the experiment were excluded from analysis. Animals were anesthetized with isoflurane and mounted under a custom-built two-photon microscope via an aluminum headbar installed during the craniotomy surgery. All imaging was performed through a Nikon 16x, 0.8 NA objective. On the first day, PSD-95mVenus and tdTomato positive dendrites were imaged in layer 1 in areas of the window that yielded barrel-responses during intrinsic signal imaging. Images of dendrites were acquired at 512 × 512 pixels, a scan speed of 2 ms/line, and a field-of-view of ~45 μm. No averaging was performed during image acquisition, but we oversampled in the z dimension (0.8 μm/step) which allowed for a running average in the z dimension. The laser power at specimen was held constant for all imaging-sessions of the same field of view and never exceeded 45 mW at sample. Presented images have been filtered by a Gaussian filter with a sigma of 1 pixel (~0.09 μm).
QUANTIFICATION AND STATISTICAL ANALYSIS
General Statement / Statistics
Data analyses were performed with custom programs written in MATLAB (Mathworks), Python 2.7 and 3.8 (https://www.python.org/downloads/release/python-380/), or R (https://cran.r-project.org). Sample sizes are indicated in text or figure legends and *p ≤ 0.05, **p ≤ 0.01, and ***p ≤ 0.001. Unless indicated otherwise, statistical tests and distributional best-fits were computed via the scipy package in Python 3.6.
Four-Dimensional Synapse Scoring and ROI Generation
PSD-95mVenus puncta were identified manually and their persistence and dynamics were scored in custom MATLAB software that allowed for the simultaneous visualization of the same synapse in three dimensions over all 8 experimental time points (Figure S2). Only dendrites with high imaging quality over all imaging sessions were included in the analysis. At each time point, PSD-95mVenus puncta were classified as residing on the shaft of the dendrite or on a spine. To reduce noise associated with analyzing four-dimensional two-photon imaging datasets, we implemented a “two-day rule”: for a synapse to be scored as eliminated, it must be absent for at least two consecutive imaging sessions. Spiny synapses were defined as synapses that protruded laterally from the dendritic shaft, with a clear emanating structure evident from the tdTomato channel. Shaft synapses were identified as PSD-95mVenus puncta that colocalized with the dendritic shaft. Due to the relatively poor axial resolution of two-photon microscopes, we only classified spines based on their geometry, relative to the dendrite, in the X-Y dimensions: all axially protruding spines were thus classified as shaft synapses.
After initial scoring for the presence and persistence of each synapse, ellipsoid ROIs were generated for each synapse and manually adjusted to ensure proper fit. Changes in the ROI size were mirrored across all imaging-days for a given synapse, ensuring that measures of changing intensity were not subject to changes in ROI size.
Weight Extraction
To compute the weight of a synapse, we first excluded all manually scored synapses that were compromised by either a) proximity to nearby synapses or b) motion artifact. We then used elliptical ROIs generated manually in custom scoring software. Next, we searched in the axial-plane (within a defined window), to find a synapse’s center-of-mass and adjusted the z-position of the synaptic ROI if necessary. Next, the average pixel value of a user-designated background ROI was subtracted from each pixel within the ROI. Additionally, we subtracted tdTomato’s bleedthrough in the mVenus collection channel. Experiments in tdTomato-only dendrites estimated this value at ~2%, which was used for these experiments. Next, the background- and bleedthrough-subtracted pixels within an ROI were integrated across 5 axial-planes (±1.6 μm). These values were normalized to the average of the 40th to 60th percentile of all such intensities on a given dendrite for a single day. This normalization assumed that the average synaptic strength along a dendritic segment is stable across dendrites and across days, but it was necessary to pool data from different dendrites and dates together due to different imaging conditions, such as subtle variations in imaging depths and variable influences by local blood vessels, and day-to-day variations in the sample (e.g., see Figures S3A and S3B). Using the average of the 40th to 60th percentile over mean or median reduces the effect of outliers (in the case of mean) and variations of individual values (in the case of median). Empirically, using other ranges for normalization (e.g., 30%–70% or the mean of all dendrites) gave qualitatively similar results (data not shown). We used this approach over an alternative strategy that normalizes using the fluorescence of a dendritic cytosolic marker, because the expression of PSD-95mVenus and tdTomato might not be stoichiometric across cells, and mVenus and tdTomato were differentially bleached over days (Figures S3C and S3D).
Markov-Chain Model Fitting Procedure
We binned the non-zero synaptic strengths into 40 equal-width bins, but grouped the last 21 bins into a single bin given that the counts were small in these last 20 bins. These bins constituted the “states” of the Markovian transition matrix, resulting in 21 total states (20 states of non-zero synaptic strength and one state reserved for a strength of 0). The number of bins was empirically determined. Other numbers of bins gave qualitatively similar results. The Markovian transition matrix was fit using a maximum likelihood estimator (MLE), in which for each pair of consecutive observation days (t and t+1), we counted the number of times the synaptic strength changed from state s1 on day t to state s2 on day t+1, for all pairs of states s1 and s2. We then normalized these counts to form a conditional probability distribution such that Σs2 P(wt+1 = s2|wt = s1) = 1. These transition probabilities were used as the elements of the Markov transition matrix. Each row of this matrix indicates the initial state s1 and each column indicates the final state s2. Thus, each row is a conditional probability distribution of future state given current state and sums to 1. The model was fit to 678 synapses from 14 dendrites across 4 animals for Pyr neurons, and 451 synapses from 21 dendrites across 7 animals for PV+ neurons.
Stationary Distribution
The stationary distribution was obtained from the right eigenvector of the Markov transition matrix with an eigenvalue of 1. This same stationary distribution can also be obtained from iterating the Markov dynamics many times from an arbitrary initial distribution. We compared this to the empirical stationary distribution fit using a maximum likelihood estimator (MLE), where the synaptic strengths were binned into the same states as used for the Markovian transition matrix, and the number of occurrences of synaptic strengths (aggregated across observation days) was counted in each bin, normalized by the total number of synapses.
To generate error bars, the original data were sampled with replacement from 30 bootstrap runs. In each bootstrap run, the data were fit with a Markov transition matrix to obtain the stationary distribution from the eigenvector (model, as described above), as well as fit by the empirical stationary distribution (experimental).
To generate Figures S4A and S4B, we started from a distribution over the 21 Markov states (including the 0 state), and then iterated the Markov chain to produce the next distribution over states.
Cross-correlation Coefficient of Weight Changes
Once the Markovian transition matrix had been established, we sampled from the chain starting at the stationary distribution. Although the Markovian transition matrix returned discrete states at each time point, we converted those states back to continuous synaptic strengths by uniformly sampling between the minimum and maximum synaptic strength values within that state bin. This procedure resulted in a continuous valued trajectory of synaptic strengths S for each synapse in the original dataset.
We then computed the cross-correlation coefficient on both S and the original dataset W(both of which were matrices of size, number of synapses N x total observation days T). First, the consecutive weight changes were computed in W, given by vt = wt - wt-1, resulting in the matrix V, and in S, , resulting in the matrix . The cross correlation was then computed from these consecutive weight change matrices. For a given increment of observation time Δ,
where f can either be the matrix V or the matrix . The “cross-correlation coefficient” was given by CCf(Δ) = Cf(Δ)/Cf(0), in order to attain a maximum value of 1.
Survival Fraction
For the simulated survival fraction in Figure 4K, we generated a continuous valued trajectory of synaptic strengths S from the Markovian transition matrix (as described above), but starting from the distribution of synaptic strengths from the first day to match the original data. The survival fraction was then computed both in the model and in the data as the fraction of synapses on each observation day that persisted from the original set of synapses on the first day. In the survival fraction simulations, synapses could only enter and exit the “0” state once to simulate synapse addition and elimination, respectively.
Kesten Model
A Kesten process is given by wt+1 = εt·wt + ηt, which can be rewritten as wt+1 = wt + (εt – 1)·wt + ηt, where wt is the synaptic size at time t and εt and ηt are random variables that can be drawn from any distribution (we set them to be Gaussians, as explained below). We set αt = εt – 1, so Δwt = (εt – 1)·wt + ηt = αt·wt + ηt. We assumed that αt and ηt were random processes as they were the results of unobserved pre- and post-synaptic activities. We simply modeled them as Gaussians, whereby αt ~N(at, bt) and ηt ~N(ct, dt). Here N(a,b) denotes a Gaussian distribution with mean a and variance b. As a result, Δwt ~N·(at·wt + ct, bt·wt2 + dt). We binned the weights wt in order to get an approximate distribution for the synaptic strengths at day t, and then plotted the average value of the consecutive weight change < Δwt > = at·wt + ct, and its variance Var(Δwt) = bt·wt2 + dt, versus the average (across synapses in that bin), wt, and the square of this average, wt2, respectively. This allowed us to first determine respectively if at, bt, ct, and dt are indeed independent of momentary synaptic strength wt (and can therefore be treated as constants in a linear regression), as well as their corresponding values.
To perform this linear regression, we binned the (nonzero) synaptic strengths, across synapses and observation days, into 20 bins with roughly equal numbers of elements, which for synapses onto the pyramidal cell type resulted in ~165 synaptic strength values per bin, and for those onto the PV cell type resulted in ~125 synaptic strength values per bin. We then computed Δwt = wt+1 - wt, for all synaptic strength values wt in that bin, from which we further computed < wt > , < wt > 2, < Δwt >, and Var(Δwt) per bin. These four values per bin were then linearly regressed, namely < Δwt > versus < wt > and Var(Δwt) versus < wt > 2 – yielding the coefficients a, b, c, and d, as described above.
Supplementary Material
Highlights.
Chronic in vivo imaging of excitatory shaft synapses via endogenous PSD-95 labeling
Synaptic weights are log normally distributed on PV+ and pyramidal neurons
PV+ synapses are more stable and less heterogeneous than pyramidal synapses
Synaptic weight distributions are intrinsically set by cell-type-specific dynamics
ACKNOWLEDGMENTS
We thank Dr. Wenzhi Sun, Dr. Na Ji, Dr. Vijay Iyer, Dr. Joseph Wekselblatt, Dr. Cris Niell, Dr. Vivek Unni, Daniel Flickinger, and Valerie Osterberg for help with surgeries, hardware, and software for in vivo two-photon imaging; Dr. Daniel O’Connor for intrinsic imaging setup; and Dr. Emmeke Aarts for pilot data analyses not included in this manuscript. We thank Drs. Lei Ma, Vivek Unni, and Yi Zuo for critical comments for the manuscript. This work was supported by three NIH BRAIN Initiative awards (to H.Z. and T.M.), U01NS094247, R01NS104944, and RF1MH120119; an NINDS R01 grant R01NS081071 (to T.M.); an NINDS R21 grant R21NS097856 (to H.Z.); awards from the Simons and James S. McDonell Foundations (to S.G.); and an NSF CAREER award (to S.G.).
Footnotes
SUPPLEMENTAL INFORMATION
Supplemental information can be found online at https://doi.org/10.1016/j.celrep.2021.109972.
DECLARATION OF INTERESTS
H.Z. is the inventor of the PSD-95-ENABLED mouse, which has been licensed to several companies. This potential conflict of interest has been reviewed and managed by OHSU.
REFERENCES
- Antoine MW, Langberg T, Schnepel P, and Feldman DE (2019). Increased Excitation-Inhibition Ratio Stabilizes Synapse and Circuit Excitability in Four Autism Mouse Models. Neuron 101, 648–661.e4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Béïque JC, and Andrade R (2003). PSD-95 regulates synaptic transmission and plasticity in rat cerebral cortex. J. Physiol 546, 859–867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bergmann I, Nitsch R, and Frotscher M (1991). Area-specific morphological and neurochemical maturation of non-pyramidal neurons in the rat hippocampus as revealed by parvalbumin immunocytochemistry. Anat. Embryol. (Berl) 184, 403–409. [DOI] [PubMed] [Google Scholar]
- Bhatt DH, Zhang S, and Gan WB (2009). Dendritic spine dynamics. Annu. Rev. Physiol 71, 261–282. [DOI] [PubMed] [Google Scholar]
- Buzsáki G, and Mizuseki K (2014). The log-dynamic brain: how skewed distributions affect network operations. Nat. Rev. Neurosci 15, 264–278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cane M, Maco B, Knott G, and Holtmaat A (2014). The relationship between PSD-95 clustering and spine stability in vivo. J. Neurosci 34, 2075–2086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen JL, Villa KL, Cha JW, So PTC, Kubota Y, and Nedivi E (2012). Clustered dynamics of inhibitory synapses and dendritic spines in the adult neocortex. Neuron 74, 361–373. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ehrlich I, and Malinow R (2004). Postsynaptic density 95 controls AMPA receptor incorporation during long-term potentiation and experience-driven synaptic plasticity. J. Neurosci 24, 916–927. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Elias GM, Elias LAB, Apostolides PF, Kriegstein AR, and Nicoll RA (2008). Differential trafficking of AMPA and NMDA receptors by SAP102 and PSD-95 underlies synapse development. Proc. Natl Acad. Sci. U S A 105, 20953–20958. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fiala JC, and Harris KM (1999). Dendrite structure. In Dendrites, Stuart G, Spruston N, and Häusser M, eds. (Oxford University Press; ), pp. 1–34. [Google Scholar]
- Fortin DA, Tillo SE, Yang G, Rah JC, Melander JB, Bai S, Soler-Cedeño O, Qin M, Zemelman BV, Guo C, et al. (2014). Live imaging of endogenous PSD-95 using ENABLED: a conditional strategy to fluorescently label endogenous proteins. J. Neurosci 34, 16698–16712. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerstner W, Kempter R, van Hemmen JL, and Wagner H (1996). A neuronal learning rule for sub-millisecond temporal coding. Nature 383, 76–81. [DOI] [PubMed] [Google Scholar]
- Goldberg JH, Tamas G, Aronov D, and Yuste R (2003). Calcium microdomains in aspiny dendrites. Neuron 40, 807–821. [DOI] [PubMed] [Google Scholar]
- Gray NW, Weimer RM, Bureau I, and Svoboda K (2006). Rapid redistribution of synaptic PSD-95 in the neocortex in vivo. PLoS Biol. 4, e370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gross GG, Junge JA, Mora RJ, Kwon HB, Olson CA, Takahashi TT, Liman ER, Ellis-Davies GCR, McGee AW, Sabatini BL, et al. (2013). Recombinant probes for visualizing endogenous synaptic proteins in living neurons. Neuron 78, 971–985. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grutzendler J, Kasthuri N, and Gan WB (2002). Long-term dendritic spine stability in the adult cortex. Nature 420, 812–816. [DOI] [PubMed] [Google Scholar]
- Guo L, Xiong H, Kim JI, Wu YW, Lalchandani RR, Cui Y, Shu Y, Xu T, and Ding JB (2015). Dynamic rewiring of neural circuits in the motor cortex in mouse models of Parkinson’s disease. Nat. Neurosci 18, 1299–1309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris KD, and Shepherd GMG (2015).The neocortical circuit: themes and variations. Nat. Neurosci 18, 170–181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harris KM, and Stevens JK (1989). Dendritic spines of CA 1 pyramidal cells in the rat hippocampus: Serial electron microscopy with reference to their biophysical characteristics. J. Neurosci 9, 2982–2997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hayashi-Takagi A, Yagishita S, Nakamura M, Shirai F, Wu YI, Loshbaugh AL, Kuhlman B, Hahn KM, and Kasai H (2015). Labelling and optical erasure of synaptic memory traces in the motor cortex. Nature 525, 333–338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hazan L, and Ziv NE (2020). Activity dependent and independent determinants of synaptic size diversity. J. Neurosci 40, 2828–2848. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He CX, Cantu DA, Mantri SS, Zeiger WA, Goel A, and Portera-Cailliau C (2017). Tactile defensiveness and impaired adaptation of neuronal activity in the Fmr1 knock-out mouse model of autism. J. Neurosci 37, 6475–6487. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hippenmeyer S, Vrieseling E, Sigrist M, Portmann T, Laengle C, Ladle DR, and Arber S (2005). A developmental switch in the response of DRG neurons to ETS transcription factor signaling. PLoS Biol. 3, e159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hofer SB, Mrsic-Flogel TD, Bonhoeffer T, and Hübener M (2009). Experience leaves a lasting structural trace in cortical circuits. Nature 457, 313–317. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holtmaat A, and Svoboda K (2009). Experience-dependent structural synaptic plasticity in the mammalian brain. Nat. Rev. Neurosci 10, 647–658. [DOI] [PubMed] [Google Scholar]
- Holtmaat AJGD, Trachtenberg JT, Wilbrecht L, Shepherd GM, Zhang X, Knott GW, and Svoboda K (2005). Transient and persistent dendritic spines in the neocortex in vivo. Neuron 45, 279–291. [DOI] [PubMed] [Google Scholar]
- Holtmaat A, Wilbrecht L, Knott GW, Welker E, and Svoboda K (2006). Experience-dependent and cell-type-specific spine growth in the neocortex. Nature 441, 979–983. [DOI] [PubMed] [Google Scholar]
- Hopfield JJ (1982). Neural networks and physical systems with emergent collective computational abilities. Proc. Natl Acad. Sci. U S A 79, 2554–2558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang ZJ (2014). Toward a genetic dissection of cortical circuits in the mouse. Neuron 83, 1284–1302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson CM, Peckler H, Tai LH, and Wilbrecht L (2016). Rule learning enhances structural plasticity of long-range axons in frontal cortex. Nat. Commun 7, 10785. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keck T, Scheuss V, Jacobsen RI, Wierenga CJ, Eysel UT, Bonhoeffer T, and Hübener M (2011). Loss of sensory input causes rapid structural changes of inhibitory neurons in adult mouse visual cortex. Neuron 71, 869–882. [DOI] [PubMed] [Google Scholar]
- Kim Y, Yang GR, Pradhan K, Venkataraju KU, Bota M, García Del Molino LC, Fitzgerald G, Ram K, He M, Levine JM, et al. (2017). Brain-wide Maps Reveal Stereotyped Cell-Type-Based Cortical Architecture and Subcortical Sexual Dimorphism. Cell 171, 456–469.e22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knott GW, Holtmaat A, Wilbrecht L, Welker E, and Svoboda K (2006). Spine growth precedes synapse formation in the adult neocortex in vivo. Nat. Neurosci 9, 1117–1124. [DOI] [PubMed] [Google Scholar]
- Lee SH, Kwan AC, Zhang S, Phoumthipphavong V, Flannery JG, Masmanidis SC, Taniguchi H, Huang ZJ, Zhang F, Boyden ES, et al. (2012). Activation of specific interneurons improves V1 feature selectivity and visual perception. Nature 488, 379–383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loewenstein Y, Kuras A, and Rumpel S (2011). Multiplicative dynamics underlie the emergence of the log-normal distribution of spine sizes in the neocortex in vivo. J. Neurosci 31, 9481–9488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma L, Qiao Q, Tsai JW, Yang G, Li W, and Gan WB (2016). Experience-dependent plasticity of dendritic spines of layer 2/3 pyramidal neurons in the mouse cortex. Dev. Neurobiol 76, 277–286. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ma L, Jongbloets BC, Xiong WH, Melander JB, Qin M, Lameyer TJ, Harrison MF, Zemelman BV, Mao T, and Zhong H (2018). A Highly Sensitive A-Kinase Activity Reporter for Imaging Neuromodulatory Events in Awake Mice. Neuron 99, 665–679.e5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Madisen L, Zwingman TA, Sunkin SM, Oh SW, Zariwala HA, Gu H, Ng LL, Palmiter RD, Hawrylycz MJ, Jones AR, et al. (2010). A robust and high-throughput Cre reporting and characterization system for the whole mouse brain. Nat. Neurosci 13, 133–140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Majewska AK, Newton JR, and Sur M (2006). Remodeling of synaptic structure in sensory cortical areas in vivo. J. Neurosci 26, 3021–3029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Masino SA, Kwon MC, Dory Y, and Frostig RD (1993). Characterization of functional organization within rat barrel cortex using intrinsic signal optical imaging through a thinned skull. Proc. Natl Acad. Sci. U S A 90, 9998–10002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Matsuzaki M, Ellis-Davies GCR, Nemoto T, Miyashita Y, lino M, and Kasai H (2001). Dendritic spine geometry is critical for AMPA receptor expression in hippocampal CA1 pyramidal neurons. Nat. Neurosci 4, 1086–1092. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mikuni T, Nishiyama J, Sun Y, Kamasawa N, and Yasuda R (2016). High-Throughput, High-Resolution Mapping of Protein Localization in Mammalian Brain by In Vivo Genome Editing. Cell 165, 1803–1817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murmu RP, Li W, Szepesi Z, and Li JY (2015). Altered sensory experience exacerbates stable dendritic spine and synapse loss in a mouse model of Huntington’s disease. J. Neurosci 35, 287–298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nishiyama J, Mikuni T, and Yasuda R (2017). Virus-Mediated Genome Editing via Homology-Directed Repair in Mitotic and Postmitotic Cells in Mammalian Brain. Neuron 96, 755–768.e5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nitsch R, Soriano E, and Frotscher M (1990). The parvalbumin-containing nonpyramidal neurons in the rat hippocampus. Anat. Embryol. (Berl) 181, 413–425. [DOI] [PubMed] [Google Scholar]
- Pfeffer CK, Xue M, He M, Huang ZJ, and Scanziani M (2013). Inhibition of inhibition in visual cortex: the logic of connections between molecularly distinct interneurons. Nat. Neurosci 16, 1068–1076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pologruto TA, Sabatini BL, and Svoboda K (2003). ScanImage: flexible software for operating laser scanning microscopes. Biomed. Eng. Online 2, 13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rimbault C, Maruthi K, Breillat C, Genuer C, Crespillo S, Puente-Muñoz V, Chamma I, Gauthereau I, Antoine S, Thibaut C, et al. (2019). Engineering selective competitors for the discrimination of highly conserved protein-protein interaction modules. Nat. Commun 10, 4521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rimbault C, Breillat C, Compans B, Toulmé E, Nunes Vicente F, Fernandez-Monreal M, Mascalchi P, Genuer C, Puente-Muñoz V, Gauthereau I, et al. (2021). Engineering paralog-specific PSD-95 synthetic binders as potent and minimally invasive imaging probes. BioRxiv. 10.1101/2021.04.07.438431. [DOI] [Google Scholar]
- Sancho L, and Bloodgood BL (2018). Functional Distinctions between Spine and Dendritic Synapses Made onto Parvalbumin-Positive Interneurons in Mouse Cortex. Cell Rep. 24, 2075–2087. [DOI] [PubMed] [Google Scholar]
- Santuy A, Rodriguez JR, DeFelipe J, and Merchan-Perez A (2018). Volume electron microscopy of the distribution of synapses in the neuropil of the juvenile rat somatosensory cortex. Brain Struct. Funct 223, 77–90. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schnell E, Sizemore M, Karimzadegan S, Chen L, Bredt DS, and Nicoll RA (2002). Direct interactions between PSD-95 and stargazin control synaptic AMPA receptor number. Proc. Natl Acad. Sci. U S A 99, 13902–13907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sheng M, and Kim E (2011). The postsynaptic organization of synapses. Cold Spring Harb. Perspect. Biol 3, a005678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Song S, Miller KD, and Abbott LF (2000). Competitive Hebbian learning through spike-timing-dependent synaptic plasticity. Nat. Neurosci 3, 919–926. [DOI] [PubMed] [Google Scholar]
- Spires TL, Meyer-Luehmann M, Stern EA, McLean PJ, Skoch J, Nguyen PT, Bacskai BJ, and Hyman BT (2005). Dendritic spine abnormalities in amyloid precursor protein transgenic mice demonstrated by gene transfer and intravital multiphoton microscopy. J. Neurosci 25, 7278–7287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Statman A, Kaufman M, Minerbi A, Ziv NE, and Brenner N (2014). Synaptic Size Dynamics as an Effectively Stochastic Process. PLoS Comput. Biol 10, e1003846. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sun YJ, Espinosa JS, Hoseini MS, and Stryker MP (2019). Experience-dependent structural plasticity at pre- and postsynaptic sites of layer 2/3 cells in developing visual cortex. Proc. Natl. Acad. Sci. USA 116, 21812–21820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suzuki K, Tsunekawa Y, Hernandez-Benitez R, Wu J, Zhu J, Kim EJ, Hatanaka F, Yamamoto M, Araoka T, Li Z, et al. (2016). In vivo genome editing via CRISPR/Cas9 mediated homology-independent targeted integration. Nature 540, 144–149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tjia M, Yu X, Jammu LS, Lu J, and Zuo Y (2017). Pyramidal neurons in different cortical layers exhibit distinct dynamics and plasticity of apical dendritic spines. Front. Neural Circuits 11, 43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Trachtenberg JT, Chen BE, Knott GW, Feng G, Sanes JR, Welker E, and Svoboda K (2002). Long-term in vivo imaging of experience-dependent synaptic plasticity in adult cortex. Nature 420, 788–794. [DOI] [PubMed] [Google Scholar]
- Tsai J, Grutzendler J, Duff K, and Gan WB (2004). Fibrillar amyloid deposition leads to local synaptic abnormalities and breakage of neuronal branches. Nat. Neurosci 7, 1181–1183. [DOI] [PubMed] [Google Scholar]
- Turrigiano G (2012). Homeostatic synaptic plasticity: local and global mechanisms for stabilizing neuronal function. Cold Spring Harb. Perspect. Biol 4, a005736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Versendaal D, Rajendran R, Saiepour MH, Klooster J, Smit-Rigter L, Sommeijer JP, De Zeeuw CI, Hofer SB, Heimel JA, and Levelt CN (2012). Elimination of inhibitory synapses is a major component of adult ocular dominance plasticity. Neuron 74, 374–383. [DOI] [PubMed] [Google Scholar]
- Villa KL, Berry KP, Subramanian J, Cha JW, Oh WC, Kwon HB, Kubota Y, So PTC, and Nedivi E (2016). Inhibitory Synapses Are Repeatedly Assembled and Removed at Persistent Sites In Vivo. Neuron 89, 756–769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu T, Yu X, Perlik AJ, Tobin WF, Zweig JA, Tennant K, Jones T, and Zuo Y (2009). Rapid formation and selective stabilization of synapses for enduring motor memories. Nature 462, 915–919. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xue M, Atallah BV, and Scanziani M (2014). Equalizing excitation-inhibition ratios across visual cortical neurons. Nature 511, 596–600. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhong H, Ceballos CC, Massengill CI, Muniak MA, Ma L, Qin M, Petrie SK, and Mao T (2021). High-fidelity, efficient, and reversible labeling of endogenous proteins using CRISPR-based designer exon insertion. eLife 10, e64911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou M, Liang F, Xiong XR, Li L, Li H, Xiao Z, Tao HW, and Zhang LI (2014). Scaling down of balanced excitation and inhibition by active behavioral states in auditory cortex. Nat. Neurosci 17, 841–850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ziv NE, and Brenner N (2018). Synaptic Tenacity or Lack Thereof: Spontaneous Remodeling of Synapses. Trends Neurosci. 41, 89–99. [DOI] [PubMed] [Google Scholar]
- Zuo Y, Yang G, Kwon E, and Gan WB (2005a). Long-term sensory deprivation prevents dendritic spine loss in primary somatosensory cortex. Nature 436, 261–265. [DOI] [PubMed] [Google Scholar]
- Zuo Y, Lin A, Chang P, and Gan WB (2005b). Development of long-term dendritic spine stability in diverse regions of cerebral cortex. Neuron 46, 181–189. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The original longitudinal imaging data are available at the Brain Image Library (https://download.brainimagelibrary.org/87/f8/87f8546092155279/), and are publicly available as of the date of publication. The accession number is listed in the Key resources table.
Manual scoring software can be found at https://github.com/HZhongLab/synscore. All code necessary to perform the analyses within this paper can be found at https://github.com/HZhongLab/melander_nayebi_2021. These codes are publically available as of the date of publication. The DOI is listed in the Key resources table.
Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Antibodies | ||
| Monoclonal Anti-Parvalbumin Antibody | Millipore Sigma | P3088-100UL |
| Hoechst 33342 Solution | ThermoFisher | Cat#62249 |
| Bacterial and virus strains | ||
| AAV2/1-Syn-Cre | Custom preparation from Boris Zemelman | N/A |
| Chemicals, peptides, and recombinant proteins | ||
| Chlorprothixene hydrochloride | Sigma-Aldrich | Cat# C1671 |
| Isoflurane | Piramal | NDC# 66794-019 |
| MNI-Glutamate | Tocris | Cat# 1490 |
| Optical Adhesive NOA81 | Norland | Cat# 2018 |
| Deposited data | ||
| Longitudinal in vivo imaging data of PSD-95-CreNABLED dendrites of Pyr and PV+ neurons | This paper | Brain Image Library ID 87f8546092155279; https://download.brainimagelibrary.org/87/f8/87f8546092155279/ |
| Experimental models: Organisms/strains | ||
| C57BL/6 mouse | Charles River | C57BL/6NCrl; RRID: IMSR_CRL:27 |
| PV-IRES-Cre (B6.129P2-Pvalbtm1(cre) Arbr/J) | Jax | 008069; RRID: IMSR_JAX:008069 |
| Ai9 (B6.Cg-Gt(ROSA)26Sortm9 (CAG-TdTomato)Hze/J) | Jax | 012569; RRID: IMSR_JAX:012569 |
| Software and algorithms | ||
| MATLAB | MathWorks | RRID: SCR_001622; https://www.mathworks.com |
| ScanImage | Svoboda Lab, HHMI Janelia / Vidrio Technologies | RRID: SCR_014307 |
| synScore | This paper | https://github.com/HZhongLab/synscore |
| Custom analysis codes | This paper | https://zenodo.org/record/5553667#.YXI6BfrMItI |
| R | n/a | RRID:SCR_001905; https://cran.r-project.org |
| Python Programming Language (2.7 and 3.6) | n/a | RRID: SCR_008394; https://www.python.org |


