Abstract
We aim to understand the spatial inequality in Coronavirus disease 2019 (COVID-19) positivity rates across New York City (NYC) ZIP codes. Applying Bayesian spatial negative binomial models to a ZIP-code level dataset (N = 177) as of May 31st, 2020, we find that (1) the racial/ethnic minority groups are associated with COVID-19 positivity rates; (2) the percentages of remote workers are negatively associated with positivity rates, whereas older population and household size show a positive association; and (3) while ZIP codes in the Bronx and Queens have higher COVID-19 positivity rates, the strongest spatial effects are clustered in Brooklyn and Manhattan.
Keywords: Spatial inequality, Bayesian spatial modeling, New York City, COVID-19
1. Introduction
Since the outbreak of the novel coronavirus disease 2019 (COVID-19), New York City (NYC) has become the epicenter of the pandemic in the United States (US) (Wadhera et al., 2020). Specifically, NYC accounts for 2.5 percent of the total US population; however, it makes up almost 10 percent of the total confirmed cases and more than 18 percent of COVID-19 deaths nationwide (authors’ calculation) in the early stage of the pandemic. Even after the spread of COVID-19 virus has been contained, the COVID-19 deaths in NYC still make up almost 6 percent of total deaths in the US by April 2021. This heavy burden has exacerbated the existing health disparities along with several social dimensions in NYC, such as race/ethnicity and income. For example, the age-adjusted case rate is at least 40 percent higher among Hispanics (7944.51 per 100,000 people), in contrast to non-Hispanic whites (5658.60) and Asian/Pacific-Islanders (4860.94 per 100,000 people). Similarly, the risk of contracting (or dying of) COVID-19 increases with neighborhood poverty (NYC Health Department, 2021a).
Although several studies have explored racial/ethnic and socioeconomic health disparities in COVID-19 outcomes in NYC (Almagro and Orane-Hutchinson, 2020; Whittle and Diaz-Artiles, 2020), little attention has been paid to the spatial health disparities within the city until recently. For example, Hamidi and Hamidi (2021) use spatial lag models to understand if subway ridership is associated with COVID-19 infection rates and Cordes and Castro (2020) identify the COVID-19 positivity rate hotspot with spatial clustering analysis techniques. Spatial health disparities are related to the sociodemographic processes underlying a certain disease and/or the dynamics between an environment and the populations who live in it (Davidson et al., 2008). A study (Wadhera et al., 2020) in NYC finds that the Bronx consistently shows the highest hospitalization and death rates and Manhattan is the least hit among the five boroughs. The authors suggest that this spatial inequality is concerning as the disadvantaged populations in NYC (e.g., the poor) suffer from COVID-19 more than others. Another study (Gonzalez-Reiche et al., 2020) sequences the COVID-19 virus in the early stage of the pandemic and identifies spatial clusters of related viruses in both Brooklyn and Manhattan. These studies mainly focus on describing the spatial inequality patterns in NYC and do not investigate the determinants associated with these spatial inequalities.
This study aims to investigate the extent to which the spatial inequality in COVID-19 positivity rates across NYC ZIP codes can be explained by various sociodemographic variables (e.g., racial/ethnic composition and occupations) and how spatial structure1 is associated with the distribution of COVID-19 positive cases. As spatial health inequalities are often geographically clustered, it is imperative to adopt spatial modeling to obtain unbiased coefficient estimates (Voss et al., 2006) and to understand how spatial structure among ZIP codes may contribute to spatial inequality (Haining and Haining, 2003; Pfeiffer et al., 2008). Prior county-level studies have overlooked spatial dependence (Mahajan and Larkins-Pettigrew, 2020; Millett et al., 2020; Zhang and Schwartz, 2020) and limited research has adopted spatial analysis (Mollalo et al., 2020). Spatial dependence may bias the statistical estimates of relationships of interest and considering spatial errors may account for spatial confounding due to unmeasured variables.
2. Data and methods
The unit of analysis is the modified ZIP codes created by the NYC Department of Health and Mental Hygiene (DOHMH). Due to the concern about the uneven distribution of population across the conventional ZIP codes, the NYC DOHMH solidifies the conventional ZIP codes by integrating ZIP codes with small population size into those with a large population. This approach yields comparable population size across the modified ZIP codes, which helps calculate stable rates (NYC Health Department, 2020a). This study uses the boundaries of the modified ZIP codes for analysis and visualization (and we discuss the generalizability issue in the discussion section).
2.1. Measures and data sources
Dependent variable: The total number of positive COVID-19 cases in a ZIP code serves as our dependent variable and the number of tests is treated as the offset variable. The data come from the NYC DOHMH as of May 31st, 2020. The NYC government suggests that the positivity rate should be lower than 5 percent (NYC Health Department, 2020b) to contain the pandemic. Since the end of May 2020, NYC has consistently observed a positivity rate lower than this threshold. Thus, this study focuses on the COVID-19 data between March and May. ZIP code is the most granular geographic unit at which the data are available in NYC. A total of 200,051 positive COVID-19 cases was reported but 6417 cases without identifiable ZIP code were excluded from the analysis. Our final sample consists of 177 ZIP codes with 193,634 positive cases (96.79% of total cases).
According to NYC DOHMH (NYC Health Department, 2021b), an individual who got a positive result (i.e., diagnosed with COVID-19) should not be re-tested during the 90 days from the date of the previous test. The reason is that those who have recovered from COVID-19 may still yield a positive test result. Moreover, people who work outside the home or work/live in a congregate setting are encouraged to get tested every month. Given these NYCDOH recommendations, the number of tests (i.e., the offset variable) may be inflated with those who do not contract COVID-19. However, the number of positive cases (i.e., the dependent variable) is unlikely to be influenced by the multiple tests of COVID-19 patients, unless an individual contracts COVID-19 again after s/he recovered from the previous infection. That is, our dependent variable tends to underestimate, rather than overestimate, the actual positivity rate at the ZIP code level.
Covariates: We consider four groups of covariates: demographic characteristics, socioeconomic status, worker characteristics, and household characteristics. Recent studies have found that age, race/ethnicity, and population density are related to COVID-19 infections (Raifman and Raifman, 2020; Rocklöv and Sjödin, 2020; Tenforde et al., 2020) and socioeconomic status has been regarded as the fundamental cause of disease (Link and Phelan, 1995). People with longer commuting time have a heightened risk of infection while those working from home may have a reduced risk (Baker et al., 2020). Similarly, large household size and poor housing conditions may be associated with higher positivity rates. Data on these covariates are from the 2014–2018 American Community Survey 5-year estimates.2
Demographic characteristics include five variables: percentage of non-Hispanic Blacks, percentage of Asians, percentage of Hispanics, percentage of population ages 65 and above, and population density (1000 people per square mile).
Socioeconomic status includes three variables: disadvantage index, income inequality, and percentage of adults (19–64) who are uninsured. The disadvantage index was constructed by applying principal component analysis (PCA) to the following variables: percentage of population who had received a bachelor’s degree or higher (factor loading = −0.881), logged household income (−0.940), percentage of population living below poverty level (0.848), unemployment rate (0.850), percentage of female-headed households (0.919), percentage of households receiving public assistance income (0.891), and percentage of workers who were employed in the “COVID-essential” occupations3 (0.843). The PCA results suggest that one factor explains almost 80% of the overall variation. Income inequality is measured with the Gini index. For both variables, higher values reflect higher neighborhood disadvantage and income inequality.
Worker characteristics in a ZIP code included two variables: percentage of non-remote workers who commute by public transportation and percentage of workers who work at home.
Finally, as for household characteristics, we consider three variables: average household size, percentage of housing units that were built before 1990, and sanitation facilities index. The sanitation facilities index is an average score of two standardized variables: percentage of housing units without complete plumbing facilities and percentage of housing units without complete kitchen facilities. Lower scores indicate better sanitation facilities among ZIP codes.
2.2. Bayesian spatial modeling
Given the nature of our dependent variable, we first examine whether a Poisson distribution, which assumes that the mean value equals the variance, fits our data with Dean’s PB score test (Dean, 1992). The results indicate that the equivalence assumption is rejected and the dependent variable is overdispersed.4 Consequently, we use the negative binomial regression, which relaxes the equivalence assumption and allows for overdispersion, to investigate the associations between the independent variables and positive COVID-19 case counts (Agresti, 2003). It can be expressed as follows:
| (1) |
where refers to the mean of the COVID-19 cases (i.e., ) and indicates the number of tests performed in a ZIP code (as an individual cannot be diagnosed with COVID-19 without a test), which is known as the population at risk. Should both parameters be combined, a negative binomial regression estimates the mean incidence rate of COVID-19 case per test (i.e., positivity rates). is the intercept and the coefficient is a parameter assessing the relationship between covariates and . Overdispersion in this model is measured by the parameter, , that reflects the level of overdispersion (the larger the value is, the greater the variance is). Additional modeling details are provided in Appendix A.
Beyond the conventional model specification above, we expand equation (1) by considering different sets of error terms, which can be expressed as equation (2):
| (2) |
is a random error specific to each ZIP code i, which is independent and identically distributed (IID) and follows a normal distribution with a mean of 0 and a variance parameter , which is defined as ( is a precision parameter). In addition, refers to the spatially structured errors and follows a normal distribution that is conditional on other neighboring locations , which can be expressed as below:
| (3) |
where refers to the variance parameter and is defined as ( is the precision parameter for spatial errors), j ~ i denotes ZIP code j is a neighbor of the ith ZIP code, and is the total number of neighbors of the ith ZIP code. Explicitly, given a set of neighbors, is assumed to have a mean equal to the mean of these neighbors and a variance that is a function of the number of neighbors. Such a specification of spatially structured errors has been commonly used in the conditional autoregressive (CAR) model (Besag et al., 1991). The spatially structured errors capture the processes associated with the variables that are not included in the analysis. For example, the level of compliance with precautionary actions (e.g., face masking) is not available at the ZIP code level and may be reflected in spatially structured errors. Any two ZIP codes sharing a common boundary or a vertex are defined as neighbors. Though there is a concern about whether the choice of spatial weight matrix alters results, recent research suggests that this concern is little supported by theories (LeSage and Pace, 2014).
We use the integrated nested Laplace approximation (INLA) method and the R-INLA package in R to obtain the Bayesian estimates for all models.5 The INLA generates the posterior distributions of parameter estimates (e.g., ) and we will present the results with the rate ratios and 95 percent credible regions (Banerjee and Fuentes, 2012). The Deviance Information Criterion (DIC) will be used to compare different models. Generally, a DIC difference that is greater than ten between two models suggests that the one with the lower value is preferred (Spiegelhalter et al., 2002).
We adopt the CAR model and the Bayesian approach for two reasons. First, the conventional spatial econometrics/regression models were developed for continuous dependent variables that follow a normal distribution. However, our dependent variable, the number of positive COVID-19 cases, is a count variable and fits the spatial generalized linear modeling approach better. The CAR model follows the Markov property and has been commonly used in spatial generalized linear modeling (Goodchild and Haining, 2004; Ver Hoef et al., 2018). While the count variable can be converted into positivity rates, the distribution of positivity rates is highly skewed to the right. Variable transformation becomes necessary in order to use the conventional regression methods, which makes the interpretation less intuitive.
The other reason is that for models like spatial lag or spatial Durbin model, the regression estimates cannot be directly interpreted because the spatial lag parameter needs to be further decomposed (LeSage and Pace, 2009). By contrast, spatial error models estimate a spatial error parameter that captures the potential effects of variables unattended in the model. Both spatial lag and spatial error estimates reflect the average effects across space and do not allow users to estimate the effects specific to each ecological unit. Since the goal of our analysis is to control for the potential bias caused by spatial structure and to further separate the structured effects from the unstructured ones, the CAR model serves this goal better than spatial regression models.
2.3. Analytic strategy
We first implement the descriptive analysis by the five boroughs of NYC and test if there is any significant difference across boroughs with one-way ANOVA. Showing results by borough is to understand the differences across boroughs and the potential role of spatial structure/inequality. We then conduct various models to investigate how the independent variables are associated with COVID-19 cases. The first model is the conventional negative binomial model without any error terms (i.e., equation (1)). The second model considers the ZIP-code specific IID errors (i.e., equation (2) without ), and the third model further includes the spatially structured errors (i.e., equation (2)). We visualize both IID and spatially structured effects. The first model serves as the baseline model and the second model aims to understand if there is any ZIP code specific error that may confound the relationships between the covariates and positive cases. The final model aims to answer if spatially autocorrelated errors alter our findings.
3. Results
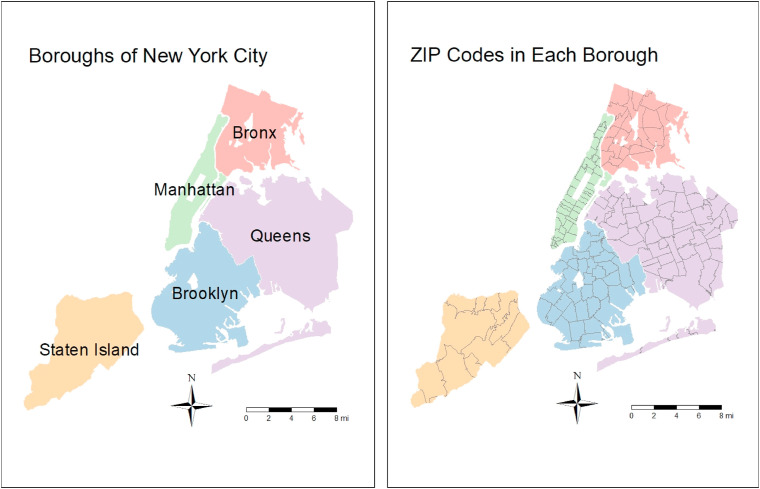
For ease of discussion, we create Fig. 1 to show ZIP codes in NYC boroughs. Table 1 presents descriptive statistics calculated for all NYC ZIP codes and by each borough. Several findings are notable. First, as of May 31st, on average, a ZIP code in NYC reports 1094 positive COVID-19 cases. Importantly, the total number of positive cases varies across boroughs as the Bronx (1762 cases) has more than three times as many cases as Manhattan (540 cases). Second, the one-way ANOVA results suggest that all variables, except for the percentage of population ages 65 and above and sanitation facilities index, are different across boroughs. Third, NYC is racially and ethnically diverse as non-Hispanic Blacks and Asians account for almost 20% and 15% of the population, respectively. Among these boroughs, the Bronx has the highest percentage of non-Hispanic Blacks and Hispanics, whereas Queens has the highest percentage of Asians. Third, these boroughs are different in terms of their socioeconomic status. In particular, ZIP codes in the Bronx are the most socioeconomically vulnerable, as reflected in their disadvantage index and percentage of uninsured adults. By contrast, ZIP codes in Manhattan have the lowest average disadvantage index. Fourth, overall, in NYC more than half of workers commute by public transportation (56%). Nonetheless, the distribution of workers who work from home is uneven because four of the five boroughs have, on average, less than five percent of workers who can work from home, except for Manhattan (6.65%). Lastly, as for household characteristics, ZIP codes in Brooklyn are more likely to have old housing units (built before 1990) without complete sanitation facilities compared to their counterparts elsewhere.
Fig. 1.
Five boroughs in New York City and the ZIP codes in each borough.
Table 1.
Means and standard deviations (S.D.) across ZIP codes within each NYC borough.
| The Bronx |
Brooklyn |
Manhattan |
Queens |
Staten Island |
NYC |
One-way ANOVA |
|||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n = 25 |
n = 37 |
n = 44 |
n = 59 |
n = 12 |
n = 177 |
||||||||
| Mean | S.D. | Mean | S.D. | Mean | S.D. | Mean | S.D. | Mean | S.D. | Mean | S.D. | p-value | |
| Dependent Variable | |||||||||||||
| Covid-19 Cases | 1761.76 | 786.77 | 1424.57 | 692.77 | 539.95 | 425.47 | 1014.34 | 767.14 | 1106.42 | 591.07 | 1093.98 | 779.60 | <0.05 |
| Independent Variables | |||||||||||||
| Demographic Characteristics | |||||||||||||
| % Non-Hispanic Blacks | 27.84 | 15.41 | 29.30 | 28.62 | 11.52 | 17.06 | 17.09 | 24.79 | 11.13 | 11.56 | 19.37 | 23.12 | <0.05 |
| % Asians | 3.53 | 3.21 | 11.29 | 11.06 | 14.32 | 10.26 | 24.06 | 16.37 | 7.48 | 3.96 | 14.95 | 13.95 | <0.05 |
| % Hispanics | 53.08 | 18.16 | 19.41 | 13.01 | 20.47 | 19.13 | 24.21 | 15.22 | 20.49 | 11.63 | 26.10 | 19.44 | <0.05 |
| % Population Ages 65 and Above | 13.25 | 5.31 | 13.45 | 4.83 | 14.28 | 6.00 | 15.25 | 4.56 | 14.49 | 2.90 | 14.30 | 5.04 | |
| Population Density | 44.91 | 26.86 | 42.95 | 15.31 | 72.46 | 38.33 | 26.40 | 20.10 | 9.69 | 3.74 | 42.79 | 32.01 | <0.05 |
| Socioeconomic Status | |||||||||||||
| Disadvantage Index | 1.23 | 0.95 | 0.24 | 0.76 | −0.77 | 1.03 | −0.08 | 0.56 | −0.07 | 0.52 | 0.00 | 1.00 | <0.05 |
| Income Inequality | 0.49 | 0.04 | 0.50 | 0.03 | 0.53 | 0.06 | 0.44 | 0.03 | 0.46 | 0.05 | 0.48 | 0.06 | <0.05 |
| % Adults 19–64 Uninsured | 13.79 | 4.42 | 11.55 | 4.40 | 6.79 | 4.13 | 12.23 | 6.18 | 7.76 | 3.79 | 10.65 | 5.57 | <0.05 |
| Worker Characteristics | |||||||||||||
| % Workers Who Commute by Public Transportation | 59.69 | 13.03 | 64.43 | 9.70 | 62.84 | 12.01 | 48.48 | 16.21 | 31.18 | 7.78 | 55.79 | 16.05 | <0.05 |
| % Workers Who Work at Home | 3.37 | 1.39 | 4.36 | 2.04 | 6.65 | 2.00 | 2.71 | 1.09 | 2.52 | 0.82 | 4.11 | 2.25 | <0.05 |
| Household Characteristics | |||||||||||||
| Average Household Size | 2.76 | 0.28 | 2.67 | 0.38 | 2.10 | 0.36 | 2.93 | 0.48 | 2.83 | 0.16 | 2.64 | 0.500 | <0.05 |
| % Housing Units Built Before 1990 | 89.06 | 6.33 | 89.57 | 6.54 | 80.34 | 21.01 | 89.16 | 13.61 | 76.58 | 13.03 | 86.18 | 14.67 | <0.05 |
| Sanitation Facilities Index | 0.11 | 0.55 | 0.17 | 1.17 | −0.28 | 0.67 | 0.06 | 1.14 | −0.03 | 0.63 | 0.00 | 0.96 | |
The Bayesian negative binomial regression results are presented in Table 2 . Before we discuss the key findings, we note that the variance inflation factors (VIFs) among the independent variables are all lower than 10 (see the VIF column), a commonly used criterion for multicollinearity correction (Kutner et al., 2004). This suggests that multicollinearity should not be a concern in our analysis. We summarize the notable findings as follows.
Table 2.
Bayesian negative binomial regression results with different specifications of models in New York city ZIP codes (N = 177).
| Conventional NB Model 1 |
NB with IID Effect Model 2 |
NB with Both CAR & IID Effect Model 3 |
VIF | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | 95% CR | Mean | 95% CR | Mean | 95% CR | |||||||
| Intercept | 0.1058 | (0.0679, | 0.1650) | 0.1034 | (0.0659, | 0.1618) | 0.1169 | (0.0718, | 0.1906) | |||
| Demographic Characteristics | ||||||||||||
| % Non-Hispanic Blacks | 1.0020 | (1.0010, | 1.0040) | 1.0024 | (1.0010, | 1.0039) | 1.0022 | (1.0005, | 1.0039) | 3.49 | ||
| % Asians | 1.0010 | (0.9990, | 1.0030) | 1.0011 | (0.9991, | 1.0031) | 1.0013 | (0.9989, | 1.0037) | 2.38 | ||
| % Hispanics | 1.0030 | (1.0010, | 1.0050) | 1.0034 | (1.0014, | 1.0055) | 1.0032 | (1.0008, | 1.0056) | 4.96 | ||
| % Population Ages 65 and Above | 1.0111 | (1.0050, | 1.0161) | 1.0105 | (1.0045, | 1.0165) | 1.0088 | (1.0021, | 1.0156) | 2.23 | ||
| Population Density | 0.9990 | (0.9980, | 0.9990) | 0.9986 | (0.9978, | 0.9994) | 0.9986 | (0.9977, | 0.9994) | 1.98 | ||
| Socioeconomic Status | ||||||||||||
| Disadvantage Index | 1.0439 | (0.9910, | 1.0997) | 1.0420 | (0.9892, | 1.0979) | 1.0507 | (0.9945, | 1.1105) | 8.08 | ||
| Income Inequality | 1.0212 | (0.5560, | 1.8757) | 1.0544 | (0.5703, | 1.9493) | 0.9849 | (0.5199, | 1.8635) | 3.11 | ||
| % Adults 19–64 Uninsured | 1.0030 | (0.9970, | 1.0090) | 1.0026 | (0.9966, | 1.0086) | 1.0026 | (0.9963, | 1.0089) | 3.44 | ||
| Worker Characteristics | ||||||||||||
| % Workers Who Commute by Public Transportation | 1.0020 | (1.0000, | 1.0040) | 1.0016 | (0.9995, | 1.0037) | 1.0007 | (0.9981, | 1.0033) | 3.30 | ||
| % Workers Who Work at Home | 0.9666 | (0.9512, | 0.9831) | 0.9662 | (0.9500, | 0.9827) | 0.9675 | (0.9504, | 0.9849) | 3.75 | ||
| Household Characteristics | ||||||||||||
| Average Household Size | 1.2324 | (1.1503, | 1.3218) | 1.2333 | (1.1500, | 1.3229) | 1.2135 | (1.1223, | 1.3118) | 3.57 | ||
| % Housing Units Built Before 1990 | 1.0010 | (0.9990, | 1.0030) | 1.0012 | (0.9993, | 1.0031) | 1.0015 | (0.9995, | 1.0035) | 1.70 | ||
| Sanitation Facilities Index | 0.9910 | (0.9704, | 1.0121) | 0.9894 | (0.9683, | 1.0109) | 0.9894 | (0.9679, | 1.0114) | 1.25 | ||
| (overdispersion hyperparameter) | 4.3598 | (4.0861, | 4.6083) | 4.7047 | (4.2507, | 5.0930) | 5.0295 | (4.4078, | 5.5826) | |||
| DIC | 2148.3800 | 2108.9000 | 2104.2400 | |||||||||
+: NB: negative binomial regression; CR: credible region; IID: independent and identically distributed; CAR: conditional autoregressive. When a credible region does not include 0, it suggests that a variable is associated with the dependent variable. Bold numbers indicate that 0 is not included in the 95% CR. VIF: variance inflation factor.
First, across the three models, the associations between racial/ethnic groups and COVID-19 positivity rates are stable and the rate ratios range between 1.0020 and 1.0034. For example, every 10-percent-point increase in non-Hispanic Blacks is associated with a 2-percent increase (1.0020∧10 = 1.0202) in COVID-19 positivity rate in a ZIP code. Moreover, the rate ratio of the percentage of older adults is 1.0111 in Model 1 but it slightly decreases to 1.0088 in Model 3 (95% CR: (1.0021, 1.0156)).
Second, none of the three socioeconomic status variables is related to COVID-19 positivity rates. ZIP codes with high disadvantage index scores do not have high COVID-19 positivity rates. Neither income inequality nor the percentage of adults without health insurance is related to the positivity rates in NYC ZIP codes. However, the results indicate that worker characteristics play a critical role in understanding why some ZIP codes have higher COVID-19 positivity rates than others. Specifically, the percentage of workers who work at home is strongly associated with positivity rates because a 10-percent-point increase in workers who work at home in a ZIP code would lead to a 28.8-percent decrease in COVID-19 positivity rates (Model 1). The percentage of workers commuting by public transportation is associated with the positivity rate in Model 1 only.
Third, household characteristics are also closely related to positivity rates. Among the three variables, we find the average household size is positively related to COVID-19 positivity rates. For example, based on Model 1, if the average household size increases by 0.5 (i.e., NYC standard deviation, see Table 1), we would expect to observe an 11 percent increase in the positivity rate in a ZIP code (1.2324, 95% CR: (1.1503, 1.3218)).
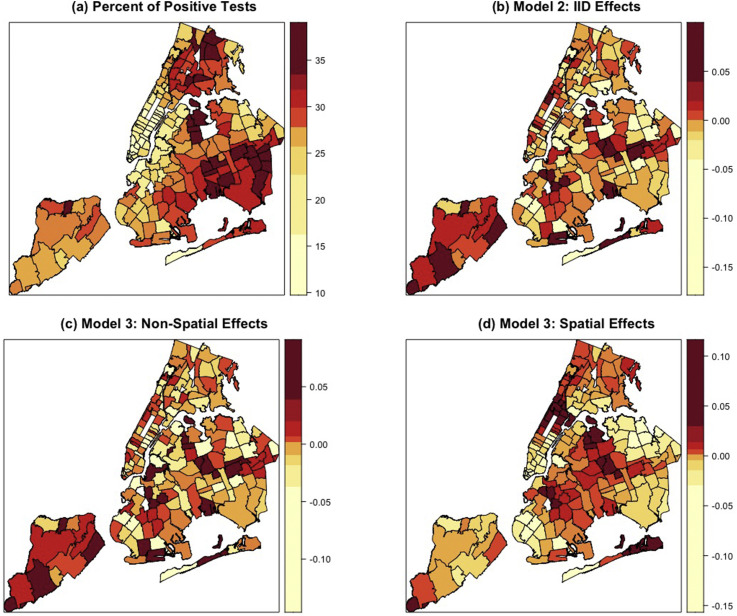
Beyond these substantive findings, we visualize the COVID-19 positivity rates and ZIP code specific effects in Fig. 2 , which allows us to further assess spatial inequality in COVID-19 positivity rates. As shown in Fig. 2(a), high percentages of positive tests are clustered in the Bronx, Queens, and Brooklyn. Our covariates are able to explain why some ZIP codes in these boroughs have high positivity rates because the IID effects (Model 2 and Fig. 2(b)) are smaller for ZIP codes with high positivity rates than those with low rates. When we consider both IID and spatially structured (i.e., CAR) errors, our results (Model 3 and Fig. 2(c) and (d)) suggest that the spatial structure among ZIP codes plays an important role in accounting for the spatial distribution of COVID-19 positivity rates. The ZIP codes in Brooklyn and Manhattan are more likely to be affected by their neighbors, compared with the ZIP codes in Queens. That is, the distribution of COVID-19 seems to be more spatially connected in Brooklyn and Manhattan than other boroughs, and the high positivity rates in Queens (and some ZIP codes in the Bronx) are a result of the ZIP-code level features considered in our regression.
Fig. 2.
Spatial distribution of COVID-19 positivity rates and patterns of spatially structured and unstructured effects.
At least two implications can be drawn from the pattern of spatially structured errors shown in Fig. 2. One is that the pattern may reflect the clusters of religious communities in Brooklyn and Queens. As it has been reported that religious communities largely overlap the hotspots of COVID-19 positivity rate in NYC (Shapiro and Silva, 2020), our spatially structured errors may reflect the potential impact of this factor on our dependent variable. The other implication is related to the pattern of uptake of preventive health care at the ZIP code level. In contrast to those with low spatially structured errors, the ZIP codes with high errors are less likely to use preventive health care, which had led to local outbreak of infectious disease between 2018 and 2019 in NYC (NYC Health Department, 2021c). The willingness to use preventive health care or take precautionary actions may affect the level of compliance with COVID-19 precautionary measures, such as face masking and social distancing, which ultimately shapes the spatial inequality in COVID-19 positivity rates.
4. Discussion
This study advances our understanding of the spatial inequality in COVID-19 positivity rates in NYC in two ways. First, we find that the relationships between socioeconomic status and demographic composition and COVID-19 positivity rates are not sensitive to spatial structure and can be used to explain why some ZIP codes have low rates but others do not. This finding echoes recent county-level studies (Mahajan and Larkins-Pettigrew, 2020; Millett et al., 2020). Nonetheless, worker and household characteristics are related to the spatial structure as their estimates change when spatially structured errors are considered. For example, ZIP codes with more workers who commute by public transportation have higher positivity rates and they may also affect the positivity rates in neighboring ZIP codes. In addition, the association between household size and positivity rate decreases after spatial errors are considered. Without a spatial perspective, this relationship may not be accurately unveiled.
Second, the option to work from home has been regarded as a privilege for individuals in advantaged positions (Felstead et al., 2002). The negative relationship between the percentage of workers who work at home and COVID-19 cases lends support to this assertion as ZIP codes with high concentrations of workers who can work from home observe fewer positive cases, indicating that working from home reduces the risk of infection, as well as the positivity rates (McNicholas and Poydock, 2020). Furthermore, the concentrations of workers commuting with public transportation may shape the spatial inequality in COVID-19 positivity rates in NYC, but this association seems to be subject to the spatial relationships among ZIP codes. However, due to the data limitation, we are unable to explicitly test this explanation. Future efforts are warranted to investigate how positivity rates are associated with COVID-19 fatality rates and whether the prevalence of various chronic conditions could serve as a mediator or moderator between positivity rates and fatality.
We situate our findings into the unique context of NYC as follows. First, NYC has a diverse population, reflected particularly by its racial/ethnic composition and foreign-born population (Census Bureau, 2020). While the black/white residential segregation has declined, minorities still consistently live in minority neighborhoods and are exposed to poverty and substandard public infrastructure (Alba and Romalewski, 2012). These features are likely to facilitate the transmission of COVID-19 virus, making NYC the epicenter in the early stage of the pandemic. Second, according to the NYC Department of City Planning (2019), more than 20 percent of NYC workers are in-commuters (i.e., commuting to the five NYC boroughs) and almost half of NYC residents work in the non-residential borough. The dynamic exchange of workers in NYC increases exposure to infection so that the percentage of workers working at home is negatively associated with COVID-19 cases. Finally, structural inequality (e.g., income inequality and deprivation) is unevenly distributed across NYC (as shown in our descriptive statistics and thematic maps) and it drives the spatial health inequalities in NYC (Cordes and Castro, 2020; Ransome et al., 2016). As found in our study, ZIP codes with high concentrations of marginalized populations report more positive cases. This association holds even after controlling for the spatially and non-spatially structured effects.
The findings and analytic approach of this study shed some light on how place shapes the spatial inequality in COVID-19 positivity rates in NYC in at least three ways. First, several recent studies report little evidence for the impact of public transportation infrastructure on COVID-19 outcomes (Adams et al., 2021; Hamidi and Hamidi, 2021). Our finding that the percentage of workers commuting by public transportation is not related to COVID-19 echoes the extant literature and we further find that this association is sensitive to spatial structure. Similarly, the significant and negative association between the percentage of workers who work at home and COVID-19 positive cases, to some extent, supports the telecommuting and social distancing measures that reduce face-to-face contacts. Second, the pattern of spatially structured errors may reflect the concentration of religious communities and uneven spatial distribution of compliance with precautionary actions. These variables are not readily available at the ZIP code level and the conventional spatial regression approach (e.g., spatial lag model) could not unveil the spatial pattern related to these factors. Visualizing the spatially structured errors helps us understand the potentially positive associations between the omitted variables and COVID-19 positivity rates, and geographical proximity to ZIP codes with high concentrations of religious communities may be a risk factor for COVID-19 positivity rates. Finally, the pattern of spatial effects (Fig. 2) suggests that the independent variables included in our analysis account for spatial variation in COVID-19 positivity rates better in some areas (e.g., southeastern Queens) than others (e.g., northern Brooklyn), which implies the existence of spatial heterogeneity within NYC. That is, the same change in a variable may invoke different levels of change in COVID-19 positivity rates, and this association depends on not only the features of a ZIP code but also those of its neighboring ZIP codes.
In light of the unique context of NYC, the findings of this study cannot be directly generalized to other metropolitan areas. However, the associations between the key independent variables (e.g., racial/ethnic composition and workers’ features) and COVID-19 positivity rates may be extended to other metropolitan areas with comparable segregation, demographic, and socioeconomic profiles, such as Chicago City. Moreover, the pattern of spatially structured errors that can be identified with the CAR model may capture the unique social and cultural clusters in other cities. It is important to focus on the heterogeneity across metropolitan areas in future research.
We implemented several sensitivity analyses to check the robustness of our findings and conclusions. For example, we separated the percent of essential workers from the disadvantage index and this change did not make the disadvantage index a significant factor (and the direction of the association between essential workers and COVID-19 positivity rate follows the expectation). Moreover, we considered more covariates than presented in the tables (e.g., percent of foreign-born population) but these covariates do not alter our findings. For model parsimony, we opted not to include them in this study. Finally, we considered other spatial error structures (e.g., combining the spatial and non-spatial effects into one overall effect) and found that the substantive findings remain the same. These sensitivity analysis results indicate that our results are robust.
This study has several limitations. First, changing the unit of analysis may change our findings and conclusions, which is known as the modifiable area unit problem among ecological studies (Fotheringham and Wong, 1991). Second, the COVID-19 cases by patients’ characteristics (e.g., race/ethnicity) are not available so that we are unable to analyze data by subgroups. Third, our results cannot be generalized to the individual level and any inference to individual behavior should be avoided. Fourth, the data and findings may be subject to several methodological concerns (Delgado-Rodriguez and Llorca, 2004), such as confounding effects, selection bias (e.g., who got tested), and systematic errors (e.g., testing practice/behavior). Finally, the number of tests performed is not evenly distributed across ZIP codes and may be affected by other ZIP-code level factors, such as trust for the government (unavailable to this study).
In sum, we find that demographic composition, worker characteristics, and household features explain the high positivity rates in the ZIP codes of Queens and the Bronx. The spatial structure among ZIP codes matters more in Brooklyn and Manhattan than in other areas. ZIP codes with fewer remote workers or larger household sizes may need special attention when implementing the reopening policies. Future research should explicitly assess the potential impacts of religious community or levels of compliance with precautionary measures on COVID-19 positivity rates.
Footnotes
Spatial structure refers to the geographical relations among ZIP codes in New York City, and this spatial structure is associated with ZIP code level covariates, including both dependent and independent variables. Our analysis with this spatial structure aims to explain the spatial variation in positive COVID-19 cases by considering the potential impacts of covariates that are embedded in this spatial structure but unattended in the analysis. This approach echoes the definition proposed by Bennett and Haining (1985).
NYC DOHMH combined several ZIP code tabulation areas into one ZIP code. When we created the independent variables for these ZIP codes, we first summed up the raw counts from the surveys and then calculated final values.
The “COVID-essential” occupations include construction and extraction occupation; farming, fishing, and forestry occupation; installation, maintenance, and repair occupation; material moving occupation; production occupation; transportation occupation; office and administrative support occupation; sales and related occupation; building and grounds cleaning and maintenance occupation; food preparation and serving related occupation; healthcare support occupation; personal care and service occupation; and protective service occupations.
The Dean’s PB score statistic is 282.80 (without covariates) and 53.85 (with all covariates), respectively. Both have a p-value less than 0.001. The likelihood ratio (LR) tests also yield the same conclusion (LR = 4718.53 and 678.93, respectively).
The comparisons between INLA and Markov chain Monte Carlo can be found in (Carroll et al., 2015).
Appendix A. Technical details of the negative binomial regression model in this study
The likelihood of the negative binomial distribution can be expressed as follows:
for and and does not have to be an integer. The mean value of the negative binomial distribution can be expressed as
where indicates the total number of tests performed in the study area and refers to the linear combination of covariates and the hyperparameter , which serves as the overdispersion parameter and can be shown as
where is shape parameter of the negative binomial distribution. In addition, is a hyperparameter and is written as
and refers to the internal presentation of and INLA gives initial value and prior.
The mean and variance of the distribution of are and . When approaches infinity, the negative binomial distribution would become the Poisson distribution.
References
- Adams M., Garcia K., Keung D., Park-Rogers F. Tracking COVID-19 and Transit: an examination of COVID-19 clusters in NYC. Tri-State Transport. Campaign. 2021:29. [Google Scholar]
- Agresti A. John Wiley & Sons; 2003. Categorical Data Analysis. [Google Scholar]
- Alba R., Romalewski S. The end of segregation? Hardly. CUNY Center Urban Res. 2012 https://www.gc.cuny.edu/page-elements/academics-research-centers-initiatives/centers-and-institutes/center-for-urban-research/cur-research-initiatives/the-end-of-segregation-hardly Accessed 20 March 2021. [Google Scholar]
- Almagro M., Orane-Hutchinson A. The differential impact of COVID-19 across demographic groups: evidence from NYC. SSRN Electr. J. 2020 doi: 10.2139/ssrn.3573619. [DOI] [Google Scholar]
- Baker M.G., Peckham T.K., Seixas N.S. Estimating the burden of United States workers exposed to infection or disease: a key factor in containing risk of COVID-19 infection. PloS One. 2020;15(4) doi: 10.1371/journal.pone.0232452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Banerjee S., Fuentes M. Bayesian modeling for large spatial datasets: Bayesian modeling for large spatial datasets. Wiley Interdiscipl. Rev.: Comput. Stat. 2012;4(1):59–66. doi: 10.1002/wics.187. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bennett R., Haining R. Spatial structure and spatial interaction: modelling approaches to the statistical analysis of geographical data. J. Roy. Stat. Soc. 1985;148:1–27. [Google Scholar]
- Besag J., York J., Mollié A. Bayesian image restoration, with two applications in spatial statistics. Ann. Inst. Stat. Math. 1991;43(1):1–20. doi: 10.1007/BF00116466. [DOI] [Google Scholar]
- Carroll R., Lawson A., Faes C., Kirby R., Aregay M., Watjou K. Comparing INLA and OpenBUGS for hierarchical Poisson modeling in disease mapping. Spatial and Spatio-Temporal Epidemiol. 2015;14:45–54. doi: 10.1016/j.sste.2015.08.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Census Bureau . 2020. QuickFacts.https://www.census.gov/quickfacts/fact/table/newyorkcitynewyork/PST045219 Accessed 20 March 2021. [Google Scholar]
- Cordes J., Castro M.C. Spatial analysis of COVID-19 clusters and contextual factors in New York City. Spatial and Spatio-Temporal Epidemiol. 2020;34:100355. doi: 10.1016/j.sste.2020.100355. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davidson R., Mitchell R., Hunt K. Location, location, location: the role of experience of disadvantage in lay perceptions of area inequalities in health. Health Place. 2008;14(2):167–181. doi: 10.1016/j.healthplace.2007.05.008. [DOI] [PubMed] [Google Scholar]
- Dean C.B. Testing for overdispersion in Poisson and binomial regression models. J. Am. Stat. Assoc. 1992;87(418):451–457. doi: 10.1080/01621459.1992.10475225. [DOI] [Google Scholar]
- Delgado-Rodriguez M., Llorca J. Bias. J. Epidemiol. Community Health. 2004;58(8):635–641. doi: 10.1136/jech.2003.008466. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Felstead A., Jewson N., Phizacklea A., Walters S. The option to work at home: another privilege for the favoured few? New Technol. Work. Employ. 2002;17(3):204–223. doi: 10.1111/1468-005X.00105. [DOI] [Google Scholar]
- Fotheringham A.S., Wong D.W. The modifiable areal unit problem in multivariate statistical analysis. Environ. Plann. 1991;23(7):1025–1044. doi: 10.1068/a231025. [DOI] [Google Scholar]
- Gonzalez-Reiche A.S., Hernandez M.M., Sullivan M.J., Ciferri B., Alshammary H., Obla A., Fabre S., Kleiner G., Polanco J., Khan Z., Alburquerque B., van de Guchte A., Dutta J., Francoeur N., Melo B.S., Oussenko I., Deikus G., Soto J., Sridhar S.H., Wang Y.-C., Twyman K., Kasarskis A., Altman D.R., Smith M., Sebra R., Aberg J., Krammer F., García-Sastre A., Luksza M., Patel G., Paniz-Mondolfi A., Gitman M., Sordillo E.M., Simon V., van Bakel H. Introductions and early spread of SARS-CoV-2 in the New York City area. Science. 2020;369(6501):297–301. doi: 10.1126/science.abc1917. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goodchild M.F., Haining R.P. GIS and spatial data analysis: converging perspectives. Pap. Reg. Sci. 2004;83(1):363–385. doi: 10.1007/s10110-003-0190-y. [DOI] [Google Scholar]
- Haining R.P., Haining R. Cambridge University Press; 2003. Spatial Data Analysis: Theory and Practice. [Google Scholar]
- Hamidi S., Hamidi I. Subway ridership, crowding, or population density: determinants of COVID-19 infection rates in New York City. Am. J. Prev. Med. 2021 doi: 10.1016/j.amepre.2020.11.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kutner M.H., Nachtsheim C.J., Neter J., Li W. McGraw-Hill Irwin; 2004. Applied Linear Statistical Models. [Google Scholar]
- LeSage J., Pace R.K. Chapman & Hall/CRC; Florida: 2009. Introduction to Spatial Econometrics. [Google Scholar]
- LeSage J.P., Pace R.K. The biggest myth in spatial econometrics. Econometrics. 2014;2(4):217–249. doi: 10.3390/econometrics2040217. [DOI] [Google Scholar]
- Link B.G., Phelan J. Social conditions as fundamental causes of disease. J. Health Soc. Behav. 1995:80–94. doi: 10.2307/2626958. [DOI] [PubMed] [Google Scholar]
- Mahajan U.V., Larkins-Pettigrew M. Racial demographics and COVID-19 confirmed cases and deaths: a correlational analysis of 2886 US counties. J. Publ. Health. 2020;42(3):445–447. doi: 10.1093/pubmed/fdaa070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McNicholas C., Poydock M. 2020. Who Are Essential Workers? A Comprehensive Look at Their Wages, Demographics, and Unionization Rates.https://www.epi.org/blog/who-are-essential-workers-a-comprehensive-look-at-their-wages-demographics-and-unionization-rates Accessed 19 June 2020. [Google Scholar]
- Millett G.A., Jones A.T., Benkeser D., Baral S., Mercer L., Beyrer C., Honermann B., Lankiewicz E., Mena L., Crowley J.S. Assessing differential impacts of COVID-19 on black communities. Ann. Epidemiol. 2020;47:37–44. doi: 10.1016/j.annepidem.2020.05.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mollalo A., Vahedi B., Rivera K.M. GIS-based spatial modeling of COVID-19 incidence rate in the continental United States. Sci. Total Environ. 2020;728:138884. doi: 10.1016/j.scitotenv.2020.138884. [DOI] [PMC free article] [PubMed] [Google Scholar]
- NYC Department of City Planning . 2019. The Ins and Outs of NYC Commuting.https://www1.nyc.gov/assets/planning/download/pdf/planning-level/housing-economy/nyc-ins-and-out-of-commuting.pdf [Google Scholar]
- NYC Health Department . 2021. COVID-19: Latest Data.https://www1.nyc.gov/site/doh/covid/covid-19-data.page Accessed 4 April 2021. [Google Scholar]
- NYC Health Department . 2021. NYC COVID-19 Testing Recommendations.https://www1.nyc.gov/assets/doh/downloads/pdf/covid/covid-19-testing-recommendations.pdf Accessed 20 March 2021. [Google Scholar]
- NYC Health Department . 2021. Measles.https://www1.nyc.gov/site/doh/health/health-topics/measles.page Accessed 20 March 2021. [Google Scholar]
- NYC Health Department . 2020. Modified ZIP Code Tabulation Area.https://nychealth.github.io/covid-maps/modzcta-geo/about.html Accessed 10 November 2020. [Google Scholar]
- NYC Health Department . 2020. COVID-19: Public Health Milestones.https://www1.nyc.gov/site/doh/covid/covid-19-goals.page Accessed 10 November 2020. [Google Scholar]
- Pfeiffer D., Robinson T.P., Stevenson M., Stevens K.B., Rogers D.J., Clements A.C. Oxford University Press; 2008. Spatial Analysis in Epidemiology. [Google Scholar]
- Raifman M.A., Raifman J.R. Disparities in the population at risk of severe illness from COVID-19 by race/ethnicity and income. Am. J. Prev. Med. 2020;59(1):137–139. doi: 10.1016/j.amepre.2020.04.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ransome Y., Kawachi I., Braunstein S., Nash D. Structural inequalities drive late HIV diagnosis: the role of black racial concentration, income inequality, socioeconomic deprivation, and HIV testing. Health Place. 2016;42:148–158. doi: 10.1016/j.healthplace.2016.09.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rocklöv J., Sjödin H. High population densities catalyse the spread of COVID-19. J. Trav. Med. 2020;27(3):1–2. doi: 10.1093/jtm/taaa038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shapiro A., Silva C. NPR; 2020. How New York's orthodox Jewish community is responding to coronavirus safety measures.https://www.npr.org/2020/10/01/919188684/how-new-yorks-orthodox-jewish-community-is-responding-to-coronavirus-safety-meas Accessed 20 March 2021. [Google Scholar]
- Spiegelhalter D.J., Best N.G., Carlin B.P., Van Der Linde A. Bayesian measures of model complexity and fit. J. Roy. Stat. Soc. B. 2002;64(4):583–639. doi: 10.1111/1467-9868.00353. [DOI] [Google Scholar]
- Tenforde M.W., Rose E.B., Lindsell C.J., Shapiro N.I., Files D.C., Gibbs K.W., Prekker M.E., Steingrub J.S., Smithline H.A., Gong M.N., others Characteristics of adult outpatients and inpatients with COVID-19—11 academic medical centers, United States, March–May 2020. MMWR (Morb. Mortal. Wkly. Rep.) 2020;69(26):841–846. doi: 10.15585/mmwr.mm6926e3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ver Hoef J.M., Peterson E.E., Hooten M.B., Hanks E.M., Fortin M.-J. Spatial autoregressive models for statistical inference from ecological data. Ecol. Monogr. 2018;88(1):36–59. doi: 10.1002/ecm.1283. [DOI] [Google Scholar]
- Voss P.R., Long D.D., Hammer R.B., Friedman S. County child poverty rates in the US: a spatial regression approach. Popul. Res. Pol. Rev. 2006;25(4):369–391. doi: 10.1007/s11113-006-9007-. [DOI] [Google Scholar]
- Wadhera R.K., Wadhera P., Gaba P., Figueroa J.F., Maddox K.E.J., Yeh R.W., Shen C. Variation in COVID-19 hospitalizations and deaths across New York City boroughs. J. Am. Med. Assoc. 2020;323(21):2192–2195. doi: 10.1001/jama.2020.7197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whittle R.S., Diaz-Artiles A. An ecological study of socioeconomic predictors in detection of COVID-19 cases across neighborhoods in New York City. BMC Med. 2020;18:1–17. doi: 10.1186/s12916-020-01731-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang C.H., Schwartz G.G. Spatial disparities in Coronavirus incidence and mortality in the United States: an ecological analysis as of May 2020. J. Rural Health. 2020;36(3):433–445. doi: 10.1111/jrh.12476. [DOI] [PMC free article] [PubMed] [Google Scholar]