Abstract
This study presents a new risk-averse multi-stage stochastic epidemics-ventilator-logistics compartmental model to address the resource allocation challenges of mitigating COVID-19. This epidemiological logistics model involves the uncertainty of untested asymptomatic infections and incorporates short-term human migration. Disease transmission is also forecasted through a new formulation of transmission rates that evolve over space and time with respect to various non-pharmaceutical interventions, such as wearing masks, social distancing, and lockdown. The proposed multi-stage stochastic model overviews different scenarios on the number of asymptomatic individuals while optimizing the distribution of resources, such as ventilators, to minimize the total expected number of newly infected and deceased people. The Conditional Value at Risk (CVaR) is also incorporated into the multi-stage mean-risk model to allow for a trade-off between the weighted expected loss due to the outbreak and the expected risks associated with experiencing disastrous pandemic scenarios. We apply our multi-stage mean-risk epidemics-ventilator-logistics model to the case of controlling COVID-19 in highly-impacted counties of New York and New Jersey. We calibrate, validate, and test our model using actual infection, population, and migration data. We also define a new region-based sub-problem and bounds on the problem and then show their computational benefits in terms of the optimality and relaxation gaps. The computational results indicate that short-term migration influences the transmission of the disease significantly. The optimal number of ventilators allocated to each region depends on various factors, including the number of initial infections, disease transmission rates, initial ICU capacity, the population of a geographical location, and the availability of ventilator supply. Our data-driven modeling framework can be adapted to study the disease transmission dynamics and logistics of other similar epidemics and pandemics.
Keywords: OR in health services, Pandemic resource and ventilator allocation, Mean-CVaR multi-stage stochastic mixed-integer programming model, Risk-averse optimization, COVID-19
1. Introduction
The world is undergoing a major health crisis, which has now turned into a pandemic. The Coronavirus Disease 2019 (COVID-19), first detected in Wuhan city of China at the end of 2019, has had a devastating effect on human life and economies in all parts of the world. Countries worldwide enforce lockdown and quarantine rules to slow down the spread of the virus. For instance, a 76-day strict lockdown was imposed starting on January 23, 2020, public transport was suspended, school re-openings after the winter vacation were delayed, and population movements were severely curtailed in Wuhan. Due to the quick response and successful interventions, China and some other Asia-Pacific countries have managed to control the pandemic rapidly and effectively (Burki, 2020). New Zealand imposed a five-week nationwide lockdown before returning to close-to-normal. The country closed its borders to foreigners for more than a year, reducing their cases and deaths considerably. On the contrary, a slow reaction delaying interventions, such as mask and social distancing, have aggravated the COVID-19 death toll in some other world countries, such as the United States and the United Kingdom (UK) (CNN, Lilleker). South Korea and Ghana gave consistent messages highlighting the risks of the new pandemic and how it could be mitigated. However, nations such as Brazil, the UK, and India gave out inconsistent messages about the threat of COVID-19 and encouraged complacency less well, worsening the pandemic’s impact (CNN, 2021).
The lockdown, imposing travel restrictions, and social distancing have also severely affected the economy, from small-scale industries to stock prices and international trading. The virus has a high transmission rate, causing more than 104.7 million cases globally, of which 2.3 million people have died by mid-February 2021 (JHU, 2020). The continuous increase seen in coronavirus cases has made a worldwide scarcity of essential resources, such as ventilators, Intensive Care Unit (ICU) beds, Personal Protective Equipment (PPE), and masks. Effective, sufficient, and timely delivery of those critical resources to serve COVID-19 patients has been a major challenge faced by nations worldwide during the pandemic.
COVID-19 is primarily an acute respiratory disease. Ventilator incubation delivers high oxygen concentrations while removing carbon dioxide and reduces the risk of hypoxia for COVID-19 patients (Meng et al., 2020). The standard Acute Respiratory Distress Syndrome protocol mandates that the most severe COVID-19 patients, who constitute of all COVID-19 patients, should receive ventilator support (Bein et al., 2016). As a result, the life of many COVID-19 patients depends on the use of ventilators. The shortage of supplies and uncertainty in disease transmission has affected the proper allocation of ventilators, causing immense distress to the healthcare system. Due to ventilator shortages worldwide during the pandemic’s peak times, hospital officials have had to make life-altering resource allocation decisions and prioritized the care of COVID-19 patients (Ranney, Griffeth, & Jha, 2020). To tackle ventilator shortages and reduce the number of COVID-19-related deaths, studies have come up with new approaches for ventilator distribution. For example, Ranney et al. (2020) suggest that the demand for ventilators can be fulfilled by the government by allowing other industries to come together and help medical industries to cater to the needs of the ventilators. Another study by Castro et al. (2020) suggests that the government in Brazil should start thinking about expanding the resource capacity rather than only focusing on the allocation of the available resources for controlling COVID-19. White & Lo (2020) develop a framework for the distribution of ICU beds and ventilators depending on the priority scores using a scale of 1 to 8 based on patients’ likelihood of survival and ethical considerations.
Operations Research (OR) methods have been widely used to determine optimal resource allocation strategies to control an epidemic or pandemic. Several studies have used multi-period OR models to optimize the allocation and redistribution of ventilators (see, e.g., Mehrotra, Rahimian, Barah, Luo, & Schantz (2020), Bertsimas et al. (2020), and Blanco, Gázquez, & Leal (2020)). Other OR research models that study the epidemic diseases and resource allocation mainly focus on the logistics and operation management to control the disease in optimal ways (Büyüktahtakın, des Bordes, Kıbış, 2018, Coşgun, Büyüktahtakın, 2018, Kaplan, Craft, Wein, 2003, Tanner, Sattenspiel, Ntaimo, 2008, Yin, Büyüktahtakın, 2021a, Zaric, Brandeau, 2001). We refer the reader to excellent reviews of Dasaklis, Pappis, & Rachaniotis (2012) and Queiroz, Ivanov, Dolgui, & Wamba (2020) for a discussion of OR models for epidemic resource allocation.
While OR has been an extremely useful tool for effective and timely allocation of resources as a response to epidemics, none of the former work has considered the ventilator allocation problem using a risk-averse spatio-temporal stochastic programming model under uncertainty of asymptomatic infections. People move between regions, states, and countries, which aggravates the disease transmission to the other areas. Evaluating undetected or asymptomatic individuals is critical for determining disease dynamics because asymptomatic individuals move around and unknowingly infect other individuals (McCrimmon, 2021). Thus, the short-term migration of people is a critical factor that needs to be considered to forecast the transmission of COVID-19 realistically. However, the short-term migration rate is hard to predict and is affected by interventions and human behaviors. Furthermore, disease transmission rates are not constant and rather evolve over time with government interventions, such as the lockdown or social distancing measures. This change in the transmission rates also should be considered in a realistic model. To our knowledge, none of the former OR ventilator allocation models have integrated the epidemiological aspects of the disease and resource allocation challenges in one optimization model.
In this paper, we address the limitation of realistically forecasting the transmission of COVID-19 and build a risk-averse multi-stage stochastic epidemics-ventilator-logistics programming model to study the ventilator allocation for the treatment of severe COVID-19 patients. Our model considers the uncertainty of untested asymptomatic individuals during the transmission of COVID-19 and involves various pandemic scenarios during each time stage of the planning horizon. Our model also incorporates the short-term migration between the highly-impacted regions while using changing transmission rates under various non-pharmaceutical intervention measures. The model optimizes the distribution of ventilators while minimizing the total expected number of infected and deceased people. We calibrate, validate, and test our epidemiological ventilator allocation model using COVID-19 data collected during the pandemic’s early stages.
Former research presents bounds and approximation methods for risk-averse multi-stage stochastic mixed-integer programming problems, see, e.g., Sandıkçı & Özaltın (2017), Mahmutoğulları, Çavuş, & Aktürk (2018), and Bakir, Boland, Dandurand, & Erera (2020). Büyüktahtakın (2021) presents a new scenario sub-problem and defines stage- scenario dominance concept for the first time. The author also defines lower and upper bounds on the problem based on scenario sub-problems and presents scenario dominance decomposition cuts based on a partial ordering of scenarios. Bushaj, Büyüktahtakın, & Haight (2021a) later extend the scenario dominance definition and decomposition cuts of Büyüktahtakın (2021) under the case of endogenous uncertainty and show their computational benefit for solving a forest insect infestation surveillance and control problem. Inspired by the approach of Büyüktahtakın (2021), we define region-based and risk-based sub-problems and new lower and upper bounds using those sub-problems. Computational results also show that the proposed bounds significantly reduce the optimality and relaxation gaps.
1.1. Organization of the paper
This paper is organized into six sections. Section 2 presents a review of the articles that estimate the transmission of COVID-19, evaluate various interventions used to control the disease, and optimize resource allocation during an epidemic or pandemic, and summarizes our paper’s contributions. Section 3 presents the model notations, the compartmental sub-model, time and space-varying transmission sub-model, the description of uncertainty and scenario tree, the risk measure used in the model, and the multi-stage stochastic programming model formulation that integrates all elements described in this section. Section 4 presents a new region sub-problem and lower and upper bounds to tackle the problem difficulty. Section 5 provides the data used in the model, including population and migration data, epidemiological data, initial infection data, and capacity and cost data. Section 6 presents the results of the model’s application to the case of COVID-19 control in the counties of New York and New Jersey states. Section 7 discusses key insights from the results and provides future research directions.
2. Literature review
This section presents a review of the articles that study mathematical models to estimate the transmission rate of COVID-19, evaluate various interventions used to control the disease, and optimize resource allocation during the pandemic. The literature covers various methods, including compartmental models, such as the Susceptible (S)-Exposed (E)-Infectious (I)-Recovered (R) [SEIR] formulations, simulations, optimization models, stochastic, statistical, or probabilistic approaches, and network or graph-theory models, and is summarized in Table 1 .
Table 1.
Summary of the Literature Review.
| Approach | Specific Method | Reference | Modeling or Logistical Feature | Outbreak |
|---|---|---|---|---|
| Compartmental, Simulation and Forecasting Models | Compartmental and Simulation | Chatterjee et al. (2020) | Estimate the impact of nonpharmacological interventions | COVID-19 |
| Ku et al. (2020) | Determine forces of infections and | COVID-19 | ||
| Li et al. (2020) | Estimate the effects of under-detection of confirmed cases | COVID-19 | ||
| Wang et al. (2020) | Estimate the impacts of required social distancing measures | COVID-19 | ||
| Weissman et al. (2020) | Estimate surges in clinical demand | COVID-19 | ||
| Stochastic Compartmental | Ambikapathy & Krishnamurthy (2020) | Assess the COVID-19 cases for lockdowns in India | COVID-19 | |
| Kucharski et al. (2020) | Estimate the transmission rate of COVID-19 infections | COVID-19 | ||
| Kretzschmar et al. (2020) | Estimate due to delays in testing and isolation | COVID-19 | ||
| Roberts et al. (2020) | Analyze the impacts of ICU bed capacity | COVID-19 | ||
| Tuan et al. (2020) | Calculate the reproduction number | COVID-19 | ||
| Wei et al. (2020) | Understand the impacts of transportation in epidemics | COVID-19 | ||
| Zeb et al. (2020) | Find the number of infections using the isolation compartment | COVID-19 | ||
| Regression and Time-Series Models | Badr et al. (2020) | Estimate transmission using mobile data | COVID-19 | |
| Katris (2020) | Estimate the number of infections | COVID-19 | ||
| Loeffler-Wirth et al. (2020) | Visualize transmission rate | COVID-19 | ||
| Manca et al. (2020) | Forecast hospital capacity | COVID-19 | ||
| Murray (2020) | Forecast ICU occupancy and ventilators | COVID-19 | ||
| Optimization | Two-Stage Stochastic Programming | Blanco et al. (2020) | Minimize the expected non-covered demand | COVID-19 |
| Mehrotra et al. (2020) | Optimize the allocation of ventilators | COVID-19 | ||
| Tanner et al. (2008) | Optimize the vaccination policy | General | ||
| Multi-Stage Stochastic Programming | Yin & Büyüktahtakın (2021a) | Optimize resources and centers allocation under uncertainty and equity | Ebola | |
| Yin & Büyüktahtakın (2021b) | Optimize vaccine allocation and treatment logistics under a mean-CVaR objective | Ebola | ||
| This paper | Optimize ventilator allocation under asymptomatic uncertainty and risk | COVID-19 | ||
| MIP and/or Machine Learning | Bertsimas et al. (2020) | Optimize ventilator allocation in the US | COVID-19 | |
| Bushaj et al. (2021b) | Integrate reinforcement learning and simulation for epidemic decision-making | COVID-19 | ||
| Büyüktahtakın et al. (2018) | Integrate compartmental and logistics models to minimize infections | Ebola | ||
| Huang et al. (2017) | Optimize the allocation of mechanical ventilators | Influenza | ||
| Lacasa et al. (2020) | Optimize ventilator and ICU bed allocation in the UK and Spain | COVID-19 | ||
| Yin et al. (2021) | Integrate agent-based simulation and MIP to optimize vaccine location-allocation | COVID-19 | ||
| Network Optimization |
Billingham et al. (2020) |
Optimize the distribution of ventilators |
COVID-19 |
|
| Robust Optimization |
Parker et al. (2020) |
Optimize resource transfer to reduce critical shortages |
COVID-19 |
|
| Approximate Dynamic Programming |
Coşgun & Büyüktahtakın (2018) |
Optimize resource allocation under a limited intervention budget |
HIV |
|
| Stochastic System Dynamics | Kaplan et al. (2003) | Vaccinate incorporating the tracing/vaccination queue | Smallpox | |
| Zaric & Brandeau (2001) | Maximize the number of new infections averted | General | ||
| Review | Systematic Review | Dasaklis et al. (2012) | Survey the literature on epidemic control logistics | General |
| Structured Review | Queiroz et al. (2020) | Survey literature on the COVID-19 pandemic supply chains | COVID-19 | |
Compartmental, Simulation and Network Models. Several studies on COVID-19 modeling use SEIR-type models with simulations, such as the Monte Carlo Simulation, to predict the disease transmission rate and analyze the effectiveness of proposed non-pharmaceutical interventions and resource allocation strategies (see, e.g., Chatterjee, Chatterjee, Kumar, & Shankar (2020), Weissman et al. (2020), Wang et al. (2020), and Li et al. (2020)). For example, Li et al. (2020) develop a novel epidemiological model called DELPHI based on an SEIR model to estimate the effectiveness of government interventions and the effects of under-detection of confirmed cases. They find that the world-widely implemented travel restriction policies, social distancing, and mass gathering restrictions play a crucial role in reducing the infection rate. Ku, Ng, & Lin (2020) develop an empirical approach based on a Bass Susceptible-Infected-Recovered model to predict specific transmission parameters, exogenous forces of infection, and effective population sizes to determine the reproductive number () for COVID-19 transmission in Chinese provinces.
Stochastic compartmental models have also been used to analyze the uncertain transmission dynamics of COVID-19. For example, Kucharski et al. (2020) develop the stochastic dynamic Susceptible, Isolated, Infected, Recovered, and Exposed model to derive the transmission rate using COVID-19 cases in Wuhan as well as the associated international infections. The initial reproductive number of 2.35 was reduced to 1.05 after imposing travel restrictions in Wuhan. Kretzschmar et al. (2020) develop a stochastic mathematical model to understand the impact of time delays in testing and isolation on the reproductive number of COVID-19 transmission. Differential equations have been mainly used to solve compartmental disease models (see, e.g., Ambikapathy, Krishnamurthy, 2020, Wei, Liu, Zhu, Qian, Ye, Li, Ji, Li, Qi, Wang, et al., 2020, Zeb, Alzahrani, Erturk, Zaman, 2020, Tuan, Mohammadi, Rezapour, 2020; and Wang et al., 2020). For example, Roberts, Seymour, & Dimitrov (2020) come up with a series of differential equations that are designed to compare the two scenarios based on delaying of ICU bed shortage - effects of hospitalizing fewer COVID-19 patients versus increasing the ICU bed capacity.
The literature also includes many studies that present statistical approaches, such as logistic regression, generalized additive, and time-series models to predict the growth of the disease over time and implement resource allocation strategies accordingly during the pandemic (see, e.g., Murray, Manca, Caldiroli, Storti, 2020; and Katris, 2020). Graph-theoretical methods have also been quite useful in studying the COVID-19 transmission patterns and finding out the practices to reduce the transmission rate (see, e.g., Hu, Lin, Wang, Xu, Tatem, Meng, Zhang, Liu, Wang, Wu, et al., 2020, Loeffler-Wirth, Schmidt, Binder, 2020; and Badr et al., 2020). For example, Badr et al. (2020) model the transmission rate of COVID-19 based on mobile phone mobility and support the role of social distancing in combating COVID-19.
Optimization Models. Optimization models have also been widely studied for resource allocation in the fight against COVID-19. Queiroz et al. (2020) provide a systematic review of various supply chain and logistics approaches for optimizing the distribution of critical resources amid COVID-19. To tackle the shortage of ventilators, Mehrotra et al. (2020) develop a two-stage stochastic programming model, optimizing ventilator allocation during the pandemic under various demand scenarios. The authors find that when 60% of the ventilator inventory is allocated to non-COVID-19 patients, there is no shortfall. In comparison, when 75% of the stock is allocated to the non-COVID-19 patients, a shortfall in the supply of the ventilators to COVID-19 patients occurs. Also, they find that it is essential to ramp up the production of the ventilators to meet the additional requirements of the ventilators that might come up during the peak times of the pandemic. Lacasa, Challen, Brooks-Pollock, & Danon (2020) come up with an algorithm for optimizing the allocation of the ventilators and ICU beds and validate their algorithm during the peak and declining times of the pandemic based on the data from the United Kingdom and Spain.
Bertsimas et al. (2020) develop a four-step approach, combining descriptive, predictive, and prescriptive analytics and propose an optimization model for the re-allocation of the ventilators throughout the U.S. during the COVID-19 pandemic. Blanco et al. (2020) present a two-stage stochastic mixed-integer programming model, which minimizes the expected non-covered demand, using robust objective functions of type min-max regret. Billingham, Widrick, Edwards, & Klaus (2020) present a network optimization model to tackle the problem of scarce ventilator distribution. Parker, Sawczuk, Ganjkhanloo, Ahmadi, & Ghobadi (2020) develop mixed-integer programming and robust optimization models to redistribute patients instead of resources, such as ventilators among different hospitals under demand uncertainty. Govindan, Mina, & Alavi (2020) develop a practical decision support system hinging on the knowledge of the physicians and the fuzzy interference system (FIS) to help manage the demands of essential hospital services in a healthcare supply chain, to break down the pandemic propagation chain, and reduce stress among the health care workers. Huang et al. (2017) introduce a two-stage forecasting and optimization framework for optimizing stockpiles of mechanical ventilators, which are critical for treating hospitalized influenza patients in respiratory failure under a pandemic situation. They also incorporate their model into a web-based decision-support tool for pandemic preparedness and response. Yin & Büyüktahtakın (2021b) develop a multi-stage stochastic programming vaccine allocation model and apply it to the case of the Ebola virus disease in the Democratic Republic of the Congo. The authors also define two new equity metrics for fair resource allocation. Bushaj, Yin, Beqiri, Andrews, & Büyüktahtakın (2021b) present an integrated simulation-deep reinforcement learning (SiRL) framework to determine best intervention strategies over time for epidemic decision-making, while Yin, Bushaj, Yuan, & Büyüktahtakın (2021) present an agent-based simulation-optimization approach to solve the vaccine center location vaccine allocation problem with an application to controlling COVID-19.
2.1. Key contributions
In summary, former stochastic programming approaches on ventilator allocation in a pandemic situation have involved a time domain of only two stages and have not integrated an epidemic model within the stochastic program. Furthermore, the mathematical models on the forecast of COVID-19 do not include the uncertainty of untested asymptomatic infections. They do not incorporate the impact of short-term migrations on COVID-19 transmission in an epidemiological model. Also, former studies on COVID-19 modeling and logistics have omitted the time consistency of the risk for making decisions over multiple stages of a stochastic program under extreme pandemic scenarios. Our methodological, modeling, and applied contributions to the epidemiology and OR literature are summarized below.
Methodological contributions: We define region- and risk-based sub-problems. Then using those sub-problem solutions, we generate new lower and upper bounds on the original problem optimal objective function value. We also present proofs for those results and bounds. Our computations demonstrate that the proposed region-based upper and lower bounds significantly reduce the optimality and relaxation gaps, respectively. We also compare and discuss the efficiency of region sub-problem bounds with respect to that of the scenario sub-problem bounds of Büyüktahtakın (2021).
Modeling contributions: First, to our knowledge, this is the first study that addresses the optimal distribution of ventilators to control a pandemic in a multi-stage stochastic mean-Conditional Value at Risk (CVaR) model. This model includes many realistic effects critical in the COVID-19 pandemic, including untested asymptomatic infections, human movement among multiple regions, and evolving transmission rates under non-pharmaceutical intervention measures. Considering multiple stages in a multi-stage SP is essential to capture uncertain disease dynamics over multiple time periods since disease transmission dynamically changes over time.
Second, we consider the uncertainty of the proportion of untested asymptomatic infections at each stage and integrate this unknown dimension of the pandemic by generating a multi-stage scenario tree. As opposed to robust optimization, which focuses on the worst-case outcomes assuming a hostile environment, in stochastic programming, decision makers consider all possible outcomes (e.g., scenarios) by assigning weights to outcomes and optimizing some aggregated measure of performance over all likely outcomes (Defourny, Ernst, & Wehenkel, 2012). Thus, our multi-stage stochastic programming approach to modeling the uncertainty in the proportion of asymptomatic infections is more advantageous and provides less conservative results compared to robust optimization (Yin & Büyüktahtakın, 2021a).
Third, we present a new susceptible (S)- tested infected (I)- untested asymptomatic (X)- hospitalized (H)- ICU (C)- recovered (R)- death (D) compartmental disease model specialized for COVID-19, and also incorporate short-term human migration among multiple regions into this epidemiological model. Fourth, we derive a new time- and space-varying disease transmission formulation, which takes into account the impact of government interventions on transmission rates. Fifth, we formulate a budget-constrained ventilator allocation logistics model. Sixth, we incorporate a time-consistent CVaR risk-measure and the expectation criterion in the objective function to alleviate the impacts of extreme pandemic scenarios. Lastly, we integrate all those elements into one epidemics-ventilator-logistics mathematical formulation, which minimizes the number of infections and deceased individuals under different intervention strategies while determining the optimal timing and location of resources (ventilators) allocated. Our model combines the forecast of the transmission of COVID-19 and the determination of optimal ventilator allocation strategies in one formulation. Accordingly, the decision-maker can evaluate possible outcomes of wait-and-see decisions while foreseeing how the disease could progress in each time period.
Applied Contributions: We apply our general multi-stage mean-risk epidemics-ventilator-logistics model to the case of controlling COVID-19 in highly-impacted counties of New York and New Jersey. We collect real data from various resources and provide researchers with compact epidemiological, population, and logistics-capacity data for COVID-19. Using this data, we calibrate, validate, and test our model, which could be used as a decision support tool for fighting against COVID-19. Our model can also be adapted to study other similar diseases’ transmission dynamics and logistics.
Key Recommendations to Decision Makers: This study provides optimal risk-averse ventilator allocation policies under different risk levels that the decision-maker can apply to control COVID-19. Based on our results, we offer the following recommendations to inform resource allocation policies under a pandemic:
-
•
The short-term movement of people influences the number of new infections even if the disease transmission rate stays the same.
-
•
The number of treated people in the ICU may stay at the capacity limit under different intervention strategies because this value depends on the minimum number of patients who require a ventilator for treatment and the scarce ventilator supply. There is also a lag time to observe the impacts of government non-pharmaceutical interventions on the number of hospitalized and deceased individuals, as well as ICU patients.
-
•
“Lockdown” is the best strategy to control COVID-19. However, the “Mask and Social Distance” intervention following a certain period of “Lockdown” is the second-best choice, considering the need for opening facilities and businesses.
-
•
The ventilator allocation under different budget levels and scenarios indicates that the number of ventilators allocated to each region depends on various factors, such as the number of initial infections, initial disease transmission rates, initial ICU capacity, and the population of a geographical location.
-
•
Overall, the region with a high initial transmission rate and low initial ICU capacity has more ventilators allocated. Under a limited budget level, the region with low initial infections and low initial ICU capacity gets more ventilators allocated when the transmission scenario changes from “All Low” to “All Medium” and “All High.”
-
•
Independent from the transmission scenarios, the region with a high initial transmission rate has more ventilators allocated when the budget level increases. There are also increasing trends in the number of ventilators allocated when either the budget level increases or the cost for each ventilator reduces. A large-enough budget also provides some flexibility in delaying ventilator allocation to some regions. In contrast, all of the ventilators are allocated at the first two stages under a limited budget.
-
•
Considering risk in decision-making improves the confidence level for reducing the loss of lives under risky pandemic scenarios. However, a risk-averse decision-maker should also expect a possible increase in the number of infections and deaths while mitigating disastrous scenarios.
3. Problem formulation
This section discusses important features and submodels used in the risk-averse multi-stage stochastic epidemics-ventilator-logistics compartmental model and then presents its formulation (5a)–(5w). Specifically, Section 3.1 presents the description of the notations used in the model, Section 3.2 describes compartment flow of population dynamics in the mathematical model, Section 3.3 introduces the formulation for time and space-varying transmission rates in the model, Section 3.4 explains the uncertainty and scenario tree generation scheme, Section 3.5 states the specific features and assumptions made in the mathematical model, and Section 3.6 provides a brief description of the measure of multi-stage risk used in the model, CVaR. Then Section 3.7 presents the mathematical formulation for our epidemics-ventilator-logistics model that integrates all elements described in this section.
3.1. Model notation and formulation
Below we provide notations used for the rest of the paper.
Sets and Indices:
: Set of time periods, .
: Set of regions, .
: Set of scenarios, .
: Set of nodes in the scenario tree, where .
: Index for time period, where .
: Index for region where .
: Index for scenario, where .
State Variables:
: Susceptible individuals in region at stage under scenario .
: Tested symptomatic and part of asymptomatic infected individuals in region at stage under scenario .
: Untested asymptomatic infected individuals in region at stage under scenario .
: Hospitalized individuals in region at stage under scenario .
: Individuals treated in the intensive care unit (ICU) in region at stage under scenario .
: Recovered individuals in region at stage under scenario .
: Deceased individuals in region at stage under scenario .
: Number of tested symptomatic infected individuals admitted to the hospital in region at stage under scenario .
: Number of tested symptomatic infected individuals who cannot be admitted to the hospital due to limited capacity in region at stage under scenario .
: Number of individuals admitted to ICU in region at stage under scenario .
: Number of hospitalized individuals not admitted to the ICU due to the limited availability of ventilators in region at stage under scenario .
: Number of cumulative ventilators (ICU capacity) in region at stage under scenario .
: Number of infections caused by short-term migration in region at stage under scenario .
Parameters:
: Recovery rate of tested symptomatic and part of asymptomatic infected individuals in region .
: The death rate of tested symptomatic and part of asymptomatic infected individuals in region .
: Hospitalization requirement rate of tested symptomatic and part of asymptomatic infected individuals in region .
: Recovery rate of the hospitalized individuals in region .
: Death rate of hospitalized individuals in region .
: Ventilator requirement rate of hospitalized individuals in region .
: Recovery rate of ICU patients in region .
: Death rate of ICU patients in region .
: Recovery rate of untested asymptomatic individuals in region .
: Transmission rate of tested symptomatic and part of asymptomatic infected individuals in region at stage .
: Proportion of untested asymptomatic infections in region at stage under scenario .
: Hospital capacity in region at stage under scenario .
: Initial number of ventilators (ICU capacity) in region .
: Cost of each ventilator.
: Total budget for ventilators.
: Initial number of susceptible individuals in region .
: Initial number of tested infected individuals in region .
: Initial number of untested asymptomatic infected individuals in region .
: Initial number of hospitalized individuals in region .
: Initial number of ICU patients in region .
: Initial number of recovered individuals in region .
: Initial number of deceased individuals in region .
Risk parameters:
: Confidence level of value-at-risk, where .
: Non-negative risk preference parameter or mean-risk trade-off coefficient.
Risk variables:
: Value at risk for each stage under scenario .
: Value exceeding the value-at-risk at the confidence level at stage under scenario .
Non-anticipativity parameters:
: The serial number of nodes in the scenario tree, where .
: The corresponding stage that node marked in the scenario tree.
: The set of scenarios that pass through node .
Decision variables:
: Number of ventilators allocated to region at the end of stage under scenario .
Other variables:
: Auxiliary variable to be substituted with .
: Auxiliary variable to be substituted with .
: Auxiliary variable to be substituted with .
: Auxiliary variable to be substituted with .
: Binary variable, which takes the value 0 if the number of infected individuals who need to be hospitalized is restricted by the number of available beds in hospitals, and the value 1 if the number of beds in hospitals is sufficiently large to hospitalize all infected individuals who need to be hospitalized.
: Binary variable, which takes the value 0 if the number of hospitalized individuals need to be treated in ICUs is restricted by the number of available ventilators, and the value 1 if the number of ventilators is sufficiently large to treat all hospitalized individuals who need to be treated in ICUs.
: Upper bound of .
: Lower bound of .
: Upper bound of .
: Lower bound of .
: Upper bound of .
: Lower bound of .
: Upper bound of .
: Lower bound of .
3.2. Compartmental disease model description
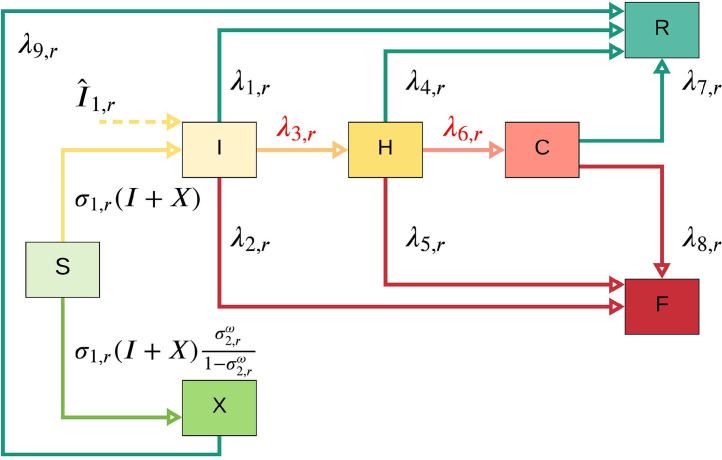
This subsection describes the compartment flow of population dynamics at each stage in each region. Figure 1 shows the transmission dynamics of COVID-19 in each region at each time period for a particular scenario . In this figure, susceptible individuals (S) can be infected and become infected (either symptomatic or asymptomatic). Asymptomatic infections (X) may have slight or no symptoms throughout the infection period and will recover with a rate of . Tested symptomatic and part of asymptomatic infections (I) may recover or die with rates of and , respectively, if they are not treated in the hospital (H). Note that with an incoming dashed arc to the I compartment represents the number of infected people coming into the region at stage under scenario from neighboring regions. Tested infected individuals (I) move to the hospital (H) compartment, depending on the number of tested infections (I) and available hospital capacity (we use to represent the associated non-constant transmission rate). Some of the treated infected people in the hospital (H) will recover with a rate of , where R represents recovered individuals. The situations of some patients in the hospital (H) may worsen, and thus they may be transferred to the intensive care unit (we use C to represent ICU), and those individuals need ventilators for their treatment (similar to , represents the non-constant rate from (H) to (C) since this number depends on the minimum number of patients who need to be treated in ICU and the available ventilator supply in the ICU).
Fig. 1.
One-step COVID-19 compartmental model. Note that and are not constant transition rates; and they depend on the available hospital and ICU capacity, respectively.
Similar to the case of admittance into the hospital, the number of hospitalized patients transferred to an ICU at each time period is equal to the minimum of the number of patients who need to be transferred to an ICU and the number of available ventilators. The patients who are not able to receive the treatment in the ICU due to the limitation on the number of available ventilators may die at a rate of , where F represents deceased individuals. After being treated in the ICU, some of the patients may recover with a rate of , while others may die with a rate of . Different from a typical compartmental model, the transfer rate from I to H and H to C is not a constant, and it depends on the available capacity in the H and C compartments, respectively, as discussed above.
3.3. Time and space-varying transmission rate
This subsection introduces how we model COVID-19 transmission under government interventions in the mathematical model. We formulate the transmission rate as a time- and space-varying parameter, which depends on the government interventions taken at time and region . Since the onset of COVID-19, many governments have imposed different intervention strategies to reduce the transmission rate. At a certain stage, each intervention has a different impact on the transmission rate for the next stage. In this paper, we incorporate three main non-pharmaceutical interventions to formulate the time-varying transmission rate — none, mask and social distancing, and lockdown. Under the mask and social distancing, people are allowed to go to public places, but they have to wear masks and keep a 6-feet distance from each other. The lockdown represents that all the public areas are closed, and people must stay where they are. During the lockdown period, people may go out to buy necessities, but they have to wear masks and keep a 6-feet distance from each other.
Let , , and be binary decision variables that correspond to none (), mask and social distancing (), and lockdown () interventions, respectively, taken at stage and region . If takes a value of 1, then intervention is employed; otherwise, it is not employed at stage and region . The transmission rate at stage in region is a function of the transmission rate and specific intervention employed at stage in the same region, as given in the below equations:
| (1) |
| (2) |
| (3) |
where represents the percent change in the transmission rate with respect to the binary decision variable for intervention taken at stage in region . Equation (1) shows that the transmission rate at stage is a function of the transmission rate at stage and the intervention strategy taken at stage . Equation (2) indicates that only one intervention measure can be taken at each stage . Equation (3) describes the binary nature of intervention decisions.
The transmission rate in our model is not equal to the basic reproduction number, . It shows how many new tested infections will be caused by the symptomatic and asymptomatic infections from the previous stage. Since the number of new asymptomatic infections is uncertain, the number of new infections (both symptomatic and asymptomatic) changes under different scenarios even if the transmission rates at each stage stay the same.
There is a delay in the impact of the government’s interventions on the number of infections and the reaction to the test results is also slow. Therefore, we calculate the transmission rate for the first two stages directly using the real data from JHU (2020), independent of the intervention type. Based on the first two-stage transmission rates, we calculate the transmission rates from stages three to five using the formulation (1)–(3) for each intervention strategy. Also, the values of are trained using the real data obtained from JHU (2020). As an example, the initial transmission rates for the first two stages in New York and New Jersey and the impacts of government intervention strategies are shown in Table 7 under Section 5.2.
Table 7.
Transmission rate in New York and New Jersey and impact of interventions.
| County | Transmission Rate | Transmission Rate | Impact of | Impact of | Impact of |
|---|---|---|---|---|---|
| at Stage 1 | at Stage 2 | None | Mask and Social Distancing | Lockdown | |
| New York | 4.5 | 0.9855 | 1 | 0.4 | 0.6 |
| Kings | 9 | 0.9855 | 1 | 0.4 | 0.6 |
| Queens | 10 | 1.095 | 1 | 0.4 | 0.6 |
| Bronx | 12 | 1.314 | 1 | 0.4 | 0.6 |
| Richmond | 12 | 1.314 | 1 | 0.4 | 0.6 |
| Hudson | 22 | 2.409 | 1 | 0.3 | 0.6 |
| Bergen | 11 | 1.408 | 1 | 0.3 | 0.6 |
| Essex | 22 | 2.409 | 1 | 0.3 | 0.6 |
3.4. Evolution of uncertainty and multi-period scenario tree
In this subsection, we explain how we address the uncertainty of disease transmission in the mathematical model. Data regarding undetected or untested asymptomatic cases is lacking and uncertain. Therefore, we model the uncertainty regarding the proportion of untested asymptomatic infections by generating a set of scenarios , each representing a specific realization of the uncertain proportion of untested asymptomatic individuals over multiple time periods. Our scenario generation approach is similar to Alonso-Ayuso, Escudero, Guignard, & Weintraub (2018)’s method developed to model the demand uncertainty in forestry management. Each scenario has a probability of and . Since data is not available to describe the probability distribution of the uncertain variable , we assume that the uncertain parameter follows a normal distribution. The lower and upper bounds for the proportion of asymptomatic infections are obtained from the study of Meller (2020). The lower bound value for the random variable is considered as the value of 0.001-quantile, and the upper bound is considered as the value of 0.999-quantile of the normal distribution.
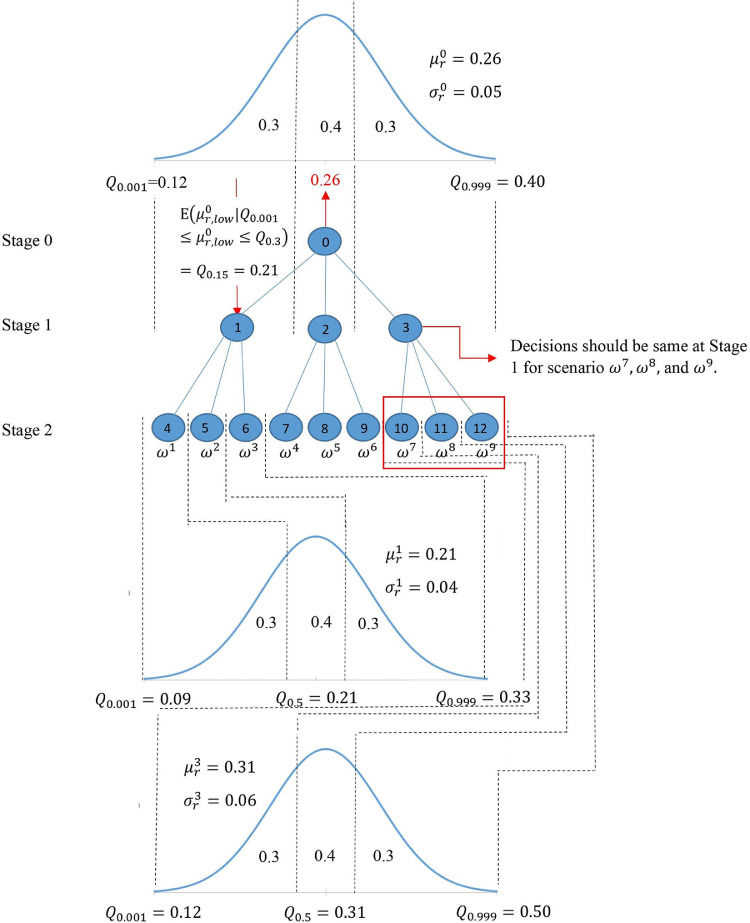
As an example, Fig. 2 shows a particular scenario tree for the proportion of untested asymptomatic infections for a two-stage problem. We consider three realizations at each node of the scenario tree by dividing its normal distribution into three discrete parts [low (L), medium (M), high (H)]. The low and high realizations have a probability of 0.3, and the medium realization has a probability of 0.4. Each path from the root node to the leaf node of the scenario tree represents a scenario . The probability of a scenario , , is calculated as the multiplication of probabilities on the path for scenario . For two stages, 9 () scenarios will be generated in this instance. The non-anticipativity constraints indicate that two scenarios are inseparable at stage if they share the same scenario path up to that stage. This means that the corresponding decision made at this stage for those two scenarios should also be the same.
Fig. 2.
Multi-stage scenario tree generation example for the uncertain proportion of untested asymptomatic infections ().
The value of the proportion of asymptomatic infections has a mean and standard deviation at stage . We use to represent the value of -quantile in the normal distribution. For each node in the scenario tree, the mean value of the low realization is the value of 0.15-quantile , the mean value of medium realization is the value of 0.50-quantile , and the mean value of high realization is the value of 0.85-quantile . For node 0 in our example, the proportion of untested asymptomatic infections at stage has = 0.26 and = 0.05. The low, medium, and high realizations at node 0 in stage and nodes 1 and 3 in stage are given in Table 2 below. According to the distributions presented in Table 2, the proportion of untested asymptomatic infections in stage 1 is realized as 0.21 (Low) at node 1, 0.26 (Medium) at node 2, and 0.31 (High) at node 3.
Table 2.
The 0.15-, 0.50-, 0.85-quantiles of the normal distribution at nodes 0, 1, and 3 of the scenario tree in Fig. 2 and the associated node of the uncertain parameter realization.
| Low (realized node) | Medium (realized node) | High (realized node) | |
|---|---|---|---|
| Node 0 Distribution | 0.21 (node 1) | 0.26 (node 2) | 0.31 (node 3) |
| Node 1 Distribution | 0.17 (node 4) | 0.21 (node 5) | 0.25 (node 6) |
| Node 3 Distribution | 0.12 (node 10) | 0.31 (node 11) | 0.50 (node 12) |
3.4.1. Decision process under uncertainty in multiple stages
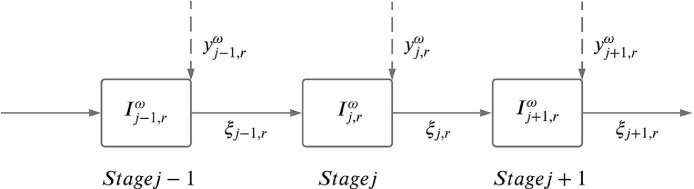
Decisions at stage are made based on the available information up to stage , which is also known as the non-anticipativity requirement. In our multi-stage stochastic program, we have two types of decision variables, namely here-and-now and wait-and-see variables. Here-and-now variables refer to ventilator allocation decision variables () that must be decided at the beginning of each time stage prior to the realization of the uncertain parameter () at that stage. Wait-and-see variables, on the other hand, refer to State Variables presented under Section 2.1 (e.g., , , and ) that are to be determined at the end of each time stage after ventilator allocation decisions at that stage are made and the outcome of the uncertain parameters are known. For example, at the beginning of stage we take a ventilator allocation action before the uncertain parameter is known at stage . Once the uncertain parameter value is realized at stage , we update the state variables at stage based on the optimal treatment actions and the ventilator allocation decisions made up to stage , and then take another ventilator allocation action before the uncertainty in stage is realized. This is followed up by updating the value of state variables based on the optimal treatment actions and the ventilator allocation decisions made up to that point in the subsequent stages.
The decision process in a multi-stage stochastic problem is equivalent to sequential decision making over multiple periods where here-and-now and wait-and-see decisions follow each other, as illustrated in an example in Fig. 3 . In this example figure, we represent here-and-now and wait-and-see decisions to be taken at each stage as and , respectively, and the uncertain parameter in stage and in region is represented by . In each time stage , the realization of is known only after the decisions at stage , , have already been made. Once is realized, we make the state decisions represented by at stage .
Fig. 3.
Decision process in a multi-stage stochastic program over stages .
3.5. Model features and assumptions
Since the transmission of COVID-19 is affected by many factors, data to calibrate some of the model parameters, such as the impact of human mobility, is either lacking or inaccurate. Therefore, we incorporate some important features and make some assumptions in the model formulation.
Important features. First, we consider the impact of different intervention strategies on the disease transmission rate and adjust the short-term migration population depending on the intervention strategy. For instance, under the lockdown strategy, we assume that the short-term migration among each county is zero. Under mask and social distancing strategies, the short-term migration population among each county is reduced to 60% of the original value, as estimated from the study of Lee et al. (2020). Second, we incorporate the cost for purchasing ventilators to provide a capacity limitation on the total number of ventilators that could be allocated for treating COVID-19 patients. Since there are significant fluctuations in the ventilator prices (Glass, 2020), we consider the minimum purchase price for each ventilator acquired. Third, we train the real data to determine the impact rate of each intervention strategy on the disease transmission rate. The trained value of the impact of interventions can only be used in the regions considered in our case study since all the selected counties in New York and New Jersey are geographically close to each other, and thus interventions have similar social effects. However, for example, the impact of intervention strategies in a rural area may be different from those taken in a city. To estimate the transmission of COVID-19 in other U.S. regions, the model should be re-trained using the associated data.
Assumptions. First, the proportion of untested asymptomatic people is an uncertain parameter in our model. Studies regarding the asymptomatic infections specific to New York City region are limited. Since studied counties in New Jersey and New York are geographically and socially close to each other, the proportions of untested asymptomatic infections at each stage under scenario are set to be the same for each region . We make this assumption based on the characteristics of these regions. Many people who live in these counties work in New York City, and the short-term migration among each region is quite frequent. Thus, we use the same lower and upper bound of untested asymptomatic infections for these regions. Although the asymptomatic proportion is the same under each scenario, the number of untested asymptomatic infections is different in each region because of the difference in the transmission rate and the initial number of infections. Second, the model considers allocating newly purchased ventilators for the treatment of COVID-19 patients instead of re-allocating existing ventilators from other counties or states since the demand for ventilators during the disease’s peak periods is high for all the counties and states, and there is a lead time for transfer of the ventilators between the states that are far from each other. Here, we also assume a central decision maker is entitled to allocate a given supply of ventilators to multiple regions. Third, the infected individuals who cannot be treated in the hospital (both severe and less severe) due to the limited capacity have the same death rate as people who cannot be treated in the ICU due to the limited ventilator supply. This is because the health condition of both groups may worsen without professional treatment. Fourth, we assume that “I” compartment represents tested infected individuals, including all symptomatic and part of the asymptomatic infections. Thus, all the symptomatic infections and part of the asymptomatic infections are tested. The uncertain parameter is the proportion of the untested asymptomatic infections. It is natural for humans to protect themselves as they learn more about an epidemic due to their survival instincts. Thus, fifth, we assume that people react to the pandemic by anticipating the government’s interventions and may start social distancing and quarantining days or weeks before an intervention is imposed, as also reported in multiple studies, see, e.g., Zhang et al. (2020) and Fischer et al. (2020). Therefore, the transmission rate with either doing nothing or mask and social distancing shows a decreasing trend in later stages of the pandemic due to physical distancing among people. Sixth, we use each county’s ICU capacity from JHU (2020) as the initial ventilator availability. We assume that non-COVID-19 patients use 60% of this capacity (Mehrotra et al., 2020). Thus, only 40% of the initial ICUs are available for treating COVID-19 patients. Lastly, the incubation period of COVID-19 ranges from 2 to 14 days (CDC, 2021). We assume that the infected compartment includes the incubation period. Thus, we use a two-week period for each time stage to make sure people who are infected but still in the incubation period at the beginning of each stage are counted as infected at the same stage.
3.6. Multi-Stage risk and time consistency
The -quantile of the cumulative distribution of a random variable , , is defined as the value-at-risk (VaR) at the confidence level and denoted by . The conditional expected value that exceeds the VaR at the confidence level is called conditional value-at-risk (CVaR), defined as . For a minimization problem, is the -quantile of the distribution of the cost, and it provides an upper bound on the cost that is exceeded only with a small probability of . measures an expectation of the cost that is more than , and can be calculated as an optimization problem as follows (Rockafellar & Uryasev, 2002):
where for any .
We formulate our model as a mean-risk minimization problem:
| (4) |
where is the expected cost function over the scenarios , represents the conditional value-at-risk at , and is a non-negative weighted risk coefficient, and it can be adjusted for a trade-off between optimizing an expectation value and the level of risk taken.
Time Consistency. Time consistency is considered as a critical issue when modeling a risk-averse multi-stage stochastic program. Time consistency means that if you solve a multi-stage stochastic programming model today, you should get the same solution if you resolve the problem tomorrow, given the information that is observed and decided today. We consider a nested risk measure, expected conditional value-at-risk (), as defined in Homem-de Mello & Pagnoncelli (2016) since it is shown to satisfy the time consistency of multi-stage stochastic programs. The can be linearized and formulated as a linear stochastic programming model. In the following section, we will utilize the as a risk measure in our formulation.
3.7. Mathematical model formulation and description
The mathematical formulation for our risk-averse multi-stage stochastic epidemics-ventilator-logistics model (5a)–(5w) is given below.
Epidemics-Ventilator-Logistics Model Formulation:
| (5a) |
| (5b) |
| (5c) |
| (5d) |
| (5e) |
| (5f) |
| (5g) |
| (5h) |
| (5i) |
| (5j) |
| (5k) |
| (5l) |
| (5m) |
| (5n) |
| (5o) |
| (5p) |
| (5q) |
| (5r) |
| (5s) |
| (5t) |
| (5u) |
| (5v) |
| (5w) |
Objective Function(5a). The objective function (5a) minimizes the total expected number of tested infected individuals and deaths and the conditional value-at-risk over all stages and scenarios .
Population Infection Dynamics Constraints(5b)–(5j). Constraints (5c) give the initial number of the susceptible, tested infected, untested asymptomatic infected, hospitalized, ICU patients, recovered, and deceased individuals, respectively, in each region at the beginning of the planning horizon. Constraint (5d) makes sure that the number of susceptible individuals in region at stage under scenario equals the number of susceptible individuals at stage minus the number of susceptible individuals who become either tested infected or untested asymptomatic infected at stage . In this equation, the number of untested asymptomatic infections equals the number of tested infections multiplied by the proportion of the untested asymptomatic infections to the tested infections. Constraint (5e) shows that the number of tested infected individuals in region at stage under scenario equals the number of tested infected individuals at stage plus the infected individuals caused by short-term migration, plus the newly tested infections at time , minus the recovered and deceased infections of tested individuals at stage , minus the hospitalized individuals at stage . Constraint (5f) implies that the number of untested asymptomatic infections in region at stage under scenario equals the number of untested asymptomatic infections at stage plus new, untested asymptomatic infections, minus the recovered untested asymptomatic infections at stage . Constraint (5g) shows that the hospitalized individuals in region at stage under scenario equals the number of hospitalized individuals at stage plus the newly hospitalized individuals at stage , minus the recovered and deceased individuals at stage , minus the individuals who move to the intensive care unit (ICU) at stage . Constraint (5h) indicates that the total number of individuals in ICU in region at stage under scenario equals the total number of individuals in ICU at stage plus the individuals who moved to an ICU at stage , minus the individuals who are recovered or died at the ICU at stage . Constraint (5i) shows that the number of recovered individuals in region at stage under scenario equals the number of recovered individuals at stage plus the recovered individuals from tested infected, untested asymptomatic infected and hospitalized individuals, and ICU patients at stage . Constraint (5j) indicates that the number of deceased individuals in region at stage under scenario equals the number of deceased individuals at stage plus the deceased individuals from tested infected and hospitalized individuals and ICU patients at stage .
Ventilator Logistics and Capacity Constraints(5k)–(5r).
Both (5k) and (5l) are, respectively, equivalent linear constraints of
| (6) |
| (7) |
with additional linearization variables, using the method presented in Yin & Büyüktahtakın (2021a), Kıbış & Büyüktahtakın (2017). Constraints (5k) [or non-linear equivalent (6)] ensure that the number of individuals admitted to the hospital in region at stage under scenario equals the minimum number of individuals who require hospitalization and the available hospital capacity at stage . Constraints (5l) [or non-linear equivalent (7)] imply that the number of individuals admitted to an ICU in region at stage under scenario equals the minimum number of individuals who require treatment in ICU and the number of available ventilators at stage . Constraint (5m) represents that the cumulative number of ICU beds (equivalent to ventilators) in region at stage under scenario equals the initial number of ICU beds plus the cumulative number of ICU beds (new ventilators) allocated from stage 1 to stage . Constraints (5n)–(5q) show that the number of individuals who can not be admitted to the hospital or the ICU due to limited capacity should be greater than or equal to zero. Constraint (5r) represents that the cost of ventilators allocated over all regions and time stages under scenario cannot exceed the total budget allocated for ventilators. The budget here also represents the maximum total ventilator supply that could be available throughout the planning horizon.
Risk Measure Constraints(5s) and (5t). Constraint (5s) indicates the difference between the objective function value and the value-at-risk for each stage under each scenario . Constraint (5t) ensures that the loss value exceeding the value-at-risk is included in the CVaR calculation, and thus should be greater than or equal to zero.
Non-Anticipativity, Non-Negativity and Integrality Constraints(5u)–(5w). Constraint (5u) is the non-anticipativity constraint, indicating that the scenarios that share the same path up to stage should also have the same corresponding decisions. Constraint (5v) indicates that the number of individuals in each compartment in region at stage under scenario should be greater or equal to zero. Constraint (5w) implies that the number of allocated ventilators should be an integer. We implement this mixed-integer linear programming (MILP) formulation (5a)–(5w) for the rest of the paper.
4. New lower and upper bounds
4.1. Region sub-problem and bounds
We present a new region sub-problem and lower and upper bounds to reduce the optimality gap of solving our risk-averse multi-stage stochastic programming problem (5a)–(5w). We are inspired by the study of Büyüktahtakın (2021), where the general risk-averse stochastic MILP problem was decomposed into scenario sub-problems, while keeping all original constraints the same in the sub-problem. However, our sub-problem is different than that of Büyüktahtakın (2021) in that we decompose the problem with respect to the regions rather than scenarios and then derive bounds based on those sub-problems. Further, we decompose the problem into two: region- and risk sub-problems. The new scenario sub-problem and bounds are described below.
Definition 4.1
(Region- Sub-problem) The region- problem is formulated as follows:
(8a)
(8b)
Specifically, in we minimize the objective function value only under region while keeping all the variables and the constraints from the original problem (5a)–(5w), .
Proposition 1
(Region-Lower Bound) Letbe the optimal solution forcorresponding to region. Then the following inequality holds:
(9)
Proof
and share the same feasible region, but minimizes the full objective function (5a), while only minimizes the objective function for only region (8a). Thus, the optimal solution of for region , , is feasible but sub-optimal for . □
In order to get a lower bound on the full objective function (5a), we define the risk sub-problem as follows:
Definition 4.2
(Risk Sub-problem) The risk sub-problem is formulated as follows:
(10a)
(10b)
Proposition 2
is superadditive on, which means that for
(11)
Proof
, , and share the same feasible region with . Thus, the optimal solution of the is feasible but sub-optimal for each of and . □
Proposition 3
(Lower Bound) Letrepresent the objective function of the original problem(5a)–(5w),. Then we have:
(12)
Proof
The proof follows from the generalization of the superadditivity result in Proposition 2 and the equivalence of and by Definition 4.1. In other words, we have:
Proposition 4
(Upper Bound) Letbe the optimal solution of region-problem,, andbe the objective value of original problem(5a)–(5w)whereis substituted in the original problem objective function(5a). Then we have:
(13)
Proof
Because is the optimal solution for , it is feasible for problem (5a)–(5w). As holds for each , is bounded above by the minimum over all . □
4.2. Computational results
In our computational experiments, we demonstrate the effectiveness of the proposed region- bounds (R) in solving our risk-averse multi-stage stochastic programming problem (5a)–(5w). We use the CPLEX solution and the scenario- bounds (S) proposed by Büyüktahtakın (2021) as comparison benchmarks under different budget levels with the following solution approaches:
-
•
cpx: Direct solution of the model (5a)–(5w) by CPLEX using its default settings.
-
•
lb: Region- lower bound inequalities (9) (lb–) or scenario- lower bound inequalities (lb–).
-
•
ub: Upper bound inequalities (13) (ub–) or scenario- upper bound inequalities (ub–).
-
•
lb+ub: Inequalities (9) and (13) (lb+ub–) or scenario- lower and upper bound inequalities (lb+ub–).
In Table 3 , we report results for a combination of columns defined as follows.
-
•
Budget: The total budget level used.
-
•
Exp: Solution approach.
-
•
CutTime: Inequality generation time in CPU seconds, including the solution of all sub-problems used to generate bounds.
-
•
Time: Total CPU seconds required to solve the problem, including inequality generation time (CutTime).
-
•
MIPGap: Final optimality gap for any given Exp (cpx, lb, ub, or lb+ub) at the end of the time limit.
-
•
GapImp: Percentage improvement in MIPGap using lb, ub, or lb+ub. For example, for ub, (GapImp = 100 (1- MIPGap/MIPGap), where MIPGap and MIPGap are the final optimality gaps by cpx and ub, respectively.
-
•
IGap: Percentage integrality gap of the formulation before inequalities are added (InitGap = 100 (bestobj - relaxlb)/bestobj), where relaxlb and bestobj are objective function values of the initial Linear Programming (LP) relaxation and the best feasible solution by cpx, respectively.
-
•
RGap: Percentage integrality gap of the formulation after inequalities are added (RootGap = 100 (bestobj - rootlb)/bestobj), where rootlb is the objective function value of the initial LP relaxation after lb and ub are added.
-
•
GapImp: Percentage improvement in the integrality gap at the root node (GapImp = 100 (1-RGap/IGap).
-
•
R: Method using region- bounds for 5 region sub-problems.
-
•
S: Method using scenario- bounds proposed by Büyüktahtakın (2021) for 40 scenario sub-problems.
Table 3.
Optimality gap results using lb, ub, and lb+ub for and under different budget levels.
| Budget | Exp | CutTime |
Time |
MIPgap |
GapImp |
Igap | Rgap | GapImp | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (CPU sec) |
(CPU sec) |
(%) |
(%) |
(%) | (%) | (%) | ||||||
| R | S | R | S | R | S | R | S | R | R | |||
| $30M | cpx | 0 | 7203 | 13.1 | 13.9 | |||||||
| lb | 797 | 1330 | 8098 | 8536 | 13.1 | 13.3 | 0.1 | 0.0 | 13.2 | 4.9 | ||
| ub | 848 | 1306 | 8068 | 8524 | 8.1 | 7.9 | 38.3 | 39.4 | 13.9 | 0.0 | ||
| lb+ub | 965 | 1331 | 8294 | 8535 | 8.0 | 9.3 | 38.6 | 29.0 | 13.2 | 4.9 | ||
| $35M | cpx | 0 | 7203 | 9.3 | 10.3 | |||||||
| lb | 171 | 1234 | 7476 | 8438 | 9.3 | 13.4 | 0.0 | 0.0 | 9.4 | 9.0 | ||
| ub | 157 | 1314 | 7393 | 8530 | 8.3 | 7.8 | 10.4 | 15.8 | 10.3 | 0.0 | ||
| lb+ub | 178 | 1270 | 7501 | 8481 | 8.3 | 10.1 | 11.0 | 0.0 | 9.4 | 9.0 | ||
| $40M | cpx | 0 | 7204 | 9.6 | 10.7 | |||||||
| lb | 434 | 1080 | 7736 | 8282 | 9.5 | 13.3 | 0.4 | 0.0 | 9.5 | 10.7 | ||
| ub | 434 | 1098 | 7654 | 8302 | 8.3 | 7.8 | 13.4 | 19.1 | 10.7 | 0.0 | ||
| lb+ub | 434 | 1088 | 7754 | 8291 | 8.3 | 9.2 | 13.1 | 4.0 | 9.5 | 10.7 | ||
| $45M | cpx | 0 | 7203 | 9.3 | 10.4 | |||||||
| lb | 1381 | 1354 | 8682 | 8358 | 9.3 | 13.4 | 0.1 | 0.0 | 9.2 | 12.1 | ||
| ub | 1252 | 1132 | 8458 | 8334 | 8.1 | 8.0 | 13.0 | 14.4 | 10.4 | 0.0 | ||
| lb+ub | 1335 | 1121 | 8639 | 8324 | 8.2 | 7.7 | 12.2 | 17.8 | 9.2 | 12.1 | ||
| $50M | cpx | 1 | 6775 | 0.0 | 1.1 | |||||||
| lb | 204 | 982 | 7086 | 8188 | 0.0 | 13.4 | 0.0 | 0.0 | 0.0 | 100.0 | ||
| ub | 215 | 969 | 7424 | 8172 | 0.0 | 7.4 | 0.0 | 0.0 | 1.1 | 0.0 | ||
| lb+ub | 220 | 956 | 7524 | 8168 | 0.0 | 7.1 | 0.0 | 0.0 | 0.0 | 100.0 | ||
| Average | cpx | 0 | 7118 | 8.3 | 9.3 | |||||||
| lb | 598 | 1156 | 7816 | 8360 | 8.2 | 13.4 | 0.1 | 0.0 | 8.3 | 27.3 | ||
| ub | 581 | 1164 | 7799 | 8372 | 6.6 | 7.8 | 15.0 | 17.7 | 9.3 | 0.0 | ||
| lb+ub | 626 | 1153 | 7942 | 8360 | 6.6 | 8.7 | 15.0 | 10.2 | 8.3 | 27.3 | ||
Table 3 presents the results for CutTime, Time, MIPgap, and GapImp over cpx and lb, ub and lb+ub for both and . Since a scenario- sub-problem is a weaker relaxation of the original problem (5a)–(5w) compared to a region- sub-problem, lb– provides a weaker lower bound for the original problem than lb–, and thus does not improve the Igap given a limited number of scenario sub-problems used in . Therefore, we only demonstrate Igap, Rgap, and GapImp for . Each row of Table 3 presents results for an instance with budget levels , , , , and , while the Average row represents average results for all instances. Overall, instances get easier as the budget level increases, GapImp and GapImp due to show a decreasing and increasing trend, respectively. Both lb and ub for and are generated within 10 and 20 CPU minutes, respectively, on average. Our preliminary results have shown that region- lower bound inequalities (9) performed better than the lower bound (12); thus we do experiments using the inequalities (9). In Table 3, ub– provides the best benefit in reducing the MIPgap at the end of the time limit, while lb– helps the most in reducing the LP relaxation gap. For example, ub– improves the MIP gap by , while lb– reduces the initial gap by on average. Thus, we recommend adding ub– as a cut into the formulation to reduce the final MIP gap and using lb– only in the branch and bound tree to strengthen the LP relaxation of the formulation. Note the instance with is relatively easy, and thus the MIP gap is zero after two hours of the time limit, and the LP relaxation gap of is completely closed by lb–. Compared with , takes more time to generate and does not provide a better final MIP gap under lb– and lb+ub– over the corresponding bounds. However, ub– provides a better MIP gap (MIPgap and GapImp ) than ub–, except for the easiest instance with the budget level.
5. Case study data
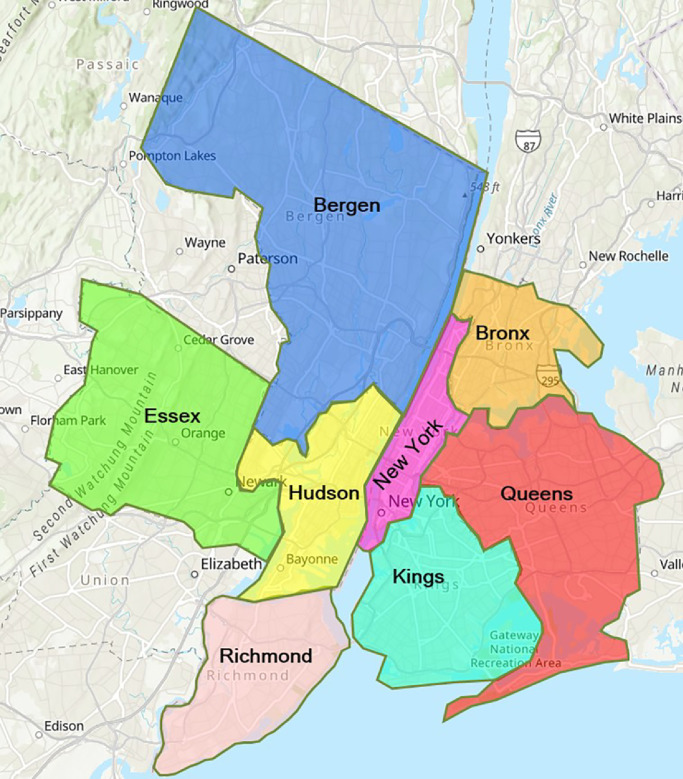
This section provides the data used to calibrate model parameters and formulate the model, including population and short-term migration data, transmission parameters, as well as the cost of a ventilator. As shown in Fig. 4 , we select eight counties that are most impacted by the pandemic in the states of New York and New Jersey for our case study. They are New York County, Kings County, Queens County, Bronx County, Richmond County, Hudson County, Bergen County, and Essex County. In our multi-stage model, each stage represents a two-week period. Thus, all the data regarding transmission and migration are bi-weekly.
Fig. 4.
Counties in New York and New Jersey (Source: Environmental Systems Research Institute (ESRI) (2021)).
5.1. Population and migration data
Table 4 shows the population data for each considered county in New York and New Jersey. Population data is obtained from JHU (2020). The migration rates among the considered counties, estimated from the data on CENSUS (2020), are presented in Table 5 . The blank areas in Table 5 represent a zero short-term migration because the movement among those counties is too small to make an impact on the model results.
Table 4.
Counties and population sizes in New York and New Jersey.
| New York | Population | New Jersey | Population | |
|---|---|---|---|---|
| New York | 1,632,480 | Hudson | 668,631 | |
| Kings | 2,600,747 | Bergen | 929,999 | |
| Queens | 2,298,513 | Essex | 793,555 | |
| Bronx | 1,437,872 | |||
| Richmond | 474,101 | |||
| Total | 8,443,713 | 2,392,185 |
Table 5.
Migration rate among counties in New York and New Jersey.
| To | New York | Kings | Queens | Bronx | Richmond | Hudson | Bergen | Essex |
|---|---|---|---|---|---|---|---|---|
| From | ||||||||
| New York | 0.015 | 0.012 | 0.009 | 0.006 | 0.007 | 0.007 | 0.007 | |
| Kings | 0.192 | 0.038 | 0.004 | 0.004 | ||||
| Queens | 0.218 | 0.044 | 0.009 | 0.002 | ||||
| Bronx | 0.209 | 0.014 | 0.028 | 0.003 | 0.003 | |||
| Richmond | 0.105 | 0.105 | ||||||
| Hudson | 0.040 | 0.001 | 0.040 | 0.040 | ||||
| Bergen | 0.126 | 0.039 | 0.039 | |||||
| Essex | 0.079 | 0.001 | 0.057 | 0.057 |
5.2. Epidemiological data
Table 6 presents the data values for transmission parameters for the studied counties in New York and New Jersey. The data contains the proportion of untested asymptomatic infections, recovery rate, and the death rate for tested infections, hospitalized infections, and ICU patients. Table 7 shows the transmission rate of each county at the first two stages and the impacts of applying different intervention strategies, as discussed in Section 3.3.
Table 6.
Transmission parameters and bi-weekly rates for COVID-19.
| Parameter | Description | Data | Reference |
|---|---|---|---|
| Proportion of untested asymptomatic infections | 0.15-0.4 | Meller (2020) | |
| Recovery rate without hospitalization | 0.69-0.79 | Hogan (2020) | |
| Death rate without hospitalization | 0.4 | Trained using real data from JHU (2020) | |
| Hospitalization rate | 0.21-0.31 | Hogan (2020) | |
| Recovery rate with hospitalization | 0.88 | Hogan (2020) | |
| Death rate with hospitalization (No ventilators) | 0.4 | Trained using real data from JHU (2020) | |
| Ventilator requirement rate of hospitalized | 0.12 | Hogan (2020) | |
| Recovery rate with ventilator | 0.643 | Bernstein (2020) | |
| Death rate with ventilator | 0.357 | Bernstein (2020) | |
| Recovery rate with asymptomatic infections | 1 | Bertsimas et al. (2020) |
5.3. Initial infection, capacity and cost data
Table 8 shows the initial number of infections, hospital capacity, and ICU capacity for each county. The data is obtained from JHU (2020).
Table 8.
Initial number of infections, hospital capacity, and ICU capacity for each county.
| County | Initial | Initial | Initial |
|---|---|---|---|
| Infections | Hospital Capacity | ICU Capacity | |
| New York | 1200 | 8650 | 944 |
| Kings | 1300 | 5838 | 282 |
| Queens | 1100 | 3210 | 146 |
| Bronx | 554 | 2816 | 274 |
| Richmond | 206 | 1177 | 72 |
| Hudson | 66 | 1764 | 89 |
| Bergen | 249 | 2874 | 122 |
| Essex | 73 | 3541 | 226 |
Ventilator Cost. The cost of each ventilator ranges from $5000 to $50,000 (Glass, 2020). In our case, we consider a cost of $5000 for each ventilator, and different budget levels are set to impose different upper bounds on the ventilator supply.
6. Results
6.1. Model validation
This section presents the validation results of the mathematical model in Eqs. (5a)–(5w) as presented in Section 3 for the 8-stage time period from April 3, 2020, to July 10, 2020. We consider a medium realization of the uncertain asymptomatic proportions at each stage of the planning horizon and compare the number of infections forecasted by our model to the real outbreak data.
The government applied a lockdown strategy from April 3, 2020, to July 10, 2020, at those considered locations in New York and New Jersey. Thus, we use the lockdown strategy and the corresponding transmission rate at each stage in our model for validation.
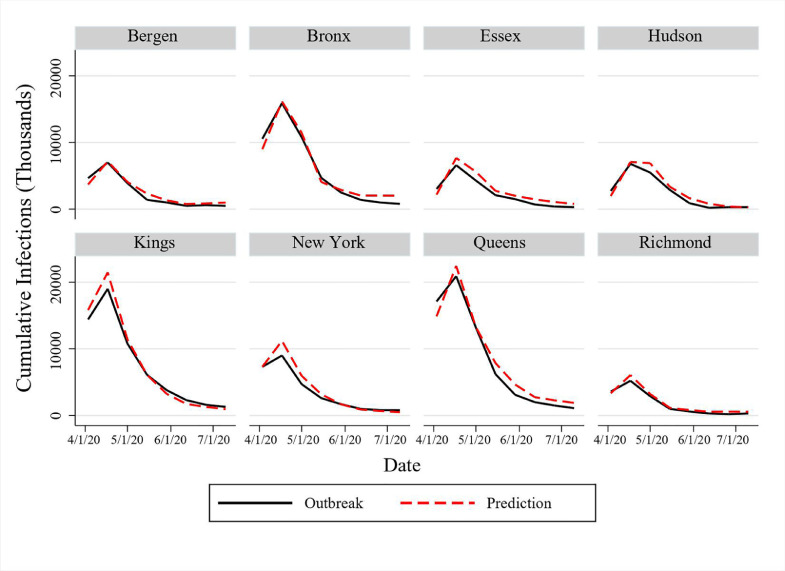
Figure 5 shows the comparison between the predicted infections and real outbreak data. The model’s predictions give a good approximation for the actual number of new infections in each region, implying that the model can capture the disease transmission dynamics under a lockdown intervention strategy. Similar to the validation approaches of Kıbış et al. (2021) and Kıbış & Büyüktahtakın (2019), we also perform a paired--test to analyze the difference between the pairs of predicted new infections and the actual data in each period. As shown in Table 9 , all -values are greater than 0.05, and thus our model provides statistically similar predictions with the real outbreak data from April 3, 2020, to July 10, 2020, for each considered county.
Fig. 5.
Comparison of predicted cases with real outbreak data for new infections in New York and New Jersey.
Table 9.
Statistical analysis to compare the bi-weekly predicted new cases and real outbreak data.
| County | Mean |
Two-tailed paired-t-test |
|||||
|---|---|---|---|---|---|---|---|
| Outbreak | Predicted | t-stat | t-critical | p-value | |||
| New York | 7300 | 7299 | 0.20 | 2.36 | 0.58 | ||
| Kings | 7413 | 7754 | 0.41 | 0.65 | |||
| Queens | 8138 | 8751 | 0.21 | 0.58 | |||
| Bronx | 5956 | 6214 | 0.46 | 0.67 | |||
| Richmond | 1762 | 2040 | 0.04 | 0.51 | |||
| Hudson | 2455 | 2806 | 0.16 | 0.56 | |||
| Bergen | 2444 | 2656 | 0.30 | 0.61 | |||
| Essex | 2366 | 2948 | 0.04 | 0.51 | |||
6.2. Case study implementation details
We apply our model described in Section 3 to the selected counties in New York and New Jersey. We first solve the risk-neutral model. We incorporate the uncertainty of the proportion of untested asymptomatic infections as well as the short-term migration in the disease transmission and forecast the number of new infections, deceased individuals, hospitalized individuals, and ICU patients under different intervention strategies. Also, we solve the model to determine the optimal location and number of ventilators allocated under different budget levels and scenarios to provide insights into resource allocation over multiple jurisdictions under uncertainty. Due to the high complexity of the mathematical formulation, we solve it for a 5-stage time period. Each stage corresponds to two weeks, resulting in a planning horizon of ten weeks from March 20, 2020, to May 29, 2020. Because each node of the scenario tree has three possible realizations of the random parameters, we solved 243 () scenarios simultaneously.
The mathematical model is solved using CPLEX 12.7.1 on a desktop computer running with Intel i7 CPU and 64.0 GB of memory. We set the time limit at 7200 CPU seconds to solve each test instance. We extend running time for specific budget levels ( Million) and interventions (“Lockdown”) due to the large optimality gap. In the following subsections, we present results from solving the multi-stage stochastic epidemics-ventilator-logistics model with an application to the case of COVID-19 using the data presented in Section 5.
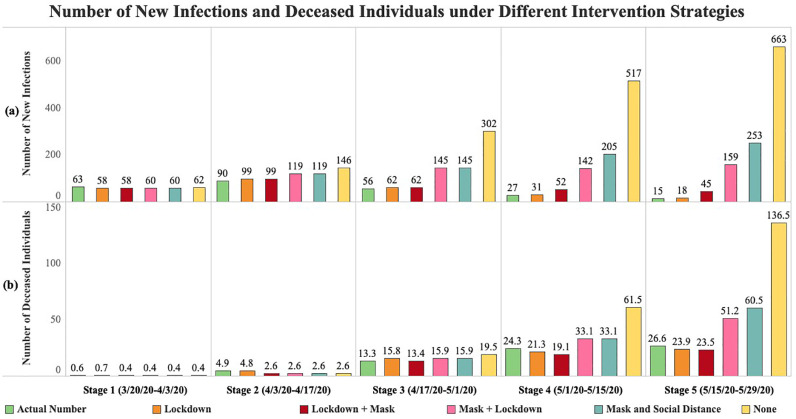
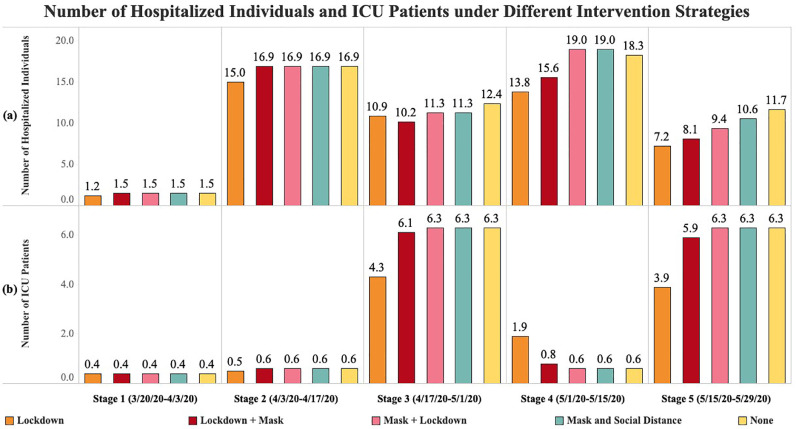
6.3. Transmission forecast under different intervention strategies
Here, we present results of our formulation for each time period under different intervention strategies: No intervention (“None”), mask and social distancing for all stages (“Mask and Social Distance”), lockdown for all stages (“Lockdown”), mask and social distancing for the first three stages and lockdown for the following two stages (“Mask + Lockdown”), lockdown for the first three stages and mask and social distancing for the following two stages (“Lockdown + Mask”). The model is solved under the million budget level. The model with the “Lockdown” strategy gives a optimality gap after a run time of 43,241 CPU seconds, while the model solved for all other strategies has a zero optimality gap within 7200 CPU seconds.
Figure 6 presents the number of infections and deceased individuals at each stage under different intervention strategies. According to the results, short-term migration influences the number of new infections even under constant transmission rates. As in the first stage, with the same initial transmission rate, the number of infections under different intervention strategies is different from each other. When the stage increases, the difference in the number of new infections among each intervention strategy becomes more and more significant. The “None” strategy has the most infections at each stage, followed by the “Mask and Social Distance” strategy. The “Lockdown” strategy results in the lowest number of new infections compared to those under other strategies at each stage. The “Lockdown” strategy provides a marginally higher number of infections compared to the actual infection data since our model slightly (but statistically insignificantly) overestimates the number of infections. Compared to the “Mask + Lockdown” strategy, the “Lockdown + Mask” intervention leads to fewer infections. This implies that applying the “Lockdown” strategy immediately at the onset of the pandemic followed by the “Mask and Social Distance” intervention is a better strategy than enforcing “Mask and Social Distance” first and delaying the lockdown.
Fig. 6.
Number of new infections and deaths under different intervention strategies and actual numbers (numbers are rounded in thousands).
The intervention strategy does not influence the number of deceased individuals as quickly as it impacts the number of infections, as shown in Fig. 6. Here, the number of deceased individuals at the first two stages is much lower than that of the last three stages. Starting from stage three, the number of deceased individuals under different intervention strategies shows a similar trend with the number of new infections. The influence of interventions is further delayed for those confirmed infections to be treated in the hospital and ICU (Fig. 7 ).
Fig. 7.
Number of hospitalized individuals and ICU patients under different intervention strategies (numbers are rounded in thousands).
To reduce both the number of new infections and deaths, “Lockdown” is the best strategy. As shown in Fig. 6b, the “Lockdown” strategy with the optimal ventilator allocation further reduces the actual number of deaths. Due to the negative impact of COVID-19 on employment and its economic burden, governments are often forced to stop the lockdown and reopen businesses. In such cases, applying “Mask and Social Distance” after a certain period of “Lockdown” will be the best choice.
Figure 7 shows the number of hospitalized individuals and ICU patients at each stage under different intervention strategies. Similar to the number of deceased individuals, there are delays in the impact of government interventions on the number of hospitalized individuals and ICU patients. An infected person may have mild symptoms for about one week, then worsen rapidly (Harvard Medical School (2021)). Thus, it may take some time for patients to be admitted to the ICU, so the impact of interventions on the number of ICU patients is delayed one more stage compared to the hospitalized cases. As shown in Fig. 7, a higher number of hospitalized individuals at stage will lead to more ICU patients at stage .
For all the stages, the “Lockdown” strategy has the lowest number of hospitalized individuals and ICU patients, followed by the “Lockdown + Mask” intervention. The ICU patients of “None,” “Mask and Social Distance,” and “Mask + Lockdown” are almost the same at stages three to five. This is because under those, the need for ventilators is large, and the number of treated individuals in ICUs depends on the minimum number of patients who require ventilators and the ventilator supply in those ICUs. Therefore, the number of treated patients in ICUs is limited by the tight ventilator availability.
6.4. Optimal ventilator allocation under varying costs and budgets
Table 10 shows the number of ventilators allocated to each region at stages one and two and the total number of ventilators allocated throughout the planning horizon under different budget levels and three select scenarios. The “All Low,” “All Medium,” and “All High” scenarios represent low, medium, and high realization of the proportion of untested asymptomatic infections at each stage of a five-stage planning horizon, respectively. To analyze the impact of budget on the optimal ventilator allocation decisions, we select M as the limited budget level, M as the medium budget level, and M as the ample budget level. The model has zero optimality gap under the M budget level, optimality gap under the M budget level, and optimality gap under the M budget level within two hours of solution time.
Table 10.
Optimal ventilator allocation under different scenarios and budgets with unit ventilator cost of $5000.
| Scenario | County | Stage | Stage | Total | Stage | Stage | Total | Stage | Stage | Total |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | Ventilator | 1 | 2 | Ventilator | 1 | 2 | Ventilator | ||
| (Budget=M) | (Budget=M) | (Budget=M) | ||||||||
| All Low | New York | 0 | 0 | 0 | 0 | 86 | 86 | 780 | 82 | |
| Kings | 119 | 0 | 119 | 418 | 0 | 418 | 120 | 1950 | ||
| Queens | 105 | 1120 | 1225 | 1225 | 0 | 1225 | 4 | 0 | 4 | |
| Bronx | 28 | 0 | 28 | 28 | 988 | 1016 | 28 | 988 | 1016 | |
| Richmond | 18 | 0 | 18 | 18 | 314 | 332 | 17 | 315 | ||
| Hudson | 0 | 250 | 250 | 247 | 3 | 0 | 250 | |||
| Bergen | 14 | 128 | 142 | 13 | 438 | 451 | 13 | 438 | ||
| Essex | 0 | 218 | 218 | 218 | 0 | 218 | 0 | 218 | ||
| Total | 284 | 1716 | 2000 | 2167 | 1829 | 962 | 4241 | |||
| All Medium | New York | 0 | 0 | 0 | 0 | 0 | 0 | 780 | 0 | 780 |
| Kings | 119 | 0 | 119 | 418 | 25 | 443 | 120 | 1950 | 2070 | |
| Queens | 105 | 776 | 881 | 1225 | 0 | 1225 | 4 | 1187 | 1191 | |
| Bronx | 28 | 44 | 72 | 28 | 988 | 1016 | 28 | 989 | 1017 | |
| Richmond | 18 | 0 | 18 | 18 | 379 | 397 | 17 | 6 | 23 | |
| Hudson | 0 | 245 | 245 | 247 | 3 | 250 | 0 | 250 | 250 | |
| Bergen | 14 | 437 | 451 | 13 | 438 | 451 | 13 | 438 | 451 | |
| Essex | 0 | 214 | 214 | 218 | 0 | 218 | 0 | 218 | 218 | |
| Total | 284 | 1716 | 2000 | 2167 | 1833 | 4000 | 9,62 | 5038 | 6000 | |
| All High | New York | 0 | 0 | 0 | 0 | 0 | 0 | 780 | 82 | |
| Kings | 119 | 0 | 119 | 418 | 0 | 418 | 120 | 1950 | 2070 | |
| Queens | 105 | 137 | 242 | 1225 | 0 | 1225 | 4 | 0 | 4 | |
| Bronx | 28 | 924 | 952 | 28 | 988 | 1016 | 28 | 988 | 1016 | |
| Richmond | 18 | 0 | 18 | 18 | 404 | 422 | 17 | 34 | 51 | |
| Hudson | 0 | 0 | 0 | 247 | 3 | 250 | 0 | 0 | 0 | |
| Bergen | 14 | 437 | 451 | 13 | 438 | 451 | 13 | 438 | 451 | |
| Essex | 0 | 218 | 218 | 218 | 0 | 218 | 0 | 218 | 218 | |
| Total | 284 | 1716 | 2000 | 2167 | 1833 | 4000 | 962 | 3710 | ||
Some of the ventilators are allocated at stages three and four.
The results in Table 10 demonstrate that the location and number of ventilators allocated depend on several factors, including the initial and evolving disease transmission rates, the population and the number of initial infections in a region, and the existing ventilator capacity. Thus, the optimal ventilator allocation should be determined case-by-case.
According to the results, the total number of ventilators allocated increases in the budget level due to the high need for ventilators. As shown in Table 10, some regions with many initial infections, e.g., New York County, do not receive ventilators. This situation occurs because the initial ventilator capacity of those regions is higher than in other counties. Also, results suggest that more ventilators should be distributed to other areas with a higher initial transmission rate than New York County, such as Kings and Queens. Both Kings and Queens have higher initial transmission rates and lower initial ICU capacity than New York. Thus, these regions get more ventilators allocated. Also, regions with a smaller population, such as Bergen and Essex in New Jersey, get a large share of ventilators due to their high transmission rates at the beginning of the pandemic and under the “All High” scenario compared to other New Jersey counties, such as Richmond and Hudson.
Under a limited budget level, some regions with low initial infections and low initial ICU capacity (e.g., Bronx) get more ventilators allocated when the scenario changes from “All Low” to “All Medium” and “All High.” Also, the number of ventilators allocated in regions with a high initial transmission rate (e.g., Kings and Queens) do not significantly increase as the scenario changes from “All Low” to “All High.” These regions usually have much more initial ICU capacity for the treatment of their patients because of their large population. On the contrary, the areas with a lower initial transmission rate but less initial ICU capacity may benefit more if they receive more ventilators as the disease transmission rates get higher. Independent from the scenarios, the majority of the regions get more ventilators allocated when the budget level increases from limited to medium and ample. This is in particular observed for the areas with high initial transmission rates (e.g., Kings). The benefit of giving resources to those regions is higher than those regions with low initial disease transmission when the budget increases.
Moreover, the model is forced to make difficult decisions, and some of the regions may not have any ventilator allocated under a limited ventilator supply or “All High” transmission scenario under a very limited budget (see, e.g., New York and Hudson counties). When the budget is too tight, the regions either with a high transmission rate or a low capacity get the priority for ventilator allocation. As the budget increases to medium and ample, the model allocates more capacity to the regions with a higher population and a larger initial number of infections but with a lower transmission rate. Also, the stage-wise distribution of ventilators has a high relationship with the available budget. If the budget is tight (see total budgets of and ), most ventilators are distributed within the first two stages. As we increase the budget, some of the ventilators are allocated in stages three and four in addition to stages one and two. Thus, a higher budget level also provides some flexibility in delaying the ventilator allocation to some regions.
6.4.1. Varying ventilator cost
In addition to considering a cost of for each ventilator, we perform a sensitivity analysis on different ventilator costs and their impact on the number of ventilators allocated to each region. Specifically, we change the ventilator unit cost from to , , and under the budget levels of , , and (see Tables S1, S2, and S3 in the Online Supplement S1 for more detailed results). Results show that all ventilators are allocated in time stages one and two when the unit ventilator cost of is increased to , , and . According to the results, the ventilator allocation decisions show similar trends under different ventilator costs. For instance, when the ventilator cost increases and the disease transmission situation worsens (medium and high scenarios), more ventilators are allocated to Bergen County. When the ventilator cost increases from to , , and , New York County and Kings county receive almost the same number of ventilators allocated under different budgets and scenarios. Under the “All High” scenario and budget level, Bronx County receives more ventilators than in other scenarios due to the ample budget.
Furthermore, we can find some trends in the ventilator allocations under different costs. Independent from the budget level and scenario, when the ventilator cost increases, the number of ventilators allocated to Queens and Bronx decreases, while other regions have a similar number of ventilators allocated (e.g., Kings). This is because the model prioritizes allocating an appropriate number of ventilators to these regions with a smaller number of ICUs to support the essential operation of the ICU. When the ventilator cost decreases (or more budget is available), more ventilators are allocated to the regions with high transmission rates and a high initial ICU capacity to reduce deaths.
6.5. Risk analysis
In this section, we perform an analysis of the risk parameters and in terms of their impact on the expected number of infected and deceased people as well as the CVaR of the impact. Specifically, under the budget level, we compare four different problems with respect to their risk-averseness level, adjusting and values accordingly-risk-neutral (), weak risk-aversion (), mild risk-aversion (), and strong risk-aversion (). The model under the mild risk-aversion results in a high optimality gap () within 7200 CPU seconds running time. Therefore, we solve the scenario- problems described in Section 4.1 and obtain the lower and upper bounds for the original problem. For our problem, we select five representative scenarios and add bounds based on the results of those select scenarios in the risk-averse model. After implementing the scenario bounds, the optimality gaps over all of the risk-averseness levels reduce to less than .
We decompose the objective function (5a) into the Expected Impact [] and the Expected Risk [], as demonstrated in Eq. (4), to analyze the impact of risk trade-off on the results. Table 11 presents the value of the objective function (5a), expected impact, and expected risk (without ) under different risk-averseness levels. Specifically, the expected impact represents the expected total number of infections and deceased individuals, and the expected risk corresponds to the expected CVaR term in (5a) without the value. According to Table 11, the risk-neutral formulation has the highest expected risk since it does not consider the risks related to high-stake scenarios. When comparing different risk-averseness levels, as both and increase, the level of risk-averseness and the expected risk increase. The optimal objective function value increases due to the additional risk term added into the objective formulation. The expected impact also increases, implying the cost of being risk-averse, which is the increased number of infections and deceased individuals while trying to mitigate specific disastrous scenarios.
Table 11.
Comparison of objective value, expected impact, and expected risk under various risk-averseness levels.
| Risk | Weak | Mild | Strong | |
|---|---|---|---|---|
| Neutral | Risk-aversion | Risk-aversion | Risk-aversion | |
| (, ) | (, ) | (, ) | (, ) | |
| Objective Value | 358,030 | 721,710 | 3,997,129 | 4,011,964 |
| Expected Impact | 358,030 | 360,438 | 362,559 | 363,526 |
| Expected Risk | 421,827 | 361,272 | 363,457 | 364,844 |
The expected impact and expected risk (without ) for various combinations of and under the budget level are presented in Table 12 . We observe the change of the expected impact and expected risk when changing one of the risk parameters and fixing all other original values. According to the results, when , the expected risk has the highest value under each value (because the risk measure is omitted). Fixing the value, both expected impact and expected risk show an increasing trend due to the increase of from 1 to 10. When we move from risk-neutral () to risk-averse (), the expected impact always increases. Similarly, increases the expected impact compared to the risk-neutral model. Besides, when fixing the value and increasing the value, the expected risk increases because we increase the confidence level for reducing the risk of having an extremely large number of infections and big losses of lives.
Table 12.
Expected impact and risk for different risk-averseness levels.
| 0.3 |
0.6 |
0.95 |
|||||||
|---|---|---|---|---|---|---|---|---|---|
| Expected |
Expected |
Expected |
Expected |
Expected |
Expected |
||||
| Impact | Risk | Impact | Risk | Impact | Risk | ||||
| 0 | 358,030 | 376,318 | 358,030 | 392,273 | 358,030 | 421.827 | |||
| 1 | 360,438 | 361,272 | 361,950 | 363,251 | 363,882 | 365,236 | |||
| 10 | 360,880 | 361,341 | 362,559 | 363,457 | 363,526 | 364,844 | |||
7. Discussion and future directions
In this paper, we present a general multi-stage mean-risk epidemics-ventilator-logistics model and apply this model to control COVID-19 in select counties of New York and New Jersey. We first explicitly formulate the uncertainty of the proportion of untested asymptomatic infections at each stage, generating a multi-stage scenario tree. We then develop a compartmental disease model and integrate the short-term human movement among multiple regions into this model. We also derive a time- and space-varying disease transmission formulation and a logistics sub-model. We then integrate all those components into one mathematical formulation, which minimizes the number of infections and deceased individuals under different intervention strategies. We also present new bounds on the problem and show their computational benefits in terms of the optimality and relaxation gaps. We find that region bounds provide a better improvement on the LP relaxation gap, while scenario bounds provide a better MIP gap for harder instances with the expense of longer sub-problem solution times.
We solve the epidemics-ventilator-logistics model under different budget levels to determine the ventilator-distribution optimal timing and location under various pandemic scenarios. Next, we apply the CVaR in a nested form over a five-stage planning horizon to minimize the total expected number of infections and deceased individuals, as well as the weighted risk of the loss. Finally, we solve the scenario sub-problems under various scenarios to generate the lower and upper bounds for the original problem, reducing the optimality gap. Our results provide key insights into the resource-allocation decisions for controlling COVID-19 and can be adapted to study the transmission and logistics of other similar diseases.
According to the results, the number of infections, deceased individuals, hospitalized individuals, and ICU patients indicates that short-term migration influences the number of infections, even if the transmission rate is constant over time. The impacts of government interventions on the number of deceased individuals, hospitalized individuals, and ICU patients are delayed because deaths and hospitalization have a higher lag period compared to zero or a small lag period in the growth of infections. Furthermore, the number of ICU patients at each time period depends on the minimum number of patients who require the ICU and the available ventilators. Thus, the number of ICU patients might be at the capacity limit even under different intervention strategies at a particular stage. The “Lockdown” strategy is the best way to control disease transmission. Nevertheless, “Mask and Social Distance” applied after the several stages of “Lockdown” is the second-best strategy to alleviate the pandemic’s economic impacts.
The region with a high initial transmission rate and low initial ICU capacity receives more ventilators. This is because other regions with low initial transmission rates have fewer infections, even if they have smaller initial ICU capacity. Independent from the transmission scenario, an area with a high initial transmission rate has more ventilators allocated. This is because the benefit of giving resources to those regions is higher than the regions with low initial disease transmission when the budget increases. Moreover, when the budget is limited, all of the ventilators are allocated at the first two stages. When the budget becomes ample, decision-makers would have some flexibility in delaying ventilator allocation to later stages of the planning horizon.
Overall, we can derive general insights based on our sensitivity analysis. However, if the decision-makers prefer to be precise in the optimal allocation, they are encouraged to solve a complicated optimization model as presented in our paper. This necessity shows the importance of using complex mathematical models to tackle the difficulty of the pandemics control problem over multiple regions and time periods.
The increase in the mean-risk trade-off coefficients in the risk-averse model improves the confidence level, reducing the loss in the right tail of the objective function values (the number of infected and deceased individuals over highly-adverse scenarios). However, we should expect more infections and deceased individuals on average considering all possible scenarios when we want to decrease the impact of adverse scenarios by increasing the risk-averseness level.
This study leads to several future directions for research. For instance, vaccine allocation is also essential as it can potentially protect people from being infected. The combination of vaccine allocation and other interventions will provide more flexible strategies to prevent and control the disease. For example, for the region with a low transmission rate and high vaccine coverage, decision-makers could consider lifting the “Lockdown” earlier to stimulate the economy. Furthermore, the mathematical model cannot allocate ventilators to some regions under a very tight budget, and so future research could investigate ethical and fair resource allocation strategies during a pandemic. Also, some of the assumptions and inferences made in our model could be updated in a future study as more data becomes available. The proposed multi-stage mean-risk epidemics-ventilator-logistics formulation is highly complex and also interesting in terms of developing new solution methodologies. In this paper, we compare our region bounds with the scenario bounds of Büyüktahtakın (2021). Future research could also investigate the performance of the scenario dominance decomposition cuts of Büyüktahtakın (2021) and other prominent decomposition approaches (e.g., the stochastic dual dynamic integer programming method of Zou, Ahmed, & Sun (2019)) proposed for multi-stage stochastic mixed-integer programs.
Acknowledgments
We gratefully acknowledge the partial support of the National Science Foundation CAREER Award co-funded by the CBET/ENG Environmental Sustainability program and the Division of Mathematical Sciences in MPS/NSF under Grant No. CBET-1554018. We also thank four anonymous referees and the editors, whose remarks helped to improve the content and clarity of our exposition.
Footnotes
Supplementary material associated with this article can be found, in the online version, at 10.1016/j.ejor.2021.11.052.
Appendix A. Supplementary materials
Supplementary Raw Research Data. This is open data under the CC BY license http://creativecommons.org/licenses/by/4.0/
References
- Alonso-Ayuso A., Escudero L.F., Guignard M., Weintraub A. Risk management for forestry planning under uncertainty in demand and prices. European Journal of Operational Research. 2018;267(3):1051–1074. [Google Scholar]
- Ambikapathy B., Krishnamurthy K. Mathematical modelling to assess the impact of lockdown on COVID-19 transmission in India: Model development and validation. JMIR Public Health and Surveillance. 2020;6(2):e19368. doi: 10.2196/19368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Badr H.S., Du H., Marshall M., Dong E., Squire M.M., Gardner L.M. Association between mobility patterns and COVID-19 transmission in the USA: A mathematical modelling study. The Lancet Infectious Diseases. 2020;20(11):1247–1254. doi: 10.1016/S1473-3099(20)30553-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bakir I., Boland N., Dandurand B., Erera A. Sampling scenario set partition dual bounds for multistage stochastic programs. INFORMS Journal on Computing. 2020;32(1):145–163. [Google Scholar]
- Bein T., Grasso S., Moerer O., Quintel M., Guerin C., Deja M.…Mehta S. The standard of care of patients with ARDS: Ventilatory settings and rescue therapies for refractory hypoxemia. Intensive Care Medicine. 2016;42(5):699–711. doi: 10.1007/s00134-016-4325-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bernstein, L. (2020). More COVID-19 patients are surviving ventilators in the ICU. https://www.washingtonpost.com/health/more-covid-19-patients-are-surviving-ventilators-in-the-icu/2020/07/03/2e3c3534-bbca-11ea-8cf5-9c1b8d7f84c6_story.html. Accessed November 30, 2020.
- Bertsimas, D., Boussioux, L., Wright, R. C., Delarue, A., Digalakis Jr, V., Jacquillat, A., Kitane, D. L., Lukin, G., Li, M. L., Mingardi, L. et al. (2020). From predictions to prescriptions: A data-driven response to COVID-19. arXiv preprint arXiv:2006.16509. [DOI] [PMC free article] [PubMed]
- Billingham S., Widrick R., Edwards N.J., Klaus S. COVID-19 (SARS-CoV-2) ventilator resource management using a network optimization model and predictive system demand. MedRxiv. 2020 [Google Scholar]
- Blanco, V., Gázquez, R., & Leal, M. (2020). Reallocating and sharing health equipments in sanitary emergency situations: The COVID-19 case in Spain. arXiv preprint arXiv:2012.02062.
- Burki, T. (2020). China’s successful control of COVID-19. https://www.thelancet.com/journals/laninf/article/PIIS1473-3099(20)30800-8/fulltext. Accessed May 30, 2021. [DOI] [PMC free article] [PubMed]
- Bushaj S., Büyüktahtakın İ.E., Haight R.G. Risk-averse multi-stage stochastic optimization for surveillance and operations planning of a forest insect infestation. European Journal of Operational Research. 2021 [Google Scholar]
- Bushaj, S., Yin, X., Beqiri, A., Andrews, D., & Büyüktahtakın, İ. E. (2021b). A simulation-deep reinforcement learning (SiRL) approach for epidemic control optimization. Under Review. [DOI] [PMC free article] [PubMed]
- Büyüktahtakın İ.E. Stage- scenario dominance for risk-averse multi-stage stochastic mixed-integer programs. Accepted for publication in Annals of Operations Research. 2021:1–36. [Google Scholar]
- Büyüktahtakın İ.E., des Bordes E., Kıbış E.Y. A new epidemics–logistics model: Insights into controlling the Ebola virus disease in West Africa. European Journal of Operational Research. 2018;265(3):1046–1063. [Google Scholar]
- Castro M.C., de Carvalho L.R., Chin T., Kahn R., Franca G.V., Macario E.M., de Oliveira W.K. Demand for hospitalization services for COVID-19 patients in Brazil. MedRxiv. 2020 [Google Scholar]
- CDC (2021). Clinical questions about COVID-19: Questions and answers. http://www.cdc.gov/coronavirus/2019-ncov/hcp/faq.htmlAccessed May 30, 2021.
- CENSUS (2020). Datasets. http://www.census.gov/data/datasets.html. Accessed November 30, 2020.
- Chatterjee K., Chatterjee K., Kumar A., Shankar S. Healthcare impact of COVID-19 epidemic in India: A stochastic mathematical model. Medical Journal Armed Forces India. 2020 doi: 10.1016/j.mjafi.2020.03.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- CNN (2021). New Zealand and Australia were Covid success stories. why are they behind on vaccine rollouts?http://edition.cnn.com/2021/04/15/asia/new-zealand-australia-covid-vaccine-intl-dst-hnk/index.html. Accessed August 2, 2021.
- Coşgun Ö., Büyüktahtakın İ.E. Stochastic dynamic resource allocation for HIV prevention and treatment: An approximate dynamic programming approach. Computers & Industrial Engineering. 2018;118:423–439. [Google Scholar]
- Dasaklis T.K., Pappis C.P., Rachaniotis N.P. Epidemics control and logistics operations: A review. International Journal of Production Economics. 2012;139(2):393–410. [Google Scholar]
- Defourny B., Ernst D., Wehenkel L. Decision theory models for applications in artificial intelligence: Concepts and solutions. IGI Global; 2012. Multistage stochastic programming: A scenario tree based approach to planning under uncertainty; pp. 97–143. [Google Scholar]
- Environmental Systems Research Institute (ESRI) (2021). ArcGIS map. http://www.arcgis.com/index.html. Accessed January 20, 2021.
- Fischer I., Avrashi S., Oz T., Fadul R., Gutman K., Rubenstein D.…Glöckner A. The behavioural challenge of the COVID-19 pandemic: Indirect measurements and personalized attitude changing treatments (impact) Royal Society Open Science. 2020;7(8):201131. doi: 10.1098/rsos.201131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glass, H. (2020). High-acuity ventilator cost guide. http://hcpresources.medtronic.com/blog/high-acuity-ventilator-cost-guide. Accessed November 30, 2020.
- Govindan K., Mina H., Alavi B. A decision support system for demand management in healthcare supply chains considering the epidemic outbreaks: A case study of coronavirus disease 2019 (COVID-19) Transportation Research Part E: Logistics and Transportation Review. 2020;138:101967. doi: 10.1016/j.tre.2020.101967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harvard Medical School (2021). Symptoms, spread and other essential information about Coronavirus and COVID-19. http://www.health.harvard.edu/diseases-and-conditions/covid-19-basicsAccessed February 12, 2021.
- Hogan, A. (2020). Watch: Ventilators are in high demand for COVID-19 patients. How do they work?http://www.statnews.com/2020/03/30/covid-19-ventilators-how-they-work/. Accessed November 30, 2020.
- Hu M., Lin H., Wang J., Xu C., Tatem A.J., Meng B.…Wu G., et al. The risk of COVID-19 transmission in train passengers: An epidemiological and modelling study. Clinical Infectious Diseases. 2020 doi: 10.1093/cid/ciaa1057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang H.-C., Araz O.M., Morton D.P., Johnson G.P., Damien P., Clements B., Meyers L.A. Stockpiling ventilators for influenza pandemics. Emerging Infectious Diseases. 2017;23(6):914. doi: 10.3201/eid2306.161417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- JHU (2020). COVID-19 United States cases by county. http://coronavirus.jhu.edu/us-mapAccessed November 30, 2020.
- Kaplan E.H., Craft D.L., Wein L.M. Analyzing bioterror response logistics: The case of smallpox. Mathematical Biosciences. 2003;185(1):33–72. doi: 10.1016/s0025-5564(03)00090-7. [DOI] [PubMed] [Google Scholar]
- Katris C. A time series-based statistical approach for outbreak spread forecasting: Application of COVID-19 in Greece. Expert Systems with Applications. 2020;166:114077. doi: 10.1016/j.eswa.2020.114077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kıbış E.Y., Büyüktahtakın İ.E. Optimizing invasive species management: A mixed-integer linear programming approach. European Journal of Operational Research. 2017;259(1):308–321. [Google Scholar]
- Kıbış E.Y., Büyüktahtakın İ.E. Optimizing multi-modal cancer treatment under 3D spatio-temporal tumor growth. Mathematical Biosciences. 2019;307:53–69. doi: 10.1016/j.mbs.2018.10.010. [DOI] [PubMed] [Google Scholar]
- Kıbış E.Y., Büyüktahtakın İ.E., Haight R.G., Akhundov N., Knight K., Flower C.E. A multistage stochastic programming approach to the optimal surveillance and control of the emerald ash borer in cities. INFORMS Journal on Computing. 2021;33(2):808–834. [Google Scholar]
- Kretzschmar M.E., Rozhnova G., Bootsma M.C., van Boven M., van de Wijgert J.H., Bonten M.J. Impact of delays on effectiveness of contact tracing strategies for COVID-19: A modelling study. The Lancet Public Health. 2020;5(8):e452–e459. doi: 10.1016/S2468-2667(20)30157-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ku C.C., Ng T.-C., Lin H.-H. Available at SSRN 3544127. 2020. Epidemiological benchmarks of the COVID-19 outbreak control in China after Wuhan’s lockdown: A modelling study with an empirical approach. [Google Scholar]
- Kucharski A.J., Russell T.W., Diamond C., Liu Y., Edmunds J., Funk S.…Munday J.D., et al. Early dynamics of transmission and control of COVID-19: A mathematical modelling study. The Lancet Infectious Diseases. 2020 doi: 10.1016/S1473-3099(20)30144-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lacasa L., Challen R., Brooks-Pollock E., Danon L. A flexible method for optimising sharing of healthcare resources and demand in the context of the COVID-19 pandemic. Plos One. 2020;15(10):e0241027. doi: 10.1371/journal.pone.0241027. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee M., Zhao J., Sun Q., Pan Y., Zhou W., Xiong C., Zhang L. Human mobility trends during the early stage of the COVID-19 pandemic in the United States. PLoS One. 2020;15(11):e0241468. doi: 10.1371/journal.pone.0241468. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li M.L., Bouardi H.T., Lami O.S., Trikalinos T.A., Trichakis N.K., Bertsimas D. Forecasting COVID-19 and analyzing the effect of government interventions. MedRxiv. 2020 [Google Scholar]
- Lilleker, D. (2021). The good, the bad and the ugly of government responses to COVID. https://www.theafricareport.com/72401/the-good-the-bad-and-the-ugly-of-government-responses-to-covid/. Accessed May 30, 2021.
- Loeffler-Wirth H., Schmidt M., Binder H. COVID-19 transmission trajectories-monitoring the pandemic in the worldwide context. Viruses. 2020;12(7):777. doi: 10.3390/v12070777. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mahmutoğulları A.İ., Çavuş Ö., Aktürk M.S. Bounds on risk-averse mixed-integer multi-stage stochastic programming problems with mean-CVaR. European Journal of Operational Research. 2018;266(2):595–608. [Google Scholar]
- Manca D., Caldiroli D., Storti E. A simplified math approach to predict ICU beds and mortality rate for hospital emergency planning under COVID-19 pandemic. Computers & Chemical Engineering. 2020:106945. doi: 10.1016/j.compchemeng.2020.106945. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCrimmon, K. K. (2021). The truth about COVID-19 and asymptomatic spread: It’s common, so wear a mask and avoid large gatherings. https://www.uchealth.org/today/the-truth-about-asymptomatic-spread-of-covid-19/. Accessed February 13, 2021.
- Mehrotra S., Rahimian H., Barah M., Luo F., Schantz K. A model of supply-chain decisions for resource sharing with an application to ventilator allocation to combat COVID-19. Naval Research Logistics (NRL) 2020 doi: 10.1002/nav.21905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meller, M. (2020). The asymptomatic and pre-symptomatic spread of COVID-19. https://www.gundersenhealth.org/covid19/the-asymptomatic-and-pre-symptomatic-spread-of-covid-19/Accessed November 30, 2020.
- Homem-de Mello T., Pagnoncelli B.K. Risk aversion in multistage stochastic programming: A modeling and algorithmic perspective. European Journal of Operational Research. 2016;249(1):188–199. [Google Scholar]
- Meng L., Qiu H., Wan L., Ai Y., Xue Z., Guo Q.…Tong C., et al. Intubation and ventilation amid the COVID-19 outbreak: Wuhan’s experience. Anesthesiology. 2020;132(6):1317–1332. doi: 10.1097/ALN.0000000000003296. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murray, C. (2020). Forecasting COVID-19 impact on hospital bed-days, ICU-Days, ventilator-days and deaths by US state in the next 4 months, 10.1101/2020.03.27.20043752.
- Parker, F., Sawczuk, H., Ganjkhanloo, F., Ahmadi, F., & Ghobadi, K. (2020). Optimal resource and demand redistribution for healthcare systems under stress from COVID-19. arXiv preprint arXiv:2011.03528.
- Queiroz M.M., Ivanov D., Dolgui A., Wamba S.F. Impacts of epidemic outbreaks on supply chains: mapping a research agenda amid the COVID-19 pandemic through a structured literature review. Annals of Operations Research. 2020:1–38. doi: 10.1007/s10479-020-03685-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ranney M.L., Griffeth V., Jha A.K. Critical supply shortages-the need for ventilators and personal protective equipment during the COVID-19 pandemic. New England Journal of Medicine. 2020;382(18):e41. doi: 10.1056/NEJMp2006141. [DOI] [PubMed] [Google Scholar]
- Roberts M.D., Seymour H.D., Dimitrov A. Selectively caring for the most severe COVID-19 patients delays ICU bed shortages more than increasing hospital capacity. MedRxiv. 2020 [Google Scholar]
- Rockafellar R.T., Uryasev S. Conditional value-at-risk for general loss distributions. Journal of Banking & Finance. 2002;26(7):1443–1471. [Google Scholar]
- Sandıkçı B., Özaltın O. A scalable bounding method for multistage stochastic programs. SIAM Journal on Optimization. 2017;27(3):1772–1800. [Google Scholar]
- Tanner M.W., Sattenspiel L., Ntaimo L. Finding optimal vaccination strategies under parameter uncertainty using stochastic programming. Mathematical Biosciences. 2008;215(2):144–151. doi: 10.1016/j.mbs.2008.07.006. [DOI] [PubMed] [Google Scholar]
- Tuan N.H., Mohammadi H., Rezapour S. A mathematical model for COVID-19 transmission by using the caputo fractional derivative. Chaos, Solitons & Fractals. 2020;140:110107. doi: 10.1016/j.chaos.2020.110107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang X., Pasco R.F., Du Z., Petty M., Fox S.J., Galvani A.P.…Meyers L.A. Impact of social distancing measures on COVID-19 healthcare demand in Central Texas. MedRxiv. 2020 doi: 10.3201/eid2610.201702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wei J.-T., Liu Y.-X., Zhu Y.-C., Qian J., Ye R.-Z., Li C.-Y.…Wang Y., et al. Impacts of transportation and meteorological factors on the transmission of COVID-19. International Journal of Hygiene and Environmental Health. 2020;230:113610. doi: 10.1016/j.ijheh.2020.113610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weissman G.E., Crane-Droesch A., Chivers C., Luong T., Hanish A., Levy M.Z.…Anesi G.L., et al. Locally informed simulation to predict hospital capacity needs during the COVID-19 pandemic. Annals of Internal Medicine. 2020;173(1):21–28. doi: 10.7326/M20-1260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- White D.B., Lo B. A framework for rationing ventilators and critical care beds during the COVID-19 pandemic. JAMA. 2020;323(18):1773–1774. doi: 10.1001/jama.2020.5046. [DOI] [PubMed] [Google Scholar]
- Yin, X., Bushaj, S., Yuan, Y., & Büyüktahtakın, İ. E. (2021). COVID-19: An agent-based simulation-optimization approach to vaccine center location vaccine allocation problem. Under Review.
- Yin X., Büyüktahtakın İ.E. A multi-stage stochastic programming approach to epidemic resource allocation with equity considerations. Published online ahead of print in Health Care Management Science. 2021:1–26. doi: 10.1007/s10729-021-09559-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yin X., Büyüktahtakın İ.E. Risk-averse multi-stage stochastic programming to optimizing vaccine allocation and treatment logistics for effective epidemic response. IISE Transactions on Healthcare Systems Engineering. 2021;0(0):1–23. doi: 10.1080/24725579.2021.1938298. [DOI] [Google Scholar]
- Zaric G.S., Brandeau M.L. Resource allocation for epidemic control over short time horizons. Mathematical Biosciences. 2001;171(1):33–58. doi: 10.1016/s0025-5564(01)00050-5. [DOI] [PubMed] [Google Scholar]
- Zeb A., Alzahrani E., Erturk V.S., Zaman G. Mathematical model for coronavirus disease 2019 (COVID-19) containing isolation class. BioMed Research International. 2020;2020 doi: 10.1155/2020/3452402. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang N., Jia W., Lei H., Wang P., Zhao P., Guo Y.…Xie J., et al. Effects of human behaviour changes during the COVID-19 pandemic on influenza spread in Hong Kong. Clinical Infectious Diseases. 2020 doi: 10.1093/cid/ciaa1818. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zou J., Ahmed S., Sun X.A. Stochastic dual dynamic integer programming. Mathematical Programming. 2019;175(1):461–502. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Raw Research Data. This is open data under the CC BY license http://creativecommons.org/licenses/by/4.0/