Abstract
We study the role of global supply chains in the impact of the Covid-19 pandemic on GDP growth using a multi-sector quantitative framework implemented on 64 countries. We discipline the labor supply shock across sectors and countries using the fraction of work in the sector that can be done from home, interacted with the stringency with which countries imposed lockdown measures. One quarter of the total model-implied real GDP decline is due to transmission through global supply chains. However, “renationalization” of global supply chains does not in general make countries more resilient to pandemic-induced contractions in labor supply. This is because eliminating reliance on foreign inputs increases reliance on the domestic inputs, which are also disrupted due to nationwide lockdowns. In fact, trade can insulate a country imposing a stringent lockdown from the pandemic-shock, as its foreign inputs are less disrupted than its domestic ones. Finally, unilateral lifting of the lockdowns in the largest economies can contribute as much as 2.5% to GDP growth in some of their smaller trade partners.
Keywords: Production networks, International transmission, Pandemic, Covid-19
1. Introduction
Much of the world is closely integrated through final and intermediate goods trade. As countries simultaneously curtail economic activity by means of domestic lockdown policies, the global economic downturn may therefore be exacerbated by reductions in the supply of foreign intermediates, or demand for a country's exports abroad (Baldwin, 2020). As a result, there is now a great deal of speculation in both policy circles and popular press that the experience of the pandemic will eventually lead to a “renationalization” of supply chains.1 However, it is an open question whether supply chain renationalization would make GDP more resilient to pandemic-type shocks. A shift from foreign to domestic intermediates would also change the structure of the domestic economy, and thus affect the reaction of the economy to a pandemic.
This paper quantifies the role of the global supply chains in the economic impact of the Covid-19 pandemic using a model of world production and trade covering 64 countries on all continents and 33 sectors spanning all economic activities. We parameterize the model using the OECD Inter-Country Input-Output (ICIO) Tables, that provide matrices of domestic and international intermediate input and final use trade. We solve the model analytically using the techniques developed in Huo et al. (2020).
We start by simulating a global lockdown as a contraction in labor supply. To discipline the relative size of the labor contraction, we combine two pieces of information. First, we use the Dingel and Neiman (2020) measure of the fraction of the work of different occupations that can be done at home. Variation across sectors in their occupation usage and of countries in their sectoral employment composition results in heterogeneous incidence of the shock across countries. Second, countries also vary in the stringency of lockdown measures. To capture this, we interact the work-from-home intensity by occupation with an index capturing the country-level lockdown stringency from Hale et al. (2020). Since this index is not a cardinal measure, we apply a monotonic transformation to match the mean and the dispersion of the drop in Industrial Production in a subsample of countries where these data are available. Though we do not target country-specific output changes, the model predictions fit the data well.
Not surprisingly, the model produces a large contraction of economic activity, with an average 29.6% GDP drop in our sample of countries for the duration of the shock. Our focus is on the role of the global supply chains in particular. To better understand how linkages between countries amplify or mitigate the effect of the shock, we report two results. First, we compute the share of each country's GDP contraction that is due to foreign, rather than domestic shocks. On average, about 23.3% of the contraction of GDP comes from foreign shocks.
Second, we answer the more substantive question of whether participation in global supply chains exacerbated or alleviated the pandemic-induced contraction in labor supply. Figuring this out requires comparing the pandemic-induced GDP change in the baseline model to the pandemic-induced GDP change in an alternative world without international trade, where supply chains have adjusted to use only domestic inputs.
We find that on average in our 64 countries the downturn would actually be slightly worse with renationalized supply chains (−30.2%) than under current levels of trade. The reason is that eliminating reliance on foreign inputs increases the reliance on domestic inputs. Since a pandemic-related lockdown also affects domestic sectors, there is generally no resilience benefit from renationalizing international supply chains.
There is a distribution of differences around the average. In some countries GDP would drop by 5–8 percentage points more if supply chains were renationalized, whereas in others GDP would fall by about 4 percentage points less. The cross-country variation is well-explained by differences in lockdown severity across countries. Some countries – most prominently Japan, Taiwan, Sweden, or Greece – impose less stringent lockdowns in response to the pandemic shock. The domestic pandemic-induced shock is therefore smaller in these countries than the shock to their trading partners with more severe lockdowns. Separating from the global supply chains would make these countries more resilient to lockdowns by eliminating the transmission of the relatively larger shock from other countries. By contrast, a country with the most severe lockdown will reduce its own domestic labor supply by more than its average trading partner. In that case, the supply of the domestic intermediate inputs falls by more than the supply of foreign ones, and thus the GDP contraction is larger when supply chains are renationalized. Thus, whether renationalizing supply chains insulates a country from the pandemic depends on whether it imposes a more or less severe lockdown than its trading partners.
It may be that while renationalizing all supply chains is not on average beneficial, doing so in specific sectors would improve resilience. To investigate this possibility, we renationalize supply chains in individual sectors one by one. There is no sector in which supply chain renationalization notably improves resilience, measured either by GDP, or by value added of the sector itself.
Next, we address the interaction between the health crisis and global supply chains, by simulating the lockdown in an environment of increased demand for health services. We first construct an alternative “high-health” economy, in which the share of final expenditure that goes to the Health sector doubles in each country. We then simulate the pandemic-driven labor supply contraction in the baseline and “high-health” economies, and compare the results. Because the Health sector is not subject to the lockdown, the GDP contraction is modestly less severe in the “high-health” scenario (on average about 1 percentage point smaller contraction). Since the Health sector is largely non-tradeable, increasing its size does not have a consistent impact on the relative importance of international transmission.
Our last counterfactual tackles the recovery from the shock. Currently, countries decide on lifting the lockdowns without international coordination. We thus simulate individual countries’ decisions to unilaterally allow workers to return to work, while the rest of the world remains in lockdown. Our quantification suggests that most of the GDP impacts of the lockdown are domestic, and these are reversed by reopening. We show that the unilateral reopenings of smaller countries such as Norway or Austria have limited impacts on GDP in other countries. By contrast, even unilateral reopening of large economies like China, US, Germany, or Russia would have a noticeable impact on others. These countries’ opening can raise GDP in some of the most tightly linked countries by up to 2.5%.
We highlight that our exercises do not take into account the health consequences of the pandemic itself, nor do we model the labor supply shock as being conditional on the infection rate in the population. We view this as reasonable in the current context where a very small fraction of the population in most countries is directly affected by the disease at any point in time. Note that incorporating the infection rate into the calibration would only amplify the aggregate labor supply shock and the GDP consequences in the baseline. We take this approach as most of our counterfactuals are meant to capture the very short-run impact consequences of the shock. During the impact period, infection rates are low and most of the labor force is not incapacitated.
1.1. Related literature
Our paper contributes to the burgeoning body of work on the macroeconomic impact of the Covid-19 pandemic. In the closed-economy setting see, among many others, Acemoglu et al. (2020), Alon et al. (2020), Atkeson, 2020, Eichenbaum et al., 2020, Glover et al. (2020), Guerrieri et al. (2020), and Kaplan et al. (2020), as well as analyses with input-output networks (Baqaee and Farhi, 2020b, Baqaee and Farhi, 2020a, Barrot et al., 2020, del Rio-Chanona et al., 2020). We study the international transmission through global supply chains, a focus we share with a growing body of contemporaneous work (e.g. Antràs et al., 2020, Çakmaklı et al., 2020, Çakmaklı et al.,, Eppinger et al., 2020, George et al., 2020, Sforza and Steininger, 2020).2
In that respect, we build on the active recent research agenda on international shock propagation in production networks. We apply the framework and tools developed in Huo et al. (2020), who study the sources of international GDP comovement in a general multi-country multi-sector multi-factor model with input linkages. Also related are Baqaee and Farhi (2019), Allen et al. (2020) and Kleinman et al. (2020), who explore the impact of productivity, factor supply, and trade cost shocks in a wide class of open-economy models. Our counterfactuals simulate the labor supply shocks in an environment with endogenous labor supply, allowing for propagation through input networks.3 Our analysis also relates to recent papers studying the short-run transmission and amplification of a natural disaster shock through trade linkages (Barrot and Sauvagnat, 2016, Boehm et al., 2019a, Carvalho et al., 2021). In contrast to these papers, the Covid-19 pandemic offers a unique opportunity to quantify the consequences of a synchronized labor supply shock. As highlighted by Imbs (2004) and Huo et al. (2020), both correlated shocks and transmission lead to synchronization of GDP growth, and the relative importance of the two is a quantitative question.
The rest of the paper is organized as follows. Section 2 introduces the quantitative framework, Section 3 describes the data and calibration, and Section 4 presents the results. Section 5 concludes.
2. Global network model
This section sets up and solves a model of the global network of production and trade. The model is an extension of the quantitative framework of Huo et al. (2020), which should be consulted for further details.
2.1. Setup
2.1.1. Preliminaries
Consider an economy comprised of N countries indexed by n and m and J sectors indexed by j and i, that produce using labor inputs from different occupations indexed by . Each country n is populated by a representative household. The household consumes the final good available in country n and supplies labor and capital to firms. Trade is subject to iceberg costs τ mnj to ship good j from country m to country n (throughout, we adopt the convention that the first subscript denotes source, and the second destination).
2.1.2. Households
There is a continuum of workers in a representative household who share the same consumption. The problem of the household is
| (1) |
subject to
where is consumption of final goods, is the labor hours supplied in occupation , is the occupation-specific labor supply shock, and K nj is the amount of installed capital in sector j which is assumed to be exogenous. Labor in occupation collects a wage , and capital is rented at the price R nj.4
The utility function is an extension of the Greenwood et al. (1988) preferences, that produce an especially simple isoelastic labor supply curve that only depends on the real wage:
We highlight two features of our preference formulation that will be important for the analysis that follows. First, labor is differentiated by occupation. This feature captures imperfect inter-occupation labor mobility in the short run, appropriate in this application. Second, the labor supply is subject to country-occupation-specific shocks . This flexibility is needed to capture the fact that not all occupations experienced the same contractions in labor supply, as some jobs can be more easily done at home. In a similar vein, there is heterogeneity in lockdown severity across countries, that once again can be captured by variation in .
2.1.3. Shocks
Through the lens of our model, the worldwide lockdown policies are a vector of labor supply shocks . Our quantitative analysis will trace the impact of these shocks on the world economy under various assumptions on the structure of production and trade.
An alternative interpretation of the labor supply shock is a change in the efficiency units. A reduction in then implies that workers in occupation will produce less in the same amount of hours worked, for instance due to frictions associated with working at home, lack of childcare, etc. In this case, the disappear from the utility function, but appear in the budget constraint
| (2) |
Appendix A.2 shows that despite the different interpretations, these two formulations are observationally equivalent in the sense that given the same value of , the two economies experience the same change in real GDP and final consumption. However, as the efficiency units approach directly affects the measured wage for the same amount of hours worked, these two specifications have different implications for labor market outcomes such as wages.
The set of sectors is partitioned into Q ≪ J groups indexed by q. The final good in the economy is a CES aggregate across groups q:
where P n is the final goods price index and D nq is the quantity consumed of category q. The q's should be thought of as large groupings, such as “goods” or “services.” Correspondingly, the substitution elasticity ρ between them should be thought of as a number less than 1. To anticipate the role of these groupings, one of these will be healthcare. In one of our simulations, we will consider a pandemic-induced increase in demand for healthcare, by raising its preference weight ζ nq.
Category q is an Armington aggregate of goods coming from different countries and sectors
where denotes the index set of sectors that belong to category q, D mnj is the final consumption by country n of sector j goods imported from country m, and γ controls the substitution elasticity between different origin-sector goods within a category. The corresponding price index is P nq, where P mj is the price of sector j country m's product “at the factory gate” in the origin country. No arbitrage in shipping implies that the price faced by the consumer in n is P mj times the iceberg cost τ mnj.
The expenditure share of a particular good from country m and sector j that belongs to category q is given by
and this share will shape the responses to shocks as we will show below.
2.1.4. Firms
A representative firm in sector j in country n operates a CRS production function
| (3) |
The composite labor in sector j, H nj, is an aggregate of labor inputs from different occupations, and similarly, the intermediate input usage X nj is an aggregate of inputs from potentially all countries and sectors:
where is the usage of labor of occupation , with κ governing the elasticity of substitution across occupations, and X mi,nj is the usage of inputs coming from sector i in country m in production of sector j in country n, with ε governing the elasticity of substitution across intermediate inputs.
Cost minimization implies that the payments to primary factors and intermediate inputs are:
where is the share of intermediates from country m sector i in total intermediate spending by n, j:
and is the share of labor expenditure on workers from occupation :
It will also be convenient to define the share of total occupation labor employed in sector j:
2.1.5. Equilibrium
An equilibrium in this economy is a set of goods and capital prices , factor allocations , and goods allocations , for all countries and sectors, and factor prices and allocations {, } for all countries and occupations, such that (i) households maximize utility; (ii) firms maximize profits; and (iii) all markets clear.
At the sectoral level, the following market clearing condition has to hold for each country n sector j:
| (4) |
Meanwhile, trade balance implies that each country's final expenditure equals the sum of value added across domestic sectors5
| (5) |
For each occupation, the following market clearing condition holds
Note that once we know the share of value added in production η j and the expenditure shares and for all n, m, i, j, we can compute the nominal output P nj Y nj for all country-sectors (n, j) after choosing a numeraire good. Together with the shares related to the occupation inputs, and , there is no need to specify further details of the model, and we will utilize this property to derive the model solution.
2.2. Analytical solution
We now provide an analytical expression for the global influence matrix. An influence matrix is the solution to the model, as it translates the vector of exogenous shocks to the vector of endogenous general equilibrium responses of output in each country and sector. In general, closed-form solutions for the exact influence matrices cannot be obtained in multi-country multi-sector models such as ours. However, Huo et al. (2020) show that in this framework we can solve for the first-order approximation of the influence matrix.
Following national accounting conventions, real GDP is defined as value added evaluated at base prices b:
| (6) |
where P nj,b is the gross output base price, and is the base price of inputs in that sector-country. Denote by “ln” the log-deviation from steady state/pre-shock equilibrium. The real GDP change in any country n following a vector of labor supply shocks is given by
| (7) |
where are the pre-shock Domar weights.
Of course, the ln H nj in (7) are equilibrium outcomes. To solve the model, we have to express them as a function of primitive shocks. Let the vector ln H of length NJ collect the worldwide sectoral composite labor changes, and the vector ln ξ of length collect the worldwide occupation-specific labor supply shocks.
Proposition 1
The response of ln H to the global vector of labor supply shocks ln ξ is to a first order approximation given by
(8) where captures the domestic labor market GE effects holding production fixed
(9) and captures the global GE effects allowing all goods markets to adjust
(10) In addition, η and α are matrices of output elasticities, Π f and Π x are matrices of final consumption and intermediate shares, respectively, is the matrix of occupational shares by sector, Λ is a matrix of sectoral employment shares by occupation, and summarizes how prices respond to output changes which combines both structural elasticities and spending shares. 6
Proof
See Appendix A. □
Eqs. (8), (9), (10) illustrate that all we need to understand the response of worldwide output to various occupation-country shocks in this quantitative framework are measures of steady state final goods consumption and production shares, the distribution of occupations across sectors, as well as model elasticities. The matrix that encodes the equilibrium responses of worldwide labor inputs to the worldwide vector of shocks is the influence matrix. In Eq. (8), the term Δ −1 ln ξ reflects how wages in different occupations respond to supply shocks holding the quantities and prices in all goods markets fixed. A shock in occupation not only affects wages for occupation , but also spills over to other occupations. The former is captured by , and the latter is captured by . Importantly, the elasticity κ has opposite effects on these two terms, leaving the total wage response independent of κ when the magnitude of the labor supply shock is uniform across occupations. The matrix measures the exposures of sectoral labor inputs to wages in different occupations, and thus translates changes in wages to changes in labor.
The expression in (9) is a block diagonal matrix, implying a null partial equilibrium response to foreign shocks. Once we allow the goods markets to respond, the global supply chain starts to play a role and transmission across countries will occur. The matrix encodes the general equilibrium response of sectoral labor composite in a country to shocks in any sector-country, taking into account the full model structure and all direct and indirect links between the countries and sectors. The model solution (8), (9), (10) resembles the typical solution to a network model, that writes the equilibrium change in output as a product of the Leontief inverse and the vector of shocks. Our expression also features a vector of shocks, and an inverse of a matrix that is more complicated due to the multi-country structure of our model combined with elastic factor supply and non-unitary elasticities of substitution.7
The main advantage of the first-order solution above is transparency. The GDP change is represented as a linear combination of primitive shocks, allowing additive decompositions of the GDP change that illuminate the forces at work. An alternative is an exact solution of the model. Figure A1 compares the exact and first-order solutions. In our application, the first-order and exact solutions are quite close.8
In a special case where the elasticities of substitution for final goods and the intermediate goods are equal to 1, the influence matrix in (8) simplifies to9
| (11) |
Clearly, the overall response of labor is increasing in the Frisch elasticity ψ. It also underscores that the exact general equilibrium feedback effects hinge on various steady-state shares. When the final goods or intermediate goods aggregates deviate from the Cobb-Douglas case, the global goods demand system (4) is more complex and the matrix that governs the responses of prices enters the influence matrix (8).
2.3. Accounting decompositions
To illustrate how we will use the model above to understand the impact of global supply chains on GDP growth during the pandemic, we next present some simple accounting decompositions of domestic GDP growth. These build on the more general accounting framework used in Huo et al. (2020) to study GDP comovement.
The linear representation of the GDP change in country n as a function of the global vector of shocks (7), (8), (9), (10) lends itself to an additive decomposition of the GDP change into the components due to domestic and foreign shocks. To first order, the log change in real GDP of country n can be written as:
| (12) |
where are the elasticities of the GDP of country n with respect to shocks in occupation , country m, characterized by (7), (8), (9), (10).
2.3.1. Contribution of foreign lockdowns to GDP contractions
To highlight the effects of domestic and foreign shocks on GDP, separate the double sum in (12) into the component due to country n's own shocks () and the component due to all the trade partners’ shocks ():
| (13) |
Below, we report the fraction of the overall downturn that can be attributed to foreign, rather than domestic, labor contractions: , for each country in our sample.10
2.3.2. Renationalization of global supply chains
There is now a great deal of speculation in policy circles and popular press that the pandemic will lead to a renationalization of the global supply chains, to protect against similar shocks in the future. In our model transmission is positive, in the sense that an adverse foreign shock lowers a country's GDP. The sign and size of the contribution of foreign shocks is informative, but does not imply that the presence of global value chains exacerbated the GDP contraction due to the lockdown.
To establish this type of result, we need to compare the contraction in the baseline model to an alternative in which the global supply chains have been renationalized. We construct such a version of the world economy by raising iceberg trade costs to infinity in both intermediate and final good uses. We then shock each country with the same size lockdown as in the baseline world economy. If the GDP contraction with renationalized supply chains is smaller than the one in the baseline, we conclude that a country's participation in the global value chains exacerbated the downturn, and vice versa. To understand the results that appear below, we can write the GDP change in the renationalized equilibrium (R) following the shock as:
| (14) |
where is the elasticity of country n's GDP to a shock in occupation in the renationalized equilibrium. By definition, in this case the country is immune to foreign shocks, and only responds to domestic shocks.
Comparing (13) and (14), the difference in the GDP response in the baseline relative to autarky is a sum of two parts:
| (15) |
The second component, , is straightforward: in autarky, the country is not subject to foreign shocks, so holding all else fixed the downturn is smaller in autarky if the rest of the world experiences a bad shock.
However, the first term captures an additional effect. Absent international trade, the responsiveness of the economy to domestic shocks would also be different. Some sectors grow in influence as a country opens to trade, others shrink. Whether or not participation in global trade exacerbates the downturn is determined by how the altered sensitivity to domestic shocks () compares to the eliminated sensitivity to foreign shocks.
To better understand the change in the domestic influence term, note that the change in the labor input can be written as a sum of the partial and general equilibrium impacts of the shocks:
| (16) |
Combining (7), (15), and (16), the difference between the trade and the renationalized equilibria can be written as:
| (17) |
The difference in the GDP change between the trade and renationalized equilibria can be decomposed into three effects. The PE effect captures the reweighting of the sectors towards, or away from, those more exposed to the lockdown. For instance, if when going from the renationalized to the trade equilibrium Domar weights grow in sectors more immune to lockdowns, the country will be more insulated from lockdowns under trade, all else equal.
The matrix governing the partial equilibrium response to shocks is simple: . By construction, D is block-diagonal by country, as only shocks to domestic occupational groups directly affect domestic hours. It can be directly constructed from data on occupational shares and labor-related elasticities, and thus does not require solving the model. The PE response matrix D captures the direct effect of the shocks to occupations in the home country on sectoral labor in the home country. That is, it traces the shift of the labor supply curve in occupation , holding all other markets fixed (including domestic labor markets in other occupations). The magnitude of this shift is (1 + ψ) ln , governed by the Frisch elasticity. The needed adjustment in the wage rate is , which encodes the information on the slope of the demand curve (ψ −1) and the supply curve (κ −1). The change in the wage rate translates into the change in the composite labor in sector j by an amount proportional to sector j's exposure to occupation , given by .
The domestic GE term captures the change in the general equilibrium effects of domestic shocks between the two equilibria. It reflects the fact that the renationalization of global supply chains will rearrange domestic input usage, and as a result the impact of domestic shocks on the home economy. The matrix of general equilibrium adjustments Γ includes the spillover effects to labor markets in other occupations, and the indirect effects on domestic and global goods markets. Computing the GE term requires the solution to the full general equilibrium model, as it encodes the change in the propagation of occupation-specific shocks through the rest of the economy through product and labor market linkages.11
2.3.3. Real GDP vs. real consumption
Our baseline analysis focuses on real GDP, as it is a concept tracked by statistical agencies and is thus the key input into policymaking. Though changes in nominal GDP have to equal changes in nominal consumption expenditure, changes in real GDP and in real consumption will generally not coincide in an open economy due to terms-of-trade effects. Real GDP measures the real quantities produced by the economy, and depends on foreign shocks only to the extent that those shocks change primary factor inputs. In contrast, as clarified in detail in Appendix A.3, real consumption would increase if terms of trade improved even if the domestic production allocation is completely unchanged. Conceptually, one could argue that the real consumption change is a better measure of the welfare change associated with the shock. In the quantitative analysis we therefore also compare the changes in real consumption due to the pandemic between the baseline and renationalized economies.
3. Data and calibration
Labor shock. To calibrate the size of the labor shock, we use three pieces of data. The first is the classification of occupations by whether they can be performed at home by Dingel and Neiman (2020).12 We then combine this occupation-specific work from home intensity with the country-specific lockdown intensity constructed by the Oxford Blavatnik School of Government Coronavirus Government Response Tracker (Hale et al., 2020, henceforth GRT). This index ranges from 0 to 100, and we treat it as a proportion indicator, 1 being a full lockdown. These data are recorded daily. We take the maximum value in each country up to April 30, 2020.13
While the variation across countries in lockdown severity can be captured by the GRT index, it is not meant to be a cardinal measure, and the elasticity of the labor supply with respect to this index is unknown. We thus curve the GRT index to fit a lognormal distribution, where we choose the mean and variance to match the mean and the range of the fall in the April 2020 Industrial Production (IP) for the countries for which these data are currently available.14
The labor supply shift in occupation and country n relative to the pre-shock steady state is then:
| (18) |
The exception is the Health Services sector, which receives no labor supply shock as it is not subject to lockdowns. The robustness section below shows that none of the main conclusions change if we simply treat the GRT index as a cardinal measure of the percentage of labor supply contraction ().15
Sectoral occupation composition. To compute the occupation shares by sector, we use US data from the Bureau of Labor Statistics. This dataset reports the number of workers in each occupation employed in each NAICS sector, together with their average annual wage. We convert this to our ISIC-based industry classification, and use it to compute the sectoral expenditure shares on each occupation. Because workers in Health Services are not affected by the lockdown measures, we create a special composite health occupation that is used by the Health Services sector only, and does not incur a negative labor supply shock. Our final occupational classification is similar to the 23 SOC “major groups”, minus the Military-Specific Occupations and with an extra “Health Composite” occupation. Appendix Table A1 lists our occupational classification together with the work from home intensities. Since data on industry occupational composition are unavailable for countries other than the US, we assume that the shares are similar across countries.16
Trade, input, and consumption shares. The data requirements for calibrating this model is the information on the world input-output matrix and final use. We use the OECD Inter-Country Input-Output (ICIO) Tables. These data cover 64 countries on all continents and 33 sectors spanning the entire economy. We use the information for the latest available year, 2015. We separate the 33 sectors into 3 groups for final consumption: Goods, Services, and Health. Appendix Table A.2 lists the countries, and Appendix Table A.3 lists the sectors along with the breakdown into groups.
Structural parameters. To construct the influence matrix (8) we must also take a stand on a few elasticities. Table 1 summarizes the parameters in our baseline calibration. Huo et al. (2020) estimate a final goods substitution elasticity γ between 1 and 2.75. Since ours is a very short-run application, we take the lower value of 1, and apply it to all groups. We set the intermediate input substitution elasticity ε to 0.5. The notion that inputs are complements at business cycle frequencies is consistent with the estimates by Atalay (2017) and Boehm et al. (2019a). We calibrate the cross-group substitution elasticity ρ to 0.2 in our baseline, following the estimates from the structural transformation literature suggesting that broad services and manufacturing aggregates are complements (Herrendorf et al., 2013, Cravino and Sotelo, 2019, Comin et al., 2021). In the baseline we set the Frisch labor supply elasticity ψ of 2 for all occupations. Finally, we set the sectoral elasticity of substitution across occupations κ to 1, close to the value of 0.9 found by Goos et al. (2014). As detailed in Sections 2.2, 2.3, the magnitudes of domestic and international GE effects are governed by these elasticities. Below we reports the results of our quantitative exercises under alternative elasticities.
Table 1.
Parameter values.
| Param. | Value | Source | Description |
|---|---|---|---|
| ρ | 0.2 | Herrendorf et al. (2013) | Cross-group substitution elasticity |
| γ | 1 | Huo et al. (2020) | Final substitution elasticity |
| ε | 0.5 | Boehm et al. (2019a) | Intermediate substitution elasticity |
| ψ | 2 | Occupational Frisch elasticity | |
| κ | 1 | Goos et al. (2014) | Cross-occupation elasticity |
| αj | [.38,.69] | KLEMS, OECD STAN | Labor and capital shares |
| ηj | [.33,.65] | KLEMS, OECD STAN | Intermediate input shares |
| OECD ICIO | Final use trade shares | ||
| OECD ICIO | Intermediate use trade shares | ||
| BLS | Occupation shares by sector |
Notes: This table summarizes the parameters and data targets used in the baseline quantitative model, and their sources. For αj and ηj, the table reports the 10th and 90th percentiles of the range of these parameters. Alternative parameters are considered in the robustness analysis.
All other parameters in the model have close counterparts in basic data and thus we compute them directly. Capital shares in total output α j and value added shares in gross output η j come from the KLEMS and OECD STAN databases, and are averaged in each sector across countries to reduce noise.
3.1. Basic facts
How economies react to the labor shock stemming from the pandemic depends on the fraction of work that can be performed from home. Appendix Table A.4 shows the sectoral shares of employees whose occupation can be done from home, computed as a sector-specific weighted average of the occupation measures. There is substantial sectoral variation in the shares, ranging from 11% in the accommodation and food services sector, to 90% in the IT sector. Overall, service sectors have a higher share, with the notable exception of the Human Health and Social Work sector. Because sectors have different labor shares, however, the share of work that cannot be done from home does not precisely capture the exposure of a sector to the labor shock. The last column of the table displays the sectoral exposure, defined as (1 − α j)η j(1 − work from homej). These are uniformly lower, since the labor shares in gross output are far less than 1, but still feature considerable variation across sectors.
The effective severity of the labor supply shock will vary across countries as a function of both sectoral composition and lockdown stringency. Table 2 lists the top 10 and bottom 10 countries according to the share of aggregate labor that can be performed at home. This share is computed as the sectoral labor compensation-weighted average of the sectoral shares of work that can be done from home. Among the top 10 are several developed economies such as the US, United Kingdom or Luxembourg, consistent with their large service sector size. Table 2 also lists the top and bottom 10 countries in terms of lockdown stringency.
Table 2.
Country-level work from home intensity and lockdown stringency.
| Country | Work from home | Country | Work from home | Country | Lockdown stringency | Country | Lockdown stringency |
|---|---|---|---|---|---|---|---|
| Top 10 | Bottom 10 | Top 10 | Bottom 10 | ||||
| LUX | 0.656 | KHM | 0.346 | PHL | 100 | TWN | 30.6 |
| IRL | 0.559 | TUN | 0.369 | ARG | 100 | SWE | 46.3 |
| MLT | 0.543 | VNM | 0.374 | IND | 100 | JPN | 47.2 |
| CYP | 0.513 | IDN | 0.402 | HRV | 96.3 | ISL | 53.7 |
| SGP | 0.510 | TUR | 0.410 | VNM | 96.3 | BRN | 58.3 |
| ISR | 0.506 | CHN | 0.423 | PER | 96.3 | FIN | 60.2 |
| USA | 0.502 | THA | 0.423 | NZL | 96.3 | LVA | 65.7 |
| GBR | 0.497 | PER | 0.431 | SAU | 94.4 | HKG | 66.7 |
| TWN | 0.496 | ARG | 0.433 | ISR | 94.4 | KHM | 68.5 |
| FRA | 0.489 | COL | 0.436 | CYP | 94.4 | DNK | 72.2 |
Notes: This table displays the countries with the top 10 and bottom 10 country-level work from home intensities, computed as the labor-compensation weighted averages of sectoral intensities. The second section reports the lockdown stringency index, out of 100.
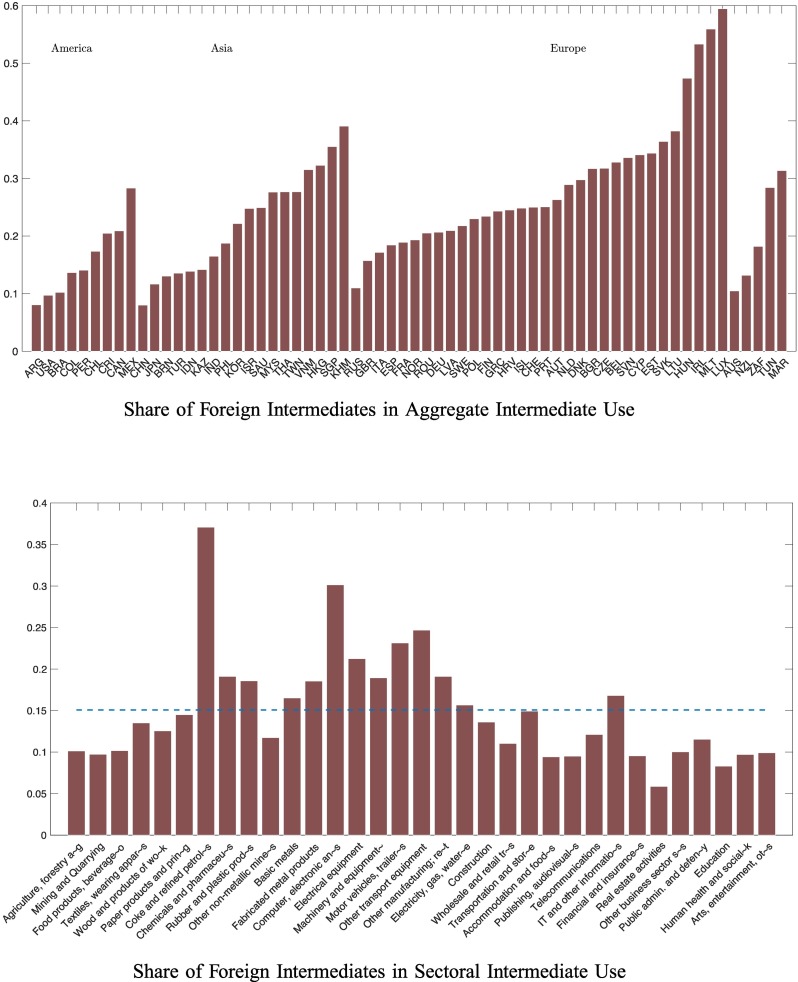
Exposure to foreign inputs will also determine the extent to which each country is affected by international shock propagation. The top panel of Fig. 1 displays the share of inputs that each country sources from abroad. There is a fair bit of variation, ranging from less than 10% in countries least integrated into global supply chains to over 50% in the most integrated countries. The bottom panel of Fig. 1 displays the world average of same measure at the sectoral level. As expected, manufacturing sectors tend to have higher imported input shares than services.
Fig. 1.
Foreign Intermediate Input Use by Country and by Sector. Notes: The top panel displays the share of foreign intermediate inputs in the total intermediate purchases for the countries in our sample in 2015. The bottom panel displays the share of foreign intermediate inputs in the total sectoral intermediate purchases. The blue dashed horizontal line is the cross-sector mean. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
4. Main results
4.1. GDP contraction and the contribution of foreign shocks
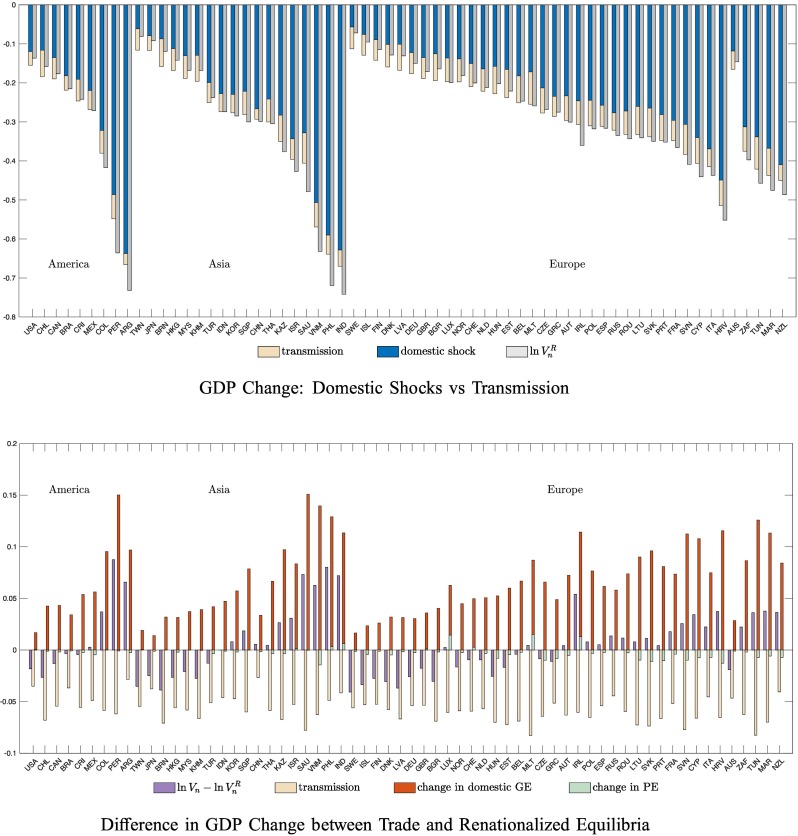
The blue-beige combination bars in the top panel of Fig. 2 display the GDP drops across all countries in our baseline model following the labor supply shock. The four panels group countries into geographical regions. The GDP reductions are dramatic, at −29.6% on average. There is a significant amount of dispersion, with GDP reductions ranging from −11% in Sweden and Taiwan to −67% in Argentina and India.
Fig. 2.
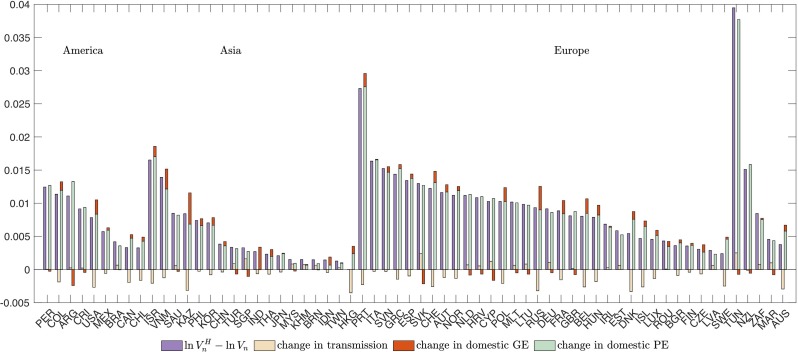
GDP Responses to the Labor Supply Shock. Notes: The top panel of this figure displays the change in GDP following the labor supply shock described in Section 3. The first bar represents the change in GDP under trade, decomposed into domestic shock (dark blue) and transmission (beige bar). The second bar represents the change in GDP under renationalization. Tables A5 and A6 in Appendix B.3 display the specific numbers. The bottom panel decomposes the change in the reaction of GDP to the labor supply shock between the baseline trade economy (ln Vn) and the renationalized supply chains economy (), according to the decomposition in Eq. (17). The purple bar is the total difference, the beige bar is the transmission, the red bar is the change in domestic GE, and the light green bar is the change in domestic PE. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
The white parts of the bars denote the contribution of foreign shocks . It is evident that foreign shocks transmitted through the global supply chains constitute a sizable minority of the overall GDP contraction. The mean contribution of foreign shocks to the fall in GDP is 23.3% of the total. Appendix Tables A.5–A.6 lists the GDP changes and the elements of the decomposition underlying Fig. 2 for every country in the sample.
4.2. Renationalization of the global supply chains
To answer whether participation in the global supply chains makes economies more vulnerable to pandemic-related lockdowns, we must solve for the GDP contraction under the same magnitude of a shock, but in a counterfactual economy in which the supply chains have been renationalized. We construct the renationalization scenario as follows. Starting from today's world economy, we increase iceberg trade costs to a very high value, and solve for the new production equilibrium following the exact hat algebra approach of Dekle et al. (2008). One subtlety with this exercise is that to find the renationalized equilibrium we raise the substitution elasticities above 1. This is because when elasticities are below 1, expenditure shares on foreign goods increase in iceberg trade costs. Raising the substitution elasticities above 1 captures the notion that supply chain renationalization will be a medium- to long-run adjustment, and thus should be governed by higher substitution elasticities. It also delivers the sensible outcome that raising trade costs to very high levels eliminates cross-border trade.17 We obtain virtually the same results if we construct the renationalized equilibrium by simply reapportioning foreign spending to domestic suppliers by fiat. Below, we present an alternative renationalization scenario, in which only intermediate input trade costs are raised while leaving final good trade costs unchanged. The results are similar.
The gray bars in the top panel of Fig. 2 plot counterfactual declines in GDP for the same shock in a world where supply chains are domestic. The mean decline in GDP in the renationalized equilibrium is −30.2% in our sample, slightly worse than the decline with international supply chains. The renationalized equilibrium also features larger cross-country dispersion of GDP changes. The standard deviation of GDP changes is 16% in the renationalized scenario compared to 13% under trade (Table A7). Not surprisingly, participation in global supply chains synchronizes GDP changes across countries.
To help understand this result, the bottom panel of Fig. 2 implements the accounting decomposition (17). The purple bars are the difference in GDP change in trade relative to autarky, the left-hand side of (17). A positive value of the bar indicates that GDP falls by less in the current trade equilibrium relative to the renationalization scenario, that is, global supply chains mitigate the fall in GDP. The beige bars are the transmission terms , which are all negative. All else equal, GDP falls by more in the trade equilibrium because foreign shocks can now also reduce domestic GDP.
The transmission terms paint an incomplete picture, however, because the influence of domestic sectors will also change. The red and green bars plot the changes in the GE and PE components of domestic influence. The total change in domestic influence (the sum of the GE and PE bars bars) is always positive: in the trade equilibrium, most economies are more resilient to their own domestic shocks than they would be in autarky. The change in the PE term is negligible for most countries, implying that most of the change in domestic influence comes through general equilibrium effects.
The net result of these opposing effects is that most countries would experience smaller GDP reductions in the current trade equilibrium than they would in a world of renationalized global supply chains. Put plainly, eliminating reliance on foreign inputs increases reliance on the domestic inputs. Since a pandemic-related lockdown also affects domestic sectors, on average there is no benefit of resilience from renationalizing the international supply chains.
There is variation across countries, however. A number of important economies: Japan, Taiwan, Sweden, and the US, among others, would be more resilient to the pandemic-related lockdown if their supply chains were renationalized. The opposite is true of some Latin American (Peru, Argentina, Colombia) and Asian (Philippines, India) countries.
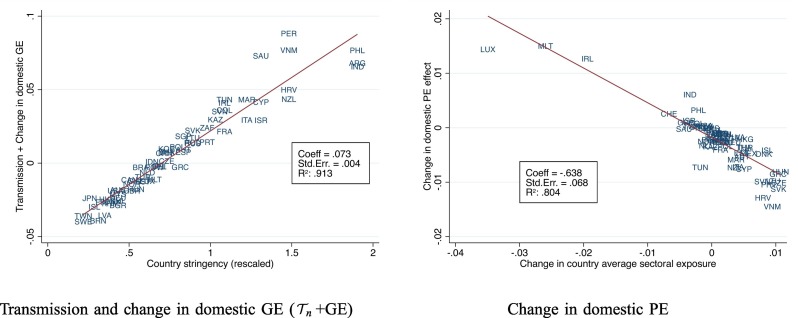
To better understand this variation, the left panel of Fig. 3 plots the combined general equilibrium terms (domestic GE term and international transmission) against a country's lockdown stringency. There is a tight positive relationship between the two, with a bivariate R 2 of about 0.9. Countries with most stringent lockdowns are better off with international supply chains, and vice versa. This is intuitive. A country with the most stringent lockdown is trading with countries with less severe lockdowns. Thus, the reduction in the supply of foreign inputs is smaller than the reduction in the corresponding domestic inputs, since these are subject to a severe lockdown.
Fig. 3.
Correlates of the PE and GE Effects. Notes: This figure presents scatterplots of the terms of the decomposition (17) against heuristic measures. The left panel displays the sum of the change in GE and Transmission against the country lockdown stringency. The right panel displays the change in domestic PE against the change in the country-level exposure, computed as the Domar-weighted sum of sectoral exposure in from Table A4. The lines through the data are OLS fits. The boxes report slope coefficient estimates, robust standard errors, and the R2's of the bivariate regression.
To highlight a source of remaining variation, the right panel of Fig. 3 plots the change in domestic PE against the change in the country-level exposure to the labor shock, defined as the Domar-weighted sectoral exposure from Table A4. A country where participation in international supply chains increases the size of sectors where work cannot be done from home becomes relatively less resilient to domestic shocks in the trade equilibrium, and vice versa. As evident from the bottom panel of Fig. 2, the PE component is barely perceptible for most countries, and so a reshuffling of employment across sectors with different work-from-home intensities is not a large effect quantitatively.
4.3. Renationalizing supply chains in individual sectors
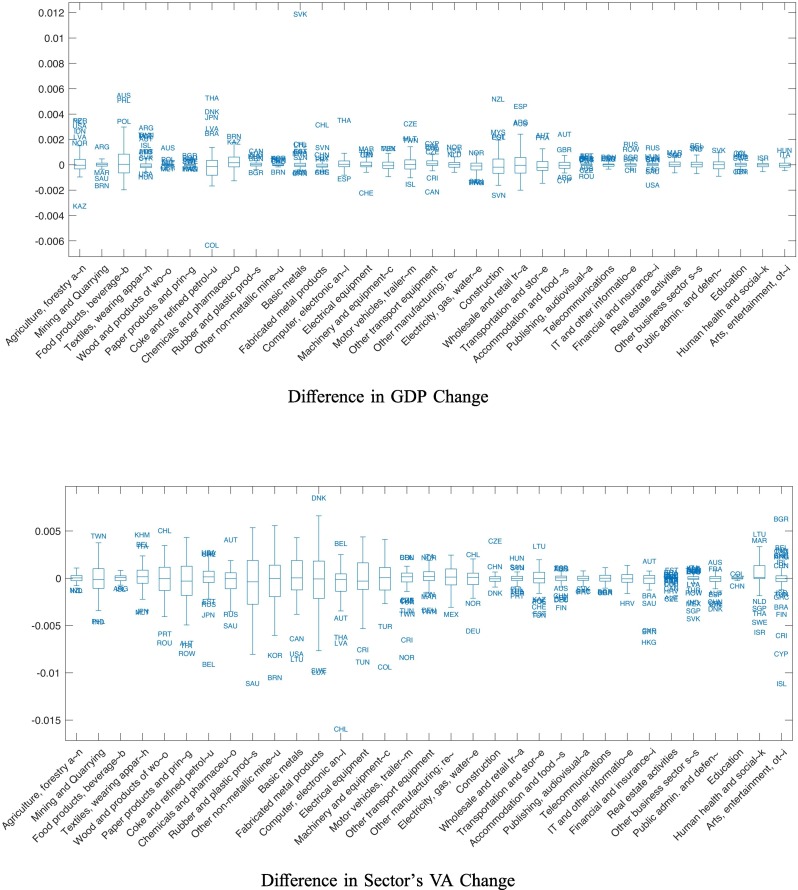
It may be that while renationalizing all trade is not generally beneficial, renationalizing specific sectors’ supply chains can systematically improve resilience. To check whether this is the case, we examine a set of counterfactuals in which we renationalize supply chains of each sector one at a time. That is, we force all inputs in one specific sector to be sourced domestically. We then subject this counterfactual economy to the lockdown shock, and compare the GDP contraction to the baseline, as we did for the full renationalization scenario.
The top panel of Fig. 4 reports the results. For each sector, it presents a box plot of the difference in the GDP change in the baseline relative to the counterfactual in which that sector's inputs are sourced domestically. A value of zero on the y-axis implies that there is no difference in the lockdown-driven GDP change in this counterfactual relative to the baseline. The box depicts the interquartile range of country-specific GDP change differences, while “whiskers” extend to the adjacent values. The outlier countries are labeled.
Fig. 4.
Sectoral Renationalization. Notes: The top panel depicts the difference in country-level GDP change due to the lockdown, between the baseline scenario and a scenario where the individual sector's supply chain is renationalized. The bottom panel depicts the difference in the sector's real value added change due to the lockdown, between the baseline scenario and a scenario where that sector's supply chain is renationalized.
The main conclusion is that when it comes to GDP changes, renationalizing individual sectors has a minimal impact. The mean difference in GDP changes is a small fraction of a percent, and the variation across countries is tight around zero. Even outliers almost never amount to a more than a 1.2% absolute difference, relative to the GDP reductions of 29.6% on average.
It may be that while the resilience benefits of renationalizing supply chains in a particular sector are small for GDP, they are large for that particular sector. The bottom panel of Fig. 4 plots instead the difference in the value added change of that sector when its supply chain is renationalized and the baseline. Once again, the averages across countries as well as the interquartile ranges are very close to zero. As expected, there are a few more visible outliers, but even for most outliers the absolute difference between the baseline and renationalization is small. Notably, the supply chain renationalization in the Health sector beings the most visible benefit on average, and the highest dispersion in outcomes. Nonetheless, while the values are large relative to other sectors, they are negligible in absolute terms. All in all, there appears to be no systematic benefit of resilience to the sector from renationalizing its supply chain.
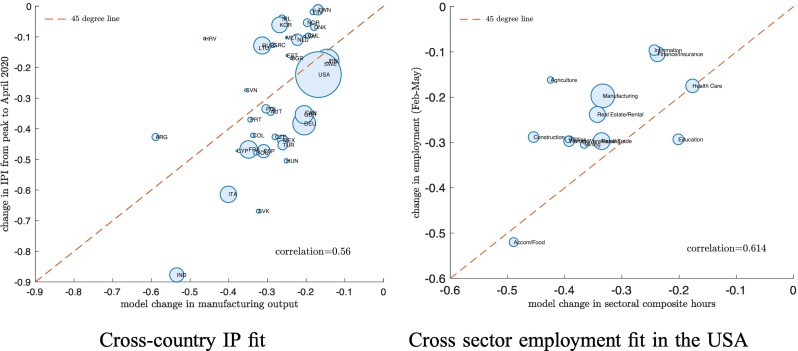
4.4. Fit
While our calibration of the size of the shock used a log-normal transformation to approximate the average fall in IP and its dispersion, we did not target the variation in output contractions across countries in the sample. The left panel of Fig. 5 plots the April 2020 IP contraction in the data on the y-axis against the manufacturing output contraction implied by the model, along with the 45-degree line. The IP data are available for 39 countries. Circle sizes are proportional to total GDP of the country. There is a clear positive correlation (0.56) between the data and the model. We do not target a perfect fit. The lack of a perfect fit is sensible, as the model is subjected to only one, fairly parsimoniously specified exogenous shock, whereas the data are presumably generated by many shocks. In addition, up-to-date IP data are available for only about two-thirds of the countries in the sample.
Fig. 5.
Model fit: IP Contraction and Employment changes. Notes: This figure plots the change in April 2020 Industrial Production in the data against the fall in real manufacturing output on the y-axis in the model for 39 countries (left panel), and changes in US sectoral hours in the model against the change in US sectoral employment in the data (right panel). The lines through the data are the 45-degree lines. The model hours changes are aggregated to Bick et al. (2020)'s classification using simple averages.
The right panel of Fig. 5 plots the February to May sectoral employment change in the US from the Real-Time Population Survey (Bick et al., 2020), against the model-implied change in sectoral composite hours. Again, while we do not target the sectoral labor input changes to calibrate our shock, the correlation is positive at 0.61.
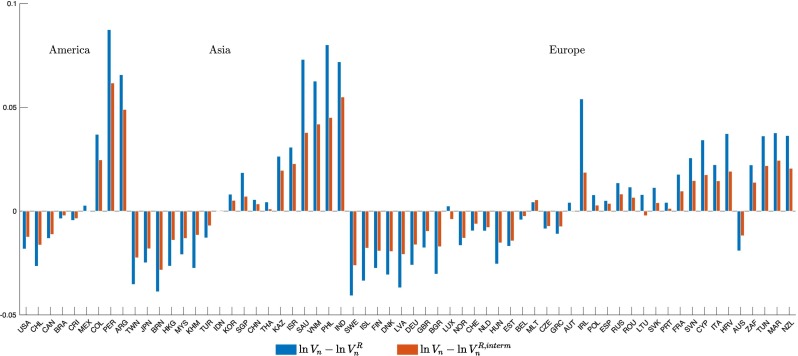
4.5. Renationalization of intermediate supply chains only
Fig. 6 displays the difference between the baseline and renationalization scenarios, under an alternative assumption that only intermediate supply chains are renationalized, but countries can still trade final goods. Appendix Table A7 summarizes the key outcomes. The difference between the intermediate renationalization scenario and the baseline is slightly muted, but the set of countries better off under trade does not change except for countries where the difference between trade and renationalized equilibria is negligible. In this alternative renationalization scenario, the average drop in GDP is 29.9% instead of 30.1% in our main renationalization scenario.
Fig. 6.
Alternative Renationalization Scenario. Notes: This figure displays the difference in the GDP change between baseline and renationalized equilibria for alternative renationalization scenarios. The blue bars represent our main renationalization exercise (ln VR), and the red bars represent an alternative in which only intermediate trade is removed, but trade in final goods continues (ln VR,interm). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
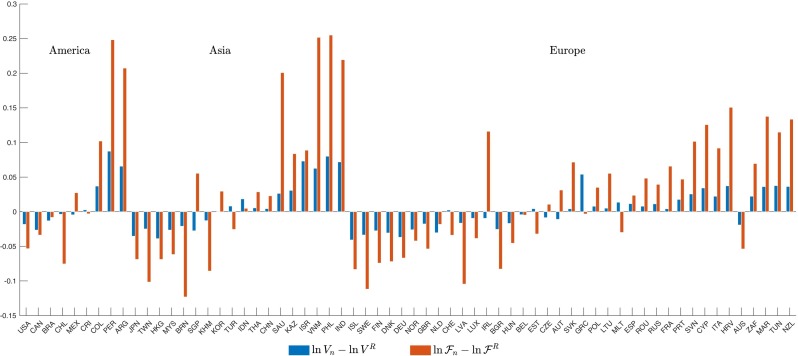
4.6. Change in real consumption
While most of our analysis focuses on real GDP (a common policy target), it is of independent interest how welfare changes in the pandemic in the baseline and renationalized equilibria. Since our main shock is to preferences (disutility of labor supply), we ignore that dimension of welfare, and present the results for real consumption. Real consumption is simply nominal GDP divided by the consumption price index: . Fig. 7 displays the difference between the baseline minus renationalization scenarios, for GDP (as above) and for real consumption , side by side. The summary statistics of the main outcomes are reported in Appendix Table A7. By and large the two track each other fairly well. However, the real consumption differentials exhibit greater dispersion: countries better off during pandemics under trade according to real GDP are even better off in terms of real consumption, and vice versa. At the mean, the real consumption drops by 2.5 percentage points more in the renationalized scenario compared to the baseline, whereas GDP drops by only 0.5 percentage points more. Thus, if anything, renationalizing supply chains is more harmful during pandemics for real consumption than for GDP.
Fig. 7.
Renationalization: Real Consumption vs. Real GDP. Notes: This figure displays the difference in the GDP change and in the real consumption change () between Trade and Renationalized Equilibria.
Our explanation for this “amplification” of the differential change for real consumption compared to GDP is that in the trade equilibrium terms-of-trade effects help countries with harsher lockdowns, and hurt countries with milder ones. Since countries with harsher lockdowns contract their output by relatively more, terms of trade move in their favor. So for these countries going to autarky takes away the favorable terms-of-trade effect, and makes the pandemic even worse. The opposite is true for countries with milder lockdowns. The alternative renationalization scenario that permits final goods trade (as in the paragraph above) retains part of the terms-of-trade effect even in the renationalized equilibrium. As a result, the overall terms-of-trade effect is attenuated, and the dispersion in consumption differentials is still present but lower than the dispersion in the full autarky scenario (not pictured).
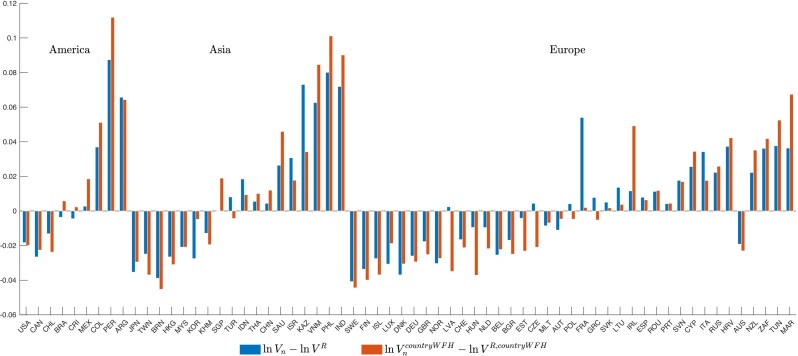
4.7. Country-specific work-from-home intensity
The baseline analysis uses a work-from-home intensity by occupation computed based on US data, as this information is not available for all the countries and occupations in our sample. Hatayama et al. (2020), henceforth HVW use survey micro data to compute comparable work-from-home intensities for 35 countries, and present normalized work-from-home intensities for 9 occupations. These data show that (i) for the US, the HVW work-from-home index has a 0.86 correlation with the Dingel-Neiman measure that we use; and (ii) the HVW work-from-home index is highly correlated across countries. Among these 35 countries, the pairwise correlations range from 0.84 to 0.99, with a mean and median of 0.96. The countries range from the wealthiest ones such as US and Norway to middle-income countries such as Ecuador, Peru, and Turkey. Thus, it appears that over a fairly wide range of income levels, the variation across occupations in work-from-home intensity is quite highly correlated.
We did not adopt this measure as the baseline, because it covers many fewer occupations and countries. As a robustness check, we used the HVW index for the 35 countries for which it is available, concording their 9 occupations to our 20. For the 29 countries not in the HVW data, we imputed country-occupation specific work-from-home intensities by fitting a bivariate relationship between the HVW work-from home intensity measure and per capita income for each occupation available in their data, and computing the predicted work-from-home intensity for each occupation and each country based on its per-capita income. While this falls short of capturing the complete heterogeneity across countries (which would be infeasible based on these data, as we have 64 countries in our model), it at least makes the adjustment for any relationship between work-from-home intensity and the level of development. Within every one of these 9 occupations, the cross-country relationship between work-from-home intensity and income is positive, and thus with this adjustment work-from-home intensity falls for countries with lower per capita income than the US. Thus, our baseline approach of using the Dingel-Neiman measure for all countries is conservative, as it implies a smaller shock to poorer countries. Fig. 8 displays the difference in GDP changes between the baseline and the renationalized equilibria when using country-specific work-from-home intensity together with the baseline results, and Appendix Table A7 summarizes the key outcomes. All of the main results are unchanged.
Fig. 8.
Country-Specific Work-from-Home Intensity. Notes: This figure displays the difference in the GDP change between baseline and renationalized equilibria when using country-specific measures of work-from-home intensity. The blue bars represent the baseline exercise (ln V − ln VR), and the red bars represent an alternative exercise that uses country-specific work-from-home intensity (ln VcountryWFH − ln VR,countryWFH). (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
4.8. Shock interpretation and the labor supply response
Our baseline analysis conceives of the lockdown as an inward shift of the occupation-specific labor supply. Conditional on this inward shift, households can still adjust their supplied hours, and this adjustment is governed by the Frisch elasticity ψ. As noted in Section 2.1, for changes in GDP and real consumption, this setup is isomorphic to one in which the lockdown instead lowers the efficiency units of every supplied hour of labor. Thus, by lowering the Frisch elasticity, we can accommodate the alternative view of the lockdown as a “quantity restriction” on the labor input. Taking away the household's ability to move along its labor supply curve, the lockdown essentially amounts to an exogenous contraction in the effective supply of labor.18
Relatedly, the GHH preferences mute the wealth effect on labor supply. In a static model, real wealth is simply real income. Thus, to quantify the wealth effect on labor supply, we would need to take a stand on the joint distribution of asset and occupation endowments across households, ideally for each country in our sample. This would clearly be infeasible with available data. A special case of an economy populated by “worker” and “capital-owner” households, where each worker household only supplies labor to one occupation yields the same isoelastic functional form of labor supply as in our baseline, albeit with a different exponent (details available upon request). So this special case can be dealt with by simply choosing a different value of the labor supply elasticity. Since the wealth effect on the labor supply is normally considered negative, adding the wealth effect in this case amounts to lowering the overall labor supply elasticity.
With these two discussions in mind, Appendix Table A7 summarizes the results under three lower values of the Frisch elasticity: 1, 0.2, and 0.01. To keep the results comparable to the baseline, we do not recalibrate the size of the labor supply shock, and thus the only change is in the ψ parameter. With a lower Frisch elasticity, workers are less responsive to negative labor supply shocks. As a result, the total fall in GDP is smaller and the international transmission less important. The main result that renationalizing the supply chains does not insulate countries from pandemic is unchanged under these alternative Frisch elasticities. As the Frisch elasticity goes to zero, the labor supply becomes exogenous, and real GDP is only driven by domestic shocks (Kehoe and Ruhl, 2008, Burstein and Cravino, 2015, Baqaee and Farhi, 2019). Since the shocks are by construction the same size in the baseline and the renationalized equilibria, exogenous factor supply yields the most stark – but perhaps least illuminating – version of the result that renationalizing global supply chains has no effect on the pandemic-driven GDP change.19
4.9. Additional sensitivity
Appendix Table A7 summarizes the main results under alternative values of ρ, ε, κ, and γ. A higher elasticity in the final goods aggregator, ρ, makes a country less sensitive to the variation in other countries’ production. Therefore the importance of the transmission term is smaller in this case. When we change ρ from 0.2 to 1, the average share of contribution of transmission in GDP reduction decreases by 1.5% in the trade economy. Raising the elasticity of substitution between intermediate inputs ε to 1 has a minimal impact on the overall GDP contraction, but reduces the importance of transmission to 16% of the total. The elasticity across occupations κ matters for how a shock in one occupation spills over to other occupations. In our exercises, almost all occupations are affected and few sectors concentrate on a particular occupation to the exclusion of others. Therefore, the quantitative effect of varying κ is mild. A lower substitution elasticity for final goods γ of 0.5 makes foreign goods more essential in consumption, and implied that the share of transmission increases to 34.6%. Renationalizing supply chains still does not insulate countries from pandemics, on average. All in all, the directions and magnitudes of the effects discussed in our baseline model are not especially sensitive to ρ, ε, κ, and γ.
The next robustness exercise treats the Government Response Tracker index as a cardinal measure of lockdown stringency. The index, that varies from 0 to 1, is treated as a percentage change in labor supply. The raw GRT index produces a similar average contraction in GDP (30.2%), but undershoots substantially on the dispersion in GDP changes across countries. The share of international transmission in the total GDP contraction, and the comparison between autarky and trade are quite similar to the baseline.
Finally, we explore the consequences of imperfect labor mobility across sectors. In our baseline analysis, within an occupation labor is perfectly mobile across sectors. Note that sectoral labor bundles are still not perfectly mobile across sectors, due to heterogeneous sectoral occupational composition. Thus, frictions to labor reallocation across sectors are accommodated in the baseline model, and could be regulated by varying κ. Nonetheless, we capture imperfect labor mobility across sectors with an alternative model in which labor is differentiated directly by sector, detailed in Huo et al. (2020). In this model, the set of occupations indexed by coincides with the set of sectors indexed by j. Then each sector only employs one type of labor, so that the sectoral labor aggregate is simply H nj = L nj. This model has one less parameter, as there is no longer κ, and the frictional reallocation across sectors is governed by ψ. For relative labor allocations across sectors, the model is isomorphic to the “Roy-Frechet” framework used in international trade (Galle et al., 2017): for any two sectors j and i, . It differs from the Roy-Frechet setup in that the aggregate labor supply is variable. The work-from-home intensity of sector j is then constructed as the occupation-share weighted occupational work-from-home intensity, and from there the sector-country specific shocks are constructed and calibrated as in Section 3. The last row of Table A7 summarizes the results. They are very similar to the baseline.
4.10. Discussion of baseline elasticity choices
Our baseline model equates the substitution elasticities across goods (within a broad product group) with the Armingon elasticity across source countries within a good. A straightforward extension would be to separate the two. In this case it would be reasonable to assume that the Armington elasticity is higher than the cross-good substitution elasticity. Empirical evidence suggests that the Armington elasticity low both in the short run (Boehm et al., 2019a) and even in the medium to long run (Boehm et al., 2020). Thus our approach of equating the two is in a sense conservative, as the overall elasticity parameter is calibrated to Armington estimates. While the main focus of our quantification is measured real GDP, we acknowledge that the choice of these elasticities may affect real consumption differently, as it would have implications for the strength of terms-of-trade effects. We leave a more complete exploration of how elasticity choices affect the distinction between real GDP and consumption for future work.
Our choice of the Frisch elasticity is higher than various micro estimates, but these lower micro elasticities are typically unable to account for business-cycle fluctuations. Extensive margin adjustments, labor hoarding, inattentive agents, variable capital utilization, and market frictions can provide a rationale for why a low micro-Frisch elasticity may result in a higher macro-Frisch elasticity (Hansen, 1985, Rogerson, 1988, Burnside et al., 1993, Chang and Kim, 2007). As discussed above, in the extreme case where the Frisch elasticity goes to zero, GDP in every country is unaffected by foreign shocks, but the terms-of-trade driven effects of foreign shocks on real consumption remain.
4.11. Increased long-run demand for health services
Our next counterfactual simulates a pandemic shock in a world with permanently increased demand for health services. To do this, we first compute a new pre-shock “high-health” steady state, in which the share of health expenditures in total final expenditures is twice as large as in the baseline. The mean share of health expenditures is 5% in our sample of countries, and thus in the “high-health” scenario it increases to 10% for the average country. We then simulate the same lockdown in this alternative economy. The experiment is designed to reflect the fact that the Health sector becomes more important in the pandemic.
The blue bars in Fig. 9 plot the difference in GDP change in the high-health economy relative to the baseline economy. A positive value indicates that the GDP downturn is less severe in the “high-health” scenario. All the values are positive, which is sensible as the Health sector is not subject to the lockdown, and thus increasing the relative size of the health sector will lead to smaller GDP contractions. The difference is small overall, ranging from 0.2% to 3% (whereas the GDP fall is on the order of 30%).
Fig. 9.
Difference in GDP Change between Large Health Sector Scenario and Baseline. Notes. This figure displays the decomposition (17) of the GDP contraction difference between the high-health scenario () and the baseline (ln Vn). The blue bar is the total difference, the beige bar is the difference in transmission, the red bar is the difference in the change in domestic GE, and the light green bar is the difference in the change in domestic PE. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
The beige, red, and light green bars in Fig. 9 implement the PE/GE/International transmission decomposition (17). The light green bar displays the difference in domestic PE. In this experiment, the domestic PE effect is the largest, accounting for the majority of the total GDP change. The difference in GDP contraction in the “high-health” economy compared to the baseline is accounted for by the fact that the high-health economy reallocates expenditure towards the sector not subject to the negative labor supply shock. The domestic GE effect is in red. It ends up being positive, but small. We conjecture that the relatively small domestic GE effect here is due to the fact that the Health sector uses relatively few intermediate inputs, and thus its ability to stimulate demand for upstream inputs is limited. The change in international transmission, in beige, is small compared to the domestic effects, and changes sign from country to country. This is consistent with the fact that the health sector is relatively non-tradeable and uses few foreign inputs.
4.12. Reopening
Finally, we simulate the lifting of the lockdown restrictions. The model does not exhibit asymmetries in the responses to positive vs. negative shocks. Thus, the GDP change following a worldwide end to the lockdown is essentially the negative of the GDP changes reported in Fig. 2. By the same token, the negative of the blue bars in the figure show what would happen to an individual country's GDP if it were the only one to reopen while the rest of the world stayed in lockdown. Since most of the GDP impact is due to the domestic lockdown policies, unilateral reopening will achieve most of the GDP rebound even if other countries stay under lockdown. Similarly, the negative of the beige portions of the bars give GDP changes in the opposite scenario: the rest of the world lifts restrictions while the country in question stays under lockdown. As long as the country itself is under lockdown, the bounceback expected from foreign opening is comparatively modest.
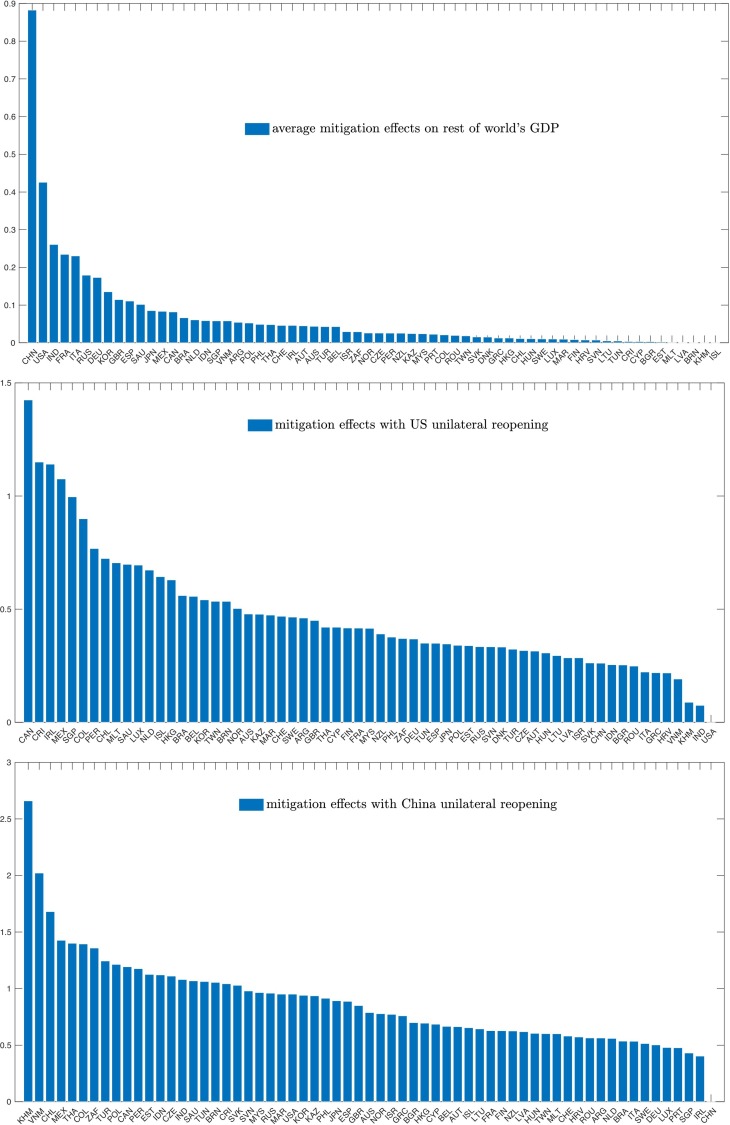
To give the opening scenarios a bit more texture, and because the timing of lockdown removals is likely to be staggered across countries, we simulate lifting the lockdowns country-by-country. The top panel of Fig. 10 plots the change in the rest of the world's GDP when the country on the x-axis lifts its lockdown. Not surprisingly, opening of the largest economies – US, China, Russia, Germany, Japan – would have the greatest impact on others. By contrast, since most countries are small, their opening will have a negligible impact on the rest of the world. The middle and bottom panels of Fig. 10 display the GDP change in the country on the x-axis following the end of the lockdowns in the US and China, respectively. These countries’ opening can raise GDP in some of the most tightly linked countries by up to 1−2.5% in some cases.
Fig. 10.
GDP Changes due to Unilateral Reopening. Notes: The top panel displays the GDP change in the rest of the world, when the country on the x-axis lifts its lockdown. The middle panel displays the GDP change of the country on the x-axis when the US lifts its lockdown. The bottom panel displays the GDP change of the country on the x-axis when China lifts its lockdown.
Appendix Figure A2 plots the entire matrix of other countries’ GDP changes. The axis labeled “Source” refers to the country whose reopening is being simulated. The axis labeled “Destination” refers to the country whose GDP change is being plotted. Thus, the figure plots the GDP change in “Destination” following the lifting of a lockdown in “Source.” Countries on both axes are sorted in descending order of average impact. Thus, countries in the left end of the Source axis are those whose opening has the largest impact on other countries in the world. Finally, we suppress the own country impact, as those values would swamp the variation in the plots (this explains the scattered “blanks” in the picture).
5. Conclusion
Global supply chains are a central feature of the world economy. As most countries go into lockdowns, there are concerns about both the present and the future. In the present, global supply chains are widely believed to transmit the crisis across countries. The future is forecasted to bring about at least some renationalization of the supply chains.
This paper performs a quantitative assessment of the role of global supply chains in the pandemic. While foreign lockdowns undoubtedly contribute to the size of economic downturns experienced by countries, the majority of GDP contractions come from the domestic lockdown policies. By and large, severing global supply chains will not make countries more resilient to pandemic-style labor supply shocks. This is because reducing the importance of foreign inputs mechanically increases the importance of domestic inputs. If domestic inputs are also subject to lockdowns, renationalization does not help mitigate the size of the contraction. Renationalization will make the economy more resilient if the country plans to have a less stringent lockdown then its trading partners, and vice versa.
Footnotes
We are grateful to the editor (Andrés Rodríguez-Clare), two anonymous referees, Costas Arkolakis, David Baqaee, Lorenzo Caliendo, Ayşegül Şahin, Sebastian Sotelo, and Meredith Startz as well as seminar participants at the IMF, Rebuilding Macroeconomics, Mason Online Pandemic Modeling Forum, the International Growth Centre, the NBER ITI Summer Institute, the NBER ITI Spring Meetings, the IMF Jacques Polak Annual Research Conference, the AEA meetings, and the Central Bank of Russia Research Workshop for helpful suggestions, and to Jonathan Dingel and Hernan Winkler for sharing their data.
See, e.g. “It's the End of the World Economy as We Know It”, The New York Times, 16 April 2020.
Hyun et al. (2020) use firm-level data to show that more internationally connected firms are more exposed to foreign shocks but less exposed to domestic shocks. Our resilience counterfactuals highlight a similar result, as decreasing foreign input exposure increases domestic input exposure.
The notion that international input trade is the key feature of the global economy goes back to Hummels et al. (2001) and Yi (2003), and has more recently been documented and quantified in a series of contributions by Johnson and Noguera, 2012, Johnson and Noguera, 2017 and Caliendo and Parro (2015). Burstein et al. (2008), Bems et al. (2010), Johnson (2014), Eaton et al. (2016), and Eaton et al. (2016), among others, explore the role of input trade in shock transmission and business cycle comovement. Also related is the large empirical and quantitative literature on the positive association between international trade and comovement (e.g. Frankel and Rose, 1998, Imbs, 2004, Kose and Yi, 2006, di Giovanni and Levchenko, 2010, Ng, 2010, Liao and Santacreu, 2015, di Giovanni et al., 2018, Drozd et al., 2021).
Our goal is to quantify the contemporaneous impact of the pandemic shock on GDP growth. Thus, the model is static and the capital stock remains fixed. To make the model dynamic requires assumptions on how lockdowns change over time as the disease spreads. The static model relies on far fewer assumptions but remains appropriate for quantifying the impact response to the shock. Huo et al. (2020) provide a quantification of the relative importance of contemporaneous vs. intertemporal correlation in a more general setting and show that the contemporaneous effect of shocks dominates.
We can incorporate deficits in a manner similar to Dekle et al. (2008), without much change in our results.
The NJ × NJ diagonal matrices η and α collect the ηj's and αj's respectively. The (n, mi) element of Πf is and the (mi, nj) element of Πx is . Typical elements of Λ and are and , respectively. The matrix is defined precisely in Appendix A.
The expression also makes clear that while we use only labor supply shocks in our analysis, the global input-output structure implies that a supply shock in a downstream sector will be a demand shock to an upstream sector, and so our approach incorporates a notion of demand disturbances as well.
The nonlinear solution yields the exact changes in all sectoral real quantities and prices following the shock. Then when we compute real GDP, which is a statistical construct, we use the base (pre-shock) Domar weights, rather than chained Domar weights.
In this case, .
It is immediate that the influence matrix can also be used to trace out the effect of shocks in a particular country (e.g. China) on the GDP growth in a partner (e.g. the US).
The first term captures how labor supply shocks on one occupation spillover to other occupations’ labor inputs. The second term captures the propagation of labor supply shocks through the input and final goods markets worldwide.
We use Dingel and Neiman (2020)'s O*NET-derived classification. Notice that in the context of the Covid-19 pandemic, this is a conservative shock, as school closures and other lockdown measures likely imply that the actual occupation-related tasks performed at home are less than those that are feasible. We also consider an alternative survey-based country-specific work-from-home measure below.
It is not known whether the April 2020 world contraction was driven by lockdown policies per se or by private decisions to stay at home for fear of the virus. For the purposes of quantifying the shock, the lockdown indices are a natural choice, both because they are likely highly correlated with the private agents’ fear of the virus, and because to our knowledge there are no internationally comparable data on the magnitude of voluntary labor supply responses due to fear.
See Appendix B.2 for details about the curving procedure. The advantage of IP data is that they are released promptly and are at the monthly frequency. The disadvantage is that they only cover the manufacturing sector, and thus must be lined up with manufacturing sector output rather than GDP in our model. We obtained April 2020 IP data for 39 of our 64 countries from the OECD, Eurostat, and some national statistical agencies. The April 2020 IP contraction is defined as the log difference with respect to the maximum 3-month moving average in the previous 12 months (meant to capture contraction relative to the peak).
In practice, the adjustment to the average size of the shock to match the IP drop is minimal. Using the raw GRT produces a 30.1% fall in manufacturing output in the set of countries for which we found IP data, compared to 28.7% in the data. Using raw GRT undershoots the dispersion in IP changes across countries substantially.
This is consistent with our assumption that sectoral production functions are the same across countries and the elasticity of substitution across occupations equals 1.
Our baseline calibration to elasticities below 1 is meant to reflect that we are capturing the very short-run effects of the pandemic lockdowns. Boehm et al., 2020 provide a mutually consistent set of trade elasticity estimates, and show that the elasticity is below 1 in the short run, but above 1 in the long run.
Alternative ways to capture the impact of the pandemic on labor inputs could include a disequilibrium approach in which quantities of either the labor inputs or firms’ outputs are capped, and thus jobs and/or goods are rationed. This approach would complicate the analysis as it would require assumptions on who receives the rents from the rationing that would be hard to justify with available data. Our exercises lowering the Frisch elasticity do not accommodate this disequilibrium view of the lockdown.
Even with exogenous factor supply, renationalizing global supply chains does affect how the pandemic changes real consumption, because the terms-of-trade effect described above still operates. Countries imposing the harshest lockdowns experience favorable terms of trade changes, and thus real consumption falls by more during the pandemic when supply chains are renationalized in those countries, and vice versa.
Supplementary data to this article can be found online at https://doi.org/10.1016/j.jinteco.2021.103534.
Appendix A. Supplementary data
Online Appendix
Data availability
References
- Acemoglu D., Chernozhukov V., Werning I., Whinston M.D. National Bureau of Economic Research; 2020. A Multi-Risk SIR Model With Optimally Targeted Lockdown. Working Paper 27102. [Google Scholar]
- Allen T., Arkolakis C., Takahashi Y. Universal gravity. J. Polit. Econ. 2020;128(2):393–433. [Google Scholar]
- Alon T., Kim M., Lagakos D., VanVuren M. National Bureau of Economic Research; 2020. How Should Policy Responses to the COVID-19 Pandemic Differ in the Developing World? Working Paper 27273. [Google Scholar]
- Antràs P., Redding S.J., Rossi-Hansberg E. National Bureau of Economic Research; 2020. Globalization and Pandemics, Working Paper 27840. [Google Scholar]
- Atalay E. How important are sectoral shocks? Am. Econ. J.: Macroecon. 2017;9(4):254–280. [Google Scholar]
- Atkeson A. National Bureau of Economic Research; 2020. What Will Be the Economic Impact of COVID-19 in the US? Rough Estimates of Disease Scenarios. Working Paper 26840. [Google Scholar]
- Baldwin R. 2020. Supply Chain Contagion Waves: THINKING AHEAD on Manufacturing ‘contagion and reinfection’ From the COVID Concussion, VoxEU.org. [Google Scholar]
- Baqaee D., Farhi E. mimeo, UCLA and Harvard; 2020. Nonlinear Production Networks With an Application to the Covid-19 Crisis. [Google Scholar]
- Baqaee D., Farhi E. Mimeo, UCLA and Harvard; 2020. Supply, Demand in Disaggregated Keynesian Economies With an Application to the Covid-19 Crisis. [Google Scholar]
- Baqaee D.R., Farhi E. mimeo, UCLA and Harvard; 2019. Networks, Barriers, and Trade. [Google Scholar]
- Barrot J.-N., Grassi B., Sauvagnat J. Mimeo, HEC-Paris and Bocconi; 2020. Sectoral Effects of Social Distancing. [Google Scholar]
- Barrot J.-N., Sauvagnat J. Input specificity and the propagation of idiosyncratic shocks in production networks. Q. J. Econ. 2016;131(3):1543–1592. [Google Scholar]
- Bems R., Johnson R.C., Yi K.-M. Demand spillovers and the collapse of trade in the global recession. IMF Econ. Rev. 2010;58(2):295–326. [Google Scholar]
- Bick A., Blandin A., Mertens K. mimeo, Arizona State, Virginia Commonwealth, and Federal Reserve Bank of Dallas; 2020. Work From Home After the COVID-19 Outbreak. [Google Scholar]
- Boehm C.E., Flaaen A., Pandalai-Nayar N. Input linkages and the transmission of shocks: firm-level evidence from the 2011 Tohoku earthquake. Rev. Econ. Stat. 2019;101(1):60–75. [Google Scholar]
- Boehm C.E., Levchenko A.A., Pandalai-Nayar N. National Bureau of Economic Research; 2020. The Long and Short (Run) of Trade Elasticities. Working paper 27064. [Google Scholar]
- Burnside C., Eichenbaum M., Rebelo S. Labor hoarding and the business cycle. J. Polit. Econ. 1993;101(2):245–273. [Google Scholar]
- Burstein A., Cravino J. Measured aggregate gains from international trade. Am. Econ. J.: Macroecon. 2015;7(2):181–218. [Google Scholar]
- Burstein A., Kurz C., Tesar L.L. Trade, production sharing, and the international transmission of business cycles. J. Monet. Econ. 2008;55:775–795. doi: 10.1016/j.jmoneco.2008.03.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caliendo L., Parro F. Estimates of the trade and welfare effects of NAFTA. Rev. Econ. Stud. 2015;82(1):1–44. [Google Scholar]
- Carvalho V.M., Nirei M., Saito Y.U., Tahbaz-Salehi A. Supply chain disruptions: evidence from the great east Japan earthquake. Q. J. Econ. 2021;136(2):1255–1321. [Google Scholar]
- Çakmaklı C., Demiralp S., Kalemli-Özcan c., Yesiltas S., Yildirim M.A. National Bureau of Economic Research; 2020. COVID-19 and Emerging Markets: An Epidemiological Model With International Production Networks and Capital Flows. Working paper 27191. [Google Scholar]
- Çakmaklı C., Demiralp S., Kalemli-Özcan c., Yesiltas S., Yildirim M.A. mimeo, Koç University and University of Maryland; 2021. The Economic Case for Global Vaccinations: An Epidemiological Model With International Production Networks. [Google Scholar]
- Chang Y., Kim S.-B. Heterogeneity and aggregation: implications for labor-market fluctuations. Am. Econ. Rev. 2007;97(5):1939–1956. [Google Scholar]
- Comin D.A., Lashkari D., Mestieri M. Structural change with long-run income and price effects. Econometrica. 2021;89(1):311–374. [Google Scholar]
- Cravino J., Sotelo S. Trade-induced structural change and the skill premium. Am. Econ. J.: Macroecon. 2019;11(3):289–326. [Google Scholar]
- Dekle R., Eaton J., Kortum S. Global rebalancing with gravity: measuring the burden of adjustment. IMF Staff Papers. 2008;55(3):511–540. [Google Scholar]
- del Rio-Chanona R., Mealy P., Pichler A., Lafond F., Farmer J. Supply and demand shocks in the COVID-19 pandemic: an industry and occupation perspective. Oxf. Rev. Econ. Policy. 2020;(Issue Supplement 1):S94–S137. [Google Scholar]
- di Giovanni J., Levchenko A.A. Putting the parts together: trade, vertical linkages, and business cycle comovement. Am. Econ. J.: Macroecon. 2010;2(2):95–124. [Google Scholar]
- di Giovanni J., Levchenko A.A., Mejean I. The micro origins of international business cycle comovement. Am. Econ. Rev. 2018;108(1):82–108. [Google Scholar]
- Dingel J.I., Neiman B. How many jobs can be done at home? J. Public Econ. 2020;189:104235. doi: 10.1016/j.jpubeco.2020.104235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drozd L.A., Kolbin S., Nosal J.B. The trade-comovement puzzle. Am. Econ. J.: Macroecon. 2021;13(2):78–120. [Google Scholar]
- Eaton J., Kortum S., Neiman B. Obstfeld and Rogoff's international macro puzzles: a quantitative assessment. J. Econ. Dyn. Control. 2016;72(C):5–23. [Google Scholar]
- Eaton J., Kortum S.S., Neiman B., Romalis J. Trade and the global recession. Am. Econ. Rev. 2016;106(11):3401–3438. [Google Scholar]
- Eichenbaum M.S., Rebelo S., Trabandt M. National Bureau of Economic Research; 2020. The Macroeconomics of Epidemics. Working paper 26882. [Google Scholar]
- Eppinger P., Felbermayr G., Krebs O., Kukharskyy B. CESifo; 2020. Decoupling Global Value Chains. Working paper 8572. [Google Scholar]
- Frankel J.A., Rose A.K. The endogeneity of the optimum currency area criteria. Econ. J. 1998;108(449):1009–1025. [Google Scholar]
- Galle S., Rodríguez-Clare A., Yi M. National Bureau of Economic Research; 2017. Slicing the Pie: Quantifying the Aggregate and Distributional Effects of Trade. Working paper 23737. [Google Scholar]
- George A., Li C., Lim J.Z., Xie T. 2020. Propagation of Epidemics’ Economic Impacts via Production Networks: The Cases of China and ASEAN during SARS and COVID-19. Working Paper. [Google Scholar]
- Glover A., Heathcote J., Krueger D., Ríos-Rull J.-V. Centre for Economic Policy Research; 2020. Health Versus Wealth: On the Distributional Effects of Controlling a Pandemic. Discussion paper 14606. [Google Scholar]
- Goos M., Manning A., Salomons A. Explaining job polarization: routine-biased technological change and offshoring. Am. Econ. Rev. 2014;104(8):2509–2526. [Google Scholar]
- Greenwood J., Hercowitz Z., Huffman G.W. Investment, capacity utilization, and the real business cycle. Am. Econ. Rev. 1988;78(3):402–417. [Google Scholar]
- Guerrieri V., Lorenzoni G., Straub L., Werning I. Mimeo, Chicago, Northwestern, Harvard, MIT; 2020. Macroeconomic Implications of COVID-19: Can Negative Supply Shocks Cause Demand Shortages. [Google Scholar]
- Hale T., Webster S., Petherick A., Phillips T., Kira B. Blavatnik School of Government. Data Use Policy: Creative Commons Attribution CC BY standard; 2020. Oxford COVID-19 Government Response Tracker. [Google Scholar]
- Hansen G.D. Indivisible labor and the business cycle. J. Monet. Econ. 1985;16(3):309–327. [Google Scholar]
- Hatayama M., Viollaz M., Winkler H. Jobs’ amenability to working from home: evidence from skills surveys for 53 countries. Covid Econ. Vetted Real-Time Papers. 2020;19:211–240. [Google Scholar]
- Herrendorf B., Rogerson R., Valentinyi Á. Two perspectives on preferences and structural transformation. Am. Econ. Rev. 2013;103(7):2752–2789. [Google Scholar]
- Hummels D., Ishii J., Yi K.-M. The nature and growth of vertical specialization in world trade. J. Int. Econ. 2001;54:75–96. [Google Scholar]
- Huo Z., Levchenko A.A., Pandalai-Nayar N. National Bureau of Economic Research; 2020. International Comovement in the Global Production Network. Working paper 25978. [Google Scholar]
- Hyun J., Kim D., Shin S.-R. 2020. The Role of Global Connectedness and Market Power in Crises: Firm-level Evidence From the COVID-19 Pandemic. Working Paper Issue 49, CEPR. [Google Scholar]
- Imbs J. Trade, finance, specialization, and synchronization. Rev. Econ. Stat. 2004;86(3):723–734. [Google Scholar]
- Johnson R.C. Trade in intermediate inputs and business cycle comovement. Am. Econ. J.: Macroecon. 2014;6(4):39–83. [Google Scholar]
- Johnson R.C., Noguera G. Accounting for intermediates: production sharing and trade in value added. J. Int. Econ. 2012;86(2):224–236. [Google Scholar]
- Johnson R.C., Noguera G. A portrait of trade in value-added over four decades. Rev. Econ. Stat. 2017;99(5):896–911. [Google Scholar]
- Kaplan G., Moll B., Violante G. mimeo; 2020. The Great Lockdown and the Big Stimulus: Tracing the Pandemic Possibility Frontier for the U.S. [Google Scholar]
- Kehoe T.J., Ruhl K.J. Are shocks to the terms of trade shocks to productivity? Rev. Econ. Dyn. 2008;11(4):804–819. [Google Scholar]
- Kleinman B., Liu E., Redding S.J. National Bureau of Economic Research; 2020. International Friends and Enemies. Working paper 27587. [Google Scholar]
- Kose M., Yi K.-M. Can the standard international business cycle model explain the relation between trade and comovement. J. Int. Econ. 2006;68(2):267–295. [Google Scholar]
- Liao W., Santacreu A.M. The trade comovement puzzle and the margins of international trade. J. Int. Econ. 2015;96(2):266–288. [Google Scholar]
- Ng E.C. Production fragmentation and business-cycle comovement. J. Int. Econ. 2010;82(1):1–14. [Google Scholar]
- Rogerson R. Indivisible labor, lotteries and equilibrium. J. Monet. Econ. 1988;21(1):3–16. [Google Scholar]
- Sforza A., Steininger M. CESifo; 2020. Globalization in the Time of COVID-19. Working paper 8184. [Google Scholar]
- Yi K.-M. Can vertical specialization explain the growth of world trade? J. Polit. Econ. 2003;111(1):52–102. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Online Appendix