Functional organization of the maternal and paternal human 4D Nucleome

Summary

Every human somatic cell inherits a maternal and a paternal genome, which work together to give rise to cellular phenotypes. However, the allele-specific relationship between gene expression and genome structure through the cell cycle is largely unknown. By integrating haplotype-resolved genome-wide chromosome conformation capture, mature and nascent mRNA, and protein binding data from a B lymphoblastoid cell line, we investigate this relationship both globally and locally. We introduce the maternal and paternal 4D Nucleome, enabling detailed analysis of the mechanisms and dynamics of genome structure and gene function for diploid organisms. Our analyses find significant coordination between allelic expression biases and local genome conformation, and notably absent expression bias in universally essential cell cycle and glycolysis genes. We propose a model in which coordinated biallelic expression reflects prioritized preservation of essential gene sets.

Graphical abstract

Highlights

• •We discover allele-specific relationships in genome architecture and gene expression
• •Integration of data modalities reveals an allele-specific 4D Nucleome
• •Allelic expression and conformation biases correspond to Pol II recruitment biases
• •We introduce a novel haplotype phasing algorithm, HaploHiC

Genomics; Bioinformatics; Genomic analysis

Introduction

Biallelic gene expression in diploid genomes inherently protects against potentially harmful mutations. Disrupted biallelic expression of certain genes increases vulnerability to disease in humans, such as in familial cancer syndromes that have loss of function in one allele (Knudson, 1971). BRCA1 and BRCA2 are quintessential examples, for which missense, nonsense, or frameshift mutations affecting function of one allele significantly increase the risk of breast cancer in women (Gudmundsson et al., 1995; Maxwell et al., 2017). Imprinted genes are also associated with multiple disease phenotypes such as Angelman and Prader-Willi syndromes (Zakharova et al., 2009; Buiting, 2010). Other genes with monoallelic or allele-biased expression (MAE, ABE) may be associated with disease, but the contribution of allelic bias to disease phenotypes remains poorly understood.

ABE can occur with single nucleotide variants (SNVs), insertions or deletions (InDels), and chromatin modifications (Consortium, 2015; Rozowsky et al., 2011; Kundaje et al., 2015; Rao et al., 2014; Tan et al., 2018). Analyses of allelic bias suggest high variance across tissues and individuals, with estimates ranging from 4% to 26% of genes in a given setting (Leung et al., 2015; Rozowsky et al., 2011). In addition, higher order chromatin conformation and spatial positioning in the nucleus shape gene expression (Rajapakse and Groudine, 2011; Misteli, 2011, 2020; Cook, 2010). As the maternal and paternal alleles can be distant in the nucleus, their spatial positions may promote ABE (Beliveau et al., 2015; Cremer and Cremer, 2010).

A major step toward understanding the contribution of allelic bias to disease is to identify ABE genes, recognizing that important biases may be transient and challenging to detect. Allele-specific expression and 3D structures are not inherently accounted for in genomics methods such as RNA-sequencing and genome-wide chromosome conformation capture (Hi-C). These limitations complicate interpretations of structure-function relationships, and complete phasing of the two genomes remains a significant challenge.

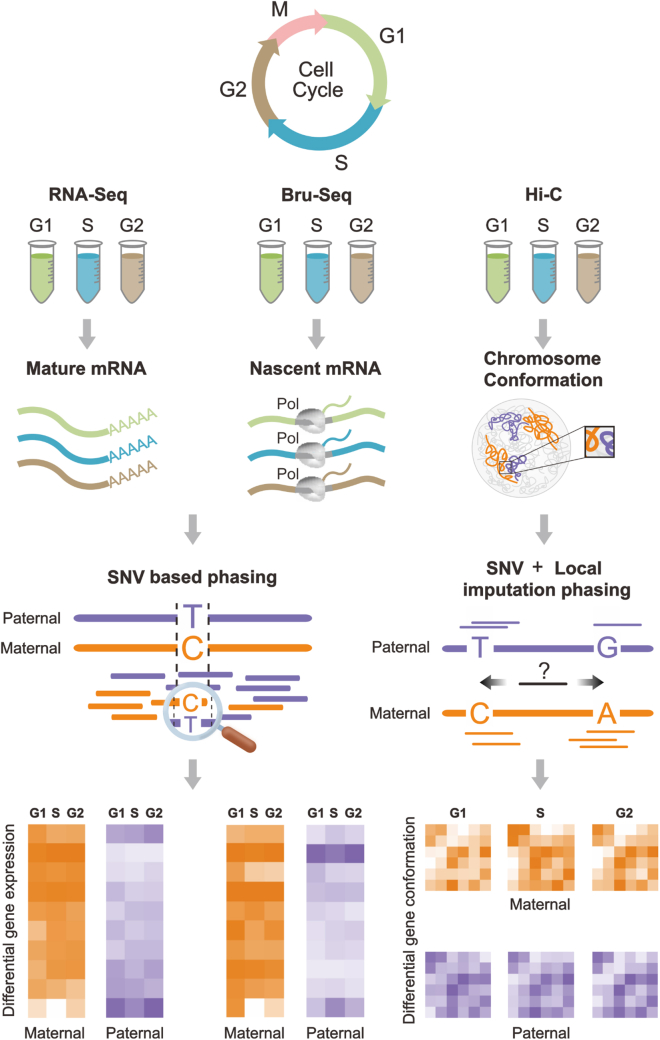
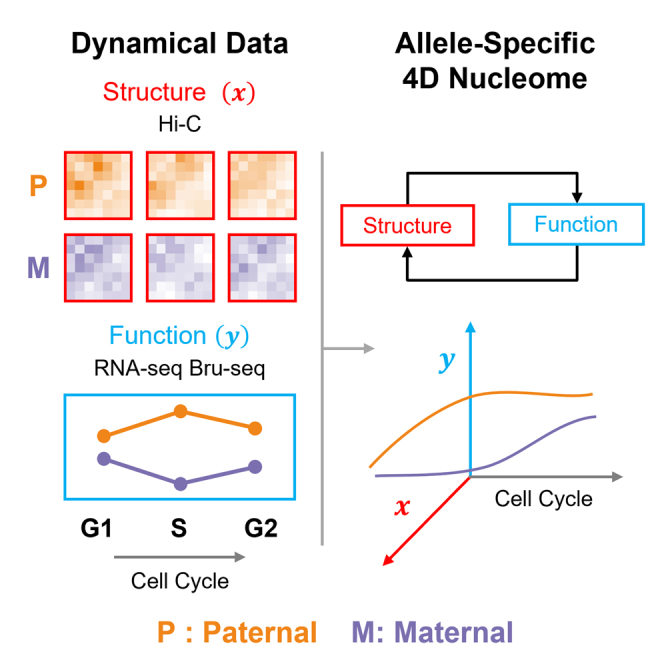
To improve understanding of ABE in genomic structure-function relationships, we developed a novel phasing algorithm for Hi-C data, which we integrate with allele-specific RNA-seq and Bru-seq data across three phases of the cell cycle in a human female B-lymphoblastoid cell line (Figure 1). RNA-seq and Bru-seq provide complementary gene expression data. RNA-seq provides information on steady state gene expression by measuring mature RNA, while Bru-seq measures nascent RNA transcription through bromouridine tagging (Paulsen et al., 2014). RNA-seq and Bru-seq data were separated into their maternal and paternal components through SNVs/InDels (Pickrell et al., 2010). Our algorithm, HaploHiC, uses phased SNVs/InDels to impute Hi-C reads of unknown parental origin. Publicly available allele-specific protein binding data (ChIP-seq) were also included to better understand potential regulatory elements involved in allelic bias (Chen et al., 2016b; Rozowsky et al., 2011). In addition to identifying known ABE genes silenced by X Chromosome inactivation (XCI) or imprinting, our analyses find novel expression biases between alleles and cell cycle phases in several hundred genes, many of which had corresponding bias in allele-specific protein binding. Furthermore, the alleles of ABE genes were significantly more likely to differ in local structure compared to randomly selected alleles. In contrast, we observed a pronounced lack of ABE in crucial biological pathways and essential genes. Our findings highlight advantages of integrating genomics analyses in a cell cycle and allele-specific manner and represent an allele-specific extension of the 4D Nucleome (4DN) (Chen et al., 2015; Ried and Rajapakse, 2017; Dekker et al., 2017; Lindsly et al., 2021). This approach will be beneficial to investigation of human phenotypic traits and their penetrance, genetic diseases, vulnerability to complex disorders, and tumorigenesis.

Figure 1.

Experimental and allelic separation workflow

Cell cycle sorted cells were extracted for RNA-seq, Bru-seq, and Hi-C (left to right, respectively). RNA-seq and Bru-seq data were allelicly phased via SNVs/InDels (left). SNV/InDel based imputation and haplotype phasing of Hi-C data using HaploHiC (right). These data provide quantitative measures of structure and function of the maternal and paternal genomes through the cell cycle. For all G2 labels after the cell cycle diagram, G2 includes both G2 and M.

Results

Chromosome-scale maternal and paternal differences

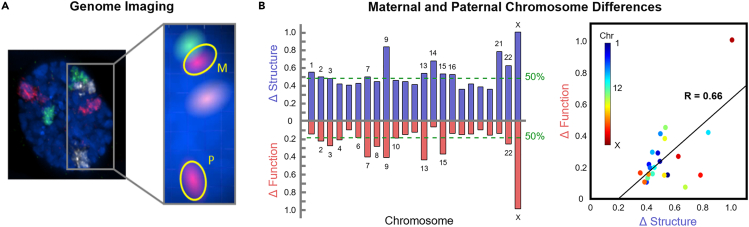
Spatial positioning of genes within the nucleus is known to be associated with transcriptional status (Rajapakse and Groudine, 2011; Misteli, 2011, 2020; Cook, 2010). One might expect that the maternal and paternal copies of each chromosome would stay close together to ensure that their respective alleles have equal opportunities for transcription. Imaging of chromosome territories has shown that this is often not the case (Figure 2A, method details) (Solovei et al., 2002; Bolzer et al., 2005; Ronquist et al., 2017). This observation inspired us to investigate whether the two genomes operate in a symmetric fashion, or if allele-specific differences exist between the genomes regarding their respective chromatin organization patterns (structure) and gene expression profiles (function). We analyzed parentally phased whole-chromosome Hi-C and RNA-seq data at 1 Mb resolution to identify allele-specific differences in structure and function, respectively. We subtracted each chromosome’s paternal Hi-C matrix from the maternal matrix and found the Frobenius norm of the resulting difference matrix. The Frobenius norm provides a measure of distance between matrices, where equivalent maternal and paternal genome structures would result in a value of zero. Similarly, we subtracted the phased RNA-seq vectors in log₂ scale and found the Frobenius norm of each difference vector. RNA-seq vectors were constructed by taking the average expression of all genes contained within each 1 Mb bin for all chromosomes. The Frobenius norms were adjusted for chromosome size and normalized for both Hi-C and RNA-seq.

Figure 2.

Genome imaging and chromosome differences

(A) Nucleus of a primary human fibroblast imaged using 3D FISH with the maternal and paternal copies of Chromosome 6, 8, and 11 painted red, green, and white, respectively (left). Subsection highlighting the separation between the maternal and paternal copies of Chromosome 11, now colored red (right).

(B) Normalized chromosome level structural and functional parental differences of GM12878 cells. Structural differences (Δ Structure, blue) represent the aggregate changes between maternal and paternal Hi-C over all 1 Mb loci for each chromosome, adjusted for chromosome size in G1. Functional differences (Δ Function, red) represent the aggregate changes between maternal and paternal RNA-seq over all 1 Mb loci for each chromosome, adjusted for chromosome size in G1. Green dashed lines correspond to the median structural (0.48, chromosome 3) and functional (0.20, chromosome 6) differences, in the top and bottom respectively, and all chromosomes equal to or greater than the threshold are labeled. Scatterplot of maternal and paternal differences in structure and function with best-fit line (R = 0.66 and p = 0.007).

We found that all chromosomes have allelic differences in both structure (Hi-C, blue) and function (RNA-seq, red) (Figure 2B). Chromosome X had the largest structural difference, as expected, followed by Chromosomes 9, 21, and 14. Chromosome X had the most extreme functional differences as well, followed by Chromosomes 13, 7, and 9. A threshold was assigned at the median Frobenius norm for Hi-C and RNA-seq (Figure 2B green dashed lines). The majority of chromosomes with larger structural differences than the median in Hi-C also have larger functional differences than the median in RNA-seq. There is a positive correlation between chromosome level differences in structure and function, which is statistically significant only when Chromosome X is included (R ₌ 0.66 and p ₌ 0.007 with Chromosome X; R ₌ 0.30 and p ₌ 0.17 without Chromosome X).

Allele-specific RNA expression

After confirming allelic differences in RNA expression at the chromosomal scale, we examined allele-specific expression of individual genes through RNA-seq and Bru-seq. We hypothesized that the chromosome scale expression differences were not only caused by known cases of ABE such as XCI and imprinting, but also by widespread ABE over many genes (Gimelbrant et al., 2007; Deng et al., 2014). Therefore, we evaluated all genes with sufficient reads covering SNVs/InDels for differential expression across the six settings: maternal and paternal in G1, S, and G2/M. These settings give rise to seven comparisons which consist of maternal versus paternal within each of the cell cycle phases (three comparisons), as well as G1 versus S and S versus G2/M for the maternal and paternal genomes, respectively (two comparisons for each genome). Within this manuscript, we define the term “allele-specific genes” as any genes with sufficient expression and SNV/InDel coverage for accurate separation of the maternal and paternal allelic contributions, although it is likely that other genes with insufficient coverage may also have biases in their allelic expression.

First, we identified genes with ABE and cell cycle-biased expression (CBE) from RNA-seq. Although ABE refers to differential expression between alleles in each cell cycle phase, CBE refers to significant changes in expression from one cell cycle phase to another in each allele. From 23,277 RefSeq genes interrogated, there were 4,193 genes with sufficient coverage on SNVs/InDels to reliably determine allele-specific expression (O’Leary et al., 2016). We performed differential expression analysis for the seven comparisons to identify which of the 4,193 genes had ABE or CBE (Anders and Huber, 2010). We identified 615 differentially expressed genes from RNA-seq: 467 ABE genes, 229 CBE genes, and 81 genes with both ABE and CBE (Tables S2 and S4). Both exons and introns containing informative SNVs/InDels were used for our Bru-seq data, from which 5,294 genes had sufficient coverage. We identified 505 differentially expressed genes from Bru-seq: 380 ABE genes, 164 CBE genes, and 39 genes with both ABE and CBE (Tables S3 and S5). We also identified 130 genes that had ABE in both RNA-seq and Bru-seq. Although this is substantially smaller than the total number of ABE genes for RNA-seq and Bru-seq (467 and 380, respectively), the number of genes that are allele-specific in both data modalities is also smaller. That is, only 285 of the ABE genes from RNA-seq are allele-specific in Bru-seq and 192 of the ABE genes from Bru-seq are allele-specific in RNA-seq. The remaining genes did not have sufficient expression or SNV coverage to be included in the downstream analysis, even though they may have biases in their allelic expression levels. We then separated the differentially expressed genes into their respective chromosomes to observe their distribution throughout the genome. From RNA-seq (Bru-seq), we found that autosomes had 3-14% (1-11%) of ABE in their allele-specific genes which is comparable to previous findings (Leung et al., 2015). As expected, Chromosome X had a particularly high percentage of ABE genes at 90% (91%).

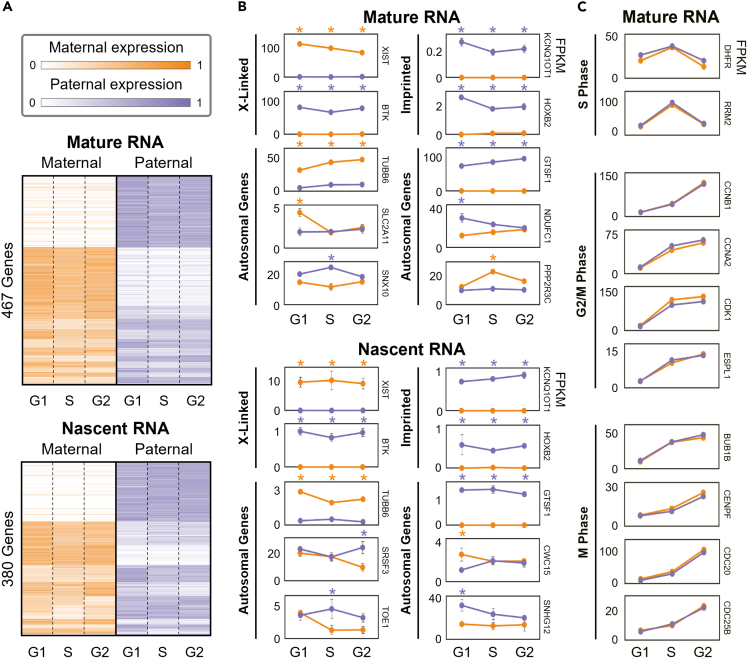
We identified 288 genes that have ABE in all three cell cycle phases from RNA-seq (160 paternally biased, 128 maternally biased) and 173 from Bru-seq (129 paternally biased, 44 maternally biased). This is the most common differential expression pattern among ABE genes and these genes form the largest clusters in Figure 3A. These clusters include, but are not limited to, XCI, imprinted, and other MAE genes. Known examples within these clusters are highlighted in the ‘X-Linked’ and ‘Imprinted’ sections of Figure 3B. We also identified hundreds of genes that are not currently appreciated in literature to have ABE, with examples shown in the ‘Autosomal Genes’ sections of Figure 3B for both mature and nascent RNA. Approximately half of all ABE genes were only differentially expressed in one or two cell cycle phases, which we refer to as transient allelic biases. These genes form the smaller clusters seen in Figure 3A. Examples of genes with transient allelic biases are also presented in the ‘Autosomal Genes’ section of Figure 3B. Transient expression biases like these may be because of coordinated expression of the two alleles in only certain cell cycle phases, though the mechanism behind this behavior is unclear.

Figure 3.

Allele-specific mature and nascent RNA expression

(A) Differentially expressed genes’ maternal and paternal RNA expression through the cell cycle. Expression heatmaps are average FPKM values over three replicates after row normalization. Genes are grouped by their differential expression patterns (Figure S1).

(B) Representative examples of X-linked, imprinted, and other autosomal genes with allelic bias. Top and bottom sections of (A) and (B) show mature RNA levels (RNA-seq) and nascent RNA expression (Bru-seq), respectively.

(C) Examples of cell cycle regulatory genes’ mature RNA levels through the cell cycle. These genes are grouped by their function in relation to the cell cycle and all exhibit CBE but none have ABE. All example genes in (B) and (C) reflect average FPKM values over three replicates, and ABE in a particular cell cycle phase is marked with an orange or purple asterisk for maternal or paternal bias, respectively. Within this figure, G2 includes both G2 and M phase. Any plots with no visible error bars in (B) and (C) have errors smaller than the marker at each cell cycle phase.

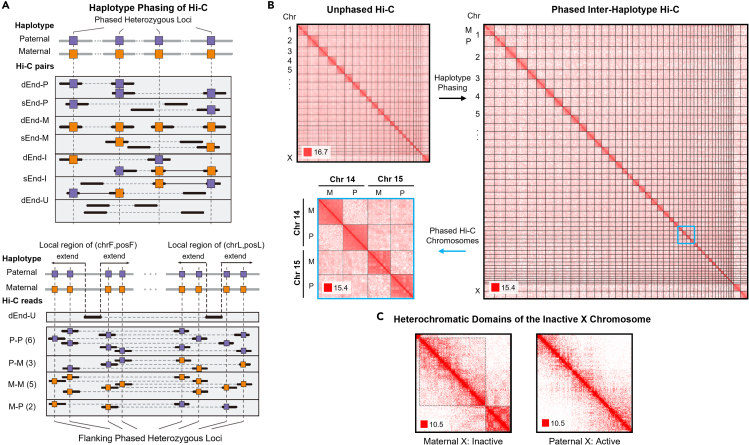
Among the ABE genes from RNA-seq analysis, we found 117 MAE genes. In addition to the requirements for differential expression, we impose the thresholds of an FC ≥ 10 and for the inactive allele to have <0.1 Fragments Per Kilobase of transcript per Million (FPKM), or FC ≥ 50 across all three cell cycle phases. Our analysis confirmed MAE for imprinted and XCI genes, with examples shown in Figure 3B. Imprinted and XCI genes are silenced via transcriptional regulation, which was verified by monoallelic nascent RNA expression (Bru-seq). The XIST gene, which is responsible for XCI, was expressed in the maternal allele reflecting the deactivation of the maternal Chromosome X. XCI was also observed from Hi-C through large heterochromatic domains in the maternal Chromosome X, and the absence of these domains in the paternal Chromosome X (Figure 4C). The inactive Chromosome X in our cells is opposite of what is commonly seen for the GM12878 cell line in literature (likely because of our specific GM12878 sub-clone), but is consistent between our data modalities (Chen et al., 2016b; Rao et al., 2014; Tan et al., 2018). The MAE genes also include six known imprinted genes, four expressed from the paternal allele (KCNQ1OT1, SNRPN, SNURF, and PEG10) and two from the maternal allele (NLRP2 and HOXB2). Some of the known imprinted genes that were confirmed in our data are associated with imprinting diseases, such as Beckwith-Wiedemann syndrome (KCNQ1OT1 and NLRP2), Angelman syndrome (SNRPN and SNURF), and Prader-Willi syndrome (SNRPN and SNURF) (Cao et al., 2017; Adams, 2008). These genes and their related diseases offer further support for allele-specific analysis, as their monoallelic expression could not be detected otherwise.

Figure 4.

Haplotype phasing of Hi-C data

(A) HaploHiC separates paired-end reads into groups based on parental origin determined through SNVs/InDels (left, method details). Reads are grouped by: (i) reads with one (sEnd-P/M) or both ends (dEnd-P/M) mapped to a single parent, (ii) reads are inter-haplotype, with ends mapped to both parents (d/sEnd-I), and (iii) reads with neither end mapped to a specific parent (dEnd-U). Abbreviations within this figure are defined as follows: dEnd, double-end; sEnd, single-end; U, unmapped; P, paternal; M, maternal; I, inter-haplotype; chrF/posF, mapped chromosome and position of forward end after sorted; chrL/posL, mapped chromosome and position of latter end after sorted. An example of a paired-end read (dEnd-U) with no SNVs/InDels has its origin imputed using nearby reads (right, method details). A ratio of paternally and maternally mapped reads is found in a dynamically sized flanking region around the haplotype-unknown read’s location (method details). The ratio then determines the likelihood of the haplotype-unknown read’s origin. This example visualization shows a slight bias toward Hi-C reads with a paternal origin, but the majority of our Hi-C data has stronger biases than what is shown here.

(B) Whole-genome Hi-C of GM12878 cells (top left). Inter-haplotype and intra-haplotype chromatin contacts after phasing Hi-C data using HaploHiC (right). Chromosomes 14 and 15 highlight inter- and intra-chromosome contacts within and between genomes (bottom left). Visualized in log₂ scale 1 Mb resolution in G1.

(C) Haplotype phasing illustrates that the inactive maternal Chromosome X is partitioned into large heterochromatic domains, outlined in dotted black boxes. Visualized in log₂ scale 100 kb resolution in G1.

After observing that approximately half of all ABE genes had transient expression biases, we hypothesized that alleles may have unique dynamics through the cell cycle. We then focused our investigation on allele-specific gene expression through the cell cycle to determine if alleles had CBE, and whether alleles were coordinated in their cell-cycle dependent expression (Figure S1B). We compared the expression of each allele between G1 and S as well as between S and G2/M, which provides insight into the differences between maternal and paternal alleles’ dynamics across the cell cycle. In the G1 to S comparison, there are 88 (55) genes in RNA-seq (Bru-seq) which have similar expression dynamics in both alleles. These genes’ maternal and paternal alleles are similarly upregulated or downregulated from G1 to S. In contrast, 87 (97) genes in RNA-seq (Bru-seq) have different expression dynamics between alleles. That is, only one allele is up or downregulated in the transition from G1 to S. In the S to G2/M comparison, there are 26 3) genes in RNA-seq (Bru-seq) that have similar expression dynamics in both alleles and 56 (12) genes with different expression dynamics between alleles. From these data, we see a coordination of expression between many, but certainly not all, alleles through the cell cycle.

Biallelic expression and cellular function

We observed from our analysis of CBE that multiple cell cycle regulatory genes had no instances of ABE (Figure 3C). We expanded this set of genes to include all allele-specific genes contained in the KEGG cell cycle pathway (Kanehisa and Goto, 2000). Again, we found zero instances of ABE. This may suggest that genes with certain crucial cellular functions, like cell cycle regulation, may have coordinated biallelic expression to ensure their sufficient presence as a means of robustness. This is supported by previous findings which showed restricted genetic variation of enzymes in the essential glycolytic pathway (Cohen et al., 1973).

We hypothesized that genes implicated in critical cell cycle processes would be less likely to have ABEs. We tested additional modules derived from KEGG pathways containing at least five allele-specific genes, with the circadian rhythm module supplemented by a known core circadian gene set (Chen et al., 2015). Examples of modules with varying proportions of ABE are shown in Table 1 (Table S7), where “Percent ABE” refers to the proportion of genes with ABE to the total number of allele-specific genes in that module. We found that there are multiple crucial modules, including the glycolysis/gluconeogenesis and pentose phosphate pathways, which also had zero ABE genes. To explore the possibility of a global phenomenon by which genes essential to cellular fitness are significantly less likely to have biased expression, we analyzed the frequency of ABE in 1,734 genes experimentally determined to be essential in human cells (Blomen et al., 2015). Using the 662 allele-specific genes in this set, we found that these essential genes were significantly less likely to have ABE than a random selection of allele-specific genes (5.8% versus 11.1%, p < 0.001, method details), consistent with our hypothesis that critical genes are likely to be expressed by both alleles. In total, we offer a model in which coordinated biallelic expression reflects prioritized preservation of essential gene sets.

Table 1.

Allelic bias in biological modules.

Module	Percent ABE
Cell cycle	0%
Glycolysis/gluconeogenesis	0%
Pentose phosphate	0%
BCR signaling	8%
Circadian rhythm	9%
p53 signaling	11%
Wnt signaling	16%
Hippo signaling	21%
Whole genome	11%

Allele-specific genome structure

Motivated by our observations of chromosome level structural differences between the maternal and paternal genomes, we examined the HaploHiC separated data in more detail to determine where these differences reside. The genome is often categorized into two compartments: transcriptionally active euchromatin and repressed heterochromatin. In studies comparing multiple types of cells or cells undergoing differentiation, areas of euchromatin and heterochromatin often switch corresponding to genes that are activated/deactivated for the specific cell type (Dixon et al., 2015). We explored this phenomenon in the context of the maternal and paternal Hi-C matrices to determine if the two genomes had differing chromatin compartments. Chromatin compartments can be identified from Hi-C data using methods such as principal component analysis or spectral clustering (method details) (Chen et al., 2016a). We applied spectral clustering to every chromosome across all three cell cycle phases at 1 Mb resolution. We found that there were slight changes in chromatin compartments for all chromosomes, but the vast majority of these changes took place on the borders between compartments rather than an entire region switching compartments. These border differences were not enriched for ABE genes. This implies that, although the structures may not be identical, the maternal and paternal genomes have similar overall compartmentalization (aside from Chromosome X).

We next applied spectral clustering recursively to the Hi-C data at 100 kb resolution to determine whether there were differences in TADs between the two genomes throughout the cell cycle (Chen et al., 2016a). While the current understanding of genomic structure dictates that TAD boundaries are invariant (between alleles, cell types, etc), it is also known that “intra-TAD” structures are highly variable (Dixon et al., 2012, 2015; Finn et al., 2019). The spectral identification method has an increased ability to discern these subtle structural changes. We found that TAD boundaries were variable between the maternal and paternal genomes and across cell cycle phases in all chromosomes. This supports previous findings of allelic differences in TADs for single cells, and we predict that they are even more variable across cell types (Chen et al., 2016a; Finn et al., 2019). Differences in TAD boundaries were observed surrounding MAE genes, ABE genes, and genes with coordinated biallelic expression (Figure S6). This indicated that changes in TAD boundaries were not directly related to allelic expression differences.

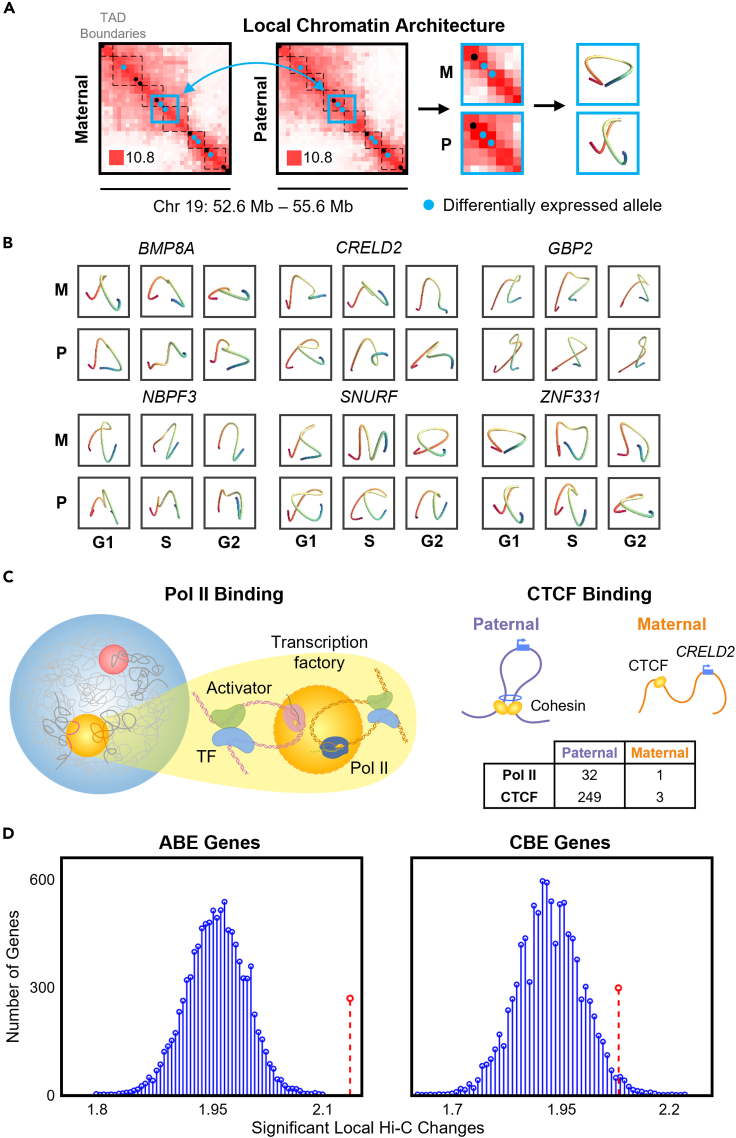
Although we did not find a direct relationship between TAD boundary differences and ABE genes, we observed during this analysis that the local genome structure around the six imprinted genes had noticeable differences. We then sought to analyze all genes with ABE or CBE to find out if they had corresponding structural differences at a local level. We analyzed the local Hi-C matrices for each of the 615 RNA-seq and 505 Bru-seq differentially expressed genes. Using a 300 kb flanking region centered at the 100 kb bin containing the transcription start site, we isolated a 7 × 7 matrix (700 kb) for each differentially expressed gene (Figures 5A and 5B). These matrices represent the local genomic structure of the differentially expressed genes, and are slightly smaller than average TAD size (_∼1 Mb). We then compared the correlation matrices of the log₂-transformed local Hi-C data and determined whether or not the matrices have statistically significant differences (p < 0.05) (Koziol et al., 1997; Lindsly et al., 2021). We applied this comparison to all genes that were differentially expressed in RNA-seq (Bru-seq) and found that 515 (403) genes had at least one comparison in which both the expression and local structure had significantly changed. Although changes in local genome structure and changes in gene expression do not have a one-to-one relationship, we found that both ABE and CBE genes are more likely to have significant architectural differences than randomly sampled allele-specific genes (p ₌ 0.001 and p = 0.004, respectively) (Figure 5D and method details). This lends further support to the idea that there is a relationship between allele-specific differences in gene expression and genome structure.

Figure 5.

Local chromatin structure and transcription factor binding

(A) Local regions around differentially expressed genes are tested for significant conformational changes. These regions are modeled to visualize the conformations around each allele through G1, S, and G2/M (method details). Example of local chromatin structure extraction is shown for ZNF331 in G1 phase (center of blue box). Hi-C matrices are shown in log₂ scale 100 kb resolution.

(B) 3D models of the local genome structure around six ABE genes with bias agreement of Pol II and significant changes in local genome structure.

(C) Schematic representation of allele-specific Pol II and CTCF binding, with highlighted gene CRELD2, which had binding biases in both. Table shows extreme binding biases of Pol II and CTCF on CRELD2 as an example.

(D) ABE and CBE genes are significantly more likely to have changes in their local genome architecture than randomly selected genes. Blue and red lines represent the average number of significant local Hi-C changes for randomly selected genes and differentially expressed genes, respectively (method details). Within this figure, G2 includes both G2 and M phase.

Allele-specific protein binding

To uncover the mechanisms behind the relationship between allele-specific gene expression and genome structure, we looked to DNA binding proteins such as RNA polymerase II (Pol II), CCCTC-binding factor (CTCF), and 35 other transcription factors. We used publicly available protein binding data from AlleleDB in tandem with RNA-seq and found 114 genes that have an allelic bias in both gene expression and binding of at least one such protein (Chen et al., 2016b). We identified 13 genes which have ABE and biased binding of Pol II, with bias agreement in 11 cases (85%). That is, the allelic expression and Pol II binding were biased toward the same allele. For CTCF, 33 of 72 cases have bias agreement (46%), and for all other transcription factors analyzed, 20 of 29 cases have bias agreement (69%) (Table S6). The CTCF binding bias agreement of around 50% is expected, based on previous studies (Rozowsky et al., 2011). This is likely because of CTCF’s role as an insulator, since an allele could be expressed or suppressed by CTCF’s presence depending on the context. To avoid potential inconsistencies between our data and the protein data from AlleleDB, we excluded Chromosome X when testing for ABE and protein binding biases.

We evaluated the relationship between TAD boundary differences between the maternal and paternal genomes and allele-specific CTCF binding sites. We found multiple instances of biased binding of CTCF and corresponding changes to the boundaries of TADs containing ABE genes. Examples of this phenomenon are shown in the center of Figure S6A, where TAD boundaries from the maternal (paternal) Hi-C data are closer to a maternally (paternally) biased CTCF binding site in some cell cycle phases near the ABE genes ANKRD19P, C9orf89, and FAM120A. Despite observing individual instances of biased CTCF binding corresponding to TAD boundary differences and ABE genes, there were insufficient data to evaluate this relationship genome-wide. We hypothesize that differences in TAD boundaries would correspond to allele-biased CTCF binding provided that there were enough data, as it has been repeatedly shown that TAD boundaries are enriched with CTCF binding (Wutz et al., 2017; Dixon et al., 2012).

We analyzed the 11 genes with allelic expression and Pol II binding bias agreement further to determine if they also had significant changes in local genome structure. Through local Hi-C comparisons, we found that all 11 of these genes had significant changes in structure in at least one cell cycle phase. 3D models for six of these genes are shown in Figure 5B, which highlight differences in local genome structure (method details) (Varoquaux et al., 2014). Local Hi-C contact maps for these example genes are shown in Figure S7. The genes with bias agreement and changes in local genome structure include known imprinted genes such as SNURF and SNRPN, as well as genes with known allele-specific expression (and suggested imprinting in other cell types) like ZNF331 (Ben-David et al., 2014). In addition, there are multiple genes with known associations with diseases or disorders such as BMP8A, CRELD2, and NBPF3 (Wu et al., 2017; Kim et al., 2017; Petroziello et al., 2004). These findings suggest that changes in local structure often coincide with changes in expression because of the increased or decreased ability of a gene to access the necessary transcriptional machinery within transcription factories (Cook, 2010; Osborne et al., 2004). We visualize this relationship for the gene CRELD2 as an example (Figure 5C).

The maternal and paternal 4D Nucleome

We define the maternal and paternal 4DN as the integration of allele-specific genome structure with gene expression data through time, adapted from Chen et al. (2015). Many complex dynamical systems are investigated using a network perspective, which offers a simplified representation of a system (Newman, 2018; Strogatz, 2001). Networks capture patterns of interactions between their components and how those interactions change over time (Chen et al., 2015). We can consider genome structure as a network, because Hi-C data captures interactions between genomic loci (Rajapakse and Groudine, 2011; Misteli, 2020). In network science, the relative importance of a node in a network is commonly determined using network centrality (Newman, 2018). For Hi-C data, we consider genomic loci as nodes and use network centrality to measure the importance of each locus at each cell cycle phase (Liu et al., 2018; Lindsly et al., 2021). We initially performed a global analysis of the maternal and paternal 4DN by combining RNA-seq with multiple network centrality measures (method details) (Lindsly et al., 2021). We found differences between the maternal and paternal genomes and across cell cycle phases, but only Chromosome X had clear maternal and paternal separation (Figures S9 and S10).

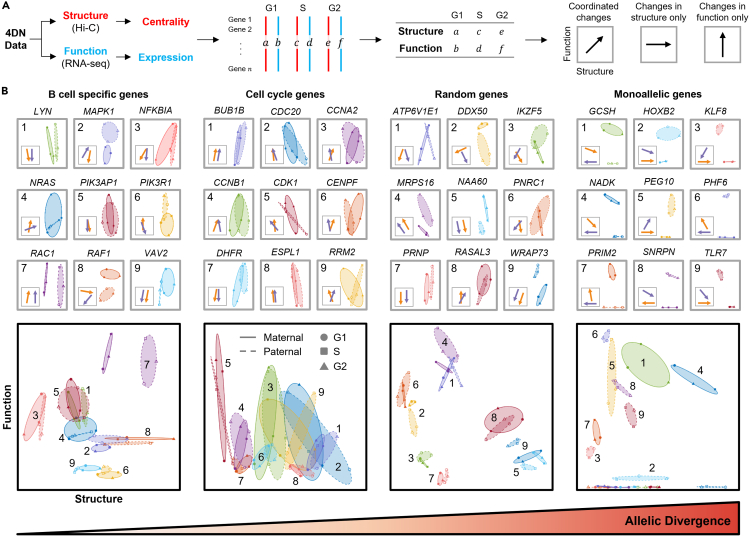
In our earlier analysis, we found a significant relationship between ABE and changes in local genome structure. We also observed that genes in multiple critical biological modules had coordinated biallelic expression. Motivated by these results, we performed an integrated analysis of structure and function to determine allele-specific dynamics of targeted gene sets. We constructed a sub-network for each gene set (analogous to an in silico 5C matrix), by extracting rows and columns of the Hi-C matrix containing genes of interest for each cell cycle phase (Dostie et al., 2006). We used eigenvector centrality (similar to Google’s PageRank) to quantify structure, and used the average expression from the three RNA-seq replicates to quantify function, for each allele in the sub-network (Page et al., 1999). We utilized the concept of a phase plane to plot the maternal and paternal 4DN (4DN phase plane, adapted from Chen et al.) (Figure 6) (Chen et al., 2015). We designated one axis as a measure of structure and the other as a measure of function. Coordinates of each point in the 4DN phase plane were determined from normalized structure data (x axis, sub-network eigenvector centrality) and function data (y axis, FPKM). The 4DN phase plane contains three points for each allele, which represent G1, S, and G2/M. We define allelic divergence (AD) as the average Euclidean distance between the maternal and paternal alleles across all cell cycle phases in the 4DN phase plane (method details).

Figure 6.

4DN phase planes reveal a wide range of allelic divergences in gene sub-networks

(A) Workflow to obtain structure and function measures. Eigenvector centrality for each gene is computed from the extracted sub-network of Hi-C contacts. Expression for each gene can be found directly from RNA-seq. Simplified phase planes are shown with linear relationships between changes in structure and function, changes in structure with no changes in function, and changes in function with no changes in structure.

(B) 4DN phase planes of genes specific to B cell function, cell cycle genes, random allele-specific genes, and MAE genes, highlighting the similarities and differences between their alleles. Genes such as BUB1B and PIK3AP1 have similar phase planes between alleles, while RAC1 differs in structure and WRAP73 differs in function. The bottom plot for each column combines the phase planes of the nine example genes, and the average allelic divergence is calculated from each of these gene sets. Circles, squares, and triangles represent phases of the cell cycle: G1, S, and G2/M, respectively. Solid and dashed lines indicate the minimum volume ellipses that contain all cell cycle phases for the maternal and paternal allele of each gene, respectively (Sun and Freund, 2004). Within this figure, G2 includes both G2 and M phase.

We show four example 4DN phase planes of gene sub-networks with various ADs in Figure 6. Genes which are known to be crucial for cell cycle regulation have a mean AD of 0.0245 (Figure 6B, middle-left). Given that GM12878 is a B-lymphoblastoid cell line, we were interested in the AD of genes which are related to B cell receptor functionality. We found that these genes had a mean AD of 0.0225 (Figure 6B, left). The ADs of cell cycle regulating genes and B cell specific genes are smaller than the mean AD of randomly selected allele-specific genes (AD ₌ 0.0301 over 10,000 samples). This may be indicative of a robust coordination between the alleles to maintain proper cellular function and progression through the cell cycle, and therefore a lack of ABE genes or large structural differences. We show a random set of allele-specific genes with a mean AD of 0.0249 as an example (Figure 6B, middle-right). MAE genes had a mean AD of 0.1748 (Figure 6B, right), significantly higher than randomly selected allele-specific genes (p = 0.001, method details). This approach is useful for quantifying differences between maternal and paternal genomes throughout the cell cycle, highlighting gene sets with large structural or expression differences over time. In previous work, we have also shown that this method may be broadly applicable to time-series analysis of different cell types (Lindsly et al., 2021).

Discussion

In this study, we present evidence for the intimate relationship among allele-specific gene expression, genome structure, and protein binding across the cell cycle. We validated our data and methods using known allele-specific properties such as the monoallelic expression of imprinted and X-linked genes, broad similarities of chromatin compartments between the maternal and paternal genomes, and large heterochromatic domains of Chromosome X (Reik and Walter, 2001; Babak et al., 2015; Baran et al., 2015; Santoni et al., 2017; Rao et al., 2014). Unique to this study, we established a coordination of allele-biased expression and changes in local genome structure, which included hundreds of genes not commonly associated with allele-biased expression. We observed further evidence of this coordination through corresponding protein binding biases.

Through our analysis of mature (nascent) RNA, we found 467 (380) genes to be differentially expressed between the two alleles and 229 (164) genes with differential expression through the cell cycle. Approximately half of the genes with allele-biased expression are only differentially expressed in certain cell cycle phases, and over half of the genes with CBE are only differentially expressed in one allele. Further research is needed to explore why certain genes have coordinated cell cycle dynamics across both alleles, while other genes have disparate expression in some cell cycle phases. We predict that these transient allelic biases may be associated with developmental pathologies and tumorigenesis, similar to imprinted and other MAE genes. Conversely, we found no allele-biased expression from genes in multiple biological modules, such as the cell cycle and glycolysis pathways (Table 1). We were not able to establish a statistical significance here due to the limited number of allele-specific genes in these modules, so we surveyed a set of 662 essential genes and found that they are significantly less likely to have allele-biased expression (Blomen et al., 2015). This supports our hypothesis of highly coordinated biallelic expression in universally essential genes.

We developed a novel phasing algorithm, HaploHiC, which uses Hi-C reads mapped to phased SNVs/InDels to predict nearby reads of unknown parental origin. This allowed us to decrease the sparsity of our allele-specific contact matrices and increase confidence in our analysis of the parental differences in genome structure. Although found that the overall compartmentalization (euchromatin and heterochromatin) of the two genomes was broadly similar, there were many differences in TAD boundaries and local genome structure between the two genomes and between cell cycle phases. We focused our search for allele-specific differences in genome structure by calculating the similarity of local contacts surrounding differentially expressed genes (Koziol et al., 1997; Lindsly et al., 2021). We found that differentially expressed genes were significantly more likely to have corresponding changes in local genome structure than random allele-specific genes.

We incorporated publicly available allele-specific protein binding data for Pol II and CTCF to explore the mechanisms behind the gene expression and local genome structure relationship (Rozowsky et al., 2011). In genes that had both allele-biased expression and Pol II binding biases, we found that 85% of these genes had allelic bias agreement. Additionally, we found that all of the genes with expression and Pol II binding bias agreement had significant changes in local genome structure. Analysis of the relationships among allele-specific gene expression, genome structure, and protein binding is currently hindered by the amount of information available and our limited understanding of the dynamics of cell-specific genome structure and gene expression variability (Finn and Misteli, 2019). The ability to separate maternal and paternal gene expression and protein binding is dependent on the presence of an SNV/InDel within the gene body and nearby protein binding motifs. As SNVs/InDels are relatively rare in the human genome, the number of genes available to study is severely limited. Once we are able to separate the maternal and paternal genomes through advances in experimental techniques, we will be able to fully study these relationships.

Overall, these data support an intimate allele-specific relationship between genome structure and function, coupled through allele-specific protein binding. Changes in genome structure, influenced by the binding of proteins such as CTCF, can affect the ability of transcription factors and transcription machinery to access DNA. This results in changes in the rate of transcription of RNA, captured by Bru-seq. The rate of transcription leads to differential steady state gene expression, captured by RNA-seq. Integration of these data into a comprehensive computational framework led to the development of a maternal and paternal 4DN, which can be visualized using 4DN phase planes and quantified using allelic divergence. Allele-specific analysis across the cell cycle will be imperative to discern the underlying mechanisms behind many diseases by uncovering potential associations between deleterious mutations and allelic bias, and may have broad translational impact spanning cancer cell biology, complex disorders of growth and development, and precision medicine.

Limitations of the study

The experiments presented in this study are limited to a single B lymphoblastoid cell line. This cell line’s maternal and paternal genome sequences are known, allowing for the separation of gene expression and chromatin conformation data. SNVs are relatively rare in the human genome, so the number of genes available to analyze is severely limited. Increasing sequencing coverage depth and length of reads may improve future analyses. This study does not present comprehensive analysis on the specific relationships between chromatin conformation changes and differences in gene expression, only that these changes frequently occur together. Targeted investigations into particular chromatin conformations and gene expression profiles are needed to further elucidate the complex relationship between genome structure and function, and how the maternal and paternal genomes compare throughout the cell cycle.

STAR★Methods

Key resources table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited data
Raw and analyzed data (RNA-seq, BRU-seq, and Hi-C)	This paper	GEO: GSE159813
Software and algorithms
Prototype MATLAB implementation for differential expression analysis	MathWorks	https://www.mathworks.com/help/bioinfo/ug/identifying-differentially-expressed-genes-from-rna-seq-data.html
HaploHiC code	This paper	https://github.com/Nobel-Justin/HaploHiC

Resource availability

Lead contact

Further information and requests for resources should be directed to and will be fulfilled by the lead contact, Dr. Indika Rajapakse (indikar@umich.edu).

Materials availability

This study did not generate new reagents.

Experimental model and subject details

Cell culture and cell cycle sorting

Human GM12878 cells were cultivated in RPMI1640 medium supplemented with 10% fetal bovine serum (FBS). Live cells were stained with Hoechst 33342 (Cat #B2261, Sigma-Aldrich), and then sorted by fluorescence-activated cell sorting (FACS) to obtain cell fractions at the corresponding cell cycle phases G1, S, and G2/M (Figure S2).

Method details

RNA-seq and Bru-seq sequencing

Total RNA was extracted from sorted live cells for both RNA-seq and Bru-seq. We performed 5′-bromouridine (Bru) incorporation in live cells for 30 minutes, and the Bru-labeled cells were then stained on ice with Hoechst 33342 for 30 minutes before sorting at 4°C to isolate G1, S, and G2/M phase cells. The sorted cells were immediately lysed in TRizol (Cat # 15596026, ThermoFisher) and frozen. To isolate Bru-labeled RNA, DNAse-treated total RNA was incubated with anti-BrdU antibodies conjugated to magnetic beads (Lieberman-Aiden et al., 2009). We converted the transcripts from the RNA-seq and Bru-seq experiments for all samples into cDNA libraries and deep-sequenced at 50-base length on an Illumina HiSeq2500 platform. The RNA-seq and Bru-seq data each consist of three biological replicates. From our RNA-seq replicates, we obtained a total of 193.4, 197.2, and 202.0 million raw reads for G1, S, and G2/M, respectively. From our Bru-seq replicates, we obtained a total of 162.5, 149.9, and 138.0 million raw reads for G1, S, and G2/M, respectively.

Hi-C sequencing

For cells used in construction of Hi-C libraries, cells were crosslinked with 1% formaldehyde, the reaction was neutralized with 0.125 M glycine, then cells were stained with Hoechst 33342 and sorted into G1, S, and G2/M fractions. Cross-linked chromatin was digested with the restriction enzyme MboI for 12 hours. The restriction enzyme fragment ends were tagged with biotin-dATP and ligated in situ. After ligation, the chromatins were de-cross-linked, and DNA was isolated for fragmentation. DNA fragments tagged by biotin-dATP, in the size range of 300–500 bp, were pulled down for sequencing adaptor ligation and polymerase chain reaction (PCR) products. The PCR products were sequenced on an Illumina HiSeq2500 platform. Respective to G1, S, and G2/M, we obtained 512.7, 550.3, and 615.2 million raw Hi-C sequence reads.

RNA-seq and Bru-seq data processing

RNA-seq and Bru-seq analysis were performed as previously described (Seaman et al., 2017; Paulsen et al., 2014). Briefly, Bru-seq used Tophat (v1.3.2) to align reads without de novo splice junction calling after checking quality with FastQC (version 0.10.1). A custom gene annotation file was used in which introns are included but preference to overlapping genes is given on the basis of exon locations and stranding where possible (see Paulsen et al. (2014) for full details). Similarly for RNA-seq data processing, the raw reads were checked with FastQC. Tophat (version 2.0.11) and Bowtie (version 2.1.0.0) were used to align the reads to the reference transcriptome (HG19). Cufflinks (version 2.2.1) was used for expression quantification, using UCSC hg19.fa and hg19.gtf as the reference genome and transcriptome, respectively. A locally developed R script using CummeRbund was used to format the Cufflinks output.

Separation of maternal and paternal RNA-seq and Bru-seq data

To determine allele-specific transcription and gene expression through Bru-seq and RNA-seq, all reads were aligned using GSNAP, a SNV aware aligner (Wu and Nacu, 2010; Kukurba and Montgomery, 2015). HG19 and UCSC gene annotations were used for the reference genome and gene annotation, respectively. The gene annotations were used to create the files for mapping to splice sites (used with –s option). Optional inputs to perform SNV aware alignment were also included. Specifically, –v was used to include the list of heterozygous SNVs and –use-sarray = 0 was used to prevent bias against non-reference alleles (Degner et al., 2009).

After alignment, the output SAM files were converted to BAM files, sorted and indexed using SAMtools (Li et al., 2009). SNV alleles were quantified using bam-readcounter to count the number of each base that was observed at each of the heterozygous SNV locations. Allele-specificity of each gene was then assessed by combining all of the SNVs in each gene. For RNA-seq, only exonic SNVs were used. Bru-seq detects nascent transcripts containing both exons and introns, so both exonic and intronic SNVs were used. Maternal and paternal gene expression were calculated by multiplying the genes’ overall read counts by the fraction of the SNV-covering reads that were maternal and paternal, respectively. We identified 266,899 SNVs from the Bru-seq data, compared with only 65,676 SNVs from RNA-seq data. However in the Bru-seq data, many SNVs have low read coverage depth. We required at least 5 SNV-covering reads for a SNV to be used to separate the maternal and paternal contributions to gene expression. This criterion found that there were similar numbers of informative SNVs (19,394 and 19,998) in the RNA-seq and Bru-seq data, respectively. Genes which did not meet these criteria were omitted from downstream allele-specific analysis.

Allele-specific differential expression

For a gene’s expression to be considered for differential expression analysis, we require each of the three replicates to have an average of at least 10 SNV-covering reads mapped to at least one of the alleles in all three cell cycle phases. This threshold was introduced to reduce the influence of technical noise on our differential expression results. From the 23,277 Refseq genes interrogated, there were 4,193 genes with at least 10 read counts mapped to either the maternal or paternal allele (or both) in the RNA-seq data. From Bru-seq, there were 5,294 genes using the same criterion. We define these genes as “allele-specific genes” for their respective data sources. We observed that there were larger variances between samples and lower read counts in the Bru-seq data set than in RNA-seq. We identified differentially expressed genes between alleles and between cell cycle phases for both RNA-seq and Bru-seq using a MATLAB implementation of DESeq (Anders and Huber, 2010). To reduce the possibility of false positives when determining differential expression, we imposed a minimum FPKM level of 0.1, a false discovery rate adjusted p-value threshold of 0.05, and a fold change cutoff of FC > 2 for both RNA-seq and Bru-seq (Benjamini and Hochberg, 1995).

Separation of maternal and paternal Hi-C data by HaploHiC

Hi-C library construction and Illumina sequencing were performed using established methods (Rao et al., 2014). In this study, we separate the maternal and paternal genomes’ contributions to the Hi-C contact matrices to analyze their similarities and differences in genome structure. In order to determine which Hi-C reads come from which parental origin, we utilize differences in genomic sequence at phased SNVs/InDels. As these variations are unique to the maternal and paternal genomes, they can be used to distinguish reads. When attempting to separate the maternal and paternal genomes, complications arise when there are sections of DNA that are identical. There are a relatively small number of allele-specific variations, and the resulting segregated maternal and paternal contact matrices are sparse. In order to combat this problem, we seek to infer contacts of unknown parental origin.

We propose a novel technique, HaploHiC, for phasing reads of unknown parental origin using local imputation from known reads. HaploHiC uses a data-derived ratio based on the following hypothesis: if the maternal and paternal genomes have different 3D structures, we can use the reads with known origin (at SNV/InDel loci) to predict the origin of neighboring unknown reads (Figure 4A, method details) (Selvaraj et al., 2013). For example, if we observe that many contacts between two loci can be directly mapped to the paternal genome but few to the maternal genome, then unphased contacts between those loci are more likely to be from the paternal genome as well, and vice versa. This process of imputing Hi-C reads of unknown origin based on nearby known reads is similar to the methods developed by Tan et al. (2018).

HaploHiC marks paired-end reads as haplotype-known or -unknown depending on their coverage of heterozygous phased SNVs/InDels. Haplotype-known reads are directly assigned to their corresponding haplotype, maternal or paternal. HaploHiC uses a local contacts-based algorithm to impute the haplotype of haplotype-unknown reads using nearby SNVs/InDels. If the minimum threshold (ten paired-ends) of haplotype-known reads for local imputation is not reached, HaploHiC randomly assigns the haplotype-unknown reads to be maternal or paternal (less than 5% of all haplotype-unknown reads).

Our validation shows that HaploHiC performs well, with an average accuracy of 84.9%, 86.1%, and 86.9% for G1, S, and G2/M, respectively, over 10 trials each (Table S12). Each validation trial randomly removed 10% of the heterozygous phased SNVs/InDels, and calculated imputation accuracy by the fraction of correctly imputed reads from the haplotype-known Hi-C reads covering these removed heterozygous mutations. Our main validation of imputation accuracy is similar to the method presented in Tan et al. (2018), but we perform additional tests and multiple simulations for further validation. HaploHiC is available through a GitHub repository.

After haplotype assignment through HaploHiC, Hi-C paired-end reads (PE-reads) were distributed to intra-haplotype (P-P and M-M) and inter-haplotype (P-M and M-P).Juicer was applied on intra-haplotype PE-reads, and outputs maternal and paternal contact matrices which were normalized through the Knight-Ruiz method of matrix balancing (Durand et al., 2016; Knight and Ruiz, 2013). Inter-haplotype contact matrices were generated by HaploHiC.Intra- and inter-haplotype contacts are shown in Figures 4B and S8. Both base pair level and fragment level matrices were constructed. The resolution of base pair level matrices are 1 Mb and 100 kb. Gene-level contacts were converted from fragment level matrices by HaploHiC.

Generation and haplotype assignment of Hi-C

Phased germline mutations of GM12878

From the AlleleSeq database (version: Jan-7-2017) (Rozowsky et al., 2011), we downloaded the VCF file of sample GM12878. This VCF file contains phased heterozygous germline mutations (SNV and InDel) with a total of 2.49 million genomic loci (Table S8). We confirmed that paternal allele is the left side of phased alleles, and the maternal allele is the right side, e.g., ‘0|1’ at HG19 genomic position chr1:2276371. This mutation list was also utilized in the realignment process of GATK.

HaploHiC utilizes heterozygous genotype information to distinguish reads’ parental origin as long as the reads cover the heterozygous genomic loci. Considering that short sequence insertions and deletions dramatically influence alignment accuracy, we applied a filtration on heterozygous InDels. All homologous and heterozygous InDel alleles were assigned a minimum distance to the next InDel on the haplotyped genome. This minimum distance considers repeatability of both the mutation sequence and local genomic context. The mutation sequence (i.e., the inserted or deleted sequence) might be repetitive and repeated at its genomic position. For example, at HG19 genomic position chr1:2277268, the maternal genome has a deletion (‘CACA’). The deleted sequence is ‘CA’-unit repetitive (2 times) and also repeated in the adjacent reference context (‘CA’-unit repeats 11 times). The minimum distance is the whole repeats’ length added by unit repeated time of mutation sequence. So, at genomic position chr1:2277268, the minimum distance of the deletion allele on maternal genome is 28, which means any InDel located within this distance on maternal genome will be excluded from following analysis. In total, 11,614 heterozygous genomic loci harboring InDel alleles were filtered (Table S8). HaploHiC outputs a list of these filtered genotypes. The minimum distance is also applied in InDel allele judgment on sequencing reads (see parental origin categories of Hi-C PE-reads).

Alignment and filtering of Hi-C PE-reads

Illumina adapter sequences and low quality ends were trimmed from raw Hi-C reads by Trimmomatic (Bolger et al., 2014). Paired-ends (PE, R1 and R2) were separately aligned to the human reference genome (HG19) using the function ‘mem’ from BWA (0.7.15) with default parameters (Li and Durbin, 2009). Then, each alignment BAM file was coordinated, sorted, and realigned by GATK (3.5) (McKenna et al., 2010). All realigned BAM files were sorted by read names before processing in HaploHiC.

HaploHiC loads Hi-C PE-reads’ mapping information from paired alignment BAM files, and filters unqualified and invalid pairs in the first step. After exclusion of unqualified and invalid pairs, remaining Hi-C PE-reads are eligible to provide chromatin contacts (Table S9).

Unqualified PE-reads are filtered out if either or both ends are un-mapped, mapped with a mapping quality less than 20, or mapped to multiple genomic positions. Note that supplementary alignments are reserved, because theoretically, a portion of sequencing reads that cover ligation site could be soft-clipped mapped to two genomic locations by BWA and provide contact information. HaploHiC sets two filtering criteria on primary and supplementary alignments: 1) the difference between their length sum and the reads’ length must be less than one fifth of the reads’ length, 2) the overlaps between primary and supplementary mapped parts must be shorter than one third of the shorter one. If the two criteria are not satisfied simultaneously, the supplementary alignment will be marked as ‘remove_SP’ and discarded.

HaploHiC detects four categories of invalid pairs: 1) dangling ends, 2) self circle, 3) dumped pair forwarded mapped, and 4) dumped pair reversed mapped. The definition of these four categories are the same as HiC-Pro (Servant et al., 2015), while the singleton type is included in the unqualified PE-reads mentioned above. The two ends of an invalid pair must map to same the enzyme fragment or within a close distance (1 kb).

Parental origin categories of Hi-C PE-reads

HaploHiC assigns a haplotype situation to sequencing reads by checking whether reads cover and support heterozygous alleles of specific parental origin. Note that, in this section, we deal with each alignment of sequencing reads. Four haplotype situations are defined (Figure 4): 1) ‘P’ (only paternal allele), 2) ‘M’ (only maternal allele), 3) ‘I’ (both maternal and paternal alleles, i.e., inter-haplotype), and 4) ‘U’ (no parental allele supported). Clearly, the former three situations (‘P’, ‘M’, and ‘I’) are haplotype-known, and the fourth (‘U’) is haplotype-unknown. Note that sequencing reads with ‘I’ support both haplotypes simultaneously, as covering the junction site of the ligated maternal and paternal fragments.

For sequencing reads covering heterozygous genomic positions and matching either parental allele, the bases that match the allele must meet two criteria: 1) base quality is not less than 20, and 2) distance to bilateral edges of this read is not less than 5 bp. Note, if the allele is determined through an InDel, the read-edge distance might use the minimum distance representing the repeatability mentioned above (see section) if the latter is larger. HaploHiC outputs a list recording all InDel alleles that have the repeatability distance. There are a total of 255,961 heterozygous loci having such InDel alleles in sample GM12878 (Table S8).

According to the haplotype status of the two ends, HaploHiC assigns Hi-C PE-reads to seven categories: dEnd-P/M/I, sEnd-P/M/I, and dEnd-U. Here, ‘dEnd’ and ‘sEnd’ represent dual-ends and single-end, respectively. Common instances of each category are shown in Figure 4. Additionally, we also set requirements on distance of alignments (Table S9).

• •dEnd-P: both ends support only paternal alleles, and are not close-aligned
• •dEnd-M: both ends support only maternal alleles, and are not close-aligned
• •dEnd-I: at least one end supports both maternal and paternal alleles, and the other one is haplotype-known
• •sEnd-P: one end supports only paternal allele, the other one has haplotype-unknown alignment
• •sEnd-M: one end supports only maternal allele, the other one has haplotype-unknown alignment
• •sEnd-I: one end supports both maternal and paternal alleles, the other one has haplotype-unknown alignment
• •dEnd-U: both ends are haplotype-unknown.

Clearly, four categories (dEnd-P/M/I and sEnd-I) have confirmed allele-specific contacts, and we call them phased Hi-C PE-reads. Conversely, the other three categories are unphased: PE-reads have one (sEnd-P/M) or two (dEnd-U) haplotype-unknown ends. The next step is to assign the haplotype to these unphased Hi-C PE-reads based on the allele-specific contact information in local regions.

Local region contacts from phased Hi-C PE-reads

By integrating all phased Hi-C PE-reads, HaploHiC records allele-specific contacts in windowed regions. For example, to record allele-specific contacts of two genomic regions (‘no.A’ window on ‘chrA’, and ‘no.B’ window on ‘chrB’), HaploHiC sorts ‘chrA’ and ‘chrB’ in ASCII order, and if ‘chrA’ and ‘chrB’ are the same chromosome, it then sorts ‘no.A’ and ‘no.B’ in ascending order. This dual-sorting process avoids duplicated records and reduces software memory consumption. After sorting, the former region is ‘chrF, no.F’ (here, ‘F’ for former), and the latter region is ‘chrL, no.L’ (here, ‘L’ for latter). HaploHiC keeps a dictionary with key-value pairs. The key is ‘chrF, no.F, chrL, no.L’, and its value is a set of phased Hi-C PE-reads that link these two regions with haplotype combinations (i.e., ‘P-P’, ‘M-M’, ‘P-M’, and ‘M-P’, Figures 4B and S4. Additionally, HaploHiC de-duplicates the Hi-C PE-reads under each haplotype combination.

HaploHiC utilizes a local allele-specific contacts based algorithm to impute the haplotype for haplotype-unknown ends. To get the local region of one end of the unphased Hi-C PE-reads, HaploHiC extends bilaterally from the mapped position. The extension length is 50 kb on each unilateral side, which is referred to as an extension unit. Note that each unilateral region cannot harbor more than 30 phased heterozygous loci, or else the unilateral region will be trimmed. The bilateral extended regions are merged as one local region. A similar extension gets the local region of the other end of the Hi-C PE-read. Then, from the dictionary of phased Hi-C pairs, HaploHiC counts PE-reads linking these two local regions of each haplotype combination. For simplicity, the contact counts of haplotype combinations are: α (‘P-P’), β (‘M-M’), γ (‘P-M’), and δ (‘M-P’), respectively. HaploHiC uses these counts to impute the haplotype for haplotype-unknown reads. Note that if the sum of these counts is zero, local regions of both ends will be iteratively extended by more extension units until the sum is non-zero or local regions reach the maximum length (10 Mb, more than 90% Hi-C pairs get imputed in local region ≤3 Mb in this study). Finally, if the sum is still zero, we define this pair of local regions as unphased.

Assign haplotype to unphased Hi-C PE-reads (sEnd-P/M)

First, HaploHiC deals with unphased Hi-C PE-reads from sEnd-P/M categories. Because these Hi-C pairs already have one haplotype-known end, some haplotype combinations should be excluded. For example, one Hi-C pair has one paternal end (mapped to ‘posA’ on ‘chrA’) and one haplotype-unknown end (mapped to ‘posB’ on ‘chrB’). After dual-sorting the mapped chromosomes and positions, ‘chrB, posB’ is the ‘chrF, posF’, and ‘chrA, posA’ is the ‘chrL, posL’. HaploHiC calculates the local regions of ‘chrF, posF’ and ‘chrL, posL’ respectively, and summarizes contacts counts of haplotype combinations recorded under key ‘chrF, posF, chrL, no.L’: α (‘P-P’), β (‘M-M’), γ (‘P-M’), and δ (‘M-P’). Because ‘chrL, posL’ is from the paternal genome in this instance, β (‘M-M’) and γ (‘P-M’) are impossible and should be excluded. HaploHiC then randomly assigns ‘P’ or ‘M’ to the haplotype-unknown end (‘chrF, posF’) with possibility defined as:

$$possibility\left(paternal\right)=\frac{\alpha }{\alpha +\delta }$$ (Equation 1)

$$possibility\left(maternal\right)=\frac{\delta }{\alpha +\delta }$$ (Equation 2)

Moreover, if the local regions are still unphased after iterative extension, i.e., the sum of contacts counts of haplotype combinations is still zero, HaploHiC will assign the haplotype with uniform possibility depending on the mapped chromosome situation. In this example, if ‘chrF, posF’ and ‘chrL, posL’ belong to same chromosome, HaploHiC assigns the haplotype of ‘chrL, posL’ (the haplotype-known end) to ‘chrF, posF’ (the haplotype-unknown end). However, if ‘chrF, posF’ and ‘chrL, posL’ belong to different chromosomes, uniform possibility (0.5) will be applied.

If intra-chromosome mapped (in this example):

$$possibility\left(paternal\right)=1$$ (Equation 3)

$$possibility\left(maternal\right)=0$$ (Equation 4)

If inter-chromosome mapped:

$$possibility\left(paternal\right)=0.5$$ (Equation 5)

$$possibility\left(maternal\right)=0.5$$ (Equation 6)

Hi-C pairs from sEnd-P/M categories are marked as ‘phased imputed’ and ‘unphased imputed’ corresponding to phased and unphased local regions, respectively.

Assign haplotype to unphased Hi-C PE-reads (dEnd-U)

Before the operations on unphased Hi-C PE-reads from dEnd-U category, HaploHiC records ‘phased imputed’ Hi-C pairs from sEnd-P/M categories to expand the contacts dictionary. For dEnd-U Hi-C pairs, calculation of local contacts counts of haplotype combinations is identical to that of sEnd-P/M mentioned above. Note that as both ends are haplotype-unknown, no haplotype combination will be excluded. Based on local regions’ contacts count (α (‘P-P’), β (‘M-M’), γ (‘P-M’), and δ (‘M-P’), Figure 4B), HaploHiC randomly assigns a haplotype combination to dEnd-U Hi-C PE-reads with possibility defined as:

$$possibility\left(paternal,paternal\right)=\frac{\alpha }{\alpha +\beta +\gamma +\delta }$$ (Equation 7)

$$possibility\left(maternal,maternal\right)=\frac{\beta }{\alpha +\beta +\gamma +\delta }$$ (Equation 8)

$$possibility\left(paternal,maternal\right)=\frac{\gamma }{\alpha +\beta +\gamma +\delta }$$ (Equation 9)

$$possibility\left(maternal,paternal\right)=\frac{\delta }{\alpha +\beta +\gamma +\delta }$$ (Equation 10)

Similar to sEnd-P/M, if the local regions are still unphased after iterative extension, HaploHiC will assign a haplotype with uniform possibility depending on the mapped chromosome status.

If intra-chromosome mapped:

$$possibility\left(paternal,paternal\right)=0.5$$ (Equation 11)

$$possibility\left(maternal,maternal\right)=0.5$$ (Equation 12)

$$possibility\left(paternal,maternal\right)=0$$ (Equation 13)

$$possibility\left(maternal,paternal\right)=0$$ (Equation 14)

If inter-chromosome mapped:

$$possibility\left(paternal,paternal\right)=0.25$$ (Equation 15)

$$possibility\left(maternal,maternal\right)=0.25$$ (Equation 16)

$$possibility\left(paternal,maternal\right)=0.25$$ (Equation 17)

$$possibility\left(maternal,paternal\right)=0.25$$ (Equation 18)

Hi-C pairs from dEnd-U category are also marked as ‘phased imputed’ and ‘unphased imputed’ corresponding to phased and unphased local regions, respectively.

Allele-specific integrated results of Hi-C PE-reads

After processing the unphased Hi-C PE-reads of sEnd-P/M and dEnd-U categories, HaploHiC successfully assigns haplotype to all valid Hi-C pairs. Finally, HaploHiC integrates Hi-C pairs of each haplotype combination: intra-paternal (‘P-P’), intra-maternal (‘M-M’), and inter-haplotype (‘P-M’ and ‘M-P’). Note that ‘P-M’ and ‘M-P’ are recorded with different tags in one file.

• •Intra-paternal includes dEnd-P category, and imputed (‘P-P’) Hi-C pairs from sEnd-P/M and dEnd-U categories
• •Intra-maternal includes dEnd-M category, and imputed (‘M-M’) Hi-C pairs from sEnd-P/M and dEnd-U categories
• •Inter-haplotype includes dEnd-I and sEnd-I categories, and imputed (‘P-M’ and ‘M-P’) Hi-C pairs from sEnd-P/M and dEnd-U categories

All integrated files are in BAM format, which keeps the original alignments of Hi-C pairs. HaploHiC adds several tags in SAM optional fields to denote processing details. A report is generated recording statistics of each category of all Hi-C pairs.

We calculated the phased rate in each sample (Table S10). The phased rate is the percentage of phased Hi-C pairs, including dEnd-P/M/I, sEnd-I, and phased Hi-C pairs with imputed haplotype from sEnd-P/M and dEnd-U categories. Phased rates in sEnd-P/M and dEnd-U categories are calculated separately.

Additionally, we introduced ‘inter-chr imbalance’ to evaluate the difference between inter-haplotype and intra-haplotype assignment of inter-chromosome Hi-C pairs. Theoretically, for inter-chromosome contacts, there is no reason to assume any difference between the intra-haplotype and inter-haplotype. The ‘inter-chr imbalance’ is defined as the difference of intra-haplotype and inter-haplotype inter-chromosome contacts divided by their larger one. Our data shows very low ‘inter-chr imbalance’ (0.01%–0.04%, Table S10), which supports the accuracy of HaploHiC phasing.

Validation of allele-specific contacts

To validate HaploHiC, we randomly removed 10% of heterozygous loci from the list of phased mutations. The Hi-C PE reads from three categories (dEnd-P/M/I) were selected for validation, as both ends of these reads have known parental origin and can be used as the ground truth. To estimate the imputation accuracy of HaploHiC, we compared the imputed haplotype and the original haplotype of all Hi-C PE that cover the removed phased mutations. This validation method is similar to the one proposed in Tan et al. (2018). We found that HaploHiC was able to correctly assign an average of 84.9%, 86.1%, and 86.9% of these Hi-C reads for G1, S, and G2/M, respectively, over 10 trials. The minimum accuracy over all trials for G1, S, and G2/M were 84.5%, 83.7%, and 84.1%. Accuracy of imputation was calculated by the fraction of correctly imputed ones from the haplotype-known Hi-C reads covering these removed heterozygous mutations (Table S12).

We performed an additional hold-out validation which randomly selects SNVs and finds 10% of Hi-C read pairs that cover these SNVs from dEnd-P/M/I categories. These Hi-C pairs are then considered to be dEnd-U to validate HaploHiC’s prediction accuracy. Unlike the validation presented in Tan et al., this validation procedure removes the entire Hi-C read instead of only removing a random set of SNVs. When random SNVs are removed, many dEnd-P/M/I Hi-C reads only lose one end’s SNV coverage which leads to easier predictions. We found that prediction accuracy for the randomly removed “dEnd-U” reads was significantly lower than the previous validation, at an average of 41.6%, 42.2%, and 42.8% for G1, S, and G2/M, respectively, over 10 trials (Table S13).

We note that during the prediction of dEnd-U Hi-C reads, it is likely that a pair of reads will be falsely assigned to the opposite haplotypes (e.g. ‘M-M’ assigned to ‘P-P’ and vice-versa), which we refer to as “reciprocal swaps.” When reciprocal swaps occur, the actual Hi-C haplotype assignment is incorrect but the final count of Hi-C contacts between loci in each haplotype remain the same. Therefore, reciprocal swaps would not affect downstream analysis of the population data. After considering this case, the accuracy of imputation increases to 58.3%, 63.0%, and 64.5% for G1, S, and G2/M, respectively, averaged over 10 trials (Table S13). In approximately 15–20% of prediction cases, only one Hi-C read existed in our validation data set (Table S13). This prevents the possibility of reciprocal swaps. Given that the full Hi-C data set has many more Hi-C reads, we expect that the number of occurrences of reciprocal swaps would increase, causing the final imputed Hi-C counts to more closely match the ground truth. As expected, we also found that as the amount Hi-C data with SNV coverage increases, the number of false contacts decreases greatly (Table S14). This means that larger Hi-C data sets with better SNV coverage will allow HaploHiC to make more accurate imputations of unknown Hi-C reads.

To further evaluate our local contacts based algorithm, we simulated Hi-C sequencing data from haplotype specific contacts between gene pairs of ten categories:

Five categories for imitation of intra-haplotype autosome contacts:

• •Cross-Chrom: inter-chromosome translocations
• •Long-Distance: intra-chromosome, but on different arms
• •Long-Distance: intra-chromosome, on same arm, gene distance is > 10 Mb
• •TAD level: intra-chromosome, on same arm, gene distance is [1 Mb, 2 Mb]
• •LOOP level: intra-chromosome, on same arm, gene distance is < 700 kb

Two categories for imitation of inter-haplotype contacts:

• •InterHap/interChr: inter-chromosome translocations
• •InterHap/intraChr: intra-chromosome, gene distance is > 10 Mb

Three categories for imitation of chrX specific activation (intra-haplotype):

• •chrX/LongDistance: gene distance is > 10 Mb
• •chrX/TAD: gene distance is [1 Mb, 2 Mb]
• •chrX/LOOP: gene distance falls into is < 700 kb

In total, 67 gene pairs were randomly selected from COSMIC cancer gene census database (Forbes et al., 2016) to construct pairwise allele-specific contacts of maternal and paternal genomes respectively (Table S11). The maternal and paternal genomes are downloaded from AlleleSeq database (version: Jan-7-2017) (Rozowsky et al., 2011). The simulations on the LOOP level are CN-based (copy number), and the others are SV-based (structure variation, Figure S5). To imitate SV-based chromatin contacts for one pair of genes, e.g. BCR and ABL1, breakpoints are randomly picked from the two genes’ genomic regions respectively. At the breakpoints, reciprocal translocations are formed via concatenating extended flanking 2 Mb genomic sequences. As the gene-pair contact is heterozygous, sequences are extracted from paternal genome FASTA file to form an allele-specific SV, and sequences from maternal genome are extracted and kept unchanged (Figure S5A). To simulate CN-based chromatin contacts on the LOOP level, we assign different copy numbers to genomic regions harboring two neighbor genes on the two haplotypes (Figure S5B). For one genomic region containing two nearby genes (gene C and D), to make the paternal genome have more contacts between these two genes, we use two copies of this region from the paternal genome, while only keeping one copy from the maternal genome. We applied simu3C (DeMaere and Darling, 2017) to simulate the Hi-C sequencing reads of the SV-based and CN-based allele-specific gene-pair contacts.

HaploHiC successfully recovers the allele-specific contacts in simulation data with 97.66% accuracy (Table S11). First, all SV-based intra-haplotype allele-specific contacts are precisely reported by HaploHiC. For example, contacts of gene pair ‘ETV6, NTRK3’ are all ‘P-P’, and contacts of gene pair ‘KCNJ5, LMO2’ are all ‘M-M’. Second, for CN-based intra-haplotype allele-specific contacts, the advantage haplotype is successfully reported by HaploHiC. For example, gene pair ‘FLT3, LNX2’ has ‘P-P’ contacts more than three times of the ‘M-M’ contacts, and gene pair ‘RUNX1, SMIM11’ has ‘M-M’ contacts more than two times of the ‘P-P’ contacts. These ratios are close to what we found in simulation. Third, all inter-haplotype gene pairs are successfully identified with correct the haplotype combination. For example, all contacts of the gene pair ‘WT1, ZMYM2’ link paternal WT1 and maternal ZMYM2. The gene pair ‘MAP2K1, NUP214’ has seven ‘M-P’ contacts (false positives), which is only 2.6% of all its contacts (273). Fourth, all the intra-haplotype chrX allele-specific activation cases are reported correctly. Two gene pairs have some bias to inactivated haplotype (‘LAS1L, ZC4H2’ and ‘GPC3, HS6ST2’). Note that even shifted, they still show enrichment on correct haplotype. Gene pair ‘LAS1L, ZC4H2’ has larger shifting (33.3%) to ‘M-M’ contact, because the neighbor gene (MSN, gene distance is about 75 kb) of LAS1L forms gene pair ‘MSN, STAG2’ which is simulated to have only ‘M-M’ contacts. ‘LAS1L, ZC4H2’ is influenced by ‘MSN, STAG2’ as we merged all simulated Hi-C sequencing data of 67 gene pairs together as one sample in HaploHiC evaluation. Finally, all Hi-C pairs with mistakenly assigned haplotype combinations are gathered as false positives (count is 1,326, total count of valid Hi-C pairs is 55,013).

Whole Chromosome probe generation and 3D FISH

Whole chromosome paint probes were generated in-house using PCR labeling techniques as described at https://ccr.cancer.gov/Genetics-Branch/thomas-ried. Chromosome 7 was labeled with Orange dUTP (Abbott Laboratories, Abbott Park, IL), Chromosome 8 was labeled with Dy505 (Dyomics, Jena, Germany) and Chromosome 11 was labeled with Biotin-16-dUTP (Roche Applied Science, Indianapolis, IL). Cells were grown on slides and fixed with 4% paraformaldehyde for 10 minutes. Cells were then washed with 0.05% Triton X100 for five minutes followed by permeabilization steps which included incubation with 0.5% Triton X100 for 20 minutes, followed by subsequent repeated (4x) freeze thaw in liquid nitro- gen/glycerol. The slides were then incubated in 20% glycerol for at least one hour before being frozen in 1xPBS at −20°C until hybridization was performed. Prior to hybridization, cells were washed in 0.05% Triton X100 followed by incubation in 0.1N HCl for 10 minutes. Cells were then washed in 2XSSC followed by incubation in 50% formamide/2XSSC for at least one hour before hybridization. Cells and probes were co-denatured at 72°C for five minutes followed by a 48 hours hybridization at 37°C. After incubation at 37°C, detection commences with posthybridization washes followed by incubation in blocking (3% BSA, 4xSSC, 0.1% Tween20) for 30 minutes at 37°C. The biotinylated probes were detected with the fluorochrome Cy5 conjugated to Streptavidin (Rockland, Gilbertsville, PA). The slides were then washed with 2XSSC before being counterstained with Prolong Gold antifade reagent with DAPI (Promega Madison, WI).

Quantification and statistical analysis

Spectral clustering: the Laplacian, Fiedler value, and Fiedler vector

The Laplacian, Fiedler value, and Fiedler vector can be summarized as follows. Consider an adjacency matrix $\mathbf{A}$, where ${\left(\mathbf{A}\right)}_{i,j}=w\left(n_i,n_j\right)$, and weight function, w, satisfying $w\left(n_i,n_j\right)=w\left(n_j,n_i\right)$ (symmetrical) and $w\left(n_i,n_j\right)\ge 0$ (nonnegative). The Laplacian, $\mathbf{L}$, of $\mathbf{A}$ is defined to be $\mathbf{L}=\mathbf{D}-\mathbf{A}$, where $\mathbf{D}=diag\left(d_1,\cdots ,d_k\right)$ and $d_i={\text{Σ}}_{j=1}^k{a}_{ij}$. The normalized Laplacian is the matrix $\overline{\mathbf{L}}={\mathbf{D}}^{-1/2}\mathbf{L}{\mathbf{D}}^{-1/2}$. The second smallest eigenvalue of $\mathbf{L}$ (or $\overline{\mathbf{L}}$) is called the Fiedler value, and the corresponding eigenvector is called the Fiedler vector (Chung and Graham, 1997). The Fiedler value is also known as the algebraic connectivity of a graph. The magnitude of the Fiedler value increases as the number of edges in the graph increases, and as the graph becomes more structurally ordered. The Fiedler vector partitions the genome into two parts that reflect underlying topology, as given by edge weights inferred from Hi-C data. The Fiedler vector plays a role similar to the eigenvector associated with the largest eigenvalue (principal component 1) of the correlation matrix of the normalized Hi-C matrix (Lieberman-Aiden et al., 2009), but it is directly related to properties of the associated graph (Chung and Graham, 1997). The Fiedler vector can be calculated recursively to identify smaller partitions in Hi-C data. These smaller partitions correspond to topologically associated domains (TADs) (Chen et al., 2016a). Description of the Laplacian, Fiedler value, and Fiedler vector adapted from Chen et al. (2015).

Structure-function visualization and the 4D Nucleome

The goal of the maternal and paternal 4DN is to understand the relationship of allele-specific genomic structure and gene function through time. Gene expression (RNA-seq) directly offers us a scalar value to represent the function of an individual gene, or for a genomic locus (total gene expression for all genes within the locus). In order to find a compatible scalar value which represents structure, we look to Hi-C contacts. Hi-C provides insight into the structural organization of the genome by finding distant regions of the genome (in terms of genomic sequence) that are close to one another in 3D space. The 3D structure of the genome can be viewed through the perspective of a ‘genomic network’. In such a network, genomic regions are considered nodes and the contacts between genomic regions are the edges.

A concept that is well known in network theory is centrality. Network centrality measurements, or features, encompass a wide range of network properties (Newman, 2018). The common goal of these features is to assign quantitative measurements to the structure of the network. One particularly important feature is the eigenvector centrality, which is the eigenvector associated with the largest eigenvalue of the adjacency matrix which defines the network. Eigenvector centrality assigns values to each node in a network corresponding to that node’s influence on the network. Other centrality features that have been shown to have biological relevance include degree, betweenness, and closeness centrality (Liu et al., 2018). We calculated these four centrality features from the Hi-C data at 1 Mb resolution and concatenated them with RNA-seq to form a new structure-function (S-F) matrix which represents both structure and function (rows correspond to genomic loci, columns correspond to centrality features and RNA-seq) (Liu et al., 2018; Lindsly et al., 2021). We derived the S-F matrix both genome-wide and for individual chromosomes. We then normalize the S-F matrix for each setting (maternal and paternal in G1, S, and G2/M) and concatenate all settings. Next, we apply t-SNE to the combined S-F matrix (containing all settings) and reduce it to two dimensions (Maaten and Hinton, 2008). Then we can visualize the two dimensional projection, and observe how the maternal and paternal genomes compare across cell cycle phases (Figure S9).

The structure-function matrix integrates genomic structure and gene expression into a common subspace, but it does not directly inform us of the relationship between structure and function. To visualize this allele-specific relationship, we use eigenvector centrality and mature RNA (RNA-seq, FPKM) for each allele at each phase of the cell cycle. In other words, eigenvector centrality and RNA-seq serve as structure (x-axis) and function (y-axis) coordinates across the cell cycle, respectively (Figure 6). The cell cycle and B cell receptor signaling genes displayed in Figure 6 are contained in a larger sub-network of genes based on their KEGG pathway, whose Hi-C contacts (1 Mb resolution) define the edges of their respective sub-networks (from which eigenvector centrality is calculated). Similarly, the MAE genes displayed are contained within a sub-network of all MAE genes identified in our ABE analysis. The allele-specific genes displayed, which serve as a control, are contained within a gene sub-network which was randomly selected from all allele-specific genes. The number of allele-specific genes selected for the control is the mean of the other three sets’ sizes. The three points (G1, S, and G2/M) in the 4DN phase plane for each allele are fit with a minimum volume ellipse to capture the 4DN variance of the allele (Sun and Freund, 2004). Allelic divergence for each gene is calculated as the mean Euclidean distance between the maternal and paternal alleles’ coordinates in the 4DN phase plane for G1, S, and G2/M, after normalization of coordinates. The allelic divergence for each group of genes displayed in Figure 6 is defined as the mean of these genes’ individual allelic divergences.

Statistical significance via permutation test

A permutation test builds the shape of null hypothesis (namely, the random background distribution) by resampling the observed data. We use a permutation test to establish statistical significance in our analysis of the relationship between local structural changes and corresponding functional changes, the frequency of ABE genes in an essential gene set, and average allelic divergence of MAE genes. This sampling procedure was repeated 10,000 times in all cases cases. A rank-based p-value is then calculated for the right-tailed event for testing likelihood of local structure changes around ABE genes and allelic divergence. The left-tailed event was tested for decreased ABE in an essential gene set (Blomen et al., 2015). The background distribution for ABE in essential genes was generated by calculating the proportion of ABE genes in a randomly selected set of 662 allele-specific genes (same number of genes as the allele-specific essential gene set). The proportion of ABE genes in the essential gene set compared to this background distribution yields the p-value (Figure S3). The background distributions for genome structure changes were generated by calculating the average number of significant changes in the Hi-C contacts surrounding random allele-specific genes. The probability of the right-tailed event of our observation of significant structural changes around ABE, CBE, and combined set of ABE and CBE genes under their respective background distributions yields the p-values (Figure 5D). The background distribution for allelic divergence in MAE genes was generated by calculating the average allelic divergence among randomly selected sets of allele-specific genes. The allelic divergence of the MAE gene set compared to this background distribution yields the p-value (Figure S11).

Structure alignment and 3D modeling

Structures computed from different distance matrices could be varied in both scale and orientation. To align different structures and superimpose them into the same coordinates, we used Procrustes analysis (Stegmann and Gomez, 2002) which applies the optimal transform to the second matrix (including scaling/dilation, rotations, and reflections) to minimize the sum of square errors of the point-wise differences. First, we translocate shapes to the origin by subtracting the mean value of all coordinates. Next, we force shapes into the same scale by dividing each shape by the Frobenius norm. For an $m\times n$ matrix A, the Frobenius norm is defined as ${\Vert \mathbf{A}\Vert }_F={\left({\sum }_{i=1}^m{\sum }_{j=1}^n{\left|a_{ij}\right|}^2\right)}^{\frac{1}{2}}.$ Finally, we find an optimal rotation matrix that will align one contact matrix $\mathbf{A}$ to matrix B by using Singular Value Decomposition (SVD) on M where $\mathbf{M}={\mathbf{A}}^{\top }\mathbf{B}$. Applying SVD to the matrix M gives $\mathbf{M}=\mathbf{U}\mathbf{\Sigma }{\mathbf{V}}^{\top }$, where ${\mathbf{V}}^{\top }$ is the rotation matrix of B. Then $\mathbf{B}{\mathbf{V}}^{\top }$ is the rotated shape. To visualize the final structure from the inferred three dimensional embedding, we smooth the curve by interpolating three dimensional scatter data using the radial basis function (RBF) kernel. The structure was visualized using the Mayavi package in Python (Ramachandran and Varoquaux, 2011).

Published: December 17, 2021

Supporting Citations

The following references appear in the Supplemental information: Santos et al., 2015.

Data and code availability

• •All RNA-seq, Bru-seq, and Hi-C data are publicly available and have been deposited at the Gene Expression Omnibus (GEO) database. The accession number is listed in the key resources table.
• •Prototype MATLAB implementation for differential expression analysis is available through MathWorks and original HaploHiC code has been deposited to a GitHub repository. DOIs are listed in the key resources table.
• •Any additional information required to reanalyze the data reported in this paper is available from the lead contact upon request.