Executive Function Assigns Value to Novel Goal-Congruent Outcomes

Abstract

People often learn from the outcomes of their actions, even when these outcomes do not involve material rewards or punishments. How does our brain provide this flexibility? We combined behavior, computational modeling, and functional neuroimaging to probe whether learning from abstract novel outcomes harnesses the same circuitry that supports learning from familiar secondary reinforcers. Behavior and neuroimaging revealed that novel images can act as a substitute for rewards during instrumental learning, producing reliable reward-like signals in dopaminergic circuits. Moreover, we found evidence that prefrontal correlates of executive control may play a role in shaping flexible responses in reward circuits. These results suggest that learning from novel outcomes is supported by an interplay between high-level representations in prefrontal cortex and low-level responses in subcortical reward circuits. This interaction may allow for human reinforcement learning over arbitrarily abstract reward functions.

Introduction

Successful actions are often not signaled by immediate receipt of primary or secondary reinforcers (e.g., food and money), but through the realization of more abstract outcomes that do not have intrinsic value. Consider the game of bridge—in bridge, the most valuable cards (“trumps”) may be hearts in one game and diamonds in the next. Thus, in each new game, players need to use a flexible cognitive mapping to immediately reassign values to various stimuli. This ability to rapidly imbue an abstract stimulus or event with value is often taken for granted. Indeed, this ability contrasts with even our closest primate cousins: Chimpanzees can learn to treat novel tokens as substitutes for reward, but they do so only after lengthy bouts of conditioning where they incrementally learn to map those tokens to the future receipt of food (Wolfe 1936; Cowles 1937). Rapid, single-shot endowment of outcomes with value may be a unique faculty of higher-level human cognition, allowing us to form flexible mappings between actions and abstract signals of success.

Parallels between learning from abstract novel outcomes versus traditional secondary reinforcers are, however, poorly understood. Here we test whether attaining novel outcome feedback can reinforce choices in a similar manner to obtaining common secondary reinforcers (numeric “points”). We pushed this concept to a logical extreme, asking if fully novel outcomes that indicate goal attainment, or goal-congruent outcomes, can substitute for secondary reinforcers during instrumental learning. We further examined the role of executive function in this process.

Our first hypothesis was that standard reinforcement learning circuits would support learning from such abstract novel outcomes. This prediction is motivated by the observation that a diverse set of primary and secondary reinforcers drive instrumental learning. Primary rewards, including intrinsically pleasant odors (Howard et al. 2015) and flavors (McClure et al. 2003), act as reliable reinforcers that engage striatal circuits. Secondary reinforcers, such as money or numeric points (Daw et al. 2006), which acquire value from repeated pairings with reward, also engage this system. More abstract secondary reinforcers, such as improvements in perceived social reputation (Izuma et al. 2008), words and symbols that explicitly signal outcome valence (Hamann and Mao 2002; Daniel and Pollmann 2010), and internally maintained representations about performance accuracy (Han et al. 2010; Satterthwaite et al. 2012), all consistently engage striatal learning systems. Lastly, information that resolves uncertainty engages mesolimbic circuits in a similar manner to rewards (Charpentier et al. 2018; White et al. 2019). These findings suggest that striatal populations operate according to a flexible definition of reward that is context dependent and includes arbitrarily abstract goals (Juechems and Summerfield 2019).

Recent evidence suggests that sensitivity to goal-congruent outcomes can sometimes even supersede reward responses: Frömer et al. (2019) observed that the brain’s value network responds to goal-congruent choice outcomes even when current goals are pitted against rewards (Frömer et al. 2019). It remains to be established how this system endows values to fully novel outcomes. Repeated experience with unfamiliar feedback may engage incremental reward learning circuits to effectively transform goal-congruent outcomes into secondary reinforcers, in the same way that social cues or numerical points acquire secondary value over time. Alternatively, as we hypothesize here, the executive system may rapidly (i.e., within a single exposure) imbue novel outcomes with value via top-down input. In order to adjudicate between these mechanisms, we designed a study in which the features of novel outcome feedback changed from trial-to-trial, requiring flexible mappings between those outcomes and the reinforcement of preceding actions.

Our hypotheses are also inspired by recent research demonstrating that top-down inputs directly influence value-based learning computations in RL circuits (Rmus et al. 2021). For instance, attention modulates RL by specifying reward-predicting features of stimuli that RL processes should operate on (Leong et al. 2017; Radulescu et al. 2019). Explicit memories of familiar rewards can be flexibly combined to endow value to novel combinations of those rewards and to drive activity in the brain’s valuation network (Barron et al. 2013). Reward prediction error responses in dopamine neurons are influenced by latent task representations that are likely maintained in the prefrontal cortex (Wilson et al. 2014; Schuck et al. 2016; Babayan et al. 2018; Starkweather et al. 2018; Sharpe et al. 2019), as well as information held in working memory (Collins et al. 2017; Collins 2018; Collins and Frank 2018). Finally, even in standard model-free reinforcement learning, a cognitive map of action–outcome contingencies appears to guide credit assignment computations in the model-free system (Moran et al. 2021). This body of work suggests that higher-level cognitive processes specify and shape key inputs (e.g., states, rewards, and credit) to RL systems.

In this experiment, we used behavioral methods, computational modeling, and neuroimaging to investigate whether canonical signals measured during learning from familiar secondary reinforcers are observed, in overlapping neural regions, during learning from novel outcomes. We then examined whether prefrontal correlates of executive function, defined via a secondary task, influence how reward-related regions respond to these outcomes.

Methods

Participants

Thirty-two healthy volunteers (aged 18–40; mean age = 25.6 years; 18 females) participated in the experiment. All subjects were right-handed, had no known neurological disorders, and had normal or corrected-to-normal vision. Subjects provided written, informed consent and received $30 for their participation in the experiment. Functional neuroimaging data from three subjects were not analyzed beyond preprocessing because of excessive head motion (see below for details on these exclusion criteria), and an additional subject was excluded from both behavioral and neural analyses for showing overall below-chance mean performance in the task (i.e., more often choosing the less-rewarding stimulus). The three subjects excluded for excessive head motion were included in the behavioral and modeling analyses, yielding an effective sample size of 31 subjects for behavior analysis; the effective sample size for imaging analysis was 28 subjects. Experimental protocols were approved by the Institutional Review Board at the University of California, Berkeley.

Probabilistic Selection Task

Subjects were tasked with learning which of two stimuli, across four pairs of stimuli, was more likely to yield a favorable outcome (Fig. 1A). For one run, the choice stimuli were black line drawings of simple shapes (e.g., diamond, circle, and triangle), and for the other run, they were differently colored squares (e.g., blue, red, and green). The order of these two runs was counterbalanced across subjects. Stimuli were presented using MATLAB software (MathWorks) and the Psychophysics Toolbox (Brainard 1997). The display was projected onto a translucent screen that subjects viewed via a mirror mounted on the head coil.

Figure 1 .

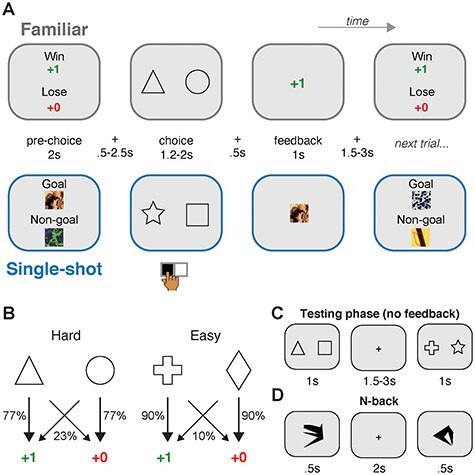
Task design. (A) Subjects (N = 32) performed a probabilistic selection task, learning which of two choice stimuli (e.g., triangle vs. circle) was more likely to yield positive feedback. Two feedback conditions were used: In the Familiar reward condition, successful choices were rewarded with numeric points. In the Single-shot condition, successful choices were signaled via prespecified “goal” fractal images. The images used as goal and nongoal stimuli were unique for each Single-shot trial. Pairs of choice stimuli were assigned to a single condition, and trials from each condition were intermixed. (B) In both feedback conditions, each choice pair was designated as either Hard or Easy, determined by the difference in success probabilities between pairs of choice stimuli. (C) After the learning phase of the probabilistic selection task, subjects experienced a testing phase, where different pairings of the eight total choice stimuli were pitted against one another and subjects rapidly chose their preference. No feedback was given in this phase. (D) Subjects also performed an N-back task, in which they responded when an image within a sequence repeated after “N” intervening images. N’s used = [1, 2, 3].

Trials proceeded as follows (Fig. 1A). First, during the prechoice phase, the type of feedback associated with the current trial was displayed (see below for details). This phase lasted 2 s. After a brief interstimulus interval (0.5–2.5 s, uniform jitter), the choice phase began, and a single pair of choice stimuli was presented (e.g., square vs. circle). The sides (left or right of the central fixation cross) where each of the two stimuli appeared were randomized across trials. Subjects had 1.2 s to render their choice with an MR-compatible button box, using their index finger to select the stimulus on the left and their middle finger to select the stimulus on the right. Successfully registered choices were signaled by the central fixation cross changing from black to blue. The choice phase ended after 1.2–2 s (uniform jitter) regardless of the reaction time, and choice stimuli stayed on screen until a second interstimulus interval with only the fixation cross displayed (0.5 s). Finally, in the feedback phase, feedback was presented for 1 s, followed by an intertrial interval of 1.5–3 s (uniform jitter). If reaction times were too fast (<0.2 s) or too slow (>1.2 s), the trial was aborted and a “Too Fast!” or “Too Slow!” message (red font) was displayed centrally for 1 s in lieu of any reward feedback and the ITI was initiated. (4.12 ± 0.73% of trials were aborted in this manner; mean ± 95% CI).

Two reward conditions were used (Familiar vs. Single-shot; Fig. 1A) as well as two difficulty levels (Easy vs. Hard; Fig. 1B). In the Familiar condition, feedback “point” stimuli were previewed during the prechoice phase, with the “+1” presented toward the top of the display and the “+0” presented toward the bottom, accompanied by the text “POINTS trial” in black font. At feedback, rewarded choices were signaled by numeric points, where a “+1” message was presented on successful trials (green font), and a “+0” message was presented on unsuccessful trials (red font). In the Single-shot condition prechoice phase, two distinct colored fractal-like patterns were displayed, with one labeled as the “Goal” (displayed toward the top of the screen) and the other as the “Non-goal” (displayed toward the bottom of the screen), accompanied by the text “GOAL trial” in black font. Here, the subject's task was to remember the identity of the fractal, so that in the feedback phase, they can appropriately reinforce their preceding stimulus choice. The set of colorful fractal stimuli were created using the randomize function of ArtMatic Pro (www.artmatic.com), and the final set of fractals was selected to maximize discriminability between any two fractals.

Trials were also evenly divided into two levels of difficulty: Easy or Hard. On Easy trials, the optimal choice stimulus yielded a favorable outcome (i.e., +1 point or the goal fractal) on 90% of trials (27 of 30 trials), and an unfavorable outcome (i.e., +0 points or the nongoal fractal) on 10% of trials. The other choice stimulus on Easy trials was associated with the inverse success probability (10%/90%). On Hard trials, the optimal choice stimulus yielded a favorable outcome (i.e., one point or the goal fractal) on ~77% of trials (23 of 30 trials), and an unfavorable outcome (i.e., 0 points or the nongoal fractal) on ~23% of trials. The other choice stimulus on Hard trials was associated with the inverse success probability (23%/77%). Reward schedules were deterministically prespecified so that the exact number of successful/unsuccessful outcomes for each stimulus was identical across subjects, though each subject received a unique pseudorandomized trial sequence. Crossing the two conditions (Familiar and Single-shot) and two difficulty levels (Easy and Hard) yielded four choice stimulus pairs for each run. Subjects performed 120 trials in each of the two runs of the task, performing 30 choices per run for each condition (i.e., for each of the four pairs of choice stimuli). To ensure that subjects understood the task, the experiment began with a thorough explanation of the conditions followed by a sequence of 16 practice trials that included both Familiar and Single-shot trial types (with deterministic reward/goal feedback), using fractal images and choice stimuli (Klingon characters) that were not seen in either subsequent learning run. These practice trials occurred during the anatomical scan.

In each run, after learning trials were completed, a “surprise” testing phase was administered (we note that the surprise aspect only existed for the first run of the experiment). Here, after a brief break cued by an instruction screen (12 s), a pseudorandom sequence of choice stimulus pairs was presented (1 s each, max RT 1 s, intertrial interval 1.5–3 s, uniform jitter). In this phase, all possible pairings of the 8 choice stimuli seen during learning were presented three times each, yielding 84 total trials. Participants made choices in the testing phase, though no feedback was given.

N-Back Task

After completing both learning runs, subjects also performed an n-back task during the third and final functional scan. In this task, subjects were shown a pseudorandomized sequence of novel opaque black shapes (ten unique stimuli; stimuli source: Vanderplas and Garvin 1959; task code modified from https://github.com/JAQuent/nBack) and asked to respond with a button press (forefinger press on the MR-compatible button box) whenever a shape repeated following N intervening different shapes. The current N-rule was specified via an instruction screen at the start of each sequence.

Four sequences (blocks) were performed at each N (Ns used: 1, 2, 3). Each sequence was 17 + N items long, had 7 target trials (hits) per sequence, and had no triple repeats of any single shape nor any repeats in the first three presented shapes. Each shape appeared centrally for 0.5 s, with a 2-s interstimulus interval. A black fixation cross was presented throughout the sequences. The order of the 12 sequences was randomized, although the first three sequences of the task were fixed to N = 1, 2, 3 in that order.

Behavioral Analysis

Behavior during the learning phase of the probabilistic selection task was quantified by a simple performance metric that reflected the percent of trials where subjects chose the optimal stimulus in each pair (i.e., the stimulus most likely to yield a reward; Fig. 1; Frank et al. 2007). In the testing phase, behavior was quantified using a logistic regression model. In this model, the response variable was a boolean based on whether the subject chose the stimulus on the right side of the screen (1) or the left side (0). Predictors included the cumulative reward difference of the stimuli (right minus left) determined by the sum of rewards (points or fractals) yielded by that stimulus during the preceding learning phase; a boolean predictor for trials that pitted two Familiar condition stimuli against one another; a boolean predictor for trials that pitted two Single-shot condition stimuli against one another; and a signed predictor capturing a Familiar condition bias, with a value of 1 when a Familiar condition stimulus appeared on the right and a Single-shot condition stimulus appeared on the left, a value of −1 for when a Single-shot condition stimulus appeared on the right and a Familiar condition stimulus appeared on the left, and a value of 0 when both stimuli were associated with the same condition. Interaction terms were included as well, and all predictors were z-scored.

N-back performance was quantified using the d-prime metric (Haatveit et al. 2010). Correlations between n-back performance (d-prime over all trials/Ns) and performance in the probabilistic selection task were computed using both Spearman and Pearson correlations and were conducted on both the full set of trials in the probabilistic selection task, or the subset that showed similar cross-condition performance (i.e., Familiar–Hard trials and Single-shot–Easy trials.

Computational Modeling Analysis

We tested several variants of standard trial-based reinforcement learning (RL) models (Sutton and Barto 1998) to account for subjects’ instrumental learning behavior and to build model-derived regressors for fMRI analyses. All models tested were built using the same basic architecture, where values of stimuli were updated according to the delta rule:

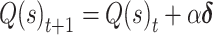(1)

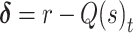(2)

Here, Q(s)_t reflects the learned value of stimulus s on trial t, α reflects the learning rate, and 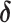reflects the reward prediction error (RPE), or the difference between the observed reward (r) and the expected reward given the choice of stimulus s. Action selection between the two presented stimuli was modeled using the softmax function,

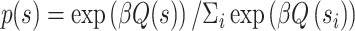(3)

where β is the inverse temperature parameter.

Two candidate models also included a decay parameter, which captured trial-by-trial forgetting of all stimulus Q-values,

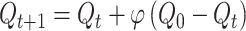(4)

where 0 < φ < 1 is a decay parameter that at each trial pulls value estimates toward their initial value Q₀ = 0. We note that a preliminary analysis found that the best-fitting value of initial Q-values, Q₀, was 0. Moreover, additional model fitting and comparison analyses found that a decay target of 0 was the most appropriate value for the decay process.

After performing a preliminary model fitting and comparison analysis across a wide range of candidate models (using maximum likelihood estimation), we narrowed our primary model fitting and comparison analysis to six candidate model variants that performed well in our first-pass analysis and represented distinct behavioral interpretations (see Supplementary Table 1 for details of each tested model).

The first model we tested reflected our hypothesis that the differences in performance we observed between the Familiar and Single-shot feedback conditions were strictly a function of weaker learning in the Single-shot condition. We implemented this by having an independent learning rate (α) for each feedback condition (Familiar vs. Single-shot). This model included a single decay parameter and a single temperature parameter.

In a second variant, we assumed that performance differences were a function of both weaker learning and increased forgetting of stimulus values in the Single-shot condition; this model matched the first model but had unique decay parameters for each feedback condition. In a third variant, we excluded the decay parameter altogether but included feedback condition-specific learning rates, and in a fourth variant, we assumed asymmetric updates (i.e., unique learning rates) for positive and negative outcomes (Frank et al. 2007; Gershman 2015).

To capture a form of rapid learning that is qualitatively distinct from incremental RL, we also tested a simple heuristic “win-stay lose-shift” model, which can be captured by equation (1) when α = 1. To allow for feedback condition differences in this simple heuristic model, we included a unique β free parameter for each feedback condition.

Finally, in our sixth model, we tried to capture the hypothesis that the learning processes (equations (1) and (2)) in both the Familiar and Single-shot conditions were identical (via equal learning rates), but that the choice process (equation (3)) was different, perhaps being noisier in the Single-shot condition due to the presence of a secondary task (i.e., having to maintain the goal fractal during the choice phase). We approximated the effect of putative choice-phase noise via an undirected noise parameter,

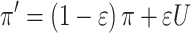(5)

Here, given the action selection policy π = p(s) (equation (3)), equation (5) introduces noise by implementing a mixed policy where U is the uniform random policy (i.e., a coin flip between stimuli) and the parameter 0 < ε < 1 controls the amount of decision noise introduced during choice (Collins et al. 2014). We included separate ε free parameters for each feedback condition.

For model fitting and model comparisons, we used a recently developed technique, Hierarchical Bayesian Inference (HBI) (Piray et al. 2019). In this method, models are compared and free parameters are estimated simultaneously. Recent work using this method has shown that fits estimated by HBI are more precise and recoverable than competing methods, and model comparison is robust and less biased toward simplicity (Piray et al. 2019). We note briefly that similar behavioral and fMRI results were obtained when we used traditional maximum likelihood estimation methods; however, clearer model comparison results and more interpretable parameter estimates were obtained in our HBI analysis. For our HBI procedure, we implemented a prior variance parameter of v = 6.00. Finally, to compare learning rate parameters across feedback conditions, we could not perform standard frequentist tests due to the hierarchical procedure; thus, in a follow-up HBI analysis, we implemented the Single-shot condition learning rate as a free parameter that was added or subtracted to the Familiar condition learning rate and performed an “HBI t-test” on the resulting parameter fit relative to zero. (Further details concerning the HBI analysis procedure, and its open-source toolbox, are given in Piray et al. 2019.)

After model fitting and comparison, we validated the winning model by simulating choice behavior using the best-fit parameters. For each subject, we simulated 100 RL agents using the schedule of rewards seen by that subject and the best-fit individual-level parameters for that subject gleaned from the HBI procedure. Results were averaged before plotting. For model-derived fMRI analyses, we simulated the model for each subject using his or her actual choice history and best-fit learning rate and decay parameters. This procedure yielded model-based predictions of trial-by-trial RPEs and trial-by-trial Q-values (of the chosen stimulus). Both of these variables were convolved with the canonical hemodynamic response function and used to model BOLD responses during, respectively, the feedback and choice phases. Lastly, in a control fMRI analysis, we instead used the group-level parameters for each subject (as given by the HBI-fitting procedure) to simulate RPEs.

Imaging Procedures

Whole-brain imaging was performed at the Henry H. Wheeler Jr Brain Imaging Center at the University of California, Berkeley, on a Siemens 3 T Trio MRI scanner using a 12-channel head coil. Functional data were acquired with a gradient-echo echo-planar pulse sequence (TR = 2.25 s, TE = 33 ms, flip angle = 74°, 30 slices, voxel size = 2.4 mm × 2.4 mm × 3.0 mm). T1-weighted MP-RAGE anatomical images were collected as well (TR = 2.30 s, TE = 2.98 ms, flip angle = 9°, 160 slices, voxel size = 1.0 mm isotropic). Functional imaging was performed in three runs, with the first two runs consisting of the probabilistic selection task (584 volumes each) and the third run consisting of the n-back task (275 volumes). A field map scan was performed between the two probabilistic selection task runs to correct for magnetic field inhomogeneities (see Image Preprocessing). Subjects’ head movements were restricted using foam padding.

Image Preprocessing

Preprocessing was performed using fMRIPrep 1.4.0 (Esteban et al. 2019). First, the T1-weighted (T1w) image was corrected for intensity nonuniformity with N4BiasFieldCorrection (Tustison et al. 2010) and then used as the T1w reference image throughout the workflow. The T1w reference image was skull-stripped (using antsBrainExtraction.sh), and brain tissue segmentation was performed on the brain-extracted T1w using the FSL tool FAST. Brain surfaces were reconstructed using the FreeSurfer tool Recon-all (FreeSurfer 6.0.1; Dale et al. 1999). Volume-based spatial normalization to standard (MNI) space was performed through nonlinear registration with ANTs, using brain-extracted versions of both the T1w reference image and the T1w template.

The functional data were resampled into standard space (MNI), generating a preprocessed BOLD time series for each run. A reference volume (average) and its skull-stripped version (using ANTs for stripping) were generated. A B0 field map was co-registered to the BOLD reference image. Head-motion parameters were estimated with respect to the BOLD reference image (transformation matrices and six corresponding rotation and translation parameters) before spatiotemporal filtering was applied with MCFLIRT (FSL 5.0.9; Jenkinson et al. 2002). Slice-time correction was applied using 3dTshift from AFNI (Cox and Hyde 1997). The BOLD time-series (including slice-timing correction) were resampled into their original, native space by applying a single transform to correct for head-motion and susceptibility distortions (Glasser et al. 2013). The unwarped BOLD reference volume for each run was co-registered to the T1w reference image using bbregister (FreeSurfer), with nine degrees of freedom to account for any distortions remaining in the BOLD reference image.

Framewise displacement was calculated for each functional run (following Power et al. 2014). Confound regressors for component-based noise correction were created using CompCor (Behzadi et al. 2007). Gridded (volumetric) resamplings were performed using antsApplyTransforms (ANTs), with Lanczos interpolation. Lastly, data were high-pass filtered (100 s) and spatially smoothed with a Gaussian kernel (4.0 mm FWHM) prior to all GLM analyses.

Imaging Analyses

Analyses involved four separate GLMs fit to learning phase BOLD data, and one GLM fit to the n-back task BOLD data. All GLM analyses were performed using FSL (version 6.0.3). Regressors of no interest were entered into the model; these included subject reaction time (a parametric regressor yoked to choice onset, convolved with the HRF), button press events (convolved with the HRF), six standard motion regressors, the framewise displacement time course, linear drift terms, and the first 6 aCompCor components. In addition, we added stick regressors corresponding to volumes with large motion artifacts (>1.0 mm framewise displacement, or >5 scaled variance as determined by SPM’s tsdiffana protocol), with additional confound stick regressors for the neighboring (subsequent) volume. This procedure was also used to determine movement-related subject exclusions: If more than 10% of volumes in either of the two learning runs were flagged as outliers, the subject was excluded (three subjects were excluded based on these criteria). Unthresholded group statistical maps (t-maps), and an average group normalized structural scan have been deposited on Neurovault (https://identifiers.org/neurovault.collection:9839).

In the first GLM (GLM 1), regressors of interest included condition-specific spike regressors for the onset of each of the following trial phases: prechoice, choice, feedback, and the choice phase in the testing trials. A feedback-locked valence regressor also was included, which effectively coded successful (+1) and unsuccessful (−1) trials within the learning phase. A model-derived parametric regressor was also included at feedback onset, which captured condition-specific RPEs (equation (2)). Including both valence and RPE regressors is important because brain responses distinguishing the feedback valence (in visual, affective, or cognitive properties) could be misidentified as parametric reward prediction errors. Each subject’s RPE time course was determined using his or her individually-fit parameters. Orthogonalization was not used, and each regressor was convolved with the canonical hemodynamic response function (double-gamma). Secondary GLMs were also run for two control analyses (Supplementary Fig. 3): In one variant of GLM 1, the RPE regressor in the model was created using group-level learning rate and decay parameter values rather than individually-fit parameters for each subject’s RPE time-course; in a second variant of GLM 1, we included separate positive and negative RPE regressors for each condition. The second GLM (GLM 2) was identical to the first, except that instead of including RPE regressors it included the model-derived Q-value for the chosen stimulus as a parametric modulation of choice onset (modeled separately for the two feedback conditions).

The third and fourth GLMs were designed to facilitate decoding and connectivity analyses: GLM 3 included identical task and confound regressors as those in GLM 1; however, feedback onset was modeled on a trial-by-trial basis, with unique stick regressors at each instance of feedback (and no regressors for valence/RPEs). This method produced individual feedback phase beta-maps for each trial of the learning task (Mumford et al. 2014). GLM 4 was also similar to GLM 1, except a single feedback onset regressor for all trials was used, and we instead modeled the prechoice phase on a trial-by-trial basis, producing individual prechoice phase beta-maps for each trial of the task.

The n-back task GLM (GLM 5) included the same confound regressors as the learning task GLMs. Regressors of interest included a block-level regressor spanning the beginning to end of each stimulus sequence, and a parametric modulation of that regressor that reflected the particular N assigned to each sequence. This latter regressor thus captured the linear effect of increasing cognitive load in the n-back task and was used as an executive function ROI localizer for later analyses.

Individual subject runs were combined in a fixed effects analysis and then brought to the group level for mixed-effect analyses. For whole-brain analyses, we imposed a family-wise error cluster-corrected threshold of P < 0.05 (FSL FLAME 1) with a cluster-forming threshold of P < 0.001.

Our region-of-interest (ROI) creation procedure was designed to both avoid double-dipping at the subject level (Kriegeskorte et al. 2009; Boorman et al. 2013) and to conservatively test our predictions about RL processes specifically in the Single-shot feedback condition. First, for each subject, we performed a leave-one-out group-level mixed-effects analysis of the main effect of interest (e.g., valence) in the Familiar condition trials only, excluding that subject’s data. Prethreshold masking was performed in this analysis to constrain results within an anatomical region using a cluster-corrected threshold of P < 0.05 (FSL FLAME 1) and cluster-forming threshold P < 0.01 (note that this threshold was relaxed relative to the whole-brain threshold for ROI creation purposes only). For striatal analyses, we used a three-partition striatal mask for anatomical masking (Choi et al. 2012). For cortical ROI masking, we used the Harvard-Oxford probabilistic atlas, thresholding all masks at 0.50. (We note that for the inferior parietal lobule mask we combined the bilateral angular and supramarginal gyri.) Because of this method, resulting Familiar and Single-shot condition ROI results were statistically valid at the subject level, and all Single-shot condition results were additionally validated out-of-set at the condition level. All neural effect sizes (betas) were extracted using featquery (FSL).

Our cross-validated encoding analysis of RPE processing was performed as follows: Beta series data for feedback onset (GLM 3) were extracted from each subject’s dorsomedial striatum ROI. Then, for each individual run, a linear regression was performed independently for each voxel, relating its activation to model-derived RPEs on rewarded Familiar condition trials only. We constrained this analysis to rewarded trials to model parametric prediction error effects independent of valence. The resulting n × 1 vector of parameter estimates, for n voxels, was then multiplied by one of three different trial × n matrices of independent beta series data: the beta series of rewarded Familiar trials in the held-out run, the beta series of rewarded Single-shot trials within-run, and the beta series of rewarded Single-shot trials in the held-out run. This produced a vector of “predicted” RPEs for each of these analyses. Predicted RPEs were then correlated (Spearman) with the model-derived RPEs for the associated run/condition and Fisher-transformed for statistical analysis (two-tailed t-tests relative to zero, with alpha set to 0.05).

Functional correlation analyses were performed as follows: First, we aimed to identify prefrontal cortex (PFC) voxels that were related to the encoding of the fractal stimuli. Thus, we created a PFC ROI using a group-level mixed-effects analysis on the Single-shot > Familiar prechoice phase contrast (using the aforementioned leave-one-out procedure to maintain statistical independence), masking those results (prethreshold) with the group main effect map from the n-back GLM (parametric N regressor; see above). Then, for each ROI (e.g., PFC and hippocampus) and phase (e.g., prechoice and feedback), we extracted trial-by-trial betas from either GLM 3 (for feedback) or GLM 4 (for prechoice) and averaged within each ROI. We performed beta series correlations (Rissman et al. 2004) by computing the spearman correlation coefficients between each ROI pair and then Fisher-transformed those values to derive a “Connectivity Index.” We measured both within-subject effects for this Connectivity Index (i.e., Single-shot vs. Familiar) and between-subject correlations between the condition differences in connectivity and the condition differences in learning and n-back performance. Connectivity analyses in control ROIs (thalamus and posterior cingulate cortex) were performed using beta-series data extracted from anatomically derived ROIs (Harvard-Oxford atlas; thresholded at 0.50). Finally, a post-hoc connectivity analysis on PFC-VTA functional correlations was performed using the probabilistic VTA atlas given by Murty et al. 2014 (thresholded at 0.50).

Results

Subjects (N = 32) performed a probabilistic selection learning task (Frank et al. 2007) adapted for fMRI, and an executive function task (n-back; Kirchner 1958). Each trial of the selection task required a binary choice between two stimuli (Fig. 1A). Subjects were required to learn which stimulus in each pair more often produced favorable outcomes. The task involved two feedback conditions: Familiar and Single-shot. The Familiar condition used numeric points (i.e., “+1” or “+0”) as secondary reinforcers. Points, like money, are secondary reinforcers due to their common association with positive outcomes in various real-world games and activities; indeed, a multitude of RL studies have used points as proxies for reward, which lead to reliable learning behaviors and robust responses in the reward system (e.g., Daw et al. 2006). Therefore, we refer to the Familiar feedback condition as generating “reward outcomes.”

The Single-shot feedback condition used randomly generated fractal stimuli as outcomes. Both the target (“goal”) and nontarget (“non-goal”) fractals were novel on each Single-shot condition trial. Thus, the Single-shot condition required subjects to use their knowledge of the current target fractal to determine whether their choices were successful. Each trial of both conditions included three phases: a prechoice phase, a choice phase, and a feedback phase (Fig. 1A). In the Single-shot condition, the two novel fractal stimuli were displayed during the prechoice phase with one designated as the “goal” and the other as the “non-goal,” explicitly mirroring, respectively, the “+1” and “+0” of the Familiar condition. To match motivational aspects of the two conditions, no performance-based monetary incentives were provided in the experiment.

To investigate differential effects of task difficulty and feedback condition, we also implemented two difficulty levels (Hard and Easy), where each pair of choice stimuli was associated with different probabilities of yielding successful outcomes (Fig. 1B). To test subjects’ retention of learned values, a subsequent testing phase was administered where subjects made choices between each possible pairing of the eight learning stimuli and no feedback was given (Fig. 1C). Finally, to capture an independent measure of executive function, subjects also performed a standard visual n-back task (Fig. 1D; Ns used: 1, 2, 3). We predicted that performance on this task would be specifically related to subjects’ ability to learn from novel outcomes.

Executive Function Supports Single-Shot Reward Learning

Subjects performed well in the learning task, selecting the better stimulus of each pair in both the Familiar (mean: 82%; chance = 50%; t(30) = 19.39, P < 1e−17) and Single-shot (mean: 75%; t(30) = 10.70, P < 1e−11) conditions (Fig. 2A,B). A repeated-measures ANOVA revealed a main effect of feedback condition (i.e., Single-shot vs. Familiar; F_1,30 = 11.67, P = 0.002), with better learning phase performance in the Familiar versus the Single-shot condition (Bonferroni-corrected; t(30) = 3.41, P = 0.002). We also observed a main effect of difficulty (F_1,30 = 22.74, P < 1e−4), with better performance on Easy versus Hard trials (t(30) = 4.77, P < 1e−4). There was no significant interaction between feedback condition and difficulty (F_1,30 = 0.34, P = 0.57). These results show that subjects could leverage Single-shot outcome stimuli to successfully learn to select actions that lead to favorable outcomes, but that this was less successful than learning via familiar rewards.

Figure 2 .

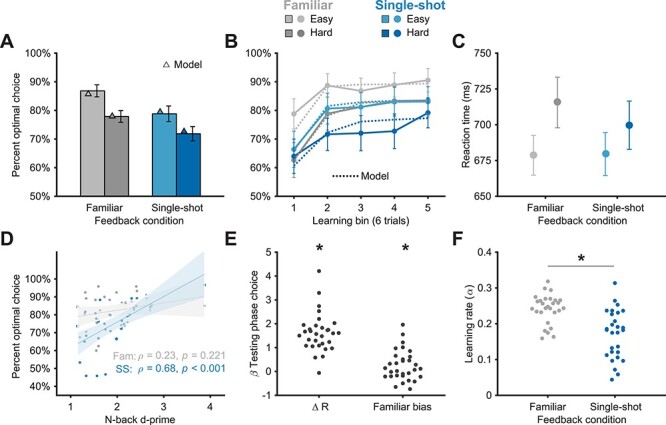
Behavioral results. (A) Average performance in the probabilistic selection task for each condition. Subjects performed well above chance (50%) in the task. We observed main effects of feedback condition (Familiar vs. Single-shot) and difficulty (Easy vs. Hard) but no interaction. Model simulation results (triangles) are depicted for each condition and difficulty level. (B) Learning curves for each condition and difficulty level, with six trials per bin. Model simulations are depicted as dashed lines. (C) Mean reaction times during learning. We observed a main effect of difficulty, but no effect of feedback condition nor any interaction. (D) Correlation of performance in the N-back task with learning performance in the probabilistic selection task (collapsed across difficulty levels). Fam = Familiar condition; SS = Single-shot condition. (E) Regression weights resulting from a logistic regression analysis on testing phase choices. Subjects’ choice of stimuli increased as a function of how often the stimulus was rewarded during learning (∆R, left) and showed a bias toward stimuli associated with Familiar reward feedback when they were paired with stimuli associated with Single-shot feedback (right). (F) Learning rate parameters from the best-fit RL model. Learning rates were significantly higher in the Familiar condition. ^*P < 0.05; Error shading = 95% CI; Error bars = 1 SEM.

One explanation for performance differences between the Familiar and Single-shot feedback conditions is the dual-task demands in the latter (i.e., holding the novel fractal in memory while also having to select a preferred stimulus). A common signature of dual-tasks is slowed reaction times (RTs) for individual subtasks (Pashler 1994). Thus, one prediction of a dual-task effect is slower RTs during choice in the Single-shot condition relative to the Familiar condition. An ANOVA on the RT data (Fig. 2C), however, revealed no main effect of feedback condition (F_1,30 = 0.57, P = 0.47), a main effect of difficulty (F_1,30 = 14.07, P = 0.001), and no significant interaction (F_1,30 = 1.83, P = 0.19). These results show that the dual-task design of the Single-shot condition did not manifest by slowing RTs, which suggests that maintaining a novel outcome image did not necessarily interfere with choice. These results also argue against a qualitatively different process (such as planning) driving behavior in the Single-shot condition: In general, planning should incur an RT cost relative to simple instrumental learning (Keramati et al. 2011).

We hypothesized that one factor differentiating performance between the conditions was the fidelity of working memory. That is, if a fractal stimulus is sufficiently encoded and maintained in memory during a Single-shot trial, it should effectively stand in as a reinforcer at feedback. If this is true, we expect working memory performance to correlate with Single-shot condition performance above and beyond performance in the Familiar condition (Fig. 2D). Indeed, Single-shot condition performance was significantly correlated with n-back d-prime values (ρ = 0.68, P < 1e−4), but Familiar condition performance was not (ρ = 0.23, P = 0.221). A permutation test revealed that these correlations were significantly different (P = 0.038; 5000 iterations of shuffled correlation differences). We also found a significant correlation between n-back performance and the learning difference between feedback conditions (i.e., Single-shot minus Familiar; ρ = 0.52, P = 0.003). Nonparametric (Spearman) correlations were used for the above correlations given the one clear n-back task outlier (Fig. 2D); results were replicated with parametric (Pearson) correlation metrics.

In an exploratory follow-up analysis, we asked if working memory performance may be linked to early learning in the Familiar condition, when executive function may be useful for formation of value representations (Collins 2018; McDougle and Collins 2021; Rmus et al. 2021). Interestingly, we found significant correlations between n-back performance and early learning (first six trials) in both the Familiar (ρ = 0.39, P = 0.03) and Single-shot conditions (ρ = 0.53, P = 0.002), consistent with a role for executive function in the earliest phases of typical RL tasks.

We next asked if executive function covaried with learning in the Single-shot condition simply because it was a harder (i.e., dual) task, or if the particular memory demands of the Single-shot condition recruited executive function. That is, the correlation results (Fig. 2D) could arise due to simple differences in the difficulty of the learning task between conditions as measured by choice performance. We controlled for difficulty by selecting difficulty-matched subsets of data—specifically, we examined Hard trials of the Familiar condition and Easy trials of the Single-shot condition, where performance was statistically indistinguishable (Bayes factor = 6.84 in favor of the null). If n-back performance covaries with Single-shot condition performance for reasons beyond simple task difficulty, the correlation results in Figure 2D should hold in these data. Indeed, Single-shot-Easy performance was significantly correlated with n-back performance (ρ = 0.74, P = 0.004) but Familiar-Hard performance was not (ρ = 0.06, P = 0.504), and these correlations were significantly different (permutation test: P = 0.046). Taken together, these results suggest that executive function played a selective role in maintaining Single-shot outcomes and helping subjects learn from them.

Learning from Single-Shot Outcome Feedback versus Familiar Rewards Is Similar, but Slower

How well were learned stimulus values retained after training was complete? One potential consequence of learning purely via top-down executive function—a plausible hypothesis for the Single-shot condition—is relatively brittle value representations that are forgotten quickly (Collins 2018). On the other hand, if learning proceeds similarly between the conditions, the amount of forgetting should be roughly the same. We addressed this question in the testing phase (Fig. 1C). When looking at pairs of testing phase stimuli that were learned under the same feedback condition, we found that subjects selected the more valuable stimulus more often for both the Familiar and Single-shot stimuli (mean: 68%; t(30) = 8.49, P < 1e−8; mean: 64%; t(30) = 5.04, P < 1e−3; respectively), with no significant difference between the feedback conditions (t(30) = 1.11, P = 0.28). In a further analysis, we looked at performance in these same testing phase trials as a function of asymptotic learning—that is, as a proxy for forgetting. We computed forgetting by taking the difference between performance on the last six trials of the learning phase for each condition and performance on the within-condition testing phase trials. The Familiar condition showed an average 19.37% forgetting effect, and the Single-shot condition showed an average 17.08% forgetting effect; forgetting was not significantly different between the conditions (t(30) = 0.62, P = 0.54).

To characterize choice behavior across the full range of testing phase trial types, we further analyzed subjects’ choices using multiple logistic regression (see Methods). The choice of stimulus in the testing phase was influenced by the difference in the cumulative number of successful outcomes associated with each stimulus (“∆R” in Fig. 2E; t-test on Betas relative to zero: t(30) = 11.17, P < 1e−11), but we did not observe a significant interaction between cumulative value and the effect of the feedback condition in which the stimuli were learned (t(30) = 0.21, P = 0.839). This suggests that subjects similarly integrated both types of outcomes (rewards and goal-congruent outcomes) into longer-term memories of stimulus value. Lastly, when the two stimuli in the testing phase had originally been learned via different feedback conditions, subjects did show a bias toward stimuli from the Familiar condition, even when controlling for cumulative reward differences within the same regression (Fig. 2E; t(30) = 2.16, P = 0.039). This suggests that values learned via familiar rewards may have been subtly more salient during recall when directly pitted against those learned via novel outcomes.

Next, we asked if performance differences between feedback conditions of the learning task resulted from choice- or learning-related effects. In order to better understand the differences between the feedback conditions, and to produce RL model regressors for fMRI analysis, we modeled subjects’ choices in this task with several variants of standard RL models (Sutton and Barto 1998). We implemented a Bayesian model selection technique (Piray et al. 2019) that simultaneously fits and compares multiple candidate models (see Methods). This analysis strongly favored a simple RL model that differentiated the Familiar and Single-shot conditions via separate learning rate parameters (Exceedance probability for this model vs. competing variants = 1.0; Supplementary Fig. 1; Supplementary Table 1). Critically, this model outperformed a competing model that used different levels of decision noise in each feedback condition—this suggests that the condition differences we observed (Fig. 2A,B) were related to learning rather than choice processes, the latter being a natural prediction of dual-task interference.

To validate our model, we simulated choices using the fit model parameters: As shown in Figure 2A,B, the model successfully reproduced subjects’ performance across feedback conditions and difficulty levels. Performance differences were successfully captured by the learning rate parameter—learning rates were significantly lower in the Single-shot condition versus the Familiar condition (P < 1e−4 via an “HBI t-test,” see Methods; Fig. 2F and Supplementary Fig. 1). Moreover, consistent with the results depicted in Fig. 2D, n-back performance was positively correlated with the difference between the Single-shot and Familiar condition reinforcement learning rates (i.e., Single-shot minus Familiar; ρ = 0.44, P = 0.019).

We note that the observed difference in learning rates could represent (at least) two non–mutually-exclusive phenomena: First, it could be that there are weaker appetitive signals for novel outcome stimuli versus familiar rewards. Second, occasional “lapses” in working memory could lead to forgetting of the fractals. The fact that n-back performance was selectively predictive of the Single-shot condition performance appears to support the lapsing interpretation, though executive function could also act to boost the appetitive strength of novel outcomes. Either way, choice and RT analyses suggest qualitatively similar, though slower, learning from Single-shot novel outcomes versus Familiar reinforcers. Next, we asked if these similarities carried over to the neural signatures of learning.

Similar Neural Regions Support Familiar Reward and Single-Shot Outcome Learning

We reasoned that Single-shot valuation of novel outcomes leveraged the same RL circuits that drive learning from Familiar rewards, and that activity in executive function-related regions of the prefrontal cortex (PFC) could support this process through an interaction with reward-sensitive regions. These results would be consistent with our behavioral results, where executive function performance covaried with Single-shot learning (Fig. 2D).

We first used whole-brain contrasts to measure univariate effects of feedback condition. In the prechoice phase, we observed significantly more activity in the Single-shot versus Familiar condition in areas across the ventral visual stream, hippocampus, and both medial and lateral regions of PFC (Supplementary Fig. 2; see also for results of Familiar > Single-shot contrasts). These results are broadly consistent with the greater visual complexity in the Single-shot condition during the prechoice phase, where text-based instructions and a complex fractal stimulus are viewed rather than simply text alone (Fig. 1A). Additionally, there were increased cognitive demands during this phase in the Single-shot condition—subjects needed to attend to and encode the novel fractals. In the choice phase, we observed more activity in the medial striatum and visual cortex in the Single-shot versus Familiar condition. The lack of any significant differences in PFC activation during the choice phase in this contrast is consistent with the relatively modest working memory demand in the Single-shot condition (Supplementary Fig. 2). However, we note that the continued activation in primary visual areas in the Single-shot condition during the choice phase could potentially reflect ongoing working memory maintenance (Emrich et al. 2013). Finally, in the feedback phase, we observed greater activation in the visual cortex and dorsolateral prefrontal cortex in the Single-shot versus Familiar condition. These increased activations could reflect, respectively, the complex visual features of the fractal stimulus and recall of its valence (Manoach et al. 2003).

We used ROI analyses to test the hypothesis that overlapping neural populations encode value signals related to traditional secondary reinforcers and novel outcomes. We used the Familiar feedback condition as a reward processing “localizer” task, generating the ROIs we used to characterize novel outcome processing in the Single-shot feedback condition. Thus, our analysis of the Single-shot condition was fully validated out-of-set (see Methods). This approach provided a stringent test of our hypothesis that overlapping neural populations would encode reward and value signals related to both traditional secondary reinforcers and novel, Single-shot outcomes. Moreover, ROIs for individual subjects were determined using a leave-one-out procedure where the group functional map used to create a particular subject’s functional ROI excluded that subject’s own data (Boorman et al. 2013; Kriegeskorte et al. 2009; see Methods for further details). Figure 3A shows example ROIs derived from the Familiar condition for one representative subject.

Figure 3 .

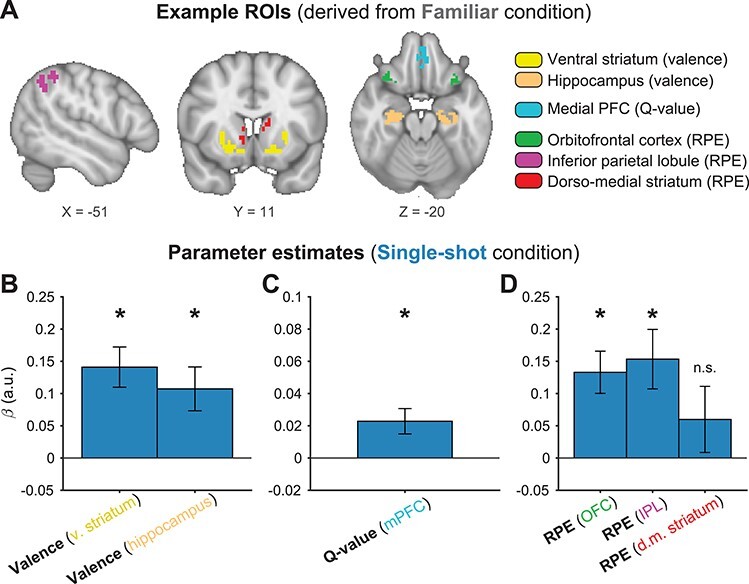
fMRI results: valence, value, and prediction errors. (A) Example ROIs for the three main effects of interest are shown for an individual subject (subject s020). ROIs were created using a leave-one-out procedure, where each subject’s data were excluded from the statistical maps used to define their ROIs. Critically, only trials from the Familiar condition were used to generate these ROIs. Held-out Single-shot condition results were then computed in these ROIs, for effects of (B) valence, (C) model-derived Q-values at choice, and (D) model-derived reward prediction errors (RPEs). All parameter estimates were significantly greater than zero at P < 0.01, except where noted. Error bars = 1 SEM. mPFC = medial prefrontal cortex; OFC = orbitofrontal cortex; IPL = inferior parietal lobule.

We first sought to test whether subcortical valence responses were comparable across feedback conditions. In the Familiar condition, we observed predicted effects of feedback valence in the anterior hippocampus (HC; t-test on neural beta values: t(27) = 5.78, P < 1e−5) and the ventral striatum (VS; t(27) = 4.20, P < 1e−3), in addition to various cortical activations (Supplementary Fig. 2). Both of these subcortical results are consistent with previous findings of reward processing in RL-related circuits (Delgado et al. 2000; McClure et al. 2004; Foerde and Shohamy 2011; Li et al. 2011; Davidow et al. 2016; Palombo et al. 2019). Crucially, in the held-out Single-shot condition, valence responses were observed in both the hippocampal (t(27) = 3.16, P = 0.004) and VS (t(27) = 4.51, P < 1e−3) ROIs defined from the Familiar condition valence response (Fig. 3B). Moreover, whole-brain contrasts revealed no clusters (cortical or subcortical) with significant differences in valence responses between conditions (Supplementary Fig. 2). These results suggest that rapid endowment of value to a novel, Single-shot feedback stimulus leads to valenced responses in the same regions of the brain that show sensitivity to conventional reinforcers.

We hypothesized that if the brain’s reinforcement system is harnessed to learn from novel outcomes, the same computational latent variables should be present in both feedback conditions. The value of the selected choice stimulus (termed “Q-values” in standard RL models) typically correlates with activation in the medial frontal cortex (Bartra et al. 2013). In the Familiar condition, we observed the predicted Q-value coding in a ventral–rostral region of medial prefrontal cortex (mPFC; t(27) = 4.26, P < 1e−3; Fig. 3A). Consistent with our predictions, we observed significant Q-value coding in this same mPFC ROI in the held-out Single-shot condition (Fig. 3B; t(27) = 2.90, P = 0.007). This result implies that comparable computational processes are involved in modifying value representations through both familiar rewards and novel outcomes, and using those values to guide decisions.

Reward prediction errors (RPEs) drive reinforcement learning and have robust neural correlates in multiple brain regions. In the Familiar condition, we observed significant RPE-linked activity in various regions (Fig. 3A and Supplementary Fig. 2), notably in a frontal ROI that included regions of bilateral orbitofrontal cortex (OFC, with some overlap in the insula; t(27) = 5.49, P < 1e−5), a second cortical ROI spanning bilateral portions of the inferior parietal lobe (IPL; t(27) = 4.98, P < 1e−4), and a bilateral ROI in dorsomedial striatum (DMS; t(27) = 3.99, P < 1e−3). These ROIs are consistent with findings from previous studies modeling the neural correlates of prediction errors (Daw et al. 2011; Garrison et al. 2013).

We observed significant effects in the two cortical RPE ROIs localized in the Familiar condition when analyzing the held-out Single-shot condition (Fig. 3B; SPL: t(30) = 3.33, P = 0.003; OFC: t(30) = 4.06, P < 1e−3), further supporting the idea that comparable computational mechanisms drove learning in both feedback conditions. Moreover, whole-brain contrasts revealed no significant differences in RPE processing between the conditions (Supplementary Fig. 2). However, contrary to our prediction, the RPE response in the dorsomedial striatum ROI, while numerically positive on average, was not significantly greater than zero in the Single-shot condition (Fig. 3B; t(30) = 1.17, P = 0.253). Control analyses using slightly different striatal ROIs also failed to reach significance (Supplementary Fig. 3). We note that this analysis of RPE-related activity is particularly conservative because the RPE regressor is included in the same model as—and thus competes for variance with—the outcome valence regressor. Consequently, significant activity in this analysis must reflect parametric RPE encoding beyond the effect of outcome valence.

To further probe if striatal RPEs were detectable in the Single-shot condition, we opted to take a cross-validated encoding-focused approach (see Methods for details). If the computations underlying RPEs in response to familiar rewards are mirrored during learning from novel outcomes, we should be able to decode goal RPEs in the striatum using a model trained on the Familiar condition data. We extracted feedback-locked betas for each individual trial of the learning task (from voxels in the striatal RPE ROI) and restricted our analysis to rewarded trials only. For each Familiar condition run, we trained linear models separately for each voxel, computing the ability of the feedback response amplitude to explain variance in the model-derived RPEs. RPEs were then decoded from the held-out BOLD data for both Single-shot and Familiar condition runs and compared with the associated held-out model-derived RPEs for those same runs.

Cross-validated RPE encoding (Fig. 4) was observed within-condition across-runs (t(27) = 3.31, P = 0.003), between-condition within-run (t(27) = 6.39, P < 1e−5), and between-condition across-runs (t(27) = 2.34, P = 0.027). We emphasize that the regression models used for the encoding analyses were trained on Familiar runs only, providing a stringent test for RPE encoding in the Single-shot condition. These results suggest that novel outcome prediction errors are represented in the same format as typical reward prediction errors in the dorsomedial striatum. However, we caution that these results were not mirrored in the conventional GLM analysis (Fig. 3B). This discrepancy suggests that novel outcome RPE signals in the DMS may be relatively weaker (or noisier) than familiar reinforcer RPE signals, consistent with our observation of slower learning in the Single-shot condition. However, we do note that Single-shot condition RPE signals in the frontal and parietal ROIs were statistically robust (Fig. 3B).

Figure 4 .

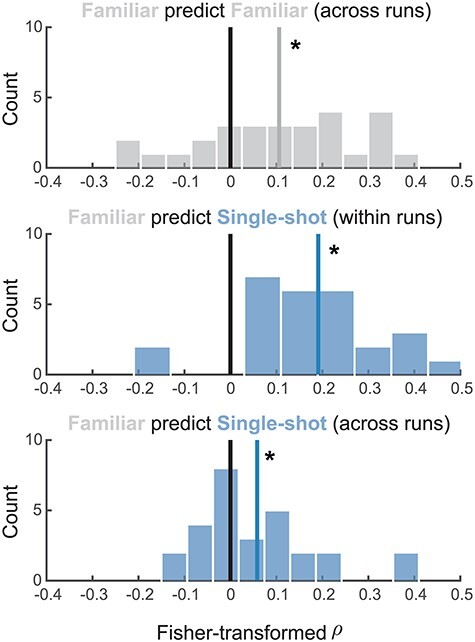
Cross-validated reward prediction error analysis. Regression analyses were run to decode model-derived RPEs from activation in dorsal striatal voxels in the Familiar condition. We used the resulting regression weights at each voxel to generate predicted trial-by-trial RPEs for the held-out runs both within and between conditions. Plots depict the distribution of correlation coefficients between predicted RPEs (derived from BOLD data) with model-derived RPEs. ^*P < 0.05.

Novel Outcome Learning Drives Increased Frontal–Striatal and Frontal–Hippocampal Functional Correlations

Our second key hypothesis was that executive prefrontal cortex (PFC) regions encode and maintain informative novel outcomes and interact with reward circuits so that those outcomes can act as reinforcers at feedback. Specifically, we predicted greater functional correlations between these networks during novel outcome versus reward-driven learning, with PFC activity during the encoding of novel outcomes covarying with reward system activity at feedback. To test this, we needed to specify an executive function prefrontal ROI. We first computed a whole-brain group-level map of neural regions that were parametrically modulated by load (“N”) in the independent n-back task (Supplementary Fig. 4). We extracted the significant PFC cluster from that analysis, which spanned regions of the precentral gyrus, middle frontal gyrus, and inferior frontal gyrus (Yeo et al. 2015). Then, for each subject, we computed a leave-one-out functional ROI using the Single-shot > Familiar contrast from the prechoice phase (Supplementary Fig. 2), masking those results with the aforementioned n-back PFC map (see Fig. 5A for an example PFC ROI). For subcortical areas, we used the three ROIs gleaned from GLM 1 (Fig. 3A; VS and hippocampal valence-based ROIs, and the DMS RPE-based ROI).

Figure 5 .

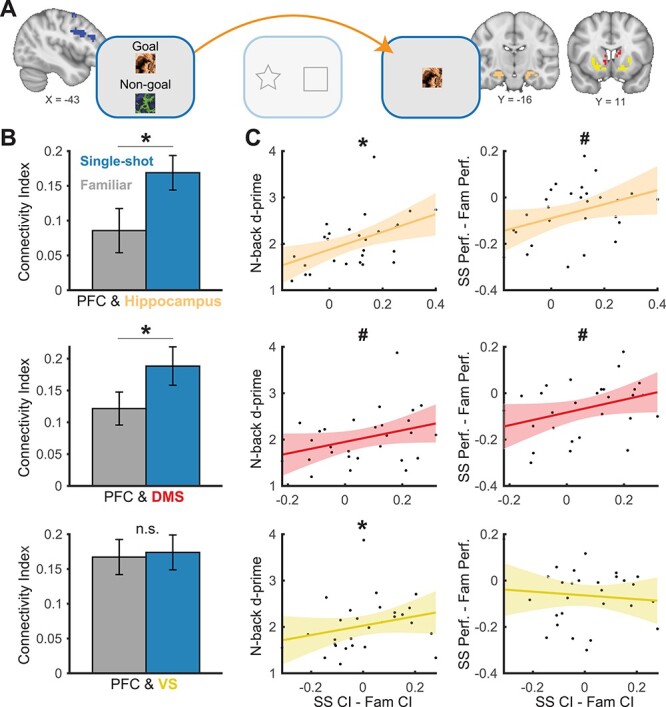
Functional correlations across brain regions and trial phases. (A) Functional correlations were computed between PFC activity during the prechoice phase and feedback-locked hippocampal and striatal activity (dorsal and ventral) on rewarded trials. (B) Within-subject functional correlation results. (C) Between-subject correlations relating differences in connectivity between conditions, and both n-back performance (left column) and learning task performance (right columns) as a function of condition. CI = connectivity index; SS = Single-shot feedback condition; Fam = Familiar feedback condition; PFC = prefrontal cortex; DMS = dorsomedial striatum; VS = ventral striatum. Shaded regions connote 95% confidence intervals. ^#P < 0.10; ^*P < 0.05.

As predicted, we found stronger functional correlations in the Single-shot condition between PFC activity during encoding and both reward (hippocampus) and RPE-related (DMS) areas at feedback (Fig. 5B; PFC-hippocampus, t(27) = 3.01, P = 0.006; PFC-DMS, t(27) = 2.36, P = 0.026). We observed no significant condition difference in PFC-VS functional correlations (t(27) = 0.25, P = 0.81). These results suggest that encoding of desirable outcomes in the PFC may drive downstream reward signals in subcortical structures when those outcomes are attained.

One alternative explanation for this result is that elevated attention or vigilance in the Single-shot condition’s prechoice phase could drive higher global activity across multiple brain regions that persists into the feedback phase. First, we note that the null PFC-VS result (Fig. 5B) speaks against this global confound. Nonetheless, we controlled for this possibility by performing the above connectivity analysis in two additional regions that have been shown to respond to rewards, the posterior cingulate cortex (PCC; McDougle et al. 2019; Pearson et al. 2011) and thalamus (Knutson et al. 2001). We did not expect these ROIs to contribute significantly to the hypothesized novel outcome learning processes. Indeed, there were no significant effects of feedback condition for PFC functional correlations with either the PCC (Supplementary Fig. 5; t(27) = 0.71, P = 0.48) or the thalamus (Supplementary Fig. 5; t(27) = 0.97, P = 0.34), rendering a global attentional account of our results unlikely.

The observed connectivity results also appeared to be uniquely related to PFC processing during the encoding of goal stimuli (the prechoice phase), rather than PFC activity during the feedback phase: We observed no significant differences between Single-shot versus Familiar functional correlations between feedback-locked PFC activity and feedback-locked hippocampal, DMS, or VS activity (all Ps > 0.47). Thus, our results did not appear to be driven by heightened PFC activity that persisted throughout Single-shot trials, but specifically related to the initial encoding of desirable outcomes (presumably in PFC) and subsequent outcome-related responses (in subcortical reward regions).

We reasoned that connectivity between executive and reward regions would also be related both to executive functioning itself (n-back performance) and, critically, to learning. Indeed, differences between PFC and hippocampus connectivity strength in the Single-shot versus Familiar condition were significantly correlated with n-back performance (ρ = 0.56, P = 0.002) and marginally correlated with Single-shot versus Familiar condition learning differences (ρ = 0.37, P = 0.052; Fig. 5C, top row). Moreover, the degree of difference between PFC and DMS connectivity strength in the Single-shot versus Familiar condition was marginally correlated with both n-back performance (ρ = 0.33, P = 0.090) and condition learning differences (ρ = 0.33, P = 0.088; Fig. 5C, middle row). We also observed a significant correlation between the difference between PFC and VS connectivity in the Single-shot versus Familiar condition and n-back performance (ρ = 0.38, P = 0.046; Fig. 5C, bottom row), but not learning differences (ρ = 0.10, P = 0.62). We note that although the connectivity results were robust in our within-subject contrasts (Fig. 5B), the mostly trend-level between-subject correlation effects (Fig. 5C) should be interpreted with caution. However, taken as a whole, these results suggest that top-down cortical processes may rapidly shape downstream reward responses to flexibly map outcomes to successful actions and promote adaptive decision-making.

PFC Interactions with Dopaminergic Regions for Learning from Novel Outcomes

In addition to the planned analyses, we also performed an additional exploratory, a posteriori analysis to examine interactions between PFC and the ascending dopaminergic system. To test this, we examined functional correlations between our PFC ROI and an anatomically defined ventral tegmental area (VTA) ROI (Murty et al. 2014), the main source of the brain’s mesolimbic and mesocortical dopamine (Fig. 6).

Figure 6 .

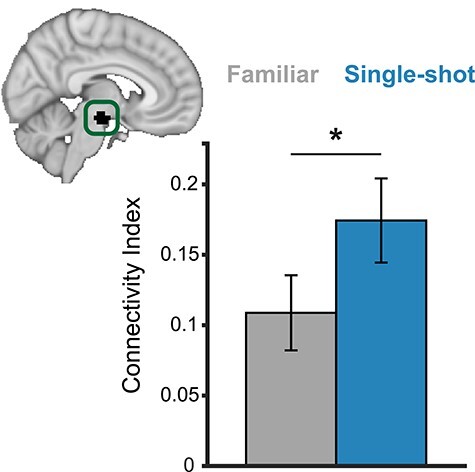
Functional correlations between PFC and the VTA. Functional correlations between PFC activity during the prechoice phase and feedback-locked ventral tegmental area (VTA) activity on successful trials. Inset: anatomical VTA ROI used in the analysis (shown in black). ^*P < 0.05.

Functional correlations between PFC (during prechoice) and VTA (during feedback) were significantly higher in the Single-shot condition relative to the Familiar condition (Fig. 6; t(27) = 2.31, P = 0.029). These effects were unique to PFC activity during the prechoice phase: Correlations between feedback-locked PFC activity and feedback-locked VTA activity were not significantly different between conditions (t(27) = 0.25, P = 0.80). However, we did not observe significant brain–behavior correlations—PFC-VTA connectivity differences between conditions did not correlate with n-back performance nor learning differences (P’s > 0.60). Taken together, these results offer preliminary evidence that single-trial learning from novel outcomes might involve PFC interactions with dopaminergic neurons (Ballard et al. 2011; Sharpe et al. 2019).

Discussion

Here, we presented evidence that learning via novel choice outcomes is behaviorally similar to learning via familiar secondary reinforcers. This type of learning appears to rely on highly similar activation of reward circuitry: We found overlapping neural responses to Single-shot novel outcome attainment and Familiar reward attainment with respect to outcome valence, suggesting that novel stimuli can substitute as rewards during instrumental learning. During choice, value representations were similar between conditions, supporting the idea that learning mechanisms were shared. Similarly, reward prediction errors, the key teaching signal of reinforcement learning, appeared to be similar between the Single-shot and Familiar reward conditions, especially in cortical regions. Lastly, successful performance in the Single-shot condition was associated with increased connectivity between prefrontal cortical regions implicated in executive control and subcortical reward circuits. Together, these findings are consistent with executive function enabling an arbitrarily flexible reward function for corticostriatal reinforcement learning (Daniel and Pollmann 2014).

The crucial feature of our experimental design was the fact that the nonfamiliar outcomes (i.e., fractal stimuli) were novel on every Single-shot condition trial. Thus, for subjects to learn in this condition, they had to rapidly endow value to these transient stimuli (Cole et al. 2013). How does a never-before-seen stimulus get rapidly imbued with value? We propose that a novel stimulus can be internally defined as a desirable outcome (e.g., through verbal/symbolic instruction) and thus be endowed with value while held in working memory. With these ingredients, attaining this outcome should then express the key features of a typical reinforcer. Testing this proposal is difficult, though our results provide some evidence in its favor: Performance on an independent executive function task predicted subjects’ ability to learn from Single-shot novel outcomes, even when controlling for task difficulty (Fig. 2D). Moreover, BOLD activity in prefrontal executive regions during encoding of the novel outcomes positively correlated with subsequent responses in the brain’s reward system (Figs 5 and 6).

We note that there is an alternative (and not mutually exclusive) interpretation of behavior in the Single-shot condition: It is possible that instead of prospectively imbuing the novel outcomes with value during encoding, people could retrospectively assign value at feedback via credit assignment. Specifically, subjects could determine if the outcome they receive had been previously mapped onto the desirable “goal” template and then assign credit to the action that produced that outcome. This interpretation echoes recent work suggesting that high-level representations (e.g., cognitive maps) are not only used prospectively for planning but can also be used retrospectively by the model-free RL system for credit assignment of familiar reward stimuli (Moran et al. 2021). Future studies, perhaps using methods with higher temporal resolution (e.g., EEG), may help dissociate these mechanisms by revealing the temporal dynamics of neural activity at feedback. That is, while a prospective valuation model would predict indistinguishable, rapid feedback responses between our conditions, a retrospective credit assignment model would predict more drawn-out processing of novel outcomes.

Important questions remain about the factors that can render a novel outcome stimulus valuable within the brain’s reward system. Good performance in the Single-shot task might require intrinsic motivation (Barto 2013), where actions are reinforced essentially “for their own sake.” Although the novel outcome stimuli were extrinsic visual cues, the motivation to learn from them in the first place—even though they lacked any prior value—could simply reflect a desire to follow the experimenter’s instructions (Doll et al. 2009), a social learning process that is reinforced over development. Interestingly, a previous study found that dopaminergic medication can boost a learner’s ability to adhere to new instructions about previously learned neutral stimulus–outcome associations that were only endowed with value after learning (Smittenaar et al. 2012). Our findings are consistent with this result, supporting a role for the dopaminergic system in treating abstract outcomes as rewards via explicit (verbal or symbolic) instructions. Further research could investigate if other independent correlates of intrinsic motivation (Deci 1971) predict one’s ability to learn from novel outcomes and engender flexibility in the subcortical reward system.

Our fMRI results also may speak to the common dichotomy between goal-directed and instrumental components of decision-making (Collins and Cockburn 2020; Dickinson and Balleine 1994; Doll et al. 2012). In our study, we observed essentially overlapping neural signatures for Single-shot novel outcomes and secondary reinforcers, the latter reflecting a conventional form of reward feedback (Fig. 3). Other studies have revealed distinct networks corresponding to two forms of feedback-based learning: For instance, Gläscher et al. (2010) showed that neural signatures of model-based “state prediction errors” (in lateral PFC and the intraparietal sulcus) were physiologically distinct from neural signatures of typical reward prediction errors (in ventral striatum). These signals reflected violations of state transition expectations during a sequence of choices. Gläscher and colleagues’ findings suggest that behavior in our Single-shot condition could, in theory, have been driven by this form of state transition learning. Much like learning a complex trajectory toward a goal, subjects could learn a transition structure between the choice stimuli and the “goal fractal” category of objects without ever needing to rely on “bottom-up” rewards. Our results do not support this interpretation, as we observed engagement of typical reward learning circuits during learning from the Single-shot outcomes. We propose that when outcome states are congruent with the task’s primary goal (as in our study, e.g., choose the correct stimulus), the line between a state prediction error and a reward prediction error might be blurred. Indeed, other studies have revealed similar overlaps between state and reward prediction errors in canonical reinforcement learning circuits (Guo et al. 2016; Langdon et al. 2017).

In contrast to the current study, previous research has highlighted important differences between attaining so-called subgoals versus attaining rewards during hierarchically organized decision-making. For example, Ribas-Fernandes et al. (2011) used a hierarchical task that included a subgoal (pick up a package in a mail delivery simulation) that had to be attained before earning a terminal reward (delivery of the package). The authors observed neural correlates of a “pseudoreward prediction error”, driven by surprising jumps in the location of the subgoal, in regions including the anterior cingulate, insula, lingual gyrus, and right nucleus accumbens. In a separate behavioral experiment, they argued that subgoal attainment was not a reliable proxy for reinforcement. It is possible that a lack of need for protracted learning from subgoals in such studies of hierarchical decision-making (Ribas-Fernandes et al. 2011) may lead to qualitatively different neural responses versus studies like ours, where attaining novel fractals (subgoals) is a requirement for learning.

Our study has several important limitations. First, our task design, where novel stimuli had to be encoded and briefly maintained in short-term memory, may have artificially introduced a dependence on executive function. That is, our task made it somewhat difficult to fully separate effects of learning from novel outcomes from effects of engaging working memory, as both were clearly required. It should be mentioned that even for tasks like the n-back, the striatum shows positive responses on correct detection trials (Satterthwaite et al. 2012), suggesting that performing such tasks correctly provides intrinsic reward. Indeed, we replicated this finding in the current data set (Supplementary Fig. 6). There are, however, cases where a novel outcome could be acted on without requiring working memory: For instance, an outcome could instead be retrieved from episodic memory, such as recalling and acting on an instruction you received hours (or days) in the past. In that case, the medial temporal lobe and medial prefrontal cortex may be involved in maintaining and communicating the features of valuable outcomes to striatal and midbrain circuits (Han et al. 2010). Either way, it is difficult to conceive of a setting where learning from novel outcomes would not carry memory demands, whether short- or long-term.

Second, the precise cause of the poorer performance we observed in the Single-shot feedback condition (Fig. 2A) was not clear. Our modeling analysis appeared to rule out the interpretation that the effect was driven by noise during choice. Although it was apparent that executive function—operationalized by performance in the independent n-back task—was selectively related to learning in the Single-shot condition (Fig. 2D), multiple psychological phenomena could have attenuated performance in that condition. These include a weaker appetitive signal for Single-shot outcomes, or an increased frequency of lapses of attention, where the fractal is either not encoded initially or forgotten by the time of feedback. Future behavioral studies could attempt to fill this gap, for example by testing subjects’ memory of the novel images themselves on intermittent probe trials or in a subsequent long-term memory test. We speculate that understanding the source of this learning difference could reveal important computational constraints on learning from unfamiliar action outcomes.

Third, we found mixed results with respect to striatal RPE encoding in the Single-shot condition (Figs 3 and 4). Surprisingly, our cross-validated encoding analysis (Fig. 4) supported the presence of striatal RPEs in the Single-shot condition, while our more liberal beta calculation showed nonsignificant RPE encoding in the Single-shot condition (Fig. 3B and Supplementary Fig. 3). These inconsistent results could suggest a lack of power or sensitivity, or a true attenuation of prediction errors when they are signaled by stimuli held in working memory. The latter interpretation would be consistent with findings showing a weakening of striatal prediction error signals when working memory is actively contributing to choice behavior (Collins et al. 2017). One approach to address this question could be to induce a wider dynamic range of RPEs, or to better match working memory demands.

Learning from novel outcomes in addition to familiar reinforcers is a key aspect of intelligent behavior and is an especially important cognitive tool for humans. Here, we asked if novel outcomes could stand in for rewards during learning, even when those outcomes are abstract stimuli with no prior meaning or value to the learner and are only observed a single time. We demonstrated that human subjects can easily perform this kind of Single-shot instrumental learning and that it shares many behavioral and physiological features with conventional instrumental learning from secondary reinforcers. The ability to rapidly direct behavior toward the achievement of abstract outcomes has been linked to executive control processes in the human prefrontal cortex (Duncan et al. 1996), an idea that our data further supports. Taken together, our findings suggest that humans can rapidly and flexibly define what constitutes a reinforcer in a single instance, harnessing the brain’s executive functions and reward circuitry to optimize decision-making.

Notes

We would like to thank the CCN Lab (UC Berkeley) and ACT Lab (Yale) for helpful discussions. Conflict of Interest: The authors declare no conflicts of interest.

Funding

National Institute of Mental Health fellowship (F32 MH119797 to S.D.M.); National Institute of Mental Health (grant R01MH119383 to A.G.E.C. and B.B.); National Institute of Mental Health (grant R01MH124108 to S.B.); National Institute of Mental Health fellowship (F32MH119796 to I.B.); Hellman Fellows Fund Award.