Abstract
Introduction:
Achieving health gains from the United Nations Sustainable Development Goals of universal coverage for water and sanitation will require interventions that can be widely adopted and maintained. Effectiveness -- how an intervention performs based on actual use -- as opposed to efficacy will therefore be central to evaluations of new and existing interventions. Incomplete compliance -- when people do not always use the intervention and are therefore exposed to contamination -- is thought to be responsible for the lower-than-expected risk reductions observed from water, sanitation, and hygiene interventions based on their efficacy at removing pathogens.
Methods:
We explicitly incorporated decision-theory into a quantitative microbial risk assessment (QMRA) model. Specifically, we assume that the usability of household water treatment (HWT) devices (filters and chlorine) decrease as they become more efficacious due to issues such as taste or flow rates. Simulations were run to examine the tradeoff between device efficacy and usability.
Results:
For most situations, HWT interventions that trade lower efficacy (i.e., remove less pathogens) for higher compliance (i.e., better usability) contribute substantial reductions in diarrheal disease risk compared to devices meeting current World Health Organization (WHO) efficacy guidelines.
Conclusions:
Recommendations that take into account both the behavioral and microbiological properties of treatment devices are likely to be more effective at reducing the burden of diarrheal disease than current standards that only consider efficacy.
Keywords: Household water treatment, risk assessment, compliance, decision theory, waterborne pathogens
1. INTRODUCTION
Despite substantial global progress across water, sanitation, and hygiene (WASH) programs, diarrheal disease remains the second leading cause of death among children under five (Fuller, Goldstick, Bartram, & Eisenberg, 2016; World Health Organization, 2017). As of 2012, roughly 11% of the population remained without safe drinking water while roughly 36% of the population lacked access to improved sanitation, representing major challenges to the United Nations Sustainable Development Goals target of complete global access to safe drinking water and sanitation (Fuller et al., 2016). Access to these resources is necessary to reduce morbidity and mortality from environmentally transmitted diarrheal disease. However, access alone may not be sufficient. While many promising interventions (e.g. household water treatment devices, latrines, and cook stoves) have been developed, health gains in field trials have often underperformed expectations. For example, modern household water treatment devices are capable of removing or inactivating nearly all pathogens in treated water. However, they have not yielded corresponding reductions in observed infection risk (B. Arnold, Arana, Mäusezahl, Hubbard, & Colford, 2009; Schmidt & Cairncross, 2009; Stauber et al., 2006; Waddington & Snilstveit, 2009). Similarly, a recent randomized trial of latrine construction and promotion demonstrated increased coverage, but no significant reduction in diarrheal disease (T. Clasen et al., 2014; D. G. McNeil Jr., 2014; Schmidt, 2015). Incomplete compliance may be responsible for some of the observed inconsistency between treatment efficacy from small scale trials (B. F. Arnold & Colford, 2007) and population health outcomes. We focus on household water treatment (HWT) interventions to demonstrate the potential impact of compliance on intervention effectiveness.
One complication in addressing HWT compliance is that treatment efficacy may not correlate to end user appeal. Instead, higher treatment efficacies may compromise end-user convenience or device reliability (Waddington & Snilstveit, 2009). For example, chlorine is increasingly detectable by taste as concentrations increase, and can render drinking water unpalatable (Mintz, Bartram, Lochery, & Wegelin, 2001; World Health Organization, 2011b). Water filtration devices can achieve similarly significant pathogen reductions without altering taste, but slow flow rates and clogging can impede adoption and long-term effectiveness (T. F. Clasen, Brown, & Collin, 2006; Murphy, Sampson, McBean, & Farahbakhsh, 2009; van Halem, van der Laan, Heijman, van Dijk, & Amy, 2009). Under these circumstances, the efficacy of a HWT method does not capture its actual capacity to reduce the burden of disease, as a more efficacious treatment device may induce lower compliance and therefore be less effective than a less efficacious but more appealing intervention. HWT efficacy is typically reported as log10-removal values (LRVs) that quantify the amount of pathogen removed from treated water, i.e., the proportion of pathogens remaining after treatment is 10-LRV. LRVs serve as a comparative measure for treatment methods within a given class or between classes. The 2011 World Health Organization (WHO) guidelines for water treatment recommend HWT efficacies of 4 LRV for bacteria, 5 LRV for viruses, and 4 LRV for protozoa in order to attain a “highly protective” standard in generic scenarios where contextual information about exposure levels and the population at risk are not available (World Health Organization, 2011b). Notably, the WHO guidelines assume perfect compliance with the treatment method. However, technological adoption is seldom complete (Rogers, 2010). HWT uptake in particular is variable but rarely widespread in lower income regions (Rosa & Clasen, 2010; Shaheed et al., 2018). More recently, the WHO International Scheme to Evaluate Household Water Treatment Technologies has begun to include usability considerations, but remains primarily focused on the microbiological performance of HWT technologies (World Health Organization, 2016).
To address the interactions between compliance and microbiological efficacy, we develop and analyze a quantitative microbial risk assessment (QMRA) model that includes decision theoretic intervention compliance. QMRA has proven to be a valuable tool to study the health risks associated with pathogen exposure from a variety of pathways as well as evaluating the potential impact of interventions on these pathways. Recent QMRA research has begun to address the impact of compliance on the effectiveness of HWT interventions (Brown & Clasen, 2012; Enger, Nelson, Clasen, Rose, & Eisenberg, 2012; Enger, Nelson, Rose, & Eisenberg, 2013). In particular, these results suggest the existence of diminishing returns in risk reduction for higher LRV. However, these studies did not directly address the causes of variable compliance, or the implications of interactions between efficacy and compliance. By contrast, decision theory models individual choices based on preferences determined by costs and benefits. Decision theory is widely used in economics and other social sciences, and applications to public health have largely focused on cost analysis for institution-level interventions (Fischer et al., 2013; B. J. McNeil & Pauker, 1984). In the context of HWT, it is likely that uptake and compliance are determined by the degree to which an intervention matches individuals’ preferences regarding trade-offs between treatment efficacy and usability. Thus overall compliance depends both on the distribution of user preferences and the specific intervention proposed. In this study, we use our model to investigate the tradeoff between efficacy and compliance on the risk of diarrheal disease. Our model also represents a novel method to integrate techniques from social science into exposure assessment.
2. METHODS
2.1. Quantitative Microbial Risk Assessment (QMRA) model
QMRA provides a framework to evaluate the risk of infection based on environmental and microbiological characteristics. Conducting a QMRA involves the following stages:
Hazard identification -- Characterize the microbiological and epidemiological properties of the pathogen.
Dose response -- Determine the relationship between a dose of pathogen and the probability of infection.
Exposure assessment -- Establish transmission pathways and the average rate of pathogen ingestion.
Risk characterization -- Compute individual or population risks using exposure level and dose response.
Risk management -- Determine strategies for reducing risk to tolerable levels.
QMRA can be implemented using either an analytical or (stochastic) simulation-based approach (Enger et al., 2012, 2013). Using an analytical approach, risk is directly calculated using data for exposure levels. For a stochastic QMRA simulation, risk is estimated from an ensemble of simulation runs. In a given simulation, exposure levels can vary, and infection is determined randomly according to the probability distribution specified by the dose-response function. We use a simulation approach in our analysis of the risk of waterborne infection. We consider three pathogens: Cryptosporidium, enterotoxigenic E. coli (ETEC), and rotavirus representing parasites, bacteria, and viruses respectively. These pathogens were selected due to their impact in developing nations (Kotloff et al., 2013; Platts-Mills et al., 2015; World Health Organization, 2017). In particular, the Global Enteric Multicenter Study (GEMS) found that Cryptosporidium, ETEC, and rotavirus were responsible for the highest attributable fractions of moderate to severe diarrhea in lower income countries, indicating that these pathogens are both prevalent and create a significant burden of disease (Kotloff et al., 2013).
2.1.1. Exposure assessment
For waterborne disease, contaminated drinking water acts as one of the primary transmission pathways, so exposure levels represent the quantity of viable pathogen ingested daily based on the quality of available drinking water. An individual’s daily volume of pathogen ingested is
| (1) |
where w is the concentration of pathogen per liter of untreated water, v is the volume of water consumed per day, and x̂ is the LRV of the specific HWT method implemented. An individual i uses an HWT device (complies) with probability Pr(use)i. The expected dose E[di] across all individuals in a population can then be characterized as:
| (2) |
where E[Pr(use)i] is the average population compliance. On average, individuals are exposed to fully contaminated water when they do not use their treatment device () or reduced pathogen content when they do (). Alternatively, average compliance can be interpreted as the fraction of a given day’s water that is effectively treated. These interpretations yield identical analytical results, but would alter the disease outcomes in an explicit simulation. This approach to exposure assessment is similar to (Enger et al., 2013), however, we choose to model compliance based on an individual’s attitude toward the specific implemented HWT, by developing a decision-theoretic model defined in Section 2.2.
2.1.2. Dose-response
The probability of infection per organism depends on interactions between the pathogen and the host immune system. Empirically, infection events can be modeled using a dose-response function fit to experimental data. We use an exponential or approximate beta-Poisson dose-response function to compute the daily probability of infection for a given quantity of pathogen. Specifically, we use an exponential dose-response function for the probability of infection by Cryptosporidium and a beta-Poisson function for E. coli and rotavirus (Table 1). Both of these functions assume that a single pathogenic organism has a non-zero probability of causing an infection, essentially treating infection as the outcome of Bernoulli trials. The exponential dose-response function is
| (3) |
with rate parameter k. Mechanistically, this function implies that the dose is Poisson distributed and that each unit of pathogen has an identical probability of surviving to reach the target site (k−1) and of causing an infection.
Table 1:
Dose-response functions and recovery time distributions for each pathogen. The average time to recovery for a gamma distribution is the product of the shape and scale parameters. For an exponential distribution the average time is equal to the scale parameter.
| Pathogen | Dose-Response | Dose-Response Parameters | Recovery Distribution | Recovery Parameters |
|---|---|---|---|---|
| Cryptosporidium | Exponential (Messner et al. 2001) | k = 5.72 × 10-2 | Gamma | shape = 4, scale = 2.5 |
| E. coli(ETEC) | Beta-Poisson (DuPont et al. 1971) | α = 0.155, N50 = 2 × 106 | Gamma | shape = 1.775, scale = 1.69 |
| Rotavirus | Beta-Poisson (Ward et al. 1986) | α = 0.253, N50 = 6.17 | Gamma | shape = 1, scale = 5.2 |
An exact beta-Poisson function can be computationally unstable due to its use of the confluent hypergeometric function. As a result, the approximate form is often used instead.
| (4) |
| (5) |
where controls the slope and N50 is the dose required to infect 50% of a population. This approximation is appropriate when and which are satisfied by our parameter values for E. coli and rotavirus (Table 1). The mechanistic interpretation of the beta-Poisson model is similar to that of the exponential model, however in this case the probability that a pathogen survives to infect (i.e., infectivity) is assumed to be given by a beta distribution. The choice of dose-response function is typically made based on both biological and statistical considerations. We use the exponential dose-response function for Cryptosporidium (Messner, Chappell, & Okhuysen, 2001). while the beta-Poisson dose-response function is used to characterize E. coli (DuPont et al., 1971) and rotavirus (Ward et al., 1986).
2.2. Decision-theoretic compliance
To accommodate variable individual compliance in a QMRA framework, we construct the following decision-theoretic model that determines the distribution of individual compliance based on attitudes toward recommended HWT levels. Given the limited data on the functional relationship between attitude and HWT levels we use functions that are heuristically derived.
Suppose we have individuals who each select a probability of compliance Pr(use)i with a treatment device chosen from the intervention space . This space represents the range of possible HWT levels quantified by their LRV. We assume that an individual’s attitude toward HWT properties map to the LRV of any given treatment method (since both the advantages and drawbacks of a given method are correlated with the LRV). That is, each individual has a most preferred LRV denoted . We will refer to the distribution of these points as the preference distribution. The shape of the preference distribution characterizes a population’s disposition toward potential HWT interventions; i.e., a population with many individuals who prefer low LRV will be more resistant to high efficacy devices than a population with higher average LRV preferences. For our analysis we assume that preferences are distributed according to a truncated normal distribution with mean and variance , bounded by [0,6] (the range from no intervention to the highest current recommendation). We use x̂ to refer to a hypothetical intervention that has been provided to the population in question. Based on this model, an optimal intervention is a function a device’s microbiological efficacy (LRV) and the aggregate of individual preferences for efficacy. By contrast, most current HWT evaluations are based on a device’s microbiological characteristics.
Based on this framework we define the following decision problem: Given their preferred LRV, individuals choose the degree to which they comply with the specific HWT intervention provided. As noted above, this choice is over the probability of compliance as opposed to the binary choice of compliance on a specific day. This is because we assume that conditions informing compliance do not change enough between days to alter an individual’s choice. Instead, individuals choose Pr(use)i when the intervention is implemented and draw their daily compliance accordingly, analogous to a mixed strategy in game theory. To represent this problem we construct a utility function, ui, which represents an individual’s preferences regarding compliance with the intervention x̂. In particular, we use the following negative quadratic form:
| (6) |
where represents the “distance” between intervention x̂ and individual i’s most preferred intervention xi (we refer to as the distance function). Note that a larger distance indicates a less appealing intervention. Qualitatively, Equation 6 reflects that individuals prefer to comply with devices that are more appealing to them (E.g. if and . Conversely, individuals prefer to not comply with devices that are not appealing. Equation 6 is meant to be a phenomenological representation of user preferences for devices in order to demonstrate our method. Additionally, a negative quadratic utility function is analytically appealing, as it is guaranteed to have a unique maximum. However, other functional forms could be chosen based on additional information regarding intervention end user behavior.
The shape of the distance function may depend on prior knowledge of how individuals compare HWT alternatives. We use two different functions to characterize different potential situations. The first function is the squared Euclidean distance
| (7) |
where min(X) and max(X) are the lowest and highest feasible LRVs, respectively. This distance function implies that individuals dislike treatments that are either more or less efficient than their ideal preference. Chemical treatment such as chlorination may be an example of an intervention for which individuals apply a symmetrical distance function. This may be because an individual who prefers some level of chlorination would be unwilling to treat their water at levels that they do not perceive as effective (lower LRV than preferred), and may not want to treat at high concentrations due to taste issues (B. F. Arnold & Colford, 2007; World Health Organization, 2011a).
Alternatively, we can use an asymmetrical piecewise distance function
| (8) |
Unlike for chlorination, this variant implies that individuals dislike LRVs greater than their ideal point, but view lower LRVs as equally favorable. This asymmetry may be appropriate for filtration methods, where individuals may not distinguish between a lower LRV device and the recommended treatment level, especially if changes in the aesthetic qualities of the filtered drinking water do not vary between devices. They may begin to become non-compliant, however, with a high LRV filter due to slow water flow or increased breakage rate. If X is normalized to the [0,1] interval, the above equations simplify to
| (9) |
and
| (10) |
Note that the steepness of our distance functions determines the degree to which individuals dislike less favorable interventions. While not explicitly included in the above equations, this could be tuned as an additional parameter by scaling the quadratic term in either distance function if appropriate data is available.
Decision theory requires that individuals will choose actions that maximize their utility.(Tadelis, 2013) The inner term of Equation 6 implies that when the provided intervention is not appealing, utility is maximized by adopting a low probability of compliance. By contrast, when an intervention is appealing, utility is maximized by adopting a high probability of compliance. Thus, maximizing Equation 6 with respect to Pr(use)i results in the following probability of compliance:
| (11) |
To account for the fact that an individual will never comply perfectly even with their most preferred HWT intervention, Equation 11 can be modified using a scaling factor as follows:
| (12) |
where cmax is the maximum possible compliance. The inclusion of cmax does not impact our estimates of optimal interventions but does have an impact on our risk estimates. In particular we would expect a lower cmax to attenuate the risk reduction for any intervention. This is because risk responds monotonically to compliance for a given intervention level, so lowering the maximum compliance probability acts as an offset.
2.2.1. Applying the decision theoretic model to household water filtration
Household water filters include a range of specific technologies including biosand (Elliott, Stauber, Koksal, DiGiano, & Sobsey, 2008), and ceramic (Oyanedel-Craver & Smith, 2008) devices. Filter types vary with respect to their filtration efficacy for viral, bacterial, and protozoan parasites as well as properties such as flow rate, capacity, and durability. While individuals facing endemic diarrheal disease are likely to value improved pathogen removal, the usability of a filter may significantly influence whether an individual is willing to treat their drinking water. Filters that are more efficient may have reduced usability as smaller pores decrease the flow rate and are more likely to clog. As a result, attitudes toward filters may become less favorable as efficacy increases, especially once the usability of a filter becomes unacceptable. However, filters below that acceptability threshold may be equally acceptable, given that individuals may not explicitly evaluate the LRV so long as a filter reduces apparent risk.
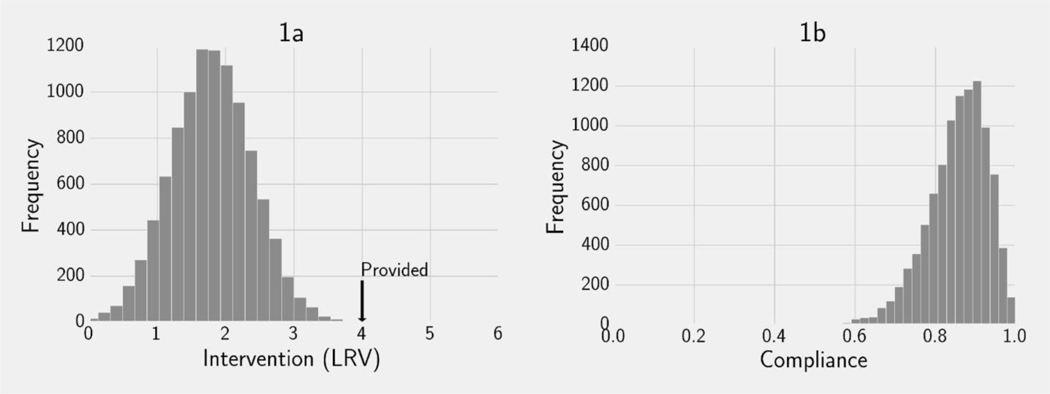
We illustrate our decision-theoretic approach using this context. To this end, suppose we have a population in which preferences regarding filter efficacy (xi) are normally distributed with a mean of 2 LRV (Figure 1a), and that we wish to determine the distribution of compliance if a 4 LRV filter (x̂) is provided. For this example, we assume that filters may have a minimum LRV of 0 and a maximum LRV of 6. Individuals select their compliance level with the 4 LRV device (Pr(use)i) based on Equation 12 using the asymmetric distance function, where x̂ = 4 LRV, and cmax= 1. All else equal, this function implies that individuals dislike filters more efficient than their ideal point but are ambivalent about filters as efficient or less. As a result, we are able to determine the distribution of compliance with the provided filter (Figure 1b). In this case, our model predicts an average compliance of approximately 85%.
Figure 1.
An example of our decision-theoretic framework. 1a: The frequency distribution of preferences for interventions (xi) represented by their LRV in a simulated example population. In this example the minimum LRV is 0, the maximum LRV is 6, and a 4 LRV treatment device has been provided (). 1b: The frequency distribution of compliance among the simulated population (Pr(use)i) determined by solving Equation 11 using an asymmetrical distance function with .
2.3. Optimizing HWT interventions
When we assume perfect compliance, we can always compute the treatment level (efficacy) necessary to obtain a given risk threshold. With incomplete compliance, however, it is possible that no feasible treatment level will reduce risk below current acceptable disease burden standards; i.e., increasing non-compliance decreases the effectiveness of an intervention. When we account for incomplete compliance, therefore, it is important to consider the optimal treatment level that will reduce infections the most relative to baseline conditions. Effective interventions from this perspective must take into account both the microbiological characteristics of the device and behavioral features of potential users. We define an optimal intervention as the LRV that most reduces risk subject to a tradeoff between compliance and device efficacy. Formally, this problem can be stated as follows:
| (13) |
Where means that we search for the intervention x̂* that minimizes the average probability of infection -- a function of the intervention level x̂ and other parameters θ (i.e. the dose response function). This procedure is equivalent to solving a game-theoretic model in which a policy maker first selects an intervention and individuals then choose their compliance probabilities (Appendix B). Conveniently, when the dose response function is monotonic, the optimal intervention can be found by minimizing the function representing the expected dose (Equation 2). Notably, this means that the solution does not depend on pathogen or exposure characteristics beyond the effect of treatment. We illustrate this framework by computing numerical solutions to Equation 13 assuming normally distributed preferences. Appendix A describes our procedure in detail.
2.4. Risk Simulation framework
We simulate a population of size N for T days. Each day healthy individuals may become infected based on their exposure level and probability of infection. Sick individuals recover based on times drawn from a gamma distribution. Table 1 describes the specific dose-response and recovery models used for each pathogen.(Enger et al., 2013) Gamma distributions characterize the expected time to recovery for diseases with multiple infectious stages assuming a Poisson process. When represented by an integer, the shape parameter denotes the number of stages. In the case where the shape parameter is one, the gamma distribution is equivalent to an exponential distribution. For Cryptosporidium and E. coli, gamma distribution parameters were drawn from existing literature on the infectious period of each disease (Eisenberg, Seto, Colford, Olivieri, & Spear, 1998; Estrada-Garcia et al., 2009). Because less data is available for rotavirus we chose a gamma distribution with an average waiting time equal to the median recovery time of 5.2 days (Gurwith, Wenman, Hinde, Feltham, & Greenberg, 1981) and a shape parameter of one. We implemented our models and analyses in Python 2.7 using Numpy, Scipy, and Matplotlib (Hunter, 2007; Jones E, Oliphant T, Peterson P, Others, 2001).
3. RESULTS
3.1. The effect of imperfect compliance
We simulate the disease burden of our three reference pathogens. For each pathogen type, we simulated our stochastic QMRA model for 1 year and computed the average yearly disease burden. Our simulations are largely consistent with the scenarios defined in the original WHO guideline analysis. For example, we assumed perfect compliance, water treatment interventions meeting the 2011 WHO Guidelines (4 LRV for bacteria/protozoa and 5 LRV for viruses), and a target disease burden of 10−6 DALY/year. Similarly, our assumptions about pathogen contamination levels, water consumption, and individual burden of disease are drawn from the methods used in the Guidelines.
Our approach differed in three ways. First, the original WHO analysis used Campylobacter Jejuni, Cryptosporidium, and rotavirus as reference pathogens. As noted above, we used data from the GEMS (published after the Guidelines) to select reference pathogens resulting in our choice of ETEC over Campylobacter. Second, our model used dose-response functions and expected recovery times specified in Table 1 for each reference pathogen. These functions have been derived from previous experimental studies. The original WHO analysis assumed linear dose-response relationships, which is likely to match our simulations for lower doses (Brouwer, Weir, Eisenberg, Meza, & Eisenberg, 2017). Third, for rotavirus, the original WHO analysis presented results corresponding to the disease burden in high income countries (low income disease burden was presented in a supplement) while we used a burden of disease corresponding to low-income countries, which reflects higher mortality in countries that will receive the greatest potential benefit from the SDGs and which have lower rotavirus vaccination coverage. Like the WHO analysis, E. coli and Cryptosporidium DALYs were only derived for developed countries.
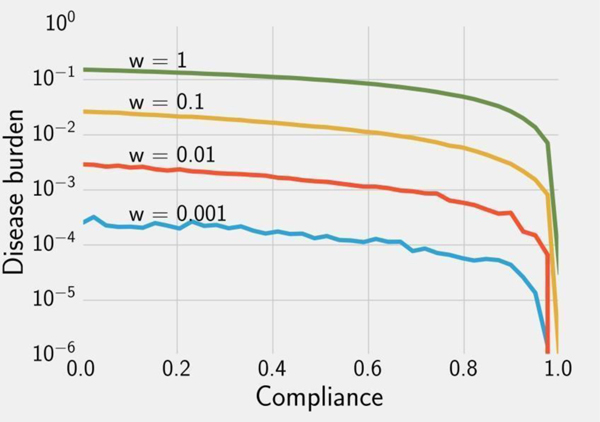
With perfect compliance, our simulations for E. coli and Cryptosporidium correspond to the WHO analytical results for bacteria and protozoa (Table 2), indicating that in the ideal case, 4 LRV treatment would reduce the burden of disease below the target threshold. Due to rotavirus’ higher burden of disease in low income countries, the 5 LRV treatment did not reduce the overall simulated disease burden below the threshold level. Next, we relax the assumption of perfect compliance for Cryptosporidium (similar results for E. coli and rotavirus can be found in the supplementary material). At all contamination levels, greater than 99% compliance is necessary to reach the WHO target (Figure 2). This finding is a consequence of two factors. The 2011 guidelines were determined by solving for the lowest efficacy that resulted in a tolerable disease burden, so we would not expect a less efficacious intervention to meet the threshold. Additionally, individuals face substantially higher disease risks whenever they do not use their treatment device, causing disease burden to be very sensitive to compliance. While the largest changes occur between compliance levels of 80–100%, substantial health gains are predicted for more modest improvements in compliance. For example, at 1 oocyst/L, if compliance increases from 20% to 60%, the disease burden decreases from 0.134 DALY/year to 0.0827 DALY/year, a 38% reduction.
Table 2:
Simulated disease burden estimates for three waterborne enteric pathogens at 6 LRV with complete compliance.
| E. coli (ETEC) | Rotavirus* | Cryptosporidium | |
|---|---|---|---|
|
| |||
| Organisms/L | 1 × 103 | 1 | 0.1 |
| Daily water consumption (L) | 1 | 1 | 1 |
| Treatment efficacy (LRV) | 4 | 5 | 4 |
|
| |||
| DALY/person | 5.47 × 10-2 | 0.482 | 1.47 × 10-3 |
| Prevalence/year | 2.92 × 10-4 | 1.36 × 10-2 | 2.26 × 10-3 |
| Disease burden (DALY/person-year) | 1.59 × 10-5 | 6.54 × 10-3 | 3.32 × 10-6 |
|
| |||
| Tolerable threshold (DALY/person-year) | 1 × 10-6 | 1 × 10-6 | 1 × 10-6 |
Rotavirus assumes 6% population at risk in a low income country.
Figure 2.
Simulated disease burden estimates for Cryptosporidium given expected doses calculated using Equation 2 for v = 1L/day, varying contamination concentrations (), and varying compliance with a 4 LRV device (Pr(use)i). A population of 5000 was simulated until equilibrium using the exponential dose-response function (Equation 3) and gamma-distributed recovery times (Table 1).
Note that the target threshold of 10−6 DALY/year implies extremely low endemic prevalence based on analytical QMRA. This is impossible to verify in practice due to the large population size required to detect any cases once the risk of infection is sufficiently low. Our stochastic model results in this phenomenon -- many simulations with near-perfect compliance had zero cases. As a result, although the disease burden for incomplete compliance is higher than the 10−6 DALY/year threshold, contamination levels of 0.01 and 0.001 oocysts/L cause a very small absolute number of cases on average.
3.2. Optimal interventions
3.2.1. Case study
We use a hypothetical water filter trial to demonstrate our optimal intervention framework when data on intervention compliance is available. For simplicity, we assume that the variance of compliance is not available. First, we calculate the average LRV preference E[xi] by solving Equation 12:
| (14) |
where cmax is the maximum compliance. We use the negative square root since our model for filters assumes an asymmetric distance function, which implies that incomplete compliance is generally a product of an intervention that is more efficacious than the average user preference. For our scenario, we assume that the maximum compliance level, cmax = 0.9, the highest possible treatment efficacy max(X) = 6 LRV, the lowest possible treatment efficacy min(X) = 0 LRV. We also assume that when given a 6 LRV filter participants do not use their device 20% of the time on average, and the average observed compliance level E[Pr(use)i] = 0.8. Plugging these values into Equation 14 results in an average preference E[xi] = 4 LRV. We then solve Equation 13 numerically to obtain the optimal intervention x̂* = 4 LRV, the same value as the average user preference. Therefore, by knowing the maximum compliance level and percent compliance for a given device, we can obtain a recommendation that suggests a 4 LRV device would be more effective than the initial 6 LRV device implemented. With more information, such as a variance estimate of the compliance distribution we could obtain a more precise estimate. While this example is highly artificial, it is intended to demonstrate that our approach can flexibly address multiple questions related to HWT compliance and intervention effectiveness.
3.2.2. Selecting HWT based on user preferences
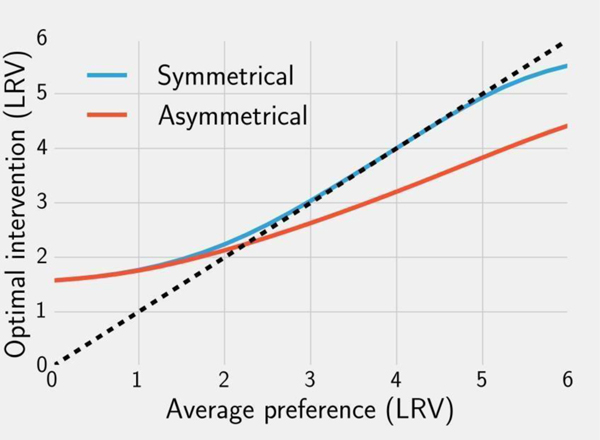
We now consider a more general case where compliance is not known but end user preferences regarding device efficacy could be estimated (e.g. stated preference surveys). In these analyses, we examine the optimal interventions for a range of possible preference distributions. Simulating a filter intervention, we assume that individuals have an asymmetrical distance function, i.e., users accept LRVs lower than their preference but are less likely to use filters that have higher LRV than their preference (Equation 8). Based on these assumptions optimal LRVs for filters tend to be higher than the average user preference when the average is low and tend to be lower than the average preference when the average preference is high (Figure 3). The transition point occurs at approximately 2 LRV. This can be seen by comparing the solution line with the dashed line indicating an intervention set at the mean of the preference distribution (Figure 3).
Figure 3.
Numerical solutions to Equation 13, i.e. optimal interventions given average population preferences μ assuming normally distributed preferences with variance . Solutions are shown using a symmetrical (blue) and asymmetrical (red) distance function. The dashed line indicates whether the optimal intervention for a given μ is higher or lower than that value.
For a chlorination intervention we assume that the distance function is symmetrical -- individuals are less likely to treat their water if the treatment LRV is either higher or lower than their preference. Like filtration, the optimal LRV for chlorination is higher than the average preference when the average preference is below 2. However, between 2 and 5 LRV optimal chlorination tracks the average preference. Above an average preference of 5 LRV the optimal value is slightly below the average user preference.
The symmetrical distance function results in higher optimal LRV interventions than the asymmetrical measure for distributions with an average preference above 2 LRV. This is because with the asymmetrical function compliance with lower LRV devices is generally high. This is not true for a symmetrical distance function. Consequently, overall compliance with any intervention under these conditions is higher than in the case where individuals also dislike less efficient treatments.
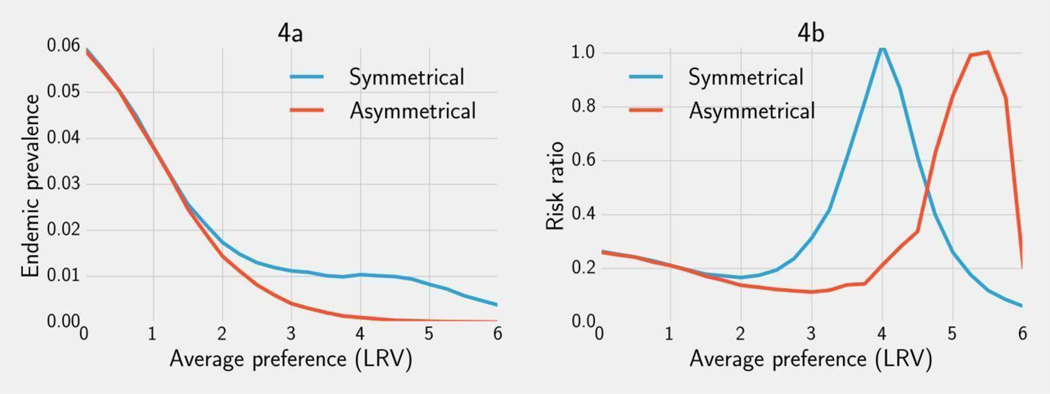
3.2.3. Risk reduction
As the average LRV preference increases, the optimal intervention becomes more effective at decreasing prevalence for both chlorination and filtration (Figure 4a). This relationship becomes more dramatic for average preferences between 1 and 2 LRV. Beyond this point, the effectiveness of chlorination plateaus while optimal filtration continues to reduce risk for populations with greater average preference. In both cases, optimal interventions are generally more effective than the implemented 4 LRV device (Figure 4b). For chlorination, the only exception is if the average preference is at 4 LRV; then the optimal intervention is also at 4 LRV (Figure 3). For filtration, the exception occurs closer to 5.5 LRV at which point the optimal intervention is 4 LRV (Figure 3). Simulations for E. coli and rotavirus can be found in the supplementary material (Figures S1, S2). While specific values differ, the qualitative features of the absolute and relative risk curves do not vary substantially by pathogen.
Figure 4.
4a: The simulated endemic Cryptosporidium prevalence when the optimal intervention from Figure 3 is implemented. 4b: The risk ratio comparing the optimal intervention vs. the current 4 LRV guideline for Cryptosporidium across a range of LRV preferences (4b). Results are shown for both an asymmetric and symmetric distance function. Endemic prevalence was calculated for a simulated population of 10,000 after one year using a contamination concentration w = 1 oocyst/L, volume v = 2L/day, and dose response and recovery parameters given in Table 1
4. DISCUSSION
Current HWT guidelines have been developed using QMRA assuming perfect compliance and focus on microbiological performance (World Health Organization, 2011a). As a result, recommended treatment devices favor high LRV capabilities. However, these recommendations become problematic if compliance is inversely related to efficacy. In fact, uptake of HWT in developing countries has been documented to vary from 13–67% (Rosa & Clasen, 2010). It is important, therefore, to characterize the causes and impact of non-compliance with HWT. Recent QMRA analyses have found evidence for diminishing returns in risk reduction for increasing LRVs under imperfect compliance (Brown & Clasen, 2012; Enger et al., 2013; Rosa & Clasen, 2010). Our simulation results broadly support these findings. Notably, we find that improving compliance from low to moderate levels can provide significant health gains (Figure 2). Conversely, even a small level of non-compliance with a high LRV treatment method can still result in a significant loss in health gains when drinking water is sufficiently contaminated (Figure 2). This suggests that once the microbiological efficacy of a device is “good enough”, focusing on improving compliance may be at least as important as increasing a device’s LRV.
Across the range of scenarios we tested, the optimal LRV from the perspective of minimizing disease burden was almost always lower than the current WHO standards that assume perfect compliance (Figure 3). In addition, we found that the risk-reductions generated by interventions chosen by our model framework as opposed to high efficacy interventions were considerable for all three pathogens (protective-ratio comparing the optimal intervention with the implemented device: 0.1 – 1). Assuming that achieving perfect compliance is unrealistic, our simulations further suggest that reaching the tolerable disease burden threshold of 10−6 DALY/year is impractical. However, balancing compliance and efficacy provides the maximum possible risk reductions. These findings indicate that multiple WASH interventions, or coupled technological-behavioral interventions may be needed in order to achieve desired reductions in diarrheal disease.
Our modeling framework further extends the scope of QMRA for environmental epidemiology by integrating decision theory into exposure assessment to explicitly represent the response of potential HWT users to a given intervention. Characterizing individual level incentives is crucial, as in many cases HWT appears to be subject to a trade-off between usability and efficacy. Specifically, studies of filter adoption have suggested that usability may decline as a function of LRV. Biosand and clay pot filters have LRV approaching 5 for bacteria, but are prone to breakage and clogging (Fiore, Minnings, & Fiore, 2010; Gupta, Islam, Johnston, Ram, & Luby, 2008; van Halem et al., 2009). By contrast cloth filters have been successfully adopted for cholera prevention in spite of a much lower (2 LRV) efficacy (Colwell et al., 2003; Huq et al., 2010). Chemical treatment involves a similar trade-off as the taste and odor of treated water become less palatable as the concentration of disinfectant increases (Mintz et al., 2001; World Health Organization, 2011b). Our decision-theoretic model captures these scenarios by assuming that usability and therefore individual preference is a function of device efficacy measured in LRV. This approach is designed to accommodate a wide range of incentive structures. Our choice of an asymmetrical or symmetrical distance function to represent filtration or chlorination respectively is based on a mechanistic hypothesis of the perceived trade-off between efficacy and usability. Specific characteristics of the function; e.g., rate of drop-off and value where drop-off begins will vary by type of intervention and the specific technology. Both consultation with experts and behavioral data will help to identify these functional forms.
Willingness to adopt more efficacious (but potentially less usable) HWT methods is likely to vary substantially by region. Ideally, HWT recommendations should be informed by data regarding the target group’s preferences and attitudes regarding treatment. Such attitudes are complex, determined by a wide range of elements including private costs, social contexts, and political forces. Our decision-theory model is designed to accommodate behavioral data at multiple levels of resolution. In particular, when data on compliance are unavailable or unreliable, attitude surveys and similar techniques can be used to assess the distribution of preferences and inform the selection or construction of a utility function (Albert, Luoto, & Levine, 2010; Mankad & Tapsuwan, 2011; Poulos et al., 2012). Alternatively, as demonstrated by our household water treatment case study, data on compliance with existing interventions can be used to infer more effective treatment levels should they be feasible.
Our QMRA model relies on a simplified representation of enteric pathogen transmission. Like other QMRA approaches, we assume that infected individuals do not shed pathogen back into drinking water sources, and that contaminated drinking water is the primary transmission pathway. In order to focus on the implications of intervention and preference-dependent compliance we omitted temporal variation in pathogen exposure due to seasonal or other periodic factors. Future work may address these factors by implementing a compartmental transmission model with environmental transmission similar to the EITS or SIWR models (Li, Eisenberg, Spicknall, & Koopman, 2009; Tien & Earn, 2010).
5. CONCLUSIONS
Realizing health gains from environmental interventions requires an understanding of the role of host behaviors in transmission systems. Our framework represents a straightforward extension to QMRA that addresses end user compliance behavior as well as environmental and microbiological factors. This systems approach can be applied to evaluate new and existing HWT interventions. In particular, our analyses suggest that it may be advisable to focus on cost-efficient and readily usable treatment options. Addressing the usability efficacy trade-off is likely to be crucial to the successful deployment of HWT in areas still lacking access to safe drinking water. Applications of our framework are not limited to decentralized HWT contexts. Indeed, even centralized water treatment can fail to attain complete coverage due to infrastructure limitations such as reliability and re-contamination.
Supplementary Material
ACKNOWLEDGMENTS
This research was funded under the Models of Infectious Disease Agent Study (MIDAS) program within the National Institute of General Medical Sciences of the National Institutes of Health (grant number U01GM110712).
REFERENCES
- Albert J, Luoto J, & Levine D. (2010). End-user preferences for and performance of competing POU water treatment technologies among the rural poor of Kenya. Environmental Science & Technology, 44(12), 4426–4432. [DOI] [PubMed] [Google Scholar]
- Arnold B, Arana B, Mäusezahl D, Hubbard A, & Colford JM Jr. (2009). Evaluation of a pre-existing, 3-year household water treatment and handwashing intervention in rural Guatemala. International Journal of Epidemiology, 38(6), 1651–1661. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arnold BF, & Colford JM Jr. (2007). Treating water with chlorine at point-of-use to improve water quality and reduce child diarrhea in developing countries: a systematic review and meta-analysis. The American Journal of Tropical Medicine and Hygiene, 76(2), 354–364. [PubMed] [Google Scholar]
- Brouwer AF, Weir MH, Eisenberg MC, Meza R, & Eisenberg JNS (2017). Dose-response relationships for environmentally mediated infectious disease transmission models. PLoS Computational Biology, 13(4), e1005481. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown J, & Clasen T. (2012). High adherence is necessary to realize health gains from water quality interventions. PloS One, 7(5), e36735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clasen T, Boisson S, Routray P, Torondel B, Bell M, Cumming O, … Schmidt W-P (2014). Effectiveness of a rural sanitation programme on diarrhoea, soil-transmitted helminth infection, and child malnutrition in Odisha, India: a cluster-randomised trial. The Lancet. Global Health, 2(11), e645–e653. [DOI] [PubMed] [Google Scholar]
- Clasen TF, Brown J, & Collin SM (2006). Preventing diarrhoea with household ceramic water filters: assessment of a pilot project in Bolivia. International Journal of Environmental Health Research, 16(3), 231–239. [DOI] [PubMed] [Google Scholar]
- Colwell RR, Huq A, Islam MS, Aziz KMA, Yunus M, Khan NH, … Russek-Cohen E. (2003). Reduction of cholera in Bangladeshi villages by simple filtration. Proceedings of the National Academy of Sciences of the United States of America, 100(3), 1051–1055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DuPont HL, Formal SB, Hornick RB, Snyder MJ, Libonati JP, Sheahan DG, … Kalas JP (1971). Pathogenesis of Escherichia coli diarrhea. The New England Journal of Medicine, 285(1), 1–9. [DOI] [PubMed] [Google Scholar]
- Eisenberg JN, Seto EY, Colford JM Jr, Olivieri A, & Spear RC (1998). An analysis of the Milwaukee cryptosporidiosis outbreak based on a dynamic model of the infection process. Epidemiology, 9(3), 255–263. [PubMed] [Google Scholar]
- Elliott MA, Stauber CE, Koksal F, DiGiano FA, & Sobsey MD (2008). Reductions of E. coli, echovirus type 12 and bacteriophages in an intermittently operated household-scale slow sand filter. Water Research, 42(10–11), 2662–2670. [DOI] [PubMed] [Google Scholar]
- Enger KS, Nelson KL, Clasen T, Rose JB, & Eisenberg JNS (2012). Linking quantitative microbial risk assessment and epidemiological data: informing safe drinking water trials in developing countries. Environmental Science & Technology, 46(9), 5160–5167. [DOI] [PubMed] [Google Scholar]
- Enger KS, Nelson KL, Rose JB, & Eisenberg JNS (2013). The joint effects of efficacy and compliance: a study of household water treatment effectiveness against childhood diarrhea. Water Research, 47(3), 1181–1190. [DOI] [PubMed] [Google Scholar]
- Estrada-Garcia T, Lopez-Saucedo C, Thompson-Bonilla R, Abonce M, Lopez-Hernandez D, Santos JI, … Long KZ (2009). Association of diarrheagenic Escherichia coli Pathotypes with infection and diarrhea among Mexican children and association of atypical Enteropathogenic E. coli with acute diarrhea. Journal of Clinical Microbiology, 47(1), 93–98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fiore MM, Minnings K, & Fiore LD (2010). Assessment of biosand filter performance in rural communities in southern coastal Nicaragua: an evaluation of 199 households. Rural and Remote Health, 10(3), 1483. [PubMed] [Google Scholar]
- Fischer AJ, Threlfall A, Meah S, Cookson R, Rutter H, & Kelly MP (2013). The appraisal of public health interventions: an overview. Journal of Public Health, 35(4), 488–494. [DOI] [PubMed] [Google Scholar]
- Fuller JA, Goldstick J, Bartram J, & Eisenberg JNS (2016). Tracking progress towards global drinking water and sanitation targets: A within and among country analysis. The Science of the Total Environment, 541, 857–864. [DOI] [PubMed] [Google Scholar]
- Gupta SK, Islam MS, Johnston R, Ram PK, & Luby SP (2008). The chulli water purifier: acceptability and effectiveness of an innovative strategy for household water treatment in Bangladesh. The American Journal of Tropical Medicine and Hygiene, 78(6), 979–984. [PubMed] [Google Scholar]
- Gurwith M, Wenman W, Hinde D, Feltham S, & Greenberg H. (1981). A prospective study of rotavirus infection in infants and young children. The Journal of Infectious Diseases, 144(3), 218–224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hunter JD (2007). Matplotlib: A 2D Graphics Environment. Computing in Science & Engineering, 9(3), 90–95. [Google Scholar]
- Huq A, Yunus M, Sohel SS, Bhuiya A, Emch M, Luby SP, … Colwell RR (2010). Simple sari cloth filtration of water is sustainable and continues to protect villagers from cholera in Matlab, Bangladesh. mBio, 1(1). 10.1128/mBio.00034-10 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones E, Oliphant T, Peterson P, Others. (2001). SciPy: Open Source Scientific Tools for Python. Retrieved from http://www.scipy.org/
- Kotloff KL, Nataro JP, Blackwelder WC, Nasrin D, Farag TH, Panchalingam S, … Levine MM (2013). Burden and aetiology of diarrhoeal disease in infants and young children in developing countries (the Global Enteric Multicenter Study, GEMS): a prospective, case-control study. The Lancet, 382(9888), 209–222. [DOI] [PubMed] [Google Scholar]
- Li S, Eisenberg JNS, Spicknall IH, & Koopman JS (2009). Dynamics and Control of Infections Transmitted From Person to Person Through the Environment. American Journal of Epidemiology, 170(2), 257–265. [DOI] [PubMed] [Google Scholar]
- Mankad A, & Tapsuwan S. (2011). Review of socio-economic drivers of community acceptance and adoption of decentralised water systems. Journal of Environmental Management, 92(3), 380–391. [DOI] [PubMed] [Google Scholar]
- McNeil BJ, & Pauker SG (1984). Decision analysis for public health: principles and illustrations. Annual Review of Public Health, 5, 135–161. [DOI] [PubMed] [Google Scholar]
- McNeil DG Jr. (2014, October 27). Latrines may not improve the health of poor children. The New York Times. [Google Scholar]
- Messner MJ, Chappell CL, & Okhuysen PC (2001). Risk assessment for Cryptosporidium: a hierarchical Bayesian analysis of human dose response data. Water Research, 35(16), 3934–3940. [DOI] [PubMed] [Google Scholar]
- Mintz E, Bartram J, Lochery P, & Wegelin M. (2001). Not just a drop in the bucket: expanding access to point-of-use water treatment systems. American Journal of Public Health, 91(10), 1565–1570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Murphy HM, Sampson M, McBean E, & Farahbakhsh K. (2009). Influence of household practices on the performance of clay pot water filters in rural Cambodia. Desalination, 248(1–3), 562–569. [Google Scholar]
- Oyanedel-Craver VA, & Smith JA (2008). Sustainable colloidal-silver-impregnated ceramic filter for point-of-use water treatment. Environmental Science & Technology, 42(3), 927–933. [DOI] [PubMed] [Google Scholar]
- Platts-Mills JA, Babji S, Bodhidatta L, Gratz J, Haque R, Havt A, … MAL-ED Network Investigators. (2015). Pathogen-specific burdens of community diarrhoea in developing countries: a multisite birth cohort study (MAL-ED). The Lancet. Global Health, 3(9), e564–e575. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poulos C, Yang J-C, Patil SR, Pattanayak S, Wood S, Goodyear L, & Gonzalez JM (2012). Consumer preferences for household water treatment products in Andhra Pradesh, India. Social Science & Medicine, 75(4), 738–746. [DOI] [PubMed] [Google Scholar]
- Rogers EM (2010). Diffusion of Innovations, 4th Edition. Simon and Schuster. [Google Scholar]
- Rosa G, & Clasen T. (2010). Estimating the scope of household water treatment in low- and medium-income countries. The American Journal of Tropical Medicine and Hygiene, 82(2), 289–300. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmidt W-P (2015). Seven trials, seven question marks. The Lancet. Global Health, 3(11), e659–e660. [DOI] [PubMed] [Google Scholar]
- Schmidt W-P, & Cairncross S. (2009). Household water treatment in poor populations: is there enough evidence for scaling up now? Environmental Science & Technology, 43(4), 986–992. [DOI] [PubMed] [Google Scholar]
- Shaheed A, Rathore S, Bastable A, Bruce J, Cairncross S, & Brown J. (2018). Adherence to Point-of-Use Water Treatment over Short-Term Implementation: Parallel Crossover Trials of Flocculation-Disinfection Sachets in Pakistan and Zambia. Environmental Science & Technology, 52(11), 6601–6609. [DOI] [PubMed] [Google Scholar]
- Stauber CE, Elliott MA, Koksal F, Ortiz GM, DiGiano FA, & Sobsey MD (2006). Characterisation of the biosand filter for E. coli reductions from household drinking water under controlled laboratory and field use conditions. Water Science and Technology: A Journal of the International Association on Water Pollution Research, 54(3), 1–7. [DOI] [PubMed] [Google Scholar]
- Tadelis S. (2013). Game Theory: An Introduction. Princeton University Press. [Google Scholar]
- Tien JH, & Earn DJD (2010). Multiple Transmission Pathways and Disease Dynamics in a Waterborne Pathogen Model. Bulletin of Mathematical Biology, 72(6), 1506–1533. [DOI] [PubMed] [Google Scholar]
- van Halem D, van der Laan H, Heijman SGJ, van Dijk JC, & Amy GL (2009). Assessing the sustainability of the silver-impregnated ceramic pot filter for low-cost household drinking water treatment. Physics and Chemistry of the Earth, Parts A/B/C, 34(1–2), 36–42. [Google Scholar]
- Waddington H, & Snilstveit B. (2009). Effectiveness and sustainability of water, sanitation, and hygiene interventions in combating diarrhoea. Journal of Development Effectiveness, 1(3), 295–335. [Google Scholar]
- Ward RL, Bernstein DI, Young EC, Sherwood JR, Knowlton DR, & Schiff GM (1986). Human rotavirus studies in volunteers: determination of infectious dose and serological response to infection. The Journal of Infectious Diseases, 154(5), 871–880. [DOI] [PubMed] [Google Scholar]
- World Health Organization. (2011a). Evaluating Household Water Treatment Options: Health-based Targets and Microbiological Performance Specifications.
- World Health Organization. (2011b). Guidelines for Drinking-water Quality.
- World Health Organization. (2016). Results of round 1 of the WHO International Scheme to Evaluate Household Water Treatment Technologies. Retrieved from http://apps.who.int/iris/bitstream/handle/10665/204284/?sequence=1
- World Health Organization. (2017). Fact sheet: Diarrhoeal disease. Retrieved from http://www.who.int/news-room/fact-sheets/detail/diarrhoeal-disease [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.