The neural basis of delayed gratification

Sustained ramping of dopaminergic activation helps individuals resist impulsivity and wait for a later but larger reward.

Abstract

Balancing instant gratification versus delayed but better gratification is important for optimizing survival and reproductive success. Although delayed gratification has been studied through human psychological and brain activity monitoring and animal research, little is known about its neural basis. We successfully trained mice to perform a waiting-for-water-reward delayed gratification task and used these animals in physiological recording and optical manipulation of neuronal activity during the task to explore its neural basis. Our results showed that the activity of dopaminergic (DAergic) neurons in the ventral tegmental area increases steadily during the waiting period. Optical activation or silencing of these neurons, respectively, extends or reduces the duration of waiting. To interpret these data, we developed a reinforcement learning model that reproduces our experimental observations. Steady increases in DAergic activity signal the value of waiting and support the hypothesis that delayed gratification involves real-time deliberation.

INTRODUCTION

To optimize survival and reproductive success, animals need to balance instant gratification versus delayed but better gratification. Repeated exposure to instant gratification may disrupt this balance, thereby increasing impulsive decisions. These decisions contribute to numerous human disorders, such as addiction and obesity (1, 2). Delayed gratification is an important process that balances time delay with increased reward (3). It is influenced by strengths in patience, willpower, and self-control (4). Psychologists and neuroscientists have long studied this important behavior through human psychological and brain activity assessments and rodent-based studies. Although the dopamine system has been implicated in delayed gratification, the precise neural activity of the dopamine system that allows better gratification has not been demonstrated. In addition, no studies to date have causally manipulated the dopamine system during delayed gratification tasks.

During a well-controlled delayed gratification task, an individual must balance the benefits versus risks of delay in receiving an available reward. The choice to continue waiting requires suppression of the constant temptation of an immediate reward, in favor of an enhanced reward in the future (3, 5, 6). Midbrain dopaminergic (DAergic) neurons are well known to play central roles in reward-related and goal-directed behaviors (7–12). Studies have revealed that DAergic activity signals spatial or operational proximity to distant rewards (7, 13, 14), which has been postulated to sustain or motivate goal-directed behaviors while resisting distractions. DAergic neurons play important roles in time judgment (15) and cost-benefit calculations, which are necessary for value-based decision-making (13, 16–18).

We successfully trained mice to perform a waiting-for-water-reward delayed gratification task. Recording and manipulation of neuronal activities during this task allowed us to explore the cellular regulation of delayed gratification. We found that the activity of ventral tegmental area (VTA) DAergic neurons ramped up consistently while mice were waiting in place for rewards. Transient activation of DAergic neurons extended, whereas inhibition reduced the duration of the waiting period. Then, we adopted reinforcement learning (RL) computational models to predict and explain our experimental observations.

RESULTS

Mice can learn to wait for greater rewards by delayed gratification task training

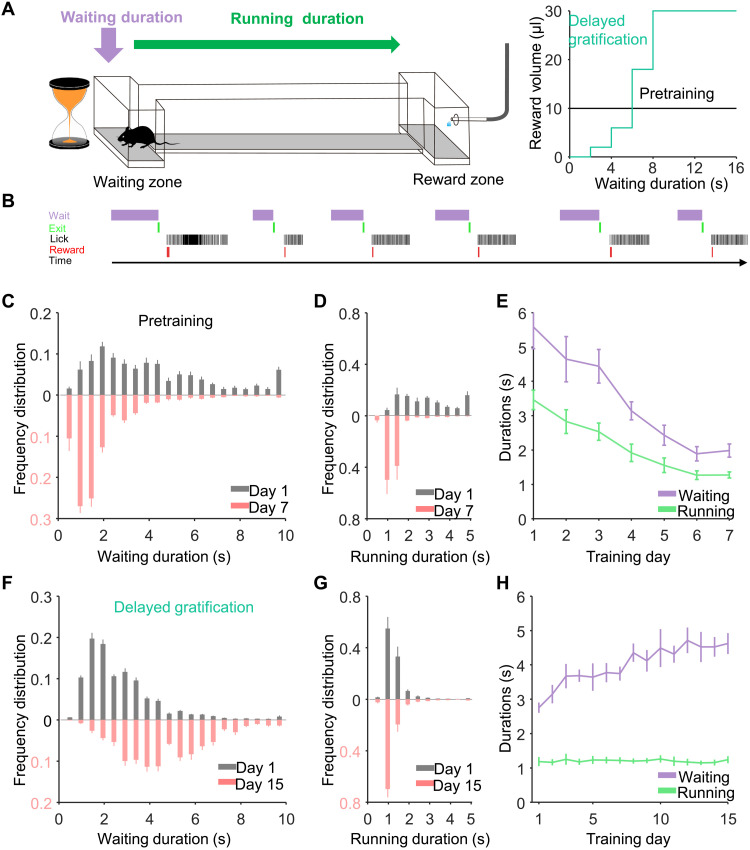
First, we trained water-restricted mice to perform a one-arm foraging task (pretraining) in which delay did not result in an increased reward (19). The period in which the mouse remained in the waiting zone was defined as the waiting duration, and the time during which the mouse traveled from the waiting zone to reach the water reward was defined as the running duration (Fig. 1A, left). When the mouse exited the waiting zone and licked the water port in the reward zone, it could receive a 10-μl water drop regardless of the time spent in the waiting zone [Fig. 1A, right (black line)]. During a week of training, the average waiting and running durations both significantly decreased from days 1 to 7 (day 1: waiting, 5.58 ± 0.63 s; running, 3.46 ± 0.28 s; P < 0.001; day 7: waiting, 1.99 ± 0.19 s; running, 1.28 ± 0.09 s; P < 0.001, n = 7 mice, Friedman test; Fig. 1, C to E, and movie S1). All mice learned the strategy of reducing durations of both waiting and running to maximize the reward rate (defined as microliters of water per second in a given trial; fig. S1C).

Fig. 1. The behavioral performance of mice during learning of a delayed gratification task.

(A) Left: Schematic of the delayed gratification task. Right: Relationship between reward volumes and waiting durations in the two behavioral tasks. (B) A plot of transistor-transistor logic signals for the chronological sequence of behavioral events in the tasks. (C to E). The waiting duration and running duration both decreased during the training process in the pretraining phase (P < 0.001). (F) The distribution of waiting durations from the behavioral session on the last analyzed day (day 15, light red), revealing significantly longer waiting durations compared to those from day 1 (day 1: gray, n = 7 mice). (G) The distribution of running durations on days 1 and 15 did not differ with training. (H) Continuous training significantly increased the average waiting duration (P < 0.001), whereas the training did not change the average running duration (P = 0.97).

Next, we trained the same mice using a delayed gratification paradigm, where the size of the reward increased quadratically with time spent in the waiting zone [Fig. 1A, right (green line)]. Over the next 3 weeks, this resulted in shifting the distributions of the waiting duration toward a longer wait. The averaged waiting period significantly increased from 2.76 ± 0.15 s on day 1 to 4.62 ± 0.30 s on day 15 (P < 0.001, n = 7 mice, Friedman test; Fig. 1, F and H, and movie S2). Continuous training steadily increased the averaged waiting duration, whereas the training did not change the average running duration from 1.19 ± 0.13 s on day 1 to 1.24 ± 0.10 s on day 15 (P = 0.97, n = 7 mice, Friedman test; Fig. 1, G and H). The reward rate increased steadily, indicating that the mice were successfully learning to successfully delay gratification (fig. S1D).

The activity of VTA DAergic neurons increases steadily during the waiting period

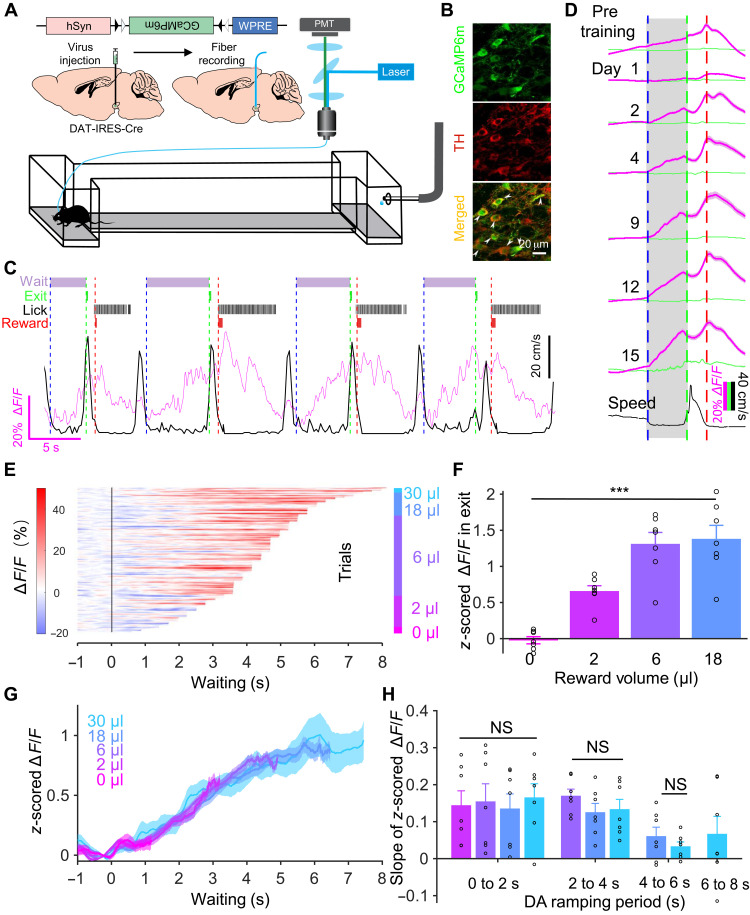
To monitor the activity of VTA DAergic neurons during the delayed gratification task, we used fiber photometry to record the calcium signals in VTA DAergic neurons in freely moving mice for as long as 1 month (Fig. 2, A to C; optical fiber placement illustrated in fig. S2). On the first day of pretask training, the calcium signal rose rapidly upon reward and quickly reached a peak. A few days of training markedly reshaped the response pattern. Once the mice reentered the waiting zone, the activity of DAergic neurons started to rise and reached the highest level when the animal received a reward (fig. S3A).

Fig. 2. VTA DAergic activity ramps up consistently while the mice are waiting for the reward.

(A) Schematic of stereotaxic virus injection procedures. (B) Confocal images illustrating GCaMP6m expression in VTA TH⁺ neurons. (C) A live recording trace (magenta) of Ca²⁺ signal in VTA DAergic neurons and running speed (black) when the mouse was performing the delayed gratification task. Task events over time (top): The dashed vertical lines indicate waiting onset (blue), waiting termination (green), and reward onset (red). (D) The scaled Ca²⁺ signals (magenta) and green fluorescent protein signal (green) curves of VTA DAergic neurons from the last day of pretraining and days in the delayed gratification task training (black, speed). (E) Waiting duration sorted ramping Ca²⁺ signal data from one mouse during the delayed gratification task training (150 trials). (F) z-scored ΔF/F values at 0.5 s before exit were significantly different when the reward volumes were different (***P < 0.001). (G) Averaged Ca²⁺ signal curves with different outcomes from (E). (H) Shown separately for different trial stages (DAergic ramping periods) during the last week of training. There were no differences in the slope of the Ca²⁺ signals between trials with different reward outcomes. NS, not significant. WPRE, Woodchuck Post-transcriptional Regulatory Element; PMT, PhotoMultiplier Tube; TH, Tyrosine Hydroxylase.

We next analyzed the activity of these same neurons in the mice as they learned the delayed gratification task. The recording traces showed that training gradually reshaped the pattern and time course of activity (Fig. 2D). The activity started to ramp up once the mice entered the waiting zone and then reached its highest level when they exited. To investigate carefully the dynamical properties of the ramping activity during waiting, we sorted the calcium signals from day 15 of one mouse by their length of waiting durations and plotted them with a heatmap (Fig. 2E). We divided trials according to the trial outcome (reward volume) and calculated the calcium signals while the mouse exited the waiting zone with different reward volumes. Our results showed that the z-scored calcium signals at 0.5 s before exit were significantly increased as reward volumes increased [F = 24.67, P < 0.001, n = 7, one-way analysis of variance (ANOVA); Fig. 2F], but the mean signal curves followed similar trajectories regardless of trial outcome (Fig. 2G). Then, we calculated the slopes of signal curves with different outcomes over four time windows (0 to 2, 2 to 4, 4 to 6, and 6 to 8 s) by linear regression analysis. The slopes during the same time window did not differ significantly between reward groups (0 to 2 s: F = 0.10, P = 0.96; 2 to 4 s: F = 1.03, P = 0.38; 4 to 6 s; F = 1.00, P = 0.34, n = 7, one-way ANOVA; Fig. 2H). We pooled and plotted the slopes of different waiting periods together and found that the activity curves kept rising steadily, almost saturating after 6 s from the time the mice entered the waiting zone. The ramp-up of DAergic activity became less variable with delayed gratification task training in our experimental data (fig. S4, A to D). All these results indicated that VTA DAergic neurons consistently ramp up their activity during waiting in as animals are trained in the delayed gratification task.

High-frequency spiking of VTA DAergic neurons sustains waiting in the delayed gratification task

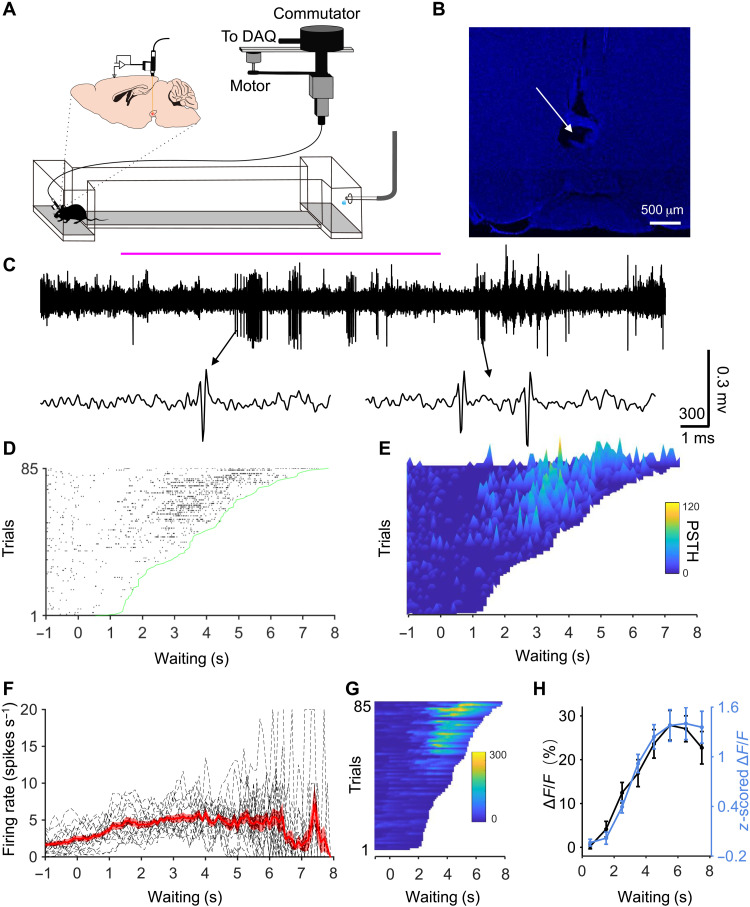
Does tonic or phasic firing of DAergic neurons underlie the ramping calcium signal? To answer this, we conducted single unit recordings when mice were performing the delayed gratification task (Fig. 3A). A custom-made head plate was placed on the skull and affixed in place with dental cement. After recording, placements of recording electrodes were confirmed with electrolytic lesion inside VTA of all five mice (Fig. 3B). We found that 17 putative DAergic neurons displayed short bursts of firing during the waiting period (Fig. 3C). On trials in which the mice waited for a short duration, the firing rate was low throughout the waiting period (Fig. 3, D to E). On trials in which the mice waited for a long duration, the firing rate was initially low before increasing during the later waiting period (Fig. 3, D to E). We averaged peristimulus time histograms (PSTHs) of all trials to obtain a response curve (n = 17 cells; Fig. 3F). Similar to calcium signal, the response curve of firing rate noticeably ramped up with increased waiting time before reaching a plateau at around 4 s. To compare with the experimental calcium signal, we used a convolution algorithm to predict calcium responses trial by trial based on the firing rate of all 17 recorded cells (Fig. 3G showed the predicted calcium responses from Fig. 3E). The average of predicted calcium signal (ΔF/F %, 0.5 s before exiting from all trials) of all cells fit the measured calcium response (z-scored ΔF/F, 0.5 s before exit from the last week of training) curve very well (r = 0.982, Pearson correlation; Fig. 3H). This analysis shows that the spiking activity of single DAergic neurons underlies the ramping calcium signal revealed by fiber photometry recording.

Fig. 3. Single unit recordings reveal that high-frequency spiking of VTA DAergic neurons sustains waiting in the delayed gratification task.

(A) Schematic of single unit electrical recordings in the delayed gratification task. DAQ, Data Acquisition. (B) An example image showing the placement of electrode tips in VTA with an electrolytic lesion. (C) An example recording trace when a mouse performed a whole trial of the delayed gratification task. The waiting period was noted with a solid magenta line. (D) Raster plot of spikes trial by trial sorted by waiting duration of the delayed gratification task. (E) Three-dimensional PSTH plot for (D). (F) Average response curve during the waiting period (n = 17 cells, each dashed line represents one cell). (G) Predicted calcium responses based on the convolution of the spike rate from (E) with a 0.1-s time bin. (H) The predicted calcium response curve (black) is based on the spiking response curves in (F), compared to the measured calcium response curve (blue line) (r = 0.982, Pearson correlation).

Optogenetic manipulation of VTA DAergic activity alters the waiting durations in the delayed gratification task

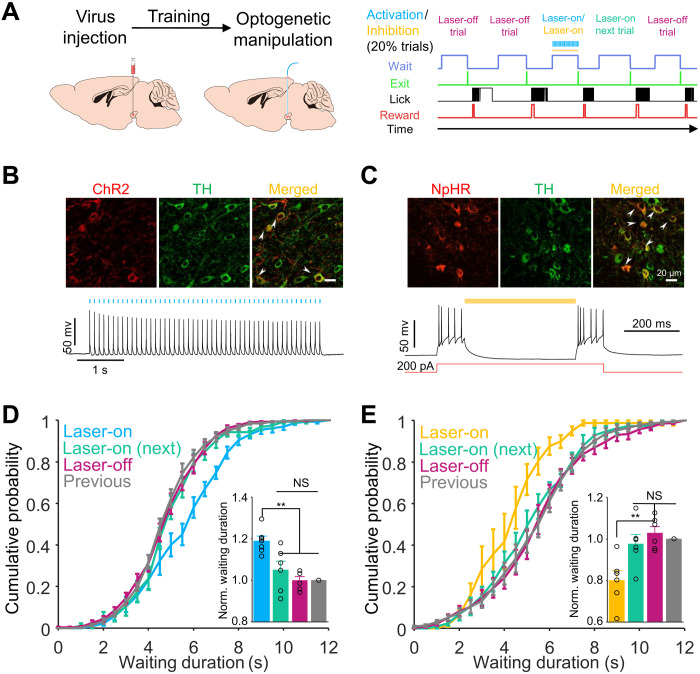
To determine whether VTA DAergic activity controls performance in the delayed gratification task, we manipulated VTA DAergic neurons temporally using optogenetic tools in 20% of pseudorandomly chosen trials while the mice were waiting during the delayed gratification task (Fig. 4, A to C). Activating the VTA DAergic neurons shifted the cumulative probability distribution toward a longer waiting duration (F = 12.93, P = 0.002, n = 6 mice, one-way ANOVA; Fig. 4D, blue), while inhibiting these same neurons shifted the distribution significantly in the opposite direction (F = 7.76, P = 0.008, n = 6 mice, one-way ANOVA; Fig. 4E, yellow). The effects of optogenetic stimulation or inhibition on the cumulative probability distributions for waiting duration were only observed in the laser-on trials. In contrast, the laser-off trials, including those immediately after the laser-on trials treated as a single group, were not significantly different from the trials from the previous day (P > 0.5; Fig. 4, D and E). The optical manipulation did not influence the running durations in the delayed gratification task in mice that expressed Channelrhodopsin-2 (ChR2) or enhanced Halorhodopsin 3.0 (eNpHR3.0) (fig. S5, A and B), nor did it change the waiting duration distribution of mice that expressed mCherry in DAergic neurons in delayed gratification tasks (fig. S6, A and B). To rule out the possibility of optogenetic manipulation–induced memory, we performed a random place preference test with the same stimulation dosage. Neither activating nor inhibiting VTA DAergic neurons significantly changed the transient waiting duration or pattern in the location in which the laser was activated in any of the tested mice (fig. S5, E to H) or in the mCherry expressing controls (fig. S6, C to F).

Fig. 4. Optogenetic manipulation of VTA DAergic activity altered the waiting durations.

(A) Left: Schematic of stereotaxic virus injection and surgical procedure. Right: Behavioral events and optogenetic manipulation protocol. (B) Images showing ChR2-mCherry expression (top) and whole-cell recordings showing action potentials evoked by 10-Hz laser flash sequences (50 flashes) in VTA TH⁺ neurons (bottom). (C) Images showing eNpHR3.0-mCherry expression (top) and whole-cell recordings showing that evoked action potentials were inhibited by continued 589-nm laser in VTA TH⁺ neurons (bottom). (D) Cumulative probabilities of waiting durations. The waiting durations of optogenetically activated trials were significantly increased (P = 0.002, blue) relative to those of the previous day’s trials (gray). Inset: Bar graph of the normalized waiting durations showing that the average waiting duration of unstimulated trials (P = 0.96, magenta) did not differ from those of the previous day’s trials or the next trials following photoactivation (P = 0.63, green). (E) The same experimental configuration as in (D) but VAT TH⁺ neurons were optogenetically inhibited by a yellow laser. Optogenetic inhibition decreased the waiting duration (P = 0.008, yellow), whereas there were no differences between other trials (P > 0.5). **P < 0.01.

An RL model suggests that ramping up VTA DAergic activity signals the value of waiting for delayed gratification

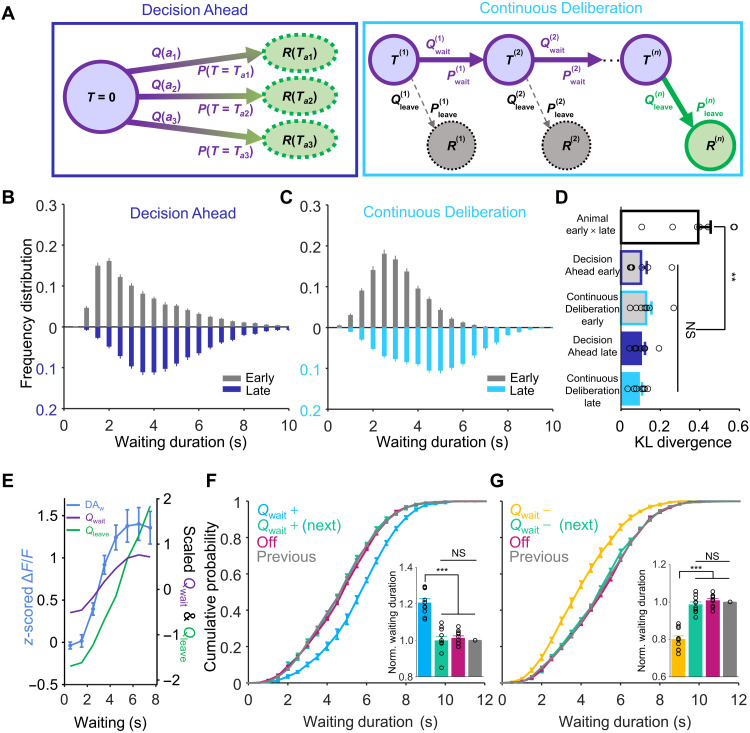
How does a mouse manage to wait longer for a larger reward while ignoring smaller but more immediate reward options? We propose two models of behavioral scenarios that exemplify possible strategies a mouse may implement to achieve extended waiting performances: (i) setting a goal of expected waiting duration before the initiation of waiting or (ii) continuously deliberating during the waiting period. According to the first hypothesis (i), we modeled an RL agent that keeps time until a predetermined moment has passed (Fig. 5A, Decision Ahead); according to (ii), we modeled a second RL agent that continuously balances the values of waiting versus leaving to control the decision to wait or to leave for the reward. To implement these models, we used a version of the state-action-reward-state-action (SARSA) algorithm with a series of states (Fig. 5A, Continuous Deliberation; see Materials and Methods) (20, 21). The behaviors of both models were able to replicate the behavioral performance that we observed in animal experiments (Fig. 5, B and C). The distributions of behavioral performances between early training days and late training days from the experimental data were very different from each other, such that the Kullback-Leibler (KL) divergence was large (0.39 ± 0.06). The KL divergences between the distributions of simulated behavioral performances and experimental data were significantly small to the large KL divergence value (P = 0.005, n = 7 mice, Friedman test), and there was no difference (P > 0.99) between Decision Ahead RL model and Continuous Deliberation RL model in either the early or late training session. (Fig. 5D). We could not determine which model is better on the basis of behavioral performance alone, given that both models reproduced the behavioral data well.

Fig. 5. Behavioral performances and ramping VTA DAergic activity are explained by the RL model.

(A) Two RL models: Decision Ahead and Continuous Deliberation. Q(a_n), value for action a(n); P(T_an), probability of action a(n); $P_{\text{wait}}^{(n)}$, the probability of waiting; $Q_{\text{wait}}^{(n)}$, waiting action value; $P_{\text{leave}}^{(n)}$, probability of leaving; $Q_{\text{leave}}^{(n)}$, leaving action value; R⁽ⁿ⁾, received reward. (B and C) The distributions of waiting durations from the early session and late session were simulated in the Decision Ahead model (B) and Continuous Deliberation model (C). (D) The Kullback-Leibler divergence between the distribution of early and late experimental data was significantly larger than the KL divergences between the distributions of simulated behavioral performances and experimental data (P = 0.005), but there was no difference (P > 0.99) between the two RL models. (E) Plots of z-scored ΔF/F values (DA_w, blue), scaled Q_wait (purple), and Q_leave (green) from the Continuous Deliberation model. The Q_wait and Q_leave both predicted the experimental calcium activity well. (F and G) Computational RL model (continuous deliberation)–simulated data, dependent on manipulating Q_wait in delayed gratification task. The simulation showed that manipulating Q_wait (i.e., simulated dopamine activity) only influenced the waiting durations of Q_wait manipulated trials [(F and G), P < 0.001]. **P < 0.01; ***P < 0.001.

What does the ramping up of DAergic activity mean in the delayed gratification task? We tried to explain it with our RL models. In the Decision Ahead model, the agent keeps time until the predetermined moment has passed, which suggests that the ramping DAergic activity may relate to timing in the delayed gratification task. Some studies have proposed that the ramping activity is consistent with a role in the classical model of timing, with the movement being initiated when the ramping activity reaches a nearly fixed threshold value, following an adjusted slope of ramping activity (22–25). In contrast, our results showed that the DAergic activity ramped up to different values with similar trajectories on at a nearly constant slope (Fig. 2, F to H). This suggests that VTA DAergic neurons may not implement a decision variable for the Decision Ahead scenario. In the Continuous Deliberation RL model, we compared the curves of the value of waiting and leaving with the ramping up of DAergic activity and found that the behavioral performance of both animals and model agents reached the asymptote. The values of waiting (r = 0.99, Pearson correlation; Fig. 5E, purple) and the leaving (r = 0.91, Pearson correlation; Fig. 5E, green) each correlated positively with the ramp of DAergic activity during waiting (z-scored ΔF/F, 0.5 s before exit from the last week of training; Fig. 5E, blue). This detailed analysis suggested that the Continuous Deliberation RL model agreed with previous studies (13, 26–28) and that ramping DAergic activity signals the value of actions, either waiting or leaving, in the delayed gratification task.

In the Decision Ahead RL model, if the agent keeps timing during the waiting period through ramping DAergic activity to encode the elapse of time (29–31), then extra VTA DAergic activation should represent a longer time, thus leading to earlier cessation of waiting. This prediction is contrary to our optogenetics result that DAergic activation led to a longer waiting (Fig. 4D). Instead, we reproduced the optogenetic manipulations in the Continuous Deliberation RL model by either increasing or decreasing the value of waiting (Q_wait) in a pseudorandom 20% of trials. The increase or decrease in waiting durations only occurred in the Q_wait-manipulated trials (P < 0.001, Friedman test, n = 10), whereas the remaining trials, including the next trials after value manipulation, did not differ significantly from controls (P > 0.999, Friedman test, n = 10; Fig. 5, F to G). Manipulating the value of leaving (Q_leave) in a pseudorandom 20% of trials induced the opposite results, inconsistent with the experimental data (fig. S8, A and B). Manipulating the reward prediction error (RPE) signal in the model led to persistent changes to the waiting time on subsequent trials (fig. S8, C and D). This is inconsistent with the experimental finding that optogenetic manipulation of dopamine neuron firing only affects waiting time on the current trial (Fig. 4, D and E). Thus, the ramping dopamine signal is not consistent with an RPE signal in the delayed gratification task. Our experimental data and the Continuous Deliberation RL model together indicated that the ramping up of VTA DAergic activity profoundly influenced the waiting behavioral performance in the delayed gratification task, which suggested that this activity signals the value of waiting, rather than the value of leaving or RPE. Conceptually, our analysis revealed that delayed gratification involves real-time deliberation.

VTA DAergic activity during waiting predicts the behavioral performance in the delayed gratification task

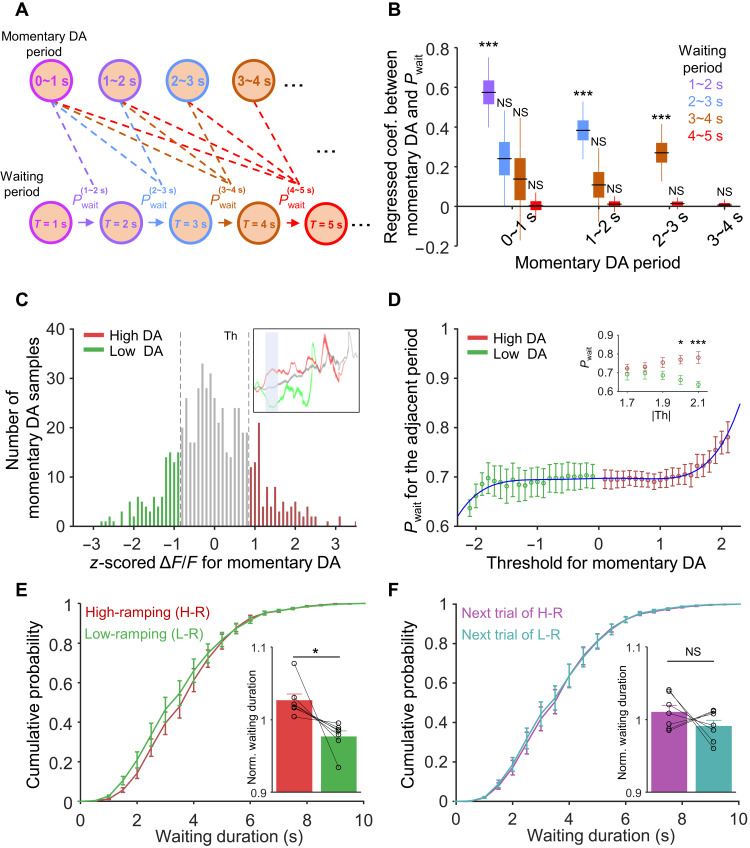
Our optogenetic manipulation experiments and Continuous Deliberation RL model indicated that VTA DAergic activity during waiting influenced the waiting durations while the mouse performed the delayed gratification task (Figs. 4, D and E, and 5, F and G). Although the activity of VTA DAergic neurons ramped up consistently during waiting (Fig. 2, G and H), it still fluctuated to a certain extent moment by moment. Therefore, we sought next to determine whether this fluctuation of DAergic activities influences the waiting behavior in the delayed gratification task. A strong prediction made by the Continuous Deliberation model is that, if DAergic activity signals the value of waiting at each specific moment, then a momentary increase in the DA signal will make the agent more likely to keep waiting in the next “time bin” but not in subsequent time bins (fig. S8, E and F). That is to say, the value of waiting is only positively correlated with the behavior of the immediately following time bin, which indicates the Markovian nature of the model (32). We thus aimed to test the relationship between the amplitude of the momentary VTA DAergic signal and the behavior (i.e., waiting or leaving) within each time bin to determine how the momentary DAergic activity (the calcium signal amplitude in 0 to 1 s, 1 to 2 s, 2 to 3 s, or 3 to 4 s after waiting onset, shown as each cluster of bars in Fig. 6B) affects the waiting performance in the subsequent periods (behavior from 1 to 2 s, 2 to 3 s, 3 to 4 s, and 4 to 5 s for DAergic activity from 0 to 1 s; behavior within 2 to 3 s, 3 to 4 s, and 4 to 5 s for DAergic from in 1 to 2 s; and so on; Fig. 6A). To integrate data from multiple sessions and multiple animals, we took advantage of the linear mixed model (LMM) analysis (see Materials and Methods) (33–35). We examined the correlation between momentary DAergic activity and behavior (i.e., the momentary binary waiting decision). For the behavior, we coded sustained waiting as 1 and leaving in that time bin as 0 (trials that stopped before the examined time window were not taken into account) for different pairs of time bins. Ten independent LMM analyses were done for each activity-behavior pair, as indicated by the dash lines in Fig. 6A. The regression coefficients, as well as the confidence intervals of each of the 10 pairs, are shown by corresponding bars in Fig. 6B. The correlation is only significantly positive between adjacent DAergic and waiting bins (P < 0.001, n = 7 mouse, black lines, regressed coefficient median; boxes, 50% confidence interval; whisker, 95% confidence interval; Fig. 6B, the first bar of each cluster, where the DA activity bin is 1 s ahead of the waiting bin). There was no significant correlation between DAergic activity at 3 to 4 s and behavior at 4 to 5 s (r = 0.007, P = 0.61, n = 7), which may result from insufficient data for those long trials. Apart from these pairs with adjacent bins, other pairs of DAergic activity and waiting behavior did not show any significant correlation (Fig. 6B, the remaining bars of each cluster). These results indicate that the waiting decision of the current moment is only influenced by the most recent DAergic signal but not by DAergic signal further in the past, which suggests that deliberation for waiting in delayed gratification may be a Markov process as we formalized in the Continuous Deliberation RL model (32).

Fig. 6. VTADAergic activity during waiting predicts the behavioral performance in the delayed gratification task.

(A) Schematic of waiting probability (P_wait) in waiting periods after momentary DAergic periods. (B) Relationship between momentary VTA DAergic activity (Ca²⁺ signals) and its waiting probability. For each momentary DAergic period, its DAergic activity is only highly correlated (P < 0.001) with P_wait in the adjacent waiting period (the left bar of each cluster). (C) The distribution of z-scored mean ΔF/F of momentary DAergic periods. Three colors are used to illustrate: high dopamine activity (high DA, red), low dopamine activity (low DA, green), and other activity (gray). (D) The P_wait of high DA and low DA activity trials for the adjacent period after the momentary DA periods. The difference between the P_w of the high DA trials and low DA trials increases with the increase of threshold (Th). (E and F) Cumulative probabilities of waiting durations for the high-DA-ramping trials [(E) H-R, red], the lower-DA-ramping trials [(E) L-R, green] and their “next-in-series” trials (F). Bar graph showing that the normalized waiting durations of the H-R trials are significantly longer than those of the L-R trials [(E) P = 0.024] but did not differ significantly between their next-in-series trials [(F) P = 0.290]. *P < 0.05; ***P < 0.001.

In the Continuous Deliberation RL model, the probability of waiting (P_w) positively correlates with the value of waiting (Q_wait). To explore the impact of DAergic activity on the probability of waiting in our experimental data, we binned DAergic activity of every trial and normalized data points (V_DA) in each momentary DAergic period [with each period lasting 1 s and starting from 0 to 9 s, as shown in Fig. 6C (top right)]. Then, we divided the trials into two groups by setting a series of arbitrary thresholds (red: high DAergic activity, V_DA-Z ≥ Th; green: low DAergic activity, V_DA-Z ≤ −Th, where Th was the threshold for the analysis of high/low DAergic activity) from these trials (Th was set to 0.9; Fig. 6C). We analyzed the P_w of low or high DAergic activity trials for the adjacent waiting period with different thresholds. In doing so, we found that the probability of waiting increased rapidly as the absolute value of the threshold increased. The P_w of high DA and low DA activity trials fit well with a fifth-degree polynomial function (R² = 0.93, −2.1 ≤ threshold ≤ 2.1). When the absolute values of the threshold are large enough (|Th| ≥ 1.7), the P_w of the high DA activity trials is significantly (P = 0.04, F_1,12 = 5.483, two-way ANOVA) higher than the P_wait of the low DA-ramping activity trials in adjacent waiting periods (|threshold| = 2.0, P = 0.02; |threshold| = 2.1, P < 0.001, Sidak’s multiple comparisons test, n = 7; Fig. 6D).

Last, we investigated the influence of fluctuations of intrinsic VTA DAergic activity on the waiting performance of mice in the delayed gratification task. There were certain trials in which DAergic activity across the whole duration of waiting was significantly higher (red, high-ramping) or lower (green, low-ramping) than the mean DAergic activity (see Materials and Methods). We then got two groups of trials and found that the cumulative distribution of waiting durations in high-ramping trials shifted to the right, with significantly higher normalized waiting durations (1.03 ± 0.01) compared to those low-ramping trials (0.98 ± 0.01, P = 0.024, n = 7, paired Student’s t test; Fig. 6E), but there was no difference between the normalized waiting durations for the trials immediately following the high-ramping and low-ramping trials (next trial of high-ramping, 1.01 ± 0.01; next trial of low-ramping, 0.99 ± 0.01; P = 0.290, n = 7, paired Student’s t test; Fig. 6F). These results accorded with our optogenetic manipulation experiment (Fig. 4, D and E), which indicated that optogenetically manipulated VTA DAergic activity transiently influences the duration of waiting in the delayed gratification task.

DISCUSSION

Here, we reported a previously unreported behavioral task in which the mice were trained to learn a foraging task with a delayed gratification paradigm. Mice learned to wait for bigger rewards that they received after waiting for longer (Fig. 1, F to H). On a neural level, we found that the calcium signal of VTA DAergic neurons ramped up consistently when mice waited in place before taking action to fetch the expected reward (Fig. 2, G and H). Further data analysis showed that the ramping VTA DA activity indeed influenced the behavioral performance of waiting (Fig. 6, B to E), which was confirmed with bidirectional optogenetic manipulations of VTA DAergic activity (Fig. 4, D and E). Last, we developed an RL model that predicted our experimental observations well and consolidated the conclusion that the ramping up of VTA DAergic activity signaled the value of waiting in the delayed gratification task, which involved real-time deliberation (Fig. 5, B to G).

DA release in the nucleus accumbens (NAc) was previously conjectured to sustain or motivate the goal-directed behavior and resistance to distractions (13, 14). Here, we explicitly implemented continuous less-optimal options during the delayed gratification process, in which, to achieve better performance, mice needed to sustain waiting and prevent/control impulsivity (3, 6, 36, 37). We found remarkable and sustained DAergic activation when mice managed to wait longer and further demonstrated a causal link between DAergic activation and the increase in transient waiting probability. Furthermore, we found DAergic activity ramps up in a consistent manner during waiting, mimicking the value of waiting along with a series of states in our Continuous Deliberation RL model, both of which presumably contributed to pursuing a more valuable future goal and resisting the distraction of the less-optimal immediate options in our task. The momentary DAergic activity was found to correlate positively with the momentary waiting probability, which also suggested that DAergic activity may be involved in the continuous deliberation process. Therefore, we not only demonstrated the behavioral significance of DAergic activity in delayed gratification but also depicted “a continuous deliberation” framework in which DAergic activity may participate to help achieve more flexible and sophisticated performance.

Numerous works have used Pavlovian conditioning in studying DAergic activity (10, 12, 38–40). Some studies paired the reward with a cue (or cues) such that the animals do not need to perform effortful work to obtain rewards. It is well known that this kind of DAergic activity signals the RPE via phasic firing. In the studies using operant conditioning or goal-directed behavior, the animals have to perform actions and need effortful work to obtain outcomes, and a ramping up of DAergic activity was reported to emerge while the animals were approaching the reward (13, 14, 41, 42). This ramping activity was suggested to signal the value of work (13) or a distant reward (14), but key evidence is lacking because the change of sensory input flow markedly alters the DAergic activity over time. Under such mutual influence, it is impossible to identify the RPE or the value of work from external cues. The RPE model of ramping activity assumes that the value increases exponentially (or at least in a convex curve) as the reward is approached. Under this model, sensory feedback is suggested to result in the RPE signal ramping up (41, 43, 44), while a lack of sensory feedback is predicted to make a flat RPE signal. In contrast, the ramping up of DAergic activity is well isolated from the external sensory inputs when performing the delayed gratification task in our model. Mice continuously deliberate about the current state and future rewards without any external sensory inputs while waiting in place. Despite the lack of external sensory inputs, we still observed the calcium signal of VTA DAergic neurons ramping up in a consistent manner, functionally mimicking an inner variable of the evolving value of waiting. This observation is consistent with the hypothesis of dopamine signaling the value that is related to time and effort investment under certain circumstances (13) but cannot be immediately explained by an RPE response to external sensory inputs.

Midbrain DAergic neurons play an important role in RL (9, 11, 12, 45, 46), where activation of DAergic neurons usually produces a reinforcement effect on an associated action, stimulus, or place. However, in our delayed gratification task, optogenetic manipulation of DAergic activity substantially influenced the ongoing behavior during the current trial without a visible reinforcement effect on later trials. Notably, this optogenetic manipulation was not sufficient to induce a reinforcement effect in the random place performance test (RPPT). These results revealed the distinct and potent instantaneous effect of DAergic activity during delayed gratification. By simulating transient manipulations of variables in the RL model, we showed that manipulating dopamine activity was equivalent to manipulating the value of waiting in the model. In contrast, manipulating the value of leaving or the RPE signal itself caused markedly different effects on behavior. The observations and analysis in our experiments suggest that the value of waiting is represented in VTA DAergic neurons during a delayed gratification task. This significantly updates the understanding of the coding mechanisms and fundamental functions of the DAergic system in delayed gratification. Our results suggested that DAergic neuron stimulation during the RPPT test is not rewarding but does lead to a shift in wait time. This control experiment was performed to exclude the rewarding effect of our DAergic stimulation paradigm during the delayed gratification task. However, such a test may not be strictly comparable with stimulation during the delayed gratification task because of the differences in the behavioral contexts.

The previous finding suggested that reasonable behavior in the face of instant gratification requires suppression of reflexive reward desiring. Human brain imaging results demonstrated that hemodynamic responses to conditioned (rewarding) stimuli in both the NAc and the VTA were significantly attenuated during the desire-reason dilemma (47). Such discrepancies with our results may be the consequence of different behavioral strategies, in which they measured the reward-related activation during a desire-reason dilemma, and we measured the DA activity during the waiting time. In addition, the different temporal and spatial resolution of human brain imaging and fiber photometry and electrophysiology may lead to the discrepancies, and our ramping pattern of DAergic activity also indicated that there are inhibitory tones in the NAc and VTA during the beginning phase of wait.

The design of our delayed gratification task recapitulates the realistic situation where immediate less-valuable choices lie in the way of pursuing a later but possibly larger benefit. A deficit in the ability to resist immediate reward for the delayed but possibly larger reward is closely related to a variety of disorders such as obesity, gambling, and addiction (1, 48). The ramping VTA DAergic activity accords with a model of NOW versus LATER decisions in which DAergic signals have a strong influence on the prefrontal cortex in favoring LATER rewards (2). We propose that the sustained phasic VTA DAergic activity during the delay period could serve as a neural basis for the power to resist a temptation close at hand and improve reward rate or goal pursuit in the long run.

MATERIALS AND METHODS

Mice

Animal care and use strictly followed institutional guidelines and governmental regulations. All experimental procedures were approved by the Institutional Animal Care and Use Committee at the Chinese Institute for Brain Research (Beijing) and ShanghaiTech University. Adult (8 to 10 weeks) dopamine transporter (DAT)–internal ribosome entry site (IRES)–Cre knock-in mice (JAX, stock no. 006660) were trained and recorded. Mice were housed under a reversed 12-hour day/12-hour night cycle at 22° to 25°C with free access to ad libitum rodent food.

Stereotaxic viral injection and optical fiber implantation

After deep anesthesia with isoflurane in oxygen, mice were placed on the stereoscopic positioning instrument. Anesthesia remained constant at 1 to 1.5% isoflurane supplied per anesthesia nosepiece. The eyes were coated with Aureomycin eye cream. The scalp was cut open, and the fascia over the skull was removed with 3% hydrogen peroxide in saline. The bregma and lambda points were used to level the mouse head. A small window of 300 to 500 μm in diameter was drilled just above the VTA [Anterior–Posterior (AP), −3.10 mm; Medial–Lateral (ML), ±1.15 mm; and Dorsal-Ventral (DV), −4.20 mm] for viral injection and fiber implantation. A total of 300 nl of AAV2/9-hSyn-DIO-GCamp6m (10¹²) solution was slowly injected at 30 nl/min unilaterally for fiber photometry recording. Either 300 nl of AAV2/9-EF1a-DIO-hChR2(H134R)-mCherry (10¹²) or 300 nl of AAV2/9-EF1a-DIO-eNpHR3.0-mCherry (10¹²) was injected bilaterally for optogenetic experiments. The injection glass pipette was tilted at an angle of 8° laterally to avoid the central sinus. After injection, the glass pipette was kept in place for 10 min and then slowly withdrawn. An optical fiber [200 μm outside diameter (O.D.), 0.37 numerical aperture (NA); Anilab] hold in a ceramic ferrule was slowly inserted into the brain tissue with the tip slightly above the viral injection sites. The fiber was sealed to the skull with dental cement. Mice were transferred to a warm blanket for recovery and then housed individually in a new home until all experiments were done.

Behavioral tasks

One week after surgery, mice started a water restriction schedule to maintain 85 to 90% of free-drinking bodyweight for 5 days. The experimenter petted the mice 5 min per day for 3 days in a row and then started task training. All behavioral tasks were conducted during the dark period of the light/dark cycle.

The foraging task shuttle box had two chambers (10 cm by 10 cm by 15 cm) connected by a narrow corridor (45 cm by 5 cm by 15 cm; Fig. 1A). A water port (1.2-mm O.D. steel tube, 3 cm above the floor) was attached to the end of one chamber, defined as the reward zone, with the other as the waiting zone. The position of the mouse in the shuttle box was tracked online with a custom MATLAB (2016b, MathWorks) program through an overhead camera (XiangHaoDa, XHD-890B). The experimental procedure control and behavioral event acquisition were implemented with a custom MATLAB program and an integrated circuit board (Arduino UNO R3).

One-arm foraging task (pretraining)

A water-restricted mouse was put in the shuttle box for free exploration for up to 1 hour. When the animal traveled from the waiting zone through the corridor to the reward zone to lick the water port, 10 μl of water was delivered by a step motor in 100 ms as a reward. A capacitor sensor monitored the timing and duration of licking. The animals return to the waiting zone to initiate the next trial. Exiting from the waiting zone triggered an auditory cue (200 ms at 4-kHz sine wave with 90 dB) to signal this exit from the waiting zone. The time spent in the waiting zone was defined as the waiting duration. The training was conducted every day for a week. All mice learned to move quickly back and forth between the two chambers to maximize the reward rate within 1 week.

Delayed gratification task

From the second week, the volume of water reward was changed to a function proportional to the waiting time: a wait time of 0 to 2 s for 0 μl; 2 to 4 s triggered delivery of 2 μl; 4 to 6 s, 6 μl; 6 to 8 s, 18 μl; and >8 s, 30 μl, as shown in Fig. 1A. The training was conducted 5 days a week, from Monday to Friday.

P_w calculation

We divided all trials into two groups, waiting trials and leaving trials, according to whether the animal remained to wait or left during a given time interval, such as 1 s after each behavioral period. Then, we calculated the P_w in this given time interval by the number of “waiting trials” [N_w(n)] and the number of “leaving trials” [N_L(n)] in the time window n

$$P_{\mathrm{w}(n)}=\frac{N_{\mathrm{w}(n)}}{N_{\mathrm{w}(n)}+N_{\mathrm{L}(n)}}$$

Then, we could calculate the P_w for a given time duration

$$P_{\mathrm{w}}=\frac{{\displaystyle {\sum }_0^9}{N}_{\mathrm{w}(n)}}{{\displaystyle {\sum }_0^9}{N}_{\mathrm{w}(n)}+{\displaystyle {\sum }_0^9}{N}_{\mathrm{L}(n)}}$$

Linear mixed model

We implemented the LMM analysis using the open-source Python package “statsmodels” (www.statsmodels.org/stable/mixed_linear.html). The binary value of waiting or leaving during a specific behavioral period t_beh was set as the dependent factor [t_beh = [1, 2), [2, 3), [3, 4), or [4, 5); unit, seconds]. The fluctuation of momentary DA signal from its mean during a preceding period t_DA was set as fixed effects [t_DA = [0, 1), [1, 2), [2, 3), [3, 4); unit, seconds; note that t_DA is always smaller than t_beh]. The animal identity and session numbers were set as a random effect (n = 5 for each animal from the third week). The parameters of the model were estimated by restricted maximum likelihood estimation.

Optogenetic stimulation

Lasers, with wavelength of 473 nm for activation and 589 nm for inhibition, were coupled to the common end of a patchcord (200-μm O.D., 1 m long, and 0.37 NA). The patchcord split through an integrated rotatory joint into two ends connected to optical fibers implanted as described above (200-μm O.D. and 0.37 NA) for bilateral light delivery. First, the mice were trained for 3 weeks to learn the delayed gratification task. Optical stimulation was delivered pseudorandomly in ~20% of behavioral trials in the test experiment. Square pulses of 20 ms at 10 Hz for activation or a continuous stimulation for inhibition were delivered. The laser was set to ON when the animal entered the reward zone and to OFF upon exiting from the reward zone. The maximal laser stimulation was no longer than 16 s, even if, in the case, a mouse stayed in the waiting zone longer than this time. Continuous laser power at the tip of the splitting patchcord was about 10 mW for the 473-nm laser and 8 mW for the 589-nm laser, respectively.

Random place performance test

After finishing optogenetic tests for delayed gratification, all mice took an RPPT. The RPPT was carried on in a rectangular apparatus consisting of two chambers (30 cm by 30 cm by 30 cm) separated by an acrylic board. With an 8-cm-wide door open, the mice could move freely between the two chambers. Before testing, each mouse was placed into the apparatus for 5-min free exploration. The RPPT consisted of two rounds of 10-min tests. First, we randomly assigned one chamber as a test chamber. Laser pulses were delivered with 20% possibility (in accord with the setting of laser pulses delivering in delayed gratification task) while the mouse entered the test chamber. The delivery of light, no longer than 16 s, stopped while the mouse exited the test chamber. Next, we switched the chamber in which laser pulses were delivered. The laser output power and pulse length were set the same as in the optogenetic manipulations in the delayed gratification task. In this task, we analyzed the time in each chamber with or without laser delivered.

Fiber photometry recording

During the behavioral task training and test, we recorded the fluorescence signal of VTA DAergic neurons. The signal was acquired with a fiber photometry system equipped with a 488-nm excitation laser and a 505- to 544-nm emission filter. The GCaMP6m signal was focused on a photomultiplier tube (Hamamatsu, R3896 and C7319) and then digitalized at 1 kHz and recorded with a 1401 digitizer and Spike2 software (Cambridge Electronic Design, Cambridge, UK). An optical fiber (200-μm O.D., 0.37 NA, and 1.5 m long; Thorlabs) was used to transfer the excitation and emission light between recording and brain tissue. The laser power output at the fiber tip was adjusted to 5 to 10 μW to minimize bleaching.

All data were analyzed with custom programs written in MATLAB (MathWorks). First, we sorted the continuously recorded data by behavioral trials. For each trial, the data spanned the range between 1 s before the waiting onset and 2 s after the reward. Before hooking up the fiber to the mouse, we recorded 20 s of data and averaged as F_b as the ground baseline. For each trial, we averaged 1 s of data before the waiting onset as the baseline F₀ and then calculated its calcium transient as

$$\mathrm{\Delta }\mathit{F}/F(\%)=(F-F_0)/(F_0-F_{\mathrm{b}})\times 100(\%)$$

In the correlation analysis between VTA DAergic activity before waiting and the waiting duration of mice, we used averaged 1-s data before the waiting onset as the DAergic activity before waiting. In the analysis of high-ramping and low-ramping DAergic activity, we compared the whole calcium signal of every trial with the average curve (the same length as the analyzed calcium signal) of all trials from one mouse in a single training day with paired a t test and then separated their waiting times into high-ramping group and low-ramping group.

To facilitate presenting the data, we divided each trial data into four segments, including 1 s before waiting onset, waiting, running, and 2 s after rewarding. For comparing the rising trends, we resampled the data segments at 100, 100, 50, and 100 data points, respectively. In the delayed gratification task, the trial data were aligned to the waiting onset and presented as the mean plots with a shadow area indicating SEM of fluctuations.

In vivo electrophysiological recording

A custom-made head plate was placed on the skull of each mouse and affixed in place with dental cement. We removed the skull and dural carefully above the recording window before the implantation. Stereotrodes were twined from 12.7-μm Ni-Cr-Fe wires (Stablohm 675, California Fine Wire, CA, USA). Then, eight stereotrodes were glued together and gold plated to reduce impedance to 250 to 500 kilohms. The stereotrodes were gradually lowered to a depth of 0.7 mm above the VTA. A silver wire (127 μm diameter; A-M System) was attached to one of the four skull-penetrating M1 screws to serve as ground (19). Mice were allowed a recovery time of 7 days. Extracellular spiking signals were detected with eight stereotrodes and amplified (1000×) through a custom-made 16-channel amplifier with built-in band-pass filters (0.5 to 6 kHz). We selected one channel that did not show spike signals and defined it as a reference ground to reduce movement artifacts. Analog signals were digitized at 25 kHz and sampled by a Power1401 digitizer and Spike2 software (Cambridge Electronic Design). Spikes recorded by the stereotrode were sorted offline using Spike2 software (Cambridge Electronic Design). Classified single units should have a high signal-to-noise ratio (>3:1), reasonable refractory period (interspike interval, >1 ms), and relatively clear boundaries among different principal components analysis clusters. The spike frequency and waveform were used to determine cell type as the DA or γ-aminobutyric acid neurons. The putative DA neurons were identified by their relatively low firing rate (the mean firing rate, <15 Hz) and a broad initial positive phase of >1 ms. Then, the spike trains were aligned with the waiting onset in delayed gratification task. PSTHs (bin width, 100 ms) for each trial were calculated and presented with averages in plots.

Calcium signal simulation

We performed a simple simulation of the “calcium fluorescence signal” contributed by each recorded unit using kernel convolution with 0.1-s time bin (49). The kernel that we used is composed of a linear rising edge and exponential decay. We set the kernel parameters, namely, the rise time and half-peak decay time, to 0.2 and 0.7 s, respectively, from the relationship between fluorescence signal and a single action potential, without concerning the nonlinear effect of multiple action potentials (50).

RL model

We investigated two potential scenarios. One was that the mouse decided on a waiting duration before entering the waiting area and then waited according to the decided goal. The other scenario was that the mouse entered the waiting zone and determined whether to wait or leave as an ongoing process throughout the whole waiting period. We called these two scenarios “Decision Ahead” and “Continuous Deliberation,” respectively, and formulated corresponding RL-based models for simulation using Python (Python Software Foundation, version 2.7, available at www.python.org/).

Decision ahead

Inspired by animal behavior, we simply set three optional “actions” with different expected waiting durations that could empirically cover the main range of animals’ waiting durations seen during training (T_a1 = 1.65 s for action 1, T_a2 = 2.72 s for action 2, and T_a3 = 4.48 s for action 3). These waiting durations were equally spaced on the log-time axis, consistent with Weber’s law [that is, ln(T_a1) = 0.5, ln(T_a2) = 1, and ln(T_a3) = 1.5]. During the execution of action a_i, we imposed additional noise on the timing so that the actual waiting time τ_ai for action a_i followed a Gaussian distribution on the log-time axis centered at the T_ai, ln ~N(ln(Τ_ai), 0.4²), i = 1,2,3. These settings allowed us to best capture the animals’ waiting performance in the model. For each trial, the agent chose an action randomly based on the three action values and a Boltzmann distribution (SoftMax)

$$P_{a_i}=\frac{e^{\mathrm{\beta }{Q}_{a_i}}}{{\sum }_{j=1,2,3}{e}^{\mathrm{\beta }{Q}_{a_j}}}$$

where P_ai was the probability of choosing action a_i and waiting for τ_ai. Q_ai was the value for a_i. β was the inverse temperature constant tuned to 5 to best fit the animal experimental data. After waiting, the agent would get a reward according to the same reward schedule used in our experiment. Each action value was updated separately during the reward delivery

$$\mathrm{\delta }=r–Q_a$$

$$r=R/(\mathrm{\tau }+1)$$

$$Q_a\leftarrow Q_a+\mathrm{\alpha }*\mathrm{\delta }$$

where the RPE δ was calculated by the difference between the hyperbolically discounted reward r (or “reward rate,” given by the absolute reward R dividing total time τ + 1 for obtaining the reward, where τ was the waiting duration and the additional 1 s was the estimated delay of running between the two zones) and the chosen action value Q_a. The RPE was then used to update the value of the chosen action. We tuned the learning rate α to 0.002 to fit the animal behavioral data.

Continuous deliberation

In each trial, the agent would go through a series of hidden states, each lasting for 0 to 2 s randomly according to a Gaussian distribution (mean at 1 s). At each hidden state, the agent had two action options, either to keep waiting or to leave. If it chose to keep waiting, then the agent would transition to the next hidden state, with the past time of the previous state cumulated to the whole waiting duration. If the choice was to leave, then the cumulation would cease and a virtual reward dependent on the duration was delivered; a new trial would then begin from the initial state. The reward schedule was identical to that used for the animals during the experiments.

The action choice for the future was determined randomly by a Boltzmann distribution (SoftMax) and action values

$$P_{a_{\mathrm{w}}}^{(T+1)}=\frac{e^{\mathrm{\beta }{Q}_{a_{\mathrm{w}}}^{(T+1)}}}{e^{\mathrm{\beta }{Q}_{a_{\mathrm{w}}}^{(T+1)}}+e^{\mathrm{\beta }{Q}_{a_{\mathrm{L}}}^{(T+1)}}}$$

$P_{a_{\mathrm{w}}}^{(T+1)}$ was the probability of choosing to wait for the next state T + 1. $Q_{a_{\mathrm{w}}}^{(T+1)}$ and $Q_{a_{\mathrm{L}}}^{(T+1)}$ were the value of waiting and leaving, respectively, for state T + 1. β was the inverse temperature constant tuned to 5 to best fit the animal experimental data. The action values for each hidden state T were updated by a temporal difference learning algorithm (SARSA)

$$\mathrm{\delta }=r+\mathrm{\gamma }*Q_{a\prime }^{(T+1)}–Q_a^{(T)}$$

$$r=R/(\mathrm{\tau }+1)$$

$$Q_a^{(T)}\leftarrow Q_a^{(T)}+\mathrm{\alpha }*\mathrm{\delta }$$

where the future action a′was determined by the Boltzmann distribution in the previous step. The current action a and the future action a′ could both be either waiting or leaving. The prediction error δ was calculated by the sum of reward rate r (r remained zero until the reward R was delivered; τ + 1 was the total time for obtaining the reward, where τ was the waiting duration and the additional 1 s was the estimated delay of running between the two zones) and the future action value $\mathrm{\gamma }*Q_{a\prime }^{(T+1)}$ discounted by γ (γ = 0.9), minus the current action value $Q_a^{(T)}$. When a was leaving, the future action value $Q_{a\prime }^{(T+1)}$ would always be zero. This error signal δ was used to update $Q_a^{(T)}$ with the learning rate α = 0.001.

As a Markovian process, each state would be identical to the agent no matter how the state was reached or what the following actions might be. Thus, we extracted the learned value of waiting as a time series along all the hidden states to compare with the averaged curve of VTA DAergic activity. For each trial, we also extracted the time series of the transient waiting value for a trial-wise analysis. Apart from the value of waiting, we could also extract the time series of RPE for each trial. We simulated optogenetic manipulation in the model after normal training was accomplished as in the animal experiments.

Value manipulation

In 20% of trials in the simulation session, the future waiting value throughout the whole waiting period was manipulated. The optogenetics activation was simulated as an extra positive value added onto the future waiting value, and the optogenetics inhibition corresponded to a proportional decrease of the future waiting value as follows

$$Q_{a_{\mathrm{w}}}^{(T+1)}\leftarrow {\tilde{Q}}_{a_{\mathrm{w}}}^{(T+1)},\text{for the current trial}$$

$$\text{where} {\tilde{Q}}_{a_{\mathrm{w}}}^{(T+1)}=\{\begin{array}{c}{Q}_{a_{\mathrm{w}}}^{(T+1)}+{∆}_{\text{value}-\text{ext}},\text{if}″\text{ChR}2-\text{lighton}″\\ {\mathrm{\kappa }}_{\text{value}-\text{inh}}{Q}_{a_{\mathrm{w}}}^{(T+1)},\text{if}″\text{eNPHR}-\text{lighton}″\end{array}$$

and $\mathrm{\delta }=r+\mathrm{\gamma }*{\tilde{Q}}_{a_{\mathrm{w}}}^{(T+1)}–Q_a^{(T)},\mathrm{\text{if}} a^{\prime }=a_{\mathrm{w}}$.

Here, we set ∆_value−ext = 0.15 and κ_value−inh = 0.9 so that the change in averaged waiting duration in the simulated “light-on” trials could capture the magnitude of the instantaneous effect of optogenetic stimulations on the current trials. Using these parameters “calibrated” by the current trial effect, we were able to compare the stimulation effect on the light-off or the following trials in both real and simulated situations. In addition, note that if the future action was chosen as waiting, then the manipulated value of waiting would be used in the RPE calculation and, thus, current action value updating as well.

RPE manipulation

Under this situation, in 20% of trials in the stimulation session, instead of the future waiting value, RPE (δ) was manipulated throughout the whole waiting period as follows

$$\tilde{\mathrm{\delta }}=\{\begin{array}{c}\mathrm{\delta }+{∆}_{\text{RPE}-\text{ext}},\text{if}″\text{ChR}2-\text{lighton}″\\ \mathrm{\delta }-{∆}_{\text{RPE}-\text{inh}},\text{if}″\text{eNPHR}-\text{lighton}″\end{array}$$

and $Q_a^{(T)}\leftarrow Q_a^{(T)}+\mathrm{\alpha }*\tilde{\mathrm{\delta }}$. We set ∆_RPE−ext = 15 and ∆_RPE−inh = 20, which was calibrated by the current trial effect of real light stimulation.

To simulate the fluctuation in real DAergic signal, we simply multiplied the future waiting value during each state by a factor of σ ~ N(1, 0.3²) (determined by the averaged signal-dependent noise magnitude/relative SD for all momentary DAergic amplitudes), as an addition to the original model [this is only implemented for fig. S8 (E and F)].

Electrophysiological recordings

Adult (8 to 10 weeks) DAT-IRES-Cre knock-in male mice 4 weeks after injection with AAV2/9-EF1a-DIO-ChR2(H134R)-mCherry or AAV-DIO-eNpHR3.0-mCherry were anesthetized with an intraperitoneal injection of pentobarbital (100 mg kg⁻¹) and then perfused transcardially with ice-cold oxygenated (95% O₂/5% CO₂) N-methyl-d-glucamine (NMDG) artificial cerebrospinal fluid (ACSF) solution [93 mM NMDG, 93 mM HCl, 2.5 mM KCl, 1.25 mM NaH₂PO₄, 10 mM MgSO₄·7H₂O, 30 mM NaHCO₃, 25 mM glucose, 20 mM Hepes, 5 mM sodium ascorbate, 3 mM sodium pyruvate, and 2 mM thiourea (pH 7.4), 295 to 305 mosM]. After perfusion, the brain was rapidly dissected out and immediately transferred into an ice-cold oxygenated NMDG ACSF solution. Then, the brain tissue was sectioned into slices horizontally at 280 μm in the same buffer with a vibratome (VT-1200 S, Leica). The brain slices containing the VTA were incubated in oxygenated NMDG ACSF at 32°C for 10 to 15 min and then transferred to a normal oxygenated solution of ACSF (126 mM NaCl, 2.5 mM KCl, 1.25 mM NaH₂PO₄, 2 mM MgSO₄·7H₂O, 10 mM glucose, 26 mM NaHCO₃, and 2 mM CaCl₂) at room temperature for 1 hour. A slice was then transferred to the recording chamber and then submerged and superfused with ACSF at a rate of 3 ml/min at 28°C. Cells were visualized using infrared differential interference contrast and fluorescence microscopy (BX51, Olympus). VTA DAergic neurons were identified by their fluorescence and other electrophysiological characteristics. Whole-cell current-clamp recordings of VTA DAergic neurons were made using a MultiClamp 700B amplifier and Digidata 1440A interface (Molecular Devices). Patch electrodes (3 to 5 megohms) were backfilled with internal solution containing the following: 130 mM K-gluconate, 8 mM NaCl, 10 mM Hepes, 1 mM EGTA, 2 mM Mg·adenosine triphosphate, and 0.2 mM Na₃·guanosine triphosphate (pH 7.2, 280 mosM). Series resistance was monitored throughout the experiments. For optogenetic activation, blue light was delivered onto the slice through a 200-μm optical fiber attached to a 470-nm light-emitting diode (LED) light source (Thorlabs, USA). The functional potency of the ChR2-expressing virus was validated by measuring the number of action potentials elicited in VTA DAergic neurons using blue light stimulation (20 ms, 10 Hz, 2.7 mW) in VTA slices. For optogenetic inhibition, yellow light (0.7 mW) was generated by a 590-nm LED light source (Thorlabs, USA) and delivered to VTA DAergic neurons expressing eNpHR3.0 through a 200-μm optical fiber. To assure eNpHR-induced neuronal inhibition, whole-cell recordings were carried out in current-clamp mode and spikes were induced by current injection (200 pA) with the presence of yellow light. Data were filtered at 2 kHz, digitized at 10 kHz, and acquired using pClamp10 software (Molecular Devices).

Immunostaining

Mice were deeply anesthetized with pentobarbital (100 mg/kg, intraperitoneally), followed by saline perfusion through the heart. After blood was drained out, 4% paraformaldehyde (PFA) was used for fixation. Upon decapitation, the head was soaked in 4% PFA at room temperature overnight. The brain was harvested the next day, postfixed overnight in 4% PFA at 4°C, and transferred to 30% sucrose in 0.1 M phosphate-buffered saline (PBS) (pH 7.4) for 24 to 48 hours. Coronal sections (20 μm) containing the VTA were cut on a cryostat (Leica CM3050 S). The slides were washed with 0.1 M PBS (pH 7.4), incubated in blocking buffer [0.3% Triton X-100 and 5% bovine serum albumin in 0.1 M PBS (pH 7.4)] for an hour, and then transferred into the primary antibody (rabbit anti-tyrosine hydroxylase antibody, 1:1000; Invitrogen) in blocking buffer overnight at 4°C. The sections were washed three times in 0.1 M PBS and then incubated with donkey anti-rabbit immunoglobulin G H&L secondary antibody (conjugated to Alexa Fluor-488 or Alexa Fluor-594, 1:1000; Jackson ImmunoResearch) at room temperature for 2 hours. The nucleus was stained with 4′,6-diamidine-2-phenylindole. Sections were mounted in glycerin and covered with coverslips sealed in place. Fluorescent images were collected using a Zeiss confocal microscope (LSM 880).

Quantification and statistics

All statistics were performed by MATLAB (R2016b, MathWorks) and Python (v2.7, Python Software Foundation) routines. Data were judged to be statistically significant when the P values were less than 0.05. Asterisks denote statistical significance: *P < 0.05, **P < 0.01, and ***P < 0.001. Unless stated otherwise, values were presented as means ± SEM.

Supplementary Materials

This PDF file includes:

Figs. S1 to S8

Other Supplementary Material for this manuscript includes the following:

Movies S1 and S2

Other file

View/request a protocol for this paper from Bio-protocol.