A Radiology-focused Review of Predictive Uncertainty for AI Interpretability in Computer-assisted Segmentation

Abstract

The recent advances and availability of computer hardware, software tools, and massive digital data archives have enabled the rapid development of artificial intelligence (AI) applications. Concerns over whether AI tools can “communicate” decisions to radiologists and primary care physicians is of particular importance because automated clinical decisions can substantially impact patient outcome. A challenge facing the clinical implementation of AI stems from the potential lack of trust clinicians have in these predictive models. This review will expand on the existing literature on interpretability methods for deep learning and review the state-of-the-art methods for predictive uncertainty estimation for computer-assisted segmentation tasks. Last, we discuss how uncertainty can improve predictive performance and model interpretability and can act as a tool to help foster trust.

Keywords: Segmentation, Quantification, Ethics, Bayesian Network (BN)

© RSNA, 2021

Summary

Interpretable, highly accurate segmentation models have the potential to provide substantial benefit for automated clinical workflows.

Essentials

• ■ Estimating the uncertainty in a model’s prediction (predictive uncertainty) can help clinicians quantify, visualize, and communicate model performance.

• ■ Variational inference, Monte Carlo dropout, and ensembles are reliable methods to estimate predictive uncertainty.

• ■ Interpretable artificial intelligence is key for clinical translation of this technology.

Introduction

Artificial intelligence (AI) has seen a resurgence in popularity since the development of deep learning (DL), a method to learn representations within data with multiple levels of abstraction (1). DL frameworks have been widely successful for a variety of applications, including image object recognition and detection tasks where there is a particular interest in applying this technology to interpret complex medical images (2). As modern DL frameworks are structured through multiple hidden layers of network weights, these networks are coined as black box models. An important question that arises from such a model is how to trust the prediction of that model, particularly in instances where that prediction can alter clinical outcomes. Even though black box models are not particularly understood, their use in the medical field is analogous to some pharmaceutical drugs, such as thalidomide, that continue to be the standard of care even when clinicians do not fully understand how they work. In contrast, clinicians can estimate the risks associated with a particular drug or procedure, whereas current DL models have yet to provide similar estimates of risk or uncertainty.

Qualitative interpretability methods for DL models have been discussed in the comprehensive review by Reyes et al (3), where there is a strong focus on classification interpretability using saliency maps, local interpretable model-agnostic explanations, and gradient-weighted class activation mapping. Building on this work, we further clarify the semantics of interpretable and explainable models and introduce various methods that estimate predictive uncertainty. Predictive uncertainty is a quantitative value, or set of values, that estimates a model’s confidence in its output: A highly confident model would have low uncertainty, and vice versa.

We narrow our focus to the application of predictive uncertainty for segmentation, a particularly important task for which DL has substantial potential to accelerate typical clinical routines. We further emphasize that interpretability is a key factor if the clinical implementation and longevity of such technology is to be successful. Therefore, throughout this review, we discuss why these uncertainty estimates are important for improving model interpretability, where they can fail, and their importance for detecting out-of-distribution (OOD) samples.

Interpretability, Explainability, and Trust

As machine learning (ML) permeates all facets of society, users and stakeholders have sought understandable ML models (4). The two key terms for understandable ML, “interpretability” and “explainability,” are used either synonymously or with explicit distinction (3–8). We borrow from Lipton (9) and state that interpretability and explainability are different concepts and should be treated as such. Rather than trying to comprehend the inner workings of a model, as is done with explainable methods, interpretability attempts to understand model predictions at a higher level of abstraction. Current interpretability methods typically act in tandem with a complex model and attempt to communicate the model’s decision through either post hoc methods or interactive approaches (8).

The lack of trust in an ML model is typically attributed to a lack of model transparency, which has led to an increase in interpretability research for ML. Some argue that model interpretability is a precursor to trust (10). We emphasize that trust is particularly important in DL, where models are notoriously complex due to the large number of parameters used to achieve state-of-the-art predictive performance. The cultivation of trust in ML models could benefit from an externalist epistemologic perspective, where trust is rationally justified through proven, repetitive, and reproducible experiences (11), rather than an attempt to understand what is “under the hood.”

The 2018 Radiological Society of North America AI Summit emphasized that building trust is a key component for the practical implementation of AI (12). Education and data curation are of top priority to build trust. Model interpretability tools should foster clinicians’ trust of computer-based models. Research has shown that individuals are more likely to follow advice when given notions of confidence (13) and that diagnostic accuracy can decrease when radiologists of all levels of expertise are given inaccurate advice (AI or not) (14). Thus, AI should lead to improved clinical outcomes if models can reach higher than expert-level diagnostic performance and indicate predictive confidence.

Interpretability through Uncertainty

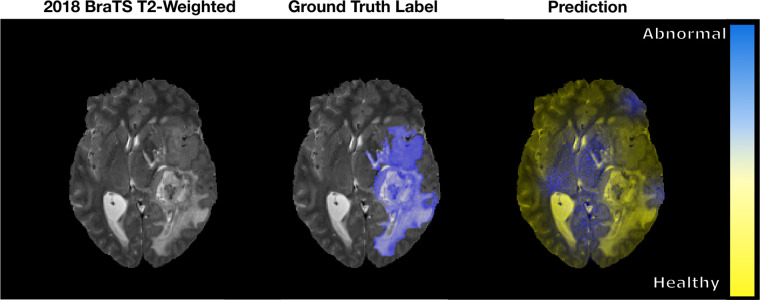
Typical DL algorithms do not assign uncertainty estimates with their output predictions. This lack seems counterintuitive, as traditional classification or segmentation (ie, pixel-wise classification) tasks output a probability that a particular object or pixel corresponds to one of the various classes that the network has been trained to identify. This probability often is interpreted erroneously as model confidence, which may lead to confusion when these algorithms are used (15). Consider an extreme case where a sophisticated DL model has randomly initialized weights and has not been trained. In a tumor segmentation task, for example, the sum of the probabilities for a pixel belonging to either of the two possible classes (tumor, not tumor) must sum to 1. Therefore, there can be instances where an untrained network can output high classwise probability where there is no basis to do so. Figure 1 illustrates such a segmentation output. In these cases, predictive uncertainty methods can provide a way to evaluate model confidence at the output, which should be low and independent of the predicted class probability.

Figure 1:

An example of a pixel-wise classification output fused to a sample axial T2-weighted MRI section from the 2018 Medical Image Computing and Computer Assisted Intervention Society Multimodal Brain Tumor Image Segmentation (BraTS) dataset (16,17). The ground truth abnormality is shown in blue. The prediction from the untrained network classifies the abnormal and healthy brain tissues as blue and yellow, respectively. As seen, the network classifies healthy brain tissue as abnormal when there is no basis to do so.

For the following discussion, we narrow our focus to provide a foundation for predictive uncertainty, a metric that is less discussed in the existing literature (3).

Predictive Uncertainty

To describe model uncertainty, we provide an illustrative example. Consider a hypothetical model that has been trained on a large dataset of routine brain MR images with the goal of determining the volume’s scanning sequence (T1 weighted, T2 weighted, T2 fluid-attenuated inversion-recovery, etc). Presumably, if the model has been trained well, it will correctly distinguish the sequence with high confidence. What would happen if the model were to be exposed to a modality it was not trained with? As Gal et al (18) describe, this question is an example of OOD data. The desired behavior of the model would be to try and provide a reasonable prediction and report the lack of confidence the model has in its output.

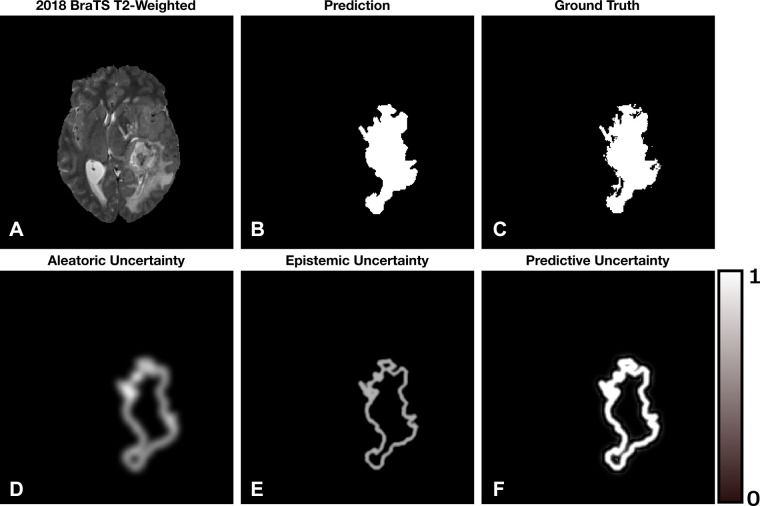
The uncertainty associated with a model’s prediction can be broken down into three categories: (a) sources of random noise within the data (otherwise known as aleatoric uncertainty), (b) parameter uncertainty (uncertainty in the model’s weights), and (c) structure uncertainty (what is the best model for the job). The addition of (b) and (c) is known as the epistemic uncertainty, where predictive uncertainty is the addition of the aleatoric and epistemic uncertainties. Epistemic uncertainty can be minimized by training the model with a diverse set of task-relevant data. Alternatively, aleatoric uncertainty has a fundamental limit to which it can be reduced because noise cannot be fully characterized. In situations where the uncertainty is estimated, indications of high or low uncertainty can benefit directly from human intervention while still providing value to the clinician. These uncertainties become particularly useful when visually displayed, as shown in Figure 2.

Figure 2:

A simulated example of the aleatoric, epistemic, and predictive uncertainties for a segmentation task. Brighter pixels indicate larger uncertainty with range 0–1. (A) Axial T2-weighted MRI section from the 2018 Medical Image Computing and Computer Assisted Intervention Society Multimodal Brain Tumor Image Segmentation dataset (16,17). (B) The hypothetical segmentation output. (C) The ground truth segmentation. (D) Aleatoric uncertainty localized to the boundaries of the segmentation. (E) Epistemic uncertainty localized to the boundary of the segmentation with less ambiguity compared with the aleatoric uncertainty. (F) Predictive uncertainty, which is the addition of (D) and (E). We notice that the model is confident within the interior of the segmented lesion and less so at the boundary.

Uncertainty can be represented in a variety of different ways depending on the application. In a segmentation task, visualizations can quickly communicate areas in which the model has low or high uncertainty and act as a proxy for the quality of the segmentation (19). Uncertainty values can be aggregated to report a single numeric uncertainty estimate to enable clinicians to directly compare predictions. Whether a reported value or set of values is given within a numeric range, as a confidence interval or a standard deviation, the representation of uncertainty should be malleable depending on the task and the individuals interpreting the model’s prediction. As such, uncertainty estimates can be standardized in relation to the task or discipline as clinicians see fit.

Estimating predictive uncertainty is indispensable in the case of DL, and there has been noteworthy work to integrate it into prediction pipelines. The methods that produce uncertainty estimates are rooted in Bayesian and frequentist statistics and are described in the following sections.

Bayesian Neural Networks

Increased data complexity has led to the development of larger neural network (NN) models to obtain state-of-the-art predictive performance. In Bayesian inference, the model parameters are seen as a set of random variables, each possessing an intrinsic probability distribution around its mean. In this formulation, we are ultimately looking to compute a Bayesian model average to determine the probability of the outcome y, given the data D and network weights ω. This is defined as the predictive probability distribution:

This integral becomes intractable with a large number of parameters and is impractical for NNs (18). As such, methods such as variational inference (VI) have been developed to obtain estimates of this integral. To do so, VI postulates an approximate distribution q(ω|D) that should be distributionally similar to p(ω|D), the true unknown distribution. To ensure that the approximate distribution is optimal, the difference between q(ω| D) and p(ω|D) is measured and iteratively minimized during training (20). Once optimized, the epistemic and aleatoric uncertainties are derived through the variance of the estimated predictive distribution, p(y|D) (21).

A noteworthy limitation of Bayesian modeling is the requirement to inject the necessary prior probability information into the model when determining q(ω|D). The designer of the model needs to make assumptions about the characteristics of the output distribution where a Gaussian approximation is typically used (22). These assumptions typically hinder the optimization process, which often results in underestimating the predictive uncertainty (20).

VI has been used for regression, classification, and segmentation tasks with varying degrees of success. Kwon et al (21) applied this technique to two multisequence MR image datasets from the 2015 Ischemic Stroke Lesion Segmentation challenge. With VI, Kwon et al were able to build on the initial work completed by Kendall and Gal (23) and proposed a new way to obtain and decompose predictive uncertainty without incorporating additional parameters into the model. The method is able to provide voxel-wise estimations of the aleatoric and epistemic uncertainties, which can then be formed into corresponding visualizations.

VI is a promising Bayesian technique, but it comes with implementation challenges. With the associated complexity of medical image data, optimizing the parameters of the network can be difficult using VI (24).

Monte Carlo Dropout

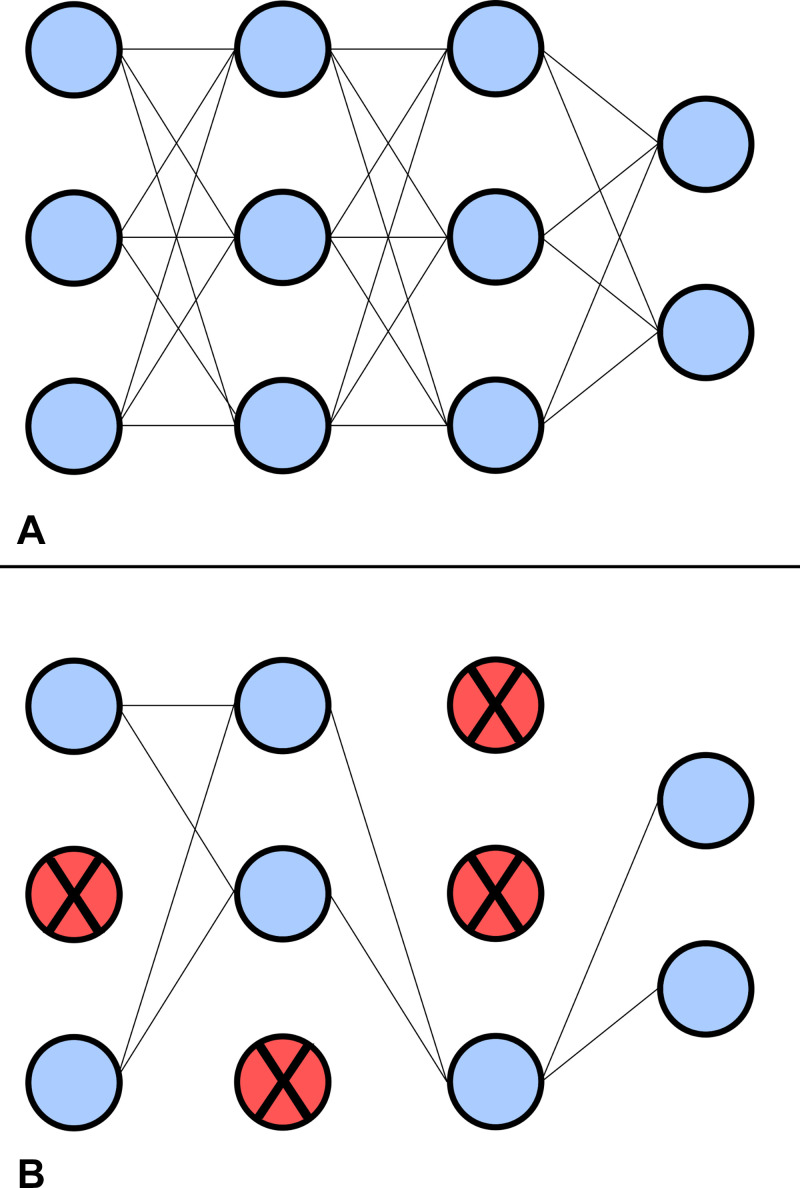
To obtain results with less computational overhead, methods such as Monte Carlo (MC) dropout have been formulated to provide a simple way to obtain Bayesian-like uncertainty estimates. In the field of DL, dropout refers to a training procedure that randomly suppresses a subset of nodes and their corresponding connections within the network to reduce the chance of coadaptation between layers (25). Figure 3 shows a simple NN with and without dropout. Effectively, dropout forces the network to learn more relevant features, reduces overfitting, and thus improves generalization ability. Initially proposed by Gal and Ghahramani (15), MC dropout uses this concept during both the training and testing procedures of the network. To acquire estimates of the epistemic and aleatoric uncertainties, each input sample is put through N stochastic forward passes. The mean and variance of the set of N predictions is used to determine the uncertainties (18).

Figure 3:

Example of a network (A) without and (B) with dropout. Nodes and corresponding connections are suppressed during dropout to improve generalization. The probability for a node to be suppressed during dropout is 0 < P < 1.

Unlike VI, MC dropout requires no prior information to be injected into the model and can obtain an approximation of the output distribution without additional bias. As such, MC dropout can be seen as a frequentist type of solution to estimating predictive uncertainty. With its comparative ease of implementation and Bayesian-like outputs, MC dropout has gained favor within the medical image analysis community compared with its Bayesian counterparts. Nair et al presented the first exploration of multiple uncertainty estimates using MC dropout with a three-dimensional multiple sclerosis lesion segmentation convolutional NN (26). The network was trained with a proprietary, large-scale, multisite, multiscanner multiple sclerosis dataset where voxel-wise and image-wise uncertainty measures were reported. Nair et al showed that by filtering predictions on the basis of its uncertainty, the model’s detection accuracy was greatly improved, particularly in the case of small lesions.

Roy et al (27) used MC dropout for full-brain segmentation with voxel-wise uncertainty along with structural uncertainty metrics per chosen anatomic brain structure. Wang et al (28) derived aleatoric uncertainties with MC dropout and test-time augmentation for fetal brain tumor segmentation. In both cases, the uncertainty estimates resulted in improved predictive performance. Although MC dropout provides a simplistic method for obtaining uncertainty, deep ensembles attempt to obtain more accurate predictions by aggregating predictions from many ML models.

Ensemble Methods

The popular method of ensemble-based DL has shown great success for a variety of prediction tasks. By training numerous models, the implementation allows for more robust prediction ability in tandem with OOD stability (29). A DL ensemble aggregates the results from multiple deterministic NNs trained with different parameter initializations. An output probability is determined through the mean of the ensembled predictions, where the variance around the mean is understood as the predictive uncertainty. Each individual prediction before ensembling is seen as a sample from the predictive distribution and as such, the variance between model predictions can be illustrated in a per-voxel fashion.

The generalization ability of an ensemble is often stronger than any of the individual models that compose the framework (30). Therefore, ensembles can result in improved performance over a larger range of relevant inputs and natively include uncertainty measures at the cost of training multiple large networks. Compared with its Bayesian counterparts, the lack of prior assumptions allows for more flexible parameter optimization. Therefore, it is advantageous to use a method such as ensembling to gather more information about the true predictive distribution and obtain greater predictive performance (22).

Ensembling was initially proposed by Lakshminarayanan et al (30) and was evaluated through a series of nonmedical regression and classification benchmarks. Since its inception, the method has been extended for other DL applications. De Fauw et al (31) presented the first clinical application of this method on a large set of three-dimensional optical coherence tomography scans, showing that ensembling was able to achieve comparable expert-level segmentation performance. Mehrtash et al (32) applied this process to two-dimensional brain, heart, and prostate segmentation tasks for confidence calibration, showing that ensembles performed better in whole-volume and subvolume cases compared with a nonensemble framework. In both studies, the uncertainty estimates were used to improve segmentation in ambiguous regions.

Reliability of Uncertainty Models

When applying uncertainty metrics to a DL model, how can we evaluate which method is optimal? In real-world applications, well-calibrated uncertainty estimates are crucial to determine if a model’s output should be trusted. In this case, proper calibration means that the model should output inference probabilities representative of the true likelihood of occurrence (33). More critically, it is important to know which methods work most reliably under dataset shift, a common problem in medical data. Dataset shift means that something has changed between the training, testing, and clinical distributions, where these shifts are normally attributed to changes in population type, acquisition protocols, and/or annotation inconsistencies (34). Therefore, the effective evaluation of predictive uncertainty is most meaningful in the OOD case and, as such, there has been specific work done in an attempt to determine how different methods behave with OOD data.

Ovadia et al (35) presented a large-scale benchmark for a variety of classification problems to investigate the effect of dataset shift on accuracy and uncertainty calibration for VI, MC dropout, and ensemble networks. Trained with nonmedical data, the quality of the uncertainty quickly degraded with increasing dataset shift independent of the model used. Overall, ensembles were consistently seen to perform more accurately across all tested datasets while being the most robust to shifting, even when using a small number of classification models.

Jungo et al (36) suggested that uncertainty estimates should be coupled with an evaluation of model calibration to ensure that the estimates are sensitive to dataset shift. In a recent study evaluating ML accuracy on ImageNet, Shankar et al (37) stated that a model’s sensitivity to small, naturally occurring dataset shifts is a performance dimension that is not addressed by current ML benchmarks but is easily handled by humans. To move toward clinical translation, considerable work must be done to ensure that interpretability metrics, such as predictive uncertainty, can capture these shifts.

Discussion

The potential for uncertainty estimates to establish trust instills hope for more informed clinical decisions, but no method comes without limitations. With algorithms reaching expert-level performance, ethical decision-making in the context of diagnostic imaging could become even more difficult when the clinician and algorithm differ in their evaluations and/or recommendations for the patient. The potential for diagnostic disparities between the clinician and the computer will lead to an ethical crossroad: who or which is correct? As Grote and Berens (38) describe, should the clinician trust their initial opinion, default to the algorithm, or bring in additional human supervision? If there is a ground truth that can alleviate this disparity, such as referring to pathologic examination, this should be the default course of action, but in some cases, knowing the ground truth is either impractical or impossible. The action made by the clinician will ultimately rest on the trust and understanding they have in the algorithm, along with their experience within the field.

Unfortunately, the dilemma described has no clear answer in many situations. What should be clear is that predictive models add an extra level of complexity that may or may not improve clinical outcomes, depending on how the clinician interacts with the AI platform. That is, additional information might not always streamline the diagnostic process. In routine clinical cases, it is reasonable to ask whether segmentation models would even need estimates of predictive uncertainty, as the radiologist could indicate if the algorithm matches their own prediction. These situations emphasize the necessity for these models to have improved or equal diagnostic performance compared with radiologists, where poor segmentation models would presumably be avoided regardless of whether uncertainty is provided or not. Therefore, the efficacy of these predictive models depends greatly on their performance with in-distribution samples, along with the proper calibration and predictive stability in OOD cases. As clinical data distributions shift, uncertainty is indeed a powerful metric to indicate poor model performance. This becomes relevant in automation pipelines where uncertain predictions can be flagged for further review.

Finally, developing causal DL frameworks provides a promising solution for explainable model composition and prediction, but further research must be done to conclude if causality in DL holds up to its proposed claims (34). Furthermore, the norms surrounding AI in health care must be carefully audited, as defaulting to the algorithm can potentially blur the lines of diagnostic accountability (38).

Conclusion

DL has revolutionized the field of ML and has substantial potential to impact clinical workflows. As model interpretability research continues to accelerate, these efforts will slowly increase clinician trust in AI applications. Furthermore, experience with these models will likely play a key role in their clinical translation. Error always exists, be it from a computational model or through expert human interpretation. We must accept some level of risk when implementing intelligent learning machines, but this risk is acceptable only if it is well understood. Collaboration between researchers, clinicians, and medical imaging regulatory bodies will be paramount to set the groundwork for interpretability, trust, and clinical translation in the coming years.