Collapse of complexity of brain and body activity due to excessive inhibition and MeCP2 disruption

Significance

How does brain function falter when inhibition is not properly balanced by excitation in cerebral cortex? Here we show in rats that excessive inhibition leads to stereotyped, low-complexity relationships among neurons in motor cortex and body movements. We observed similar phenomena in rats with disrupted MeCP2 function, suggesting that imbalanced inhibition may contribute to motor dysfunction in Rett syndrome.

Abstract

Complex body movements require complex dynamics and coordination among neurons in motor cortex. Conversely, a long-standing theoretical notion supposes that if many neurons in motor cortex become excessively synchronized, they may lack the necessary complexity for healthy motor coding. However, direct experimental support for this idea is rare and underlying mechanisms are unclear. Here we recorded three-dimensional body movements and spiking activity of many single neurons in motor cortex of rats with enhanced synaptic inhibition and a transgenic rat model of Rett syndrome (RTT). For both cases, we found a collapse of complexity in the motor system. Reduced complexity was apparent in lower-dimensional, stereotyped brain–body interactions, neural synchrony, and simpler behavior. Our results demonstrate how imbalanced inhibition can cause excessive synchrony among movement-related neurons and, consequently, a stereotyped motor code. Excessive inhibition and synchrony may underlie abnormal motor function in RTT.

A diverse and complex repertoire of body movements requires diverse and complex neural activity among cortical neurons. Moreover, interactions between movement-related neurons and the body must be sufficiently high dimensional to carry these movement signals with high fidelity. The complexity of movement-related neural activity and neuron–body interactions can be compromised if synchrony among neurons is excessive. Indeed, it is well understood theoretically that excessive correlations can limit the information capacity of any neural code (1–3)—if all neurons are perfectly synchronized, then different neurons cannot encode different motor signals. Synchrony is also known to play a role in pathophysiology of movement-related disorders, like Parkinson’s disease (4–6). However, synchrony and correlations also contribute to healthy function in the motor system (7–14). For instance, particular groups of synchronized neurons seem to send control signals to particular muscle groups (7, 8) and propagation of correlated firing contributes to motor planning (10). Synchrony can also play a role in motor learning (12–14). These findings suggest that correlated activity among specific subsets of neurons encodes specific motor functions. Thus, it stands to reason that if this synchrony became less selective and more stereotyped across neurons, then the motor code would become less complex and lose specificity, resulting in compromised motor function.

Here we explored this possibility in rats, in the caudal part of motor cortex where neurons associated with hindlimb, forelimb, and trunk body movement are located (15–17). We focused on two conditions. First, we studied a transgenic rat model of Rett syndrome (RTT), which has disrupted expression of the MeCP2 gene. Second, we studied normal rats with acutely altered inhibitory neural interactions. Both of these cases are associated with abnormal motor behavior and, possibly, abnormal synchrony. Abnormal synchrony is a possibility, because both of these cases are linked to an imbalance between excitatory (E) and inhibitory (I) neural interactions, which in turn is likely to result in abnormal synchrony. For instance, many computational models suggest that synchrony is strongly dependent on E/I interactions (18–21). Likewise, in experiments, pharmacological manipulation of E/I causes changes in synchrony (19, 22, 23) and the excessive synchrony that occurs during epileptic seizures is often attributed to an E/I imbalance (24, 25). Similarly, the majority of people with RTT suffer from seizures (26) and many previous studies establish E/I imbalance as a common problem in RTT (27). MeCP2 dysfunction, which is known to cause RTT, seems to be particularly important in inhibitory neurons (28). For instance, two studies have shown that disrupting MeCP2 only in specific inhibitory neuron types can recapitulate the effects of brain-wide disruption of MeCP2 (29, 30). However, whether the E/I imbalance favors E or I at the population level seems to vary across different brain regions in RTT. Studies of visual cortex (29) and hippocampus (31) suggest that the balance tips toward too much excitation (perhaps explaining the prevalence of seizures), while studies of somatosensory cortex (32, 33) and a brain-wide study of Fos expression (34) suggest that frontal areas, including motor cortex, are tipped toward excessive inhibition. These facts motivated our choice to study pharmacological disruption of inhibition here. While it is clear that E/I imbalance is important in RTT, it is much less clear how it manifests at the level of dynamics and complexity of neural activity that is responsible for coordinating body movements. Thus, in addition to pursuing the general questions about synchrony and complexity in the motor system discussed above, a second goal of our work was to improve understanding of motor dysfunction due to MeCP2 disruption.

Taken together, these facts led us to the following questions: How does MeCP2 disruption impact the complexity of body movements, movement-related neural activity, and motor coding? Are abnormalities in the MeCP2-disrupted motor system consistent with excessive inhibition in motor cortex? We hypothesized that both MeCP2 disruption and excessive inhibition lead to reduced complexity of interactions between cortical neurons and body movements, excessive cortical synchrony, and reduced complexity of body movements. Our findings confirmed this hypothesis and suggest that RTT-related motor dysfunction may be due, in part, to excessive synchrony and inhibition in motor cortex.

Results

We performed simultaneous measurements of body movements and spiking activity of many single neurons in motor cortex of rats (Fig. 1 A–C). We compared five different experimental groups: normal rats (Rattus norvegicus, n = 6, Sprague–Dawley; Harlan Laboratories), normal rats with systemic pharmacological changes to inhibition (n = 3), normal rats with pharmacological changes to inhibition locally in motor cortex (n = 3), transgenic RTT rats (n = 4, HET KO, SD-Mecp2tm1sage; Horizon Laboratories), and RTT rats with systemically altered inhibition. The rat model of RTT we study here has been shown to recapitulate important dysfunctions and behaviors found in RTT humans, including impaired motor functions (35–37). During each 30-min recording session (n = 234 sessions in total), the rats behaved freely—e.g., walking, grooming, and changing posture—on a 30 × 30-cm platform inside a dark enclosure. To capture body movement, we recorded the three-dimensional positions of eight reflective beads positioned along the neck, back, rear hips, and the base of the tail of each rat, using an infrared multicamera motion-tracking system (Optitrack Flex: V100R2) with millimeter spatial resolution and 10-ms temporal resolution. We note that basic motility was not significantly different between normal (wild type [WT]) rats and the RTT rats, but application of gamma-Aminobutyric acid (GABA) agonist muscimol tended to cause a decrease in animal movement (SI Appendix, Fig. S1). Neural activity was recorded (Cerebus; Blackrock Microsystems) with a 32-channel, four-shank microelectrode array chronically implanted in deep layers (1,300µm from the pia) of caudal motor cortex. The electrode array location targeted neurons associated with hindlimb, forelimb, and trunk control (15–17, 38, 39). After spike sorting (Kilosort) (40), we obtained 5,922 single units in total (n = 2,079 from normal rats, n = 3,843 from RTT rats, average n = 25 units per recording; SI Appendix, Fig. S2 A–C). Spike rates were not significantly different between WT and RTT rats, but were reduced by muscimol (mus) application, as expected (SI Appendix, Fig. S2D).

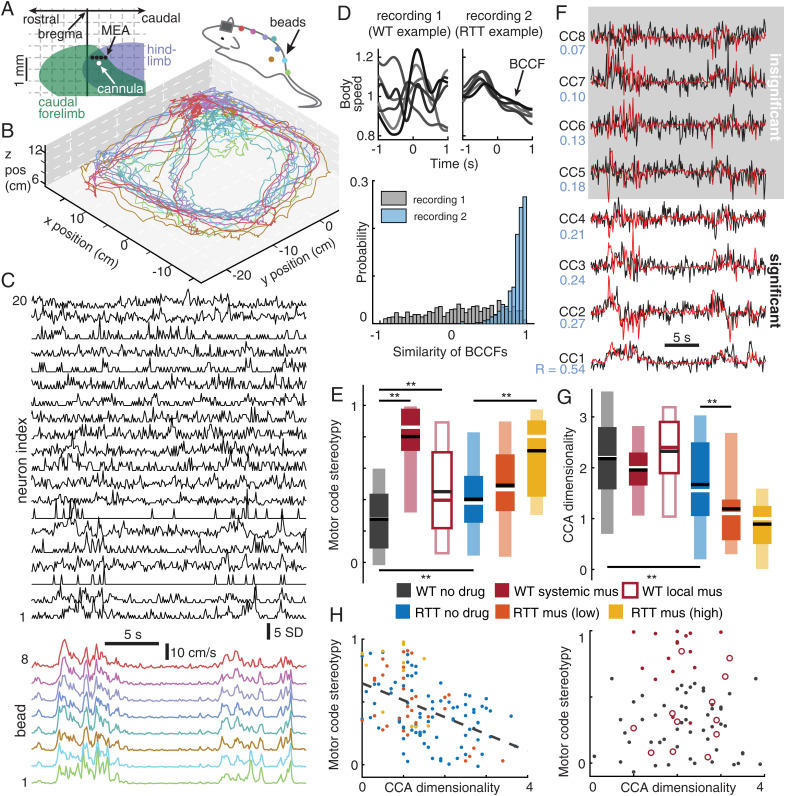
Fig. 1.

Reduced complexity of brain–body interactions due to MeCP2 disruption and excessive inhibition in motor cortex. (A) Diagram of electrode array (black dots) and microcannula (white dot) locations relative to approximate map of caudal forelimb motor area (green) and hindlimb motor area (blue). (B) Motion tracking beads were located along the spine from head to tail and on rear hips. Shown are example three-dimensional trajectories of tracking beads during one recording. Rat cartoon is drawn to approximate scale with these axes. (C) Single-unit neural activity (Top) and body movement (Bottom) were recorded simultaneously. Colors indicate corresponding bead locations shown in B. (D) Spike-triggered average body speed functions (BCCFs) for two example recordings (Top). Note diverse shapes of BCCFs for recording 1 and stereotyped BCCF shapes for recording 2. (Bottom) Distributions of similarity for all pairs of BCCFs for the two example recordings. Motor code stereotypy was defined as the average similarity across all BCCF pairs for each recording. (E) Motor code stereotypy was lowest in normal rats. RTT rats and conditions with elevated inhibition had significantly increased motor code stereotypy (**P < 0.01, t test). Dark and light boxes delineate 0.25 to 0.75 and 0.05 to 0.95 quantiles, respectively. Lines mark median (white, red) and mean (black). (F) Time series of neural activity (black) and bead speeds (red) projected onto CCA dimensions. Note that correlations (blue number) between neurons and body are decreasing from CC1 to CC8. Insignificance of correlations (gray shading) was determined by comparison to time-shuffled data (Materials and Methods). (G) CCA dimensionality is the number of significantly correlated CCA components. CCA dimensionality was significantly less for RTT compared to WT (**P < 0.01, Wilcoxon rank sum test). (H) For RTT animals (Left) motor code stereotypy was significantly correlated with CCA dimensionality (P < 0.01, Spearman’s correlation), but not in WT animals (Right).

Neuron–Body Interactions

Our first goal was to quantitatively assess relationships between neurons and body movements. We met this goal in two ways. First, we asked how each single neuron fired in relation to body movements. For each neuron, we calculated a spike-triggered average of body speed in a 2-s window centered on the triggering spike time, similar to a cross-correlation function (CCF) between the triggering neuron’s spikes and the body speed (Fig. 1D). (See ref. 41 for similar analyses.) Hereafter, we refer to this spike-triggered average body speed function as a body cross-correlation function (BCCF). Here, for simplicity, we used the center-of-mass speed of the eight motion-tracking beads to calculate the BCCFs; below we consider more detailed aspects of body motion. We obtained one BCCF for each neuron and compared the shape of BCCFs across neurons in each recording. The shape of a BCCF reveals whether and how the trigger neuron leads or lags body movement. A flat line in the BCCF would indicate a neuron that fires independently of the body. Additional example BCCFs are shown in SI Appendix, Fig. S3. Further considerations for interpreting BCCFs are in Discussion.

We found that neurons recorded in RTT animals tended to have stereotyped BCCFs, while normal rats tended to have more diverse BCCFs across neurons (e.g., Fig. 1 D, Top). To quantify the similarity of BCCFs across neurons we calculated the correlation of each pair of BCCFs and then averaged these correlations across all pairs. Distributions of all of these pairwise correlations are shown in Fig. 1 D, Bottom for the two example recordings in Fig. 1 D, Top. Thus, we obtain a single number for each recording that we interpret as a measure of the stereotypy of the motor code. As summarized in Fig. 1 E, motor code stereotypy was significantly higher (P < 0.01, t test) for RTT animals (0.40 ±0.27, mean ± SD) than for normal rats (0.28 ±0.21) and was also significantly increased due to enhancement of inhibition (P < 0.01, t test, 0.80 ±0.21 for WT + systemic muscimol, 0.45 ±0.30 for WT + local mus, 0.49 ±0.25 for RTT + low-dose mus, 0.71 ±0.26 for RTT + high-dose mus).

One limitation of our analysis of BCCFs was that it was based on the center-of-mass speed of the rat, thus reducing the potentially complex motion of the rat to a one-dimensional variable. To account for higher-dimensional relationships between neurons and body movements, we adopted a second approach based on canonical correlation analysis (CCA) (for a review of CCA see refs. 42 and 43). If many neurons have similar BCCFs, i.e., high motor code stereotypy, this would suggest that they have a low-dimensional motor code. We used CCA to test this possibility, treating both the neural activity and body movements as high-dimensional variables: n neural dimensions for a population of n recorded neurons and eight body dimensions, and one dimension for the speed of each tracking bead. CCA identifies special directions in these two high-dimensional “spaces.” When projected onto these special dimensions, the neural activity and body activity are correlated with each other; the first dimension (CC1) is most correlated, the second dimension (CC2) is the second-most correlated, and so on (Fig. 1F). Here we define the dimensionality of interactions between the neurons and the body as the number of CCA dimensions with a statistically significant correlation between brain and body (Materials and Methods). We considered only periods when the animal was active to avoid confounding movement complexity with general motivation to move (Materials and Methods).

In line with our analysis of BCCFs, we found that the dimensionality of interactions between neurons and the body for RTT animals (1.67 ±0.89) was significantly lower (P < 0.01, Wilcoxon rank sum test) than that of WT rats (2.18 ±0.90), as summarized in Fig. 1G. Moreover, we found that CCA dimensionality was significantly anticorrelated with motor code stereotypy in RTT animals (P < 0.01, Spearman correlation, Fig. 1H). In WT rats, CCA dimensionality did not correlate with motor code stereotypy, which may explain why CCA dimensionality was not reduced by muscimol for the WT group.

Neural Complexity

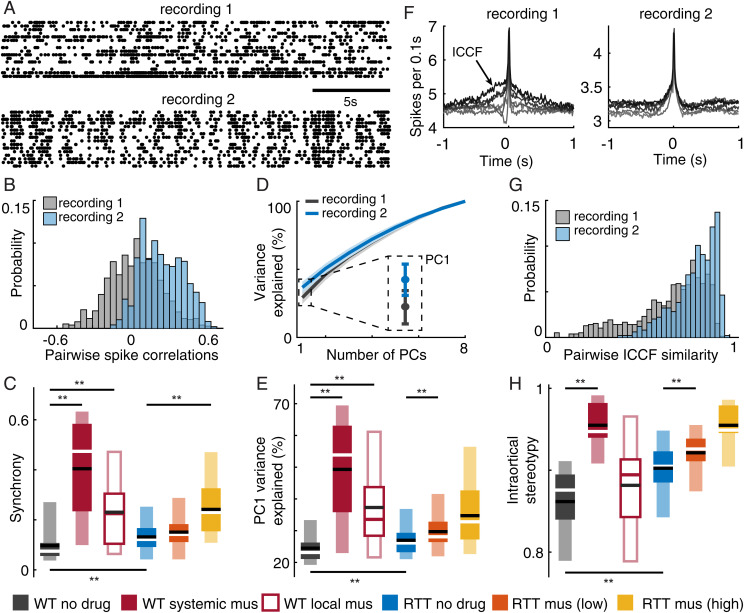
So far, the findings we present in Fig. 1 demonstrate that both MeCP2 disruption (RTT) and increased inhibition result in a motor code with reduced complexity compared to that in normal rats. This suggests that the complexity of the neural activity by itself, independent of body movement, could also be reduced in these cases. Alternatively, it is also possible that the complexity of neural activity does not change and that the trends in Fig. 1 manifest in subspaces of neural activity that are not apparent when considering neural activity separately from the body activity. To test these possibilities, we quantified complexity of neural activity in three ways (Fig. 2). First, we examined pairwise spike count correlations among the recorded neurons. We constructed spike count time series for each neuron and then computed the correlation coefficient of these time series for each pair of neurons (Fig. 2 A and B); distributions of such pairwise correlation coefficients are shown in Fig. 2B for two example recordings, one from a normal rat and the other from an RTT rat. We averaged across all pairwise correlations to obtain a single number for each recording, termed “synchrony” in Fig. 2C, which quantifies the tendency for neurons to fire together. We interpret higher levels of synchrony as less complex neural activity. Similar to the trends in Fig. 1, we found that synchrony in RTT animals (0.13 ±0.06) was significantly higher (P < 0.01, t test) than in WT animals (0.10 ±0.08). These results are summarized for all recordings and experimental groups in Fig. 2C. Pharmacological enhancement of inhibition (both local and systemic) also resulted in increased synchrony (P < 0.01, t test, 0.40 ±0.19 for WT + systemic muscimol, 0.23 ±0.14 for WT + local mus, 0.15 ±0.07 for RTT + low-dose mus, 0.24 ±0.11 for RTT + high-dose mus). This result is somewhat surprising considering that stronger inhibition is often associated with reduced synchrony in theory (18, 44) and GABA agonists can result in reduced synchrony (19), but our finding is consistent with a recent study that applied low-dose muscimol in motor cortex of awake rats (23).

Fig. 2.

Decreased complexity of neural activity due to MeCP2 disruption and excessive inhibition. (A) Example spike rasters from a WT no-drug recording (recording 1) with weaker correlations among neurons and an example RTT no-drug recording (recording 2) with stronger correlations. (B) Distributions of all pairwise spike count correlations for the two recordings in A. We defined the average across all pairs as synchrony. (C) Summary of all recordings shows increased synchrony in RTT rats compared to WT rats. Similarly, increasing inhibition results in increased synchrony. (D) For the example recording with greater synchrony (blue), PCA analysis shows that PC1 explains more variance. (E) Summary of the variance explained by PC1 follows the same trends as synchrony in C. (F) Several example spike-triggered average spike histograms (ICCFs) are shown for the example recordings. Note that the ICCFs are more similar in shape for recording 2 (RTT) than recording 1 (WT). (G) Distributions summarize the similarity for all possible pairs of ICCFs. The average of all similarities defines the “intracortical stereotypy” for each recording. (H) Summary of intracortical stereotypy for all recordings and experimental groups. Normal rats (WT) were the least stereotyped; RTT and increased inhibition have elevated stereotypy. Asterisks indicate t-test significance: **P < 0.01. Dark and light boxes delineate 0.25 to 0.75 and 0.05 to 0.95 quantiles, respectively. Lines mark mean (black) and median (white, red).

Next, we assessed complexity of neural activity using principal component analysis (PCA) (Materials and Methods). Similar to CCA, PCA identifies special directions in high-dimensional neural space. But, instead of finding directions that are correlated with the body (as in CCA), PCA finds directions along which the neural activity has the greatest variance (without regard to the body). The first principal component (PC1) explains the most variance, the second component (PC2) explains the second-most variance, and so on. In this context, higher-complexity neural activity requires more components to explain its variance; if a greater fraction of the total variance can be explained by the first PC, we interpret this as lower complexity (Fig. 2D). We found that the amount of variance explained by the first principal component was highly correlated with our synchrony measurements (SI Appendix, Fig. S4A; Pearson’s R = 0.96, P < 0.01). Like synchrony, the variance explained by PC1 for RTT rats (26.97 ±4.80) was significantly higher (P < 0.01, t test) than in WT animals (24.49 ±6.09). These results are summarized for all recordings and experimental groups in Fig. 2E. Increased inhibition (both local and systemic) also resulted in increased variance explained by PC1 (P < 0.01, t test, 49.30 ±15.55 for WT + systemic muscimol, 37.31 ±12.40 for WT + local mus, 29.70 ±5.65 for RTT + low-dose mus, 34.73 ±10.42 for RTT + high-dose mus).

We quantified complexity of neural activity in a third way, similar to our analysis of BCCFs and motor code stereotypy (Fig. 1 D and E). For each single neuron, we computed a spike-triggered average of the spike activity of the rest of the population of neurons from the same recording (Fig. 2F). We refer to these as intracortical cross-correlation functions (ICCFs). ICCFs have been used in previous studies of population coupling (23, 45, 46). We obtained one ICCF for each neuron in a recording and compared the shape of the ICCFs across neurons. The shape of an ICCF reveals whether and how the trigger neuron leads or lags the activity of the network in which it is embedded. A flat line in the ICCF would indicate a neuron that fires independently of the population. Additional considerations for interpreting ICCFs are in Discussion. After obtaining one ICCF for each single neuron, we then asked how similar the ICCFs were across neurons.

We found that for normal rats, ICCFs were diverse: Some neurons lead, others lag the population; some neurons had sharply peaked ICCFs, others had broader peaks (Fig. 2F, gray). In contrast, in the RTT rats, neurons tended to have stereotyped ICCFs (Fig. 2F); each neuron tends to participate with the population in the same way in RTT rats. We quantified this stereotypy of intracortical interactions by calculating correlations between all pairs of ICCFs (Fig. 2G) for each recording and then averaging across all pairs, to obtain a single intracortical stereotypy number for each recording. Intracortical stereotypy was correlated with synchrony, but not as strongly as PC1 variance (SI Appendix, Fig. S4B; Pearson’s R = 0.54, P < 0.01). Comparing across our experimental groups, we found that intracortical stereotypy in RTT rats (0.90 ±0.03) was significantly greater (P < 0.01, t test) than in normal rats (0.86 ±0.05), as summarized in Fig. 2H. We found that systemic application of muscimol increased intracortical stereotypy for both normal and RTT rats (P < 0.01, t test, 0.95 ±0.03 for WT + systemic muscimol, 0.92 ±0.03 for RTT + low-dose mus, 0.95 ±0.02 for RTT + high-dose mus), but the increase due to local muscimol application was not significant (0.88 ±0.05 for WT + local mus).

Complexity of Body Motion

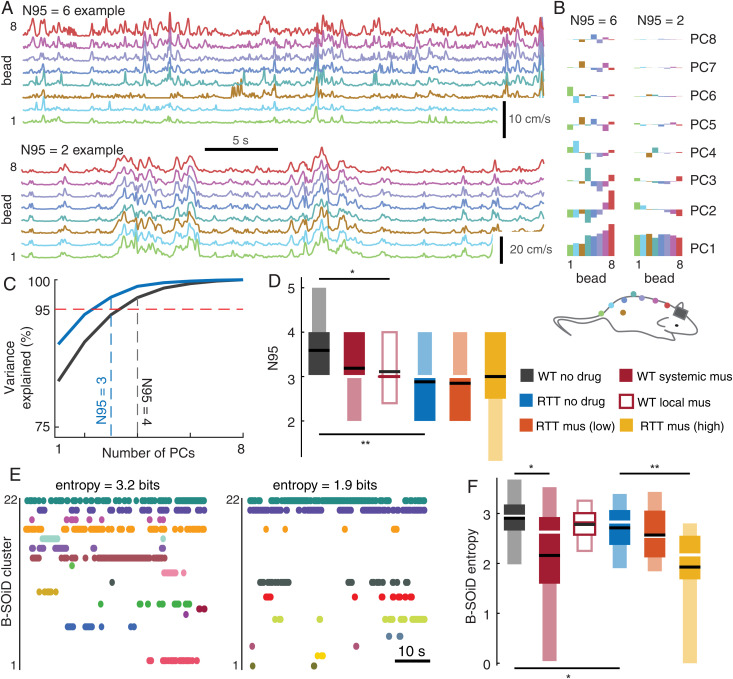
Figs. 1 and 2 show that both neural activity and its relationship to body movements are reduced in complexity for RTT animals and for enhanced inhibition. Does this reduced complexity also manifest in the body movements considered alone, without reference to neural activity? This is a possibility but is not guaranteed; it could be that the trends in Figs. 1 and 2 are fully explained by trends in neural activity, with body movements playing a lesser role. To sort this out, we next aimed to directly measure body movement complexity. We did this in two ways. First, we used a PCA-based analysis of the eight-dimensional bead speed data during periods when the rats were not at rest (as for our CCA analysis in Fig. 1). Similar to our PCA analysis of neural activity, we defined the complexity of body movements based on the variance explained by different principle components. However, correlations among neurons were weak compared to correlations among the eight motion-tracking beads on the body (Fig. 3A). Thus, the variance explained by PC1 was always quite high and did not serve well as a measure of complexity. A more sensitive measure of complexity was the number of PCs needed to explain 95% of variance (termed N95 in Fig. 3C). As demonstrated in Fig. 3A, N95 was low when body movements were highly correlated across all eight tracking beads (e.g., during locomotion) and N95 was higher when different body parts moved more independently (e.g., moving the head, grooming, or changing posture). This is also apparent when examining how different body parts contribute to different PCs for low and high N95 (Fig. 3B). Compared to high-N95 cases, low-N95 cases tended to have all beads contribute more equally to PC1. We found that N95 for RTT rats (2.88 ±0.87) was significantly lower (P < 0.01, Wilcoxon rank sum test) than that for normal rats (3.59 ±0.87). Local muscimol application also resulted in reduced N95 compared to that for normal rats (P < 0.05, Wilcoxon rank sum test). In RTT animals, muscimol application did not further lower N95. Fig. 3D summarizes N95 results across all recordings and experimental groups (3.19 ±0.75 for WT + systemic muscimol, 3.11 ±0.47 for WT + local mus, 2.85 ±0.71 for RTT + low-dose mus, 3.00 ±0.95 for RTT + high-dose mus).

Fig. 3.

Reduced body movement complexity due to MeCP2 disruption and excessive inhibition. (A) Examples of tracking bead speed data with higher complexity (Top, speeds less correlated across beads) and lower complexity (Bottom, highly correlated bead speeds). Vertical scales differ for these two examples. (B) Principal components for the two examples in A. Each component is scaled by the variance it explains. Color indicates bead location. For the low-complexity example, note that PC1 has similar contributions from all beads and other PCs explain a relatively small amount of variance. (C) The number of PCs needed to explain 95% of variance, i.e., N95, is lower for less complex body movements. (D) Summary of N95 for all recordings and experimental groups reveals that N95 is highest for the WT rats. N95 is significantly lower for local muscimol application (*P < 0.05, Wilcoxon rank sum) and for RTT rats (**P < 0.01). (E) Two example recordings showing behavioral classification time series from B-SOiD analysis. The example with less complex behavior, i.e., smaller entropy, spends most time in just a few behaviors. (F) Summary of B-SOiD entropy across all recordings and experimental groups. WT rats had the highest entropy. Systemic muscimol application and RTT rats had significantly lower entropy (*P < 0.05). Muscimol also reduced entropy for the RTT group (**P < 0.01).

Finally, we assessed complexity of body motion with an alternative approach based on the recently developed B-SOiD algorithm (47). B-SOiD was originally developed for classifying behaviors based on limb position data obtained from markerless pose estimation software (e.g., DeepLabCut) (48). Here we applied the B-SOiD algorithm to classify repeating behaviors based on the data from our eight tracking beads (Materials and Methods). In addition to the eight speeds we used in our PCA-based analysis, B-SOiD also uses distances and angles among the eight beads to identify behaviors. The output of the B-SOiD algorithm is a behavioral state time series—a sequence of labels, with a unique label for each behavior, and one label at each time point (e.g., Fig. 3E). After excluding periods of rest (as we did for our N95 and CCA analyses), we calculated the Shannon entropy of the behavioral state time series (Materials and Methods). Entropy, in this context, measures the complexity of behavior. The highest possible entropy would occur for an animal that spent equal time in every behavioral state. The lowest possible entropy (0 bits) would occur if the animal spent the entire time in one behavioral state. We found that entropy was highest in the normal rats (2.91 ±0.46) and was significantly reduced (P < 0.05, t test) for RTT animals (2.71 ±0.54) and for systemically applied muscimol (2.16 ±1.20). Fig. 3F summarizes entropy across all recordings and experimental groups (2.78 ±0.30 for WT + local mus, 2.57 ±0.55 for RTT + low-dose mus, 1.93 ±0.91 for RTT + high-dose mus).

Discussion

Here we have shown that MeCP2 disruption and increased inhibition cause a similar reduction in complexity of the rat motor system. Compared to normal rats with intact inhibition, this reduced complexity manifested in multiple ways. First, the dimensionality of the motor system was reduced. This lower dimensionality was apparent at three levels: neural activity in caudal motor cortex (Fig. 2 D and E), body movements (Fig. 3 A–D), and interactions between neurons and body movements (Fig. 1 F and G). Second, neural activity became more synchronized (Fig. 2 A–C). Third, the way that different neurons participate in motor system dynamics became more stereotyped. This stereotypy was apparent when considering how each neuron participates in the collective activity of the neural population (Fig. 2 G and H) and when considering how each neuron relates to body movements (Fig. 1 D and E).

Returning to the questions we posed at the start, one possible interpretation of our observations is that MeCP2 disruptions cause an imbalance favoring inhibition in motor cortex. This E/I imbalance results in excessive neural synchrony, thereby limiting the information capacity of the motor code; the commands sent from cortex to spinal cord are less complex. In this view, the reductions in complexity of behavior and neuron-to-body relationships are a natural consequence of the less complex commands issued from cortical neurons.

This interpretation is supported by the fact that local application of muscimol in motor cortex of normal rats recapitulated many of our observed differences between RTT rats and normal rats. This observation is also consistent with previous studies that point to an imbalance favoring too much inhibition in frontal areas as a circuit-level problem associated with RTT (32–34). Also consistent with this possibility, we found that spike rates are lower for RTT rats compared to normal rats (SI Appendix, Fig. S2). However, this observation also deserves more careful attention. A few aspects of our measurements of RTT rats did not parallel the effects of local muscimol application in normal rats. The most prominent example of this was the CCA dimensionality of neuron–body interactions, which was not lower than normal for local muscimol application. How is this possible, considering that the synchrony and dimensionality of neural activity and dimensionality of body movements were reduced for local muscimol application? The most general answer to this question could be compensatory mechanisms, which are a well-known challenge of studying long-term E/I imbalance in neural disorders that may differ for acute E/I manipulations (27). Nonetheless, a more specific possible explanation is suggested by a recent study of neurons in the same part of motor cortex. In that study we showed, in normal rats, that the neurons that are most correlated with each other are also the least correlated with body activity (23). This relationship suggests that the prominent low-dimensional neural activity that occurs for local muscimol in WT rats will not be noticed by CCA, which selects dimensions that are correlated with body movements. Our results in Fig. 1H suggest that this distinction is present in normal rats, but may not be present in RTT rats. Further studies will be required to better understand these issues.

To further explore the role of inhibition in our RTT rat model, we performed additional experiments in which we reduced inhibition by applying systemic GABA antagonists. Our original motivation for this was the possibility of rescuing normal motor function in RTT rats. However, we found that partially blocking inhibition did not recover normal motor function. Perhaps consistent with compensatory mechanisms, we found that RTT rats were more sensitive to reduced inhibition than normal rats, but we did not find a return to normal motor function (SI Appendix, Fig. S5).

Thus far, we have interpreted our results in terms of motor coding. However, a potentially important additional interpretation arises when considering our recording location more completely. We chose our recording location because it has a high density of corticospinal neurons related to hindlimb and forelimb control (15, 17). But, this location also contains hindlimb somatosensory neurons (38). Such sensory neurons could provide sensory feedback used to guide hindlimb movements. In this context, the reduced complexity we observed for RTT and muscimol may manifest as limits on somatosensorimotor activity. Moreover, there could be a purely sensory component to the reductions in complexity we observed; sensory coding among the recorded neurons could be stereotyped in RTT and for increased inhibition. Sorting out these interesting possibilities requires further study.

Finally, we point out a limitation to our interpretations of spike-triggered average body speed (BCCF) and spike-triggered average population spike activity (ICCF). We interpreted these spike-triggered average functions in terms of “interactions” between the triggering neuron and the body (BCCF, Fig. 1 D and E) or interactions between the triggering neuron and the population neural activity (ICCF, Fig. 2 F–H). However, in principle, such spike-triggered averages can reveal not only cross-correlations (i.e., interactions), but also the autocorrelation of the triggering neuron. To clarify whether our results are related to such autocorrelations we performed a control analysis, repeating our measurements of motor code stereotypy and intracortical stereotypy, but with a random time shift applied to the spike times of each neuron. This control keeps autocorrelations intact, but destroys cross-correlations. We found that motor code stereotypy was very low and with no significant differences across groups for this control (SI Appendix, Fig. S6A), indicating that our motor code stereotypy is indeed appropriately interpreted in terms of interactions (cross-correlations). However, as shown in SI Appendix, Fig. S6 B and C, for intracortical stereotypy, autocorrelations may play a role in the difference between WT and RTT (but not for the effects of muscimol). This may indicate that the functional implications of different autocorrelations (49–51) should also be considered in etiology of RTT-related dysfunction.

Our work highlights the complex role of synchrony and high-dimensional interactions in motor system function and dysfunction. We show that MeCP2 disruption can lead to excessive synchrony and a collapse of complexity in the relationships among cortical neurons and the relationships between neurons and the body. Our findings suggest that stereotypy at the level of motor coding may play a role in the stereotyped body movements of Rett syndrome.

Materials and Methods

Animals

All procedures followed the Guide for the Care and Use of Laboratory Animals of the National Institutes of Health and were approved by University of Arkansas Institutional Animal Care and Use Committee (protocol 14048). We studied normal Sprague–Dawley male rats (n = 6, Harlan Laboratories; 3 for systemic pharmacological manipulation and 3 for local pharmacological manipulation) and transgenic MeCP2 knockout female rats (n = 4, HET KO, SD-Mecp2^tm1sage; Horizon Laboratory). The raw data from the normal rats were collected and first reported in our previous study (23), but reanalyzed here. The RTT rats have a 71-bp deletion in exon 4 and are maintained by breeding heterozygous females with wild-type males, both with Sprague–Dawley backgrounds. This animal model has been shown in other studies to recapitulate important dysfunctions and behaviors found in RTT humans including breathing abnormalities, unusual social interactions, exaggerated response to auditory stimuli, reduced gross locomotion, weak grip, and shortened lifespan (35, 36). In addition, these rats have also been shown to manifest many of the same behavioral abnormalities found in some RTT mouse models including stunted body growth, maloccluded teeth, and reduced interest in social novelty (35).

Pharmacology

On each recording day, we performed one no-drug recording first and one muscimol recording after at least 1 h for each rat. We used muscimol to induce pharmacological enhancement of inhibition. Muscimol is a GABA_A agonist that increases the strength of inhibitory signaling (52). For systemic pharmacological manipulation, the rats were given 2 mL muscimol diluted in saline solution through intraperitoneal (i.p.) injection 50 min before every recording. For normal rats, the dose for muscimol was 2 mg/kg body weight; for RTT rats, we applied a lower dose varying from 0.25, to 0.5, to 1 to 2 mg/kg body weight because these animals seemed to be more sensitive to altered inhibition than normal rats. In the main text and figures, the concentration of 0.25 mg/kg body weight is referred to as “low-dose muscimol”; higher concentrations are grouped into “high-dose muscimol” for RTT animals. For local drug delivery, a microcannula was included in the chronic implant (26-GA guide cannula, 33-GA injection cannula; Plastics One), where the guide cannula had its tip touching, but not penetrating the surface of cortex. The outer diameter of the guide cannula tip was positioned 0.35 mm from the electrode array, such that the center of the cannula was 0.5 mm posterior to bregma and 2.5 mm lateral from midline. The injection cannula also did not penetrate the surface of cortex. The cannula was used to inject 1 µL of muscimol dissolved in sterile saline solution with a syringe pump (Bioanalytical Systems, Inc.) slowly over a 5-min period. Multiple concentrations were tested and grouped for local muscimol, including 80, 160, 320, 640, and 1,280 µM. For no-drug recordings preceding systemic muscimol application a sham i.p. injection of 2 mL saline was performed. For no-drug recordings preceding local muscimol application, a sham injection of 1 µL saline was injected via the microcannula.

Electrophysiology

Microelectrode arrays were chronically implanted 1,300 μm deep in a 2 × 2-mm craniotomy with the center located 0.5 mm posterior to bregma and 2 mm lateral from midline. Thus, the recorded neurons were located in deep layers of caudal motor cortex and at positions associated with hindlimb, forelimb, and trunk movement (15, 17, 38). For the normal rat systemic manipulation group, we used one type of microelectrode array (A8x4–2mm-200–200–413-CM32; Neuronexus); for the normal rat local manipulation group and RTT rats, we used a different type of microelectrode array (Buzsaki32-CM32; Neuronexus) for improved spike sorting (53). For all groups, the plane of microelectrode arrays was oriented perpendicular to the dorsal surface and parallel to the midline. After implantation surgery, the rats recovered for at least 2 wk before recordings began. During each 30-min recording, extracellular voltage fluctuations were recorded with 30-kHz sample rate (Cerebus; Blackrock Microsystems). Signals were digitized by a headstage connected to the electrode and transmitted by a commutator connected to the recording system. Spike sorting was done with the Kilosort (54), a fast and accurate spike sorting algorithm for high-channel count probes (40). Then, we manually curated the spike sorting results with the graphical user interface Phy (55). Criteria for a good unit included clear and distinct waveform shapes, refractory periods in autocorrelograms, stability in amplitudes, and distinct principal components in feature space (SI Appendix, Fig. S2 A–C).

Motion Tracking

As in our previous work (23), body movement was recorded with an infrared nine-camera motion tracking system (OptiTrack Flex:V100R2), where the three-dimensional coordinate of eight reflective beads (MCP1125, Naturalpoint; 3 mm diameter) temporarily adhered along the spine from neck to tail and on each lateral side of rear hips. The tracking system has 10 ms time resolution and millimeter spatial resolution. The recordings took place in a dark enclosed space. During a 30-min recording, the rats were allowed to freely move on a 30 × 30-cm platform placed at the center of the recording space. The lightweight cable is attached to the ceiling and the length is carefully measured so that it does not impede the free movement of the rats. Each rat went through three acclimatization sessions before recording with the same setup to avoid animal stress and anxiety. After recordings were completed, the tracking trajectories were manually corrected with the software Motive (56) and smoothed by a 5-Hz low-pass filter. The speeds of center of mass and beads were then obtained by calculating differentiated positions.

Body Motion Data Analysis

We used the distance traveled by the rat during the recording to represent the general motility (SI Appendix, Fig. S1). The distance traveled was calculated for each recording as the cumulative distance traveled by the center of mass of the tracking beads. Complexity of movements was assessed in two ways: PCA-based analysis and B-SOiD analysis (Fig. 3). For PCA-based analysis, we performed principal component analysis on the speed of eight beads using the Matlab function “pca.” We excluded time periods when the rats were at rest for more than 1.5 s. We defined the animal to be “at rest” if it met two conditions: 1) speed of center of mass less than 0.8 cm/s and 2) speed of each bead less than 1 cm/s. Brief periods of motion, shorter than 0.5 s, preceded and followed by rest were considered rest. After excluding rest periods and applying principal component analysis, we counted the number of principal components that explains 95% of variance, defined as N95.

Our B-SOiD analysis was performed using B-SOiD version 2.0 (57). Version 2.0 builds upon the first version, which was previously described (58). We used 12 representative recordings (2 from each of the experimental groups: WT, WT + systemic mus, WT + local mus, RTT, RTT + low mus, RTT + high mus) to train a classifier. And then we used the classifier on all recordings. We used the two-dimensional horizontal position coordinates (x and y in Fig. 1A) of the eight tracking beads as input to B-SOiD. For classification, B-SOiD 2.0 uses 28 distances among the eight tracking beads, 28 angles, and the speeds of the eight beads. The interbead angles and speeds were the most useful for B-SOiD classification (SI Appendix, Fig. S7). We set the B-SOiD parameters as follows: Frame rate was 100 fps, training input fraction was 1, cluster size range was 0.14 to 0.64%. The output of B-SOiD was a behavioral state time series, s(t), where s is a label that ranges from 1 to m if there are m behavioral states defined by B-SOiD. We excluded periods when the animal was inactive (as done for CCA and N95 analysis). We found that $m=26.4\pm 14.4$ (mean ± SD) for our recordings. Considering all recordings together, 58 behavioral states were identified that had at occurred for at least 1 min (totaled over all recordings). To assess complexity of body movements, we computed Shannon entropy H of the behavioral state time series: $H=-{\displaystyle {\sum }_i{p}_i}lo{g}_2(p_i)$, where i ranges from 1 to m and $p_i=n_i/N$ is the probability of state i estimated by the number of occurrences n_i of state i divided by the total number of time points N.

Spike Data Analysis

Spike rate of a recording was obtained by the average spike rate across all units during the recording (SI Appendix, Fig. S2D). Synchrony was defined as the average of pairwise correlations of spike count time series across all pairs of neurons (Fig. 2 A–C). The spike count time series were calculated for each neuron using 1-s time bins. The PCA-based analysis of spikes (Fig. 2 D and E) was also done on spike count time series with 1-s time bins. We performed principal component analysis on the spike count times series of eight randomly picked neurons in the recording and repeated 10 times to obtain an average for each recording. We used the percentage of variance explained by the first component, named “PC1 variance explained,” to represent complexity of neural activity.

Intracortical stereotypy (Fig. 2 F–H) was defined based on spike-triggered average population activity functions, ICCFs. For each neuron (trigger neuron), we counted the number of spikes from the population (with a 10-ms time bin) in a ±1-s time window centered on the spike times of the trigger neuron. We then averaged these spike-triggered spike counts across all spikes from the trigger neuron to obtain ICCFs (Fig. 2F). Intracortical stereotypy was calculated by averaging pairwise correlations of ICCFs across all pairs of units as a single number for each recording (Fig. 2G).

Analysis of Interactions between Body and Neural Activity

Motor code stereotypy (Fig. 1 D and E) was defined based on spike-triggered average body speed functions, BCCFs. Similar to ICCFs, we obtained BCCFs for each neuron (the trigger neuron) by averaging the speed of center of mass in a ±1-s time window centered on the spike times of the trigger neuron (Fig. 1D). BCCFs were then smoothed by a 1.5-Hz low-pass filter and normalized by its mean. Motor code stereotypy was defined as the average of pairwise correlations of BCCFs across all pairs of units to obtain a single number for each recording.

We performed CCA on the two high-dimensional variables: neural activity and body activity. For neural activity, we used the spike count time series (with a 10-ms time bin) of eight randomly selected neurons as neural dimensions; for body activity, we used the speeds of eight reflective beads as body dimensions. We excluded time periods when the rats were at rest (same as in PCA-based and B-SOiD analysis of body motion). Then, we performed CCA (using Matlab function “canoncorr”) to obtain canonical correlations between the two variables on each of eight CCA dimensions. We defined a P value to measure whether the canonical correlation coefficient in each dimension is significant, compared to chance. Our P value is the probability of a chance-level canonical correlation coefficient being greater than the measured value. To define chance-level canonical correlations, we repeated the CCA calculation using randomly shuffled temporal order of bead speeds measurements, keeping the temporal order of spike counts fixed. We repeated this control CCA calculation 200 times to obtain $8\times 200=1,600$ chance-level canonical correlation coefficients. The dimensions with P value < 0.01 were defined as dimensions having significant correlation between neural activity and body activity. We defined CCA dimensionality as the number of CCA dimensions with significant correlation. CCA dimensionality was calculated 10 times for each recording, each time with eight different randomly selected neurons. Then we averaged over these 10 repeats to finally obtain a single CCA dimensionality for each recording.

Statistics

We examined the statistical significance of the difference between two groups using a P value of t test for continuous variables and a Wilcoxon rank sum test for discrete variables. The P value represents the probability of accepting the null hypothesis that the means of two groups are not different. Spearman’s correlation coefficient and its corresponding P value were used to test the correlations between two quantities in Fig. 1H. Pearson’s correlation coefficient and its corresponding P value were used in SI Appendix, Fig. S4. For both types of correlation, the P value represents the null hypothesis that the two quantities are uncorrelated. We obtained n = 234 recordings with at least 5 good units in total (n = 57 for WT, n = 17 for WT + systemic mus, n = 23 for WT + local mus, n = 86 for RTT, n = 37 for RTT + low mus, n = 14 for RTT + high mus). All these recordings were included in our analysis of spike rate, synchrony, and intracortical stereotypy. Recordings with less than 8 good units (n = 10) were excluded for the PCA-based analysis of spikes and CCA dimensionality. For analysis of distance traveled, complexity of movements (N95), B-SOiD entropy, motor code stereotypy, and CCA dimensionality, n = 6 recordings were excluded due to absence of motion tracking data. Recordings with no active period in behavior (n = 4) were excluded for the analysis of complexity of movements (N95), B-SOiD entropy, and CCA dimensionality.

Data Availability

All data presented in this paper are publicly available in Figshare (DOI: 10.6084/m9.figshare.16559976) (59).