Cochlear outer hair cell electromotility enhances organ of Corti motion on a cycle-by-cycle basis at high frequencies in vivo

Significance

The remarkable high-frequency sensitivity of mammalian hearing depends on the amplification of sound-evoked cochlear vibrations by outer hair cells. One way that outer hair cells are proposed to generate amplifying forces is through voltage-driven changes in cell length. However, it remains unclear whether this electromotility can work fast enough in vivo to provide amplification at the necessary frequencies. Here, we show that sound elicits motions within the living mouse cochlea that are fully consistent with electromotility. These motions are large relative to the motion of the underlying cochlear partition, including at high frequencies. The data therefore suggest that electromotility can indeed provide high-speed amplification in vivo.

Abstract

Mammalian hearing depends on an amplification process involving prestin, a voltage-sensitive motor protein that enables cochlear outer hair cells (OHCs) to change length and generate force. However, it has been questioned whether this prestin-based somatic electromotility can operate fast enough in vivo to amplify cochlear vibrations at the high frequencies that mammals hear. In this study, we measured sound-evoked vibrations from within the living mouse cochlea and found that the top and bottom of the OHCs move in opposite directions at frequencies exceeding 20 kHz, consistent with fast somatic length changes. These motions are physiologically vulnerable, depend on prestin, and dominate the cochlea’s vibratory response to high-frequency sound. This dominance was observed despite mechanisms that clearly low-pass filter the in vivo electromotile response. Low-pass filtering therefore does not critically limit the OHC’s ability to move the organ of Corti on a cycle-by-cycle basis. Our data argue that electromotility serves as the primary high-frequency amplifying mechanism within the mammalian cochlea.

Sound stimulation of the mammalian ear launches traveling waves that propagate along the basilar membrane (BM), a tuned structure that stretches longitudinally from the base to the apex of the cochlear spiral (1). The sensory cells within the organ of Corti detect these waves when deflection of their stereociliary bundles varies the ionic current flow through mechanically gated transduction channels, creating a receptor potential. For inner hair cells (IHCs), this triggers afferent synaptic transmission to the auditory nerve. For outer hair cells (OHCs), the receptor potential primarily serves to elicit force generation by the cell. These forces amplify BM motion in response to quiet sounds but not loud sounds, both improving the cochlea’s mechanical sensitivity by ∼1,000-fold and compressing its responses to a wide array of sound pressures into a physiologically useful range (2, 3). It is commonly assumed that OHCs provide amplification by generating force on a cycle-by-cycle basis with the timing required to deliver power to the BM (4) and counteract viscous drag (5). However, it remains controversial whether or how OHCs can do this at the speeds necessary to provide amplification over the frequency range of mammalian hearing, which can exceed 100 kHz in some species.

OHCs are mainly thought to generate amplifying forces due to voltage-driven changes in cell length (6–8). This somatic electromotility is endowed by prestin, a motor protein in the OHC lateral wall that changes conformation upon membrane depolarization and hyperpolarization, causing the cell to contract and elongate, respectively (9, 10). The resulting forces are then transmitted to the surrounding structures in the organ of Corti. In vitro, isolated and electrically stimulated OHCs have been shown to produce constant force at frequencies exceeding 50 kHz (11). However, it is unclear whether OHCs can generate forces sufficient for providing amplification at such high frequencies in vivo. This is largely because receptor potentials are low-pass filtered by the OHC’s electrical impedance, which reduces the voltage drive to prestin by 6 dB/octave above the cell’s corner frequency (12). Even for OHCs in high-frequency cochlear regions, this corner frequency has typically been placed below 1 kHz (13–15), with the highest estimate being ∼6 kHz for OHCs from the 10-kHz region (16). Furthermore, recent studies suggest that the kinetics of prestin-based electromotility may be inherently limiting at high frequencies (17, 18). While various mechanisms could circumvent or compensate for low-pass filtering (19–21), effective amplification may require processes other than cycle-by-cycle somatic electromotility. For instance, stereociliary bundle motility is the sole amplifying mechanism in nonmammals (22) and has been shown to generate force in mammals as well (23, 24). Slow modulation of OHC properties (e.g., length and/or stiffness) could also regulate the organ of Corti’s response to high-frequency sound (25, 26).

Compelling though indirect evidence that OHCs provide fast somatic force generation has come from in vivo measurements of cochlear vibrations. Intracochlear electrical stimulation produces vibrations of both the BM and the apical surface of the OHCs at frequencies >60 kHz (27, 28), indicating that OHC electromotility can follow fast, cycle-by-cycle voltage changes. Recently, optical coherence tomography (OCT) has been used to measure organ of Corti vibrations in the gerbil cochlear base, revealing that sound elicits large motions within the OHC region at frequencies up to 20 to 30 kHz (26, 29). These motions resemble intracochlear electrical potentials (29), suggesting that electrically driven OHC force generation is evoked by high-frequency sound. Nevertheless, observation of the out-of-phase motions expected to result from OHC elongation and contraction has proved elusive (26), and vibrations of the OHC region show signs of low-pass filtering (30). Thus, it is unclear whether cycle-by-cycle OHC length changes occur and whether they have sufficient magnitude to effect high-frequency amplification. Here, we directly assess the influence of OHC electromotility on sound-evoked motions within the mouse organ of Corti in vivo.

Results

Examining Nonlinear Vibrations within the Mouse Organ of Corti.

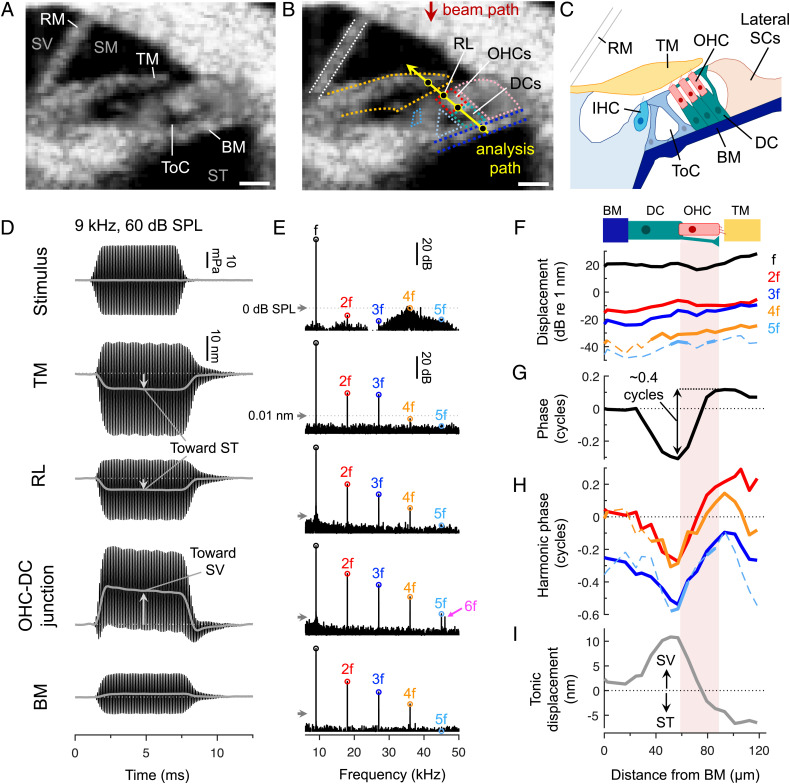
We used a custom-built OCT system to image through the intact cochlear bone in anesthetized, adult mice and measure sound-evoked vibrations from within the organ of Corti (Fig. 1 A–C and SI Appendix, Fig. S1 A–C) (31–33). While our system’s lateral and axial imaging resolutions were ∼9.8 and ∼12.5 μm (full width at half maximum), respectively, and thus did not allow visualization of individual cells, we could identify the three fluid-filled cochlear scalae (scala vestibuli, SV; scala media, SM; and scala tympani, ST), the tectorial membrane (TM), and the tunnel of Corti, which separates the IHCs from the OHCs (Fig. 1A). After inferring the location of the OHCs and their supporting Deiters’ cells (DCs), we measured vibrations along a path connecting the BM, DCs, OHCs, and TM (Fig. 1 B and C) and looked for contractile motions consistent with electromotility. Measurements were made in an apical region tuned to a characteristic frequency (CF) of ∼9 kHz, where we have previously shown that vibrations of the OHC region are strongly influenced by nonlinear amplification (33, 34) (SI Appendix, Fig. S1 D–I).

Fig. 1.

Sound causes contractile motion within the organ of Corti on both a tonic and a cycle-by-cycle basis. (A) Cross-sectional OCT image of the apical cochlear turn. The three scalae (SV, SM, and ST) are indicated, along with Reissner’s membrane (RM), the TM, and the BM. The cellular organ of Corti is situated between the BM and TM. (Scale bar = 50 μm.) (B) The same OCT image with the inferred location of various structures outlined. Displacements parallel to the beam path were measured at locations along the yellow line. (Scale bar = 50 μm.) (C) Schematic of the anatomy. (D and E) Waveforms and spectra of a 9-kHz, 60-dB SPL stimulus and the resulting displacements of locations indicated by black circles in B. Low-pass filtered waveforms (gray lines) reveal the tonic displacements. Waveforms were obtained for 7-ms tones while spectra were obtained using ∼100-ms tones for improved frequency resolution (arrows indicate 0-dB SPL or 0.01 nm, for scale). Responses at the stimulus frequency (f) and its harmonics (2f, 3f, etc.) are labeled, including a 54-kHz component (6f) that was aliased to 46 kHz. (F–I) Cycle-by-cycle displacement magnitudes (F) and phases (G and H), as well as tonic displacements (I), in ∼7-μm steps along the analysis path for a mouse with relatively large harmonics (stimulus = 9-kHz, 60-dB SPL). All phases were referenced to the BM phase at f. Dashed portions of the magnitude and phase curves indicate data falling below the noise floor.

To assess the speed of electromotility in vivo, we exploited the fact that nonlinearity introduces high-frequency harmonic distortion (35, 36). The nonlinearity is thought to originate from the sigmoidal relationship between stereociliary bundle displacement and mechanotransduction current (SI Appendix, Fig. S2). Sinusoidal bundle displacement (at frequency f) introduces harmonic components (at 2f, 3f, etc.) into the OHC’s receptor potential and thus its electromotile response. Additionally, any asymmetry in the mechanotransduction current will introduce a tonic (0 Hz) component, which would elicit a tonic OHC length change. Low-pass filtering will alter the magnitude and phase relationships among these responses. We therefore assessed the influence of low-pass filtering by examining both cycle-by-cycle and tonic displacements within the organ of Corti.

As shown in Fig. 1 D and E (and SI Appendix, Fig. S3), near-CF tones elicited vibrations of the OHC region that were indeed strongly asymmetric and distorted. This was particularly true near the OHC–DC junction, where harmonics were evident at frequencies exceeding 50 kHz (our system’s Nyquist frequency). Previous OCT measurements in gerbil have similarly identified the OHC–DC junction as a “hotspot” of vibratory nonlinearity (26, 30). Importantly, harmonics in our acoustic stimulus were small and were at frequencies too high to elicit waves that could travel to our measurement site. The vibratory harmonics must therefore have originated within the organ of Corti.

Sound Causes the Top and Bottom of the OHC Region to Move in Opposite Directions on Both a Tonic and a Cycle-by-Cycle Basis.

Low-pass filtering the response waveforms to visualize the tonic displacements revealed that the top and bottom of the OHC region moved toward one another during sound stimulation (Fig. 1D). The apical portion of the OHCs near the reticular lamina (RL) moved down toward ST while the OHC–DC junction moved up toward SV. Nearby structures exhibited similar tonic movements, with the TM being displaced toward ST and the BM displaced toward SV. These motions are consistent with these structures being pulled closer together by sustained OHC contraction, which would occur in response to tonic depolarization during the sound stimulus.

To determine whether similar motion patterns could be observed on a cycle-by-cycle basis, we mapped the vibratory magnitude and phase at the stimulus frequency and its harmonics in ∼7-μm steps along the diagonal path connecting the BM to the TM. Displacements for a 9-kHz tone presented at 60-dB sound pressure level (SPL) in a mouse with particularly large harmonics are shown in Fig. 1 F–I (average data for eight mice are shown in SI Appendix, Fig. S4A). Relative to the BM, OHC–DC displacements exhibited a ∼0.25 cycle phase lag, while RL and TM displacements exhibited a ∼0.1 to 0.15 cycle phase lead. The bottom and top of the OHC region therefore moved ∼0.4 cycles out of phase (0.5 cycles = antiphasic). The spatial phase variations mirrored the tonic displacements, which were large and positive near the OHC–DC junction, where the largest phase lags were observed, and negative above the OHC region’s midpoint, where the phase transitioned to a lead. These patterns are consistent with OHCs producing contractile motions on both a tonic and a cycle-by-cycle basis, including at frequencies much higher than the CF.

We also examined displacements along the width of the RL and BM (SI Appendix, Fig. S4 B and C). While there was little spatial variation in the phases of BM displacements at the stimulus frequency, RL displacements exhibited ∼0.5 cycle phase jumps near the lateral supporting cells (31), where the tonic displacements also changed sign. Similar pivoting motions of the RL are induced by electrical stimulation of OHCs ex vivo (37, 38), further suggesting that our measurements capture motions that are associated with electromotility.

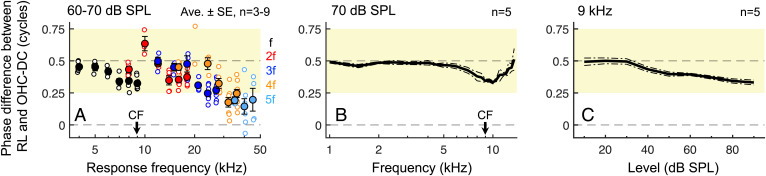
Average spatial maps of responses to 4- to 9-kHz tones presented at 60- to 70-dB SPL confirmed that the top and bottom of the OHCs moved out of phase at frequencies up to at least 20 kHz (Fig. 2A and SI Appendix, Fig. S5). For harmonics at frequencies above 20 kHz, the phase difference between the RL and OHC-DC became more variable and tended to fall below 0.25 cycles, with values often being near 0 cycles for the highest harmonic frequencies. The overall decline in the phase difference at these very high harmonic frequencies could result if our OCT beam path was angled so that RL and OHC–DC motions were measured at slightly different longitudinal locations, where the harmonics would be generated at different times. This would affect higher-order harmonics more because, as a function of cochlear distance, the phase of the n^th harmonic is expected to vary a factor of n times more rapidly than the phase of the response at the stimulus frequency (36).

Fig. 2.

The top and bottom of the OHC region move most out of phase at low frequencies and low stimulus levels. (A) Phase differences between the RL and OHC-DC from spatial maps of responses to 4- to 9-kHz tones presented at 60- or 70-dB SPL. Roughly out-of-phase motion (indicated by shaded area; 0.5 cycles = truly antiphasic) was observed up to ∼20 kHz. Individual/average phase differences (open/closed symbols) at f and its harmonics are plotted versus the response frequency. Averages are shown when data were available from at least three mice. When responses at both 60- and 70-dB SPL were obtained in individual mice, phase differences were first averaged across levels prior to plotting and inclusion in the group average. (B and C) Average phase differences between the RL and OHC-DC (at f) for 70-dB SPL tones swept in frequency (B) or 9-kHz tones swept in level (C), demonstrating antiphasic motion at low frequencies and low SPLs. Data in B and C were derived from measurements from isolated points near the RL and OHC-DC rather than detailed spatial maps, which could only be obtained at a few stimulus frequencies and levels in each mouse.

Noting that phase differences for responses at the stimulus frequency also declined near the CF, we further characterized the displacements of points close to the RL and OHC–DC junction across stimulus frequency and level (Fig. 2 B and C and SI Appendix, Fig. S6 A–F). Nearly antiphasic motion was observed for 1- to 7-kHz tones presented at 70-dB SPL, as well as for 9-kHz tones presented below 40-dB SPL. Similar frequency- and level-dependent phase differences were observed between displacements of the OHC–DC junction and the TM (SI Appendix, Fig. S6 G–L). The reduced phase difference for near-CF stimuli at higher SPLs is likely due to the increasing relative influence of the organ of Corti’s passive mechanical response, which could obscure the active motions associated with electromotility.

Out-of-Phase Motions Are Strongly Reduced Postmortem.

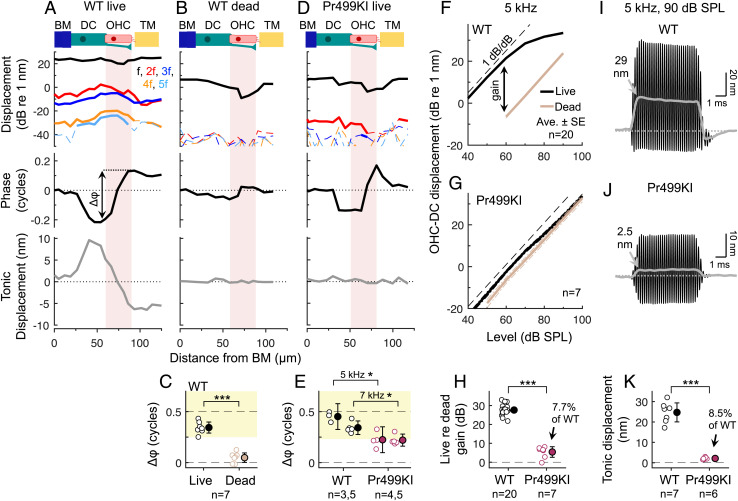
To verify that the out-of-phase motions were due to an active mechanical process, we repeated our measurements after euthanasia. Death eliminates the electrical potential that is necessary for large mechanotransduction currents and thus reduces the voltage drive to OHC electromotility. As expected, death reduced displacements at the stimulus frequency and its harmonics, greatly diminished the phase difference between the RL and OHC–DC, and nearly abolished the tonic displacements (Fig. 3 A–C and SI Appendix, Fig. S7). While harmonics were measurable at stimulus levels above 70-dB SPL postmortem, tonic displacements were <2 nm, even at stimulus levels as high as 100-dB SPL (SI Appendix, Fig. S7). The harmonics observed postmortem may result from small, residual receptor potentials driving OHC electromotility and/or from passive nonlinearities in the organ of Corti’s mechanics.

Fig. 3.

Out-of-phase motions depend on active, prestin-mediated electromotility. (A and B) Displacements in a WT mouse alive (A) and postmortem (B) for a 7-kHz, 70-dB SPL stimulus. Phases were referenced to the BM phase and are only shown for the response at f, for clarity. Dashed portions of the magnitude curves indicate data falling below the noise floor. (C) Phase differences (Δφ) between the RL and OHC-DC in live and dead mice for 70-dB SPL tones at 7 or 8 kHz (paired t test: t₆ = 10.14, P < 0.0005). Individual/average data are indicated by closed/open symbols. (D) Displacements in a live Pr499KI mouse for a 7-kHz, 70-dB SPL stimulus, plotted as in A and B. (E) Phase differences between the RL and OHC-DC were significantly smaller in Pr499KI versus WT mice at 5 and 7 kHz (t test: 5 kHz, t₅ = 4.27, P = 0.0079; 7 kHz, t₈ = 3.79, P = 0.0053). (F and G) Average OHC-DC displacements in live and dead WT (F) and Pr499KI (G) mice for 5-kHz tones varied in level. (H) The displacement gain in live re dead Pr499KI mice for a 5-kHz, 60-dB SPL tone was significantly different from 0 (t test: t₆ = 4.72, P = 0.0033) and was 7.7% of the WT gain (t test: t₂₅ = 17.90, P < 0.0005), consistent with the residual electromotility in Pr499KI mice. (I and J) OHC-DC displacement waveforms from WT (I) and Pr499KI (J) mice for a 5-kHz, 90-dB SPL stimulus. (K) Tonic displacement magnitudes (for 5-kHz, 90-dB SPL tones) in Pr499KI mice were significantly different from 0 (t test: t₅ = 9.25, P < 0.0005) and were 8.5% of those in WT mice (t test: t₁₁ = 10.87, P < 0.0005). Error bars in C, E, H, and K indicate 95% CIs.

Out-of-Phase Motions Depend on Normal Prestin.

To confirm that the out-of-phase motions in live mice depended on prestin, we measured vibrations in Prestin 499 knockin (Pr499KI) mice, which have mutant prestin that confers ∼7.5% of the electromotility observed in wild-type (WT) mice (10). While prior vibration measurements in Pr499KI mice have demonstrated that nonlinear amplification of BM motion is largely absent (31, 39), measurements from within the OHC region have not been previously examined.

Responses to 70-dB SPL tones in Pr499KI mice were much smaller than in WT mice, particularly in the OHC region, but contained measurable harmonics (Fig. 3D and SI Appendix, Fig. S8). This is consistent with the presence of normal, nonlinear mechanotransduction but reduced OHC electromotility in these mice. Interestingly, while the tonic displacements in Pr499KI mice were negligible for stimulus levels ≤70-dB SPL, the top and bottom of the OHC region still exhibited modest phase leads and lags relative to the BM, respectively, with phase differences between the RL and OHC–DC being reduced to <65% of the WT value.

Further examination of vibrations in Pr499KI mice indicated that these phase differences were due to residual electromotility conferred by the mutant prestin. First, the phase differences were strongly reduced postmortem (SI Appendix, Fig. S8), indicating that they depended on mechanotransduction currents. Second, OHC–DC vibrations in live Pr499KI mice grew compressively (<1 dB/dB) for stimulus levels above 70-dB SPL, revealing ∼5.4 dB of nonlinear amplification that was eliminated by death (Fig. 3 F–H and SI Appendix, Fig. S9). The gain in live relative to dead Pr499KI mice for a 5-kHz, 60-dB SPL tone was ∼7.7% of the WT value (Fig. 3H), consistent with the amount of electromotility observed in vitro (10). Furthermore, tonic displacements could be elicited in Pr499KI mice at stimulus levels >80 dB SPL, with amplitudes saturating at ∼8.5% of WT values (Fig. 3 I–K), confirming the presence of residual electromotility. Since the electromotility in Pr499KI mice appeared to be strong enough to amplify the OHC region’s cycle-by-cycle vibrations by a factor of ∼2, the RL and OHC–DC phases would be expected to partially reflect the out-of-phase motions associated with electromotility, as we observed.

OHC stereocilia and mechanotransduction are unaffected in Pr499KI mice (10), such that active stereociliary bundle motility may be present and operating in response to sound-evoked motions of the organ of Corti. However, our data show that this mechanism alone is incapable of driving large motions of the bottom and the top of the OHC region or of the TM (Fig. 3D and SI Appendix, Fig. S9). Bundle motility is also clearly insufficient for directly amplifying BM motion at high frequencies (31, 39, 40). Our measurements in Pr499KI mice therefore argue that prestin-based electromotility, and not bundle motility, is responsible for both the out-of-phase OHC region motions and the degree of cochlear amplification observed in WT mice. In addition, while motions at harmonic frequencies >20 kHz did not always resemble OHC contraction and elongation in WT mice, their dependence on prestin indicates that they are attributable to OHC electromotility.

Low-pass Filtering Does Not Critically Limit OHC Electromotility.

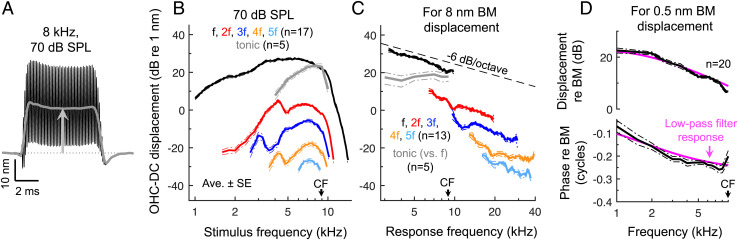
While OHCs may be capable of somatic force generation at high frequencies, we found that the motions induced by electromotility were influenced by low-pass filtering. Primary evidence for this was that the tonic OHC–DC displacement could be larger than the displacement at the stimulus frequency, particularly for near-CF tones (Fig. 4 A and B). Since the tonic component in the output of a sigmoidal nonlinearity is never larger than the response at the stimulus frequency, the output of the nonlinearity must be low-pass filtered.

Fig. 4.

Motions associated with OHC electromotility are low-pass filtered. (A) OHC-DC displacement waveform for an 8-kHz, 70-dB SPL stimulus in a WT mouse. Low-pass filtering is indicated by the fact that the tonic displacement (gray curve) was larger than the cycle-by-cycle displacements (note that the waveform’s downward excursions do not reach the OHC-DC’s initial baseline position; dotted line). (B) Average cycle-by-cycle OHC-DC displacements for 70-dB SPL tones swept from 1 to 15 kHz (in ∼200-Hz steps) and tonic displacements for stimuli swept from 3 to 11 kHz (in ∼1-kHz steps). Tonic displacements were sharply tuned to the CF, where they were typically as large as displacements at the stimulus frequency and much larger than the harmonic responses. (C) Average interpolated OHC-DC displacements for stimulus levels producing 8 nm of BM displacement across frequency. Tonic displacements (plotted versus f) were roughly flat with stimulus frequency, while the cycle-by-cycle displacements (plotted versus their own frequency) declined by ∼7 dB/octave. Averages are shown when data from at least three mice were above the noise floor. (D) Average interpolated OHC-DC displacement (at f) for stimulus levels producing 0.5 nm of BM displacement across frequency. Magnitudes and phases were referenced to the those of the BM. The response of a first-order low-pass filter with corner frequency of 1.75 kHz is shown for comparison, with the filter’s phase response shifted by −0.02 cycles. Data analyzed in D were obtained over a wider range of stimulus levels but using coarser frequency steps (0.5 kHz) compared to the data presented in B and C.

To confirm the presence of low-pass filtering, we used interpolation to calculate OHC–DC responses at stimulus levels that produced a fixed amount of BM displacement across frequency, assuming that this provides a constant input to the OHC stereocilia (30). First, we set the criterion BM displacement to 8 nm in order to generate measurable harmonic and tonic distortions. While these levels yielded nearly constant tonic OHC–DC displacements as the stimulus frequency was increased, the cycle-by-cycle displacements all declined by an average of ∼7 dB/octave (Fig. 4C). This is roughly consistent with the 6-dB/octave attenuation expected of a first-order low-pass filter. However, a corner frequency could not be detected in the interpolated responses, indicating that it fell below ∼4 kHz.

To examine responses at lower frequencies, we calculated OHC–DC displacements at the stimulus frequency for a criterion BM displacement of 0.5 nm. The resulting OHC–DC displacement magnitudes and phases (referenced to the BM) resembled those of a low-pass filter response with corner frequency between 1 and 2 kHz (Fig. 4D). This corner frequency estimate was supported by comparisons of OHC–DC displacements with the low-pass filtered output of a Boltzmann function (simulating the OHC nonlinearity) when using BM displacement as the function’s input (SI Appendix, Figs. S10 and S11 and SI Appendix, Supplementary Text). Low-pass filtering was necessary to reproduce the relative magnitude of the tonic component and the phases of displacements at the stimulus frequency and its harmonics (SI Appendix, Fig. S11). A corner frequency of ∼1 to 2 kHz is consistent with extrapolation from in vivo displacement data in gerbil, which placed the corner frequency >2.5 octaves below the CF (30).

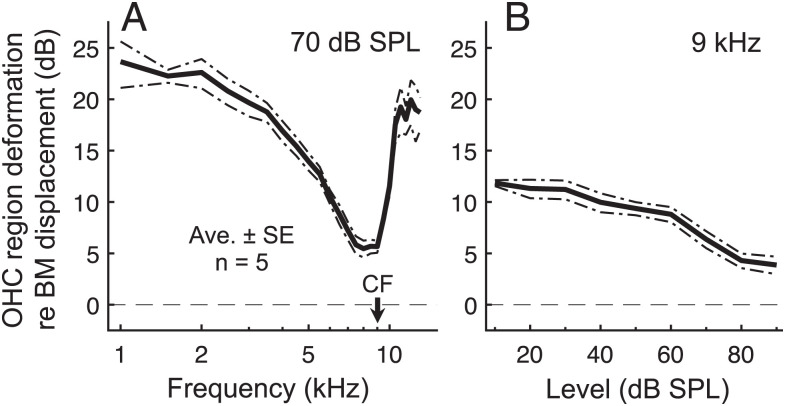
While our data confirm the presence of low-pass filtering, they also demonstrate that this filtering does not critically limit the influence of OHC electromotility on the motion of the organ of Corti at the CF. At the CF, both RL and OHC–DC displacements were ∼3 to 6 dB larger than those of the BM for stimulus levels <70 dB SPL (SI Appendix, Fig. S6D). By taking the vector difference between RL and OHC-DC displacements, we estimated the net cycle-by-cycle deformation of the OHC region induced by electromotility (Fig. 5). OHC region deformations exceeded BM motion at all stimulus frequencies and levels and were four times larger than BM motion for CF tones presented at low levels. Cycle-by-cycle electromotility therefore remains substantial near the CF, despite low-pass filtering.

Fig. 5.

Despite low-pass filtering, cycle-by-cycle deformations of the OHC region are large relative to the motion of the underlying BM at all frequencies. (A and B) Average vector difference between RL and OHC-DC displacements, normalized to BM displacement, for 70-dB SPL tones swept in frequency (A) or 9-kHz tones swept in level (B). The vector difference approximates the net deformation within the OHC region induced by electromotility. Despite the steep drop in deformation magnitude (re BM) for 70-dB SPL tones above ∼2 kHz, the deformations were still ∼2× as large as the BM displacement near the CF. At low stimulus levels, deformations were ∼4× as large as BM displacements.

Discussion

Here, we show that OHC electromotility generates forces in vivo that move the organ of Corti at frequencies more than five times the CF. Despite being low-pass filtered, contractile motions within the organ of Corti remained larger than BM displacements at the CF, particularly at the low SPLs where amplification is most important. Taken together, this argues that OHCs are capable of operating with both the speed and the strength necessary to subserve high-frequency amplification in the mammalian cochlea.

How amplification works remains unresolved (26, 41, 42). While the classic view is that OHCs primarily act by pushing and pulling on the BM via the DCs (4), the present data reinforce our previous finding that the structure that moves the most at the CF is actually the TM (32, 33). This suggests that a major role of OHC electromotility at the CF is to preferentially amplify motion at the top of the organ of Corti. This mechanism may serve to tune and enhance the fluid flow that stimulates IHCs (43), which is ultimately the goal of cochlear amplification.

Our data contrast with recent OCT measurements in the base of the gerbil cochlea that did not show out-of-phase motions within the OHC region (26). Instead, these measurements revealed frequency- and imaging-angle–dependent phase differences between the BM and OHC–DC junction, which were argued to result from longitudinal motion. This would not be surprising because electrically stimulated OHCs produce both longitudinal and radial motions of the organ of Corti ex vivo (37). While our results could also be influenced by these complex motions, they cannot simply be attributed to our imaging angle. We found the same antiphasic motion pattern at both 1 and 9 kHz, indicating that our results were not due to a fortuitous interaction between the imaging angle and the wavelength of the traveling wave, which is long at low frequencies and short near the CF (44). We also observed a stimulus-dependent phase lead of RL relative to BM motion (SI Appendix, Fig. S6 C and F) that was consistent with data from the basal cochlear turn in mouse (42), gerbil (45), and guinea pig (41, 46). Our measurement approach therefore replicates key findings from other laboratories and in other species.

Our data further indicate that OHC electromotility was responsible for the out-of-phase motions we observed. The cycle-by-cycle displacements within the OHC region depended on physiological state and prestin. They also followed the same motion pattern as the tonic displacements, which are almost certainly attributable to OHC electromotility. For instance, tonic displacements of the BM and RL were similar to those observed during sustained electrical stimulation ex vivo (47). Since tonic displacements of the OHC–DC junction could exceed the cycle-by-cycle displacements, they cannot be due to rectification in the passive mechanical response to a sinusoidal force. Thus, the simplest interpretation is that the tonic and cycle-by-cycle displacements resulted from the OHC’s electromotile response to sustained and cycle-by-cycle changes in membrane potential, respectively.

Consistent with this, the asymmetry in OHC–DC displacement waveforms resembled that observed in receptor potentials of apical guinea pig OHCs, which are tonically depolarizing for near-CF stimuli (48). However, basal guinea pig OHC receptor potentials are nearly symmetric at the CF (49), and the OHC’s stereociliary bundle is thought to be positioned such that nearly half of the mechanotransduction current is activated at rest, resulting in roughly symmetric receptor currents and potentials (16). It is hard to reconcile these different findings at present. The in vivo resting position of OHC stereociliary bundles in the mouse apical turn is unknown, and there may be other sources of receptor potential asymmetry, such as the OHC’s basolateral conductances (50). Whether the tonic OHC length changes play a modulatory role in the amplification process also remains uncertain.

The relatively large magnitude of the OHC–DC tonic displacements may be due to the influence of what could be approximated by a first-order low-pass filter with corner frequency of ∼1 to 2 kHz. While it is tempting to attribute this to membrane filtering of the OHC’s receptor potential, it likely represents the summed effect of a cascade of various mechanisms. For instance, the organ of Corti’s impedance has been characterized as viscoelastic, resulting in displacements that decline by ∼4.8 dB/octave in response to constant force (51, 52). Prestin kinetics have also been shown in vitro to confer a frequency-dependent roll-off that is a few decibels/octave up to ∼10 kHz but more severely limiting at higher frequencies (17, 18, 53). However, modeling work suggests that the OHC’s piezoelectric properties and how the cell is loaded in vivo may help to tune the OHC’s power output to the requisite high frequencies (54). Nevertheless, such model speculations require experimental verification, particularly at frequencies above 50 kHz, where prestin kinetics are expected to be frequency limiting (55).

Traveling-wave amplification is a spatially distributed process that not only depends on OHCs but also strongly depends on the properties of the BM, the cytoarchitecture of the organ of Corti, and the hydrodynamics within the cochlear duct (56). For example, a recent model has shown that broadband OHC-generated forces, acting through cochlear hydrodynamics, can yield realistic, narrowband BM amplification (57). Indeed, while low-frequency OHC force generation produces large displacements of the OHC and DC region, these low-frequency forces have little impact on BM motion, which is only amplified at frequencies within approximately one octave of the CF (26, 34, 42). These low-frequency motions also appear to produce relatively minor IHC stimulation (49, 58), possibly due to high-pass mechanical filtering of the motions at the top of the organ of Corti (33). Thus, the electro–hydro–mechanical environment of the OHCs may serve to effectively counteract the low-pass characteristic of OHC electromotility. Still, it remains to be determined whether low-pass filtering does critically limit OHC electromotility at the highest frequencies of mammalian hearing. This could be addressed through future micromechanical measurements in the basal turn of the mouse cochlea, where CFs exceed 50 kHz.

Materials and Methods

Detailed methods are provided in SI Appendix, Supplementary Methods.

OCT Vibrometry.

OCT was used to perform cochlear imaging and vibrometry after surgically accessing the left middle ear space of anesthetized, adult WT CBA/CaJ and Pr499KI mice of either sex. All procedures were approved by the Institutional Animal Care and Use Committee at the University of Southern California. Our custom-built OCT system and related methodology have been previously described (31–34). The current system uses a light source with a reliable, linear sweep (Insight akinetic swept source; center wavelength = 1,310 nm; bandwidth = 95 nm), which permits higher phase stability and thus a lower noise floor in the vibration measurements than was previously possible. To further reduce the noise floor, significant time-domain averaging of sound-evoked responses was employed. This allowed us to study the low-magnitude, higher-order harmonics in the responses and to reliably quantify tonic displacements from the vibratory waveforms.

In each experiment, the mouse was positioned so that structures within an apical cochlear region (tuned to ∼9 kHz in WT mice) could be visualized in two-dimensional cross-sectional scans. To primarily capture the transverse motions of the relevant structures, the mouse’s head was further oriented so that the BM was at an angle ∼20° or less relative to the horizontal plane. Though each structure may move in three dimensions, only the motions in line with the path of the light source were measured. Details regarding sound stimuli, number of stimulus repetitions used, and analysis methods for different measurement paradigms are provided in SI Appendix, Supplementary Methods.

Statistical Analysis.

Reported values are the mean ± SE unless otherwise noted. Statistical analyses were performed with MATLAB (2020b, MathWorks, Natick). Two-tailed unpaired or paired Student’s t tests were used to assess statistical significance at the P = 0.05 level. Significance is indicated in figures by asterisks (*P < 0.05, **P < 0.005, and ***P < 0.0005).

Data Availability

Data supporting the findings of this study are included in the main text and SI Appendix and are available for download at GitHub (https://github.com/jso111/Dewey2021).