Abstract
Numerical simulations of Magic Angle Spinning Dynamic Nuclear Polarization (MAS-DNP) have transformed the way the DNP process is understood in rotating samples. In 2012, two methods were concomitantly developed to simulate small spin systems (less than 4 spin-1/2). The development of new polarizing agents, including those containing metal centers with S > 1/2, makes it necessary to further expand the numerical tools with minimal approximations that will help rationalize the experimental observations and build approximate models. In this paper, three strategies developed in the past five years are presented: an adaptive integration scheme, a hybrid Hilbert/Liouville formalism, and a method to truncate the Liouville space basis for periodic Hamiltonian. Each of these methods enable time savings ranging from a factor of 3 to >100. We illustrate the code performance by reporting for the first time the MAS-DNP field profiles for “AMUPol”, in which the couplings to the nitrogen nuclei are explicitly considered, as well as Cross-Effect MAS-DNP field profiles with two electrons spin 5/2 interacting with a nuclear spin 1/2.
Graphical Abstract
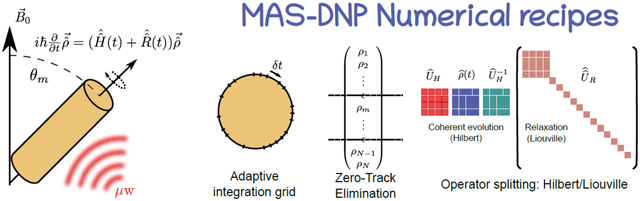
Faster MAS-DNP simulations in Liouville space via adaptive integration
Zero-Track Elimination algorithm for periodic Hamiltonians
Operator splitting using Hilbert and Liouville formalism to compute larger spin systems
First bis-nitroxide MAS-DNP field profiles with explicit Nitrogen hyperfine couplings
First solid-effect and cross-effect MAS-DNP field profiles with electron spins S = 5/2
Introduction
In the past two decades, Magic Angle Spinning Dynamic Nuclear Polarization (MAS-DNP) has enabled very difficult solid-state NMR experiments by increasing the resolution (MAS) and the sensitivity (DNP) [1–3]. First developed for low magnetic fields [4–6], MAS-DNP for high fields [1,7] has been a game changer for difficult systems [8–15], thanks to hardware developments [3,16–20] and the introduction of biradicals as polarizing agents [21–24]. MAS-DNP complements room temperature solid-state NMR experiments and enables ssNMR applications where the system of interest has a low concentration [14,25–31] and/or cannot be isotopically enriched [32–34].
DNP is a process that involves a complex interplay between the coherent and incoherent behavior of the spin system. The time dependence induced by MAS generates fast energy level (anti)crossing [35,36] and so-called rotor events [37]. These rotor events impact the populations and coherences in the density matrix, the effects of which depend on the strengths of the interactions and the rates of the crossings [35,37]. The deep complexity of this problem makes numerical simulations the only viable tool for the analysis of these mechanisms [35–39].
To simulate an experiment under MAS-DNP conditions, one needs to account for both the coherent (time dependent) behavior of the spin dynamics and its coupling to the environment, i.e., the relaxation. The integration of the resulting time dependent quantum master equation requires significant computing power. Due to the potentially large anisotropies and the amplitude of the interactions, it is integrated in a stepwise fashion [35–37]. This integration can be done over a long evolution time [35] or can take advantage of the periodicity of the problem [36,37] by just computing the evolution operator for one rotor period and applying it stroboscopically [36,37]. Hilbert space simulations are best suited for the former, while the Liouville space approach is better for the latter, and turns out to be faster for small spin systems [36,37,40–42].
This integration of the quantum master equation involves many matrix multiplications and exponential matrix operations. As the size of the spin system increases, the matrices become very large (exponential scaling), making the simulations cumbersomely slow. Improving the efficiency of MAS-DNP simulations is critical, as currently, they are the only way to understand time-dependent DNP mechanisms [35–40,42–48] and may be the best pathway for enabling the rational design of better biradicals [40,43,44,49,50]. While the numerical efficiency problem seems largely contained for bisnitroxide, with the advent of quantitative simulations [44,51], it may remain an open problem for biradicals with strong exchange interactions [49,52–54]. In addition, the MAS-DNP community has a strong interest in using other paramagnetic species for DNP that are reduction resistant, can be used to dope bulk materials [55–65], and/or may offer increasingly important structural information [66,67].
The current literature offers a variety of approaches to accelerate numerical spin dynamic simulations, such as the Liouville space basis truncation [68,69] using symmetry considerations or the contribution of the state to the spin dynamics [70,71], truncations using the Krylov-Bogoliubov approximation [72], block diagonalization [73,74], or the use of efficient exponential matrices [74–77]. For Hilbert space simulations, larger spin systems can be simulated with the coupled cluster approach [78–81]. For very large spin systems, one can use Krylov propagation [74,82] and prevent matrix size explosion using tensor trains to avoid opening the Kronecker products [83]. In addition, simulations of frozen systems routinely require powder averaging to provide an accurate representation of the system’s properties. To this end, efficient interpolation algorithms have been implemented and yield considerable time savings [84–87]. However, most of these approaches have not been implemented into MAS-DNP simulations but have great potential to improve the speed of the simulations.
In this article we describe additional numerical methods that can lead to orders-of-magnitude time savings in simulations of MAS-DNP experiments. First, a simple adaptive integration scheme that enables time savings on the order of three to five times is presented. Second, a hybrid Hilbert/Liouville formalism is introduced to study larger spin systems, which enables simulations of MAS-DNP field profiles with more spins and with electron spin S > ½ with times savings greater than one hundred times for short spin evolution times (< 1 s). Third, this hybrid formalism is used to truncate the Liouville space basis. This process, similar to the Zero-Track-Eliminations [88], enables truncation of the Liouville space basis, which combined with the adaptive integration scheme, yields times savings on the order of five to nine times, and is perfectly suitable for 3-spin steady state studies. Finally, the advantages, limitations, and potential improvements of each method are discussed.
Simulations
Hamiltonian and Integration of the Master equation
In this section the spin system and Hamiltonian are presented together with the standard numerical simulation approach to numerically integrate the time dependent Liouvillian [36,37].
For a spin system containing Ne electron spins and Nn nuclei, the Hamiltonian for MAS-DNP simulations is defined as:
| Eq. (1) |
Where
| Eq. (2) |
| Eq. (3) |
Herein, the electrons spins are designated by a, b, c, … while nuclear spins designated by 1, 2, 3… gi stands for the electron g-tensor value of electron spin i, Di,j, the electron dipolar coupling between electron spin and i, Ji,j, the exchange interaction between electron spin i and j, Ai,j, the hyperfine coupling between electron spin i and nucleus n, ωn, the nuclear Larmor frequency of nucleus n, ωμw, the microwave frequency, and ω1, the microwave nutation frequency. If the electron spin has S > ½ the Zero-Field Splitting (ZFS) term must be accounted for. This interaction is treated as a perturbation of the Zeeman interaction to enable the simulations in the microwave rotating frame. Using the Irreducible Spherical Tensor (IST) representation, the ZFS Hamiltonian can be written up to second order as
| Eq. (4) |
Where and are the spatial tensor components of the ZFS and the IST, respectively, and is the Larmor frequency of the electron spin (detailed expressions are given in references [73,89])
The simulations are carried out by propagating the density matrix either in Hilbert space with the Liouville-von Neuman equation [35]
| Eq. (5) |
where and are the coherent and relaxation operators, respectively in Hilbert space, or in Liouville space using the Master equation [36,37,41]
| Eq. (6) |
where and are the coherent and relaxation super-operators. We use one hat for an operator O in Hilbert space, and two hats for O in Liouville space. In the Liouville basis made of the projectors |ϕi〉〈ϕj|, where |ϕi〉 are the Hilbert space states, . is just reshaped as a vector. This basis is called wave-function basis [90] (but also the Bra-Flipper [91]). To simplify the equations, we set ℏ = 1.
In this article the relaxation super-operator was generated in the eigenbasis of the Rotating Frame Hamiltonian (without microwaves), . Details about the relaxation and propagation of such equations can be found in a previous publication [37]. Other relaxation models may be valid [92,93], but might not benefit from the same performance gains.
The numerical solution of the MAS-DNP master equation in the Liouville space is obtained by slicing the rotor period in small time intervals δt (typically ~103-104 steps per rotor period). At each step k, the Liouvillian is assumed to be constant, and the evolution super-operators are computed:
| Eq. (7) |
The calculation of this matrix exponential is often the slowest step of the simulation, and this step must be repeated many times. For one rotor-period, τr, the complete evolution super-operator is given by
| Eq. (8) |
The density matrix at an integer multiple of any rotor period, N, is obtained as
| Eq. (9) |
from which the expectation values of the operators are extracted. For example, the polarization of electron spin a, Pa, is defined as
| Eq. (10) |
and the polarization gain, ϵB, is defined as
| Eq. (11) |
More details can be found in earlier publications [38,44,51].
Simulation parameters
Unless otherwise specified, all the simulations were carried out assuming a microwave frequency ωμw = 2π × 263.45 GHz, a temperature T = 100 K, a MAS frequency vr = 8 kHz, and a nutation frequency ω1 = 2π × 0.4 MHz. Using Liouville space formalism, the steady-orbit density matrices were computed for 30 s of free evolution. When using the Hilbert/Liouville formalism, the density matrix was propagated for 100 ms of free evolution. For all nuclei we assumed T2,n = 10 ms.
For single orientation bisnitroxide simulations, we used an arbitrary biradical geometry. The g-tensor principal axis frame values were g = [2.00924, 2.0061, 2.00205], Da,b = 30 MHz, Ja,b = 0 MHz. The electron a is coupled to a proton through a dipolar hyperfine coupling of Aa,1 = 3 MHz. The g-tensors relative orientation was set to (α,β,γ) = (90°,90°,90°), the electron-electron dipolar angles to (θ,ϕ) = (90°,180°), and the electron-proton dipolar angles to (θn,ϕn) = (0°,0°). The electron relaxation times were set at T1,e = 0.3 ms and T2,e = 2.5 μs for bis-nitroxide, and the nuclear relaxation time was set to T1,n = 0.1 s for the protons. The single crystal orientation was chosen to be [0°,137.5°,275°] (Figure 2 and Figure 4). The electron-nucleus dipolar angles are arbitrary but for the chosen hyperfine coupling strength, they have no effect on the outcome of simulations which are dominated by the electron spins’ dynamics [37].
Figure 2:
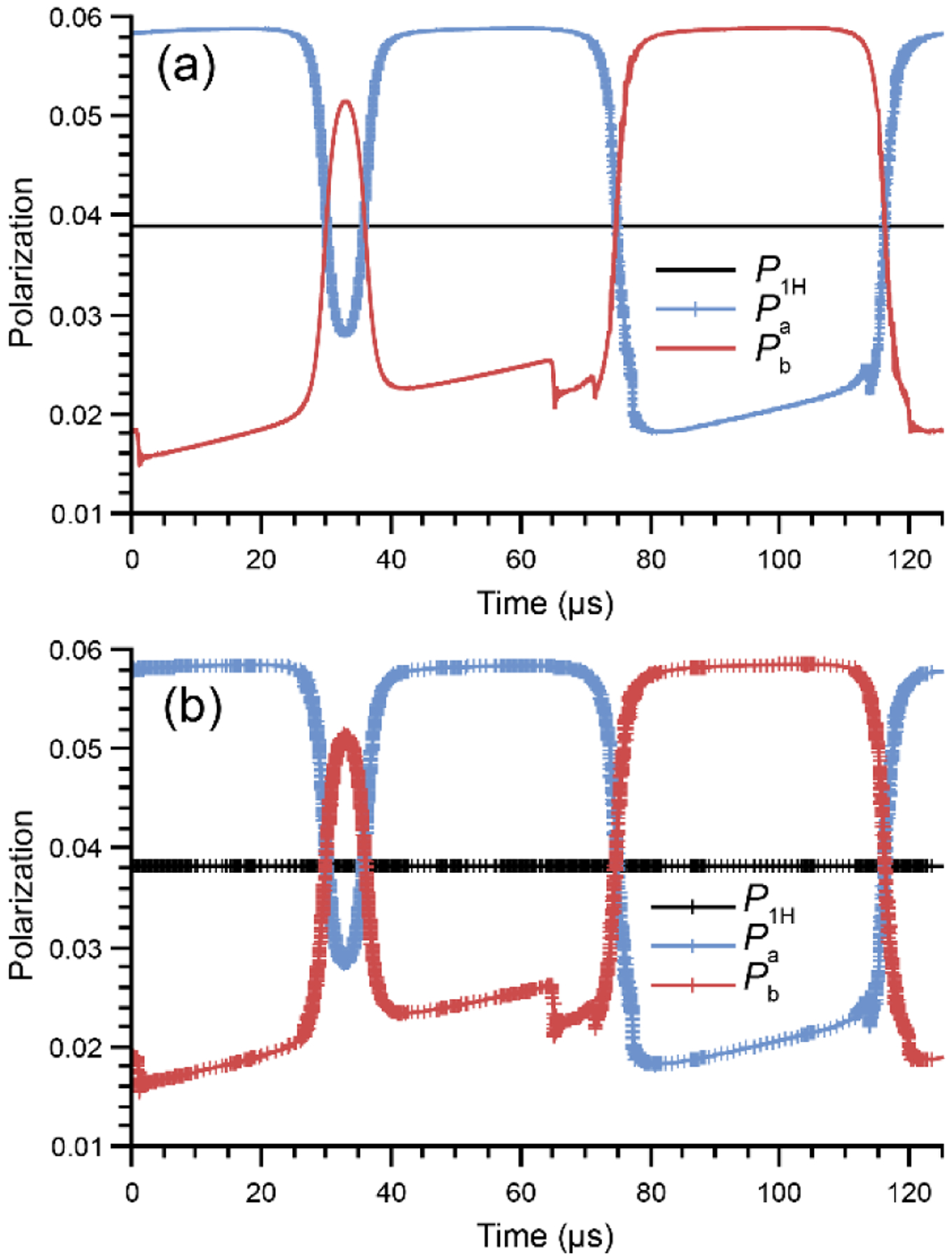
Single crystal, time dependence after 30 s of at “steady orbit” of the polarization of electrons spin a Pa (blue), electron spin b Pb (red) and nuclear spin P1H(black), in the case of constant step integration with 8192 steps (a) obtained in 35 s, and adaptive integration (b) obtained in 2225 steps and 10 s. The integration steps can be seen in figure (a) as Pa is represented with a blue line and crosses. In figure (b) the Pa, Pb and P1H are represented with vertical crosses which illustrates where finer and coarser steps where used.
Figure 4:
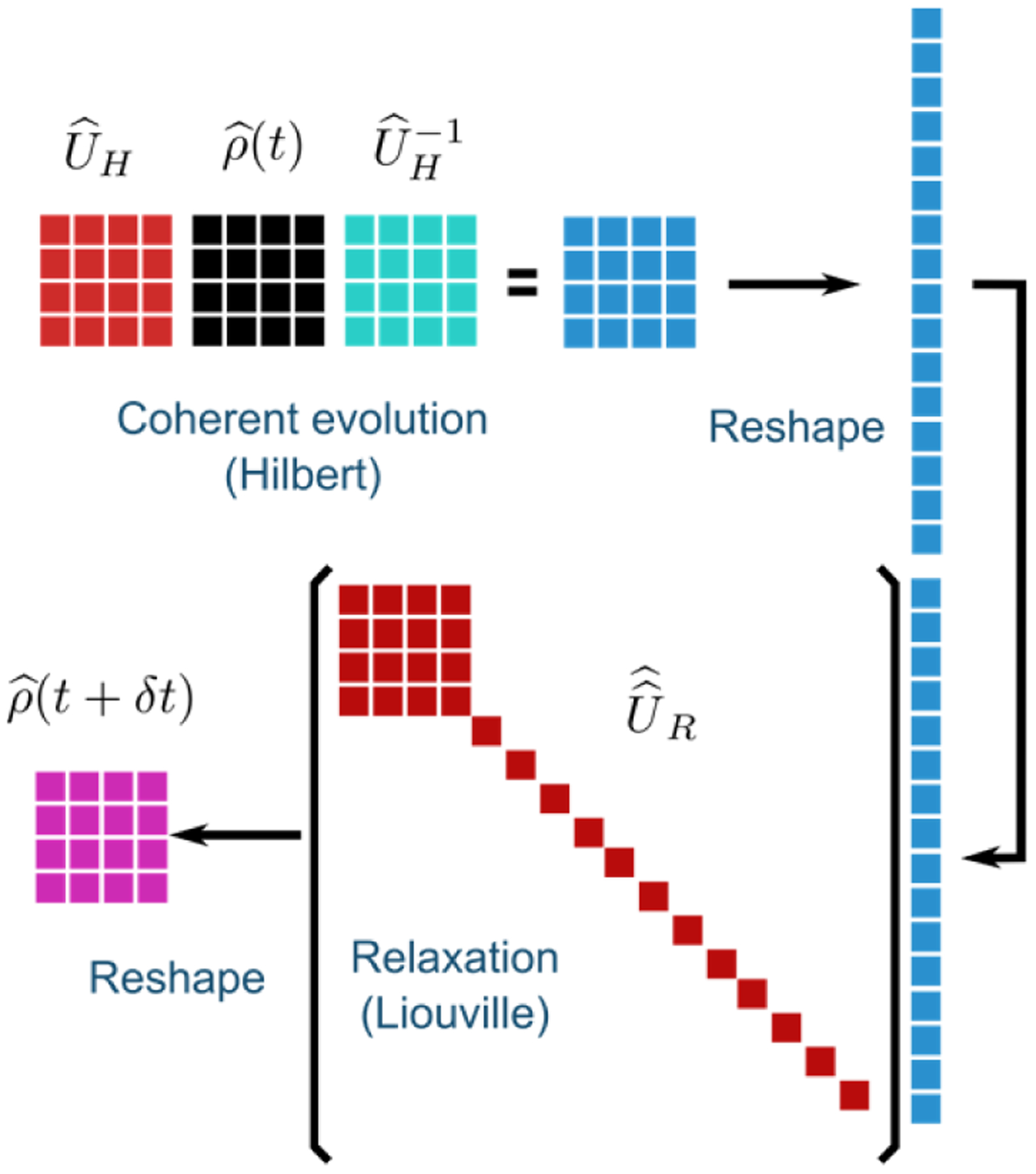
Schematic of Hilbert/Liouville formalism. First the density matrix is propagated in Hilbert space, then reshaped and Relaxation is applied. Finally, it is reshaped back into the Hilbert Space. In this schematic, the rotation “into” and “from” the lab-frame Hamiltonian eigenbasis were omitted for clarity. They occur at the beginning and the end of this cycle.
The MAS-DNP field profiles of “AMUPol” used parameters extracted from DFT and EPR experiments [44]. The g-tensors relative orientation was set to (α,β,γ) = (58°,57°,126°), Da,b = 35 MHz, Ja,b = −16 MHz, the electron-electron dipolar angles to (θ,ϕ) = (78°,167°), and the proton hyperfine coupling was identical to the single orientation case. In this case, the electron T1,e was assumed anisotropic, i.e., T1,e = f(g), where f is a second order polynomial [51,94] and T2,e = 2.5 μs.
For “AMUPol” and the fictious bisnitroxide, the 14N nitrogen hyperfine coupling was set to AN = [20 18 101] MHz. Each electron spin is coupled to one 14N nuclear spins. The hyperfine coupling can be implicitly or explicitly considered. In Figure 3 and Figure 8, the 14N were implicitly accounted for by considering that the hyperfine coupling shifts only the electron Larmor frequency
| Eq. (12) |
Figure 3:
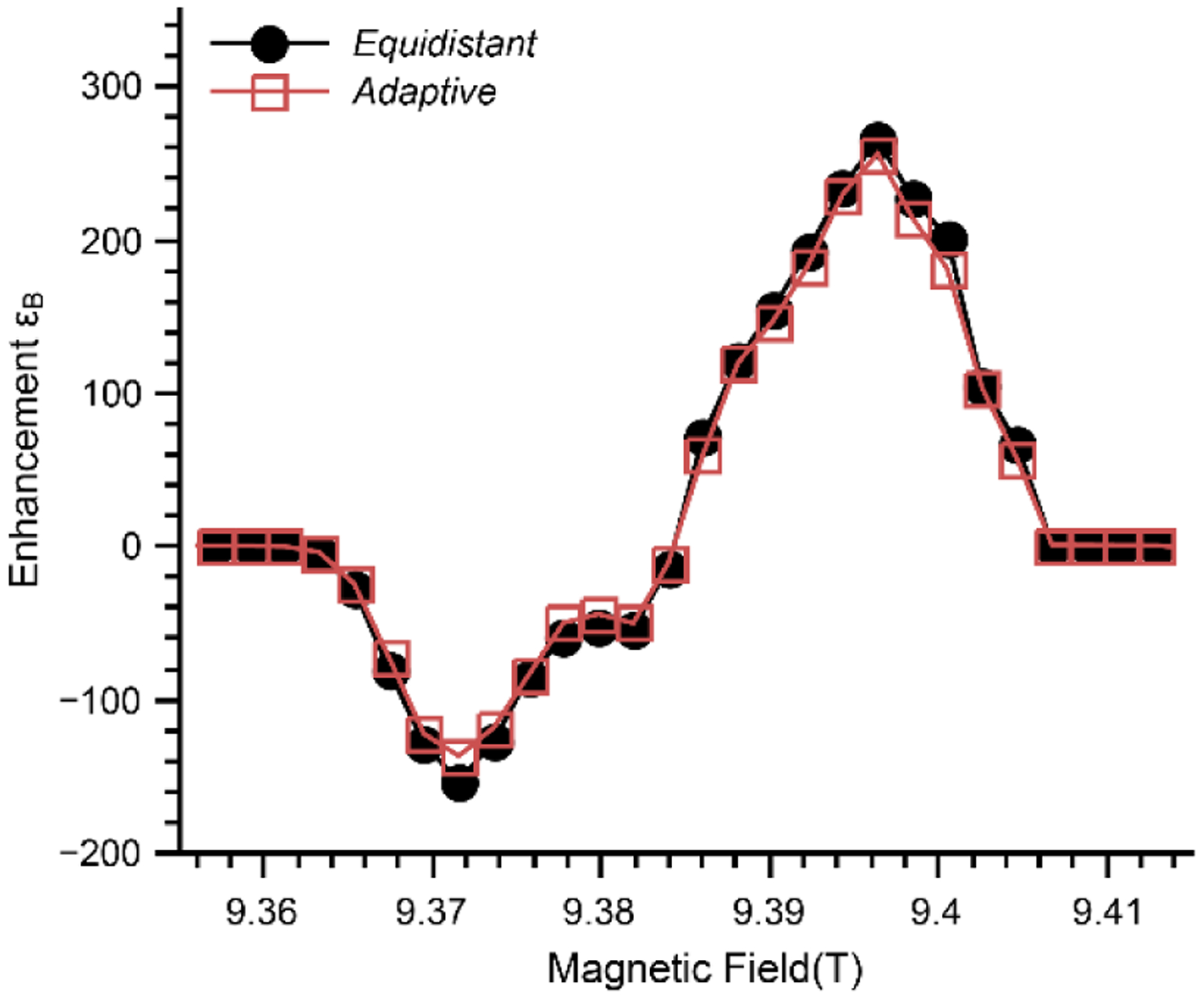
MAS-DNP field profile of AMUPol computed with two different methods: equidistant (black circles) and adaptive integration (open red squares). The equidistant was computed in 5h 48 min as compared to 1h 39 min for the adaptive. The maximum number of steps was set to 8192 (N=13) and the convergence criteria were [10−3,10−6]
Figure 8:
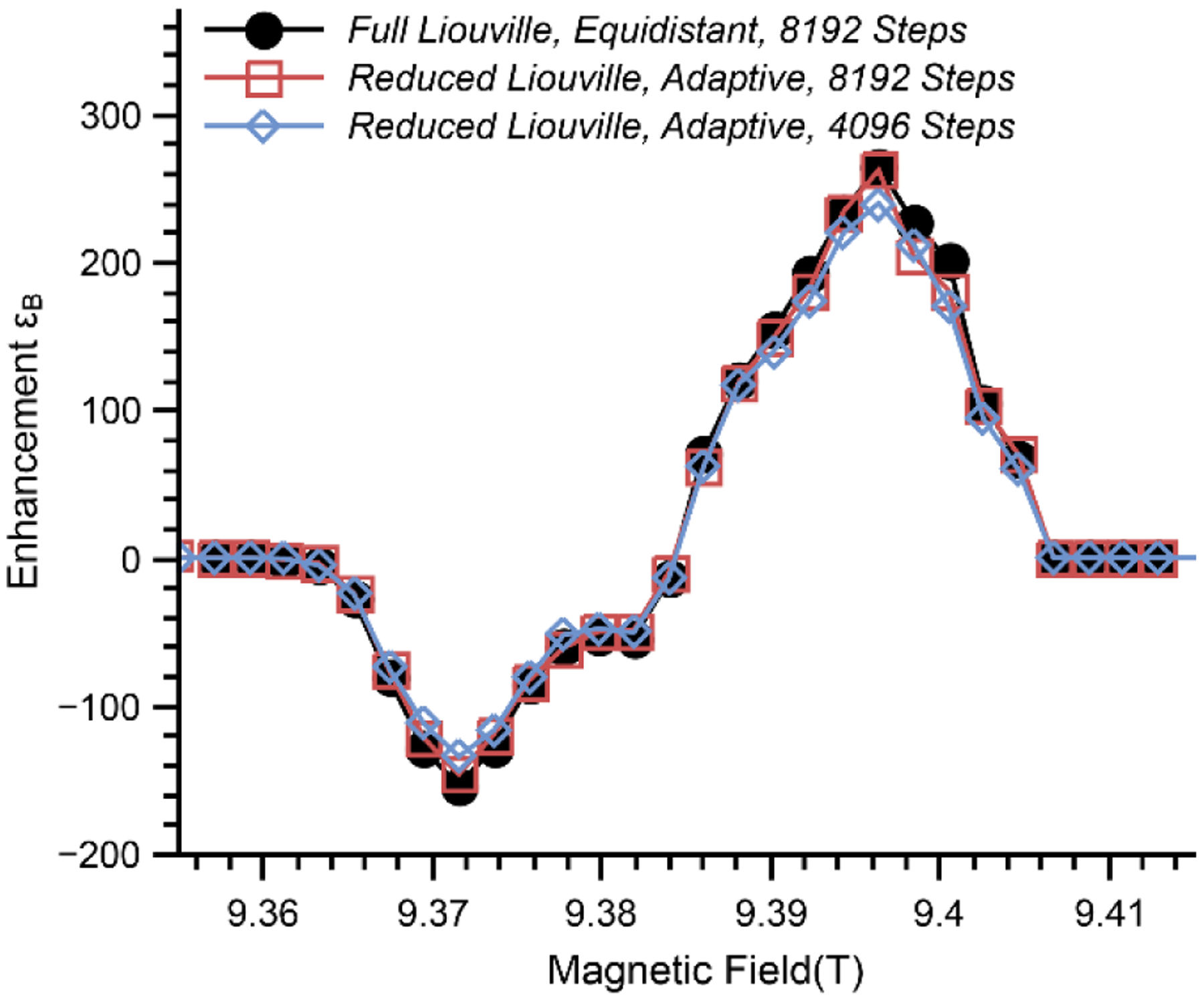
MAS-DNP field profile of AMUPol computed with equidistant integrations steps (black circles, in 5h48min), computed with adaptive integration and reduced Liouville space (open red squares, 1 h). The maximum number of steps was set to 8192 in these simulations. Adaptive integration, reduced Liouville (42 states vs 64) and a maximum number of steps set to 4096 obtained in 40 minutes (open blue diamonds). For all simulations the convergence criteria were [10−3,10−6].
In these simulations, mI,i was randomly picked between [1,0,−1] for each radical of each crystal orientation.
In Figure 4, the 14N are explicitly accounted for and their relaxation times were . In Figure 6, the 15N hyperfine coupling, [28 25 142] MHz, are explicitly accounted for. The relaxation times were .
Figure 6:
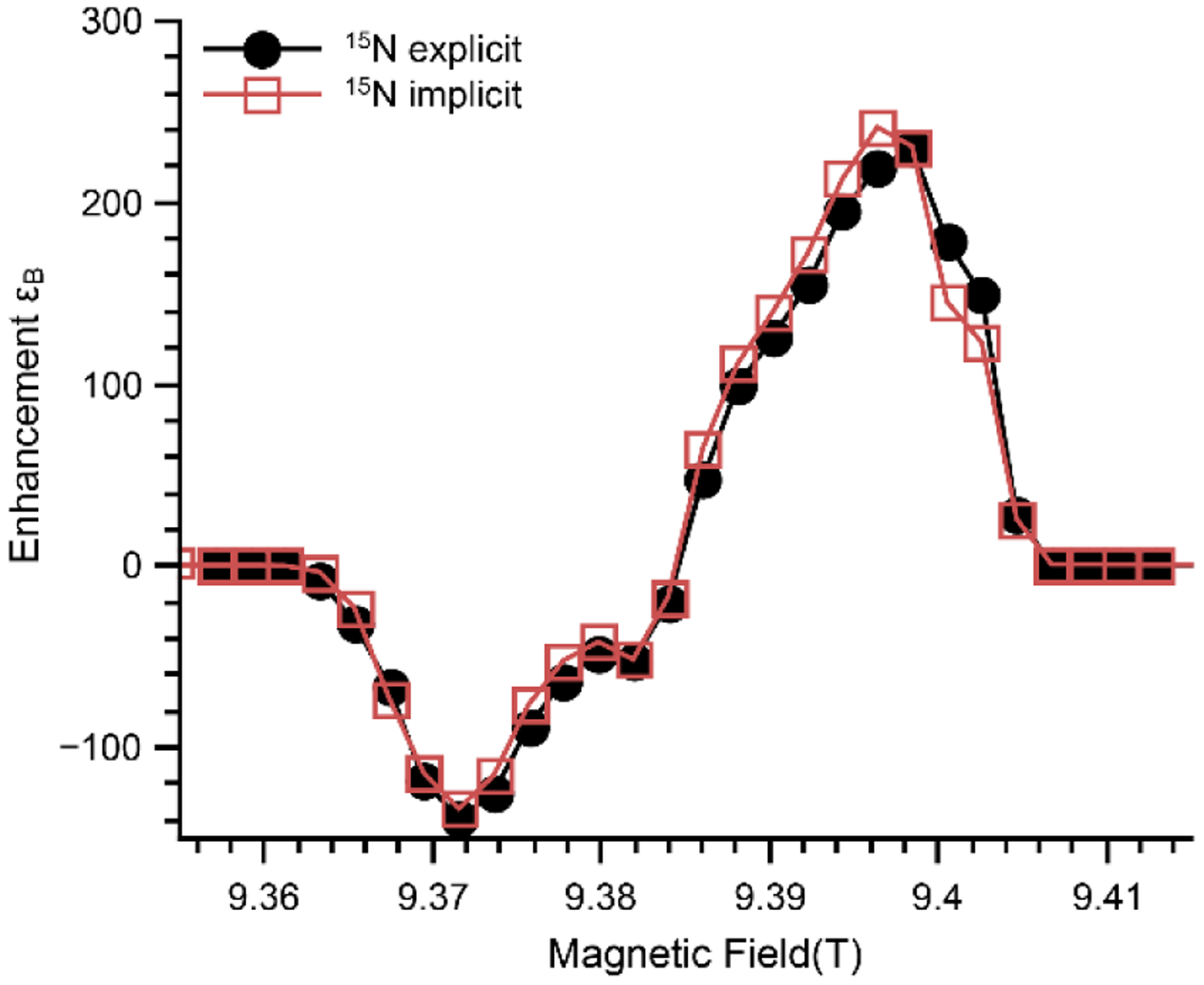
MAS-DNP field profiles after 100 ms of free evolution of a spin system mimicking a AMUPol labelled with 15N. Black circles represent a 5-spin system {2 electrons spin ½, 2 15N, 1 proton} computed with the Hilbert/Liouville method. Both secular and pseudo-secular 15N hyperfine coupling terms are considered. Red open squares represent adaptive Liouville space simulations where the 15N hyperfine coupling are implicitly accounted for.
Large integration grid made of 800 three angles REPULSION single crystal orientations [95], were used to ensure convergence of the simulations for bisnitroxide.
The quadrupolar interaction of the 14N was ignored as it is relatively small compared to the hyperfine coupling and Larmor frequency [96].
For simulations with S = 3/2 and 5/2 (Figure 9), a Dzfs = 1 GHz was assumed (i.e., with Principal Axis Frame values [−1 −1 2] GHz). The g-tensor was assumed to be isotropic and set, for convenience, to 2.0023. The dipolar coupling between the electron spins was set to Da,b = 30 MHz. The nucleus was assumed to be a 13C with a hyperfine coupling was set to 0.75 MHz. The ZFS relative orientation was (α,β,γ) = (90°,90°,90°), the electron-electron dipolar angles to (θ,ϕ) = (90°,180°) and the electron a - proton dipolar angles to (θ,ϕ) = (0°,0°). The relaxation times were set to T1,e = 0.1 ms and T2,e = 2.5 μs, an T1,n = 10 s. 200 three angles REPULSION single crystal orientations were sufficient to reach convergence.
Figure 9:
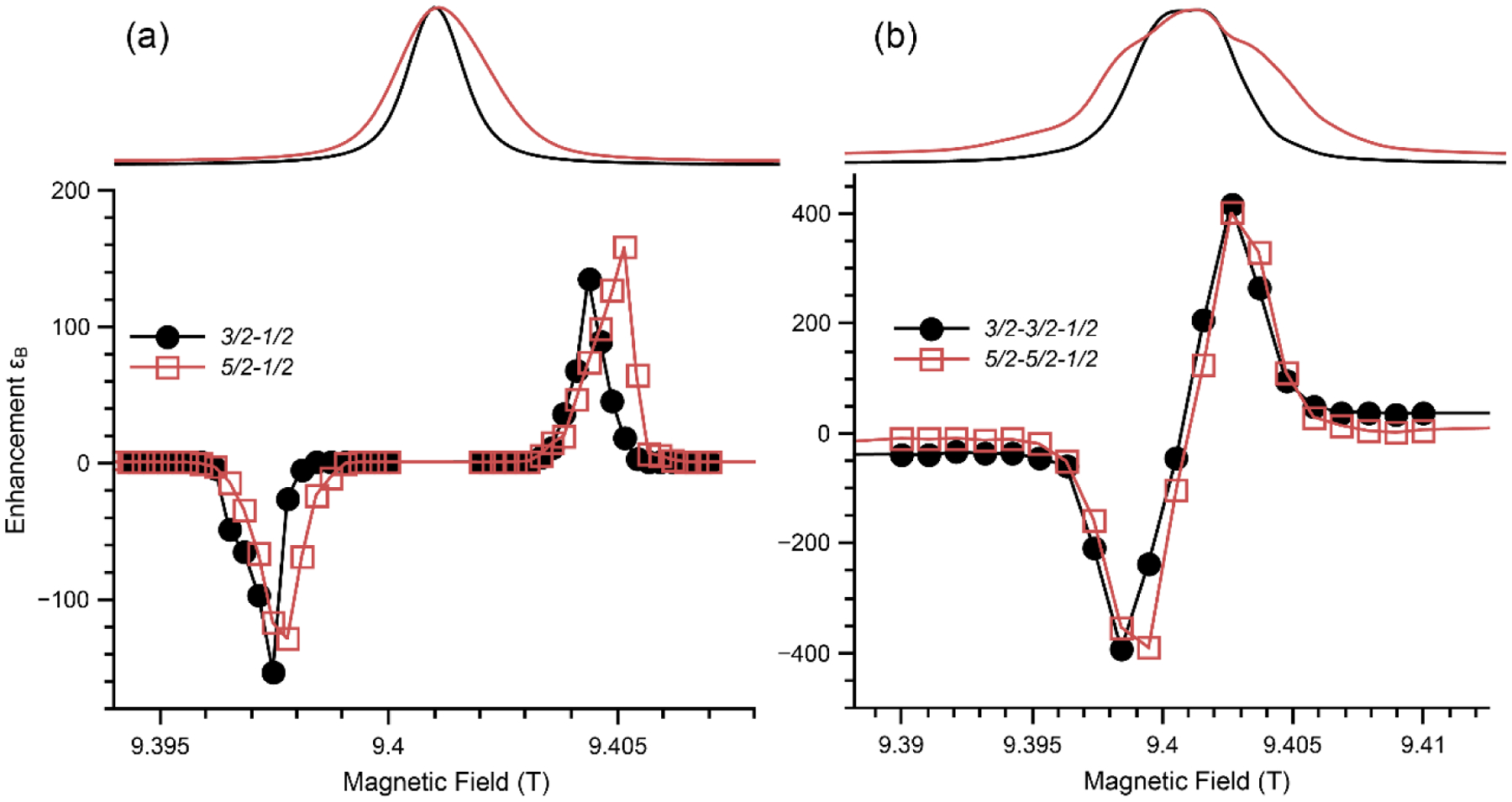
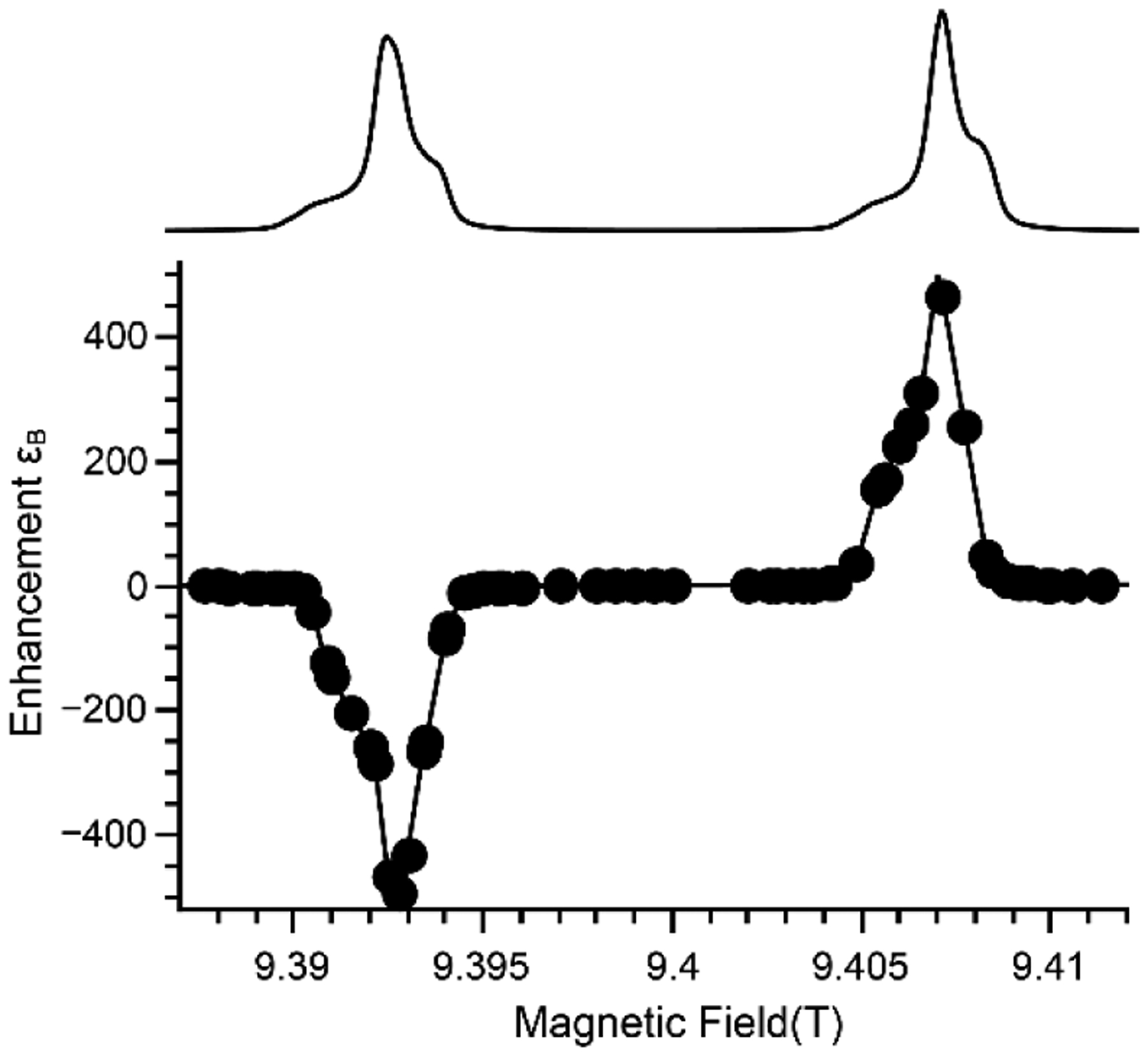
MAS-DNP field profile computed with the hybrid Hilbert/Liouville method after 25 ms evolution. (a, bottom), Solid Effect case with one electron spin 3/2 (black circles) or 5/2 (red open squares) and one carbon atom; (b, bottom) Cross-Effect case with two electrons spin 3/2 (black circles) or 5/2 (red open squares) and one carbon. Top of (a) and (b) are the corresponding EPR spectra of the spin systems used for the MAS-DNP simulations. The EPR spectra were computed with Easyspin assuming a line broadening [0.5 0.5] mT and a D strain of 100%, using the “matrix” method. In the MAS-DNP no strain was included.
All the simulations were carried out on a Dell Precision 7820, equipped with two Intel XEON gold 6130 CPUs, with 96 GB of RAM, and operating under Ubuntu 20.04.2 and using MATLAB 2020b (The MathWorks, Inc). The code was written in MATLAB and optimized to maximize calculation speed.
Adaptive integration in MAS-DNP
Principles
One obvious improvement to MAS-DNP simulations, and MAS simulations in general, is to avoid the constant time step integration and use an adaptive grid instead. So far, the MAS-DNP codes described in the literature use uniform/equidistant integration steps [35–37,41] which could be improved with an algorithm that automatically determines the optimal integration step size to achieve a given accuracy level.
The algorithm presented herein aims to (1) be simple to implement, (2) be accurate, (3) have low overhead (i.e., does not slow down the simulations), and (4) avoid re-computation of the Liouvillian and propagator super-operators.
The workflow of this procedure is shown in Figure 1. It is a modified two steps forward Euler method that computes accurately the spin dynamics during the rotor-events. First, the integration interval, i.e. one rotor period, τr = 1/vr, is divided into two different grids, each containing 2n elements. The largest time step allowed for the simulations is δtmax = τr/27 and the smallest time step allowed is δtmin = τr/2N (N = 12–14). The code determines on the fly, the optimal δt ∈ [δtmin,δtmax] for each “integration step”.
Figure 1:
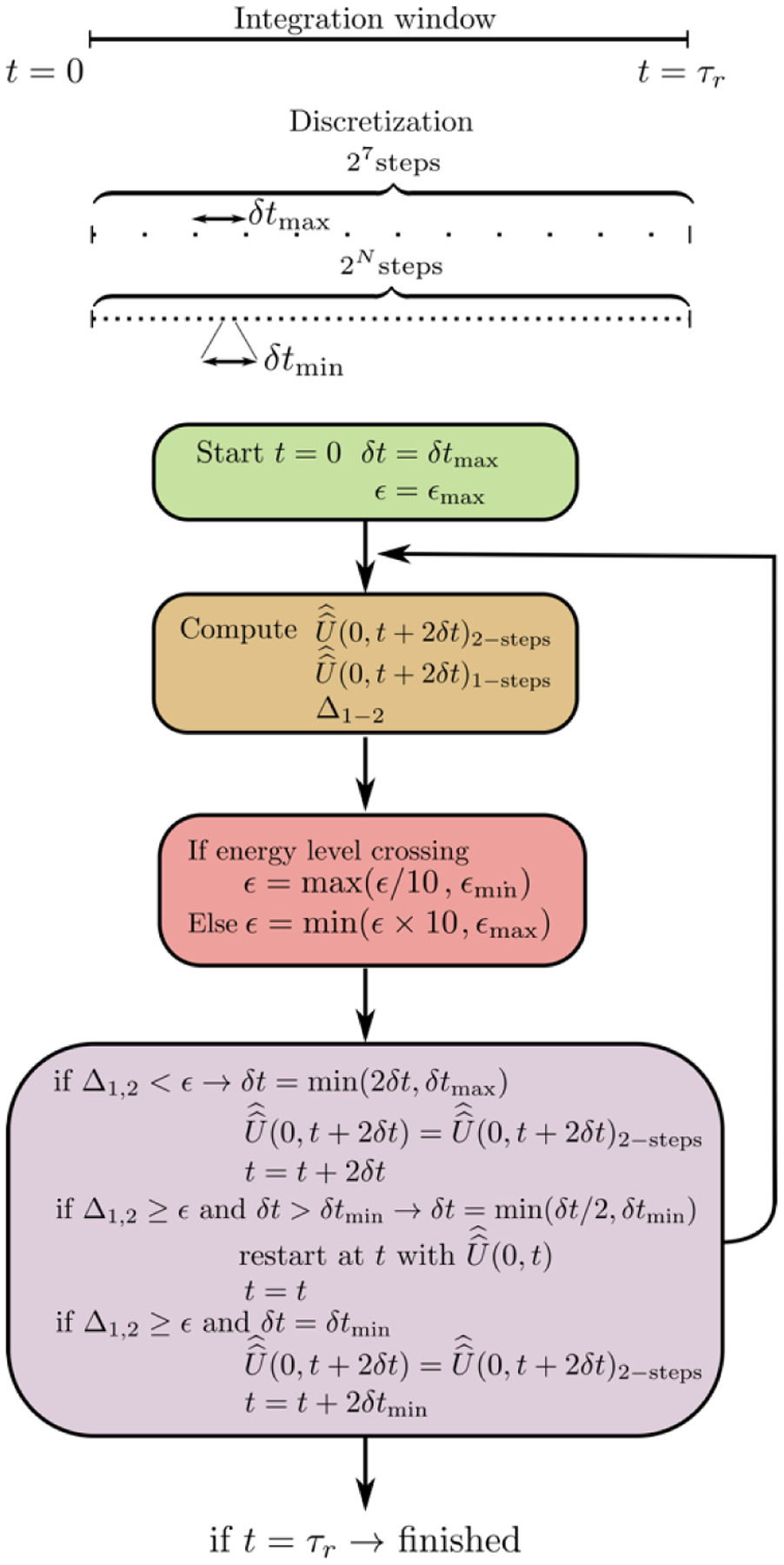
Schematics of the adaptive integration scheme for MAS-DNP simulations in the case of the Liouville space simulations. Typically, N = 12–14.
The master equation is first integrated with the largest step interval δtmax and the largest convergence criterion ϵ = ϵmax. Then, and for all following integration step, two computations are carried out: one super-operator propagator is computed with a time step δt and a second one with 2δt:
| Eq. (13) |
| Eq. (14) |
To assess convergence, the Frobenius norm of the difference between the two super-operator propagators, Δ1 − 2, is calculated:
| Eq. (15) |
If Δ1 − 2 is smaller than a user determined threshold ϵ (typically 10−3) the simulation proceed to the next integration step, and sets
| Eq. (16) |
The integration step is increased by a factor two (if δt is smaller than δtmax)
| Eq. (17) |
If the difference is greater than ϵ the calculation is carried out with a time step smaller by a factor 2
| Eq. (18) |
The code loops back and computes
| Eq. (19) |
| Eq. (20) |
The procedure is carried out until convergence is achieved, i.e. Δ1 − 2 < ϵ. To avoid recomputing the super operator propagators at each step, they are evaluated for the smallest δt = δtmin
| Eq. (21) |
and stored propagators in memory. They can later be scaled up by computing
| Eq. (22) |
which is “fast” when δt/δtmin is an integer.
This integration scheme is notoriously insufficient to capture rapid changes such as the rotor events. Without additional constraints, the code requires a stringent convergence criterion ϵ to be accurate, annihilating the benefit of the adaptive integration. To overcome it, and find a balance between accuracy and speed, two convergence criteria were introduced: one, used away from the rotor events, ϵmax, one used nearby the rotor events, ϵmin.
In addition, the existence of a rotor event is determined at each step with a sub-routine that checks if an energy level crossing/anti-crossing exists in the interval [t,t +2δt]. If this is the case, then a new convergence tolerance then ϵ is set:
| Eq. (23) |
where ϵmin is user-defined (typically 10−6). This ensures proper assessment at the rotor-events. This criterion is then slowly re-increased towards ϵmax after the energy crossing:
| Eq. (24) |
It is sufficient with this approach to check the energy level crossings occurring in the rotating frame since the energy diagram is dominated by the off-resonance generated by the g-tensors’ anisotropies under typical MAS-DNP conditions.
Applications
This algorithm leads to a factor >3 in time savings for MAS-DNP simulations while maintaining very good accuracy (≤ 5%). This is illustrated in Figure 2 which shows the computation for a single crystal orientation at “steady orbit” (or “quasi-periodic steady state”). The full lines, Figure 2 (a) show the constant time step integration carried out with 213 = 8192 steps. Figure 2 (b) lines with crosses show the same simulation with the adaptive integration algorithm which lead to only 2225 steps. The time saving is a factor 35 s/10 s ≈ 3.5. This value is very close to the ratio of number of steps 8192/2225 ~ 3.6, meaning that subroutine that determines the optimal time steps has minimal overhead.
This is confirmed with simulations of a AMUPol’s MAS-DNP field profile using both methods and reported in Figure 3. The equidistant method took 3.5 times longer than the adaptive version leading to identical profiles and a maximum error of ~8 % and an average error < 5 %.
All in all, and despite its simplicity, the adaptive integration scheme presented here is very powerful. It significantly reduces computation time, by a factor 3–5 depending on the convergence criteria and the spin system, while remaining accurate. It thus enables computing MAS-DNP field profiles, probe the effect of spin or experimental parameters to be tested, in a shorter timescale.
The method presented here still suffers from Liouville space simulations exponential scaling with the number of spins. To address this problem an alternative formalism was developed, a hybrid between Hilbert and Liouville space.
Operator splitting, the hybrid Hilbert/Liouville formalism
Taking advantage of Hilbert space scaling
In this section, a simulation method that combines Hilbert space and Liouville space components is presented. This method avoids, in part, the Liouville space simulations scaling issue. In absence of any Liouville basis truncation, a M spin ½ system is represented with a Liouvillian and evolves under a super-operator propagator of size of 4M while the corresponding Hilbert space size is 2M. The Liouvillian of a five-spin system has a size (1024 × 1024) and while the Hamiltonian size is only 32 × 32. The exponentiation is in general computationally intensive and scales unfavorably, even when the Liouvillian is sparse [74]. For a Liouvillian containing both the coherent and incoherent processes, there are often no “hidden” symmetries, and the full matrix must be exponentiated. One would thus want to take advantage of the more favorable Hilbert space scaling, as previously done by Thurber and Tycko [35], but also keep the convenience of Liouville space to introduce relaxation. This is possible under certain conditions and relies on 3 observations.
Observations (1), if the relaxation super-operator is written in the laboratory frame eigenbasis wavefunction, it takes a “kite shape” [97]. It is the direct sum of the terms related to the population and those related to the coherences such that
| Eq. (25) |
being a square non-diagonal matrix of size 2M and is a square diagonal matrix of dimension 2M(2M-1) ~ 22M.
The exponentiation preserves the kite shape and is thus fast and straightforward. It maps as
| Eq. (26) |
Only a 2M×2M matrix, , must be exponentiated, and the exponential of the numbers populating the diagonal of must calculated.
Observation (2), the MAS-DNP simulations are often carried out in small steps (~ 10 ns) and for the typical interactions/relaxation rates found under MAS-DNP conditions (T2,e~μs, ω1~MHz, Da,b/Ja,b~MHz) the Lie-Trotter product formula [98] (or Suzuki–Trotter expansion up to the first order [99]), is valid. Thus,
| Eq. (27) |
Observation (3), (Liouville space) is a very large matrix and slow to compute. However, using this Suzuki–Trotter approach, one can use a Hilbert space computation instead if the density matrix is re-written in Hilbert space for this step.
The resulting Hilbert/Liouville formalism, is illustrated in Figure 4. First, the density matrix, written as a 2M × 2M matrix and written in eigenbasis. It is then propagated in the Hilbert space using
| Eq. (28) |
where and are operators in the Hilbert space. is then turned into a Liouville space vector of size 4M by a simple “reshape” command, which corresponds to written in the Laboratory frame eigenbasis wavefunction. The relaxation (super-operator) propagator can be applied
| Eq. (29) |
The density matrix “vector” is then written back into the Hilbert space, as a simple “reshape” command, and finally rotated back into the Zeeman basis. and and the eigenvectors can be computed for one rotor period and stored in memory for subsequent calling.
Applications
The advantages of this approach are not obvious: (1) the number of computations is doubled, (2) it is more memory demanding, (3) it does not take advantage of the periodicity offered by Liouville space simulations. However, the execution time of exponential matrices and matrix multiplication are the main bottlenecks leading to slower simulations in full Liouville space. The combined Hilbert/Liouville method is massively faster for larger spin systems, with literally no accuracy difference between the Hilbert/Liouville and full Liouville approach (see Figure SI 1 for a 3 spins system). Figure 5 illustrates the potential of this formalism by exploring the evolution of a 5-spin system: 2 electrons spin 1/2, 2 14N, and a proton after it evolved for (100 ms). The simulation took 890 seconds on a single CPU core. In comparison, this 5184 × 5184 problem in Liouville space, combined with the Zero-Track Elimination (vide infra) and a basis size reduction by 75 % (cutoff criteria 10−5), vastly exceeded 15 h.
Figure 5:
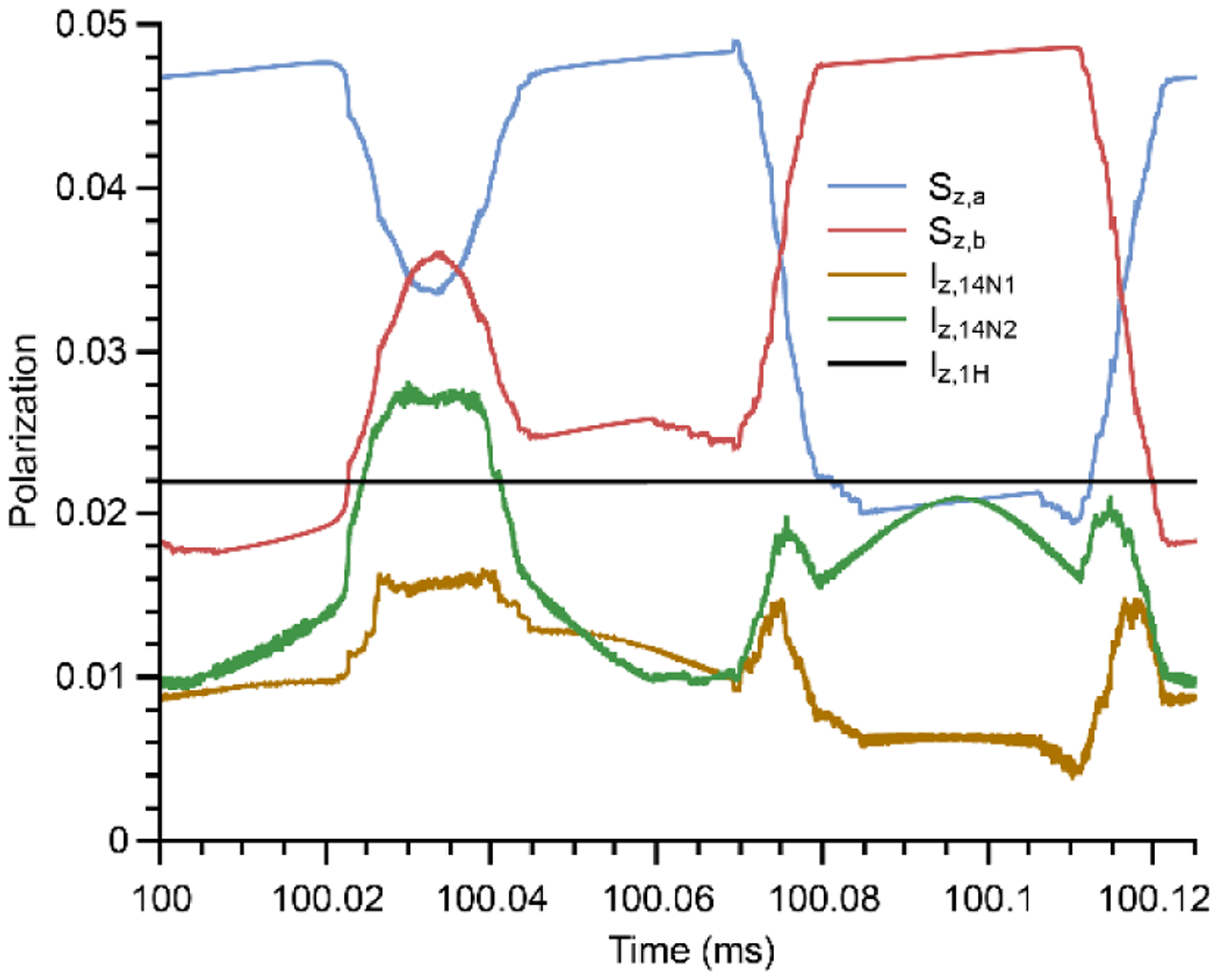
Time dependence of the polarization for nitroxide biradical made of 2 electrons, 2 14N, and one 1H across one rotor period after 100 ms of evolution. Blue, polarization of electron spin a Pa, red, polarization electron spin b Pb, gold, polarization of the 14N connected to electron a P14N,1, green, polarization of the 14N connected to electron b P14N,2, and black for spin P1H computed in 15 minutes.
The simulations reveals that all the rotor events are now “split” into sub-rotor events due to the significant 14N coupling and that 14N undergo very strong CE rotor event occurring close to the dipolar/exchange rotor events. They affect the electron spins’ dynamics by creating significant changes in their polarization. It also shows that, as the number of spins is increased, the sharp nature of the rotor-events gets smeared into a more continuous form as anticipated in earlier work [39].
This brings up the question: can the spin dynamics of nitrogen be ignored for bis-nitroxides? Figure 5 shows they impact all the rotor events and the electrons’ polarization, but so far, their dynamics have been left out of MAS-DNP simulations due to scaling issues. The Hilbert/Liouville method enables answering this question. The MAS-DNP field profile of “AMUPol” made of {2 electrons, 2 nitrogens, 1 proton} was computed in two cases: (1) by explicitly including the nitrogens’ nuclear spins, i.e. with the secular and pseudo secular hyperfine to the nitrogen spins, (2) by considering only the shift induced by secular hyperfine to the nitrogen spins (see Eq. (12)). In case (1), the simulations consider the contribution of the nitrogen spin to the total spin dynamics, while in case (2), the nitrogen only shifts the electron Larmor frequency.
To keep the simulation time down (i.e., less than a day), 15N were used. The results are reported in Figure 6. The black circles correspond to the full treatment of the 15N hyperfine coupling while the open red square correspond to the implicit case. The two MAS-DNP field profiles are very similar. The relative intensities of the maximum positive and negative sides are identical. The profiles are identical in the low field region but slightly differ in the high field one. The approximation (Eq. (12)) repeatedly underestimates the DNP efficiency on the right edge of the MAS-DNP field profile. The optimal field position is slightly shifted as well. Overall, these effects are small and these simulations (and others, see figure SI 4) confirm that one can safely ignore the impact of the nitrogen on the MAS-DNP performance of bis-nitroxides.
Lastly, the adaptive integration scheme and the Hilbert/Liouville formalism can be combined. The algorithm is identical with exception of the convergence criteria Δ1 − 2 is applied to the density matrix and becomes
| Eq. (30) |
This adaptive integration generates significant time savings when the number of rotor events is low. This is illustrated on a model biradical made of 2 electrons and 2 nuclei with large isotropic hyperfine couplings matching the Larmor frequency of the proton. This spin system is similar to the ideal biradical proposed by Thurber and Tycko [35], except that the EPR line is not split due to different isotropic g-tensors but due to the isotopic hyperfine coupling. The corresponding MAS-DNP field profile is reported in Figure 7. It was obtained in less than 6 hours, ~9 times faster than the equidistant computation.
Figure 7:
Top high field EPR spectrum of the hypothetical biradical computed with Easyspin. Bottom 73 points MAS-DNP field profile computed with the hybrid Hilbert/Liouville method after 100 ms evolution, for a 5-spin system {2 electron spins, 2 15N, 1H}. The 15N couplings are isotropic and equal to 400 MHz, the g-tensors are [2.0027, 2.0024, 2.0023]. The biradical geometry was identical to the fictious bisnitroxide used in figure 2. T1,e = 0.5 ms and T2,e = 2.5 μs.
Expectedly this type of spin system can generate significant enhancement and could be superior to bis-nitroxides. One should note that such a mechanism may occur in Mn2+ when polarizing certain nuclei (e.g. 31P at ~14.1 T) or with 13C-labelled bis-trityl that exhibit very large hyperfine interactions [100].
All in all, the Hilbert/Liouville formalism is very efficient for larger spin system. Its speed makes this method pertinent to determine which terms in the density matrix are getting populated, thus enabling a speed up the Liouville space simulations via the reduction of the Liouville basis. This process, called Zero-Track Elimination [88], is described in the following section for periodic Hamiltonian used in MAS-DNP simulations.
The Zero-Track Elimination (ZTE) for periodic Hamiltonians
In this section the Liouville/Hilbert method is used to reduce the space size of the conventional Liouville method. As demonstrated by Kuprov et al. [69] the Liouville space is often sparsely populated during magnetic resonance simulations. States that do not contribute to spin dynamics can be safely discarded, leading to smaller super-operators [71,88]. For a time-independent Hamiltonian, it is sufficient to propagate the full density matrix over a few time steps to assess which terms are not populated and therefore can be discarded. This is the ZTE algorithm [71,88].
However, the time dependence induced by MAS complicates the application of the ZTE algorithm. As MAS-DNP involves periodic, quasi-instantaneous energy level anti-crossing (rotor event), the spin system must be propagated over at least one rotor period to assess which terms can be discarded. For large spin systems, this is nearly impossible when using the full Liouville formalism. Instead, the propagation can be carried out with the Hilbert/Liouville formalism, thus enabling the ZTE and the shrinking of the Liouville basis used in Liouville space simulations.
In the current implementation, the density matrix is propagated over Nr = 21 rotor periods. The density matrices computed at each step of the last rotor period, , are stored in memory. The module of the density matrices elements |ρi,j(Nr − 1)τr + kδt| is averaged over the last rotor period as
| Eq. (31) |
If ∥ρi,j∥ < ϵ the state can be discarded from the basis.
As MAS-DNP requires powder averaging, two strategies can be devised: 1/ apply the ZTE for each single crystal orientation prior to executing the reduced Liouville space simulations, or 2/ try to find the minimal basis size common to all crystal orientations and then run the reduced Liouville space simulations. The ZTE being still time consuming, option 2 is a smarter choice. The minimal common basis can be found by executing the ZTE for multiple crystal orientations. For Cross-Effect MAS-DNP, 40 REPULSION crystal orientations are sufficient to determine these commonly populated states. The final basis consists of all the states that meet the criteria ∥ρi,j∥ > ϵ at least once for all the crystal orientation, i.e.
| Eq. (32) |
Figure 8 reports the MAS-DNP field profile computed in the case of AMUPol with ZTE as compared to the full space, equidistant integration. Keeping the terms that are ∥ρi,j∥ > ϵ = 5 × 10−5, only 42 of the 64 terms survived. The simulations using adaptive integration and ZTE were 5.2 times faster when the maximum number of angular steps was set to 8192. The ZTE execution took 40 s and was executed once at B0 = 9.394 T. The average error is < 5 % on average. A factor > 8 in time savings is obtained by setting the maximum number of angular steps to 4096. The errors are larger, about 8 % on average, but simulations still provide an accurate MAS-DNP field profile and are thus sufficient for that purpose.
Discussion
Numerical simulations of MAS-DNP are time consuming, even for a small spin system made of 3 spins 1/2. They can take a few hours up to a few days depending on the number of parameters scanned and the extent of the powder averaging. Thus, three different strategies with minimal approximations, and their implementations, have been described: the adaptive integration for Liouville space simulations, the hybrid Hilbert/Liouville method, the ZTE for time dependent problem. The first two are independent while the ZTE relies on the Hilbert/Liouville formalism but benefits the Liouville space simulations. The improvement in the simulation times should not be compared with what was achieved in recent work [39,44]. The methods are not intended to simulate thousands of spins, instead, the absence of additional assumptions makes these methods ideal to probe cases where there is no prior knowledge of spin dynamics. This is essential to understand the spin dynamics and be able to make assumptions/simplifications in order to build larger spin systems.
Adaptive and ZTE
The adaptive integration scheme for the Master equation is a simple scheme that improved the speed of the simulations by a factor 3–5 without affecting the accuracy. Combined with the ZTE the gains are even more important as displayed in Figure 8. Specifically, the Liouville basis of a 3-spin system (2 electrons spin 1/2, one nucleus 1/2) was reduced by ZTE from 64 to 42 states (≈ 65% or the original size). Scanning through experimental or magnetic parameters is made accessible on a reasonable time scale for 3 spin systems. The method was successfully used at screening stages of biradical design [49].
The adaptive integration scheme performs well for small spin systems because few rotor events occur. This means that the overhead induced by checking the convergence criteria, the scaling of the propagator, is vastly compensated by the reduction of the number of steps. As the number of spins increases, the rotor events become more continuous, and the adaptive integration becomes slower than the brute force equidistant integration.
The ZTE implementation for periodic problem can be straightforwardly applied to any system and any basis. In practice, the ZTE leads to drastic basis size reduction when the interaction graph is sparsely connected, in other words, when each spin is connected to very few neighbors [88]. The ZTE used for a 5-spin system (2 electrons, 2 14N, 1 proton) reduced the problem size from 5180 to 1106, i.e. a factor 5, with a cutoff criteria of 10−5.
Here, the ZTE algorithm uses the hybrid Hilbert/Liouville method to propagate large spin systems and then reduce the basis for Liouville space simulations. It could have been implemented with a Krylov propagation [70,75,82] that only involves fast matrix/vector propagator instead of matrix exponential. For speed purposes it may be possible to use a Hilbert space propagation, albeit with a lower efficiency as high order of coherences may not decay quickly enough [101].
These algorithms are subject to improvements, further boosting their efficiency. Cleverer adaptive integration schemes may provide better results both in terms of accuracy and computation time if their overhead is significantly lower than the proposed algorithm. So far, the algorithm described above “slows” down for each energy level crossing whether it contributes to the spin dynamics or not. This clearly can be improved by using the approximated eigen-energy diagram, as used to compute field swept EPR spectra [87,102].
Another significant improvement may be obtained by using “Iserles” integrators [103,104], that are equivalent to the trapezoidal integrations. In Spinach v.2.6, their implementation yields time savings > 5 [74].
Finally, the ZTE could be made more efficient with more Liouville basis adapted for truncation, such as IST [68,74,97,105,106].
Hybrid Hilbert/Liouville
Despite these two improvements simulations in Liouville space (even truncated) remain exceedingly slow for large spin system. For example, it is nearly impossible to compute a single crystal orientation containing spins systems with a Hilbert space size > 32×32 on a reasonable time-scale. This led to the development of an alternative approach to compute larger spin systems: the hybrid Hilbert/Liouville formalism. The method takes advantage of the need for small integration steps, to benefit from the scaling of the Hilbert space. This enables the propagation of spin system that are significantly larger and that include spins >1/2. To fully take advantage of the Hilbert space scaling, the relaxation was introduced in the eigenbasis wavefunction of the lab-frame Hamiltonian . This basis was used to compute the coherent propagator and make the relaxation super-operator exponentiation simple. Introducing the relaxation in the eigenbasis of requires the diagonalization which might be a bottleneck [107]. However, is always block-diagonal and the diagonalization is very fast when combined with the Tarjan algorithm [108].
This method does not fully take advantage of the periodicity of the problem. This is a difficulty also faced by Thurber and Tycko in their implementation of the MAS-DNP simulations [35] where Hilbert space simulations and a separation of coherent and relaxation processes were used.
As the relaxation model used here only considered exponential decays it enables the propagators/relaxation super-operator of the Hilbert/Liouville approach to be stored in memory. The buffering facilitates longer propagation. To illustrate this, a MAS-DNP simulation of a three-spin system (2 electron spin ½ and a nucleus ½) was carried out for 1.25 s of free evolution. This simulation took approximately 15 minutes with buffering 16 hours without. The Hilbert/Liouville simulations even with buffering remains impractical for a small spin system as the full Liouville space simulations only take ~30 s.
The Hilbert/Liouville implementation is designed for larger spin systems. It is, so far, the only viable numerical method without significant approximations. As a demonstration, simulations with 2 electron spins, 2 14N and one proton was carried out over 100 ms in just 15 mins for a single crystal, on a single core! We used it to show that the dynamics of the bis-nitroxide nitrogen are not essential for the MAS-DNP process and can be omitted. Additionally, the formalism is compatible with the adaptive integration saving significant computation time when the spin system does not involve too many rotor events. This was perfectly adapted to the model biradical where two well defined EPR lines are separated by the proton Larmor frequency.
The hybrid Hilbert/Liouville formalism can compute MAS-DNP field profile with two electrons spin 5/2 and one nucleus spin ½ as illustrated in Figure 9. In Figure 9 (a, bottom) the Solid-Effect MAS-DNP field profiles were computed in two different spin systems, an electron spin 3/2 or 5/2 connected to a 13C spin (black circles and red squares respectively). The corresponding high field EPR spectra are reported in Figure 9 (a, top). For readability, the MAS-DNP field profiles were centered around the central transition but broader field profiles were computed and reported in the SI (Fig. SI 2). The MAS-DNP field profiles presents the expected positive and negative enhancement outside of the EPR spectra. The simulations were carried out in 28 and 40 minutes respectively correspond to an evolution of 25 ms. The speed of the simulations indicated that even spin 7/2, as found in Gd3+, could be simulated.
Similarly, Figure 9 (b, bottom) reports the Cross-Effect MAS-DNP field profiles for two different spin systems, two electron spins 3/2 with or two electron spin 5/2 connected to a 13C spin (black circles and red squares respectively). The corresponding high field EPR spectra are reported in Figure 9 (b, top). The MAS-DNP field profiles presents the expected positive and negative enhancement inside of the EPR spectra. Again, the MAS-DNP field profiles are centered around the central transition for readability, broader field profiles are reported in the SI (Fig. SI 2). They reveal significant enhancement arising for these higher spin number states transition. The simulations took 2 h and 18 h respectively for 25 ms of evolution time. The simulations are significantly slower than the SE case. It may be possible to compute two electron spins 7/2 and a nuclei, or two Mn2+ and a nuclei using a more powerful computing setup.
This operator splitting method could be used to confirm the theoretical prediction by Corzilius of the MAS-DNP mechanism when electron spin ≥ 5/2 are involved [45], test the effect of the relative ZFS orientation and build an equivalence with the g-tensors’ distance [43]. It may then be possible to build faster MAS-DNP model that uses Landau-Zener approximation and severely truncated Liouville basis as was done for bis-nitroxides [39,44,46,47]. This remains beyond the scope of this manuscript.
In general, the hybrid Hilbert/Liouville is not immediately suitable to compute polarization gains ϵB at the steady orbit. A shorter evolution time may affect the shape of the MAS-DNP field profiles.
For CE in small spin system, the nuclear polarization at steady orbit is usually obtained in hundreds of milliseconds [35], meaning that the Hilbert/Liouville method could be used to compute accurate Cross-Effect MAS-DNP field profiles.
This was observed for the MAS-DNP field profiles which is identical for shorter (12.5 ms) or longer evolution time (100 ms) (see figure SI 3). This illustrates that reliable MAS-DNP field profiles are possible in a reasonable time scale, i.e. within a few hours to a day.
For the Solid-Effect and Overhauser case, the steady state is reached after a much longer evolution time [109–111]. Approximate MAS-DNP field profile may be obtained by computing them with short evolution time (e.g. 25 ms) and scale them by computing the steady state for a single magnetic field point.
Steady state polarization may nonetheless be accessible with a cleverer approach than brute-force time propagation. For example, it is possible to use optimization Monte Carlo algorithms to compute the steady state polarization as previously done for large spin systems [50].
Finally, this hybrid method could also be improved, using the already mentioned Iserles integrators, a cleverer adaptive integration and different basis. Together they would provide enable reducing the number of angular steps required and the basis size, thereby limiting the memory requirements, and speeding the simulations up.
Conclusion
In this article we showed three numerical methods to make MAS-DNP simulations faster. The three methods, adaptive integration, hybrid Hilbert/Liouville approach and ZTE each have their domain of applications and combination. The ZTE combined with adaptive integration leads to time saving ranging from 5 to 10 depending on the level of accuracy enabling computation of MAS-DNP field profiles of small spin systems straightforward. The hybrid Hilbert/Liouville approach is powerful to look at spin systems with more spins or spins greater than ½. This enables computing spin systems that corresponds to a Liouville space 80 times greater than the commonly used 3 spin ½ system that mimics the Cross-Effect. The formalism can serve as a platform to analyze the spin physics in these systems and seems sufficient to computer properties such as MAS-DNP field profiles but is ineffective to compute the steady state polarization. Each of these methods were illustrated with examples that provided a glimpse of what is accessible and how the spin dynamics changes with the nature of the paramagnetic species. We finally discussed potential improvement that could be made to the codes to further improve them.
Supplementary Material
Acknowledgements
The National High Magnetic Field laboratory (NHMFL) is funded by the National Science Foundation Division of Materials Research (DMR-1644779) and the State of Florida. A portion of this work was supported by the NIH P41 GM122698. FMV thanks Dr. Zhehong Gan, Faith Scott and Robert Schurko for their suggestions to improve this manuscript. In addition, FMV thanks Lucio Frydman for the idea resulting in figure 7.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Declaration of interests
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- [1].Becerra LR, Gerfen GJ, Temkin RJ, Singel DJ, Griffin RG, Dynamic nuclear polarization with a cyclotron resonance maser at 5 T, Phys. Rev. Lett 71 (1993) 3561–3564. doi: 10.1103/PhysRevLett.71.3561. [DOI] [PubMed] [Google Scholar]
- [2].Barnes AB, De Paepe G, van der Wel PCA, Hu K-N, Joo C-G, Bajaj VS, Mak-Jurkauskas ML, Sirigiri JR, Herzfeld J, Temkin RJ, Griffin RG, High-Field Dynamic Nuclear Polarization for Solid and Solution Biological NMR, Appl. Magn. Reson 34 (2008) 237–263. doi: 10.1007/s00723-008-0129-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [3].Rosay M, Tometich L, Pawsey S, Bader R, Schauwecker R, Blank M, Borchard PM, Cauffman SR, Felch KL, Weber RT, Temkin RJ, Griffin RG, Maas WE, Solid-state dynamic nuclear polarization at 263 GHz: spectrometer design and experimental results, Phys. Chem. Chem. Phys 12 (2010) 5850. doi: 10.1039/c003685b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Wind RA, Duijvestijn MJ, van der Lugt C, Manenschijn A, Vriend J, Applications of dynamic nuclear polarization in 13C NMR in solids, Prog. Nucl. Magn. Reson. Spectrosc 17 (1985) 33–67. doi: 10.1016/0079-6565(85)80005-4. [DOI] [Google Scholar]
- [5].Singel DJ, Seidel H, Kendrick RD, Yannoni CS, A spectrometer for EPR, DNP, and multinuclear high-resolution NMR, J. Magn. Reson 81 (1989) 145–161. doi: 10.1016/0022-2364(89)90273-4. [DOI] [Google Scholar]
- [6].Afeworki M, Vega S, Schaefer J, Direct electron-to-carbon polarization transfer in homogeneously doped polycarbonates, Macromolecules 25 (1992) 4100–4105. doi: 10.1021/ma00042a009. [DOI] [Google Scholar]
- [7].Hall DA, Maus DC, Gerfen GJ, Inati SJ, Becerra LR, Dahlquist FW, Griffin RG, Polarization-enhanced NMR spectroscopy of biomolecules in frozen solution., Science (80-.) 276 (1997) 930–2. doi: 10.1126/science.276.5314.930. [DOI] [PubMed] [Google Scholar]
- [8].Rossini AJ, Zagdoun A, Lelli M, Lesage A, Copéret C, Emsley L, Dynamic Nuclear Polarization Surface Enhanced NMR Spectroscopy, Acc. Chem. Res 46 (2013) 1942–1951. doi: 10.1021/ar300322x. [DOI] [PubMed] [Google Scholar]
- [9].Ni QZ, Daviso E, Can TV, Markhasin E, Jawla SK, Swager TM, Temkin RJ, Herzfeld J, Griffin RG, High Frequency Dynamic Nuclear Polarization, Acc. Chem. Res 46 (2013) 1933–1941. doi: 10.1021/ar300348n. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [10].Lee D, Hediger S, De Paepe G, Is solid-state NMR enhanced by dynamic nuclear polarization?, Solid State Nucl. Magn. Reson 66–67 (2015) 6–20. doi: 10.1016/j.ssnmr.2015.01.003. [DOI] [PubMed] [Google Scholar]
- [11].Lilly Thankamony AS, Wittmann JJ, Kaushik M, Corzilius B, Dynamic nuclear polarization for sensitivity enhancement in modern solid-state NMR, Prog. Nucl. Magn. Reson. Spectrosc 102–103 (2017) 120–195. doi: 10.1016/j.pnmrs.2017.06.002. [DOI] [PubMed] [Google Scholar]
- [12].Rankin AGM, Trébosc J, Pourpoint F, Amoureux J-P, Lafon O, Recent developments in MAS DNP-NMR of materials, Solid State Nucl. Magn. Reson 101 (2019) 116–143. doi: 10.1016/j.ssnmr.2019.05.009. [DOI] [PubMed] [Google Scholar]
- [13].Hediger S, Lee D, Mentink-Vigier F, De Paëpe G, MAS-DNP Enhancements : Hyperpolarization, Depolarization, and Absolute Sensitivity, eMagRes, WILEY-VCH Verlag, 2018. doi: 10.1002/9a780470034590.emrstm1559. [DOI] [Google Scholar]
- [14].Paioni AL, Renault MAM, Baldus M, DNP and cellular solid-state NMR, EMagRes 7 (2018) 51–62. doi: 10.1002/9780470034590.emrstm1561. [DOI] [Google Scholar]
- [15].Akbey U, Franks WT, Linden A, Orwick-Rydmark M, Lange S, Oschkinat H, Dynamic Nuclear Polarization Enhanced NMR in the Solid-State, in: Top. Curr. Chem, 2013: pp. 181–228. doi: 10.1007/128_2013_436. [DOI] [PubMed] [Google Scholar]
- [16].Rosay M, Blank M, Engelke F, Instrumentation for solid-state dynamic nuclear polarization with magic angle spinning NMR, J. Magn. Reson 264 (2016) 88–98. doi: 10.1016/j.jmr.2015.12.026. [DOI] [PubMed] [Google Scholar]
- [17].Thurber KR, Potapov A, Yau W-M, Tycko R, Solid state nuclear magnetic resonance with magic-angle spinning and dynamic nuclear polarization below 25 K, J. Magn. Reson 226 (2012) 100–106. doi: 10.1016/j.jmr.2012.11.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Bouleau E, Saint-Bonnet P, Mentink-Vigier F, Takahashi H, Jacquot J-F, Bardet M, Aussenac F, Purea A, Engelke F, Hediger S, Lee D, De Paepe G, Pushing NMR sensitivity limits using dynamic nuclear polarization with closed-loop cryogenic helium sample spinning, Chem. Sci 6 (2015) 6806–6812. doi: 10.1039/C5SC02819A. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [19].Matsuki Y, Fujiwara T, Cryogenic Platforms and Optimized DNP Sensitivity, EMagRes 7 (2018) 9–24. doi: 10.1002/9780470034590.emrstm1553. [DOI] [Google Scholar]
- [20].Blank M, Felch KL, Millimeter-wave Sources for DNP-NMR, EMagRes 7 (2018) 155–166. doi: 10.1002/9780470034590.emrstm1582. [DOI] [Google Scholar]
- [21].Hu K-N, Yu H, Swager TM, Griffin RG, Dynamic Nuclear Polarization with Biradicals, J. Am. Chem. Soc 126 (2004) 10844–10845. doi: 10.1021/ja039749a. [DOI] [PubMed] [Google Scholar]
- [22].Matsuki Y, Maly T, Ouari O, Karoui H, Le Moigne F, Rizzato E, Lyubenova S, Herzfeld J, Prisner TF, Tordo P, Griffin RG, Dynamic Nuclear Polarization with a Rigid Biradical, Angew. Chemie Int. Ed 48 (2009) 4996–5000. doi: 10.1002/anie.200805940. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [23].Sauvée C, Rosay M, Casano G, Aussenac F, Weber RT, Ouari O, Tordo P, Highly Efficient, Water-Soluble Polarizing Agents for Dynamic Nuclear Polarization at High Frequency, Angew. Chemie Int. Ed 52 (2013) 10858–10861. doi: 10.1002/anie.201304657. [DOI] [PubMed] [Google Scholar]
- [24].Zagdoun A, Casano G, Ouari O, Schwarzwälder M, Rossini AJ, Aussenac F, Yulikov M, Jeschke G, Copéret C, Lesage A, Tordo P, Emsley L, Large Molecular Weight Nitroxide Biradicals Providing Efficient Dynamic Nuclear Polarization at Temperatures up to 200 K, J. Am. Chem. Soc 135 (2013) 12790–12797. doi: 10.1021/ja405813t. [DOI] [PubMed] [Google Scholar]
- [25].Lesage A, Lelli M, Gajan D, Caporini MA, Vitzthum V, Miéville P, Alauzun J, Roussey A, Thieuleux C, Mehdi A, Bodenhausen G, Coperet C, Emsley L, Surface Enhanced NMR Spectroscopy by Dynamic Nuclear Polarization, J. Am. Chem. Soc 132 (2010) 15459–15461. doi: 10.1021/ja104771z. [DOI] [PubMed] [Google Scholar]
- [26].Piveteau L, Dirin DN, Gordon CP, Walder BJ, Ong T-C, Emsley L, Copéret C, Kovalenko MV, Colloidal-ALD-Grown Core/Shell CdSe/CdS Nanoplatelets as Seen by DNP Enhanced PASS–PIETA NMR Spectroscopy, Nano Lett 20 (2020) 3003–3018. doi: 10.1021/acs.nanolett.9b04870. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [27].Chow WY, Norman BP, Roberts NB, Ranganath LR, Teutloff C, Bittl R, Duer MJ, Gallagher JA, Oschkinat H, Pigmentation Chemistry and Radical-Based Collagen Degradation in Alkaptonuria and Osteoarthritic Cartilage, Angew. Chemie Int. Ed 59 (2020) 11937–11942. doi: 10.1002/anie.202000618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [28].Linden AH, Lange S, Franks WT, Akbey U, Specker E, van Rossum B-J, Oschkinat H, Neurotoxin II Bound to Acetylcholine Receptors in Native Membranes Studied by Dynamic Nuclear Polarization NMR, J. Am. Chem. Soc 133 (2011) 19266–19269. doi: 10.1021/ja206999c. [DOI] [PubMed] [Google Scholar]
- [29].Hirsh DA, Rossini AJ, Emsley L, Schurko RW, 35 Cl dynamic nuclear polarization solid-state NMR of active pharmaceutical ingredients, Phys Chem Chem Phys 18 (2016) 25893–25904. doi: 10.1039/C6CP04353D. [DOI] [PubMed] [Google Scholar]
- [30].Gupta R, Zhang H, Lu M, Hou G, Caporini M, Rosay M, Maas W, Struppe J, Ahn J, Byeon I-JL, Oschkinat H, Jaudzems K, Barbet-Massin E, Emsley L, Pintacuda G, Lesage A, Gronenborn AM, Polenova T, Dynamic Nuclear Polarization Magic-Angle Spinning Nuclear Magnetic Resonance Combined with Molecular Dynamics Simulations Permits Detection of Order and Disorder in Viral Assemblies, J. Phys. Chem. B 123 (2019) 5048–5058. doi: 10.1021/acs.jpcb.9b02293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [31].Lee D, Leroy C, Crevant C, Bonhomme-Coury L, Babonneau F, Laurencin D, Bonhomme C, De Paepe G, Interfacial Ca2+ environments in nanocrystalline apatites revealed by dynamic nuclear polarization enhanced 43Ca NMR spectroscopy, Nat. Commun 8 (2017) 14104. doi: 10.1038/ncomms14104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [32].Zhang L, Gao C, Mentink-Vigier F, Tang L, Zhang D, Wang S, Cao S, Xu Z, Liu X, Wang T, Zhou Y, Zhang B, Arabinosyl Deacetylase Modulates the Arabinoxylan Acetylation Profile and Secondary Wall Formation, Plant Cell 31 (2019) 1113–1126. doi: 10.1105/tpc.18.00894. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [33].Perras FA, Chaudhary U, Slowing II, Pruski M, Probing Surface Hydrogen Bonding and Dynamics by Natural Abundance, Multidimensional, 17 O DNP-NMR Spectroscopy, J. Phys. Chem. C 120 (2016) 11535–11544. doi: 10.1021/acs.jpcc.6b02579. [DOI] [Google Scholar]
- [34].Smith AN, Märker K, Piretra T, Boatz JC, Matlahov I, Kodali R, Hediger S, van der Wel PCA, De Paepe G, Structural Fingerprinting of Protein Aggregates by Dynamic Nuclear Polarization-Enhanced Solid-State NMR at Natural Isotopic Abundance, J. Am. Chem. Soc 140 (2018) 14576–14580. doi: 10.1021/jacs.8b09002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [35].Thurber KR, Tycko R, Theory for cross effect dynamic nuclear polarization under magic-angle spinning in solid state nuclear magnetic resonance: The importance of level crossings, J. Chem. Phys 137 (2012) 084508. doi: 10.1063/1.4747449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [36].Mentink-Vigier F, Akbey U, Hovav Y, Vega S, Oschkinat H, Feintuch A, Fast passage dynamic nuclear polarization on rotating solids, J. Magn. Reson 224 (2012) 13–21. doi: 10.1016/j.jmr.2012.08.013. [DOI] [PubMed] [Google Scholar]
- [37].Mentink-Vigier F, Akbey U, Oschkinat H, Vega S, Feintuch A, Theoretical aspects of Magic Angle Spinning - Dynamic Nuclear Polarization, J. Magn. Reson 258 (2015) 102–120. doi: 10.1016/j.jmr.2015.07.001. [DOI] [PubMed] [Google Scholar]
- [38].Mentink-Vigier F, Paul S, Lee D, Feintuch A, Hediger S, Vega S, De Paepe G, Nuclear depolarization and absolute sensitivity in magic-angle spinning cross effect dynamic nuclear polarization, Phys Chem Chem Phys 17 (2015) 21824–21836. doi: 10.1039/C5CP03457D. [DOI] [PubMed] [Google Scholar]
- [39].Mentink-Vigier F, Vega S, De Paepe G, Fast and accurate MAS–DNP simulations of large spin ensembles, Phys Chem Chem Phys 19 (2017) 3506–3522. doi: 10.1039/C6CP07881H. [DOI] [PubMed] [Google Scholar]
- [40].Mentink-Vigier F, Mathies G, Liu Y, Barra AL, Caporini MA, Lee D, Hediger S, Griffin RG, De Paepe G, Efficient cross-effect dynamic nuclear polarization without depolarization in high-resolution MAS NMR, Chem. Sci 8 (2017) 8150–8163. doi: 10.1039/C7SC02199B. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [41].Mance D, Gast P, Huber M, Baldus M, Ivanov KL, The magnetic field dependence of cross-effect dynamic nuclear polarization under magic angle spinning, J. Chem. Phys 142 (2015) 234201. doi: 10.1063/1.4922219. [DOI] [PubMed] [Google Scholar]
- [42].Perras FA, Sadow A, Pruski M, In Silico Design of DNP Polarizing Agents: Can Current Dinitroxides Be Improved?, ChemPhysChem 18 (2017) 2279–2287. doi: 10.1002/cphc.201700299. [DOI] [PubMed] [Google Scholar]
- [43].Mentink-Vigier F, Optimizing nitroxide biradicals for cross-effect MAS-DNP: the role of g-tensors’ distance, Phys. Chem. Chem. Phys 22 (2020) 3643–3652. doi: 10.1039/C9CP06201G. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [44].Mentink-Vigier F, Dubroca T, Van Tol J, Sigurdsson ST, The distance between g-tensors of nitroxide biradicals governs MAS-DNP performance: The case of the bTurea family, J. Magn. Reson 329 (2021) 107026. doi: 10.1016/j.jmr.2021.107026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [45].Corzilius B, Theory of solid effect and cross effect dynamic nuclear polarization with half-integer high-spin metal polarizing agents in rotating solids, Phys. Chem. Chem. Phys 18 (2016) 27190–27204. doi: 10.1039/C6CP04621E. [DOI] [PubMed] [Google Scholar]
- [46].Thurber KR, Tycko R, Perturbation of nuclear spin polarizations in solid state NMR of nitroxide-doped samples by magic-angle spinning without microwaves., J. Chem. Phys 140 (2014) 184201. doi: 10.1063/1.4874341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [47].Perras FA, Pruski M, Large-scale ab initio simulations of MAS DNP enhancements using a Monte Carlo optimization strategy, J. Chem. Phys 149 (2018) 154202. doi: 10.1063/1.5042651. [DOI] [PubMed] [Google Scholar]
- [48].Equbal A, Tagami K, Han S, Balancing dipolar and exchange coupling in biradicals to maximize cross effect dynamic nuclear polarization, Phys. Chem. Chem. Phys 22 (2020) 13569–13579. doi: 10.1039/D0CP02051F. [DOI] [PubMed] [Google Scholar]
- [49].Mentink-Vigier F, Marin-Montesinos I, Jagtap AP, Halbritter T, van Tol J, Hediger S, Lee D, Sigurdsson ST, De Paepe G, Computationally Assisted Design of Polarizing Agents for Dynamic Nuclear Polarization Enhanced NMR: The AsymPol Family, J. Am. Chem. Soc 140 (2018) 11013–11019. doi: 10.1021/jacs.8b04911. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [50].Perras FA, Raju M, Carnahan SL, Akbarian D, van Duin ACT, Rossini AJ, Pruski M, Full-Scale Ab Initio Simulation of Magic-Angle-Spinning Dynamic Nuclear Polarization, J. Phys. Chem. Lett (2020). doi: 10.1021/acs.jpclett.0c00955. [DOI] [PubMed] [Google Scholar]
- [51].Mentink-Vigier F, Barra A-L, van Tol J, Hediger S, Lee D, De Paepe G, De novo prediction of cross-effect efficiency for magic angle spinning dynamic nuclear polarization, Phys. Chem. Chem. Phys 21 (2019) 2166–2176. doi: 10.1039/C8CP06819D. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [52].Mathies G, Caporini MA, Michaelis VK, Liu Y, Hu K-N, Mance D, Zweier JL, Rosay M, Baldus M, Griffin RG, Efficient Dynamic Nuclear Polarization at 800 MHz/527 GHz with Trityl-Nitroxide Biradicals, Angew. Chem. Int. Ed 127 (2015) 11936–11940. doi: 10.1002/ange.201504292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [53].Wisser D, Karthikeyan G, Lund A, Casano G, Karoui H, Yulikov M, Menzildjian G, Pinon AC, Purea A, Engelke F, Chaudhari SR, Kubicki DJ, Rossini AJ, Moroz IB, Gajan D, Copéret C, Jeschke G, Lelli M, Emsley L, Lesage A, Ouari O, BDPA-Nitroxide Biradicals Tailored for Efficient Dynamic Nuclear Polarization Enhanced Solid-State NMR at Magnetic Fields up to 21.1 T, J. Am. Chem. Soc 140 (2018) 13340–13349. doi: 10.1021/jacs.8b08081. [DOI] [PubMed] [Google Scholar]
- [54].Lund A, Casano G, Menzildjian G, Kaushik M, Stevanato G, Yulikov M, Jabbour R, Wisser D, Renom-Carrasco M, Thieuleux C, Bernada F, Karoui H, Siri D, Rosay M, Sergeyev IV, Gajan D, Lelli M, Emsley L, Ouari O, Lesage A, TinyPols: a family of water-soluble binitroxides tailored for dynamic nuclear polarization enhanced NMR spectroscopy at 18.8 and 21.1 T, Chem. Sci 11 (2020) 2810–2818. doi: 10.1039/C9SC05384K. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [55].Wolf T, Kumar S, Singh H, Chakrabarty T, Aussenac F, Frenkel AI, Major DT, Leskes M, Endogenous Dynamic Nuclear Polarization for Natural Abundance 17 O and Lithium NMR in the Bulk of Inorganic Solids, J. Am. Chem. Soc 141 (2019) 451–462. doi: 10.1021/jacs.8b11015. [DOI] [PubMed] [Google Scholar]
- [56].Harchol A, Reuveni G, Ri V, Thomas B, Carmieli R, Herber RH, Kim C, Leskes M, Endogenous Dynamic Nuclear Polarization for Sensitivity Enhancement in Solid-State NMR of Electrode Materials, J. Phys. Chem. C 124 (2020) 7082–7090. doi: 10.1021/acs.jpcc.0c00858. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [57].Paterson AL, Perras FA, Besser MF, Pruski M, Dynamic Nuclear Polarization of Metal-Doped Oxide Glasses: A Test of the Generality of Paramagnetic Metal Polarizing Agents, J. Phys. Chem. C 124 (2020) 23126–23133. doi: 10.1021/acs.jpcc.0c05676. [DOI] [Google Scholar]
- [58].Jardón-Álvarez D, Kahn N, Houben L, Leskes M, Oxygen Vacancy Distribution in Yttrium-Doped Ceria from 89Y−89Y Correlations via Dynamic Nuclear Polarization Solid-State NMR, J. Phys. Chem. Lett (2021). doi: 10.1021/acs.jpclett.1c00221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [59].Jardón-Álvarez D, Reuveni G, Harchol A, Leskes M, Enabling Natural Abundance 17 O Solid-State NMR by Direct Polarization from Paramagnetic Metal Ions, J. Phys. Chem. Lett 11 (2020) 5439–5445. doi: 10.1021/acs.jpclett.0c01527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [60].Chakrabrty T, Goldin N, Feintuch A, Houben L, Leskes M, Paramagnetic metal ion dopants as polarization agents for DNP NMR spectroscopy in inorganic solids, ChemPhysChem 5 (2018) 644–656. doi: 10.1002/cphc.201800462. [DOI] [PubMed] [Google Scholar]
- [61].Hope MA, Rinkel BLD, Gunnarsdóttir AB, Märker K, Menkin S, Paul S, Sergeyev IV, Grey CP, Selective NMR observation of the SEI–metal interface by dynamic nuclear polarisation from lithium metal, Nat. Commun 11 (2020) 2224. doi: 10.1038/s41467-020-16114-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [62].Hope MA, Björgvinsdóttir S, Grey CP, Emsley L, A Magic Angle Spinning Activated 17 O DNP Raser, J. Phys. Chem. Lett (2020) 345–349. doi: 10.1021/acs.jpclett.0c03457. [DOI] [PubMed] [Google Scholar]
- [63].Corzilius B, Michaelis VK, Penzel SA, Ravera E, Smith AA, Luchinat C, Griffin RG, Dynamic Nuclear Polarization of 1H, 13C, and 59Co in a Co(III) tris-ethylenediamine crystalline lattice doped with Cr(III)., J. Am. Chem. Soc (2014). doi: 10.1021/ja5044374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [64].Kaushik M, Qi M, Godt A, Corzilius B, Bis-Gadolinium Complexes for Solid Effect and Cross Effect Dynamic Nuclear Polarization, Angew. Chemie Int. Ed 56 (2017) 4295–4299. doi: 10.1002/anie.201612388. [DOI] [PubMed] [Google Scholar]
- [65].Carnahan SL, Venkatesh A, Perras FA, Wishart JF, Rossini AJ, High-Field Magic Angle Spinning Dynamic Nuclear Polarization Using Radicals Created by γ-Irradiation, J. Phys. Chem. Lett 10 (2019) 4770–4776. doi: 10.1021/acs.jpclett.9b01655. [DOI] [PubMed] [Google Scholar]
- [66].Kaushik M, Bahrenberg T, Can TV, Caporini MA, Silvers R, Heiliger J, Smith AA, Schwalbe H, Griffin RG, Corzilius B, Gd(III) and Mn(II) complexes for dynamic nuclear polarization: small molecular chelate polarizing agents and applications with site-directed spin labeling of proteins, Phys Chem Chem Phys (2016). doi: 10.1039/C6CP04623A. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [67].Heiliger J, Matzel T, Çetiner EC, Schwalbe H, Kuenze G, Corzilius B, Site-specific dynamic nuclear polarization in a Gd(III)-labeled protein, Phys. Chem. Chem. Phys 22 (2020) 25455–25466. doi: 10.1039/D0CP05021K. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [68].Butler MC, Dumez J-N, Emsley L, Dynamics of large nuclear-spin systems from low-order correlations in Liouville space, Chem. Phys. Lett 477 (2009) 377–381. doi: 10.1016/j.cplett.2009.07.017. [DOI] [Google Scholar]
- [69].Kuprov I, Wagner-Rundell N, Hore PJ, Polynomially scaling spin dynamics simulation algorithm based on adaptive state-space restriction, J. Magn. Reson 189 (2007) 241–250. doi: 10.1016/j.jmr.2007.09.014. [DOI] [PubMed] [Google Scholar]
- [70].Hogben HJ, Hore PJ, Kuprov I, Strategies for state space restriction in densely coupled spin systems with applications to spin chemistry, J. Chem. Phys 132 (2010) 1–10. doi: 10.1063/1.3398146. [DOI] [PubMed] [Google Scholar]
- [71].Krzystyniak M, Edwards LJ, Kuprov I, Destination state screening of active spaces in spin dynamics simulations, J. Magn. Reson 210 (2011) 228–232. doi: 10.1016/j.jmr.2011.03.010. [DOI] [PubMed] [Google Scholar]
- [72].Karabanov A, Kwiatkowski G, Kockenberger W, Quantum Mechanical Simulation of Cross Effect DNP Using Krylov-Bogolyubov Averaging, Appl. Magn. Reson 43 (2012) 43–58. doi: 10.1007/s00723-012-0367-0. [DOI] [Google Scholar]
- [73].Bak M, Rasmussen JT, Nielsen NC, SIMPSON: A General Simulation Program for Solid-State NMR Spectroscopy, J. Magn. Reson 147 (2000) 296–330. doi: 10.1006/jmre.2000.2179. [DOI] [PubMed] [Google Scholar]
- [74].Hogben HJ, Krzystyniak M, Charnock GTP, Hore PJ, Kuprov I, Spinach – A software library for simulation of spin dynamics in large spin systems, J. Magn. Reson 208 (2011) 179–194. doi: 10.1016/j.jmr.2010.11.008. [DOI] [PubMed] [Google Scholar]
- [75].Moler C, Van Loan C, Nineteen dubious ways to compute the exponential of a matrix, twenty-five years later, SIAM Rev 45 (2003) 3–49. doi: 10.1137/S00361445024180. [DOI] [Google Scholar]
- [76].Veshtort M, Griffin RG, SPINEVOLUTION: A powerful tool for the simulation of solid and liquid state NMR experiments, J. Magn. Reson 178 (2006) 248–282. doi: 10.1016/j.jmr.2005.07.018. [DOI] [PubMed] [Google Scholar]
- [77].Giscard P-L, Bonhomme C, Dynamics of quantum systems driven by time-varying Hamiltonians: Solution for the Bloch-Siegert Hamiltonian and applications to NMR, Phys. Rev. Res 2 (2020) 023081. doi: 10.1103/PhysRevResearch.2.023081. [DOI] [Google Scholar]
- [78].Yang W, Liu RB, Quantum many-body theory of qubit decoherence in a finite-size spin bath, Phys. Rev. B 78 (2008) 1–13. doi: 10.1103/PhysRevB.78.085315. [DOI] [Google Scholar]
- [79].Yang W, Liu RB, Quantum many-body theory of qubit decoherence in a finite-size spin bath. II. Ensemble dynamics, Phys. Rev. B 79 (2009) 1–7. doi: 10.1103/PhysRevB.79.115320. [DOI] [Google Scholar]
- [80].Canarie ER, Jahn SM, Stoll S, Quantitative Structure-Based Prediction of Electron Spin Decoherence in Organic Radicals, J. Phys. Chem. Lett 11 (2020) 3396–3400. doi: 10.1021/acs.jpclett.0c00768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [81].Kveder M, Rakvin B, You J, A quantum many body model for the embedded electron spin decoherence in organic solids, J. Chem. Phys 151 (2019) 164124. doi: 10.1063/1.5124561. [DOI] [PubMed] [Google Scholar]
- [82].Sidje RB,Expokit, ACM Trans. Math. Softw 24 (1998) 130–156. doi: 10.1145/285861.285868. [DOI] [Google Scholar]
- [83].Allami AJ, Concilio MG, Lally P, Kuprov I, Quantum mechanical MRI simulations: Solving the matrix dimension problem, Sci. Adv 5 (2019). doi: 10.1126/sciadv.aaw8962. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [84].Alderman DW, Solum MS, Grant DM, Methods for analyzing spectroscopic line shapes. NMR solid powder patterns, J. Chem. Phys 84 (1986) 3717–3725. doi: 10.1063/1.450211. [DOI] [Google Scholar]
- [85].Hohwy M, Bildsøe H, Jakobsen HJ, Nielsen NC, Efficient Spectral Simulations in NMR of Rotating Solids. The γ-COMPUTE Algorithm, J. Magn. Reson 136 (1999) 6–14. doi: 10.1006/jmre.1998.1593. [DOI] [PubMed] [Google Scholar]
- [86].Stevensson B, Edén M, Interpolation by fast Wigner transform for rapid calculations of magnetic resonance spectra from powders, J. Chem. Phys 134 (2011) 124104. doi: 10.1063/1.3561094. [DOI] [PubMed] [Google Scholar]
- [87].Stoll S, Schweiger A, EasySpin, a comprehensive software package for spectral simulation and analysis in EPR., J. Magn. Reson 178 (2006) 42–55. doi: 10.1016/j.jmr.2005.08.013. [DOI] [PubMed] [Google Scholar]
- [88].Kuprov I, Polynomially scaling spin dynamics II: Further state-space compression using Krylov subspace techniques and zero track elimination, J. Magn. Reson 195 (2008) 45–51. doi: 10.1016/j.jmr.2008.08.008. [DOI] [PubMed] [Google Scholar]
- [89].Gan Z, Satellite transition magic-angle spinning nuclear magnetic resonance spectroscopy of half-integer quadrupolar nuclei, J. Chem. Phys 114 (2001) 10845–10853. doi: 10.1063/1.1374958. [DOI] [Google Scholar]
- [90].Aspuru-Guzik A, Dutoi AD, Love PJ, Head-Gordon M, Simulated quantum computation of molecular energies., Science (80-.) 309 (2005) 1704–7. doi: 10.1126/science.1113479. [DOI] [PubMed] [Google Scholar]
- [91].Gyamfi JA, Fundamentals of quantum mechanics in Liouville space, Eur. J. Phys 41 (2020). doi: 10.1088/1361-6404/ab9fdd. [DOI] [Google Scholar]
- [92].Karabanov A, Kwiatkowski G, Kockenberger W, Spin dynamic simulations of solid effect DNP: the role of the relaxation superoperator, Mol. Phys 0 (2014) 1–17. doi: 10.1080/00268976.2014.884287. [DOI] [Google Scholar]
- [93].Bengs C, Levitt MH, A master equation for spin systems far from equilibrium, J. Magn. Reson 310 (2020) 106645. doi: 10.1016/j.jmr.2019.106645. [DOI] [PubMed] [Google Scholar]
- [94].Geiger MA, Jagtap AP, Kaushik M, Sun H, Stöppler D, Sigurdsson ST, Corzilius B, Oschkinat H, Efficiency of Water-Soluble Nitroxide Biradicals for Dynamic Nuclear Polarization in Rotating Solids at 9.4 T: bcTol-M and cyolyl-TOTAPOL as New Polarizing Agents, Chem Eur J 24 (2018) 13485–13494. doi: 10.1002/chem.201801251. [DOI] [PubMed] [Google Scholar]
- [95].Bak M, Nielsen NC, REPULSION A Novel Approach to Efficient Powder Averaging in Solid-State NMR, J. Magn. Reson 125 (1997) 132–139. doi: 10.1006/jmre.1996.1087. [DOI] [PubMed] [Google Scholar]
- [96].Florent M, Kaminker I, Nagarajan V, Goldfarb D, Determination of the 14N quadrupole coupling constant of nitroxide spin probes by W-band ELDOR-detected NMR., J. Magn. Reson 210 (2011) 192–9. doi: 10.1016/j.jmr.2011.03.005. [DOI] [PubMed] [Google Scholar]
- [97].Ernst RR, Bodenhausen G, Wokaun A, Redfield AG, Principles of Nuclear Magnetic Resonance in One and Two Dimensions, 1987.
- [98].Lie S, Theorie der Transformationsgruppen I, Math. Ann 16 (1880) 441–528. doi: 10.1007/BF01446218. [DOI] [Google Scholar]
- [99].Suzuki M, Generalized Trotter’s formula and systematic approximants of exponential operators and inner derivations with applications to many-body problems, Commun. Math. Phys 51 (1976) 183–190. doi: 10.1007/BF01609348. [DOI] [Google Scholar]
- [100].Huffman JL, Poncelet M, Moore W, Eaton SS, Eaton GR, Driesschaert B, Perchlorinated Triarylmethyl Radical 99% Enriched 13C at the Central Carbon as EPR Spin Probe Highly Sensitive to Molecular Tumbling, J. Phys. Chem. B 125 (2021) 7380–7387. doi: 10.1021/acs.jpcb.1c03778. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [101].Karabanov A, Kuprov I, Charnock GTP, van der Drift A, Edwards LJ, Köckenberger W, On the accuracy of the state space restriction approximation for spin dynamics simulations, J. Chem. Phys 135 (2011) 084106. doi: 10.1063/1.3624564. [DOI] [PubMed] [Google Scholar]
- [102].Stoll S, Spectral Simulations in Solid-State Electron Paramagnetic Resonance, ETH Zürich (2003) 141. doi: 10.3929/ethz-a-004529758. [DOI] [Google Scholar]
- [103].Casas F, Iserles A, Explicit Magnus expansions for nonlinear equations, J. Phys. A. Math. Gen 39 (2006) 5445–5461. doi: 10.1088/0305-4470/39/19/S07. [DOI] [Google Scholar]
- [104].Blanes S, Iserles A, Explicit adaptive symplectic integrators for solving Hamiltonian systems, Celest. Mech. Dyn. Astron 114 (2012) 297–317. doi: 10.1007/s10569-012-9441-z. [DOI] [Google Scholar]
- [105].Sanctuary BC, Multipole N.M.R., Mol. Phys 48 (1983) 1155–1176. doi: 10.1080/00268978300100841. [DOI] [Google Scholar]
- [106].Perras FA, Pruski M, Linear-scaling ab initio simulations of spin diffusion in rotating solids, J. Chem. Phys 151 (2019) 034110. doi: 10.1063/1.5099146. [DOI] [PubMed] [Google Scholar]
- [107].Kuprov I, Defeating the Matrix, J. Magn. Reson 306 (2019) 75–79. doi: 10.1016/j.jmr.2019.07.031. [DOI] [PubMed] [Google Scholar]
- [108].Tarjan R,Depth-First Search and Linear Graph Algorithms, SIAM J. Comput 1 (1972) 146–160. doi: 10.1137/0201010. [DOI] [Google Scholar]
- [109].Can TV, Caporini M. a., Mentink-Vigier F, Corzilius B, Walish JJ, Rosay M, Maas WE, Baldus M, Vega S, Swager TM, Griffin RG, Overhauser effects in insulating solids, J. Chem. Phys 141 (2014) 064202. doi: 10.1063/1.4891866. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [110].Chaudhari SR, Wisser D, Pinon AC, Berruyer P, Gajan D, Tordo P, Ouari O, Reiter C, Engelke F, Copéret C, Lelli M, Lesage A, Emsley L, Dynamic Nuclear Polarization Efficiency Increased by Very Fast Magic Angle Spinning, J. Am. Chem. Soc (2017) jacs.7b05194. doi: 10.1021/jacs.7b05194. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [111].Lelli M, Chaudhari SR, Gajan D, Casano G, Rossini AJ, Ouari O, Tordo P, Lesage A, Emsley L, Solid-State Dynamic Nuclear Polarization at 9.4 and 18.8 T from 100 K to Room Temperature, J. Am. Chem. Soc 137 (2015) 14558–14561. doi: 10.1021/jacs.5b08423. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


