Amyloid β 42 fibril structure based on small-angle scattering

Significance

Alzheimeŕs disease is one of the major global health challenges. Neuronal cell dysfunction and death are connected to the self-assembly of the amyloid β peptide (Aβ42) into oligomeric and fibrillar aggregates. The fibril surface can catalyze the formation of toxic oligomers via secondary nucleation. Access to a high-resolution structure of Aβ42 fibrils would provide a valuable basis for design of inhibitors of oligomer generation and toxicity in the form of fibril-binders and thus significantly contribute to the development of therapeutics against Alzheimer’s disease. A combination of methods may be most fruitful toward this aim. We show that small-angle X-ray scattering data, in combination with a solid-state NMR structure of the filament core, can reveal a detailed fibril model.

Abstract

Amyloid fibrils are associated with a number of neurodegenerative diseases, including fibrils of amyloid β42 peptide (Aβ42) in Alzheimer’s disease. These fibrils are a source of toxicity to neuronal cells through surface-catalyzed generation of toxic oligomers. Detailed knowledge of the fibril structure may thus facilitate therapeutic development. We use small-angle scattering to provide information on the fibril cross-section dimension and shape for Aβ42 fibrils prepared in aqueous phosphate buffer at pH = 7.4 and pH 8.0 under quiescent conditions at 37 °C from pure recombinant Aβ42 peptide. Fitting the data using a continuum model reveals an elliptical cross-section and a peptide mass-per-unit length compatible with two filaments of two monomers, four monomers per plane. To provide a more detailed atomistic model, the data were fitted using as a starting state a high-resolution structure of the two-monomer arrangement in filaments from solid-state NMR (Protein Data Bank ID 5kk3). First, a twofold symmetric model including residues 11 to 42 of two monomers in the filament was optimized in terms of twist angle and local packing using Rosetta. A two-filament model was then built and optimized through fitting to the scattering data allowing the two N-termini in each filament to take different conformations, with the same conformation in each of the two filaments. This provides an atomistic model of the fibril with twofold rotation symmetry around the fibril axis. Intriguingly, no polydispersity as regards the number of filaments was observed in our system over separate samples, suggesting that the two-filament arrangement represents a free energy minimum for the Aβ42 fibril.

The association of neurodegenerative diseases with amyloid deposits has stimulated investigations of fibril structures over a range of length scales (1–8). Alzheimer’s disease (AD) is the most common form of dementia, which strongly impacts the affected individuals and their caregivers, as well as the economy of the society. Over 50 million people worldwide are diagnosed with AD, and the number is expected to double by 2050, meaning that worldwide, 1 person in 85 will develop the disease (9, 10).

Previous studies have shown that metabolites of Amyloid precursor protein, generated by the β- and γ-secretase, play a critical role in the onset of AD (11, 12). The amyloid β42 peptide (Aβ42) is the variant predominately found in fibril-like deposits in the substancia nigra of the brains of AD patients, together with other length variants (13). While low–molecular-weight aggregates known as oligomers are believed to be the toxic species against neuronal cell functions (14), systematic kinetic analyses have revealed that the secondary nucleation pathway plays a key role in the generation of Aβ42 oligomers (15, 16). Thus, monomer conversion into toxic oligomeric species is catalyzed by the surface of fibrils (for a recent review, see ref. 17).

While no effective treatments are currently available (14), the Food and Drug Administration (FDA) recently approved (18) the antibody Aducanumab, which reduces brain amyloid load as well as clinical symptoms (19, 20) and inhibits the generation of toxic oligomers through surface-catalyzed nucleation (21).

Deciphering the structure of Aβ fibrils will be of importance for the design of future therapeutics.

Small-angle scattering is a powerful and useful technique for investigating the structure of matter on the nanometer-length scale (22) including the studies of amyloid fibrils (23). It is thus complementary to direct imaging techniques, like transmission electron cryomicroscopy (cryo-TEM) (24, 25), with the added advantage that it is essentially nondestructive, apart from the case of radiation damage that can be a serious issue at a high brilliance synchrotron source, and one measures the structure directly in solution.

The structure of Aβ42 fibrils has been studied using solid state nuclear magnetic resonance (ss-NMR) (1–3) spectroscopy, cryo-electron microscopy (cryo-EM) (4, 26), and atomic force microscopy (AFM) (27–29).

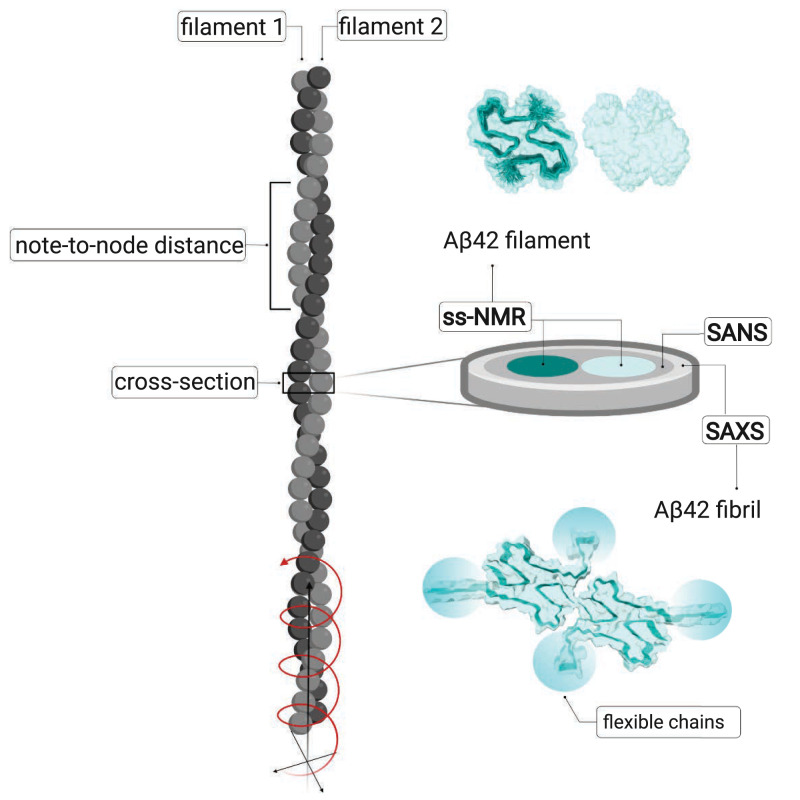
These methods provide information at different structural levels ranging from short distance and atomic-level resolution of the filament core to longer length-scale observations such as number of filaments per fibril, node-to-node distance, and fibril length. Several independent studies revealed highly similar structural models with parallel cross-β structure in neutral or slightly basic phosphate buffer (1–3) implying a stable and reproducible fibril fold. However, a change in solution conditions to strongly acidic water-acetonitrile mixture was found to govern a very different fold (4) for fibrils with a small width of 7.4 ± 0.4 nm and a short cross-over (node-to-node) distance of 41.5 ± 2.3 nm. Recent AFM studies on mature Aβ42 fibrils suggest a rigid cylindrical structure with a mean diameter of 9.6 ± 0.7 nm (30). Fig. 1 illustrates an amyloid fibril, its constituting structural hierarchy, and the level of information that can be obtained with various methods.

Fig. 1.

Cartoon illustrating a fibril (gray) with its two filaments in light and dark gray. The node-to-node distance can be obtained from AFM or cryo-EM, which can also provide information of the detailed packing. To the Right is shown an excised cross-section plane, the dimensions of which are studied by SAXS and SANS, with the cores of the two filaments in tile and light cyan. Above the cross-section is shown one plane of each filament, seen from the Top, based on the ss-NMR structure (1) PDB ID 5KK3, DOI: 10.2210/pdb5KK3/pdb, with one filament as space-filling model and the other one as space-filling model with the backbone of the two monomers outlined. Below the cross-section is shown one plane of the fibril with the backbone of all four monomers outlined and the flexible N-termini indicated by cyan ovals, as modeled in the current work. (Created with BioRender.com.)

ss-NMR studies of recombinant ¹³C- and ¹⁵N-labeled Aβ42 fibrils (1, 2) revealed that each plane in a filament contains two monomers with a significant number of buried hydrophobic side-chains. Such planes stack on top of each other along the filament’s propagation axis, and the highly organized hydrophobic cores are continuous inside the fibril along its entire length. The filament core is formed by amino acid residues 15 to 42 (20 of these 27 residues are hydrophobic); however, ss-NMR provides little structural information on the more flexible N-terminal region (1), where a limited number of distance restraints are seen for residues 11 to 14 only. Moreover, because ss-NMR provides short-distance restraints only, it cannot reveal information on the assembly of filaments in the fibril.

In this framework, small-angle X-ray (SAXS) and neutron (SANS) scattering may provide complementary information not accessible by ss-NMR, cryo-EM, or AFM (31). Small-angle scattering and X-ray fiber diffraction studies have been reported for synthetic amyloid-like peptides and in presence of organic solvents (5, 32–34).

In this work, we present SAXS/SANS data obtained for recombinant Aβ42 fibrils in aqueous phosphate buffer solution at physiological pH. The experimental SAXS data are also compared with simulations, based on the locally folded ss-NMR structure of Aβ42 filaments, to provide a model of the fibril structure.

Results and Discussion

Fibril Cross-Section Shape and Size.

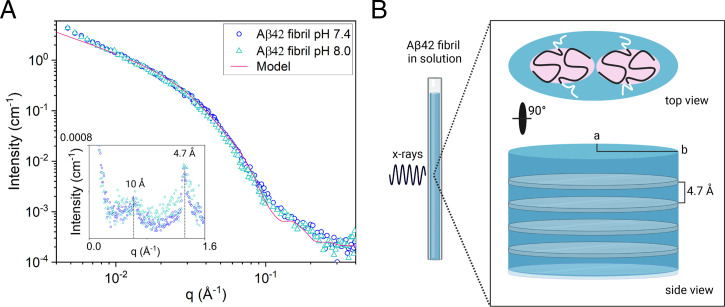
The SAXS patterns of 350 μM Aβ42 fibrils, formed at pH = 7.4 and 8.0, respectively, are presented in Fig. 2. As can be seen, the two patterns are essentially identical, both in shape and in absolute intensity. Combined SAXS/wide-angle X-ray scattering (WAXS) experiments were performed in a q-range from 0.004 to 2 Å⁻¹, where q = 4πsin(θ/2)/λ is the scattering vector magnitude, with θ being the scattering angle. In the experimental q-range, the SAXS pattern mainly reports on the size and shape of the fibril cross-section, which clearly are the same at the two pH values. In Fig. 2, we also show, as an inset, the WAXS patterns. Here, we observe in both cases a relatively sharp reflection at q = 1.3 Å⁻¹ corresponding to the periodic β-strand separation, $d_{\mathit{\beta }}=2\mathit{\pi }/q=$4.7 Å in addition to a broader hump, centered at q = 0.6 Å⁻¹, which reports on a characteristic distance of 10 Å in the packing perpendicular to the fibril axis (35). The β-strand separation of 4.7 Å is a characteristic feature of parallel and antiparallel β-sheets in folded monomeric proteins as well as in aggregates (36, 37) and is observed also in the case of β-sheet aggregates of short peptides (38, 39). Interestingly, the characteristic distance of 10 Å is also observed for β-sheet aggregates of the core segment Aβ (16–22, 40), where it clearly corresponds to the separation between β-sheets in a two-dimensional (2D) crystalline lattice (40).

Fig. 2.

(A) Absolute-scaled SAXS patterns of Aβ42 fibrils formed at pH 7.4 (circles) and 8.0 (triangles). The solid line is a calculated scattering pattern, where the fibrils are modeled as elliptical cylinders. The Inset shows the WAXS pattern, where the dashed lines indicate the reflections at q = 1.3 and 0.6 Å⁻¹, respectively. (B) Schematic representation in scale of Aβ42 fibril cross-section dimensions obtained by SAXS/WAXS (light blue color) and Aβ42 filaments-core dimensions (residues 15 to 42) obtained by ss-NMR (light red color). Residues 0 to 14, shown in white, are flexible, and exposed to the solvent. (Created with BioRender.com.)

The fibrils are very long with overall length $L\gg q_{\mathit{min}}^{-1}$, where q_min is the minimum q-value accessible in the experimental q-range. Hence, L cannot be measured in present experiments, besides the fact that the fibrils overlap and form a network. Furthermore, because of the large L, the fibril form factor can be factorized into a product of overall length and cross-section contributions (41). With $L\gg q_{\mathit{min}}^{-1}$, we can write the model scattered intensity as

$$I\left(q\right)=\frac{C}{q}{P}_c(q),$$ [1]

where P_c(q) is the normalized 2D cross-section form factor, and C is given by

$$C=\mathit{\pi }\mathrm{\Delta }{\mathit{\rho }}^2\mathit{\varphi }\frac{V_p}{L}.$$ [2]

Here, $\mathrm{\Delta }\mathit{\rho }={\mathit{\rho }}_p-{\mathit{\rho }}_b$ is the scattering length density difference between protein (p) and buffer (b), $\mathit{\varphi }$ is the fibril (protein) volume fraction, and V_p/L is the protein volume per unit length in the fibrils (V_p is the total protein volume in a fibril, and L is the fibril length). The X-ray scattering length densities are given by ${\mathit{\rho }}_p$ = 13 10¹⁰ cm⁻² and ${\mathit{\rho }}_b$ = 9.5 10¹⁰ cm⁻², respectively. The normalized cross-section form factor of an elliptical cylinder can be written as

$$P_c\left(q\right)=\frac{2}{\mathit{\pi }}{\displaystyle {\int }_0^{\mathit{\pi }/2}d\mathit{\phi }{\left(\frac{2J_1(qr)}{qr}\right)}^2}.$$ [3]

Here, J₁(x) is the first order Bessel function and

$$r={\left({\left(a\sin \mathit{\phi }\right)}^2+{\left(b\cos \mathit{\phi }\right)}^2\right)}^{1/2},$$ [4]

and r is an effective radius that varies with the polar angle $\mathit{\phi }$. Eq. 3 is obtained from the full elliptical cross-section cylinder model given for example in ref. 42 after performing the factorization (Eq. 1). An elliptical cross-section with minor semiaxis a = 3.0 nm and major semiaxis b = 9.0 nm was found to describe the SAXS pattern satisfactorily. In the SI Appendix we compare with the cylinder form factor of a circular cross-section with the same cross-section area (SI Appendix, Fig. S5).

Next, we address the question how many filaments, N, are found in the fibril structure, where each filament is made of two stacks of folded Aβ42 molecules (i.e., two monomers per plane). Thus, we have

$$V_p/L=2N{v}_p/d_{\mathit{\beta }},$$ [5]

where $v_p$ = 5.4 nm³ is the Aβ42 molecular volume, assuming a mass density of 1.43 g/cm³ (42).

Shown as a solid line in Fig. 2 is the result of a model calculation assuming an elliptical cross-section with a = 3.0 nm, b = 9.0 nm (axial ratio b/a = 3), and n = 2 (SI Appendix, Table S1). As can be seen, this simple model describes the data well within the experimental q-range. We see a small deviation at lower q-values, where the model approaches a q⁻¹ dependence, while the experimental data show a slightly steeper upturn. We ascribe this to the presence of attractive fibril–fibril interactions, most likely due to hydrophobic interactions (43). The origin of similar effects were recently analyzed for α-synuclein fibrils (6). We also see a minor deviation in the q-range 0.1 to 0.3 Å⁻¹. This is due to the oscillations in the model form factor that arise from the assumed sharp interface between the model elliptical cylinder and the solvent, resulting in discontinuous change in the scattering length density. In the real system, the fibril–solvent interface is more diffuse.

We can then conclude that each protein molecule adopts a 2D folded structure in the fibril core, fibril cross-section is made by tetramers, and the molecules stack, with intermolecular β-sheets along the fibril direction with a periodic repeat distance, d_β = 4.7 Å.

Aβ42 Fibrils in Solution: Number of Filaments and Orientation.

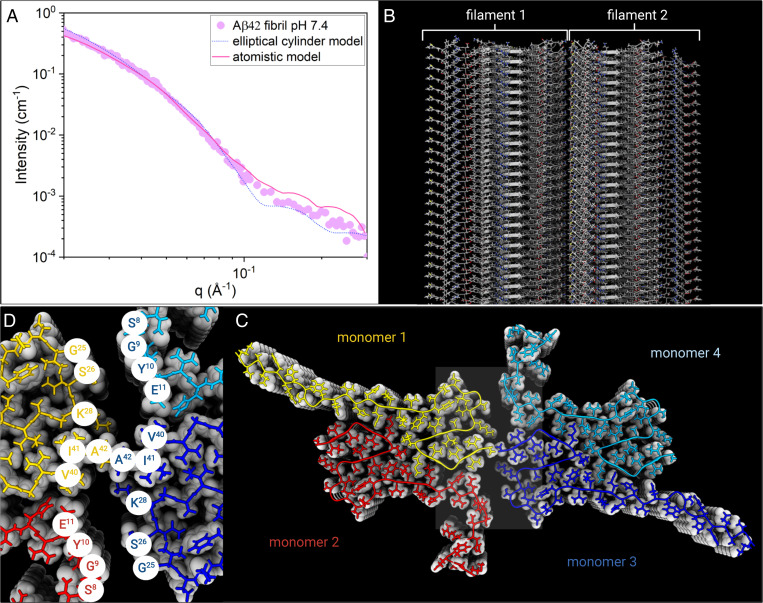
We now proceed with a more detailed SAXS data analysis and construct an atomistic model of the fibrils. To do so, we use an ss-NMR structure [Protein Data Bank (PDB) ID 5KK3 (1)] as a model for a single filament, from which we then build a fibril model composed of two filaments by varying the parameters describing the helical symmetry of the system, as outlined in detail in the Materials and Methods. Structure-based scattering calculations were then used to identify which model fits the experimental data best. The ss-NMR model covers residues 11 to 42 in each Aβ42 monomer, of which residues 15 to 42 are part of the ordered core. Scattering calculations based on models without residues 0 to 14 did not result in curves that fit well to the experimental data (SI Appendix, Fig. S3), suggesting the N-termini contribute significantly to the scattering. We modeled different conformations of the N-terminus using symmetrical loop modeling. Each monomer in the Aβ42 is found in a different structural environment. Hence, we allow the two N-termini of each plane in the filament, constituting the asymmetric unit, to have different conformations. This resulted in considerably better fit to data than assuming a single conformation for both N-termini (SI Appendix, Fig. S3). For each generated model, we used Pepsi-SAXS (44) to predict the scattering curve and compared it to the experimental data. A deep minimum of χ² was found for the degree of freedom corresponding to the rotation of the asymmetric unit, which controls which residues are found at the interface between filaments (SI Appendix, Fig. S3). Attempts to account for conformational flexibility by fitting the data to a structural ensemble rather than a single structure did not lead to improvements in the fit. This suggests that the model represents the average conformation of the termini well. The modeled termini sample a range of conformations from the compact to the extended. The best fitting models consistently have the two N-termini in extended conformations. Also the C-terminal carboxylate groups are in two different locations with the C termini of two out of four monomers at the interface between filaments. Each Ala42 C-terminal carboxylate group is in close contact with the terminal amino group of a Lys28 side-chain, meaning that this arrangement will likely not cause any net electrostatic repulsion between the filaments. In Fig. 3, the best model fit is plotted together with the experimental SAXS pattern obtained at pH = 7.4. As can be seen, there is a good agreement between the model fit and the experimental data, giving strong support for the two-filament fibril structure, in which the filament core structure is given by the molecular fold obtained from ss-NMR.

Fig. 3.

(A) Experimental SAXS profile for Aβ42 fibril in 20 mM sodium phosphate buffer at pH = 7.4 (purple circles), plotted together with the best fit of the atomistic model by Pepsi-SAXS (pink line) and the elliptical cylinder model calculation (blue dots). (B) Illustration of the atomistic model structure of the fibrils made by two filaments. (C) A fibril Top view illustrates the fibril cross-section made by tetramer units (monomers 1 to 4, color coded) that form β-sheets stacked along the fibril axis. (D) Zoom of Aβ42 fibril core showing the amino acid residues of contact between filament 1 and 2.

In Fig. 3, we also compare with the analytical continuum elliptical cylinder model. Both the continuum model formfactor and the discrete atomistic model form factor show small oscillations for q > 0.1 Å⁻², which are not present in the experimental data. As mentioned above for the case of the continuum model, the origin of the oscillations is the assumed sharp fibril–solvent interface. In the case of the atomistic model, on the other hand, the oscillations report on an internal variation in the electron density within the fibril having fixed positions of the atoms. In the real system, we expect thermal fluctuations to smear many of such features.

Intriguingly, in vitro studies of synthetic peptides show that Aβ42 fibrils might exist as different polymorphs as a consequence of changes in the amino acid sequence or experimental conditions (45). Thus, the amino acid sequence might dictate which segment of the chain forms the amyloid core and the fibril packing. On the other hand, polydispersity based on the number and arrangement of the filaments may occur without changes in the sequence and seems strongly dependent on the fibril sample preparation (27). Recent cryo-EM studies on fibril extracts from AD patients reports polydispersity of brain-derived Aβ fibrils (26). Three main fibril morphologies where found made by one, two, or three filaments, respectively. In contrast, our SAXS studies on Aβ42 fibrils formed in phosphate buffer solution at pH 7.4 and 8.0, with or without thioflavin T, a fluorescent dye commonly used to detect amyloid fibrils, or in buffer with different contrasts, show repeatedly a cross-section corresponding to two filaments. The polymorphism of brain-derived fibril structures obtained from AD patients might reflect a true polymorphism in brain, or might in part be a result of the extraction procedures. Our findings suggest that when Aβ42 fibrils are formed in vitro from recombinant peptide under quiescent conditions, there is little polydispersity as regards the number of filaments per fibril and only the two-filament structure (Fig. 3) is obtained.

In total, five different small-angle scattering experiments on Aβ42 fibrils were performed. Apart from the SAXS data shown in Fig. 2, SAXS/WAXS experiments were also performed in the presence of thioflavin T (SI Appendix, Fig. S1) to investigate whether the presence of the dye influenced the fibril morphology. Furthermore, additional SAXS and SANS experiments were performed on fibrils in heavy water (100% D₂O buffer), as shown in SI Appendix, Fig. S2. All small-angle scattering data presented in this work are consistent with the two-filament fibril structure. The four samples studied by SAXS have essentially identical scattering patterns (SI Appendix, Figs. S1 and S2). This suggest that the two-filament structure might represent a free energy minimum that is deep enough to show a reproducible and monodisperse fibril morphology. The interesting question that then arise is the following: why is there a free energy minimum for a two-filament fibril structure rather than one or three? And what are the important interactions, the balance of which, being responsible for the observed fibril morphology?

The individual filaments seem to consist of two twisted stacks of folded Aβ42 molecules. The interactions that hold these two stacks together were discussed in ref. 1 and are mainly hydrophobic interactions. Also, as concluded in ref. 1, the dimer-filament shows hydrophobic patches, containing the side-chains of V18, A21, V40, and A42, exposed on its surface. If these four residues are replaced with polar ones (serine), the fibril takes another fold exposing other hydrophobic patches on each filament (46). It is thus likely that the attractive cohesive force holding the two filaments together results from hydrophobic interactions and that these filament–filament interactions stabilize the fold of each filament. Having hydrophobic attractive filaments, the question is what limits the number of filaments to an optimum value. We note that amyloid fibrils in general have a cross-section diameter of around 10 nm, indicating that there may be a general mechanism for limiting the cross-section width. A likely explanation for a limited width (low number of filaments) can in fact be derived from the twisting as a consequence of chirality (38, 47) but also of the attractive hydrophobic interactions (48) as a consequence of the increasing contact between filaments. In addition, electrostatic interactions may be involved (49, 50). Twisting of filaments around a central axis involves a deformation of the β-sheet hydrogen bonds. The deformation increases with the distance from the central axis and hence overall fibril radius (38, 47) and acts as a limiting factor for the fibril cross-section dimension and hence the number of filaments. Essentially the same arguments were recently invoked to explain the finite width of peptide ribbon aggregates using a quantitative thermodynamic model (38).

Materials and Methods

All chemicals and reagents were of analytical grade and were used without further purification. Buffers solutions were prepared with deuterium oxide (99% D isotope purity, Sigma-Aldrich) and deionized water of resistivity not more than 18.2 MΩ cm⁻¹.

Aβ42 Monomers: Expression and Purification.

Aβ(M1-42) peptide, MDAEFRHDSGYEVHHQKLVFFAEDVGSNKGAIIGLMVGGVVIA, here called Aβ42, with a molar mass of 4,645 g ⋅ mol⁻¹, was expressed in Escherichia coli and purified from inclusion bodies as described (15, 51, 52). The isolated monomers were aliquoted, lyophilized, and the powder stored at −20 °C.

Aβ42 Fibril Sample Preparation: SAXS Studies.

Aβ42 aliquots were dissolved in 1 mL 6 M GuHCl at pH 8.4 and the sample injected on an Increase 10/300 GL (GE Healthcare) column with a flow rate of 0.7 mL/min and eluted in 20 mM ammonium acetate, pH 8.5. Aβ42 gel filtration fractions were lyophilized and the powder was dissolved in 20 mM sodium phosphate, 0.2 mM ethylenediaminetetraacetic acid (EDTA), 0.02% NaN₃ at pH 7.4 at a final monomer concentration of 350 µM and a minimum volume of 250 µL. Aβ42 monomer samples were then incubated at 37 °C under quiescent conditions for 5 d to ensure aggregation end state.

SAXS/WAXS.

Each sample (150 µL) was loaded in a 1-mm–diameter quartz capillary. All measurements were made in an air-evacuated space at a pressure below 1.6 mbar and at room temperature and were performed using a Saxslab Ganesha pinhole instrument, JJ X-ray System Aps (JJ X-ray) with an X-ray microsource (Xenocs) and a 2D 300 k Pilatus detector (Dectris Ltd.). The scattering experiments were performed with Cu Kα radiation having a wavelength (λ) of 1.54 Å. Samples were measured at three given sample-to-detector distances, and the evolution of the scattering profile was monitored by data acquisition at different time points in order to detect possible fibril sedimentation. The 2D images from the Pilatus detector were azimuthally averaged after subtracting the dark counts. The background, recorded in a capillary with buffer at the same contrast, was subtracted from the acquired one-dimensional scattering data, I(q).

Atomistic Modeling.

Atomistic modeling of fibril structures was based on the ss-NMR structure by Colvin et al. (1) (PDB ID 5kk3). The ss-NMR structure includes residues 11 to 42 and involves a short section of a filament with 18 Aβ42 monomers arranged in two tightly interacting β-sheet stacks. A symmetrized version of this filament section was generated by the procedures described in ref. 53. The twist of the filament was allowed to vary from −4.4 to 28 degrees per plane using a symmetric energy refinement protocol (symmetric relax) in Rosetta (54). The twist value with the lowest Rosetta energy was selected, corresponding to 0 degrees. The 0 degree minimum is expected as the model neglects a preferred twist angle (38, 47).

Next, we built a model of a fibril being composed of two filaments as supported by the cross-section dimensions of the elliptical cylinder compatible with the SAXS data. Two Aβ42 monomers, from the symmetrically optimized single-filament model, were used as the smallest repeating unit for building the two-filament structure with helical symmetry. The double helix model formed from two filaments contained 79 repeating units (each with two Aβ42 monomers) and had a length of around 230 Å. The degrees of freedom explored in the modeling of this helix were the distance between the two filaments of the helix, the twist, and the rotation of the asymmetric unit (which controls which parts of the Aβ42 dimers that are in close proximity). To determine the optimum twist, different models with varying twist values were constructed with helical symmetry. The twist value was varied within the range estimated from electron microscopy data reporting, 2.6 ± 2 degrees (55) and 1.2 ± 0.2 degrees (56) per plane, respectively. The value (1.0 degree) giving the lowest Rosetta energy after symmetric backbone refinement, was used in the subsequent modeling. This analysis suggested a right-handed twist of 1 degree. To optimize the distance between the two filaments, the rotation of the dimeric Aβ42 asymmetric unit was evaluated from 0 to 360 degrees in steps of 10 degrees. For each rotation, the optimal distance was determined by gridding the distance between the two filaments. The distance giving rise to the lowest Rosetta energy value was used for further modeling.

The ss-NMR model suggests high order for residues 15 to 42, more variation for residues 11 to 14, and no information for residues 1 to 10. In this work, we modeled different conformations of residues 1 to 11 of the N-terminus by symmetric loop modeling onto the symmetrized fibril structure (one strand) using the loop model application in Rosetta. This modeling was done in the coarse-grained centroid mode, followed by addition of side-chains using the Rosetta side-chain optimization procedure. A unit composed of two monomers from a single filament was then used as the repeating units for modeling of the double filament fibril. Each repeating unit has two N-termini that will be in two different chemical environments in the structure. We allowed these two termini to have different conformations, which improved the fit to data considerably. For each rotation, we evaluated 100 different conformation of the terminus of each of the two Aβ42 monomers. All combinations were then generated, resulting in 10,000 models (100 × 100) per rotation. The predicted model was selected by identifying the model with the minimal χ² between scattering predicted from the model and the experimental data. Since the low q region is primarily determined by the length of the fibrillar model, we compared to experimental data for q > 0.18 Å⁻¹. Pepsi-SAXS (44) was used to calculate the scattering profile, I(q), from the atomistic models.

Data Availability

All study data are included in the article and/or SI Appendix.